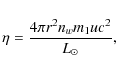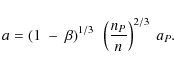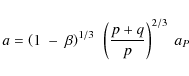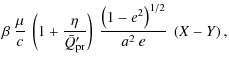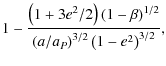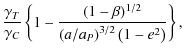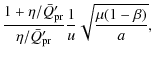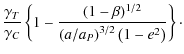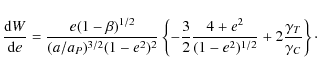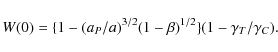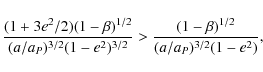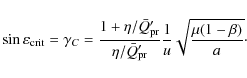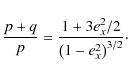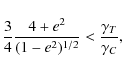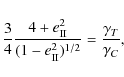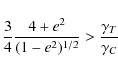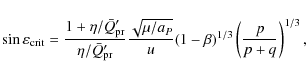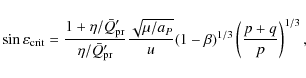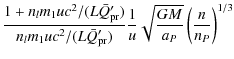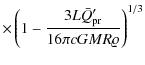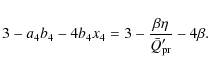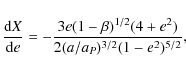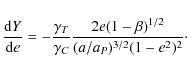| Issue |
A&A
Volume 501, Number 1, July I 2009
|
|
|---|---|---|
| Page(s) | 367 - 374 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200811286 | |
| Published online | 08 April 2009 | |
Eccentricity evolution in mean motion resonance and non-radial solar wind
P. Pástor - J. Klacka - J. Petrzala - L. Kómar
Department of Astronomy, Physics of the Earth, and Meteorology, Faculty of Mathematics, Physics and Informatics, Comenius University, Mlynská dolina, 842 48 Bratislava, Slovak Republic
Received 4 November 2008 / Accepted 4 March 2009
Abstract
Eccentricity evolution of a dust particle in a mean motion orbital
resonance with a planet in circular orbit is investigated. The action
of solar electromagnetic and corpuscular radiation, including non-radial
components of the solar wind velocity, is taken into account.
Various types of eccentricity evolution depend on the angle between
the radial direction and the direction of the solar wind velocity.
The evolution changes at the analytically derived angles.
Its application to exosolar systems is included.
Key words: Sun: solar wind - interplanetary medium - celestial mechanics - stars: planetary systems
1 Introduction
The motion of interplanetary dust particles is influenced by gravitational forces of the Sun and planets and by non-gravitational effects. The effect of solar electromagnetic radiation in the form of the Poynting-Robertson (P-R) effect and the effect of the radial solar wind are conventionally taken into account (see, e.g. Robertson 1937; Wyatt & Whipple 1950; Whipple 1955; Dohnanyi 1978; Leinert & Grün 1990; Dermott et al. 2001; Grün 2007).
Physics of resonances with Solar System planets has been investigated mainly for the last three decades. The orbital motion of dust particles in mean motion orbital resonances with a planet has been intensively studied since Jackson & Zook (1989) predicted a ring of dust particles in resonances with the Earth. The ring was observed by satellites IRAS (Brownlee 1994; Dermott et al. 1994) and COBE (Reach et al. 1995). The orbital evolution of interplanetary dust particles near zones of mean motion resonances was investigated in many papers (Weidenschilling & Jackson 1993; Beaugé & Ferraz-Mello 1994; Sidlichovský & Nesvorný 1994; Liou et al. 1995; Liou & Zook 1999; Kuchner & Holman 2003; Klacka & Pástor 2004). Liou & Zook (1997) derived the relation between the secular time derivative of eccentricity and the secular time derivative of the inclination of dust particles in mean motion resonance with a planet in a circular restricted three-body problem with the P-R effect and the radial solar wind (the authors incorrectly accounted for the radial solar wind). As for the planar case, it is possible to obtain secular time derivative of a particle's eccentricity using the method presented in Liou & Zook (1997). The orbital evolution in mean motion resonance in the planar elliptical restricted three-body problem with the P-R effect is discussed in Pástor et al. (2007). The evolution of eccentricity of the particle under the action of the P-R effect and the non-radial solar wind in mean motion resonances with a planet in a circular orbit is investigated in Klacka et al. (2008). Measurement of the non-radial component of the solar wind velocity was performed by Helios 2 during its first solar mission in 1976 (Bruno et al. 2003). According to these results, the angle between the direction of the solar wind velocity and the radial direction is practically independent of heliocentric distance, at least for the distances covered by observations. A constant value of this angle is also in accordance with the results of Parker (1958).
We are motivated mainly by the results of Klacka et al. (2008). We want to obtain detailed predictions of orbital evolution in the orbital resonances when the P-R effect and the non-radial solar wind are considered.
2 Equation of motion
Let us consider a spherical dust grain under the action of gravitational forces
generated by the Sun and a planet moving around the Sun. Moreover, the grain
is evolving under the action of solar electromagnetic radiation and solar wind.
The equation of motion of the particle is considered in the form
where
where nw is the concentration of the solar wind particles at distance r from the Sun, and m1 is the mass of the solar wind particle(s).
3 Mean motion orbital resonances with planets
A particle is in the qth order exterior mean motion resonance with a planet if the ratio of its mean motion n and the mean motion of the planet nP approximately satisfies the equation nP/n = (p+q)/p, where p and q are natural numbers. Similarly, the qth order interior mean motion resonance is defined by the relation nP / n = p / ( p + q ). The special case mean motion 1/1 resonance corresponds to q = 0. In terms of orbital periods: T / TP = ( p + q ) / p for the exterior, T / TP = p / ( p + q ) for the interior resonance and T / TP = 1 for mean motion 1/1 resonance.
We can determine the semimajor axis of the particle in the mean motion
resonance from Kepler's third law. We have
where a, aP are semimajor axes of the particle characterized by the optical parameter
On the basis of the definition of mean motion resonance and Eq. (5), we can write
for the semimajor axis of the particle in the qth order exterior resonance with a planet of mass mP. A similar relation can be obtained for the interior resonance. For mean motion 1/1 orbital resonance we can put q = 0 in Eq. (6).
4 Evolution of eccentricity in a mean motion resonance
A dust particle is captured in a mean motion orbital resonance with a planet
and the P-R effect and the non-radial solar wind affect its motion.
The secular time derivative of the eccentricity of the particle
is (Klacka et al. 2008)
where
We define a new function W (e) as
The differentiation of the function W (e) with respect to eccentricity is
It is easy to show that d
4.1 Exterior mean motion resonances
Figure 1 depicts the function W (e) for exterior mean motion
4/3 resonance for various values of
![]() .
If W (e) is positive, then the eccentricity increases
from a given value of eccentricity e. If W (e) is negative,
then the eccentricity decreases.
.
If W (e) is positive, then the eccentricity increases
from a given value of eccentricity e. If W (e) is negative,
then the eccentricity decreases.
For the exterior mean motion resonances, Eq. (10) reduces to
The value W (0) is positive or zero for
![\begin{figure}
\par\includegraphics[height=0.21\textheight]{1286_F1.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg67.png) |
Figure 1:
The function W (e) for exterior mean motion 4/3 resonance.
Various values of
|
| Open with DEXTER | |
4.1.1
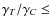 1
1
If
![]() ,
then the function W(e)is a decreasing function of eccentricity (see Eq. (9) and Fig. 1).
One root of the function W(e) exists,
since W(0) > 0 and
,
then the function W(e)is a decreasing function of eccentricity (see Eq. (9) and Fig. 1).
One root of the function W(e) exists,
since W(0) > 0 and
![]() .
We denote this root as
.
We denote this root as ![]() .
Various functions W (e) in Fig. 1
intersect at eccentricity ey for which is Y (e) = 0. W (ey)is negative. The statement follows from the inequality
.
Various functions W (e) in Fig. 1
intersect at eccentricity ey for which is Y (e) = 0. W (ey)is negative. The statement follows from the inequality
which holds for all e
Let us denote ex the value of the eccentricity at which X(e) = 0for exterior resonances. We have (see also Liou et al. 1995)
If the value of
4.1.2 1 <
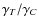 < 3
< 3
If
![]() for an exterior mean motion resonance,
then W (e) does not have a root for e
for an exterior mean motion resonance,
then W (e) does not have a root for e ![]() [0,1), since W (0) < 0
and W (e) is a decreasing function of eccentricity. The secular evolution of
eccentricity is always a decreasing function of time and the eccentricity
non-asymptotically decreases to 0 (zero eccentricity can be reached).
[0,1), since W (0) < 0
and W (e) is a decreasing function of eccentricity. The secular evolution of
eccentricity is always a decreasing function of time and the eccentricity
non-asymptotically decreases to 0 (zero eccentricity can be reached).
4.1.3
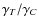
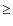 3
3
If
![]()
![]() 3
for exterior mean motion resonances, then W (0) < 0. The
function W (e) also can be an increasing function of eccentricity, but only
if the following inequality holds:
3
for exterior mean motion resonances, then W (0) < 0. The
function W (e) also can be an increasing function of eccentricity, but only
if the following inequality holds:
see Eq. (9).
Three possibilities exist:
- 1.
- W (e) does not have a root for e
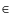 [0,1);
[0,1);
- 2.
- W (e) has only one root for e
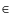 [0,1) -
we will denote it
[0,1) -
we will denote it
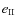 ;
;
- 3.
- W (e) has two roots for e
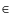 [0,1) -
we will denote them
[0,1) -
we will denote them
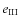 and
and
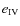 .
.
Possibility 1:
The secular evolution of eccentricity is always a decreasing
function of time. The eccentricity non-asymptotically decreases to 0.
Possibility 2:
We can write for
![]()
since
Possibility 3:
In this case we put
![]() .
If the initial eccentricity is greater than
.
If the initial eccentricity is greater than
![]() ,
then the eccentricity asymptotically decreases to the value
,
then the eccentricity asymptotically decreases to the value
![]() .
If the initial eccentricity lies between
.
If the initial eccentricity lies between
![]() and
and
![]() ,
the eccentricity asymptotically increases to the value
,
the eccentricity asymptotically increases to the value
![]() .
Finally, if the initial eccentricity is smaller than the value
.
Finally, if the initial eccentricity is smaller than the value
![]() ,
then the eccentricity non-asymptotically decreases to 0.
,
then the eccentricity non-asymptotically decreases to 0.
4.2 Interior mean motion resonances
The graph of the function W (e) for the interior mean motion 2/3 resonance
is depicted in Fig. 2. Various values of
![]() are used.
are used.
For interior mean motion resonances, Eq. (10) reduces to
The value W (0) is negative for
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F2.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg92.png) |
Figure 2:
The function W (e) for interior mean motion 2/3 resonance
for various values of
|
| Open with DEXTER | |
4.2.1
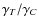 < 1
< 1
If
![]() ,
then W (0) < 0 and W (e) is
a decreasing function. Secular evolution eccentricity is always a decreasing
function of time. The eccentricity non-asymptotically decreases
to 0.
,
then W (0) < 0 and W (e) is
a decreasing function. Secular evolution eccentricity is always a decreasing
function of time. The eccentricity non-asymptotically decreases
to 0.
4.2.2
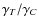
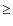 1
1
If
![]() ,
then W (0) = 0.
Thus,
,
then W (0) = 0.
Thus, ![]() = 0 is a root of W (e).
The eccentricity asymptotically decreases to
= 0 is a root of W (e).
The eccentricity asymptotically decreases to
![]() (circular orbit). For the value
(circular orbit). For the value
![]() we can define (similarly
to exterior resonances) an angle
we can define (similarly
to exterior resonances) an angle
![]() for
which
for
which
![]() .
We can calculate
.
We can calculate
![]() for the interior resonances from the condition
for the interior resonances from the condition
![]() .
.
If
![]() ,
then W (0) > 0. In this case, at
least one root
,
then W (0) > 0. In this case, at
least one root ![]() of W (e) exists. We will show that W (e)has only one root
of W (e) exists. We will show that W (e)has only one root ![]() for e
for e ![]() [0,1). If eccentricity fulfills
the inequality given by Eq. (15) (we can apply this inequality also for
interior resonances), then W (e) is an increasing function.
If the following inequality
[0,1). If eccentricity fulfills
the inequality given by Eq. (15) (we can apply this inequality also for
interior resonances), then W (e) is an increasing function.
If the following inequality
is fulfilled, then the function W (e) is a decreasing function (see Eq. (9)). Since W (0) > 0 and
4.3 Mean motion 1/1 resonance
Finally, let us consider the special case mean motion 1/1 orbital
resonance (q = 0). The graph of the function W (e) for 1/1 resonance
is shown in Fig. 3. Various values of
![]() are used.
are used.
For the mean motion 1/1 resonance, Eq. (10) reduces to
Thus, one root
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F3.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg99.png) |
Figure 3:
The function W (e) for mean motion 1/1 resonance
for various values of
|
| Open with DEXTER | |
4.3.1

W (e) is a decreasing function and W (0) = 0. Thus, W (e) < 0for e ![]() (0,1). The eccentricity asymptotically decreases to 0.
(0,1). The eccentricity asymptotically decreases to 0.
4.3.2
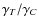 > 3
> 3
If
![]() > 3, then another root
> 3, then another root
![]() of W (e) exists, because W (e) is also an increasing function for the
values of eccentricity determined by inequality Eq. (15) and W (0) = 0.
If the initial eccentricity is greater than
of W (e) exists, because W (e) is also an increasing function for the
values of eccentricity determined by inequality Eq. (15) and W (0) = 0.
If the initial eccentricity is greater than
![]() ,
then the eccentricity asymptotically decreases to
,
then the eccentricity asymptotically decreases to
![]() .
If the initial eccentricity is less than
.
If the initial eccentricity is less than
![]() ,
then the
eccentricity asymptotically increases to
,
then the
eccentricity asymptotically increases to
![]() .
.
5 Discussion
The case
![]() yields, qualitatively,
the same secular evolution of eccentricity as the case
yields, qualitatively,
the same secular evolution of eccentricity as the case
![]() .
For the exterior mean motion resonances, eccentricity exhibits two
monotonous parts (an increasing and a decreasing one) asymptotically
approaching the limiting value of the eccentricity. For
the interior mean motion resonances, eccentricity is a decreasing function
of time and the eccentricity non-asymptotically decreases to 0.
The evolution of eccentricity changes for both types of resonances,
exterior and interior, at the value
.
For the exterior mean motion resonances, eccentricity exhibits two
monotonous parts (an increasing and a decreasing one) asymptotically
approaching the limiting value of the eccentricity. For
the interior mean motion resonances, eccentricity is a decreasing function
of time and the eccentricity non-asymptotically decreases to 0.
The evolution of eccentricity changes for both types of resonances,
exterior and interior, at the value
![]() .
Evolution of the eccentricity changes to a non-asymptotically
decreasing evolution for the exterior mean motion resonances, and
to an asymptotic behavior for the interior mean motion resonances.
.
Evolution of the eccentricity changes to a non-asymptotically
decreasing evolution for the exterior mean motion resonances, and
to an asymptotic behavior for the interior mean motion resonances.
![]() represents the smallest value of
represents the smallest value of
![]() for which the secular evolution of eccentricity changes
(two such values exist for exterior resonances,
but only one value for interior resonances).
If we use Eq. (6) and a similar equation for
the interior resonances, then we get (see Eq. (13))
for which the secular evolution of eccentricity changes
(two such values exist for exterior resonances,
but only one value for interior resonances).
If we use Eq. (6) and a similar equation for
the interior resonances, then we get (see Eq. (13))
for the exterior resonances and
for the interior resonances.
Table 1 presents the values of
![]() for
for
![]() ,
,
![]() ,
u= 400 km s-1,
,
u= 400 km s-1,
![]() ,
1 and 3/2,
for several exterior and interior resonances with a planet in a circular
orbit of radius
aP= 30.058 AU (approximately the semimajor axis of planet
Neptune).
,
1 and 3/2,
for several exterior and interior resonances with a planet in a circular
orbit of radius
aP= 30.058 AU (approximately the semimajor axis of planet
Neptune).
Table 1:
Values of
![]() (in degrees) for various exterior
and interior resonances with a planet in a circular orbit of radius aP= 30.058 AU. The particle is characterized by
(in degrees) for various exterior
and interior resonances with a planet in a circular orbit of radius aP= 30.058 AU. The particle is characterized by
![]() and the solar wind by
and the solar wind by
![]() and u = 400 km s-1.
and u = 400 km s-1.
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F4.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg108.png) |
Figure 4:
Evolution of eccentricity obtained from Eq. (7). A dust particle
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F5.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg109.png) |
Figure 5:
Evolution of eccentricity obtained from Eq. (7). A dust particle
with
|
| Open with DEXTER | |
Figures 4 and 5 depict secular evolution of the particle's eccentricity
in the exterior mean motion 4/3 resonance with a planet in a circular
orbit of radius
aP= 30.058 AU for the case
![]() and
and
![]() .
Figure 4 holds for
.
Figure 4 holds for
![]() and Fig. 5 holds for
and Fig. 5 holds for
![]() .
If
.
If
![]() ,
then
the evolution of the eccentricity is similar to Fig. 4.
If 1.762
,
then
the evolution of the eccentricity is similar to Fig. 4.
If 1.762
![]()
![]() ,
then the
secular evolution of the eccentricity is similar to Fig. 5. The detailed
numerical integrations of Eq. (1) are consistent with Eq. (7).
Evolutions depicted in Figs. 4 and 5 are calculated from the numerical
solution of Eq. (7).
,
then the
secular evolution of the eccentricity is similar to Fig. 5. The detailed
numerical integrations of Eq. (1) are consistent with Eq. (7).
Evolutions depicted in Figs. 4 and 5 are calculated from the numerical
solution of Eq. (7).
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{NEW-FIGS/1286_F6NEW.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg115.png) |
Figure 6:
Evolution of eccentricity of a dust particle with
|
| Open with DEXTER | |
Figure 6 depicts the evolution of eccentricity for the case when the
function W (e) has two roots (
![]() ). Various
evolutions differ only in initial values of eccentricity. A dust
particle with
). Various
evolutions differ only in initial values of eccentricity. A dust
particle with
![]() and
and
![]() is captured in
the exterior mean motion 5/4 resonance with an artificial planet in
a circular orbit of radius aP= 80 AU. The speed of the solar wind is
u=400 km s-1 and the angle between the radial direction and the direction of
the solar wind velocity is
is captured in
the exterior mean motion 5/4 resonance with an artificial planet in
a circular orbit of radius aP= 80 AU. The speed of the solar wind is
u=400 km s-1 and the angle between the radial direction and the direction of
the solar wind velocity is
![]() .
An asymptotic approach
to the limiting value
.
An asymptotic approach
to the limiting value
![]() is evident.
The evolution of eccentricity is always a decreasing function of time, below
the initial eccentricity
is evident.
The evolution of eccentricity is always a decreasing function of time, below
the initial eccentricity
![]() .
.
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{NEW-FIGS/1286F7a-NEW...
...
\includegraphics[height=0.25\textheight]{NEW-FIGS/1286F7w-New.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg119.png) |
Figure 7:
Orbital evolution of a spherical dust particle with
|
| Open with DEXTER | |
Figure 7 depicts results of numerical integration of Eq. (1).
A particle with
![]() and
and
![]() is captured in
a mean motion 5/4 resonance with a planet of mass
mP = 20
is captured in
a mean motion 5/4 resonance with a planet of mass
mP = 20
![]() (
(
![]() kg)
in a circular orbit with a semimajor axis 80 AU. The solar wind is
characterized by u= 400 km s-1,
kg)
in a circular orbit with a semimajor axis 80 AU. The solar wind is
characterized by u= 400 km s-1,
![]() ,
,
![]() .
As the mass of the star we use solar mass. Initial conditions
of the particle are
.
As the mass of the star we use solar mass. Initial conditions
of the particle are
![]() AU,
e = 0.6,
AU,
e = 0.6,
![]() ,
,
![]() ,
where
a5/4 0.01 is the semimajor axis calculated from Eq. (6)
using p = 4, q = 1 and
,
where
a5/4 0.01 is the semimajor axis calculated from Eq. (6)
using p = 4, q = 1 and
![]() .
.
![]() is
the argument of perihelion and f is the true anomaly. The planet's
initial position is on the X-axis (the axis from which the argument
of perihelion is measured). The initial eccentricity of the fifth
evolution of eccentricity from the top of Fig. 6 is also 0.6.
This evolution of eccentricity corresponds to the evolution
of eccentricity obtained by numerical integration
of Eq. (1) shown in Fig. 7. Numerical integration shown in Fig. 7 is in
accordance with our analytical theory, since evolution of eccentricity
asymptotically increases to the value
is
the argument of perihelion and f is the true anomaly. The planet's
initial position is on the X-axis (the axis from which the argument
of perihelion is measured). The initial eccentricity of the fifth
evolution of eccentricity from the top of Fig. 6 is also 0.6.
This evolution of eccentricity corresponds to the evolution
of eccentricity obtained by numerical integration
of Eq. (1) shown in Fig. 7. Numerical integration shown in Fig. 7 is in
accordance with our analytical theory, since evolution of eccentricity
asymptotically increases to the value
![]() .
.
We found that the function W(e) can have two roots for the first order
exterior resonances also for smaller values of
![]() if we use greater p (when the other parameters in the function W (e)are constant). But the resonance overlap begins to be significant for the
first order exterior resonances with higher p (see e.g.
Murray & Dermott
1999). The particle is captured into a 1/1 resonance with a higher probability
than into the first order exterior resonance with a high value of p.
if we use greater p (when the other parameters in the function W (e)are constant). But the resonance overlap begins to be significant for the
first order exterior resonances with higher p (see e.g.
Murray & Dermott
1999). The particle is captured into a 1/1 resonance with a higher probability
than into the first order exterior resonance with a high value of p.
Now, we find how
![]() depends on the individual physical
quantities characterizing the star, planetary orbit and dust grain.
We will carry out our analysis for a given resonance, defined by numbers p and q. Putting Eqs. (2) and (3) into Eq. (7) yields
depends on the individual physical
quantities characterizing the star, planetary orbit and dust grain.
We will carry out our analysis for a given resonance, defined by numbers p and q. Putting Eqs. (2) and (3) into Eq. (7) yields
using Eq. (5) and the notation 4
Now, we can find how
![]() depends on individual variables.
It is evident that the value of
depends on individual variables.
It is evident that the value of
![]() decreases with
an increasing value of the semimajor axis of the planet aP(see Eq. (22)).
decreases with
an increasing value of the semimajor axis of the planet aP(see Eq. (22)).
![]() is an increasing function
of a particle's radius R and mass density
is an increasing function
of a particle's radius R and mass density ![]() .
The function
f1(x1)=(1+a1x1)/(a1x1) has a derivative with
respect to x1 equal to
f'1(x1)=- 1/(a1x12).
f1(x1) is a decreasing function for positive values of a1.
Thus,
.
The function
f1(x1)=(1+a1x1)/(a1x1) has a derivative with
respect to x1 equal to
f'1(x1)=- 1/(a1x12).
f1(x1) is a decreasing function for positive values of a1.
Thus,
![]() will be a decreasing function of nl and m1.
The function
will be a decreasing function of nl and m1.
The function
![]() has a derivative equal to
has a derivative equal to
![]() .
.
![]() .
Since
.
Since ![]() for particles captured
in a mean motion resonance, we obtain
for particles captured
in a mean motion resonance, we obtain
![]() .
Thus,
.
Thus,
![]() will be an increasing function of M.
The function
f3(x3)=(1 + a3x3)/(a3x32) has a derivative
equal to
f'3(x3)=-(2 + a3x3)/(a3x43). f3 is a decreasing
function of x3, for positive a3 and x3. Thus,
will be an increasing function of M.
The function
f3(x3)=(1 + a3x3)/(a3x32) has a derivative
equal to
f'3(x3)=-(2 + a3x3)/(a3x43). f3 is a decreasing
function of x3, for positive a3 and x3. Thus,
![]() is a decreasing function of u.
The function
f4(x4)=(1+a4/x4)(1-b4x4)1/3/(a4/x4)has a derivative equal to
f'2(x4)=(3-a4b4-4b4x4)/[3a4(1-b4x4)2/3],
a4 > 0 and
is a decreasing function of u.
The function
f4(x4)=(1+a4/x4)(1-b4x4)1/3/(a4/x4)has a derivative equal to
f'2(x4)=(3-a4b4-4b4x4)/[3a4(1-b4x4)2/3],
a4 > 0 and
Thus,
We can conclude that
![]() will be always a decreasing function
of aP, nl, m1, u, and, an increasing function of M, R,
will be always a decreasing function
of aP, nl, m1, u, and, an increasing function of M, R,
![]() .
Equation (22) yields that
.
Equation (22) yields that
![]() may be neither an increasing
nor a decreasing function of L and
may be neither an increasing
nor a decreasing function of L and
![]() if the other
parameters are fixed (we do not take into account that luminosity
of a star may depend on its mass).
if the other
parameters are fixed (we do not take into account that luminosity
of a star may depend on its mass).
To obtain the evolution presented in Fig. 6 we need to minimize
the value of
![]() or maximize value of
or maximize value of
![]() in order to have the maximum of the value
in order to have the maximum of the value
![]() .
Thus,
.
Thus,
![]() is larger for stars with strong stellar
wind (high nl, m1, u) or with large a value of
is larger for stars with strong stellar
wind (high nl, m1, u) or with large a value of
![]() .
The value of
.
The value of
![]() can be sufficiently high also
for a particle in a resonance with a planet in orbit with a large semimajor
axis aP. Known systems with a star similar to the Sun and a planet
in an orbit with large a semimajor axis are: GQ Lup
(
can be sufficiently high also
for a particle in a resonance with a planet in orbit with a large semimajor
axis aP. Known systems with a star similar to the Sun and a planet
in an orbit with large a semimajor axis are: GQ Lup
(
![]() ,
Seperuelo et al. 2008;
,
Seperuelo et al. 2008;
![]() AU, Neuhäuser et al. 2005),
1RXS J160929.1-210524 (
M = 0.85+0.20-0.10
AU, Neuhäuser et al. 2005),
1RXS J160929.1-210524 (
M = 0.85+0.20-0.10 ![]() ;
;
![]() AU, Lafreniere et al. 2008).
Also AB Pic has a planet candidate
at a separation of
AU, Lafreniere et al. 2008).
Also AB Pic has a planet candidate
at a separation of ![]() 258 AU (Chauvin et al. 2005).
But AB Pic is classified as a dwarf star, similar
to many known systems with large semimajor axes.
If we calculate
258 AU (Chauvin et al. 2005).
But AB Pic is classified as a dwarf star, similar
to many known systems with large semimajor axes.
If we calculate
![]() for an exosolar system
and its value is higher than 3, then secular evolution of
the particle's eccentricity in an exterior mean motion resonance
can be similar to some of the evolutions shown in Fig. 6.
for an exosolar system
and its value is higher than 3, then secular evolution of
the particle's eccentricity in an exterior mean motion resonance
can be similar to some of the evolutions shown in Fig. 6.
6 Conclusion
We investigated the evolution of eccentricity of an interplanetary spherical dust particle under the action of resonant perturbation of a planet in a circular orbit, the P-R effect and non-radial solar wind.
Eccentricity asymptotically approaches (increases or
decreases) a limiting value in exterior mean motion resonances
(simple asymptotic behavior) if the P-R effect
and radial solar wind are considered.
If also the non-radial component of the solar wind velocity
is taken into account, then various possibilities exist.
If the angle between the radial direction and the velocity of the
solar wind fulfills 0
![]() ,
then
the eccentricity evolution is similar to the case of a radial
solar wind. If
,
then
the eccentricity evolution is similar to the case of a radial
solar wind. If
![]() ,
then the
eccentricity is a decreasing function of time and
the eccentricity non-asymptotically decreases to zero.
,
then the
eccentricity is a decreasing function of time and
the eccentricity non-asymptotically decreases to zero.
For interior mean motion orbital resonances, eccentricity is always a
non-asymptotically decreasing function of time for the P-R effect
and the radial solar wind. The behavior of particle's eccentricity
is inverse to the behavior in the exterior resonances for
![]() .
If we take
into account the non-radial component of the solar wind velocity and
.
If we take
into account the non-radial component of the solar wind velocity and
![]() ,
then the evolution of eccentricity
is similar to the case of the radial solar wind. If
,
then the evolution of eccentricity
is similar to the case of the radial solar wind. If
![]() ,
then eccentricity
asymptotically approaches the limiting value
(simple asymptotic behavior).
,
then eccentricity
asymptotically approaches the limiting value
(simple asymptotic behavior).
If
![]() ,
then
the eccentricity non-asymptotically decreases to 0 or may asymptotically
decrease or increase to a limiting value, for exterior resonances.
If
,
then
the eccentricity non-asymptotically decreases to 0 or may asymptotically
decrease or increase to a limiting value, for exterior resonances.
If
![]() ,
then the eccentricity evolution
has a simple asymptotic behavior for interior resonances.
,
then the eccentricity evolution
has a simple asymptotic behavior for interior resonances.
For the special case of the mean motion 1/1 resonance, the eccentricity
asymptotically decreases to 0, for
![]() .
If
.
If
![]() ,
then simple asymptotic behavior of
the eccentricity exists.
,
then simple asymptotic behavior of
the eccentricity exists.
For the case
![]() ,
the evolution of eccentricity
of a particle captured in an exterior mean motion resonance is characterized
by simple asymptotic behavior. Eccentricity non-asymptotically
decreases to 0 in an interior resonance. The special case of the mean
motion 1/1 resonance is characterized by an asymptotic decrease of eccentricity
to 0.
,
the evolution of eccentricity
of a particle captured in an exterior mean motion resonance is characterized
by simple asymptotic behavior. Eccentricity non-asymptotically
decreases to 0 in an interior resonance. The special case of the mean
motion 1/1 resonance is characterized by an asymptotic decrease of eccentricity
to 0.
We have not found eccentricity evolution characterized by two roots of the function W (e), for a dust particle under the action of electromagnetic and corpuscular radiation of the Sun in an exterior mean motion resonance with a planet in the Solar System.
The values of
![]() ,
,
![]() and numbers pand q determine types of eccentricity evolution.
The value of
and numbers pand q determine types of eccentricity evolution.
The value of
![]() is:
is:
- i)
- an increasing function of mass of a star and particle's radius and mass density,
- ii)
- a decreasing function of stellar wind speed, mass and concentration
of the stellar wind particles, and
- iii)
- an increasing or a decreasing function of luminosity of the star and particle's dimensionless efficiency factor of radiation pressure.
Acknowledgements
The authors would like to thank the anonymous reviewer for fruitful comments. The paper was supported by the Scientific Grant Agency VEGA grant No. 2/0016/09 and by the Comenius University grants UK/405/2009.
Appendix A: Exterior mean motion resonances -
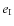
We will show how the value of the root ![]() depends on
depends on
![]() .
We calculate derivatives of the functions
X (e) and Y (e) with respect to the eccentricity
.
We calculate derivatives of the functions
X (e) and Y (e) with respect to the eccentricity
A.1
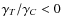
According to Eq. (9), W (e) is a decreasing function of eccentricity,
for
![]() .
Derivatives of the functions X (e) and -Y (e)fulfill d
.
Derivatives of the functions X (e) and -Y (e)fulfill d
![]() and
and
![]() .
Thus, the functions X (e) and -Y (e) are decreasing functions of
eccentricity.
.
Thus, the functions X (e) and -Y (e) are decreasing functions of
eccentricity.
Inserting ex (given by Eq. (14)) into the function W (e),
we obtain
W (ex) > 0. The statement follows from the
inequality Eq. (12). This means that ![]() must be greater
than ex, since the function W (e) is a decreasing function of
eccentricity. If we assume that eccentricity is greater than ex and
less than
must be greater
than ex, since the function W (e) is a decreasing function of
eccentricity. If we assume that eccentricity is greater than ex and
less than ![]() ,
then X (e) < 0 and
W (e) = X (e) - Y (e)> 0, thus
-Y (e) > 0. Both X (e) and -Y (e) decrease with increasing
eccentricity. A positive value of -Y (e) is proportional
to
,
then X (e) < 0 and
W (e) = X (e) - Y (e)> 0, thus
-Y (e) > 0. Both X (e) and -Y (e) decrease with increasing
eccentricity. A positive value of -Y (e) is proportional
to
![]() .
If we decrease the ratio
.
If we decrease the ratio
![]() ,
then the value of X (e) < 0 must decrease more
rapidly in order to reach the condition
,
then the value of X (e) < 0 must decrease more
rapidly in order to reach the condition
![]() .
If X (e) and Y (e) approach such values that
.
If X (e) and Y (e) approach such values that
![]() ,
then the eccentricity e approaches
,
then the eccentricity e approaches ![]() .
The condition will be fulfilled since
.
The condition will be fulfilled since
![]() and
and
![]() (only decreasing X (e) and -Y (e) is not sufficient to fulfill this
condition). Thus,
(only decreasing X (e) and -Y (e) is not sufficient to fulfill this
condition). Thus, ![]() will be a decreasing function of
will be a decreasing function of
![]() .
.
A.2 0 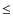
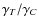
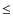 1
1
Derivatives of functions X (e) and Y (e) with
respect to eccentricity are d
![]() and d
and d
![]() (see Eqs. (A.1) and (A.2)). Thus,
the functions X (e) and Y (e) are decreasing functions of
eccentricity. It is easy to show that dX/d
(see Eqs. (A.1) and (A.2)). Thus,
the functions X (e) and Y (e) are decreasing functions of
eccentricity. It is easy to show that dX/d
![]() for all
e
for all
e ![]() (0, 1), if
(0, 1), if
![]() .
.
Inserting ex into the function W (e), for the case
![]() ,
we obtain
W (ex) < 0.
This means that
,
we obtain
W (ex) < 0.
This means that ![]() must be smaller than ex, since the
function W (e) is a decreasing function of eccentricity.
If we assume that eccentricity is greater than
must be smaller than ex, since the
function W (e) is a decreasing function of eccentricity.
If we assume that eccentricity is greater than
![]() and less than ex, then
X (e) > 0 and Y (e) > 0. We have also
W (e) = X (e) - Y (e) < 0, i.e.
X (e) < Y (e). X (e) increases faster than
Y (e) for decreasing e. If X (e) and Y (e) approach
such values that
and less than ex, then
X (e) > 0 and Y (e) > 0. We have also
W (e) = X (e) - Y (e) < 0, i.e.
X (e) < Y (e). X (e) increases faster than
Y (e) for decreasing e. If X (e) and Y (e) approach
such values that
![]() ,
then the eccentricity e approaches
,
then the eccentricity e approaches ![]() .
The value of Y (e) is
proportional to
.
The value of Y (e) is
proportional to
![]() .
The greater
.
The greater
![]() the more rapid an increase of X (e) is necessary in order to reach the
condition
X (e)-Y (e)
the more rapid an increase of X (e) is necessary in order to reach the
condition
X (e)-Y (e) ![]() 0. Thus,
0. Thus, ![]() is a decreasing
function of
is a decreasing
function of
![]() .
If the value of
.
If the value of
![]() increases
from 0 to
increases
from 0 to
![]() ,
then the value of
,
then the value of ![]() decreases from
ex to 0.
decreases from
ex to 0.
Appendix B: Interior mean motion resonances -

The root ![]() was derived for
was derived for
![]() .
Derivatives of the functions X (e) and Y (e) are d
.
Derivatives of the functions X (e) and Y (e) are d
![]() and
d
and
d
![]() (see Eqs. (A.1) and (A.2)). Thus, the functions X (e) and Y (e) are
decreasing functions of eccentricity.
(see Eqs. (A.1) and (A.2)). Thus, the functions X (e) and Y (e) are
decreasing functions of eccentricity.
If
![]() ,
inequalities
X (e) < 0 and Y (e) < 0 hold for the case of the interior resonances. If the initial
eccentricity is smaller than
,
inequalities
X (e) < 0 and Y (e) < 0 hold for the case of the interior resonances. If the initial
eccentricity is smaller than ![]() ,
then W (e) > 0, and thus
- X (e) < - Y (e). If the inequality represented by Eq. (18)
is fulfilled, then the function -X (e) increases faster than
the function -Y (e), with an increasing eccentricity (see Eqs. (A.1) and (A.2)).
This is necessary in order to reach the condition
X (e) - Y (e)
,
then W (e) > 0, and thus
- X (e) < - Y (e). If the inequality represented by Eq. (18)
is fulfilled, then the function -X (e) increases faster than
the function -Y (e), with an increasing eccentricity (see Eqs. (A.1) and (A.2)).
This is necessary in order to reach the condition
X (e) - Y (e) ![]() 0.
The value of -Y (e) is proportional to
0.
The value of -Y (e) is proportional to
![]() ,
and, thus,
,
and, thus,
![]() is an increasing function of
is an increasing function of
![]() .
.
References
- Bahcall, J. N. 2002, Phys. Rev. C, 65, 025801 [NASA ADS] [CrossRef] (In the text)
- Beaugé, C., & Ferraz-Mello, S. 1994, Icarus, 110, 239 [NASA ADS] [CrossRef] (In the text)
- Brownlee, D. E. 1994, Nature, 369, 706 [NASA ADS] [CrossRef]
- Bruno, R., Carbone, V., Sorriso-Valvo, L., & Bavassano, B. 2003, J. Geophys. Res., 108(A3), 1130 (In the text)
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dermott, S. F., Jayaraman, S., Xu, Y. L., Gustafson, B. A. S., & Liou, J. C. 1994, Nature, 369, 719 [NASA ADS] [CrossRef] (In the text)
- Dermott, S. F., Grogan, K., Durda, D. D., et al. 2001, in Interplanetary Dust, ed. E. Grün, B. A. S. Gustafson, S. F. Dermott, & H. Fechtig (Berlin: Springer-Verlag), 569 (In the text)
- Dohnanyi, J. S. 1978, Particle dynamics, in Cosmic Dust, ed. J. A. M. McDonnell (Wiley-Interscience, Chichester), 527 (In the text)
- Grün, E. 2007, Solar System Dust, in Encyclopedia of the Solar System, ed. L.-A. McFadden, P. R. Weissman, & T. V. Johnson 2nd edn. (San Diego: Academic Press-Elsevier Inc.), 621 (In the text)
- Jackson, A. A., & Zook, H. A. 1989, Nature, 337, 629 [NASA ADS] [CrossRef] (In the text)
- Klacka, J. 1994, Earth Moon Planets, 64, 125 [NASA ADS] [CrossRef] (In the text)
- Klacka, J. 2008a [arXiv:0807.2795] (In the text)
- Klacka, J. 2008b [arXiv:0807.2915]
- Klacka, J., & Saniga, M. 1993, Earth Moon Planets, 60, 23 [NASA ADS] [CrossRef] (In the text)
- Klacka, J., Petrzala, J., Pástor, P., & Kómar, L. 2009 [arXiv:0904.0368] (In the text)
- Klacka, J., Kómar, L., Pástor, P., & Petrzala, J. 2008, A&A, 489, 787 [NASA ADS] [CrossRef] [EDP Sciences]
- Klacka, J., & Pástor, P. 2004 [arXiv:astro-ph/0411691] (In the text)
- Kuchner, M. J., & Holman, M. J. 2003, ApJ, 588, 1110 [NASA ADS] [CrossRef] (In the text)
- Lafreniere, D., Jayawardhana, R., & van Kerkwijk, M. H. 2008, ApJL, submitted [arXiv:0809.1424] (In the text)
- Leinert, Ch., & Grün, E. 1990, Interplanetary dust, in Physics of the Inner Heliosphere I, ed. R. Schwen, & E. Marsch (Berlin: Springer-Verlag), 207 (In the text)
- Liou, J.-Ch., & Zook, H. A. 1997, Icarus, 128, 354 [NASA ADS] [CrossRef] (In the text)
- Liou, J.-Ch., & Zook, H. A. 1999, AJ, 118, 580 [NASA ADS] [CrossRef] (In the text)
- Liou, J.-Ch., Zook, H. A., & Jackson, A. A. 1995, Icarus, 116, 186 [NASA ADS] [CrossRef] (In the text)
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (New York: Cambridge Univ. Press) (In the text)
- Neuhäuser, R., Guenther, E. W., & Wuchterl, G., et al. 2005, A&A, 435, L13 [NASA ADS] [CrossRef] [EDP Sciences]
- Parker, E. N. 1958, ApJ, 128, 664 [NASA ADS] [CrossRef] (In the text)
- Pástor, P., Klacka, J., & Kómar, L. 2009, Cel. Mech. and Dynam. Astron., 103, 343 [NASA ADS] [CrossRef]
- Poynting, J. M. 1903, MNRAS , 64, A 1 (In the text)
- Reach, W. T., Franz, B. A., & Welland, et al. 1995, Nature, 374, 521 [NASA ADS] [CrossRef] (In the text)
- Robertson, H. P. 1937, MNRAS, 97, 423 [NASA ADS] (In the text)
- Seperuelo, E., Alencar, S. H. P., Batalha, C., & Lopes, D. 2008, A&A, 489, 349 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sidlichovský, M., & Nesvorný, D. 1994, A&A, 289, 972 [NASA ADS] (In the text)
- Weidenschilling, S. J., & Jackson, A. A. 1993, Icarus, 104, 244 [NASA ADS] [CrossRef] (In the text)
- Whipple, F. L. 1955, ApJ, 121, 750 [NASA ADS] [CrossRef] (In the text)
- Wyatt, S. P., & Whipple, F. L. 1950, ApJ, 111, 134 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1:
Values of
![]() (in degrees) for various exterior
and interior resonances with a planet in a circular orbit of radius aP= 30.058 AU. The particle is characterized by
(in degrees) for various exterior
and interior resonances with a planet in a circular orbit of radius aP= 30.058 AU. The particle is characterized by
![]() and the solar wind by
and the solar wind by
![]() and u = 400 km s-1.
and u = 400 km s-1.
All Figures
![\begin{figure}
\par\includegraphics[height=0.21\textheight]{1286_F1.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg67.png) |
Figure 1:
The function W (e) for exterior mean motion 4/3 resonance.
Various values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F2.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg92.png) |
Figure 2:
The function W (e) for interior mean motion 2/3 resonance
for various values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F3.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg99.png) |
Figure 3:
The function W (e) for mean motion 1/1 resonance
for various values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F4.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg108.png) |
Figure 4:
Evolution of eccentricity obtained from Eq. (7). A dust particle
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{1286_F5.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg109.png) |
Figure 5:
Evolution of eccentricity obtained from Eq. (7). A dust particle
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{NEW-FIGS/1286_F6NEW.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg115.png) |
Figure 6:
Evolution of eccentricity of a dust particle with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=0.25\textheight]{NEW-FIGS/1286F7a-NEW...
...
\includegraphics[height=0.25\textheight]{NEW-FIGS/1286F7w-New.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11286-08/Timg119.png) |
Figure 7:
Orbital evolution of a spherical dust particle with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



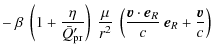
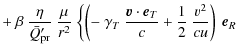
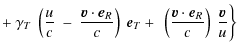
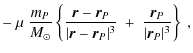
![\begin{displaymath}
\beta = \frac{3 L_{\odot} \bar{Q}'_{\rm pr}}{16 \pi c G~ M_{...
...Q}'_{\rm pr}}{R ~[\mbox{m}] ~\varrho ~[\mbox{kg/m}^{3}]} \cdot
\end{displaymath}](/articles/aa/full_html/2009/25/aa11286-08/img38.png)