R-matrix electron-impact excitation data for the Na-like iso-electronic sequence

G. Y. Liang; A. D. Whiteford; N. R. Badnell

doi:10.1051/0004-6361/200911866

Free Access

Issue		A&A Volume 500, Number 3, June IV 2009


Page(s)		1263 - 1269
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200911866
Published online		08 April 2009

R-matrix electron-impact excitation data for the Na-like iso-electronic sequence

G. Y. Liang - A. D. Whiteford - N. R. Badnell

Department of Physics, University of Strathclyde, Glasgow, G4 0NG, UK

Received 17 February 2009 / Accepted 26 March 2009

Abstract
We present results for the outer-shell electron-impact excitation of all Na-like ions from Mg⁺ to Kr²⁵⁺ obtained using the intermediate-coupling frame transformation R-matrix approach. For each ion's calculation, the target and close-coupling expansions are both taken to be the 18 LS terms (32 levels) belonging to configurations ${\rm [1s^22s^22p^6]3}l$ , 4l, 5l and 6l (l=0-5). Effective collision strengths ( $\Upsilon$ s) are presented at temperatures ranging from $2\times10^2(q+1)^2$ K to $2\times10^6(q+1)^2$ K (where q is the residual charge of ions, i.e. Z-11). Detailed comparisons for the $\Upsilon$ s are made with the results of previous calculations for several ions, which span the sequence. Furthermore, we examine the iso-electronic trends of both low- and high-temperature effective collision strengths

Key words: atomic data - atomic processes - plasmas

1 Introduction

Emission lines arising from outer-shell transitions in ions of the sodium iso-electronic sequence are widely detected in astrophysical objects (see e.g. Acton et al. 1985; Thomas & Neupert 1997; Behar et al. 2001; Keenan et al. 2003) using present ground and space observatories. These emission lines are potential diagnostics of the electron temperature and density of coronal-like hot plasmas (Flower & Nussbaumer 1975; Feldman & Doschek 1977). The most frequently observed emission lines in Na-like ions are from Fe¹⁵⁺ in stars, which is due to its large cosmic abundance. Such line identifications and diagnostics in astrophysical spectroscopy require accurate atomic data.

The astrophysical analysis (e.g. for solar flare spectra obtained with the X-ray Spectrometer/Spectrograph Telescope and observation of Capella with the Low-Energy Transmission Grating Spectrometer on the Chandra X-ray observatory) based upon updated R-matrix excitation data for Fe¹⁵⁺ has shown a considerable improvement (Keenan et al. 2007) in recent years over earlier theoretical predictions for the Fe¹⁵⁺ spectrum. The large amount of high-resolution astrophysical spectroscopy available from past, present & future and ground & space observatories and fusion research provides the need for a large set of accurate baseline atomic data (see e.g. Brown et al. 2008; Summers et al. 2002).

To-date, a large amount of excitation data has been calculated using the distorted-wave (DW) method, using different sizes of configuration interaction (CI) expansions. Sampson et al. (1990) first reported comprehensive relativistic DW collision strengths of outer-shell ( $n \leq5$ ) excitations for Na-like ions with $22\leq Z \leq 92$ . The first R-matrix calculations for outer-shell excitations of the Na-like iso-electronic sequence were the work of Dufton & Kingston (1987) for Al²⁺, Si³⁺ and S⁵⁺, in which results for excitations among 5-states (3s, 3p, 3d, 4s and 4p) were reported. Kimura et al. (1998) made extensive (for the 11 terms of 3l, 4l and 5l, l=0-3configurations) LS-coupling R-matrix calculations for Al²⁺, Si³⁺, S⁵⁺, Ar⁷⁺ and Ca⁹⁺. Thereafter, more elaborate calculations have been performed for several ions. For example, Eissner et al. (1999) presented Breit-Pauli R-matrix results for electron-impact excitations amongst the 12 fine-structure levels of the $n \leq4$ configurations of Fe¹⁵⁺; Hudson & Bell (2005) reported R-matrix results for level-resolved excitations among the lowest 17 fine-structure levels belonging to 3l, 4l, 5s, 5p and 5d configurations of Al²⁺ by re-coupling LS-coupling results via the JAJOM code; Aggarwal & Keenan (2006) reported results for level-resolved excitations among the lowest 39 levels amongst the $n \leq7$ ( $l \leq4$ ) configurations of Fe¹⁵⁺ by using the Dirac atomic R-matrix code DARC.

Due to the advantages (high accuracy and less-time demanding) of the intermediate coupling frame transformation (ICFT) R-matrix codes and the high capability of parallel computer clusters, it is now feasible to provide the excitation data for iso-electronic sequences across the entire range of astrophysical interest within the R-matrix framework (see the work of Witthoeft et al. 2007, for the F-like iso-electronic sequence - Ne⁺ to Kr²⁷⁺). Based upon the robustness of the current suite of R-matrix codes, the R-matrix calculation of effective collision strengths currently can be performed automatically for each ion without manual intervention along an iso-electronic sequence. This ensures that each calculation is performed uniformly and reliably. Careful analysis of the results is still essential so as to further validate the accuracy of the data along the sequence.

In the present work, we study the outer-shell electron impact excitation of Na-like iso-electronic sequence (from Mg⁺ to Kr²⁵⁺), via the ICFT R-matrix approach. In Sect. 2, we discuss details of the calculational method and compare our structure results with those of previous calculations, for the iso-electronic sequence. The excitation results are discussed in Sect. 3. Our work is a part of ongoing collaborative work - the UK Atomic Processes for Astrophysical Plasmas (APAP) network, a broadening of scope of the original UK RmaX network.

2 Sequence calculation

The aim of this work is to perform R-matrix calculation employing intermediate-coupling frame transformation (ICFT) method (see Griffin et al. 1998) for all Na-like ions from Mg⁺to Kr²⁵⁺. The details of the calculation for each ion follow closely to those in the work of Witthoeft et al. (2006) for Fe¹⁹⁺. In our calculations we included the following configuration basis set: [ ${\rm 1s^22s^22p^6}]3l$ , 4l, 5l and 6l (l=0-5) in both the target and close-coupling expansions.

2.1 Structure: levels

The orbital basis functions were obtained from AUTOSTRUCTURE (Badnell 1986) using the Thomas-Femi-Dirac-Amaldi model potential. Relativistic effects were included perturbatively from the one-body Breit-Pauli operators (viz. mass-velocity, spin-orbit and Darwin). The radial scaling parameters were obtained separately for each ion by minimizing the weighted sum of energies of all 18 LS terms.

The resulting energies along the sequence are displayed in Fig. 1a, in which they have been scaled by a factor of 1/(q+1)² (where q=Z-11 for the Na-like sequence), as well as listed in Table 1 for 13 ions spanning Mg⁺ to Kr²⁵⁺.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig1a.eps}\par\includegraphics[width=9cm,clip]{1866fig1b.eps} \end{figure}$	Figure 1: Energy levels for all ions considered. a) The present theoretical energies in units of (q+1)² Ryd (where q=Z-11). b) Comparison with observed energies listed in NIST v.3 for several levels.
Open with DEXTER

In order to maintain consistency and not to introduce arbitrary changes in comparisons across the sequence, we performed the optimization procedure automatically in AUTOSTRUCTURE without manual re-adjustment. So, the energies for the first couple of ions in the sequences show poorer agreement with available experimental values (from NIST v.3) as shown in Fig. 1b. Coupling to the continuum and highly-excited bound states would need to be taken account of, either explicitly via Laguerre pseudo-states or implicitly via a polarization potential, to improve results here. Thereafter (Z=14), the agreement is within 1% of NIST values.

2.2 Structure: gf-values

A further test of the accuracy our structure is to compare gf-values with those of other calculations. Our main comparison is with previous sequence calculations of Sampson et al. (1990) for Ti¹¹⁺-U⁸¹⁺ and Kimura et al. (1998) for Al²⁺-Ca⁹⁺.

The present results show good agreement with those of Sampson et al. (1990), within 10% for $22\leq Z\leq 36$ , e.g. for the ${\rm 2p^63p~^2P_{1/2,3/2}} {-} {\rm 2p^63s~^2S_{1/2}}$ transitions shown in Fig. 2a. The data of Aggarwal & Keenan (2006) in Fe¹⁵⁺ are also overlapped for comparison. For Al²⁺-S⁵⁺, Kimura et al. (1998) reported the gf-values between LS terms. We partition statistically - such an assumption is a good one at low nuclear charge. With increasing charge, of course, this assumption breaks down: the gf-value ratio ${\rm ^2P_{3/2}} {-} {\rm ^2S_{1/2}}$ to ${\rm ^2P_{1/2}} {-} {\rm ^2S_{1/2}}$ deviates from the factor of 2, changing to $\approx$ 2.5 by Kr²⁵⁺, as shown in Fig. 2a. The derived gf-values from Kimura et al.'s data show poorer agreement with the present AUTOSTRUCTURE results, and are worse for lower charge, but they are still within 20% as shown in Fig. 2a. The data from the NIST compilation shows better agreement with the present results (see Fig. 2a). The transitions decaying from more highly excited levels, e.g. 4s and 5f (see Fig. 2b), also show good agreement, to within 20%. For lower-charge ions, the data from the NIST compilation are compared and show good agreement with the present AUTOSTRUCTURE results. We also note that there are spikes and dips for the isoelectronic trend of the gf-values from NIST, which is due to the different data sources in their database.

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{1866fig2a.eps}\par\includegraphics[width=8.7cm,clip]{1866fig2b.eps} \end{figure}$

Figure 2:

Comparison of gf-values from the present AUTOSTRUCTURE calculation with those of previous calculations along the sequence. a) ${\rm 2p^63p~^2P_{1/2}}$ and ${\rm ^2P_{3/2}} {-} {\rm 2p^63s~^2S_{1/2}}$ transitions. SZF90 refers to the work of Sampson et al. (1990), KON98 to Kimura et al. (1998), and AK06 to Aggarwal & Keenan (2006), for Fe¹⁵⁺. NIST compiled data are given for lower charge ions. b) As above, but for the ${\rm 2p^64s~^2S_{1/2}} {-} {\rm 2p^63p~^2P_{1/2}}$ and ${\rm 2p^65f~^2F_{5/2}} {-} {\rm 2p^63d~^2D_{3/2}}$ transitions.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{1866fig3.eps} \end{figure}$

Figure 3:

Scatter plot showing the ratio of gf-values of other workers to the present ones, for transitions from the 5 lowest-lying levels to all levels up to 6g. For Al²⁺: from Hudson & Bell (2005), denoted by HB05, and from NIST v3. For Fe¹⁵⁺: from Aggarwal & Keenan (2006), denoted by AK06. For Kr²⁵⁺: from Sampson et al. (1990), denoted by SZF90 and from Younis et al. (2007), denoted by YAE06. The horizontal dash-dotted lines mark agreement of 20%.

Open with DEXTER

We make a further complete comparison with the results of previous calculations for three ions which span the sequence, viz. Al²⁺, Fe¹⁵⁺ and Kr²⁵⁺, by way of a scatter plot in Fig. 3 (only decays to the 5 lowest-lying levels are shown). For Al²⁺, the present results agree to within 20% when compared with those available from Hudson & Bell (2005) and NIST's v.3 compilation. For Fe¹⁵⁺, a complete set of data from Aggarwal & Keenan (2006) is available and so more transitions are compared. They show that the present gf-values agree to within 20% for most transitions. For Kr²⁵⁺, the present results also show good agreement (within 20%) with those given by Sampson et al. (1990, see Fig. 3). However, the data of Younis et al. (2007) show a large scatter.

2.3 Scattering

Our ICFT R-matrix calculations over the sequence used 40 continuum basis per orbital angular momentum. Contributions from partial waves up to J=12 were included in the exchange R-matrix calculation. The contribution from higher partial waves up to J=42 were included via a non-exchange R-matrix calculation. A ``top-up'' was used to complete the partial collision strength sum over higher J-values by using the Burgess (1974) sum rule for dipole transitions and a geometric series for non-dipole transitions, taking care of the degenerate limit (Badnell & Griffin 2001). In the F-like iso-electronic sequence calculations, Witthoeft et al. (2007) repeated the calculation for some ions with different energy meshes in order to check the convergence of the effective collision strengths ( $\Upsilon$ s) with respect to resonance resolution. In the outer-region calculation, we adopted the finer energy meshes of the work of Witthoeft et al. (2007) to ensure the convergence of $\Upsilon$ s along the Na-like sequence, see Table 2. Beyond the resonance region, for the exchange calculation, an energy mesh of 0.01 or 0.005 was used. For the non-exchange calculation, we used a step of $1\times10^{-3}q^2$ Ryd over the entire energy range. The R-matrix calculation was carried out up to an incident energy of 3 times the ionization potential for each ion. We then used the infinite energy Born limits (non-dipole allowed) and line-strengths (dipole-allowed) from AUTOSTRUCTURE so that the reduced collision strengths ( $\Omega$ s), as defined by Burgess & Tully (1992), are interpolated for all additional higher energies that are necessary to converge the Maxwellian-averaging. The effective collision strengths ( $\Upsilon$ s) at 13 electron temperatures ranging from $2\times10^2(q+1)^2$ K to $2\times10^6(q+1)^2$ K (q=Z-11), are produced as the end product of the calculation. The data were stored in the ADAS adf04 format (Summers 2004).

Table 1: The level energies (Ryd) for ions over the sequence.

Table 2: The energy meshes (in unit of q², residual charge of ion) used for each ion.

3 Results and discussion

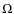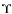
3.1 Comparison with previous results for $\Omega$ and $\Upsilon$

We compare the present ICFT R-matrix results with those of previous works for three ions (Al²⁺, Fe¹⁵⁺and Kr²⁵⁺) which span the range of astrophysical interest for the iso-electronic sequence. Aggarwal & Keenan (2006) noted sudden rises and drops in the background of the ordinary collision strength ( $\Omega$ ) in the Breit-Pauli R-matrix results of Eissner et al. (1999), and suggested it could be a numerical problem in their adopted code. So, we selected the affected ${\rm 4p~^2P_{1/2}} {-} {\rm 4s~^2S_{1/2}}$ transition (see the bottom panel in Fig. 6) as a check. As shown in Fig. 4a, for Al²⁺ and Fe¹⁵⁺, our results show an excellent agreement over the entire temperatures with the JAJOM and Dirac R-matrix results of Hudson & Bell (2005) and Aggarwal & Keenan (2006), respectively. Moreover, there is no sudden jump in the present ordinary $\Omega$ (see Fig. 6) as reported in the work of Eissner et al. (1999), which results in a reduction of $\Upsilon$ at low temperatures in their results. For transitions without sudden jumps in their $\Omega$ , Eissner et al.'s results show good agreement with the present ICFT results and the DARC results at the low temperature. For example, in the ${\rm 4s~^2S_{1/2}}$ $\to$ ${\rm 3p~^2P_{1/2}}$ transition, the $\Upsilon$ is 0.104 (Breit-Pauli), 0.113 (ICFT) and 0.106 ( DARC) at $T_{\rm e}=10^5$ K, respectively.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig4a.eps}\par\includegraphics[width=9cm,clip]{1866fig4b.eps} \end{figure}$

Figure 4:

Comparison of the present ICFT R-matrix results with those of other workers for several ions spanning the iso-electronic sequence. a) Effective collision strengths ( $\Upsilon _{i, j}$ ) for the transitions ${\rm 4s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ and ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ . Top: Al²⁺; HB05 refers to the JAJOM R-matrix results of Hudson & Bell (2005). Middle: Fe¹⁵⁺; EGM99 refers to the Breit-Pauli R-matrix results of Eissner et al. (1999) and AK06 to the Dirac R-matrix results of Aggarwal & Keenan (2006). Bottom: Kr²⁵⁺; SZF90 refers to the relativistic distorted-wave results of Sampson et al. (1990). b) Ordinary collision strengths ( $\Omega$ ) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ in Kr²⁵⁺.

Open with DEXTER

For the highly-charged ion, Kr²⁵⁺, no R-matrix data and no data for excitations from n=4 levels are available, to our knowledge. So the ${\rm 3p~^2P_{3/2}} {-} {\rm 3s~^2S_{1/2}}$ transition was used to test our calculation against DW. Sampson et al. (1990) presented the DW $\Omega$ s at 6 scaled energies grids ranging from 1.9 to 306.0 Ryd for Kr²⁵⁺, from which we derived the effective collision strengths at several temperatures. The enhancement of the present ICFT R-matrix results at low temperatures is due to the resonances near the threshold of the transition with respect to the non-resonant DW calculations, which is confirmed by the comparison of the original collision strengths between the two calculations, as displayed in Fig. 4b. The background of the present ICFT R-matrix calculation shows excellent agreement with the DW values of Sampson et al. (1990). With increasing temperature, the difference between the two calculations decreases and comes into close agreement.

By way of a scatter plot of $\Upsilon$ ratios between the results of the two different calculations, we make a complete comparison for the effective collision strengths in Fe¹⁵⁺ at a low (10⁵ K) and a high (10⁷ K) temperature, see Fig. 5. At the low temperature, the Dirac R-matrix results of Aggarwal & Keenan (2006) are systematically slightly higher than the present ones. There are 64% and 100% transitions showing agreement within 20% and a factor of 2, respectively. The weaker excitations show poorer agreement, for example, excitations with $\Upsilon\leq 0.05$ occupy 91% of the excitations with the difference over 20%. On increasing the temperature to 10⁷ K, 82% transitions of all points in the scatter plot are in agreement within 20%. This indicates that the background of the two R-matrix calculations show agood agreement, and that indirectly reveals that the structure calculations in the two works are in agreement again. For those transitions with differences being larger than 20%, the most likely reason maybe due to the resolution and/or positioning of near threshold resonances. In the present sequence calculations, the energy mesh in the resonance region for Fe¹⁵⁺ is 10^-5q² Ryd (q=15here), which is two times larger than that (0.001 Ryd) used in work of Aggarwal & Keenan (2006). So, we performed an additional calculation with a comparable energy mesh ( $5\times10^{-6}q^2$ Ryd) to that used in the work of Aggarwal & Keenan (2006), which reveals only a slight improvement in the agreement. Therefore, it is likely that the differences are mainly from the differences in near-threshold resonance positions, which results from the two different structures used. As such, it gives an indication of current theoretical accuracy.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig5.eps} \end{figure}$	Figure 5: Scatter plot showing the ratio of $\Upsilon$ s of the Dirac R-matrix results of Aggarwal & Keenan (2006), denoted by AK06, to the present ICFT R-matrix ones, for Fe¹⁵⁺ at the temperatures of 10⁵ and 10⁷ K. (For clarity, only excitations from the 5 lowest-lying levels are shown.) Horizontal dashed lines mark an agreement of 20%.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig6.eps} \end{figure}$	Figure 6: Collision strengths ( $\Omega$ ) for the ${\rm 4s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ transition in Fe¹⁵⁺. The present ICFT R-matrix results are compared to those of the Dirac R-matrix results of Aggarwal & Keenan (2006), denoted by AK06, and the Breit-Pauli R-matrix results of Eissner et al. (1999), denoted by EGM99.
Open with DEXTER

In work of Aggarwal & Keenan (2006), the authors noticed sudden dips in their background $\Omega$ for some transitions and attributed it to numerical difficulties in their adopted code. For example, the ${\rm 4p~^2P_{1/2}} {-} {\rm 4s~^2S_{1/2}}$ transition (see middle panel in Fig. 6). A check on the $\Omega$ from our calculation shows that the phenomenon does not appear and the resonance structure basically agrees with the DARC result (see Fig. 6). Moreover, no sudden jumps, as reported by Eissner et al. (1999, see bottom panel in Fig. 6) appear in the present ICFT R-matrix results.

3.2 Iso-electronic trends

Following-on the above comparison for ordinary collision strengths, we examine their Maxwell-averaged effective collision strengths ( $\Upsilon$ ) trends along the iso-electronic sequence. In the F-like iso-electronic sequence studied by Witthoeft et al. (2007), complicated and periodic spikes and dips of the effective collision strengths appear at low temperatures along the iso-electronic sequence. It is of interest to see if this phenomenon appears in the Na-like iso-electronic sequence.

As noted in the work of Witthoeft et al. (2007), the level mixing of higher excited levels strongly affects the behaviour of the $\Upsilon$ s along the sequence. Here, we first examine the gf-values along the iso-electronic sequence, because the gf-values should vary smoothly along the sequence. In this way, we can exclude errors induced from mis-indexing of transitions resulting from the level mixing for different ions.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig7a.eps}\par\includegraphics[width=9cm,clip]{1866fig7b.eps} \end{figure}$

Figure 7:

Present ICFT R-matrix effective collision strengths ( $\Upsilon$ ) compared with those of other workers at temperatures of $T_{{\rm e}}=10^{3, 4, 5}(q+1)^2$ K along the iso-electronic sequence. KON98 denotes the LS-coupling R-matrix results of Kimura et al. (1998), AK06 the Dirac R-matrix results of Aggarwal & Keenan (2006) (Fe¹⁵⁺ only) and SZF90 the relativistic DW results of Sampson et al. (1990) a) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ ; b) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ .

Open with DEXTER

In Fig. 7a, we show the effective collision strengths along the iso-electronic sequence at a temperature of 10³(q+1)², 10⁴(q+1)² and 10⁵(q+1)² K for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ . As seen in this figure, $\Upsilon$ varies smoothly along the iso-electronic sequence. This same behaviour as reported by Kimura et al. (1998) for their LS-coupling results for Al²⁺, Si³⁺, S⁵⁺, Ar⁷⁺ and Ca⁹⁺, also shown here. Excellent agreement between the two sets of results is obtained at both low and high temperatures. For highly-charged ions ( $Z\geq22$ ), Sampson et al. (1990) presented the original DW collision strengths at 6 scaled energies along the sequence. Using their data, we derived the $\Upsilon$ s at the temperatures of 10³(q+1)² and 10⁴(q+1)² K. The values at $T_{\rm e}=10^{5}(q+1)^2$ K are not given because they require contributions from $\Omega$ at higher energies, i.e. we would have to extrapolate Sampson et al.'s data. The derived $\Upsilon$ s show good agreement with the present R-matrix values, even at the low temperature, which indicates the resonance contribution is negligible for this dipole transition. For Fe¹⁵⁺, the Dirac R-matrix results of Aggarwal & Keenan (2006) are also compared and show good agreement with the present ones.

On the other hand, see Fig. 7b, a check on a $\Delta n=1$ excitation, for example ${\rm 3s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ , shows that the $\Upsilon$ does not vary as smoothly along the iso-electronic sequence at the low temperature, of 10³(q+1)² K, but it has weak bumps or dips. This differs from the iso-electronic trend reported by Kimura et al. (1998). For their selected ions, the present results shows good agreement with theirs. At the higher temperatures, 10⁴(q+1)² and 10⁵(q+1)² K, the two sets of results vary smoothly, and show good agreement. For higher charged ions, the present $\Upsilon$ s are significantly higher than those derived from the relativistic DW $\Omega$ s of Sampson et al. (1990) by nearly a factor of 5 at $T_{\rm e}=10^{3}(q+1)^2$ K. By 10⁴(q+1)² K, the differences decreases to 20%, which is due to the contribution from strong resonances around the threshold becoming weaker at higher temperatures. As pointed out by Witthoeft et al. (2007), such spikes and dips along the iso-electronic sequence at low temperatures are due to the steady shifting of groups of resonances down to threshold, and below, with increasing ionic charge. The difference with results derived from Sampson et al.'s work decreases with increasing $T_{\rm e}$ , tending to zero.

Finally, we note that for transitions with strong resonances, the resonance enhancement is more important for lower charged ions. The $\Upsilon$ ratio along the sequence between the low ( 10³(q+1)² K) and high ( 10⁵(q+1)² K) temperatures clearly demonstrates this - see Fig. 8. The resonance contribution reaches a maximum at Si³⁺, and decreases again with lower charges.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig8.eps} \end{figure}$	Figure 8: Ratio of effective collision strengths ( $\Upsilon$ ) at $T_{\rm e}=10^{3}(q+1)^2$ K to $T_{\rm e}=10^{5}(q+1)^2$ K for the ${\rm 4p~^2P_{1/2}}{\rm 3s~^2S_{1/2}}$ transition along the iso-electronic sequence.
Open with DEXTER

4 Summary

We have performed 32-level ICFT R-matrix calculations for the outer-shell excitation of the Na-like iso-electronic sequence for all ions from Mg⁺ to Kr²⁵⁺.

Good agreement with the results of others for level energies and gf-values for the iso-electronic sequence supports the reliability of the present R-matrix excitation data. This was confirmed specifically, by detailed comparisons of ordinary and effective collision strengths, for Al²⁺, Fe¹⁵⁺ and Kr²⁵⁺.

Poorer structure for ( Z=12 - 14) increases the uncertainty of our excitation data of these ions. A more elaborate R-matrix calculation, e.g. with pseudostates (RMPS), is necessary to test the present data here. This exceeds the scope of the present work. Similarly, fully relativistic calculations may be required for the upper end of the sequence ( Z=34 - 36). For the rest of the sequence ( Z=15 - 33), the present excitation data are useful and reliable for spectroscopy/diagnostic research in the astrophysical and fusion communities. These data are made available through archives of APAP website¹ in the ADAS adf04 format (Summers 2004), ADAS and CHIANTI.

Furthermore, we examined the iso-electronic trends of the effective collision strengths. A complicated pattern of spikes and dips at low temperatures was noted again along the sequence, which precludes interpolation in Z. An extensive check reveals that the spikes and dips are not significant as that in F-like sequence (Witthoeft et al. 2007). Comparison with the results of previous R-matrix calculations shows good agreement for ions along the sequence. With increasing temperature, the difference between the present ICFT R-matrix and previous DW results decreases. For excitations with strong resonances, the resonance contribution at low temperatures becomes stronger for lower charge ions.

In conclusion, we have generated an extensive set of reliable excitation data utilizing the ICFT R-matrix method. This will update the DW data presently used by the astronomical community and its use may overcome some shortcomings in the present astrophysical modelling, as seen in cases of Mg IX (Del Zanna et al. 2008) and Si X (Liang et al. 2009).

Acknowledgements

The work of the UK APAP Network is funded by the UK STFC under grant No. PP/E001254/1 with the University of Strathclyde.

References

Acton, L. W., Bruner, M. E., Brown, W. A., et al. 1985, ApJ, 291, 865 [NASA ADS] [CrossRef] (In the text)
Aggarwal, K. M., & Keenan, F. P. 2006, A&A, 450, 1249 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Badnell, N. R. 1986, J. Phys. B: At. Mol. Opt. Phys., 19, 3827 [NASA ADS] [CrossRef] (In the text)
Badnell, N. R., & Griffin, D. C. 2001, J. Phys. B: At. Mol. Opt. Phys., 34, 681 [NASA ADS] [CrossRef] (In the text)
Behar, E., Cottam, J., & Kahn, S. M. 2001, ApJ, 548, 966 [NASA ADS] [CrossRef] (In the text)
Brown, C. M., Feldman, U., Seely, J. F., et al. 2008, ApJS, 176, 511 [NASA ADS] [CrossRef] (In the text)
Burgess, A. 1974, J. Phys. B: At. Mol. Opt. Phys., 7, L364 [NASA ADS] [CrossRef] (In the text)
Burgess, A., & Tully, J. A. 1992, A&A, 254, 436 [NASA ADS] (In the text)
Del Zanna, G., Rozum, I., & Badnell, N. R. 2008, A&A, 487, 1203 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Dufton, P. L., & Kingston, A. E. 1987, J. Phys. B: At. Mol. Opt. Phys., 20, 3899 [NASA ADS] [CrossRef] (In the text)
Eissner, W., Galavís, M. E., Mendoza, Z., et al. 1999, A&AS, 136, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Feldman, U., & Doschek, G. A. 1977, J. Opt. Soc. Am., 67, 726 [NASA ADS] [CrossRef] (In the text)
Flower, D. R., & Nussbaumer, H. 1975, A&A, 42, 265 [NASA ADS] (In the text)
Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B: At. Mol. Opt. Phys., 31, 3713 [NASA ADS] [CrossRef] (In the text)
Hudson, C. E., & Bell, K. L. 2005, A&A, 436, 1131 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Keenan, F. P., Katsiyannis, A. C., Brosius, J. W., Davila, J. M., & Thomas, R. J. 2003, MNRAS, 343, 513 [NASA ADS] [CrossRef] (In the text)
Keenan, F. P., Drake, J. J., & Aggarwal, K. M. 2007, MNRAS, 381, 1727 [NASA ADS] [CrossRef] (In the text)
Kimura, E., Ohsaki, A., Nakazaki, S., & Itikawa, Y. 1998, A&AS, 132, 99 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Liang, G. Y., Whiteford, A. D., & Badnell, N. R. 2009, A&A, 499, 943 [NASA ADS] [CrossRef] [EDP Sciences] DOI: 10.1051/0004-6361/200811423 (In the text)
Sampson, D. H., Zhang, H. L., & Fontes, C. J. 1990, At. Data and Nucl. Data Tables, 44, 209 [NASA ADS] (In the text)
Summers, H. P., Badnell, N. R., O'Mullane, M. G., et al. 2002, Plasma Phys. Control. Fusion, 44, B323 [CrossRef] (In the text)
Summers, H. P. 2004, The ADAS User manual version 2.6, http://www.adas.ac.uk/
Thomas, R. J., & Neupert, W. M. 1994, ApJS, 91, 461 [NASA ADS] [CrossRef] (In the text)
Witthoeft, M. C., Badnell, N. R., Del Zanna, G., et al. 2006, A&A, 446, 361 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Witthoeft, M. C., Whiteford, A. D., & Badnell, N. R. 2007, J. Phys. B: At. Mol. Opt. Phys., 40, 2969 [NASA ADS] [CrossRef] (In the text)
Younis, W. O., Allam, S. H., & El-Sherbini, Th. M. 2006, At. Data and Nucl. Data Tables, 92, 187 [NASA ADS] [CrossRef] (In the text)

Footnotes

... sequence: These data are made available in the archives of APAP via http://www.apap-network.org, OPEN-ADAS via http://open.adas.ac.uk as well as anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/500/1263
... network: http://www.apap-network.org
... v.3: http://physics.nist.gov/PhysRefData/ASD/levels_form.html
... ADAS: http://www.adas.ac.uk/
... CHIANTI: http://www.chianti.rl.ac.uk/

All Tables

Table 1: The level energies (Ryd) for ions over the sequence.

Table 2: The energy meshes (in unit of q², residual charge of ion) used for each ion.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig1a.eps}\par\includegraphics[width=9cm,clip]{1866fig1b.eps} \end{figure}$	Figure 1: Energy levels for all ions considered. a) The present theoretical energies in units of (q+1)² Ryd (where q=Z-11). b) Comparison with observed energies listed in NIST v.3 for several levels.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{1866fig2a.eps}\par\includegraphics[width=8.7cm,clip]{1866fig2b.eps} \end{figure}$	Figure 2: Comparison of gf-values from the present AUTOSTRUCTURE calculation with those of previous calculations along the sequence. a) ${\rm 2p^63p~^2P_{1/2}}$ and ${\rm ^2P_{3/2}} {-} {\rm 2p^63s~^2S_{1/2}}$ transitions. SZF90 refers to the work of Sampson et al. (1990), KON98 to Kimura et al. (1998), and AK06 to Aggarwal & Keenan (2006), for Fe¹⁵⁺. NIST compiled data are given for lower charge ions. b) As above, but for the ${\rm 2p^64s~^2S_{1/2}} {-} {\rm 2p^63p~^2P_{1/2}}$ and ${\rm 2p^65f~^2F_{5/2}} {-} {\rm 2p^63d~^2D_{3/2}}$ transitions.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{1866fig3.eps} \end{figure}$	Figure 3: Scatter plot showing the ratio of gf-values of other workers to the present ones, for transitions from the 5 lowest-lying levels to all levels up to 6g. For Al²⁺: from Hudson & Bell (2005), denoted by HB05, and from NIST v3. For Fe¹⁵⁺: from Aggarwal & Keenan (2006), denoted by AK06. For Kr²⁵⁺: from Sampson et al. (1990), denoted by SZF90 and from Younis et al. (2007), denoted by YAE06. The horizontal dash-dotted lines mark agreement of 20%.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig4a.eps}\par\includegraphics[width=9cm,clip]{1866fig4b.eps} \end{figure}$	Figure 4: Comparison of the present ICFT R-matrix results with those of other workers for several ions spanning the iso-electronic sequence. a) Effective collision strengths ( $\Upsilon _{i, j}$ ) for the transitions ${\rm 4s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ and ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ . Top: Al²⁺; HB05 refers to the JAJOM R-matrix results of Hudson & Bell (2005). Middle: Fe¹⁵⁺; EGM99 refers to the Breit-Pauli R-matrix results of Eissner et al. (1999) and AK06 to the Dirac R-matrix results of Aggarwal & Keenan (2006). Bottom: Kr²⁵⁺; SZF90 refers to the relativistic distorted-wave results of Sampson et al. (1990). b) Ordinary collision strengths ( $\Omega$ ) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ in Kr²⁵⁺.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig5.eps} \end{figure}$	Figure 5: Scatter plot showing the ratio of $\Upsilon$ s of the Dirac R-matrix results of Aggarwal & Keenan (2006), denoted by AK06, to the present ICFT R-matrix ones, for Fe¹⁵⁺ at the temperatures of 10⁵ and 10⁷ K. (For clarity, only excitations from the 5 lowest-lying levels are shown.) Horizontal dashed lines mark an agreement of 20%.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig6.eps} \end{figure}$	Figure 6: Collision strengths ( $\Omega$ ) for the ${\rm 4s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ transition in Fe¹⁵⁺. The present ICFT R-matrix results are compared to those of the Dirac R-matrix results of Aggarwal & Keenan (2006), denoted by AK06, and the Breit-Pauli R-matrix results of Eissner et al. (1999), denoted by EGM99.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig7a.eps}\par\includegraphics[width=9cm,clip]{1866fig7b.eps} \end{figure}$	Figure 7: Present ICFT R-matrix effective collision strengths ( $\Upsilon$ ) compared with those of other workers at temperatures of $T_{{\rm e}}=10^{3, 4, 5}(q+1)^2$ K along the iso-electronic sequence. KON98 denotes the LS-coupling R-matrix results of Kimura et al. (1998), AK06 the Dirac R-matrix results of Aggarwal & Keenan (2006) (Fe¹⁵⁺ only) and SZF90 the relativistic DW results of Sampson et al. (1990) a) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 3p~^2P_{3/2}}$ ; b) for the transition ${\rm 3s~^2S_{1/2}} {-} {\rm 4p~^2P_{1/2}}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1866fig8.eps} \end{figure}$	Figure 8: Ratio of effective collision strengths ( $\Upsilon$ ) at $T_{\rm e}=10^{3}(q+1)^2$ K to $T_{\rm e}=10^{5}(q+1)^2$ K for the ${\rm 4p~^2P_{1/2}}{\rm 3s~^2S_{1/2}}$ transition along the iso-electronic sequence.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

R-matrix electron-impact excitation data for the Na-like iso-electronic sequence

1 Introduction

2 Sequence calculation

2.1 Structure: levels

2.2 Structure: gf-values

2.3 Scattering

3 Results and discussion

3.1 Comparison with previous results for and

3.2 Iso-electronic trends

4 Summary

References

Footnotes

All Tables

All Figures

3.1 Comparison with previous results for $\Omega$ and $\Upsilon$