| Issue |
A&A
Volume 500, Number 3, June IV 2009
|
|
|---|---|---|
| Page(s) | 1045 - 1063 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200911771 | |
| Published online | 16 April 2009 | |
A new population of cool stars and brown dwarfs
in the Lupus clouds![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
F. Comerón1,![]() - L. Spezzi2,3 - B. López Martí4
- L. Spezzi2,3 - B. López Martí4
1 - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
2 - INAF - Osservatorio Astrofisico di Catania, via S. Sofia, 78, 95123 Catania, Italy
3 - Research and Scientific Support Department, European Space Agency (ESTEC), PO Box 299, 2200 AG Noordwijk, The Netherlands
4 - Laboratorio de Astrofísica Estelar y Exoplanetas - Centro de Astrobiología (LAEX-CAB/INTA-CSIC, LAEFF-Apdo. 78, 28691 Villanueva de la Cañada, Spain
Received 2 February 2009 / Accepted 6 April 2009
Abstract
Context. Most studies of the stellar and substellar populations of star-forming regions rely on using the signatures of accretion, outflows, disks, or activity characterizing the early stages of stellar evolution. However, these signatures rapidly decay with time.
Aims. We present the results of a wide-area study of the stellar population of clouds in the Lupus star-forming region. When combined with 2MASS photometry, our data allow us to fit the spectral energy distributions of over 150 000 sources and identify possible new members based on their photospheric fluxes, independent of any display of the signposts of youth.
Methods. We used the Wide Field Imager (WFI) at the La Silla 2.2 m telescope to image an area of more than 6 square degrees in the Lupus 1, 3 and 4 clouds in the ![]() ,
,
![]() ,
and
,
and
![]() bands, selected so as to overlap with the areas observed in the Spitzer Legacy Program ``From molecular cores to planet-forming disks''. We complement our data with 2MASS photometry to sample the spectral energy distribution from 0.6
bands, selected so as to overlap with the areas observed in the Spitzer Legacy Program ``From molecular cores to planet-forming disks''. We complement our data with 2MASS photometry to sample the spectral energy distribution from 0.6 ![]() m to 2.2
m to 2.2 ![]() m. We validate our method on the census of known members of the Lupus clouds, for which spectroscopic classification is available. The temperatures derived for cool objects are generally accurate, with most of the exceptions attributed to veiling, strong emission lines at short wavelengths, near-infrared excess, variability, or the presence of close companions.
m. We validate our method on the census of known members of the Lupus clouds, for which spectroscopic classification is available. The temperatures derived for cool objects are generally accurate, with most of the exceptions attributed to veiling, strong emission lines at short wavelengths, near-infrared excess, variability, or the presence of close companions.
Results. Considering that the dereddened fluxes of most cool (
![]() K) young stellar objects at the distance of Lupus occupy a gap between those typical both of field cool dwarfs and of background giants, we identify a new population of cool members of Lupus 1 and 3. The approximately 130 new members are only moderately concentrated toward the densest clouds, they appear to have ages in the same range as the known members, and very few show the infrared excess caused by warm disks. This population is absent in Lupus 4.
K) young stellar objects at the distance of Lupus occupy a gap between those typical both of field cool dwarfs and of background giants, we identify a new population of cool members of Lupus 1 and 3. The approximately 130 new members are only moderately concentrated toward the densest clouds, they appear to have ages in the same range as the known members, and very few show the infrared excess caused by warm disks. This population is absent in Lupus 4.
Conclusions. This new population of Lupus members seems to be composed of stars and brown dwarfs that have lost their inner disks on a timescale of a few Myr or less. Almost all these objects are in low extinction regions. We speculate that dissipation of unshielded disks caused by nearby O stars or fast collapse of the pre-(sub)stellar cores triggered by the passage of old supernova shocks may have led to disk properties and evolutionary paths very different from those resulting from the more quiescent environment provided by dense molecular clouds.
Key words: stars: low-mass, brown dwarfs - stars: formation - stars: pre-main sequence - ISM: individual objects: Lupus - ISM: clouds
1 Introduction
Much of our current knowledge of the earliest stages of the evolution of very low mass stars and brown dwarfs, the signatures of stellar and substellar youth, and the build-up and shape of the initial mass function comes from the observation of a number of star-forming regions within 150-200 pc from the Sun (see Reipurth 2008 for an extensive collection of reviews). The availability of instruments with large format, sensitive detectors operating at different wavelengths both on the ground and in space has made it possible to obtain an increasingly complete census of the young populations in all these regions down to masses well below the substellar limit. The approach normally adopted consists of using different telltale features displayed by young stellar objects as a way to identify members, and derive their intrinsic properties by means of detailed follow-up observations or with the help of photometric information.
The Lupus clouds, a complex of low-mass star-forming regions in
the Scorpius-Centaurus OB association, has been the target of a
number of such investigations (see Comerón 2008 for a historical
review and a summary of existing results). Those clouds are spread
over a large area of the sky, nearly ![]() across, with
galactic longitudes in the range
across, with
galactic longitudes in the range
![]() and
latitudes
and
latitudes
![]() .
Following early slitless
spectroscopy surveys by Thé (1962) and Schwartz (1977) which
revealed for the first time the rich T Tauri content of the Lupus
clouds, their lowest mass component has been probed by more recent
studies at different wavelengths. Hughes et al. (1994) obtained
spectroscopy and infrared photometry for the members listed by
Schwartz (1977). The Lupus 3 cloud, which contains the largest number
and density of members, has been the target of several surveys:
Nakajima et al. (2000) identified some possible very low luminosity members
by means of near-infrared excesses. Comerón et al. (2003) added four new
members identified through their H
.
Following early slitless
spectroscopy surveys by Thé (1962) and Schwartz (1977) which
revealed for the first time the rich T Tauri content of the Lupus
clouds, their lowest mass component has been probed by more recent
studies at different wavelengths. Hughes et al. (1994) obtained
spectroscopy and infrared photometry for the members listed by
Schwartz (1977). The Lupus 3 cloud, which contains the largest number
and density of members, has been the target of several surveys:
Nakajima et al. (2000) identified some possible very low luminosity members
by means of near-infrared excesses. Comerón et al. (2003) added four new
members identified through their H![]() emission, including a M 8
brown dwarf. López Martí et al. (2005) have proposed 22 additional candidate
members of Lupus 3 based on a wide-area survey using a combination
of filters that allowed them to identify possible H
emission, including a M 8
brown dwarf. López Martí et al. (2005) have proposed 22 additional candidate
members of Lupus 3 based on a wide-area survey using a combination
of filters that allowed them to identify possible H![]() -emitting
members and to estimate their temperatures from intermediate-band
differential photometry near selected spectral features. Deep X-ray
observations of Lupus 3, sensitive to the emission from brown
dwarfs, have been presented by Gondoin (2006).
-emitting
members and to estimate their temperatures from intermediate-band
differential photometry near selected spectral features. Deep X-ray
observations of Lupus 3, sensitive to the emission from brown
dwarfs, have been presented by Gondoin (2006).
The most comprehensive recent searches for members of the Lupus clouds have been based on the results obtained by the Spitzer Space Observatory. As a result of the Spitzer Legacy program From molecular cores to planet-forming disks (Evans et al. 2008,2003), a number of papers (Merín et al. 2008; Allers et al. 2006; Chapman et al. 2007) have reported on the discovery of new low-mass members and the confirmation of previously suspected ones. Further Spitzer observations of the region have been presented by Allen et al. (2007). These identifications are based on the determination of spectral energy distributions at infrared wavelengths, where warm dust dominates the emission. Merín et al. (2008) have synthesized the Spitzer findings on the Lupus 1, 3, and 4 clouds, and have discussed the properties of both the central objects and their circumstellar material. Together with the results of previous surveys, the member lists presented by Merín et al. (2008) represent the most complete census to date of stars and brown dwarfs in Lupus 1, 3, and 4.
Despite their wide coverage and the ability to reveal very
low mass members, surveys based on the detection of H![]() emission or infrared excesses caused by warm dust leave the question
open about the fraction of members of a star-forming region that
may not be accreting or surrounded by a sufficient amount of dust.
Observational evidence points toward disk lifetimes of only a few Myr, with a significant fraction of stars losing their disks over a
timescale that is comparable to the duration of the embedded phase (e.g.
Haisch et al. 2001). In fact, as pointed out by Merín et al. (2008), some confirmed
members of the star-forming region observed by Spitzer do not meet the
infrared excess-based color criteria for their selection of
candidates. Unbiased surveys where the identification of
members is based solely on the photospheric properties (e.g.
Luhman 2007) appear thus as a necessary complement of those based
on the identification of signatures of accretion, dust, or the
strong chromospheric activity characteristic of young stellar objects.
emission or infrared excesses caused by warm dust leave the question
open about the fraction of members of a star-forming region that
may not be accreting or surrounded by a sufficient amount of dust.
Observational evidence points toward disk lifetimes of only a few Myr, with a significant fraction of stars losing their disks over a
timescale that is comparable to the duration of the embedded phase (e.g.
Haisch et al. 2001). In fact, as pointed out by Merín et al. (2008), some confirmed
members of the star-forming region observed by Spitzer do not meet the
infrared excess-based color criteria for their selection of
candidates. Unbiased surveys where the identification of
members is based solely on the photospheric properties (e.g.
Luhman 2007) appear thus as a necessary complement of those based
on the identification of signatures of accretion, dust, or the
strong chromospheric activity characteristic of young stellar objects.
In this paper we present the results of a broad-band, wide-area
visible imaging survey of the Lupus 1, 3, and 4 clouds complemented
with near-infrared photometry from the 2MASS point source catalog.
Our new observations, presented in Sect. 2, cover the
interval between 0.6 and 0.96 ![]() m and, when combined with JHKSphotometry from 2MASS, provide a good sampling of the spectral
energy distribution in the region around its peak for young low mass
stars and brown dwarfs. The wide wavelength baseline allows us to
perform a robust fit to the intrinsic spectral energy distribution
predicted by model atmospheres and pre-main sequence evolutionary
tracks, which we describe in Sect. 3. In this way we
produce lists of candidate members of the star-forming region, which
can be compared to the census of members obtained by previous works
like those outlined above using different approaches.
m and, when combined with JHKSphotometry from 2MASS, provide a good sampling of the spectral
energy distribution in the region around its peak for young low mass
stars and brown dwarfs. The wide wavelength baseline allows us to
perform a robust fit to the intrinsic spectral energy distribution
predicted by model atmospheres and pre-main sequence evolutionary
tracks, which we describe in Sect. 3. In this way we
produce lists of candidate members of the star-forming region, which
can be compared to the census of members obtained by previous works
like those outlined above using different approaches.
A major uncertainty factor in deriving intrinsic properties of young stellar objects is the rather poor accuracy with which the distances to their host star-forming regions are generally known. In the case of Lupus, the existent distance determinations have been reviewed by Comerón (2008). Following the discussion in that work we will adopt 150 pc for Lupus 1 and 4, and 200 pc for Lupus 3.
The areas covered by the survey presented here were chosen so as to have a large overlap with the regions observed by the Spitzer legacy program From molecular cores to planet-forming disks, and data presented here have already been used in the analyses of Merín et al. (2007) and Merín et al. (2008). Therefore, this paper provides the detailed description of the visible observations used in those works.
2 Observations and data reduction
The material presented in this paper is based on imaging of the
Lupus 1, 3, and 4 clouds obtained with the Wide Field Imager (WFI)
at the MPI-ESO 2.2m telescope on La Silla, Chile (Baade et al. 1999).
Images were obtained through filters approximately covering the
Cousins ![]() and
and ![]() bands, as well as through an intermediate-width band near 0.96
bands, as well as through an intermediate-width band near 0.96 ![]() m to which we will refer as
m to which we will refer as
![]() .
The detector plane of WFI is covered by an array of
.
The detector plane of WFI is covered by an array of
![]() individual CCD chips, each with
individual CCD chips, each with
![]() pixel2, covering a field of view of
pixel2, covering a field of view of
![]() with small gaps of 14'' and 23'' between adjacent chips. The pixel scale is 0''238 pixel-1.
with small gaps of 14'' and 23'' between adjacent chips. The pixel scale is 0''238 pixel-1.
A total of 24 fields were observed covering the areas of highest dust column density in each of the clouds according to IRAS 100 ![]() m emission maps, selected to include most of the areas
surveyed in the Spitzer Legacy program From molecular cores to planet-forming disks. The area of the sky covered in each cloud is 2.84 square degrees in Lupus 1, 2.78 in Lupus 3, and 1.11
in Lupus 4. The observations were carried out in Service Mode
during ESO periods 69 (April-October 2002) and 71 (April-October 2003). Since the
execution in Service Mode implies that the observations are carried
out when the external conditions are within a pre-specified range,
rather than on fixed dates (Comerón 2004), individual observations
were spread over many observing nights, spanning a few months every
period. The observations scheduled in 2003 included fields that
could not be observed at all in the previous year, as well as the
completion of the observations of fields that could be imaged only
in some of the filters in 2002.
m emission maps, selected to include most of the areas
surveyed in the Spitzer Legacy program From molecular cores to planet-forming disks. The area of the sky covered in each cloud is 2.84 square degrees in Lupus 1, 2.78 in Lupus 3, and 1.11
in Lupus 4. The observations were carried out in Service Mode
during ESO periods 69 (April-October 2002) and 71 (April-October 2003). Since the
execution in Service Mode implies that the observations are carried
out when the external conditions are within a pre-specified range,
rather than on fixed dates (Comerón 2004), individual observations
were spread over many observing nights, spanning a few months every
period. The observations scheduled in 2003 included fields that
could not be observed at all in the previous year, as well as the
completion of the observations of fields that could be imaged only
in some of the filters in 2002.
The observations of each individual field were distributed in two
Observation Blocks (OBs). The first OB described the instrument
setup and exposure parameters in the R and I filters, while the
second one described the observation in the
![]() filter.
Such split was needed due to the long exposure time per field when
adding the integrations in all the filters, and facilitated the
scheduling of the observations. The disadvantage is that
observations in R and I on one side, and
filter.
Such split was needed due to the long exposure time per field when
adding the integrations in all the filters, and facilitated the
scheduling of the observations. The disadvantage is that
observations in R and I on one side, and
![]() on the
other, were in general not simultaneous. Furthermore, most of the
on the
other, were in general not simultaneous. Furthermore, most of the
![]() observations were carried out on the second year,
whereas the R and I observations were roughly evenly distributed
between both periods. As a result, for many fields the lag between
the RI and the
observations were carried out on the second year,
whereas the R and I observations were roughly evenly distributed
between both periods. As a result, for many fields the lag between
the RI and the
![]() observations can approach or slightly
exceed one year. The total exposure times per field and filter were
1600s in R, 240s in I, and 1320s in
observations can approach or slightly
exceed one year. The total exposure times per field and filter were
1600s in R, 240s in I, and 1320s in
![]() .
The observations in
each filter were split into four individual exposures, shifting the
telescope pointing by small amounts (between 1' and 2') between
consecutive pointings so as to cover the gaps between the individual
chips forming the WFI detector. The total coverage of each field led
to an overlap band 5' wide between adjacent fields.
.
The observations in
each filter were split into four individual exposures, shifting the
telescope pointing by small amounts (between 1' and 2') between
consecutive pointings so as to cover the gaps between the individual
chips forming the WFI detector. The total coverage of each field led
to an overlap band 5' wide between adjacent fields.
The observations were processed by using a number of dedicated
IRAF![]() scripts in charge of
the different steps of the data reduction. Master bias frames were
constructed, for each night in which observations for our program
were obtained, from the standard calibration data products supplied
with the Service Mode data package. Regarding flat fields, the best
results were obtained with twilight sky flat field frames rather
than with dome flat field frames. The stability of the sky flat
field frames was found to be sufficiently good for the use of a
single master sky flat field frame in each filter for each of the
observing seasons, which was obtained by combining all the sky flat
field frames included in our data packages.
scripts in charge of
the different steps of the data reduction. Master bias frames were
constructed, for each night in which observations for our program
were obtained, from the standard calibration data products supplied
with the Service Mode data package. Regarding flat fields, the best
results were obtained with twilight sky flat field frames rather
than with dome flat field frames. The stability of the sky flat
field frames was found to be sufficiently good for the use of a
single master sky flat field frame in each filter for each of the
observing seasons, which was obtained by combining all the sky flat
field frames included in our data packages.
Fringing strongly affects the WFI observations taken in the Iand
![]() filters. To remove the fringing pattern, we first
identified the science frames in those filters in our data sets that
were virtually free from nebulosity. After inspection of the
fringing pattern we grouped those sharing the same pattern, since
2-3 pattern changes typically took place during the period spanned
by our observations in each of the two seasons. Then, a master
fringing frame in each of the two affected filters was constructed
by subtracting from each frame its average sky level, and median
filtering all the frames of each group together. The suitable master
fringing frame was then scaled by a factor of order unity to account
for the amplitude of the fringes in the individual science frames.
The precise value of the scaling factor was determined by
iteratively subtracting from each science frame the master fringing
pattern with different values of this factor, until finding one that
left no visible residual fringing. We found that visual inspection
provided the best criterion to determine the fringing scaling
factor. In all cases a good solution could be found that effectively
removed the fringing pattern of the science frames after proper
scaling.
filters. To remove the fringing pattern, we first
identified the science frames in those filters in our data sets that
were virtually free from nebulosity. After inspection of the
fringing pattern we grouped those sharing the same pattern, since
2-3 pattern changes typically took place during the period spanned
by our observations in each of the two seasons. Then, a master
fringing frame in each of the two affected filters was constructed
by subtracting from each frame its average sky level, and median
filtering all the frames of each group together. The suitable master
fringing frame was then scaled by a factor of order unity to account
for the amplitude of the fringes in the individual science frames.
The precise value of the scaling factor was determined by
iteratively subtracting from each science frame the master fringing
pattern with different values of this factor, until finding one that
left no visible residual fringing. We found that visual inspection
provided the best criterion to determine the fringing scaling
factor. In all cases a good solution could be found that effectively
removed the fringing pattern of the science frames after proper
scaling.
Another factor affecting WFI frames, common to focal reducers, is
the existence of sky concentration, which requires the determination
of an illumination correction map. This effect is well known to
exist at the WFI to the level of a few hundredths of a magnitude
throughout most of the field, reaching slightly above 0.1 mag near
the edges of the field. Since no calibrations suitable for a quantification of this effect in our images were obtained, we applied instead the WFI illumination correction map in the R band derived by Koch et al. (2003) and assumed it to be approximately applicable to the I and
![]() filters as well. Judging from the residual differences between the illumination correction
maps computed by Koch et al. in different filters, we expect the
systematic error introduced in this way not to exceed 0.03 mag
anywhere in the field. On the other hand, we examined the residuals
of the fits of photometric solutions derived from observations of
Landolt (1992) standard star fields (Sect. 2.1) obtained
as a part of the WFI calibration plan during the nights in which our
observations were carried out. Although the crowding of these fields
with standard stars is far too sparse to independently derive
illumination correction maps, the absence of systematic positional
trends in the residuals gives us confidence that the applied
procedure is indeed sufficiently accurate down a few hundredths of a
magnitude.
filters as well. Judging from the residual differences between the illumination correction
maps computed by Koch et al. in different filters, we expect the
systematic error introduced in this way not to exceed 0.03 mag
anywhere in the field. On the other hand, we examined the residuals
of the fits of photometric solutions derived from observations of
Landolt (1992) standard star fields (Sect. 2.1) obtained
as a part of the WFI calibration plan during the nights in which our
observations were carried out. Although the crowding of these fields
with standard stars is far too sparse to independently derive
illumination correction maps, the absence of systematic positional
trends in the residuals gives us confidence that the applied
procedure is indeed sufficiently accurate down a few hundredths of a
magnitude.
Once corrected for bias, flat field, fringing and illumination, individual images in each filter were combined into a single mosaic per field. This was done by determining the offsets among the four exposures of each field for each individual detector chip using the stellar images as references, and then combining the images in each chip correcting for the offsets. Because the amplitude of the offsets was larger than the size of the interchip gaps, the combined, offset-corrected images of each chip overlapped, thus making it possible to precisely determine the offsets between adjacent chips using the stars in the overlap regions as reference. In this way a single full field image was produced for each filter by stacking together the four individual exposures.
Astrometric calibration of each field was carried out by using stellar positions in the USNO-A2.0 catalog, which provides several thousand stars per field. A distortion correction was then applied to the images through scripts making use of the IRAF GEOMAP and GEOTRANS tasks. The rms error in stellar coordinates is found to be better than 0''3 by comparison to the USNO-A2.0 astrometry, and confirmed by cross-matching with the 2MASS point source catalog (see Sect. 2.1.3).
The distortion-corrected images of each field in the three observed filters were stacked together into a single combined image where source detection was carried out using DAOFIND. Aperture photometry, using IRAF scripts based on DAOPHOT (Stetson 1987) on each position where a source was detected, was then carried out on the original combined image in each filter, thus producing a catalog with the coordinates and instrumental magnitude of each object in each of the three filters. The aperture radius was individually set for each image taking as a reference the full-width at half-maximum (FWHM) of bright unsaturated stars, in order to account for the varying image quality among the different fields. An aperture radius of five times the FWHM (i.e. typically about 6'') was used.
2.1 Photometric calibration
2.2.1
 and
and
 filters
filters
At least one, and frequently more, observations of Landolt standard star fields (Landolt 1992) were carried out every night that R and I observations were obtained for our program. This allowed us to determine both photometric zeropoints and color terms for each of those two filters in order to convert instrumentally determined magnitudes to the Cousins system. No attempt was made to determine in addition extinction terms, since the small number of standard star fields observed per night prevented their determination on a nightly basis. Instead, average extinction coefficients for La Silla in those filters were used.
Whereas the R and the
![]() filters used were the same
in the 2002 and 2003 periods, the standard I filter used at WFI,
denominated Ic in 2002, was replaced shortly after the beginning
of the 2003 period by the so-called I/203 filter. As a result,
part of our observations carried out in 2003 were obtained with a
I filter different from that used for the rest of the
observations. Comparing the zeropoints obtained from the analysis of
the Landolt standard star fields with both filters, we find that
observations with the I/203 filter are approximately 0.3 mag deeper. Furthermore, the I/203 filter is closer to the Cousins
filters used were the same
in the 2002 and 2003 periods, the standard I filter used at WFI,
denominated Ic in 2002, was replaced shortly after the beginning
of the 2003 period by the so-called I/203 filter. As a result,
part of our observations carried out in 2003 were obtained with a
I filter different from that used for the rest of the
observations. Comparing the zeropoints obtained from the analysis of
the Landolt standard star fields with both filters, we find that
observations with the I/203 filter are approximately 0.3 mag deeper. Furthermore, the I/203 filter is closer to the Cousins ![]() filter, as shown by the lower value of the color terms. These were determined by solving the following equations for each standard star field observed:
filter, as shown by the lower value of the color terms. These were determined by solving the following equations for each standard star field observed:
| |
= | (1) | |
| = | (2) | ||
| = | (3) |
where r, i203, and ic are instrumental magnitude measurements in the R, I/203, and Ic filters; Cr, Ci203, and
| k''r | = | ||
| k''i203 | = | ||
| = |
These average values were then used to recompute the nightly zeropoints for each individual field.
Since the goal of our observations is to characterize the low-mass population of the Lupus clouds, the long exposure times used lead to detector saturation even at relatively faint magnitudes. Table 1 lists both the saturation magnitudes in each filter and approximate 3![]() detection limits. Moderate variations within the 0.2 mag level in these values occur from field to field due to the different external conditions under which our observations were carried out.
detection limits. Moderate variations within the 0.2 mag level in these values occur from field to field due to the different external conditions under which our observations were carried out.
Table 1:
Saturation limits and limiting magnitudes at 3![]() level.
level.
2.1.2
 filter
filter
The calibration of the
![]() filter was carried out based on
observations of the star Wolf 629, which has been adopted
as a standard both in the Johnson-Cousins system, and in the Gunn
system used by the Sloan Digital Sky Survey (Fukugita et al. 1996). A cycle
of observations consisting of short
filter was carried out based on
observations of the star Wolf 629, which has been adopted
as a standard both in the Johnson-Cousins system, and in the Gunn
system used by the Sloan Digital Sky Survey (Fukugita et al. 1996). A cycle
of observations consisting of short
![]() exposures of the field
around Wolf 629 immediately followed by also short exposures at the
centers of the Lupus 1, 3, and 4 areas in the same filter was
obtained in order to set up a network of secondary standards in each
of the individual clouds. Each of the deep fields imaged in
exposures of the field
around Wolf 629 immediately followed by also short exposures at the
centers of the Lupus 1, 3, and 4 areas in the same filter was
obtained in order to set up a network of secondary standards in each
of the individual clouds. Each of the deep fields imaged in
![]() was then calibrated with reference to this shallow
exposure. For the fields where an overlap region with the shallow
exposure on the center of the field existed, bright, unsaturated
stars in the area of overlap were used. For fields farther from the
cloud center not overlapping with the shallow reference exposure,
cross-calibration was achieved by using stars in the overlap region
with contiguous fields, which typically provided a few hundred
suitable stars in common.
was then calibrated with reference to this shallow
exposure. For the fields where an overlap region with the shallow
exposure on the center of the field existed, bright, unsaturated
stars in the area of overlap were used. For fields farther from the
cloud center not overlapping with the shallow reference exposure,
cross-calibration was achieved by using stars in the overlap region
with contiguous fields, which typically provided a few hundred
suitable stars in common.
The
![]() filter is characterized by an effective wavelength of
957 nm, which is somewhat longer than that of the Gunn z' filter
(911.4 nm), and a width of 53.4 nm. Using the STIS
spectrophotometric calibration of Vega (Bohlin & Gilliland 2004), the flux at
zero magnitude at the effective wavelength of the
filter is characterized by an effective wavelength of
957 nm, which is somewhat longer than that of the Gunn z' filter
(911.4 nm), and a width of 53.4 nm. Using the STIS
spectrophotometric calibration of Vega (Bohlin & Gilliland 2004), the flux at
zero magnitude at the effective wavelength of the
![]() filter
was determined to be
filter
was determined to be
![]() W cm-2 s-1
W cm-2 s-1 ![]() m. The magnitude of Wolf 629 in that filter was then determined using its Gunn r', i', and z' photometry as given in Smith et al. (2002) and a template M4 star spectrum, thus obtaining
m. The magnitude of Wolf 629 in that filter was then determined using its Gunn r', i', and z' photometry as given in Smith et al. (2002) and a template M4 star spectrum, thus obtaining
![]() .
.
2.1.3 Final catalog including 2MASS data
Three merged catalogs (one for each of the observed clouds) with position and photometry, as well as the date of the observation in each filter, were produced. For each star appearing in more than one field, the entry corresponding to the field where its angular distance to the field center was smaller was retained, rather than averaging the magnitudes derived in each field. This was preferred in order to reduce the effects of the higher uncertainty of the illumination correction towards the edges of the fields.
Each entry in the catalog was further complemented with near-infrared JHKS photometry by cross-matching it with the 2MASS Point Source Catalog (Skrutskie et al. 2006). A matching radius of 2'' was defined, which appears to be by far sufficient given that in all fields over 94% of the matches corresponded to differences between the 2MASS positions and those determined by us of less than 1''. When more than one 2MASS source was found within the 2'' circle, the one closer to the position derived from our observations was chosen as the counterpart.
Table 2 gives bulk numbers reflecting the contents
of our catalogs. In total, our observations contain nearly 1.4
million objects for which the magnitude in at least one of the R,
I, or
![]() filters has been measured, and 157 415 for which
six-band photometry from 0.6 to 2.2
filters has been measured, and 157 415 for which
six-band photometry from 0.6 to 2.2 ![]() m is available. The numbers
given in Table 2 show the ability of our
observations to image sources too faint to be detected by 2MASS, as
only 15% of the sources that we detect in all three WFI filters
have a counterpart detected in 2MASS. The catalogs used in this
study are available from the authors upon request.
m is available. The numbers
given in Table 2 show the ability of our
observations to image sources too faint to be detected by 2MASS, as
only 15% of the sources that we detect in all three WFI filters
have a counterpart detected in 2MASS. The catalogs used in this
study are available from the authors upon request.
Table 2: Number of sources for which photometry is available.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1771f01.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg51.png) |
Figure 1: Photometric errors versus magnitudes and relative exponential fits for all the point-like sources detected in Lupus 3. The ``multiple sequence'' is due to different seeing conditions during the observation of the different fields. |
| Open with DEXTER | |
3 Analysis
The multiband photometry available from the merging of our
observations and the 2MASS Point Source Catalog enables a highly
reliable determination of the spectral energy distributions of a
vast number of objects covering a sizeable fraction of the volume of
the star-forming regions in Lupus 1, 3 and 4. The available
wavelength range from the ![]() to the KS bands samples the peak
emission of cool, low mass objects. We thus expect the flux
in all these bands to be generally dominated by photospheric emission,
although exceptions due to veiling, emission lines or warm circumstellar
dust may exist as discussed in Sect. 4. The long
wavelength baseline makes it possible to disentangle the intrinsic
spectral energy distribution from the reddening effects caused by
dust associated to the host clouds along the line of sight. Finally,
the effects of extinction in those bands are expected to be
relatively small taking into account the moderate extinction levels
present in the observed regions (Cambrésy 1999).
to the KS bands samples the peak
emission of cool, low mass objects. We thus expect the flux
in all these bands to be generally dominated by photospheric emission,
although exceptions due to veiling, emission lines or warm circumstellar
dust may exist as discussed in Sect. 4. The long
wavelength baseline makes it possible to disentangle the intrinsic
spectral energy distribution from the reddening effects caused by
dust associated to the host clouds along the line of sight. Finally,
the effects of extinction in those bands are expected to be
relatively small taking into account the moderate extinction levels
present in the observed regions (Cambrésy 1999).
As noted in Sect. 2.1.3, the depth of our WFI observations
is such that nearly 85% of the sources detected in them are too
faint to appear in the 2MASS catalog. On the other hand, wavelength
coverage restricted to the
![]() bands is too limited to
carry out a reliable simultaneous fit of the spectral energy
distribution and the foreground reddening, thus preventing us from
determining the characteristics of these faint sources in the same
way as we do for those for which photometric data extend to the
near-infrared. We thus preferred to confine this study to the
portion of our source catalog for which at least complete
bands is too limited to
carry out a reliable simultaneous fit of the spectral energy
distribution and the foreground reddening, thus preventing us from
determining the characteristics of these faint sources in the same
way as we do for those for which photometric data extend to the
near-infrared. We thus preferred to confine this study to the
portion of our source catalog for which at least complete
![]() coverage is available, as our results indicate that
a fit in the 0.8-2.2
coverage is available, as our results indicate that
a fit in the 0.8-2.2 ![]() m interval is the minimum required for a
reliable determination of the intrinsic spectral energy distribution.
Whenever available we also use the flux measured at
m interval is the minimum required for a
reliable determination of the intrinsic spectral energy distribution.
Whenever available we also use the flux measured at ![]() to improve
the reliability of the fit. The requirement of having 2MASS
measurements available is likely to leave out of the current analysis
some interesting very low mass members of the Lupus clouds, which we are
not able to reliably identify as such on the basis of the
to improve
the reliability of the fit. The requirement of having 2MASS
measurements available is likely to leave out of the current analysis
some interesting very low mass members of the Lupus clouds, which we are
not able to reliably identify as such on the basis of the
![]() data alone. The identification of the lowest-mass population of the clouds
potentially detected in our WFI survey using the same methodology described in this paper is thus deferred to further work making use of deeper near-infrared photometry.
data alone. The identification of the lowest-mass population of the clouds
potentially detected in our WFI survey using the same methodology described in this paper is thus deferred to further work making use of deeper near-infrared photometry.
Although limited to sources for which photometry between 0.6/0.8 and
2.2 ![]() m is available, the sensitivity of the combined WFI and 2MASS data is sufficient to probe deep into the substellar mass function of the Lupus clouds. At the 2MASS limiting magnitude of
m is available, the sensitivity of the combined WFI and 2MASS data is sufficient to probe deep into the substellar mass function of the Lupus clouds. At the 2MASS limiting magnitude of
![]() ,
assuming as typical parameters for a source in Lupus 3 (probably the most distant of the three clouds) a distance of 200 pc, an age of 5 Myr, and an extinction AV = 5 mag, evolutionary models indicate that our survey should be able to detect brown dwarfs with masses down to 0.02
,
assuming as typical parameters for a source in Lupus 3 (probably the most distant of the three clouds) a distance of 200 pc, an age of 5 Myr, and an extinction AV = 5 mag, evolutionary models indicate that our survey should be able to detect brown dwarfs with masses down to 0.02 ![]() (Baraffe et al. 2003), having temperatures as low as 2400 K corresponding to a spectral type L0-L1 (Kirkpatrick 2005), and even cooler and later objects if their age is younger. On the other hand, for lightly reddened members the saturation limit is first reached in the R band, with the limit of
(Baraffe et al. 2003), having temperatures as low as 2400 K corresponding to a spectral type L0-L1 (Kirkpatrick 2005), and even cooler and later objects if their age is younger. On the other hand, for lightly reddened members the saturation limit is first reached in the R band, with the limit of
![]() given in Table 1 corresponding to an unreddened star of 0.6
given in Table 1 corresponding to an unreddened star of 0.6 ![]() and 5 Myr age at the distance of the nearest cloud, Lupus 1, with a temperature of
and 5 Myr age at the distance of the nearest cloud, Lupus 1, with a temperature of ![]() 3600 K and spectral type M1 (Luhman et al. 2003). While the actual limits vary depending on the actual age, distance, and extinction, the dynamic range of the merged WFI/2MASS photometry thus samples well the very low mass stellar and massive brown dwarf domains and the early-M to early-L spectral type interval.
3600 K and spectral type M1 (Luhman et al. 2003). While the actual limits vary depending on the actual age, distance, and extinction, the dynamic range of the merged WFI/2MASS photometry thus samples well the very low mass stellar and massive brown dwarf domains and the early-M to early-L spectral type interval.
3.1 Temperature and luminosity fits
The procedure that we used to estimate the individual
temperature and luminosity of each object is based on the
simultaneous fit of all the measured broad-band fluxes to model
spectra of cool stellar and substellar photospheres, and is similar
to that used by Spezzi et al. (2007) in their study of the stellar
population in Chamaeleon II. The grid of reference model spectra
used is that of Hauschildt et al. (1999) and Allard et al. (2000), covering the
effective temperature (
![]() )
range 1700 K-10 000 K. A single
value of the surface gravity,
)
range 1700 K-10 000 K. A single
value of the surface gravity,
![]() ,
was chosen as being
representative of very low mass stars and brown dwarfs, since
broad-band colors have only a mild dependency on the actual surface
gravity in this range. Using the flux per unit of stellar surface
provided by the synthetic spectra, absolute magnitudes in each of
the filters used,
,
was chosen as being
representative of very low mass stars and brown dwarfs, since
broad-band colors have only a mild dependency on the actual surface
gravity in this range. Using the flux per unit of stellar surface
provided by the synthetic spectra, absolute magnitudes in each of
the filters used,
![]() ,
are obtained for fiducial
stars of different
,
are obtained for fiducial
stars of different
![]() ,
each with a radius arbitrarily set to
1
,
each with a radius arbitrarily set to
1 ![]() .
The observed magnitude
.
The observed magnitude
![]() at each band
can then be expressed as
at each band
can then be expressed as
where AV is the foreground extinction in the visible,
The ratio
Assuming a certain input value of
![]() for a star, one equation
like Eq. (4) can be set for each photometric band.
These equations form an overdetermined system with the two
unknowns
for a star, one equation
like Eq. (4) can be set for each photometric band.
These equations form an overdetermined system with the two
unknowns ![]() and S, which can be solved by least squares. The
temperature that minimizes the residual of the fit is then taken as
the temperature of the object, and the luminosity L is derived
from the value of S obtained for the best fitting temperature as
and S, which can be solved by least squares. The
temperature that minimizes the residual of the fit is then taken as
the temperature of the object, and the luminosity L is derived
from the value of S obtained for the best fitting temperature as
![]() ,
where
,
where ![]() is the
Stefan-Boltzmann constant. The residuals for this best fit give in
turn an estimate of the quality of the solution. It should be in
principle possible to obtain a more reliable fit by weighting each equation by the inverse of the magnitude uncertainty,
is the
Stefan-Boltzmann constant. The residuals for this best fit give in
turn an estimate of the quality of the solution. It should be in
principle possible to obtain a more reliable fit by weighting each equation by the inverse of the magnitude uncertainty,
![]() .
However, we
preferred not to use such weights, which are composed of the
random measurement error and a possible systematic error caused by
shortcomings in the models. The latter is poorly known, but it is
likely to dominate especially at infrared wavelengths where the
objects are brightest and the magnitude uncertainty is very small.
We carried out numerical experiments comparing the results
obtained for known cloud members with well constrained temperatures,
where we computed their temperatures by solving the system of
Eqs. (4) either without weighting them, or by weighting them with the inverse of the photometric uncertainty alone. In general we find a better match in the non-weighted results, seemingly confirming our suspicion that systematic errors dominate over the photometric ones.
.
However, we
preferred not to use such weights, which are composed of the
random measurement error and a possible systematic error caused by
shortcomings in the models. The latter is poorly known, but it is
likely to dominate especially at infrared wavelengths where the
objects are brightest and the magnitude uncertainty is very small.
We carried out numerical experiments comparing the results
obtained for known cloud members with well constrained temperatures,
where we computed their temperatures by solving the system of
Eqs. (4) either without weighting them, or by weighting them with the inverse of the photometric uncertainty alone. In general we find a better match in the non-weighted results, seemingly confirming our suspicion that systematic errors dominate over the photometric ones.
The best-fitting
![]() derived for each star, and the
corresponding values of
derived for each star, and the
corresponding values of ![]() and S, are expected to be close to their true values regardless of whether or not the object is a member of the star-forming region, since the
colors of young stellar objects, main sequence late dwarfs, and cool
giants of a given temperature are to a first approximation similar.
On the other hand, it is straightforward to transform S into the
luminosity if the object is a member of the star-forming region. For
background and foreground members, the luminosity remains however
undetermined due to their unknown distances.
and S, are expected to be close to their true values regardless of whether or not the object is a member of the star-forming region, since the
colors of young stellar objects, main sequence late dwarfs, and cool
giants of a given temperature are to a first approximation similar.
On the other hand, it is straightforward to transform S into the
luminosity if the object is a member of the star-forming region. For
background and foreground members, the luminosity remains however
undetermined due to their unknown distances.
The suitability of the wavelength range used to sample the spectral energy distribution of the objects of interest is illustrated in Fig. 2, where we show the fit of the photometric data points to the reddened synthetic spectrum of a
![]() K photosphere. The pronounced change of slope of the spectral energy distribution in the region around its peak allows us to reliably disentangle the effect of temperature from that of extinction.
K photosphere. The pronounced change of slope of the spectral energy distribution in the region around its peak allows us to reliably disentangle the effect of temperature from that of extinction.
The residuals of the spectral energy distribution fits are used to estimate their quality. After producing fits for all the sources in our sample, we find that 87% of them yield averages residuals below 0.2 mag, which we consider of good quality in view of the accuracy of our photometry. The percentage actually varies between 86% for Lupus 3 and 4, and 91% for Lupus 1. The reason is mainly the higher galactic latitude of the latter, which leads to a smaller number of close pairs not disentangled by our automatic photometry. Poor fits are also obtained for variable sources due to the non-simultaneity of the photometry, as we discuss in Sect. 4. The extinction is derived to a typical accuracy of
![]() mag, and the luminosity to
mag, and the luminosity to
![]() .
As discussed in Sect. 4, the accuracy in the determination of the temperature is estimated to be
.
As discussed in Sect. 4, the accuracy in the determination of the temperature is estimated to be ![]() 200 K in the range of temperatures of interest,
200 K in the range of temperatures of interest,
![]() K.
K.
It must be stressed that, whereas the method described here can be efficiently used to derive parameters of cool stars in the field, it is not intended to provide by itself a membership criterion. However, under certain circumstances that we describe in Sect. 5 the value of S can be used as a strong indicator of membership within a certain range of distances and ages.
![\begin{figure}
\par\includegraphics[height=8.5cm,angle=-90,clip]{1771f02.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg78.png) |
Figure 2:
Example of the fit of the
|
| Open with DEXTER | |
3.2 Estimating the contamination
The derivation of the best-fitting values of
![]() and S for
each star allows us to plot them in a diagram that is closely linked
to the commonly used L vs.
and S for
each star allows us to plot them in a diagram that is closely linked
to the commonly used L vs.
![]() diagram in the case of members
of the star-forming region. It is also easy to convert theoretical isochrones and evolutionary tracks so that ages and masses of the members can be determined by relation to them. In this diagram, the isochrones delimiting the age range set by the time span in which the aggregate has been forming stars can be expressed as
diagram in the case of members
of the star-forming region. It is also easy to convert theoretical isochrones and evolutionary tracks so that ages and masses of the members can be determined by relation to them. In this diagram, the isochrones delimiting the age range set by the time span in which the aggregate has been forming stars can be expressed as
![]() and
and
![]() ,
where
,
where
![]() and
and
![]() are respectively the ages of the youngest and oldest members of the aggregate. All members of the aggregate are thus expected to be found in the band defined by these isochrones. This is illustrated in Fig. 3, where the position of all the stars for which
are respectively the ages of the youngest and oldest members of the aggregate. All members of the aggregate are thus expected to be found in the band defined by these isochrones. This is illustrated in Fig. 3, where the position of all the stars for which
![]() and S can be determined in the field of Lupus 3 are plotted together with two representative isochrones. For the latter we used the evolutionary tracks of Baraffe et al. (1998) for stellar masses down to 0.075
and S can be determined in the field of Lupus 3 are plotted together with two representative isochrones. For the latter we used the evolutionary tracks of Baraffe et al. (1998) for stellar masses down to 0.075 ![]() ,
and the models allowing dust formation in the photosphere of Chabrier et al. (2000) for substellar masses.
,
and the models allowing dust formation in the photosphere of Chabrier et al. (2000) for substellar masses.
![\begin{figure}
\par\includegraphics[width=6.5cm,angle=-90]{1771f03.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg83.png) |
Figure 3:
S vs.
|
| Open with DEXTER | |
The band occupied by members of the aggregate may be expected to be populated also by foreground and background stars of similar temperature, whose D/R ratios lead to a value of S within the same range. In the cool temperature range of interest in this work, these potential contaminants are split into two well separated categories with similar temperatures but very different luminosities. Foreground sources are expected to be main sequence cool dwarfs, whereas red giants are expected to dominate the background population. This is most clearly seen at the lowest temperatures shown in Fig. 3.
3.2.1 Main sequence contamination
To estimate the number of main sequence contaminants we used the log-normal local initial mass function of Chabrier (2005), assuming that all foreground stars at a given
![]() are on the main sequence and thus have a well-defined
are on the main sequence and thus have a well-defined
![]() vs. mass relationship, which we derive from the 5 Gyr isochrone from Baraffe et al. (1998). The number of stars per logarithmic mass (M) interval that enter the region between S1 and S2 in an area of the sky that subtends an angle
vs. mass relationship, which we derive from the 5 Gyr isochrone from Baraffe et al. (1998). The number of stars per logarithmic mass (M) interval that enter the region between S1 and S2 in an area of the sky that subtends an angle ![]() is then
is then
![\begin{displaymath}\frac{{\rm d}N(M)}{{\rm d} \log M} = \frac{1}{3} \ \xi (\log ...
... R^3(M) 10^3
\bigl[10^{0.6 S_2} - 10^{0.6 S_1} \bigr] \ \Omega
\end{displaymath}](/articles/aa/full_html/2009/24/aa11771-09/img85.png) |
(6) |
where R(M) is the stellar radius in units of
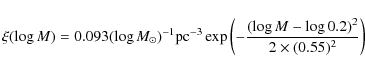 |
(7) |
with the mass given in
Table 3:
Expected numbers of non-members in the Lupus
![]() - S locus.
- S locus.
Some illustrative results are presented in Table 3, where the number of contaminants expected up to a certain temperature in each region is given. The upper part of the table shows that the number of foreground stars with both
![]() and S in the range covered by members of the clouds with ages between 1 and 20 Myr is in general small. The expected foreground contamination in Lupus 3 is somewhat stronger due to the greater distance assumed for this cloud, which moves the isochrones down by 0.6 mag in S. However, this is also the most densely populated cloud according to previous studies, and the contamination is thus lower in relative terms.
and S in the range covered by members of the clouds with ages between 1 and 20 Myr is in general small. The expected foreground contamination in Lupus 3 is somewhat stronger due to the greater distance assumed for this cloud, which moves the isochrones down by 0.6 mag in S. However, this is also the most densely populated cloud according to previous studies, and the contamination is thus lower in relative terms.
3.2.2 Background cool stars
We estimated the expected level of background contamination using the volume density laws for the different galactic structural components described by Wainscoat et al. (1992). Red giant stars dominate the background contribution to the star counts in the direction of Lupus. We adopted for these stars the effective
temperatures and radii from Fluks (1998). As in the case of foreground stars, background cool giants at a given
![]() and radius appear in the region of the
and radius appear in the region of the
![]() ,
S) diagram occupied by cloud members if they lie within a range of distances set by those intrinsic properties, the distance of the clouds, and the limiting isochrones of cloud members. To estimate the background contribution we thus integrated the volume density seen in the direction of each cloud over this distance range.
,
S) diagram occupied by cloud members if they lie within a range of distances set by those intrinsic properties, the distance of the clouds, and the limiting isochrones of cloud members. To estimate the background contribution we thus integrated the volume density seen in the direction of each cloud over this distance range.
The results are also presented in Table 3. The most obvious feature when comparing
the background contamination towards each cloud is the much higher level expected in Lupus 3 and 4, which is a consequence of their lower galactic latitude (
![]() and
and
![]() for Lupus 3 and 4 respectively, as compared to
for Lupus 3 and 4 respectively, as compared to
![]() 5 for Lupus 1). Also noticeable is the great decrease in the number of background stars above the isochrone corresponding to the oldest stars in the clouds when the temperature range is reduced from T < 3500 K to
5 for Lupus 1). Also noticeable is the great decrease in the number of background stars above the isochrone corresponding to the oldest stars in the clouds when the temperature range is reduced from T < 3500 K to
![]() K. This is due to the fact that red
giants in the
K. This is due to the fact that red
giants in the
![]() range (corresponding to early M spectral types) having values of S in the range covered by Lupus cloud members are located in dense regions of the galactic bulge in that direction. Conversely, as we move towards cooler and intrinsically brighter stars above the oldest limiting isochrone, the contributors with S values in the proper range are located in more remote regions of the Galaxy, where they are rarer. Remarkably, for
range (corresponding to early M spectral types) having values of S in the range covered by Lupus cloud members are located in dense regions of the galactic bulge in that direction. Conversely, as we move towards cooler and intrinsically brighter stars above the oldest limiting isochrone, the contributors with S values in the proper range are located in more remote regions of the Galaxy, where they are rarer. Remarkably, for
![]() K almost no background stars are
expected to be found in the locus occupied by Lupus members with ages between 1 and 20 Myr, since nearly all such background stars appear much brighter than Lupus members of the same
K almost no background stars are
expected to be found in the locus occupied by Lupus members with ages between 1 and 20 Myr, since nearly all such background stars appear much brighter than Lupus members of the same
![]() .
This is seen in the results of Oliveira et al. (2009), who spectroscopically confirm that the brightest cool stars in the direction of the Serpens star-forming region are background giants. Our case is more favorable in terms of the numbers of such background giants expected, given the higher galactic latitude of Lupus.
.
This is seen in the results of Oliveira et al. (2009), who spectroscopically confirm that the brightest cool stars in the direction of the Serpens star-forming region are background giants. Our case is more favorable in terms of the numbers of such background giants expected, given the higher galactic latitude of Lupus.
We thus conclude that only foreground cool main sequence stars can contribute noticeably to the contamination of the locus of Lupus cloud members, and they are expected to do so in numbers similar to those given in Table 3. A more detailed analysis is presented in Sect. 5, allowing us to produce lists of reliable candidate members of each region.
It must be noted that a particular complication in the interpretation of the census of Lupus is due to the existence of an additional component to those characterized above. By analyzing the results of the ROSAT All-Sky Survey in the direction of Lupus and other regions of the sky and carrying out follow-up spectroscopy, Krautter et al. (1997) noted the existence of an older, extended population of weak-line T Tauri stars. This population is not particularly concentrated towards the clouds, and an analysis of its large-scale distribution rather links it to the Gould Belt (Wichmann et al. 1997). If the weak-line T Tauri stars in Lupus are at the same distance as the Lupus clouds, as suggested by Wichmann et al. (1997), their older ages should place them below the oldest limiting isochrone, thus making it easy to reject them as possible members. However, studies of the distribution of weak-line T Tauri stars across the Gould Belt by Guillout et al. (1998) rather indicate that these stars span a wide range in distance towards any given direction. Their results further suggest that the Lupus clouds lie near the far end of this distance range in that direction of the sky, with most of the weak-line T Tauri stars being foreground and extending to distances as close as 30 pc from the Sun. Foreground old T Tauri stars unrelated to the Lupus clouds can thus have S values in the range expected for true cloud members, and thus be photometrically indistinguishable from them. The possible influence of the presence of this component on our results will be discussed in Sect. 6.
4 The known members of the Lupus clouds
The many studies carried out over the last decades dealing with the identification and characterization of the stellar and substellar population of the Lupus clouds has provided an abundant census of members. For many of them detailed information on circumstellar environment, intrinsic properties of the central source, or variability is available, thus providing a sound basis to test the validity of the methods outlined in Sect. 3.1.
A compilation of all known members of Lupus 1, 3, and 4, selected by different techniques, has been presented by Merín et al. (2008), who also estimated the spectral type, luminosity, and foreground extinction for most objects based on photometric fits to synthetic spectra, using a procedure similar to ours. The
![]() photometry data that they used are the same as in this paper, complemented with data from the literature for saturated sources.
photometry data that they used are the same as in this paper, complemented with data from the literature for saturated sources.
The derived parameters for the known members of each cloud that
are detected and unsaturated in at least ![]() and
and
![]() are presented in Table 4. It may be noted that Table 4
does not represent a validation of membership based on our new data, but only a derivation of parameters of objects already known to be members from their youth signatures, based on the method described in Sect. 3. For most of the objects we obtain low temperatures, and luminosities and ages consistent with
their membership in the Lupus clouds. The vast majority of objects in
Merín et al. (2008) are detected in our WFI observations, with some exceptions that we list in Table 5. As expected, the comparison shows that our visible/red survey is particularly incomplete near the high extinction regions of the clouds, most notably Lupus 3, where members are too deeply embedded to be detectable at short wavelengths. Other objects are close to bright sources or their associated nebulosity, outside the field surveyed with WFI or, in a few cases, misclassified as a stellar object whereas the WFI images show it to be a resolved galaxy.
are presented in Table 4. It may be noted that Table 4
does not represent a validation of membership based on our new data, but only a derivation of parameters of objects already known to be members from their youth signatures, based on the method described in Sect. 3. For most of the objects we obtain low temperatures, and luminosities and ages consistent with
their membership in the Lupus clouds. The vast majority of objects in
Merín et al. (2008) are detected in our WFI observations, with some exceptions that we list in Table 5. As expected, the comparison shows that our visible/red survey is particularly incomplete near the high extinction regions of the clouds, most notably Lupus 3, where members are too deeply embedded to be detectable at short wavelengths. Other objects are close to bright sources or their associated nebulosity, outside the field surveyed with WFI or, in a few cases, misclassified as a stellar object whereas the WFI images show it to be a resolved galaxy.
Table 5: Objects classified as candidate Lupus members by Merín et al. (2008) for which no fits are obtained.
The availability of spectral classifications for many of the objects
listed in Table 4 provides a check on our derived
temperatures. The result of the comparison is presented in
Fig. 4, where we also plot the spectral type vs.
effective temperature relationships derived by Luhman et al. (2003) for
M-type young stellar objects, and by Kenyon & Hartmann (1995) for main sequence
stars of types K and M. The relative abundance of spectral
types later than M0 in the diagram is due to earlier types being
generally saturated in our observations, and is not related to the
overabundance of mid-M types reported by Hughes et al. (1994). We excluded
from the comparison the objects in Table 4 showing evidence of
variability as indicated in the notes at the end of the table. Since our
observations in ![]() and
and ![]() were obtained at epochs generally
different from those in
were obtained at epochs generally
different from those in
![]() ,
and were combined with 2MASS
JHKS photometry obtained on a yet different epoch, the fit to the
spectral energy distribution for variable sources is not meaningful. This
is the most likely cause of the relative large fraction of poor fits with a high residual that we obtain among the known members of the clouds.
,
and were combined with 2MASS
JHKS photometry obtained on a yet different epoch, the fit to the
spectral energy distribution for variable sources is not meaningful. This
is the most likely cause of the relative large fraction of poor fits with a high residual that we obtain among the known members of the clouds.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{1771f04.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg95.png) |
Figure 4:
Comparison between the temperatures obtained with our
fitting procedure and the published spectral types of known members
of the Lupus clouds (Table 4). Stars known to display
photometric variability are excluded from the plot. The outlier near
the upper right corner is Lup 654. For SSTc2d160815.0-385715, which is
characterized by a noticeable near-infrared excess, we used
|
| Open with DEXTER | |
The appearance of Fig. 4 shows a distinct
distribution with most of the objects used for the comparison
clustering along the expected spectral type-temperature
relationship, whereas some objects appear as clear outliers for
which we estimate temperatures well above those expected from their
spectral types. Part of the temperature scatter at any given
spectral type is undoubtedly due to the limited accuracy with which
the temperature can be determined by our fits. However, the
different techniques and wavelength ranges used to determine
spectral types in different studies are likely
to play a role as well. We note in this regard that most of the
later stars for which the spectral type is taken from Hughes et al. (1994) lie
below the spectral type vs.
![]() calibration. As shown
by Comerón et al. (2003), the spectral types in that study tend to
systematically differ by about 2 subtypes from those determined by
Hughes et al. (1994), in the sense of the Comerón et al. (2003) types being later.
The latter authors tentatively attribute the difference to their use
of a redder spectral region, less affected by veiling and more
suitable for classification based on the shapes of the TiO and VO molecular bands. The application of a correction by two spectral
subtypes to the classifications of Hughes et al. (1994) indeed improves their
agreement with the calibration beyond M3. On the other hand, we include
in Table 4 the classification of López Martí et al. (2005) that
is based on intermediate-band photometry of a single selected
temperature-dependent spectral feature, being therefore less
accurate than an actual spectral classification. The comparison to
the calibrations suggests that the spectral types assigned by
López Martí et al. (2005) tend to be only slightly earlier than corresponding to the actual
temperature. Spectra obtained from the other sources listed at the
bottom of Table 4 are in general in better
agreement with the calibration.
calibration. As shown
by Comerón et al. (2003), the spectral types in that study tend to
systematically differ by about 2 subtypes from those determined by
Hughes et al. (1994), in the sense of the Comerón et al. (2003) types being later.
The latter authors tentatively attribute the difference to their use
of a redder spectral region, less affected by veiling and more
suitable for classification based on the shapes of the TiO and VO molecular bands. The application of a correction by two spectral
subtypes to the classifications of Hughes et al. (1994) indeed improves their
agreement with the calibration beyond M3. On the other hand, we include
in Table 4 the classification of López Martí et al. (2005) that
is based on intermediate-band photometry of a single selected
temperature-dependent spectral feature, being therefore less
accurate than an actual spectral classification. The comparison to
the calibrations suggests that the spectral types assigned by
López Martí et al. (2005) tend to be only slightly earlier than corresponding to the actual
temperature. Spectra obtained from the other sources listed at the
bottom of Table 4 are in general in better
agreement with the calibration.
Table 6:
Fits to
![]() photometry of stars with suspected veiling.
photometry of stars with suspected veiling.
Table 7:
Fits to
![]() photometry of stars with suspected infrared excess.
photometry of stars with suspected infrared excess.
The outliers in Fig. 4 are Lup 654, classified by
López Martí et al. (2005) as L1 but for which we fit a temperature of
![]() K;
and, to a lesser extent, the M 5 star SSTc2dJ160853.7-391437, for which we obtain
K;
and, to a lesser extent, the M 5 star SSTc2dJ160853.7-391437, for which we obtain
![]() K. No variability information exists for either of these
objects, which leaves variability as a possible reason for a temperature
overestimate as discussed later in this Section. The rather high values of extinction needed to fit the spectral energy distribution of both object, particularly
SSTc2dJ160853.7-391437, hint at an overestimate of the temperature by our method.
For this latter object, Allen et al. (2007) note the presence of emission lines, which
may hint at veiling or the contribution of the H
K. No variability information exists for either of these
objects, which leaves variability as a possible reason for a temperature
overestimate as discussed later in this Section. The rather high values of extinction needed to fit the spectral energy distribution of both object, particularly
SSTc2dJ160853.7-391437, hint at an overestimate of the temperature by our method.
For this latter object, Allen et al. (2007) note the presence of emission lines, which
may hint at veiling or the contribution of the H![]() emission to the
emission to the ![]() -band
flux as another possible cause for an incorrect fit. Finally, a
rather large departure from the spectral type vs. temperature calibration is noted for
SSTc2d160815.0-385715, an object for which Allen et al. (2007) note a strong
near-infrared excess which is supported by our fits when the KS measurement
is excluded. The still significant deviation from the expected temperature for
its M4.75 spectral type may indicate that other effects may be still present.
Still, a low-residual fit (<0.2 mag rms) can be attained for these three objects.
-band
flux as another possible cause for an incorrect fit. Finally, a
rather large departure from the spectral type vs. temperature calibration is noted for
SSTc2d160815.0-385715, an object for which Allen et al. (2007) note a strong
near-infrared excess which is supported by our fits when the KS measurement
is excluded. The still significant deviation from the expected temperature for
its M4.75 spectral type may indicate that other effects may be still present.
Still, a low-residual fit (<0.2 mag rms) can be attained for these three objects.
Among the objects classified as members in Table 4, we find some whose fitted luminosities appear to be inconsistent with membership in Lupus, apparently placing them near or below the main sequence. Most are located in Lupus 3, most likely just because of a size-of-the-sample effect since that cloud contains by far the richest aggregate. Out of the 86 Lupus 3 members for which we obtain a fit, nearly one third (26) are in this category. In at least two cases, Sz 102 and Par-Lup3-4, their underluminosity is well known. It may be explained by the fact that these objects are surrounded by abundant circumstellar material and display jets moving in a direction that is close to the plane of the sky, suggesting substantial obscuration of the central object by a disk seen close to an edge-on orientation (Graham & Heyer 1988; Fernández & Comerón 2005).
Another possible explanation is that the spectral energy distributions of some other objects may be
affected by the signatures of accretion and warm circumstellar dust in the visible (veiling and strong emission lines) and near-infrared (infrared excess), leading to an erroneous estimate of the temperature. In both situations, our fits tend to overestimate both the temperature and the extinction. We thus produced fits to all the objects in Table 4 excluding the data points in the ![]() and KS bands, respectively. Significantly cooler temperatures are estimated for 7 objects when the
and KS bands, respectively. Significantly cooler temperatures are estimated for 7 objects when the ![]() band is excluded from the fit, as listed in Table 6. The peculiar objects Sz 102 and Par-Lup-4 are among them. Furthermore, the new parameters derived for four of the objects place them above the main sequence. The most remarkable one is Lup 706 (SSTc2dJ160837.3-392311), which is best fitted as a very young brown dwarf (age <1 Myr) with
band is excluded from the fit, as listed in Table 6. The peculiar objects Sz 102 and Par-Lup-4 are among them. Furthermore, the new parameters derived for four of the objects place them above the main sequence. The most remarkable one is Lup 706 (SSTc2dJ160837.3-392311), which is best fitted as a very young brown dwarf (age <1 Myr) with
![]() K when the
K when the ![]() measurement is excluded, in excellent agreement with the independent spectral type estimate of López Martí et al. (2005). Similarly, a good fit is now obtained for SSTc2dJ160927.0-383628, whose derived age (2.8 Myr) places it now in the same range as most of the Lupus 3 population. Two other objects, SSTc2dJ160754.7-391545 and SSTc2dJ160708.6-391407, now appear above the main sequence, but still with ages much older than those expected for Lupus 3 members. The low luminosities still obtained by the best fit to the photometry of these objects, and to the remaining four objects in Table 6 for which no age could be estimated, perhaps indicates that some degree of veiling still subsists at
measurement is excluded, in excellent agreement with the independent spectral type estimate of López Martí et al. (2005). Similarly, a good fit is now obtained for SSTc2dJ160927.0-383628, whose derived age (2.8 Myr) places it now in the same range as most of the Lupus 3 population. Two other objects, SSTc2dJ160754.7-391545 and SSTc2dJ160708.6-391407, now appear above the main sequence, but still with ages much older than those expected for Lupus 3 members. The low luminosities still obtained by the best fit to the photometry of these objects, and to the remaining four objects in Table 6 for which no age could be estimated, perhaps indicates that some degree of veiling still subsists at ![]() ,
or that other causes such as variability between the different epochs in which the photometry was obtained produce a fit with an incorrect temperature. This is supported by the fact that only a poor quality fit can be obtained for 28% of the members that apparently lie below the main sequence.
,
or that other causes such as variability between the different epochs in which the photometry was obtained produce a fit with an incorrect temperature. This is supported by the fact that only a poor quality fit can be obtained for 28% of the members that apparently lie below the main sequence.
Similar results are obtained when the KS measurement is excluded from our fit to minimize the effect
of circumstellar emission in that band. However, the numbers of objects for which the best-fitting temperature substantially changes when excluding the KS measurement is much smaller than those affected by the exclusion of ![]() .
The effect of the KS band exclusion on the derived temperature is typically a change by less than 200 K, even among those objects known or suspected to possess important infrared excesses. For the known members, among which such excesses are expected to be most frequent, best-fitting temperatures obtained in this way are significantly different from those obtained by including the KS measurement in only four cases (including SSTc2d160815.0-385715 as noted above), all of which yield a cooler temperature when the KS measurement is discarded (Table 7). The new positions in the temperature-luminosity diagram rises two of them above the main sequence, but still well below the age strip occupied by most members of Lupus 3.
.
The effect of the KS band exclusion on the derived temperature is typically a change by less than 200 K, even among those objects known or suspected to possess important infrared excesses. For the known members, among which such excesses are expected to be most frequent, best-fitting temperatures obtained in this way are significantly different from those obtained by including the KS measurement in only four cases (including SSTc2d160815.0-385715 as noted above), all of which yield a cooler temperature when the KS measurement is discarded (Table 7). The new positions in the temperature-luminosity diagram rises two of them above the main sequence, but still well below the age strip occupied by most members of Lupus 3.
As a summary of our comparison, both with members of known spectral types and with suspected members still lacking spectral classification, we conclude that our method produces good fits to the spectral energy distribution and reliable estimates of the temperature, luminosity, and foreground extinction towards most of the objects under consideration. A number of discrepancies are found however, either through an estimated temperature significantly different from that expected from the observed spectral type, or through a derived luminosity placing the object near or below the main sequence at the distance of its star-forming region. In a number of cases, the source of the discrepancy can be traced back to variability, suspected veiling or strong emission lines at short wavelengths, or known peculiarities such as an apparent strong underluminosity of the object. It must be noted that, whereas veiling, strong emission lines, and infrared excess as causes of discrepant fits can be suspected by discarding measurements at the shortest and longest wavelengths respectively, variability can be confirmed for only a few objects due to the general unavailability of multi-epoch measurements at either visible or infrared wavelengths. Variability thus remains as just a tentative explanation for the inconsistent fits to the spectral energy distributions of most of the objects.
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{1771f05.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg100.png) |
Figure 5: Histograms of S values obtained at different temperature ranges in each of the observed regions. The thick histogram bars denote the contribution by known members of the star-forming region. The dashed lines indicate the expected contamination by field main sequence stars, and the dotted lines the contamination by background giants. Incompleteness due to the limiting magnitudes affects the bins with highest values of S, whereas saturation depopulates the low S bins at the right. The presence of a significant population of objects in Lupus 1 and 3 is obvious as a local peak in the valley left between the S regions dominated respectively by field main sequence and background giant contamination. It is also noticeable that only a relatively minor fraction of the objects contributed to this peak is composed of previously known members. |
| Open with DEXTER | |
5 Evidence for new members
The distributions in the S vs.
![]() diagram predicted for field low-mass main sequence stars and background cool giants, based on the estimates presented in Sect. 3.2, open up a very useful window for the detection of cool populations associated to the Lupus clouds and, in general, for all the low-mass star-forming regions located in the
diagram predicted for field low-mass main sequence stars and background cool giants, based on the estimates presented in Sect. 3.2, open up a very useful window for the detection of cool populations associated to the Lupus clouds and, in general, for all the low-mass star-forming regions located in the ![]() 100-300 pc distance range from the Sun. This window can be qualitatively understood in the following way: at a given temperature, the number n(S) of field main sequence stars per unit area decreases with decreasing S as
100-300 pc distance range from the Sun. This window can be qualitatively understood in the following way: at a given temperature, the number n(S) of field main sequence stars per unit area decreases with decreasing S as
![]() ,
as can be easily derived from the assumption of a constant volume density of stars and from the definition of S. At the distance of Lupus, this results in an almost negligible value of n(S) for temperatures below
,
as can be easily derived from the assumption of a constant volume density of stars and from the definition of S. At the distance of Lupus, this results in an almost negligible value of n(S) for temperatures below ![]() 3500 K for the typical values of S expected among members of the clouds, as shown in Table 3. On the other hand, cool giants in that same range of temperatures have low values of S due to their large radii, unless they are extremely distant and thus located in regions of the Galaxy where the stellar density is exceedingly small. This yields a surface density of cool giants that is significant only for values of S generally lower than those accessible to the pre-main sequence members of the star-forming regions. As a result for
3500 K for the typical values of S expected among members of the clouds, as shown in Table 3. On the other hand, cool giants in that same range of temperatures have low values of S due to their large radii, unless they are extremely distant and thus located in regions of the Galaxy where the stellar density is exceedingly small. This yields a surface density of cool giants that is significant only for values of S generally lower than those accessible to the pre-main sequence members of the star-forming regions. As a result for
![]() below
below ![]() 3500 K, the members of the Lupus clouds, and of other star-forming regions located at a comparable distance, are largely located within a range of values of S that is not populated either by field cool dwarfs or by background cool giants. The location of this range, which depends on the distance, would move into the background-dominated part for aggregates closer than
3500 K, the members of the Lupus clouds, and of other star-forming regions located at a comparable distance, are largely located within a range of values of S that is not populated either by field cool dwarfs or by background cool giants. The location of this range, which depends on the distance, would move into the background-dominated part for aggregates closer than ![]() 100 pc, and is masked by the field stars for regions more distant than
100 pc, and is masked by the field stars for regions more distant than ![]() 300 pc.
300 pc.
To reveal this effect in our surveyed region, Fig. 5 shows the histogram of values of S for four different ranges of temperature for each of the three surveyed clouds. The expected contribution to the source number counts by field dwarfs and giants in the same temperature range is given as well. Such contribution varies as a function of the area covered in each cloud and its position on the sky, mainly through its proximity to the galactic plane, which determines the level of background contamination.
At large values of S (to the left in the plots) the field dwarf population dominates, with numbers
being in rough agreement with the expectations yielded by the local initial mass function. The latter has been modeled using the log-normal forms given by Chabrier (2003,2005), whose differences, according to Chabrier (2005), largely reflect the uncertainties in the present determinations. We find that Chabrier (2003) provides a closer match to the high-S part of our histograms. The agreement is particularly good in the
![]() range and to some extent also below
range and to some extent also below ![]() 2800 K, where the number of stars that we observe is close to the model predictions for all three clouds. The discrepancies are larger for the
2800 K, where the number of stars that we observe is close to the model predictions for all three clouds. The discrepancies are larger for the
![]() interval, where our number counts fall significantly below the predicted ones, and for the
interval, where our number counts fall significantly below the predicted ones, and for the
![]() interval, where the opposite is seen. Possible causes for this discrepancy are deviations between the actual initial mass function and its adopted form, inaccuracies in the adopted mass-temperature relationship for field dwarfs (for which we adopted the 5 Gyr isochrone of Baraffe et al. 1998), or systematic effects in the temperature derived for evolved field objects of higher surface gravity when using the
interval, where the opposite is seen. Possible causes for this discrepancy are deviations between the actual initial mass function and its adopted form, inaccuracies in the adopted mass-temperature relationship for field dwarfs (for which we adopted the 5 Gyr isochrone of Baraffe et al. 1998), or systematic effects in the temperature derived for evolved field objects of higher surface gravity when using the
![]() synthetic spectra that are more appropriate for the young population of the Lupus clouds. An additional cause for the lower-than-expected number of field stars observed in the
synthetic spectra that are more appropriate for the young population of the Lupus clouds. An additional cause for the lower-than-expected number of field stars observed in the
![]() interval comes from the fact that the highest values of S covered by our histograms correspond to main sequence stars located beyond the Lupus clouds, and thus subjected to obscuration by them. Although such effect is no doubt present in our data, the relatively small fraction of the field observed toward each cloud that is covered by highly obscuring dust leads us to conclude that this cause alone cannot explain the observed discrepancy.
interval comes from the fact that the highest values of S covered by our histograms correspond to main sequence stars located beyond the Lupus clouds, and thus subjected to obscuration by them. Although such effect is no doubt present in our data, the relatively small fraction of the field observed toward each cloud that is covered by highly obscuring dust leads us to conclude that this cause alone cannot explain the observed discrepancy.
It is more difficult to compare our results with the contamination expected from background cool giants since such contamination, which becomes important at the lowest values of S, corresponds mostly to stars that are saturated in our images, unless they are sufficiently obscured by dust for their magnitudes to fall below our saturation limits. The fact that our number counts of unsaturated stars fall in all cases below the predicted number of background cool stars is consistent with this. The effect of galactic latitude on the expected contamination by cool giants is rather dramatic, as discussed in Sect. 3.2. Very few cool giants are expected in the direction of Lupus 1 as compared to Lupus 3 and even more with Lupus 4.
The plots in Fig. 5 show the evidence of substantial young populations in Lupus 1 and
especially in Lupus 3, and only a trace of such a population in Lupus 4. Such populations appear as an excess in the histograms of detected objects with respect to the sum of the contamination due to field dwarfs and background giants within a range of values of S. Our histograms also indicate as a function of S the number of previously known members of the clouds within the considered temperature interval. In this way it is also clearly seen that both Lupus 1 and Lupus 3 contain significant amounts of thus far unrecognized cool members. It should be noted that the known members contributing to the histograms plotted in Fig. 5 are only those that we detect in at least ![]() and
and
![]() and for which we therefore derive S and
and for which we therefore derive S and
![]() in exactly the same way as we do for all other stars in our images. Therefore, such contribution to the histograms does not include known embedded members that are too obscured to be detected in those bands or, at the brighter end, members within the relevant range of temperatures that are saturated in either of those bands.
in exactly the same way as we do for all other stars in our images. Therefore, such contribution to the histograms does not include known embedded members that are too obscured to be detected in those bands or, at the brighter end, members within the relevant range of temperatures that are saturated in either of those bands.
Although the approach to recognize the existence of the populations associated with the clouds is in principle statistical, the fact that such populations occur in regions of the S histogram devoid of contamination allows us to produce lists of individual new candidate members whose intrinsic parameters are derived with the procedure outlined in Sect. 3.1. We note that the new members that we report here are unlikely to possess significant excess emission in the 0.6 ![]() m-2.2
m-2.2 ![]() m range or veiling at short wavelengths, since the warm disks and accretion that produce them would most likely have been detected in previous studies. This increases our confidence in the derivation of their properties, as their spectral energy distributions are expected to be free from some of the causes that distort the fits to the objects listed in Table 4. Indeed, good quality fits (residual <0.2 mag rms) are obtained for virtually all the new candidate members.
m range or veiling at short wavelengths, since the warm disks and accretion that produce them would most likely have been detected in previous studies. This increases our confidence in the derivation of their properties, as their spectral energy distributions are expected to be free from some of the causes that distort the fits to the objects listed in Table 4. Indeed, good quality fits (residual <0.2 mag rms) are obtained for virtually all the new candidate members.
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f06.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg107.png) |
Figure 6:
Diagram showing the positions of both known and new candidate members of Lupus 1 based on their presence in regions of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=12cm,clip]{1771f07.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg108.png) |
Figure 7:
Distribution of previously known (filled triangles) and newly identified (open squares) members of Lupus 1, plotted on a R-band mosaic of the region constructed from our WFI observations. Note that in order to produce a homogeneous comparison between the distributions of known and new members, only the known members lying within the limits of S defining the contamination-free region of the
|
| Open with DEXTER | |
5.1 Lupus 1
The histogram of cool stars with
![]() of Lupus 1 peaks at 5 < S < 6, just where contamination by field dwarfs and giants is expected to reach a minimum, thus clearly revealing the signature of the population associated with the cloud. None of the stars contributing to this bin has been previously recognized as a member of Lupus 1. In this range of temperatures such values of S correspond to members of the cloud population with typical ages between 2 and more than 10 Myr, the actual limits depending on the precise temperature. Younger objects with S < 5 are generally above our saturation limit, which may explain why the peak moves to 4 < S < 5 in the next temperature interval,
of Lupus 1 peaks at 5 < S < 6, just where contamination by field dwarfs and giants is expected to reach a minimum, thus clearly revealing the signature of the population associated with the cloud. None of the stars contributing to this bin has been previously recognized as a member of Lupus 1. In this range of temperatures such values of S correspond to members of the cloud population with typical ages between 2 and more than 10 Myr, the actual limits depending on the precise temperature. Younger objects with S < 5 are generally above our saturation limit, which may explain why the peak moves to 4 < S < 5 in the next temperature interval,
![]() .
The presence of the cool Lupus 1 members with S > 6 and
.
The presence of the cool Lupus 1 members with S > 6 and
![]() K is difficult to ascertain from our observations, since foreground contamination dominates in this range.
K is difficult to ascertain from our observations, since foreground contamination dominates in this range.
Virtually no contamination by non-members is expected for S < 8 below
![]() K. However, we find 15 objects in this range, only three of which were previously known and listed in
Table 4. We also consider all the stars with S < 6 in the
K. However, we find 15 objects in this range, only three of which were previously known and listed in
Table 4. We also consider all the stars with S < 6 in the
![]() range, and the stars with 5 < S < 6 in the
range, and the stars with 5 < S < 6 in the
![]() range, as candidate new members, although these latter are likely to include a few field stars. None of these 53 additional stars had been previously identified as a possible member. We thus propose a census of 65 new members of Lupus 1 with T < 3700 K, which we list in Table 9. The actual census of previously unidentified members most probably extends beyond the S ranges that we chose here on the basis of the weak contamination.
range, as candidate new members, although these latter are likely to include a few field stars. None of these 53 additional stars had been previously identified as a possible member. We thus propose a census of 65 new members of Lupus 1 with T < 3700 K, which we list in Table 9. The actual census of previously unidentified members most probably extends beyond the S ranges that we chose here on the basis of the weak contamination.
The location of these new members in the
![]() -S diagram is plotted in
Fig. 6, together with the isochrones, evolutionary tracks, and the limiting values of S described above for each temperature range. The narrow limits of S chosen for
-S diagram is plotted in
Fig. 6, together with the isochrones, evolutionary tracks, and the limiting values of S described above for each temperature range. The narrow limits of S chosen for
![]() K imply that we sample a narrow range of ages at such temperatures, probably leaving aside the youngest members as they lie in an area where contamination by background stars becomes substantial. Evidence for such a younger population, with ages below 2 Myr, appears at lower temperatures where no lower limit in S is needed due to the expected absence of background contamination. In addition, the recently identified member SSTc2dJ153803.1-331358 (Merín et al. 2008), with
K imply that we sample a narrow range of ages at such temperatures, probably leaving aside the youngest members as they lie in an area where contamination by background stars becomes substantial. Evidence for such a younger population, with ages below 2 Myr, appears at lower temperatures where no lower limit in S is needed due to the expected absence of background contamination. In addition, the recently identified member SSTc2dJ153803.1-331358 (Merín et al. 2008), with
![]() K, also appears in the zone corresponding to ages below 1 Myr.
K, also appears in the zone corresponding to ages below 1 Myr.
Only one of our proposed new members, J154433.9-335254, displays signatures of warm circumstellar dust detectable by Spitzer, which appears as a moderate excess at 24 ![]() m and perhaps a slight excess at 8
m and perhaps a slight excess at 8 ![]() m indicating the absence of dust warmer than a few hundred K. Although most of the other new Lupus 1 members have been detected by Spitzer, all of them have mid-infrared spectral energy distributions typical of pure photospheres.
m indicating the absence of dust warmer than a few hundred K. Although most of the other new Lupus 1 members have been detected by Spitzer, all of them have mid-infrared spectral energy distributions typical of pure photospheres.
The S < 8 limit imposed to avoid contamination by field stars prevent us from identifying cool stars (
![]() K) with ages above 5-10 Myr. However, the younger end of this range is accessible at temperatures above 3400 K as noted before. The abundance of new members found in this range leads us to suspect that star formation in Lupus 1 started well over 10 Myr ago, although the identification at present of the oldest members is problematic since most of them may not be accreting significantly or have detectable disk emission anymore.
K) with ages above 5-10 Myr. However, the younger end of this range is accessible at temperatures above 3400 K as noted before. The abundance of new members found in this range leads us to suspect that star formation in Lupus 1 started well over 10 Myr ago, although the identification at present of the oldest members is problematic since most of them may not be accreting significantly or have detectable disk emission anymore.
The distribution on the sky of the new members that we identify is plotted in
Fig. 7. Together with the new members we also plotted the position of those known members that are selected using the same criteria. The known members plotted in those figures are therefore not the complete list, since it excludes both objects for which we cannot produce a fit (such as those too deeply embedded to be detected in the visible or those saturating in either ![]() or
or
![]() )
and objects falling outside the ranges of S used to select samples uncontaminated by field and background stars. We preferred to proceed in this way so that an unbiased comparison can be established between the distributions of known and new members. The same procedure has been followed in the plots of the distribution of members of Lupus 3 and 4, discussed in the next Sections. The number of members thus excluded from the plots is 10 in Lupus 1, 72 in Lupus 3, and 10 in Lupus 4.
)
and objects falling outside the ranges of S used to select samples uncontaminated by field and background stars. We preferred to proceed in this way so that an unbiased comparison can be established between the distributions of known and new members. The same procedure has been followed in the plots of the distribution of members of Lupus 3 and 4, discussed in the next Sections. The number of members thus excluded from the plots is 10 in Lupus 1, 72 in Lupus 3, and 10 in Lupus 4.
The few previously known members of the Lupus 1 clouds (including those not plotted in Fig. 7) tend to concentrate toward the two main masses of dark nebulosity covered by our observations, TGU H2079 (Dobashi et al. 2005), the elongated cloud running from SE to NW) and TGU H2072 (the more round cloud on the SW region of the field). In contrast, the new members show a concentrated distribution roughly centered in the area between both dark clouds, with no particular association with either of them.
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f08.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg113.png) |
Figure 8:
Same as Fig. 6 for Lupus 3. Note the different limits in the temperature axis, since stars with temperatures above
|
| Open with DEXTER | |
5.2 Lupus 3
Qualitatively, the histograms of S values in Lupus 3 are similar to those obtained for Lupus 1. However, the lower galactic latitude of Lupus 3 leads to a dramatic increase in the surface density of background cool giants expected to appear in our surveyed field. Thus, although the histogram of S values for the range
![]() clearly shows an excess of sources associated with the Lupus 3 young stellar population and a peak at the same position as in Lupus 1, all the bins in that temperature range are expected to contain significant contamination by either foreground or background sources. We thus preferred to leave the
clearly shows an excess of sources associated with the Lupus 3 young stellar population and a peak at the same position as in Lupus 1, all the bins in that temperature range are expected to contain significant contamination by either foreground or background sources. We thus preferred to leave the
![]() range outside our discussion of Lupus 3, since the likelihood for any star in it to be a non-member is high. Restricting ourselves to the 5 < S < 7 range where the excess of sources over the contamination prediction stands out, we estimate the existence of roughly 60 thus far unidentified members of the Lupus 3 aggregate.
range outside our discussion of Lupus 3, since the likelihood for any star in it to be a non-member is high. Restricting ourselves to the 5 < S < 7 range where the excess of sources over the contamination prediction stands out, we estimate the existence of roughly 60 thus far unidentified members of the Lupus 3 aggregate.
The signature of the Lupus 3 population is much clearer at lower temperatures. The excess of sources over the predicted numbers of field dwarfs and giants in the 4 < S < 7 range for
![]() is more than 40, out of which only 6 are known. The signature is also clear for 3 < S < 8 at
is more than 40, out of which only 6 are known. The signature is also clear for 3 < S < 8 at
![]() ,
where we find 58 objects, 31 of them previously unrecognized. The 72 new candidate members that we find with
,
where we find 58 objects, 31 of them previously unrecognized. The 72 new candidate members that we find with
![]() K within these boundaries are listed in Table 9; we estimate the number of contaminants in this range to be no more than 10. Although the number of new candidates that we identify in Lupus 3 is similar to that in Lupus 1, we note that most of the candidates in the latter cloud have
K within these boundaries are listed in Table 9; we estimate the number of contaminants in this range to be no more than 10. Although the number of new candidates that we identify in Lupus 3 is similar to that in Lupus 1, we note that most of the candidates in the latter cloud have
![]() K, which we exclude from our Lupus 3 census.
K, which we exclude from our Lupus 3 census.
Unlike in the case of Lupus 1 discussed above, we need now to use a lower limit to the values of S for candidate members due to the significant expectation of background contamination. We note in this respect that the two coolest stars in our list of candidate members, J160523.5-391849 (S = 3.1) and J161353.9-380850 (S = 3.5), although formally within the boundaries of our member selection criterion, are close to the values of
![]() where background contamination becomes significant. We therefore consider them as likely background stars, and we note it accordingly in Table 9. Another object with even lower S, outside our boundary, is SSTc2dJ161001.1-385401, which Merín et al. (2008) classify as a heavily obscured early-type member of Lupus 3. The fit that we obtain with a low temperature leads us to consider it instead as another likely cool giant as noted in Table 4, or perhaps a AGB star, which may explain its mid-infrared excess.
where background contamination becomes significant. We therefore consider them as likely background stars, and we note it accordingly in Table 9. Another object with even lower S, outside our boundary, is SSTc2dJ161001.1-385401, which Merín et al. (2008) classify as a heavily obscured early-type member of Lupus 3. The fit that we obtain with a low temperature leads us to consider it instead as another likely cool giant as noted in Table 4, or perhaps a AGB star, which may explain its mid-infrared excess.
![\begin{figure}
\par\includegraphics[angle=0,width=12cm,clip]{1771f09.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg116.png) |
Figure 9:
Same as Fig. 7 for Lupus 3. The field is in this case
|
| Open with DEXTER | |
An intriguing difference between the populations identified in Lupus 1 and 3 is the considerably larger fraction of members that are already known from previous studies, which is readily apparent from Fig. 5. At first sight the difference might be attributed to the greater attention that Lupus 3 has traditionally received, with more studies aimed at revealing new members. However, the comprehensive surveys carried out with Spitzer dealt with both regions in the same manner, with very similar sensitivity levels and using identical criteria for the detection of young stellar object candidates, yet they detected many more in Lupus 3 than in Lupus 1; see Table 4 of Merín et al. (2008). It thus seems very unlikely that the difference is largely due to the more detailed study received by Lupus 3 in the past. Instead, the fraction of Lupus 3 members displaying characteristic mid-infrared excess is truly higher than in Lupus 1.
A small group of 7 new Lupus 3 members display mid-infrared excess as well. Based on the position in the
[3.6]-[4.5],
[5.8]-[8.0] diagram we identify three objects with excesses characteristics of young stellar objects. The source J160836.2-392302 displays clear excess emission starting at 4.5 ![]() m, and is also detected at the MIPS 70
m, and is also detected at the MIPS 70 ![]() m band. According to the classification criteria defined by the extensive disk simulation grid of Robitaille et al. (2006) it belongs to Stage I, corresponding to an object surrounded by an infalling envelope and possibly a disk. The other two excess sources in this diagram are J160800.2-390259 and J160822.8-390058, lying in the area Stage II corresponding to objects surrounded by optically thick disks. The use of similar criteria in the
[3.6]-[5.8],
[8.0]-[24] diagram now places J160836.2-392302 in the Stage II area and confirms the classification of J160800.2-390259 within this same stage. The use of those two colors also shows the infrared excess displayed by two additional sources, J160804.8-390449 and J160831.6-384729, which shows clearly only at 24
m band. According to the classification criteria defined by the extensive disk simulation grid of Robitaille et al. (2006) it belongs to Stage I, corresponding to an object surrounded by an infalling envelope and possibly a disk. The other two excess sources in this diagram are J160800.2-390259 and J160822.8-390058, lying in the area Stage II corresponding to objects surrounded by optically thick disks. The use of similar criteria in the
[3.6]-[5.8],
[8.0]-[24] diagram now places J160836.2-392302 in the Stage II area and confirms the classification of J160800.2-390259 within this same stage. The use of those two colors also shows the infrared excess displayed by two additional sources, J160804.8-390449 and J160831.6-384729, which shows clearly only at 24 ![]() m. Both sources are near the dividing line between Stages II and III, marking the transition from thick to thin disks. Also J160822.8-390058, previously classified as Stage II and whose mid-infrared excess appears longwards of 5.8
m. Both sources are near the dividing line between Stages II and III, marking the transition from thick to thin disks. Also J160822.8-390058, previously classified as Stage II and whose mid-infrared excess appears longwards of 5.8 ![]() m, lies close to this boundary. Finally two other sources, J160836.4-393119 and J160826.8-384101, show clear excess in MIPS observations at 24
m, lies close to this boundary. Finally two other sources, J160836.4-393119 and J160826.8-384101, show clear excess in MIPS observations at 24 ![]() m. Unfortunately, they lie in an area that was not observed by IRAC at shorter wavelengths.
m. Unfortunately, they lie in an area that was not observed by IRAC at shorter wavelengths.
We show the distribution of the new members of Lupus 3 in the
![]() vs. S diagram in Fig. 8, and their spatial distribution in Fig. 9, together with the distribution of those previously known members that are selected according the same criteria. Among the new members a similar degree of concentration as in Lupus 1 is observed, which in this case form a distribution roughly centered on the dense star-forming cloud TGU H-2084 hosting most of the known members and the Herbig Ae/Be stars HR 5999/6000. Although the dark cloud lies near the center of the distribution very few new members appear projected on it, in stark difference with the distribution of the known members. The fact that the known members were selected according to the same criteria argues against the difference between both distributions being due to extinction.
vs. S diagram in Fig. 8, and their spatial distribution in Fig. 9, together with the distribution of those previously known members that are selected according the same criteria. Among the new members a similar degree of concentration as in Lupus 1 is observed, which in this case form a distribution roughly centered on the dense star-forming cloud TGU H-2084 hosting most of the known members and the Herbig Ae/Be stars HR 5999/6000. Although the dark cloud lies near the center of the distribution very few new members appear projected on it, in stark difference with the distribution of the known members. The fact that the known members were selected according to the same criteria argues against the difference between both distributions being due to extinction.
5.3 Lupus 4
The histogram of stars detected as a function of S for Lupus 4 differs markedly from those of Lupus 1 and 3 in all the temperature bins in which Fig. 5 is organized. The source counts in this cloud are in general in good consistency with the contribution from the field dwarfs and giants alone, and the trace of a young population associated with it is only marginal. Given is galactic latitude
![]() ,
the expected contamination by unrelated stars is very similar to that expected in the direction of Lupus 3, scaled down due to the smaller area covered by our observations of Lupus 4. The peak at 5 < S < 6 at
,
the expected contamination by unrelated stars is very similar to that expected in the direction of Lupus 3, scaled down due to the smaller area covered by our observations of Lupus 4. The peak at 5 < S < 6 at
![]() can now be accounted for by background early M giants alone. We only identify 6 apparent members of the cloud with
can now be accounted for by background early M giants alone. We only identify 6 apparent members of the cloud with
![]() K, one of them previously known. The other 5 are listed in Table 9. Three additional members may be present in the
K, one of them previously known. The other 5 are listed in Table 9. Three additional members may be present in the
![]() range with 4 < S < 5, although background giants are expected to contribute to this bin of the histogram and we do not consider this excess to be sufficiently significant. We only identify two stars in the virtually uncontaminated 5 < S < 7 range, one of which is a known member. Only one of the newly identified candidate members of Lupus 4, J160019.2-415635, has its mid-infrared flux measured by Spitzer, without indication of significant excess flux through the 3.6
range with 4 < S < 5, although background giants are expected to contribute to this bin of the histogram and we do not consider this excess to be sufficiently significant. We only identify two stars in the virtually uncontaminated 5 < S < 7 range, one of which is a known member. Only one of the newly identified candidate members of Lupus 4, J160019.2-415635, has its mid-infrared flux measured by Spitzer, without indication of significant excess flux through the 3.6 ![]() m-24
m-24 ![]() m range. The positions of all these objects in the
m range. The positions of all these objects in the
![]() vs. S diagram is shown in Fig. 10.
vs. S diagram is shown in Fig. 10.
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f10.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg117.png) |
Figure 10: Same as Fig. 6 for Lupus 4. Like in Lupus 1, the limits of the temperature axis are conveniently adjusted. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f11.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg118.png) |
Figure 11:
Same as Fig. 7 for Lupus 4. The field is in this case
|
| Open with DEXTER | |
The spatial distribution of the few objects identified in Lupus 4, shown in Fig. 11 does not show any hints of concentration toward the central cloud, TGU H-2063, and none of them appears projected on it. In this respect, it is worth noting the striking difference between Lupus 1 and 4. Previous to the present study, and even after the surveys carried out by Spitzer, the number of known members in Lupus 1 and 4 was very similar (see Table 9 in Merín et al. 2008). However, whereas our results add 64 objects to the 17 known in Lupus 1, the increase is a modest 6 to the 18 known in Lupus 4, and the true members in this latter case may be even less as noted in Sect. 6. In this regard, our results for Lupus 4 closely resemble those of Spezzi et al. (2007), who found only a small number of additional candidate members of the Chamaeleon II clouds beside those already identified through the emission of their circumstellar envelopes. Both the selection criteria of known members of Chamaeleon II, mainly based on Spitzer colors, and the method used to identify new candidates from broad-band imaging were very similar to those used in the present paper.
6 Discussion
The discovery of such a numerous population of new members of the Lupus 1 and 3 clouds is in itself an intriguing result, since it reveals that much of the stellar content of these clouds, and even most of it in the case of Lupus 1, has remained unidentified to date. The examination of the bulk properties of the new population and its comparison with those of the known members leads to some surprising results. Since we restrict our identification of new members to regions in the
![]() -S diagram devoid of contamination by other cool stars, with a subsequent restriction on the age range from which the new members are drawn, we have limited information on the age distribution of the Lupus stellar population. In particular we cannot tell from our results if the total population of non-identified members reaches to older ages than that of known members, and we cannot use the newly identified members to reconstruct the history of star formation in Lupus, although the hotter stars of Lupus 1 hint at significant star-forming activity over 10 Myr ago. For similar reasons there is little we can conclude about the stellar mass function in the Lupus clouds. Nevertheless, a comparison between the positions in the
-S diagram devoid of contamination by other cool stars, with a subsequent restriction on the age range from which the new members are drawn, we have limited information on the age distribution of the Lupus stellar population. In particular we cannot tell from our results if the total population of non-identified members reaches to older ages than that of known members, and we cannot use the newly identified members to reconstruct the history of star formation in Lupus, although the hotter stars of Lupus 1 hint at significant star-forming activity over 10 Myr ago. For similar reasons there is little we can conclude about the stellar mass function in the Lupus clouds. Nevertheless, a comparison between the positions in the
![]() vs. S diagram of previously known and new candidate members presented in Figs. 6 and 8 does not show any significant differences between both groups in either age or mass distribution.
vs. S diagram of previously known and new candidate members presented in Figs. 6 and 8 does not show any significant differences between both groups in either age or mass distribution.
Our results show that the large population of newly discovered candidate members found in Lupus 1 and 3 contains numerous members with ages below 5 Myr or even 1 Myr and with no detectable signatures of disks or accretion, in the same range of ages covered by members that do display those signatures. The lack of noticeable infrared excess at 24 ![]() m for most of the new members implies the clearing of the inner parts of disks within at least the inner 1 AU from the central object. The large number of new members without such disk signatures appears to be at variance with the research on the disk-bearing fraction of young stellar populations, which indicates a typical duration of 2 Myr for the optically thick disk phase (see Evans et al. 2008 for a summary of lifetime estimates for the different evolutionary phases, as derived by a large number of studies in different star-forming regions). Haisch et al. (2001) show that about half of the stars in clusters are able to retain inner disks producing excess at 3.4
m for most of the new members implies the clearing of the inner parts of disks within at least the inner 1 AU from the central object. The large number of new members without such disk signatures appears to be at variance with the research on the disk-bearing fraction of young stellar populations, which indicates a typical duration of 2 Myr for the optically thick disk phase (see Evans et al. 2008 for a summary of lifetime estimates for the different evolutionary phases, as derived by a large number of studies in different star-forming regions). Haisch et al. (2001) show that about half of the stars in clusters are able to retain inner disks producing excess at 3.4 ![]() m in the first 3 Myr. The fraction seems to be similar or even higher at very low masses (Jayawardhana et al. 2003), including the giant-planet-mass regime (Scholz & Jayawardhana 2008). On the other hand, low mass stars and brown dwarfs have been shown to frequently retain their disks for ages as old as
m in the first 3 Myr. The fraction seems to be similar or even higher at very low masses (Jayawardhana et al. 2003), including the giant-planet-mass regime (Scholz & Jayawardhana 2008). On the other hand, low mass stars and brown dwarfs have been shown to frequently retain their disks for ages as old as ![]() 10 Myr (Riaz & Gizis 2008; Uchida et al. 2004), as well as to maintain a low accretion rate (Lawson et al. 2004) at those ages. The existence of coeval members with differing disk and accretion characteristics, such as classical T Tauri stars, weak-line T Tauri stars, and transition objects has been observed in other clusters, including the 9 Myr-old
10 Myr (Riaz & Gizis 2008; Uchida et al. 2004), as well as to maintain a low accretion rate (Lawson et al. 2004) at those ages. The existence of coeval members with differing disk and accretion characteristics, such as classical T Tauri stars, weak-line T Tauri stars, and transition objects has been observed in other clusters, including the 9 Myr-old ![]() Cha (Lyo et al. 2003; Lawson et al. 2004), indicating that different paths towards disk dissipation, acting on different timescales, must exist. Additional evidence of the complexity of the disk dissipation process is presented by Merín et al. (2008), on the basis of basic parameters of the mid-infrared spectral energy distribution that characterize the sizes of the inner clearings and the optical thickness and flaring of disks. The broad range of values and poor correlations between such a parameters indicate a wide variety of disk inner holes and geometries during the dissipation process. On the other hand, an examination of the mid-infrared excesses of weak T Tauri stars (WTTS) by Cieza et al. (2007) has shown that WTTS as young as 1 Myr exist with no trace of circumstellar dust, in consonance with our results.
Cha (Lyo et al. 2003; Lawson et al. 2004), indicating that different paths towards disk dissipation, acting on different timescales, must exist. Additional evidence of the complexity of the disk dissipation process is presented by Merín et al. (2008), on the basis of basic parameters of the mid-infrared spectral energy distribution that characterize the sizes of the inner clearings and the optical thickness and flaring of disks. The broad range of values and poor correlations between such a parameters indicate a wide variety of disk inner holes and geometries during the dissipation process. On the other hand, an examination of the mid-infrared excesses of weak T Tauri stars (WTTS) by Cieza et al. (2007) has shown that WTTS as young as 1 Myr exist with no trace of circumstellar dust, in consonance with our results.
Table 8: Possible binaries.
We examined the fraction of wide binaries among the new population by searching for companions within a radius of 10'' from each new candidate member (projected distance 1500 AU at the distance of Lupus 1 and 4, and 2000 AU at that of Lupus 3), and having
![]() and S compatible with membership in the corresponding cloud. Although most of the new candidate members have sources within that angular distance, in nearly all cases where their spectral energy distribution can be fitted the possible companions have S values placing them below the main sequence, indicating that they are unrelated foreground stars instead. We only identify two possible binaries, both in Lupus 1, which are tabulated in Table 8. The first one, J153815.5-350342B, is a possible brown dwarf companion with a derived age similar to that of the primary, lying slightly above the S-cutoff that we set at its temperature,
and S compatible with membership in the corresponding cloud. Although most of the new candidate members have sources within that angular distance, in nearly all cases where their spectral energy distribution can be fitted the possible companions have S values placing them below the main sequence, indicating that they are unrelated foreground stars instead. We only identify two possible binaries, both in Lupus 1, which are tabulated in Table 8. The first one, J153815.5-350342B, is a possible brown dwarf companion with a derived age similar to that of the primary, lying slightly above the S-cutoff that we set at its temperature,
![]() K. The second companion candidate, 154018.5-342614B, is more doubtful, as we obtain a temperature slightly higher than that of its primary but a lower luminosity, which if taken at face value would imply an older age. However, the uncertainties in the derivation of the temperatures using our methods do not allow us to rule out the possibility that it forms a physical pair with its primary. While this hints at a low binary frequency among the new members, we must stress that our criteria for the identification of binaries is rather restrictive. On the one hand, we are unable to verify as likely companions low luminosity sources fainter than the detection limits of 2MASS, as a reliable fit cannot be derived from
K. The second companion candidate, 154018.5-342614B, is more doubtful, as we obtain a temperature slightly higher than that of its primary but a lower luminosity, which if taken at face value would imply an older age. However, the uncertainties in the derivation of the temperatures using our methods do not allow us to rule out the possibility that it forms a physical pair with its primary. While this hints at a low binary frequency among the new members, we must stress that our criteria for the identification of binaries is rather restrictive. On the one hand, we are unable to verify as likely companions low luminosity sources fainter than the detection limits of 2MASS, as a reliable fit cannot be derived from
![]() photometry alone. On the other hand, some of our new candidate members may be companions to brighter stars that appear saturated in some of our images. A dedicated investigation is thus necessary to derive the true incidence of binarity in our sample, and its possible relationship with its lack of disk signatures.
photometry alone. On the other hand, some of our new candidate members may be companions to brighter stars that appear saturated in some of our images. A dedicated investigation is thus necessary to derive the true incidence of binarity in our sample, and its possible relationship with its lack of disk signatures.
Could the new population be actually related to the Gould Belt, rather than to the star-forming Lupus clouds? Given the radial extent of the Gould Belt (see Sect. 3.2) such explanation would remove the problem of having to account for the quick dispersal of disks, since the position of these objects in the same
![]() -S diagram would then be due to their closer distance to us rather than to a young age. However, our results provide several arguments against that explanation. In the first place, the new members of both Lupus 1 and Lupus 3 clearly show a concentrated spatial distribution, rather than a random scatter as would be expected from the Gould Belt population on the angular scale covered by our observations (see for instance Fig. 3 of Krautter et al. 1997, see also Wichmann et al. 1997, and Sterzik et al. 1995 for similar observations in the Orion region). Secondly, the surface density of our objects is much smaller in Lupus 4, which is close to Lupus 3 on the sky and should be affected by Gould Belt members to a very similar degree. A third argument is given by the
-S diagram would then be due to their closer distance to us rather than to a young age. However, our results provide several arguments against that explanation. In the first place, the new members of both Lupus 1 and Lupus 3 clearly show a concentrated spatial distribution, rather than a random scatter as would be expected from the Gould Belt population on the angular scale covered by our observations (see for instance Fig. 3 of Krautter et al. 1997, see also Wichmann et al. 1997, and Sterzik et al. 1995 for similar observations in the Orion region). Secondly, the surface density of our objects is much smaller in Lupus 4, which is close to Lupus 3 on the sky and should be affected by Gould Belt members to a very similar degree. A third argument is given by the
![]() -S diagrams of Lupus 1 and, more notably, of Lupus 3, where no members, either new or already known, are found above a temperature-dependent value of S, which probably marks the location of the stellar birthline (Stahler 1983) in Lupus. Unless the inner edge of the Gould Belt casually happens to lie at the right distance, there is no reason why its members should not occupy the part of the diagram above this line.
-S diagrams of Lupus 1 and, more notably, of Lupus 3, where no members, either new or already known, are found above a temperature-dependent value of S, which probably marks the location of the stellar birthline (Stahler 1983) in Lupus. Unless the inner edge of the Gould Belt casually happens to lie at the right distance, there is no reason why its members should not occupy the part of the diagram above this line.
Of course, the arguments above do not exclude the possibility that some of the new members that we identify do belong to a foreground population associated with the Gould Belt. As noted in Table 9, some of them were identified by Krautter et al. (1997) thanks to their X-ray emission as weak-line T Tauri stars and possible members of that population. The small number of new candidate members that we detect toward Lupus 4 and their lack of noticeable clustering toward the cloud suggest that perhaps all the objects that we tentatively identify as new members of Lupus 4 may belong instead to the foreground Gould Belt population. However, there is no doubt that this is at most a minor contributor to the number of new members that we find toward Lupus 1 and 3.
6.1 The origin of the new members
A surprising result of our study is the different spatial distribution between the newly discovered objects often without disk signatures, mostly located outside the main clouds, and those that preserve their youth signposts. The locations of the latter are very closely correlated to the densest concentrations of molecular gas and dust, as noted by Merín et al. (2008). A difference in ages could in principle be an obvious cause for the spatial segregation between both populations, reflected also on their different disk properties. In this picture, the oldest objects would have had time to slowly drift away from the parental clouds while their disks evolved toward dissipation. However, as noted above we find no evidence of the age differences between both populations that would be required by such explanation. We cannot rule out that such differences might be revealed by future studies that will more accurately determine the intrinsic properties of the new candidate members, including their ages, but at the moment the available data provide no support for their existence.
It is very unlikely that the halo of new members around TGU-H2084, the main molecular condensation of Lupus 3, might be composed by objects formed in the cloud and then ejected shortly after their formation, losing the disk in the process. Taking as typical values for our new members an angular distance to the cloud of ![]() and a travel time of
and a travel time of ![]() 0.5 Myr, the ejection velocities that are required are not very high, of order of
0.5 Myr, the ejection velocities that are required are not very high, of order of ![]() 4 km s-1. However, the efficiency of the process of ejection involving stripping of the disk would need to be extremely high to account for the production of roughly 70 objects or more displaying such features, a number that is comparable to that of objects in the same age range that retain their disks. We thus regard this as a very unlikely explanation. Furthermore, it is doubtful that it may apply to Lupus 1 as well, since the concentration of new members without disk signatures does not appear to be centered on any of the observed clouds -and where, if correct, the ejection plus disk-stripping mechanism should have affected to most of the members to account for the ratio of diskless to disk-bearing stars.
4 km s-1. However, the efficiency of the process of ejection involving stripping of the disk would need to be extremely high to account for the production of roughly 70 objects or more displaying such features, a number that is comparable to that of objects in the same age range that retain their disks. We thus regard this as a very unlikely explanation. Furthermore, it is doubtful that it may apply to Lupus 1 as well, since the concentration of new members without disk signatures does not appear to be centered on any of the observed clouds -and where, if correct, the ejection plus disk-stripping mechanism should have affected to most of the members to account for the ratio of diskless to disk-bearing stars.
Alternatively, all the objects may have formed near their present locations and their disks may have then followed an environment-dependent path, with objects embedded in the dense clouds being able to retain their inner disks and accretion rates for millions of years, whereas those forming outside the clouds lost them much more quickly. A reason for these different evolutionary paths may be related to the shielding provided to forming disks by the parental molecular cloud, which would protect them from being externally irradiated, whereas this would not be the case for exposed disks. The fast evaporation of disks by the ultraviolet radiation of nearby O stars is well known in the Trapezium cluster, where protoplanetary disks resolved by the Hubble Space Telescope appearing in silhouette against a bright background are often distorted due to the proximity to the hot Trapezium stars, in agreement with the results of numerical simulations (Richling & Yorke 1998). Johnstone et al. (1998) and Bally et al. (1998) estimate mass loss rates due to disk photoevaporation as high as
![]() yr-1, and disk lifetimes as short as 0.1 Myr or less in these conditions. Further evidence is presented by Robberto et al. (2004), who derive mass accretion rates on low-mass stars in the Trapezium cluster. The typical accretion rates found are on the average one order of magnitude below those derived for other star-forming regions such as the Taurus clouds or adjacent regions in Orion itself, despite the similar distributions in mass and age. The authors attribute this difference to the fast exhaustion of the disk reservoirs for accretion as the O-type members of the Trapezium evaporate them. They also propose that the early suppression of accretion by the dissipation of the disk should result in a peculiar Initial Mass Function biased toward low mass members, as their further growth is prematurely terminated. The effects of external disk irradiation are nevertheless detectable only on the close surroundings of the Trapezium, on distances of
yr-1, and disk lifetimes as short as 0.1 Myr or less in these conditions. Further evidence is presented by Robberto et al. (2004), who derive mass accretion rates on low-mass stars in the Trapezium cluster. The typical accretion rates found are on the average one order of magnitude below those derived for other star-forming regions such as the Taurus clouds or adjacent regions in Orion itself, despite the similar distributions in mass and age. The authors attribute this difference to the fast exhaustion of the disk reservoirs for accretion as the O-type members of the Trapezium evaporate them. They also propose that the early suppression of accretion by the dissipation of the disk should result in a peculiar Initial Mass Function biased toward low mass members, as their further growth is prematurely terminated. The effects of external disk irradiation are nevertheless detectable only on the close surroundings of the Trapezium, on distances of ![]() 0.1 pc, which are over one order of magnitude smaller than the size of the region occupied by the new members of Lupus. Evidence for fast disk dissipation on a longer length scale has been reported in the Rosette nebula cluster, where two jets are detected emanating from stars otherwise lacking any signatures of the existence of a disk (Li & Rector 2007). This is interpreted as the result of the early and fast transition from the classical to the weak-line T Tauri phase triggered by the external erosion of the disk by nearby O stars, which leaves the jet as the only recognizable signpost of youth. In this case the distance between the jet-driving stars and the nearest massive stars is in the 2-3 pc range, but the eroding radiation field is more intense by more than one order of magnitude than in the Trapezium, mainly because of the presence of very massive O4V(f) and O5V stars within that distance range.
0.1 pc, which are over one order of magnitude smaller than the size of the region occupied by the new members of Lupus. Evidence for fast disk dissipation on a longer length scale has been reported in the Rosette nebula cluster, where two jets are detected emanating from stars otherwise lacking any signatures of the existence of a disk (Li & Rector 2007). This is interpreted as the result of the early and fast transition from the classical to the weak-line T Tauri phase triggered by the external erosion of the disk by nearby O stars, which leaves the jet as the only recognizable signpost of youth. In this case the distance between the jet-driving stars and the nearest massive stars is in the 2-3 pc range, but the eroding radiation field is more intense by more than one order of magnitude than in the Trapezium, mainly because of the presence of very massive O4V(f) and O5V stars within that distance range.
In our case, the candidate sources of external irradiation may be the OB stars of the Scorpius-Centaurus
OB association, one of whose groups, Upper Centaurus-Lupus, is adjacent to the Lupus clouds (Blaauw 1991). However, no O-type stars are found at present within few parsecs of either Lupus 1 or Lupus 3 (de Zeeuw et al. 1999), thus rendering such explanation highly unlikely. With the disk mass loss rate ![]() decreasing with increasing distance d to the ionizing source as
decreasing with increasing distance d to the ionizing source as
![]() (Richling & Yorke 1998), the mechanism quickly loses efficiency in the absence of very nearby massive stars.
(Richling & Yorke 1998), the mechanism quickly loses efficiency in the absence of very nearby massive stars.
Preibisch & Zinnecker (1999) suggested that star formation in the Lupus clouds may have been triggered by a supernova explosion about 5 Myr ago in the Upper Scorpius OB association. At a distance of several parsecs, the shock wave driven by the explosion in the surrounding interstellar medium would have slowed down by collecting intervening material, most probably being in the radiative shock phase (Chevalier 1977) by the time it reached the Lupus clouds. Slow shocks can trigger the outside-in collapse of preexisting clouds, as described by Boss (1995), via the thermal pressure by the post-shock material. This results in the fast collapse of the cloud giving rise to a high accretion rate (up to
![]() yr-1) on the central object, which rapidly declines in the absence of a massive reservoir of gas. This provides another possible explanation for the existence of an off-cloud population, which may have formed as a result of the direct exposure of isolated small molecular cores to one or several successive shock waves from the neighboring OB association. The outside-in character of the collapse, as opposed to the inside-out collapse of the cores embedded in the more quiescent environment of the larger molecular clouds, may explain the very different disk properties that we identify. With respect to the previous explanation based on the external irradiation of disks, the advantage of the supernova-triggered star formation scenario is that it does not require the presence of very nearby massive stars, which renders it more plausible in the scenario of Lupus 1 and 3. The absence of this population in Lupus 4 (and probably also in other clouds, such as Chamaeleon II; Spezzi et al. 2007) may then be simply due to the lack of nearby supernovae having provided this triggering mechanism.
yr-1) on the central object, which rapidly declines in the absence of a massive reservoir of gas. This provides another possible explanation for the existence of an off-cloud population, which may have formed as a result of the direct exposure of isolated small molecular cores to one or several successive shock waves from the neighboring OB association. The outside-in character of the collapse, as opposed to the inside-out collapse of the cores embedded in the more quiescent environment of the larger molecular clouds, may explain the very different disk properties that we identify. With respect to the previous explanation based on the external irradiation of disks, the advantage of the supernova-triggered star formation scenario is that it does not require the presence of very nearby massive stars, which renders it more plausible in the scenario of Lupus 1 and 3. The absence of this population in Lupus 4 (and probably also in other clouds, such as Chamaeleon II; Spezzi et al. 2007) may then be simply due to the lack of nearby supernovae having provided this triggering mechanism.
7 Conclusions
We have presented the results of a wide survey of the Lupus 1, 3, and 4 clouds which, when combined with 2MASS photometry, provides a broad wavelength coverage well suited for the determination of temperatures of cool stars and their line-of-sight extinctions by means of fits to synthetic spectra. We estimate in this way the temperatures of over 150 000 stars in the directions of the Lupus clouds, including many previously known members with temperatures independently derived from their spectral types, and conclude that our method provides a generally good fit to the temperature, except when veiling, strong emission lines, variability, or nearby companions are present.
We introduce a parameter S related to the ratio of the distance to the star and its radius. Using it, we show that members of the Lupus clouds at a given temperature and within a restricted set of ages that are in the range expected for a star-forming region are characterized by values of S virtually unreachable by non-members of similar temperature. We take advantage of this property, shared by other star-forming regions at similar distances from the Sun, to demonstrate the existence of an important population of members of Lupus 1 and 3 thus far undetected by previous surveys. This population is either much less significant or non-existing in Lupus 4.
The properties of this new population are puzzling in several respects. The ages of its components are young, in the range of the previously known members of the same regions, but their non-detection until now
implies that they are surrounded by little or no circumstellar material within at least ![]() 1 AU from the central object, as confirmed by the Spitzer photometry available for most of these objects. Furthermore, while the new populations discovered in Lupus 1 and 3 tend to be spatially concentrated (toward a region between the two main clouds forming the Lupus 1 complex, and toward the main cloud in Lupus 3), most of their members are located outside those clouds.
1 AU from the central object, as confirmed by the Spitzer photometry available for most of these objects. Furthermore, while the new populations discovered in Lupus 1 and 3 tend to be spatially concentrated (toward a region between the two main clouds forming the Lupus 1 complex, and toward the main cloud in Lupus 3), most of their members are located outside those clouds.
Taking together the absence of significant disk emission among the newly identified members and their preferential location away from the main molecular concentrations of their host complexes, we tentatively interpret our results in terms of the rapid disappearance (on timescales of less than 1 Myr) of the inner disks of stars formed outside the shielding environment of a molecular cloud. We consider it unlikely that the agent responsible for the fast dispersal of off-cloud stars in Lupus 1 and 3 may be the ultraviolet radiation of OB stars belonging to the Upper Centaurus-Lupus group of the Scorpius-Centaurus OB association, which is located adjacent to the Lupus clouds on the sky but whose individual members are too far away from the Lupus clouds. While evidence of disk ablation by external irradiation by O stars has been previously reported in the Trapezium and Rosette clusters, the applicability of this explanation to the Lupus clouds remains very doubtful due to the much less extreme radiation environment. We consider as more likely an alternative explanation by which the formation of the off-cloud population may have been caused by the passage of one or more shock fronts associated with evolved supernova remnants, triggering the outside-in collapse of preexisting cloudlets.
Regardless of its ultimate interpretation, the discovery of a substantial and even dominant population of thus far unnoticed members of one of our nearest star-forming regions stresses the important unknowns that still subsist in their observational characterization, despite the important advancements that recent surveys from the ground and from space have made possible.
Acknowledgements
We are pleased to thank the staff of La Silla Science Operations for the careful execution of our observing runs in Service Mode at the 2.2 m telescope, as well as to the ESO User Support Department for their assistance with the preparation of the observations. This paper benefitted from comments on the manuscript by Drs. Ewine van Dishoeck and Neal Evans, as well as by a careful review by the referee, Dr. Bruno Merín. F. C. is also thankful to Dr. Ewine van Dishoeck for first having invited him to become involved in the 'Cores to Disk' effort, and to the hospitality of the Vatican Observatory staff during the final stages of preparation of this paper. B.L.M. acknowledges the financial support of the ESO Director General Discretionary Fund and from the Spanish MICINN under the Consolider-Ingenio 2010 Program, through grant CSD2006-00070. This research has made use of the SIMBAD database operated at CDS, Strasbourg, France. It also makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work is based in part on archival data obtained with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA.
References
- Allard, F., Hauschildt, P. H., & Schwenke, D. 2000, ApJ, 540, 1005 [NASA ADS] [CrossRef] (In the text)
- Allen, P. R., Luhman, K. L., Myers, P. C., et al. 2007, ApJ, 655, 1095 [NASA ADS] [CrossRef] (In the text)
- Allers, K. N., Kessler-Silacci, J. E., Cieza, L. A., & Jaffe, D. T. 2006, ApJ, 644, 364 [NASA ADS] [CrossRef]
- Baade, D., Meisenheimer, K., & Iwert, O. 1999, The Messenger 95, 15 (In the text)
- Bally, J., Testi, L., Sargent, A., & Carlstrom, J. 1998, AJ, 116, 854 [NASA ADS] [CrossRef] (In the text)
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] (In the text)
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Blaauw, A. 1991, in The Physics of Star Formation and Early Stellar Evolution, ed. C. J. Lada, & N. D. Kylafis, NATO ASI Ser. C, 342 (In the text)
- Bohlin, R. C., & Gilliland, R. L. 2004, 127, 3508 (In the text)
- Boss, A. P. 1995, ApJ, 439, 224 [NASA ADS] [CrossRef] (In the text)
- Burgasser, A. J. 2004, ApJS, 155, 207 [NASA ADS] [CrossRef]
- Burgasser, A. J., Kirkpatrick, J. D., McGovern, M. R., et al. 2004, ApJ, 604, 827 [NASA ADS] [CrossRef]
- Cambrésy, L. 1999, A&A, 345, 965 [NASA ADS] (In the text)
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef]
- Chabrier, G. 2005, in The initial mass function 50 years later, ed. E. Corbelli, et al. (Springer) (In the text)
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] (In the text)
- Chapman, N. L., Lai, S.-P., Mundy, L. G., et al. 2007, ApJ, 667, 288 [NASA ADS] [CrossRef]
- Chevalier, R. A. 1977, ARA&A, 15, 175 [NASA ADS] [CrossRef] (In the text)
- Cieza, L., Padgett, F. L., Stapelfeldt, K. R., et al. 2007, ApJ, 667, 308 [NASA ADS] [CrossRef] (In the text)
- Comerón, F. 2004, in Organizations and Strategies in Astronomy, 5, ed. A. Heck (Kluwer Acad. Publ.) (In the text)
- Comerón, F. 2008, in Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, ASP Monograph Publ., 5, 295 (In the text)
- Comerón, F., Fernández, M., Baraffe, I., et al. 2006, A&A, 406, 1001 [NASA ADS] [CrossRef] (In the text)
- Dahn, C. C., Harris, H. C., Vrba, F. J., et al. 2002, AJ, 124, 1170 [NASA ADS] [CrossRef]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H .J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] (In the text)
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, S1 [NASA ADS] (In the text)
- Evans, N. J., II, Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef]
- Evans, N. J., et al. 2009, ApJS, in press
- Fernández, M., & Comerón, F., A&A, 2005, 440, 1119 (In the text)
- Fluks, M. A. 1998, Ph.D. Thesis, Univ. of Amsterdam (In the text)
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] (In the text)
- Gondoin, P. 2006, A&A, 454, 595 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Graham, J. A., & Heyer, M. H. 1988, PASP, 100, 1529 [NASA ADS] [CrossRef] (In the text)
- Guillout, P., Sterzik, M. F., Schmitt, J. H. M. M., Motch, C., & Neuhäuser, R. 1998, A&A, 337, 113 [NASA ADS] (In the text)
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] (In the text)
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] (In the text)
- Herbig, G. H. 1998, ApJ, 497, 736 [NASA ADS] [CrossRef]
- Hughes, J. H., Hartigan, P., Krautter, J., & Kelemen, J. 1994, AJ, 108, 1071 [NASA ADS] [CrossRef] (In the text)
- Jayawardhana, R., & Ivanov, V. D. 2006, ApJ, 647, L167 [NASA ADS] [CrossRef]
- Jayawardhana, R., Ardila, D. R., Stelzer, B., & Haisch, K. E., 2003, AJ, 126, 1515 [NASA ADS] [CrossRef] (In the text)
- Johnstone, D., Hollenbach, D., & Bally, J. 1998, ApJ, 499, 758 [NASA ADS] [CrossRef] (In the text)
- Kainulainen, J., Lehtinen, K., & Harju, J. 2006, A&A, 447, 597 [NASA ADS] [CrossRef] [EDP Sciences]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] (In the text)
- Kirkpatrick, J. D. 2005, ARA&A, 43, 195 [NASA ADS] [CrossRef] (In the text)
- Koch, A., Grebel, E. K., Odenkirchen, M., & Caldwell, J. A. R. 2003, The Messenger, 115, 37 [NASA ADS] (In the text)
- Krautter, J., Wichmann, R., Schmitt, J. H. M. M., et al. 1997, A&AS, 123, 329 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] (In the text)
- Lawson, W. A., Lyo, A.-R., & Muzerolle, J. 2004, MNRAS, 351, L39 [NASA ADS] [CrossRef] (In the text)
- Lee, H. T., Chen, W. P., Zhi, W. Z., & Jing, Y. H. 2005, ApJ, 624, 808 [NASA ADS] [CrossRef]
- Li, J. Z., & Rector, T. A. 2007, NewA, 12, 441 [NASA ADS] [CrossRef] (In the text)
- López Martí, B., Eislöffel, J., & Mundt, R. 2005, A&A, 440, 139 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Luhman, K. L. 1999, ApJ, 525, 466 [NASA ADS] [CrossRef]
- Luhman, K. L. 2007, ApJS, 173, 104 [NASA ADS] [CrossRef] (In the text)
- Luhman, K. L., & Rieke, G. H. 1999, ApJ, 525, 440 [NASA ADS] [CrossRef]
- Luhman, K. L., Stauffer, J. R., Muench, A. A. et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef] (In the text)
- Luhman, K. L., Allers, K. N., Jaffe, D. T., et al. 2007, ApJ, 659, 1629 [NASA ADS] [CrossRef]
- Luhman, K. L., Allen, L. E., Allen, P. R., et al. 2008, ApJ, 675, 1375 [NASA ADS] [CrossRef]
- Lyo, A.-R., Lawson, W. A., Mamajek, E. E., & Feigelson, E. D. 2003, MNRAS 38, 616 (In the text)
- Merín, B., Augereau, J.-C., van Dishoeck, E. F. et al. 2007, ApJ, 661, 361 [NASA ADS] [CrossRef] (In the text)
- Merín, B., Jørgensen, J., Spezzi, L., et al. 2008, ApJ, submitted
- Meyer, M. R., Calvet, N., & Hillenbrand, L. A. 1997, ApJ, 114, 288 [NASA ADS]
- Nakajima, Y., Tamura, M., Oasa, Y., & Nakajima, T. 2000, AJ, 119, 873 [NASA ADS] [CrossRef] (In the text)
- Oliveira, I., Merín, B., Pontoppidan, K. M., et al. 2009, ApJ, 691, 672 [NASA ADS] [CrossRef] (In the text)
- Preibisch, T., & Zinnecker, H. 1999, AJ, 117, 2381 [NASA ADS] [CrossRef] (In the text)
- Reipurth, B. 2008, Handbook of Star Forming regions, ASP Monograph (In the text)
- Riaz, B., & Gizis, J. E. 2008, ApJ, 681, 1584 [NASA ADS] [CrossRef] (In the text)
- Richling, S., & Yorke, H. W. 1998, A&A, 340, 508 [NASA ADS] (In the text)
- Robberto, M., Song, J., Mora Carrillo, G., et al. 2004, ApJ, 606, 952 [NASA ADS] [CrossRef] (In the text)
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] (In the text)
- Scholz, A., & Jayawardhana, R. 2008, ApJ, 672, L49 [NASA ADS] [CrossRef] (In the text)
- Schwartz, R. D. 1977, ApJS, 35, 161 [NASA ADS] [CrossRef] (In the text)
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
- Smith, J., Allyn, Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [NASA ADS] [CrossRef] (In the text)
- Spezzi, L., Alcalá, J. M., Frasca, A., et al. 2007, A&A, 470, 281 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stahler, S. W. 1983, ApJ, 274, 822 [NASA ADS] [CrossRef] (In the text)
- Steenman, H., Thé, P.-S. 1989, Ap&SS, 159, 189 [NASA ADS] [CrossRef] (In the text)
- Sterzik, M. F., Alcalá, J. M., Neuhäuser, R., & Schmitt, J. H. M. M. 1995, A&A, 297, 418 [NASA ADS] (In the text)
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] (In the text)
- Thé, P. S. 1962, Contrib. Bosscha Obs., 15 (In the text)
- Uchida, K. I., Calvet, N., Hartmann, L., et al. 2004, ApJS, 154, 439 [NASA ADS] [CrossRef] (In the text)
- Vrba, F. J., & Rydgren, A. E. 1984, ApJ, 283, 123 [NASA ADS] [CrossRef] (In the text)
- Wainscoat, R. J., Cohen, M., Volk, K., Walker, H. J., & Schwartz, D. E. 1992, ApJS, 83, 111 [NASA ADS] [CrossRef] (In the text)
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [CrossRef] (In the text)
- Wichmann, R., Krautter, J., Covino, E., et al. 1997, A&A, 320, 185 [NASA ADS] (In the text)
Online Material
Table 4: Derived physical parameters for known, non-saturated members of Lupus 1, 3, and 4.
Table 9:
New candidate members of Lupus 1, 3, and 4.
Table 1:
Saturation limits and limiting magnitudes at 3 Table 2:
Number of sources for which photometry is available.
Table 3:
Expected numbers of non-members in the Lupus
Table 5:
Objects classified as candidate Lupus members by Merín et al. (2008) for which no fits are obtained.
Table 6:
Fits to
Table 7:
Fits to
Table 8:
Possible binaries.
Table 4:
Derived physical parameters for known, non-saturated members of Lupus 1, 3, and 4.
Table 9:
New candidate members of Lupus 1, 3, and 4.
Photometric errors versus magnitudes and relative
exponential fits for all the point-like sources detected in Lupus 3.
The ``multiple sequence'' is due to different seeing conditions during the observation of the different fields.
Example of the fit of the
Footnotes
![]()
![]()
![]()
![]()
All Tables
![]() level.
level.
![]() - S locus.
- S locus.
![]() photometry of stars with suspected veiling.
photometry of stars with suspected veiling.
![]() photometry of stars with suspected infrared excess.
photometry of stars with suspected infrared excess.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1771f01.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg51.png)
Figure 1:
Open with DEXTER In the text
![\begin{figure}
\par\includegraphics[height=8.5cm,angle=-90,clip]{1771f02.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg78.png)
Figure 2:
![]() photometry (dots) to a synthetic spectrum (grey line). In this case, the model providing the best fit corresponds to a temperature of 3000 K. The sampling around the peak of the spectral energy distribution allows us to determine the temperature to an accuracy of few hundreds K, as discussed in Sect. 4.
photometry (dots) to a synthetic spectrum (grey line). In this case, the model providing the best fit corresponds to a temperature of 3000 K. The sampling around the peak of the spectral energy distribution allows us to determine the temperature to an accuracy of few hundreds K, as discussed in Sect. 4.Open with DEXTER In the text
![\begin{figure}
\par\includegraphics[width=6.5cm,angle=-90]{1771f03.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg83.png) |
Figure 3:
S vs.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{1771f04.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg95.png) |
Figure 4:
Comparison between the temperatures obtained with our
fitting procedure and the published spectral types of known members
of the Lupus clouds (Table 4). Stars known to display
photometric variability are excluded from the plot. The outlier near
the upper right corner is Lup 654. For SSTc2d160815.0-385715, which is
characterized by a noticeable near-infrared excess, we used
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{1771f05.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg100.png) |
Figure 5: Histograms of S values obtained at different temperature ranges in each of the observed regions. The thick histogram bars denote the contribution by known members of the star-forming region. The dashed lines indicate the expected contamination by field main sequence stars, and the dotted lines the contamination by background giants. Incompleteness due to the limiting magnitudes affects the bins with highest values of S, whereas saturation depopulates the low S bins at the right. The presence of a significant population of objects in Lupus 1 and 3 is obvious as a local peak in the valley left between the S regions dominated respectively by field main sequence and background giant contamination. It is also noticeable that only a relatively minor fraction of the objects contributed to this peak is composed of previously known members. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f06.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg107.png) |
Figure 6:
Diagram showing the positions of both known and new candidate members of Lupus 1 based on their presence in regions of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=12cm,clip]{1771f07.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg108.png) |
Figure 7:
Distribution of previously known (filled triangles) and newly identified (open squares) members of Lupus 1, plotted on a R-band mosaic of the region constructed from our WFI observations. Note that in order to produce a homogeneous comparison between the distributions of known and new members, only the known members lying within the limits of S defining the contamination-free region of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f08.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg113.png) |
Figure 8:
Same as Fig. 6 for Lupus 3. Note the different limits in the temperature axis, since stars with temperatures above
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=12cm,clip]{1771f09.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg116.png) |
Figure 9:
Same as Fig. 7 for Lupus 3. The field is in this case
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f10.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg117.png) |
Figure 10: Same as Fig. 6 for Lupus 4. Like in Lupus 1, the limits of the temperature axis are conveniently adjusted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{1771f11.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa11771-09/Timg118.png) |
Figure 11:
Same as Fig. 7 for Lupus 4. The field is in this case
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.