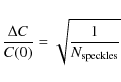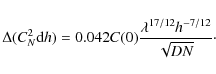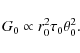First single star scidar measurements at Dome C, Antarctica

J. Vernin; M. Chadid; E. Aristidi; A. Agabi; H. Trinquet; M. Van der Swaelmen

doi:10.1051/0004-6361/200811119

Home

All issues

Volume 500 / No 3 (June IV 2009)

A&A, 500 3 (2009) 1271-1276

Full HTML

Free Access

Issue		A&A Volume 500, Number 3, June IV 2009


Page(s)		1271 - 1276
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/200811119
Published online		16 April 2009

First single star scidar measurements at Dome C, Antarctica

J. Vernin - M. Chadid - E. Aristidi - A. Agabi - H. Trinquet - M. Van der Swaelmen

Laboratoire H. Fizeau, UMR6525, Université de Nice, Observatoire de la Côte d'Azur, Parc Valrose, 06108 Nice - France

Received 9 October 2008 / Accepted 30 January 2009

Abstract
Aims. We investigate the first operational running of the Single Star Scidar (SSS instrument) under harsh weather conditions at Dome C in Antarctica and examine continuous monitoring of the optical turbulence and wind speed profiles throughout the atmosphere.
Methods. SSS is mainly composed of commercially available light-weight components and a 16 inch telescope installed on an equatorial mount. Scintillation patterns were computed (auto and cross-correlations) in real time and analyzed off line to retrieve continuously vertical profiles of optical turbulence C_N²(h) and wind speed V(h), from the ground up to 20 km.
Results. Using a simulated annealing method, we have analyzed about 6.5 h of observations, revealing the strong surface layer contribution to seeing degradation. SSS results show a good seeing agreement with simultaneous measurements with a Differential Image Motion Monitor, even under very good seeing as low as 0.2 arcsec, as well as wind speed agreement when compared to the weather archive from NOAA.
Conclusions. SSS has shown its usefulness for site characterization since it simultaneously measures C_N² and V profiles, from which most adaptative optic parameters are deduced, such as isoplanatic angle and coherence time of the wavefront. Due to its small size, it is well adapted for site characterization, even when low infrastructure is available.

Key words: atmospheric effects - site testing - turbulence - instrumentation: detectors - methods: data analysis - methods: observational

1 Introduction

Vernin et al. (2007) gave a brief history of site testing at Dome C, located on the high Antarctica plateau. Studies began in 1992, with a congress (Vernin 1994) organized by the French Académie des Sciences, and soon the decision was taken to begin a two-year site testing campaign at the South Pole. Marks et al. (1999) showed that most of the optical turbulence came from the 200 m boundary layer (BL) triggered by katabatic winds and this motivated the site testing campaign at Dome C where less katabatic winds were expected.

In 1995, one of us, Jean Vernin, participated in the first scientific expedition to Dome C, but at that time no winter infrastructure was available. In 2005, the Astro-Concordia station was first opened for winterover during which two DIMMs were set up and 40 meteorological balloons, instrumented for C_N²(h) and $\vec{V}(h)$ profiling, were launched. Again, it became obvious that most of the turbulence was generated within the surface layer (Agabi et al. 2006), as was found at the South Pole, but with a depth of only 30 m.

There are very few instruments which are able to simultaneously retrieve C_N²(h) and $\vec{V}(h)$ profiles from the ground level up to ${\approx}25{-}30$ km where the optical turbulence begins to be negligible. To our knowledge, only the Scidar family, i.e.the double star scidar (Vernin & Azouit 1983b,a) and the single star scidar (Habib et al. 2006) and the instrumented balloon (Azouit & Vernin 2005) are among these sound techniques. The Multi Aperture Scintillation Sensor (Kornilov et al. 2003) or MASS, delivers C_N² profiles along six slabs in the atmosphere, but it does not give access to ground turbulence nor the wind speed at any altitude. Echo soundings (SODAR) are not well calibrated in terms of C_N² since they require extra knowledge of the humidity profile, and their altitude range is around $30~ {\rm m} \la h \la 1~ \rm km$ , which may have a serious impact on site testing (Lawrence et al. 2004). SLODAR (Wilson 2002), based upon wavefront slope analysis on a double star, delivers optical turbulent profiles. To our knowledge, there are no cross calibrations of the SLODAR with other techniques or profiles of the wind speed.

Double Star Scidar requires at least a 1 to 1.5 m telescope since it uses a triangulation method and the maximum reachable altitude $h_{\rm max}$ is related to the diameter D of the entrance pupil through $h_{\rm max}=D/\theta$ , where $\theta$ is the angular separation of the double star. If one want to probe the atmosphere up to 20-25 km with double stars separated by 4-10 arcsec, such a telescope is needed. The same argument applies also to the SLODAR technique. Instrumented balloons require a great deal of ground infrastructure for balloon preparation, balloon launching and then for data reception, but they can be operated even at new sites where no telescope is available. Thus, for the purpose of investigation of new modern astronomical site one needs a light-weight experimental setup such as the Single Star Scidar, because it only requires a ``small'' 40 cm telescope.

Here we present the first results obtained at Dome C in 2006 during the second polar winter. In Sect. 2 we present the instrument which was prepared to resist polar conditions. In Sect. 3 we detail the campaign of observations and in Sect. 4 the Single Star Scidar (SSS) results. In Sect. 5 the results are discussed and compared to other sources like DIMM and meteorological re-analysis from the National Oceanic and Atmospheric Administration (NOAA).

2 Instrument

As seen in Fig. 1, the SSS is made with standard components. The telescope is based on a Meade M 16 (40 cm diameter) Ritchey Chrétien optical combination supported by an Astro-Physics 1200 equatorial mount. At the focus of the telescope, a collimating lens makes the beam parallel, as seen in the optical scheme in Fig. 2. In order to make the low altitude layers scintillate, one uses the ``generalized '' scidar mode (Fuchs et al. 1998) in which displacing the photoelectric receiver by a distance $\Delta z$ along the optical axis, one introduces an extra altitude difference $\Delta H=G^2\Delta z$ , where $G=F_{\rm telescope}/f_{\rm collimation}$ is the optical magnification.

The photoelectric receiver is a Pixelfly CCD with a fast readout of ${\sim}140$ images per second and a low readout noise ( ${\sim}13\rm e^-$ ). Auto-correlations and cross-correlations between images separated by a temporal lag $\Delta T= 0$ , $\Delta T= 7$ and $2 \Delta T= 14$ ms are computed in real time and averaged over $N\sim2000$ images. In order to disentangle the broadening effect of the altitude and the wind velocity fluctuations during the time to process the N images, two cross-correlations are necessary (more details are found in Habib et al. 2006).

$\begin{figure} \par\includegraphics[width=9cm]{1119fig1} \end{figure}$	Figure 1: Installation of the SSS above one of the two plateforms at Dome C during polar summer 2005-2006.
Open with DEXTER

2.1 C_N² and V retrieval

To retrieve the respective vertical profiles of C_n²(h), $\vec{V}(h)$ and $\sigma _v(h)$ (the variance of wind speed fluctuations at altitude h), we use a ``Simulated Annealing'' (SA) algorithm which is also described in Habib et al. (2006). Here, we recall only that altitudes are sampled from 0 to 20 km, with a 1 km vertical resolution which is about the natural vertical resolution of the SSS. Since the surface layer, ${\sim}30~\rm m$ thick, is very turbulent (Trinquet et al. 2008) we gave the SA algorithm the possibility of reconstructing four turbulent layers all situated at zero altitude, but with different wind speed components $\left\lbrace v_x,v_y\right\rbrace$ . Knowing that the wind speed is increasing with altitude in the Ekman layer, we sorted these four layers according to increasing wind speed. Above this surface layer, the first reconstructed altitude is 1 km and then 2 km, 3 km up to 20 km. If the refractive index structure constant is less than some threshold ( C_N² < 10^-18 m^-2/3), we assume that there is not enough turbulence to detect it and to assess its velocity. When the wind speed is zero in the first slab of the four boundary turbulent layers, it is assumed that turbulence is relevant to ``mirror seeing'' and is removed from our analysis, as already discussed by Avila et al. (2001). An ambiguity might remain if the velocity of a boundary turbulent layer is less than the first detectable speed $\Delta V$ given by:

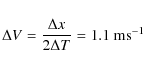$\begin{displaymath}\Delta V=\frac{\Delta x}{2\Delta T}=1.1~\rm ms^{-1} \end{displaymath}$

(1)

where $\Delta x=1.6$ cm is the size of a CCD pixel projected onto the entrance pupil, and $2 \Delta T= 14$ ms is the time lag between image i and image i + 2, from which the second cross-correlation is computed, giving the best velocity accuracy.

Six minutes of CPU time are required to compute vertical profiles of C_N², $\vec{V}$ and $\sigma _{{v}}$ deduced from the auto and cross-correlations averaged over a set of 2000 images, corresponding to an acquisition time of about 14 s. This means that 180 h, i.e. one week, of CPU (Opteron processor) time is required to process 6 h of observations.

$\begin{figure} \par\includegraphics[width=9cm]{1119fig2} \end{figure}$	Figure 2: Principle of the generalized SSS. After passing through the telescope, light is collimated by a short focal lens. In order to make the low altitude layers scintillate, the photoelectric receiver is displaced by a distance $\Delta z$ which corresponds to an altitude shift of $\Delta H=G^2\Delta z$ , where $G=F_{\rm telescope}/f_{\rm collimation}$ .
Open with DEXTER

2.2 SSS detectivity

The detectivity of the SSS depends on the noise in the scintillation auto and cross-correlations. As expressed by Vernin & Azouit (1983b), the relative error on the correlation function is given by:

$\begin{displaymath}\frac{\Delta C}{C(0)}=\sqrt{\frac{1}{N_{\rm speckles}}} \end{displaymath}$

(2)

where $N_{\rm speckles}$ is the number of independant atmospheric speckles which have been analysed, C(0) is the scintillation variance which is produced by all the turbulent layers:

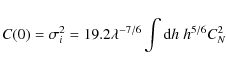$\begin{displaymath}C(0)= \sigma_i^2 = 19.2 \lambda^{-7/6} \int {\rm d}h \; h^{5/6} C_N^2 \end{displaymath}$

(3)

and $\Delta C$ is the estimation error. Equation (2) can be written as:

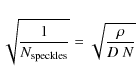$\begin{displaymath}\sqrt{\frac{1}{N_{\rm speckles}}}= \sqrt{\frac{\rho}{D~N}} \end{displaymath}$

(4)

where $\rho$ is the diameter of the spatial scintillation correlation, D the telescope diameter and N the number of images which have been analysed. Knowing that $\rho=0.67\sqrt{\lambda h}$ (Vernin & Azouit 1983b), the first Fresnel zone, and knowing that the scintillation index (Roddier 1981) for a given turbulent layer at altitude h is:

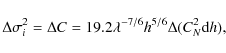$\begin{displaymath}\Delta\sigma_i^2=\Delta C = 19.2 \lambda^{-7/6} h^{5/6} \Delta(C_N^2{\rm d}h), \end{displaymath}$

(5)

one can relate the SSS detectivity $\Delta(C_N^2{\rm d}h)$ and the statistical noise through:

$\begin{displaymath} \Delta(C_N^2{\rm d}h)=0.042 C(0) \frac{\lambda^{17/12}h^{-7/12}}{\sqrt{DN}}\cdot \end{displaymath}$

(6)

This result allows us to determine the absolute error on the C_N²(h) profile and which will be used later in the text.

3 Observations at Dome C in 2006

3.1 Description of the observing campaign

The SSS instrument was designed and constructed in our laboratory and sent to Dome C, Antarctica, lat. $-75\hbox{$^\circ$ }$ 06', long. $123\hbox{$^\circ$ }$ 23'E at 3230 m altitude. It was designed to resist the harsh Antarctic conditions such as temperatures as low as $-80\hbox{$^\circ$ }$ C. All the motors and encoders driving the equatorial mount, as well as the optical bench, are thermo-regulated with resistors. The same star (Canopus, RA = 06 23 45, Dec = -52 41 44 and m_v=-0.72) was tracked all along the polar night. At Dome C latitude, Canopus is circumpolar and thus can be tracked 24 h a day, with an air mass comprized between 1.09 and 1.66. Due to the fact that SSS is not fully automatized, that the sky is not dark enough when the sun approaches the horizon and that ice crystals build up on the entrance window of the telescope, we use continuous observing windows of approximately 12-15 h, separated into smaller blocks of about one hour. From time to time a sky background correction is needed which requires that we remove Canopus from the CCD field of view.

Observations began in March 2006, ending in September of the same year. For the reason explained in Sect. 2, we present here only one observing ``night'', on 20 March 2006, of 6.5 h with comparisons to other types of measurements.

3.2 C _N²(h), V(h) and 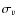$\sigma _{{v}}$ (h) profiles deduced from scintillation auto and cross-correlations

In Fig. 3, from left to right, an auto-correlation of the scintillation moving pattern and the first and second cross-correlations, taken respectively at $\Delta T= 7$ ms and 14 ms, are visible. In the second cross-correlation, several bumps are detected, each one corresponding to a different turbulent layer. In Fig. 4, the same cross-correlation computed at $\Delta T=14$ ms, as in Fig. 3, and the theoretical reconstructed cross-correlation at the end of the SA process have been plotted. All the bumps corresponding to different turbulent layers are well detected.

$\begin{figure} \par\includegraphics[width=9cm]{1119fig3} \end{figure}$	Figure 3: From left to right, two-dimensional auto-correlation, first and second cross-correlation of the scintillation pattern on the 40 cm entrance pupil of the telescope corresponding to time lags $1\Delta T$ and $2\Delta T$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{1119fig4} \end{figure}$	Figure 4: Measured temporal cross-correlation ( left) at $2\Delta T$ , and the same function after ``simulated annealing'' reconstruction ( right).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=18cm]{1119fig5} \end{figure}$

Figure 5:

Top left: median vertical profile of the optical turbulence on a logarithmic scale C_N²(h)and ${\pm} \sigma_{\log(CN2)}$ error bars. Top right: number of detected layers within 1 km slabs among the about 1900 profiles which have been analysed. Bottom left: mean wind speed modulus profile $\vert\vec{V}(h)\vert$ and ${\pm } \sigma$ error bars, of the rms variation of the wind speed $\sigma _v(h)$ and mean wind direction. Bottom right: mean vertical profile of the wind speed standard deviation $\sigma _V(h)$ . All profiles have been averaged over 6.5 h on 20 March 2006 with the SSS technique, at Dome C, Antarctica. Green dashed lines of the bottom figures refer to weather data extracted from the National Oceanic and Atmospheric Administration-Air Resources Laboratory. The dash-dotted line in the top-left panel refers to SSS detectivity corresponding to this particular period.

Open with DEXTER

4 Results

In Fig. 5 top panel, we present the mean vertical profiles averaged over the whole ``night'' of 20 March. For clarity, the four first layers at zero altitude have been averaged. Almost all the optical turbulence is concentrated within the surface layer, the rest being scattered through the free atmosphere, as reported by Trinquet et al. (2008). The dash-dotted line represents the detectivity of the SSS, as deduced from Eq. (6), with C(0)=0.1, N = 2000, $\Delta h = 1$ km and D = 0.4 m, which correspond to the observing conditions during this night. Close to the BL, the detectivity is about $4\times 10^{-18}$ , and less than 10^-18 above, in accordance with the threshold given in Sect. 2.1.

The wind speed, which corresponds to turbulent slabs, increases from ice level to reach 13 ms^-1 at 8 km and remains stable above. In Fig. 6, the temporal evolution of C_N²(h) (top) and $\vec{V}(h)$ (bottom) profiles during the same night are shown. For clarity, the free atmosphere and surface layer are plotted separately, one on top and the other at the bottom of each sub-figure. The first colored line, corresponding to a [0-1] km slab, refers to the average of the four turbulent slabs which are detailed below. It is clear again that most of the OT is concentrated within the surface layer, and that the free atmosphere is quite stable.

Trinquet et al. (2008) & Roddier (1981) showed that, from the knowledge of both C_N²(h) and $\vec{V}(h)$ , one can compute the seeing $\varepsilon _0$ , the isoplanatic angle for adaptive optics $\theta _0$ and the coherence time $\tau _0$ for adaptive optics.

It is clear that the greater r₀, $\theta _0$ and $\tau _0$ , the better the conditions for adaptive optics or interferometry. A more general approach is given by Lloyd (2004). He defines a ``coherence étendue'' G₀in which a photon remains coherent and which takes into account a combination of Fried's radius, isoplanatic angle and coherence time:

$\begin{displaymath}G_0\propto r_0^2 \tau_0 \theta_0^2. \end{displaymath}$

(7)

This new formulation shows a strong dependency on r₀ and $\theta _0$ . Fig. 7 shows the temporal evolution of the seeing, related to the integral of the optical turbulence, the coherence étendue G₀, the coherence time $\tau _0$ and the isoplanatic angle $\theta _0$ which can be deduced from the knowledge of optical turbulence and wind speed profiles. In Eq. (7), we arbitrarily chose to express r₀ in m, $\tau _0$ in ms and $\theta _0$ in arcsec. In red we plot the same parameter evolution, but only taking into account the free atmosphere, excluding the surface layer contribution. As expected, the whole atmosphere seeing varies between 0.25 and 1.5 arcsec and the free atmosphere seeing is between 0.1 and 0.5 arcsec. The isoplanatic angle is not affected by the surface layer. The coherence time is three times better when the surface layer is excluded. The coherence étendue, which is a combination of the three later parameters, is about 20 times better for a telescope above the surface layer.

From Fig. 7, one notes that the three variables, seeing, isoplanatic angle and coherence time vary on small time scales and with large amplitude.

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig6a} \includegraphics[angle=270,width=9cm]{1119fig6b} \end{figure}$	Figure 6: Temporal evolution of the optical turbulence C_n²(h,t) ( top) and of the wind speed modulus $\vert\vec{V}(h,t)\vert$ during 6.5 h on 20 March 2006.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig7} \end{figure}$

Figure 7:

From top left to bottom right: temporal evolution of the seeing $\varepsilon _0$ , the coherence étendue G₀ (see text), the isoplanatic angle $\theta _0$ and the time coherence $\tau _0$ as given by the SSS, same night as Fig. 5. Black dots refers to integrals over the whole atmosphere and red crosses to integrals above the surface layer. In both cases, ``mirror seeing'' has been removed according to the Sect. 2.1.

Open with DEXTER

5 Discussion

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig8} \end{figure}$	Figure 8: Temporal evolution of seeing measured by SSS (red crosses) and DIMM (line) during 6.5 h on 20 March 2006.
Open with DEXTER

During the 2006 polar winter a DIMM (Agabi et al. 2006) was operating on an other platform, 15 m away from the SSS platform, both at 8 m above ice level. The DIMM measures the seeing continuously and it allows a direct comparison with SSS seeing measurements. In Fig. 8, the temporal evolution of the seeing as measured by the DIMM (black line) and the SSS (red crosses) are superimposed. Both instruments are in very good agreement. From 17:15 to 17:30 some discrepancies are visible which can be explained by the fact that the distance between the two experiments, 15 m, is comparable to the thickness of the surface layer, 30 m, which accounts for 80% of the whole optical turbulence (Trinquet et al. 2008). The overall good agreement means that SSS detects all the turbulent layers in a quantitative way. We recall that SSS is an ``auto-calibrated'' instrument, where no calibration parameter is introduced. This is related to the fact that the scintillation variance $\sigma_I^2$ is auto-calibrated, by definition, with the square of the mean flux $\sigma_I^2={<I^2>}/{<I>^2}$ . In Fig. 9 we plot the DIMM seeing v.s the SSS seeing. The slope of the line is 0.97 with a 0.75 correlation coefficient. The regression slope is very close to 1 and seeing amplitude variations of both DIMM and SSS are between 0.2-0.5 and 1.5-1.7 arcsec.The SSS is even able to detect very low turbulence conditions, as shown in Fig. 10, where the seeing lies around 0.2-0.3 arcsec.

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig9} \end{figure}$	Figure 9: Correlation between seeings measured by SSS and DIMM.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig10} \end{figure}$	Figure 10: Temporal evolution of seeing measured by SSS (red crosses) and DIMM (line) during 0.5 h over 21 March 2006. 0.2 to 0.3 arcsec seeings are detected both by SSS and DIMM.
Open with DEXTER

In order to check for the validity of the wind speed deduced from SSS measurements, we used the National Oceanic and Atmospheric Administration re-analysis which is available on their web site (http://www.arl.noaa.gov/READYcmet.php). NOAA profiles are vertically sampled from ground level up to 26 km over 14 levels, starting at 0 UT, and every three hours a new re-analysis is issued. The first level, or Surface Level, corresponds to ${\sim}10$ m above ground. In the bottom of Fig. 5, NOAA wind speed and direction are plotted in green. Excellent agreement! Fig. 11 gives a comparison of the temporal evolution of the wind speed deduced from the first four levels of the SSS and the first two levels, 10m (rectangles) and 400 m (triangles) from the NOAA re-analysis. The wind speed at these two levels are compatible with the second and third SSS levels, at the surface layer.

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig11} \end{figure}$

Figure 11:

Temporal evolution of the wind speed modulus deduced from SSS measurements in the four layers within the boundary layer, with a one-hour sliding triangle convolution. The two measurements from NOAA re-analysis at $\sim$ 10 m and $\sim$ 400 m are in red stars and in red circles, plotted at 12, 15 and 18 UT. SSS wind measurements were convolved with a one hour, at half maximum, triangle function in order to smooth rapid variations, in comparison with the three hour delay between NOAA profiles.

Open with DEXTER

6 Conclusion

We have shown that the Single Star Scidar technique is extremely well suited for astronomical site characterization, even under he worst weather conditions on the high Antarctic plateau. The instrument is robust, reliable, well calibrated and allows the access of vertical profiles of both C_N²(h) and $\vec{V}(h)$ from groundlevel up to 20 km, with a temporal resolution of about 12 s, over tens of hours. These profiles allow us to assess most of the major parameters relevant to high angular resolution such as seeing, coherence time, isoplanatic angle and ``étendue volume'' G₀, which is a combination of the three last variables.

SSS seeing measurements obtained for 6.5 h on 20 March 2006 are consistent with other optical experiment like DIMM, even under very low turbulence conditions. SSS wind speed profiles are well comparable with NOAA meteorological re-analysis, from the ground up to 25 km. As expected, above the high Antarctica plateau, SSS shows the same optical turbulence distribution, mainly concentrated within the surface layer.

Acknowledgements

We are indebted to the technical staff of Fizeau laboratory for its help in the construction of the SSS prototype. We thank the Institut Paul-Emile Victor personnel as well as the members of Antarctica expedition who helped in the infrastructure at Dome C. The SSS prototype working at Dome C has been funded by the French ``Institut National des Sciences de l'Univers''. National Oceanic and Atmospheric Administration is acknowledged for access to its meteorological re-analysis profiles through its ARL web-site. Part of the development of the SSS technique was undertaken in the framework of the contract #F61775-02-C0002 with the US Air Force EOARD.

References

Agabi, A., Aristidi, E., Azouit, M., et al. 2006, PASP, 118, 344 [NASA ADS] [CrossRef] (In the text)
Avila, R., Vernin, J., & Sánchez, L. J. 2001, A&A, 369, 364 [NASA ADS] [CrossRef] [EDP Sciences]
Azouit, M., & Vernin, J. 2005, PASP, 117, 536 [NASA ADS] [CrossRef] (In the text)
Fuchs, A., Tallon, M., & Vernin, J. 1998, PASP, 110, 86 [NASA ADS] [CrossRef] (In the text)
Habib, A., Vernin, J., Benkhaldoun, Z., & Lanteri, H. 2006, MNRAS, 368, 1456 [NASA ADS] [CrossRef] (In the text)
Kornilov, V., Tokovinin, A. A., Vozyakova, O., et al. 2003, in Adaptive Optical System Technologies II., ed. P. L. Wizinowich, & D. Bonaccini, SPIE, 4839, 837 (In the text)
Lawrence, J. S., Ashley, M. C. B., Tokovinin, A., & Travouillon, T. 2004, Nature, 431, 278 [NASA ADS] [CrossRef] (In the text)
Lloyd, J. P. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, 5491, 190 (In the text)
Marks, R. D., Vernin, J., Azouit, M., Manigault, J. F., & Clevelin, C. 1999, A&AS, 134, 161 [NASA ADS] [CrossRef] [EDP Sciences]
Roddier, F. 1981, Prog. Optics, 19, 281 (In the text)
Trinquet, H., Agabi, A., Vernin, J., et al. 2008, PASP, 120, 203 [NASA ADS] [CrossRef] (In the text)
Vernin, J. 1994, in Recherches polaires: une stratégie pour l'an 2000, Académie des Sciences (Paris, Tec & Doc, Lavoisier), 91 (In the text)
Vernin, J., Agabi, A., Aristidi, E., et al. 2007, Highlights of Astronomy, 14, 693 [NASA ADS] (In the text)
Vernin, J., & Azouit, M. 1983a, Journal d'Optique, 14, 5 [NASA ADS]
Vernin, J., & Azouit, M. 1983b, Journal d'Optique, 14, 131 [NASA ADS] (In the text)
Wilson, R. W. 2002, MNRAS, 337, 103 [NASA ADS] [CrossRef] (In the text)

All Figures

$\begin{figure} \par\includegraphics[width=9cm]{1119fig1} \end{figure}$	Figure 1: Installation of the SSS above one of the two plateforms at Dome C during polar summer 2005-2006.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{1119fig2} \end{figure}$	Figure 2: Principle of the generalized SSS. After passing through the telescope, light is collimated by a short focal lens. In order to make the low altitude layers scintillate, the photoelectric receiver is displaced by a distance $\Delta z$ which corresponds to an altitude shift of $\Delta H=G^2\Delta z$ , where $G=F_{\rm telescope}/f_{\rm collimation}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{1119fig3} \end{figure}$	Figure 3: From left to right, two-dimensional auto-correlation, first and second cross-correlation of the scintillation pattern on the 40 cm entrance pupil of the telescope corresponding to time lags $1\Delta T$ and $2\Delta T$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{1119fig4} \end{figure}$	Figure 4: Measured temporal cross-correlation ( left) at $2\Delta T$ , and the same function after ``simulated annealing'' reconstruction ( right).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=18cm]{1119fig5} \end{figure}$	Figure 5: Top left: median vertical profile of the optical turbulence on a logarithmic scale C_N²(h)and ${\pm} \sigma_{\log(CN2)}$ error bars. Top right: number of detected layers within 1 km slabs among the about 1900 profiles which have been analysed. Bottom left: mean wind speed modulus profile $\vert\vec{V}(h)\vert$ and ${\pm } \sigma$ error bars, of the rms variation of the wind speed $\sigma _v(h)$ and mean wind direction. Bottom right: mean vertical profile of the wind speed standard deviation $\sigma _V(h)$ . All profiles have been averaged over 6.5 h on 20 March 2006 with the SSS technique, at Dome C, Antarctica. Green dashed lines of the bottom figures refer to weather data extracted from the National Oceanic and Atmospheric Administration-Air Resources Laboratory. The dash-dotted line in the top-left panel refers to SSS detectivity corresponding to this particular period.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig6a} \includegraphics[angle=270,width=9cm]{1119fig6b} \end{figure}$	Figure 6: Temporal evolution of the optical turbulence C_n²(h,t) ( top) and of the wind speed modulus $\vert\vec{V}(h,t)\vert$ during 6.5 h on 20 March 2006.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig7} \end{figure}$	Figure 7: From top left to bottom right: temporal evolution of the seeing $\varepsilon _0$ , the coherence étendue G₀ (see text), the isoplanatic angle $\theta _0$ and the time coherence $\tau _0$ as given by the SSS, same night as Fig. 5. Black dots refers to integrals over the whole atmosphere and red crosses to integrals above the surface layer. In both cases, ``mirror seeing'' has been removed according to the Sect. 2.1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig8} \end{figure}$	Figure 8: Temporal evolution of seeing measured by SSS (red crosses) and DIMM (line) during 6.5 h on 20 March 2006.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig9} \end{figure}$	Figure 9: Correlation between seeings measured by SSS and DIMM.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig10} \end{figure}$	Figure 10: Temporal evolution of seeing measured by SSS (red crosses) and DIMM (line) during 0.5 h over 21 March 2006. 0.2 to 0.3 arcsec seeings are detected both by SSS and DIMM.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=270,width=9cm]{1119fig11} \end{figure}$	Figure 11: Temporal evolution of the wind speed modulus deduced from SSS measurements in the four layers within the boundary layer, with a one-hour sliding triangle convolution. The two measurements from NOAA re-analysis at $\sim$ 10 m and $\sim$ 400 m are in red stars and in red circles, plotted at 12, 15 and 18 UT. SSS wind measurements were convolved with a one hour, at half maximum, triangle function in order to smooth rapid variations, in comparison with the three hour delay between NOAA profiles.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Homepage

Table of Contents