| Issue |
A&A
Volume 500, Number 3, June IV 2009
|
|
|---|---|---|
| Page(s) | 1089 - 1108 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200810841 | |
| Published online | 08 April 2009 | |
Planetary nebulae in the direction of the Galactic bulge:
on nebulae with emission-line central stars![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
S. K. Górny1 - C. Chiappini2,3 - G. Stasinska4 - F. Cuisinier5
1 - Copernicus Astronomical Center, Rabianska 8,
87-100 Torun, Poland
2 -
Geneva Observatory,
Geneva University,
51 Chemin des Maillettes,
1290 Sauverny, Switzerland
3 -
Osservatorio Astronomico di Trieste,
OAT-INAF,
via Tiepolo 11,
Trieste, Italy
4 -
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot,
Place Jules Janssen, 92190 Meudon, France
5 -
GEMAC, Observatório do Valongo/UFRJ,
Ladeira do Pedro Antônio 43, 20.080-090 Rio de Janeiro, Brazil
Received 21 August 2008 / Accepted 12 February 2009
Abstract
Aims. We present a homogeneous set of spectroscopic measurements secured with 4-m class telescopes for a sample of 90 planetary nebulae (PNe) located in the direction of the Galactic bulge.
Methods. We derive their plasma parameters and chemical abundances. For half of the objects this is done for the first time. We discuss the accuracy of these data and compare it with other recently published samples. We analyze various properties of PNe with emission-line central stars in the Galactic bulge.
Results. Investigating the spectra we found that 7 of those PNe are ionized by Wolf-Rayet ([WR]) type stars of the very late (VL) spectral class [WC 11] and 8 by weak emission-line (WEL) stars. From the analysis we conclude that the PN central stars of WEL, VL and remaining [WR] types form three, evolutionary unconnected forms of enhanced mass-loss among central stars of PNe. [WR] PNe seem to be intrinsically brighter than other PNe. Overall, we find no statistically significant evidence that the chemical composition of PNe with emission-line central stars is different from that of the remaining Galactic bulge PNe.
Key words: ISM: planetary nebulae: general -Galaxy: bulge - Galaxy: abundances - stars: Wolf-Rayet
1 Introduction
Planetary nebulae (PNe) are a short evolutionary phase in the life of low and intermediate mass stars occurring after they leave the Asymptotic Giant Branch (AGB). This basic fact was established decades ago (Shklovsky 1956; Paczynski 1971) yet the details of processes leading to the creation of the nebula and its subsequent evolution remain unclear. It is not known for example if the central stars (CSs) of PNe are predominantly hydrogen or helium burning. In fact, only for a small subclass of them, with spectra similar to massive Wolf-Rayet stars, do we know what is powering their evolution: since such stars are practically hydrogen free, they must be burning helium. For the remaining CSs it is believed that they are burning hydrogen in a shell and in fact most of the available evolutionary models assume hydrogen as a fuel of the nuclear reactions at these stages of evolution (see Górny & Tylenda 2000).
Table 1: Log of observations.
The atmospheres of Wolf-Rayet type CSs are peculiar and very different from
most CSs. Their outermost layers are mostly composed of helium, carbon and
oxygen (see review by Werner & Herwig 2006). They are also characterized by
enhanced mass-loss which triggers the occurrence of prominent stellar
emission bands of C, O and He. The origin of their name comes from the
appearance of their stellar spectra as they
closely resemble those of genuine massive Wolf-Rayet population I stars of
the WC spectral subclass. The similarity is so close that the same
classification scheme can be used (Crowther et al. 1998; Acker & Neiner 2003)![]() .
To mark the difference with population I WR stars, a notation between
brackets is used: [WR] or [WC].
.
To mark the difference with population I WR stars, a notation between
brackets is used: [WR] or [WC].
The general question of the origin of Wolf-Rayet type central stars
at the center of some PNe is one of the open problems in the PN
field. But [WR] PNe![]() have other secrets of their own. For example, it is not understood
why in the Milky Way there are so few CSs with intermediate-class [WC]
spectral types. Those that are known are located predominantly in the bulge
of our Galaxy while there is clearly an underpopulation of such objects in
the disk (Górny 2001). The picture of Galactic bulge/disk dichotomy of
[WR] PNe seemed to be disturbed when Górny et al. (2004) reported on a large number of
PNe central stars classified as [WC 11] in the bulge. Before that,
[WR] PNe of this type were known only in the Galactic disk. In addition,
the number of PNe with ``weak emission-line'' (WEL) central stars (a class
introduced by Tylenda et al. 1993) found by Górny et al. (2004) in the
bulge was also surprisingly high.
have other secrets of their own. For example, it is not understood
why in the Milky Way there are so few CSs with intermediate-class [WC]
spectral types. Those that are known are located predominantly in the bulge
of our Galaxy while there is clearly an underpopulation of such objects in
the disk (Górny 2001). The picture of Galactic bulge/disk dichotomy of
[WR] PNe seemed to be disturbed when Górny et al. (2004) reported on a large number of
PNe central stars classified as [WC 11] in the bulge. Before that,
[WR] PNe of this type were known only in the Galactic disk. In addition,
the number of PNe with ``weak emission-line'' (WEL) central stars (a class
introduced by Tylenda et al. 1993) found by Górny et al. (2004) in the
bulge was also surprisingly high.
In this paper we present new spectra of 90 PNe in the Galactic bulge direction. The goal of our observational program was to increase the sample of bulge PNe with homeogenous abundance determinations and to discover new emission-line CSs. Combined with high quality literature data we have gathered spectroscopic data of 245 PNe, most of them with a high probability of physically belonging to the bulge of the Milky Way. The remaining PNe most probably belong to the inner disk of our Galaxy. In this work, we use the spectroscopic information combined with other data to discuss the evolutionary status of Galactic bulge PNe with different types of emission-line CSs as compared to PNe with normal nuclei.
This paper is organized as follows. In Sect. 2 we present the observations and describe the reduction procedures. In Sect. 3 the data quality is assessed. In Sect. 4 we describe the method applied to derive the plasma parameters and abundances. In Sect. 5 for common objects we compare our results with those of other authors. Section 6 presents our newly discovered PNe with emission-line CSs including a discussion on their classification, rate of occurrence and selection effects, both in the bulge and inner disk samples. In Sect. 7 various properties of these objects are described and compared to normal PNe. A summary of our results and our conclusions can be found in Sect. 8.
2 Observations and reduction
We present results of spectroscopic observations of 90 PNe secured during three runs on two different 4-m class telescopes by C. Chiappini and F. Cuisinier. The observations were performed in July 2001 and April/May 2002 at the Cerro Tololo Interamerican Observatory (CTIO) using the RC-spectrograph attached to the 4-m telescope and in July 2002 with the 3.6 m telescope and the EFOSC II instrument of the European Southern Observatory (ESO). The log of observations is presented in Table 1.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f1.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg15.png) |
Figure 1: Distribution of the observed PNe in Galactic coordinates. Objects observed during different runs are marked: CTIO 2001 - squares, CTIO 2002 - diamonds, ESO 2002 - triangles. Objects observed during both seasons at CTIO are marked with circles. |
| Open with DEXTER | |
In Fig. 1 we show the sky distribution of the observed objects in
Galactic coordinates. Practically all these PNe can be regarded as belonging
to the Galactic bulge as they satisfy the standard criteria (Stasinska
& Tylenda 1994), namely: a) they are located within 10 degrees from the
center of the Galaxy; b) have diameters smaller than 20
![]() and c) known
radio fluxes at 5 GHz smaller than 100 mJy.
and c) known
radio fluxes at 5 GHz smaller than 100 mJy.
For the majority of PNe in our sample the presented spectroscopic observations allowed us to derive accurate plasma parameters and chemical abundances for the first time. For the remaining objects such data had already been published elsewhere, e.g. 24 PNe are in common with Górny et al. (2004) and 9 with Wang & Liu (2007). There are also 44 objects in common with Exter et al. (2004) however in this case information on some crucial diagnostic lines is often available only in our spectra.
A series of spectra with different exposures were taken for each observed PN. The times ranged from a few seconds to 1 h, to secure unsaturated detections of the strongest nebular lines as well as good signal for the weak but important features. On-sky projected slit apertures of 4 arcsec for PN observations and 10 arcsec in the case of standard star spectra were used. Each night at least three different standard stars (Feige 58, Feige 110, EG 274, GD 108 or LT 6248) were observed together with appropriate calibration lamp spectra, dome and sky flats.
The spectra obtained at CTIO have a spectral resolution R=1000 and span from
3900 Å to 7580 Å for observations taken in year 2001 and from
3700 Å to 7390 Å in 2002. The spectra obtained at ESO have a spectral
resolution of about R=2000 and span from 3600 Å to 7350 Å. In both cases,
due to the fact that no order blocking filters were used, the spectra of
standard stars can be contaminated in their red part with light coming from
the second order blue wing. The effect on PN spectra is much smaller
since most of the radiation is emitted in narrow lines. In some
PN observations, the use of broad-band filters is not desirable if one
is interested in registering blue lines, like the [O II] ![]() 3727 line. However
it is possible to use transmission curves as derived from
different standard stars of different effective temperatures to
disentangle the effects of second order contamination. In Appendix A we
describe our method to account for second order contamination during data
reduction and find that it adds only a few percent of
uncertainty in the line fluxes.
3727 line. However
it is possible to use transmission curves as derived from
different standard stars of different effective temperatures to
disentangle the effects of second order contamination. In Appendix A we
describe our method to account for second order contamination during data
reduction and find that it adds only a few percent of
uncertainty in the line fluxes.
Procedures from the long-slit spectral package of MIDAS![]() were used to
reduce and calibrate the spectra. These involved bias subtraction, flatfield
correction, atmospheric extinction correction, and wavelength and flux
calibration.
were used to
reduce and calibrate the spectra. These involved bias subtraction, flatfield
correction, atmospheric extinction correction, and wavelength and flux
calibration.
The 1-dimensional spectra of standard stars were obtained in the usual manner by summing over the appropriate rows of a sky-subtracted frame. In the case of PNe spectra a multi-step method had to be adopted. This was due to the fact that many lines of the observed nebulae are weak and that the objects are located in crowded Galactic bulge fields with many nearby contaminating stars. For this reason before extracting 1D spectra we removed all the underlying background sources leaving only nebular emission lines. This involved both sky continuum emission and telluric and interstellar lines (perpendicular to the dispersion direction) and all the stellar continuum components (spanning along the dispersion). The complicated system of contaminating features could not be satisfactorily removed in just one step. A separate fitting to both directions had to be performed starting from test removing of sky background components, followed by removing spectra of stars and finally performing a proper sky subtraction. In some cases this process had to be repeated in an iterative way.
The final step was to detect the nebular lines in the frame. The procedure we used considered that a signal can be attributed to a nebular line only if it was stronger than 2 sigmas of the averaged background noise and at least half of its neighboring pixels were also found above that level. In this way spatial contours of all secure nebular lines were established while the remaining background could be set to zero. After summing the frame in the direction perpendicular to the dispersion, a 1D spectrum of the PN was obtained. The applied procedure helps to maximize the S/N of weak nebular features as fewer noise-dominated pixels are integrated.
Intensities of the lines were measured from the 1D spectra by
employing the REWIA package![]() adopting Gaussian profiles and performing multi-Gaussian fits when necessary.
adopting Gaussian profiles and performing multi-Gaussian fits when necessary.
The line intensities have been corrected for extinction using an iterative
procedure, adopting the extinction law of Seaton (1979) in order to
reproduce the theoretical case B Balmer lines ratios at the electron
temperature and density derived for the object. For the CTIO and ESO
observations in 2002 the H![]() /H
/H![]() ratio was used while for the
CTIO 2001 observations only the H
ratio was used while for the
CTIO 2001 observations only the H![]() /H
/H![]() could be used
could be used![]() . Therefore the
line intensities for the latter subsample of observations have in fact been
derived with respect to H
. Therefore the
line intensities for the latter subsample of observations have in fact been
derived with respect to H![]() and only later recalculated to the
expected H
and only later recalculated to the
expected H![]() intensity.
intensity.
In the case of 2002 CTIO and ESO observations the basic reddening procedure
described above did not always give the theoretically expected ratios of
H![]() /H
/H![]() and/or H
and/or H![]() /H
/H![]() .
This is not unusual and can be
attributed to many factors like deviations from the adopted extinction law or
flux calibration problems (we have tried to evaluate the importance of such
effects, see below). It is crucial however that the intensities of the
[O III]
.
This is not unusual and can be
attributed to many factors like deviations from the adopted extinction law or
flux calibration problems (we have tried to evaluate the importance of such
effects, see below). It is crucial however that the intensities of the
[O III] ![]() 4363 and [O II]
4363 and [O II] ![]() 3727 lines are reddening-corrected in the best possible way.
For this reason we have applied an additional correction procedure (similar
to the one described in Górny et al. 2004) to bring the H
3727 lines are reddening-corrected in the best possible way.
For this reason we have applied an additional correction procedure (similar
to the one described in Górny et al. 2004) to bring the H![]() /H
/H![]() and/or H
and/or H![]() /H
/H![]() ratios to their theoretically expected values and
then used a proportional correction to all the nearby lines. The principal
refinement to the recipe described in Górny et al. (2004) was that we took
due consideration of the possible random errors involved in line
measurements and applied the procedure only if the deviations were
substantial compared to expected inaccuracies. We thus avoided translating
uncertainties from individual measurements of (sometimes rather weak)
H
ratios to their theoretically expected values and
then used a proportional correction to all the nearby lines. The principal
refinement to the recipe described in Górny et al. (2004) was that we took
due consideration of the possible random errors involved in line
measurements and applied the procedure only if the deviations were
substantial compared to expected inaccuracies. We thus avoided translating
uncertainties from individual measurements of (sometimes rather weak)
H![]() and H
and H![]() lines onto other lines.
lines onto other lines.
In Table 2![]() we present the dereddened intensities of all important lines on the
scale of H
we present the dereddened intensities of all important lines on the
scale of H![]() .
The lines additionally corrected in the way described above
are marked with ``c'' in the table.
.
The lines additionally corrected in the way described above
are marked with ``c'' in the table.
3 Evaluation of data quality
In the ESO 2002 observations the spectral resolving power of ![]() 2000
resulted in a substantial blending of the H
2000
resulted in a substantial blending of the H![]() line at 6563 Å with
the [N II] line at 6548 Å. Since the [N II]
line at 6563 Å with
the [N II] line at 6548 Å. Since the [N II] ![]() 6584/6548 ratio is given
by atomic physics to be 3.05, we obtained the H
6584/6548 ratio is given
by atomic physics to be 3.05, we obtained the H![]() intensity by
subtracting from the measured sum of H
intensity by
subtracting from the measured sum of H![]() and [N II]
and [N II] ![]() 6548
intensities the value of the [N II]
6548
intensities the value of the [N II] ![]() 6584 intensity divided by 3.05.
The cases when this approach was necessary are marked with ``b'' in Table 2.
The accuracy of the H
6584 intensity divided by 3.05.
The cases when this approach was necessary are marked with ``b'' in Table 2.
The accuracy of the H![]() line intensities obtained in such a way is
estimated to be around 10%.
line intensities obtained in such a way is
estimated to be around 10%.
The same mark ``b'' is placed for cases with strong blending of lines of the
[S II] ![]() 6731/6716 doublet. The accuracy of the inferred ratio of these two lines can
probably be as low as 40% in the most difficult cases marked additionally
with a colon (:b) in Table 2.
6731/6716 doublet. The accuracy of the inferred ratio of these two lines can
probably be as low as 40% in the most difficult cases marked additionally
with a colon (:b) in Table 2.
The accuracies of all the remaining line measurements are estimated to be of roughly 5%. This includes all direct sources of errors like photon shot noise as well as CCD readout, bias and sky background induced noises. The standard star measurement and interstellar/atmospheric extinction related uncertainties further increase the possible errors. In cases marked with a colon in Table 2 the uncertainty is around 20% and in the rare cases of extremely weak lines or lines contaminated with sky features or field stars (marked with semicolon) this can be as high as 40%.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f2.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg21.png) |
Figure 2:
Intensity ratio of the [O III] |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f3.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg23.png) |
Figure 3:
Relative differences in line measurements (reddening uncorrected) from two
different spectra at CTIO in 2001 and in 2002 as a function of line
intensity (
|
| Open with DEXTER | |
Because the ratios of some lines should be practically constant and are
known from atomic physics they can be used to evaluate the quality of
spectroscopic observations. One of them is the [O III] ![]() 5007/4959 line ratio which should be 2.98 (Storey & Zeippen
2000). Note that these lines are usually so bright they easily saturate and
therefore have to be extracted from the shortest exposure frames. The
measured values for our data are plotted in Fig. 2. The dispersion
of the observed ratios for the strong and intermediate brightness lines is
in agreement with the estimated 5% error of the line intensity
measurements
5007/4959 line ratio which should be 2.98 (Storey & Zeippen
2000). Note that these lines are usually so bright they easily saturate and
therefore have to be extracted from the shortest exposure frames. The
measured values for our data are plotted in Fig. 2. The dispersion
of the observed ratios for the strong and intermediate brightness lines is
in agreement with the estimated 5% error of the line intensity
measurements![]() .
.
We have tried also to use the already mentioned [N II] ![]() 6584/6548
ratios derived from our spectra. In this case the deviations from the
theoretical value turned out to be much larger. We have checked, however,
that the main reason for the discrepancy is due to contamination of [N II]
6584/6548
ratios derived from our spectra. In this case the deviations from the
theoretical value turned out to be much larger. We have checked, however,
that the main reason for the discrepancy is due to contamination of [N II] ![]() 6548 line from the wing of the strong adjacent H
6548 line from the wing of the strong adjacent H![]() line. It
therefore turns out that the [N II]
line. It
therefore turns out that the [N II] ![]() 6584/6548 ratio is simply not
applicable as a tracer of line measurement quality for our observations.
6584/6548 ratio is simply not
applicable as a tracer of line measurement quality for our observations.
A final test of the accuracy of line measurements is shown in
Fig. 3. This plot presents relative differences of all lines of 4 PNe (H 2-1, H 1-9, M 2-11 and H1-46) registered during CTIO observations
in 2001 and repeated in 2002. In this case the differences reflect the
combined effect of more factors since during the two nights e.g. standard star
selection could be different and the atmospheric conditions or detailed
instrument settings are certainly not identical. As can be seen in
Fig. 3, most of the differences in line measurements are again
within 5% and only very few exceed 10%. Many of the outlying points
correspond to lines already acknowledged to be uncertain while inspecting
the spectra and measuring the line intensities (open symbols). It is
important to note that the measurement of the [O II] ![]() 7325 lines seems
to be rather uncertain (shown with larger symbols) even though their
intensities are relatively high - at the level of 1/10 of the H
7325 lines seems
to be rather uncertain (shown with larger symbols) even though their
intensities are relatively high - at the level of 1/10 of the H![]() intensity. This is due to the difficulty in establishing the instrument
response function with a high confidence at both extreme red and
blue ends of the spectral range
intensity. This is due to the difficulty in establishing the instrument
response function with a high confidence at both extreme red and
blue ends of the spectral range![]() . An additional argument for a systematic rather than statistical character
of these errors is that they are biased in the same direction in all four
PNe presented in Fig. 3. With CTIO 2001 observations the [O II]
. An additional argument for a systematic rather than statistical character
of these errors is that they are biased in the same direction in all four
PNe presented in Fig. 3. With CTIO 2001 observations the [O II] ![]() 7325 intensities seem always larger than in CTIO 2002. For this reason
we have adopted 10% as a default error for [O II]
7325 intensities seem always larger than in CTIO 2002. For this reason
we have adopted 10% as a default error for [O II] ![]() 7325 measurements in further calculations.
7325 measurements in further calculations.
4 Plasma parameters and chemical abundances
We use the classical empirical method to derive the plasma parameters.
First, the electron densities are deduced from the [S II] ![]() 6731/6716 ratio and electron
temperatures from the [O III]
6731/6716 ratio and electron
temperatures from the [O III] ![]() 4363/5007 and/or [N II]
4363/5007 and/or [N II] ![]() 5755/6584 ratios. These are used to refine
the inferred reddening correction as described above. The chemical
abundances are derived with the code ABELION as in Górny et al. (2004),
but the atomic data have been updated using sources listed in Stasinska
(2005) as well as Tayal (2007) for [O II] and Porter et al. (2007) for He I.
5755/6584 ratios. These are used to refine
the inferred reddening correction as described above. The chemical
abundances are derived with the code ABELION as in Górny et al. (2004),
but the atomic data have been updated using sources listed in Stasinska
(2005) as well as Tayal (2007) for [O II] and Porter et al. (2007) for He I.
The [N II] ![]() 5755 and [O II]
5755 and [O II]
![]()
![]() 7320,7330 lines can be affected by recombination from
N++ and O++ ions. This was taken into account by using the
expressions given in Liu et al. (2000), the [N II]
7320,7330 lines can be affected by recombination from
N++ and O++ ions. This was taken into account by using the
expressions given in Liu et al. (2000), the [N II] ![]() 5755/6584 temperature and assuming
that N++/H = O++/H
5755/6584 temperature and assuming
that N++/H = O++/H ![]() N+/O+. This has a negligible
effect on the computed abundances. The real effect could be larger if, as
suggested by Liu (2006, and references therein), the recombination lines were
actually coming from a much cooler zone. In the most extreme cases from Wang
& Liu (2007), where the observational data allow a better correction for
the effect of recombination, the resulting abundances are modified by a few
percent at most.
N+/O+. This has a negligible
effect on the computed abundances. The real effect could be larger if, as
suggested by Liu (2006, and references therein), the recombination lines were
actually coming from a much cooler zone. In the most extreme cases from Wang
& Liu (2007), where the observational data allow a better correction for
the effect of recombination, the resulting abundances are modified by a few
percent at most.
Thus the recombination contribution cannot solve the known problem of a
frequent difference in O+ ionic abundance derived from ![]() 7325 as
compared to
7325 as
compared to ![]() 3727. The discrepancy between these two O+ values
varies from object to object. For some PNe there is almost perfect agreement
while for other PNe the difference exceeds a factor of 2. We have noticed
however that the abundance ratios O+(
3727. The discrepancy between these two O+ values
varies from object to object. For some PNe there is almost perfect agreement
while for other PNe the difference exceeds a factor of 2. We have noticed
however that the abundance ratios O+(![]() 3727)/O+(
3727)/O+(![]() 7325)
that we derive seem to cluster around a value characteristic for a given
observing run and PN environment (e.g. bulge or inner-disk objects). We have
therefore used the relevant median ratio to correct the
O+(
7325)
that we derive seem to cluster around a value characteristic for a given
observing run and PN environment (e.g. bulge or inner-disk objects). We have
therefore used the relevant median ratio to correct the
O+(![]() 7325) abundance down when necessary to obtain an O+estimation scaled to the value expected from the O+(
7325) abundance down when necessary to obtain an O+estimation scaled to the value expected from the O+(![]() 3727) line. For
example, in the case of CTIO 2002 when the blue O+ line was not observed
due to high extinction, a factor of 0.66 was used to correct the other line. The
same factor was applied to CTIO 2001 observations that all missed the [O II]
3727) line. For
example, in the case of CTIO 2002 when the blue O+ line was not observed
due to high extinction, a factor of 0.66 was used to correct the other line. The
same factor was applied to CTIO 2001 observations that all missed the [O II] ![]() 3727 line since it was outside the observed range. Thanks to this procedure, the
results are not biased by the selection of data sources (whether the
3727 line since it was outside the observed range. Thanks to this procedure, the
results are not biased by the selection of data sources (whether the
![]() 3727 could be registered in a particular observing run) or the line
being unobserved for some PNe (e.g. due to high extinction). In a last step
if there were O+ estimates from both lines a final value for a given PN
was calculated by taking an average weighted by their respective
uncertainties.
3727 could be registered in a particular observing run) or the line
being unobserved for some PNe (e.g. due to high extinction). In a last step
if there were O+ estimates from both lines a final value for a given PN
was calculated by taking an average weighted by their respective
uncertainties.
Table 4: Differences in dex on plasma parameters and chemical abundances adopting data from this work versus data taken from the literature. The number of analyzed PNe in common is given in parenthesis.
The uncertainties in abundance ratios and other derived parameters were obtained by propagating uncertainties in the observed emission line intensities using Monte-Carlo simulations. It should be noted that our approach does not take into account such sources of possible errors like variations in extinction law or unknown structure of the nebulae. This should be compensated to some degree by our conservative assumption of line intensity errors of at least 5% even for the strongest lines. In order to avoid dealing with uncertain values we remove from consideration any parameter for which the two-sigma error from the Monte-Carlo simulation is larger than 0.3 dex. In cases where we will include more uncertain parameters, this will be indicated.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f4.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg27.png) |
Figure 4:
The electron temperature derived from [O III] |
| Open with DEXTER | |
Similarly to Górny et al. (2004) we use ![]() (N II), the temperature
derived from [N II]
(N II), the temperature
derived from [N II] ![]() 5755/6584 for lines from ions with low ionization potential
(S+, N+, O+) and
5755/6584 for lines from ions with low ionization potential
(S+, N+, O+) and ![]() (O III), the temperature derived from
[O III]
(O III), the temperature derived from
[O III] ![]() 4363/5007 for hydrogen and lines from other ions with intermediate and high
ionization potentials. If neither of these temperatures is available (only 6
cases) we refrain from abundance determinations. In Fig. 4 we plot
4363/5007 for hydrogen and lines from other ions with intermediate and high
ionization potentials. If neither of these temperatures is available (only 6
cases) we refrain from abundance determinations. In Fig. 4 we plot
![]() (O III) versus
(O III) versus ![]() (N II) for our PN data. The observed
behavior of these temperatures is quite similar to the one shown in Fig. 2
of Górny et al. (2004). The only difference is that in the new sample there are no PNe
with measured values of
(N II) for our PN data. The observed
behavior of these temperatures is quite similar to the one shown in Fig. 2
of Górny et al. (2004). The only difference is that in the new sample there are no PNe
with measured values of ![]() (O III) larger than 16 000 K. As in Górny et al. (2004) in about 25% of cases
(O III) larger than 16 000 K. As in Górny et al. (2004) in about 25% of cases ![]() (N II) was very uncertain and we used the
(N II) was very uncertain and we used the
![]() (O III) for all the ions.
(O III) for all the ions.
After computing ionic abundances, the elemental abundances are obtained
using the ionization correction factors (ICFs) from Kingsburgh & Barlow
(1994). In the present work we derive additionally the abundance of
chlorine, adopting the ICF from Liu et al. (2000).
Table 3![]() lists
the plasma diagnostics and ionic and elemental abundances ordered by PN G
numbers. In this table, there are three rows for each object, and a fourth
row used to separate them. The first row gives the values of parameters
computed from the nominal values of the observational data. The second and
third row give the upper and lower limits respectively of these parameters.
Column (1) of Table 3 gives the PNG number; Col. (2) gives the usual name
of the PN; Col. (3) gives the electron density deduced from [S II]
lists
the plasma diagnostics and ionic and elemental abundances ordered by PN G
numbers. In this table, there are three rows for each object, and a fourth
row used to separate them. The first row gives the values of parameters
computed from the nominal values of the observational data. The second and
third row give the upper and lower limits respectively of these parameters.
Column (1) of Table 3 gives the PNG number; Col. (2) gives the usual name
of the PN; Col. (3) gives the electron density deduced from [S II] ![]() 6731/6716; Cols. (4) and (5) give the electron temperature deduced from [O III]
6731/6716; Cols. (4) and (5) give the electron temperature deduced from [O III] ![]() 4363/5007 and [N II]
4363/5007 and [N II] ![]() 5755/6584 respectively (the value of
5755/6584 respectively (the value of ![]() (N II) is in parenthesis if
(N II) is in parenthesis if ![]() (O
III) was chosen for all ions). Column (6) gives the He/H ratio, Cols. (7) to (12) the N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the logarithmic extinction C at HH
(O
III) was chosen for all ions). Column (6) gives the He/H ratio, Cols. (7) to (12) the N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the logarithmic extinction C at HH![]() derived from the spectra.
derived from the spectra.
5 Comparison with other samples
We now compare the quality of our results with previously published data. For this purpose we derived the plasma parameters and abundances using exactly the same procedures, assumptions and atomic data for the objects of the sample introduced here and taking the data of PNe originally observed by Górny et al. (2004), objects observed by Escudero & Costa (2001) and Escudero et al. (2004) and also those of Wang & Liu (2007). In the latter case we used only the optical data to be consistent with what was available from our own observations. Finally, the same method was applied to objects from Exter et al. (2004).
First we analyse the electronic temperatures. Columns 2 and 3 of Table 4
present the median of the differences of derived temperatures for PNe in
common between this work and other samples. As it can be seen, the agreement
between the different authors is good, typically well below 0.1 dex. The
differences are therefore of the same order as individual errors derived
with the Monte-Carlo method, suggesting that our error estimates were
reasonable. Larger differences are found with respect to the PNe in common
with Exter et al. (2004). Inspecting the individual cases of PNe
with ![]() (N II) much larger than
(N II) much larger than ![]() (O III) we have noticed that
usually this property is confirmed by data of different observers.
(O III) we have noticed that
usually this property is confirmed by data of different observers.
The derived electron densities from [S II] ![]() 6731/6716 ratio for objects in common
between different samples are compared in Col. 4 of Table 4. As can be
seen the agreement is also usually good. However, for objects with weaker
lines we have checked that the deviations are larger, especially with
respect to the Exter et al. (2004) sample.
6731/6716 ratio for objects in common
between different samples are compared in Col. 4 of Table 4. As can be
seen the agreement is also usually good. However, for objects with weaker
lines we have checked that the deviations are larger, especially with
respect to the Exter et al. (2004) sample.
The typical differences in O/H between the computations using our data and literature data are within 0.1 dex (Col. 5 of Table 4). Only comparing with data from Exter et al. (2004) did we find a typical difference of almost 0.2 dex. What is more important however, is that we noticed that using measurements from Exter et al. (2004) would make the observed O/H distribution of bulge PNe much broader simply due to the lower quality of that data. In particular, analyzing PNe in common with our list of targets one finds in Exter et al. (2004) three cases with log O/H > 9 - a value that otherwise seems a strong upper cut off for derived oxygen abundances of PNe in the Galactic bulge direction (compare with Fig. 11 of Górny et al. 2004 and a discussion on possible flattening of the O/H gradient or see Fig. 15 below).
In Cols. 6 and 7 of Table 4 we present differences in derived N/O and S/Ar. In the latter cases the uncertainties can be larger, particularly when the lines are extremely weak. In addition, the S/Ar ratios of Exter et al. (2004) are systematically lower than what we find.
From the results presented in this section we can conclude that the quality
of our data is comparable to that found in the best recent literature
sources. On the other hand, the comparison with Exter et al. (2004) shows our
data to be of superior quality, especially for ![]() and O/H. This is
probably due to the indirect flux calibration procedure adopted by Exter
et al. In addition, due to the apparently lower sensitivity of their
observations, temperature diagnostic lines are not available for about 40%
of the PNe included in Exter et al. (2004), making the data unusable for
abundance determinations.
and O/H. This is
probably due to the indirect flux calibration procedure adopted by Exter
et al. In addition, due to the apparently lower sensitivity of their
observations, temperature diagnostic lines are not available for about 40%
of the PNe included in Exter et al. (2004), making the data unusable for
abundance determinations.
6 Discovery of new emission-line central stars
6.1 Spectra of the newly discovered objects
With our new uniform high quality spectra of 90 PNe seen in the direction of the Galactic bulge we were able to perform a search for new emission-line CSs. This was motivated by the previous search for such objects towards the Galactic bulge, which revealed a large number of very late type [WR] CSs (see Fig. 6 of Górny et al. 2004) and several new WEL CSs. As mentioned in Sect. 1, this was unexpected, since no [WC 11] CSs were known previously in this zone. It seemed therefore that the distribution of spectral [WC] types among objects located in the Galactic bulge was different from that in the Galactic disk, but not in the way assumed by Górny (2001).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0841f5a.eps}\par\vspace*{2...
...s}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{0841f5g.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg28.png) |
Figure 5: Spectra of the new VL PNe (very late type [WC 11]-like emission-line central stars PNe). |
| Open with DEXTER | |
In the present work we discovered a further 7 CSs with very late emission-line
spectra![]() (hereafter called VL).
With the classical classification scheme (Hu & Bibo 1990) they would be
described as [WC 11]. The spectra are presented in Fig. 5.
Both C III
(hereafter called VL).
With the classical classification scheme (Hu & Bibo 1990) they would be
described as [WC 11]. The spectra are presented in Fig. 5.
Both C III ![]() 5695 and C II
5695 and C II ![]() 7235 lines can be
identified while the C IV
7235 lines can be
identified while the C IV ![]() 5805 feature is absent. The list of
stellar emission lines we looked for was the same as in Górny et al. (2004).
5805 feature is absent. The list of
stellar emission lines we looked for was the same as in Górny et al. (2004).
As in the case of objects discovered by Górny et al. (2004) the nebulae surrounding
[WC 11] stars in the bulge are all of very low ionization with spectra
dominated by the [N II] doublet and hydrogen Balmer series. Only for two of
these PNe (H 2-1 and H 1-9) are the central stars apparently hot enough,
leading to an [O III] ![]() 5007 intensity comparable to that of H
5007 intensity comparable to that of H![]() .
The
same was found by Górny et al. (2004) for M 3-17. For all the other PNe
with [WC 11] CSs in our sample, the [O III]
.
The
same was found by Górny et al. (2004) for M 3-17. For all the other PNe
with [WC 11] CSs in our sample, the [O III] ![]() 5007 line (often the strongest
nebular line in normal PNe) is either undetectable or at a level of a few
percent of H
5007 line (often the strongest
nebular line in normal PNe) is either undetectable or at a level of a few
percent of H![]() .
This means that there are no conditions for higher
ionization potential ions in the nebula and at least the C III
.
This means that there are no conditions for higher
ionization potential ions in the nebula and at least the C III
![]() 5695 line has to be of stellar origin. Some nebular contribution to
the recombination C II
5695 line has to be of stellar origin. Some nebular contribution to
the recombination C II ![]() 7235 cannot however be totally ruled
out. The objects with the highest probability of such contribution are
H 1-9 and Ap 1-12. It is interesting that other extremely low ionization
PNe in the bulge do show the C II recombination line (the C III
bands are not observed) though in most cases the emission clearly comes from
a spatially extended region and is therefore of nebular nature.
7235 cannot however be totally ruled
out. The objects with the highest probability of such contribution are
H 1-9 and Ap 1-12. It is interesting that other extremely low ionization
PNe in the bulge do show the C II recombination line (the C III
bands are not observed) though in most cases the emission clearly comes from
a spatially extended region and is therefore of nebular nature.
We also identified 8 new WEL PNe![]() .
According to the definition of Tylenda et al. (1993), the spectra of these
objects usually present only the C IV emission at 5805 Å and
this feature is anyhow much weaker and narrower than in [WR] PNe. The spectra of
the new WEL CSs are shown in Fig. 6. Two of these objects were
previously inspected by Górny et al. (2004) but no emission lines were
detected. On the other hand none of the previously known [WR] or WEL CSs
escaped identification
.
According to the definition of Tylenda et al. (1993), the spectra of these
objects usually present only the C IV emission at 5805 Å and
this feature is anyhow much weaker and narrower than in [WR] PNe. The spectra of
the new WEL CSs are shown in Fig. 6. Two of these objects were
previously inspected by Górny et al. (2004) but no emission lines were
detected. On the other hand none of the previously known [WR] or WEL CSs
escaped identification![]() .
.
6.2 Number of objects
With the aim of performing a statistical analysis of the population of PNe with emission-line CSs we combined our present sample with the ones of Cuisinier et al. (2000), Escudero & Costa (2001), Escudero et al. (2004), Górny et al. (2004) and Wang & Liu (2007). These PNe can be divided into two distinct populations: one composed of the objects pertaining physically to the Galactic bulge and a second with most of the objects related to the Galactic inner-disk. To distinguish the members of the first group, hereafter referred to as the b subsample, we used the same criteria as in Górny et al. (2004). The objects that do not fulfill these criteria are likely to be located in the disk (the d subsample). Since all of the latter have been chosen at small angular distances from the center of the Galaxy, the majority of them probably belongs to the inner-disk population. It has been shown by Górny et al. (2004) that although the abovementioned selection criteria do not contain any reference to kinematical properties, a clear distinction can be observed also in radial velocities of the members of the b and d subsamples (see Figs. 12 and 13 of Górny et al. 2004). Of course, as the criteria are of a statistical nature, individual objects assigned to one of the groups may in reality belong to a different population. This can be also the case of some PNe with emission-line CSs as discussed in the next section.
![\begin{figure}
\par\includegraphics[width=5.78cm,clip]{0841f6a.eps}\par\vspace*{...
...par\vspace*{1.1mm}
\includegraphics[width=5.78cm,clip]{0841f6h.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg29.png) |
Figure 6: Spectra of the newly discovered WEL PNe (weak emission-line central stars PNe). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0841f7.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg30.png) |
Figure 7:
The relation of apparent diameter and reddening corrected H |
| Open with DEXTER | |
6.3 Selection effects
In Fig. 7 we show the reddening corrected H![]() fluxes of
the PNe from our subsample b as a function of their apparent diameters. As
all of the nebulae under consideration should be located at approximately
8.5 kpc, the distance-dependence of both parameters can be ignored in this
case. PNe with emission-line CSs are represented by large symbols. The PNe
with CSs that do not exhibit emission lines are marked with small black
symbols. We will refer to them as normal or other PNe throughout
the rest of this text.
fluxes of
the PNe from our subsample b as a function of their apparent diameters. As
all of the nebulae under consideration should be located at approximately
8.5 kpc, the distance-dependence of both parameters can be ignored in this
case. PNe with emission-line CSs are represented by large symbols. The PNe
with CSs that do not exhibit emission lines are marked with small black
symbols. We will refer to them as normal or other PNe throughout
the rest of this text.
It is striking that the [WR] PNe are among the brightest PNe of the subsample. Extrapolating this property of the b sample to other samples of PNe, we can infer that the estimated occurrence frequency of [WR] PNe can be severely biased in magnitude limited samples. This could explain why, in external galaxies, the rate of occurrence of [WR] PNe is much higher than in our Galaxy (e.g. in the Sagittarius dwarf galaxy, see Zijlstra et al. 2006).
There are some outliers. One of them is M 2-8 (PN G 352.1+05.1) a [WR] PN
with ![]() (H
(H![]() )0=-11.6 and a central star classified as [WC 2-3].
Its angular position is 9.4 arcsec away from the center of Galaxy so it is
very close to the border value of 10 arcsec usually adopted to define bulge
objects. The physical distance from the Sun can be evaluated with
statistical methods (see next section) as 10.7 to 13.3 kpc. It is therefore
not excluded that this PN is actually located behind the bulge region. The
radial velocity
)0=-11.6 and a central star classified as [WC 2-3].
Its angular position is 9.4 arcsec away from the center of Galaxy so it is
very close to the border value of 10 arcsec usually adopted to define bulge
objects. The physical distance from the Sun can be evaluated with
statistical methods (see next section) as 10.7 to 13.3 kpc. It is therefore
not excluded that this PN is actually located behind the bulge region. The
radial velocity
![]()
![]() of only 2.8 km s-1 is also not in contradiction with
the hypothesis that M 2-8 more likely belongs to the disk population (see
Figs. 12 and 13 of Górny et al. 2004).
of only 2.8 km s-1 is also not in contradiction with
the hypothesis that M 2-8 more likely belongs to the disk population (see
Figs. 12 and 13 of Górny et al. 2004).
The other nebulae outlying their group location in Fig. 7 are
M 1-27 (PN G356.5-02.3) and Ap 1-12 (PNG 003.3-04.6) of VL type. In this
case both the large observed diameter and H![]() brightness do not fit the
rest of VL PNe and seem too large. The distance estimation gives 4 to about
6 kpc for both of them - almost half of what is usually adopted as a
distance to the Galactic bulge. One could therefore suspect that in reality
these PNe are disk objects located in the foreground of the bulge. The
radial velocities of M 1-27 is
brightness do not fit the
rest of VL PNe and seem too large. The distance estimation gives 4 to about
6 kpc for both of them - almost half of what is usually adopted as a
distance to the Galactic bulge. One could therefore suspect that in reality
these PNe are disk objects located in the foreground of the bulge. The
radial velocities of M 1-27 is
![]() km s-1 and not in contradiction
with the object belonging either to the disk or to the bulge system. In the
case of Ap 1-12 the
km s-1 and not in contradiction
with the object belonging either to the disk or to the bulge system. In the
case of Ap 1-12 the
![]() km s-1 clearly indicates however that the
PN should be kinematically associated with the bulge system.
km s-1 clearly indicates however that the
PN should be kinematically associated with the bulge system.
If having a high brightness nebula is a general property of [WR] PNe in different galactic systems it would explain why so many previously known [WR] PNe are missing in our d subsample. The reason is that most of the targets included in the present analysis (except for observations by Cuisinier et al. 2000 and Wang & Liu 2007) were secured in programs deliberately concentrated on obtaining spectra for the previously unobserved or poorly observed PNe that are intrinsically fainter. Given the fact that [WR] PNe are probably the brightest PNe in a given population, this will certainly introduce a bias in the estimated occurrence frequency. In the samples limited to only the brightest PNe the relative number of [WR] PNe could be overestimated. In the case of our d subsample, on the contrary, many [WR] PNe have been excluded.
Figure 7 shows that VL PNe are generally at least a factor 2 weaker than [WR] PNe. This is a first indication that these classes should be analyzed separately. The number of WEL PNe and that of VL PNe can easily be underestimated in samples limited to only the brightest PNe. However in the case of our d sample, since it is biased towards low luminosity PNe as mentioned above, the fraction of WEL PNe and VL PNe is expected to be larger than in a complete inner-disk sample.
6.4 Rate of occurrence
Assuming that the abovementioned selection effects are nonetheless small for VL PNe we can attempt a comparison of their rate of occurrence in the Galactic bulge and inner-disk. The 14 VL PNe from the b sample represent 7.8% of the total number of PNe in this sample, whereas the single confirmed VL PN in our d sample suggests 1.5% in the inner-disk. However, if we consider that Ap 1-12 and/or M 1-27 are also in fact located in the disk rather than bulge then the difference will substantially diminish. Given the small absolute numbers involved, it is therefore not certain that there is a statistically meaningful difference in the rate of occurrence of VL PNe between these two Galactic populations. On the other hand, the observational selection effects do not have to work in favor of detecting relatively more VL PNe in the d sample (see discussion in Górny et al. 2004).
Analyzing the spectra of VL PNe, an easily noticeable property is that they
are associated with PNe of very low excitation. Eight out of fourteen VL PNe
in the b sample have [O III] ![]() 5007 lines either not detected or
fainter than 1% of H
5007 lines either not detected or
fainter than 1% of H![]() .
In only one object, H 1-9, this line is
stronger than H
.
In only one object, H 1-9, this line is
stronger than H![]() .
We can therefore check if the relatively high number
of VL PNe found in the Galactic bulge is not related to the fact that they
are associated with a particular population of very low-ionization PNe
possibly more frequent in this region. In our b sample there are 21 (12.1%) PNe with [O III]
.
We can therefore check if the relatively high number
of VL PNe found in the Galactic bulge is not related to the fact that they
are associated with a particular population of very low-ionization PNe
possibly more frequent in this region. In our b sample there are 21 (12.1%) PNe with [O III] ![]() 5007 < H
5007 < H![]() ,
whereas in the d sample there are 5
such objects (8.5%). The relative population of very low-ionization PNe in
both subsamples is therefore similar. Unfortunately, again the
absolute numbers are too small to judge if the fact that VL CSs have been
found in 67% of low ionization PNe in the b subsample is statistically
significant. An analysis of a much larger number of inner-disk PNe would be
necessary to conclude if the rate of occurrence of VL PNe in the disk
(presently derived as
,
whereas in the d sample there are 5
such objects (8.5%). The relative population of very low-ionization PNe in
both subsamples is therefore similar. Unfortunately, again the
absolute numbers are too small to judge if the fact that VL CSs have been
found in 67% of low ionization PNe in the b subsample is statistically
significant. An analysis of a much larger number of inner-disk PNe would be
necessary to conclude if the rate of occurrence of VL PNe in the disk
(presently derived as ![]() 20% to
20% to ![]() 40%) is indeed much lower than in
the bulge.
40%) is indeed much lower than in
the bulge.
Finally, assuming that the selection effects are reasonably small also for WEL PNe, we can evaluate their rates in both subsamples. There are 25 (or 14.5%) such objects in the b subsample and 10 (16.9%) of them in d subsample. Obviously there is no difference in the frequency of occurrence of WEL PNe in both groups despite the fact that the Galactic bulge and inner disk PNe should originate from different stellar populations and different epochs of Galactic evolution.
In conclusion, as can be seen from the above considerations, the answer to the question of how frequent are the different types of emission-line CSs remains open, until additional similarly large and uniform samples of deep PNe spectra are collected. In particular, the analysis of PNe in the Milky Way inner-disk should shed more light on the connection between VL PNe and low excitation nebulae (Górny, in preparation). Since the number of low excitation PNe is relatively easy to establish (e.g. using existing surveys) it would help to investigate if the presence of the VL PNe group is characteristic only of the metallicity/age conditions of the bulge population. It cannot be totally excluded that the surprisingly large number of discoveries of VL PNe by Górny et al. (2004) and this work is simply due to the fact that they were not expected to exist and therefore not searched for by surveys of other Galactic regions.
7 Properties of the bulge PNe with emission-line central stars
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0841f8.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg35.png) |
Figure 8: Locations of different types of bulge PNe in Galactic coordinates (absolute values). The meaning of the symbols is the same as in Fig. 7. |
| Open with DEXTER | |
The aim of this section is to compare the properties of PNe with emission-line CSs with the ``normal'' ones. We will restrict our analysis to PNe with emission-line CSs of our b subsample, i.e. pertaining to the Galactic bulge. This sample is more numerous, statistically more meaningful and likely more complete and homogeneous than the much smaller d subsample we have collected.
7.1 Spatial distribution
We begin with the simplest property i.e. the spatial distribution on the sky in the Galactic coordinates l,b (Fig. 8). Because of the small number of objects we present the absolute values of the coordinates assuming a perfect point-symmetry of the bulge PNe distribution. It is clear from Fig. 8 that the locations of [WR] PNe, WEL PNe and VL PNe differ, suggesting that they may originate from different populations of stars.
More than a half of bulge [WR] PNe are located at longitudes
larger than 4.5 degrees from the Galactic center, whereas there are very few
WEL PNe and VL PNe at such locations. From simple geometric considerations
the [WR] PNe seem therefore to form the most external system and it would be
tempting to consider the [WR] PNe as members of the inner disk
population and not physically pertaining to the bulge. Indeed, the object
with the largest angular separation from the center is M 2-8, already
suspected to belong to the Galactic disk based on its relatively low
H![]() flux and low radial velocity. The other [WR] PNe seem however not in
contradiction in this respect with their bulge association. On the other
hand, the distances of [WR] PNe derived with the
Shklovsky statistical method suggest they could be located at 4.3 kpc i.e.
only half-way to the bulge. We strongly argue however (see the next
section) that these distances are not reliable because the common
assumptions, e.g. on the typical nebular mass, are not met by [WR] PNe.
flux and low radial velocity. The other [WR] PNe seem however not in
contradiction in this respect with their bulge association. On the other
hand, the distances of [WR] PNe derived with the
Shklovsky statistical method suggest they could be located at 4.3 kpc i.e.
only half-way to the bulge. We strongly argue however (see the next
section) that these distances are not reliable because the common
assumptions, e.g. on the typical nebular mass, are not met by [WR] PNe.
Most of the bulge [WR] CSs fall within the range [WC4]-[WC6] of spectral classes that are uncommon among the disk [WR] PNe (see e.g. Fig. 1 of Górny 2001). It is a particular feature of this group, and it seems very unlikely that these objects would be Galactic disk members only by chance located in the direction of Galactic bulge. Nonetheless, the spectral type cannot be used as a parameter discriminating [WR] PNe pertaining to the bulge from those in the Galactic inner-disk. In the latter system there are also four objects with similar [WC] type (see Table 1 of Górny et al. 2004). Interestingly, the Shklovksy distances of these objects are, as should be expected, convincingly smaller than the bulge [WR] PNe distances mentioned above.
For the VL PNe in Fig. 8 the distribution is completely different.
They are practically all within 4.5 degrees from the Galactic center with
the exception of H 1-65 PNe![]() . It can be noticed also in Fig. 8 that the low
ionization PNe not classified as VL PNe (small open circles) are
not distributed like the VL PNe but rather like the [WR] PNe.
. It can be noticed also in Fig. 8 that the low
ionization PNe not classified as VL PNe (small open circles) are
not distributed like the VL PNe but rather like the [WR] PNe.
WEL PNe show a distribution similar to that of VL PNe, suggesting that both groups can be physically closer to the center of the Milky Way and originate from a different stellar population or epoch of the bulge history than the [WR] PNe.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0841f9.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg36.png) |
Figure 9: Apparent diameter vs. electron density for different types of bulge PNe. Bottom panel is for PNe too small to be reliably measured. The meaning of the symbols is the same as in Fig. 7. Filled symbol marks inner-disk VL PN. |
| Open with DEXTER | |
7.2 Masses of the nebulae
Figure 9 presents the nebular diameter as a function of electron density for the b sample PNe. The solid line shown in this plot is a linear fit to the distribution of normal PNe. As can be seen, most PNe with emission-line CSs, irrespective of the particular spectral type, are located to the right of this line. This means that the ionized matter in these nebulae is denser than in the average PNe. If all the nebulae would be uniformly filled with gas and ionized at the same percentage of their volume that would also mean that the nebulae around emission-line CSs are more massive.
The hypothesis that the nebulae around [WR] CSs are more massive than the normal PNe was proposed by Górny (1996) as a result of the analysis of statistical distances to these objects. Taking the average distance calculated with the Shklovsky method it was suggested that the [WR] PNe are closer by a factor of 2 to the observer than the other Galactic PNe. As that investigation concerned 350 PNe with known types of the central star (appropriate spectroscopic observations available) there seemed to be no observational selection effect responsible for this behavior nor physical reason why [WR] PNe should be closer to the Sun. Górny (1996) concluded that the apparent difference can be explained if the nebulae around [WR] CSs are almost 5 times more massive than the typical nebula or/and if their filling factor parameters are considerably lower. The second possibility is quite likely as the morphological images of [WR] PNe reveal a larger number of sub-structures (Górny 2001) while their expansion velocity profiles are characterized by large scale turbulence component sometimes found also in WEL PNe but seldom in normal PNe (Gesicki et al. 2006).
Here, we will adopt a similar reasoning to that of Górny (1996). Using distances derived with statistical methods is equivalent to assuming that all the nebulae can be represented by a simple model of hydrogen gas occupying uniformly a sphere with a certain filling factor (like in the Shklovsky distance method) or that this gas has a constant density equal to that derived from spectroscopic observations (as in the distance method proposed by Barlow 1987). The mass of the gas is assumed to be the same for all objects. Since we are dealing with Galactic bulge PNe, if the model assumptions are correct and hold for all nebulae then using either method the derived average distance for each subsample should be the same. We assume a Galactic bulge distance of 8.5 kpc from the Sun.
Starting with the method proposed by Barlow (1987), making the common
assumption that the typical ionized mass of the nebula is 0.2 ![]() and
taking the densities as derived from our observations of [S II]
and
taking the densities as derived from our observations of [S II] ![]() 6731/6716 lines one
obtains a distance scale that is too long for the normal PNe with non
emission-line CSs. The adopted Galactic bulge distance would be obtained if
the mass of the average nebula assumed in the model is 0.13
6731/6716 lines one
obtains a distance scale that is too long for the normal PNe with non
emission-line CSs. The adopted Galactic bulge distance would be obtained if
the mass of the average nebula assumed in the model is 0.13 ![]()
![]() .
If we now use the Shklovsky method to derive the same distance adopting the
ionized nebular mass of 0.13
.
If we now use the Shklovsky method to derive the same distance adopting the
ionized nebular mass of 0.13 ![]() it is necessary to assume also that the
average filling factor is
it is necessary to assume also that the
average filling factor is
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f10.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg38.png) |
Figure 10: Distances derived with the Shklovsky method vs. method of Barlow (1987) for different types of bulge PNe. The meaning of the symbols is the same as in Figs. 7 and 9. |
| Open with DEXTER | |
The distances for all the Galactic bulge PNe of our b sample computed
using both methods with the abovementioned assumptions on nebular parameters
are plotted in Fig. 10. One can see in this plot that the distances
of [WR] PNe calculated with such a nebular model are too short compared to
the adopted bulge distance (arrow), meaning that their true ionized masses must
be larger. The only [WR] PN with a distance exceeding 8.5 kpc is M 2-8,
declared before as a probable background object not truly associated with
the bulge. On the other hand the distances to VL PNe are generally too large,
again except for M 1-17 and Ap 1-12 already suspected rather to be
foreground disk objects based on their large relative brightness. Excluding
these two nebulae to obtain a mean distance of 8.5 kpc for VL PNe, their
average filling factor should be closer to
![]() and their ionized
masses as small as
and their ionized
masses as small as
![]()
![]() .
Taking into account that VL PNe are
very low ionization nebulae, they can be only partially ionized and in that
case their total nebular mass could be larger (but see the discussion on
evolutionary status below). For the 5 [WR] PNe in
Fig. 10 with short distances one obtains
.
Taking into account that VL PNe are
very low ionization nebulae, they can be only partially ionized and in that
case their total nebular mass could be larger (but see the discussion on
evolutionary status below). For the 5 [WR] PNe in
Fig. 10 with short distances one obtains
![]()
![]() .
As
far as the WEL PNe are concerned they do not seem to distinguish themselves from the
normal PNe in
Fig. 10. Finally, because the derivation of typical ionized masses or
the filling factor by reversing statistical distance methods is very
uncertain, the quoted numbers should be regarded as a rough estimate giving
only an indication of the scale of possible differences between different
groups of PNe.
.
As
far as the WEL PNe are concerned they do not seem to distinguish themselves from the
normal PNe in
Fig. 10. Finally, because the derivation of typical ionized masses or
the filling factor by reversing statistical distance methods is very
uncertain, the quoted numbers should be regarded as a rough estimate giving
only an indication of the scale of possible differences between different
groups of PNe.
As already discussed, in Fig. 7 one can compare the locations
of the sample b PNe in the diameter versus flux F(H![]() )0 plane with a
set of theoretical tracks. These tracks have been calculated assuming that
the central star is radiating like a black-body and evolving according to
the Blöcker (1995) models. Three different stellar masses are shown:
0.57
)0 plane with a
set of theoretical tracks. These tracks have been calculated assuming that
the central star is radiating like a black-body and evolving according to
the Blöcker (1995) models. Three different stellar masses are shown:
0.57 ![]() (long dashed lines), 0.6
(long dashed lines), 0.6 ![]() (dotted) and 0.64
(dotted) and 0.64 ![]() (solid).
The model of the surrounding nebula was a simple constant-density sphere
uniformly filled with gas and expanding with a constant velocity. Such
simple PNe models are not realistic as e.g. they do not take into account the
interaction between the stellar winds and the nebula. They are however
sufficient for our illustrative purposes. Three different sets of models are
presented in the plot for each stellar mass assuming a total nebular mass of
(solid).
The model of the surrounding nebula was a simple constant-density sphere
uniformly filled with gas and expanding with a constant velocity. Such
simple PNe models are not realistic as e.g. they do not take into account the
interaction between the stellar winds and the nebula. They are however
sufficient for our illustrative purposes. Three different sets of models are
presented in the plot for each stellar mass assuming a total nebular mass of
![]() ,
0.20 and 0.35
,
0.20 and 0.35 ![]() (see labels). The adopted expansion
velocity was set to 20 km s-1 and the filling factor
(see labels). The adopted expansion
velocity was set to 20 km s-1 and the filling factor
![]() in all the cases.
in all the cases.
The model calculations presented in Fig. 7 indicate what kinds
of nebulae can produce the bright [WR] PNe. They cannot be directly compared
as the [WR] CSs are helium-burning objects whereas the presented
models are based on evolutionary tracks of hydrogen-burning stars. It can be
deduced however that more massive nebulae can easily be the brightest
objects in a given population even if they surround intermediate mass
CSs. The high-mass stars (M* >0.64 ![]() )
cannot produce
objects like bulge [WR] PNe because they evolve too quickly. The time-scale
of their evolution would have to be slowed-down considerably compared with
what the stellar Blöcker (1995) models predict. This is however not very
likely, knowing that the [WR] CSs have high mass loss. Intensive mass
loss will rather speed up the evolution bringing the star faster to high
temperatures due to the stripping of the external layers of the
star
)
cannot produce
objects like bulge [WR] PNe because they evolve too quickly. The time-scale
of their evolution would have to be slowed-down considerably compared with
what the stellar Blöcker (1995) models predict. This is however not very
likely, knowing that the [WR] CSs have high mass loss. Intensive mass
loss will rather speed up the evolution bringing the star faster to high
temperatures due to the stripping of the external layers of the
star![]() .
.
Concerning the WEL PNe it is not certain (as for most of the normal nebulae as well) if their CSs are powered by burning helium or hydrogen. From their locations in Fig. 7 it may be suspected they represent a diversity of possible parameter combinations and can have CSs of different masses and/or very different nebulae. The VL PNe on the other hand are probably more uniform and more obviously distinct from [WR] PNe.
7.3 Evolutionary status
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f11.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg44.png) |
Figure 11:
Surface brightness
|
| Open with DEXTER | |
Figure 11 presents the locations of sample b PNe (open symbols)
in the
![]() versus
versus ![]() plot,
plot,
![]() being the nebular H
being the nebular H![]() surface brightness and
surface brightness and ![]() a similarly defined parameter
based on the stellar flux in the visual V band and on the nebular diameter
a similarly defined parameter
based on the stellar flux in the visual V band and on the nebular diameter
![]() (Górny et al. 1997):
(Górny et al. 1997):
This parameter is very useful for distinguishing stars at different stages of post-AGB evolution. Both
It is seen in Fig. 11 that the locations of [WR] PNe and VL PNe are clearly separated. The VL PNe seem to be originating from stars of lower masses than the [WR] (but again the exact values of plotted parameters depend on selected nebular model and details of central star evolution - see Górny & Tylenda 2000 for some examples). The lines presenting model calculations allow us to follow the typical evolution of a PN and its central star that is going from young high surface brightness objects to old, dispersed and low surface brightness nebulae. None of them links regions occupied by the VL and [WR] PNe. The VL PNe locations in this frame form a very narrow strip suggesting that the masses of their CSs may be very similar and that one can in fact observe an evolutionary sequence within this group. The direction of their evolution would be in agreement with model predictions but clearly not towards [WR] PNe.
There seems to be only one VL object in the present b subsample that could evolve into a [WR]-type star: H 1-9. Its location in Fig. 11 is close to the position of the long-known, unusual very late type object SwSt 1 and other Galactic disk [WC11] or [WC10] central stars (see e.g. Fig. 5 of Górny 2001 for comparison). As can be learned from Fig. 7, H 1-9 is possibly the brightest true bulge VL PN in our sample and at the same time an object with the smallest observed diameter in this group. In fact, the known disk [WC11] PNe are characterized by small angular diameters, with the clear exception of K2-16 and possibly PM1-188 - see Górny & Tylenda (2000) and Peña (2005). It is interesting that the location of the inner-disk VL object H 2-1 is also rather close to the abovementioned region in Fig. 11. It is noteworthy that the locations of the other inner-disk-suspected M 1-27 and Ap 1-12 are within the bulk of the region occupied by VL PNe in this plane (not marked).
One can also notice in Fig. 11 that the positions occupied by the VL PNe are clearly separated from regions where the WEL PNe are found (compared to Fig. 7 with a significant number of VL PNe and WEL PNe sharing similar locations). It can therefore be argued that although VL PNe have central stars of lower temperatures they probably form a separate class of objects and will evolve neither into [WR] PNe nor WEL PNe.
7.4 Nebular properties
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f12.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg47.png) |
Figure 12: Ionization level of different types of bulge PNe as indicated by the relative abundance of O++ ions versus relative abundance of He++ ions. [WR] PNe are marked with magenta triangles, WEL PNe blue squares and VL PNe ([WC 11]-like spectra) with green circles. Normal PNe are marked with diamonds: black mark objects with high level of ionization (O++/O++O++ > 0.8), grey mark remaining objects. Open symbols indicate PNe with lines from relevant ions below the detection limit. |
| Open with DEXTER | |
In this section the general properties of PNe surrounding emission-line and non-emission line CSs in the Galactic bulge will be presented. We start with the detected level of ionization of the nebular gas. For this purpose in Fig. 12 we present the ionic ratio O++/O++O++ versus He++/He++He++ for all PNe from our b sample. As can be noticed, if judged only by the relative numbers of doubly to singly ionized oxygen atoms the WEL PNe would appear among the PNe of highest ionization with almost all of them having O++/O++O++ > 0.85. Surprisingly, on the other hand only a few WEL PNe have any significant amounts of doubly ionized helium and, on average, the He++/He++He++ ratio is lower than in normal PNe. This could be due to a difference in the spectral energy distribution of the ionizing radiation field between WEL CSs and normal CSs i.e. those without enhanced mass loss. It has to be noted that this is not only an interesting fact distinguishing the CSs. It can have some important consequences e.g. for the determination of chemical abundances since in many cases the use of ICFs is necessary to correct for unobserved ionization stages. The assumption that ionizing radiation fields of the CSs are similar is important, but as can be seen clearly not totally justified in this case.
For [WR] PNe the interpretation of Fig. 12 is more difficult since in the spectra of these objects one may expect also the presence of stellar recombination lines of helium. This is a consequence of the strong winds from these stars and adds additional uncertainty to the interpretation. Nevertheless, in two out of nine bulge [WR] PNe in our sample a measurable nebular He++ line has undoubtedly been identified. This is a comparable ratio to what we noticed for WEL PNe and in agreement with the fact that e.g. judging from their positions in Fig. 11 the range of temperatures of their CSs and their present phase in the evolution of the nebula should on average be quite similar for the two groups.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f13a.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f13b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg48.png) |
Figure 13:
Distributions of electron temperatures derived from [N II] |
| Open with DEXTER | |
In Fig. 9 we presented the derived electron densities of the observed nebulae. It was quite apparent from that figure that taking nebulae of a given nebular diameter (that can be regarded as an indicator of evolutionary advancement) all the types of nebulae with emission-line CSs seemed to be denser than their normal counterparts.
Another important parameter of the plasma - electron temperatures are
presented in Fig. 13. It displays the distributions of ![]() (N
II) and
(N
II) and ![]() (O III) temperatures derived respectively from [N II] lines and from [O III] line ratios for all the four groups of the b sample PNe. The inspection
of histograms in the right panel reveals that in the case of [WR] PNe and WEL PNe the distributions of
(O III) temperatures derived respectively from [N II] lines and from [O III] line ratios for all the four groups of the b sample PNe. The inspection
of histograms in the right panel reveals that in the case of [WR] PNe and WEL PNe the distributions of ![]() (O III) temperature differ from what is
derived for normal PNe. There seem to be more objects with lower
temperatures in the former two groups. For the WEL PNe the
Kolmogorov-Smirnov and Wilcoxon nonparametric tests confirm that this
difference is statistically significant while in the case of [WR] PNe it may
still be a result of random effects due to the small number of objects in the
sample.
(O III) temperature differ from what is
derived for normal PNe. There seem to be more objects with lower
temperatures in the former two groups. For the WEL PNe the
Kolmogorov-Smirnov and Wilcoxon nonparametric tests confirm that this
difference is statistically significant while in the case of [WR] PNe it may
still be a result of random effects due to the small number of objects in the
sample.
In Fig. 13 (left panel) it can be seen that the ![]() (N
II) of VL PNe tend to be substantially lower than for other PNe. The
median value of log
(N
II) of VL PNe tend to be substantially lower than for other PNe. The
median value of log ![]() (N II) is 3.83 for VL PNe as compared to 4.02 for the normal PNe. On the other hand, the
(N II) is 3.83 for VL PNe as compared to 4.02 for the normal PNe. On the other hand, the ![]() (N II) temperatures
of [WR] PNe and WEL PNe show near perfect similarity to the distribution of
the normal PNe.
(N II) temperatures
of [WR] PNe and WEL PNe show near perfect similarity to the distribution of
the normal PNe.
Figure 14 compares ![]() (N II) and
(N II) and ![]() (O III) for PNe
where both electron temperatures could be derived. In general we see from
this plot that both values are relatively well correlated as could be
expected from the similarity of histograms in the bottom left and right panel of
Fig. 14. Despite that, there is a tendency for higher
(O III) for PNe
where both electron temperatures could be derived. In general we see from
this plot that both values are relatively well correlated as could be
expected from the similarity of histograms in the bottom left and right panel of
Fig. 14. Despite that, there is a tendency for higher
![]() (N II) with respect to
(N II) with respect to ![]() (O III) values for PNe with higher
levels of oxygen ionization (black diamonds, O++/O++O++ > 0.8 - see
Fig. 12). The WEL PNe show similarity with this group
as practically all plotted objects display
(O III) values for PNe with higher
levels of oxygen ionization (black diamonds, O++/O++O++ > 0.8 - see
Fig. 12). The WEL PNe show similarity with this group
as practically all plotted objects display ![]() (N II) >
(N II) > ![]() (O
III). For the [WR] PNe the situation is not clear as most of them seem to be
located much closer to the one-to-one relation plotted with the dotted line in
Fig. 14.
(O
III). For the [WR] PNe the situation is not clear as most of them seem to be
located much closer to the one-to-one relation plotted with the dotted line in
Fig. 14.
In the case of VL PNe the ![]() (O III) is available for only one PN as due
to their extremely low ionization the oxygen is only singly ionized or lines
are too faint to be measured. The locations of grey symbols in
Fig. 14 indicate that the lower values of
(O III) is available for only one PN as due
to their extremely low ionization the oxygen is only singly ionized or lines
are too faint to be measured. The locations of grey symbols in
Fig. 14 indicate that the lower values of ![]() (N II) are a
general tendency of low ionization PNe. Nonetheless, the distributions
observed in the left panel of Fig. 13 clearly demonstrate that
(N II) are a
general tendency of low ionization PNe. Nonetheless, the distributions
observed in the left panel of Fig. 13 clearly demonstrate that
![]() (N II) temperatures of VL PNe are lower than in any other group of
bulge PNe.
(N II) temperatures of VL PNe are lower than in any other group of
bulge PNe.
7.5 Chemical abundances
7.5.1 The O/H ratio
In Fig. 15 we present the histograms of the oxygen abundance. This element is believed to be generally unmodified during the life of intermediate mass stars, reflecting the primordial composition of the matter from which the star was born (see Stasinska 2007; Chiappini et al. 2009). The four histograms present the distributions for the normal, [WR], WEL and VL PNe subsamples analyzed here. The hatched parts of histograms represent the component of the distribution derived from the data of best quality - the individual errors are smaller than the median of errors of a given parameter in the b subsample (i.e. non-emission and the emission-line central star PNe combined). The remaining objects have errors not larger that 0.3 dex as results with larger uncertainties have been rejected. An exception has been made in the case of the distribution of VL PNe (dashed line, top panel of Fig. 15) where we have used all the available data regardless of this condition.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f14.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg49.png) |
Figure 14:
The electron temperature derived from [O III] |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0841f15a.eps}\par\vspace*{2mm}
\includegraphics[width=7.7cm,clip]{0841f15b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg50.png) |
Figure 15: Distributions of O/H abundance ratio for Galactic bulge VL PNe ([WC 11]-like spectra), [WR] PNe, WEL PNe and normal PNe. The same notation as in Fig. 13 except for the dashed histogram of VL PNe that presents the distribution including all available data while the solid line histogram marks the part derived with data of satisfactory quality (errors <0.3 dex). |
| Open with DEXTER | |
The oxygen abundances of VL PNe seem lower than in any other group of
PNe![]() . One can raise the question of whether the extreme low ionization of these objects
does not contribute to this fact as some atoms may remain neutral and
unobserved. In Fig. 16 one can see that other nebulae with
equally low oxygen ionization level (O++/O++O++ < 0.35) apparently have higher
O/H ratios than VL PNe. This comparison suffers however from the large
errors of the derived O/H ratio for these objects.
. One can raise the question of whether the extreme low ionization of these objects
does not contribute to this fact as some atoms may remain neutral and
unobserved. In Fig. 16 one can see that other nebulae with
equally low oxygen ionization level (O++/O++O++ < 0.35) apparently have higher
O/H ratios than VL PNe. This comparison suffers however from the large
errors of the derived O/H ratio for these objects.
The O/H abundance in [WR] PNe and WEL PNe also appears different from normal
nebulae. There are hardly any objects with log O/H > 9 in either group
but the median O/H values are approximately 0.1 dex larger for
[WR] PNe and WEL PNe. The difference is small and in reality not confirmed by
nonparametric tests. However, the statistically confirmed fact that the
![]() (O III) temperatures are lower in [WR] PNe and WEL PNe (see above) is in
accordance with a higher oxygen abundance in these objects as it
(O III) temperatures are lower in [WR] PNe and WEL PNe (see above) is in
accordance with a higher oxygen abundance in these objects as it
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{0841f16.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg51.png) |
Figure 16: The relation of O/H abundance ratio with ionization parameter O++/O++O++ for Galactic bulge PNe. Different symbols mark: [WR] PNe - magenta triangles; WEL PNe - blue squares; VL PNe ([WC 11]-like spectra) - green circles; normal PNe - black or grey diamonds. Filled symbols mark objects with best quality data. Objects with derived O/H quality beyond adopted rejection limit (errors >0.3 dex) are represented with open thin-line symbols. Red dashed lines mark the median O/H values for normal PNe divided into four bins of O++/O++O++ parameter: <0.35; 0.35-0.7; 0.7-0.9 and >0.9. (Note, three low-metallicity PNe fall below the presented range of O/H - see Sect. 7.5.4 and Fig. 21, available on-line.) |
| Open with DEXTER | |
Nonetheless, there are some possible systematic effects that have to be
considered. From Fig. 16 it seems evident that a comparison
limited only to the PNe with O++/O++O++ > 0.9 would
leave no doubt that the derived O/H ratios for WEL PNe are higher than for the
normal PNe (note their locations above the dashed line marking the median
value). One has to be aware though of the effects brought in by the use
of ICFs. For the O/H ratio the ICF should correct for the possible
presence of ions more charged than O2+ and has the form:
For the WEL PNe, as well as for the [WR] PNe, due to the fact that there is very little or no He2+ detected, the ICF will be close to or equal to 1. This means that no correction is necessary as lines of all oxygen ions are accessible in optical spectra. For the other nebulae however any systematic error in the form of ICF applied will have a direct impact on the derived O abundance and therefore on the conclusions we infer about possible differences between normal PNe and subtypes with emission-line CSs.
An additional factor that may add some uncertainty is the already mentioned
(Sect. 4) problem of a difference between O+ abundances derived from
[O II] ![]() 3727 and [O II]
3727 and [O II] ![]() 7325. For the total oxygen abundance
in WEL PNe this problem may be ignored as most of the oxygen is in the form
of doubly ionized O2+. But for the PNe with lower ionization it is
important especially if the electron temperatures are low presenting
favorable conditions for a significant contribution from recombination.
7325. For the total oxygen abundance
in WEL PNe this problem may be ignored as most of the oxygen is in the form
of doubly ionized O2+. But for the PNe with lower ionization it is
important especially if the electron temperatures are low presenting
favorable conditions for a significant contribution from recombination.
7.5.2 The N/O and He/H abundance ratios
In Fig. 17 the distributions of log N/O for the four subsamples of bulge PNe are presented. The nonparametric tests do not indicate strong, statistically significant differences between them. The derived median N/O value for WEL PNe is smaller than for normal PNe but the distributions have similar width and range. It should be noted also that this abundance ratio is derived assuming N/O = N+/O+, therefore the uncertainty in the O+could directly influence the nitrogen abundances.
Figure 18 presents the distributions of the He/H ratio. In reality the computed He abundances do not take into account the possible presence of neutral helium. For this reason, the He/H abundance ratios for objects with O++/O++O++ < 0.4 have been excluded from further considerations as being significantly underestimated. All VL PNe fall into this category and are therefore absent in Fig. 18.
Applying nonparametric tests one finds out that the distributions presented
in Fig. 18 are not distinguishable in a statistically meaningful
way. It can be noticed however that neither the [WR] PNe (but the overall
number of objects is small) nor the WEL PNe have helium abundances higher
than
![]() whereas for almost 1/3rd of the normal PNe the helium
abundances have been found to be higher than this value. This is surprising,
since [WR] CSs have very strong He-rich winds, and one would expect this to
be reflected in the nebulae.
whereas for almost 1/3rd of the normal PNe the helium
abundances have been found to be higher than this value. This is surprising,
since [WR] CSs have very strong He-rich winds, and one would expect this to
be reflected in the nebulae.
Both helium and nitrogen are expected to be produced in more massive
progenitors of PNe. In Fig. 19 we present a relation of the
abundances of both elements for [WR], WEL and normal PNe. For the latter two
groups we also plot a linear fit to the locations of objects with
![]() (but rejecting PNe with presumably underestimated
(but rejecting PNe with presumably underestimated
![]() ,
i.e. below solar). As can be noticed for WEL PNe there
is a tight correlation of He and N enrichment in the parent star (dotted
line). Surprisingly, though the dispersion of points is much larger, an
almost identical correlation is derived for the normal PNe. The [WR] PNe also
seem to follow a similar relation as the WEL PNe although the number of
nebulae is too small to derive firm conclusions.
,
i.e. below solar). As can be noticed for WEL PNe there
is a tight correlation of He and N enrichment in the parent star (dotted
line). Surprisingly, though the dispersion of points is much larger, an
almost identical correlation is derived for the normal PNe. The [WR] PNe also
seem to follow a similar relation as the WEL PNe although the number of
nebulae is too small to derive firm conclusions.
7.5.3 Abundances of other elements
Figure 20 presents the distributions of neon, argon, sulfur
and chlorine abundances for the Galactic bulge [WR], WEL and normal PNe. The
VL PNe have been omitted because of their very low ionization, which leads
to uncertain abundances as the ICFs used are not applicable. To minimize ICF
related effects for other types of objects only nebulae with O++/O++O++ > 0.4
have been used to derive the distributions of Ne, Ar and S abundances and
objects with O++/O++O++ > 0.8 in the case of Cl abundance![]() .
.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f17a.eps}\par\includegraphics[width=7.8cm,clip]{0841f17b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg56.png) |
Figure 17: Distributions of N/O abundance ratio for Galactic bulge VL PNe, [WR] PNe, WEL PNe and normal PNe. The same notation as in Fig. 15. |
| Open with DEXTER | |
The sample of Galactic bulge [WR] PNe again does not seem numerous enough to draw firm conclusions concerning the investigated abundances. The ranges of all four abundance ratios would suggest similarity with normal PNe. On the other hand, the derived median S/H and Ar/H abundances are approximately 0.3 dex larger for [WR] PNe. While the median log Ar/H = 6.61 for [WR] PNe there are only 14% of normal PNe with that argon abundance. The same holds for sulfur with median log S/H = 7.10 for [WR] PNe and only 17% of normal PNe lie above this abundance. The nonparametric tests do not allow to reject also the hypothesis that the distributions of abundances of [WR] and normal PNe are identical.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f18.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg57.png) |
Figure 18: Distribution of He/H abundance ratio for Galactic bulge [WR], WEL and normal PNe. The same notation as in Fig. 13. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f19.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg58.png) |
Figure 19:
N/O versus He/H for Galactic bulge [WR], WEL and normal PNe. The same
notation of symbols as in Fig. 14. Lines are fits obtained by
using WEL (short-dashed) and normal PNe (long-dashed) for objects with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f20a.eps}\hspace*{2mm}
\...
...0c.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f20d.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg59.png) |
Figure 20: Distributions of neon, argon, sulfur and chlorine abundance for Galactic bulge [WR], WEL and normal PNe. The same notation as in Fig. 13. |
| Open with DEXTER | |
In the case of the WEL PNe there seems to be even less doubt that there are no major
differences in distributions of Ar/H and S/H compared to the normal PNe.
If there is possibly any difference in abundances it seems the largest in
the case of neon as the median log Ne/H is 0.15 dex larger than
for normal PNe. The difference would be more pronounced if the WEL PNe were
compared with the normal PNe of O++/O++O++ > 0.8 only![]() . A similar situation holds for the distribution of
Cl/H with a derived median abundance for WEL PNe larger by 0.36 dex and
higher total proportion of WEL PNe with derived chlorine abundance (50%) than
for normal PNe (25%). But even in this case there remains a 5% probability
that the difference in Cl/H is purely of random statistical origin.
. A similar situation holds for the distribution of
Cl/H with a derived median abundance for WEL PNe larger by 0.36 dex and
higher total proportion of WEL PNe with derived chlorine abundance (50%) than
for normal PNe (25%). But even in this case there remains a 5% probability
that the difference in Cl/H is purely of random statistical origin.
In Fig. 23 the relations between oxygen abundance and the abundances
of neon and argon are presented for the three PNe
subsamples. For the WEL and normal PNe we also overplot the lines
of fitted correlations between element abundances(dotted and dashed
respectively) derived for objects with
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f23a.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f23b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg61.png) |
Figure 23:
Relations of Ne/H and Ar/H versus O/H for Galactic bulge [WR],
WEL and normal PNe. The same notation of symbols as in Fig. 14.
Lines are fits obtained by using WEL (short-dashed) and normal PNe
(long-dashed) for objects with
|
| Open with DEXTER | |
Inspection of the left panel of Fig. 23 suggests that the same tight relation between derived O and Ne abundances holds for WEL and normal PNe. A closer analysis reveals, though, the already mentioned fact that the neon abundances of the WEL PNe better match the values derived for normal PNe with intermediate levels of oxygen ionization (grey symbols) than the highly ionized PNe (black symbols). The slightly higher oxygen abundance of WEL PNe is therefore apparently compensated by an equally increased neon abundance preserving the relation between the two elements at practically the same level for both WEL and normal PNe.
A different situation can be observed in the right panel of Fig. 23 presenting the relation between O and Ar. The two correlation lines have the same slope but are shifted by approximately 0.1 dex reflecting the difference in average oxygen abundance between the WEL and normal PNe samples. In other words, if the difference in oxygen abundances is real and not introduced by the method (see discussion above), then the enhanced O abundance in WEL PNe is apparently not accompanied by an increase in nebular Ar.
7.5.4 Objects with peculiar abundances
In Figs. 19 and 23 one can notice three PNe with emission-line CSs distinguished by their low metallicity: MaC 1-10, M 2-39 and Th 3-12.
The main reason for deriving low O/H ratio in these PNe is the unusually
high electron temperature of the nebular plasma. For the two
peculiar WEL PNe we determined:
![]() (N II) = 10 270 K and
(N II) = 10 270 K and
![]() (O III) = 26 960 K for M 2-39,
and
(O III) = 26 960 K for M 2-39,
and ![]() (N II) = 26 950 K for Th 3-13
(
(N II) = 26 950 K for Th 3-13
(![]() (O III) not available).
For both nebulae we have two independent spectroscopic observations by
different observers confirming that the derived values are not due to incidental
errors.
(O III) not available).
For both nebulae we have two independent spectroscopic observations by
different observers confirming that the derived values are not due to incidental
errors.
In the case of MaC 1-10 - the [WR] PN with peculiar nebular composition -
![]() (O III) = 25 870 K while
(O III) = 25 870 K while ![]() (N II) cannot be derived as the
[N II]
(N II) cannot be derived as the
[N II] ![]() 5755/6584 ratio 0.11 exceeds the usable range. These values are based on a single
spectroscopic observation in a set of sources we use in this paper. It finds
however confirmation in recently published lower quality spectra by Suarez
et al. (2006).
5755/6584 ratio 0.11 exceeds the usable range. These values are based on a single
spectroscopic observation in a set of sources we use in this paper. It finds
however confirmation in recently published lower quality spectra by Suarez
et al. (2006).
Nonetheless, the MaC 1-10 nebula is exceptional for other reasons. The
[WC 8] spectral class of its central star makes it different from the rest of
bulge [WR] PNe and resembling more the [WR] type nuclei known in the Galactic
disk. Neither the distance nor radial velocity is available for this object
to judge wether MaC 1-10 indeed belongs to the disk population. The total
nebular H![]() or radio flux are also unknown and the physical relation
of this nebula to the Galactic bulge was inferred from its apparent
location and diameter well below the 20
or radio flux are also unknown and the physical relation
of this nebula to the Galactic bulge was inferred from its apparent
location and diameter well below the 20
![]() limit (MacConnell 1978).
From the recent image published by Suarez et al. (2006) it looks as the
nebula is of clearly bipolar morphology with the maximum extension measured
as
limit (MacConnell 1978).
From the recent image published by Suarez et al. (2006) it looks as the
nebula is of clearly bipolar morphology with the maximum extension measured
as
![]()
![]() - that makes the latter argument questionable. To add to
the mystery of the chemical composition and origin of this PN, in a recent survey
a H20 maser emission was discovered by Suarez et al. (2007) in the
direction of MaC 1-10.
- that makes the latter argument questionable. To add to
the mystery of the chemical composition and origin of this PN, in a recent survey
a H20 maser emission was discovered by Suarez et al. (2007) in the
direction of MaC 1-10.
The oxygen ionization level of MaC 1-10 measured by the O++/O++O++ ratio is only marginally above 0.4. We have chosen this value (see above) as a minimum for the derived abundances to be accepted and not seriously biased by the ICFs used. It is not excluded though that the form of the ICFs adopted could add some additional contribution to the apparent under-abundance of MaC 1-10 in oxygen and other elements. However, we can compare this nebula to PNe with a similar level of excitation (see Fig. 21) and therefore similar ICF factors. It is then evident that the ratios He/H, O/H, N/H, Ar/H and S/H derived for MaC 1-10 are the lowest among them. On the other hand, abundance ratios N/O, Ar/O and S/O are all larger than average in this group suggesting that oxygen is the most depleted element in MaC 1-10.
In the left panel of Fig. 23 presenting Ne/H abundance ratios as a function of O/H another two [WR] PNe stand out with their noticeably low neon abundances. Combined with their oxygen abundance slightly above average makes the Ne/O ratios of these objects unusually low. One of these PNe is M 1-25 reported for that property by Peña et al. (2001). The other object is M 2-20 sharing with the former also a similar [WC5-6] spectral type.
8 Discussion and conclusions
We have presented a homogeneous set of spectroscopic measurements for a sample of 90 PNe located in the direction of the Galactic bulge secured with 4-m telescopes. For about a half of these objects, plasma parameters and chemical abundances have been derived for the first time. We have discussed the accuracy of the data based on internal tests of reliability and on comparison with other recently published samples. We conclude that our data is superior in quality to the data presented by Exter et al. (2004) and is comparable to Wang & Liu (2007) and Górny et al. (2004). We have therefore merged our observations with the latter two sources into a large common sample comprising 245 Galactic bulge and inner-disk PNe.
Using the new spectroscopic material, we performed a search for emission-line CSs. We have discovered 8 new WEL CSs and 7 PNe with very late (VL) emission-line CSs. The latter objects are associated with PNe of extremely low ionization level. Despite the surprisingly large number of objects discovered, it is not certain if the relative populations of WEL and VL PNe are different in the bulge as compared to the inner-disk region of the Galaxy. A similar extensive search for these types of objects in other regions of the Milky Way would be desirable to draw firm conclusions.
Analyzing the spatial distribution of WEL, VL and classic [WR] PNe belonging to the bulge we have discovered that there is a clear distinction
between the three groups in Galactic coordinates. WEL and VL PNe are
typically found at longitudes below 4
![]() 5 from the center of the
Milky Way whereas [WR] PNe are located further away.
5 from the center of the
Milky Way whereas [WR] PNe are located further away.
The properties of PNe surrounding emission-line stars have also been
analyzed. We have found the electron densities derived for these objects to
be larger than that of normal PNe. There seems also to be a difference in
electron temperatures with ![]() (O III) of WEL PNe and [WR] PNe lower
by 0.1 dex on average than in normal PNe. The
(O III) of WEL PNe and [WR] PNe lower
by 0.1 dex on average than in normal PNe. The ![]() (N II) derived for
VL PNe also differs from normal PNe as their average temperature is of
6.760 K only. The fact that the
(N II) derived for
VL PNe also differs from normal PNe as their average temperature is of
6.760 K only. The fact that the ![]() (O III) can be lower for [WR] PNe and WEL PNe as compared to normal PNe has been noticed recently by Girard
et al. (2007). The distribution of electron densities of disk [WR] PNe have
seemed so far indistinguishable from their normal counterparts (Górny
& Tylenda 2000; Górny 2001).
(O III) can be lower for [WR] PNe and WEL PNe as compared to normal PNe has been noticed recently by Girard
et al. (2007). The distribution of electron densities of disk [WR] PNe have
seemed so far indistinguishable from their normal counterparts (Górny
& Tylenda 2000; Górny 2001).
[WR] PNe appear peculiar also by the fact that they are among the brightest in the bulge. This explains why we were not successful in discovering any new classic [WR] PNe in our enlarged sample, which consists mainly of fainter PNe. On the other hand the same property can lead to strong overestimation of the [WR] PNe rate of occurrence in magnitude limited samples of PNe, e.g. in other galaxies. The large luminosities of bulge [WR] PNe are likely due to the fact that their nebulae are more massive than the average normal PNe. This can have important evolutionary implications.
The matter later ionized in the form of a planetary nebula is ejected during late AGB stages of evolution. The higher masses of [WR] PNe would directly point to that stage of evolution as a period when the triggering mechanism of a change from a normal intermediate-mass star into a future hydrogen-depleted [WR]-type nucleus has started. It therefore favors the hypothesis of a direct origin of [WR] PNe from the AGB (either as a single star or from a binary system) as opposied to a very late thermal pulse scenario (VLTP) - see also Górny & Tylenda (2000). In the first case, the creation of a more massive nebula and transformation of the surface chemical composition of the star can naturally work together. In the VLTP case, on the contrary, there is no possibility of increasing the mass of the nebula considerably.
Investigating the present evolutionary state of the central stars and
surrounding nebulae we have found additional evidence that the WEL PNe,
VL PNe and [WR] PNe form three evolutionary unconnected manifestations of
enhanced mass loss phenomenon from PNe central stars. With the help of comparison with simple model
calculations one can deduce from their locations in
evolutionary diagrams that the three groups differ in at least one
important property: the mass of the central star (closely related to
mass/age of the progenitor) or the mass of the surrounding nebula. Both
factors may be working at the same time. From our study, it seems that the
VL PNe will not evolve into intermediate-type [WR] PNe. In fact, although
the VL central stars satisfy the appropriate criteria and can be classified
as [WC 11] objects![]() they nevertheless seem different from the previously known
Galactic PNe with central stars of similar spectral class.
they nevertheless seem different from the previously known
Galactic PNe with central stars of similar spectral class.
From the analysis of our sample it looks as if CSs with VL type spectra are quite common among Galactic bulge low-ionization PNe. In fact the presence of such central stars may be a necessary condition for these PNe to exist and be observable. Evolutionary time scales from model calculations indicate that very low mass post-AGB stars would require an enhanced mass-loss (manifested by emission lines in the spectra) to be able to reach temperatures sufficient to ionize the surrounding matter before it disperses. The range of masses of the stars from which the VL PNe originate may be very narrow.
Finally, we analyzed the chemical abundances of the PNe with emission-line
CSs and compared them to those of normal PNe. We have found no significant
differences among the various groups. Such a conclusion had previously been
reached by Górny & Stasinska (1995) and by Peña et al. (2001),
however, in those studies, the abundances were not obtained in a homogeneous
way. Recently Girard et al. (2007) have published an analysis of new
observations of 30 [WR] PNe (including some bulge and inner-disk objects) presenting
some indications that in these nebulae the N/O, Ar/H and S/H abundance
ratios are larger than in normal PNe. Interestingly, at least in the case of
the latter two ratios, our results would suggest a similar possibility.
On the other hand the O/H ratio may be higher for WEL PNe (and perhaps
[WR] PNe) in comparison with other PNe. This would be consistent with the lower
![]() (O III) of these PNe suggesting a larger number of effectively
cooling atoms in the nebular plasma. However the result may also be biased
by the method used to derive the abundances.
(O III) of these PNe suggesting a larger number of effectively
cooling atoms in the nebular plasma. However the result may also be biased
by the method used to derive the abundances.
Three PNe with emission-line CSs: Th 3-13, M 2-29 (WEL) and MaC 1-10 ([WR]), have been found to be extremely metal-poor compared to the rest. These nebulae deserve further investigation. We have also confirmed the unusually low Ne/O abundance in M 1-25 reported by Peña et al. (2001) and found another [WR] PN with this property: M 2-20.
A detailed analysis of the chemical abundances of the collected PNe sample and a discussion of their consequences for our understanding of the formation and evolution of the Galactic bulge itself and the PNe population in particular are presented in Chiappini et al. (2009).
Acknowledgements
C.C. and F.C. thank CTIO and ESO staff in Chile and Pronex-Brazil for partial support. C.C. would like to acknowledge the Swiss National Science Foundation (SNF) for partial support. S.K.G. and G.S. acknowledge support by the European Associated Laboratory ``Astronomy Poland-France''. Discussions with R. Walterbos and J. Danziger are greatly appreciated.
Appendix A: Recovering correct intensities from second order contaminated spectra
We describe here a procedure developed for our second order contaminated spectra. This type of spectrum can be corrected if at least two different standard stars were observed. The advantage of the presented approach is an easy implementation within MIDAS routines requiring no labour-intensive manual correcting or editing of every observed spectrum.
It is well known that the spectra at wavelengths longer than 5800 Å (double
the atmospheric UV cutoff at 2900 Å) can be subject to
contamination from second order effects. However, the exact amount of this
contamination can vary depending on the site and instrument
transmissivity to UV photons as well as the specific object properties.
Therefore this effect may be quite small or even negligible in many
cases. The use of order blocking filters is also not advised when one deals
with spectra covering a wide wavelength range and does not want to decrease the
sensitivity of its blue part. This was our case as we were equally
concerned with both an intrinsically weaker [O II] ![]() 7325 line at the red
end and the usually more poorly exposed lines at the blue end, especially
the crucial [O II]
7325 line at the red
end and the usually more poorly exposed lines at the blue end, especially
the crucial [O II] ![]() 3727 line.
3727 line.
Nevertheless after starting to reduce the spectra it became evident that the
order contamination problem of our CTIO observations is very prominent.
It first appears when the flux calibration is attempted. Using the nomenclature of
MIDAS routines this is known as deriving the instrument response
function from standard star(s) observations and applying it to observed
objects. The response function at a given wavelength is defined as:
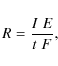
where I is the flux registered and measured from the CCD after flat-field correction and bias and background subtraction, F is the tabulated flux of the star at the base of the atmosphere, t is the exposure time and E is a correction for atmospheric extinction. E is computed from the actual airmass of the observation and the atmospheric extinction constant A as:
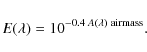
However in the case of second order contaminated spectra at wavelength
| (A.1) |
Thus for the first observed but contaminated standard star to have a correct response function we would have to solve the equation:
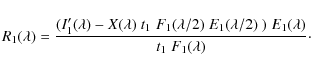
X(
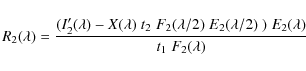
and solve them with the condition that the response functions from observations of both stars should (ideally) give the same response solution:
| (A.2) |
or in full form as:
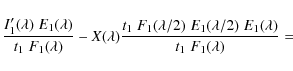
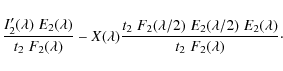
This can be noted also as
leading to:
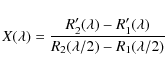 |
(A.3) |
where
The creation of the modified extinction table and separate
![]() frames for each standard star observed are the only steps requiring any
manual modifications of existing tables or data. Since the created files
follow the standard MIDAS image and table formats, the extinction correction
frames for each standard star observed are the only steps requiring any
manual modifications of existing tables or data. Since the created files
follow the standard MIDAS image and table formats, the extinction correction
![]() and
and
![]() can be executed with a standard MIDAS
procedure extinction/long and the response function can be
derived with the
commands integrate/long and response/long.
can be executed with a standard MIDAS
procedure extinction/long and the response function can be
derived with the
commands integrate/long and response/long.
Once this is done it is easy to calculate the
![]() factors using
Eq. (A.3) and then to derive the corrected response function.
factors using
Eq. (A.3) and then to derive the corrected response function.
Having observed more that two standard stars during a given night, we can
compute slightly different X parameters using different standard star
pairs. We can also choose different stars to compute the final response:
Our tests have shown however that due to the errors involved and the accuracy of the computations it is best to correct the response function of the star with the lowest UV/R light intensity ratio. On the other hand the X factors should be computed using all pairs including this star and stars with a high UV/R ratio. In this way we are inferring the true R by making only a small correction to R' and using X that has been determined with high accuracy from a few independent measurements
The fact that the adopted procedure works correctly can be judged from Fig. A.1. In this figure, black lines present the original registered spectra of four standard stars observed during one night. Their corrected shapes computed using Eq. (A.1) are shown with green lines in this plot.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841fa1.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg84.png) |
Figure A.1: Registered and atmospheric extinction corrected spectra of four standard stars observed at CTIO on May 21st, 2002 (black lines) and after removing second order contamination effects (green lines). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841fa2.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg85.png) |
Figure A.2: Response functions derived from observations of four different standard stars during the CTIO run on May 21st, 2002 (black lines) and the final average response after removing second order contamination effects (red line). |
| Open with DEXTER | |
In Fig. A.2 an average corrected response function is shown as a red curve. The part between 5600 Å and 6400 Å has been derived by a linear interpolation between the original function at shorter wavelengths and the re-calculated one at longer wavelength. This was a necessary step since the order contamination may still take place in this intermediate spectral region but the necessary standard fluxes below 3200 Å are not available.
References
- Acker, A., & Neiner, C. 2003, A&A, 403, 659 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barlow, M. J. 1987, MNRAS, 227, 161 [NASA ADS] (In the text)
- Beaulieu, S. F., Freeman, K. C., Kalnajs, A. J., et al. 2000, AJ, 120, 855 [NASA ADS] [CrossRef]
- Blöcker, T. 1995, A&A, 229, 755 [NASA ADS] (In the text)
- Chiappini, C., Górny, S. K., Stasinska, G., & Barbuy, B. 2009, A&A, 494, 591 [NASA ADS] [CrossRef] [EDP Sciences] [arXiv:0812.0558] (In the text)
- Crowther, P. A., De Marco, O., & Barlow, M. J. 1998, MNRAS, 296, 367 [NASA ADS] [CrossRef] (In the text)
- Cuisinier, F., Maciel, W. J., Köppen, J., et al. 2000, A&A, 353, 543 [NASA ADS] (In the text)
- Durand, S., Acker, A., & Zijlstra, A. 1998, A&AS, 132, 13 [NASA ADS] [CrossRef] [EDP Sciences]
- Escudero, A. V., & Costa, R. D. D. 2001, A&A, 380, 300 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Escudero, A. V., Costa, R. D. D., & Maciel, W. J. 2004, A&A, 414, 211 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Exter, K. M., Barlow, M. J., & Walton, N. A. 2004, MNRAS, 349, 1291 [NASA ADS] [CrossRef] (In the text)
- Gesicki, K., Zijlstra, A. A., Acker, A., et al. 2006, A&A, 451, 925 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Girard, P., Köppen, J., & Acker, A. 2007, A&A, 463, 265 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Górny, S. K. 1996, Ap&SS, 238, 79 [NASA ADS] (In the text)
- Górny, S. K. 2001, Ap&SS, 275, 67 [NASA ADS] [CrossRef] (In the text)
- Górny, S. K., & Stasinska, G. 1995, A&A, 303, 893 [NASA ADS] (In the text)
- Górny, S. K., Stasinska, G., Escudero, A. V., & Costa, R. D. D. 2004, A&A, 427, 231 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Górny, S. K., Stasinska, G., & Tylenda, R. 1997, A&A, 318, 256 [NASA ADS] (In the text)
- Górny, S. K., & Tylenda, R. 2000, A&A, 362, 1008 [NASA ADS] (In the text)
- Górny, S. K., Tylenda, R., & Szczerba, R. 1994, A&A, 284, 949 [NASA ADS]
- Hu, J. Y., & Bibo, E. A. 1990, A&A, 234, 435 [NASA ADS] (In the text)
- Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 275, 605
- Liu, X.-W. 2006, in Planetary Nebulae in our Galaxy and Beyond, ed. M. J. Barlow, & R. H. Méndez (Cambridge University Press), IAU Symp., 234, 219 (In the text)
- Liu, X.-W., Storey, P. J., Barlow, M. J., et al. 2000, MNRAS, 312, 585 [NASA ADS] [CrossRef] (In the text)
- MacConnell, D. J. 1978, A&ASS, 33, 219 [NASA ADS] (In the text)
- Paczynski, B. 1971, Acta Astron., 21, 417 [NASA ADS] (In the text)
- Peña, M. 2005, Rev. Mex. A&A, 41, 423 [NASA ADS] (In the text)
- Peña, M., Stasinska, G., & Medina, S. 2001, A&A, 367, 983 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Porter, R. L., Ferland, G. J., & MacAdam, K. B. 2007, ApJ, 657, 327 [NASA ADS] [CrossRef] (In the text)
- Schönberner, D., & Tylenda, R. 1990, A&A, 234, 439 [NASA ADS]
- Seaton, M. J. 1979, MNRAS, 187, 73 [NASA ADS] (In the text)
- Shklovsky, I. 1956, AZh, 33, 222 (In the text)
- Stasinska, G. 2005, A&A, 434, 507 [NASA ADS] [CrossRef] [EDP Sciences]
- Stasinska, G. 2007, in Stellar Nucleosynthesis: 50 years after B2FH, ed. C. Charbonnel, & J.-P. Zahn, EAS Publ. Ser., in press (In the text)
- Stasinska, G., & Tylenda, R. 1994, A&A, 289, 225 [NASA ADS] (In the text)
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [NASA ADS] [CrossRef]
- Suáez, O., García-Lario, P., Manchado, A., et al. 2006, A&A, 458, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Suáez, O., Gomez, J. F., & Morata, O. 2007, A&A, 467, 1085 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tayal, S. S. 2007, ApJS, 171, 331 [NASA ADS] [CrossRef] (In the text)
- Tylenda, R., Acker, A., & Stenholm, B. 1993, A&AS, 102, 595 [NASA ADS] (In the text)
- Wang, W., & Liu, X.-W. 2007, MNRAS, 381, 669 [NASA ADS] [CrossRef] (In the text)
- Zijlstra, A. A., Gesicki, K., Walsh, J. R., et al. 2006, MNRAS, 369, 875 [NASA ADS] [CrossRef] (In the text)
Online Material
Table 2:
Logarithmic extinction C at HH![]() and dereddened line intensities
on the scale H
and dereddened line intensities
on the scale H![]() .
.
Table 3:
Plasma parameters and abundances. The first row for each PN gives
parameters computed from the nominal values of the observational data. The
second and third row give the upper and lower limits respectively of these
parameters. Column (1) gives the PNG number; Col. (2) usual name; Col. (3) electron density deduced from [S II] ![]() 6731/6716; Cols. (4) and (5)
electron temperatures from [O III]
6731/6716; Cols. (4) and (5)
electron temperatures from [O III] ![]() 4363/5007 and [N II]
4363/5007 and [N II] ![]() 5755/6584 respectively (the
value of
5755/6584 respectively (the
value of ![]() (N II) is in parenthesis if
(N II) is in parenthesis if ![]() (O III) was chosen
for all ions). Columns (6) to (12) give the
He/H, N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the
logarithmic extinction C at HH
(O III) was chosen
for all ions). Columns (6) to (12) give the
He/H, N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the
logarithmic extinction C at HH![]() derived from our spectra.
derived from our spectra.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{0841f21a.eps}\hspace*{2.5m...
...s}\hspace*{2.5mm}
\includegraphics[width=5.5cm,clip]{0841f21l.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg86.png) |
Figure 21: The relation of different abundance ratios with ionization parameter O++/O++O++ for Galactic bulge PNe: [WR] PNe - magenta triangles; WEL PNe - blue squares; VL PNe - green circles; normal PNe - black or grey diamonds. Filled symbols mark objects with best quality data. PNe with a quality of the derived abundance ratio above the adopted rejection limit (i.e. error >0.3 dex) are represented with open thin-line symbols. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{0841f22a.eps}\hspace*{2.5m...
...ps}\hspace*{2.5mm}
\includegraphics[width=5.5cm,clip]{0841f22l.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg87.png) |
Figure 22: The relation of different abundance ratios with ionization parameter He++/He++He++ for Galactic bulge PNe. The same notation as in Fig. 21. |
| Open with DEXTER | |
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Based on observations made at the Cerro Tololo Interamerican Observatory and the European Southern Observatory.
- ...
![[*]](/icons/foot_motif.png)
- Tables 2 and 3 and Figs. 21 and 22 are only available in electronic form at http://www.aanda.org
- ...2003)
![[*]](/icons/foot_motif.png)
- In this work we will continue to use the older classification scheme with spectral classes ranging from coolest [WC 11] to hottest [WC 2] stars because they are easier to apply to the central stars with lower quality spectra - see Górny et al. (2004) for more detailed justification.
- ... [WR] PNe
![[*]](/icons/foot_motif.png)
- In the rest of the paper, we use the notation [WR] PNe for PNe with [WR] central stars and [WR] CSs referring to such stars.
- ... MIDAS
![[*]](/icons/foot_motif.png)
- MIDAS is developed and maintained by the European Southern Observatory.
- ... package
![[*]](/icons/foot_motif.png)
- J. Borkowski; www.ncac.torun.pl/cgi-bin/rewia2html
- ... used
![[*]](/icons/foot_motif.png)
- In the CTIO 2001 run, the H
 line was registered on hot pixels of one
of the bad CCD columns and could not be reliably measured.
line was registered on hot pixels of one
of the bad CCD columns and could not be reliably measured.
- ...
![[*]](/icons/foot_motif.png)
- Table 2 is available in electronic form only.
- ...
measurements
![[*]](/icons/foot_motif.png)
- The most outlying points in Fig. 2 are evolved, faint nebulae: H 1-64, H 2-22, Pe 2-12 and H 2-30. The first three are low excitation PNe without emission-line CSs. The latter PN is high excitation object but no nebular parameters could be calculated due to the quality of the spectra.
- ... range
![[*]](/icons/foot_motif.png)
- Compare e.g. the different shapes of response functions from individual standard stars at these wavelengths shown in Fig. A.2 in the Appendix.
- ...
![[*]](/icons/foot_motif.png)
- Table 3 is available in electronic form only.
- ...
spectra
![[*]](/icons/foot_motif.png)
- One of them, H 1-55 should be confirmed when better spectra are available.
- ... WEL PNe
![[*]](/icons/foot_motif.png)
- Additional three WEL PNe pertaining to the Galactic disk can be identified by examination of measured lines tabulated by Wang & Liu (2007): M 1-20, IC 4699 & IC 4846. However, IC 4846 has coordinates too far-off to be regarded an inner-disk member and was not included in the analyzed sample.
- ... identification
![[*]](/icons/foot_motif.png)
- The only exception is M 2-34 (PN G007.8-03.7) which has a doubtful spectral classification and was not confirmed as [WR] type central star by Górny et al. (2004).
- ...
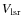
![[*]](/icons/foot_motif.png)
- All the radial velocities used in this paper have been taken from Durand et al. (1998) and corrected for solar motion using the formulae of Beaulieu et al. (2000).
- ... PNe
![[*]](/icons/foot_motif.png)
- Note that H 1-65 has been classified as WEL PN by Acker & Neiner (2003) nonetheless our spectrum in Fig. 5 clearly shows the C III emission at 5695 Å and the absence of C IV 5805 Å that is present in other WEL PNe.
- ...
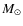
![[*]](/icons/foot_motif.png)
- The typical
nebular mass would be
 0.19
0.19 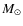 if we consider only 33 normal PNe
with CSs hotter than
if we consider only 33 normal PNe
with CSs hotter than
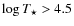 assuming such nebulae are density
bounded.
assuming such nebulae are density
bounded.
- ...
star
![[*]](/icons/foot_motif.png)
- Compare with Górny et al. (1994) to see how an enhanced mass-loss is reflected in evolutionary diagrams for H-burning central stars or Górny & Tylenda (2000) for He-burning models.
- ...
PNe
![[*]](/icons/foot_motif.png)
- Due to the small number of objects the difference cannot be confirmed by Kolmogorov-Smirnov and Wilcoxon nonparametric tests to be statistically significant.
- ... abundance
![[*]](/icons/foot_motif.png)
- Figures 21 and 22 available on-line present the relations of important abundance ratios of all the bulge PNe as a function of O++/O++O++(and He++/He++He++) and can be analyzed for effects of imperfect ICF correction.
- ... only
![[*]](/icons/foot_motif.png)
- see upper-right panel of Fig. 21.
- ... objects
![[*]](/icons/foot_motif.png)
- Similarly Peña et al. (2001) were able to apply [WC] classification to some WEL CSs.
- ... measurements
![[*]](/icons/foot_motif.png)
- If two stars with similar and high UV/R are used it can lead to large errors or even a false solution.
All Tables
Table 1: Log of observations.
Table 4: Differences in dex on plasma parameters and chemical abundances adopting data from this work versus data taken from the literature. The number of analyzed PNe in common is given in parenthesis.
Table 2:
Logarithmic extinction C at HH![]() and dereddened line intensities
on the scale H
and dereddened line intensities
on the scale H![]() .
.
Table 3:
Plasma parameters and abundances. The first row for each PN gives
parameters computed from the nominal values of the observational data. The
second and third row give the upper and lower limits respectively of these
parameters. Column (1) gives the PNG number; Col. (2) usual name; Col. (3) electron density deduced from [S II] ![]() 6731/6716; Cols. (4) and (5)
electron temperatures from [O III]
6731/6716; Cols. (4) and (5)
electron temperatures from [O III] ![]() 4363/5007 and [N II]
4363/5007 and [N II] ![]() 5755/6584 respectively (the
value of
5755/6584 respectively (the
value of ![]() (N II) is in parenthesis if
(N II) is in parenthesis if ![]() (O III) was chosen
for all ions). Columns (6) to (12) give the
He/H, N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the
logarithmic extinction C at HH
(O III) was chosen
for all ions). Columns (6) to (12) give the
He/H, N/H, O/H, Ne/H, S/H, Ar/H, Cl/H ratios, respectively. Column (13) gives the
logarithmic extinction C at HH![]() derived from our spectra.
derived from our spectra.
All Figures
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f1.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg15.png) |
Figure 1: Distribution of the observed PNe in Galactic coordinates. Objects observed during different runs are marked: CTIO 2001 - squares, CTIO 2002 - diamonds, ESO 2002 - triangles. Objects observed during both seasons at CTIO are marked with circles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f2.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg21.png) |
Figure 2:
Intensity ratio of the [O III] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f3.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg23.png) |
Figure 3:
Relative differences in line measurements (reddening uncorrected) from two
different spectra at CTIO in 2001 and in 2002 as a function of line
intensity (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f4.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg27.png) |
Figure 4:
The electron temperature derived from [O III] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0841f5a.eps}\par\vspace*{2...
...s}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{0841f5g.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg28.png) |
Figure 5: Spectra of the new VL PNe (very late type [WC 11]-like emission-line central stars PNe). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.78cm,clip]{0841f6a.eps}\par\vspace*{...
...par\vspace*{1.1mm}
\includegraphics[width=5.78cm,clip]{0841f6h.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg29.png) |
Figure 6: Spectra of the newly discovered WEL PNe (weak emission-line central stars PNe). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0841f7.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg30.png) |
Figure 7:
The relation of apparent diameter and reddening corrected H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0841f8.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg35.png) |
Figure 8: Locations of different types of bulge PNe in Galactic coordinates (absolute values). The meaning of the symbols is the same as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0841f9.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg36.png) |
Figure 9: Apparent diameter vs. electron density for different types of bulge PNe. Bottom panel is for PNe too small to be reliably measured. The meaning of the symbols is the same as in Fig. 7. Filled symbol marks inner-disk VL PN. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f10.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg38.png) |
Figure 10: Distances derived with the Shklovsky method vs. method of Barlow (1987) for different types of bulge PNe. The meaning of the symbols is the same as in Figs. 7 and 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f11.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg44.png) |
Figure 11:
Surface brightness
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f12.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg47.png) |
Figure 12: Ionization level of different types of bulge PNe as indicated by the relative abundance of O++ ions versus relative abundance of He++ ions. [WR] PNe are marked with magenta triangles, WEL PNe blue squares and VL PNe ([WC 11]-like spectra) with green circles. Normal PNe are marked with diamonds: black mark objects with high level of ionization (O++/O++O++ > 0.8), grey mark remaining objects. Open symbols indicate PNe with lines from relevant ions below the detection limit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f13a.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f13b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg48.png) |
Figure 13:
Distributions of electron temperatures derived from [N II] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f14.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg49.png) |
Figure 14:
The electron temperature derived from [O III] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0841f15a.eps}\par\vspace*{2mm}
\includegraphics[width=7.7cm,clip]{0841f15b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg50.png) |
Figure 15: Distributions of O/H abundance ratio for Galactic bulge VL PNe ([WC 11]-like spectra), [WR] PNe, WEL PNe and normal PNe. The same notation as in Fig. 13 except for the dashed histogram of VL PNe that presents the distribution including all available data while the solid line histogram marks the part derived with data of satisfactory quality (errors <0.3 dex). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{0841f16.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg51.png) |
Figure 16: The relation of O/H abundance ratio with ionization parameter O++/O++O++ for Galactic bulge PNe. Different symbols mark: [WR] PNe - magenta triangles; WEL PNe - blue squares; VL PNe ([WC 11]-like spectra) - green circles; normal PNe - black or grey diamonds. Filled symbols mark objects with best quality data. Objects with derived O/H quality beyond adopted rejection limit (errors >0.3 dex) are represented with open thin-line symbols. Red dashed lines mark the median O/H values for normal PNe divided into four bins of O++/O++O++ parameter: <0.35; 0.35-0.7; 0.7-0.9 and >0.9. (Note, three low-metallicity PNe fall below the presented range of O/H - see Sect. 7.5.4 and Fig. 21, available on-line.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0841f17a.eps}\par\includegraphics[width=7.8cm,clip]{0841f17b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg56.png) |
Figure 17: Distributions of N/O abundance ratio for Galactic bulge VL PNe, [WR] PNe, WEL PNe and normal PNe. The same notation as in Fig. 15. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f18.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg57.png) |
Figure 18: Distribution of He/H abundance ratio for Galactic bulge [WR], WEL and normal PNe. The same notation as in Fig. 13. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f19.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg58.png) |
Figure 19:
N/O versus He/H for Galactic bulge [WR], WEL and normal PNe. The same
notation of symbols as in Fig. 14. Lines are fits obtained by
using WEL (short-dashed) and normal PNe (long-dashed) for objects with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f20a.eps}\hspace*{2mm}
\...
...0c.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f20d.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg59.png) |
Figure 20: Distributions of neon, argon, sulfur and chlorine abundance for Galactic bulge [WR], WEL and normal PNe. The same notation as in Fig. 13. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841f23a.eps}\hspace*{2mm}
\includegraphics[width=8cm,clip]{0841f23b.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg61.png) |
Figure 23:
Relations of Ne/H and Ar/H versus O/H for Galactic bulge [WR],
WEL and normal PNe. The same notation of symbols as in Fig. 14.
Lines are fits obtained by using WEL (short-dashed) and normal PNe
(long-dashed) for objects with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841fa1.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg84.png) |
Figure A.1: Registered and atmospheric extinction corrected spectra of four standard stars observed at CTIO on May 21st, 2002 (black lines) and after removing second order contamination effects (green lines). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0841fa2.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg85.png) |
Figure A.2: Response functions derived from observations of four different standard stars during the CTIO run on May 21st, 2002 (black lines) and the final average response after removing second order contamination effects (red line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{0841f21a.eps}\hspace*{2.5m...
...s}\hspace*{2.5mm}
\includegraphics[width=5.5cm,clip]{0841f21l.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg86.png) |
Figure 21: The relation of different abundance ratios with ionization parameter O++/O++O++ for Galactic bulge PNe: [WR] PNe - magenta triangles; WEL PNe - blue squares; VL PNe - green circles; normal PNe - black or grey diamonds. Filled symbols mark objects with best quality data. PNe with a quality of the derived abundance ratio above the adopted rejection limit (i.e. error >0.3 dex) are represented with open thin-line symbols. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{0841f22a.eps}\hspace*{2.5m...
...ps}\hspace*{2.5mm}
\includegraphics[width=5.5cm,clip]{0841f22l.eps}
\end{figure}](/articles/aa/full_html/2009/24/aa10841-08/Timg87.png) |
Figure 22: The relation of different abundance ratios with ionization parameter He++/He++He++ for Galactic bulge PNe. The same notation as in Fig. 21. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


