| Issue |
A&A
Volume 500, Number 2, June III 2009
|
|
|---|---|---|
| Page(s) | L13 - L16 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200912297 | |
| Published online | 13 May 2009 | |
LETTER TO THE EDITOR
Double or binary: on the multiplicity of open star clusters![[*]](/icons/foot_motif.png)
R. de la Fuente Marcos - C. de la Fuente Marcos
Suffolk University Madrid Campus, C/ Viña 3, 28003 Madrid, Spain
Received 7 April 2009 / Accepted 30 April 2009
Abstract
Context. Observations indicate that the fraction of potential binary star clusters in the Magellanic Clouds is about 10%. In contrast, it is widely accepted that the binary cluster frequency in the Galaxy disk is much lower.
Aims. Here we investigate the multiplicity of clusters in the Milky Way disk to either confirm or disprove this dearth of binaries.
Methods. We quantify the open cluster multiplicity using complete, volume-limited samples from WEBDA and NCOVOCC.
Results. At the Solar Circle, at least 12% of all open clusters appear to be experiencing some type of interaction with another cluster; i.e., are possible binaries. As in the Magellanic Clouds, the pair separation histogram hints at a bimodal distribution. Nearly 40% of identified pairs are probably primordial. Most of the remaining pairs could be undergoing some type of close encounter, perhaps as a result of orbital resonances. Confirming early theoretical predictions, the characteristic time scale for destruction of bound pairs in the disk is 200 Myr, or one galactic orbit.
Conclusions. Our results show that the fraction of possible binary clusters in the Galactic disk is comparable to that in the Magellanic Clouds.
Key words: methods: statistical - Galaxy: open clusters and associations: general - stars: formation - Galaxy: disk - Galaxy: evolution - solar neighborhood
1 Introduction
In a little known paper, Rozhavskii et al. (1976) claimed that the fraction of multiple systems among open clusters in the Milky Way was roughly 20%. This largely neglected result was
obtained before any research was undertaken to assess the importance of cluster binarity in the Magellanic Clouds. The firsts of such studies (LMC, Bhatia & Hatzidimitriou 1988; SMC, Hatzidimitriou & Bhatia 1990) inferred that the fraction of star clusters in pairs was nearly 10%. Slightly higher values, 12%, were found by Pietrzynski & Udalski (2000).
These results were later confirmed by a more rigorous, extensive work completed by Dieball et al. (2002). In contrast, and for the Galaxy, the only widely accepted double or binary cluster
system is the ![]() Persei pair (NGC 869/NGC 884), although the actual physical separation between the pair members is >200 pc (see, e.g., de la Fuente Marcos & de la Fuente Marcos 2009). Nevertheless, Subramaniam et al. (1995) were able to identify a number of additional candidates, concluding that about 8% of open clusters may be actual
binaries, challenging the traditional view. In spite of this result, it is still emphasized (see, e.g., Dieball & Grebel 1998; Bekki et al. 2004) that the number of cluster pairs in the Milky Way is small compared to that in the Clouds. This is usually interpreted as supporting evidence for the higher formation efficiency of bound stellar groups in the Clouds. In all these studies, projected, not three-dimensional, distances were used.
Persei pair (NGC 869/NGC 884), although the actual physical separation between the pair members is >200 pc (see, e.g., de la Fuente Marcos & de la Fuente Marcos 2009). Nevertheless, Subramaniam et al. (1995) were able to identify a number of additional candidates, concluding that about 8% of open clusters may be actual
binaries, challenging the traditional view. In spite of this result, it is still emphasized (see, e.g., Dieball & Grebel 1998; Bekki et al. 2004) that the number of cluster pairs in the Milky Way is small compared to that in the Clouds. This is usually interpreted as supporting evidence for the higher formation efficiency of bound stellar groups in the Clouds. In all these studies, projected, not three-dimensional, distances were used.
In reality, star clusters which have small angular separations are not necessarily physically associated. In most cases, they happen by chance to lie nearly along the same line of sight; they are merely ``optical doubles''. This is to be expected, as clusters are born in complexes (Efremov 1978) which are observed in projection, with some objects formed along shock fronts induced by supernovae. These complexes may also be inclined with respect to the galaxy disk (e.g. the Gould Belt) and this fact is customarily neglected in Magellanic Cloud studies. In this context and without information on three-dimensional separations, misidentification of large numbers of double clusters as binaries is, statistically speaking, highly likely. These preliminary considerations pose some obvious questions; if 3D data are used, is there a real scarcity of binary clusters in our Galaxy with respect to the Magellanic Clouds? How similar are their binary cluster fractions? and their pair separation distributions? Here we attempt to provide statistically robust answers to these and other questions regarding the multiplicity of open clusters. This Letter is organized as follows: in Sect. 2, we discuss possible formation channels for binary/double clusters. In Sect. 3, we provide a quantitative analysis of the Galactic binary cluster frequency using samples of open clusters. Individual candidates are considered in Sect. 4. Results are discussed and conclusions summarized in Sect. 5.
2 Double or binary: formation channels
Pairs, triplets or higher multiplicity star clusters may form as a result of a number of processes:
- a)
- Simultaneous formation. Open cluster binaries formed inside a star complex and out of the same molecular cloud are expected to share a common space velocity, but also have very similar
ages and chemical composition. They may also be the final products of multiple mergers of smaller clusters. Coformation scenarios have been suggested by Fujimoto & Kumai (1997) and Bekki et al. (2004). Objects formed are genetic pairs and therefore true binaries if bound.
- b)
- Sequential formation. In this scenario, stellar winds or supernova shocks generated by one cluster induce the collapse of a nearby cloud, triggering the formation of a companion cluster (see, e.g., Brown et al. 1995; Goodwin 1997). A finite but relatively small age difference should be
observed. Post-supernova metal contamination may produce different metallicity. If the companion is born out of the same cloudlet forming the originator cluster, common kinematics is expected; if the shocked cloud is unrelated, the kinematics may be different. Pairs formed may be binaries or not.
- c)
- Tidal capture. Open cluster binaries formed by tidal capture must share a common space velocity, but their ages and chemical composition are expected to be rather different. Details of the actual mechanism are discussed in, e.g., van den Bergh (1996). Even if they are true binaries, they are not primordial.
- e)
- Resonant trapping. Dehnen (1998) pointed out that orbital resonances may be responsible for most stellar moving groups present in the solar neighbourhood. This idea was further explored by De Simone et al. (2004), Quillen & Minchev (2005), Famaey et al. (2005) and Chakrabarty (2007) for the case of resonances induced by the Galactic bar and spiral structure. Extrapolating this scenario to entire clusters, we may have formation of double or multiple clusters as a result of resonances of the non-axisymmetric component of the Galactic potential. Cluster pairs must share a common kinematics with rather different ages and metallicities. However, they are not true binaries but pseudo-binaries, transient pairs or multiples. Tidal capture may operate within resonant trapping regions.
- f)
- Optical doubles: hyperbolic encounters. As in the stellar case, optical doubles are not physical binaries. Although they occupy a limited volume of space (following our criterion, see below, one sphere of radius 15 pc), they do not share common kinematics, but they may have similar ages and metallicities, especially if they are young and belong in the same star complex. Given their small separation, they may well be undergoing some type of close, even disruptive, gravitational encounter.
3 Double or binary? The data and the evidence
In this section we describe the databases and the classification scheme used. The basic criterion used in our preliminary selection is purely dynamical: the pair physical (not projected) separation must be less than three times the average value of the tidal radius for clusters in the Milky Way disk (10 pc, Binney & Tremaine 2008). Following Innanen et al. (1972), for two clusters separated by a distance larger than three times the outer radius of each cluster, the amount of mutual disruption is negligible. On the other hand, general open cluster samples are biased against older clusters because they contain less luminous stars. If any reliable conclusions on the open cluster binary frequency have to be obtained, a complete sample must be used. Completeness of general open cluster samples has been customarily approached assuming uniform surface density in the solar neighborhood (Battinelli & Capuzzo-Dolcetta 1989, 1991). Piskunov et al. (2006) have concluded that, assuming uniform density, the completeness limit for clusters of any age could be 0.85 kpc. In the following, we consider this group of clusters, forming a volume limited sample, as the best sample.
WEBDA. The Open Cluster Database![]() (WEBDA, Mermilliod & Paunzen 2003) is one of the most widely used open cluster databases. The latest update of WEBDA (April 2009, Paunzen & Mermilliod 2009) includes 1756 objects. The number of clusters with both age and distance in the database is 1051 (59.9%). Out of the resulting 551 775 pairs, the number of systems with separation
(WEBDA, Mermilliod & Paunzen 2003) is one of the most widely used open cluster databases. The latest update of WEBDA (April 2009, Paunzen & Mermilliod 2009) includes 1756 objects. The number of clusters with both age and distance in the database is 1051 (59.9%). Out of the resulting 551 775 pairs, the number of systems with separation ![]() 30 pc is 34 (see Table 1). Therefore and for the general sample, the fraction of candidate clusters involved in some type of close range
dynamical interaction is 6.2%. If we restrict the analysis to the best sample, 281 objects are included with 39 340 pairs. Out of this best sample, the number of pairs with separation
30 pc is 34 (see Table 1). Therefore and for the general sample, the fraction of candidate clusters involved in some type of close range
dynamical interaction is 6.2%. If we restrict the analysis to the best sample, 281 objects are included with 39 340 pairs. Out of this best sample, the number of pairs with separation ![]() 30 pc is 19 or 12.4%. Hence, and based only on spatial considerations (as in Magellanic Clouds studies), our best value for the fraction of multiple clusters in the Galactic disk is
comparable to that in the Clouds. Most of these cluster pairs have proper motions in WEBDA, with a smaller number also having radial velocities. A very small percentage of open clusters in pairs have known metallicity.
30 pc is 19 or 12.4%. Hence, and based only on spatial considerations (as in Magellanic Clouds studies), our best value for the fraction of multiple clusters in the Galactic disk is
comparable to that in the Clouds. Most of these cluster pairs have proper motions in WEBDA, with a smaller number also having radial velocities. A very small percentage of open clusters in pairs have known metallicity.
NCOVOCC. The New Catalogue of Optically Visible Open Clusters and Candidates![]() (NCOVOCC, Dias et al. 2002) is also widely used in open cluster studies. The February 2009 version (v2.10, Dias 2009) of NCOVOCC includes 1787 clusters and 982 of these (54.9%) have known distances and ages, generating 481 671 pairs. After performing the same type of analysis that we did on WEBDA data, we obtain
the following values for the binary fractions: 5.3% and 11.4%. Now we have a total of 27 pairs with 14 in the best sample (see Table 2).
(NCOVOCC, Dias et al. 2002) is also widely used in open cluster studies. The February 2009 version (v2.10, Dias 2009) of NCOVOCC includes 1787 clusters and 982 of these (54.9%) have known distances and ages, generating 481 671 pairs. After performing the same type of analysis that we did on WEBDA data, we obtain
the following values for the binary fractions: 5.3% and 11.4%. Now we have a total of 27 pairs with 14 in the best sample (see Table 2).
The values obtained for the binary fraction of a sample of open clusters in the solar neighbourhood using WEBDA and NCOVOCC are statistically consistent and they include the effect of presumed triple systems. Our best value for the open cluster binary fraction in the solar neighbourhood (complete sample) and, therefore in the Galactic disk, is ![]() 12%. This value matches that of the Magellanic Clouds. If results from both databases are combined, the fraction of possible binary clusters is nearly 15%. The number of pairs common to WEBDA and NCOVOCC is 18 (ASCC 16
12%. This value matches that of the Magellanic Clouds. If results from both databases are combined, the fraction of possible binary clusters is nearly 15%. The number of pairs common to WEBDA and NCOVOCC is 18 (ASCC 16 ![]() Briceño 1 and ASCC 50
Briceño 1 and ASCC 50 ![]() Alessi 43) with an additional 3 clusters in common but assigned to different companions. Evidence for systems with a multiplicity higher than 2 is weak, with a few possible triple or even quadruple systems. The average distances between clusters in the best sample for WEBDA and NCOVOCC are 765.1
Alessi 43) with an additional 3 clusters in common but assigned to different companions. Evidence for systems with a multiplicity higher than 2 is weak, with a few possible triple or even quadruple systems. The average distances between clusters in the best sample for WEBDA and NCOVOCC are 765.1 ![]() 1.8 pc and 754
1.8 pc and 754 ![]() 2 pc, respectively. Our list in Table 1 has only two pairs (#2 and #27) in common with Subramaniam et al. (1995); Table 2 shares only 1 pair (#21).
2 pc, respectively. Our list in Table 1 has only two pairs (#2 and #27) in common with Subramaniam et al. (1995); Table 2 shares only 1 pair (#21).
The distribution of separations between open clusters in Table 1 shows an apparent peak at 10 pc (see Fig. 1). Similar peaks are observed for the LMC (![]() 6 pc) and the SMC (
6 pc) and the SMC (![]() 11 pc) but not in Subramaniam et al. (1995) for open clusters or in NCOVOCC data. In spite of the low number of cluster pairs, the peak seems to be statistically robust as it appears for both the general and best samples. On the other hand, the age of a given cluster pair or multiple system is the age of its youngest member. If we represent the age difference between clusters in a pair as a function of the age of the pair (see Fig. 2), we observe that the vast majority, except three, of almost coeval pairs (age difference <80 Myr) are younger than 25 Myr. This implies that primordial pairs do not survive for long and is consistent with similar findings for the LMC and the SMC (Hatzidimitriou & Bhatia 1990). If the unusual pair #31 is neglected, no primordial pairs older than 300 Myr exist in the disk, which is also consistent with theoretical expectations discussed in Innanen et al. (1972). Either way, the number of candidate binary clusters among young ones in the best sample is almost 7 times larger than for the general age group. An unexpected age gap is observed for the age range 25-70 Myr. This could be the result of orbit expansion (and subsequent pair destruction) due to mass loss, as observed in N-body simulations by Portegies Zwart & Rusli (2007), but also of early cluster disruption after gas expulsion (Hills 1980). If we further analyze the cluster pairs in these two clearly distinct age ranges (
11 pc) but not in Subramaniam et al. (1995) for open clusters or in NCOVOCC data. In spite of the low number of cluster pairs, the peak seems to be statistically robust as it appears for both the general and best samples. On the other hand, the age of a given cluster pair or multiple system is the age of its youngest member. If we represent the age difference between clusters in a pair as a function of the age of the pair (see Fig. 2), we observe that the vast majority, except three, of almost coeval pairs (age difference <80 Myr) are younger than 25 Myr. This implies that primordial pairs do not survive for long and is consistent with similar findings for the LMC and the SMC (Hatzidimitriou & Bhatia 1990). If the unusual pair #31 is neglected, no primordial pairs older than 300 Myr exist in the disk, which is also consistent with theoretical expectations discussed in Innanen et al. (1972). Either way, the number of candidate binary clusters among young ones in the best sample is almost 7 times larger than for the general age group. An unexpected age gap is observed for the age range 25-70 Myr. This could be the result of orbit expansion (and subsequent pair destruction) due to mass loss, as observed in N-body simulations by Portegies Zwart & Rusli (2007), but also of early cluster disruption after gas expulsion (Hills 1980). If we further analyze the cluster pairs in these two clearly distinct age ranges (![]() 25 Myr and >70 Myr), we observe some obvious trends (see Fig. 3). The vast majority of primordial pairs appear to have separations in the range 20-30 pc. Most cluster pairs with separations <20 pc appear to be old and/or non-primordial and they may have formed by resonant trapping. Notable exceptions are pair #3 (perhaps part of a primordial triple, see below), pair #7 (a likely long-lived binary) and pair #31 (another long-lived binary, if real). Older pairs appear to exhibit two disparate groupings: all pairs with separation <20 pc have age
differences <400 Myr or two galactic rotations at the Solar Circle. Wider pairs show random age differences. This may well be a characteristic time scale for disruption of close transient pairs formed by resonant trapping.
25 Myr and >70 Myr), we observe some obvious trends (see Fig. 3). The vast majority of primordial pairs appear to have separations in the range 20-30 pc. Most cluster pairs with separations <20 pc appear to be old and/or non-primordial and they may have formed by resonant trapping. Notable exceptions are pair #3 (perhaps part of a primordial triple, see below), pair #7 (a likely long-lived binary) and pair #31 (another long-lived binary, if real). Older pairs appear to exhibit two disparate groupings: all pairs with separation <20 pc have age
differences <400 Myr or two galactic rotations at the Solar Circle. Wider pairs show random age differences. This may well be a characteristic time scale for disruption of close transient pairs formed by resonant trapping.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig1.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg6.png) |
Figure 1: Pair separation histogram. WEBDA data, Table 1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig2.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg7.png) |
Figure 2: Age difference of open cluster pairs as a function of their age. WEBDA data. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig3.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg8.png) |
Figure 3: Age difference of open cluster pairs as a function of their physical separation. WEBDA data. |
| Open with DEXTER | |
4 Candidates
In Tables 1 and 2 we compile a preliminary list of candidate binary open clusters from WEBDA (34 pairs) and NCOVOCC (27 pairs), respectively. In these tables, pairs are sorted in order of increasing heliocentric distance; the horizontal line separates clusters in the complete or best sample. Clusters in both databases appear in boldface.
- i)
- Binary open clusters. In order to classify a pair as binary we restrict the age difference to
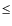 50 Myr and having similar kinematics. In WEBDA, clear candidates are pairs #6, #7, #18, #30, and #34. All of them have similar ages, radial velocity and proper motions. Pair #7 (Loden 1171/Loden 1194) is interesting as the clusters appear to have been able to survive as a bound pair for more than one entire orbit around the Galactic centre. Additional possible binaries with not enough kinematic information are pairs #19, #27 and #30. The unstudied pair Carraro 1/Loden 165 is rather peculiar as both objects have intermediate age. Assuming that they are real clusters, it is hard to understand how they have been able to survive as a pair for such a long period of time; they may well be a resonant pair or a close encounter. Another obvious primordial binary is the NCOVOCC pair #24 (Bica 1/Bica 2), which is coeval, has similar proper motion and with a separation of only 3 pc.
50 Myr and having similar kinematics. In WEBDA, clear candidates are pairs #6, #7, #18, #30, and #34. All of them have similar ages, radial velocity and proper motions. Pair #7 (Loden 1171/Loden 1194) is interesting as the clusters appear to have been able to survive as a bound pair for more than one entire orbit around the Galactic centre. Additional possible binaries with not enough kinematic information are pairs #19, #27 and #30. The unstudied pair Carraro 1/Loden 165 is rather peculiar as both objects have intermediate age. Assuming that they are real clusters, it is hard to understand how they have been able to survive as a pair for such a long period of time; they may well be a resonant pair or a close encounter. Another obvious primordial binary is the NCOVOCC pair #24 (Bica 1/Bica 2), which is coeval, has similar proper motion and with a separation of only 3 pc.
- ii)
- Triple open clusters. The system NGC 1981/NGC 1976/ Collinder 70 (#2 and #3) appears to be a bona fide triple candidate using WEBDA data. These three clusters may constitute a hierarchical triple system with the inner pair being NGC 1981/NGC 1976 with Collinder 70 orbiting around them. NCOVOCC indicates that the triple may be NGC 1976/
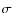 Ori/Collinder 70 (#3 and #4). If we consider both databases simultaneously, the system may well be a quadruple cluster. WEBDA pairs #8/#9 and #10/#12 cannot be primordial triples but perhaps transient pseudo-triples.
Ori/Collinder 70 (#3 and #4). If we consider both databases simultaneously, the system may well be a quadruple cluster. WEBDA pairs #8/#9 and #10/#12 cannot be primordial triples but perhaps transient pseudo-triples.
- iii)
- Tidal capture/resonant trapping. Using the available information, it is currently impossible to distinguish pairs formed by tidal capture from those resulting from resonant trapping. On the other hand, tidal capture via three-body encounters within resonant trapping regions
is also a possibility and resonant trapping may be a first step towards tidal capture. WEBDA pairs to be included in this group are #5, #8, #9, #10 or #12.
- iv)
- Hyperbolic encounters. In this group we include those pairs that are physically close but with disparate kinematics. Clear examples in WEBDA are pairs #4, #20, #23 or #32. Pair #1 is regarded as controversial: the member objects may not be true clusters. The same concern applies to many other ASCC candidates.
5 Discussion and conclusions
In this Letter, we have shown that binary open clusters appear to constitute a statistically significant sample and that the fraction of possible binary clusters in the Galactic disk is comparable to that in the Magellanic Clouds. The spatial proximity of two almost coeval open clusters, compared to the large distances which typically separate these objects, suggests that both objects were formed together. In star-forming complexes, one star cluster might capture another to form a bound state in the presence of a third body or of energy dissipation. This mechanism may also be at work within orbital resonances for non-coeval clusters. However, nearly 40% of candidate binary clusters that exist in the Milky Way may have been formed in a bound state. Only a small fraction of them, ![]() 17%, can survive as pairs for more than 25 Myr. Our data indicates that binary clusters appear to form both simultaneously and sequentially; multiple clusters form only sequentially. The bimodal nature of the distribution of separations suggests that two formation mechanisms are at work: coformation and resonant trapping.
17%, can survive as pairs for more than 25 Myr. Our data indicates that binary clusters appear to form both simultaneously and sequentially; multiple clusters form only sequentially. The bimodal nature of the distribution of separations suggests that two formation mechanisms are at work: coformation and resonant trapping.
How reliable are our present results? Unfortunately, they are affected by the inherent errors associated with the determination of open cluster parameters. The current status of the accuracy of open cluster data has been reviewed by Paunzen & Netopil (2006). There, they concluded that distances are rather well known because for about 80% of 395 of the best studied objects, the absolute error is <20%. For cluster ages, the situation is the opposite: only 11% of the best studied objects have errors <20% and 30% have absolute errors >50%. Accordingly, we may assume that our conclusions based on distances are probably quite robust but those based on ages may not be as reliable. However, they are probably more reliable than those obtained using Magellanic Clouds data. A Monte Carlo simulation of 100 000 artificial data sets using original WEBDA data altered by errors of 10%, 20%, and 30% in both distance and cluster centre determination gives average binary fractions of 10 ![]() 2%, 9
2%, 9 ![]() 2%, and 8
2%, and 8 ![]() 2%, respectively, where the error quoted is the standard deviation. The binary fraction decreases, as expected, but not dramatically. It is therefore statistically safe to conclude that the open cluster binary fraction is very likely at least 10%.
2%, respectively, where the error quoted is the standard deviation. The binary fraction decreases, as expected, but not dramatically. It is therefore statistically safe to conclude that the open cluster binary fraction is very likely at least 10%.
Acknowledgements
We would like to thank the anonymous referee for a particularly constructive and quick report. In preparation of this Letter, we made use of the NASA Astrophysics Data System and the ASTRO-PH e-print server. This research has made use of the WEBDA database operated at the Institute of Astronomy of the University of Vienna, Austria. This work also made use of the SIMBAD database, operated at the CDS, Strasbourg, France.
References
- Battinelli, P., & Capuzzo-Dolcetta, R. 1989, Ap&SS, 157, 75 [NASA ADS] [CrossRef] (In the text)
- Battinelli, P., & Capuzzo-Dolcetta, R. 1991, MNRAS, 249, 76 [NASA ADS] (In the text)
- Bekki, K., Beasley, M. A., Forbes, D. A., & Couch, W. J. 2004, ApJ, 602, 730 [NASA ADS] [CrossRef] (In the text)
- Bhatia, R. K., & Hatzidimitriou, D. 1988, MNRAS, 230, 215 [NASA ADS] (In the text)
- van den Bergh, S. 1996, ApJ, 471, L31 [NASA ADS] [CrossRef] (In the text)
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd Ed. (Princeton: Princeton University Press) (In the text)
- Brown, J. H., Burkert, A., & Truran, J. W. 1995, ApJ, 440, 666 [NASA ADS] [CrossRef] (In the text)
- Chakrabarty, D. 2007, A&A, 467, 145 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dehnen, W. 1998, AJ, 115, 2384 [NASA ADS] [CrossRef] (In the text)
- Dieball, A., & Grebel, E. K. 1998, A&A, 339, 773 [NASA ADS] (In the text)
- Dieball, A., Müller, H., & Grebel, E. K. 2002, A&A, 391, 547 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dias, W. S. 2009, Catalog of Optically Visible Open Clusters and Candidates, v. 2.10, http://www.astro.iag.usp.br/wilton/ (In the text)
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Efremov, Y. N. 1978, Sov. Astr. Lett., 4, 66 [NASA ADS] (In the text)
- Famaey, B., Jorrissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- de la Fuente Marcos, R., & de la Fuente Marcos, C. 2009, New Astron., 14, 180 [NASA ADS] [CrossRef] (In the text)
- Fujimoto, M., & Kumai, Y. 1997, AJ, 113, 249 [NASA ADS] [CrossRef] (In the text)
- Goodwin, S. P. 1997, MNRAS, 284, 785 [NASA ADS] (In the text)
- Hatzidimitriou, D., & Bhatia, R. K. 1990, A&A, 230, 11 [NASA ADS] (In the text)
- Hills, J. G. 1980, ApJ, 235, 987 [NASA ADS] [CrossRef] (In the text)
- Innanen, K. A., Wright, A. E., House, F. C., & Keenan, D. 1972, MNRAS, 160, 249 [NASA ADS] (In the text)
- Mermilliod, J.-C., & Paunzen, E. 2003, A&A, 410, 511 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641 [NASA ADS] [CrossRef] (In the text)
- Paunzen, E., & Mermilliod, J.-C. 2009, Open Cluster Database, http://www.univie.ac.at/webda (In the text)
- Pietrzynski, G., & Udalski, A. 2000, Acta Astron., 50, 355 [NASA ADS] (In the text)
- Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R.-D. 2006, A&A, 445, 545 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Portegies Zwart, S. F., & Rusli, S. P. 2007, MNRAS, 374, 931 [NASA ADS] [CrossRef] (In the text)
- Quillen, A. C., & Minchev, I. 2005, AJ, 130, 576 [NASA ADS] [CrossRef] (In the text)
- Rozhavskii, F. G., Kuz'mina, V. A., & Vasilevskii, A. E. 1976, Astrophys., 12, 204 [NASA ADS] (In the text)
- De Simone, R. S., Wu, X., & Tremaine, S. 2004, MNRAS, 350, 627 [NASA ADS] [CrossRef] (In the text)
- Subramaniam, A., Gorti, U., Sagar, R., & Bhatt, H. C. 1995, A&A, 302, 86 [NASA ADS] (In the text)
Online Material
Table 1: List of candidate binary clusters (WEBDA).
Table 2: List of candidate binary clusters (NCOVOCC).
Footnotes
- ... clusters
![[*]](/icons/foot_motif.png)
- Tables 1 and 2 are only available in electronic form at http://www.aanda.org
- ... Database
![[*]](/icons/foot_motif.png)
- http://www.univie.ac.at/webda/
- ... Candidates
![[*]](/icons/foot_motif.png)
- http://www.astro.iag.usp.br/~wilton/
All Tables
Table 1: List of candidate binary clusters (WEBDA).
Table 2: List of candidate binary clusters (NCOVOCC).
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig1.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg6.png) |
Figure 1: Pair separation histogram. WEBDA data, Table 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig2.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg7.png) |
Figure 2: Age difference of open cluster pairs as a function of their age. WEBDA data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2297fig3.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12297-09/Timg8.png) |
Figure 3: Age difference of open cluster pairs as a function of their physical separation. WEBDA data. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


