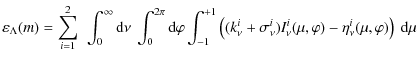| Issue |
A&A
Volume 500, Number 2, June III 2009
|
|
|---|---|---|
| Page(s) | 891 - 899 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200912121 | |
| Published online | 29 April 2009 | |
Models of magnetized neutron star atmospheres: thin atmospheres and partially ionized hydrogen atmospheres with vacuum polarization
V. Suleimanov1,2 - A. Y. Potekhin3,4 - K. Werner1
1 - Institut für Astronomie und Astrophysik, Kepler Center for Astro and
Particle Physics, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
2 - Kazan State University, Kremlevskaja str., 18, Kazan 420008, Russia
3 - Ioffe Physical-Technical Institute, Polytekhnicheskaya str., 26, St. Petersburg 194021, Russia
4 - Isaac Newton Institute of Chile, St. Petersburg Branch, Russia
Received 20 March 2009 / Accepted 14 April 2009
Abstract
Context. Observed X-ray spectra of some isolated magnetized neutron stars display absorption features, sometimes interpreted as ion cyclotron lines. Modeling the observed spectra is necessary to check this hypothesis and to evaluate neutron star parameters.
Aims. We develop a computer code for modeling magnetized neutron star atmospheres in a wide range of magnetic fields (
1012-1015 G) and effective temperatures (
![]() K). Using this code, we study the possibilities to explain the soft X-ray spectra of isolated neutron stars by different atmosphere models.
K). Using this code, we study the possibilities to explain the soft X-ray spectra of isolated neutron stars by different atmosphere models.
Methods. The atmosphere is assumed to consist either of fully ionized electron-ion plasmas or of partially ionized hydrogen. Vacuum resonance and partial mode conversion are taken into account. Any inclination of the magnetic field relative to the stellar surface is allowed. We use modern opacities of fully or partially ionized plasmas in strong magnetic fields and solve the coupled radiative transfer equations for the normal electromagnetic modes in the plasma.
Results. Spectra of outgoing radiation are calculated for various atmosphere models: fully ionized semi-infinite atmosphere, thin atmosphere, partially ionized hydrogen atmosphere, or novel ``sandwich'' atmosphere (thin atmosphere with a hydrogen layer above a helium layer). Possibilities of applications of these results are discussed. In particular, the outgoing spectrum using the ``sandwich'' model is constructed. Thin partially ionized hydrogen atmospheres with vacuum polarization are shown to be able to improve the fit to the observed spectrum of the nearby isolated neutron star RBS 1223 (RX J1308.8+2127).
Key words: stars: individual: RX J1308.8+2127- radiative transfer - methods: numerical - stars: neutron - stars: atmospheres - X-rays: stars
1 Introduction
In the last two decades, several new classes of neutron stars (NSs) have
been discovered by X-ray observatories. They include X-ray dim isolated NSs
(XDINSs), or Magnificent Seven (see review by Haberl 2007),
central compact objects (CCOs) in supernova remnants (Pavlov et al. 2004,2002), anomalous X-ray pulsars and soft-gamma repeaters (AXPs and SGRs; see reviews by
Kaspi 2007; Mereghetti et al. 2007; Mereghetti 2008). The NSs in the last two classes have superstrong magnetic fields (
![]() G) and are commonly named magnetars. The XDINSs can have
G) and are commonly named magnetars. The XDINSs can have
![]() G, as evaluated from period changes and from absorption features in the observed spectra, if they are interpreted as ion cyclotron lines (see reviews by van Kerkwijk & Kaplan 2007; Haberl 2007).
G, as evaluated from period changes and from absorption features in the observed spectra, if they are interpreted as ion cyclotron lines (see reviews by van Kerkwijk & Kaplan 2007; Haberl 2007).
These NSs are relatively young with ages ![]() 106 yr and
sufficiently hot (
106 yr and
sufficiently hot (
![]() K) to be observed as soft X-ray sources. The thermal spectra of
these objects can be described by blackbody spectra with (color) temperatures
from 40 to 700 eV (see, for example, Mereghetti et al. 2002).
Some of the XDINSs and CCOs in supernova remnants have one or more absorption features in their X-ray spectrum at the energies 0.2-0.8 keV (Haberl 2007). The central energies of these features appear to be harmonically spaced (van Kerkwijk & Kaplan 2007; Schwope et al. 2007; Sanwal et al. 2002; Haberl 2007). The optical counterparts of some XDINSs are also known (see review by Mignani et al. 2007), and their optical/ultraviolet fluxes are a few times larger than the blackbody extrapolation of the X-ray spectra (Motch et al. 2003; Burwitz et al. 2001,2003; Kaplan et al. 2003).
K) to be observed as soft X-ray sources. The thermal spectra of
these objects can be described by blackbody spectra with (color) temperatures
from 40 to 700 eV (see, for example, Mereghetti et al. 2002).
Some of the XDINSs and CCOs in supernova remnants have one or more absorption features in their X-ray spectrum at the energies 0.2-0.8 keV (Haberl 2007). The central energies of these features appear to be harmonically spaced (van Kerkwijk & Kaplan 2007; Schwope et al. 2007; Sanwal et al. 2002; Haberl 2007). The optical counterparts of some XDINSs are also known (see review by Mignani et al. 2007), and their optical/ultraviolet fluxes are a few times larger than the blackbody extrapolation of the X-ray spectra (Motch et al. 2003; Burwitz et al. 2001,2003; Kaplan et al. 2003).
The XDINs are nearby objects, and parallaxes of some of them can be measured (Kaplan et al. 2002a). Therefore, they give a good possibility to measure the NS radii, yielding useful information on the equation of state (EOS) for the NS inner core (Lattimer & Prakash 2007; Trümper et al. 2004), which is one of the most important problems in the NS physics. For example, the EOS is necessary for computations of templates of gravitational wave signals which arise during neutron stars merging (e.g. Baiotti et al. 2008).
For a sufficiently accurate evaluation of NS radii,
a good model of the NS surface radiation for
the observed X-ray spectra fitting is necessary. The isolated NS surface
layers can either be condensed or have a plasma envelope (Lai 2001; Lai & Salpeter 1997). In the latter case, the outer envelope layer forms an NS
atmosphere. The structure and emergent spectrum of this atmosphere can be
computed by using stellar model atmosphere methods (e.g. Mihalas 1978). Such modeling has been performed by many scientific groups for NS model
atmospheres without magnetic field (Zavlin et al. 1996; Romani 1987; Gänsicke et al. 2002; Werner & Deetjen 2000; Rajagopal & Romani 1996; Pons et al. 2002) and by several groups for models with strong (
![]() G) magnetic fields (Shibanov et al. 1992; Özel 2001; Ho & Lai 2004; van Adelsberg & Lai 2006; Ho & Lai 2001,2003; Rajagopal et al. 1997). These model spectra were used to fit the observed isolated NS X-ray spectra (see review by Zavlin 2009).
G) magnetic fields (Shibanov et al. 1992; Özel 2001; Ho & Lai 2004; van Adelsberg & Lai 2006; Ho & Lai 2001,2003; Rajagopal et al. 1997). These model spectra were used to fit the observed isolated NS X-ray spectra (see review by Zavlin 2009).
Modeling of magnetized NS star atmospheres is based on the theory of electromagnetic wave propagation in a magnetized plasma in two normal modes, extraordinary (X) and ordinary (O) ones (Mészaros 1992; Ginzburg 1970), and on the methods of opacity calculations for these two modes (Kaminker et al. 1982,1983; Ventura 1979). Methods of fully ionized model atmospheres modeling are well developed (see, e.g., Zavlin 2009 for references). Partially ionized hydrogen atmospheres have been modeled (Ho & Lai 2004; Ho et al. 2008; Potekhin et al. 2004), using the opacity and EOS calculations by Potekhin & Chabrier (2003,2004), which accurately take into account the motional Stark effect and plasma nonideality effects in quantizing magnetic fields. Mid-Z element atmospheres for strongly magnetized NSs have been modeled by Mori & Ho (2007), who treat the motional Stark effect using a perturbation theory (Pavlov & Mészáros 1993) valid at relatively low T.
For magnetar atmospheres, polarization of the vacuum can be significant, which was studied by Pavlov & Gnedin (1984) and recently by Lai & Ho (2003,2002). Model atmospheres with partial mode conversion due to the vacuum polarization have been computed by Ho & Lai (2003) and van Adelsberg & Lai (2006).
If the temperature is sufficiently low or the magnetic field is sufficiently strong, the thick atmosphere can be replaced by a condensed surface (Lai 2001; Lai & Salpeter 1997; Medin & Lai 2007) as a result of the plasma phase transition (cf. Potekhin et al. 1999; Potekhin & Chabrier 2004). Emission and absorption properties of such surfaces in strong magnetic fields have been studied by Turolla et al. (2004), van Adelsberg et al. (2005), and Pérez-Azorín et al. (2005).
In recent years, evidence has appeared that some of the XDINSs may have a ``thin'' atmosphere above the condensed surface. Such atmosphere could be optically thick to low-energy photons and optically thin to high-energy photons. Motch et al. (2003) fitted the spectrum of RX J0720.4-3125 using a nonmagnetic thin hydrogen atmosphere model, and Ho et al. (2007) fitted the spectrum of RX J1856.4-3754 using a magnetic, partially ionized, thin hydrogen atmosphere model.
In this paper we present a new computer code for model atmospheres of magnetized NSs and some new results, which were obtained by using this code. The code is applicable to modeling of fully ionized NS atmospheres and partially ionized hydrogen atmospheres accounting for the partial mode conversion due to the vacuum polarization. The magnetic field can be normal or inclined to NS surface. We use this code to study various thin atmospheres above a condensed NS surface. In particular, we consider a novel ``sandwich'' atmosphere model, where a thin atmosphere is composed of a hydrogen layer above a helium layer. We also discuss the possibility to apply our thin partially ionized hydrogen model atmospheres with vacuum polarization to fit the spectrum of RBS 1223. Our numerical method is outlined in Sect. 2. Results are presented and discussed in Sect. 3. Conclusions are summarized in Sect. 4.
2 Method of atmosphere structure calculations
We compute model
atmospheres of hot, magnetized NSs subject to the constraints
of hydrostatic and radiative equilibrium assuming planar geometry
and homogeneous magnetic field.
There are two versions of the code.
In the first one, we consider the magnetic field
![]() perpendicular to the surface. In
this case the angle
perpendicular to the surface. In
this case the angle ![]() between
between ![]() and a radiation
wave vector
and a radiation
wave vector ![]() is equal to the angle
is equal to the angle ![]() between
between
![]() and the normal
and the normal ![]() to the surface
(see Fig. 1).
It is the simplest case,
because opacities depend on
to the surface
(see Fig. 1).
It is the simplest case,
because opacities depend on ![]() ,
and the geometry of radiation
propagation depends on
,
and the geometry of radiation
propagation depends on ![]() .
In the second version, the angle
.
In the second version, the angle
![]() between
between ![]() and
and ![]() is arbitrary,
and calculations are more expensive. In this case the
opacities depend not only on the polar angle
is arbitrary,
and calculations are more expensive. In this case the
opacities depend not only on the polar angle
![]() ,
but also on the azimuthal angle
,
but also on the azimuthal angle
![]() between the projections of
between the projections of ![]() and
and ![]() onto the stellar surface, therefore it is necessary to solve radiation
transfer equations for a significantly larger number of directions.
onto the stellar surface, therefore it is necessary to solve radiation
transfer equations for a significantly larger number of directions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg1.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg29.png) |
Figure 1: Geometry of the radiation transfer. |
| Open with DEXTER | |
The model atmosphere structure for a NS with effective temperature
![]() ,
surface gravity g, magnetic field B, and given chemical composition
is described by the following set of equations:
,
surface gravity g, magnetic field B, and given chemical composition
is described by the following set of equations:
- 1.
- The hydrostatic equilibrium equation
where
g = 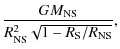
(2) 
= 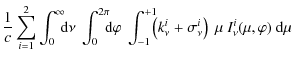
(3)
allows for the radiation pressure, and![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg2.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg35.png)
Figure 2: Dependence of the free-free and electron scattering opacities in two modes on the photon energy at different angles in a fully ionized hydrogen plasma. The proton cyclotron and vacuum resonances are also shown. The plasma temperature is
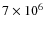 K, the plasma density is 30 g cm-3, the magnetic field strength is 1014 G.
K, the plasma density is 30 g cm-3, the magnetic field strength is 1014 G.Open with DEXTER 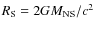 is the Schwarzschild radius of the NS. Here
is the Schwarzschild radius of the NS. Here
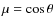 ,
,
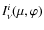 is the specific intensity in mode i,
is the specific intensity in mode i, 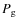 is the gas pressure, and the column density m is determined as
is the gas pressure, and the column density m is determined as
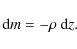
(4)
The variable denotes the gas density and z is the vertical distance.
Radiation pressure is unimportant in the models presented below,
but it can be significant at higher effective temperatures.
denotes the gas density and z is the vertical distance.
Radiation pressure is unimportant in the models presented below,
but it can be significant at higher effective temperatures.
- 2.
- The radiation transfer equations for the two modes
where
is the source function,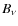 is the blackbody (Planck) intensity, and the optical depth
is the blackbody (Planck) intensity, and the optical depth
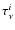 is defined as
is defined as
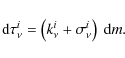
(7)
Here, the true absorption and electron scattering opacities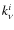 and
and
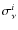 depend on
depend on 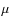 and
and 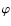 .
Specific intensity in given direction and mode can be scattered in some other direction and in both modes
.
Specific intensity in given direction and mode can be scattered in some other direction and in both modes
- 3.
- The energy balance equation
with emissivity
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg3.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg54.png) |
Figure 3: Dependence of the free-free and electron scattering opacities in two modes on the angle between the magnetic field lines and the direction of photon propagation for two photon energies: 1 keV and at the proton cyclotron energy. Plasma parameters and magnetic field strength are the same as in Fig. 2. |
| Open with DEXTER | |
In the first (simplest) case, a fully ionized atmosphere are calculated. Therefore, the EOS is the ideal gas law
where
The second considered case is a partially ionized hydrogen atmosphere. In this case the EOS and the corresponding opacities are taken from tables calculated by Potekhin & Chabrier (2003,2004). The normal mode polarization vectors are taken from the calculations by Potekhin et al. (2004). The vacuum polarization effect is also included.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg4.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg57.png) |
Figure 4:
Dependence of the true opacities in two
modes on the photon energy for fully (dashed curves) and partially ionized
(solid curves) hydrogen. The vacuum polarization effect is taken into account. The plasma temperature is 106 K, the plasma density is 1 g cm-3, the magnetic field strength is
|
| Open with DEXTER | |
For solving the above equations and computing the model atmosphere, we used a version of the computer code ATLAS (Kurucz 1970,1993), modified to deal with strong magnetic fields. A nonmagnetic version of this modified code was previously used to model atmospheres of super-soft X-ray sources (Swartz et al. 2002; Ibragimov et al. 2003), atmospheres of non-magnetized NSs (Suleimanov & Werner 2007; Rauch et al. 2008), and atmospheres of spreading layers on the surface of accreting NSs (Suleimanov & Poutanen 2006).
The scheme of calculations is as follows. First of all, the input
parameters of the model atmosphere are defined:
![]() ,
g,
,
g, ![]() and the chemical composition.
Then a starting model using a grey temperature distribution is calculated.
The calculations are performed with a set of 90 depth points mj
distributed logarithmically in equal steps from
and the chemical composition.
Then a starting model using a grey temperature distribution is calculated.
The calculations are performed with a set of 90 depth points mj
distributed logarithmically in equal steps from
![]() g cm-2 to
g cm-2 to
![]() g cm-2 in the case
of a semi-infinite atmosphere. It is also possible to calculate
thin atmospheres with arbitrary values of
g cm-2 in the case
of a semi-infinite atmosphere. It is also possible to calculate
thin atmospheres with arbitrary values of
![]() .
In
this case the temperature at the inner boundary is considered as
the temperature of a condensed NS surface.
.
In
this case the temperature at the inner boundary is considered as
the temperature of a condensed NS surface.
In the starting model, all number densities and opacities at all depth points and all photon energies are calculated. We use 200 logarithmically equidistant energy points in our computations in the range 0.001-20 keV with 9 additional points near each ion
cyclotron resonance
where Z is the ionic charge and A the atomic weight in the atomic units. If the vacuum resonance is taken into consideration, then another photon energy grid is used, which is constructed using the ``equal grid'' method (Ho & Lai 2003). In this method every point in the depth grid mj corresponds to the point in the energy grid defined by the equation
| (13) |
(if this energy point is in the considered energy range 0.001-20 keV). Here
The radiation transfer Eq. (5) is solved on a set of 40 polar angles ![]() and 6 azimuthal angles
and 6 azimuthal angles ![]() (in the case of inclined magnetic field)
by the short characteristic method (Olson & Kunasz 1987).
(in the case of inclined magnetic field)
by the short characteristic method (Olson & Kunasz 1987).
We use the conventional condition (no external radiation) at the outer boundary
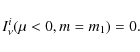 |
(14) |
The diffusion approximation is used as the inner boundary condition
The code allows one to take into account the partial mode conversion according to van Adelsberg & Lai (2006). At the vacuum resonance, the intensity in the extraordinary mode partially converts with the probability
where
The value
The solution of the radiative transfer Eq. (5) is checked for the energy balance Eq. (9), together with the surface flux condition
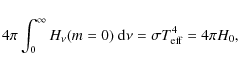 |
(18) |
where the Eddington flux at any given depth m is defined as
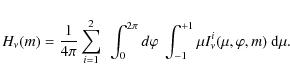 |
(19) |
The relative flux error
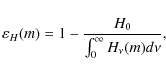 |
(20) |
and the energy balance error as functions of depth
are calculated.
Temperature corrections are then evaluated using three different procedures. The first is the integral ![]() -iteration method, modified for the two-mode radiation transfer, based on the energy balance Eq. (9). In this method the temperature correction for a particular depth is found from
-iteration method, modified for the two-mode radiation transfer, based on the energy balance Eq. (9). In this method the temperature correction for a particular depth is found from
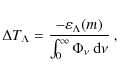 |
(22) |
where
![\begin{displaymath}\Phi_{\nu} = \sum_{i=1}^2 \left[
\left(\Lambda_{\nu{\rm diag...
...}}^i) \right]
\overline{k}_{\nu}^i ({\rm d}B_{\nu}/{\rm d}T)
\end{displaymath}](/articles/aa/full_html/2009/23/aa12121-09/img77.png) |
(23) |
and
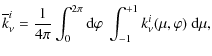 |
(24) | ||
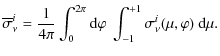 |
(25) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg5.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg87.png) |
Figure 5:
Emergent spectra and temperature structures of fully ionized hydrogen model atmospheres of neutron stars with
|
| Open with DEXTER | |
The iteration procedure is repeated until the relative flux error is smaller than 1% and the relative flux derivative error is smaller than 0.01%. As a result of these calculations, we obtain a self-consistent isolated NS model atmosphere, together with the emergent spectrum of radiation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg6.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg89.png) |
Figure 6:
Top panel: emergent spectra of the partially ionized hydrogen semi-infinite (dashed curve) and thin (
|
| Open with DEXTER | |
Our method of calculation has been tested by a comparison to models for magnetized NS atmospheres (Shibanov et al. 1992; Pavlov et al. 1994; Özel 2001; Ho & Lai 2001,2003). Model atmospheres with partially ionized hydrogen are compared to models computed by Ho et al. (2007). We have found that our models are in a good agreement with these calculations. Our results are presented in Fig. 5, where the temperature structures and the emergent spectra of models with and without vacuum polarization are compared to a model without magnetic field. In Fig. 6 we present emergent spectra and temperature structures of the semi-infinite and thin model atmospheres with the same parameters as used by Ho et al. (2007).
3 Results
In this work we use the developed code mainly for studies of thin atmospheres above a condensed NS surface. In all calculations below we use the same surface gravity,
![]() .
.
One of the problem related to magnetars (in particular, AXPs) is the lack of any absorption feature at the proton cyclotron energy, although early models of the magnetized NS
atmospheres predicted a strong feature at the magnetar field strengths
(Ho & Lai 2001; Zane et al. 2001). Ho & Lai (2003)
suggested that a possible solution of this problem is the suppression of the cyclotron absorption feature due to the vacuum polarization. We confirm this result (see Fig. 5). In addition, we demonstrate that this absorption line is further reduced in a thin atmosphere without vacuum polarization. Figure 7 demonstrates emergent spectra of thin atmospheres without allowance for the vacuum polarization effect.
In the semi-infinite atmosphere, a wide proton cyclotron line
forms in agreement with the results of Ho & Lai (2001); Zane et al. (2001).
However, the absorption feature disappears with decreasing
the atmosphere surface density ![]() .
The thin atmosphere is transparent to the
continuum and absorption line wings, therefore the emergent spectrum approaches the
spectrum of the condensed surface everywhere except for a narrow energy band at the center of the cyclotron line. The width of this absorption depends on the atmosphere thickness.
.
The thin atmosphere is transparent to the
continuum and absorption line wings, therefore the emergent spectrum approaches the
spectrum of the condensed surface everywhere except for a narrow energy band at the center of the cyclotron line. The width of this absorption depends on the atmosphere thickness.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg7.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg90.png) |
Figure 7:
Emergent spectra of the thin fully ionized hydrogen atmospheres above a solid surface with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg8.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg91.png) |
Figure 8:
Emergent spectrum ( top panel) and temperature structure ( bottom panel) of the ``sandwich'' model atmosphere above a solid surface with
|
| Open with DEXTER | |
Some XDINSs and CCOs show one or two
absorption features
(Schwope et al. 2007; Sanwal et al. 2002; Haberl 2007).
Various hypothesis (so far inconclusive) were
considered for an explanation
(see Mori & Ho 2007 and references therein).
Here we
suggest another one, which we name ``sandwich atmosphere''.
A thin, chemically layered atmosphere above a condensed NS surface can arise from
accretion of interstellar gas with cosmic chemical composition. In
this case, hydrogen and helium quickly
separate due to the high
gravity
(according to Brown et al. 2002, the He/H stratification timescale
can be estimated as
![]()
![]() s,
where
s,
where
![]() g cm-3,
T6=T/106 K, and
g14=g/1014 cm s-2). In this ``sandwich atmosphere'' a layer
of hydrogen is located above a helium slab,
and the emergent spectrum has two absorption features, corresponding to proton and
g cm-3,
T6=T/106 K, and
g14=g/1014 cm s-2). In this ``sandwich atmosphere'' a layer
of hydrogen is located above a helium slab,
and the emergent spectrum has two absorption features, corresponding to proton and ![]() -particle cyclotron energies. In Fig. 8 the emergent spectrum for one of these models is shown. The emission feature at the helium absorption line
arises due to a local temperature bump at the boundary between the helium and
hydrogen layers. This bump is due to sharp changes of the plasma density and
the opacity between helium and hydrogen layers. Clearly, some transition zone with
mixed H/He chemical composition must exist between layers, and this rapid temperature
change should be reduced. We plan to calculate models with this kind of transition
zone in future work.
-particle cyclotron energies. In Fig. 8 the emergent spectrum for one of these models is shown. The emission feature at the helium absorption line
arises due to a local temperature bump at the boundary between the helium and
hydrogen layers. This bump is due to sharp changes of the plasma density and
the opacity between helium and hydrogen layers. Clearly, some transition zone with
mixed H/He chemical composition must exist between layers, and this rapid temperature
change should be reduced. We plan to calculate models with this kind of transition
zone in future work.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg9.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg95.png) |
Figure 9:
Emergent spectra and temperature structures of partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
For comparison to observations, it is necessary to integrate the local model spectra over the NS surface. The effective temperature and magnetic field strengths are not uniform over the NS surface, and generally the magnetic field is not perpendicular to the surface (see Ho et al. 2008). Therefore, it is necessary to compute model atmospheres with inclined magnetic field. This possibility is included in our code. For example, Fig. 9 shows spectra and temperature structures of model atmospheres with magnetic field perpendicular and parallel to the NS surface.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f10.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg96.png) |
Figure 10:
Emergent spectra and temperature structures of the partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
Most of the XDINSs have magnetic fields
![]() G and color temperatures
G and color temperatures ![]() 106 K (Haberl 2007).
Hydrogen model atmospheres are partially ionized under these conditions
and the vacuum polarization effect is also significant.
Here we present first results of modeling of partially ionized
hydrogen atmospheres using our radiative transfer code. In
Fig. 10 we compare spectra and temperature
structures of the partially ionized hydrogen model atmospheres with and
without the partial mode conversion
effect. When the X-mode (having smaller opacity) partially converts to the
O-mode in the surface layers of the atmosphere, the energy absorbed by
the O-mode heats these upper layers. As a
result, the emergent spectra are closer to the blackbody.
106 K (Haberl 2007).
Hydrogen model atmospheres are partially ionized under these conditions
and the vacuum polarization effect is also significant.
Here we present first results of modeling of partially ionized
hydrogen atmospheres using our radiative transfer code. In
Fig. 10 we compare spectra and temperature
structures of the partially ionized hydrogen model atmospheres with and
without the partial mode conversion
effect. When the X-mode (having smaller opacity) partially converts to the
O-mode in the surface layers of the atmosphere, the energy absorbed by
the O-mode heats these upper layers. As a
result, the emergent spectra are closer to the blackbody.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f11.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg99.png) |
Figure 11:
Emergent spectra and temperature structures of the partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
For some of the XDINSs, optical counterparts have been found
(Mignani et al. 2007). The observed optical fluxes are a
few times larger compared to the blackbody extrapolation from X-rays
to the optical range
(see top panel of Fig. 12 for illustration).
Ho et al. (2007) demonstrated, that a single partially ionized thin
hydrogen atmosphere can explain this problem in the case of brightest
isolated NS RX J1856.4-3754: the model fits well both,
the observed optical flux and the X-ray spectrum.
RX J1856.4-3754 has very low pulsed fraction of radiation
(![]() 1.2%, Tiengo & Mereghetti 2007), therefore it is possible to fit the radiation of this star by the single model atmosphere. Other XDINSs have larger pulse fractions, up to 18% (RBS 1223, Haberl et al. 2004). In this case the temperature distribution across the NS surface is not homogenous, and the excess optical flux can be explained by the radiation from cool surface parts (Schwope et al. 2005).
1.2%, Tiengo & Mereghetti 2007), therefore it is possible to fit the radiation of this star by the single model atmosphere. Other XDINSs have larger pulse fractions, up to 18% (RBS 1223, Haberl et al. 2004). In this case the temperature distribution across the NS surface is not homogenous, and the excess optical flux can be explained by the radiation from cool surface parts (Schwope et al. 2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f12.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg100.png) |
Figure 12:
Top panel: emergent spectrum of the partially ionized hydrogen model atmosphere of neutron stars with
|
| Open with DEXTER | |
We now investigate properties of partially ionized hydrogen modes,
which can be applied to the RBS 1223 atmosphere. The color
temperature of this star, found from X-ray spectra fitting,
is close to 106 K, with magnetic field
![]() G
(Schwope et al. 2007). In particular, we investigate the optical flux excess
in comparison to the X-ray fitted blackbody flux in this kind of models.
For this aim we have calculated two sets of
models with vacuum polarization and partial mode
conversion. The models in the first set have
effective temperatures
G
(Schwope et al. 2007). In particular, we investigate the optical flux excess
in comparison to the X-ray fitted blackbody flux in this kind of models.
For this aim we have calculated two sets of
models with vacuum polarization and partial mode
conversion. The models in the first set have
effective temperatures
![]() K and the models of second one
have effective temperatures
K and the models of second one
have effective temperatures
![]() K. In both
sets
K. In both
sets
![]() G, and models with
surface densities
G, and models with
surface densities
![]() ,
3, 10, 30, 100 and 105 (semi-infinite
model) g cm-2 are computed. In Fig. 11 we show emergent spectra
and temperature structures for some models from the second set.
Clearly, the X-ray spectra of the models with
,
3, 10, 30, 100 and 105 (semi-infinite
model) g cm-2 are computed. In Fig. 11 we show emergent spectra
and temperature structures for some models from the second set.
Clearly, the X-ray spectra of the models with
![]() g cm-2 are close to a blackbody and, therefore, better fit
the observed X-ray spectrum.
g cm-2 are close to a blackbody and, therefore, better fit
the observed X-ray spectrum.
In Fig. 12 (bottom panel) we show
the ratio of the model
atmosphere flux to the X-ray fitted blackbody flux in the optical band
depending on ![]() for
both sets.
The observed ratio is about 5 (Kaplan et al. 2002b), in
agreement with the semi-infinite atmosphere models. However, the
observed blackbody like X-ray spectrum agrees with the thin
atmosphere models, for which this ratio is close to 1. Therefore,
the observed optical excess cannot be explained by the thin
atmosphere model alone; instead, it can arise due to a nonuniform
surface temperature distribution, in agreement with the RBS 1223
light curve modeling (Schwope et al. 2005).
for
both sets.
The observed ratio is about 5 (Kaplan et al. 2002b), in
agreement with the semi-infinite atmosphere models. However, the
observed blackbody like X-ray spectrum agrees with the thin
atmosphere models, for which this ratio is close to 1. Therefore,
the observed optical excess cannot be explained by the thin
atmosphere model alone; instead, it can arise due to a nonuniform
surface temperature distribution, in agreement with the RBS 1223
light curve modeling (Schwope et al. 2005).
4 Conclusions
In this paper a new code for the computation of magnetized
NS model atmosphere is presented. It can model fully ionized
and partially ionized hydrogen atmospheres in a wide range
of effective temperatures (
![]() -107 K) and magnetic
fields (1012-1015 G), with any inclination
of the magnetic
field to the stellar surface. The vacuum polarization effect with
partial mode conversion is taken into consideration. Calculated
emergent spectra and temperature structures of the model
atmospheres agree with previously published ones.
-107 K) and magnetic
fields (1012-1015 G), with any inclination
of the magnetic
field to the stellar surface. The vacuum polarization effect with
partial mode conversion is taken into consideration. Calculated
emergent spectra and temperature structures of the model
atmospheres agree with previously published ones.
We presented new results obtained using this code. We have studied the properties of thin atmospheres above condensed NS surfaces. We demonstrated that the proton cyclotron absorption line disappears in the thin hydrogen model atmospheres. A new thin ``sandwich'' model atmosphere (hydrogen layer above helium layer) is proposed to explain the occurrence of two absorption features in the observed X-ray spectra of some isolated NSs.
We analyzed the optical excess (relative to the X-ray fitted blackbody flux) in the model spectra of partially ionized hydrogen atmospheres with vacuum polarization and partial mode conversion.
A set of model atmospheres with parameters (effective
temperature and the magnetic field strength) close to the probable parameters
of the isolated NS RBS 1223 were calculated.
We found the optical flux excess ![]() 5 for the semi-infinite model
atmospheres decreases down to 1 with decreasing surface density
5 for the semi-infinite model
atmospheres decreases down to 1 with decreasing surface density ![]() of the atmosphere. Spectra of thin model atmospheres fit the observed
RBS 1223 X-ray spectrum better, therefore we conclude that the observed optical
excess should be explained by nonuniform surface temperature
distribution.
of the atmosphere. Spectra of thin model atmospheres fit the observed
RBS 1223 X-ray spectrum better, therefore we conclude that the observed optical
excess should be explained by nonuniform surface temperature
distribution.
The accuracy of the thin and sandwich model atmospheres is currently limited by the inner boundary condition for the radiation transfer equation. We used blackbody radiation as this condition, but a higher accuracy can be achieved by replacing it by the condensed surface condition (van Adelsberg et al. 2005). This will be done in a future work. We are also planning to include the effect of magnetic field and temperature distributions over the stellar surface to compute an integral emergent spectrum from isolated NSs.
Acknowledgements
VS thanks DFG for financial support (grant We 1312/35-1 and grant SFB/Transregio 7 ``Gravitational Wave Astronomy'') and the President's programme for support of leading science schools (grant NSh-4224.2008.2). The work of A.Y.P. is supported by RFBR grants 05-02-2203 and 08-02-00837 and the President's programme for support of leading science schools (grant NSh-2600.2008.2).
References
- Baiotti, L., Giacomazzo, B., & Rezzolla, L. 2008, Phys. Rev. D, 78, 084033 [NASA ADS] [CrossRef] (In the text)
- Brown, E. F., Bildsten, L., & Chang, P. 2002, ApJ, 574, 920 [NASA ADS] [CrossRef] (In the text)
- Burwitz, V., Zavlin, V. E., Neuhäuser, R., et al. 2001, A&A, 379, L35 [NASA ADS] [CrossRef] [EDP Sciences]
- Burwitz, V., Haberl, F., Neuhäuser, R., et al. 2003, A&A, 399, 1109 [NASA ADS] [CrossRef] [EDP Sciences]
- Gänsicke, B. T., Braje, T. M., & Romani, R. W. 2002, A&A, 386, 1001 [NASA ADS] [CrossRef] [EDP Sciences]
- Ginzburg, V. L. 1970, The Propagation of Electromagnetic Waves in Plasmas, (2nd edn. Oxford: Pergamon)
- Haberl, F., Motch, C., Zavlin, V. E. et al. 2004, A&A, 424, 635 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Haberl, F. 2007, A&SS, 308, 181 [NASA ADS] (In the text)
- Ho, W. C. G., & Lai, D. 2001, MNRAS, 327, 1081 [NASA ADS] [CrossRef]
- Ho, W. C. G., & Lai, D. 2003, MNRAS, 338, 233 [NASA ADS] [CrossRef]
- Ho, W. C. G., & Lai, D. 2004, ApJ, 607, 420 [NASA ADS] [CrossRef]
- Ho, W. C. G., Kaplan, D. L., Chang, P., van Adelsberg, M., & Potekhin, A. Y. 2007, MNRAS, 375, 821 [NASA ADS] [CrossRef] (In the text)
- Ho, W. C. G., Potekhin, A. Y., & Chabrier, G. 2008, ApJS, 178, 102 [NASA ADS] [CrossRef]
- Ibragimov, A. A., Suleimanov, V. F., Vikhlinin, A., & Sakhibullin, N. A. 2003, Astron. Rep., 47, 186 [NASA ADS] [CrossRef]
- Kaminker, A. D., Pavlov, G. G., & Shibanov, Yu. A. 1982, Ap&SS, 86, 249 [NASA ADS] [CrossRef]
- Kaminker, A. D., Pavlov, G. G., & Shibanov, Yu. A. 1983, Ap&SS, 91, 167 [NASA ADS] [CrossRef]
- Kaplan, D. L., van Kerkwijk, M. H., Anderson, J. 2002a, ApJ, 571, 447 [NASA ADS] [CrossRef] (In the text)
- Kaplan, D. L., Kulkarni, S. R., & van Kerkwijk, M. H. 2002b, ApJ, 579, L29 [NASA ADS] [CrossRef] (In the text)
- Kaplan, D. L., van Kerkwijk, M. H., Marshall, H. L., et al. 2003, ApJ, 590, 1008 [NASA ADS] [CrossRef]
- Kaspi, V. M. 2007, A&SS, 308, 1 [NASA ADS]
- Kurucz, R. L. 1970, SAO Spec. Rep., 309
- Kurucz, R. 1993, Atomic data for opacity calculations. Kurucz CD-ROMs, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 1
- Lai, D. 2001, Rev. Mod. Phys., 73, 629 [NASA ADS] [CrossRef]
- Lai, D., & Salpeter, E. E. 1997, ApJ, 491, 270 [NASA ADS] [CrossRef]
- Lai, D., & Ho. W. C. G. 2002, ApJ, 566, 373 [NASA ADS] [CrossRef]
- Lai, D., & Ho. W. C. G. 2003, ApJ, 588, 962 [NASA ADS] [CrossRef]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef]
- Medin, Z., & Lai, D. 2007, MNRAS, 382, 1833 [NASA ADS]
- Mereghetti, S. 2008, A&A Rev., 15, 225 [NASA ADS]
- Mereghetti, S., Tiengo, A., & Israel, G. L. 2002, ApJ, 569, 275 [NASA ADS] [CrossRef] (In the text)
- Mereghetti, S., Esposito, P., & Tiengo, A. 2007, A&SS, 308, 13 [NASA ADS]
- Mészaros, P. 1992, High-Energy Radiation from Magnetized Neutron Stars (Chicago: Univ. Chicago Press)
- Mignani, R. P., Bagnulo, S., De Luca, A., et al. 2007, A&SS, 308, 203 [NASA ADS] (In the text)
- Mihalas, D. 1978, Stellar atmospheres, 2nd edition (San Francisco: W. H. Freeman and Co.) (In the text)
- Mori, K., & Ho, W. C. G. 2007, MNRAS, 377, 905 [NASA ADS] [CrossRef] (In the text)
- Motch, C., Zavlin, V. E., & Haberl, F. 2003, A&A, 408, 323 [NASA ADS] [CrossRef] [EDP Sciences]
- Olson, G. L., & Kunasz, P. B. 1987, JQSRT, 38, 325 [NASA ADS] (In the text)
- Özel, F. 2001, ApJ, 563, 276 [NASA ADS] [CrossRef]
- Pavlov, G. G., & Gnedin, Yu. N. 1984, Astrophys. Space Phys. Rev., 3, 197 [NASA ADS] (In the text)
- Pavlov, G. G., & Mészáros, P. 1993, ApJ, 416, 752 [NASA ADS] [CrossRef] (In the text)
- Pavlov, G. G., Shibanov, Yu. A., Ventura, J. & Zavlin, V. E. 1994, A&A, 289, 837 [NASA ADS]
- Pavlov, G. G., Sanwal, D., & Garmire, G. P. 2002, In Neutron Stars in Supernova Remnants, ed. P. O. Slane, & B. M. Gaensler, ASP Conf. Ser. 271, 247
- Pavlov, G. G., Sanwal, D., Teter, M. A. 2004, in Young Neutron Stars and Their Enviroments ed. F. Camilo, & B. M. Gaensler (San Francisco: ASP), Proc. IAU Symp., 218, 239
- Pérez-Azorín, J. F., Miralles, J. A., & Pons, J. A. 2005, A&A, 433, 275 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pons, J. A., Walter, F. M., Lattimer, J., et al. 2002, ApJ, 564, 981 [NASA ADS] [CrossRef]
- Potekhin, A. Y., & Chabrier, G. 2003, ApJ, 585, 955 [NASA ADS] [CrossRef]
- Potekhin, A. Y., & Chabrier, G. 2004, ApJ, 600, 317 [NASA ADS] [CrossRef]
- Potekhin, A. Y., Chabrier, G., & Shibanov, Yu. A. 1999, Phys. Rev. E, 60, 2193 [NASA ADS] [CrossRef]
- Potekhin, A. Y., Lai, D., Chabrier G., & Ho, W. C. G. 2004, ApJ, 612, 1034 [NASA ADS] [CrossRef]
- Rajagopal, M., & Romani, R. W. 1996, ApJ, 461, 327 [NASA ADS] [CrossRef]
- Rajagopal, M., Romani, R. W., & Miller, M. C. 1997, ApJ, 479, 347 [NASA ADS] [CrossRef]
- Rauch, T., Suleimanov, V., & Werner, K. 2008, A&A, 490, 1127 [NASA ADS] [CrossRef] [EDP Sciences]
- Romani, R. W. 1987, ApJ, 313, 718 [NASA ADS] [CrossRef]
- Sanwal, D., Pavlov, G. G., Zavlin, V. E., et al. 2002, ApJ, 574, L61 [NASA ADS] [CrossRef]
- Schwope, A. D., Hambaryan, V., Haberl, F., et al. 2005, A&A, 441, 597 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schwope, A. D., Hambaryan, V., Haberl, F., & Motch, C. 2007, Ap&SS, 308, 619 [NASA ADS] [CrossRef]
- Shibanov, I. A., Zavlin, V. E., Pavlov, G. G., & Ventura, J. 1992, A&A, 266, 313 [NASA ADS]
- Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] (In the text)
- Suleimanov, V., & Werner, K. 2007, A&A, 466, 661 [NASA ADS] [CrossRef] [EDP Sciences]
- Swartz, D. A., Ghosh, K. K., Suleimanov, V., Tennant, A. F., & Wu, K. 2002, ApJ, 574, 382 [NASA ADS] [CrossRef]
- Tiengo, A., & Mereghetti, S. 2007, ApJ, 657, L101 [NASA ADS] [CrossRef] (In the text)
- Trümper, J. E., Burwitz, V., Haberl, F., & Zavlin, V. E. 2004, Nucl. Phys. B Proc. Suppl., 132, 560 [NASA ADS] [CrossRef]
- Turolla, R., Zane, S., & Drake, J. J. 2004, ApJ, 603, 265 [NASA ADS] [CrossRef] (In the text)
- van Adelsberg, M., & Lai, D. 2006, MNRAS, 373, 1495 [NASA ADS] [CrossRef]
- van Adelsberg, M., Lai, D., Potekhin, A. Y., & Arras, P. 2005, ApJ, 628, 902 [NASA ADS] [CrossRef] (In the text)
- van Kerkwijk, M. H., & Kaplan, D. L. 2007, Ap&SS, 308, 191 [NASA ADS] [CrossRef]
- Ventura, J. 1979, Phys. Rev. D, 19, 1684 [NASA ADS] [CrossRef]
- Werner, K., & Deetjen, J. 2000, in Pulsar Astronomy-2000 and Beyond, ed. M. Kramer, N. Wex, & R. Wielebinski, ASP Conf. Ser., 202, 623
- Zane, S., Turolla, R., Stella, L., & Treves, A. 2001, ApJ, 560, 384 [NASA ADS] [CrossRef]
- Zavlin, V. E. 2009, in Neutron Stars and Pulsars, ed. W. Becker (Berlin: Springer), ASSL, 357, 181 (In the text)
- Zavlin, V. E., Pavlov, G. G., & Shibanov, I. A. 1996, A&A, 315, 141 [NASA ADS]
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg1.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg29.png) |
Figure 1: Geometry of the radiation transfer. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg2.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg35.png) |
Figure 2:
Dependence of the free-free and electron scattering opacities in two modes on the photon energy at different angles in a fully ionized hydrogen plasma. The proton cyclotron and vacuum resonances are also shown. The plasma temperature is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg3.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg54.png) |
Figure 3: Dependence of the free-free and electron scattering opacities in two modes on the angle between the magnetic field lines and the direction of photon propagation for two photon energies: 1 keV and at the proton cyclotron energy. Plasma parameters and magnetic field strength are the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12121fg4.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg57.png) |
Figure 4:
Dependence of the true opacities in two
modes on the photon energy for fully (dashed curves) and partially ionized
(solid curves) hydrogen. The vacuum polarization effect is taken into account. The plasma temperature is 106 K, the plasma density is 1 g cm-3, the magnetic field strength is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg5.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg87.png) |
Figure 5:
Emergent spectra and temperature structures of fully ionized hydrogen model atmospheres of neutron stars with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg6.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg89.png) |
Figure 6:
Top panel: emergent spectra of the partially ionized hydrogen semi-infinite (dashed curve) and thin (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg7.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg90.png) |
Figure 7:
Emergent spectra of the thin fully ionized hydrogen atmospheres above a solid surface with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg8.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg91.png) |
Figure 8:
Emergent spectrum ( top panel) and temperature structure ( bottom panel) of the ``sandwich'' model atmosphere above a solid surface with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121fg9.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg95.png) |
Figure 9:
Emergent spectra and temperature structures of partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f10.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg96.png) |
Figure 10:
Emergent spectra and temperature structures of the partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f11.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg99.png) |
Figure 11:
Emergent spectra and temperature structures of the partially ionized
hydrogen model atmospheres with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12121f12.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa12121-09/Timg100.png) |
Figure 12:
Top panel: emergent spectrum of the partially ionized hydrogen model atmosphere of neutron stars with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



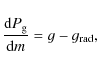
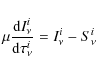
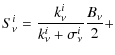
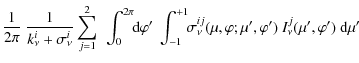
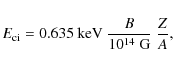
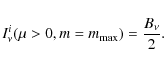
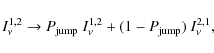
![\begin{displaymath}
P_{\rm jump} = \exp \left[-\frac{\pi}{2}(E/E_{\rm ad})^3\right].
\end{displaymath}](/articles/aa/full_html/2009/23/aa12121-09/img68.png)