| Issue |
A&A
Volume 500, Number 2, June III 2009
|
|
|---|---|---|
| Page(s) | 693 - 703 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200811469 | |
| Published online | 29 April 2009 | |
Ram pressure stripping of tilted galaxies
P. Jáchym1 - J. Köppen1,2,3,4 - J. Palous1 - F. Combes5
1 - Astronomical Institute, Academy of Sciences of the Czech Republic,
Bocní II 1401, 141 31 Prague 4, Czech Republic
2 -
Observatoire Astronomique de Strasbourg,
11 Rue de l'Université,
67000 Strasbourg, France
3 -
International Space University,
Parc d'Innovation,
1 Rue Jean-Dominique Cassini,
67400 Illkirch-Graffenstaden, France
4 -
Institut für Theoretische Physik und Astrophysik,
Universität Kiel,
24098 Kiel, Germany
5 -
Observatoire de Paris, LERMA,
61 Av. de l'Observatoire,
75014 Paris, France
Received 4 December 2008 / Accepted 30 March 2009
Abstract
Context. Ram pressure stripping of galaxies in clusters can yield gas deficient disks. Previous numerical simulations based on various approaches suggested that, except for near edge-on disk orientations, the amount of stripping depends very little on the inclination angle.
Aims. Following our previous numerical and analytical study of face-on stripping, we extend the set of parameters with the disk tilt angle and explore in detail the effects of the ram pressure on the interstellar content (ISM) of tilted galaxies that orbit in various environments of clusters, with compact or extended distributions of the intra-cluster medium (ICM). We further study how results of numerical simulations could be estimated analytically. To isolate the effect of inclination, galaxies on strictly radial orbits are considered.
Methods. A grid of numerical simulations with varying parameters is produced using the tree/SPH code GADGET with a modified method for calculating the ISM-ICM interaction. These SPH calculations extend the set of existing results obtained from different codes using various numerical techniques.
Results. The simulations confirm the general trend of less stripping at orientations close to edge-on. The dependence on the disk tilt angle is more pronounced for compact ICM distributions, however it almost vanishes for strong ram pressure pulses. Although various hydrodynamical effects are present in the ISM-ICM interaction, the main quantitative stripping results appear to be roughly consistent with a simple scenario of momentum transfer from the encountered ICM. This behavior can also be found in previous simulations. To reproduce the numerical results we propose a fitting formula depending on the disk tilt angle and on the column density of the encountered ICM. Such a dependence is superior to that on the peak ram pressure used in previous simple estimates.
Key words: galaxies: clusters: general - galaxies: intergalactic medium - galaxies: general - ISM: structure - galaxies: interactions
1 Introduction
Ram pressure of the inter-galactic medium in the dense environments of galaxy clusters and groups can significantly affect the interstellar content of galaxies. Together with tidal stripping and gas outflows due to galaxy mergers, ram pressure stripping is an efficient mechanism removing their gas component. This quenches the star formation. Local enhancement of the gas density by the ram pressure, however, can increase the star formation rate in the central disk regions and in the tail of stripped material (Kronberger et al. 2008). Current observations showing gaseous tails and extra-planar gas (e.g. Chung et al. 2007; Crowl et al. 2005), and a number of numerical simulations (e.g. Vollmer et al. 2001; Roediger & Brüggen 2007) confirm the importance of gas stripping in the evolution of galaxies. Although some gas tails could be due to tidal interactions between galaxies in the cluster (Chung et al. 2007), these are rapidly destroyed by the ram pressure (Kapferer et al. 2008). Ram pressure then creates its own long gas tails (Roediger & Brüggen 2008).
When the galaxy plunges into the intracluster medium (ICM), a complex hydrodynamical interaction of the interstellar matter (ISM) and ICM takes place. Several phases of ISM-ICM interaction were recognized by Roediger & Brüggen (2006): the initial ram pushing of the ISM out of the disk, followed by stripping of elements accelerated to the escape velocity, in a background supported by continuous stripping. A simple estimate of the stripping amount suggests that if the ram pressure of the wind exceeds the local gravitational restoring force per unit area, the gas is released from the potential of the galaxy (Gunn & Gott 1972, GG72). This approximation works well for face-on cases with constant long-lasting flows of the ICM. However, in real situations, galaxies experience a time-varying ram pressure due to their evolving orbital velocity and radially changing ICM density. An approximative criterion where the stripping is proportional to the momentum of the ICM encountered along the orbit was introduced by Jáchym et al. (2007).
A long-term ram pressure corresponding to the overall cluster ICM density profile can be accompanied by short pressure spikes from local clumps in the ICM distribution or wakes caused by previous stripping events. Tonnesen & Bryan (2008) studied the role of ICM overdensities and their infalling motions, and suggested that even small substructures in the ICM may evoke a stronger stripping than that corresponding to the given position in the cluster. In short ICM-ISM encounters, not all the ISM is accelerated to the escape speed and its re-accretion can occur. Very recently, Tonnesen & Bryan (2009) took into account the multi-phase nature of the ISM, and found different results, according to the clumpiness of the gas. Vollmer et al. (2009) argue that ram pressure is more efficient on ionized gas, and they see evidence of differential ram pressure efficiency according to the nature of the multiphase gas.
The question of how the orientation of the galaxy relative to the orbital direction influences the final stripping was touched on by many authors (Roediger & Brüggen 2006; Schulz & Struck 2001; Vollmer et al. 2001; Quilis et al. 2000; Hidaka & Sofue 2002; Marcolini et al. 2003). For tilted galaxies the effect of the hydrodynamical shielding is more pronounced in comparison to the face-on case and yields weaker stripping. Moreover, due to galactic rotation, near edge-on ram pressures evoke asymmetric shapes of the ISM disks (e.g. Roediger & Brüggen 2006). From previous simulations, only close-to edge-on orientations were identified as less efficient in the stripping than face-on cases (Roediger & Brüggen 2006; Quilis et al. 2000). The tilted stripping was found to be delayed compared to face-on (Vollmer et al. 2001), and takes a longer time (Farouki & Shapiro 1980). Other features, like tails of stripped material forming on the disk side where the gas rotates against the wind (Phookun & Mundy 1995), or annealing of inclined galaxies by a stronger loss of angular momentum (Schulz & Struck 2001), were noticed. Mimicking the hydrodynamical shielding of tilted galaxies with a simple geometrical prescription, Vollmer et al. (2001) performed a set of sticky-particle simulations with time-varying ram pressure peaks. Roediger & Brüggen (2006,2007), using hydrodynamical adaptive-mesh-refinement simulations, introduced models of galaxies experiencing a constant ICM flow in a periodic boundary box, or orbiting on realistic orbits in clusters.
What is the role of the galactic disk tilt angle in various distributions of the ICM, and could a simple dependence between the stripping amount and the tilt angle be found from simulations? To answer these questions we perform in this paper an extensive grid of Smoothed particle hydrodynamics (SPH) simulations with time-varying large or small ram pressure peaks of generally tilted ram pressure stripping events. This completes other existing simulations based on different numerical approaches (AMR, sticky-particles etc.) and follows our simulations on the face-on study made by Jáchym et al. (2007). Rather than describing in detail the process of stripping itself (that shall be studied in a forthcoming paper), we focus on the quantitative outcomes of the tilted ISM-ICM interactions. To isolate the effect of the disk inclination, we deal with galaxies on strictly radial orbits freely falling from the cluster outskirts. This condition however does not imply a strong limitation since ram pressure profiles experienced by galaxies along slightly elliptical orbits may be modeled with strictly-radial ones through an ICM distribution with a lower value of the central density and a lower concentration towards the center. With the results of the simulation grid in hand, we use a simplified test particle model to separate the various effects taking place in the ISM-ICM interactions, and to search for a simple dependence that would fit the numerical results.
Our model, initial conditions and simulation method are introduced in Sect. 2. The results of simulations are presented and analyzed in Sects. 3 and 4. Their comparison with a simple test model is discussed in Sect. 5. How can the results of the tilted stripping be estimated? This question is answered in Sect. 6, which deals with a momentum delivery criterion. In the discussion of Sect. 7, we compare our results with outcomes of previous numerical simulations.
2 Modeling
2.1 Galaxy model
Our model galaxy is a late-type massive galaxy (LM-type in
Jáchym et al. 2007): a three-component system with Plummer bulge
and dark halo, and with Toomre-Kuzmin-sech2(z/z0) disk. The
values of the model parameters are
![]()
![]() ,
,
![]() kpc, z0=0.25 kpc,
kpc, z0=0.25 kpc,
![]()
![]() ,
,
![]() kpc, and
kpc, and
![]()
![]() ,
,
![]() kpc. All three
components are represented with particles (12 000 for the stellar disk,
12 000 for the halo, and 6000 for the bulge). Their
distribution is truncated at 16 kpc (disk), 4 kpc (bulge), and 40 kpc
(halo). The corresponding rotation curve is flat with a velocity of
about 250 km s-1. The ISM in the disk follows the same density
profile as the stellar component with the same radial scale (
kpc. All three
components are represented with particles (12 000 for the stellar disk,
12 000 for the halo, and 6000 for the bulge). Their
distribution is truncated at 16 kpc (disk), 4 kpc (bulge), and 40 kpc
(halo). The corresponding rotation curve is flat with a velocity of
about 250 km s-1. The ISM in the disk follows the same density
profile as the stellar component with the same radial scale (
![]() kpc). Its mass forms 10% of the total disk mass. The ISM disk
consists of 12 000 SPH particles which provides sufficient resolution
for the large-scale effects of interest in this paper.
kpc). Its mass forms 10% of the total disk mass. The ISM disk
consists of 12 000 SPH particles which provides sufficient resolution
for the large-scale effects of interest in this paper.
2.2 Cluster model
The galaxy cluster is modeled with dark matter (DM) and ICM gas. Their
volume densities follow a ![]() -profile (Schindler et al. 1999; Cavaliere & Fusco-Femiano 1976):
-profile (Schindler et al. 1999; Cavaliere & Fusco-Femiano 1976):
![]() .
For the standard cluster model we use
.
For the standard cluster model we use
![]() ,
,
![]() cm
cm
![]() g cm-3
and
g cm-3
and
![]() kpc. The fixed DM, which provides the
gravitational potential, has
kpc. The fixed DM, which provides the
gravitational potential, has
![]()
![]() pc-3,
pc-3,
![]() kpc, and
kpc, and
![]() .
The ICM is introduced with 120 000 SPH particles distributed within
a 140 kpc truncation radius about the cluster center. Initially, the
ICM particles are assigned velocity dispersions calculated from the
hydrostatic equilibrium equation of the cluster. The system then
slightly relaxes to a stable state. Particles that reach the truncation
radius of 140 kpc are relocated to the centrally symmetric position.
See Jáchym et al. (2007) for more details.
.
The ICM is introduced with 120 000 SPH particles distributed within
a 140 kpc truncation radius about the cluster center. Initially, the
ICM particles are assigned velocity dispersions calculated from the
hydrostatic equilibrium equation of the cluster. The system then
slightly relaxes to a stable state. Particles that reach the truncation
radius of 140 kpc are relocated to the centrally symmetric position.
See Jáchym et al. (2007) for more details.
2.3 Initial conditions
The model galaxy initially starts with zero velocity from the cluster periphery (R=1 Mpc) and freely falls along a strictly radial orbit towards the cluster center. In the standard model the galaxy reaches the center at time T=1.64 Gyr with a velocity of about 1300 km s-1. The simulation is followed until T=2 Gyr when the galaxy has already left the central part of the cluster filled with ICM particles. Thus, each simulation run corresponds to one orbit of the galaxy through the cluster center.
To treat various cluster environments, we vary the values of the
![]() and
and
![]() parameters, multiplying each
standard value by factors of 8, 4, 1, and 0.25. Table 1
defines the basic set of simulation runs which are labeled with the
corresponding factors (0 stands for the factor of 0.25).
Table 1 gives for each run the combination of
parameters, multiplying each
standard value by factors of 8, 4, 1, and 0.25. Table 1
defines the basic set of simulation runs which are labeled with the
corresponding factors (0 stands for the factor of 0.25).
Table 1 gives for each run the combination of
![]() and
and
![]() parameters, the peak value of the ram
pressure along the orbit, and the column density of the ICM encountered
on the orbit. Note that narrow ICM distributions or those with low
values of density may represent ICM overdensities or debris structures
left over in the cluster from recent stripping events.
parameters, the peak value of the ram
pressure along the orbit, and the column density of the ICM encountered
on the orbit. Note that narrow ICM distributions or those with low
values of density may represent ICM overdensities or debris structures
left over in the cluster from recent stripping events.
Table 1:
Set of basic simulation runs. We refer to ![]() as to the
standard run. Values of
as to the
standard run. Values of
![]() correspond to
correspond to
![]() kpc.
kpc.
Abadi et al. (1999) warned against too massive ICM particles that can punch
holes in the gas disk and cause a large artificial drag on the ISM
particles. In our standard model (![]() )
one ICM particle has a
mass of about
)
one ICM particle has a
mass of about
![]()
![]() ,
which is almost equal to the mass of
an individual ISM particle. Concerning the ICM component setup, its
truncation radius of 140 kpc was chosen so that ram pressure in the
standard cluster exceeds at that distance the gravitational restoring
force in the disk outskirts of an approaching galaxy.
,
which is almost equal to the mass of
an individual ISM particle. Concerning the ICM component setup, its
truncation radius of 140 kpc was chosen so that ram pressure in the
standard cluster exceeds at that distance the gravitational restoring
force in the disk outskirts of an approaching galaxy.
We introduce the tilt angle of the disk with respect to the orbital
direction of the galaxy as ![]() for edge-on and
for edge-on and
![]() for
face-on orientation, throughout the paper.
for
face-on orientation, throughout the paper.
2.4 Simulation method
The simulations were carried out with the tree/SPH code GADGET (Springel et al. 2001) adapted by Jáchym et al. (2007) for calculations of ISM-ICM interactions. Smoothed particle hydrodynamics (SPH, Lucy 1977; Gingold & Monaghan 1977) in its standard formulation has significant problems with contact discontinuities where the density jump is very large. Across such contact discontinuities, fluid instabilities can be suppressed (e.g. Agertz et al. 2007), or other artifacts can occur when the sampling is poor (e.g. Okamoto et al. 2003). The problem of ICM-ISM interaction is basically a special case of this. Jáchym et al. (2007) modified GADGET to estimate smoothing lengths of either ICM or ISM particles separately from neighbors of a corresponding phase. This means that the search of the neighboring particles continues until a desired number of proper neighbors are found, while ignoring those of the second phase. It ensures that even a moderate number of ICM particles will fully cover during the interaction the ISM disk, as the ICM particles do not shrink when approaching the dense ISM in the disk. This modified code was used by Jáchym et al. (2007) for simulations of face-on ram pressure stripping events.
Although large ICM particles result in a low spatial resolution and ISM particles that lack pressure gradients from the wind, our suggestion provides a simple way to avoid the above limitation of the standard SPH method, and it may be used for the quantitative purposes of this paper. An ideal solution could involve a new self-consistent way to estimate densities that allows a better representation of contact discontinuities - e.g. based on a tessellation scheme (recently published by Springel 2009), implementation of the particle splitting mechanism (Kitsionas & Whitworth 2007) into the standard SPH, or the new SPH scheme of Kawata et al. (2009).
![\begin{figure}
\par\includegraphics[height=8.8cmcm,angle=270]{1469fig1.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg43.png) |
Figure 1: Zero-order test vs. isolated evolution: Disk radii encompassing 95%, 90%, 80%, ..., 10% of the total ISM mass ( from top down) as functions of time in the case of the galaxy evolving at rest in the center of the standard cluster ( solid curves), and in an isolated galaxy ( dashed). |
| Open with DEXTER | |
| |
Figure 2:
Pole-on views of the ISM disk crossing edge-on through
the |
| Open with DEXTER | |
2.5 Zero-order simulation run
In order to test the influence of the simulation technique used, and the effect of resolution on the results of our stripping simulations, we present a zero-order test: The galaxy is placed at rest at the center of the cluster and left to evolve surrounded by the ICM for about 300 Myr (the time comparable to the duration of the standard ISM-ICM interaction discussed later). The evolution of the galaxy's gaseous disk is displayed in Fig. 1 showing radii that encompass fixed fractions of the total ISM mass (solid curves) evolving with time. The ISM disk (or at least its outer layers) is compressed by an abrupt introduction of the static external pressure of the ICM on a time scale of about 100 Myr. After this period the outer layers start to slightly oscillate while the disk slowly continues to settle towards an equilibrium. All the ISM particles during the simulation stay bound to the galaxy. The stellar disk component is unchanged during the simulation. For comparison, the evolution of the ISM disk of an isolated galaxy, not exposed to any external pressure, is plotted in Fig. 1 with dashed curves.
The ISM component is treated isothermally in our simulations. This simple approach is used to roughly mimic an efficient radiative cooling of the ISM gas. The disk confinement in Fig. 1 may thus be understood in terms of an abrupt increase of the external pressure after the galaxy has been placed into the ICM - due to its isothermality the ISM cannot heat up (to compensate the increased external pressure) and is compressed instead. In Fig. 1, an extreme effect is shown due to a maximum pressure corresponding to the cluster center. However, in the ram pressure stripping simulations that we deal with further in this paper, the galaxy arrives at the cluster center only gradually from its outskirts. This aspect will be treated in the following section.
Concerning the influence of our numerical technique on the simulation outputs, no Rayleigh-Taylor instabilities or spurious effects due to the lack of resolution appeared in the zero-order test simulation.
3 Process of stripping
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig3.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg45.png) |
Figure 3:
Effect of the inclination: Evolution of the ISM mass bound to the
galaxy ( solid curves) or enclosed within an evaluation cylinder
around the disk plane ( dashed) in simulations with disk tilt
decreasing from face-on to edge-on ( from bottom up) of the
standard |
| Open with DEXTER | |
For non-face-on orientations of the galaxy with respect to the ICM
wind, the galactic rotation starts to play a role. Its effect is most
pronounced for near edge-on cases when it evokes an asymmetry in
the gaseous disk. This can be seen in Fig. 2 where
snapshots of the galaxy passing edge-on through the center of a wide
![]() cluster are depicted. (For illustrative purposes the
cluster are depicted. (For illustrative purposes the
![]() run is studied here rather than the standard one where
edge-on stripping is less prominent.) Due to rotation, the disk side
moving parallel to the wind (upper side in Fig. 2)
experiences ram pressure that is lower by a factor of
run is studied here rather than the standard one where
edge-on stripping is less prominent.) Due to rotation, the disk side
moving parallel to the wind (upper side in Fig. 2)
experiences ram pressure that is lower by a factor of
![]() with respect to the opposite disk side;
v is the orbital speed of the galaxy and
with respect to the opposite disk side;
v is the orbital speed of the galaxy and
![]() is the
rotational velocity of the disk. However, as e.g. the second panel of
the figure shows, the parallel-rotating side is more severely stripped
than the opposite one and it is thus not the highest ram pressure that
yields the strongest stripping. This paradox was noted by
Roediger & Brüggen (2006) as well. The explanation is in terms of time
delay: on the parallel-rotating side, the gas is accelerated towards
more rotational velocity and exits the galaxy almost at once. At the
opposite side, the gas is being braked from
is the
rotational velocity of the disk. However, as e.g. the second panel of
the figure shows, the parallel-rotating side is more severely stripped
than the opposite one and it is thus not the highest ram pressure that
yields the strongest stripping. This paradox was noted by
Roediger & Brüggen (2006) as well. The explanation is in terms of time
delay: on the parallel-rotating side, the gas is accelerated towards
more rotational velocity and exits the galaxy almost at once. At the
opposite side, the gas is being braked from
![]() towards v
and with lower or no centrifugal force it has time to fall towards the
center of galaxy. Then, it still has to rotate half a turn around the
galaxy, and it has time to be re-accreted (or at least it stays around
the galaxy for a longer time).
Snapshots in Fig. 2 further show how, due to rotation,
the tail of the stripped material winds up around the disk.
towards v
and with lower or no centrifugal force it has time to fall towards the
center of galaxy. Then, it still has to rotate half a turn around the
galaxy, and it has time to be re-accreted (or at least it stays around
the galaxy for a longer time).
Snapshots in Fig. 2 further show how, due to rotation,
the tail of the stripped material winds up around the disk.
To measure the actual level of stripping we set up a cylindrical zone
about the galactic disk plane (r=16 kpc and ![]() kpc), and
follow the enclosed ISM mass and the flow of the material through the
zone boundary. This is shown in Figs. 3 and 4 for
five simulations of the standard run with different tilt angles,
together with the ISM mass fraction bound to the galaxy (solid curves
in Fig. 3). It confirms the expected trend: with the tilt
angle growing towards face-on, more material is stripped. The maximum
departure of the curves of the bound and in-the-zone-enclosed ISM mass
in Fig. 3 indicates the amount of material that is
re-accreted after the ISM-ICM interaction. The bound mass in
Fig. 3 is given by the sum of the ISM particles for
which
kpc), and
follow the enclosed ISM mass and the flow of the material through the
zone boundary. This is shown in Figs. 3 and 4 for
five simulations of the standard run with different tilt angles,
together with the ISM mass fraction bound to the galaxy (solid curves
in Fig. 3). It confirms the expected trend: with the tilt
angle growing towards face-on, more material is stripped. The maximum
departure of the curves of the bound and in-the-zone-enclosed ISM mass
in Fig. 3 indicates the amount of material that is
re-accreted after the ISM-ICM interaction. The bound mass in
Fig. 3 is given by the sum of the ISM particles for
which
![]() .
Note that the system of the galaxy
is not closed - it experiences a changing effect of the external
potential of the cluster and an external pressure. A slight growth of
the solid curves in Fig. 3 may be found at later simulation
times.
.
Note that the system of the galaxy
is not closed - it experiences a changing effect of the external
potential of the cluster and an external pressure. A slight growth of
the solid curves in Fig. 3 may be found at later simulation
times.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig4.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg51.png) |
Figure 4: Mass flow of the ISM through the boundary of the evaluation cylinder for five simulations of Fig. 3. |
| Open with DEXTER | |
The ``stripping rate''
![]() ,
i.e. the flow of the ISM
through the boundary of the evaluation zone, exceeds almost 400
,
i.e. the flow of the ISM
through the boundary of the evaluation zone, exceeds almost 400 ![]() yr-1 for a face-on galaxy, the peak value decreases towards
the edge-on orientation to about 50
yr-1 for a face-on galaxy, the peak value decreases towards
the edge-on orientation to about 50 ![]() yr-1 (see
Fig. 4). This figure shows not only the removal rate
(
yr-1 (see
Fig. 4). This figure shows not only the removal rate
(
![]() )
but also a reversed re-accretion rate of the
shifted material (
)
but also a reversed re-accretion rate of the
shifted material (
![]() )
- in the face-on case it
reaches about 50
)
- in the face-on case it
reaches about 50 ![]() yr-1 after the passage of the galaxy
through the central cluster part. (Note that the amount of re-accretion
is dependent on the extent of the evaluation zone.)
yr-1 after the passage of the galaxy
through the central cluster part. (Note that the amount of re-accretion
is dependent on the extent of the evaluation zone.)
The re-accretion process may be better followed in Fig. 5
which traces the actual distances of the bound ISM behind the galaxy (in
the direction of the wind) for face-on and edge-on cases. In the
face-on orientation, the ISM is by an increasing ram pressure first
gradually pushed out of the disk plane, and then rapidly ``thrown'' to
large distances, shortly after the cluster center passage. This material
returns to the disk at later simulation times.
In the edge-on orientation, the disk is first compressed by the rising
ram pressure, and then some material is shifted to larger distances.
The peak in Fig. 5 is, however, much smaller than in the
face-on case.
The reason why in near edge-on orientations the pushed material stays
close to the disk is in the conservation of the angular momentum of the
ISM particles rotating in the disk. When pushed by the ram pressure,
the particles wind up around the disk. We checked this behavior in a
more efficient run ![]() where almost the same amount of ISM is
stripped as in the standard face-on run.
where almost the same amount of ISM is
stripped as in the standard face-on run.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig5.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg55.png) |
Figure 5:
ISM re-accretion: Distances behind the galaxy (in the direction of the
wind) within which a certain fraction of actually bound ISM particles
are enclosed (from 95% to 80%, curves from top down). Face-on
( black) and edge-on simulations of |
| Open with DEXTER | |
Apart from the total stripped amount, no radical differences in the duration of the stripping process of variously tilted galaxies can be seen from our simulations. Several details, like a slight time shift of the maximum of the stripping rate, or the course of re-accretion, look different in edge-on and face-on orientations, however these effects seem to be of secondary nature.
Table 2: List of performed simulations - results. From left to right: fraction of the stripped ISM mass for simulations with decreasing inclination, stripped mass fraction estimate of GG72 criterion, corresponding stripping radii and the estimate of GG72.
3.1 Static vs. dynamic ICM pressure
How does the effect of the disk radius reduction due to ram pressure compete with the disk confinement due to the static ICM pressure discussed in Sect. 2.5? In Fig. 6 the rate of the disk radius reduction caused by the ram pressure stripping in the standard face-on run is compared with the upper curve of Fig. 1. It shows that the effect of the ram pressure is more important, even though the zero-order test took place in the center of the standard cluster where the disk experienced the maximum external pressure possible. In the ram pressure simulation the in-flying galaxy enters the ICM distribution at the truncation radius where the ICM density (and its pressure) is only small, and plunges deeper towards the cluster center, which is crossed very fast. Thus the actual role of the static ICM pressure will be even less than in Fig. 6.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig6.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg68.png) |
Figure 6:
Ram pressure stripping vs. zero-order test: Actual estimate of the
stripping radius of the face-on galaxy in the standard |
| Open with DEXTER | |
Although the disk confinement due to the static ICM pressure operates against ram pressure - it does not strip the gas but makes the disk more resistant to the ram pressure - the tendency of the increasing effect of the static ICM pressure in ``larger'' clusters goes in the same direction as the effect of ram pressure stripping. Recently, Tonnesen & Bryan (2009) have taken into account the multi-phase nature of the gas disk and found that the stripping radius is considerably smaller for galaxies with radiative cooling, although the amount of stripping is similar to that in galaxies without cooling. This goes in the same direction as the above effect observed in our simulations.
We conclude that the disk confinement due to static external ICM pressure is much less important than the stripping due to ram pressure and we neglect this effect in analyzing the simulations in the following sections.
4 Results
In this section the results of the basic set of simulation runs
introduced in Table 1 are described. For each run listed
we have performed five simulations with increasing disk inclination:
![]() (edge-on), 20
(edge-on), 20![]() ,
45
,
45![]() ,
70
,
70![]() and 90
and 90![]() (face-on). The overall Table 2 provides the results:
mass fraction of the stripped material (
(face-on). The overall Table 2 provides the results:
mass fraction of the stripped material (
![]() )
at the end of
the simulation for five disk inclinations, stripped mass fraction
estimated with the GG72 formula, stripping radii
)
at the end of
the simulation for five disk inclinations, stripped mass fraction
estimated with the GG72 formula, stripping radii
![]() for five
inclinations, and the stripping radius corresponding to GG72.
for five
inclinations, and the stripping radius corresponding to GG72.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig7.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg70.png) |
Figure 7:
Stripped mass fraction as a function of disk inclination for runs from
Table 2. Each run is labeled with the peak value of
the ram pressure. The inclination is 0 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig8.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg71.png) |
Figure 8:
Stripping efficiency with respect to inclination
|
| Open with DEXTER | |
4.1 Stripped amount
The fraction of the ISM particles that is no longer bound to the galaxy at the final simulation time yields the stripped mass fractions, whose dependence on inclination is shown in Fig. 7. The general tendency of the plot is evident - with the inclination decreasing from face-on to edge-on, the amount of stripping declines. Furthermore:
- Previous simulations of Quilis et al. (2000),
Roediger & Brüggen (2006) and others have shown that there is almost no
difference between
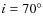 and face-on stripping (
and face-on stripping (
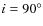 ). This is true in
Fig. 7 for all runs.
). This is true in
Fig. 7 for all runs.
- For large pressure peaks (runs
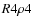 and
and 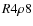 ), the
stripping amount is almost independent of the inclination (for angles
higher than about 20
), the
stripping amount is almost independent of the inclination (for angles
higher than about 20 ).
).
- The dependence of the stripping amount on inclination is more pronounced for smaller ram pressure peaks.
- Runs with the same value of
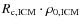 quantity show close profiles of the
quantity show close profiles of the
 curves
- e.g. (
curves
- e.g. ( and
and 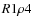 ), or (
), or (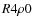 ,
,
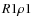 ,
and
,
and
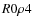 ).
).
Thus,
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig9.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg78.png) |
Figure 9: Stripped mass fraction as a function of the column density of the encountered ICM. The symbols denote the results of the SPH simulations for various inclinations. The curves correspond to the fitting curve in Eq. (2). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig10.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg79.png) |
Figure 10: Stripping efficiency with respect to inclination as a function of the column density of the encountered ICM. The curves correspond to the fitting curve in Eq. (2). |
| Open with DEXTER | |
Stripping of face-on galaxies depends on the amount of the ICM
encountered along the trajectory (Fig. 15 in Jáchym et al. 2007):
galaxies crossing clusters with such combinations of
![]() and
and
![]() parameters that
parameters that
![]() were stripped to the same level. For inclined cases this hypothesis
is tested in Figs. 9 and 10, which show
the stripped mass fraction and the stripping efficiency with respect to
inclination as a
function of the column density of the encountered ICM, respectively.
Different colors refer to simulations with different inclination
angles. The following trends are apparent
were stripped to the same level. For inclined cases this hypothesis
is tested in Figs. 9 and 10, which show
the stripped mass fraction and the stripping efficiency with respect to
inclination as a
function of the column density of the encountered ICM, respectively.
Different colors refer to simulations with different inclination
angles. The following trends are apparent
- with increasing amount of encountered ICM the stripped mass fraction and the efficiency increase;
- there is a tendency for the results from each inclination to follow a certain close relationship, despite some systematic deviations due to the different ICM density distributions;
- for high
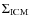 ,
these relations saturate towards
complete stripping;
,
these relations saturate towards
complete stripping;
- for lower ICM column densities, edge-on stripping is reduced with respect to face-on by a constant factor.
The numerical results in Fig. 9 can be fitted with
the following formula
The exponent 1.5 provides a rather satisfactory match to the results with intermediate inclinations, as can be seen in both Figs. 9 and 10.
In Table 2, the stripped mass fraction estimated with
the GG72 criterion is added. For the largest ram pressure peak (![]() ),
the values match well the face-on results of the SPH simulations. For
smaller peaks, however, GG72 overestimates the real stripped fraction.
Of course, no dependence on the tilt angle is included in the GG72
criterion, and its multiplication by a simple
),
the values match well the face-on results of the SPH simulations. For
smaller peaks, however, GG72 overestimates the real stripped fraction.
Of course, no dependence on the tilt angle is included in the GG72
criterion, and its multiplication by a simple ![]() term does not
resolve the problem, as it yields zero stripping in edge-on cases.
term does not
resolve the problem, as it yields zero stripping in edge-on cases.
4.2 Stripping radii
Due to an asymmetric shape of the gas disk that develops, especially after an inclined stripping event, the determination of its final radius, i.e. the stripping radius, is not trivial (see Roediger & Brüggen 2006). In close to edge-on cases, all the stripped and shifted material stays in the plane of the disk and makes the determination difficult.
In Table 2, the given values of stripping radii correspond to radii within which 90% of the bound ISM is enclosed in the final simulation time. This may slightly underestimate the radius for the face-on orientation, while overestimating it for the edge-on case. The values do not show a strong dependence for large and small peak ram pressures; however, for medium pressure the trend of increasing stripping radii towards edge-on orientations is visible.
As shown in Fig. 11, the stripping radii for all
simulations can be quite reasonably fitted with
The stripping radii estimated in the last column of Table 2 using the GG72 criterion show quite a good agreement for the largest run. However, there is a tendency to overestimate the SPH results. For smaller peaks, GG72 predicts less stripping corresponding only to the peak ram pressure.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig11.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg84.png) |
Figure 11:
Stripping radii
|
| Open with DEXTER | |
5 A simple test particle model
In order to study the influence of the parameters more efficiently, and to separate various effects - the direct kinematics on the ISM induced by the ram-pressure, and the related hydrodynamical consequences - we construct a very simplified model for the removal of gas from a galaxy. The gas disk is represented by 10 000 point masses distributed as in an exponential disk and held in the potential well composed of the bulge, stellar disk, and dark halo, with parameters identical to those used in the SPH computations. Initially, all these particles are in circular orbits about the center of the galaxy. Then, they are subjected to a Gaussian-shaped force pulse of specified tilt angle with respect to the galactic plane, duration, and maximum amplitude. The simulation starts at a time that is three times the pulse duration before the maximum. In the computation of the acceleration, the inertial mass of each particle is taken to be proportional to the gas surface density of the exponential disk, in order to account for the correct computation of the ram pressure in that part of the disk. For each particle, the equation of motion is integrated, and when the total energy becomes positive and the particle becomes unbound, it is marked and counted as having been stripped. If all particles were to experience this force pulse, the fraction of stripped particles is independent of the tilt angle, because all reach escape velocity within time-spans that depend little on their initial position in the galaxy and the force tilt angle.
![\begin{figure}
\par\includegraphics[clip=true,bb=73 72 543 745,height=8.8cm,angle=270]{1469fig12.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg85.png) |
Figure 12: The dependence of the stripped mass fraction on the column density of the swept-up ICM, for different tilt angles. The dots are results from a grid of simplified point-mass models, covering a range from 1/16 to 16 times in both duration and strength of the ram pressure force pulse, centered about the value for our standard model. The curves are the analytical fit to the SPH results. The symbols and colors are identical to those of Fig. 9. Note that the range of parameters in both axes is much wider. |
| Open with DEXTER | |
In order to simulate the thickness of the disk, we introduce a shielding or shadowing of the particles downstream of those particles facing the force. In this, we follow the modeling by sticky particles by Vollmer et al. (2001). Particles that are shielded by at least one upstream particle are assumed to experience only the galaxy's internal forces. Experiments show that with the choice of a suitable value for the shadowing radius (typically 200 pc), we are able to reproduce well the amount of stripping for the standard model of the SPH computations, as well as its dependence on the tilt angle.
As is seen in Fig. 12, the stripped mass fractions from these simplified models behave in a very similar way as the SPH results. While at high values of the ICM column density the stripping is less severe and the relation is slightly flatter, the influence on the tilt angle is nearly identical - one obtains the same amount of stripping in the edge-on configuration as in the face-on case for an ICM column density that is larger by about a factor of 6. This indicates that this modeling approach, and hence also the sticky-particle computations by Vollmer et al. (2001), appears to be quite reliable in capturing the main features of ram-pressure stripping. However, this simplified approach has notable differences to the full hydrodynamical approach, in features that we consider below.
The stripping efficiencies with respect to inclination (Fig. 13) show that the ratios of face-on and edge-on results are as large as from the SPH models, but that there are some limitations. First of all, at intermediate angles the simplified modeling gives results that are closer to the face-on case than we find in SPH. Furthermore, at high ICM column densities, one does not find such a steep increase of stripping as experienced in SPH. We searched quite extensively in parameter space, but could not find situations where the behavior matched the SPH results more closely. Evidently, this is a consequence of the limitations of the simplified treatment. We take this as an indication that this kind of diagram is sensitive to the different treatment of the (hydro-)dynamics of the problem.
![\begin{figure}
\par\includegraphics[clip=true,bb=73 72 543 745,height=8.8cm,angle=270]{1469fig13.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg86.png) |
Figure 13: Similar to Fig. 12, but for the dependence of the stripping efficiencies with respect to inclination as a function of the column density of the encountered ICM. |
| Open with DEXTER | |
The simplified modeling does allow us to separate the different physical phenomena in the ram-pressure process. In particular it helps to identify the hydrodynamical shielding by the matter lying upstream as the principal cause for the dependence of stripping on tilt angle, seen in our SPH results. The deviations seen with respect to the SPH results suggest that the details of the behavior changes with tilt angle comes from the finer details of the hydrodynamics involved in the problem.
6 Comparison with the analytical criterion
From the consideration of the momentum provided by the in-streaming ICM
to the gas in the galactic disk Jáchym et al. (2007) derived the
condition under which a volume element of disk gas (with column density
![]() for the face-on situation) would escape from a
galaxy,
for the face-on situation) would escape from a
galaxy,
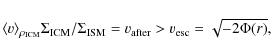 |
(4) |
i.e. if the speed
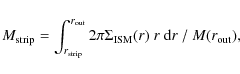 |
(5) |
where
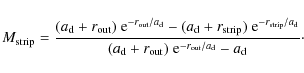 |
(6) |
On the other hand, the escape velocity as a function of galactocentric radius is the sum of the contributions from all components, i.e. bulge, disk, and dark halo. At the stripping radius the escape velocity equals the speed
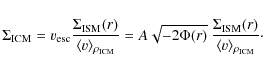 |
(7) |
Figure 14 depicts the relation between
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig14.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg97.png) |
Figure 14: The relation between stripped mass fraction and the column density of the swept-up ICM gas, computed for our standard model from our analytical criterion. The dots are results from the SPH models for the face-on configuration, compared to the predictions, adopting a value of A=0.5 ( solid curve). The open circles are results in edge-on orientation, and the dashed curves are the predictions with an adopted value A=0.12. The dotted curves come from the fitting formula Eq. (2). |
| Open with DEXTER | |
Although the SPH results from the edge-on case do exhibit a larger
scatter than the face-on data, it is quite remarkable that they can
still be matched by the analytical prediction for the face-on case, if
one simply increases the necessary ICM column density. This means that
the edge-on models can well be considered as having a lower stripping
efficiency, with a reduction factor of about 5. This factor may be
regarded as depending only on the tilt angle i, as
| (8) |
A sine-type dependence could be understandable as a geometrical projection effect, in that the edge-on galaxy presents a smaller cross section to the ICM. If it were such a pure effect of the effective cross sections, one should expect for our standard model a ratio of the areas of 4/0.25 = 16, from the disk radial scale being 4 kpc and its height being 0.25 kpc. For the moment, we prefer to take our analytical formula as a convenient expression which encapsulates essential features of the problem rather than as giving a complete description.
7 Discussion
We compare our results to the findings of previous numerical studies which treated inclined ram pressure stripping. These investigations differ in their numerical treatment of hydrodynamics, the model for the galaxy, and the way the ICM gas flows around the galaxy.
7.1 General trends
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig15.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg99.png) |
Figure 15: Stripped mass fraction as a function of the disk inclination, from Vollmer et al. (2001) - black, Roediger & Brüggen (2006) - red, Roediger & Brüggen (2007) - green, and Schulz & Struck (2001) - blue. Labels give values of the peak ram pressure, in units of cm-3 (km s-1)2. For Roediger & Brüggen (2007) the actual values of the inclination are given for the instant of pericenter passage. |
| Open with DEXTER | |
The fraction of the ISM mass that is stripped in the simulations of Vollmer et al. (2001), Roediger & Brüggen (2006), Roediger & Brüggen (2007), and Schulz & Struck (2001) is plotted in Fig. 15 as a function of inclination angle. The curves join runs with different disk inclinations, and are labeled by the maximum ram pressure. It must be stressed that for different curves not only does the maximum value of the ram pressure vary, but also its duration. These general features are apparent in Fig. 15:
- for inclinations larger than about 50
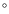 there is very
little dependence of the stripped fraction;
there is very
little dependence of the stripped fraction;
- towards the edge-on orientation, on the contrary, the amount of stripping drops strongly;
- the curves flatten for higher peak ram pressures.
For the same values of the stripped mass fraction, the simulations by Roediger & Brüggen (2006) require a substantially lower value of the peak ram pressure than our models or those by Vollmer et al. (2001), because Roediger & Brüggen (2006) consider the flow of the ICM to be constant in time, hence much longer than in the other models.
The stripping efficiency with respect to inclination (![]() )
measures
the relative stripping
potential of individual inclinations with respect to the face-on case.
It might thus serve as a good instrument for comparing results from
different numerical codes. From Fig. 16 it is obvious
that the results of different authors give very similar dependences
on the inclination angle. In spite of the basic difference in the
absolute values for the maximum ram pressure, the results of both
Roediger & Brüggen (2006) and Vollmer et al. (2001) show that higher ram
pressures result in a lower dependence of the stripping on inclination
angle, i.e. making the inclined stripping as effective as the face-on
case. Thus, the features of the inclination dependence, which our
present study shows in a systematic way, has already been seen
in earlier studies.
)
measures
the relative stripping
potential of individual inclinations with respect to the face-on case.
It might thus serve as a good instrument for comparing results from
different numerical codes. From Fig. 16 it is obvious
that the results of different authors give very similar dependences
on the inclination angle. In spite of the basic difference in the
absolute values for the maximum ram pressure, the results of both
Roediger & Brüggen (2006) and Vollmer et al. (2001) show that higher ram
pressures result in a lower dependence of the stripping on inclination
angle, i.e. making the inclined stripping as effective as the face-on
case. Thus, the features of the inclination dependence, which our
present study shows in a systematic way, has already been seen
in earlier studies.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig16.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg100.png) |
Figure 16: Stripping efficiency with respect to inclination as a function of the angle for the same results as in Fig. 15. |
| Open with DEXTER | |
7.2 Vollmer's fitting formula
Vollmer et al. (2001) derived from their simulation results a formula
which relates the fraction of the final and initial total gas mass
to the peak ram pressure and inclination angle (their Eq. (21)):
![]() ,
where
,
where
![]() is normalized by
p0=100 cm-3 (km s-1)2. Using this fitting formula we
reproduce Vollmer's Fig. 17 in Fig. 17: as a
function of angle we plot the stripping efficiency with respect to
inclination
is normalized by
p0=100 cm-3 (km s-1)2. Using this fitting formula we
reproduce Vollmer's Fig. 17 in Fig. 17: as a
function of angle we plot the stripping efficiency with respect to
inclination ![]() .
It shows that although the fitting function does
not match the simulations perfectly (and even gives for low ram
pressures negative values of
.
It shows that although the fitting function does
not match the simulations perfectly (and even gives for low ram
pressures negative values of ![]() )
the general trend corresponds well
to the numerical results, and to our findings as well: that for high
ram pressures the efficiency of stripping is high and less dependent on
the tilt angle than for low ram pressure values.
)
the general trend corresponds well
to the numerical results, and to our findings as well: that for high
ram pressures the efficiency of stripping is high and less dependent on
the tilt angle than for low ram pressure values.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig17.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg103.png) |
Figure 17:
Curves of stripping efficiency with respect to
inclination |
| Open with DEXTER | |
7.3 Dependence on ICM column density
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig18.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg104.png) |
Figure 18:
Stripping efficiency with respect to inclination |
| Open with DEXTER | |
To look for the dependence of the stripping results on
![]() in the previous simulations, we estimate these values from the
parameters of their runs. In Roediger & Brüggen (2006), a constant flow
of ICM with three values of density (0.01, 0.1, and
in the previous simulations, we estimate these values from the
parameters of their runs. In Roediger & Brüggen (2006), a constant flow
of ICM with three values of density (0.01, 0.1, and
![]() g cm-3) provokes a wind at 800 km s-1 lasting for 1 Myr. This yields values of the ICM column density of
0.4, 4, and 36
g cm-3) provokes a wind at 800 km s-1 lasting for 1 Myr. This yields values of the ICM column density of
0.4, 4, and 36 ![]() pc-2 for their weak, medium, and strong
pressure models, respectively. Vollmer et al. (2001) approximate ram
pressure profiles with Lorentz functions, whose duration is determined
by the condition that 500 Myr before the peak, a constant pressure of
50 cm-3(km s-1)2 is reached. For their four peak ram pressures of
1000, 2000, 5000, and 10 000 cm-3 (km s-1)2 we derive widths
pc-2 for their weak, medium, and strong
pressure models, respectively. Vollmer et al. (2001) approximate ram
pressure profiles with Lorentz functions, whose duration is determined
by the condition that 500 Myr before the peak, a constant pressure of
50 cm-3(km s-1)2 is reached. For their four peak ram pressures of
1000, 2000, 5000, and 10 000 cm-3 (km s-1)2 we derive widths
![]() ,
80, 50, and 35 kpc, respectively, which yield values
of
,
80, 50, and 35 kpc, respectively, which yield values
of
![]() :
4.4, 6.2, 9.4, and 13.5
:
4.4, 6.2, 9.4, and 13.5 ![]() pc-2.
pc-2.
Figure 18 compares the
![]() dependence for the results of Vollmer et al. (2001) and
Roediger & Brüggen (2006). We do not include the results of
Roediger & Brüggen (2007), as the tilt angle changes along the galaxy's
orbit. The results of both Vollmer et al. (2001) and
Roediger & Brüggen (2006) show the same trend as that revealed in our
simulations: with increasing
dependence for the results of Vollmer et al. (2001) and
Roediger & Brüggen (2006). We do not include the results of
Roediger & Brüggen (2007), as the tilt angle changes along the galaxy's
orbit. The results of both Vollmer et al. (2001) and
Roediger & Brüggen (2006) show the same trend as that revealed in our
simulations: with increasing
![]() the inclination
efficiency grows. It is worth noting that the increase is much steeper
in the case of Vollmer et al. (2001), in comparison to
Roediger & Brüggen (2006) and our own results. Since the parameters of
the model galaxies are rather similar and the stripping efficiency
the inclination
efficiency grows. It is worth noting that the increase is much steeper
in the case of Vollmer et al. (2001), in comparison to
Roediger & Brüggen (2006) and our own results. Since the parameters of
the model galaxies are rather similar and the stripping efficiency
![]() measures the relative potential of inclined stripping with
respect to the face-on case, it could well be that these differences
are due to the different ways the hydrodynamics is treated.
measures the relative potential of inclined stripping with
respect to the face-on case, it could well be that these differences
are due to the different ways the hydrodynamics is treated.
7.4 Limitations of strictly radial orbits
To separate the effects of the disk tilt angle on the stripping results we have focused in this paper on galaxies on strictly radial orbits. Then the tilt angle stays constant along the orbit. In more realistic orbits however, the disk inclination usually changes with time. Thus, almost all galaxies are likely to experience once along their orbit an efficient (close-to) face-on ram pressure phase. Its duration and strength is then determined by the parameters of the orbit. As the results of our simulations have shown, the tilt-variance might be important for situations with compact ICM distributions where the face-on stripping really is more efficient than the tilted ones. In extended clusters, however, the dependence on the disk inclination vanishes as the stripping tends to saturate.
Concerning the stripping potential of individual models, note that the strictly radial orbits used in our calculations may be considered as being equivalent to slightly elliptical ones: The ram pressure profile along a strictly radial orbit through a given ICM distribution may well be the same as the ram pressure profile along an elliptical orbit, however through a modified ICM distribution that is more centrally peaked (higher) and less extended (more compact). In other words, on an elliptical orbit the galaxy passes through the slope of the ICM density peak.
8 Conclusion
We have studied in detail the influence of disk tilt angle on the ram pressure stripping efficiency in galaxy clusters. A grid of N-body/SPH numerical simulations, varying the density of the ICM, the peak ram-pressure, its duration, and the orientation of the galaxy was performed. We summarize below the main results of the simulations:
- the stripping amount is lower for galaxies moving edge-on with respect to the ICM wind, in agreement with previous simulations;
- apart from the total stripped amount, there is no radical difference in the duration of the stripping process of variously tilted galaxies;
- due to conservation of angular momentum, ram pressure shifts the ISM in near-edge-on orientations to smaller distances behind the galaxy than in the face-on case;
- the dependence of the stripping amount on the disk tilt angle
vanishes for large clusters, where the amount of the encountered
ICM (
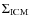 )
is large;
)
is large;
- on the other hand, for galaxies crossing small ICM overdensities or debris structures left over in the cluster from recent stripping events, the dependence on the tilt angle is more pronounced;
- we emphasize the role of the amount of the encountered ICM to the ram pressure stripping results;
- the stripping efficiency with respect to inclination
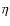 (i.e.
the ratio of the stripped mass fraction relative to the face-on case)
depends strongly on the disk tilt angle for small ram pressure peaks
but again vanishes for large values of
(i.e.
the ratio of the stripped mass fraction relative to the face-on case)
depends strongly on the disk tilt angle for small ram pressure peaks
but again vanishes for large values of
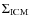 when
stripping saturates;
when
stripping saturates;
- for non-face-on orientations, the sense of rotation plays a role: contrary to expectations, it is not the side with highest ram pressure which is more stripped;
- we propose a fitting formula (Eq. (2)), which should now be tested against observations, deriving the ICM density from X-ray imaging of clusters, and the gas stripping from HI observations.
The values of a, b, and
Using simple test particle models taking schematically into account the
``shadowing'' of the gas disk by the material occurring upstream, we can
roughly obtain the main features of the stripping. The imparted momentum
![]() proves to be the
key parameter of the ICM-ISM interaction. Such particle models however
fail to reflect the true dependence of the stripping efficiency on ICM
density and inclination revealed by the full hydrodynamics.
proves to be the
key parameter of the ICM-ISM interaction. Such particle models however
fail to reflect the true dependence of the stripping efficiency on ICM
density and inclination revealed by the full hydrodynamics.
Acknowledgements
The authors gratefully acknowledge support by the Institutional Research Plan AV0Z10030501 of the Academy of Sciences of the Czech Republic, by the project 205/08/P556 of the Grant Agency of the Czech Republic, and by the Center for Theoretical Astrophysics (LC06014). We thank Volker Springel for valuable advice. The simulations have been carried outon the Ondrejov Cluster for Astrophysical Simulations (OCAS, Czech Republic) and the VIRGO computational cluster in Prague. We thank Jim Dale for English revision of the text. We would like to thank the referee for helping us to improve this paper considerably.
References
- Abadi, M. G., Moore, B., & Bower, R. G. 1999, MNRAS, 308, 947 [NASA ADS] [CrossRef] (In the text)
- Agertz, O., Moore, B., Stadel, J., et al. 2007, MNRAS, 380, 963 [NASA ADS] [CrossRef] (In the text)
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., & Vollmer, B. 2007, ApJ, 659, L115 [NASA ADS] [CrossRef]
- Crowl, H. H., Kenney, J. D. P., van Gorkom, J. H., & Vollmer, B. 2005, AJ, 130, 65 [NASA ADS] [CrossRef]
- Farouki, R., & Shapiro, S. L. 1980, ApJ, 241, 928 [NASA ADS] [CrossRef] (In the text)
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [NASA ADS]
- Gunn, J. E., & Gott, J. R. I. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] (In the text)
- Hidaka, M., & Sofue, Y. 2002, PASJ, 54, 33 [NASA ADS]
- Jáchym, P., Palous, J., Köppen, J., & Combes, F. 2007, A&A, 472, 5 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kapferer, W., Kronberger, T., Ferrari, C., Riser, T., & Schindler, S. 2008, MNRAS, 389, 1405 [NASA ADS] [CrossRef] (In the text)
- Kawata, D., Okamoto, T., Cen, R., & Gibson, B. K. 2009, ArXiv e-prints (In the text)
- Kitsionas, S., & Whitworth, A. P. 2007, MNRAS, 378, 507 [NASA ADS] [CrossRef] (In the text)
- Kronberger, T., Kapferer, W., Ferrari, C., Unterguggenberger, S., & Schindler, S. 2008, A&A, 481, 337 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef]
- Marcolini, A., Brighenti, F., & D'Ercole, A. 2003, MNRAS, 345, 1329 [NASA ADS] [CrossRef]
- Okamoto, T., Jenkins, A., Eke, V. R., Quilis, V., & Frenk, C. S. 2003, MNRAS, 345, 429 [NASA ADS] [CrossRef] (In the text)
- Phookun, B., & Mundy, L. G. 1995, ApJ, 453, 154 [NASA ADS] [CrossRef] (In the text)
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 1617 [NASA ADS] [CrossRef]
- Roediger, E., & Brüggen, M. 2006, MNRAS, 369, 567 [NASA ADS] [CrossRef] (In the text)
- Roediger, E., & Brüggen, M. 2007, MNRAS, 380, 1399 [NASA ADS] [CrossRef]
- Roediger, E., & Brüggen, M. 2008, MNRAS, 388, 465 [NASA ADS] [CrossRef] (In the text)
- Schindler, S., Binggeli, B., & Böhringer, H. 1999, A&A, 343, 420 [NASA ADS]
- Schulz, S., & Struck, C. 2001, MNRAS, 328, 185 [NASA ADS] [CrossRef]
- Springel, V. 2009, ArXiv e-prints (In the text)
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [NASA ADS] [CrossRef] (In the text)
- Tonnesen, S., & Bryan, G. L. 2008, ApJ, 684, L9 [NASA ADS] [CrossRef] (In the text)
- Tonnesen, S., & Bryan, G. L. 2009, ApJ, 694, 789 [NASA ADS] [CrossRef] (In the text)
- Vollmer, B., Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef]
- Vollmer, B., Soida, M., Chung, A., et al. 2009, A&A, 496, 669 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
All Tables
Table 1:
Set of basic simulation runs. We refer to ![]() as to the
standard run. Values of
as to the
standard run. Values of
![]() correspond to
correspond to
![]() kpc.
kpc.
Table 2: List of performed simulations - results. From left to right: fraction of the stripped ISM mass for simulations with decreasing inclination, stripped mass fraction estimate of GG72 criterion, corresponding stripping radii and the estimate of GG72.
All Figures
![\begin{figure}
\par\includegraphics[height=8.8cmcm,angle=270]{1469fig1.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg43.png) |
Figure 1: Zero-order test vs. isolated evolution: Disk radii encompassing 95%, 90%, 80%, ..., 10% of the total ISM mass ( from top down) as functions of time in the case of the galaxy evolving at rest in the center of the standard cluster ( solid curves), and in an isolated galaxy ( dashed). |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Pole-on views of the ISM disk crossing edge-on through
the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig3.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg45.png) |
Figure 3:
Effect of the inclination: Evolution of the ISM mass bound to the
galaxy ( solid curves) or enclosed within an evaluation cylinder
around the disk plane ( dashed) in simulations with disk tilt
decreasing from face-on to edge-on ( from bottom up) of the
standard |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig4.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg51.png) |
Figure 4: Mass flow of the ISM through the boundary of the evaluation cylinder for five simulations of Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig5.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg55.png) |
Figure 5:
ISM re-accretion: Distances behind the galaxy (in the direction of the
wind) within which a certain fraction of actually bound ISM particles
are enclosed (from 95% to 80%, curves from top down). Face-on
( black) and edge-on simulations of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig6.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg68.png) |
Figure 6:
Ram pressure stripping vs. zero-order test: Actual estimate of the
stripping radius of the face-on galaxy in the standard |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig7.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg70.png) |
Figure 7:
Stripped mass fraction as a function of disk inclination for runs from
Table 2. Each run is labeled with the peak value of
the ram pressure. The inclination is 0 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig8.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg71.png) |
Figure 8:
Stripping efficiency with respect to inclination
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig9.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg78.png) |
Figure 9: Stripped mass fraction as a function of the column density of the encountered ICM. The symbols denote the results of the SPH simulations for various inclinations. The curves correspond to the fitting curve in Eq. (2). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig10.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg79.png) |
Figure 10: Stripping efficiency with respect to inclination as a function of the column density of the encountered ICM. The curves correspond to the fitting curve in Eq. (2). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig11.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg84.png) |
Figure 11:
Stripping radii
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[clip=true,bb=73 72 543 745,height=8.8cm,angle=270]{1469fig12.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg85.png) |
Figure 12: The dependence of the stripped mass fraction on the column density of the swept-up ICM, for different tilt angles. The dots are results from a grid of simplified point-mass models, covering a range from 1/16 to 16 times in both duration and strength of the ram pressure force pulse, centered about the value for our standard model. The curves are the analytical fit to the SPH results. The symbols and colors are identical to those of Fig. 9. Note that the range of parameters in both axes is much wider. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[clip=true,bb=73 72 543 745,height=8.8cm,angle=270]{1469fig13.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg86.png) |
Figure 13: Similar to Fig. 12, but for the dependence of the stripping efficiencies with respect to inclination as a function of the column density of the encountered ICM. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig14.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg97.png) |
Figure 14: The relation between stripped mass fraction and the column density of the swept-up ICM gas, computed for our standard model from our analytical criterion. The dots are results from the SPH models for the face-on configuration, compared to the predictions, adopting a value of A=0.5 ( solid curve). The open circles are results in edge-on orientation, and the dashed curves are the predictions with an adopted value A=0.12. The dotted curves come from the fitting formula Eq. (2). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig15.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg99.png) |
Figure 15: Stripped mass fraction as a function of the disk inclination, from Vollmer et al. (2001) - black, Roediger & Brüggen (2006) - red, Roediger & Brüggen (2007) - green, and Schulz & Struck (2001) - blue. Labels give values of the peak ram pressure, in units of cm-3 (km s-1)2. For Roediger & Brüggen (2007) the actual values of the inclination are given for the instant of pericenter passage. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig16.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg100.png) |
Figure 16: Stripping efficiency with respect to inclination as a function of the angle for the same results as in Fig. 15. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig17.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg103.png) |
Figure 17:
Curves of stripping efficiency with respect to
inclination |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=270]{1469fig18.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11469-08/Timg104.png) |
Figure 18:
Stripping efficiency with respect to inclination |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



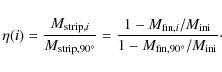
![\begin{displaymath}
\frac{M_{\rm strip}}{M_{\rm ini}} = 1 - \exp\left[-0.01~ \Sigma_{\rm
ICM} (1 + 6 \sin^{1.5} i)\right].
\end{displaymath}](/articles/aa/full_html/2009/23/aa11469-08/img81.png)