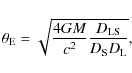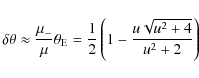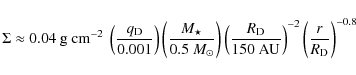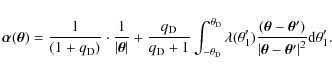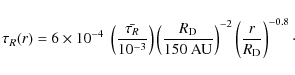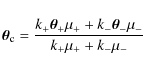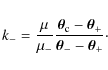EDP Sciences
Home All issues Volume 500 / No 2 (June III 2009) A&A, 500 2 (2009) 929-934 Full HTML
Free Access
Issue
A&A
Volume 500, Number 2, June III 2009
Page(s) 929 - 934
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200811458
Published online 29 April 2009

Detecting circumstellar disks around gravitational microlenses

M. Hundertmark - F. V. Hessman - S. Dreizler

Institute for Astrophysics, University of Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany

Received 2 December 2008 / Accepted 23 March 2009

Abstract
Aims. We investigate the chance of detecting proto-planetary or debris disks in stars that induce microlensing event (lenses), and consider the modification of the light curve shapes due to occultation and extinction by the disks, as well as the gravitational deflection caused by the additional mass.
Methods. The magnification of gravitational microlensing events is calculated using the ray shooting method. The occultation is taken into account by neglecting or weighting the images on the lens plane according to a transmission map of the corresponding disk for a point source point lens (PSPL) model. The estimated frequency of events is obtained by considering the possible inclinations and optical depths of the disk.
Results. We conclude that gravitational microlensing can be used, in principle, as a tool for detecting debris disks beyond 1 kpc, but estimate that each year around 1 debris disk is expected for lens stars of F, G, or K spectral type and about 10 debris disks might have shown signatures in existing datasets.

Key words: gravitational lensing - astrometry - circumstellar matter - methods: data analysis

1 Introduction

Since the discovery of the first circumstellar dust disk around Vega by the Infrared Astronomy Satellite (Aumann et al. 1984), at least 101 circumstellar disks have been resolved around pre-main and main sequence stars out to a distance of 1 kpc[*], including 17 so-called debris disks. Proto-planetary disks may be quite common during the pre-main sequence life of a star; but with a maximum life span of only 10 Myr, a galactic star formation rate of $5\ \textrm{stars}/\textrm{yr}$, an upper limit of 400 billion stars in the MilkyWay (McKee & Williams 1997; Diehl et al. 2006), the chance of a random star containing a proto-planetary disk is only about 0.01%. The debris disks that remain thereafter last much longer, perhaps as long as 10 Gyr (e.g. Greaves 2005), so should be much more common. Trilling et al. (2008) have shown that the occurrence of 70 $\mu$m excess emission in a sample of F, G, and K stars - presumedly due to dust in some form of debris disk - is $16\pm 3$%. In contrast, practically no main sequence M-stars show excess $70~\mu$m emission: Rhee et al. (2007) have found only one disk (AU Mic) from a sample of $\sim$900 M-stars.

While a common phenomenon, circumstellar disks around main sequence stars can be difficult to detect using the standard methods of coronography and the detection of excess infrared emission. A third method - detecting the disks in absorption against a background source - works very well for dense proto-planetary disks seen against an emission nebula (``proplyds''; McCaughrean & O'Dell 1996), but debris disks around main sequence stars are optically thin and unlikely to be found in front of a bright background.

Gravitational lensing could provide an additional method for detecting and characterizing circumstellar disks by creating a well-defined and bright, if temporary and geometrically complicated, background source. If the projected distance between the lens star and the background source is small enough, the source star appears to separate into two geometrically extended objects - the source of the photometric magnification in so-called microlensing, where the lensed object is not resolved. The angular scale of gravitational lensing is given by the Einstein radius

\begin{displaymath}\theta_{\rm E} = \sqrt{ \frac{4GM}{c^2} \frac{D_{\rm LS}}{D_{\rm S} D_{\rm L}} }, \end{displaymath} (1)

where $D_{\rm LS}$ denotes the lens-source distance, $D_{\rm L}$ the lens-observer distance, $D_{\rm S}$ the source-observer distance, and M is the lens mass. For a typical galactic microlensing event observed towards the galactic bulge (Paczynski 1991) with a $0.5~M_{\odot}$ lens at 6 kpc and a source at 8 kpc, one obtains an angular scale of approximately a mas(Wambsganss 2006), corresponding to a distance of $\sim$2.5 AU at the distance of the lens. Thus, the typical microlensing events studied primarily to detect low-mass exoplanets around lens stars (Beaulieu et al. 2006; Bennett et al. 2008) may also contain information about much more diffuse circumstellar matter.

 \begin{figure} \par\includegraphics[width=16cm,clip]{1458fig1.eps} \end{figure} Figure 1:

Light curve of the point source point lens model occulted by an optically thick edge-on disk is plotted along with the corresponding source and image tracks and the astrometrically detectable astrometric offset from the source. Features A and B are caused by the occultation of the less magnified image while feature C is obtained from the occultation of both images. The impact parameter is $0.4\ \theta _{\rm {E}}$, the inclination $89.8^{\circ }$ and the disk is rotated by $15^{\circ }$.
Open with DEXTER

Bozza & Mancini (2002a) and Bozza et al. (2002b) have studied the effects of microlensing by lenses consisting of gas clouds and interacting binaries, which may be used as an approximation for a face-on proto-planetary disk and Zheng & Ménard (2005) have considered the effects of disks around microlensing source stars, but to our knowledge the detectibility of circumstellar disks around lens stars has not been considered in the literature. About $70\%$ of the observed lens stars towards Baade's window are M stars and smaller, and only $\sim$25% are of spectral type F, G, or K (Dominik 2006). Given that the microlensing survey groups OGLE (Udalski et al. 1994) and MOA (Abe et al. 1997) are detecting about 1000 events per year, the fraction of events containing a debris disk should be significant: about 4.0% or currently $\sim$40/year. The chance of detecting proto-planetary disks among lens stars is correspondingly lower: 0.025% or $\sim$0.25 per year (neglecting the additional absorption likely to be found within star-forming regions). Although only 1 in 8000 lensed stars have proto-planetary disks, future surveys like the Microlensing Planet Finder (Bennett et al. 2004) or EUCLID (e.g. Beaulieu et al. 2008) have a chance of detecting a significant number of such rare events.

The effects of a circumstellar disk on microlensing light curves can be separated into two very different regimes. The disk can occult or at least extinct the light of the source star as it is bent around the lens star - a simple geometric effect given a description of the geometry and matter distribution of the disk and the geodesic paths of the photons from the source. Alternatively, the mass of the disk itself can distort the geodesic paths of the photons and hence change the apparent areas of the distorted source images and the resulting light curve independent of any occultation or extinction effects. The purely geometric disk parameters are the projected size, shape, inclination, and orientation angle $\phi $ of the major axis of the disk relative to the path of the source star and the size of the lens star's Einstein radius. The typical outer radii of proto-planetary disks are about 100-800 AU and of debris disks about 50 to 100 AU, (e.g. Greaves 2005) corresponding to 20-320  $\theta_{\rm E}$ for a typical lens. In both cases we adapt an outer radius of 150 AU as chosen by Brauer et al. (2008).

In the following we discuss the chance of detecting circumstellar disks by simulating a variety of potential light curves. We will start with optically thick disks, where the optical depth is greater than one (cf. Krivov 2005) representing the young proto-planetary disk phase and show that the corresponding magnification structure is scaled according to the ratio of the disk mass and its stellar host. This insight leads us to the most likely case of a microlens surrounded by an old debris disk modeled as optically thin and geometrically thick attenuating disks with optical depths $\tau \approx 0.01$.

2 Optically thick proto-planetary disks

Given that the major microlensing effects occur for impact parameters less than a few Einstein radii, a magnified background source will only be visible behind proto-planetary disks with high inclinations; disks with low inclinations may be too large to show any light deflection effects and will only show simpler occultations of non-magnified sources. Similarly, debris disks with high inclinations are more likely to be detected because both the projected extinction and the projected mass-density responsible for any additional lensing effect will be higher.

An optically thick disk can be modeled as an occulting disk with given inclination and orientation angles as parameters. The features of the corresponding light curves and the astrometrically observable change of the centroid (see Han & Lee 2002) of both images are illustrated in Fig. 1, neglecting the gravitational deflection due to the disk mass. The less magnified image is occulted close to the maximum of magnification. Because the disk structure is bound to the lens, it is unlikely to occult the magnified image exclusively, unless the edge-on-disk is nearly parallel to the straight line through the two images and the lens. An asymmetric total occultation of both images as in Fig. 1 indicates that an optically thick disk structure is present.

In addition to the purely photometric effect, the occultation also produces a shift in the center-of-light position of the lensed source, albeit small. The astrometric offset due to the occultation of the less magnified images, without parallax effects (see Gould 1992), can be estimated by assuming that these images are located close to the Einstein radius

\begin{displaymath}\delta \theta \approx \frac{\mu_{-}}{\mu} \theta_{\rm {E}}= \frac{1}{2} \left(1 - \frac{u \sqrt{u^2 + 4}}{u^2 + 2 }\right) \end{displaymath} (2)

where u denotes the lens-source separation in $\theta_{\rm E}$, $\mu$ the total magnification and $\mu_{\pm}$ the magnification factor of magnified and demagnified image. For a typical galactic microlensing event, the angular Einstein radius is $\approx$0.4 mas: if the source-lens separation is below 1 Einstein radius, the pre-factor in Eq. (2) takes values between 0.12 and 0.5 and the total offset is of the order of 10  $\mu\textrm{as}$ Fig. 1), which is detectable using the planned GAIA (Lindgren & Perryman 1996) or SIM (Paczynski 1998; Unwin et al. 2008) satellites. For ground-based observations Rattenbury & Mao (2006) propose using closure phase interferometry, which could provide the desired accuracy in this context.

Given the rarity of such young disks and the difficulty of seeing microlensing effects, detecting such disks photometrically and astrometrically is not impossible but unlikely.

3 Optically thin debris disks

3.1 Geometrically thin disks

Up to now, we have neglected the gravitational deflection by the mass content of the circumstellar disk, represented by the mass surface density

\begin{displaymath}\Sigma \approx 0.04~{\rm g~cm}^{-2} ~ \left(\frac{q_{\rm D}}{... ...~{\rm AU}}\right)^{-2} \left(\frac{r}{R_{\rm D}}\right)^{-0.8} \end{displaymath} (3)

(e.g. Brauer et al. 2008), where $q_{\rm D} \equiv M_{\rm D} / M_\star$ is the ratio of the disk mass to the stellar mass, and $R_{\rm D}$ is the effective outer radius.

Assuming $q_{\rm D}$ is small, the maximum change in deflection angle and magnification is for edge-on oriented disks, whose effective linear mass distribution can be calculated by integrating the surface density. The deflection angle of the combined point source point lens (PSPL) and edge-on disk model has no rotational symmetry, so we have to consider the vectorial deflection angle $\vec{\alpha}$. An analytical expression can be derived if one integrates the normalized line density in the lens plane $\lambda(\theta_{1})$ along the disk radius $\theta_{\rm D}$, expressed in units of the Einstein radius (cf. Schneider et al. 1992):

\begin{displaymath}\vec{\alpha}(\vec{\theta}) = \frac{1}{\left(1+q_{\rm D}\right... ...vec{\theta}-\vec{\theta}'\right\vert^2} \textrm{d}\theta_{1}'. \end{displaymath} (4)

The normalized line density for a mass distribution parallel to $\theta_1$ is given by

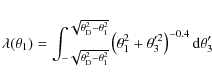\begin{displaymath}\lambda(\theta_{1}) = \int_{-\sqrt{\theta_{\rm D}^2-\theta_{1... ...left(\theta_1^2+\theta_{3}'^2\right)^{-0.4} \rm {d}\theta_{3}' \end{displaymath} (5)

where $\theta_{1,2}$ define the lens plane and the integral over $\theta_3$projects the surface density distribution onto the line. The resulting expression contains the hypergeometric function 2F1(Abramowitz & Stegun 1972):
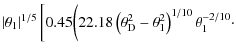                           $\displaystyle \lambda(\theta_{1})$ = $\displaystyle \left\vert\theta_1\right\vert^{1/5} \bigg[ 0.45 \bigg(22.18 \left(\theta_{\rm D}^2-\theta_1^2\right)^{1/10} \theta_1^{-2/10} \cdot$  
    $\displaystyle _2F_1 \left(-\frac{1}{10};\frac{4}{10};\frac{9}{10};\frac{\theta_1^2}{\theta_{\rm D}^2-\theta_1^2}\right)-18.94 \bigg) \bigg],$ (6)

which can be efficiently evaluated when separated far enough from the singularities at $\pm \theta_{\rm D}$. When a third-order polynomial fit is used outside a 40  $\theta_{\rm E}$ radius, as shown in Fig. 2, the total deflection angle (Eq. (4)) can be numerically integrated.

 \begin{figure} \par\includegraphics[width=8cm,clip]{1458fig2.eps} \end{figure} Figure 2:

The normalized line density of an edge-on oriented disk with a surface density $\Sigma \propto \left(\frac{r}{1 \rm{AU}}\right)^{-0.8}$, and a disk with $r_{\rm{in}}=0.03~\rm{AU}$ and $\theta_{\rm D}=60~\theta_{\rm{E}}$.
Open with DEXTER

Even though the lens equation with the additional term for the deflection angle cannot be solved analytically, the disk can be embedded in a ray shooting framework (Kayser et al. 1986, Wambsganss 1997, 1999). For $q_{\rm D} \sim0.2$, the calculated magnification offset within 1  $\theta_{\rm E}$ from the disk is $\sim$1; hence potentially observable. Close to the linear mass distribution representing the disk, one sees an additional rectangular magnification caused by the attraction of rays (Fig. 3). For small source-lens separations u (here $u<0.05~\theta_{\rm E}$), the singular peak splits in two in the central region. For $q_{\rm D} \sim0.20$, the affected region of the extended box is 0.02  $\theta_{\rm E}$ and the central distortion has a relative deviation greater than 1% for 0.2  $\theta_{\rm E}$, where the Einstein radius is calculated for the total mass of the system.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1458fig3.eps} \end{figure} Figure 3:

Top: magnification map for a linear mass distribution created by ray shooting (Eq. (4)) for the combination of a point lens and a disk mass of 20% of the stellar host along with contour lines of magnifications at $\mu =2.5,\ 3.7,\ 4.8,\ \textrm {and}\ 6$. Profiles extracted from the magnification map located in the source plane correspond to light curves. Middle: change relative to a point source point lens (PSPL) model. Bottom: vertical cuts corresponding to deviations in the light curves for two perpendicular trajectories of the lens and source for $0, 0.5.~\theta_{\rm{E}}$.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=17cm,clip]{1458fig4.eps} \end{figure} Figure 4:

Contour lines of maximal relative deviation from PSPL and a grid of attenuated light curves with $u_0=0.1~\theta_{\rm{E}}$ are plotted for a surface density $\Sigma \propto r^{-0.8}$, different outer disk radii $r_{\rm D} = 50,\ 100,\ 150$ AU, an inner disk radius of 10 AU, and a constant mean optical depth of $\bar{\tau} =5 \times 10^{-4}$.
Open with DEXTER

According to Eq. (4), the width of the distortion is proportional to $\lambda(\theta_{1})$ and thus to the mass ratio $q_{\rm D}$ for $q_{\rm D} \ll 1$. The rectangular distortion is redistributed in case of an inclined disk due to the conservation of rays: for $i=89^{\circ}$ the conserved integral of the rectangular distortion reduces the peak deviation to 2% and a face-on rotational symmetric disk has no effect at all. If the disk has no central gap, a deviation containing a split singularity is observable as long as the finite size of the source star does not smooth it out. Considering a bright giant source star with 10 $R_{\odot}$ and thus $0.014~\theta_{\rm E}$ at 8 kpc, this limit is reached at a mass ratio of 0.014 and, in the case of inclined disks, even earlier.

Calculating the extinction in a geometrically and optically thin debris disk requires an estimation of the vertical optical depth $\tau_\lambda (r) = \kappa_\lambda \Sigma(r)$. The mean R-band optical depth of AU Mic is in the range 10-3 to 10-4 (Kalas 2004). Using Eq. (3) and an area-weighting of $\tau$, one obtains an estimate of the extinction coefficient (assumed to be constant)

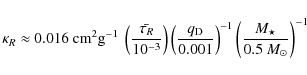\begin{displaymath}\kappa_R \approx 0.016~{\rm cm}^2 {\rm g}^{-1} ~ \left(\frac{... ...01}\right)^{-1} \left(\frac{M_\star}{0.5~M_\odot}\right)^{-1} \end{displaymath} (7)

and a final R-band optical depth distribution

\begin{displaymath}\tau_{R}(r) = 6\times10^{-4} ~ \left(\frac{\bar{\tau_R}}{10^{... ... AU}}\right)^{-2} \left(\frac{r}{R_{\rm D}}\right)^{-0.8}\cdot \end{displaymath} (8)

For a typical inner disk radius of 0.03 AU, $\tau_R$ is smaller than unity even in the disk center. A thin disk with such low optical depths produces relative deviations of the light curve on the order of 0.1%. Current ground-based microlensing observations require an order of magnitude higher deviation and so could detect an average optical depth > $5 \times 10^{-3}$; according to Augereau & Beust (2006). This would be the maximal optical depth in the visible for the AU Mic debris disk, transversed in the vertical direction, but for an edge-on orientation, optical depths of $4 \times 10^{-2}$ could be reached. Consequently, edge-on configurations are much more likely to be detected from microlensing, too.

 \begin{figure} \par\includegraphics[width=15cm,clip]{1458fig5.eps} \end{figure} Figure 5:

Differential light curves of a geometrically thick disk with a central hole are shown for different inclinations i and orientations $\phi $ of the source track. The disk has an inner radius of 10 AU and an outer radius of 50 AU, $\Sigma \propto r^{-0.8}$; $H=2.5~\rm{AU}$, and the average optical depth $\tau \approx 5\times 10^{-4}$
Open with DEXTER

3.2 Geometrically thick disks

The attenuating effect of a circumstellar disk depends especially on the path length of the light ray through the disk and thus on its shape. For an edge-on configuration and a 0.5 $M_{\odot}$ star of 0.6 $R_{\odot}$, the deflection causes a vertical shift of 10-3 AU at 150 AU in the vertical direction and can be neglected. In the following, a geometrically thick disk with a Gaussian vertical dust distribution and a scale height $H(r)=0.47\left(\frac{r}{50~{\rm AU}}\right)+0.34~{\rm AU}$ is used (for AU Mic cf. Metchev et al. 2005; Krist et al. 2005). The density $\rho$ of the disk is given by

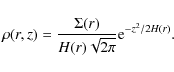\begin{displaymath}\rho(r,z)= \frac{\Sigma(r)}{H(r) \sqrt{2\pi}} {\rm e}^{-z^2/2H(r)}. \end{displaymath} (9)

The normalization constant is determined by integrating $\rho$ parallel to the disk normal

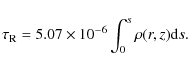\begin{displaymath}\tau_{\rm {R}}=5.07\times 10^{-6} \int_{0}^{s} \rho(r,z) \textrm{d} s. \end{displaymath} (10)

In PSPL models the light path is usually parameterized using two straight lines according to the thin lens approximation. To first order, the true light path is a hyperbola: according to Gönner (1996, p. 206), the maximal deviation of the distance of closest approach R from the hyperbola is

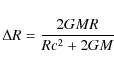\begin{displaymath}\Delta R = \frac{2 G M R}{R c^2 + 2 G M} \end{displaymath} (11)

where M is the mass of the deflecting star. The maximal deviation from the thin lens approximation for grazing incidence is $10^{-5}~{\rm AU}$ at $0.6~R_{\odot}$ and a deflector mass of $0.5~M_{\odot}$.

The sensitivity of different models for $\tau \sim 5 \times 10^{-4}$ is shown in Fig. 4. The source track for each pair of $(i,\phi)$ was limited to a range from -1 to 1 $\theta_{\rm E}$ and the impact parameter $u_0=0.1~\theta_{\rm{E}}$ has been kept fixed. It does not change the maximal variation of the transmissivity, only the maximal distance from the center. While the two-dimensional model (projected surface density) with $\Sigma \propto r^{-0.8}$ shows a maximal deviation below 1%, the more realistic three-dimensional model with $\Sigma \propto r^{-0.8}$ shows an increased deviation at high inclinations, because the transversed matter is taken into account. The smaller the outer radius of the disk, the poorer the detectability. From the calculated sensitivity pattern the fraction of the parameter space exceeding 1%, i.e. 10 mmag, can be calculated: 17% for $r_{\rm D} = 50$ AU, 34% for $r_{\rm D}=100$ AU, and 50% for $r_{\rm D} =150$ AU. These results are valid for a system without any inner clearing, but Wyatt et al. (2007) have concluded from observations that $2\pm2\%$ show hot dust close to the star. Assuming an inner radius of 10 AU changes the detectability to 10% for $r_{\rm D} = 50$ AU , to 18% for $r_{\rm D}=100$ AU, and to 23% for $r_{\rm D} =150$ AU. Changing the scale height redistributes the sensitivity to smaller inclinations.

In Fig. 5, five different sensitivity configurations are calculated for $r_{\rm D} = 50$ AU and an inner gap with 10 AU radius. Simulations for 100 AU and 150 AU show similar results: all of them show a systematic decrease in the residuals close to the maximal magnification, especially at high inclination. The source and image tracks plotted over the map of transmissivity explain this behavior for a surface density modeled as an inverse power law. The image with positive parity reaches its maximal separation from the lens when the source-lens distance is minimal, therefore the optical depth $\propto \Sigma$ is also minimal. This indicates one possibility of detecting circumstellar disks - fitting a PSPL model and analyzing the structure of the residuals within a few Einstein radii. The simulated light curves show deviations between 0.1% and 1% (i.e. 1 and 10 mmag without blending flux), a signal that is detectable by a dedicated space mission like the Microlensing Planet Finder or EUCLID.

4 Relative extinction curves

It is possible to tell a priori whether a certain microlens is surrounded by attenuating matter if a wavelength-dependent extinction signal can be seen. When fitting a PSPL model, the residuals can be used to show where relative attenuation in the lens plane occurs between images taken at different wavelengths. A combination of photometric and astrometric follow-up could then infer the extinction structure of the central zone by measuring the extinction coefficient for each image: the centroid of the lensed source star will move slightly to the less dimmed image. The centroid $\vec{\theta}_{\rm c}$ with extinction is located at

\begin{displaymath}\vec{\theta}_{\rm c}=\frac{k_{+} \vec{\theta}_{+} \mu_{+} + k_{-} \vec{\theta}_{-} \mu_{-} }{k_{+} \mu_{+} + k_{-} \mu_{-}} \end{displaymath} (12)

where $k_{\pm}$ denote the measured transmission coefficients, $\mu_{\pm}$ the unextincted magnifications, $\vec{\theta{\pm}}$ the image positions and $\vec{\theta}_{\rm c}$ the trajectories on the sky. The total magnification is described as

\begin{displaymath}\mu = k_{+} \mu_{+}+k_{-}\mu_{-}. \end{displaymath} (13)

One of the transmission coefficients can be calculated from Eqs. (12) and (13):

\begin{displaymath}k_{-}= \frac{\mu}{\mu_{-}} \frac{\vec{\theta}_{\rm c} -\vec{\theta}_{+}}{\vec{\theta}_{-}-\vec{\theta}_{+}}\cdot \end{displaymath} (14)

Ideally, brightness and position are measured simultaneously and thus the measured magnification $\mu$ and position $\vec{\theta}_{\rm c}$ can be jointly used in Eq. (14), after correcting for blended flux and baseline. Finally k+ is calculated from Eq. (13) by using the image positions $\vec{\theta}_{\pm}$ from the fitted PSPL model.

5 Conclusions

We have shown that gravitational microlensing can - in principle - be used as a tool for detecting circumstellar disks beyond 1 kpc when the photometric residuals relative to a PSPL model are searched for deviations between -3 and 3  $\theta_{\rm E}$ around the maximal magnification. We estimate that 4% of all F, G, & K-microlenses contain debris disks. However, if the optical depth $\tau \geq 5\times 10^{-4}$ (age $\sim$1 Gyr), a tenth of these objects should have detectable disks. Assuming a power-law model for the surface density $\Sigma \propto r^{-0.8}$ and depending on the inner and outer radii distribution of debris disks, between 10 and 50% of all remaining light curves could show deviations greater than 1%. For $\sim$4000 existing light curves from the OGLE collaboration, we expect that around 10 of the F, G & K-lenses show a detectable signature induced by a debris disk. If we consider that anomalous microlensing events, i.e. events that are not well-described by a PSPL model, can also display systematic variations and blending occurs, it is unlikely that debris disks can be discovered from the existing datasets. Nevertheless, future space missions will almost certainly provide the required accuracy for detecting debris disks and probing the attenuating matter.

Acknowledgements

This work was inspired by the Wilhelm und Else Heraeus Physics School ``The Early Phase of Planet Formation''. M.H. would like to acknowledge the support by the German-Israeli Foundation and from the Graduiertenkolleg 1351.

References

Footnotes

... 1 kpc[*]
http://www.circumstellardisks.org/

All Figures

  \begin{figure} \par\includegraphics[width=16cm,clip]{1458fig1.eps} \end{figure} Figure 1:

Light curve of the point source point lens model occulted by an optically thick edge-on disk is plotted along with the corresponding source and image tracks and the astrometrically detectable astrometric offset from the source. Features A and B are caused by the occultation of the less magnified image while feature C is obtained from the occultation of both images. The impact parameter is $0.4\ \theta _{\rm {E}}$, the inclination $89.8^{\circ }$ and the disk is rotated by $15^{\circ }$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{1458fig2.eps} \end{figure} Figure 2:

The normalized line density of an edge-on oriented disk with a surface density $\Sigma \propto \left(\frac{r}{1 \rm{AU}}\right)^{-0.8}$, and a disk with $r_{\rm{in}}=0.03~\rm{AU}$ and $\theta_{\rm D}=60~\theta_{\rm{E}}$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1458fig3.eps} \end{figure} Figure 3:

Top: magnification map for a linear mass distribution created by ray shooting (Eq. (4)) for the combination of a point lens and a disk mass of 20% of the stellar host along with contour lines of magnifications at $\mu =2.5,\ 3.7,\ 4.8,\ \textrm {and}\ 6$. Profiles extracted from the magnification map located in the source plane correspond to light curves. Middle: change relative to a point source point lens (PSPL) model. Bottom: vertical cuts corresponding to deviations in the light curves for two perpendicular trajectories of the lens and source for $0, 0.5.~\theta_{\rm{E}}$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{1458fig4.eps} \end{figure} Figure 4:

Contour lines of maximal relative deviation from PSPL and a grid of attenuated light curves with $u_0=0.1~\theta_{\rm{E}}$ are plotted for a surface density $\Sigma \propto r^{-0.8}$, different outer disk radii $r_{\rm D} = 50,\ 100,\ 150$ AU, an inner disk radius of 10 AU, and a constant mean optical depth of $\bar{\tau} =5 \times 10^{-4}$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{1458fig5.eps} \end{figure} Figure 5:

Differential light curves of a geometrically thick disk with a central hole are shown for different inclinations i and orientations $\phi $ of the source track. The disk has an inner radius of 10 AU and an outer radius of 50 AU, $\Sigma \propto r^{-0.8}$; $H=2.5~\rm{AU}$, and the average optical depth $\tau \approx 5\times 10^{-4}$
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.