| Issue |
A&A
Volume 500, Number 2, June III 2009
|
|
|---|---|---|
| Page(s) | 785 - 799 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200811453 | |
| Published online | 16 April 2009 | |
Dissolution is the solution: on the reduced mass-to-light ratios of Galactic globular clusters
J. M. D. Kruijssen1,2 - S. Mieske3
1 - Astronomical Institute, Utrecht University, PO Box 80000, 3508TA Utrecht, The Netherlands
2 - Sterrewacht Leiden, Leiden University, PO Box 9513, 2300RA Leiden, The Netherlands
3 - European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
Received 1 December 2008 / Accepted 27 March 2009
Abstract
Context. The observed dynamical mass-to-light (M/L) ratios of globular clusters (GCs) are systematically lower than the value expected from ``canonical'' simple stellar population models, which do not account for dynamical effects such as the preferential loss of low-mass stars due to energy equipartition. It has recently been shown that low-mass star depletion can qualitatively explain this discrepancy for globular clusters in several galaxies.
Aims. To verify whether low-mass star depletion is indeed the driving mechanism behind the M/L decrease, we aim to predict the M/LV ratios of individual GCs for which orbital parameters and dynamical V-band mass-to-light ratios M/LV are known. There is a sample of 24 Galactic GCs for which this is possible.
Methods. We used the SPACE cluster models, which include dynamical dissolution, low-mass star depletion, stellar evolution, stellar remnants, and various metallicities. We derived the dissolution timescales due to two-body relaxation and disc shocking from the orbital parameters of our GC sample and used these to predict the M/LV ratios of the individual GCs. To verify our findings, we also predicted the slopes of their low-mass stellar mass functions.
Results. The computed dissolution timescales agree well with earlier empirical studies. The predicted M/LV are in ![]() agreement with the observations for 12 out of 24 GCs. The discrepancy for the other GCs probably arises because our predictions give global M/L ratios, while the observations represent extrapolated central values that are different from global ones in the case of mass segregation and a long dissolution timescale. The GCs in our sample that likely have dissimilar global and central M/L ratios can be excluded by imposing limits on the dissolution timescale and King parameter. For the remaining GCs, the observed and predicted average M/LV are 78
+9-11% and 78
agreement with the observations for 12 out of 24 GCs. The discrepancy for the other GCs probably arises because our predictions give global M/L ratios, while the observations represent extrapolated central values that are different from global ones in the case of mass segregation and a long dissolution timescale. The GCs in our sample that likely have dissimilar global and central M/L ratios can be excluded by imposing limits on the dissolution timescale and King parameter. For the remaining GCs, the observed and predicted average M/LV are 78
+9-11% and 78 ![]() 2% of the canonically expected values, while the values are 74
+6-7% and 85
2% of the canonically expected values, while the values are 74
+6-7% and 85 ![]() 1% for the entire sample. The predicted correlation between the slope of the low-mass stellar mass function and M/LV drop is found to be qualitatively consistent with observed mass function slopes.
1% for the entire sample. The predicted correlation between the slope of the low-mass stellar mass function and M/LV drop is found to be qualitatively consistent with observed mass function slopes.
Conclusions. The dissolution timescales of Galactic GCs are such that the ![]() % gap between canonically expected and observed M/LV ratios is bridged by accounting for the preferential loss of low-mass stars, also when considering individual clusters. It is concluded that the variation in M/L ratio due to dissolution and low-mass star depletion is a plausible explanation for the discrepancy between the observed and canonically expected M/L ratios of GCs.
% gap between canonically expected and observed M/LV ratios is bridged by accounting for the preferential loss of low-mass stars, also when considering individual clusters. It is concluded that the variation in M/L ratio due to dissolution and low-mass star depletion is a plausible explanation for the discrepancy between the observed and canonically expected M/L ratios of GCs.
Key words: Galaxy: globular clusters: general - Galaxy: stellar content - galaxies: star clusters
1 Introduction
The topic of dynamical mass-to-light (M/L) ratios of old compact stellar systems has attracted increasing attention during recent years (Mieske et al. 2008; Evstigneeva et al. 2007; Forbes et al. 2008; Hilker et al. 2007; Hasegan et al. 2005; Rejkuba et al. 2007; Baumgardt & Mieske 2008; Kruijssen 2008; Dabringhausen et al. 2008; McLaughlin & van der Marel 2005; Chilingarian et al. 2008). The outcome of these studies can be summarised as follows.
- For the mass regime of ultra-compact dwarf galaxies (UCDs,
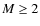
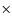
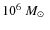 ), dynamical M/L ratios tend to be some 50% above predictions from stellar population models (Mieske et al. 2008; Forbes et al. 2008; Dabringhausen et al. 2008).
), dynamical M/L ratios tend to be some 50% above predictions from stellar population models (Mieske et al. 2008; Forbes et al. 2008; Dabringhausen et al. 2008).
- For the mass regime of globular clusters (GCs,
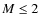
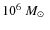 ), dynamical M/L ratios tend to be some 25% below predictions from simple stellar population (SSP) models that assume a canonical IMF (Kruijssen 2008; Mieske et al. 2008; Kruijssen & Lamers 2008; Rejkuba et al. 2007).
), dynamical M/L ratios tend to be some 25% below predictions from simple stellar population (SSP) models that assume a canonical IMF (Kruijssen 2008; Mieske et al. 2008; Kruijssen & Lamers 2008; Rejkuba et al. 2007).
- As a consequence, the dynamical M/L ratios of UCDs are on average about twice as high as those of GCs, at comparable metallicities.
As noted already in Kruijssen & Lamers (2008, hereafter KL08), the next step is to apply these analytical cluster models including preferential loss of low-mass stars to individual clusters. This would then account for variations in metallicity and dissolution timescale. Such a study will naturally be restricted to GCs with measured M/L ratios for which realistic estimates of their individual dissolution timescale are available from information on their actual orbit within the Milky Way potential. With the database of individual dissolution time scales at hand, the loss of low-mass stars can be quantified according to the prescriptions of Kruijssen (2008) and KL08, leading to predictions for the drop of M/L for individual GCs. Those predictions are to be contrasted with the actual observed M/L ratios of these GCs. This will allow us to quantitatively test the hypothesis that the loss of low-mass stars is responsible for the too low M/L ratios of GCs, and hence also partially for the discrepancy of M/L between GCs and UCDs.
Previous studies assessing the preferential loss of low-mass stars in Galactic GCs focus both on observations (e.g., De Marchi et al. 2007) and theory (e.g., Baumgardt et al. 2008). In De Marchi et al. (2007), the slopes of the stellar mass functions in GCs are measured for stars between 0.3 and 0.8
![]() ,
thereby directly reflecting possible low-mass star depletion. The study by Baumgardt et al. (2008) predicts the same slopes using N-body models and different degrees of mass segregation, assuming dissolution by two-body relaxation. The aforementioned papers both do not consider the M/L ratios of the GCs in question.
,
thereby directly reflecting possible low-mass star depletion. The study by Baumgardt et al. (2008) predicts the same slopes using N-body models and different degrees of mass segregation, assuming dissolution by two-body relaxation. The aforementioned papers both do not consider the M/L ratios of the GCs in question.
Table 1:
Observed properties for the cluster sample, together with their ![]() standard errors.
standard errors.
Table 2:
Orbital parameters for the cluster sample, together with their ![]() standard errors.
standard errors.
In this study, the reference sample for dynamical M/L ratios of Galactic GCs is that of McLaughlin & van der Marel (2005), obtained by the fitting of single-mass King profiles. It contains data for 38 GCs. Only a subsample can be used for our analysis, namely those clusters for which accurate proper motions and radial velocities are measured and can be translated to orbital parameters. Next to the destruction rates due to two-body relaxation, also the influence of disc shocking on the cluster dissolution needs to be taken into account. Both have to be derived from the orbital parameters. Several studies in which orbital information is derived and used to compute destruction rates are available in the literature (Allen et al. 2008,2006; Dinescu et al. 1999; Gnedin & Ostriker 1997), all with certain benefits and trade-offs. Specifically, Gnedin & Ostriker (1997) assign statistically sampled orbits conforming to the bulk motion of the GC system in an axisymmetric potential to derive destruction rates of 119 globular clusters. Dinescu et al. (1999) use proper motions and radial velocities to compute the orbits and destruction rates of 38 clusters in two axisymmetric potentials (Johnston et al. 1995; Paczynski 1990). Allen et al. (2008,2006) follow the same procedure, but consider both axisymmetric and barred potentials (Pichardo et al. 2004; Allen & Santillan 1991, respectively) for 54 globular clusters. They do not find a significant deviation between the results for both potentials. However, they do note that their calculated destruction rates are multiple orders of magnitude lower than others in literature and recommend combining their orbital information with the more rigorous Fokker-Planck approach used by Gnedin & Ostriker (1997) to derive the destruction rates.
We choose to adopt the orbital data and destruction rate due to disc shocking from Dinescu et al. (1999). Our study cannot be based on statistically assigned orbits but requires the actual orbits of individual clusters, thus excluding the estimated orbits from Gnedin & Ostriker (1997). In addition, the Dinescu et al. (1999) destruction rates seem to be in better agreement with the observations than those from Allen et al. (2008,2006).
In Table 1 the observed properties are listed of the 24 Galactic globular clusters for which the V-band mass-to-light ratios (M/LV) and orbital parameters are available, i.e., the sample that is covered both by Dinescu et al. (1999) and McLaughlin & van der Marel (2005). The masses and observed M/LV ratios represent dynamical values. For all clusters, the standard error in [Fe/H] is assumed to be 0.15 when computing the error propagation (see Sect. 3), which represents a conservative accuracy estimate (see, e.g., Carretta & Gratton 1997). These errors determine the uncertainty on
![]() in the last column, since the canonical M/L ratio only depends on metallicity. The galactocentric radii used to compute the orbits in Dinescu et al. (1999) are from Zinn, private communication. In extreme cases this may cause a small disagreement between the galactocentric radius quoted here and the apogalactic distance predicted by Dinescu et al. (1999, see Table 2).
in the last column, since the canonical M/L ratio only depends on metallicity. The galactocentric radii used to compute the orbits in Dinescu et al. (1999) are from Zinn, private communication. In extreme cases this may cause a small disagreement between the galactocentric radius quoted here and the apogalactic distance predicted by Dinescu et al. (1999, see Table 2).
A first inspection of the observed M/LV ratios in Table 1 can be made by comparing them to the (``canonical'') M/LV ratios from SSP models, which only depend on metallicity due to the invariance of the shape of the stellar mass function in these models. In Fig. 1 (left), the observed M/LV ratios of our sample are plotted versus the canonically expected values that were computed by interpolating SSP models. These were emulated with the models from KL08 neglecting the preferential loss of low-mass stars. The discrepancy between observed and expected M/LV ratio is evident, as the canonical M/LV are constrained to a much narrower and generally higher range than the observed ones. The number histogram of the two M/LV (Fig. 1, right) further substantiates this dissimilarity. The observed M/LV ratios are on average 74 +6-7% of the canonically expected values.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f1a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f1b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg172.png) |
Figure 1:
Left: observed mass-to-light ratio
|
| Open with DEXTER | |
With the present paper we aim to quantify the contribution of dynamical effects such as the preferential loss of low-mass stars and the selective loss of stellar remnants (see KL08) to the discrepancy between the observed and canonically expected M/L ratios. In Sect. 2, we summarise the cluster models from KL08 and highlight the aspects that are particularly relevant to this study. The dissolution timescales for the cluster sample are computed in Sect. 3, whereas the predicted mass and M/LV evolution are considered and compared to the observations in Sect. 4. We predict slopes of the low-mass stellar mass function and discuss observational tests to verify the preferential loss hypothesis for appropriate clusters in Sect. 5. In the final Sect. 6, we discuss the results and present our conclusions.
2 Cluster evolution models and M/L
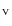 evolution
evolution
In order to study the evolution of clusters on specific orbits, we use analytical cluster models (SPACE, see KL08) that incorporate the effects of stellar evolution, stellar remnant production, cluster dissolution and energy equipartition. They are summarised here and are treated in more detail in KL08. In the second part of this section, the dependence of mass-to-light ratio evolution on initial mass, metallicity and dissolution timescale is assessed (for a more detailed description, see Kruijssen 2008).
2.1 Summary of the models
In the SPACE cluster models, clusters gradually lose mass due to stellar evolution and dissolution. The total cluster mass evolution is determined by
where the first term denotes mass loss due to stellar evolution and the second represents mass loss by dissolution. Additionally, the formation of stellar remnants and the mass-dependent loss of stars by dissolution are taken into account, thus providing a description of the changing mass function and cluster mass in remnants.
Stellar evolution is included by using the Padova 1999 isochrones![]() . These are available for metallicities Z =
. These are available for metallicities Z = ![]() 0.0004, 0.004, 0.008, 0.02, 0.05
0.0004, 0.004, 0.008, 0.02, 0.05![]() (or [Fe/H] =
(or [Fe/H] = ![]() -1.7, -0.7, -0.4, 0.0, 0.4
-1.7, -0.7, -0.4, 0.0, 0.4![]() ), which thus restricts our model computations to these values. Stellar evolution removes the most massive stars from the cluster and increases the non-luminous cluster mass by turning stars into remnants, which is included by adopting an initial-remnant mass relation
), which thus restricts our model computations to these values. Stellar evolution removes the most massive stars from the cluster and increases the non-luminous cluster mass by turning stars into remnants, which is included by adopting an initial-remnant mass relation![]() . A Kroupa (2001) IMF is assumed.
. A Kroupa (2001) IMF is assumed.
Cluster dissolution represents the dynamical cluster mass loss due to stars passing the tidal radius, which acts on the timescale
![]() :
:
where
The characteristic timescale t0 depends on the environment and determines the strength of dissolution. For example, in the case of dissolution by two-body relaxation t0 depends on tidal field strength and therefore on the angular velocity of the cluster orbit. Typical values are t0=105-108 yr (e.g., Lamers et al. 2005b), translating into a total disruption time
The effect of dissolution on the mass function depends on the dynamical state of the cluster. As it evolves towards energy equipartition, low-mass stars are preferentially lost from the cluster. This mass loss (in the ``preferential mode'', KL08) is approximated by increasing the minimum stellar mass (Lamers et al. 2006), while evaporation that is independent of stellar mass (mass loss in the ``canonical mode'', KL08) is accounted for by decreasing the normalisation of the mass function. In our models, both modes coexist to allow for intermediate modes of mass loss. Their relative contributions are fitted such that the M/LV ratio evolution matches the N-body simulations by Baumgardt & Makino (2003).
Cluster photometry is computed by integrating the stellar mass function over the stellar isochrones, yielding cluster magnitude evolution
![]() for a passband
for a passband ![]() and a cluster with initial mass
and a cluster with initial mass
![]() .
.
2.2 Dependence of mass-to-light ratio on model parameters
The models described in Sect. 2.1 yield a mass-to-light ratio evolution that depends on the dissolution timescale, metallicity and initial cluster mass. In canonical models, i.e., without the preferential loss of low-mass stars, M/L monotonously increases with time. For a given age and metallicity, these models provide M/L ratios that are independent of cluster mass. On the other hand, our models including dynamical effects predict a mass-dependent drop in mass-to-light ratio due to the ejection of low-mass, high-M/L stars (Kruijssen 2008, KL08). In Fig. 2, the V-band mass-to-light ratio evolution M/LV is shown for two metallicities and several initial cluster masses. In both panels, the upper curve marks the canonical mass-to-light ratio evolution, while the others correspond to cluster evolution including the preferential loss of low-mass stars for different initial masses. Since low-mass clusters evolve on shorter timescales than massive ones, the deviation of their mass-to-light ratio evolution with respect to canonical models arises at earlier times than for massive clusters.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f2.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg189.png) |
Figure 2:
Left: V-band mass-to-light ratio evolution M/LV for t0=1 Myr, Z=0.0004 and initial masses in the range
|
| Open with DEXTER | |
The mass-to-light ratio decrease can be quantified by considering the ratio of the observed or predicted M/L to its canonical value to divide out their metallicity dependence:
Figure 3 shows the predicted fraction of the canonical M/L ratio
which applies for all initial conditions, i.e., is independent of the cluster properties or environment
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f3.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg196.png) |
Figure 3:
The ratio of predicted to canonical mass-to-light ratio
|
| Open with DEXTER | |
The relation between the predicted fraction of the canonical mass-to-light ratio
![]() and the elapsed fraction of the total disruption time is expected, since in our models the decrease of M/L is the result of dynamical evolution. It is in agreement with studies by Richer et al. (1991) and Baumgardt & Makino (2003), who find that the depletion of the low-mass stellar mass function in globular clusters is closely related to the elapsed fraction of the total disruption time. Considering the physical processes driving dissolution, the result is not surprising either. Two-body relaxation is known to preferentially eject low-mass stars and tidal shocks remove the outer parts of the cluster, which in the case of mass segregation are constituted by low-mass stars.
and the elapsed fraction of the total disruption time is expected, since in our models the decrease of M/L is the result of dynamical evolution. It is in agreement with studies by Richer et al. (1991) and Baumgardt & Makino (2003), who find that the depletion of the low-mass stellar mass function in globular clusters is closely related to the elapsed fraction of the total disruption time. Considering the physical processes driving dissolution, the result is not surprising either. Two-body relaxation is known to preferentially eject low-mass stars and tidal shocks remove the outer parts of the cluster, which in the case of mass segregation are constituted by low-mass stars.
The evolution of cluster mass and M/LV can both be considered in the
![]() -plane. The resulting ``evolutionary tracks'' are shown in Fig. 4 for two different dissolution timescales and again for two metallicities and a range of initial cluster masses as in Fig. 2. Clusters start with their initial masses and with M/LV ratios close to zero, corresponding to an initial position on the x-axis of Fig. 4. As time progresses, clusters initially evolve to lower masses and increasing M/LV due to the death of massive stars, translating into up- and leftward motion in the
-plane. The resulting ``evolutionary tracks'' are shown in Fig. 4 for two different dissolution timescales and again for two metallicities and a range of initial cluster masses as in Fig. 2. Clusters start with their initial masses and with M/LV ratios close to zero, corresponding to an initial position on the x-axis of Fig. 4. As time progresses, clusters initially evolve to lower masses and increasing M/LV due to the death of massive stars, translating into up- and leftward motion in the
![]() -plane. When the preferential loss of low-mass stars becomes an important mechanism (the onset of which is marked by dots for each evolutionary track), the M/LV increase is turned into a decrease instead, as also illustrated in Fig. 2. In Fig. 4, the thus attained maximum in the M/LV evolution is best visible for low cluster masses and t0=1 Myr.
-plane. When the preferential loss of low-mass stars becomes an important mechanism (the onset of which is marked by dots for each evolutionary track), the M/LV increase is turned into a decrease instead, as also illustrated in Fig. 2. In Fig. 4, the thus attained maximum in the M/LV evolution is best visible for low cluster masses and t0=1 Myr.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f4.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg198.png) |
Figure 4:
Cluster evolution in the
|
| Open with DEXTER | |
Since Galactic globular clusters generally share the same ages (e.g., Vandenberg et al. 1990), the observed distribution of GCs in the
![]() -plane would follow curves of equal age in Fig. 4 if there were no spreads in metallicity and dissolution timescale. These curves, or cluster isochrones, are shown for ages
-plane would follow curves of equal age in Fig. 4 if there were no spreads in metallicity and dissolution timescale. These curves, or cluster isochrones, are shown for ages
![]() Gyr. Along the isochrones, M/LV increases with cluster mass since massive clusters have spent a smaller fraction of their total disruption time than low-mass clusters and will therefore have experienced a smaller M/LV decrease due to low-mass star depletion. The curves flatten at the highest masses, since these clusters have not yet exhibited significant preferential low-mass star ejection.
Gyr. Along the isochrones, M/LV increases with cluster mass since massive clusters have spent a smaller fraction of their total disruption time than low-mass clusters and will therefore have experienced a smaller M/LV decrease due to low-mass star depletion. The curves flatten at the highest masses, since these clusters have not yet exhibited significant preferential low-mass star ejection.
From Fig. 4 we infer the influences of dissolution timescale and metallicity on the mass-to-light ratio evolution. The dissolution timescale sets the cluster mass for which the down-bend of the cluster evolutionary tracks can occur and therefore also determines the location of the ``knee'' in the cluster isochrones. The metallicity determines the vertical extent of the cluster evolutionary tracks and thus the M/LV-normalisation of the cluster isochrones. As set forth in Kruijssen (2008), the natural spread in dissolution timescale and metallicity thus explains the scatter around the relation between M/L and cluster mass observed by Mandushev et al. (1991).
3 Determining the dissolution timescale
To assess the influence of the preferential loss of low-mass stars on the low observed mass-to-light ratios, the orbital parameters of individual clusters are to be translated into the appropriate dissolution timescales t0 for use in our cluster models. The computation is treated in this section.
3.1 Cluster dissolution timescales from orbital parameters
For globular clusters, dissolution due to two-body relaxation in the Galactic tidal field![]() and disc shocking are the main dissolution mechanisms (e.g., Chernoff et al. 1986). The total dissolution timescale
and disc shocking are the main dissolution mechanisms (e.g., Chernoff et al. 1986). The total dissolution timescale
![]() can be written as
can be written as
where
For the dissolution timescale due to two-body relaxation, we use the expression for the total disruption time from Baumgardt & Makino (2003, Eq. (10)) as approximated by Lamers et al. (2005b) to write
with
The dissolution timescale due to disc shocking can be obtained from the globular cluster destruction rates due to disc shocking
![]() from Dinescu et al. (1999). Following from Eq. (3), a present destruction rate
from Dinescu et al. (1999). Following from Eq. (3), a present destruction rate ![]() is related to a dissolution timescale t0 by
is related to a dissolution timescale t0 by
with
with the numerator the constant mass-to-light ratio
Substitution of Eqs. (7) and (10) into Eq. (6) then yields the total dissolution timescale
Table 3:
Computed dissolution timescales (for
![]() )
due to two-body relaxation (
)
due to two-body relaxation (
![]() ), disc shocking (
), disc shocking (
![]() )
and both mechanisms (
)
and both mechanisms (
![]() ), together with their
), together with their ![]() standard errors. All values are rounded to one decimal.
standard errors. All values are rounded to one decimal.
In Table 2, our cluster sample is listed with the orbital parameters from Dinescu et al. (1999) for the Paczynski (1990) potential and our computed circular velocities of the gravitational potential at the distance of apogalacticon. The circular velocities are computed in the galactic plane (z=0). Because the gravitational potentials of the disc and bulge decrease with |z|, this implies that for clusters with
![]() kpc the actual
kpc the actual
![]() can be 5-15% lower.
can be 5-15% lower.
The corresponding dissolution timescales can be found in Table 3. The values for the dissolution timescale range from
![]() -20 Myr, corresponding to total disruption times for a 10
-20 Myr, corresponding to total disruption times for a 10
![]() cluster in the range
cluster in the range
![]() -300 Gyr. This is is in good agreement with the range that is required for low-mass star depletion to explain the observed mass-to-light ratio drop (Kruijssen 2008). By comparing the dissolution timescales for two-body relaxation
-300 Gyr. This is is in good agreement with the range that is required for low-mass star depletion to explain the observed mass-to-light ratio drop (Kruijssen 2008). By comparing the dissolution timescales for two-body relaxation
![]() and disc shocking
and disc shocking
![]() ,
we can see that the latter destruction mechanism is important (i.e., lowers the total dissolution timescale
,
we can see that the latter destruction mechanism is important (i.e., lowers the total dissolution timescale
![]() by more than 40% with respect to
by more than 40% with respect to
![]() )
for the clusters NGC 288, 5139 (
)
for the clusters NGC 288, 5139 (![]() Cen), 6362, and 6779. These clusters all have perigalactic radii smaller than 3 kpc (see Table 2). For the error analysis of Tables 2 and 3 and of the rest of this paper we refer to Appendix A.
Cen), 6362, and 6779. These clusters all have perigalactic radii smaller than 3 kpc (see Table 2). For the error analysis of Tables 2 and 3 and of the rest of this paper we refer to Appendix A.
4 Predicted and observed mass-to-light ratios
In this section we combine our cluster models and the derived dissolution timescales to study the mass-to-light ratio evolution for our sample of 24 Galactic globular clusters. Present-day M/LV ratios are predicted for the cluster sample and are compared to the observations. We also discuss the possible causes for the individual clusters that still lack convincing agreement.
4.1 Predicted mass-to-light ratios for the cluster sample
We employ the cluster models treated in Sects. 2 and 3 to predict M/LV ratios for the cluster sample. The input parameters for the models are the dissolution timescale t0 and metallicity Z. The latter is derived from the iron abundance [Fe/H] (see Table 1) according to
with
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f5.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg294.png) |
Figure 5:
Top left: time-evolution of M/LV for NGC 5466. The solid line represents the Z=0.0004 model with the dissolution timescale of the cluster (t0=10.2 Myr), while the dotted curve indicates the canonical M/LV evolution, i.e., if the preferential loss of low-mass stars were omitted. The dashed line denotes constant age of t=12 Gyr. The predicted M/LV of NGC 5466 is marked by a cross and the onset of the preferential loss of low-mass stars is specified with a dot. Top right: evolution in the
|
| Open with DEXTER | |
Table 4:
Our model predictions with their ![]() standard errors.
standard errors.
Examples of the M/LV evolution with time and mass are shown in Fig. 5 for NGC 5466 and 6779. The predicted M/LV are slightly offset with respect to the model curves because the models here are computed at Z=0.0004 while the predictions are interpolated over metallicity. However, the variation with metallicity is small for the displayed clusters, since their metallicities are close to Z=0.0004. It is evident that low-mass star depletion has a much stronger effect in the case of NGC 6779 than for NGC 5466. Considering their dissolution timescales (t0=1.2 Myr versus t0=10.2 Myr, respectively) and the resulting mass evolution, this is not surprising since NGC 6779 has suffered much stronger mass loss than NGC 5466.
The predicted mass-to-light ratios M/LV, initial masses
![]() and remaining lifetimes
and remaining lifetimes
![]() are listed for our entire GC sample in Table 4. In addition, the observed and predicted fractions of the canonical M/LV ratios
are listed for our entire GC sample in Table 4. In addition, the observed and predicted fractions of the canonical M/LV ratios
![]() and
and
![]() are shown, as well as the agreement between our predicted M/LV and the observed values. Combining Tables 3 and 4, we see that GCs with short dissolution timescales indeed have low predicted M/L ratios.
are shown, as well as the agreement between our predicted M/LV and the observed values. Combining Tables 3 and 4, we see that GCs with short dissolution timescales indeed have low predicted M/L ratios.
4.2 Comparison of predictions to observations
The fifth column in Table 4 indicates the ratio between observed and predicted mass-to-light ratio
![]() .
Analogously, the sixth column gives the ratio between predicted and canonical mass-to-light ratio
.
Analogously, the sixth column gives the ratio between predicted and canonical mass-to-light ratio
![]() .
On average, the former ratio is 0.74
+0.06-0.07, while the latter ratio is 0.85
.
On average, the former ratio is 0.74
+0.06-0.07, while the latter ratio is 0.85 ![]() 0.01 for the 24 GCs investigated. There are factors that introduce biases when comparing the predictions to the observations. Specifically, the observations are likely biased to central M/L ratios for some GCs, while we predict global values. In Sect. 4.3 a more detailed consideration is provided in which the comparison of the predictions to the observations is refined.
0.01 for the 24 GCs investigated. There are factors that introduce biases when comparing the predictions to the observations. Specifically, the observations are likely biased to central M/L ratios for some GCs, while we predict global values. In Sect. 4.3 a more detailed consideration is provided in which the comparison of the predictions to the observations is refined.
The seventh column in Table 4 gives the level of agreement between the observed and predicted mass-to-light ratios, which is defined as n if
![]() for
for
![]() and
and
![]() .
Within the
.
Within the ![]() uncertainty, the predicted M/LV agree with the observed values for 12 clusters out of the 24-cluster sample. A Gaussian distribution of errors would yield an expected 16 out of 24 clusters to be found within
uncertainty, the predicted M/LV agree with the observed values for 12 clusters out of the 24-cluster sample. A Gaussian distribution of errors would yield an expected 16 out of 24 clusters to be found within ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f6.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg418.png) |
Figure 6:
Observed (crosses) and predicted (triangles) distribution of GCs in the
|
| Open with DEXTER | |
As a first comparison and analogously to the presentation in Mandushev et al. (1991) and Rejkuba et al. (2007), in Fig. 6 the distribution of GCs in the
![]() -plane is shown for the observed and predicted mass-to-light ratios. Both populations fall within the same range and follow comparable trends of increasing M/LV with cluster mass. Mandushev et al. (1991) already provided an expression for the observed logarithm of the mass as a function of magnitude, which allows for a derivation of the expected trend in Fig. 6. They fit
-plane is shown for the observed and predicted mass-to-light ratios. Both populations fall within the same range and follow comparable trends of increasing M/LV with cluster mass. Mandushev et al. (1991) already provided an expression for the observed logarithm of the mass as a function of magnitude, which allows for a derivation of the expected trend in Fig. 6. They fit
where MV represents the V-band absolute magnitude of the cluster. Adopting a solar value of
A first-order Taylor expansion of M/LV around
which has a linear slope of 0.38. The best fitting slope for our sample is 0.41
The trend of increasing mass-to-light ratio with mass is expected from the models shown in Fig. 4 and the discussion in Sect. 2.2. However, there the slope is ![]() -1.0 for metallicities Z=0.0004-0.004 and increases with Z. For some metallicities, the model slope is thus more than
-1.0 for metallicities Z=0.0004-0.004 and increases with Z. For some metallicities, the model slope is thus more than ![]() steeper than the fitted slope. This is not surprising, because the models each have a single dissolution timescale and metallicity, while in reality both quantities have a spread that causes horizontal and vertical scatter, respectively. It turns out that the spread in dissolution timescale has a stronger effect on M/L than the spread in metallicity (Kruijssen 2008), implying that the scatter in the horizontal direction is largest and that the slope fitted to the entire sample is shallower than that of a single model.
steeper than the fitted slope. This is not surprising, because the models each have a single dissolution timescale and metallicity, while in reality both quantities have a spread that causes horizontal and vertical scatter, respectively. It turns out that the spread in dissolution timescale has a stronger effect on M/L than the spread in metallicity (Kruijssen 2008), implying that the scatter in the horizontal direction is largest and that the slope fitted to the entire sample is shallower than that of a single model.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f7a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f7b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg425.png) |
Figure 7:
Left: observed mass-to-light ratio
|
| Open with DEXTER | |
In Fig. 7, a more specific comparison is made between the observations and model predictions using the same framework as for the canonical expectations in Fig. 1. Again, the left-hand panel plots the observed versus the predicted mass-to-light ratios, while the right-hand panel shows the number histograms of the two. In the left-hand panel it is shown that the predictions for half of the clusters are such that they reach down to the appropriate mass-to-light ratios. When comparing this panel to its analog in Fig. 1, the improved agreement with the observations is evident. Nonetheless, there is an aggregate of deviating GCs below the 1:1 relation at
![]() ,
representing the clusters for which no strong low-mass star depletion is expected from the models due to their long disruption times. Consequently, the predicted M/LV for these clusters are similar or equal to the canonical values. Except for NGC 6809, there are no clusters above the 1:1 relation that are inconsistent with the observations. The number histogram of the observed and predicted mass-to-light ratios in the right-hand panel of Fig. 7 confirms both the improved agreement between observed and predicted M/LV with respect to Fig. 1 and the accumulation of a number of clusters near the canonical M/LV in the model predictions.
,
representing the clusters for which no strong low-mass star depletion is expected from the models due to their long disruption times. Consequently, the predicted M/LV for these clusters are similar or equal to the canonical values. Except for NGC 6809, there are no clusters above the 1:1 relation that are inconsistent with the observations. The number histogram of the observed and predicted mass-to-light ratios in the right-hand panel of Fig. 7 confirms both the improved agreement between observed and predicted M/LV with respect to Fig. 1 and the accumulation of a number of clusters near the canonical M/LV in the model predictions.
4.3 Discussion of discrepant clusters
In total, there are twelve clusters with a worse than ![]() agreement between the model predictions and observations. Five of these have worse than
agreement between the model predictions and observations. Five of these have worse than ![]() agreement, while we would expect only one. Here, we discuss possible reasons behind the discrepancy.
agreement, while we would expect only one. Here, we discuss possible reasons behind the discrepancy.
The deviant clusters below the 1:1 relation in the left-hand panel of Fig. 7, being NGC 104, 1851, 1904, 4147, 4590, 5272, 5904, 6205, 6341, 6934 and 7089, generally share properties such as relatively wide orbits and long dissolution timescales. Due to their long dissolution timescales, they are all predicted to have near-canonical M/LV. This is illustrated in Fig. 8, where the fraction of
![]() and
and
![]() with respect to the canonical
with respect to the canonical
![]() is shown in panels similar to Fig. 7. In both the left- and right-hand panels of Fig. 8, the accumulation of too high predicted
mass-to-light ratios occurs near or at
is shown in panels similar to Fig. 7. In both the left- and right-hand panels of Fig. 8, the accumulation of too high predicted
mass-to-light ratios occurs near or at
![]() .
Since per definition
.
Since per definition
![]() ,
no values
,
no values
![]() are found. In that range, the apparent disagreement between the observed and predicted histograms is disputable since all but one cluster (NGC 6809) are in
are found. In that range, the apparent disagreement between the observed and predicted histograms is disputable since all but one cluster (NGC 6809) are in ![]() agreement with their canonical mass-to-light ratios.
agreement with their canonical mass-to-light ratios.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f8a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f8b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg431.png) |
Figure 8:
Left: the ratio of the observed mass-to-light ratio
|
| Open with DEXTER | |
While our predicted mass-to-light ratios are global (i.e., cluster-wide) values, the observations from McLaughlin & van der Marel (2005) are derived from central velocity dispersion measurements from Pryor & Meylan (1993) and are extrapolated to global values using surface brightness profiles (McLaughlin & van der Marel 2005, and references therein). They fit isotropic single-mass King models and thus neglect any radial gradients of M/L ratio or mass function slope. Consequently, the values of
![]() do not contain any information about such gradients and for some clusters only accurately reflect the M/LV ratio in their central parts. The global M/LV ratios of clusters with strong radial M/L gradients are at best approximated (McLaughlin, private communication). For instance, the centre of a mass-segregated cluster may be populated with massive, i.e., luminous stars, yielding a lower M/LV ratio than its global value.
do not contain any information about such gradients and for some clusters only accurately reflect the M/LV ratio in their central parts. The global M/LV ratios of clusters with strong radial M/L gradients are at best approximated (McLaughlin, private communication). For instance, the centre of a mass-segregated cluster may be populated with massive, i.e., luminous stars, yielding a lower M/LV ratio than its global value.
The disagreement between the global and central M/L is expected to be largest for clusters that have suffered relatively weak mass loss but are internally evolved. In that case, the low-mass stars are outside the core but still bound to the cluster and are included in the global M/L, while they do not play a role in the value derived by McLaughlin & van der Marel (2005). This indeed applies for the discrepant GCs in our sample, which not only have long dissolution timescales but also higher King parameters W0, implying that mass segregation can be reached on relatively shorter timescales. For the GCs with worse than ![]() agreement below the 1:1 line in Figs. 7 and 8 we have average King parameter
agreement below the 1:1 line in Figs. 7 and 8 we have average King parameter
![]() ,
while for the
,
while for the ![]() -consistent GCs we find
-consistent GCs we find
![]() ,
both with standard errors <0.1. This further validates our explanation for the difference between the central and global M/L ratios of these GCs.
,
both with standard errors <0.1. This further validates our explanation for the difference between the central and global M/L ratios of these GCs.
In a recent study, De Marchi et al. (2007) find that extended (low-concentration and low-W0) GCs are depleted in low-mass stars, which they confirm to be in accordance with predictions by theoretical studies (Chernoff & Weinberg 1990; Takahashi & Portegies Zwart 2000), while GCs with high values of W0 have close to canonical mass functions. This is in agreement with our predicted M/LV for these clusters and suggests that the observed M/LV are indeed underestimated. A more precise check can be made by comparing the low-mass star depletion from De Marchi et al. (2007) with the observed and predicted fractions of the canonical M/LV ratios
![]() .
This can be done for four GCs with worse than
.
This can be done for four GCs with worse than ![]() agreement, being NGC 104, 5272, 6341 and 6809. For NGC 104 and 5272 the observed depletion is not strong enough to draw any definitive conclusions, while for NGC 6341 and 6809 the results from De Marchi et al. (2007) are clearly more consistent with our predictions than with the observed M/LV (see also Sect. 5 and Fig. 9). This substantiates the claim that some GCs have observed M/L ratios that are biased to lower numbers. To test this assertion, global observational measurements of the velocity dispersion would be needed to enhance the accuracy of the present observed M/L ratios.
agreement, being NGC 104, 5272, 6341 and 6809. For NGC 104 and 5272 the observed depletion is not strong enough to draw any definitive conclusions, while for NGC 6341 and 6809 the results from De Marchi et al. (2007) are clearly more consistent with our predictions than with the observed M/LV (see also Sect. 5 and Fig. 9). This substantiates the claim that some GCs have observed M/L ratios that are biased to lower numbers. To test this assertion, global observational measurements of the velocity dispersion would be needed to enhance the accuracy of the present observed M/L ratios.
We now revisit the mean M/LV fractions of the canonical value presented in Sect. 4.2 by leaving out the GCs that may have strongly different central and global M/L ratios. It was shown by Baumgardt & Makino (2003) that for a
![]() cluster core collapse is reached within a Hubble time if
cluster core collapse is reached within a Hubble time if ![]() .
This timescale is increased by a factor three for a GC with typical initial mass of
.
This timescale is increased by a factor three for a GC with typical initial mass of
![]() ,
but mass segregation manifests itself on a shorter timescale than the core collapse time. The relative mass loss due to dissolution of a
,
but mass segregation manifests itself on a shorter timescale than the core collapse time. The relative mass loss due to dissolution of a
![]() GC is smaller than 10% after 12 Gyr for dissolution timescales
GC is smaller than 10% after 12 Gyr for dissolution timescales
![]() Myr. These limits could separate GCs with similar global and central M/L ratios from those with pronounced differences between the two. We exclude GCs with both
Myr. These limits could separate GCs with similar global and central M/L ratios from those with pronounced differences between the two. We exclude GCs with both
![]() Myr and
Myr and ![]() ,
as well as NGC 6809 (which has a M/LV ratio that cannot be explained by any model as it is 1.6 times the canonical value). This yields an average observed fraction of the canonical M/LV of
,
as well as NGC 6809 (which has a M/LV ratio that cannot be explained by any model as it is 1.6 times the canonical value). This yields an average observed fraction of the canonical M/LV of
![]() and a predicted value of
and a predicted value of
![]()
![]() 0.02. For the excluded GCs, we have
0.02. For the excluded GCs, we have
![]() and
and
![]()
![]() 0.01, reflecting the fundamental difference between both values. Although the cuts we made represent only ``educated guesses'', it is evident that the agreement between theory and observations is much better for those GCs for which we can be more certain that the central M/LV reflects the global value. For these GCs, our models confirm an average M/L ratio drop of about 20% due to low-mass star depletion, corresponding to about 1/4 of the observed difference in M/LV between GCs and UCDs.
0.01, reflecting the fundamental difference between both values. Although the cuts we made represent only ``educated guesses'', it is evident that the agreement between theory and observations is much better for those GCs for which we can be more certain that the central M/LV reflects the global value. For these GCs, our models confirm an average M/L ratio drop of about 20% due to low-mass star depletion, corresponding to about 1/4 of the observed difference in M/LV between GCs and UCDs.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f9.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg444.png) |
Figure 9:
Correlation between the observed slope of the low-mass stellar mass function
|
| Open with DEXTER | |
Another option could be that the dissolution timescales of GCs on wide orbits are overestimated (as suggested for different reasons by Kruijssen & Portegies Zwart 2009), possibly due to a dissolution mechanism that is not included in our analysis. White dwarf kicks (Fregeau et al. 2009) could be a candidate for such a mechanism. This would imply that some of our predicted dissolution timescales and M/L ratios are overestimated. Also, we do not assume clusters to be initially mass-segregated. Some of the clusters under consideration here are likely not to have reached energy equipartition within a Hubble time, but still exhibit evidence of mass segregation (e.g., Anderson & King 1996). This points to primordial mass segregation in these cases, which is shown by Baumgardt et al. (2008) to effect additional low-mass star depletion that we did not account for (see also Sect. 2.2). The additional modeled M/L ratio decrease would be ![]() % (KL08). However, this is not sufficient to lift the discrepancy for any of the deviating GCs.
% (KL08). However, this is not sufficient to lift the discrepancy for any of the deviating GCs.
5 Observational verification
If the decrease of M/L ratio with respect to the canonical value is indeed due to low-mass star depletion, one would expect a correlation between the observed slope of the low-mass MF
![]() and the ratio of the predicted and canonical M/LV ratios
and the ratio of the predicted and canonical M/LV ratios
![]() .
Specifically, for a powerlaw MF with
.
Specifically, for a powerlaw MF with
![]() ,
a low value of
,
a low value of
![]() would be signified by a reduced value of
would be signified by a reduced value of
![]() .
.
In a study by De Marchi et al. (2007), MF slopes are determined in the stellar mass range m=0.3-
![]() for several Galactic globular clusters, based on a compilation of results
from HST imaging of different sources. By reanalysing the Baumgardt & Makino (2003) N-body data, Baumgardt et al. (2008) conclude that for a Kroupa (2001) IMF the canonical slope in that mass range is
for several Galactic globular clusters, based on a compilation of results
from HST imaging of different sources. By reanalysing the Baumgardt & Makino (2003) N-body data, Baumgardt et al. (2008) conclude that for a Kroupa (2001) IMF the canonical slope in that mass range is
![]() ,
which is thus expected to be measured for clusters with canonical M/L ratios or
,
which is thus expected to be measured for clusters with canonical M/L ratios or
![]() .
In addition, they provide a fourth-order powerlaw fit to the N-body
simulations from Baumgardt & Makino (2003) for
.
In addition, they provide a fourth-order powerlaw fit to the N-body
simulations from Baumgardt & Makino (2003) for ![]() as a function of
as a function of
![]() ,
the elapsed fraction of the total disruption time. By inverting our relation between
,
the elapsed fraction of the total disruption time. By inverting our relation between
![]() and
and
![]() (Eq. (5)) and inserting the outcome into
(Eq. (5)) and inserting the outcome into
![]() from Baumgardt et al. (2008, Eq. (4)), we obtain an expression for the predicted MF slope
from Baumgardt et al. (2008, Eq. (4)), we obtain an expression for the predicted MF slope
![]() between 0.3 and 0.8
between 0.3 and 0.8
![]() as a function of the fraction of the canonical M/LV ratio
as a function of the fraction of the canonical M/LV ratio
![]() .
Inversion of Eq. (5) yields
.
Inversion of Eq. (5) yields
where the uncertainty
with the coefficients
Table 5:
Coefficients for the fourth-order powerlaw approximation of
![]() as a function of
as a function of
![]() (see Eq. (16)).
(see Eq. (16)).
In Fig. 9, the correlation between
![]() and the observed low-mass MF slope
and the observed low-mass MF slope
![]() is assessed for the subsample of clusters from the present study that is also considered in De Marchi et al. (2007). For comparison, the relation for the predicted low-mass MF slope
is assessed for the subsample of clusters from the present study that is also considered in De Marchi et al. (2007). For comparison, the relation for the predicted low-mass MF slope
![]() as a function of
as a function of
![]() is included as well. Most of the observed data match the predicted relation between
is included as well. Most of the observed data match the predicted relation between ![]() and
and
![]() within their error bars, albeit with substantial scatter. This is due to the large uncertainties of the observations and possibly also related to biases introduced by comparing central and global mass-to-light ratios (see Sect. 4.3). The poor quality of the observations is illustrated by this spread and by the large error bars. For the predicted mass-to-light ratios the trend is more well-defined, but for low values of
within their error bars, albeit with substantial scatter. This is due to the large uncertainties of the observations and possibly also related to biases introduced by comparing central and global mass-to-light ratios (see Sect. 4.3). The poor quality of the observations is illustrated by this spread and by the large error bars. For the predicted mass-to-light ratios the trend is more well-defined, but for low values of
![]() it does not extend down to the mass-to-light ratios that are predicted by theory. This could imply that either
it does not extend down to the mass-to-light ratios that are predicted by theory. This could imply that either
![]() or
or
![]() are biased. If the latter is true, it suggests that some GCs perhaps dissolve more rapidly than presently included in the models.
are biased. If the latter is true, it suggests that some GCs perhaps dissolve more rapidly than presently included in the models.
As shown in Sect. 4.3, comparison of
![]() with the observed and predicted fractions of the canonical M/LV ratios
with the observed and predicted fractions of the canonical M/LV ratios
![]() for the GCs with agreement parameter
for the GCs with agreement parameter ![]() (see Table 4) provides an independent check of our predicted M/LV ratios. While for NGC 104 and 5272 this does not allow for any definitive conclusions, for NGC 6341 and 6809 the observed mass functions are clearly more consistent with our predicted M/LV ratios than with the observed values.
(see Table 4) provides an independent check of our predicted M/LV ratios. While for NGC 104 and 5272 this does not allow for any definitive conclusions, for NGC 6341 and 6809 the observed mass functions are clearly more consistent with our predicted M/LV ratios than with the observed values.
Table 6:
Observed and predicted stellar mass function (MF) slopes ![]() in the range m=0.3-
in the range m=0.3-
![]() .
.
With Eq. (16), we can also predict the slope of the low-mass MF for clusters that where not considered by De Marchi et al. (2007). The predicted slopes are listed in Table 6. For most clusters with observed values of ![]() ,
the agreement between observed and predicted
,
the agreement between observed and predicted ![]() is reasonable. Only for NGC 6218 and 6712 there is a strong
discrepancy. For NGC 6218, we expect the deviation to arise from the observed value of
is reasonable. Only for NGC 6218 and 6712 there is a strong
discrepancy. For NGC 6218, we expect the deviation to arise from the observed value of
![]() ,
since the predicted and observed M/LV are in excellent agreement (see Table 4). On the other hand, for NGC 6712 the incompatibility may be due to a slight overestimation of
,
since the predicted and observed M/LV are in excellent agreement (see Table 4). On the other hand, for NGC 6712 the incompatibility may be due to a slight overestimation of
![]() and thus of
and thus of
![]() and
and
![]() .
.
In this context it must be noted that the compilation of ![]() values from De Marchi et al. (2007) is drawn from a sample of literature estimates, most based on HST data, observed in somewhat different
radial regions of each cluster. Four of the eleven GCs that coincide with our sample of 24 GCs do have a direct estimate for their global mass function (see Table 6). For the remaining seven other GCs from De Marchi et al. (2007), that estimate is taken from measurements restricted to the region around the half-mass radius
values from De Marchi et al. (2007) is drawn from a sample of literature estimates, most based on HST data, observed in somewhat different
radial regions of each cluster. Four of the eleven GCs that coincide with our sample of 24 GCs do have a direct estimate for their global mass function (see Table 6). For the remaining seven other GCs from De Marchi et al. (2007), that estimate is taken from measurements restricted to the region around the half-mass radius ![]() ,
of which it is known that the shape of the MF is comparable to the global (i.e., cluster-wide) MF (De Marchi & Pulone 2007; Baumgardt & Makino 2003; Richer et al. 1991). However, the uncertainty of these slopes is larger, and they do not provide a self-consistent way to derive the global MF. It is clear that a direct determination of the global stellar mass function for most of the 24 GCs investigated in this study would allow one to verify the predictions of the present study with much higher confidence.
,
of which it is known that the shape of the MF is comparable to the global (i.e., cluster-wide) MF (De Marchi & Pulone 2007; Baumgardt & Makino 2003; Richer et al. 1991). However, the uncertainty of these slopes is larger, and they do not provide a self-consistent way to derive the global MF. It is clear that a direct determination of the global stellar mass function for most of the 24 GCs investigated in this study would allow one to verify the predictions of the present study with much higher confidence.
In Fig. 10 we investigate how feasible it is to observationally verify the predicted drop of ![]() for our full sample of 24 GCs. We plot the apparent V-band magnitude of stars with 0.3 solar masses V0.3 for each cluster versus the predicted slope
for our full sample of 24 GCs. We plot the apparent V-band magnitude of stars with 0.3 solar masses V0.3 for each cluster versus the predicted slope
![]() of the stellar mass function for
of the stellar mass function for
![]() .
V0.3 is obtained from the distance modulus of each GC and from the assumption that
MV0.3=9.8 mag (Baraffe et al. 1997). We also plot the angular size of each cluster versus
.
V0.3 is obtained from the distance modulus of each GC and from the assumption that
MV0.3=9.8 mag (Baraffe et al. 1997). We also plot the angular size of each cluster versus
![]() .
As a consequence of their generally higher galactocentric distance, those GCs with the faintest
V0.3>25 mag would not be
expected to exhibit a strong low-mass star depletion. The angular half-mass diameters of the GCs with
V0.3<25 range between 2 and 8 arcmin. To obtain a representative estimate of the global mass function, it is clear that wide-field ground-based imaging is required for most GCs. For this
wide-field imaging, a completeness magnitude of V
.
As a consequence of their generally higher galactocentric distance, those GCs with the faintest
V0.3>25 mag would not be
expected to exhibit a strong low-mass star depletion. The angular half-mass diameters of the GCs with
V0.3<25 range between 2 and 8 arcmin. To obtain a representative estimate of the global mass function, it is clear that wide-field ground-based imaging is required for most GCs. For this
wide-field imaging, a completeness magnitude of V ![]() 26 mag is desirable, which will allow moderately precise photometry already for
26 mag is desirable, which will allow moderately precise photometry already for ![]() mag. For 8 m class telescopes and with optical seeing in the range 0.8 to 1.0'', this requires 1-2 h integration time per filter, or 2-4 h for a two-band exposure. With wide-field imagers such as VIMOS@VLT, IMACS@Magellan, or SuprimeCam@SUBARU, single-shot images will be sufficient to cover at least 2-3 half-light radii for most clusters. From Fig. 10 we conclude that the best candidate that also complements the compilation by De Marchi et al. (2007) is NGC 6779, followed by NGC 6362 and possibly NGC 6171.
mag. For 8 m class telescopes and with optical seeing in the range 0.8 to 1.0'', this requires 1-2 h integration time per filter, or 2-4 h for a two-band exposure. With wide-field imagers such as VIMOS@VLT, IMACS@Magellan, or SuprimeCam@SUBARU, single-shot images will be sufficient to cover at least 2-3 half-light radii for most clusters. From Fig. 10 we conclude that the best candidate that also complements the compilation by De Marchi et al. (2007) is NGC 6779, followed by NGC 6362 and possibly NGC 6171.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1453f10a.eps}\hspace*{0.6cm}
\includegraphics[width=8.3cm,clip]{1453f10b.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg493.png) |
Figure 10:
Feasibility of observational tests of low-mass star depletion. Left: for the 24 GCs investigated in this paper, the apparent V-band magnitude of stars with 0.3 solar masses V0.3 is plotted versus the predicted slope
|
| Open with DEXTER | |
6 Discussion and conclusions
In this section, we provide a summary and a discussion of our results. We consider the effects of the assumptions that were made and reflect on the implications of the results.
6.1 Summary
In this study, we have investigated the dynamical mass-to-light ratios of 24 Galactic globular clusters. We have tested the hypothesis of the preferential loss of low-mass stars as the main explanation for the fact that the average observed mass-to-light ratios of the Galactic GCs in our entire sample are only 74 +6-7% of the expectations from stellar population models. Accounting for the orbital parameters we derived dissolution timescales due to two-body relaxation and disc shocking for our globular cluster sample and calculated the evolution of their masses and photometry using the SPACE analytical cluster models from Kruijssen & Lamers (2008, throughout this paper KL08). These models account for the preferential loss of low-mass stars which is fitted to the N-body simulations by Baumgardt & Makino (2003) and therefore provide non-canonical M/LV predictions. We find the derived dissolution timescales to be in good agreement with the range required for low-mass star depletion to explain the observed M/L ratio decrease from Kruijssen (2008).
The present-day (t=12 Gyr) M/LV ratios have been compared to the observed values from McLaughlin & van der Marel (2005), yielding ![]() agreement for 12 out of 24 GCs. We considered possible causes for the remaining
agreement for 12 out of 24 GCs. We considered possible causes for the remaining
![]() discrepancies that occur for the other GCs. It is found that 11 of these clusters have predicted M/LV very close to the canonically expected M/LV ratios due to their long dissolution timescales and the correspondingly modest low-mass star depletion, while their observed M/LV are lower. This is probably due to the method by which the observed M/LV are derived, which is biased towards the central M/LV while our models predict global M/LV. For mass-segregated GCs with long dissolution timescales, both values can be substantially different. The discrepant GCs have higher than average King parameters W0, which should indeed reach mass segregation on shorter timescales (see e.g., Baumgardt & Makino 2003). This explanation for the discrepancy between some of the observed and predicted M/L ratios is confirmed by a study of low-mass star depletion in GCs by De Marchi et al. (2007), whose observed mass functions are in good agreement with our predictions. The average observed M/LV ratio of 74
+6-7% of the canonical expectations would therefore be underestimated. Excluding GCs which likely have dissimilar global and central M/L ratios by making cuts in dissolution timescale and King parameter, we find that the observed and predicted M/LV ratios are consistent at 78
+9-11% and 78
discrepancies that occur for the other GCs. It is found that 11 of these clusters have predicted M/LV very close to the canonically expected M/LV ratios due to their long dissolution timescales and the correspondingly modest low-mass star depletion, while their observed M/LV are lower. This is probably due to the method by which the observed M/LV are derived, which is biased towards the central M/LV while our models predict global M/LV. For mass-segregated GCs with long dissolution timescales, both values can be substantially different. The discrepant GCs have higher than average King parameters W0, which should indeed reach mass segregation on shorter timescales (see e.g., Baumgardt & Makino 2003). This explanation for the discrepancy between some of the observed and predicted M/L ratios is confirmed by a study of low-mass star depletion in GCs by De Marchi et al. (2007), whose observed mass functions are in good agreement with our predictions. The average observed M/LV ratio of 74
+6-7% of the canonical expectations would therefore be underestimated. Excluding GCs which likely have dissimilar global and central M/L ratios by making cuts in dissolution timescale and King parameter, we find that the observed and predicted M/LV ratios are consistent at 78
+9-11% and 78 ![]() 2% of the canonical values, respectively. For the entire sample, the average predicted fraction of the canonical M/LV ratio is 85
2% of the canonical values, respectively. For the entire sample, the average predicted fraction of the canonical M/LV ratio is 85 ![]() 1%.
1%.
To assess the imprint of low-mass star depletion on the slope of the low-mass stellar mass function, we compared the observed mass function slopes
![]() from De Marchi et al. (2007) for 11 GCs contained in our study to the values predicted by our models as well as to the observed and predicted mass-to-light ratio fractions of the canonical values
from De Marchi et al. (2007) for 11 GCs contained in our study to the values predicted by our models as well as to the observed and predicted mass-to-light ratio fractions of the canonical values
![]() and
and
![]() .
Most of the measured slopes agree with the predictions, but exhibit considerable scatter. Since most of them are values derived at around the half-mass radius and are extrapolated to global values, we also discuss the feasibility of observations for directly measuring global mass functions of most of the GCs investigated. We show that deep (ground-based) wide-field imaging would be necessary, with point source detection limits
.
Most of the measured slopes agree with the predictions, but exhibit considerable scatter. Since most of them are values derived at around the half-mass radius and are extrapolated to global values, we also discuss the feasibility of observations for directly measuring global mass functions of most of the GCs investigated. We show that deep (ground-based) wide-field imaging would be necessary, with point source detection limits ![]() mag. The most suitable candidate for such a campaign would be NGC 6779.
mag. The most suitable candidate for such a campaign would be NGC 6779.
6.2 Propagation of assumptions
In the course of the study presented in this paper, several assumptions were made that affect the results to different extents. Their implications are as follows.
- (1)
- We have adopted the SPACE cluster models (KL08), of which the stellar evolution and photometry are based on the Padova 1999 isochrones (see Sect. 2). Consequently, the predicted cluster photometry and corresponding mass-to-light ratios are affected by that choice. To indicate the level of the deviation with the cluster models from Bruzual & Charlot (2003), in Fig. 1 we compared the canonically expected M/LV from SPACE to the Bruzual & Charlot (2003) values for our cluster sample. The difference between both is inadequate to explain any systematic tendency of low mass-to-light ratio with respect to the SPACE models. Therefore, we conclude that the adopted cluster models do not effect substantial implications for the predicted M/L ratios
![[*]](/icons/foot_motif.png) .
.
- (2)
- Due to the treatment of the preferential loss of low-mass stars in the SPACE cluster models, there are indications that the predicted mass-to-light ratios could be underestimated during the final
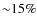 of the total cluster lifetime (KL08). Table 4 shows that none of the GCs in our sample reside in this regime. On the other hand, we did not include primordial mass segregation, which could decrease the predicted M/L ratios by
of the total cluster lifetime (KL08). Table 4 shows that none of the GCs in our sample reside in this regime. On the other hand, we did not include primordial mass segregation, which could decrease the predicted M/L ratios by 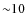 % (KL08).
% (KL08).
- (3)
- By adopting the average cluster orbits from Dinescu et al. (1999), we assume constant orbital parameters over the total cluster lifetimes. Considering the ballistic nature of the orbits, such an assumption is legitimate as long as the external conditions do not strongly differ. The Galactic potential was only substantially different from its present state during the formation of the Milky Way. A more extended distribution of mass during these early epoch would obviously increase the dissolution timescale due to disc shocking, and would affect the dissolution timescale due to two-body relaxation in a similar way because of the reduced tidal field. Consequently, this would imply that the mass loss during the first
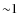 Gyr of our models is overestimated, causing our initial masses to be overestimated as well. However, the extended nature of the Milky Way would cause dissolution due to giant molecular cloud encounters to become an important mechanism (e.g., Gieles et al. 2006), thereby counteracting the previous effect. Although we cannot rule out any consequences, a residual influence would only be relevant for a small fraction (the first
Gyr of our models is overestimated, causing our initial masses to be overestimated as well. However, the extended nature of the Milky Way would cause dissolution due to giant molecular cloud encounters to become an important mechanism (e.g., Gieles et al. 2006), thereby counteracting the previous effect. Although we cannot rule out any consequences, a residual influence would only be relevant for a small fraction (the first 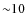 %) of the total cluster lifetime, where mass loss by dissolution is much less effective than later on during cluster evolution. Therefore, this likely only affects our analysis within the error margins.
%) of the total cluster lifetime, where mass loss by dissolution is much less effective than later on during cluster evolution. Therefore, this likely only affects our analysis within the error margins.
- (4)
- We have compared our predictions to the observed mass-to-light ratios from McLaughlin & van der Marel (2005), which are biased towards central M/L values. As treated more extensively in Sect. 4.3, this yields underestimated observed M/L ratios for mass-segregated clusters with long dissolution timescales. Therefore, based on the earlier discussion and the parameter range in which discrepancies arise, we consider the dynamical
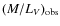 from McLaughlin & van der Marel (2005) to be subject to improvement for GCs with both dissolution timescales
from McLaughlin & van der Marel (2005) to be subject to improvement for GCs with both dissolution timescales
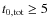 Myr and King parameters
Myr and King parameters 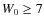 .
.
6.3 Consequences and conclusions
The consequences of our findings are not only relevant to studies of the M/L ratios of compact stellar systems, but also to other properties of these structures. Here we list them together with the conclusions of this work.
- (1)
- When constraining our sample to the subset for which the observed M/LV likely reflect the global values, we find that the preferential loss of low-mass stars can account for the
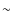 20% discrepancy between observed dynamical mass-to-light ratios of Galactic GCs and those expected from stellar population models that assume a canonical present day mass function (Kroupa 2001). This alleviates the factor of two offset in M/L between GCs and UCDs by about 25%. Still, some additional dark mass with respect to a canonical IMF is required to explain the M/L of most UCDs.
20% discrepancy between observed dynamical mass-to-light ratios of Galactic GCs and those expected from stellar population models that assume a canonical present day mass function (Kroupa 2001). This alleviates the factor of two offset in M/L between GCs and UCDs by about 25%. Still, some additional dark mass with respect to a canonical IMF is required to explain the M/L of most UCDs.
- (2)
- Accounting for the orbital parameters, present-day masses and chemical compositions of individual clusters, we find that there is good agreement between our model predictions and observations of the M/LV ratios of these clusters. For the GCs with worse than
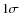 agreement there are strong indications that the discrepancy is due to an underestimation of the observed M/L ratio. In mass-segregated clusters with long dissolution timescales, the observed M/LV ratios represent central values that do not reflect the global M/LV ratio.
agreement there are strong indications that the discrepancy is due to an underestimation of the observed M/L ratio. In mass-segregated clusters with long dissolution timescales, the observed M/LV ratios represent central values that do not reflect the global M/LV ratio.
- (3)
- The ideal way to confirm the validity of our explanation for the reduced M/L ratios of GCs for individual clusters will be to obtain a homegeneous set of deep wide-field imaging for most GCs. This would expand and complement the currently available heterogeneous data sets of space based GC imaging, which is restricted to small fields in each GC, at different radial ranges. By this, the global mass and luminosity functions could be measured directly for individual GCs and be compared quantitatively to the predictions of this paper regarding the low-mass star depletion due to dynamical evolution. In addition, velocity dispersion measurements would allow for the determination of global M/L ratios, thus providing an update to those from McLaughlin & van der Marel (2005).
- (4)
- The topic of globular cluster self-enrichment and multiple stellar populations can also be considered within the framework of this paper. In a recent study by Marino et al. (2008) it is shown that NGC 6121 contains two stellar populations that are probably due to primordial variations in their respective chemical compositions. It is mentioned that the present-day mass of NGC 6121 is an order of magnitude smaller than that of known multiple-population GCs such as NGC 1851, 2808 and 5139. Consequently, Marino et al. (2008) pose the question how the enriched material could have remained in such a shallow potential and argue that multiple populations are unlikely to be strictly internal to GCs, unless they are the remnant of much larger structures. In the case of NGC 6121, our calculations seem to explain the issue, as it is the initially fifth most massive GC of our sample (
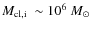 ). As a result, mass could have been retained much more easily, implying that the multiple populations of NGC 6121 are no reason to invoke external processes for enrichment and to abandon the self-enrichment scenario.
). As a result, mass could have been retained much more easily, implying that the multiple populations of NGC 6121 are no reason to invoke external processes for enrichment and to abandon the self-enrichment scenario.
Acknowledgements
We thank the anonymous referee for valuable comments that improved the manuscript. We are grateful to Dana Casetti-Dinescu for interesting discussions and for providing the disc shocking destruction rates from Dinescu et al. (1999). Christine Allen is acknowledged for providing the data from Allen et al. (2008,2006) in electronic form. We thank Guido De Marchi for sharing the uncertainties on the mass function slopes from De Marchi et al. (2007). We particularly enjoyed stimulating discussions with Holger Baumgardt, Mark Gieles, Dean McLaughlin, Simon Portegies Zwart, Frank Verbunt and Reinier Zeldenrust. J.M.D.K. is grateful to Henny Lamers for support, advice and constructive comments on the manuscript, and is supported by a TopTalent fellowship from the Netherlands Organisation for Scientific Research (NWO), grant number 021.001.038.
Appendix A: Error analysis
In this Appendix, the error propagation through our computations is discussed. The errors in Tables 2 and 3 are standard errors, most of them determined by computing the formal error propagation. For a function
f(x1,x2,...,xi) this implies
with
where
The error margins on our predictions in Table 4 are determined by numerically evaluating Eq. (A.1) for the desired quantities. Our predictions depend on the observed mass, metallicity and dissolution timescale. The derivatives of M/LV with respect to the former two are trivial since M/LV is determined by interpolating over these parameters. For the dissolution timescale, we compute additional models at
![]() to obtain the numerical derivative of M/LV with respect to
to obtain the numerical derivative of M/LV with respect to
![]() .
In fact, this is the differential rather than the derivative, because for long dissolution timescales M/LV can be locally constant, while it varies over a larger range. The only case were a non-linearity forces us to derive alternative errors is for the positive standard error on M/LV. Although the uncertainty in metallicity could increase the predicted mass-to-light above its canonical value, the uncertainty in mass and dissolution timescale cannot due to the flattening of the cluster isochrones in the
.
In fact, this is the differential rather than the derivative, because for long dissolution timescales M/LV can be locally constant, while it varies over a larger range. The only case were a non-linearity forces us to derive alternative errors is for the positive standard error on M/LV. Although the uncertainty in metallicity could increase the predicted mass-to-light above its canonical value, the uncertainty in mass and dissolution timescale cannot due to the flattening of the cluster isochrones in the
![]() -plane (see Fig. 4). Therefore, the combined positive standard error of the mass-to-light ratio due to the uncertainty in mass and dissolution timescale
-plane (see Fig. 4). Therefore, the combined positive standard error of the mass-to-light ratio due to the uncertainty in mass and dissolution timescale
![]() is defined as
is defined as
with
Except for the alternative error in Eq. (A.3) that is specific to M/LV, the standard errors on the predicted initial masses are determined analogously to the above. For the remaining lifetimes, numerical derivatives with respect to mass, metallicity and dissolution timescale are simply obtained by reintegrating Eq. (1) for slightly different initial conditions.
Finally, for the predicted slopes in Table 6, the errors are computed using Eq. (A.1) and restricted such that
![]() (analogous to
Eq. (A.3)).
(analogous to
Eq. (A.3)).
References
- Allen, C., & Santillan, A. 1991, Rev. Mex. Astron. Astrofis., 22, 255 [NASA ADS]
- Allen, C., Moreno, E., & Pichardo, B. 2006, ApJ, 652, 1150 [NASA ADS] [CrossRef]
- Allen, C., Moreno, E., & Pichardo, B. 2008, ApJ, 674, 237 [NASA ADS] [CrossRef]
- Anderson, J., & King, I. R. 1996, in Formation of the Galactic Halo...Inside and Out, ed. H. L. Morrison, & A. Sarajedini, ASP Conf. Ser., 92, 257 (In the text)
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1997, A&A, 327, 1054 [NASA ADS] (In the text)
- Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef]
- Baumgardt, H., & Mieske, S. 2008, MNRAS, 391, 942 [NASA ADS] [CrossRef]
- Baumgardt, H., De Marchi, G., & Kroupa, P. 2008, ApJ, 685, 247 [NASA ADS] [CrossRef] (In the text)
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS]
- Boutloukos, S. G., & Lamers, H. J. G. L. M. 2003, MNRAS, 338, 717 [NASA ADS] [CrossRef]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Casares, J. 2007, in Black Holes from Stars to Galaxies - Across the Range of Masses, ed. V. Karas, & G. Matt, IAU Symp., 238, 3
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
- Chernoff, D. F., & Weinberg, M. D. 1990, ApJ, 351, 121 [NASA ADS] [CrossRef]
- Chernoff, D. F., Kochanek, C. S., & Shapiro, S. L. 1986, ApJ, 309, 183 [NASA ADS] [CrossRef] (In the text)
- Chilingarian, I. V., Cayatte, V., & Bergond, G. 2008, MNRAS, 390, 906 [NASA ADS] [CrossRef]
- Dabringhausen, J., Hilker, M., & Kroupa, P. 2008, MNRAS, 386, 864 [NASA ADS] [CrossRef]
- De Marchi, G., & Pulone, L. 2007, A&A, 467, 107 [NASA ADS] [CrossRef] [EDP Sciences]
- De Marchi, G., Paresce, F., & Pulone, L. 2007, ApJ, 656, L65 [NASA ADS] [CrossRef] (In the text)
- Dinescu, D. I., Girard, T. M., & van Altena, W. F. 1999, AJ, 117, 1792 [NASA ADS] [CrossRef]
- Evstigneeva, E. A., Gregg, M. D., Drinkwater, M. J., & Hilker, M. 2007, AJ, 133, 1722 [NASA ADS] [CrossRef]
- Forbes, D. A., Lasky, P., Graham, A. W., & Spitler, L. 2008, MNRAS, 389, 1924 [NASA ADS] [CrossRef]
- Fregeau, J. M., Richer, H. B., Rasio, F. A., & Hurley, J. R. 2009, ApJ, 695, L20 [NASA ADS] [CrossRef] (In the text)
- Gieles, M., Bastian, N., Lamers, H. J. G. L. M., & Mout, J. N. 2005, A&A, 441, 949 [NASA ADS] [CrossRef] [EDP Sciences]
- Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006, MNRAS, 371, 793 [NASA ADS] [CrossRef] (In the text)
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Gnedin, O. Y., & Ostriker, J. P. 1997, ApJ, 474, 223 [NASA ADS] [CrossRef]
- Hasegan, M., Jordán, A., Côté, P., et al. 2005, ApJ, 627, 203 [NASA ADS] [CrossRef]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] (In the text)
- Hilker, M., Baumgardt, H., Infante, L., et al. 2007, A&A, 463, 119 [NASA ADS] [CrossRef] [EDP Sciences]
- Johnston, K. V., Spergel, D. N., & Hernquist, L. 1995, ApJ, 451, 598 [NASA ADS] [CrossRef]
- Kalirai, J. S., Hansen, B. M. S., Kelson, D. D., et al. 2008, ApJ, 676, 594 [NASA ADS] [CrossRef]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] (In the text)
- Kruijssen, J. M. D. 2008, A&A, 486, L21 [NASA ADS] [CrossRef] [EDP Sciences]
- Kruijssen, J. M. D., & Lamers, H. J. G. L. M. 2008, A&A, 490, 151 [NASA ADS] [CrossRef] [EDP Sciences] (KL08)
- Kruijssen, J. M. D., & Portegies Zwart, S. F. 2009, ApJL, accepted, [arXiv:0905.3744] (In the text)
- Lamers, H. J. G. L. M., & Gieles, M. 2006, A&A, 455, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005a, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamers, H. J. G. L. M., Gieles, M., & Portegies Zwart, S. F. 2005b, A&A, 429, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamers, H. J. G. L. M., Anders, P., & De Grijs, R. 2006, A&A, 452, 131 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamers, H. J. G. L. M., Gieles, M., & Baumgardt, H. 2009, A&A, in prep. (In the text)
- Mandushev, G., Staneva, A., & Spasova, N. 1991, A&A, 252, 94 [NASA ADS] (In the text)
- Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef]
- Mieske, S., Hilker, M., Jordán, A., et al. 2008, A&A, 487, 921 [NASA ADS] [CrossRef] [EDP Sciences]
- Nomoto, K., Shigeyama, T., & Hashimoto, M. 1988, in Supernovae, Remnants, Active Galaxies, Cosmology, ed. G. Boerner, 34
- Paczynski, B. 1990, ApJ, 348, 485 [NASA ADS] [CrossRef]
- Pichardo, B., Martos, M., & Moreno, E. 2004, ApJ, 609, 144 [NASA ADS] [CrossRef]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, ed. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357 (In the text)
- Rejkuba, M., Dubath, P., Minniti, D., & Meylan, G. 2007, A&A, 469, 147 [NASA ADS] [CrossRef] [EDP Sciences]
- Richer, H. B., Fahlman, G. G., Buonanno, R., et al. 1991, ApJ, 381, 147 [NASA ADS] [CrossRef] (In the text)
- Takahashi, K., & Portegies Zwart, S. F. 2000, ApJ, 535, 759 [NASA ADS] [CrossRef]
- Vandenberg, D. A., Bolte, M., & Stetson, P. B. 1990, AJ, 100, 445 [NASA ADS] [CrossRef] (In the text)
- Vesperini, E., & Heggie, D. C. 1997, MNRAS, 289, 898 [NASA ADS]
Footnotes
- ... isochrones
![[*]](/icons/foot_motif.png)
- These isochrones are based on Bertelli et al. (1994), but use the AGB treatment as in Girardi et al. (2000).
- ... relation
![[*]](/icons/foot_motif.png)
- For white dwarfs, this relation is taken from Kalirai et al. (2008), while for neutron stars the relation from Nomoto et al. (1988) is used. Black hole masses are assumed to be constant at
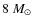 ,
in agreement with observations (Casares 2007). For more details, see KL08.
,
in agreement with observations (Casares 2007). For more details, see KL08.
- ... environment
![[*]](/icons/foot_motif.png)
- Please note that a Kroupa IMF was assumed here. For substantially different IMFs the relation will vary.
- ... field
![[*]](/icons/foot_motif.png)
- This includes the effect of bulge shocks, which occur in clusters on eccentric orbits.
- ... earlier
![[*]](/icons/foot_motif.png)
- Consequently, it represents the same uncertainty as
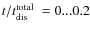 ,
with
,
with
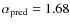 corresponding to
corresponding to
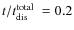 and
and
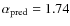 to
to
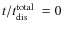 .
Since for most GCs under consideration the elapsed fractions of the total disruption time are closer to
.
Since for most GCs under consideration the elapsed fractions of the total disruption time are closer to
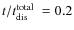 than to
than to
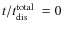 (see Table 4), we adopt
(see Table 4), we adopt
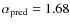 if
if
 .
.
- ... ratios
![[*]](/icons/foot_motif.png)
- Of course, if the preferential loss of low-mass stars is accounted for, i.e., non-canonical models are considered, the SPACE cluster models predict very different photometric evolution than canonical cluster models such as Bruzual & Charlot (2003).
All Tables
Table 1:
Observed properties for the cluster sample, together with their ![]() standard errors.
standard errors.
Table 2:
Orbital parameters for the cluster sample, together with their ![]() standard errors.
standard errors.
Table 3:
Computed dissolution timescales (for
![]() )
due to two-body relaxation (
)
due to two-body relaxation (
![]() ), disc shocking (
), disc shocking (
![]() )
and both mechanisms (
)
and both mechanisms (
![]() ), together with their
), together with their ![]() standard errors. All values are rounded to one decimal.
standard errors. All values are rounded to one decimal.
Table 4:
Our model predictions with their ![]() standard errors.
standard errors.
Table 5:
Coefficients for the fourth-order powerlaw approximation of
![]() as a function of
as a function of
![]() (see Eq. (16)).
(see Eq. (16)).
Table 6:
Observed and predicted stellar mass function (MF) slopes ![]() in the range m=0.3-
in the range m=0.3-
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f1a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f1b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg172.png) |
Figure 1:
Left: observed mass-to-light ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f2.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg189.png) |
Figure 2:
Left: V-band mass-to-light ratio evolution M/LV for t0=1 Myr, Z=0.0004 and initial masses in the range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f3.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg196.png) |
Figure 3:
The ratio of predicted to canonical mass-to-light ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f4.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg198.png) |
Figure 4:
Cluster evolution in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f5.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg294.png) |
Figure 5:
Top left: time-evolution of M/LV for NGC 5466. The solid line represents the Z=0.0004 model with the dissolution timescale of the cluster (t0=10.2 Myr), while the dotted curve indicates the canonical M/LV evolution, i.e., if the preferential loss of low-mass stars were omitted. The dashed line denotes constant age of t=12 Gyr. The predicted M/LV of NGC 5466 is marked by a cross and the onset of the preferential loss of low-mass stars is specified with a dot. Top right: evolution in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f6.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg418.png) |
Figure 6:
Observed (crosses) and predicted (triangles) distribution of GCs in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f7a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f7b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg425.png) |
Figure 7:
Left: observed mass-to-light ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1453f8a.ps}\hspace*{1.5cm}
\includegraphics[width=9cm,clip]{1453f8b.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg431.png) |
Figure 8:
Left: the ratio of the observed mass-to-light ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1453f9.ps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg444.png) |
Figure 9:
Correlation between the observed slope of the low-mass stellar mass function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1453f10a.eps}\hspace*{0.6cm}
\includegraphics[width=8.3cm,clip]{1453f10b.eps}
\end{figure}](/articles/aa/full_html/2009/23/aa11453-08/Timg493.png) |
Figure 10:
Feasibility of observational tests of low-mass star depletion. Left: for the 24 GCs investigated in this paper, the apparent V-band magnitude of stars with 0.3 solar masses V0.3 is plotted versus the predicted slope
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



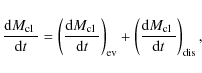
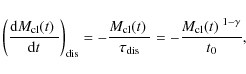
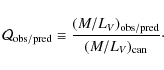
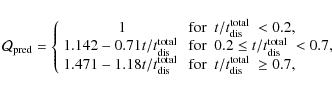
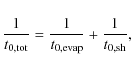
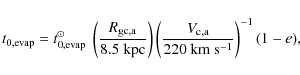
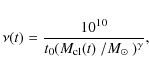

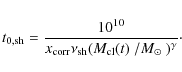
![\begin{displaymath}%
Z = Z_\odot\times 10^{\rm [Fe/H]},
\end{displaymath}](/articles/aa/full_html/2009/23/aa11453-08/img292.png)
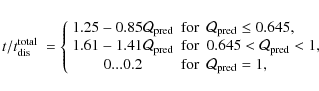

![\begin{displaymath}%
\sigma_{M/L_V}^{+,M,t_0} = {\rm min}\left[\bar{\sigma}_{M/L_V}^{+,M,t_0},(M/L_V)_{\rm can}-(M/L_V)_{\rm pred}\right],
\end{displaymath}](/articles/aa/full_html/2009/23/aa11453-08/img509.png)