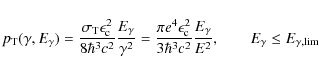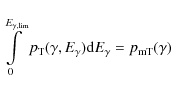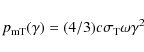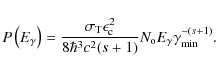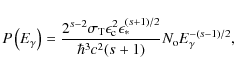| Issue |
A&A
Volume 499, Number 3, June I 2009
|
|
|---|---|---|
| Page(s) | 643 - 648 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200811596 | |
| Published online | 08 April 2009 | |
Approximation of the radiation power of electrons due to the inverse-Compton process in the black-body photon field
(Research Note)
O. Petruk
Institute for Applied Problems in Mechanics and Mathematics, Naukova St. 3-b, Lviv 79060, Ukraine
Received 25 December 2008 / Accepted 25 February 2009
Abstract
Aims. An approximation is presented for the inverse-Compton radiation power of electrons in the isotropic black-body photon field.
Methods. This approximation allows calculation of the inverse-Compton emissivity as an integral over the energies of incident electrons rather than over the field photon energies. Such an approach allows for accurate modeling of IC emission of electrons with energy spectra different from power law, in tasks where essential CPU resources are needed.
Results. The high accuracy of this approximation allows it to be used in a wide range of conditions, from Thomson to extreme Klein-Nishina limits, in different astrophysical objects. This approach also results in some new analytic expressions representing the known results in the Thomson limit.
Key words: radiation mechanisms: non-thermal - gamma rays: theory
1 Introduction
Inverse Compton (IC) electron-photon interactions are among the most important processes in gamma-ray production in many astrophysical objects. It is (or may be) important in, e.g., diffuse gamma-ray emission from the Galaxy, galaxy clusters, gamma-ray production in supernova remnants (SNRs), pulsar-wind nebulae, or in the case of the IC pair cascade processes in the isotropic radiation field, i.e. propagation of gamma-rays over cosmological distances.
Cherenkov detectors open an era of imaging gamma-ray astronomy. Surface brightness distribution of gamma-ray emission of astrophysical objects, in addition to the broad-band spectrum, offers an important possibility of testing models of kinetics of astroparticles, as well as the dynamics of magnetic field and turbulence in astrophysical plasmas. Thus, an important task appears to model the respective gamma-ray maps. Applying the exact formalism of IC emission to such a problem requires, in most cases, essential CPU resources and simulations result therefore simulations therefore lead to very long computations even with the use of modern powerful PC clusters. In such a situation, an accurate approximation may be useful because it considerably reduces CPU time (and also results in some new formulae in classical analysis, see Sects. 2.2 and 2.3 below).
A common approach is to deal with IC emissivity for a given energy of the initial (monochromatic) photons (e.g. Jones 1968; Blumenthal & Gould 1970) with assumption of a given a priori shape of the electron spectrum, power law as a common choice. The resulting IC photon spectrum is then given by the integration over the energy distribution of the field photons. Such an approach is essential for special cases of the energy distribution of the field photons.
It is known, however, that the conditions when the IC gamma-ray photons are produced by relativistic electrons propagating in the isotropic blackbody radiation field are often met in astrophysical sources. In particular, for SNRs under typical conditions, one may just consider black-body photons, with a few different temperatures representing CMB/IR/optical radiation. Even more, in SNRs not assosiated with IR emission, the contribution from CMB photons takes over the role of infrared and optical photons (see discussion in Appendix in Lazendic et al. 2004). The IR/optical photon fields may typically contribute 10-15% of the IC flux in such SNRs (Gaisser et al. 1998; Baring et al. 1999). Similar situations are found in other astrophysical environments, too.
On the other hand, the shape of the electron spectrum at energies that are important for IC gamma-ray emission may differ considerably from a power law, especially, if one considers the emission of electrons with energy E around maximum possible values.
It is known that contribution from electrons accelerated by the SNR shock to
![]() TeV is important for interpreting the HESS observations of shell SNRs. The shape of the end of an electron spectrum is commonly assumed to be maximally curved
TeV is important for interpreting the HESS observations of shell SNRs. The shape of the end of an electron spectrum is commonly assumed to be maximally curved
![]() .
Some observational and theoretical evidence suggests that the shape is broader around cut-off,
.
Some observational and theoretical evidence suggests that the shape is broader around cut-off,
![]() with
with
![]() ,
at least in SN 1006 and G347.3-0.5 (Ellison et al. 2000, 2001; Uchiyama et al. 2003; Lazendic et al. 2004). This broadening is not an artifact of observation, e.g. from superposition of local spectra along the line of sight, but most probably an internal property caused by processes at the acceleration site (Petruk 2006).
,
at least in SN 1006 and G347.3-0.5 (Ellison et al. 2000, 2001; Uchiyama et al. 2003; Lazendic et al. 2004). This broadening is not an artifact of observation, e.g. from superposition of local spectra along the line of sight, but most probably an internal property caused by processes at the acceleration site (Petruk 2006).
Nonlinear acceleration theory predicts the concave shape of the electron spectrum, i.e.
varying spectral index:
![]() where p is momentum. The function
where p is momentum. The function
![]() monotonically decreases from
monotonically decreases from ![]() at the low-energy end of the spectrum of nonthermal electrons to
at the low-energy end of the spectrum of nonthermal electrons to ![]() around
around
![]() (Berezhko & Ellison 1999).
(Berezhko & Ellison 1999).
Also, the interplay between the synchrotron and IC energy losses can play an essential role in modifying the electron energy spectrum, especially in situations when the ratio of the ambient radiation field to source's magnetic-field energy density, significantly exceeds unity (Moderski et al. 2005). In such a situation, the Klein-Nishina decline may cause the electron spectrum to harden starting from some energy that results in a bump around the cut-off energy. This effect may not be significant for a ``typical'' SNR, like SN 1006, because the
energy density of magnetic field of the strength
![]() is much higher than the energy density of initial photons. (The magnetic field strength with energy density equal to that in the CMB is
is much higher than the energy density of initial photons. (The magnetic field strength with energy density equal to that in the CMB is
![]() .) However, for SNRs in radiation-dominated environments (e.g. in the Galactic center), the implications of this effect may be important (Vannoni et al. 2009).
.) However, for SNRs in radiation-dominated environments (e.g. in the Galactic center), the implications of this effect may be important (Vannoni et al. 2009).
This effect of the Klein-Nishina reduction also influences nonthermal radiation from blazars, micro-quasars, pulsar binaries, and clusters of galaxies (Moderski et al. 2005; Moderski & Sikora 2005; Vannoni et al. 2009).
In this note, we present an approximation for IC emissivity that may be applied to IC emission originating from the isotropic black-body photon field with temperature T. Our approximation is given in terms of an energy of incident electrons rather than in the commonly used terms of the field photon energy. Such an approach gives the possibility of accurately modeling IC emission of electrons with energy spectra different from power law, a situation often appearing in astrophysical objects.
Since the temperature of the initial photons T is a parameter in our approach, our approximation may be used for calculating IC radiation from different photon fields (CMB, IR, optical). The target radiation field in some circumstances (e.g. around Galactic center) may not be black-body and/or the contribution from IR/optical photons may dominate CMB there (Porter et al. 2006; Hinton & Aharonian 2007). In cases where the different components of the target radiation field may be approached by a superposition of multiple Planck distributions with different T, our approximation may be used in a similar fashion. The overall IC emission will be the weighted sum of single approximations, each with a different value for the temperature. In cases where the initial radiation field may not be approximately described by a sum of black-body distributions, our formulae do not apply.
Another assumption in the present paper is the isotropy of the electron and photon fields. A thorough treatment of anisotropic IC scattering from cosmic-ray electrons is done by Moskalenko & Strong (2000).
2 Approximation
The spectral distribution of the volume emissivity of (isotropically distributed) electrons due to the IC process is (Jones 1968; Blumenthal & Gould 1970; Schlickeiser 2002)
where
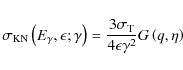 |
(2) |
is the angle-integrated IC cross-section,
and
The last term in G reflects the Klein-Nishina decline; recoil is embedded in the q parameter. The KN effect is more important than recoil for
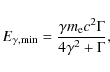 |
(5) |
that simplifies to
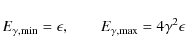 |
(7) |
in Thomson limit (
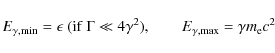 |
(8) |
in extreme Klein-Nishina limit (
electron should have in order to scatter photon with energy
(The Klein-Nishina decline is negligible for
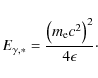 |
(11) |
2.1 Method of approximation
In some astrophysical environments, the initial photon field may well be represented by the isotropic black-body radiation
with
Let us re-write Eq. (1) in the form
where the spectral distribution of IC radiation power of a ``single'' electron with Lorenz factor
with the function
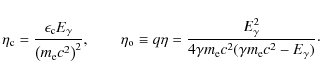 |
(16) |
Let us introduce
| (17) |
| (18) |
In the limit
| (19) |
The minimum value of
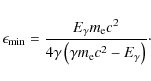 |
(20) |
In the limit
With decreasing
| (22) |
The integral
where the dilogarithm function
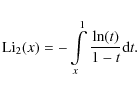 |
(24) |
An accurate approximation of (23) is
This expression restores
The original integral ![]() has an important property, because it may be split as
has an important property, because it may be split as
![]() with
with
where
The possibility of scaling these integrands (integral
Using
![]() in the scale laws (28), one has
in the scale laws (28), one has
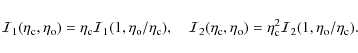 |
(29) |
This means that it is enough to check how accurate approximate expressions will be in approximation of just
Let us slightly correct exponential part in each terms of (25) by introducing into the exponents the second terms of the form
![]() where c1 and c2 are constant. These terms make (25) more accurate in the representation of
where c1 and c2 are constant. These terms make (25) more accurate in the representation of
![]() and
and
![]() .
It is important that the terms are also scaled with (28). With these corrections, we come to approximations
.
It is important that the terms are also scaled with (28). With these corrections, we come to approximations
The values of c1 and c2 are obtained by fitting the exact
The scaling property is a reason that the sum of approximations (30) and (31)
is accurate to represent
Equation (32) is good for any
![]() .
We may suggest two simpler approximations for different ranges of
.
We may suggest two simpler approximations for different ranges of
![]() .
If mostly interested in
.
If mostly interested in
![]() (e.g. the case of IC emission of electrons accelerated by the forward shock in SNRs), then one can use an expression
(e.g. the case of IC emission of electrons accelerated by the forward shock in SNRs), then one can use an expression
Figure 2 shows that the second term here (the one proportional to
Figure 4 shows the accuracy of Eq. (33) in approximation of emission power (14) for electrons with energies
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figa.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg109.png) |
Figure 1:
The accuracy of the approximation (32) as the sum
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figb.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg110.png) |
Figure 2:
Accuracy of approximation (33). Integrals |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figc.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg111.png) |
Figure 3:
Accuracy of approximation (34). Integrals |
| Open with DEXTER | |
2.2 ``Delta-function'' approximation
Figure 4 demonstrates that a ``single'' electron with Lorentz factor ![]() - being scattered by all black-body photons - emits most of its IC radiation at photons with some characteristic energy
- being scattered by all black-body photons - emits most of its IC radiation at photons with some characteristic energy
![]() .
One can introduce a ``delta-function approximation'', in addition to the classical ``monochromatic approximation'' where the electron is scattered by the photons with a fixed energy
.
One can introduce a ``delta-function approximation'', in addition to the classical ``monochromatic approximation'' where the electron is scattered by the photons with a fixed energy
![]() (e.g. Schlickeiser 2002). One can namely assume that a ``single'' electron (scattered by all black-body photons) emits all of its IC power at photons with
(e.g. Schlickeiser 2002). One can namely assume that a ``single'' electron (scattered by all black-body photons) emits all of its IC power at photons with
![]() :
:
where
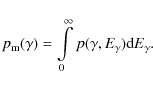 |
(36) |
There are well known approximations for the total IC energy loss
Our numerical calculations show (Fig. 4) that
![]() may be approximated by
may be approximated by
| (37) |
where
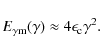 |
(38) |
In the classical ``monochromatic approximation'' (e.g. Schlickeiser 2002), the average
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figd.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg124.png) |
Figure 4:
The spectrum
|
| Open with DEXTER | |
2.3 Thomson limit
The use of (21) in (14) allows us to write down the expression for IC emissivity in the Thomson limit
![]() .
The spectral distribution of IC radiation power of a ``single'' electron with energy
.
The spectral distribution of IC radiation power of a ``single'' electron with energy
![]() is
is
where
The power
![]() is the increasing function of
is the increasing function of
![]() ,
while
,
while
![]() decreases rather rapidly after the maximum (Fig. 4).
We define an energy
decreases rather rapidly after the maximum (Fig. 4).
We define an energy
![]() by the condition
by the condition
where
is the total energy loss of electron due to IC in the Thomson limit, and
![\begin{displaymath}%
E_{{\rm\gamma,lim}}=\frac{4}{\pi}\epsilon_{{\rm c}}\gamma^2...
...}z}{\exp(z)-1} \right]^{1/2}
=2.65\epsilon_{{\rm c}}\gamma^2.
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img133.png) |
(42) |
Note that
The volume emissivity of electrons distributed as
is
For
with the known slope
![\begin{displaymath}%
{\cal A}(s)=\left[
\frac{12}{\pi^2}\frac{(s^2+4s+11)}{(s+5...
...\frac{z^{(s+3)/2} {\rm d}z}{\exp(z)-1}
\right]^{2/(s+1)}\cdot
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img143.png) |
(46) |
Numerically,
3 Conclusions
Numerical evaluation of the spatial distribution of the IC emission (e.g. in SNRs) requires essential computational resources because the IC volume emissivity (1) consists in two enclosed integrations (over initial photon and electron energies).
We developed the approximation (32) of the spectral distribution of the IC emission power
![]() of electrons with Lorentz factor
of electrons with Lorentz factor ![]() ,
which are interacting with the isotropic black-body photon field. Equation (32) restores the known results (Blumenthal & Gould 1970) with sufficient accuracy in any regime, from Thomson to extreme Klein-Nishina limits. It may be used for different astrophysical objects, from pulsar wind nebulae to clusters of galaxies. For
,
which are interacting with the isotropic black-body photon field. Equation (32) restores the known results (Blumenthal & Gould 1970) with sufficient accuracy in any regime, from Thomson to extreme Klein-Nishina limits. It may be used for different astrophysical objects, from pulsar wind nebulae to clusters of galaxies. For
![]() ,
e.g. for IC
,
e.g. for IC ![]() -ray emission from electrons accelerated by the forward shock of SNRs, it is suitable to use a simpler approximation (33). In the Thomson limit, our approach results in a simple expression (39).
-ray emission from electrons accelerated by the forward shock of SNRs, it is suitable to use a simpler approximation (33). In the Thomson limit, our approach results in a simple expression (39).
Our approximation may be used in situations where the initial radiation field may be approximated with the Planck function with some temperature T or when it may be represented by a superposition of the black-body distributions with different T. In addition, it assumes the isotropy of electron and photon fields.
The approximation is given in terms of an energy of incident electrons rather than in terms of the field photon energy. (There are known approximations for the latter approach, see e.g. Schlickeiser 2002.) Therefore, our approximation may be useful for analysing the role of the electron spectrum with shapes that differ from the power law.
The main idea behind our approach is the possibility of splitting the initial integral into two parts that may be scaled, contrary to the original integral. This scaling is the reason for the accuracy of the approximation over the wide range of parameters, from the Thomson to extreme Klein-Nishina regime.
There is a well known ``monochromatic approximation'' where an electron is scattered by the monochromatic photons with energy
![]() (e.g. Schlickeiser 2002). Figure 4 shows that the spectral distribution of the radiation power of a ``single'' electron with Lorentz factor
(e.g. Schlickeiser 2002). Figure 4 shows that the spectral distribution of the radiation power of a ``single'' electron with Lorentz factor ![]() scattered by photons distributed with the Planck function peaks at energy
scattered by photons distributed with the Planck function peaks at energy
![]() .
This allows us to introduce - as for the case of synchrotron emission - the ``delta-function'' approximation for IC emission. In this approximation, Eq. (35), all radiated energy of electron is assumed to be at
.
This allows us to introduce - as for the case of synchrotron emission - the ``delta-function'' approximation for IC emission. In this approximation, Eq. (35), all radiated energy of electron is assumed to be at
![]() .
In the Thomson limit,
.
In the Thomson limit,
![]() where
where
![]() .
In the classical ``monochromatic approximation'' (where electrons meet monochromatic photons with energy
.
In the classical ``monochromatic approximation'' (where electrons meet monochromatic photons with energy
![]() ), the average
), the average
![]() is used as an estimator for the energy of emitted IC photons.
is used as an estimator for the energy of emitted IC photons.
Our approach results in some new expressions that represent known results. Equation (39) yields the spectral distribution of IC radiation power of a ``single'' electron and Eq. (45) represents the spectrum of IC emission from the power-law spectrum of electrons in the Thomson limit. These expression account for integration over all possible energies of the seed black-body photons. They can be derived thanks to the possibility of analytical integration of ![]() in the Thomson regime, Eq. (21).
in the Thomson regime, Eq. (21).
References
- Baring, M. G., Ellison, D. C., Reynolds, S. P., Grenier, I. A., & Goret, P. 1999, ApJ, 513, 311 [NASA ADS] [CrossRef] (In the text)
- Berezhko, E., & Ellison, D. 1999, ApJ, 526, 385 [NASA ADS] [CrossRef] (In the text)
- Blumenthal, G., & Gould, R. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
- Ellison, D. C., Berezhko, E. G., & Baring, M. G. 2000, ApJ, 540, 292 [NASA ADS] [CrossRef] (In the text)
- Ellison, D. C., Slane, P., & Gaensler, B. M. 2001, ApJ, 563, 191 [NASA ADS] [CrossRef] (In the text)
- Gaisser, T. K., Protheroe, R. J., & Stanev, T. 1998, ApJ, 492, 219 [NASA ADS] [CrossRef] (In the text)
- Hinton, J. A., & Aharonian, F. A. 2007, ApJ, 657, 302 [NASA ADS] [CrossRef] (In the text)
- Jones, F. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] (In the text)
- Lazendic, J. S., Slane, P. O., Gaensler, B. M., et al. 2004, ApJ, 602, 271 [NASA ADS] [CrossRef] (In the text)
- Moderski, R., & Sikora, M. 2005, Ap&SS, 297, 369 [NASA ADS] [CrossRef] (In the text)
- Moderski, R., Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNRAS, 363, 954 [NASA ADS] [CrossRef] (In the text)
- Moskalenko, I. V., & Strong, A. W. 2000, ApJ, 528, 357 [NASA ADS] [CrossRef] (In the text)
- Petruk, O. 2006, A&A, 460, 375 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Springer) (In the text)
- Uchiyama, Y., Aharonian, F. A., & Takahashi, T. 2003, A&A, 400, 567 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vannoni, G., Gabici, S., & Aharonian, F. 2009, A&A, 497, 17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figa.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg109.png) |
Figure 1:
The accuracy of the approximation (32) as the sum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figb.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg110.png) |
Figure 2:
Accuracy of approximation (33). Integrals |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figc.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg111.png) |
Figure 3:
Accuracy of approximation (34). Integrals |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1596figd.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11596-08/Timg124.png) |
Figure 4:
The spectrum
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



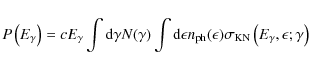
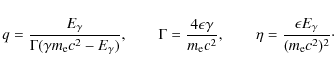
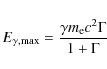
![\begin{displaymath}%
\gamma_{{\rm\min}}=\frac{E_{{\rm\gamma}}}{2m_{{\rm e}}c^2}
...
...{{\rm e}}c^2)^2}{\epsilon E_{{\rm\gamma}}}\right)^{1/2}\right]
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img43.png)
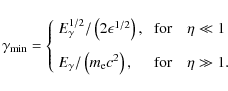
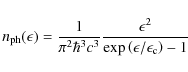
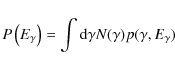
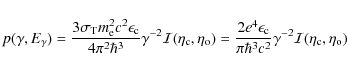
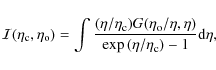
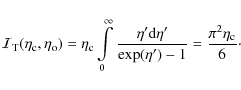
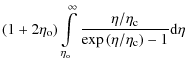
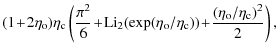
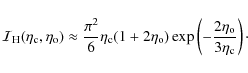
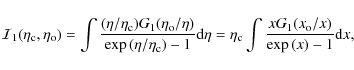
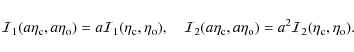
![\begin{displaymath}%
{\cal I}_1\approx \frac{\pi^2}{6}\eta_{{\rm c}}
\exp\left[...
...eft(\frac{\eta_{{\rm o}}}{\eta_{{\rm c}}}\right)^{1/2}\right],
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img96.png)
![\begin{displaymath}%
{\cal I}_2\approx
\frac{\pi^2}{3}\eta_{{\rm c}}
\eta_{{...
...\frac{\eta_{{\rm o}}}{\eta_{{\rm c}}}\right)^{0.7}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img97.png)
![$\displaystyle \frac{\pi^2}{6}\eta_{{\rm c}} \left(
\exp\left[-\frac{5}{4}\left(\frac{\eta_{{\rm o}}}{\eta_{{\rm c}}}\right)^{1/2}\right]
\right.$](/articles/aa/full_html/2009/21/aa11596-08/img100.png)
![$\displaystyle \displaystyle\left.
+2\eta_{{\rm o}}
\exp\left[-\frac{5}{7}\left(...
...^{0.7}\right]
\right)
\exp\left[-\frac{2\eta_{{\rm o}}}{3\eta_{{\rm c}}}\right]$](/articles/aa/full_html/2009/21/aa11596-08/img101.png)
![\begin{displaymath}%
{\cal I}(\eta_{{\rm c}},\eta_{{\rm o}})\approx
\frac{\pi^...
...\frac{\eta_{{\rm o}}}{\eta_{{\rm c}}}\right)^{1/2}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img103.png)
![\begin{displaymath}%
{\cal I}(\eta_{{\rm c}},\eta_{{\rm o}})\approx
\frac{\pi^...
...\frac{\eta_{{\rm o}}}{\eta_{{\rm c}}}\right)^{0.7}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/21/aa11596-08/img107.png)