| Issue |
A&A
Volume 499, Number 3, June I 2009
|
|
|---|---|---|
| Page(s) | 923 - 934 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200811559 | |
| Published online | 16 April 2009 | |
Response of optical hydrogen lines to beam heating
I. Electron beams
J. Kasparová1 - M. Varady2,1 - P. Heinzel1 - M. Karlický1 - Z. Moravec2
1 - Astronomický ústav Akademie ved Ceské republiky, v.v.i., Fricova 298,
251 65 Ondrejov, Czech Republic
2 -
Katedra fyziky, Universita J. E. Purkyne, Ceské mládeze 8,
400 24 Ústí nad Labem, Czech Republic
Received 20 December 2008 / Accepted 27 March 2009
Abstract
Context. Observations of hydrogen Balmer lines in solar flares remain an important source of information on flare processes in the chromosphere during the impulsive phase of flares. The intensity profiles of optically thick hydrogen lines are determined by the temperature, density, and ionisation structure of the flaring atmosphere, by the plasma velocities and by the velocity distribution of particles in the line formation regions.
Aims. We investigate the role of non-thermal electrons in the formation regions of H![]() ,
H
,
H![]() ,
and H
,
and H![]() lines in order to unfold their influence on the formation of these lines. We concentrate on pulse-beam heating varying on a subsecond timescale. Furthermore, we theoretically explore possibility that a new diagnostic tool exists indicating the presence of non-thermal electrons in the flaring chromosphere based on observations of optical hydrogen lines.
lines in order to unfold their influence on the formation of these lines. We concentrate on pulse-beam heating varying on a subsecond timescale. Furthermore, we theoretically explore possibility that a new diagnostic tool exists indicating the presence of non-thermal electrons in the flaring chromosphere based on observations of optical hydrogen lines.
Methods. To model the evolution of the flaring atmosphere and the time-dependent hydrogen excitation and ionisation, we used a 1-D radiative hydrodynamic code combined with a test-particle code that simulates the propagation, scattering, and thermalisation of a power-law electron beam in order to obtain the flare heating and the non-thermal collisional rates due to the interaction of the beam with the hydrogen atoms. To not bias the results by other effects, we calculate only short time evolutions of the flaring atmosphere and neglect the plasma velocities in the radiative transfer.
Results. All calculated models have shown a time-correlated response of the modelled Balmer line intensities on a subsecond timescale, with a subsecond timelag behind the beam flux. Depending on the beam parameters, both line centres and wings can show pronounced intensity variations. The non-thermal collisional rates generally result in an increased emission from a secondary region formed in the chromosphere.
Conclusions. Despite the clear influence of the non-thermal electron beams on the Balmer line intensity profiles, we were not able on the basis of our simulations to produce any unambiguous diagnostic of non-thermal electrons in the line-emitting region, which would be based on comparison of individual Balmer line intensity profiles. However, fast line intensity variations, well-correlated with the beam flux variations, represent an indirect indication of pulsating beams.
Key words: Sun: flares - radiative transfer - hydrodynamics - line: formation - line: profiles
1 Introduction
In the context of interpreting flare loop hard X-ray footpoint sources (Hudson & Fárník 2002; Hoyng et al. 1981), all contemporary flare models (Fletcher & Hudson 2008; Sturrock 1968; Turkmani et al. 2005; Kopp & Pneuman 1976; Shibata 1996), regardless of their nature, assign a fundamental role during the flare energy release, transport and deposition to the high-energy non-thermal particle beams. In the impulsive phase of flares, the beams formed by charged particles are also guided from the acceleration site (wherever it is located) downwards along the magnetic field lines into the transition region, chromosphere and possibly photosphere. At lower atmospheric layers due to the high density of local plasma, their kinetic energy is efficiently dissipated by Coulomb collisions, the corresponding regions are rapidly heated, and dramatic changes of temperature and ionisation occur. This results in explosive evaporation (Doschek et al. 1996). The manifestations of the early flare processes can be observed in the microwaves, soft and hard-X rays, and optical lines (Tandberg-Hanssen & Emslie 1988). Later on in the thermal (gradual) phase, the heating leads to the evaporation of chromospheric and transition region plasma into the corona which is gradually filled with relatively dense (up to
We concentrate on modelling the formation of optically thick hydrogen spectral
lines H![]() ,
H
,
H![]() ,
and H
,
and H![]() in the early phases of solar flares by
the means of
numerical radiative hydrodynamics combined with a test particle approach to
simulate the propagation, scattering and energy loss of an electron beam with
the power-law spectrum and prescribed time-dependent energy flux
propagating through the solar atmosphere and depositing its energy into the
solar plasma. In this context we address three main questions:
in the early phases of solar flares by
the means of
numerical radiative hydrodynamics combined with a test particle approach to
simulate the propagation, scattering and energy loss of an electron beam with
the power-law spectrum and prescribed time-dependent energy flux
propagating through the solar atmosphere and depositing its energy into the
solar plasma. In this context we address three main questions:
- 1.
- Does rapidly varying electron beam flux manifest itself in the Balmer line intensities?
- 2.
- How do the non-thermal particles in the Balmer lines formation regions influence the line profiles and intensities?
- 3.
- Can an unambiguous diagnostic method be developed that is applicable to observations of Balmer lines recognising the presence of the non-thermal particles in the line formation regions?
In this paper we concentrate on fast time variations on a subsecond time scale.
In previous works on this topic, plasma dynamics was neglected. Simplified
time-dependent non-LTE
simulations of H![]() line were then performed e.g. by
using a prescribed time evolution of a flare atmosphere from independent hydrodynamic simulations
of pulse-beam heating (Heinzel 1991) or by solving approximate energy equation (Ding et al. 2001).
Both results showed significant H
line were then performed e.g. by
using a prescribed time evolution of a flare atmosphere from independent hydrodynamic simulations
of pulse-beam heating (Heinzel 1991) or by solving approximate energy equation (Ding et al. 2001).
Both results showed significant H![]() line response to pulse-beam heating on subsecond time scales.
Here, we solve 1-D radiative hydrodynamics of a solar atmosphere subjected to a subsecond electron beam heating
and study emissions in the H
line response to pulse-beam heating on subsecond time scales.
Here, we solve 1-D radiative hydrodynamics of a solar atmosphere subjected to a subsecond electron beam heating
and study emissions in the H![]() ,
H
,
H![]() ,
and H
,
and H![]() lines.
lines.
The paper is organised as follows: Sect. 2 describes the numerical code and models of beam heating. Results of simulations concerning flare atmosphere dynamics and Balmer line emission are presented in Sect. 3. There, we also analyse several proposed diagnostic methods for recognising the presence of electron beams in line formation regions. Section 4 summarises our results.
2 Model
The model covers three important classes of processes whose importance was identified in flares:
- 1.
- propagation of charged, high-energy particle beams with power-law spectra and time-dependent energy flux downwards through the solar atmosphere and their gradual thermalisation due to the Coulomb collisions with the ambient plasma in the solar atmosphere (Emslie 1978; Bai 1982).
- 2.
- the hydrodynamic response of low-
 solar plasma corresponding
to the energy deposited by the beam.
solar plasma corresponding
to the energy deposited by the beam.
- 3.
- time evolution of the ionisation structure and formation of optical emission in the chromosphere and photosphere where non-LTE conditions apply.
2.1 Flare heating
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1559f1a.eps}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{1559f1b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg23.png) |
Figure 1:
Time modulations of the beam flux. Solid lines show g(t),
dotted lines denote
|
| Open with DEXTER | |
The flare heating caused by an electron beam propagating from
the top of the loop located in the corona (
![]() km
corresponding to T=1 MK)
downwards is calculated using a test-particle code (TPC) based on
Karlický (1990); Karlický & Hénoux (1992). We assume an electron beam with a power-law
electron flux spectrum [electrons cm-2 s-1 per unit energy]
(Nagai & Emslie 1984)
km
corresponding to T=1 MK)
downwards is calculated using a test-particle code (TPC) based on
Karlický (1990); Karlický & Hénoux (1992). We assume an electron beam with a power-law
electron flux spectrum [electrons cm-2 s-1 per unit energy]
(Nagai & Emslie 1984)
where
where t1 is the duration of the energy deposit. The energy fluxes
Table 1: Model parameters.
The TPC simulates the propagation, scattering and energy loss of an electron beam with a specified energy flux and power-law index as it propagates through partly ionised hydrogen plasma in the solar atmosphere. The losses of the beam electron kinetic energy caused by Coulomb collisions due to electron and neutral (hydrogen) components of solar plasma are given by Emslie (1978)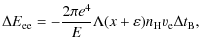 |
(3) | ||
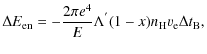 |
(4) |
where E is the kinetic energy of the non-thermal electron,
The scattering of the beam due to Coulomb collisions is taken into account
using a Monte-Carlo method combined with the analytical expressions for the
cumulative effects described by Bai (1982). The relation between the mean square of the beam
electron deflection angle
![]() and the corresponding energy loss
and the corresponding energy loss ![]() (which holds if
(which holds if
![]() or equivalently if
or equivalently if
![]() )
is given by formula
)
is given by formula
where
| (6) |
where
The TPC in principle follows the motion of statistically
important number of test particles representing clusters of electrons
in the time varying atmosphere which responses through the 1-D HD code and
the non-LTE radiative transfer code to the flare heating by TPC.
The test particles with a time-dependent power-law spectra are
generated in the corona at the loop-top and at
each timestep the positions, energies and pitch angles
of the particle clusters are calculated.
The macroscopic energy deposits into the electron
![]() and neutral hydrogen
and neutral hydrogen
![]() component of solar plasma are
obtained by summing the energy losses (
component of solar plasma are
obtained by summing the energy losses (
![]() and
and
![]() )
of a huge number of particle clusters for each position in the atmosphere using a fine
equidistant grid.
This approach allows not only to
calculate the total flare heating
)
of a huge number of particle clusters for each position in the atmosphere using a fine
equidistant grid.
This approach allows not only to
calculate the total flare heating
but also to distinguish between the beam energy deposited into the electron and hydrogen component of solar plasma and therefore to calculate the non-thermal contribution to the transition rates in hydrogen atoms which is the crucial point for the present study. The test-particle approach used here naturally takes into account propagation effects of the beam and time evolution of ionisation structure of the atmosphere. This leads us to a more realistic description of beam energy losses as compared to the approach of Abbett & Hawley (1999) or Allred et al. (2005) who used an analytic heating function corresponding to a stationary solution of beam propagation through the atmosphere (Hawley & Fisher 1994).
2.2 1-D plasma dynamics
The state and time evolution of originally hydrostatic low-![]() plasma
along magnetic field lines is calculated using a 1-D hydrodynamic code.
The temperature, density and ionisation profiles of the initial atmosphere
correspond to the VAL 3C atmosphere (Vernazza et al. 1981) with a hydrostatic
extension into the corona.
The half-length of the loop is 10 Mm.
The time evolution of the atmosphere is initiated by the energy deposited by
the beam. The main processes that determine plasma evolution in flare loops
are: convection and conduction (both in 1-D due to the magnetic field),
radiative losses and indeed the dominant factor is the flare heating here
calculated by the TPC. The evolution of plasma in the flare loop can be
described by a system of hydrodynamic conservation laws
plasma
along magnetic field lines is calculated using a 1-D hydrodynamic code.
The temperature, density and ionisation profiles of the initial atmosphere
correspond to the VAL 3C atmosphere (Vernazza et al. 1981) with a hydrostatic
extension into the corona.
The half-length of the loop is 10 Mm.
The time evolution of the atmosphere is initiated by the energy deposited by
the beam. The main processes that determine plasma evolution in flare loops
are: convection and conduction (both in 1-D due to the magnetic field),
radiative losses and indeed the dominant factor is the flare heating here
calculated by the TPC. The evolution of plasma in the flare loop can be
described by a system of hydrodynamic conservation laws
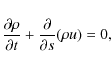 |
(7) |
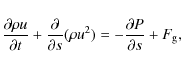 |
(8) |
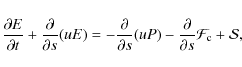 |
(9) |
where s is the position and u the macroscopic plasma velocity along the magnetic field line and
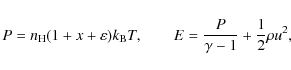 |
(10) |
where
includes all other considered energy sources and sinks, i.e. the dominant flare heating
The 1-D gas dynamics is treated using the explicit LCPFCT solver (Oran & Boris 1987), the Crank-Nicolson algorithm for the heat transfer and the time step splitting technique to couple the individual source terms of the energy equation with hydrodynamics (Oran & Boris 2000).
2.3 Time-dependent non-LTE radiative transfer
Using the instant values of T, ![]() ,
and
,
and
![]() obtained by the hydrodynamic
and test-particle codes, a time-dependent non-LTE radiative transfer
for hydrogen is solved in lower part of the loop in a 1-D plan-parallel approximation.
The hydrogen atom is approximated by a five
level plus continuum atomic model.
obtained by the hydrodynamic
and test-particle codes, a time-dependent non-LTE radiative transfer
for hydrogen is solved in lower part of the loop in a 1-D plan-parallel approximation.
The hydrogen atom is approximated by a five
level plus continuum atomic model.
The level populations ni are determined by the solution of a time-dependent
system of equations of statistical equilibrium (ESE)
where Pijcontain sums of thermal collisional rates Cij and radiative rates Rij, and Rij are preconditioned in the frame of MALI method (Rybicki & Hummer 1991). The excitation and ionisation of hydrogen by the non-thermal electrons from the beam are also included into Pij using the non-thermal collisional rates
For transitions from the ground level we thus get
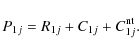 |
(13) |
Non-thermal collisional rates from excited levels as well as three-body recombination rates are not considered here since Karlický et al. (2004) and Stepán et al. (2007) found them to be negligible compared to thermal ones.
In order not to bias the effects of the non-thermal collisional processes by effects caused
by macroscopic plasma velocities, we excluded the advection term
![]() from
Eq. (11). The omission of the advection term can be justified by small velocities
(
from
Eq. (11). The omission of the advection term can be justified by small velocities
(![]() 10 km s-1) in the Balmer line formation regions (Nejezchleba 1998)
attained
during the first few seconds of the flare atmosphere evolution. On the other hand, the benefit is
a significant simplification of the radiative transfer code.
The system of ESE (11) is closed by
charge and particle conservation equations
10 km s-1) in the Balmer line formation regions (Nejezchleba 1998)
attained
during the first few seconds of the flare atmosphere evolution. On the other hand, the benefit is
a significant simplification of the radiative transfer code.
The system of ESE (11) is closed by
charge and particle conservation equations
where
The non-LTE transfer is solved on the shortest time step given by the time step splitting technique in the hydrodynamic part, see Sect. 2.2. Resulting electron density (ionisation) is then fed back to the hydrodynamic equations and the TPC.
3 Results of flare simulations
We computed the atmosphere dynamics and time evolution of the H
3.1 Flare dynamics
Figures 2 and 3 show the time evolution of temperature, hydrogen ionisation, energy deposit
In the low-flux models the heating leads to a gradual increase of temperature above ![]() 1000 km.
The steep rise of temperature from chromospheric to coronal values is shifted by about 200 km from
the preflare height to
1000 km.
The steep rise of temperature from chromospheric to coronal values is shifted by about 200 km from
the preflare height to
![]() km, see Fig. 2.
Heating by a higher flux results in a secondary region of a steep temperature rise at
km, see Fig. 2.
Heating by a higher flux results in a secondary region of a steep temperature rise at
![]() km
which is formed at
km
which is formed at ![]() s, see Fig. 3.
Due to the locally efficient radiative losses, the temperature structure
in all models up to
s, see Fig. 3.
Due to the locally efficient radiative losses, the temperature structure
in all models up to
![]() km
follows the time modulation of the beam flux; i.e. it rises and drops - compare the temperature
structure e.g. at t=1.5 s and t=2 s for 3T models and TP models in
Figs. 2 and 3 and the time evolution of temperature at two selected heights
in Fig. 4.
km
follows the time modulation of the beam flux; i.e. it rises and drops - compare the temperature
structure e.g. at t=1.5 s and t=2 s for 3T models and TP models in
Figs. 2 and 3 and the time evolution of temperature at two selected heights
in Fig. 4.
Similarly to the temperature evolution, ionisation increases above
![]() km shortly after the beam
injection, see the middle panel in Figs. 2 and 3. Again,
due to beam flux modulation and the dependence of the energy deposit on
km shortly after the beam
injection, see the middle panel in Figs. 2 and 3. Again,
due to beam flux modulation and the dependence of the energy deposit on ![]() ,
the increase of ionisation at those layers
is most significant for 3T models with
,
the increase of ionisation at those layers
is most significant for 3T models with ![]() .
As the heating continues, the layers
above
.
As the heating continues, the layers
above ![]() 1200 km become completely ionised (at
1200 km become completely ionised (at ![]() s and
s and
![]() s for low and high flux models, respectively - see thick lines in
Figs. 2 and 3)
and ionisation does not change during further heating - see also Fig. 4.
s for low and high flux models, respectively - see thick lines in
Figs. 2 and 3)
and ionisation does not change during further heating - see also Fig. 4.
On the contrary, lower heights, below
![]() km, exhibit most significant increase
of ionisation for models with
km, exhibit most significant increase
of ionisation for models with ![]() .
The ionisation at these layers reacts to the beam flux time modulation
more for the flatter beams - see Fig. 4 which also demonstrates that the
relaxation of ionisation to preheating values lags behind the time evolution of temperature.
.
The ionisation at these layers reacts to the beam flux time modulation
more for the flatter beams - see Fig. 4 which also demonstrates that the
relaxation of ionisation to preheating values lags behind the time evolution of temperature.
This effect previously shown by Heinzel (1991) and Heinzel & Karlický (1992) is due to time evolution of the ratio of the number of recombinations to photoionisations. Detailed behaviour of photoionisations followed by photorecombinations was discussed by Abbett & Hawley (1999, Sect. 4).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1559f2.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg99.png) |
Figure 2:
Temperature, ionisation, and energy deposit corresponding to the low-flux models (L)
and their evolution in time ( from top to bottom). Different line styles denote four low-flux models.
Thin solid line shows initial VAL C temperature and ionisation structure.
Left: temperature. Middle: ionisation. Thick lines denote the models with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1559f3.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg100.png) |
Figure 3: Temperature, ionisation, and energy deposit corresponding to the high-flux models (H) and their evolution in time ( from top to bottom). The notation is the same as in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm,clip]{1559f4a.eps}\hspace{...
...ps}\hspace{10mm}
\includegraphics[width=5.5cm,clip]{1559f4d.eps} }\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg101.png) |
Figure 4:
Time evolution of temperature ( left) and ionisation ( right) at two heights s=1000 and 1500 km.
Top: low-flux models L_3T_D3 (dotted) and L_3T_D5 (dash-dotted). Bottom: high-flux models H_3T_D3
(dotted) and H_3T_D5 (dash-dotted).
|
| Open with DEXTER | |
3.2 Influence of non-thermal collisional rates
To evaluate the influence of the non-thermal collisional rates, two separate runs with and without
Taking into account
![]() leads only to marginal changes of temperature and density structure of the atmosphere
(up to 17%).
On the contrary, hydrogen ionisation and emission in Balmer lines may significantly differ in models with and without
leads only to marginal changes of temperature and density structure of the atmosphere
(up to 17%).
On the contrary, hydrogen ionisation and emission in Balmer lines may significantly differ in models with and without
![]() .
Generally, the effect of
.
Generally, the effect of
![]() is stronger for models with larger
is stronger for models with larger ![]() or lower
or lower ![]() .
In the low-flux models,
.
In the low-flux models,
![]() significantly modify the time evolution of ionisation structure. They
lead to a faster complete ionisation of layers above
significantly modify the time evolution of ionisation structure. They
lead to a faster complete ionisation of layers above
![]() km and cause an increase of ionisation in the layers below,
compare thin and thick lines in Fig. 2.
The influence of
km and cause an increase of ionisation in the layers below,
compare thin and thick lines in Fig. 2.
The influence of
![]() in the high-flux models is localised mainly
in the layers below
in the high-flux models is localised mainly
in the layers below
![]() km where the flatter beams increase the ionisation. The upper parts of the atmosphere
are affected by
km where the flatter beams increase the ionisation. The upper parts of the atmosphere
are affected by
![]() only temporarily, till
only temporarily, till ![]() s, when they contribute to the fast ionisation of those layers - see Fig. 3.
s, when they contribute to the fast ionisation of those layers - see Fig. 3.
Since
![]() are directly proportional to the energy deposit on hydrogen
are directly proportional to the energy deposit on hydrogen
![]() (Eq. (12)),
their influence is strongly linked to the
(Eq. (12)),
their influence is strongly linked to the
![]() as a function of height. Consequently,
as a function of height. Consequently,
![]() affect Balmer line intensities according to their formation heights. That can be understood in terms of
the contribution function
affect Balmer line intensities according to their formation heights. That can be understood in terms of
the contribution function ![]() to the outgoing intensity
to the outgoing intensity ![]()
where
![\begin{figure}
\mbox{\includegraphics[width=4cm,clip]{1559f5a.eps}\includegraphi...
...{4cm}\includegraphics[width=5cm,clip]{1559f5g.eps}\hspace*{3.2cm}}\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg111.png) |
Figure 5:
H |
| Open with DEXTER | |
3.3 Time variation of line intensities
The intensity variations depend on the maximum beam flux. The low beam flux results in gradual increase of intensities (models L), whereas high beam flux (models H) causes rapid heating of the atmosphere and hence fast and larger increase of line intensities - see Fig. 6 which compares time variations of H ![\begin{figure}
\mbox{\includegraphics[width=4cm,clip]{1559f6a.eps}\includegraphi...
...,clip]{1559f6k.eps}\includegraphics[width=4cm,clip]{1559f6l.eps} }\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg112.png) |
Figure 6:
Time evolution of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1559f7a.eps}\hspace*{0.5mm}
...
...{6cm}\includegraphics[width=4cm,clip]{1559f7i.eps}\hspace*{6.5cm}}\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg113.png) |
Figure 7:
Time evolution of |
| Open with DEXTER | |
Figure 7 demonstrates the time variation and changes induced by
![]() of formation regions of
the H
of formation regions of
the H![]() line centre (
line centre (
![]() Å), line wing
Å), line wing
![]() Å, H
Å, H![]() line centre (
line centre (
![]() Å),
and H
Å),
and H![]() line
wing (
line
wing (
![]() Å) for L_3T_D3 model.
Shortly after the first beam injection into the VAL C atmosphere, at
Å) for L_3T_D3 model.
Shortly after the first beam injection into the VAL C atmosphere, at ![]() s, line intensities decrease by a factor
of
s, line intensities decrease by a factor
of ![]() 2 and more - see Fig. 6. Such a dip appears due to a temporal increase in optical
depth,
2 and more - see Fig. 6. Such a dip appears due to a temporal increase in optical
depth, ![]() ,
which is caused by
,
which is caused by
![]() .
A similar decrease appearing later, at
.
A similar decrease appearing later, at ![]() s is present also in the models without
s is present also in the models without
![]() - compare
- compare ![]() with and
without
with and
without
![]() in Fig. 7.
That dip is a result of relative importance of the thermal collisional rates C1j.
This behaviour was explained by Heinzel (1991) for the case of a 3-level model of hydrogen as a consequence of steeper rise of
second level population, n2, in comparison to n3 with time.
Figure 7 also shows that a region of secondary H
in Fig. 7.
That dip is a result of relative importance of the thermal collisional rates C1j.
This behaviour was explained by Heinzel (1991) for the case of a 3-level model of hydrogen as a consequence of steeper rise of
second level population, n2, in comparison to n3 with time.
Figure 7 also shows that a region of secondary H![]() wing emission is formed shortly after the beam injection
and its intensity slowly increases in time.
wing emission is formed shortly after the beam injection
and its intensity slowly increases in time.
In the case of the high-flux model, the emission from the secondary formation
region dominates and photospheric contribution to the wing intensities diminishes; this behaviour is typical for all studied Balmer lines.
As regards H![]() line, formation of the H
line, formation of the H![]() line centre is due to
line centre is due to
![]() completely moved from the photosphere
to the layers above
completely moved from the photosphere
to the layers above
![]() km. Contrary to the model without
km. Contrary to the model without
![]() ,
no emission from the photosphere
contributes to the outgoing intensity.
Furthermore,
,
no emission from the photosphere
contributes to the outgoing intensity.
Furthermore,
![]() again lead to the prominent secondary wing formation region at
again lead to the prominent secondary wing formation region at
![]() km which occurs
in the model without
km which occurs
in the model without
![]() at much later time
at much later time ![]() s - see last panel in Fig. 7.
s - see last panel in Fig. 7.
Intensities of all three studied lines show a good correlation with the beam
flux on a time scale of the beam flux variation, i.e. on a subsecond time scale.
Depending on the amount of heating, time variations are caused by the time-dependent temperature structure, e.g. H![]() line centre in the high-flux models, and influence of
line centre in the high-flux models, and influence of
![]() .
Line intensities which are affected by
.
Line intensities which are affected by
![]() (line centres in the low-flux models and
line wings in the high-flux models) show more significant time variations.
Maxima of line intensities lag behind the beam flux maxima, the
time lags are generally larger for line wing intensities than for
line centre intensities. Such a time lag is not a beam propagation effect but it is related to different
time variations of electron density at different heights.
We are aware of the fact that velocities would cause asymmetry of lines and modify the line intensities.
Here we concentrate on the beam influence on line formation. For detailed comparison with observed Balmer lines,
velocity should be considered in calculating the line intensities.
(line centres in the low-flux models and
line wings in the high-flux models) show more significant time variations.
Maxima of line intensities lag behind the beam flux maxima, the
time lags are generally larger for line wing intensities than for
line centre intensities. Such a time lag is not a beam propagation effect but it is related to different
time variations of electron density at different heights.
We are aware of the fact that velocities would cause asymmetry of lines and modify the line intensities.
Here we concentrate on the beam influence on line formation. For detailed comparison with observed Balmer lines,
velocity should be considered in calculating the line intensities.
3.4 Diagnostic tools
Having obtained the time evolution of Balmer line profiles for various electron beam parameters, we can search for observable signatures that could provide a method for diagnostic of the electron beam presence in the Balmer line formation regions. In order to distinguish between the flare energy transport by the non-thermal electrons and other agents (e.g. Alfvén waves - Fletcher & Hudson 2008), we consider a method suitable for such a diagnostics only if3.4.1 Intensity ratios
Recently, Kashapova et al. (2008) reported on so-called sidelobes in H
Using our simulations we are able to check whether the observed sidelobes are a feature related to the
electron beams.
An example of a sidelobe is shown in Fig. 8 (left). It appears as a local maximum
at
![]() Å and varies on a timescale similar to the beam flux modulation.
Due to velocities, such sidelobes could be asymmetric with respect to the line centre. On the other hand,
there are observations of almost symmetric Balmer lines and H
Å and varies on a timescale similar to the beam flux modulation.
Due to velocities, such sidelobes could be asymmetric with respect to the line centre. On the other hand,
there are observations of almost symmetric Balmer lines and H![]() /H
/H![]() ratios in the flare kernels
associated with hard X-ray emission (Kotrc et al. 2008),
thus our models which do not consider velocities in radiative transfer can be applied to such situations.
ratios in the flare kernels
associated with hard X-ray emission (Kotrc et al. 2008),
thus our models which do not consider velocities in radiative transfer can be applied to such situations.
Figure 9 shows the time evolution of H![]() /H
/H![]() at several
at several
![]() ,
,
![]() (indicated also in Fig. 8),
for all considered models of the beam heating (see Table 1).
In these plots, a sidelobe
at a certain
(indicated also in Fig. 8),
for all considered models of the beam heating (see Table 1).
In these plots, a sidelobe
at a certain
![]() would appear as an increased line above the others, varying according to the beam time modulation.
would appear as an increased line above the others, varying according to the beam time modulation.
![\begin{figure}
\par\includegraphics[width=4.4cm,clip]{1559f8a.eps}\hspace*{2mm}
\includegraphics[width=4.4cm,clip]{1559f8b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg122.png) |
Figure 8:
Intensity ratio
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1559f9a.eps}\hspace*{0.5mm}
...
...g.eps}\hspace*{0.5mm}
\includegraphics[width=4cm,clip]{1559f9h.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg123.png) |
Figure 9:
The intensity ratios
|
| Open with DEXTER | |
To consider a sidelobe being caused by the electron beam, the sidelobe should correspond to a simulation with
![]() included.
For some beam parameters
included.
For some beam parameters
![]() exhibits the
reported sidelobe behaviour with the exception of the high-flux models with
exhibits the
reported sidelobe behaviour with the exception of the high-flux models with ![]() - see
Fig. 8 (right) or the corresponding
third panel in the top and bottom row in Fig. 9 - where
- see
Fig. 8 (right) or the corresponding
third panel in the top and bottom row in Fig. 9 - where
![]() rapidly drops below
rapidly drops below
![]() and no sidelobe exists in
and no sidelobe exists in
![]() on a beam timescale.
H
on a beam timescale.
H![]() /H
/H![]() ratio shows a similar behaviour to
ratio shows a similar behaviour to
![]() whereas H
whereas H![]() /H
/H![]() ratio is much weakly sensitive to beam parameters.
ratio is much weakly sensitive to beam parameters.
On the other hand, neglecting the effect of
![]() ,
i.e. assuming other agents than electron beams for the flare energy transport,
sidelobes at
,
i.e. assuming other agents than electron beams for the flare energy transport,
sidelobes at
![]() Å are present at all models. Thus, the observed sidelobes cannot be considered as
a unique signature of beam presence in the atmosphere but they are probably related to an impulsive heating.
Å are present at all models. Thus, the observed sidelobes cannot be considered as
a unique signature of beam presence in the atmosphere but they are probably related to an impulsive heating.
Note that the maximal sidelobes from our simulations may appear, for some models, at wavelength positions slightly
different from
![]() Å.
Å.
Furthermore, other kinds of intensity ratios, e.g. a relative line intensity with respect to the line centre value such as
![]() ,
do not show any systematic difference between the models
with and without
,
do not show any systematic difference between the models
with and without
![]() either. Therefore, the intensity ratios do not provide
a reliable diagnostic tool suitable for analysing
the presence of the electron beams in the Balmer line formation regions.
either. Therefore, the intensity ratios do not provide
a reliable diagnostic tool suitable for analysing
the presence of the electron beams in the Balmer line formation regions.
![\begin{figure}
\par\includegraphics[height=4.7cm,width=4.4cm,clip]{1559f10a.eps}...
....5mm}
\includegraphics[height=4.7cm,width=4.4cm,clip]{1559f10b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg128.png) |
Figure 10:
Time evolution of H |
| Open with DEXTER | |
3.4.2 Wavelength-integrated intensity
Wavelength-integrated intensity
![]() (proportional to equivalent width)
was recently proposed by Cheng et al. (2006) as a tool for diagnostics of the non-thermal effects in the solar flares.
On the basis of static semiempirical models, they propose to judge the relative importance of thermal and non-thermal heating
in flares by analysis of
(proportional to equivalent width)
was recently proposed by Cheng et al. (2006) as a tool for diagnostics of the non-thermal effects in the solar flares.
On the basis of static semiempirical models, they propose to judge the relative importance of thermal and non-thermal heating
in flares by analysis of
![]() (H
(H![]() )
and
)
and
![]() (CaII 8542 Å) which show significantly different sensitivity to
(CaII 8542 Å) which show significantly different sensitivity to
![]() .
Using this idea, we analyse in detail the wavelength-integrated intensity
.
Using this idea, we analyse in detail the wavelength-integrated intensity
of the studied Balmer lines for more general radiative hydrodynamic models. k is a normalisation to scale intensities, here we use line centre intensity at t=0 s.
From our simulations it follows that maximum reached values of
![]() are predominantly given by the total deposited energy
are predominantly given by the total deposited energy
![]() (see Eq. (2) and Fig. 10).
Detailed time evolution of the beam flux is reflected as ``loopy structures'' in
(see Eq. (2) and Fig. 10).
Detailed time evolution of the beam flux is reflected as ``loopy structures'' in
![]() plots - see the top row of Fig. 11 - and the time variation of
plots - see the top row of Fig. 11 - and the time variation of
![]() correlates with the beam
flux variation, see Fig. 10.
However, there is no unique dependence of Balmer line
correlates with the beam
flux variation, see Fig. 10.
However, there is no unique dependence of Balmer line
![]() on
on ![]() ,
see
the right panel of Fig. 10 which shows gradual increase of
,
see
the right panel of Fig. 10 which shows gradual increase of
![]() with local minima and maxima corresponding
to the time modulation of the beam flux.
Moreover, in the case of the high-flux models,
with local minima and maxima corresponding
to the time modulation of the beam flux.
Moreover, in the case of the high-flux models,
![]() depend also on
depend also on ![]() .
As a consequence of
increased wing emission for lower
.
As a consequence of
increased wing emission for lower ![]() ,
see Fig. 6,
,
see Fig. 6,
![]() of all studied Balmer lines
reach large values for flatter electron spectra (compare centre and bottom panel in Fig. 11).
of all studied Balmer lines
reach large values for flatter electron spectra (compare centre and bottom panel in Fig. 11).
Taking
![]() into account leads to a significant increase of
into account leads to a significant increase of
![]() - see Figs. 10 and 11,
but similar increase can be caused by stronger heating by other mechanisms than electron beams. Due to this reasons,
neither wavelength-integrated intensities of Balmer lines are good indicators of electron beam presence in the Balmer line
formation regions.
- see Figs. 10 and 11,
but similar increase can be caused by stronger heating by other mechanisms than electron beams. Due to this reasons,
neither wavelength-integrated intensities of Balmer lines are good indicators of electron beam presence in the Balmer line
formation regions.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1559f11a.eps}\par\includeg...
...]{1559f11b.eps}\par\includegraphics[width=8.2cm,clip]{1559f11c.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg131.png) |
Figure 11:
Time evolution of
|
| Open with DEXTER | |
4 Conclusions
Presented radiative hydrodynamic simulations revealed the complexity of the response of hydrogen Balmer lines to the electron beam heating. At the same time, they proved to be a very useful tool to obtain answers to questions raised in the Introduction.- 1.
- We showed that the Balmer line intensities do vary on beam flux variation time scales, i.e.
on a subsecond time scale.
The time variations are caused by time evolution of the temperature structure, electron density and influence
of the non-thermal collisional rates. Depending on the amount of the beam flux,
time evolution of line intensities may also exhibit both fast (pulse like), and gradual (e.g. an increase
of intensity on a time scale larger than the beam flux time variation) components,
see e.g. the case of model L_3T_D3 in Fig. 6.
Such behaviour is known for the H
 line from observations (Trottet et al. 2000).
Therefore, we conclude that the fast pulse-like variations seem to be a good indicator
of the particle beams, namely when correlated with HXR or radio pulsations.
line from observations (Trottet et al. 2000).
Therefore, we conclude that the fast pulse-like variations seem to be a good indicator
of the particle beams, namely when correlated with HXR or radio pulsations.
- 2.
- Influence of the non-thermal rates on the Balmer lines depends on the beam parameters, both
the energy flux and power-law index.
 significantly alter the ionisation structure, leading
to a modification of the line formation regions which are not ionised due to the heating.
Depending on the beam parameters,
significantly alter the ionisation structure, leading
to a modification of the line formation regions which are not ionised due to the heating.
Depending on the beam parameters,
 can affect line centres, wings or both, but generally
can affect line centres, wings or both, but generally
 result in an increased emission from a secondary formation region in the chromosphere.
result in an increased emission from a secondary formation region in the chromosphere.
- 3.
- Concerning the diagnostic tools based on Balmer lines, except for the close correlation
of the time variation of the beam flux and the line intensities,
we did not found any systematic behaviour that would uniquely indicate the presence of the non-thermal
electrons in the atmosphere solely from observations of Balmer lines.
Complementary information such
as hard X-ray emission or spectral lines having different sensitivity to
 ,
e.g. Ca II (8542 Å),
are needed to assess the presence of the non-thermal particles.
,
e.g. Ca II (8542 Å),
are needed to assess the presence of the non-thermal particles.
Acknowledgements
We thank the referee, S. L. Hawley, for many valuable comments. This work was supported by grants 205/04/0358, 205/06/P135, 205/07/1100 of the Grant Agency of the Czech Republic and the research project AV0Z10030501 (Astronomický ústav). Computations were performed on OCAS (Ondrejov Cluster for Astrophysical Simulations) and Enputron, a computer cluster for extensive computations (Universita J. E. Purkyne).
References
- Abbett, W. P., & Hawley, S. L. 1999, ApJ, 521, 906 [NASA ADS] [CrossRef] (In the text)
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] (In the text)
- Bai, T. 1982, ApJ, 259, 341 [NASA ADS] [CrossRef]
- Canfield, R. C., Gunkler, T. A., & Ricchiazzi, P. J. 1984, ApJ, 282, 296 [NASA ADS] [CrossRef] (In the text)
- Cheng, J. X., Ding, M. D., & Li, J. P. 2006, ApJ, 653, 733 [NASA ADS] [CrossRef] (In the text)
- Czaykowska, A., de Pontieu, B., Alexander, D., & Rank, G. 1999, ApJ, 521, L75 [NASA ADS] [CrossRef] (In the text)
- Ding, M. D., Qiu, J., Wang, H., & Goode, P. R. 2001, ApJ, 552, 340 [NASA ADS] [CrossRef] (In the text)
- Doschek, G. A., Mariska, J. T., & Sakao, T. 1996, ApJ, 459, 823 [NASA ADS] [CrossRef] (In the text)
- Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef]
- Fang, C., Henoux, J. C., & Gan, W. Q. 1993, A&A, 274, 917 [NASA ADS] (In the text)
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985, ApJ, 289, 414 [NASA ADS] [CrossRef] (In the text)
- Fletcher, L., & Hudson, H. S. 2008, A&A, 675, 1645 [NASA ADS]
- Hawley, S. L., & Fisher, G. H. 1994, ApJ, 426, 387 [NASA ADS] [CrossRef] (In the text)
- Heinzel, P. 1991, Sol. Phys., 135, 65 [NASA ADS] [CrossRef] (In the text)
- Heinzel, P. 1995, A&A, 299, 563 [NASA ADS]
- Heinzel, P., & Karlický, M. 1992, in Eruptive Solar Flares, Proc. Colloq. 133, ed. Z. Svestka, B. V. Jackson, & M. E. Machado, IAU Colloq., 399, 359 (In the text)
- Hoyng, P., Duijveman, A., Machado, M. E., et al. 1981, ApJ, 246, L155 [NASA ADS] [CrossRef]
- Hudson, H. S., & Fárník, F. 2002, in Solar Variability: From Core to Outer Frontiers, ed. J. Kuijpers, ESA SP, 506, 261
- Karlický, M. 1990, Sol. Phys., 130, 347 [NASA ADS] [CrossRef]
- Karlický, M., & Hénoux, J.-C. 1992, A&A, 264, 679 [NASA ADS]
- Karlický, M., Kasparová, J., & Heinzel, P. 2004, A&AL, 416, L13 [NASA ADS] [CrossRef] (In the text)
- Kashapova, L. K., Kotrc, P., & Kupryakov, Y. A. 2008, Annales Geophysicae, 26, 2975 [NASA ADS] (In the text)
- Kasparová, J., Heinzel, P., Varady, M., & Karlický, M. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 544
- Kopp, R. A., & Pneuman, G. W. 1976, Sol. Phys., 50, 85 [NASA ADS] [CrossRef]
- Kotrc, P., Kashapova, L. K., & Kuprjakov, Y. A. 2008, 12th European Solar Physics Meeting, Freiburg, Germany, held September, 8-12, http://espm.kis.uni-freiburg.de/, 2.61, 12, 2 (In the text)
- Nagai, F., & Emslie, A. G. 1984, ApJ, 279, 896 [NASA ADS] [CrossRef] (In the text)
- Nejezchleba, T. 1998, A&AS, 127, 607 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Oran, E. S., & Boris, J. P. 1987, NASA STI/Recon Technical Report A, 88, 44860 [NASA ADS] (In the text)
- Oran, E. S., & Boris, J. P. 2000, Numerical Simulation of Reactive Flow, ed. E. S. Oran, & J. P. Boris, ISBN 0521581753 (Cambridge, UK: Cambridge University Press), 550 (In the text)
- Peres, G., Serio, S., Vaiana, G. S., & Rosner, R. 1982, ApJ, 252, 791 [NASA ADS] [CrossRef] (In the text)
- Radziszewski, K., Rudawy, P., & Phillips, K. J. H. 2007, A&A, 461, 303 [NASA ADS] [CrossRef] [EDP Sciences]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] (In the text)
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] (In the text)
- Shibata, K. 1996, Advances in Space Research, 17, 9 [NASA ADS] [CrossRef]
- Sturrock, P. A. 1968, in Structure and Development of Solar Active Regions, ed. K. O. Kiepenheuer, IAU Symp., 35, 471
- Tandberg-Hanssen, E., & Emslie, G. A. 1988, The physics of solar flares (Cambridge University Press) (In the text)
- Trottet, G., Rolli, E., Magun, A., et al. 2000, A&A, 356, 1067 [NASA ADS] (In the text)
- Turkmani, R., Vlahos, L., Galsgaard, K., Cargill, P. J., & Isliker, H. 2005, ApJ, 620, L59 [NASA ADS] [CrossRef]
- Stepán, J., Kasparová, J., Karlický, M., & Heinzel, P. 2007, A&A, 472, L55 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Model parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1559f1a.eps}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{1559f1b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg23.png) |
Figure 1:
Time modulations of the beam flux. Solid lines show g(t),
dotted lines denote
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1559f2.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg99.png) |
Figure 2:
Temperature, ionisation, and energy deposit corresponding to the low-flux models (L)
and their evolution in time ( from top to bottom). Different line styles denote four low-flux models.
Thin solid line shows initial VAL C temperature and ionisation structure.
Left: temperature. Middle: ionisation. Thick lines denote the models with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1559f3.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg100.png) |
Figure 3: Temperature, ionisation, and energy deposit corresponding to the high-flux models (H) and their evolution in time ( from top to bottom). The notation is the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm,clip]{1559f4a.eps}\hspace{...
...ps}\hspace{10mm}
\includegraphics[width=5.5cm,clip]{1559f4d.eps} }\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg101.png) |
Figure 4:
Time evolution of temperature ( left) and ionisation ( right) at two heights s=1000 and 1500 km.
Top: low-flux models L_3T_D3 (dotted) and L_3T_D5 (dash-dotted). Bottom: high-flux models H_3T_D3
(dotted) and H_3T_D5 (dash-dotted).
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=4cm,clip]{1559f5a.eps}\includegraphi...
...{4cm}\includegraphics[width=5cm,clip]{1559f5g.eps}\hspace*{3.2cm}}\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg111.png) |
Figure 5:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=4cm,clip]{1559f6a.eps}\includegraphi...
...,clip]{1559f6k.eps}\includegraphics[width=4cm,clip]{1559f6l.eps} }\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg112.png) |
Figure 6:
Time evolution of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1559f7a.eps}\hspace*{0.5mm}
...
...{6cm}\includegraphics[width=4cm,clip]{1559f7i.eps}\hspace*{6.5cm}}\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg113.png) |
Figure 7:
Time evolution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.4cm,clip]{1559f8a.eps}\hspace*{2mm}
\includegraphics[width=4.4cm,clip]{1559f8b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg122.png) |
Figure 8:
Intensity ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1559f9a.eps}\hspace*{0.5mm}
...
...g.eps}\hspace*{0.5mm}
\includegraphics[width=4cm,clip]{1559f9h.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg123.png) |
Figure 9:
The intensity ratios
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=4.7cm,width=4.4cm,clip]{1559f10a.eps}...
....5mm}
\includegraphics[height=4.7cm,width=4.4cm,clip]{1559f10b.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg128.png) |
Figure 10:
Time evolution of H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1559f11a.eps}\par\includeg...
...]{1559f11b.eps}\par\includegraphics[width=8.2cm,clip]{1559f11c.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11559-08/Timg131.png) |
Figure 11:
Time evolution of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



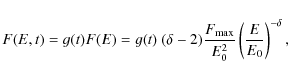
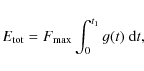
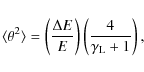
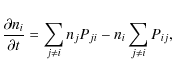
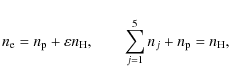
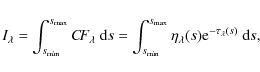
![\begin{displaymath}
I_{\rm tot} = k \int\limits_{-\Delta\lambda_{\max}}^{+\Delta\lambda_{\max}} [I(\lambda,t) - I(\lambda,t=0)]\ ~{\rm d}\lambda
\end{displaymath}](/articles/aa/full_html/2009/21/aa11559-08/img129.png)