Multiphase ISM simulations: comparing NIRVANA and ZEUS

R. A. Piontek; O. Gressel; U. Ziegler

doi:10.1051/0004-6361/20078822

Home

All issues

Volume 499 / No 2 (May IV 2009)

A&A, 499 2 (2009) 633-641

Full HTML

Free Access

Issue		A&A Volume 499, Number 2, May IV 2009


Page(s)		633 - 641
Section		Numerical methods and codes
DOI		https://doi.org/10.1051/0004-6361/20078822
Published online		08 April 2009

Multiphase ISM simulations: comparing NIRVANA and ZEUS

R. A. Piontek - O. Gressel - U. Ziegler

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 9 October 2007 / Accepted 12 February 2009

Abstract
Aims. Our aim is to compare the ZEUS and NIRVANA MHD codes in their application to multi-phase ISM simulations. A contrast in density of about 100 between the warm and cold ISM phases is typical, and discontinuities such as these can be difficult to handle numerically. It is plausible that the details of implementing a particular numerical method could affect the results of the simulation, particularly with regard to the mass and volume fractions of the warm, unstable, and cold gas. This work takes a step towards quantifying to what extent this may occur.
Methods. Using the NIRVANA code, we simulate a multi-phase ISM with turbulence driven by the magnetorotational instability. We make comparisons to our previously published ZEUS models and assess the impact of the numerical method on quantities such as the mass and volume fractions in the ISM phases, turbulent velocities, and probability distribution functions of density, temperature, pressure, and magnetic field strength. We also compare models with which turbulence is driven by an artificial forcing function.
Results. For the models that include turbulence driven by the magnetorotational instability, we find differences in the mass fractions that are typically on the order of 10%. This comparison, however, is complicated by the result that the saturation level of the MRI is different between the two codes. This suggests that, at the same saturation level, we would expect to find larger differences in the mass fractions, and this is indeed what we have found for our artificially forced models. For these runs we find differences in the cold mass fraction of approximately 30%, which is significant.

Key words: magnetohydrodynamics (MHD) - ISM: kinematics and dynamics - ISM: magnetic fields - methods: numerical - galaxies: ISM - turbulence

1 Introduction

Today's modern simulations of the ISM go far beyond solving the conservation equations of hydrodynamics, including many additional physical effects. The numerical methods are typically tested on various hydrodynamic and magnetohydrodynamic test problems, of which the standard is the shock-tube (Sod 1978). When additional physical effects are involved, the testing procedure is less straightforward, as there is often no test problem available that yields an analytic solution with which one can make comparisons.

When comparing results from simulations with analytic solutions is difficult or impossible, the next best option is to perform the same problem with different numerical methods. Numerical cosmologists have adopted this approach, and large collaborations have been formed to attempt to distinguish physical from numerical effects (Frenk et al. 1999; Heitmann et al. 2005; O'Shea et al. 2005). Detailed comparisons between different numerical methods in application to the ISM have not been published yet.

Many researchers in the field of ISM simulations, from both observational (Heiles & Troland 2003) and theoretical (Joung & Mac Low 2006) viewpoints, would like to determine basic properties, such as the fractions of gas that exist in the warm, unstable, and cold phases (Field et al. 1969). It can only be said that there is general agreement between simulations and observations with regard to this question. Observationally it has been found that significant amounts of gas exist in the thermally unstable state (Heiles & Troland 2003), and numerical models have confirmed that turbulence can indeed force gas into this regime (Hennebelle & Audit 2007; de Avillez & Breitschwerdt 2005; Mac Low et al. 2005). There are uncertainties on both the theoretical and observational sides, but this was not a prediction of classical ISM models (Field et al. 1969; McKee & Ostriker 1977). One step that can be taken to reduce or at least quantify uncertainties on the side of simulations is to compare results from one or more different numerical schemes as applied to a particular problem.

Hydrodynamics codes have different strengths and weaknesses, one of which is the ability to accurately capture shocks and discontinuities. When heating and cooling processes in the atomic ISM are taken into account, most commonly by adopting an approximate cooling function, a two-phase medium forms that has a strong contrast in density between the warm and cold phases of factor ${\sim}100$ . The thermal state of the gas is completely altered with the inclusion of this additional physics module. Separating these two stable phases is the gas in the thermally unstable regime, which may be only a few zones thick. The structure of this transition regime may change with one's choice of numerical method, and this could naturally lead to the result of finding varying proportions of gas in the warm, unstable, and cold phases. The extent to which this may or may not be the case is unknown. One of the main goals of this paper is to quantify this effect.

In three previous works, Piontek & Ostriker (2007,2005,2004) (hereafter Papers I-III), we used the ZEUS code (Stone & Norman 1992a,b) to perform numerical simulations of the ISM. The models include shear from the galactic rotation curve, which when combined with magnetic fields, results in turbulence driven by the magnetorotational instability (MRI). In addition, we include a radiative heating and cooling function to model the multi-phase ISM, as well as include conduction to properly resolve thermal instability (TI). Our unstratified models showed that the MRI can drive turbulence at levels that are typically observed in the ISM, at mean densities that are typical of the outer galaxy. Our stratified models of Paper III again showed that the MRI is probably more important at driving turbulence in the outer galaxy compared to the inner galaxy.

One important caveat of this work, however, and a second key point in the motivation for this paper, is that ZEUS does not solve a conservative energy equation. Thus, energy is lost when oppositely directed shear flows and magnetic fields are advected into a single grid zone during the flux update within the numerical finite volume scheme. We performed an analysis of the energy budget in Paper II, and found that we were losing a significant amount of energy due to this effect. The primary question, which was left open, is to what extent the thermal state of the gas might be changed had this energy been properly captured.

In this paper we reproduce one of the simulations from Paper II, using NIRVANA (Ziegler 2005,2004), which solves a total energy equation and is therefore conservative. We make comparisons between the results, and address what impacts are observed on the physical state of the gas. This allows us to not only address the specific issue of energy conservation with ZEUS, but also to comment on the much broader issue of whether or not the numerical scheme can have a significant impact on multi-phase ISM simulations. In our previous works we found the signature of TI, which we take to be a bi-modal density and temperature probability distribution function (PDF), present even in our simulations with large velocity dispersions. With this paper we can gain some insight into whether or not the choice of numerical method might be responsible for maintaining this bi-modal density distribution.

The organization of this paper is as follows: in Sect. 2 we briefly describe the numerical methods employed by ZEUS and NIRVANA, and introduce our model. Results are presented in Sect. 3, and comparisons with previously published works and concluding remarks are found in Sect. 4.

2 Numerical methods and model parameters

In the following subsections we briefly describe the numerical methods used in NIRVANA and ZEUS. We further discuss the issue of energy conservation, and the approach each of the two codes takes to solve the energy equation. Also outlined is how the subroutines for cooling and conduction were included and tested, and to close this section we describe the initial conditions for the simulations.

2.1 ZEUS

ZEUS (Stone & Norman 1992a,b) has been widely used to perform astrophysical MHD simulations for more than 10 years. Two and three dimensional versions are publicly available, including MPI parallel versions for use on distributed computing platforms (Hayes et al. 2006; Vernaleo & Reynolds 2006). ZEUS adopts a staggered mesh approach to implementing the framework for solving the MHD equations. Scalar quantities (density and internal energy) are stored at cell centers, and vector quantities (velocity and magnetic field) are located at the cell faces. Zone-centered variables are interpolated to the faces, and face-centered variables are interpolated to the cell centers, when needed.

ZEUS uses the method of characteristics and constrained transport (Evans & Hawley 1988; Hawley & Stone 1995) to evolve the magnetic field, which guarantees the divergence-free constraint will be satisfied. If the magnetic field is initially divergence-free, it will remain so, provided errors are not introduced by the boundary conditions. Our version of the ZEUS code has been modified to run on parallel clusters using a standard domain decomposition method implemented with the Message Passing Interface.

2.2 NIRVANA

NIRVANA (Ziegler 2005,2004) is a modern MHD code designed with adaptive mesh refinement (AMR) in mind, though AMR is not used in the simulations presented here. It employs a central-upwind, directionally-unsplit scheme in semi-discrete form as proposed by Kurganov et al. (2001) combining a Godunov-type flux computation (HLL equivalent) with the method of constrained transport for a divergence-free evolution of the magnetic field. Essentially, the constrained transport step uses as input upwinded electric field components computed via spatial averaging of MHD fluxes obtained from the base central-upwind scheme. The reconstruction of conserved (or primitive) variables is piecewise linear and allows the use of various TVD slope limiters. The space discretization is second-order accurate. The resulting set of ODE's is solved with a third-order strong-stability-preserving Runge-Kutta scheme as described in Shu & Osher (1988). NIRVANA is in active development, and an MPI parallel version is available to the public.

2.3 Energy conservation

A specific issue that motivated this work is one of energy conservation. ZEUS does not solve a conservative form of the energy equation, but instead evolves the internal energy. The advantage of this approach is that a more accurate solution is obtained for the internal energy in situations where the kinetic (or magnetic) energy is dominating. The major disadvantage is that kinetic and magnetic energy can be dissipated at the grid scale during the flux update, which is not captured by the code and thus lost.

This effect was apparent, and indeed appeared to be significant, in our analysis of the energy budget of our models in Paper II. The extent to which this could affect our results was not known, but it is possible that had this energy not been lost due to numerical effects, the relative fractions of gas in the different ISM phases could be affected, for example.

NIRVANA, on the other hand, treats the energy equation in the conservative form, i.e., it evolves the total rather than the internal energy. Turbulent motions and magnetic fields will still be dissipated at the grid scale in the same way as in ZEUS, but because NIRVANA computes the thermal energy by subtracting the kinetic plus magnetic energy from the total energy, the dissipated energy is converted into heat.

The main drawback of the conservative scheme is that it becomes difficult to accurately compute the thermal energy when kinetic and magnetic pressures dominate. NIRVANA therefore employs a dual-energy formalism in which the code switches from evolving either the total or internal energy depending on which is more appropriate at any point in time or space. The scheme is rather simple: NIRVANA evolves the internal energy as an additional fluid variable. Whenever the thermal energy, computed from the difference of the total and kinetic plus magnetic energies, falls below a threshold, it is overwritten with the internal energy, and the total energy is set accordingly. For the simulations presented here, the threshold was set at 10%.

2.4 Additional numerics and physics

Our versions of ZEUS and NIRVANA have been further modified to include shearing-periodic boundary conditions (Gressel & Ziegler 2007; Hawley & Balbus 1992; Hawley et al. 1995). These boundary conditions permit one to investigate rotating, shearing flows within a local framework, allowing the study of the MRI when magnetic fields are included in the calculation.

Subroutines have been added to both codes to include a radiative heating and cooling function (Sánchez-Salcedo et al. 2002), which is based on the standard curve from Wolfire et al. (1995). The cooling rate is simply a piecewise power law of temperature, with a cold stable phase below 141 K, and a warm stable phase above 6102 K. The heating rate is taken to be constant, with a value of $0.015~{\rm erg~s^{-1}~g^{-1}}$ . The equilibrium cooling curve, which is the sum of the cooling and heating terms, is shown in Figs. 4 and 5. Contours of constant temperature are shown here, which correspond to the temperatures (as indicated) at which the power-law index of the cooling function changes.

Conduction has been included as well, in both codes, to allow the most unstable modes of thermal instability to be resolved (Koyama & Inutsuka 2004). These additions have been tested, and for ZEUS the results were previously published in Paper I. The primary test was to verify that the code can reproduce the linear growth rates of thermal instability for three different levels of conduction. For each of these, three or four simulations were performed, varying the wavelength of the single mode of the instability with which the code is initialized. Growth rates were computed while the perturbations remained in the linear regime, and these compared favorably with the theoretical curves.

2.5 Initial conditions and evolution

Using NIRVANA, we have reproduced the ``Standard'' model of Paper II, of which the initial number density is constant at $1~{\rm cm^{-3}}$ . The simulation domain of the 3D model is 200 pc on each side, with a resolution of 128³ zones. Periodic boundary conditions are employed on the vertical and azimuthal boundaries, and shearing-periodic on the radial boundary. The shearing parameter, q, is set to 1.0, as is appropriate for a flat rotation curve. The box is assumed to be located at 8 kpc from the galactic center, with an orbital time scale of $\Omega = 250~{\rm Myr^{-1}}$ . The initial pressure is $P/k=2000~{\rm cm^{-3}~K}$ , to which we add random white-noise perturbations.

At this pressure and density the gas is initially thermally unstable, and it quickly forms a two-phase medium. Small high-density cold clouds are embedded in the low-density warm ambient medium. We have found that turbulence can be generated by TI itself in the first few orbits of these models (as have others: see Koyama & Inutsuka 2002,2006; Kritsuk & Norman 2002), though the turbulent amplitude is small compared to what is produced by the MRI later in the simulation. Whether or not TI can generate sustained turbulence is a matter of continuing debate, and it will be discussed further in Sect. 4. As a result of these small random motions, combined with the global shear from the rotation curve, small clouds interact with each other and tend to combine to form larger clouds. There is some limit to this growth, however, as large clouds can also be torn apart by way of the same mechanisms. The MRI begins to develop after approximately four orbits, at which point the level of turbulence increases dramatically. Although the model is relatively chaotic at this point, it is clear that the MRI drives turbulence mostly on large scales in the radial direction. In the next section we present a comparison of selected results from the two codes.

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig1.ps} \end{figure}$	Figure 1: We plot, for the conservative NIRVANA run, the net energy gain/loss rate from the net heating/cooling function, the volume-averaged energy density input rates for the Reynolds stress, and the sum of the Maxwell and Reynolds stresses, as well as the $-P(\nabla \cdot v)$ term. A positive value of the cooling term implies net cooling is occurring in the simulation.
Open with DEXTER

3 Results

3.1 Energy budget

We present an analysis of the energy budget in a manner similar to that of Paper II, Sect. 3.6. If shearing-periodic boundary conditions are adopted, following Hawley et al. (1995), and when accounting for the radiative cooling term, the change in total energy should obey the relation

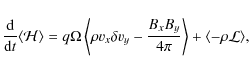$\begin{displaymath}% \frac{{\rm d}}{{\rm d}t}\langle {\cal H} \rangle = q\Omega ... ...ac{B_xB_y}{4\pi}\right\rangle + \langle -\rho{\cal L} \rangle, \end{displaymath}$

(1)

where ${\cal H}$ is the total energy, and ${\cal L}$ the sum of the radiative heating and cooling terms. The first term on the righthand side is the Reynolds stress, and the second the Maxwell stress. In a quasi-steady state, the lefthand side of the above equation should be approximately equal to zero, and if energy is properly conserved, the energy inputs from the Maxwell and Reynolds stresses should equal the rate of energy loss from the cooling function.

Table 1: Time-averaged results for the three MRI runs. Data is averaged spatially over the entire domain, and temporally over the final two orbits.

We plot the Reynolds stress, the sum of the Maxwell and Reynolds stresses, the radiative net heating-cooling rate (a positive value implies net cooling), as well as the $-P(\nabla \cdot v)$ work in Fig. 1. Compared to each other, the Maxwell and Reynolds stresses are quite similar to those of Paper II for ZEUS, both in time and relative amplitude. We found in Paper II that the net heating-cooling term was significantly less than the sum of these stresses, and this was the primary source of our concern regarding the energy conservation issue. With NIRVANA, this is no longer the case, and the sum of the Maxwell and Reynolds stresses are very tightly correlated in time with the net heating-cooling rate. This result illustrates that energy losses and gains are balanced, and energy is conserved correctly, as we expected would be the case.

To continue the comparison with our results from Paper II, we performed an additional model with the dual-energy threshold set to 100%. Using this threshold forces NIRVANA to behave essentially like a non-conservative code, and so it should be susceptible to the same dissipation issues as ZEUS with regard to the energy equation. We plot the same quantities in Fig. 2 for the non-conservative NIRVANA run, as were previously shown in Fig. 1. The results are quite remarkable. The cooling no longer follows the sum of the stresses, but switches signs to follow the $-P(\nabla \cdot v)$ term. In the conservative case we always find net cooling, while in the non-conservative case there is always net heating.

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig2.ps} \end{figure}$	Figure 2: We plot the same quantities as shown in Fig. 1, but for the non-conservative NIRVANA run. In this case the net heating/cooling term has the opposite sign as was found for the conservative NIRVANA run, and is now well correlated with the $-P(\nabla \cdot v)$ term.
Open with DEXTER

This can be understood as there being two sources (sinks) of thermal energy, compressions (and expansions), and dissipation at the grid scale in the conservative run. We know that energy is conserved, as it should be, because the cooling rate follows the energy input due to the stresses. The difference between the compressional work and the cooling rate must be dissipational heating, which we did not track explicitly.

The non-conservative run does not conserve energy, so the cooling rate does not equal the sum of the Maxwell and Reynolds stresses. In the non-conservative case, the same dissipation on the grid scale occurs, but this dissipation is not converted to thermal energy, and is simply lost on the grid scale. The only source of heating (or cooling) is compressions (or expansions). In this case the $-P(\nabla \cdot v)$ work is negative, so the cooling function is found to heat at approximately the same rate. The ZEUS run behaves in essentially the same manner as the NIRVANA non-conservative run, except that an additional source of heating is present, the artificial viscosity in shocks. For ZEUS, we found that the sum of the compressional work and heating due to artificial viscosity was approximately equal to the cooling rate.

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{8822fig3.eps} \end{figure}$

Figure 3:

Comparison of pressure, temperature, magnetic field and density PDFs, averaged over the final two orbits of the simulation. The dark line is for ZEUS, and the light line for NIRVANA. Generally the agreement is quite good, but there are some differences worth noting. For ZEUS the distributions of pressure, temperature, and density all extend to both higher and lower values as compared to NIRVANA. We also note the slightly larger fraction of unstable gas in the temperature PDF. Finally, the peak of the magnetic field PDF of ZEUS is shifted to slightly higher values, and extends much farther towards higher values of B.

Open with DEXTER

Perhaps even more remarkable than our finding that the net heating-cooling rate actually changes signs between the conservative and non-conservative runs, though perhaps not surprisingly given the short time-scale for cooling, is that the phase structure of the gas is essentially unchanged. This is because the typical net change in energy from the cooling function is close to one percent per time step during the MRI phase of evolution. Whether this is a positive or negative change apparently does not significantly alter the phase structure of the gas. In the next section we examine the relative fractions of gas in the three phases of gas.

3.2 Time and volume-averaged quantities

In Table 1, we show time-averaged values for the mass and volume fractions, the rms velocity, and the magnetic field strength, taken over the final two orbits of the simulation. The quantities are shown for the cold (H), unstable (G), and warm (F) phases. Results for the ZEUS, conservative NIRVANA, and non-conservative NIRVANA are shown. We now discuss each in turn.

For the time-averaged values of the mass and volume fractions, the two NIRVANA runs are essentially unchanged. In the ZEUS run, on the other hand, we do observe some differences. We find approximately 10% more cold gas in the ZEUS run, somewhat less unstable gas, and about the same warm mass fraction. The volume fractions are more alike between ZEUS and NIRVANA, with the only notable difference being an increase in the cold volume fraction from 4 to 5% from NIRVANA to ZEUS. Taken together with the mass fractions, this indicates that turbulence tends to alter the distribution of mass within a phase, i.e. the peak density changes within a phase, but the filling fractions remain about the same.

The rms velocities show more significant differences between all three simulations. The conservative NIRVANA simulation is the least turbulent of the three, followed by the non-conservative NIRVANA, then by ZEUS with the highest rms velocities, for all three phases. There is generally a trend toward increasing turbulent velocity from the cold, to the unstable, and finally the warm phase, for all three simulations. Higher levels of turbulence should force gas from the stable cold and warm phases into the unstable phase. While this is likely to be the case when comparing a single code with different levels of turbulence, our results show that the picture is somewhat more complicated. In our models, the ZEUS run is the most turbulent, but contains the smallest fraction of unstable gas. Also, the conservative NIRVANA run is less turbulent than the non-conservative model, but the mass and volume fractions are nearly identical.

The time-averaged magnetic field values appear to show a correlation with the turbulent velocities. ZEUS, with the highest rms velocities, has the highest magnetic field strength, followed by the non-conservative NIRVANA, and finally the conservative NIRVANA. All three simulations show an increasing trend in magnetic field strength from the warm, to unstable, to cold phases, of around 0.5 $\mu$ G, respectively. We note, however, that this correlation may be misleading, because we found no such result in Paper II. Regardless of the saturated state rms velocity, which was a function of the mean density, the time-averaged magnetic field strength was the same for all runs.

3.3 Probability distribution functions

Mass-weighted PDFs for pressure, temperature, magnetic field strength, and density are shown in Fig. 3. These PDFs are averaged over the final two orbits of the simulation. The PDFs of pressure, temperature, and density are all very similar between the two codes. In the case of pressure, the distribution extends to slightly lower and higher values for ZEUS, and is somewhat more peaked with a steeper decline towards low pressures. The mass-weighted pressure for the ZEUS simulation, averaged over the last two orbits, is 1340, 1050, and 1402 ${\rm erg~K~cm^{-3}}$ for the warm, unstable, and cold phases. For NIRVANA, averaged over the same time period, we find 1430, 1140, and 1410 ${\rm erg~K~cm^{-3}}$ for the warm, unstable, and cold phases.

Table 2: Time-averaged results for the forced models. Data is averaged spatially and temporally over the second half of the simulation.

The temperature PDFs are nearly identical, the only exception being that the distribution for ZEUS extends to slightly lower temperatures. The peaks of the temperature PDF are in the same location, and the distribution through the unstable phase is very similar. The density PDFs also agree well. The ZEUS density PDF extends to somewhat lower and higher densities as compared to NIRVANA, but the peaks for the warm and cold phases are in the same location, and the distribution between the peaks is nearly indistinguishable. The PDFs of magnetic field strength show the most significant differences. The peak in the distribution for ZEUS is around 2.5 $\mu {\rm G}$ , while for NIRVANA the peak lies at about 2.0 $\mu {\rm G}$ . The ZEUS magnetic field PDF extends to higher fields strengths, approximately 6 $\mu {\rm G}$ , while NIRVANA reaches only 4.5 $\mu {\rm G}$ .

The PDFs of the non-conservative NIRVANA run are very similar to those of the conservative NIRVANA run, so we do not show them here. There are, however, two differences worth noting. In the magnetic field PDF, the peak in the distribution is shifted to a slightly higher field strength, by perhaps $0.25~\mu {\rm G}$ . The distribution also extends by about $0.5~\mu {\rm G}$ to higher levels at the tail end of the distribution. We also note that the low-density peak of the density PDF is slightly smaller in the non-conservative NIRVANA run compared to the conservative NIRVANA run, and the tail end of the distribution is shifted slightly to lower densities.

3.4 Phase space diagrams

In Figs. 4 and 5 we show phase-space diagrams of pressure and density for ZEUS and NIRVANA, along with the equilibrium cooling curve, and lines of constant temperature, representing the transitions between the different regimes of the cooling function. In both cases, the data is averaged over the final two orbits of the simulation. The intensity of the grey scale represents the fraction of gas that is found at a particular pressure and density, with darker areas corresponding to higher proportions of gas. In both cases most of the gas is distributed along the equilibrium cooling curve. In the case of ZEUS, in both the warm and cold phases, the gas is distributed throughout a wider range of densities as compared to NIRVANA.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{8822fig4.eps} \end{figure}$

Figure 4:

Phase-space diagram of pressure and density for ZEUS, where intensity indicates the relative fraction of gas at a particular density and pressure. The dashed line represents thermal equilibrium, when heating and cooling rates are equal. The solid diagonal lines are contours of constant temperature, and are labeled individually. These temperatures correspond to those that define the transitions for the piece-wise continuous cooling function. The majority of the gas exists in thermal equilibrium in the warm and cold phases.

Open with DEXTER

3.5 Forced models

The significant difference between the saturated state rms velocity in the ZEUS and NIRVANA simulations does not afford us a very straightforward comparison of the thermal state of the gas. We have therefore performed an additional set of simulations to enable a more detailed comparison between the two codes. Turbulence in this final set of simulations is not driven by the MRI (and in fact MHD is disabled), but through an additional subroutine.

Sinusoidal velocity perturbations are added at a specified time interval. The scale of the perturbations was chosen to be k=2, or 100 pc, similar to the driving scale of the MRI. The phase and direction of the perturbations were chosen randomly. The amplitude and time interval of the forcing was chosen to give an rms velocity that is comparable to what was found in the MRI models.

Mass and volume fractions, and rms velocities, averaged over the second half of the simulation, are shown in Table 2. As can be seen, the rms velocities of the two codes are much closer to each other than in the MRI runs. We can now better compare between the models with regard to the phase structure of the gas.

We first compared the results using the same code between the MRI and forced runs. For ZEUS the forced models were significantly less turbulent than the MRI models. Nevertheless the mass and volume fractions compare quite well with each other. For NIRVANA, the rms velocity for all three phases in the forced models are about the same (as is also the case for ZEUS), and comparable to the unstable phase in the MRI models. There is less cold gas, and more unstable gas, in the forced NIRVANA simulation. With the general view in mind that turbulence drives gas from the stable phases into the unstable phase, we can conclude that our artificial forcing routine is more effective at this than the MRI. For a lower level of turbulence in the ZEUS run, we find the same unstable mass fraction, and for the same level of turbulence in the NIRVANA run we find a higher unstable mass fraction.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{8822fig5.eps} \end{figure}$	Figure 5: Same as plotted in Fig. 4, but for the conservative NIRVANA run. Compared to ZEUS, gas in the warm stable phase does not extend to as high temperatures, and gas in the cold phase does not extend to as cool temperatures. The unstable region, however, is significantly broadened, most notably between 141 K and 313 K to higher pressure and higher density.
Open with DEXTER

Comparing the ZEUS and NIRVANA forced runs together, we see significant differences in the mass fractions. The mass fraction of cold gas increases from 45% for NIRVANA to 62% for ZEUS. The unstable fraction decreases by about the same percentage, while the warm fraction is essentially unchanged. For a more detailed comparison, the mass-weighted density PDFs are shown in Fig. 6. Clearly the NIRVANA runs contains more unstable gas at all densities between the warm and cold phases. NIRVANA actually contains more gas in the cold phase if we examine only the high-density tail of the distribution, but overall this is less important than the increased cold mass fraction at the peak of the distribution.

It is interesting to note that the difference between the warm and cold phase rms velocity is much greater in the MRI runs than in the forced runs, which must stem from to the nature of the driving. In the MRI runs, turbulence is primarily driven by the MRI acting on the warm phase, which is a large-scale flow and somewhat correlated in time and space. Interactions between cold clouds tend to reduce their rms velocity. In our forced run, all phases are essentially driven at the same rate, and the forcing is random, leading to the result that different phases have a similar rms velocity dispersion.

4 Discussion and conclusions

4.1 Comparison with previously published results

We now compare our results to recently published works in which the primary ingredients are also a two-phase medium and turbulence. Brandenburg et al. (2007, hereafter BKM07) perform simulations using the Pencil code, and they adopt a cooling function that is very similar to ours (Sánchez-Salcedo et al. 2002). Explicit viscosity is included, along with conduction. The level of conduction varies linearly with density, and so is much greater in the cold medium than the warm medium. Though this description is somewhat unphysical, it helps numerically to prevent conduction from reducing the required time step. In our simulations, we have adopted a constant conduction coefficient. Two different 3D simulations were performed, one with turbulence driven only by TI (which decays), and another with forced turbulence.

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig6.eps} \end{figure}$	Figure 6: Mass-weighted density PDFs for NIRVANA and ZEUS averaged over the second half of the simulation for the forced TI simulation.
Open with DEXTER

We first examine the PDFs of the BKM07 simulation without forcing. The entire medium exists in almost exact pressure equilibrium. One reason for this is that the level of turbulence at the end of the non-turbulent simulation is quite low. Early in time in our simulations with both NIRVANA and ZEUS, the turbulent velocity driven by TI is higher, but comparable to, the level of turbulence at the end of the non-turbulent BKM07 model. At densities above $1~{\rm cm^{-3}}$ gas exists within a range of pressures in both of our models, and the phase-space diagrams of NIRVANA and ZEUS as compared to the Pencil code look significantly different.

We can also compare our MRI models to their forced simulations, that have an rms velocity which steadily increases from around 10 ${\rm km~ s^{-1}}$ at the beginning of the run to 100 ${\rm km~ s^{-1}}$ at the end. The most significant difference between the simulations of BKM07 and ours, is that turbulence does not force gas to exist at either lower densities or higher temperatures compared to the non-turbulent case. In our simulations with both NIRVANA and ZEUS, the PDFs of density are broadened to extend to both higher and lower values with the development of MRI-driven turbulence. With the Pencil code, the temperature PDFs are broadened to lower densities, but the high temperature cutoff increases only slightly. Our pressure PDFs also differ somewhat. Our peak in the pressure PDF shifts to lower pressure, while theirs shifts to higher pressure with increased turbulence. All these differences can be easily seen in the phase-space diagrams. For BKM07, in the warm phase (i.e. low density, low pressure) most of the gas is found within a narrow range of pressures. In our case, gas in the warm phase is found distributed over a much broader range of pressures, found along the equilibrium cooling curve. It should be kept in mind that these differences are present with BKM07 having a higher level of turbulence - the opposite of what might be expected. The difference in comparing the results of the Pencil code as compared to NIRVANA are somewhat less dramatic, but keeping in mind that the level of turbulence in the simulations of BKM07 is significantly higher, the opposite result would actually be expected. The unstable and cold phases for all three codes appear to agree fairly well.

Finally, we note that BKM07 found that turbulence driven by TI decays over the length of the simulation, 2.5 Gyr. In our models, the turbulence that is driven by TI does not appear to show any signs of decaying over the first 500 Myr of our simulation, before the MRI has begun to develop. Early in the simulation it is possible that MRI may be contributing at a low level so as to mask what would otherwise be a slight decay. However, in Paper I, we performed 2D models without the MRI, and these models also did not show a decline in the level of turbulence over the duration of the simulation, which lasted 500 Myr. Koyama & Inutsuka (2006) perform simulations of TI without external forcing, and find that turbulence is sustained if the domain size is three times larger than the cooling length. Viscosity and conduction are both included, but these models are followed for at most 100 Myr, much shorter than BKM07, as are our own models.

To allow us to come to a stronger conclusion regarding this issue, we performed a final simulation with NIRVANA attempting to reproduce the results of BKM07. We adopted the same prescription for conduction and viscosity, and we confirm that TI turbulence does decay. Whether this is a result of the conduction or viscosity, or both, is not clear, and further study is necessary and forthcoming.

Hennebelle & Audit (2007) perform two-phase simulations of a converging warm medium, from which a cold phase forms from shocks of the interaction. The cooling function includes Lyman-alpha, C+, and O line cooling, which are the primary coolants considered in the Wolfire et al. (1995) model, on which our cooling function is also based. The relative flow speed between the two phases is 3 times the sound speed of the warm medium, and so is much more turbulent than our models. There appear to be some significant differences between the density PDFs. Their density peaks appear at approximately 1.0 ${\rm cm^{-3}}$ for the warm phase and 100 ${\rm cm^{-3}}$ for the cold phase. In our case these numbers are shifted approximately an order of magnitude lower, to around $0.1~{\rm cm^{-3}}$ for the warm phase and 10 ${\rm cm^{-3}}$ for the cold phase. The initial density of these simulations is 0.76 ${\rm cm^{-3}}$ and the initial pressure 7 $\times$ $10^{-13}~{\rm erg~cm^{-3}}$ . This pressure and density combination is too high for the warm medium to be in thermal equilibrium for our cooling curve. The shift to higher densities is likely a result of the combination of the differing cooling curves adopted, as well as the increased density of the warm medium (which results in a higher average density of the box), and the higher level of turbulence. Phase-space diagrams from similar lower resolution simulations are presented in Audit & Hennebelle (2005), and here it can easily be seen that most of the warm medium is out of thermal equilibrium at higher pressures. The initial pressure and density of the warm medium put it at the peak of the thermal equilibrium curve, i.e. the highest value of pressure for which a two-phase medium is possible.

Joung & Mac Low (2006) simulate a stratified ISM with SNe driven turbulence using the Flash code (Fryxell et al. 2000), with AMR, to solve the equations of hydrodynamics using the piecewise parabolic method (Colella & Woodward 1984). The cooling curve for gas below 10⁴ K is that of Dalgarno & McCray (1972). This cooling curve is qualitatively similar to that of Sánchez-Salcedo et al. (2002), but differs in the transition temperatures and slopes, especially at low temperatures. PDFs are presented, but comparisons with these are very difficult, most likely due to both the differences in cooling, as well as the inclusion of SNe, with which comes a hot phase of gas that is not present in our models. Nevertheless, by neglecting the low-density hot phase, comparisons can be made between the phase diagrams, which are qualitatively similar. High-density gas falls mostly on the equilibrium cooling curve. The low-density warm medium is distributed among a variety of densities and pressures, similar to our models. Wada & Norman (2007) perform global simulations of a SNe-driven ISM, but for similar reasons comparisons are difficult, as is the case for Slyz et al. (2005), Korpi et al. (1999), and Tasker & Bryan (2006). A similar code comparison such as the one presented here, but with SNe driven turbulence, would be very useful.

4.2 Summary and conclusions

In this paper we have addressed the question as to what extent the choice of numerical method can affect the results of a two-phase ISM simulation. We compared the results of the same simulation using two different codes, ZEUS and NIRVANA. We performed two different comparisons, one in which turbulence is driven by the MRI, and a second that utilizes an artificial forcing function. We find NIRVANA correctly conserves energy with regard to comparing the net heating-cooling rates to the energy input from the Reynolds and Maxwell stresses, which was a specific issue raised concerning our results in Paper II, and also a large part of the motivation for the current work. It was foreseen that this additional energy could have increased the unstable fraction of gas in our models. For the MRI runs, the PDFs of temperature, density, and pressure show mostly minor deviations from one another, at the level of around 10%. The comparison is complicated, however, by the result that the turbulent rms velocities in the NIRVANA run are around 2.0 ${\rm km~ s^{-1}}$ , compared to 3.0 ${\rm km~ s^{-1}}$ for ZEUS. If the saturation level of the MRI had been the same for both codes, we were to have likely observed larger differences in the mass fractions and PDFs.

It is beyond the scope of this paper to determine precisely why the saturated state rms velocities and magnetic field strengths vary between the two codes. The saturation level of the MRI is itself a topic of active research. We do, however, consider a possible explanation taken from two recently published papers. Lesur & Longaretti (2007) have shown that the saturated state of the MRI is dependent on the ``numerical'' magnetic Prandtl number $({\rm Pm})$ , which is the ratio of the magnetic Reynolds number to the Reynolds number. In particular the dependence is $\alpha = {\rm Pm}^{\delta}$ , with $\delta$ ranging from 0.25 to 0.5. The parameter $\alpha$ is the dimensionless transport coefficient, which is computed from the Reynolds and Maxwell stresses. Fromang & Papaloizou (2007) recently investigated the convergence properties of ZEUS when performing local MRI shearing-box simulations such as ours. They found that ZEUS has an intrinsic ${\rm Pm} > 1$ .

We believe that NIRVANA may have a ${\rm Pm}$ that is smaller than one, as the magnetic part of the numerical scheme is probably more diffusive than the hydrodynamical part. This is because the electromotive forces in the NIRVANA scheme are computed in the same manner as the hydrodynamic fluxes, i.e., at the face centers. The constrained transport scheme, however, assumes the EMFs to be staggered at the edges. Thus NIRVANA requires an additional interpolation in the induction equation, which leads to an increased truncation error in the magnetic field. If this is the case, we would expect $\alpha$ , as well as the saturated state magnetic field strength and turbulent velocities from which $\alpha$ is computed, to be smaller, as we have observed.

We also note that Fromang & Papaloizou (2007) find $\alpha$ to vary with resolution in their models, which is a result that is particularly relevant to our own MRI models, implying that the level of turbulence or magnetic field strength might depend on resolution. We did, however, perform a resolution test, in Paper II, and found the results compared quite well between models with 128³ and 256³ zones. Our lack of dependence on resolution is likely a result of the initial conditions, for which we adopt a vertical magnetic field, whereas Fromang & Papaloizou (2007) perform models with zero net flux. Hawley et al. (1995) also performed local 3D MRI models with a net vertical flux, and did not find any strong dependence of the saturation level on resolution.

Our forced models, which have a similar level of turbulence, allow us to make a better comparison of the two codes. In these models, ZEUS contains approximately one third more cold gas mass, and one third less unstable gas, as compared to NIRVANA. This difference is significant. A convenient explanation is that the extra energy that is lost to dissipation in the ZEUS simulation, but captured by NIRVANA through the solution of a total energy equation, forces gas into the unstable state. Our MRI tests, however, indicate this is not the cause, as running NIRVANA in a non-conservative mode showed very small differences as compared to the conservative NIRVANA. It is possible that, under more turbulent conditions as might found in SNe driven simulations, this issue could become more important.

We therefore attribute the root cause of the differing mass fractions to be the numerical methods used in ZEUS and NIRVANA. We conclude that one might expect to see variations in the cold and unstable mass fractions in the ISM phases to occur at the level of 25%, depending on which code is used to solve the problem. This result should serve as a valuable point of reference for both observers and theoreticians when making future comparisons between published works. Further study is required. There are many numerical issues related to the increased complexity of modeling the ISM, which have not been investigated and are certainly worth the time and effort.

Acknowledgements

This work used the NIRVANA code v3.2 developed at the Astrophysical Institute Potsdam. The ZEUS simulations were performed at the Center for Theory and Computational cluster in the University of Maryland Department of Astronomy. We thank Eve Ostriker and Mordecai-Mark Mac Low for useful discussions and comments concerning this paper. We also thank the anonymous referee for comments that lead to significant improvements in this paper.

References

Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [NASA ADS] [CrossRef] [EDP Sciences]
Brandenburg, A., Korpi, M. J., & Mee, A. J. 2007, ApJ, 654, 945 [NASA ADS] [CrossRef] (In the text)
Colella, P., & Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [NASA ADS] [CrossRef] (In the text)
Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [NASA ADS] [CrossRef]
de Avillez, M. A., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences]
Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [NASA ADS] [CrossRef]
Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] (In the text)
Frenk, C. S., White, S. D. M., Bode, P., et al. 1999, ApJ, 525, 554 [NASA ADS] [CrossRef]
Fromang, S., & Papaloizou, J. 2007, A&A, 476, 1113 [NASA ADS] [CrossRef] [EDP Sciences]
Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] (In the text)
Gressel, O., & Ziegler, U. 2007, Comp. Phys. Commun., 176, 652 [NASA ADS] [CrossRef]
Hawley, J. F., & Balbus, S. A. 1992, ApJ, 400, 595 [NASA ADS] [CrossRef]
Hawley, J. F., & Stone, J. M. 1995, Comp. Phys. Commun., 89, 127 [NASA ADS] [CrossRef]
Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef]
Hayes, J. C., Norman, M. L., Fiedler, R. A., et al. 2006, ApJS, 165, 188 [NASA ADS] [CrossRef]
Heiles, C., & Troland, T. H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] (In the text)
Heitmann, K., Ricker, P. M., Warren, M. S., & Habib, S. 2005, ApJS, 160, 28 [NASA ADS] [CrossRef]
Hennebelle, P., & Audit, E. 2007, A&A, 465, 431 [NASA ADS] [CrossRef] [EDP Sciences]
Joung, M. K. R., & Mac Low, M.-M. 2006, ApJ, 653, 1266 [NASA ADS] [CrossRef] (In the text)
Korpi, M. J., Brandenburg, A., Shukurov, A., Tuominen, I., & Nordlund, Å. 1999, ApJ, 514, L99 [NASA ADS] [CrossRef] (In the text)
Koyama, H., & Inutsuka, S.-I. 2002, ApJ, 564, L97 [NASA ADS] [CrossRef]
Koyama, H., & Inutsuka, S.-I. 2004, ApJ, 602, L25 [NASA ADS] [CrossRef] (In the text)
Koyama, H., & Inutsuka, S.-I. 2006, arXiv Astrophysics e-prints
Kritsuk, A. G., & Norman, M. L. 2002, ApJ, 569, L127 [NASA ADS] [CrossRef] (In the text)
Kurganov, A., Noelle, S., & Petrova, G. 2001, SIAM J. Sci. Comput., 23, 707 [CrossRef] (In the text)
Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] (In the text)
Mac Low, M.-M., Balsara, D. S., Kim, J., & de Avillez, M. A. 2005, ApJ, 626, 864 [NASA ADS] [CrossRef]
McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef]
O'Shea, B. W., Nagamine, K., Springel, V., Hernquist, L., & Norman, M. L. 2005, ApJS, 160, 1 [NASA ADS] [CrossRef]
Piontek, R. A., & Ostriker, E. C. 2004, ApJ, 601, 905 [NASA ADS] [CrossRef]
Piontek, R. A., & Ostriker, E. C. 2005, ApJ, 629, 849 [NASA ADS] [CrossRef]
Piontek, R. A., & Ostriker, E. C. 2007, ApJ, 663, 183 [NASA ADS] [CrossRef]
Sánchez-Salcedo, F. J., Vázquez-Semadeni, E., & Gazol, A. 2002, ApJ, 577, 768 [NASA ADS] [CrossRef] (In the text)
Shu, C., & Osher, S. 1988, J. Comp. Phys., 77, 439 [NASA ADS] [CrossRef] (In the text)
Slyz, A. D., Devriendt, J. E. G., Bryan, G., & Silk, J. 2005, MNRAS, 356, 737 [NASA ADS] [CrossRef] (In the text)
Sod, G. 1978, J. Comput. Phys., 27, 1 [NASA ADS] [CrossRef] (In the text)
Stone, J. M., & Norman, M. L. 1992a, ApJS, 80, 753 [NASA ADS] [CrossRef]
Stone, J. M., & Norman, M. L. 1992b, ApJS, 80, 791 [NASA ADS] [CrossRef]
Tasker, E. J., & Bryan, G. L. 2006, ApJ, 641, 878 [NASA ADS] [CrossRef] (In the text)
Vernaleo, J. C., & Reynolds, C. S. 2006, ApJ, 645, 83 [NASA ADS] [CrossRef]
Wada, K., & Norman, C. A. 2007, ApJ, 660, 276 [NASA ADS] [CrossRef] (In the text)
Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [NASA ADS] [CrossRef] (In the text)
Ziegler, U. 2004, J. Comput. Phys., 196, 393 [NASA ADS] [CrossRef]
Ziegler, U. 2005, Comp. Phys. Commun., 170, 153 [NASA ADS] [CrossRef]

All Tables

Table 1: Time-averaged results for the three MRI runs. Data is averaged spatially over the entire domain, and temporally over the final two orbits.

Table 2: Time-averaged results for the forced models. Data is averaged spatially and temporally over the second half of the simulation.

All Figures

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig1.ps} \end{figure}$	Figure 1: We plot, for the conservative NIRVANA run, the net energy gain/loss rate from the net heating/cooling function, the volume-averaged energy density input rates for the Reynolds stress, and the sum of the Maxwell and Reynolds stresses, as well as the $-P(\nabla \cdot v)$ term. A positive value of the cooling term implies net cooling is occurring in the simulation.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig2.ps} \end{figure}$	Figure 2: We plot the same quantities as shown in Fig. 1, but for the non-conservative NIRVANA run. In this case the net heating/cooling term has the opposite sign as was found for the conservative NIRVANA run, and is now well correlated with the $-P(\nabla \cdot v)$ term.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{8822fig3.eps} \end{figure}$	Figure 3: Comparison of pressure, temperature, magnetic field and density PDFs, averaged over the final two orbits of the simulation. The dark line is for ZEUS, and the light line for NIRVANA. Generally the agreement is quite good, but there are some differences worth noting. For ZEUS the distributions of pressure, temperature, and density all extend to both higher and lower values as compared to NIRVANA. We also note the slightly larger fraction of unstable gas in the temperature PDF. Finally, the peak of the magnetic field PDF of ZEUS is shifted to slightly higher values, and extends much farther towards higher values of B.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{8822fig4.eps} \end{figure}$	Figure 4: Phase-space diagram of pressure and density for ZEUS, where intensity indicates the relative fraction of gas at a particular density and pressure. The dashed line represents thermal equilibrium, when heating and cooling rates are equal. The solid diagonal lines are contours of constant temperature, and are labeled individually. These temperatures correspond to those that define the transitions for the piece-wise continuous cooling function. The majority of the gas exists in thermal equilibrium in the warm and cold phases.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{8822fig5.eps} \end{figure}$	Figure 5: Same as plotted in Fig. 4, but for the conservative NIRVANA run. Compared to ZEUS, gas in the warm stable phase does not extend to as high temperatures, and gas in the cold phase does not extend to as cool temperatures. The unstable region, however, is significantly broadened, most notably between 141 K and 313 K to higher pressure and higher density.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{8822fig6.eps} \end{figure}$	Figure 6: Mass-weighted density PDFs for NIRVANA and ZEUS averaged over the second half of the simulation for the forced TI simulation.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.