| Issue |
A&A
Volume 499, Number 2, May IV 2009
|
|
|---|---|---|
| Page(s) | L13 - L16 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200811609 | |
| Published online | 29 April 2009 | |
Dynamical stability of the inner belt around Epsilon Eridani
M. Brogi1 - F. Marzari2 - P. Paolicchi1
1 - University of Pisa, Department of Physics, Largo Pontecorvo 3, 56127
Pisa, Italy
2 -
University of Padua, Department of Physics, via Marzolo 8, 35131 Padua, Italy
Received 31 December 2008 / Accepted 17 April 2009
Abstract
Context. Recent observations with Spitzer and the Caltech Submillimeter Observatory have discovered the presence of a dust belt at about 3 AU, internal to the orbit of known exoplanet ![]() Eri b.
Eri b.
Aims. We investigate via numerical simulations the dynamical stability of a putative belt of minor bodies, as the collisional source of the observed dust ring. This belt must be located inside the orbit of the planet, since any external source would be ineffective in resupplying the inner dust band.
Methods. We explore the long-term behaviour of the minor bodies of the belt and how their lifetime depends on the orbital parameters of the planet, in particular for reaching a steady state.
Results. Our computations show that for an eccentricity of ![]() Eri b equal or higher than 0.15, the source belt is severely depleted of its original mass and substantially reduced in width. A ``dynamical'' limit of
Eri b equal or higher than 0.15, the source belt is severely depleted of its original mass and substantially reduced in width. A ``dynamical'' limit of
![]() comes out, which is inconsistent with the first estimate of the planet eccentricity (
comes out, which is inconsistent with the first estimate of the planet eccentricity (
![]() ), while the alternate value (
), while the alternate value (
![]() )
can be consistent within the uncertainties.
)
can be consistent within the uncertainties.
Key words: stars: planetary systems - minor planets - asteroids - celestial mechanics - stars: individual: Epsilon Eridani
1 Introduction
The nearby star ![]() Eridani might have a miniature solar system
around it.
A long-period Jupiter class planet orbiting at about 3.4 AU, named
planet ``b'', was discovered by Hatzes et al. (2000) from radial velocity
measurements. Graves et al. (1998) and Graves (2005) took submillimeter
images of the star environment and found evidence of a nearly circular dusty
ring extending from 30 to 110 AU from the star. This debris disk might be
material left over from the early stages of planetary formation.
The properties of the disk suggest the possibility of a planet ``d'' at about
40 AU from the star. Moreover, an infrared excess within 4.5'' of the star may
indicate an additional internal structure.
Eridani might have a miniature solar system
around it.
A long-period Jupiter class planet orbiting at about 3.4 AU, named
planet ``b'', was discovered by Hatzes et al. (2000) from radial velocity
measurements. Graves et al. (1998) and Graves (2005) took submillimeter
images of the star environment and found evidence of a nearly circular dusty
ring extending from 30 to 110 AU from the star. This debris disk might be
material left over from the early stages of planetary formation.
The properties of the disk suggest the possibility of a planet ``d'' at about
40 AU from the star. Moreover, an infrared excess within 4.5'' of the star may
indicate an additional internal structure.
A recent analysis, made on Spitzer observations of ![]() Eridani by
Backman et al. (2009), suggests a more complex spatial structure of the dusty
disk. The infrared excess has been interpreted as the result of two additional
warm dusty rings: a narrow belt of small (about 3
Eridani by
Backman et al. (2009), suggests a more complex spatial structure of the dusty
disk. The infrared excess has been interpreted as the result of two additional
warm dusty rings: a narrow belt of small (about 3 ![]() m) silicate grains
located at about 3 AU and a second belt at 20 AU.
We concentrate on the innermost belt by exploring the possibility that it can
be caused by fragmentation and cratering events involving a population of
bodies large enough not to be affected by P-R drag.
These bodies must be stable against the perturbations of planet ``b'';
otherwise, the whole belt would have been wiped away by now. The star is in
fact from 500 Myr to 1 Gyr old.
Additional sources external to the planet orbit cannot in fact supply
material, drifting inwards by non-gravitational forces (P-R drag), to the inner
belt due to the barrier raised by the planet strong gravity.
m) silicate grains
located at about 3 AU and a second belt at 20 AU.
We concentrate on the innermost belt by exploring the possibility that it can
be caused by fragmentation and cratering events involving a population of
bodies large enough not to be affected by P-R drag.
These bodies must be stable against the perturbations of planet ``b'';
otherwise, the whole belt would have been wiped away by now. The star is in
fact from 500 Myr to 1 Gyr old.
Additional sources external to the planet orbit cannot in fact supply
material, drifting inwards by non-gravitational forces (P-R drag), to the inner
belt due to the barrier raised by the planet strong gravity.
A pioneering work by Moran et al. (2004) described the evolution of the dusty belt under the dynamical perturbations of the inner planet and P-R drag, showing that the primary features of the resulting central dust distribution are clumps of particles trapped in mean motion resonances. However, Figs. 2 and 4 of their paper show that the particle density dramatically drops within the orbit of planet ``b''.
As a further test, we numerically integrated the trajectories of a large
number of
![]() dust grains (the size obtained from the model in Backman
et al.) started outside the orbit of the planet. We consider 4 different
rings (centred at 5, 6, 7, 8 AU) and let the particle evolve for
dust grains (the size obtained from the model in Backman
et al.) started outside the orbit of the planet. We consider 4 different
rings (centred at 5, 6, 7, 8 AU) and let the particle evolve for
![]() yr under P-R drag and planetary perturbations.
We find that less than 5% of the dust grains can pass the planet orbit and
reach the inner region (Fig. 1). In addition, their lifetime once
inside the planet is very short either because they are ejected out of the
system after a close encounter with the planet or because their drift rate is
very high due to their large eccentricity. The dust grains travelling within
the planet orbit have on average an eccentricity greater than 0.5 and reach the
star on a timescale of about 104 yr driven by P-R drag. The peaks in
Fig. 1, giving the fraction of particles inside the planet orbit,
decay in fact very rapidly for any outer source considered.
yr under P-R drag and planetary perturbations.
We find that less than 5% of the dust grains can pass the planet orbit and
reach the inner region (Fig. 1). In addition, their lifetime once
inside the planet is very short either because they are ejected out of the
system after a close encounter with the planet or because their drift rate is
very high due to their large eccentricity. The dust grains travelling within
the planet orbit have on average an eccentricity greater than 0.5 and reach the
star on a timescale of about 104 yr driven by P-R drag. The peaks in
Fig. 1, giving the fraction of particles inside the planet orbit,
decay in fact very rapidly for any outer source considered.
The total mass in the innermost belt, estimated by Backman et al. (2009) from
infrared fluxes, is about 1021 g. Invoking an external source would
require at least
![]() g (about 0.03 Earth masses) of material
flowing past 5 AU in the past 100 Myr. This estimate accounts for the short
lifetime of dust inside the planet orbit (shorter than 104 yr) and for
the lack of efficiency of the transport mechanism. It seems unlikely that such
a huge flux of mass can be produced by the collisional evolution of an
external belt, also accounting for the reduction of the transport efficiency
getting farther away from the planet (see Fig. 1).
If the inner belt is not the result of a very recent event (within the past
104 yr), the most reliable way to explain its existence is to invoke the
possibility of a local belt of large bodies producing dust by mutual
collisions. They might be planetesimals left over from the planet formation
process.
g (about 0.03 Earth masses) of material
flowing past 5 AU in the past 100 Myr. This estimate accounts for the short
lifetime of dust inside the planet orbit (shorter than 104 yr) and for
the lack of efficiency of the transport mechanism. It seems unlikely that such
a huge flux of mass can be produced by the collisional evolution of an
external belt, also accounting for the reduction of the transport efficiency
getting farther away from the planet (see Fig. 1).
If the inner belt is not the result of a very recent event (within the past
104 yr), the most reliable way to explain its existence is to invoke the
possibility of a local belt of large bodies producing dust by mutual
collisions. They might be planetesimals left over from the planet formation
process.
The most critical parameter for the stability of the parent belt is the
eccentricity ![]() of planet ``b''. Beyond a certain value of
of planet ``b''. Beyond a certain value of ![]() ,
a large
chaotic region appears within the planet orbit, triggered by mean-motion
resonance overlap. No kind of disk debris can survive long enough in this
region to explain the observed ring of dust.
,
a large
chaotic region appears within the planet orbit, triggered by mean-motion
resonance overlap. No kind of disk debris can survive long enough in this
region to explain the observed ring of dust.
Previous estimates of the planetary eccentricity, based on radial velocity and
astrometric measurements, gave
![]() (Benedict et al. 2006).
This value clearly contradicts the existence of the inner belt, as already
suggested by Backman et al. (2009); a different estimate reduces
(Benedict et al. 2006).
This value clearly contradicts the existence of the inner belt, as already
suggested by Backman et al. (2009); a different estimate reduces ![]() to
to
![]() (Butler et al. 2006).
(Butler et al. 2006).
We use the symplectic code SyMBA (Levison & Duncan 2000) to explore the stability of the
parent belt for different values of ![]() .
We concentrate on dust precursors
and in our simulations neglect any non-gravitational force. We first analyse
the source of instability for bodies populating the belt and then compute its
evolution towards the steady state by integrating over 20 Myr.
.
We concentrate on dust precursors
and in our simulations neglect any non-gravitational force. We first analyse
the source of instability for bodies populating the belt and then compute its
evolution towards the steady state by integrating over 20 Myr.
Section 2 describes the numerical model and the simulation set up, while Sect. 3 shows the results. Section 4 is devoted to some final considerations.
![\begin{figure}
\par\includegraphics[angle=270, width=9cm]{1609f1.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg14.png) |
Figure 1: Evolution with time of the fraction of dust particles residinginside the planet orbit for different possible outer sources. |
| Open with DEXTER | |
| |
Figure 2: Different behaviours of a test particle in the range 1.9-2.9 AU, during a short-time dynamical evolution (100 kyr). Further explanations in the text. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270, width=8cm]{1609f3a.eps} \includegraphics[angle=270, width=8cm]{1609f3b.eps} }\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg16.png) |
Figure 3:
Examples of particles jumping between overlapped resonances in the
inner belt before escaping. Planetary eccentricity is
|
| Open with DEXTER | |
2 Numerical set up
According to Backman et al. the innermost dusty belt in ![]() Eridani is centred at about
Eridani is centred at about
![]() AU with a width of
AU with a width of
![]() AU. Our model starts with a belt of massless bodies orbiting between 1.9
and 2.9 AU. This belt is moved slightly inside with respect to the model
proposed by Backman et al., but it accounts for the strong instability
caused by planet ``b'' when we approach its orbit.
AU. Our model starts with a belt of massless bodies orbiting between 1.9
and 2.9 AU. This belt is moved slightly inside with respect to the model
proposed by Backman et al., but it accounts for the strong instability
caused by planet ``b'' when we approach its orbit.
The bodies were initially placed in the orbital plane of the planet assuming
circular planar orbits. The planet ![]() Eri b is set at 3.39 AU, with
zero initial longitude of pericentre, and its eccentricity has been kept fixed
during the simulation: this is probably an approximation, because the suspected
presence of - at least - a second planet would cause a secular oscillation of
the eccentricity and the circulation of the pericentre argument.
Eri b is set at 3.39 AU, with
zero initial longitude of pericentre, and its eccentricity has been kept fixed
during the simulation: this is probably an approximation, because the suspected
presence of - at least - a second planet would cause a secular oscillation of
the eccentricity and the circulation of the pericentre argument.
We used two different sets of test particles:
- the first set consists in 100 bodies equally spaced between 1.9 and 2.9
AU, with pericentres initially aligned with the planetary one. It has been
used to grasp the basic dynamical features of the belt caused by the
gravitational pull of the planet. We varied the eccentricity of the planet
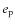 from 0 to 0.45 at equal steps of 0.05. The outcomes of these
simulations were also used to approximately detect a tentative limiting
value of
from 0 to 0.45 at equal steps of 0.05. The outcomes of these
simulations were also used to approximately detect a tentative limiting
value of 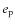 compatible with the inner belt;
compatible with the inner belt;
- the second set consists in 1000 equally spaced bodies, but with initial
pericentre arguments chosen randomly. In this case we recorded the number of
bodies (and their orbital elements) surviving within the belt every
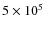 yr. For the most interesting range of planet eccentricity values
(
yr. For the most interesting range of planet eccentricity values
(
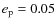 ,
0.10, and 0.15), we extended the numerical integrations for
,
0.10, and 0.15), we extended the numerical integrations for
 yr when a steady state was reached.
yr when a steady state was reached.
3 Belt evolution and stability
3.1 Dynamical behaviour
From the outcome of the short-term integrations, we divided the dynamical behaviour of the bodies into three classes:
- Stable: the semimajor axis and eccentricity oscillate regularly in time with constant amplitude (Fig. 2, left panel);
- Quickly unstable: their orbital elements vary rapidly with time, leading to ejection from the belt on a relatively short timescale (Fig. 2 middle panel);
- Mildly unstable: the bodies jump chaotically between different resonant states because of resonance overlap, but remain in the belt for an extended period of time. As the planetary eccentricity increases, this behaviour is more frequently only transient, followed by a final ejection of the particle, as shown in Fig. 3. A reliable identification of the regions strongly influenced by resonances requires a longer integration time and a more systematic exploration of the initial conditions. We discuss this point in the next section.
3.2 Reaching a steady state
The number of bodies in the belt surviving as long as 20 Myr is shown
in Fig. 4, for three values of ![]() (0.05, 0.10, and 0.15).
In all cases we have a rapid initial depletion until a steady state is
reached. On average, the population stabilises after 106 yr or
less, with a decrease of a few units in the past ten million years; therefore,
our relatively short timespan seems to be sufficient to predict the long-term
survival of the belt.
(0.05, 0.10, and 0.15).
In all cases we have a rapid initial depletion until a steady state is
reached. On average, the population stabilises after 106 yr or
less, with a decrease of a few units in the past ten million years; therefore,
our relatively short timespan seems to be sufficient to predict the long-term
survival of the belt.
These results are obtained within a 3-body model. As previously stated, the possibility of a second planet would further decrease the belt stability perturbing the orbit of planet ``b''. In this case the timescale for the belt evolution might be different and possibly related to the secular evolution of the planetary system.
![\begin{figure}
\par\includegraphics[angle=270, width=8.6cm]{1609f4.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg25.png) |
Figure 4:
Time evolution of the belt population for three different values of |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270, width=5.7cm]{1609f5a.eps} \...
...9f5b.eps} \includegraphics[angle=270, width=5.7cm]{1609f5c.eps} }
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg26.png) |
Figure 5: Eccentricities and semimajor axes of the belt particles after 20 Myr of dynamical integration. The vertical lines indicate the position of the most relevant resonances. In the lower plots, we represent the corresponding histograms. |
| Open with DEXTER | |
The observed initial fast depletion, on timescales of 104 yr, mostly stems
from strong instability quickly leading to a close encounter with the
planet. Moreover, for
![]() the Hill's sphere of the planet reaches
a minimum radius of
the Hill's sphere of the planet reaches
a minimum radius of
corresponding to the inner boundary of the belt, depleting it completely in a very short time. In a simulation performed with
In Fig. 5 we plot the orbital element distribution of the bodies
surviving at the end of the simulations in the (a, e) plane.
Dashed vertical lines mark the most relevant mean motion resonances. We
also plot the histogram of the number of bodies corresponding to various
semimajor axis bins.
For
![]() and 0.10, some excess survivors are clustered around the 3:2
and 4:3 resonances. At the 7:5 resonance location, an unstable region is
clearly visible in the plot with
and 0.10, some excess survivors are clustered around the 3:2
and 4:3 resonances. At the 7:5 resonance location, an unstable region is
clearly visible in the plot with
![]() .
The behaviour of the other
major resonances is unclear, even if a marked increase in eccentricity around
the 2:1 can be observed.
.
The behaviour of the other
major resonances is unclear, even if a marked increase in eccentricity around
the 2:1 can be observed.
For
![]() ,
resonances produce large gaps not only at their locations but
also in between, a clear indication of resonance overlap.
Almost the whole belt is depleted beyond 2.25 AU, and the inner residual
belt cannot replenish the outer regions since non-gravitational forces only
move particles inwards.
A few bodies appear to be permanently trapped at the 3:2 resonance, however
their total mass is less than 2% of the original mass.
According to Chen & Jura (2001), the amount of mass in source bodies
needed to produce the observed dust ring exceeds that of the present
asteroid belt in our Solar System. As a consequence, the bodies trapped at
the 3:2 resonance could be the source of the observed dust ring only if
they were part of an original belt almost 2 orders more massive than our
asteroid belt. This is an unlikely scenario.
,
resonances produce large gaps not only at their locations but
also in between, a clear indication of resonance overlap.
Almost the whole belt is depleted beyond 2.25 AU, and the inner residual
belt cannot replenish the outer regions since non-gravitational forces only
move particles inwards.
A few bodies appear to be permanently trapped at the 3:2 resonance, however
their total mass is less than 2% of the original mass.
According to Chen & Jura (2001), the amount of mass in source bodies
needed to produce the observed dust ring exceeds that of the present
asteroid belt in our Solar System. As a consequence, the bodies trapped at
the 3:2 resonance could be the source of the observed dust ring only if
they were part of an original belt almost 2 orders more massive than our
asteroid belt. This is an unlikely scenario.
In conclusion, the dust properties obtained from the spectral energy
distribution seem to be consistent with a planet eccentricity not greater than
about
![]() .
For larger eccentricities the source planetesimal belt
would be too depleted.
.
For larger eccentricities the source planetesimal belt
would be too depleted.
4 Discussion of results
An inner debris belt in the
As previously discussed, we have two different estimates of ![]() obtained
from radial velocities and astrometric measurements: the former
(Benedict et al. 2006) is clearly inconsistent with our limit; the latter
(Butler et al. 2006) seems to be rather high, but consistent with our results
within the error bars.
obtained
from radial velocities and astrometric measurements: the former
(Benedict et al. 2006) is clearly inconsistent with our limit; the latter
(Butler et al. 2006) seems to be rather high, but consistent with our results
within the error bars.
We note that our conclusions could be falsified essentially in two ways, both of them rather unlikely:
- The source of the dust is extremely massive (in this case it could come also from the region external to planet ``b'');
- The dust has been created by a recent event.
Acknowledgements
We are grateful to the referee M. Kuchner for useful suggestions. The work has been supported by ASI funds.
References
- Backman, D., Marengo, M., Stapelfeldt, K., et al. 2009, ApJ, 690, 1522 [NASA ADS] [CrossRef] (In the text)
- Benedict, G. F., McArthur, B. E., Gatewood, G., et al. 2006, AJ, 132, 2206 [NASA ADS] [CrossRef] (In the text)
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef] (In the text)
- Chen, C. H., & Jura, M. 2001, ApJ, 560, L171 [NASA ADS] [CrossRef] (In the text)
- Graves, J. 2005, Proceedings of the Miniworkshop on Nearby Resolved Debris Disks (In the text)
- Graves, J. S., Holland, W. S., Moriarty-Schieven, G., et al. 1998, ApJ, 506, L133 [NASA ADS] [CrossRef] (In the text)
- Hatzes, A. P., Cochran, W. D., McArthur, B., et al. 2000, ApJ, 544, L145 [NASA ADS] [CrossRef] (In the text)
- Levison, H. F., & Duncan, M. J. 2000, AJ, 120, 2117 [NASA ADS] [CrossRef] (In the text)
- Moran, S. M., Kuchner, M. J., & Holman, M. J. 2004, ApJ, 612, 1163 [NASA ADS] [CrossRef] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[angle=270, width=9cm]{1609f1.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg14.png) |
Figure 1: Evolution with time of the fraction of dust particles residinginside the planet orbit for different possible outer sources. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Different behaviours of a test particle in the range 1.9-2.9 AU, during a short-time dynamical evolution (100 kyr). Further explanations in the text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270, width=8cm]{1609f3a.eps} \includegraphics[angle=270, width=8cm]{1609f3b.eps} }\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg16.png) |
Figure 3:
Examples of particles jumping between overlapped resonances in the
inner belt before escaping. Planetary eccentricity is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270, width=8.6cm]{1609f4.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg25.png) |
Figure 4:
Time evolution of the belt population for three different values of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270, width=5.7cm]{1609f5a.eps} \...
...9f5b.eps} \includegraphics[angle=270, width=5.7cm]{1609f5c.eps} }
\end{figure}](/articles/aa/full_html/2009/20/aa11609-08/Timg26.png) |
Figure 5: Eccentricities and semimajor axes of the belt particles after 20 Myr of dynamical integration. The vertical lines indicate the position of the most relevant resonances. In the lower plots, we represent the corresponding histograms. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


