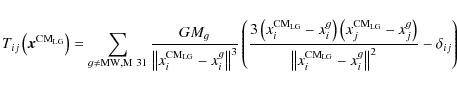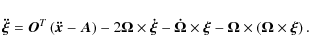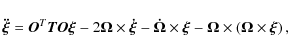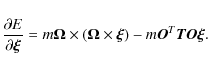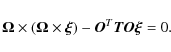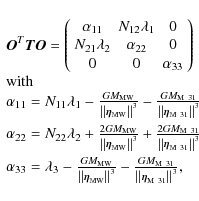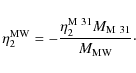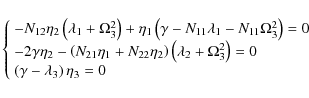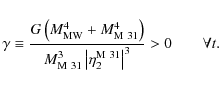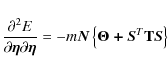| Issue |
A&A
Volume 499, Number 2, May IV 2009
|
|
|---|---|---|
| Page(s) | 385 - 394 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200811153 | |
| Published online | 16 April 2009 | |
Tidal effects on the spatial structure of the Local Group
S. Pasetto1,2 - C. Chiosi3,4
1 - Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12-14,
69120 Heidelberg, Germany
2 -
Max Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
3 -
Department of Astronomy, Padova University, Vicolo
dell'Osservatorio 2, 35122 Padova, Italy
4 -
Max Planck Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
Received 15 October 2008 / Accepted 18 February 2009
Abstract
Aims. The spatial distribution of galaxies in the Local Group (LG) is the footprint of its formation mechanism and the gravitational interactions among its members and the external massive galaxies or galaxy groups. Using a 3D-geometrical description of the spatial distribution of all the members of the LG (not only the satellites of the MW and M 31) based on present-day data of positions and distances, we found in our previous study that all galaxies (MW, M 31, their satellites, and even the most distant objects) are confined within a slab of about 200 kpc thickness. Examining how external galaxies or groups would gravitationally affect (and eventually alter) the planar structure (and its temporal evolution) of the LG, they found that the external force field acts parallel to the plane determined by geometry and studied this with the Least Action Principle.
Methods. In this paper, we thoroughly investigated the role played by the tidal forces exerted by external galaxies or galaxy groups on the LG galaxies (the most distant dwarfs in particular) in shaping their large-scale distribution. We studied in particular an idea based on the well-known effect of tidal interactions, according to which a system of mass-points can undergo not only tidal stripping but also tidal compression and thus become flatter.
Results. Excluding the dwarf galaxies tightly bound to the MW and M 31, the same tidal forces can account for the planar distribution of the remaining dwarf galaxies. We analytically recover our previous results and prove that a planar distribution of the LG dwarf galaxies is compatible with the external force field. We also highlight the physical cause of this result.
Key words: galaxies: Local Group - galaxies: dwarf - galaxies: kinematics and dynamics
1 Introduction
Over the years, many attempts have been made to find the spatial
distribution of the LG galaxies. Limiting ourselves to a few
pioneering studies
Kahn & Woltjer (1959) and
Raychaudhury & Lynden-Bell (1989) suggested a planar distribution based on
studies of the LG dynamics; Hartwick (2000) found a
flat ellipsoid with axial ratios
![]() ,
which does not differ too much from a plane; and finally
Kunkel (1979), (), and
Fusi Pecci et al. (1995) suggested that the satellite dwarf
galaxies of the MW and M 31 lie on planes
,
which does not differ too much from a plane; and finally
Kunkel (1979), (), and
Fusi Pecci et al. (1995) suggested that the satellite dwarf
galaxies of the MW and M 31 lie on planes![]() .
.
Kroupa et al. (2005) and Metz et al. (2007) suggested the satellites of the MW occupied a planar distribution, which however could also be explained as a consequence of the distribution of sub-haloes (Zentner et al. 2005) in the early cosmological stages (Kang et al. 2005). The same problem was investigated by Koch & Grebel (2006) for the satellites of M 31 with similar conclusions.
Starting from the basic idea that an off-center hydrodynamical collision occurred some 10 Gyr ago between the primordial gas-rich M 31 galaxy and the MW, and compressed the halo gas to form all the LG dwarf galaxies, Sawa & Fujimoto (2005) suggested that the new-born dwarf galaxies would be located near the orbital plane of the MW and M 31. They argued that this view is also consistent with their visual inspection of the 2D sky distribution of the LG members and that a well-defined plane of finite thickness is found, within which most of the member galaxies are confined.
Pasetto & Chiosi (2007, hereafter PC07) attacked the problem from a completely different perspective. In summary, adopting known positions and distances and using analytical geometry, they looked for the plane that minimizes the distances of all galaxies in the LG with respect to it (not only the MW and M 31 and their satellites, but also the distant dwarfs). The second part of their study was to find a dynamical justification of the planar distribution. To this aim, they applied the Hamilton Method (Minimum Action) to investigate the dynamics of the LG complex and the action of the gravitational forces exerted by external nearby galaxies or groups. They found that the planar distribution is fully compatible with the minimum action and that the external force field is probably compatible within the plane determination. This field would then pull the LG galaxies along, without altering their planar distribution. Special care was taken to evaluate the robustness of the result.
To explain the different results obtained by Kroupa et al. (2005), Koch & Grebel (2006), and Sawa & Fujimoto (2005), we note that the various studies did not use identical galaxy samplings, they did not start from the same working physical hypotheses nor they deal with the same dynamical regime. In brief:
- (i)
- the planes for the MW and M 31 satellites (Koch & Grebel 2006; Kroupa et al. 2005,
respectively) are of a
local nature because they are the consequence of strong collisional
dynamics with the host galaxy (hereafter HG). No easy explanation can be found as to why these planes survive for long time (more
than a few dynamical time scales) due to the peculiar proper motions
of the dwarfs that determine these planes (see, e.g., the ideas in Lynden-Bell & Lynden-Bell 1995; Palma et al. 2002; Lynden-Bell 1983;
applied then by Metz et al. 2008). The role of
distant dwarfs in determining the structure of the whole LG is
not considered. Therefore, these planes cannot be extended
to the whole LG;
- (ii)
- in Sawa & Fujimoto (2005), the solution for a
common plane is based on the ad hoc initial hypothesis concerning the
origin of the angular momentum. The
sample of dwarf galaxies used to determine the plane is
limited to the satellites of the two HGs. Finally, the
orbits of these dwarfs are constrained to lie on this plane;
- (iii)
- in PC07, the common plane is chosen by assuming that it contains the MW and M 31 and minimizing the distances of all remaining LG galaxies to this plane, including also the distant ones. This can be justified by considering that the HG satellites are strongly influenced by local dynamics (with continuous modification of their orbits, including possible captures by the HGs) and that if a common planar distribution for all LG galaxies exists, this should evidenced by the more external galaxies. They are much less likely to be affected by strong interactions with one of the HGs and therefore more sensitive to the influence of external galaxies and/or groups. The plane found by PC07 is a slab of about 200 kpc thickness, i.e., the largest apo-center of the HG satellites most probably falls inside this slab.
The main goal of this study is to highlight the physical nature of the results obtained by PC07, which had a rather complicated dynamical description requiring a numerical approach. We therefore develop a simpler linear approximation that is much easier to handle and yet able to provide a physical insight.
The plan of the paper is as follows. In Sect. 2, we define the tidal-force field acting on the whole LG. The tidal forces are those developed by external groups of galaxies. We combine the MW with its satellites (M 31 and its satellites) for which a suitable treatment is required and look at the remaining dwarf galaxies. On a long timescale, the external tidal forces can engender a planar distribution of these dwarf galaxies in the LG. In Sect. 3, we go deeper into this issue and check whether the planar distribution is a mere coincidence or the consequence of fundamental laws of mechanics. The answer is the latter: the planar distribution corresponds to a minimum energy and stable configuration of the whole system. The dwarf galaxies must lie on a plane because of the long timescale influence of the tidal forces exerted by massive galaxies or galaxy groups external to the LG. Furthermore, the plane found by PC07 and the minimum energy plane are coincident and the situation is stable. Finally, in Sect. 4 we summarize our results and present some general considerations.
2 LG structure and tidal forces
Looking at the composition of the LG, three main components can be identified: two massive galaxies (MW and M 31), their respective groups of bounded satellites, and a large number of distant dwarfs galaxies loosely interacting or even uncoupled to the dominant galaxies. As far as the gravitational interaction is concerned, there are two questions we are interested in addressing:
- (1)
- How does the external force field change with time?
- (2)
- Have the dwarf galaxies that are not members of the MW or the M 31 family been affected by the tidal interaction with the external force field?
Frame of reference. The true mutual interaction between the MW and M 31 suggests
that they can be considered as a privileged system, whose center of
mass (CM) can be assumed to be the origin of a reference frame
(presented in Fig. 1 and described in more detail
below). The positions and motions of any other dwarf in
the LG that is not a member of the MW and M 31 families can be given relative to this CM. This is
reminiscent of the geometry of the restricted three-body problem (e.g.,
Szebehely 1967) but here the time evolution of the CM will be followed. In particular, the stationary action principle was applied in PC07 to produce a possible solution for the motion of the external groups acting gravitationally on the LG as well as MW and M 31 (their Table 4). From this solution, we can infer the spatial evolution in the time, t, of the entire LG-barycentric system
![]() ,
which is nearly coincident with the center of mass of the
MW + M 31 system.
,
which is nearly coincident with the center of mass of the
MW + M 31 system.
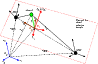 |
Figure 1:
Sketch of the geometrical framework we have
adopted. First, we define the inertial reference frame, always named S0,
with axis
|
| Open with DEXTER | |
Table 1: External galaxy groups gravitationally influencing the LG dynamics.
We started by considering the general expression for the
external tidal tensor as function of any potential ![]() expressed in the reference system S0 of Fig. 1, to describe the
external tidal tensor acting on the complex MW+M 31
expressed in the reference system S0 of Fig. 1, to describe the
external tidal tensor acting on the complex MW+M 31
where G is the gravitational constant, xg are the coordinates of the external galaxy groups of Table 1 of mass Mg,
To obtain an idea of the effects we are looking for, we make the
following preliminary considerations. We assume that the most distant dwarfs defining the plane ![]() discovered by PC07 have positions that are determined, in their initial conditions (e.g., 9 Gry ago), by the tidal
tensor of external objects. We then expect the total tidal tensor
(TTT),
discovered by PC07 have positions that are determined, in their initial conditions (e.g., 9 Gry ago), by the tidal
tensor of external objects. We then expect the total tidal tensor
(TTT),
![]() ,
defined by
Eq. (1) including in the sum also the MW and M 31, to
give, if reduced to its normal form, a single most negative eigenvalue. Between the three eigenvectors of TTT, the one corresponding to this most negative eigenvalue will indicate the direction of the
tidal compression (see classical textbooks such as
Misner et al. 1973, Chap. 1; Binney & Tremaine 1987,
Chap. 7; or some applications as in Raychaudhury & Lynden-Bell 1989). Thus, if
we also find this behavior in our TTT evaluated at the position of a dwarf galaxy
far away from the MW or M 31, this could imply that the compression does indeed occur.
For example, a simple case would be
that a dwarf presently belonging to the plane
,
defined by
Eq. (1) including in the sum also the MW and M 31, to
give, if reduced to its normal form, a single most negative eigenvalue. Between the three eigenvectors of TTT, the one corresponding to this most negative eigenvalue will indicate the direction of the
tidal compression (see classical textbooks such as
Misner et al. 1973, Chap. 1; Binney & Tremaine 1987,
Chap. 7; or some applications as in Raychaudhury & Lynden-Bell 1989). Thus, if
we also find this behavior in our TTT evaluated at the position of a dwarf galaxy
far away from the MW or M 31, this could imply that the compression does indeed occur.
For example, a simple case would be
that a dwarf presently belonging to the plane ![]() was also formed
by some mechanism in the plane
was also formed
by some mechanism in the plane ![]() or close to it. In this case we can hypothesize that the tidal force acting on this dwarf
should be similar to the tidal force that acted on the plane
in the past, say 9 Gyr ago. We can estimate these eigenvalues and their eigenvector directions by combining the
equations of the plane
or close to it. In this case we can hypothesize that the tidal force acting on this dwarf
should be similar to the tidal force that acted on the plane
in the past, say 9 Gyr ago. We can estimate these eigenvalues and their eigenvector directions by combining the
equations of the plane ![]() (see Eq. (2)), obtained by considering the current dwarf galaxy distribution, and
Eq. (1), which can also be evaluated backwards in time. If we find compatible values between different points at different epochs, then we can
claim that the effect we are searching for may have occurred.
(see Eq. (2)), obtained by considering the current dwarf galaxy distribution, and
Eq. (1), which can also be evaluated backwards in time. If we find compatible values between different points at different epochs, then we can
claim that the effect we are searching for may have occurred.
If the plane ![]() is a slab with a diameter of 4 Mpc and 200 kpc thick, we can evaluate the TTT at any point on this plane
is a slab with a diameter of 4 Mpc and 200 kpc thick, we can evaluate the TTT at any point on this plane
![]() ,
say 2 Mpc away from the barycenter of the LG,
,
say 2 Mpc away from the barycenter of the LG,
![]() .
The
resulting eigenvalue of this tidal tensor, e.g., 9 Gyr ago, is
.
The
resulting eigenvalue of this tidal tensor, e.g., 9 Gyr ago, is
![]() .
The same
evaluation can then be repeated for the barycenter position
.
The same
evaluation can then be repeated for the barycenter position
![]() ,
obtaining
,
obtaining
![]() .
This result strongly suggests that in the past the force
determining the subsequent orbital evolution of a generic dwarf had
a component that squeezed the motion toward the plane. Proceeding in this way, we can prove the compatibility of the eigenvalues of the TTT for every position on the plane
.
This result strongly suggests that in the past the force
determining the subsequent orbital evolution of a generic dwarf had
a component that squeezed the motion toward the plane. Proceeding in this way, we can prove the compatibility of the eigenvalues of the TTT for every position on the plane ![]() ,
i.e.,
,
i.e.,
![]() .
This clearly allows us
to explore the possibility that the plane
.
This clearly allows us
to explore the possibility that the plane ![]() of PC07 is produced by the tidal forces acting on the LG during a large
fraction of the Hubble time, i.e., we want to extend this estimation not only to the present time t=t0 but also to the time
of PC07 is produced by the tidal forces acting on the LG during a large
fraction of the Hubble time, i.e., we want to extend this estimation not only to the present time t=t0 but also to the time![]() t<t0.
t<t0.
Table 2:
Temporal evolution of the eigenvalues
and eigenvectors as a function of the look-back time
![]() in Gyr.
in Gyr.
To proceed further, we need to search the eigenvectors
associated with the tidal tensor that have the most negative eigenvalues.
In the limits of our approximation, they should retain a
direction with respect to an inertial reference frame not too far from the normal to the geometrically plane
![]() for most of
the Hubble time, which can nowadays be inferred by simple inspection of the dwarf galaxies' distribution in the LG. To prove this, we solve the eigensystem for the
tidal tensor of Eq. (1) as a function of time. The solutions are presented in
Table 2: the three eigenvalues are in Cols. (2) to (4) and the
corresponding eigenvectors are in Cols. (5) through (13). The results in which we are interested are limited in time to a range where monotonicity of the trend of the eigenvalues can be exploited to reveal an integrated cumulative effect of compression or expansion. We find that our range of interest must cover the past
9 Gyr, imposing a lower limit to our analysis of
for most of
the Hubble time, which can nowadays be inferred by simple inspection of the dwarf galaxies' distribution in the LG. To prove this, we solve the eigensystem for the
tidal tensor of Eq. (1) as a function of time. The solutions are presented in
Table 2: the three eigenvalues are in Cols. (2) to (4) and the
corresponding eigenvectors are in Cols. (5) through (13). The results in which we are interested are limited in time to a range where monotonicity of the trend of the eigenvalues can be exploited to reveal an integrated cumulative effect of compression or expansion. We find that our range of interest must cover the past
9 Gyr, imposing a lower limit to our analysis of
![]() Gyr. Before this
Gyr. Before this
![]() ,
the configuration of the eigenvalues differs slightly. From Table 2, we see that the time evolution of the eigenvalues shows a phase with one compressive direction compared to two positive expansion directions, and before that, as well as after
,
the configuration of the eigenvalues differs slightly. From Table 2, we see that the time evolution of the eigenvalues shows a phase with one compressive direction compared to two positive expansion directions, and before that, as well as after
![]() ,
we see two negative directions compared with one positive. For simplicity, we do not be treat analytically these switchings between the configurations. We are only interested in the last most-dominant time-evolution of the monotonic behavior of the eigenvalues.
Since we exclude the first three rows of Table 2 (the primordial evolution prior to
,
we see two negative directions compared with one positive. For simplicity, we do not be treat analytically these switchings between the configurations. We are only interested in the last most-dominant time-evolution of the monotonic behavior of the eigenvalues.
Since we exclude the first three rows of Table 2 (the primordial evolution prior to
![]() )
from our analysis, from now on, we uniquely identify (unless otherwise specified) with
)
from our analysis, from now on, we uniquely identify (unless otherwise specified) with ![]() ,
,
![]() ,
and
,
and ![]() ,
the positive eigenvalue, the second negative eigenvalue, and the most negative eigenvalue, respectively, for the eigenvectors of the external tidal tensor defined in Eq. (1) followed in their time t evolution exclusively for
,
the positive eigenvalue, the second negative eigenvalue, and the most negative eigenvalue, respectively, for the eigenvectors of the external tidal tensor defined in Eq. (1) followed in their time t evolution exclusively for
![]() .
The most negative eigenvalue (Col. 4) and its evolution in the
past 9 Gyr and projections of the associated eigenvector onto the
axes of the inertial system are highlighted in italics. The
time variations in the three eigenvalues are shown in
Fig. 2.
.
The most negative eigenvalue (Col. 4) and its evolution in the
past 9 Gyr and projections of the associated eigenvector onto the
axes of the inertial system are highlighted in italics. The
time variations in the three eigenvalues are shown in
Fig. 2.
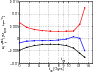 |
Figure 2:
Evolution of the eigenvalues
|
| Open with DEXTER | |
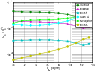 |
Figure 3:
Here we tracked back the influence of each individual component in the sum of Eq. (1) for the most negative eigenvalue,
|
| Open with DEXTER | |
From the data displayed in Fig. 2, it is evident that one of the negative eigenvalues dominates. Therefore, the external field acting on the LG may produce the planar distribution of the dwarf galaxies. This is an interesting result because:
- 1.
- it proves that, using the tidal tensor,
we can obtain analytically the same
results as PC07 for the behavior of the external field.
The external force field turns out to be
compatible with the dwarf galaxies being in a flat spatial distribution
that remains constant for a large fraction of the Hubble
time. Moreover, we can argue that the external force field
had already started to flatten the spatial distribution of the dwarf galaxies
prior to
 .
If we investigate the relevance of the different groups on this flattening effect in more detail, we can plot in Fig. 3 the normalized trend of the most negative eigenvalues of Eq. (1) divided into its components. Here we see the most negative eigenvalues of the sum in Eq. (1) normalized to the overall sum (hence the black line in Fig. 2 represents the unitary constant upper bound to the figure). As we can infer from the figure, the influence of the IC342 group has always been the most significant, followed by the effects of Maffei, Sculptor, and Cen A groups. This is expected from their masses and positions listed in Table 1. The time evolution shown in this Figure confirms their relative importance in the compressing effect on the LG for its temporal evolution. The contribution of the M 83 group is slightly less important, although is was nevertheless as important as that of the M81 group 11 Gyr ago;
.
If we investigate the relevance of the different groups on this flattening effect in more detail, we can plot in Fig. 3 the normalized trend of the most negative eigenvalues of Eq. (1) divided into its components. Here we see the most negative eigenvalues of the sum in Eq. (1) normalized to the overall sum (hence the black line in Fig. 2 represents the unitary constant upper bound to the figure). As we can infer from the figure, the influence of the IC342 group has always been the most significant, followed by the effects of Maffei, Sculptor, and Cen A groups. This is expected from their masses and positions listed in Table 1. The time evolution shown in this Figure confirms their relative importance in the compressing effect on the LG for its temporal evolution. The contribution of the M 83 group is slightly less important, although is was nevertheless as important as that of the M81 group 11 Gyr ago;
- 2.
- we must clarify once and for all that the present result does not
prove that the spatial distribution of dwarf galaxies in the LG must be flat, but only that the external force field is compatible
with such a flat distribution;
- 3.
- the external force field acting only on the two
main HGs (MW and M 31) of the LG is compatible with a flat spatial
distribution of the distant dwarfs, but this does not provide any constraint on the
distribution of the nearby dwarf satellites around their HG (both MW and
M 31);
- 4.
- furthermore, the planar distribution detected in the geometrical analysis of PC07 cannot a priori be related to the planar distribution suggested by the compression effect described by the tidal tensor affecting the LG. The subject of the following analysis is to explain the coincidence claimed by PC07 between the geometrical and dynamical planes.
The equation for the plane ![]() can be rewritten here in
the reference frame S0 as
can be rewritten here in
the reference frame S0 as
with a direction
| |
Figure 4:
The Hammer projection of the sky position of the normal
to the plane found by PC07 (from purely geometrical arguments). The color code from light red to dark brown corresponds to
the 3 |
| Open with DEXTER | |
Considering that every point in this map has an error radius of about
![]() ,
inherited from the Minimum Action analysis, and
considering the uncertainty in the angular definition of the
direction of
,
inherited from the Minimum Action analysis, and
considering the uncertainty in the angular definition of the
direction of
![]() ,
the
normal to the geometrical plane and the direction of the vector
associated with the most negative eigenvalue are compatible at the present time at
the 3
,
the
normal to the geometrical plane and the direction of the vector
associated with the most negative eigenvalue are compatible at the present time at
the 3![]() -level of confidence. Moreover, the eigenvector of the most negative
eigenvalue
-level of confidence. Moreover, the eigenvector of the most negative
eigenvalue ![]() of the tidal tensor moves, maintaining a direction not so far from the direction that we can nowadays deduce from the observation for
of the tidal tensor moves, maintaining a direction not so far from the direction that we can nowadays deduce from the observation for
![]() .
This result, which was already present in PC07, is recovered
here in a semi-analytical treatment of the whole problem.
The key question to be answered now is whether the
coincidence is causal or casual and what the meaning
of all this is.
.
This result, which was already present in PC07, is recovered
here in a semi-analytical treatment of the whole problem.
The key question to be answered now is whether the
coincidence is causal or casual and what the meaning
of all this is.
3 Causal or casual?
The tidal tensor can be derived from the Taylor expansion of the force field (see next section). This implies that the object we want to investigate (a dwarf galaxy) is influenced by a smoothly varying potential in the course of its evolution.
The large-scale description of the gravitational interaction adopted here and by PC07 becomes inaccurate on the distance scales of the closer HG-dwarf satellite interactions where satellite dwarf galaxies experience kick-off, are continually absorbed into the halo of the HG (MW and M 31 in our case) and the collisionless description is incorrect. A dwarf galaxy in these closer samples, which experiences a far stronger direct interaction with the HG, does not respond significantly to the weaker external field acting on it. On the other hand, the collisionless description is suited to deal with the effects of distant galaxy groups (see the list in Table 1) and hence the influence of the external field on the other dwarf galaxies far away from a HG (see e.g., Raychaudhury & Lynden-Bell 1989; Dunn & Laflamme 1993; Peebles 1994,1990).
To formalize out results in the previous section, we present the following two hypotheses, one about the directions of the eigenvectors and the other about their values:
- 1.
- we do not consider the evolutionary stages of the
Universe older than
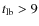 Gyr (look-back time) when assuming a monotonic behavior of a single negative eigenvalue;
Gyr (look-back time) when assuming a monotonic behavior of a single negative eigenvalue;
- 2.
- we assume that the eigenvector corresponding to the most negative eigenvalue always points in the same direction as the inertial reference frame in the non-comoving coordinate system.
Equations of motion. We note only that the generic position vectors in the two reference frames are now written as
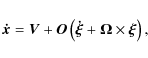
where
The time derivative of the velocity equation yields the equation of motion
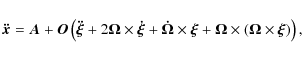
where in the second equation the vector
From this last equation it is evident that the acceleration
From Eq. (3), it is clear how the term
providing the acceleration of a generic dwarf can be evaluated,
![]() .
The acceleration of a dwarf galaxy in S0 is due
to three contributions: the gradient in the external potential
.
The acceleration of a dwarf galaxy in S0 is due
to three contributions: the gradient in the external potential
![]() ,
the gradient in the MW potential
,
the gradient in the MW potential
![]() ,
and the gradient in the M 31 potential,
,
and the gradient in the M 31 potential,
![]() ,
i.e.,
,
i.e.,
After applying a Taylor expansion to
| (5) |
together with two other similar relations for the potentials of MW and M 31 that are not given here for the sake of brevity, with
By introducing the TTT as defined in the preceding section with
and using
where we have dropped the explicit dependence on the position of the tidal tensor
3.1 Energy states of equilibrium
Our aim now is to understand whether the equation of motion in Eq. (6) can lead to stable equilibrium configurations. There are several techniques for attacking this problem based on the integration of the force or the impulse over a time interval (see e.g., Binney & Tremaine (1987, Chap. 7), the elegant Lagrangian treatment of Gnedin et al. (1999), or the sophisticated analysis in the action space of Weinberg (1994b,a).
To proceed further, we identify for the energy equilibrium configurations and the stability of a system governed by the equations of motion Eq. (6). Here, we take advantage of being able to follow the evolution of the angular velocity of the non-inertial reference frame by looking at the motion on the sky of the eigenvector of the tidal tensor as already achieved in previous sections for the quadrupole (see Fig. 2).
It can be demonstrated that the Lagrangian leading to Eq. (6), up to a total derivative, can be written as
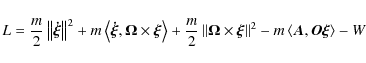
(see for instance Landau & Lifshitz 1969). Therefore, taking the linear momentum
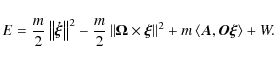
Taking the derivative with respect to the positions, we obtain
The equilibrium energy is then given by the solution of the equation
In the reference frame S1, by definition the external tidal tensor is always diagonal, i.e.,
On the basis of these considerations, we can suppose that
![]() ,
i.e., there
exists a linear operator represented by a rotational matrix
,
i.e., there
exists a linear operator represented by a rotational matrix
![]() such that the generic position vector of a
dwarf galaxy in S1,
such that the generic position vector of a
dwarf galaxy in S1, ![]() ,
can be written as a function of
the generic position vector in S2,
,
can be written as a function of
the generic position vector in S2,
![]() ,
and the tidal
tensor of the external potential
can be written as:
,
and the tidal
tensor of the external potential
can be written as:
| |
= | 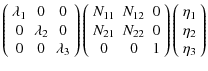 |
|
| = | 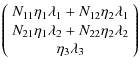 |
where we have adopted a rotation matrix spinning about
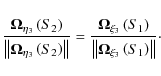
For example, we can explicitly write the matrix
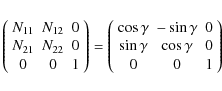
where
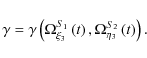
This also means that the angular velocity is not related to the angular momentum in a straightforward way. It will indeed be the result of the combined action of the centrifugal force due to the rotation of the frame tightened to the external force field, i.e.,
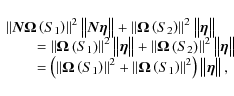
where
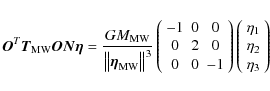
where for simplicity we have assumed that
which provides a simple description of the tidal effects. The above relation can be simplified further by recalling that, from the definition of barycenter in the reference frame in use, we can write
Inserting this expression into Eq. (8), written in the S2 frame, and using the relation
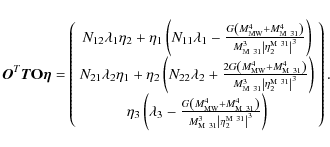
In the same way, we can derive the term due to the apparent force. Switching to the revolving system S2, we apply another rotation expressed by

The associated equilibrium energy state is given by the solution of the systems
where
The system of equations given in Eq. (10) is the result we are looking for. It is evident from these equations that the plane
The above result is fully adequate for our purposes because the total potential is separated into radial and vertical components. This is a standard consequence of the linear approximation obtained by truncating the Taylor expansion of the potential at the second order. Equivalently, one could use a generating function satisfying the Stakel theorem for separability in a Hamilton-Jacobi equation for the above system (e.g. Boccaletti & Pucacco 1998).
As far as the temporal evolution is concerned (
![]() ), we have
), we have
![]() which, translated into our spatial resolution,
simply means a physical spatial resolution
which, translated into our spatial resolution,
simply means a physical spatial resolution
![]() .
Furthermore, one can never have
.
Furthermore, one can never have
![]() because this would imply that
because this would imply that
![]() ,
whereas according to the
definition in Eq. (11), we have
,
whereas according to the
definition in Eq. (11), we have
![]() ,
and finally
,
and finally
![]() Gyr as shown by
Fig. 2. These last two conditions are clearly inconsistent leading to a contradiction that concludes our proof as required.
Gyr as shown by
Fig. 2. These last two conditions are clearly inconsistent leading to a contradiction that concludes our proof as required.
Therefore, the major conclusion of this demonstration is that the only possible solution is the following one: the statistical minimization of PC07 is compatible with a planar distribution of the dwarfs and it is not a mere coincidence. This result completes the missing interpretation of the result already included in PC07.
3.2 Stability of the equilibrium configuration
Finally, we examine the stability of the equilibrium plane that we have found by solving Eq. (10). We take the energy of Eq. (7) written for the system S2![\begin{displaymath}\frac{{\partial E}} {{\partial {\vec{\eta }}}} =
m{\vec{N}}\l...
...eta }}} \right)} \right] -
m{\vec{O}}^T {\vec{T{\rm O}N\eta }}
\end{displaymath}](/articles/aa/full_html/2009/20/aa11153-08/img152.png)
and calculate the derivative
![\begin{displaymath}\frac{{\partial ^2 E}} {{\partial {\vec{\eta }}\partial
{\vec...
...\left[ {{\vec{\Gamma N}}} \right]_{{ij}} \eta _{j} }
\right\},
\end{displaymath}](/articles/aa/full_html/2009/20/aa11153-08/img153.png)
where
where we have defined another matrix
| |
|||
| = | 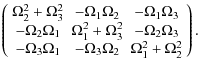 |
This matrix has no inverse, determinant
At this stage, the usual procedure would be to solve for the eigensystem in
Eq. (12). However, we can avoid this complication by
noticing that in the linear approximation the vertical potential
decouples from the radial one. In other words, by applying the full
procedure we would obtain three eigenvalues
![]() ,
where
,
where
![]() and
and
![]() are two complicated functions of
time, whereas the last eigenvalue has to be exactly the most
negative eigenvalue of the external tidal field for which we have
already calculated the time dependence as shown in Fig.
2. As long as the eigenvalue
remains negative, the relation
are two complicated functions of
time, whereas the last eigenvalue has to be exactly the most
negative eigenvalue of the external tidal field for which we have
already calculated the time dependence as shown in Fig.
2. As long as the eigenvalue
remains negative, the relation
![]() holds because
holds because
![]() by definition (Eq. (10)) whereas
by definition (Eq. (10)) whereas
![]() as required in
Fig. 2. Therefore,
the plane
as required in
Fig. 2. Therefore,
the plane ![]() is stable.
is stable.
3.3 Equations of motion and force balance
Finally, we can obtain a much deeper insight into the physical reasons
for the existence of the plane ![]() by analyzing
the equation of motion in S2. If the plane
by analyzing
the equation of motion in S2. If the plane ![]() is a stable configuration of the spatial distribution of dwarf galaxies,
it is important to isolate the force acting
on it. The equations of motion in S2 are, from e.g., Eq. (6),
is a stable configuration of the spatial distribution of dwarf galaxies,
it is important to isolate the force acting
on it. The equations of motion in S2 are, from e.g., Eq. (6),
| |
= | ||
where for the different elements of the tidal tensor we can now write

an analogous equation for MW, and
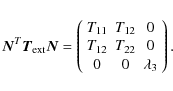
The equilibrium in the
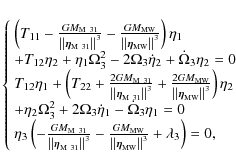
which sheds light on what is happening in reality
Along the direction orthogonal to the plane ![]() ,
three forces
are present. One is due to the MW,
,
three forces
are present. One is due to the MW,
![]() ,
another due to M 31,
,
another due to M 31,
![]() ,
and the third one due to the external field
,
and the third one due to the external field
![]() .
They
all accumulate and act by influencing the initial motion conditions of the proto-dwarf galaxies and by preventing the dwarfs to escape from the equilibrium positions within the plane.
Therefore these forces are responsible for the flattening of the whole system.
This tendency of flattening the distribution of dwarf galaxies, and
ensuring the stability of the plane
.
They
all accumulate and act by influencing the initial motion conditions of the proto-dwarf galaxies and by preventing the dwarfs to escape from the equilibrium positions within the plane.
Therefore these forces are responsible for the flattening of the whole system.
This tendency of flattening the distribution of dwarf galaxies, and
ensuring the stability of the plane ![]() ,
can be considered valid
in the limit of the linear approximation, i.e., roughly for 150 kpc
above and below the plane and for a period of time of roughly 9 Gyr,
thus being partially able to imprint the initial proper motions of
the dwarf galaxies taken into consideration for the Local Group.
,
can be considered valid
in the limit of the linear approximation, i.e., roughly for 150 kpc
above and below the plane and for a period of time of roughly 9 Gyr,
thus being partially able to imprint the initial proper motions of
the dwarf galaxies taken into consideration for the Local Group.
Along the directions parallel to the plane, the situation is more
complicated and described by relations such as
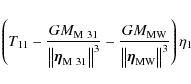
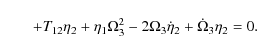
The first two terms in the sum on the left hand side are due to the tidal field that has to balance the third term due to the centrifugal force, the last term is due to the Coriolis effect and the extra term is derived from a non-uniform rotation of the system S2. The same kind of relation holds for the other coordinates.
4 Summary, conclusions, and consideration about the limits of the approach used
The spatial distribution of the galaxies in the LG is the footprint of its formation mechanism, the internal gravitational interactions among the galaxies, and the gravitational action of external massive galaxies or galaxy groups on the LG members.
In this paper, we have thoroughly addressed the whole subject focusing attention on the role played by the tidal force field exerted by external galaxies or galaxy groups on the dwarf galaxies of the LG, excluding those that are clearly under the dominant gravitational effects of the HGs, in shaping the large-scale distribution of the LG galaxies.
The idea stands on the well-known effect of tidal interactions, which can be expressed as a function of the gradient in the gravitational force. While the gravitational force never changes sign, its gradient can do so. Moreover, while the gravitational force field at any distance from the center of mass of a system depends only on the inner distribution of matter, the tidal force field does not; it is indeed the result of both internal and external distributions of matter. The tidal force acting on a body moving along a certain direction will pull it away from the origin of the reference frame and, at the same time, push it along directions perpendicular to the motion toward the origin of the reference frame. Therefore, a system subjected to tidal interactions can undergo not only tidal stripping but also tidal compression. In other words, the space distribution of galaxies undergoing tidal interactions tends to become flat.
The results of this study can be summarized as follows:
- The tidal forces
can be the cause of the planar distribution of these dwarf galaxies.
We analytically obtain the same numerical results as
Pasetto & Chiosi (2007). We prove that a planar distribution of
all dwarf galaxies, excluding those tightly bounded to a HG, is compatible
with the presence of an external force field.
- The planar geometrical distribution found
by Pasetto & Chiosi (2007) was not known to relate to the most negative
eigenvalue (and associated eigenvector) of the tidal tensor. In this respect, our
previous work was partially incomplete. Here we have studied this
issue further by following the original idea of Raychaudhury & Lynden-Bell (1989) to
check whether the planar distribution is a mere coincidence or the
consequence of fundamental laws of mechanics. To address this, we first
check, using different arguments, the coincidence between the
direction given by the vector orthogonal to the geometrical plane
and that corresponding to the eigenvector with the most negative
eigenvalue. Second, we
analyze the energy of the orbital motion of the LG galaxies and find
that the minimum energy corresponds to a planar distribution that correspond exactly to the geometrical plane
 .
Therefore, the planar distribution is the consequence of the long
time-scale influence of the tidal forces exerted by massive galaxies
or galaxy groups external to the LG. Finally, we demonstrate that
this situation has been stable over the last 9 Gyr.
.
Therefore, the planar distribution is the consequence of the long
time-scale influence of the tidal forces exerted by massive galaxies
or galaxy groups external to the LG. Finally, we demonstrate that
this situation has been stable over the last 9 Gyr.
The equilibrium and stability of the plane is a consequence of the minimum in the Action and of the orbits that come from this minimum. Although Pasetto & Chiosi (2007) have carefully investigated the nature of the Minimum Action (whether local or absolute), the uncertainty affecting the orbits derived from the Action minimization could lead to an uncertainty in the energy analysis, the stability of the plane, and the compression effectas we have demonstrated here. This problem is still unsolved and cannot be resolved at the present time because higher quality observational data would be required (e.g., proper motions, velocities, distance moduli, absolute positions, masses). Hence, the analytical approach presented here still requires further support from independent arguments. Along this line of thought, we note that the study of van der Marel & Guhathakurta (2008) found compatibility between their results what in Pasetto & Chiosi (2007).
The completeness of the sample of external galaxies listed in Table 1 is another factor influencing results developed here as well as in Pasetto & Chiosi (2007). In the previous paper, special care was taken to confirm the results based on the minimization of the action with an extended catalog from Peebles et al. (2001). We can also confirm an excellent concordance between the direction of the quadrupole tensor eigenvectors in Raychaudhury & Lynden-Bell (1989) and that derived here with the independent catalog compilation of Peebles et al. (2001). Nevertheless the continuous discoveries of new LG members suggest that the true census of the LG galaxies cannot yet be considered complete (e.g., Loeb & Narayan 2008).
- The minimum action and the study of the equilibrium
by means of the first derivative of the energy of the system is a
method that can be used to constrain the energy of dwarf galaxies with
unknown proper motions. The missing proper motion prevents us from being able to obtain the true energy of any given dwarf, but the minimization of the
action, together with the study of the tidal tensor, enable us
to evaluate the derivative of the energy in this particular situation.
- We can find another example of a flat structure in the supergalactic plane, a slab of roughly
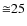 Mpc in thickness and of a diameter greater than
110 Mpc (Lahav et al. 2000), which was already proposed by
de Vaucouleurs in 1953 (de Vaucouleurs 1953). All the groups of galaxies used here
(Table 1) lie within this plane. With respect to this supergalactic plane the normal of the plane
Mpc in thickness and of a diameter greater than
110 Mpc (Lahav et al. 2000), which was already proposed by
de Vaucouleurs in 1953 (de Vaucouleurs 1953). All the groups of galaxies used here
(Table 1) lie within this plane. With respect to this supergalactic plane the normal of the plane 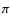 has a direction
has a direction
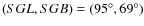 .
This plane was determined by assuming that the vector joining the MW and M 31 explicitly belongs to
.
This plane was determined by assuming that the vector joining the MW and M 31 explicitly belongs to 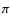 .
If you attempt to identify the best fit solution of the plane, say
.
If you attempt to identify the best fit solution of the plane, say
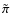 ,
for the overall sample of the LG galaxies, without forcing the MW and M 31 to belong to such a plane, we have, from PC07,
,
for the overall sample of the LG galaxies, without forcing the MW and M 31 to belong to such a plane, we have, from PC07,
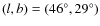 ,
i.e.,
,
i.e.,
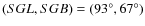 ,
for the normal to the plane
,
for the normal to the plane
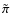 .
Thus, this is even closer to the direction of the vector associated with the most negative eigenvalue of the tidal tensor but slightly more distant from the direction of the supergalactic North Pole.
The proximity of the direction of the normal to
.
Thus, this is even closer to the direction of the vector associated with the most negative eigenvalue of the tidal tensor but slightly more distant from the direction of the supergalactic North Pole.
The proximity of the direction of the normal to 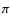 and the supergalactic North Pole cannot yet be claimed as a significant result without further investigation. However, it is also not yet possible to study this problem fully, given the incompleteness of the catalogue of nearby galaxies (see Karachentsev et al. 2004). The mass estimation together with the distances for the systems involved are still the major source of uncertainty that we considered. Finally, in none of the external groups taken into account in Table 1 can we claim the existence of a similar flat distribution of dwarf galaxies that could be a first indication of a common external effect acting on all these groups.
It seems that the local dwarf galaxies are primarily influenced by the external potential of nearby groups, not by the higher and more distant mass accumulation responsible for the supergalactic plane.
and the supergalactic North Pole cannot yet be claimed as a significant result without further investigation. However, it is also not yet possible to study this problem fully, given the incompleteness of the catalogue of nearby galaxies (see Karachentsev et al. 2004). The mass estimation together with the distances for the systems involved are still the major source of uncertainty that we considered. Finally, in none of the external groups taken into account in Table 1 can we claim the existence of a similar flat distribution of dwarf galaxies that could be a first indication of a common external effect acting on all these groups.
It seems that the local dwarf galaxies are primarily influenced by the external potential of nearby groups, not by the higher and more distant mass accumulation responsible for the supergalactic plane.
- The issue of the spatial distribution of nearby satellite galaxies bound to their HG remains to be addressed. These dwarf galaxies have orbits whose typical distance lies inside the dark matter halo of the hosting galaxy. Many N-body simulations have shown that galaxies in close proximity to a HG are affected by strong collisional interactions. The satellite dwarf galaxies may experience kick-off and interactions, and be absorbed into the halo of the HG (MW and M 31 in our case), and may abruptly change the phase-space density distribution function. In other words, the large-scale description of the gravitational interaction adopted here and in Pasetto & Chiosi (2007) is ineffective on the short distance scales of the HG-dwarf satellite interactions. This will be the subject of a forthcoming study, in which simulations of the interaction between a HG and its satellites will be investigated in the framework of strong collisional dynamics along the line of work already initiated by Pasetto et al. (2003) and Pasetto et al. (2009).
Acknowledgements
We thank the anonymous referee for useful comments and substantial improvement in the first release of the paper. We thank E. Grebel for stimulating discussions and a critical reading of the paper. We thank S. Jin for careful reading of this manuscript. C.C. is pleased to acknowledge the hospitality and stimulating environment provided by the Max-Planck Institut fürAstrophysik in Garching during his visits in July 2007 and February 2008. This study has been financed by the University of Padua by means of a postdoc fellowship to S.P. and by EARA funds.
References
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press), 747 (In the text)
- Boccaletti, D., & Pucacco, G. 1998, Astrophys. Lett. Commun., 35, 461
- de Vaucouleurs, G. 1953, AJ, 58, 30 [NASA ADS] [CrossRef] (In the text)
- Dunn, A. M., & Laflamme, R. 1993, MNRAS, 264, 865 [NASA ADS]
- Fusi Pecci, F., Bellazzini, M., Cacciari, C., & Ferraro, F. R. 1995, AJ, 110, 1664 [NASA ADS] [CrossRef] (In the text)
- Gnedin, O. Y., Hernquist, L., & Ostriker, J. P. 1999, ApJ, 514, 109 [NASA ADS] [CrossRef] (In the text)
- Grebel, E. K., Kolatt, T., & Brandner, W. 1999, ed. P. Whitelock, & R. Cannon, IAU Symp., 447
- Hartwick, F. D. A. 2000, AJ, 119, 2248 [NASA ADS] [CrossRef] (In the text)
- Holmberg, E. 1969, Arkiv Astron., 5, 305 [NASA ADS]
- Kahn, F. D., & Woltjer, L. 1959, ApJ, 130, 705 [NASA ADS] [CrossRef] (In the text)
- Kang, X., Mao, S., Gao, L., & Jing, Y. P. 2005, A&A, 437, 383 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [NASA ADS] [CrossRef] (In the text)
- Koch, A., & Grebel, E. K. 2006, AJ, 131, 1405 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P., Theis, C., & Boily, C. M. 2005, A&A, 431, 517 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kunkel, W. E. 1979, ApJ, 228, 718 [NASA ADS] [CrossRef] (In the text)
- Lahav, O., Santiago, B. X., Webster, A. M., et al. 2000, MNRAS, 312, 166 [NASA ADS] [CrossRef] (In the text)
- Landau, L. D., & Lifshitz, E. M. 1969, Mechanics 2nd edn. (Course of Theoretical Physics, Oxford: Pergamon Press) (In the text)
- Loeb, A., & Narayan, R. 2008, MNRAS, 386, 2221 [NASA ADS] [CrossRef] (In the text)
- Lynden-Bell, D. 1983, in Internal Kinematics and Dynamics of Galaxies, ed. E. Athanassoula, IAU Symp., 100, 89
- Lynden-Bell, D., & Lynden-Bell, R. M. 1995, MNRAS, 275, 429 [NASA ADS]
- Metz, M., Kroupa, P., & Jerjen, H. 2007, MNRAS, 374, 1125 [NASA ADS] [CrossRef] (In the text)
- Metz, M., Kroupa, P., & Libeskind, N. I. 2008, ApJ, 680, 287 [NASA ADS] [CrossRef] (In the text)
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: W.H. Freeman and Co.) (In the text)
- Palma, C., Majewski, S. R., & Johnston, K. V. 2002, ApJ, 564, 736 [NASA ADS] [CrossRef]
- Pasetto, S., & Chiosi, C. 2007, A&A, 463, 427 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pasetto, S., Chiosi, C., & Carraro, G. 2003, A&A, 405, 931 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pasetto, S., Grebel, E. K., Berczik, P., & Spurzem, R. 2009, A&A, submitted (In the text)
- Peebles, P. J. E. 1990, ApJ, 362, 1 [NASA ADS] [CrossRef]
- Peebles, P. J. E. 1994, ApJ, 429, 43 [NASA ADS] [CrossRef]
- Peebles, P. J. E., Phelps, S. D., Shaya, E. J., & Tully, R. B. 2001, ApJ, 554, 104 [NASA ADS] [CrossRef] (In the text)
- Raychaudhury, S., & Lynden-Bell, D. 1989, MNRAS, 240, 195 [NASA ADS] (In the text)
- Sales, L., & Lambas, D. G. 2004, MNRAS, 348, 1236 [NASA ADS] [CrossRef]
- Sawa, T., & Fujimoto, M. 2005, PASJ, 57, 429 [NASA ADS] (In the text)
- Szebehely, V. 1967, Theory of orbits. The restricted problem of three bodies (New York: Academic Press) (In the text)
- van der Marel, R. P., & Guhathakurta, P. 2008, ApJ, 678, 187 [NASA ADS] [CrossRef] (In the text)
- Weinberg, M. D. 1994a, AJ, 108, 1398 [NASA ADS] [CrossRef]
- Weinberg, M. D. 1994b, AJ, 108, 1403 [NASA ADS] [CrossRef]
- Yang, X., van den Bosch, F. C., Mo, H. J., et al. 2006, MNRAS, 369, 1293 [NASA ADS] [CrossRef]
- Zentner, A. R., Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2005, ApJ, 629, 219 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... planes
![[*]](/icons/foot_motif.png)
- Closely related to this problem is the issue of the anisotropic distribution of inner sub-haloes with respect to larger haloes in relation to the Holmberg effect (Holmberg 1969) with dissimilar results, e.g. Sales & Lambas (2004), Yang et al. (2006). What matters here (and is still debated) is whether disruptions and tidal effects can create the apparent polar alignment of the dwarf satellites around the host galaxy or, for the particular case of the LG, the position of the dwarf galaxies is the consequence of peculiar directions of pre-existing cosmological filaments.
- ... time
![[*]](/icons/foot_motif.png)
- Of course a more correct computation could have been performed by knowing distribution of the dwarf galaxies in the past, but unfortunately we cannot track back the past orbits of the dwarf galaxies belonging to the plane
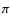 today; therefore
Eq. (2) for the plane
today; therefore
Eq. (2) for the plane 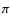 cannot be directly determined in its time evolution.
cannot be directly determined in its time evolution.
- ... reality
![[*]](/icons/foot_motif.png)
- Here we did not use the Eq. (9) previously necessary for the energy analysis, in favor of a clearer and easier physical interpretation of the terms in the equation.
All Tables
Table 1: External galaxy groups gravitationally influencing the LG dynamics.
Table 2:
Temporal evolution of the eigenvalues
and eigenvectors as a function of the look-back time
![]() in Gyr.
in Gyr.
All Figures
 |
Figure 1:
Sketch of the geometrical framework we have
adopted. First, we define the inertial reference frame, always named S0,
with axis
|
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
Evolution of the eigenvalues
|
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
Here we tracked back the influence of each individual component in the sum of Eq. (1) for the most negative eigenvalue,
|
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
The Hammer projection of the sky position of the normal
to the plane found by PC07 (from purely geometrical arguments). The color code from light red to dark brown corresponds to
the 3 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.