EDP Sciences
Home All issues Volume 499 / No 2 (May IV 2009) A&A, 499 2 (2009) 503-513 Full HTML
Highlight
Free Access
Issue
A&A
Volume 499, Number 2, May IV 2009
Page(s) 503 - 513
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361:200810905
Published online 04 December 2008

Imaging galactic diffuse clouds: CO emission, reddening and turbulent flow in the gas around 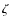$\zeta $ Ophiuchi

H. S. Liszt1 - J. Pety2,3 - K. Tachihara4

1 - National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA, USA 22903-2475, USA
2 - Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint-Martin d'Hères, France
3 - Observatoire de Paris, 61 Av. de l'Observatoire, 75014 Paris, France
4 - National Astronomical Observatory of Japan, 2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan

Received 2 September 2008 / Accepted 20 November 2008

Abstract
Context. Most diffuse clouds are only known as kinematic features in absorption spectra, but those with appreciable H2 content may be visible in the emission of such small molecules as CH, OH, and CO.
Aims. We interpret in greater detail the extensive observations of 12CO emission from diffuse gas seen around the archetypical line of sight to $\zeta $ Oph.
Methods. The 12CO emission is imaged in position and position-velocity space, analyzed statistically, and then compared with maps of total reddening $E^\infty _{B-V}$ and with models of the C+ - CO transition in H2-bearing diffuse clouds.
Results. Around $\zeta $ Oph, 12CO emission appears in two distinct intervals of reddening centered near $E^\infty _{B-V}$ $\approx$ 0.4 and 0.65 mag, of which $\la$0.2 mag is background material. Within either interval, the integrated 12CO intensity varies up to 6-12 K km s-1, compared to 1.5 K km s-1 toward $\zeta $ Oph. Nearly 80% of the individual profiles have velocity dispersions ${\sigma }_{v}$ < 0.6 km s-1, which are subsonic at the kinetic temperature derived from H2 toward $\zeta $ Oph, 55 K. Partly as a result, 12CO emission exposes the internal, turbulent, supersonic (1-3 km s-1) gas flows with especial clarity in the cores of strong lines. The flows are manifested as resolved velocity gradients in narrow, subsonically-broadened line cores.
Conclusions. The scatter between N(CO) and EB-V in global, CO absorption line surveys toward bright stars is present in the gas seen around $\zeta $ Oph, reflecting the extreme sensitivity of N(12CO) to ambient conditions. The two-component nature of the optical absorption toward $\zeta $ Oph is coincidental and the star is occulted by a single body of gas with a complex internal structure, not by two distinct clouds. The very bright 12CO lines in diffuse gas arise at N(H2) $\approx$  $ 10^{21}~{\rm cm}^{-2}$ in regions of modest density n(H) $\approx$  $ 200{-}500~{\rm cm}^{-3}$ and somewhat more complete C+-CO conversion. Given the variety of structure in the foreground gas, it is apparent that only large surveys of absorption sightlines can hope to capture the intrinsic behavior of diffuse gas.

Key words: astrochemistry - ISM: molecules - ISM: clouds

1 Introduction

The line of sight to the nearby (140-160 pc) runaway O9.5 V star HD 149 757, $\zeta $ Oph, has served as the archetype for detailed observational studies of the internal composition of diffuse ($A_{\rm V}$ $\la 1$ mag) clouds (Herbig 1968; Morton 1975), for optical/uv detection of new molecules in diffuse gas (Maier et al. 2001) and for theoretical models of molecular gas in diffuse clouds (Kopp et al. 1996; Van Dishoeck & Black 1988,1986; Black & Dalgarno 1977). The H2-bearing portions of the gas occulting $\zeta $ Oph are dense enough to host appreciable column densities of carbon monoxide, N(12CO)  $ \approx 2.4 \times 10^{15}~{\rm cm}^{-2}$ (Wannier et al. 1982; Morton 1975; Sonnentrucker et al. 2007; Lambert et al. 1994), and these are readily detectable in mm-wave emission toward the star (Liszt 1979; Langer et al. 1987; Knapp & Jura 1976). They were very partially mapped in CO emission (Liszt 1997; Kopp et al. 1996), as well as CH and OH (Liszt 1997; Crutcher 1979).

CO J=1-0 emission around $\zeta $ Oph was imaged in much more complete fashion by Tachihara et al. (2000), who focused their discussion on the properties of the nearby dark cloud complex L204 seen several degrees to the galactic South. L204 is clearly outlined against the H$\alpha$ emission from the ionized gas in the star's H II region (Gaustad et al. 2001). In this work, the 12CO datacube from Tachihara et al. (2000) is employed to study the diffuse gas at $A_{\rm V}$ $\approx$ 1 mag seen nearer the star. We scrutinize the entire CO image of the absorption-line host whose overall properties have so often been inferred from one microscopic absorption sightline toward the star, and we inquire to what extent that line of sight faithfully represents the host gas. Moreover, large-scale maps of reddening and extinction have become available at comparable resolution (though only along the entire line of sight, see Schlegel et al. 1998; and Dobashi et al. 2005), and we employ these to control against possible confusion between diffuse and darker sightlines, a source of concern given the strong CO lines we see.

The plan of this work is as follows. Section 2 summarizes what is known observationally of the line of sight toward the star and describes the pre-existing H I, CO, $A^\infty _{\rm V}$ and $E^\infty _{B-V}$ datasets which are discussed here. Section 3 discusses the appearance of the sky around $\zeta $ Oph in terms of the statistics of 12CO emission and reddening. Section 4 discusses CO profiles and linewidths in terms of the turbulent flows which are prominent in the emission profiles. Section 5 discusses physical conditions in the CO and H2-bearing host gas, especially the regions of extremely bright (11-12 K) CO emission. Section 6 is a summary and Sect. 7 (available online) discusses the relationship between the extinction and reddening measurements over the $\zeta $ Oph field and presents some additional views of the 12CO observations.

2 Observations

2.1 Carbon monoxide

The datacube of Tachihara et al. (2000) comprises nearly 11 000 spectra from the NANTEN telescope with a beamwidth HPBW = 2.7$^\prime $ on a 4$^\prime $ grid in galactic coordinates. The spectra have 0.1 km s-1 resolution and the single-channel rms at this resolution, 0.5 K, is relatively high compared to that in the small numbers of demonstration spectra typically shown in earlier work (Liszt 1997). Statisically significant detections of the CO require $W_{\rm CO}$ $\ga 1$ km s-1, where $W_{\rm CO}$ is the integrated intensity.

Toward the star, we show the profile of Liszt (1997) from the then-NRAO Kitt Peak 12 m telescope at 1$^\prime $ (HPBW) spatial resolution and 0.12 km s-1 spectral resolution (see Sect. 3). To ensure that this profile is compatible with those from NANTEN we recently used the ARO 12 m Kitt Peak telescope to re-observe several positions having comparatively strong emission in the NANTEN datacube. The 12 m spectra agree with the NANTEN data to better than 5%, a remarkable coincidence considering the difference in hardware and spatial resolution.

2.2 H I

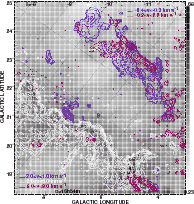 \begin{figure} { \psfig{figure=10905f1.eps,height=18cm} }\end{figure} Figure 1:

Limiting reddening (Schlegel et al. 1998) and 12CO J=1-0 emission (Tachihara et al. 2000) in the vicinity of $\zeta $ Oph. The 12CO emission contours are shown at levels 1, 2, 4, 6, 8, 10, 12, 16, 20, 24 K km s-1 and have been calculated over different velocity ranges in the upper right and lower left portions of the map, as indicated at the map corners. The dark cloud complex to the South of $\zeta $ Oph is known as L204 and the gas at the upper right, around $\zeta $ Oph, as L121.
Open with DEXTER

To help distinguish between foreground and background material, or atomic and molecular gases, we employed the H I profiles from the Leiden-Dwingeloo all-sky H I survey (Hartmann & Burton 1997). These data have 35$^\prime $ resolution on a 0.5$^\circ $ grid in galactic coordinates.

2.3 Reddening and extinction

The reddening toward $\zeta $ Oph is known to be EB-V = 0.32 mag (Morton 1975), but maps of the foreground extinction over only the first 140 pc are unavailable. Instead, we employ the limiting reddening (from here to infinity) from the work of Schlegel et al. (1998), denoted by $E^\infty _{B-V}$, with a spatial resolution of 6.1$^\prime $, published on a 2.5$^\prime $ grid; the stated global rms error of this dataset is 16% (a percentage at each pixel). Their values are based on a determination of the dust column density estimated from the IRAS 100 micron flux adopting the temperature variation derived from COBE/DIRBE 240 micron data. The minimum limiting reddening in the region, approximately 0.23 mag (Fig. 1), is likely hosted in atomic gas over long paths, as opposed to the more-localized diffuse and dark clouds of interest here.

A comparison between the limiting reddening of Schlegel et al. (1998) and maps of the limiting extinction $A^\infty _{\rm V}$ computed from star counts by Dobashi et al. (2005) can be found in Sect. 7 (online only).

2.4 Some general conditions in the gas along the line of sight to 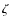$\zeta $ Oph

In front of the star, EB-V = 0.32 mag, N(H I)  $ = 5.2 \times 10^{20}~{\rm cm}^{-2}$, N(H2)  $ = 4.5 \times 10^{20}~{\rm cm}^{-2}$ (Savage et al. 1977), N(12CO)  $ \approx 2.4 \times 10^{15}~{\rm cm}^{-2}$ (Wannier et al. 1982; Morton 1975; Sonnentrucker et al. 2007), N(C0) = N(12CO) (Morton 1975) and N(C+)  $\ga 3 \times 10^{17}~{\rm cm}^{-2}$ (Cardelli et al. 1993). The mean kinetic temperature of the molecular gas inferred from H2 absorption is 54 K (Savage et al. 1977).

Toward the star the limiting extinction from the work of Schlegel et al. (1998) is $E^\infty _{B-V}$ = 0.55 mag, so that the background reddening is approximately 0.23 mag.

The distance to the occulting material is generally taken to be very close to that of the star, just outside the nearer edge of the star's H II region (Wood et al. 2005). At a distance of 140 pc, 1$^\prime $ corresponds to 0.041 pc and 1$^\circ $ to 2.44 pc.

3 The sky around 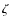$\zeta $ Oph viewed in reddening and CO emission

Figure 1 is a composite image of the limiting reddening $E^\infty _{B-V}$ and integrated 12CO J=1-0 emission, an updated version of Fig. 1 in Tachihara et al. (2000). The gray-scale underlay is the limiting reddening (Schlegel et al. 1998) normalized to white at the minimum value seen over the region, $E^\infty _{B-V}$ = 0.23 mag. Superposed on the reddening map, the integrated 12CO intensity $W_{\rm CO}$ has been calculated separately over the diffuse/translucent northwest region, referred to as L121, and the translucent/dark southeast region, L204. For the diffuse gas of L121 at upper right, the red and blue contours correspond to the velocity ranges above and below v = -0.25 km s-1 as indicated in the upper right corner: this division corresponds to the natural separation between the two components of CO, CH and OH emission found toward and around $\zeta $ Oph, as shown in the profiles and position-velocity maps of Liszt (1997). For the darker gas of L204 to the southeast $W_{\rm CO}$ was calculated over three intervals but nearly all of the emission from L204 occurs in the velocity interval 2-6 km s-1 represented by the white contours (see Fig. 5). The noise level is somewhat larger for these contours, because $W_{\rm CO}$ was calculated over a somewhat broader interval.

The strong CO emission associated with L204 often follows the ridge lines of the extinction with something of a setback (reddening without apparent CO) in the direction of the star. This is consistent with the edge-on geometry for L204 described by Tachihara et al. (2000). Nearly all of the CO emission in the L204 dark cloud complex is found in the interval ${v}_{\rm lsr}$ = 2-6 km s-1 and so does not overlap that of the more diffuse gas to the north, seen at ${v}_{\rm lsr}$ $\la$ 2 km s-1. The extent to which the two regions are at rest in the directions joining them, and might partake of the optical pumping excitation mechanism for diffuse gas described by Wannier et al. (1997) is unknown. Tachihara et al. (2000) assumed that the two clouds were co-moving at the edge of the H II region around $\zeta $ Oph in order to discuss the energetics of the gas.

To the North of L204, on either side of the star is the $\zeta $ Oph diffuse cloud, described as the L121 complex by Tachihara et al. (2000). Most of the emission from that gas occurs at -2.4 km s-1 <  ${v}_{\rm lsr}$ < 2.2 km s-1. The red-shifted kinematic component at -0.2 km s-1 <  ${v}_{\rm lsr}$ < 2.2 km s-1 which is seen in CO emission and in many species in absorption toward the star, is very much confined to the northern and northwestern edges of the broader distribution of blue-shifted gas. Its separate identity as a second cloud is somewhat marginal in the emission maps and hardly supported by a more detailed examination of the turbulent gas kinematics (also see Fig. 7).

The diffuse gas in the L121 complex around $\zeta $ Oph is separated from the L204 dark cloud by an extended trough in the reddening whose overall mean value is $E^\infty _{B-V}$ $\approx$ 0.43 mag. Immediately below the star is a pronounced minimum whose mean is $E^\infty _{B-V}$ $\approx$ 0.34 mag and whose absolute minimum is $E^\infty _{B-V}$ = 0.29 mag. The overall impression is of a cylindrical shell geometry and perhaps a separate, more circular shell of radius $\approx$1$^\circ $ around the star. However, a yet-larger map of the extinction shows that L204 is part of a much larger ridge.

 \begin{figure} { \psfig{figure=10905f2.eps,height=8.5cm} }\end{figure} Figure 2:

Integrated H I line brightness from the LDSS survey of Hartmann & Burton (1997) at 35$^\prime $ resolution, converted to equivalent reddening EB-V = N(H I)/ $5.8\times 10^{21}~{\rm cm}^{-2}$, N(H I) =  $1.823 \times 10^{18}~ ~{\rm cm}^{-2} \int {T}_{\rm B} \rm{(H~I~dv)}$/(K km s-1).

Open with DEXTER

3.1 Separating foreground and background reddening

As noted above, we wish to understand the relationships between $W_{\rm CO}$ and reddening, but we only have maps of the reddening which include all of the unrelated background and foreground gas. Immediately around $\zeta $ Oph $E^\infty _{B-V}$ = 0.55 mag, compared to EB-V = 0.32 mag in front of the star, so some 0.55-0.32 mag = 0.23 mag of reddening occurs behind the star. This also corresponds well to the absolute minimum in Fig. 1, $E^\infty _{B-V}$ = 0.23 mag found some 1.5$^\circ $ North of the star.

To estimate the amount of extraneous foreground material, we note that this is expected to be in atomic form and, in absorption against the star, N(H I)  $= 5.25 \times 10^{20}$ (Savage et al. 1977) corresponding to EB-V $\la$ 0.1 mag. This leaves EB-V $\ga$ 0.22 mag of foreground material associated with the pure H2 component and gives the general idea that perhaps as much as 0.32 mag should be subtracted from the map of $E^\infty _{B-V}$ to infer the local reddening intrinsic to the H2-bearing gas. However, this is probably an overestimate of the required correction because some of the foreground atomic gas is in the vicinity of L121 and L204, providing shielding.

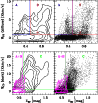 \begin{figure} \par\psfig{figure=10905f3.eps,height=9cm} \end{figure} Figure 3:

Integrated intensity of the CO line $W_{\rm CO}$ vs. limiting reddening $E^\infty _{B-V}$. Top: for the diffuse region L121 at upper right in Fig. 1; bottom: for the darker L204 gas at lower left in Fig. 1. In each case the data are shown twice, at right as individual data points, at left binned and contoured at logarithmic (factor two) intervals: the contour representation of the L121 data is superposed at bottom. Also, in each case the data are divided into regions of lower and higher extinction with the separation occuring at the mean $E^\infty _{B-V}$ over datapoints which lack statistically significant detections of CO emission (0.46 mag and 0.67 mag at top and bottom, respectively). The locus of the sightline toward $\zeta $ Oph in the B-region of the upper panel is indicated by a (red) cross. Mean 12CO emission profiles are shown in Fig. 5.

Open with DEXTER

Figure 2 is a map of the integrated H I brightness, scaled to the mean relationship between hydrogen column density and extinction, that is, the map shows $1.823 \times 10^{18} ~{\rm cm}^{-2}\int {T}_{\rm B} {\rm (H I) {\rm d}}v/ 5.8 \times 10^{21} ~{\rm cm}^{-2}~{\rm mag}^{-1}$ where the velocity integral is in units of K km s-1. Several of the local reddening peaks which lack CO emission in Fig. 1 even at $E^\infty _{B-V}$ = 0.65 mag are present as peaks in Fig. 2, for instance at (l,b) = (7.5$^\circ $, 21.5$^\circ $) and (4$^\circ $, 20$^\circ $). Some of this gas must be indigenous to the region of interest, but the extinction associated with the H I peaks is only $\approx$0.06 mag, judging from the peak levels in Fig. 2 (0.28 mag) compared to the nearby background level (0.22 mag).

The minima in Figs. 1 and 2 and the difference between the foreground and limiting reddening toward the star consistently imply a background reddening contribution of $\approx$0.2 mag over the region of interest.

3.2 Quantitative relationship between CO emission and reddening

To quantify the relationship between reddening and CO emission, and to compare and contrast the diffuse and dark sightlines we divided the extent of Fig. 1 along a Northeast-Southwest diagonal in the trough of reddening between L121 and L204, along a line running from (l,b) = (3$^\circ $, 19.333$^\circ $) to (10$^\circ $, 25$^\circ $). Figure 3 shows the integrated CO intensities $W_{\rm CO}$ and limiting reddening $E^\infty _{B-V}$ for all points in both regions: the profile integral was taken over the range -2.4 km s-1 <  ${v}_{\rm lsr}$ < 2.2 km s-1 for the diffuse L121 gas shown in the top panel, and 2 km s-1 <  ${v}_{\rm lsr}$ < 8 km s-1 for the darker L204 region in the lower portion of the map of Fig. 1 and the lower panel in Fig. 3. The rms noise in integrated intensity is 0.5-0.6 K km s-1. Profile integrals above 1 K km s-1 generally represent real detections.

Once we realized that the CO emission in the diffuse region was bimodal, as illustrated in the top panels of Fig. 3, we further sub-divided the diffuse gas into A and B portions corresponding to the two branches of the emission distribution. The A and B portions were separated at $E^\infty _{B-V}$ = 0.455 mag, which is the mean $E^\infty _{B-V}$ for those sightlines along which $W_{\rm CO}$ < 1 K km s-1 and which therefore lack statistically significant detections of CO emission. The A-branch pixels have strong CO emission at $E^\infty _{B-V}$ substantially below the mean of those sightlines lacking CO emission at all. For the diffuse gas in L121 there is actually a substantial spatial segregation of the A and B portion pixels, with unweighted mean $\langle (l,b)\rangle$ = (6.0$^\circ $ $\pm~0.7$$^\circ $, 23.8$^\circ $ $\pm~0.7$$^\circ $) and $\langle (l,b)\rangle$ = (4.0$^\circ $ $\pm~0.9$$^\circ $, 22.3$^\circ $ $\pm~1.0$$^\circ $) for the A and B portions, respectively. These centroids are on opposite sides of $\zeta $ Oph and separated by more than $1\sigma + 1\sigma$ in each coordinate. The red-shifted gas appears mostly in the higher-extinction B-portion while the blue-shifted gas appears more nearly in both the A and B-portions.

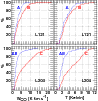 \begin{figure} \par\psfig{figure=10905f4.eps,height=9cm} \end{figure} Figure 4:

Cumulative probability distributions of the integrated intensity $W_{\rm CO}$ ( left) and peak line temperature ( right) over the diffuse, northeastern L121 (at top) and dark southeast L204 sightlines shown in Fig. 1. Only those sightlines at which $W_{\rm CO}$ $\ge 1$ K km s-1 have been considered.

Open with DEXTER

In either emission branch, $W_{\rm CO}$ varies widely over a relatively narrow range in $E^\infty _{B-V}$, mimicing the extreme sensitivities of N(CO) which are seen in global absorption line surveys of single sightlines over widely-separated regions (see Liszt 2007a). The widths of the two branches are comparable to the stated rms noise of the $E^\infty _{B-V}$ data (16%) and they are separated by 0.2 mag, which is of the same order as the background contribution: it is possible that they would more nearly coincide in EB-V if the background contribution were strongly variable. However, the B-branch at higher $E^\infty _{B-V}$ is more heavily populated at $W_{\rm CO}$ > 5 K km s-1, suggesting that it actually is somewhat more strongly shielded, fostering a higher CO abundance and brightness: in this regime, $W_{\rm CO}$ $\propto$ N(CO) (ibid and see Sect. 6) and the conversion of free carbon from C+ to CO occurs over a very narrow interval in EB-V and/or N(H2).

The distribution of brightness in the darker L204 region is not similarly bimodal at all $E^\infty _{B-V}$ and there is less rationale for a simple division into sub-portions. However when this is done, at $E^\infty _{B-V}$ = 0.67 mag corresponding again to the mean over pixels lacking statistically significant CO emission, the resultant lower- $E^\infty _{B-V}$ portion corresponds (in $E^\infty _{B-V}$ and $W_{\rm CO}$) to the entirety of the diffuse region. Consequently the lower- $E^\infty _{B-V}$ part of L204 is labelled L204 AB and the other L204 C. The behavior of $W_{\rm CO}$ with $E^\infty _{B-V}$ in the dark gas is complex but clearly bimodal for $W_{\rm CO}$ $\ga$ 12 K km s-1; the strongest emission is by no means limited to the darkest regions. Statistics of the brightness distribution over L121 and L204 are shown in Fig. 4 and discussed in the following sections.

3.3 Statistics of the line brightness

Figure 4 presents the distribution of integrated and peak brightness. The differences between the A (lower $E^\infty _{B-V}$) and B portions of the diffuse gas are somewhat more pronounced in the distribution of the line profile integral at left and somewhat less so in the peak, so that the line widths differ more than the line heights. Although the median brightness is at most only 3 K or 3 K km s-1 in the diffuse gas and the tail of the distribution seems very poorly populated above, say, 8 K peak brightness, paths which traverse L121 even in the short dimension have a very substantial chance of containing at least one such bright line, as discussed in Sect. 5 (see Fig. 7).

It is not the intention here to discuss the dark gas, but it should be noted that the difference in mean brightness between the diffuse and dark regions is modest and corresponds approximately to the difference in $E^\infty _{B-V}$, thereby preserving the possibility of a common CO-H2 conversion factor; the same is also true for the A and B portions of L121, see Fig. 5. This occurs despite the fact that most of the free gas-phase carbon is in C+in L121 (99% toward $\zeta $ Oph) and in CO in the dark gas of L204 (where N(CO)  $\approx 3\times 10^{17}~ ~{\rm cm}^{-2}$) implying a difference in CO column density and $W_{\rm CO}$/N(CO) by a factor of order 50. In Sect. 5 we discuss the very different proportionality $W_{\rm CO}$ $\propto$ N(CO) which is observed within the diffuse regime alone (Liszt 2007a).

3.4 An incidental bound on N(H2) over the diffuse gas

Because the line of sight to $\zeta $ Oph occurs at such a high value of $E^\infty _{B-V}$ relative to the rest of L121 we infer that N(H2) is never very much larger in L121 than toward the star. For instance, if we take $E^\infty _{B-V}$ = 0.65 mag characteristic of the B-portion and subtract a background contribution 0.23 mag equal to that toward the star, the remaining gas column with $E^\infty _{B-V}$ = 0.65-0.23 = 0.42 mag corresponds to N(H)  $\approx 2.4\times10^{21}$ H-nuclei  $~{\rm cm}^{-2}$ and N(H2)  $< 1.2 \times 10^{21}~{\rm cm}^{-2}$. Conversely, because the line of sight toward the star has such a high value $E^\infty _{B-V}$ = 0.55 mag relative to the rest of the region, emission from the A-branch at $E^\infty _{B-V}$ = 0.4 mag, probably arises in regions whose reddening and N(H2) are actually below those seen toward the star.

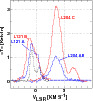 \begin{figure} { \psfig{figure=10905f5.eps,height=9cm} }\end{figure} Figure 5:

Mean spectra over the diffuse and dark sub-portions defined in Fig. 3: the profiles in the diffuse gas (L121) are those at lower velocity. The integrated brightnesses are $W_{\rm CO}$ = 2.9 and 4.0 K km s-1 for L121 and 2.3 and 7.4 K km s-1 for L204. Also shown (dashed black line) is a spectrum at 1$^\prime $ resolution toward $\zeta $ Oph from the 12 m telescope.

Open with DEXTER

4 Line profiles, linewidths and turbulent flows in diffuse gas

4.1 CO line profiles and profile widths

For a pure-H2 gas, the Doppler temperature equivalent to a given linewidth is $T_{\rm dopp} = 43.6$ K FWHM2 or $T_{\rm dopp} = 242$ K ${\sigma }_{v}$2 where ${\sigma }_{v}$ is the velocity disperson in km s-1. Typical kinetic temperatures in CO-bearing diffuse gas are above 30 K (Liszt 2007a; Burgh et al. 2007; Sonnentrucker et al. 2007) and the mean kinetic temperature seen in surveys of H2 absorption is 70-80 K (Rachford et al. 2002; Savage et al. 1977). CO profiles with ${\it FWHM}\la 1$ km s-1 are subsonic at diffuse cloud temperatures and the purely-thermal velocity dispersions of CO molecules, 0.1 km s-1 at K = 50 K, do not contribute importantly to the observed linewidths.

Unweighted mean profiles formed over the sub-portions of the diffuse L121 and dark L204 regions are shown in Fig. 5. The mean profiles have linewidths which are supersonic, FWHM of typically 2-3 km s-1 but the individual sightlines in L121 typically have subsonic linewidths; the FWHM of the two kinematic components seen toward the star at 1$^\prime $ resolution (shown in Fig. 5 as the dark dashed line) are 0.6 km s-1 and 1.1 km s-1, equivalent to Doppler temperatures of only 16 K and 53 K in a pure H2 gas, compared to a measured temperature in H2 of 54 K as noted in Sect. 2.4.

The distribution of velocity dispersions found over the L121 region is shown in Fig. 6. To produce this figure we used the following windowing technique to measure the widths of spectra which might contain more than one kinematic component: select the overall velocity interval of the diffuse gas; find the peak channel; select those contiguous channels around this peak with temperatures above a noise threshold of 0.25 K; calculate the brightness-weighted velocity dispersion over those channels; mask off that portion of the profile; repeat until no channel above 1 K remains unmasked. The dispersions measured en masse in this way are subject to overestimating the width in cases of unrecognizd blending, but they agree to within 10% for a series of test profiles which were fit with Gaussian components (for instance, those shown in Fig. 8).

The general properties of the gas in L121 have often been inferred from profiles seen along the single, microscopic absorption line of sight toward the star and a sensitive CO profile toward $\zeta $ Oph at 1$^\prime $ spatial resolution is also included in Fig. 5. How representative is it of the larger-scale distributions of the host gas? The stronger CO component at ${v}_{\rm lsr}$ = -0.7 km s-1 toward $\zeta $ Oph is one of the narrowest lines known in a diffuse cloud, with ${\it FWHM} = 0.60$ km s-1. Broad consideration of this question is given in the discussion of Fig. 7 which displays most of the profiles seen in the L121 region, immediately following.

4.2 Velocity gradients and turbulent flows

The connections between the profiles seen at individual pixels and the mean profiles shown in Fig. 5 are the flows and velocity gradients in the host medium, i.e. the character of the turbulence. Although very elaborate analyses of line profile centroids (Pety & Falgarone 2003) and fluctuations in the wings of optically thick profiles (Falgarone & Phillips 1996) have been used to infer the properties of turbulence in denser neutral media, turbulent flows in the nearby diffuse gas of L121 are immediately visible in the line cores and (usually) spatially resolved into the shifts of individual, subsonic profiles.

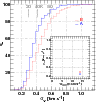 \begin{figure} { \psfig{figure=10905f6.eps,height=9cm} }\end{figure} Figure 6:

Statistics of line profile velocity dispersions in the diffuse gas. Large outer panel: cumulative probability distribution histograms of the measured velocity dispersion ${\sigma }_{v}$ shown separately for the A and B portions of the diffuse gas (see Sect. 4 of the text). The one-dimensional thermal velocity dispersions corresponding to kinetic temperatures of 20, 40 and 80 K in a gas of pure H2 are shown at upper left. Inset at lower right: variation of ${\sigma }_{v}$ with $W_{\rm CO}$.
Open with DEXTER

This is illustrated for $\zeta $ Oph in Fig. 7, where we show a comprehensive series of longitude-velocity diagrams spaced at one-pixel (4$^\prime $) intervals in galactic latitude, as labelled in the individual panels. The peak line brightnesses (K) seen in the individual panels of Fig. 7 are labelled on the bars showing the color scaling in each panel. Although lines with peak brightnesses above 8 K seem relatively rare in Fig. 4, they are common enough that peak brightnesses 7.5 K and higher appear in 40%, 18 of the 44 individual panels of Fig. 7. As shown in Fig. 3, the most intense lines in the diffuse gas are by no means limited to the more heavily-reddened sightlines.

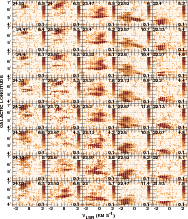 \begin{figure} \par\psfig{figure=10905f7.eps,angle=-90,height=19.4cm} \end{figure} Figure 7:

Longitude-velocity diagrams traversing the $\zeta $ Oph diffuse cloud at many latitudes within the Northwest portion of the region shown in Fig. 1. The vertical separation between panels is 4$^\prime $ (1 pixel) and the galactic latitude within each panel is labelled. The color scale in each panel is separately normalized within a range (Kelvins) shown on the individual color bars.
Open with DEXTER

Figure 7 shows that a description of the gas in terms of two identifiable foreground clouds at the absorption line or CO emission line velocities toward $\zeta $ Oph is not appropriate. The line of sight to the star could just as well have occured behind any of the profiles exhibited in Fig. 7, leading to a wide variety of possible interpretations of the intervening medium. Discussing the map in Fig. 1, we saw that the red-shifted component generally appears as something of a fringe at the northern edges of more broadly-distributed, negative-velocity gas. Viewed in position-velocity space in Fig. 7, the red-shifted gas is often seen as a pronounced kinematic excursion or wing, for instance, at b = 22.8$^\circ $ or 23.4$^\circ $. Further to the North, at b > 23.2$^\circ $, the kinematic pattern undulates across the positive-velocity portion. At b= 23.4$^\circ $ the resolved velocity gradient spans the entire range of velocities in the diffuse gas: viewed from a different perspective, this same region might have been seen as a single, broad line.

Figure 8 is an expanded view of the panel in Fig. 7 at b= 22.6$^\circ $, where we also show several included line profiles, their Gaussian decomposition and the resultant FWHM. Except at the center of the diagram where there is a partially spatially-resolved velocity gradient, the FWHM are small enough to be subsonic for an H2 gas at typical diffuse cloud temperatures above 30 K. Thus the observations show in detail how supersonic profiles might arise from the coincidental superposition or addition (for instance through beam-smearing) of velocity-shifted quiescent regions.

As in Fig. 8 there are many highly-localized, relatively broad lines in 4$^\prime $ pixels, often joined to abrupt but spatially-resolved velocity gradients and reversals in narrow-lined gas. This suggests that broader lines are themselves composed of unresolved velocity gradients and it seems possible that any profile in Fig. 7 with a width substantially above sonic is an unresolved gradient. For instance, compare the velocity span at b=22.87$^\circ $, which is spatially resolved, with that at the edge of the emission region at b=23.33$^\circ $. Recalling the extremely narrow blue-shifted CO component toward $\zeta $ Oph and the low implied Doppler temperature, we wonder whether and at what scale profiles having linewidths that are subsonic at the higher temperatures expected for diffuse gas, say 60 K, might show velocity or spatial substructure. The geometry of the turbulent flows producing the patterns in Fig. 7 will be considered in a subsequent paper.

5 Physical conditions in the diffuse gas

There are some 1000 sightlines with $W_{\rm CO}$ $\ga$ 1 K km s-1 in the diffuse, Northwest portion of the map in Fig. 1. At a distance of 140 pc, the H2-mass associated with these sightlines, parametrized by their average H2 column density $\langle N$(H2)$\rangle$, is M = 430  ${M_0}\langle N$(H2)/ $1\times 10^{21}~{\rm cm}^{-2}\rangle$ where typical values of N(H2) along the L121 sightlines are $0.5 {-} 1.2 \times 10^{21}~{\rm cm}^{-2}$ (see Sects. 2.4 and 3.4). This may be compared with the value 520 M0 given by Tachihara et al. (2000) based on a CO-H2 conversion factor N(H2)/ $W_{\rm CO}$ = $1.56\times10^{20}~{\rm cm}^{-2}$/(K km s-1).

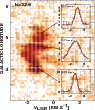 \begin{figure} \par\psfig{figure=10905f8.eps,height=9.8cm} \end{figure} Figure 8:

The longitude-velocity diagram at b = 22.6$^\circ $ from Fig. 7, expanded and decomposed into its constituent profiles at three positions (shown inset). Overlaid on each inset spectrum is a one-component Gaussian fit whose FWHM is shown at the upper left.
Open with DEXTER

Nonetheless, deriving the physical parameters of host diffuse gas from CO profiles is challenging. Strong fractionation of the carbon isotopes (Liszt 2007a; Burgh et al. 2007; Liszt & Lucas 1998; Sonnentrucker et al. 2007) causes the N(12CO)/N(13CO) to vary in the range 15-150, thus making it impossible to derive the line excitation temperatures and optical depths, or the kinetic temperatures and column densities, under the usual assumption (valid in dark gas) that the relative abundances of 12CO and 13CO only reflect the general interstellar carbon isotope ratio. However, it is straightforward to show that the general properties of the CO observations, even including the rather unexpectedly bright lines, fit easily into the framework of diffuse gas at typical temperatures 30-60 K and modest density. The real underlying mysteries are the working of the poorly-understood polyatomic chemistry which forms the CO and other species at such modest densities (Liszt et al. 2006), and the origin of the turbulent flows which may power the chemistry.

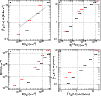 \begin{figure} \par\psfig{figure=10905f9.eps,height=8.5cm} \end{figure} Figure 9:

Models of 12CO formation and excitation. Results are shown for models having n(H) = n(H I) + 2n(H2) =  $256~{\rm cm}^{-3}$ and $512~{\rm cm}^{-3}$. Upper left: variation of integrated 12CO brightness $W_{\rm CO}$ with N(H2); the shaded line labelled ``2'' is a CO-H2 conversion factor $2\times10^{20}~\mbox{H$_2$ }~{\rm cm}^{-2}$ (K km s-1)-1. Upper right: variation of $W_{\rm CO}$ with N(12CO). Bottom left: variation of N(12CO) with N(H2). Lower right: comparison of 12CO line brightnesses in the lowest two rotational transitions.
Open with DEXTER

Figure 9 reports some results from the models which were used to interpret CO absorption line data by Liszt (2007a). The underlying physics are: to heat a uniform-density gas sphere by the photoelectric effect on small grains, as in the work of Wolfire et al. (1995,2003), to calculate the ionization balance including grain-assisted neutralization of atomic ions (including most importantly the protons, ibid), to allow equilibrium of the self-shielding of H2 formed on grains and the formation of CO by thermal electron-recombination of a fixed quantity of HCO+ X(HCO+) = N(HCO+)/N(H2) =  $2\times 10^{-9}$ (the actual secular evolution is traced by Liszt 2007b); and, to calculate the rotational excitation of CO assuming microturbulent radiative transfer with a linewidth determined by the local sound speed. Note that the interstellar radiation field in the models has not been increased above the mean interstellar value to account for the presence of the star and that all of the aspects shown here for the model results are present in the absorption line data summarized by Liszt (2007a).

Model results are shown for just two fairly high densities $n({\rm H}) = 256~{\rm cm}^{-3}$ and $512~{\rm cm}^{-3}$. To form the graphs in Fig. 9, results were derived by integrating along sightlines ranging across the faces of model spheres from center to edge. The graphs summarize results gleaned from models whose central column densities N(H) varied widely, so that the same value of N(H2) might occur at different positions across the faces of models with differing n(H) and N(H), and therefore have different N(CO) and $W_{\rm CO}$. For N(H2) =  $1\times 10^{21}~{\rm cm}^{-2}$ the models have typical sizes of 1.2-2.5 pc but the CO abundance is concentrated into smaller central portions of the host bodies owing to the chemistry of CO and that of H2, and the CO emission is more concentrated still owing to geometry and radiative pumping.

As noted above N(H2)  $ = 0.5 {-} 1\times10^{21}~{\rm cm}^{-2}$ in the CO-emitting regions around the star. As shown in panel c at the lower left, this is precisely the regime where carbon is about to recombine fully to CO at the quoted densities: the increase of N(CO) with N(H2) is very rapid. Both N(CO) and $W_{\rm CO}$ vary rapidly and have large scatter when plotted against N(H2). Substantial CO column densities can accumulate in gas which is still relatively warm, 30-50 K, giving rise to 12 K lines as observed in the brightest profiles.

The most important consideration is as shown at the upper right in panel b, $W_{\rm CO}$ $\propto$ N(CO) for $W_{\rm CO}$ $\la$ 10 K km s-1, explicitly independent of density and implicitly independent of N(H2) and other cloud properties. This is a very general consequence of very sub-thermal excitation, as first shown by Goldreich & Kwan (1974) and does not require low optical depth. As shown in Fig. 4, some 80-90% of the diffuse cloud spectra have $W_{\rm CO}$ < 5-6 K km s-1 and virtually all are below 10-12 K km s-1, just in the regime characteristic of sightlines studied in uv and mm-wave CO absorption work generally, see Fig. 6 of Liszt (2007a). Therefore, the 12CO brightness map in Fig. 1 is a map of N(12CO) in the diffuse gas and the same would be true for N(13CO) and the brightness of the 13CO line. This is the one unambiguous result of mapping CO emission in any diffuse gas.

The extreme sensitivity of $W_{\rm CO}$ to N(H2) therefore arises because $W_{\rm CO}$ $\propto$ N(CO), so that a plot of $W_{\rm CO}$ vs. N(H2) is equivalent to plotting N(CO) against N(H2). The net result is that although commonly-used values of the CO-H2 conversion factor apply to some gas (as indicated in panel a of Fig. 9) the CO-H2 conversion factor varies widely in diffuse gas and the actual N(CO)/N(H2) ratio is small but very uncertain. A map of CO emission from diffuse gas is an image of the chemistry, not the mass distribution.

Last, note that the J=1-0 CO line brightness is insensitive to density at fixed N(CO), indicating that other tracers are required to measure the local density when mm-wave emission profiles are analyzed. The J=2-1/J=1-0 line brightness ratios at lower right in Fig. 9 are not very sensitve to density, which explains why line brightness ratios 0.7-0.75 are indeed so commonly observed in diffuse and translucent gas (Pety et al. 2008; Falgarone et al. 1998). The J=3-2/J=1-0 brightness ratio is a better indicator of density in the CO lines, but care must be taken to match the spatial resolution of the two lines.

6 Summary

The line of sight to the nearby (140-160 pc) runaway 09.5V star $\zeta $ Oph has for many years been used as an archetype for studying the properties of diffuse clouds in optical and ${\it uv}$ absorption. Because the material has an appreciable molecular content, the host diffuse clouds can actually be imaged on the sky in space and radial velocity. Because the gas is well extended and comparatively close, it provides an unusual opportunity for study of diffuse gas and its interaction with its surroundings, including the star.

We began by comparing the 12CO J=1-0 emission line datacube of Tachihara et al. (2000) (HPBW 2.7$^\prime $ observations on a 4$^\prime $ = 0.1 pc pixel grid) with a map of the limiting reddening $E^\infty _{B-V}$ from the work of Schlegel et al. (1998) having similar resolution 6.1$^\prime $ (Fig. 1). The reddening in the L121 complex near and around $\zeta $ Oph ranges from $E^\infty _{B-V}$ = 0.23-0.75 mag and the integrated CO emission up to $W_{\rm CO}$ = 12 K km s-1, with 12 K peak temperatures, which are very bright lines indeed. Comparison of reddening of the star (0.32 mag) and through the Milky Way ( $E^\infty _{B-V}$ = 0.55 mag) in the same direction, and comparison of H I seen toward the star in ${\it uv}$ absorption and around the star in 21 cm emission (Fig. 2), suggests that $\approx$0.2 mag of $E^\infty _{B-V}$ should be ascribed to unrelated background material.

CO emission from diffuse L121 gas seen around $\zeta $ Oph is bimodal in $E^\infty _{B-V}$, clustering around $E^\infty _{B-V}$ = 0.4 mag and 0.65 mag and varying widely (1 K km s-1 <  $W_{\rm CO}$ < 6-12 K km s-1) with $E^\infty _{B-V}$ in one of two narrow ranges, see Fig. 3: the same large scatter in CO column density with reddening and N(H) which is seen globally in galactic absorption line surveys also occurs in the single region studied here. The lower-reddening branch of the emission is spatially segregated to the galactic northeast of the star and has somewhat smaller mean integrated brightness $W_{\rm CO}$ (Fig. 4) and velocity dispersion ${\sigma }_{v}$ (0.35 km s-1 vs. 0.42 km s-1; Fig. 6). However, peak temperatures 8-12 K are present in both branches.

 \begin{figure} \par\psfig{figure=10905f10.eps,height=8.7cm} \end{figure} Figure 10:

Comparison of the limiting extinction $A^\infty _{\rm V}$ of Dobashi et al. (2005) with the limiting reddening data $E^\infty _{B-V}$ of Schlegel et al. (1998). There is a left-offset of the $A^\infty _{\rm V}$ data of 0.78 mag, which is also seen toward $\zeta $ Oph itself, see Sect. 6 of the text (available online).
Open with DEXTER

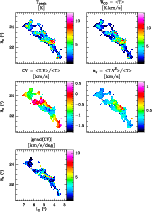 \begin{figure} \par {\psfig{figure=10905f11.eps,height=18.5cm,angle=-90} }\end{figure} Figure 11:

Maps of various quantities, available online. Top left and right, peak and integrated brightness. Middle: mean velocity and velocity dispersion. Bottom, the velocity gradient.
Open with DEXTER

The two most striking observational results of this study are the strong lines which emanate from the diffuse gas, up to $W_{\rm CO}$ = 12 K km s-1, and the velocity structure present in the strongly emitting 12CO line cores there (Figs. 7 and 8). The turbulent flows in this gas are in general directly visible as the spatially and kinematically resolved velocity gradients in simple, narrow, bright lines whose widths ( ${\sigma }_{v}$ < 0.6 km s-1) are subsonic at diffuse cloud temperatures K = 30-60 K (Figs. 4 and 8). Other, locally-broader line profiles will likely be resolved into such velocity shifts of narrow line cores with higher (than 4$^\prime $) resolution although this remains to be tested. Conversely, it also remains to be seen whether CO line profiles which are subsonic but still supra-thermal at 2.7$^\prime $ resolution will show spatial or velocity sub-structure when mapped at higher resolution.

We briefly discussed some modelling results of the formation and excitation of CO in diffuse media (Fig. 9). The brightness of the strongest CO lines can be understood by noting that the H2 column densities in the gas around $\zeta $ Oph are near the point (N(H2)  $\approx 10^{21}~{\rm cm}^{-2}$) where carbon fully recombines to CO at even modest densities n(H)  $= 200{-}500~{\rm cm}^{-3}$, so that substantial columns of CO may form in gas which is at typical diffuse cloud temperatures (above 30 K). In turn, such densities will excite CO to the required degree even though they are far too low to thermalize the lower rotational level populations.

In the range $W_{\rm CO}$ $\la$ 10 K km s-1 it is the case that $W_{\rm CO}$ $\propto$ N(CO), as a consequence of very sub-thermal excitation. The CO-H2 conversion factor therefore varies widely in diffuse gas (because N(CO) varies rapidly with N(H2) and with great scatter), but it takes on values N(H2)/ $W_{\rm CO}$  $=2 \times 10^{20} ~\mbox{H$_2$ }~{\rm cm}^{-2}$/(K km s-1) in limited circumstances (Fig. 9 panel a at upper left).

If $W_{\rm CO}$ $\propto$ N(CO), a sky map of $W_{\rm CO}$ like that in Fig. 1 is a map of the interstellar diffuse cloud chemistry. This should be contrasted with the more usual assumption of a constant CO conversion factor N(H2)/ $W_{\rm CO}$, in which case a CO map traces the contours of the mass (i.e. the bulk molecular material) largely independent of physical conditions. Even the darker gas seen in the L204 complex South of $\zeta $ Oph is not immune to the influences of chemistry, which are clearly visible in the displacements between regions of higher $W_{\rm CO}$ and $E^\infty _{B-V}$.

The wealth of structure seen in the foreground CO brightness map has important implications for absorption line study of diffuse clouds. Since the viewing geometry is an accident of the relative locations of the Sun and $\zeta $ Oph, our line of sight to the star could equally well have intercepted any of the wide variety of profiles shown in Fig. 7. This belies our ability to infer the general properties of the host gas from studies along any single sightline, no matter how comprehensive; studies of individual absorption sightlines must be viewed demographically, as datapoints within a large family of possible outcomes, even in nominally similar conditions. Even beyond this, there are some obvious fundamental limits to the use of absorption lines to derive the properties of the intervening gas. In the present case only a map could correct the false impression that the star is occulted by two separate foreground clouds. Likewise, the turbulent flows in the foreground gas appear clearly in maps of the gas but not at most individual positions, thereby conveying the false impression of an overly-quiescent medium.

We intend to map with higher angular resolution some regions of the L121 gas whose line profiles are thermal at the 2.7$^\prime $ NANTEN resolution, to see what kind of substructure might be present when some forms of line-broadening are absent. We will also map some L121 gas whose profiles are broader and whose velocity gradients are not fully resolved in Fig. 7 at 4$^\prime $ (0.16 pc) beam-spacing.

This is the second paper in a loose series (see Pety et al. 2008) which will also report observations of similar kinematics on smaller angular scales and at higher angular resolution 6 $^{\prime\prime}$-22 $^{\prime\prime}$ in other diffuse clouds of unknown distance whose presence was first manifested in our mm-wave absorption studies of polyatomic molecules. In a subsequent paper we will discuss the geometrical and physical interpretation of the internal structures responsible for the flows seen there and in Fig. 7.

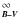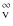
7 Comparison of measured E $^\infty_{\tiny\textit{\textbf{{B--V}}}}$ and A $^{\infty }_{\rm {{V}}}$

As an alternative source of extinction data we considered the results of Dobashi et al. (2005) who constructed a sky map of limiting extinction $A^\infty _{\rm V}$ at latitudes |b| < 40$^\circ $ based on star counts. We generated $A^\infty _{\rm V}$ from a FITS file downloaded from the survey website, with pixels on a 2$^\prime $ grid. The features in a map of that data strongly resemble those shown in Fig. 1 but $A^\infty _{\rm V}$ = 0.25 mag toward $\zeta $ Oph, which substantially underestimates the known foreground extinction since it is accepted that EB-V = 0.32 mag and $A_{\rm V}$  $\approx 3.1 \times 0.32 = 1.0$ mag.

A more general comparison with the limiting extinction of Schlegel et al. (1998) is shown in Fig. 10: we generated $A^\infty _{\rm V}$ and $E^\infty _{B-V}$ on a 4$^\prime $ grid for 3$^\circ $  $ \le l \le 9$$^\circ $, 18$^\circ $  $ \le b \le 25$$^\circ $ as in Fig. 1. The $E^\infty _{B-V}$-intercept (0.32 mag) and slope (0.41) indicate an offset of 0.32 mag/0.41 = 0.78 mag in the $A^\infty _{\rm V}$ dataset with respect to $E^\infty _{B-V}$, which corresponds to the disparity in $E^\infty _{B-V}$ and $A^\infty _{\rm V}$ values toward the star itself or to the minimum $E^\infty _{B-V}$ = 0.23 mag over the region. We infer that a uniform foreground componentof the extinction, which might have renormalized the star count, is absent in the $A^\infty _{\rm V}$ maps for this region.

Acknowledgements

The National Radio Astronomy Observatory is operated by Associated Universites, Inc. under a cooperative agreement with the US National Science Foundation. IRAM is operated by CNRS (France), the MPG (Germany) and the IGN (Spain). This research made use of the Simbad astronomical database and the NASA ADS astrophysical database system. This work profited from discussions of CO excitation with Michel Guelin.

References

All Figures

  \begin{figure} { \psfig{figure=10905f1.eps,height=18cm} }\end{figure} Figure 1:

Limiting reddening (Schlegel et al. 1998) and 12CO J=1-0 emission (Tachihara et al. 2000) in the vicinity of $\zeta $ Oph. The 12CO emission contours are shown at levels 1, 2, 4, 6, 8, 10, 12, 16, 20, 24 K km s-1 and have been calculated over different velocity ranges in the upper right and lower left portions of the map, as indicated at the map corners. The dark cloud complex to the South of $\zeta $ Oph is known as L204 and the gas at the upper right, around $\zeta $ Oph, as L121.
Open with DEXTER
In the text

  \begin{figure} { \psfig{figure=10905f2.eps,height=8.5cm} }\end{figure} Figure 2:

Integrated H I line brightness from the LDSS survey of Hartmann & Burton (1997) at 35$^\prime $ resolution, converted to equivalent reddening EB-V = N(H I)/ $5.8\times 10^{21}~{\rm cm}^{-2}$, N(H I) =  $1.823 \times 10^{18}~ ~{\rm cm}^{-2} \int {T}_{\rm B} \rm{(H~I~dv)}$/(K km s-1).

Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f3.eps,height=9cm} \end{figure} Figure 3:

Integrated intensity of the CO line $W_{\rm CO}$ vs. limiting reddening $E^\infty _{B-V}$. Top: for the diffuse region L121 at upper right in Fig. 1; bottom: for the darker L204 gas at lower left in Fig. 1. In each case the data are shown twice, at right as individual data points, at left binned and contoured at logarithmic (factor two) intervals: the contour representation of the L121 data is superposed at bottom. Also, in each case the data are divided into regions of lower and higher extinction with the separation occuring at the mean $E^\infty _{B-V}$ over datapoints which lack statistically significant detections of CO emission (0.46 mag and 0.67 mag at top and bottom, respectively). The locus of the sightline toward $\zeta $ Oph in the B-region of the upper panel is indicated by a (red) cross. Mean 12CO emission profiles are shown in Fig. 5.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f4.eps,height=9cm} \end{figure} Figure 4:

Cumulative probability distributions of the integrated intensity $W_{\rm CO}$ ( left) and peak line temperature ( right) over the diffuse, northeastern L121 (at top) and dark southeast L204 sightlines shown in Fig. 1. Only those sightlines at which $W_{\rm CO}$ $\ge 1$ K km s-1 have been considered.

Open with DEXTER
In the text

  \begin{figure} { \psfig{figure=10905f5.eps,height=9cm} }\end{figure} Figure 5:

Mean spectra over the diffuse and dark sub-portions defined in Fig. 3: the profiles in the diffuse gas (L121) are those at lower velocity. The integrated brightnesses are $W_{\rm CO}$ = 2.9 and 4.0 K km s-1 for L121 and 2.3 and 7.4 K km s-1 for L204. Also shown (dashed black line) is a spectrum at 1$^\prime $ resolution toward $\zeta $ Oph from the 12 m telescope.

Open with DEXTER
In the text

  \begin{figure} { \psfig{figure=10905f6.eps,height=9cm} }\end{figure} Figure 6:

Statistics of line profile velocity dispersions in the diffuse gas. Large outer panel: cumulative probability distribution histograms of the measured velocity dispersion ${\sigma }_{v}$ shown separately for the A and B portions of the diffuse gas (see Sect. 4 of the text). The one-dimensional thermal velocity dispersions corresponding to kinetic temperatures of 20, 40 and 80 K in a gas of pure H2 are shown at upper left. Inset at lower right: variation of ${\sigma }_{v}$ with $W_{\rm CO}$.
Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f7.eps,angle=-90,height=19.4cm} \end{figure} Figure 7:

Longitude-velocity diagrams traversing the $\zeta $ Oph diffuse cloud at many latitudes within the Northwest portion of the region shown in Fig. 1. The vertical separation between panels is 4$^\prime $ (1 pixel) and the galactic latitude within each panel is labelled. The color scale in each panel is separately normalized within a range (Kelvins) shown on the individual color bars.
Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f8.eps,height=9.8cm} \end{figure} Figure 8:

The longitude-velocity diagram at b = 22.6$^\circ $ from Fig. 7, expanded and decomposed into its constituent profiles at three positions (shown inset). Overlaid on each inset spectrum is a one-component Gaussian fit whose FWHM is shown at the upper left.
Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f9.eps,height=8.5cm} \end{figure} Figure 9:

Models of 12CO formation and excitation. Results are shown for models having n(H) = n(H I) + 2n(H2) =  $256~{\rm cm}^{-3}$ and $512~{\rm cm}^{-3}$. Upper left: variation of integrated 12CO brightness $W_{\rm CO}$ with N(H2); the shaded line labelled ``2'' is a CO-H2 conversion factor $2\times10^{20}~\mbox{H$_2$ }~{\rm cm}^{-2}$ (K km s-1)-1. Upper right: variation of $W_{\rm CO}$ with N(12CO). Bottom left: variation of N(12CO) with N(H2). Lower right: comparison of 12CO line brightnesses in the lowest two rotational transitions.
Open with DEXTER
In the text

  \begin{figure} \par\psfig{figure=10905f10.eps,height=8.7cm} \end{figure} Figure 10:

Comparison of the limiting extinction $A^\infty _{\rm V}$ of Dobashi et al. (2005) with the limiting reddening data $E^\infty _{B-V}$ of Schlegel et al. (1998). There is a left-offset of the $A^\infty _{\rm V}$ data of 0.78 mag, which is also seen toward $\zeta $ Oph itself, see Sect. 6 of the text (available online).
Open with DEXTER
In the text

  \begin{figure} \par {\psfig{figure=10905f11.eps,height=18.5cm,angle=-90} }\end{figure} Figure 11:

Maps of various quantities, available online. Top left and right, peak and integrated brightness. Middle: mean velocity and velocity dispersion. Bottom, the velocity gradient.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.