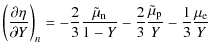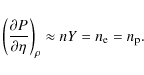| Issue |
A&A
Volume 499, Number 2, May IV 2009
|
|
|---|---|---|
| Page(s) | 557 - 566 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200810895 | |
| Published online | 01 April 2009 | |
Stable magnetic equilibria and their evolution in the upper main sequence, white dwarfs, and neutron stars
A. Reisenegger1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching bei München, Germany
2 -
Permanent address: Departamento de Astronomía y Astrofísica, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
Received 2 September 2008 / Accepted 20 March 2009
Abstract
Context. Long-lived, large-scale magnetic field configurations exist in upper main sequence, white dwarf, and neutron stars. Externally, these fields have a strong dipolar component, while their internal structure and evolution are uncertain but highly relevant to several problems in stellar and high-energy astrophysics.
Aims. We discuss the main properties expected for the stable magnetic configurations in these stars from physical arguments and the ways these properties may determine the modes of decay of these configurations.
Methods. We explain and emphasize the likely importance of the non-barotropic, stable stratification of matter in all these stars (due to entropy gradients in main-sequence envelopes and white dwarfs, due to composition gradients in neutron stars). We first illustrate it in a toy model involving a single, azimuthal magnetic flux tube. We then discuss the effect of stable stratification or its absence on more general configurations, such as axisymmetric equilibria involving poloidal and toroidal field components. We argue that the main mode of decay for these configurations are processes that lift the constraints set by stable stratification, such as heat diffusion in main-sequence envelopes and white dwarfs, and beta decays or particle diffusion in neutron stars. We estimate the time scales for these processes, as well as their interplay with the cooling processes in the case of neutron stars.
Results. Stable magneto-hydrostatic equilibria appear to exist in stars whenever the matter in their interior is stably stratified (not barotropic). These equilibria are not force-free and not required to satisfy the Grad-Shafranov equation, but they do involve both toroidal and poloidal field components. In main sequence stars with radiative envelopes and in white dwarfs, heat diffusion is not fast enough to make these equilibria evolve over the stellar lifetime. In neutron stars, a strong enough field might decay by overcoming the compositional stratification through beta decays (at the highest field strengths) or through ambipolar diffusion (for somewhat weaker fields). These processes convert magnetic energy to thermal energy, and they occur at significant rates only once the latter is less than the former; therefore, they substantially delay the cooling of the neutron star, while slowly decreasing its magnetic energy.
Key words: magnetic fields - magnetohydrodynamics (MHD) - stars: early-type - stars: magnetic fields - stars: neutron - stars: white dwarfs
1 Introduction
Upper main sequence stars, white dwarfs, and neutron stars appear to have long-lived magnetic fields. These fields are organized on large scales, in the sense that the dipole field components (and perhaps some other, low-order multipoles, e.g. Bagnulo et al. 1999,2000) are not much weaker than the rms surface field, unlike the highly chaotic field of the Sun.
The highest detected (surface dipole) magnetic field strengths are
![]() in O
stars (radius
in O
stars (radius
![]() ,
Donati et al. 2002,2006; Petit et al. 2008),
,
Donati et al. 2002,2006; Petit et al. 2008),
![]() in chemicallly peculiar A and B stars (Ap/Bp stars,
in chemicallly peculiar A and B stars (Ap/Bp stars,
![]() ,
Bagnulo et al. 1999; Mathys et al. 1997),
,
Bagnulo et al. 1999; Mathys et al. 1997),
![]() in white dwarfs
(
in white dwarfs
(
![]() ,
Schmidt et al. 2003), and
,
Schmidt et al. 2003), and
![]() in ``magnetars'', a subclass of
strongly magnetized neutron stars (
in ``magnetars'', a subclass of
strongly magnetized neutron stars (
![]() ,
Kouveliotou et al. 1998; Woods et al. 1999), in all cases yielding very
similar total magnetic fluxes,
,
Kouveliotou et al. 1998; Woods et al. 1999), in all cases yielding very
similar total magnetic fluxes,
![]() .
This coincidence has often been interpreted as an
argument for flux freezing during stellar evolution
(Ferrario & Wickramasinghe 2005b; Reisenegger 2003; Ferrario & Wickramasinghe 2006,2005a; Reisenegger 2001b; Ruderman 1972),
although its feasibility has been called into question
(Thompson & Duncan 1993; Spruit 2008). Of course, a large fraction
of the original magnetic flux might be ejected with the stellar
envelope. On the other hand, substantial field amplification through
differential rotation, convection, and various instabilities could plausibly occur
in proto-neutron stars if they are born rapidly rotating (Thompson & Duncan 1993; Spruit 2002,2008).
.
This coincidence has often been interpreted as an
argument for flux freezing during stellar evolution
(Ferrario & Wickramasinghe 2005b; Reisenegger 2003; Ferrario & Wickramasinghe 2006,2005a; Reisenegger 2001b; Ruderman 1972),
although its feasibility has been called into question
(Thompson & Duncan 1993; Spruit 2008). Of course, a large fraction
of the original magnetic flux might be ejected with the stellar
envelope. On the other hand, substantial field amplification through
differential rotation, convection, and various instabilities could plausibly occur
in proto-neutron stars if they are born rapidly rotating (Thompson & Duncan 1993; Spruit 2002,2008).
Connected to the similar fluxes is that
these stars also have similar ratios of fluid pressure (
![]() ,
where G is the gravitational constant and
M is the mass of the star) to magnetic pressure (
,
where G is the gravitational constant and
M is the mass of the star) to magnetic pressure (![]() ),
),
a large number, even for the most highly magnetized objects, implying that the magnetic field causes only very minor perturbations to their hydrostatic equilibrium structure.
Another similarity among these stars is that much or all of their
structure is stably stratified, i.e. stable to convection.
The radiative envelopes of upper main sequence stars, as well
as the whole interior of white dwarfs, are stabilized by the
radially increasing specific entropy s, while in neutron stars
the same effect is caused by a radially varying mix of different
particle species (Reisenegger & Goldreich 1992; Reisenegger 2001a; Pethick 1992), which in the outer
core reduces to a radially varying proton and electron
fraction,
![]() ,
where ni stands for the number densities of neutrons (
,
where ni stands for the number densities of neutrons (![]() ), protons (
), protons (![]() )
and
electrons (
)
and
electrons (![]() ).
).
The structure of the magnetic field inside these stars is not known, although it is highly relevant to their evolution:
- 1)
- it affects the radial transport of angular momentum and
chemical elements (e.g. Heger et al. 2005);
- 2)
- it is plausibly the dominant source of energy for both
the outbursts and the persistent emission of soft gamma repeaters
(SGRs) and anomalous X-ray pulsars (AXPs), for this reason collectively
called ``magnetars'' (Thompson & Duncan 1996,1993);
- 3)
- it is likely to play an important role in the frequency
spectrum of quasi-periodic oscillations observed after SGR
flares (Levin 2007);
- 4)
- it leads to slight deformations of neutron stars that could give rise to precession of pulsars (Wasserman 2003) and to the emission of gravitational waves (Cutler 2002).
In Sect. 2, we present arguments to the effect that the stable stratification of the stellar matter should be an essential ingredient to these equilibria. This means that, contrary to assumptions in the recent literature (e.g. Pérez-Azorín et al. 2006; Broderick & Narayan 2008; Mastrano & Melatos 2008), these are definitely not force-free fields. In fact, it is shown in Appendix A that there are no true force-free equilibria in stars, while those proposed in the literature actually have singular magnetic forces on the stellar surface. Moreover, the fluid cannot be treated as barotropic, therefore the field components are not required to satisfy the Grad-Shafranov equation (Mestel 1956), contrary to the popular belief (Yoshida et al. 2006; Kiuchi & Kotake 2008; Haskell et al. 2008; Akgün & Wasserman 2008; Tomimura & Eriguchi 2005). In fact, the range of available equilibria becomes much wider in a stably stratified, non-barotropic fluid. The constraints imposed by the stability of these equilibria are far from obvious, but we argue that there are probably no equilibria in barotropic stars, while it is likely that there are equilibria with linked toroidal and poloidal fields in stably stratified stars.
Of course, the specific entropy s and the proton fraction Y are not perfectly conserved quantities within each fluid element, but can be changed by dissipative processes, discussed in Sect. 3: in the case of s, through heat diffusion (Parker 1974), in the case of Y, by (direct or inverse) beta decays or by ambipolar diffusion (motion of charged relative to neutral particles, Thompson & Duncan 1996; Hoyos et al. 2008; Pethick 1992; Goldreich & Reisenegger 1992). Thus, the condition of stable stratification, and with it the hypothetically associated stable magnetic equilibrium configuration, although excellent approximations on short (Alfvén-like) time scales, are eroded on the time scales of the dissipative processes mentioned above, leading to the decay of these structures (Goldreich & Reisenegger 1992), and perhaps to a sudden loss of stability (Braithwaite & Spruit 2006; Braithwaite & Nordlund 2006; Braithwaite & Spruit 2004). In main-sequence stars, white dwarfs, and weakly magnetized neutron stars, these appear to be too long to act on the stellar life time, but in strongly magnetized neutron stars their time scales become shorter, so they might plausibly drive magnetic field decay, leading to internal heating and to the magnetar phenomenon (Arras et al. 2004; Thompson & Duncan 1996).
In principle, the Hall drift might also play a role in the field evolution in neutron stars (Pons & Geppert 2007; Urpin & Shalybkov 1991; Reisenegger et al. 2007,2005; Jones 1988; Goldreich & Reisenegger 1992). However, its time scale in neutron star cores tends to be somewhat longer than those of the other processes considered here (Goldreich & Reisenegger 1992). Moreover, in an axially symmetric, equilibrium magnetic field configuration, the effect of the Hall drift is exactly cancelled by bulk fluid motions (Reisenegger & Thompson 2009), so we do not take it into account. For simplicity, we also refrain from discussing the role of the solid crust of the neutron star, as well as the effects of superconductivity and superfluidity, which alter the magnetic stresses (Akgün & Wasserman 2008; Easson & Pethick 1977) as well as the dissipative processes. We also ignore the process of initial set-up of the magnetic equilibrium, which might be a highly dynamical process involving differential rotation and possibly a dynamo (Thompson & Duncan 1993; Spruit 2002), but concentrate on the properties imposed by the equilibrium and stability conditions and on the long-term evolution of the field.
A concise summary of our conclusions is given in Sect. 4. Parts of this discussion have already been given elsewhere (Reisenegger 2007,2008).
2 Magnetic equilibria and stable stratification
2.1 Force balance
In a conducting, fluid star, a general MHD equilibrium is set
by the condition that the net force on the fluid vanishes
everywhere, i.e.
where
is the magnetic (Lorentz) force per unit volume, written in terms of the magnetic field,
is the fluid force, which depends on its pressure, P, density
In all the stars of interest, the fluid is non-barotropic, i.e. the density is not a function of pressure only, but depends on an additional, non-trivial variable X, which is conserved on dynamical (sound or Alfvén wave crossing) time scales: specific entropy (X=s) in the case of upper main sequence stars and white dwarfs, and the fraction of protons (X=Y) or other minor constituent particles required by beta equilibrium in the case of neutron stars (Reisenegger & Goldreich 1992; Pethick 1992).
As shown in Eq. (1), the fluid pressure is much higher than
the magnetic pressure, so we take the point of view that the magnetic forces create
only a slight perturbation to the background hydrostatic equilibrium state
(
![]() )
the star would have in their absence. In addition, we invoke
the standard Cowling approximation of neglecting perturbations to the gravitational
potential, also used in the simulations of Braithwaite and
collaborators.
)
the star would have in their absence. In addition, we invoke
the standard Cowling approximation of neglecting perturbations to the gravitational
potential, also used in the simulations of Braithwaite and
collaborators.
We do not assume that the unperturbed
star is spherically symmetric, so our arguments can also be
applied to stars that are uniformly rotating, in which case
![]() has to be interpreted as the effective potential, also
including centrifugal effects. However, we ignore the effects
of meridional circulation. The time
scale for this process, due to the interaction of stellar rotation and
internal heat flow, is
has to be interpreted as the effective potential, also
including centrifugal effects. However, we ignore the effects
of meridional circulation. The time
scale for this process, due to the interaction of stellar rotation and
internal heat flow, is
![]() ,
where
,
where
![]() is the stellar rotation rate,
is the stellar rotation rate,
![]() is its maximum
(Keplerian or ``break-up'') value, and
is its maximum
(Keplerian or ``break-up'') value, and
![]() is the
(Kelvin-Helmholtz) time scale required to radiate away the
thermal energy content of the star. For main sequence stars,
is the
(Kelvin-Helmholtz) time scale required to radiate away the
thermal energy content of the star. For main sequence stars,
![]() is substantially shorter than their
main-sequence life time, so meridional circulation can modify
the magnetic field structure of sufficiently fast rotators,
is substantially shorter than their
main-sequence life time, so meridional circulation can modify
the magnetic field structure of sufficiently fast rotators,
![]() (Mestel 1999; Moss 1990,1984), to which our
analysis will therefore not apply. For white
dwarfs,
(Mestel 1999; Moss 1990,1984), to which our
analysis will therefore not apply. For white
dwarfs,
![]() is their cooling time, i.e.
essentially their age, so meridional circulation is unimportant
unless they rotate near break-up (Tassoul & Tassoul 1983). In
none of these cases, the magnetic field is expected to be
strong enough to have a substantial influence on the pattern or
time scale of meridional circulation. For neutron stars,
since the main source of stratification is not entropy but chemical
composition (Reisenegger & Goldreich 1992), meridional circulation will not occur at all.
is their cooling time, i.e.
essentially their age, so meridional circulation is unimportant
unless they rotate near break-up (Tassoul & Tassoul 1983). In
none of these cases, the magnetic field is expected to be
strong enough to have a substantial influence on the pattern or
time scale of meridional circulation. For neutron stars,
since the main source of stratification is not entropy but chemical
composition (Reisenegger & Goldreich 1992), meridional circulation will not occur at all.
Thus, we write the fluid force in terms of the Eulerian
perturbations (changes at fixed spatial positions) of density
and pressure,
![]() and
and ![]() ,
respectively, as
,
respectively, as
The perturbations can be viewed as being produced by a displacement field
where the gradient operator acts on the corresponding unperturbed ``background'' quantity,
If the displacement is fast enough, it can be taken to
conserve specific entropy and chemical composition, so the Lagrangian perturbations
are related by the adiabatic index
which is generally different from the analogous quantity characterizing the hydrostatic equilibrium profile of the star,
Then, also using the condition of mass conservation,
where the first term would be present as well in a barotropic, homogeneous fluid, whereas the second accounts for buoyancy effects. The latter is stabilizing if
In upper main sequence stars, the fluid is a classical,
monatomic ideal gas with
![]() ,
with their
radiative envelopes well described by
,
with their
radiative envelopes well described by
![]() (MacGregor & Cassinelli 2003), so
(MacGregor & Cassinelli 2003), so
![]() .
In white dwarfs, the electrons are highly degenerate (
.
In white dwarfs, the electrons are highly degenerate (
![]() ,
where k is Boltzmann's constant,
,
where k is Boltzmann's constant,
![]() is the interior temperature, and
is the interior temperature, and
![]() is the electron Fermi energy, not including the relativistic rest-mass term, mc2) and dominate the pressure, but the entropy is contained in the
ions, so
is the electron Fermi energy, not including the relativistic rest-mass term, mc2) and dominate the pressure, but the entropy is contained in the
ions, so
![]() .
Finally,
in the case of neutron stars, entropy becomes negligible
a few seconds after their birth, but they remain stably stratified due
to the density-dependent proton fraction,
.
Finally,
in the case of neutron stars, entropy becomes negligible
a few seconds after their birth, but they remain stably stratified due
to the density-dependent proton fraction,
![]() (Lai 1994; Reisenegger & Goldreich 1992; Reisenegger 2001a).
(Lai 1994; Reisenegger & Goldreich 1992; Reisenegger 2001a).
Equation (9) shows that, in a stably stratified fluid (with
![]() ), the fluid force has two parts that are determined by two independent, scalar functions, e.g.
), the fluid force has two parts that are determined by two independent, scalar functions, e.g. ![]() and
and
![]() ,
which give the fluid a
greater freedom to balance the magnetic force than it would
have in the barotropic case (
,
which give the fluid a
greater freedom to balance the magnetic force than it would
have in the barotropic case (
![]() ).
It should be noted that, if the buoyancy term in
Eq. (9) is crucial to balance a particular field configuration of characteristic
length scale comparable to the stellar radius,
the characteristic field strength is constrained by
).
It should be noted that, if the buoyancy term in
Eq. (9) is crucial to balance a particular field configuration of characteristic
length scale comparable to the stellar radius,
the characteristic field strength is constrained by
Thus, its maximum value is not set by the condition
yielding maximum allowed field strengths of
2.2 Hierarchy of equilibria and variational principles
Given this physical background, we now explore the more mathematical issue of how magnetic equilibria obtained under progressively more stringent (and, for our purposes, more realistic) constraints can be represented by constrained stationary points of the magnetic energy. We note that, contrary to the previous section, where ``perturbations'' were deviations from the non-magnetic, hydrostatic equilibrium caused by the magnetic field, here perturbations are taken with respect to successive, magnetic equilibria.
2.2.1 Field-free
Consider the total magnetic energy within a fixed volume,
![]() .
The only way to
obtain
.
The only way to
obtain
![]() under a weak, but otherwise arbitrary
magnetic field variation is to have
under a weak, but otherwise arbitrary
magnetic field variation is to have
![]() everywhere. This
is the absolute minimum of the magnetic energy, and it is
eventually obtained in a star placed in vacuum, without external
fields, and in which a sufficiently effective dissipation
mechanism (such as resistive diffusion) is active.
everywhere. This
is the absolute minimum of the magnetic energy, and it is
eventually obtained in a star placed in vacuum, without external
fields, and in which a sufficiently effective dissipation
mechanism (such as resistive diffusion) is active.
2.2.2 Current-free
Of course,
![]() is not fully
arbitrary, but must be divergenceless, so we now consider the
slightly more restricted case
is not fully
arbitrary, but must be divergenceless, so we now consider the
slightly more restricted case
![]() .
Now,
.
Now,
In the last result, the first integral can be made to vanish by imposing appropriate boundary conditions on the surface, for example that the magnetic flux through any surface element is fixed (
2.2.3 Force-free
In stars, dissipative processes such as the resistive diffusion of
magnetic flux are slow (see Sect. 3 for details)
and therefore often negligible. In this context, the only possible
perturbations of the magnetic field are those which can be
produced by plasma displacements,
![]() ,
with
,
with
![]() an arbitrary vector field. In
this case, neglecting the divergence term of Eq. (12),
an arbitrary vector field. In
this case, neglecting the divergence term of Eq. (12),
![]() ,
so the stationarity of the magnetic energy
implies the vanishing of the Lorentz force,
,
so the stationarity of the magnetic energy
implies the vanishing of the Lorentz force,
![]() .
This case is relevant in very diffuse plasmas such as those in stellar magnetospheres, where the
conductivity is high, but gas pressures and densities are low
(
.
This case is relevant in very diffuse plasmas such as those in stellar magnetospheres, where the
conductivity is high, but gas pressures and densities are low
(
![]() ), so the dynamics is dominated by the magnetic
field. However, as shown in Appendix A, it is
not possible to have magnetic field structures that are force-free
everywhere in a star, unless it is confined by (unrealistic)
surface forces.
), so the dynamics is dominated by the magnetic
field. However, as shown in Appendix A, it is
not possible to have magnetic field structures that are force-free
everywhere in a star, unless it is confined by (unrealistic)
surface forces.
2.2.4 Force balance
As we saw in Sect. 2.1, the plasma inside stars has
![]() ,
so the fluid forces, due to pressure and gravity,
can by no means be neglected. The total energy perturbation (with
respect to some hydrostatic or hydromagnetic equilibrium state)
caused by an arbitrary fluid displacement field
,
so the fluid forces, due to pressure and gravity,
can by no means be neglected. The total energy perturbation (with
respect to some hydrostatic or hydromagnetic equilibrium state)
caused by an arbitrary fluid displacement field
![]() can be
calculated by integrating the work per unit volume
can be
calculated by integrating the work per unit volume
![]() done against the forces of Eqs. (3) and (5) in order to build up this displacement field. In the absence of a magnetic field, the result can be written as
done against the forces of Eqs. (3) and (5) in order to build up this displacement field. In the absence of a magnetic field, the result can be written as
where we ignored a surface term that vanishes for appropriate boundary conditions. Clearly, the
When a magnetic field is introduced, the total energy perturbation
becomes more complicated,
(Bernstein et al. 1958), and negative-energy perturbations exist for some field configurations, even if
Barotropic fluid:
Thus, for a barotropic fluid with high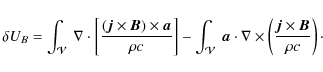 |
(15) |
Consistent with the condition that
i.e. that the Lorentz force per unit mass be a gradient (consistent with it having to be balanced by the first term in Eq. (9)). This is the case considered in most explicit descriptions of neutron star magnetic fields so far (Yoshida et al. 2006; Kiuchi & Kotake 2008; Haskell et al. 2008; Akgün & Wasserman 2008; Tomimura & Eriguchi 2005).
Stably stratified fluid:
Finally, in the strongly non-barotropic, stably stratified case (the most realistic, according to our discussion in Sect. 2.1), vertical motions are strongly suppressed, so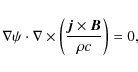 |
(17) |
a weaker condition than Eq. (16), that is satisfied if
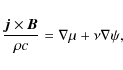 |
(18) |
where
It is clear that both the limit of a very diffuse plasma
(
![]() )
applicable to Sect. 2.2.3 and the very
dense plasma (
)
applicable to Sect. 2.2.3 and the very
dense plasma (
![]() )
of the present section are
idealizations. A more rigorous description would minimize the
total energy of the star, including internal and gravitational
energies in addition to the magnetic energy, and not impose the
additional conditions of this section on the displacement field
)
of the present section are
idealizations. A more rigorous description would minimize the
total energy of the star, including internal and gravitational
energies in addition to the magnetic energy, and not impose the
additional conditions of this section on the displacement field
![]() .
Moreover, the Tayler instability (Tayler 1973; see
also Sect. 2.4 of the present paper), although
active for arbitrarily high values of
.
Moreover, the Tayler instability (Tayler 1973; see
also Sect. 2.4 of the present paper), although
active for arbitrarily high values of ![]() ,
requires to account
explicitly for these other contributions to the energy, and
consistently to relax the constraints on
,
requires to account
explicitly for these other contributions to the energy, and
consistently to relax the constraints on
![]() .
For our purposes,
the idealized description given here appears to be sufficient.
.
For our purposes,
the idealized description given here appears to be sufficient.
2.2.5 A note on helicity conservation
A variation of the magnetic helicity,
![]() ,
can
be written, aside from a surface term (Spruit 2008), as
,
can
be written, aside from a surface term (Spruit 2008), as
![]() ,
so (for appropriate boundary conditions) helicity
is automatically conserved if
,
so (for appropriate boundary conditions) helicity
is automatically conserved if
![]() .
If we initially allow for an arbitrary
.
If we initially allow for an arbitrary
![]() ,
but
then search for a stationary point of UB at fixed
,
but
then search for a stationary point of UB at fixed
![]() (as done by Woltjer 1958; and more recently by
Broderick & Narayan 2008), we obtain
(as done by Woltjer 1958; and more recently by
Broderick & Narayan 2008), we obtain
![]() ,
where
,
where ![]() is a constant Lagrange multiplier. This condition
is less restrictive than those obtained in Sects. 2.2.1
and 2.2.2, but more restrictive than those of
Sects. 2.2.3 and 2.2.4. In
particular, the force-free condition of Sect. 2.2.3
allows for
is a constant Lagrange multiplier. This condition
is less restrictive than those obtained in Sects. 2.2.1
and 2.2.2, but more restrictive than those of
Sects. 2.2.3 and 2.2.4. In
particular, the force-free condition of Sect. 2.2.3
allows for
![]() with
with
![]() ,
so
,
so ![]() is constant on a given field
line, but possibly different on different field lines. Thus, the
condition of helicity conservation is most relevant in cases where
is constant on a given field
line, but possibly different on different field lines. Thus, the
condition of helicity conservation is most relevant in cases where
![]() is not exactly satisfied,
i.e. resistive dissipation allows some motion of magnetic flux
lines with respect to the fluid. Strictly speaking, such motion
does not conserve either energy or helicity. However, helicity is
more strongly dominated by large spatial scales than the magnetic
energy, so small-scale resistive dissipation may conserve the
former to a better approximation than the latter (Field 1986).
is not exactly satisfied,
i.e. resistive dissipation allows some motion of magnetic flux
lines with respect to the fluid. Strictly speaking, such motion
does not conserve either energy or helicity. However, helicity is
more strongly dominated by large spatial scales than the magnetic
energy, so small-scale resistive dissipation may conserve the
former to a better approximation than the latter (Field 1986).
2.3 Toy model: a thin flux tube
As a basis for later, educated guesses about the stability and
evolution of MHD equilibria in stars, we examine the stability of
a thin, azimuthal torus of cross section A lying in the
equatorial plane of the star, at a distance ![]()
![]() from the center, and containing a weak, roughly uniform azimuthal
magnetic field
from the center, and containing a weak, roughly uniform azimuthal
magnetic field ![]()
![]() .
For a general discussion
of the properties of thin magnetic flux tubes, see
Parker (1979) and references therein.
.
For a general discussion
of the properties of thin magnetic flux tubes, see
Parker (1979) and references therein.
In order to be in equilibrium, the forces across the flux tube's
cross section must balance, which requires the fluid pressure
inside to be lower by
![]() .
This is achieved on
the very short Alfvén crossing time
.
This is achieved on
the very short Alfvén crossing time ![]()
![]() ,
where
,
where
![]() is the Alfvén speed inside the flux
tube. On a longer time
is the Alfvén speed inside the flux
tube. On a longer time ![]()
![]() ,
the net forces on each
section of the flux tube must also come into balance. Its tension,
,
the net forces on each
section of the flux tube must also come into balance. Its tension,
![]() (Parker 1979), causes a radial force per unit
length
(Parker 1979), causes a radial force per unit
length
![]() that tends to contract the flux tube.
On the other hand, if the entropy and composition of the matter
inside and outside the flux tube are the same, the mass density
inside will be lower than outside,
that tends to contract the flux tube.
On the other hand, if the entropy and composition of the matter
inside and outside the flux tube are the same, the mass density
inside will be lower than outside,
![]() ,
causing a radially outward buoyancy force per
unit length,
,
causing a radially outward buoyancy force per
unit length,
![]() ,
where
,
where
![]() is the
gravitational acceleration.
is the
gravitational acceleration.
We take the point of view that the flux tube is initially placed
at a radius r where the matter outside has the same composition
and entropy as inside, and then allowed to displace to ![]() ,
enforcing
,
enforcing
![]() at each point, while the net
force
at each point, while the net
force
![]() controls the radial motion. Using the
notation of Sect. 2, we note that
controls the radial motion. Using the
notation of Sect. 2, we note that
so the net force per unit length can be written as
where the pressure scale height
In a stably stratified fluid (
![]() ), an equilibrium
will be reached at the displacement
), an equilibrium
will be reached at the displacement
Clearly, this equilibrium is stable with respect to radial, azimuthally symmetric displacements. However, it is intuitive that the flux tube could contract towards the axis by moving away from the equatorial plane, roughly on a sphere of radius r. This motion would be driven by the tension, without being opposed by the buoyancy force. It could only be prevented by an additional, poloidal magnetic field, which can either be enclosed by the toroidal flux tube under consideration or be present in the form of a twist of the magnetic field in the tube.
In all other cases (
![]() ), including that of a
barotropic fluid (
), including that of a
barotropic fluid (
![]() ), there will be no
equilibrium except at
), there will be no
equilibrium except at
![]() ,
and the flux tube will
either expand (if
,
and the flux tube will
either expand (if
![]() )
or contract (if
)
or contract (if
![]() )
indefinitely, at a speed determined by the fluid drag force
(Parker 1974).
)
indefinitely, at a speed determined by the fluid drag force
(Parker 1974).
This simple example suggests that, in the general case, the stratification of the fluid is likely to play an important role in determining the structure of magnetic equilibria, in the sense that there should be a much wider variety of possible equilibria in a stably stratified fluid than in a barotropic one.
2.4 Axially symmetric equilibria
The stable equilibria found by Braithwaite and collaborators (Braithwaite & Spruit 2006; Braithwaite & Nordlund 2006; Braithwaite & Spruit 2004) can be described ideally as axially symmetric (but see Braithwaite 2008, for highly asymmetric equilibria), involving two distinct regions: a thick torus fully contained in the star and containing a twisted toroidal-poloidal field combination, and the rest of space, containing a purely poloidal field that goes through the hole in the torus, and closing outside the star, in this way giving the external field an essentially dipolar appearance. It had long been speculated that such stable configurations might exist, but this has never been confirmed analytically (see Braithwaite & Nordlund 2006, for a discussion of earlier work).
For this reason, here we assume axial symmetry, allowing for
both poloidal and toroidal field components. In this case, all
the fluid variables depend only on two of the
three cylindrical coordinates, ![]() and z. The most general,
axially symmetric magnetic field can be
decomposed into a toroidal component
and z. The most general,
axially symmetric magnetic field can be
decomposed into a toroidal component
and a poloidal component
(Chandrasekhar & Prendergast 1956). This decomposition makes it explicit that the field depends only on two scalar functions,
where
In axial symmetry, the gradients in Eqs. (4) and (5) do not
have an azimuthal component, and therefore Eq. (2)
requires
![]() ,
or equivalently
,
or equivalently
i.e.
i.e. the surfaces
with only two vector components (in the
The possible equilibria are much more restricted in the barotropic case, in which
the stabilizing
![]() term in Eq. (5) vanishes and
the fluid force depends on a single scalar function
term in Eq. (5) vanishes and
the fluid force depends on a single scalar function
![]() .
Using this, together with
Eq. (28), in the force-balance Eq. (2), one finds that
.
Using this, together with
Eq. (28), in the force-balance Eq. (2), one finds that ![]() is parallel to
is parallel to
![]() ,
so
,
so
![]() ,
and eventually one
obtains the popular Grad-Shafranov equation (e.g. Kulsrud 2005, Sect. 4.9),
,
and eventually one
obtains the popular Grad-Shafranov equation (e.g. Kulsrud 2005, Sect. 4.9),
which is often assumed to characterize stellar magnetic fields (Yoshida et al. 2006; Kiuchi & Kotake 2008; Haskell et al. 2008; Akgün & Wasserman 2008; Tomimura & Eriguchi 2005). We emphasize that, in all the stars of interest here, the fluid is not barotropic, but stably stratified, with stabilizing buoyancy forces much stronger than the Lorentz forces, so the magnetic equilibria are not required to satisfy Eq. (29), but only the condition contained in Eqs. (26) and (27).
Of course, the existence of an equilibrium does not guarantee its stability, which is clearly illustrated by the two simplest cases of purely toroidal and purely poloidal fields, for which there are equilibria, which however are always unstable to non-axisymmetric perturbations. For a purely toroidal field, flux rings can shift with respect to each other on spherical surfaces, in this way reducing the total energy of the configuration (Tayler 1973). For a purely poloidal field, one can imagine cutting the star along a plane parallel to the symmetry axis and rotating one half with respect to the other, eliminating the dipole moment and reducing the energy of the external field, without changing the internal one (Flowers & Ruderman 1977).
In the long-lived configurations found numerically by Braithwaite and collaborators, it is clear that the toroidal and poloidal field components might stabilize each other against both kinds of instabilities mentioned in the previous paragraph. We can add here, based on the previous discussion, that the toroid of twisted field lines can be seen as a collection of nested, toroidal surfaces on which lie both the magnetic field lines and the current density lines (although their winding angles are generally different). As a consequence, the configuration has no toroidal Lorentz force component, although it generally does have poloidal components that are balanced by a pressure gradient and gravity.
We stress that Braithwaite's and his colleagues' simulations
considered a single-fluid, stably stratified star.
We can view the toroid, at least qualitatively, as a thick version of the
thin flux tube discussed in Sect. 2.3. It is impeded
from contracting onto the axis by the presence of the poloidal
flux going through it, as well as by the material between
the torus and the axis. In the stably
stratified star, the matter inside the toroid may have a
slightly different entropy or composition than outside,
cancelling its tendency to radial expansion due to buoyancy.
However, if the star were not stably stratified (or this
stratification could be overcome somehow; see Sect. 3), then a
toroid sufficiently close to the surface would tend to rise and
eventually move out of the star. If instead it were deep inside
the star, it would naturally tend to contract due to tension,
but be impeded from closing on its center by the poloidal flux.
However, in this case, a small displacement of the whole
configuration along the axis would cause a net buoyancy force
that would tend to move it out of the star, along the axis.
Although it is by no means clear whether this effect leads
to an instability or instead is quenched by other effects, such
as the progressive thickening of the toroidal ring or the
material trapped by the poloidal field, we conjecture that
stable equilibria occur only in stably
stratified stars, and not in barotropic ones. If this
conjecture were correct, it would make the usual search for
barotropic (Grad-Shafranov) equilibria in fluid stars astrophysically
meaningless![]() .
.
3 Long-term field evolution
From the previous discussion, it becomes natural to suggest that, as an alternative to the generally slow Ohmic diffusion (Cowling 1945; Baym et al. 1969), the decay of the magnetic energy may be promoted by processes that progressively erode the stable stratification of the stellar matter.
For example, in an entropy-stratified, plane-parallel atmosphere,
a horizontal flux tube with a purely longitudinal magnetic field
B can reach a mechanical equilibrium in which the interior
entropy differs from the external one by
![]() ,
so as to
compensate for the fluid pressure difference induced by the
magnetic field,
,
so as to
compensate for the fluid pressure difference induced by the
magnetic field,
![]() ,
yielding the same mass
density inside as outside,
,
yielding the same mass
density inside as outside,
![]() and thus zero net
buoyancy. However, in this state, the temperature inside the flux
tube is also lower than outside, so heat will stream inwards,
reducing
and thus zero net
buoyancy. However, in this state, the temperature inside the flux
tube is also lower than outside, so heat will stream inwards,
reducing
![]() and making the flux tube rise
(MacGregor & Cassinelli 2003; Parker 1974). This is the main alternative to
resistive diffusion in the case of entropy-stratified stars, i.e.
upper main sequence stars and white dwarfs.
and making the flux tube rise
(MacGregor & Cassinelli 2003; Parker 1974). This is the main alternative to
resistive diffusion in the case of entropy-stratified stars, i.e.
upper main sequence stars and white dwarfs.
Similarly, magnetic equilibria in a neutron star rely on a
perturbation of the proton fraction, ![]() ,
which can be
reduced by two processes (Goldreich & Reisenegger 1992):
,
which can be
reduced by two processes (Goldreich & Reisenegger 1992):
- 1)
- direct and inverse beta decays, converting neutrons into charged
particles (protons and electrons) and vice-versa; and
- 2)
- ambipolar diffusion, i.e. diffusion of charged particles, pushed
by Lorentz forces, with respect to neutral ones.
Since these processes and the corresponding ![]() differ
substantially from one type of star to another, we now discuss
each type separately.
differ
substantially from one type of star to another, we now discuss
each type separately.
3.1 Upper main sequence stars
The Ohmic dissipation time for a magnetic field in a
non-degenerate star is
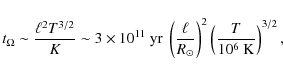 |
(30) |
with Spitzer magnetic diffusivity
According to the discussion above, the time scale for decay of the
field due to destabilization by heat exchange is
![]() ,
where, in this case,
,
where, in this case, ![]() is the heat diffusion time into a
magnetic structure of characteristic scale
is the heat diffusion time into a
magnetic structure of characteristic scale ![]() ,
related to the
Kelvin-Helmholtz time,
,
related to the
Kelvin-Helmholtz time,
![]() ,
of the star (of radius R) by
,
of the star (of radius R) by
![]() ;
therefore
;
therefore
| tB | 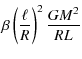 |
||
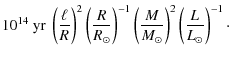 |
(31) |
For realistic numbers, this time scale is comparable or somewhat longer than the Ohmic time, thus not likely to be relevant for the star's magnetic evolution.
3.2 White dwarfs
In white dwarfs, the same processes are active as in main sequence
envelopes, although modified by the degenerate conditions. The
Ohmic time scale is reduced (factor ![]() 10-5) by the smaller
length scale, and increased (factor
10-5) by the smaller
length scale, and increased (factor ![]() 106) by the higher
kinetic energy of the electrons (Fermi energy rather than thermal
energy). Thus, again, the resistive decay of a large-scale field
is too slow to play a substantial role in the evolution of these
stars (Wendell et al. 1987).
106) by the higher
kinetic energy of the electrons (Fermi energy rather than thermal
energy). Thus, again, the resistive decay of a large-scale field
is too slow to play a substantial role in the evolution of these
stars (Wendell et al. 1987).
Heat diffusion occurs chiefly through transport by the degenerate
electrons, with conductivity
![]() ,
where
,
where
![]() is Planck's constant, Z is the atomic number of the
ions, e is the proton charge,
is Planck's constant, Z is the atomic number of the
ions, e is the proton charge,
![]() is the effective mass of
the electrons (relativistic Fermi energy divided by c2, and
is the effective mass of
the electrons (relativistic Fermi energy divided by c2, and
![]() is the dimensionless ``Coulomb logarithm'' (see
Potekhin et al. 1999), which we take
is the dimensionless ``Coulomb logarithm'' (see
Potekhin et al. 1999), which we take ![]() 1 for the estimates
that follow. Most of the heat is contained in the non-degenerate
ions, whose number density is
1 for the estimates
that follow. Most of the heat is contained in the non-degenerate
ions, whose number density is
![]() ,
so the heat diffusion
time
,
so the heat diffusion
time![]() through
a scale
through
a scale ![]() is
is
Imposing the magnetic flux loss time
Since
Unlike the case of neutron stars (Sect. 3.3), in known white dwarfs the thermal energy appears to be always larger than the magnetic energy, thus the eventual feedback of the magnetic dissipation on the stellar cooling is negligible.
3.3 Neutron stars
Like white dwarfs, neutron stars are passively cooling objects, in which the progressive decrease of the temperature makes the reaction rates and transport coefficients (but not the spatial structure) change with time. In particular, with decreasing temperature, beta decay rates decrease dramatically, while collision rates also decrease and thus make particle diffusion processes proceed more quickly.
In the discussion below, we ignore the possibility of Cooper pairing of nucleons, which is expected to occur at least in some parts of the neutron star core and turns neutrons into a superfluid and protons into a superconductor. This is likely to have a strong effect on the rates mentioned in the previous paragraph. However, this effect is difficult to quantify; therefore we rely on the better-known properties of ``normal'' degenerate matter and leave it to future work to explore the Cooper-paired analog.
3.3.1 Direct and inverse beta decays
We first consider a hot neutron star (in the neutrino cooling regime, e.g. Yakovlev & Pethick 2004), in which the collision rates are so high as to effectively bind all particle species together, but weak interaction processes proceed at non-negligible rates.
For illustration, let us again consider the toy model of a thin,
horizontal magnetic flux tube that is rising due to magnetic
buoyancy through a degenerate gas of neutrons (n), protons
(p), and electrons (e). Since the time scale to reach chemical
equilibrium is much longer than any dynamical times, the flux tube
can be considered to be in hydrostatic equilibrium, e.g. its
internal mass density is equal to that of its surroundings,
![]() ,
and its internal fluid pressure is reduced to
compensate for the magnetic pressure,
,
and its internal fluid pressure is reduced to
compensate for the magnetic pressure,
![]() .
These two conditions are only compatible if the fluid inside the
flux tube is not in chemical equilibrium, namely
.
These two conditions are only compatible if the fluid inside the
flux tube is not in chemical equilibrium, namely
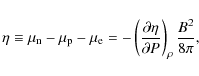 |
(34) |
where
For a simplified equation of state with non-interacting fermions
(see, e.g. Shapiro & Teukolsky 1983), we show in Appendix
B that
![]() ,
so
,
so
where we have assumed small perturbations,
In order for the flux tube to move, ![]() has to decrease by
inverse beta decays,
has to decrease by
inverse beta decays,
![]() ,
i.e. by one of the
same processes (direct or modified Urca) that control the cooling
of the star.
,
i.e. by one of the
same processes (direct or modified Urca) that control the cooling
of the star.
In the ``subthermal'' regime (Haensel et al. 2002),
![]() ,
the available phase space for these reactions is determined by the
temperature, and the time scale for the decay of
,
the available phase space for these reactions is determined by the
temperature, and the time scale for the decay of ![]() is
is ![]() 10 times shorter than that for the decrease of T (Reisenegger 1995).
On this time scale,
10 times shorter than that for the decrease of T (Reisenegger 1995).
On this time scale, ![]() would approach zero if the flux tube
was held at its initial position. What happens is that, as Y is
decreased by the beta decays, the pressure inside the flux tube
increases, the tube expands and rises to find a new hydrostatic
equilibrium in which it continues to be in a slight chemical
imbalance as described by Eq. (35). This allows us to
relate the logarithmic changes in the proton fraction inside the
flux tube and the temperature in the star as the latter cools and
the flux tube rises,
would approach zero if the flux tube
was held at its initial position. What happens is that, as Y is
decreased by the beta decays, the pressure inside the flux tube
increases, the tube expands and rises to find a new hydrostatic
equilibrium in which it continues to be in a slight chemical
imbalance as described by Eq. (35). This allows us to
relate the logarithmic changes in the proton fraction inside the
flux tube and the temperature in the star as the latter cools and
the flux tube rises,
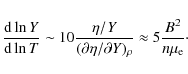 |
(36) |
A substantial displacement of the flux tube corresponds to this quantity being
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0895fig1.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa10895-08/Timg227.png) |
Figure 1: Magnetic field - temperature plane for a non-superfluid neutron star core. The dot-dashed horizontal lines show the initial temperature (just after core collapse), and the transition from neutrino-dominated (modified Urca) to photon-dominated cooling. The dashed diagonal line corresponds to the equality of magnetic and thermal energy. Above and to the left of the solid line, the star cools passively, on the time scales indicated in parenthesis along the vertical axis, without substantial magnetic field decay, so the evolution of the star is essentially a downward vertical line. Once the solid line is reached, magnetic dissipation mechanisms become important and generate heat that stops the cooling. The subsequent evolution is expected to be roughly along this line, with temperature and magnetic field decreasing together, much more slowly than the passive cooling. |
| Open with DEXTER | |
On the other hand, in the strongly ``suprathermal'' regime,
![]() ,
the induced inverse beta decays leave more
thermal energy in the star than is emitted in the form of
neutrinos, i.e. in the region in which this chemical imbalance is
present, the Urca processes have a net heating effect (Fernández & Reisenegger 2005)
and might therefore be able to keep the star warm during a time
long enough for the field to decay (Thompson & Duncan 1996). This
heating-cooling balance occurs at
,
the induced inverse beta decays leave more
thermal energy in the star than is emitted in the form of
neutrinos, i.e. in the region in which this chemical imbalance is
present, the Urca processes have a net heating effect (Fernández & Reisenegger 2005)
and might therefore be able to keep the star warm during a time
long enough for the field to decay (Thompson & Duncan 1996). This
heating-cooling balance occurs at
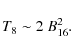 |
(37) |
On this line (see Fig. 1), the thermal energy in the star,
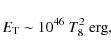 |
(38) |
is less than its magnetic energy,
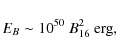 |
(39) |
by a factor
| (40) |
and therefore the cooling process of the star will be delayed by the inverse of this factor.
3.3.2 Ambipolar diffusion
At somewhat lower temperatures, collision rates are reduced (due to the increased degeneracy and reduced number of available quantum states), allowing different particle species to drift with respect to each other. The Lorentz force only acts directly on the charged particles (protons, electrons, and perhaps others), pushing them through the neutrons. The magnetic flux is only frozen into the charged particle fluid, which moves through the neutral fluid as fast as the balance of Lorentz force and collisions allows. If the charged fluid contains only protons and electrons, it will be barotropic. If additional particle species are present, it will be stably stratified due to their density-dependent abundances.
Goldreich & Reisenegger (1992) decompose the charged particle flux
![]() of
ambipolar diffusion into two modes:
of
ambipolar diffusion into two modes:
- 1)
- irrotational, with
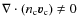 and
and
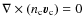 ,
which builds up pressure gradients
in the charged particle fluid, which need to be eliminated by weak
interactions in order for the motion to proceed;
,
which builds up pressure gradients
in the charged particle fluid, which need to be eliminated by weak
interactions in order for the motion to proceed;
- 2)
- solenoidal, with
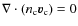 and
and
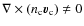 ,
corresponding to an
incompressible charged-particle flow, which does not cause
pressure gradients and only needs to overcome the frictional force
due to charged-neutron collisions.
,
corresponding to an
incompressible charged-particle flow, which does not cause
pressure gradients and only needs to overcome the frictional force
due to charged-neutron collisions.
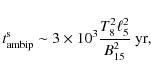 |
(41) |
causing a magnetic energy dissipation
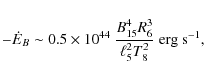 |
(42) |
that can, at sufficiently low temperatures, balance the dominant cooling luminosity, be it neutrinos (here for the modified Urca process),
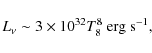 |
(43) |
or thermal electromagnetic radiation from the stellar surface,
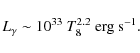 |
(44) |
The first will happen at
3.3.3 Neutron star summary
Strongly magnetized neutron stars appear to be subject to processes that can erode the stable stratification and therefore cause an MHD-stable field to decay on time scales shorter than their observable lifetime. These processes are weak decays, which are dominant at very high field strengths, and ambipolar diffusion, at somewhat lower field strengths. In both cases, these processes become important only once the thermal energy in the star is substantially less than the magnetic energy, and therefore the latter acts as a large reservoir that keeps the star hot for much more than its cooling time in the un-magnetized case (see also Thompson & Duncan 1996; Pons et al. 2007). If the field decayed homologously, the star would evolve following the line of heating-cooling balance in Fig. 1. In fact, the evolution is likely more complex, involving loss of stability, followed by abrupt re-arrangements of the field (Braithwaite & Spruit 2004), but these effects should occur roughly on the heating-cooling balance line.
Of course, neutron stars also have a solid crust, whose elastic and yielding properties are still highly uncertain. At very high field strengths, the Lorentz forces will distort the crust, which might act essentially as a fluid. At lower field strengths, the crust might act as a valve, controlling the loss of magnetic flux. The relative importance of the decay mechanisms in the crust (Hall drift, crust cracking) and core is still unclear, depending on the uncertain properties of both.
4 Conclusions
This paper contains a general discussion of several physical issues related to the existence of large-scale, coherent magnetic structures in upper main sequence stars, white dwarfs, and neutron stars. The main conclusions are the following:
- 1)
- Magnetic forces in these objects are generally weak
compared to pressure and gravity forces, and their matter is
strongly stratified by entropy or composition gradients. This
means that at least some components of the magnetic forces can
easily be balanced by other forces. Thus, there can be a wide
variety of possible equilibria. These equilibria are not
force-free; in fact, force-free equilibria are not possible in
stars.
- 2)
- If the magnetic structure is axially symmetric, the only
constraint it has to satisfy to be balanced by pressure and
gravity forces is that the azimuthal component of the Lorentz
force must vanish. This means that there must be a set of magnetic
surfaces of toroidal topology containing both the magnetic field
lines and the current flow lines. Since the fluid is not
barotropic, there is no need for the magnetic field to satisfy a
Grad-Shafranov equation.
- 3)
- It is difficult to give general criteria for stability.
However, it is likely that, in a stably stratified star, poloidal
and toroidal field components of similar strength could stabilize
each other. In a barotropic fluid, it is possible that no stable
equilibria exist, as the magnetic field might rise buoyantly and
be lost from the star.
- 4)
- The long-term evolution of the magnetic field is likely to be governed by dissipative processes that erode the stable stratification. Heat diffusion in main sequence stars and white dwarfs appears to be too slow to cause an observable effect over the life time of these stars. In strongly magnetized neutron stars, ambipolar diffusion and beta decays might be causing the magnetic energy release observed in magnetars.
Appendix A: No force-free fields in stars
Consider the following integral over a volume containing the star
of interest:
(e.g. Kulsrud 2005, Chap. 4), where the Einstein summation convention is being used, and the magnetic stress tensor is
 |
(A.2) |
The last term in Eq. (A.1) is minus the total magnetic energy within
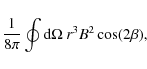 |
(A.3) |
where
Appendix B: Thermodynamic properties of a degenerate npe fluid
Taking the neutrons and protons to be nonrelativistic, the
electrons extremely relativistic, and all highly degenerate, the
total energy density and pressure are
where
The chemical imbalance
So,
Acknowledgements
The author thanks Stefano Bagnulo, Jon Braithwaite, Peter Goldreich, Swetlana Hubrig, Maxim Lyutikov, Friedrich Meyer, and Chris Thompson for many stimulating and informative conversations, Henk Spruit and an anonymous referee for insightful comments that improved the manuscript, and Cristóbal Petrovich for preparing Fig. 1. This work was supported by Proyecto Regular FONDECYT 1060644 and Proyecto Basal PFB-06/2007.
References
- Akgün, T., & Wasserman, I. 2008, MNRAS, 383, 1551 [NASA ADS]
- Arras, P., Cumming, P., & Thompson, C. 2004, ApJ, 608, L49 [NASA ADS] [CrossRef]
- Bagnulo, S., Landolfi, M., & Landi degl'Innocenti, M. 1999, A&A, 343, 865 [NASA ADS]
- Bagnulo, S., Landolfi, M., Mathys, G., & Landi degl'Innocenti, M. 2000, A&A, 358, 929 [NASA ADS]
- Baym, G., Pethick, C., & Pines, D. 1969, Nature, 224, 675 [NASA ADS] [CrossRef]
- Bernstein, I. B., Frieman, E. A., Kruskal, M. D., & Kulsrud, R. M. 1958, Proc. Roy. Soc. A, 2, 44, 17 (In the text)
- Braithwaite, J. 2008, MNRAS, 386, 1947 [NASA ADS] [CrossRef] (In the text)
- Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences]
- Braithwaite, J., & Spruit, H. 2004, Nature, 431, 819 [NASA ADS] [CrossRef]
- Braithwaite, J., & Spruit, H. 2006, A&A, 450, 1097 [NASA ADS] [CrossRef] [EDP Sciences]
- Broderick, A. E., & Narayan, R. 2008, MNRAS, 383, 943 [NASA ADS] [CrossRef]
- Chandrasekhar, S., & Prendergast, K. H. 1956, Proc. Nat. Acad. Sci., 42, 5 [NASA ADS] [CrossRef] (In the text)
- Cowling, T. G. 1945, MNRAS, 105, 166 [NASA ADS]
- Cutler, C. 2002, Phys. Rev. D, 66, 084025 [NASA ADS] [CrossRef] (In the text)
- Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef]
- Donati, J.-F., Howarth, I. D., Bouret, J.-C., et al. 2006, MNRAS, 365, L6 [NASA ADS]
- Easson, I., & Pethick, C. J. 1977, Phys. Rev. D, 16, 275 [NASA ADS] [CrossRef]
- Fernández, R., & Reisenegger, A. 2005, ApJ, 625, 291 [NASA ADS] [CrossRef] (In the text)
- Ferrario, L., & Wickramasinghe, D. T. 2005a, MNRAS, 356, 615 [NASA ADS] [CrossRef]
- Ferrario, L., & Wickramasinghe, D. T. 2005b, MNRAS, 356, 1576 [NASA ADS] [CrossRef]
- Ferrario, L., & Wickramasinghe, D. T. 2006, MNRAS, 367, 1323 [NASA ADS] [CrossRef]
- Ferraro, V. C. A. 1937, MNRAS, 97, 458 [NASA ADS]
- Field, G. 1986, in Magnetospheric phenomena in astrophysics (New York: American Institute of Physics), AIP Conf. Proc., 144, 324 (In the text)
- Flowers, E., & Ruderman, M. A. 1977, ApJ, 215, 302 [NASA ADS] [CrossRef]
- Goldreich, P., & Reisenegger, A. 1992, ApJ, 395, 250 [NASA ADS] [CrossRef]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2002, A&A, 394, 213 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Haskell, B., Samuelsson, L., Glampedakis, K., & Andersson, N. 2008, MNRAS, 385, 531 [NASA ADS] [CrossRef]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] (In the text)
- Hoyos, J., Reisenegger, A., & Valdivia, J. A. 2008, A&A, 487, 789 [NASA ADS] [CrossRef] [EDP Sciences]
- Jones, P. B. 1988, MNRAS, 233, 875 [NASA ADS]
- Kiuchi, K., & Kotake, K. 2008, MNRAS, 385, 1327 [NASA ADS] [CrossRef]
- Kouveliotou, C., Dieters, S., Strohmayer, T., et al. 1998, Nature, 393, 235 [NASA ADS] [CrossRef]
- Kulsrud, R. M. 2005, Plasma Physics for Astrophysics (Princeton University Press) (In the text)
- Lai, D. 1994, MNRAS, 270, 611 [NASA ADS]
- Levin, Y. 2007, MNRAS, 377, 159 [NASA ADS] [CrossRef] (In the text)
- Lüst, R., & Schlüter, A. 1954, Z. Astrophys., 34, 263 [NASA ADS] (In the text)
- Lyutikov, M., & Reisenegger, A. 2009, in preparation
- MacGregor, K. B., & Cassinelli, J. P. 2003, ApJ, 586, 480 [NASA ADS] [CrossRef] (In the text)
- Mastrano, A., & Melatos, A. 2008, MNRAS, 387, 1735 [NASA ADS] [CrossRef]
- Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353 [NASA ADS] [CrossRef] [EDP Sciences]
- Mestel, L. 1952, MNRAS, 112, 583 [NASA ADS] (In the text)
- Mestel, L. 1956, MNRAS, 116, 324 [NASA ADS] (In the text)
- Mestel, L. 1999, Stellar Magnetism (Oxford: Clarendon Press)
- Moss, D. 1984, MNRAS, 209, 607 [NASA ADS]
- Moss, D. 1990, MNRAS, 244, 272 [NASA ADS]
- Parker, E. N. 1974, Ap&SS, 31, 261 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1979, Cosmical Magnetic Fields (Oxford University Press) (In the text)
- Pérez-Azorín, J. F., Pons, J. A., Miralles, J. A., & Miniutti, G. 2006, A&A, 459, 175 [NASA ADS] [CrossRef] [EDP Sciences]
- Pethick, C. J. 1992, in The Structure and Evolution of Neutron Stars, ed. D. Pines, R. Tamagaki, & S. Tsuruta, 115
- Petit, V., Wade, G. A., Drissen, L., Montmerle, T., & Alecian, E. 2008, MNRAS, 387, L23 [NASA ADS]
- Pons, J. A., & Geppert, U. 2007, A&A, 470, 303 [NASA ADS] [CrossRef] [EDP Sciences]
- Pons, J. A., Link, B., Miralles, J. A., & Geppert, U. 2007, , 98, 071101
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345 [NASA ADS] (In the text)
- Reisenegger, A. 1995, ApJ, 442, 749 [NASA ADS] [CrossRef] (In the text)
- Reisenegger, A. 2001a, ApJ, 550, 860 [NASA ADS] [CrossRef]
- Reisenegger, A. 2001b, in Magnetic Fields across the Hertzsprung-Russell Diagram, ed. G. Mathys, S. K. Solanki, & D. T. Wickramasinghe, ASP Conf. Ser., 248, 469
- Reisenegger, A. 2003, in Proceedings of the International Workshop on Strong Magnetic Fields and Neutron Stars, ed. C. Z. Vasconcelos, et al. [arXiv:astro-ph/0307133]
- Reisenegger, A. 2007, Astron. Nachr., 328, 1173 [NASA ADS] [CrossRef]
- Reisenegger, A. 2008, Rev. Mex. Astron. Astrofis., in press [arXiv:0802.2227]
- Reisenegger, A., & Goldreich, P. 1992, ApJ, 395, 240 [NASA ADS] [CrossRef]
- Reisenegger, A., & Thompson, C. 2009, in preparation (In the text)
- Reisenegger, A., Prieto, J. P., Benguria, R., Lai, D., & Araya, P. A. 2005, in Magnetic Fields in the Universe: From Laboratory and Stars to Primordial Structures, AIP Conf. Proc., 784, 263
- Reisenegger, A., Benguria, R., Prieto, J. P., Araya, P. A., & Lai, D. 2007, A&A, 472, 233 [NASA ADS] [CrossRef] [EDP Sciences]
- Ruderman, M. 1972, ARA&A, 10, 427 [NASA ADS] [CrossRef]
- Schmidt, G., Harris, H. C., Liebert, J., et al. 2003, ApJ, 595, 1101 [NASA ADS] [CrossRef] (In the text)
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars (New York: Wiley) (In the text)
- Spruit, H. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences]
- Spruit, H. C. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars, and More, AIP Conf. Proc., 983, 391 [arXiv:0711.3650] (In the text)
- Tassoul, M., & Tassoul, J.-L. 1983, ApJ, 267, 334 [NASA ADS] [CrossRef] (In the text)
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS]
- Thompson, C., & Duncan, R. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef] (In the text)
- Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef]
- Tomimura, Y., & Eriguchi, Y. 2005, MNRAS, 359, 1117 [NASA ADS] [CrossRef]
- Urpin, V. A., & Shalybkov, D. A. 1991, Sov. Phys. JETP, 73, 703
- Wasserman, I. 2003, MNRAS, 341, 1020 [NASA ADS] [CrossRef] (In the text)
- Wendell, C. E., van Horn, H. M., & Sargent, D. 1987, ApJ, 313, 284 [NASA ADS] [CrossRef] (In the text)
- Woltjer, L. 1958, Proc. Nat. Acad. Sci., 44, 489 [NASA ADS] [CrossRef] (In the text)
- Woods, P. M. 1999, ApJ, 524, L55 [NASA ADS] [CrossRef]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] (In the text)
- Yoshida, S., Yoshida, S., & Eriguchi, Y. 2006, ApJ, 651, 462 [NASA ADS] [CrossRef]
Footnotes
- ... meaningless
![[*]](/icons/foot_motif.png)
- They might, however, play a role as stable ``Hall equilibria'' in solid neutron star crusts (Lyutikov & Reisenegger 2009).
- ...
time
![[*]](/icons/foot_motif.png)
- For white dwarfs, the diffusion time through scale
 in the degenerate interior is not the
Kelvin-Helmholtz or cooling time, as the bottleneck for the latter
is the conduction through the non-degenerate atmosphere.
in the degenerate interior is not the
Kelvin-Helmholtz or cooling time, as the bottleneck for the latter
is the conduction through the non-degenerate atmosphere.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0895fig1.eps}
\end{figure}](/articles/aa/full_html/2009/20/aa10895-08/Timg227.png) |
Figure 1: Magnetic field - temperature plane for a non-superfluid neutron star core. The dot-dashed horizontal lines show the initial temperature (just after core collapse), and the transition from neutrino-dominated (modified Urca) to photon-dominated cooling. The dashed diagonal line corresponds to the equality of magnetic and thermal energy. Above and to the left of the solid line, the star cools passively, on the time scales indicated in parenthesis along the vertical axis, without substantial magnetic field decay, so the evolution of the star is essentially a downward vertical line. Once the solid line is reached, magnetic dissipation mechanisms become important and generate heat that stops the cooling. The subsequent evolution is expected to be roughly along this line, with temperature and magnetic field decreasing together, much more slowly than the passive cooling. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



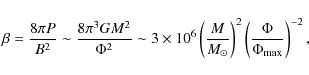

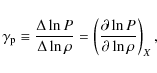
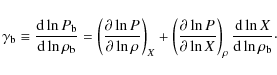
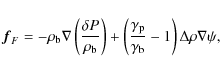
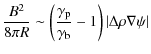
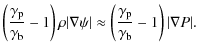
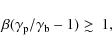
![$\displaystyle {1\over 4\pi}\left[\int_\mathcal V \nabla\cdot(\delta{\vec A}\tim...
...nt_\mathcal V \delta{\vec A}\cdot\nabla\times{\vec B}~{\rm d}\mathcal V\right].$](/articles/aa/full_html/2009/20/aa10895-08/img73.png)
![$\displaystyle \delta U=\int{1\over 2\gamma_{\rm p}P_{\rm b}}\left[\delta
P^2+\l...
...right)(\mbox{\boldmath$\xi$ }\cdot\nabla
P_{\rm b})^2\right]~{\rm d}\mathcal V,$](/articles/aa/full_html/2009/20/aa10895-08/img85.png)

![$\displaystyle +(\mbox{\boldmath$\xi$ }\cdot\nabla
P)\nabla\cdot\mbox{\boldmath$...
...cdot\nabla\psi)\nabla\cdot(\rho\mbox{\boldmath$\xi$ }) \bigg]~{\rm d}\mathcal
V$](/articles/aa/full_html/2009/20/aa10895-08/img92.png)
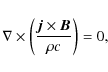
![\begin{displaymath}
\delta\rho={\rho_{\rm b}\over \gamma_{\rm p} P_{\rm b}}\left...
...\rm p}\over\gamma_{\rm b}}-1\right)\rho_{\rm b} g\xi_r\right],
\end{displaymath}](/articles/aa/full_html/2009/20/aa10895-08/img136.png)
![\begin{displaymath}
f_{\rm net}={A\over\gamma_{\rm p}H}\left[\left(1-{2\gamma_{\...
...\rm p}\over\gamma_{\rm b}}-1\right)\rho_{\rm b}
g\xi_r\right],
\end{displaymath}](/articles/aa/full_html/2009/20/aa10895-08/img137.png)
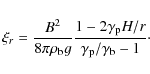

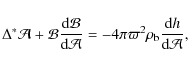
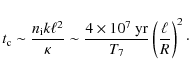
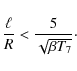
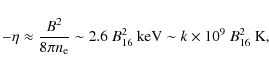
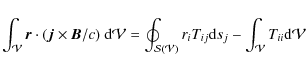
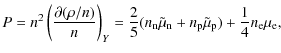
![$\displaystyle \left(\partial
P\over\partial Y\right)_n=n\left[{2\over 3}(-\mu_{\rm n}+\mu_{\rm p})+{1\over
3}\mu_{\rm e}\right]$](/articles/aa/full_html/2009/20/aa10895-08/img260.png)