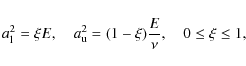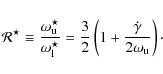EDP Sciences
Home All issues Volume 499 / No 2 (May IV 2009) A&A, 499 2 (2009) 535-540 Full HTML
Free Access
Issue
A&A
Volume 499, Number 2, May IV 2009
Page(s) 535 - 540
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200810740
Published online 19 March 2009

Internal resonance in nonlinear disk oscillations and the amplitude evolution of neutron-star kilohertz QPOs

J. Horák1 - M. A. Abramowicz2,3,6 - W. Kluzniak4,3 - P. Rebusco5 - G. Török6

1 - Astronomical Institute of the Academy of Sciences, Bocní II 1401/1a, 141-31 Praha 4, Czech Republic
2 - Department of Physics, Göteborg University, 41296 Göteborg, Sweden
3 - Copernicus Astronomical Centre PAN, Bartycka 18, 00-716 Warsaw, Poland
4 - Johannes Kepler Institute of Astronomy, Zielona Góra University, ul. Lubuska 2, 65-265 Zielona Góra, Poland
5 - MIT Kavli Institute for Astrophysics and Space Research, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
6 - Institute of Physics, Faculty of Philosophy and Science, Silesian University in Opava, Bezrucovo nám. 13, 746-01 Opava, Czech Republic

Received 4 August 2008 / Accepted 6 January 2009

Abstract
We study the properties of twin kilohertz quasiperiodic oscillations (QPOs) with a simple toy model consisting of two oscillation modes coupled with a general nonlinear force. We examine resonant effects by slowly varying the values of the tunable, and nearly commensurable, eigenfrequencies. The behavior of the true oscillation frequencies and amplitudes during a slow transition through the 3:2 resonance is examined in detail, and it is shown that both are affected significantly by the nonlinearities in the governing equations. In particular, the amplitudes of oscillations reflect a resonant exchange of energy between the modes, and as a result the initially weaker mode may become dominant after the transition. We note that a qualitatively similar behavior was reported for several neutron-star sources where the difference in the amplitudes of neutron-star twin-peak QPOs changes sign as the observed frequency ratio of the QPOs passes through the value 3:2.

Key words: X-rays: binaries - stars: neutron - accretion, accretion disks

1 Introduction

There is little doubt that kHz QPOs observed in low mass X-ray binaries originate in the inner region of accretion disks of the neutron star or black hole sources. The very fact that these quasi-periodic modulations are observed in the X-ray flux, i.e., in the most luminous part of the source spectrum - and at the same time at high photon energies - implies an origin in the inner part of the accretion flow, where most of the gravitational potential energy of the accreting matter is released. Time-of-flight arguments also imply that a kHz modulation of unbeamed radiation must originate in a region not larger than $\sim$100 km, an even tighter constraint being placed when the high degree of coherence of the observed modulation is taken into account.

In the present paper, we focus on kHz QPOs that appear in pairs, the so-called twin-peak QPOs (see van der Klis 2000, for a review), and we assume that they correspond to oscillations of an accretion-disk structure. Reproducible features of these high-frequency QPOs imply that they reflect some fundamental properties of the systems, such as their mass and spin.

Many models have been proposed, some involving orbital motions (Stella & Vietri 1999; Kluzniak et al. 1990), others based on oscillations of the accretion disk (Kato 2001,2008,2005b,2004a,2005a; Wagoner 1999; Wagoner et al. 2001; Pétri 2005, 2006) and of tori (Rezzolla et al. 2003b; Schnittman & Rezzolla 2006; Blaes et al. 2007; Montero et al. 2007; Zanotti et al. 2005; Montero et al. 2004; Horák 2008; Bursa et al. 2004; Rezzolla et al. 2003a; Blaes et al. 2006). Most models involve two or more oscillatory motions, which may interact in a nonlinear manner.

The appearance of rational ratios (mainly 3:2) of frequencies in twin-peak QPOs implies that nonlinear coupling is present between different modes of oscillations (Abramowicz & Kluzniak 2001). The importance of a resonant process was also emphasized by Kluzniak & Abramowicz (2001); Psaltis & Norman (2000); Titarchuk (2002); Kluzniak et al. (2004) and investigated in more detail, e.g., in Horák & Karas (2006); Abramowicz et al. (2003b); Lee et al. (2004); Rebusco (2004); Horák et al. (2004).

One example of an investigation of resonances between specific modes in an accretion disk can be found in the work of Kato (2005a), who proposed a model in which the two kHz QPOs are due to a nonlinear resonant interaction between the oscillations of a thin accretion disk and an oscillatory perturbation induced by the non-axisymmetric, rotating neutron-star. Both kHz oscillations are localized close to a resonant radius, where the interaction with the perturbation is most prominent. The spatial proximity of the two oscillations may facilitate an internal resonance between them. As pointed out by Mao et al. (2008), a resonance may also occur between two modes with non-overlapping wavefunctions, when it is mediated by a traveling wave. In other words, the two oscillators in resonance need not be located in the same annulus of the accretion disk. Kato (2008) relaxed the local approximation and analyzed the nonlinear, resonant excitation of inertial-acoustic, disk oscillations in deformed disks (a warped disk or a one-armed pattern that is symmetric with respect to the equator).

Other QPO models involve vortices in the disk or magnetic interactions. For example, Tagger & Varnière (2006) proposed the formation of two or three Rossby-wave vortices in microquasar disks, while Li & Narayan (2004) suggested a model in which the two QPOs are identified with two Rayleigh-Taylor or Kelvin-Helmholtz unstable modes developed at the interface between the disk and the magnetosphere. Similarly, in the Alfvén-wave-oscillation model (Zhang et al. 2007; Zhang 2004), the two QPOs correspond to the Keplerian orbital frequency and the frequency of the Alfvén waves excited at the same radius. It is less clear whether the resonant interaction described in this paper would apply to those models as well.

In this paper, we consider some general properties of nonlinear resonance that may be applicable to many systems. We specify neither the physical nature of the oscillators, nor the couplings necessary for a resonance to occur. In the context of kHz QPOs, the oscillators could be taken to be eigenmodes of either the accretion disk or an associated structure, perhaps as already discussed in the theoretical literature cited above. We do not address the crucial question of the excitation and damping of the modes in the turbulent disk, particularly when MRI-induced turbulence is present; in the framework of two coupled oscillators, this issue was addressed already by Vio et al. (2006). Eventually, one would hope to identify these resonances in numerical models of accretion flow. Inertial modes are beginning to be detected in numerical simulations (Brandenburg 2005; Machida & Matsumoto 2008; Kato 2004b; Reynolds & Miller 2008; Arras et al. 2006). It may be premature to look for a numerical validation of the idea of resonance in accretion disks, at least until two distinct frequencies in a 3:2 ratio are identified with some regularity in the simulations. Nevertheless, numerical work may already be offering new insights.

We review some general properties of internal resonance and investigate the amplitude evolution of the oscillations by modeling a slow passage of the frequencies through the 3:2 resonance. The results presented in this paper are more relevant to neutron-star QPOs where the frequencies vary over ranges of hundreds of hertz on the timescale of several hours, than to black-hole QPOs, whose frequencies are more stable.

2 Mathematics of the internal resonance

We model the QPOs using two coupled, nonlinear oscillators governed by the equations

 
$\displaystyle \ddot{x}_{\rm l}+ \omega_{\rm l}^2 x_{\rm l}= \omega_{\rm l}^2 f_{\rm l}(x_{\rm l},x_{\rm u},\dot{x}_{\rm l},\dot{x}_{\rm u}),$     (1)
$\displaystyle \ddot{x}_{\rm u}+ \omega_{\rm u}^2 x_{\rm u}= \omega_{\rm u}^2 f_{\rm u}(x_{\rm l},x_{\rm u},\dot{x}_{\rm l},\dot{x}_{\rm u}).$     (2)

The oscillations underlying the upper and lower QPOs are identified with the dimensionless solutions $x_{{\rm u}}(t)$ and $x_{\rm l}(t)$, respectively. The coupling functions $f_{\rm l}$ and $f_{\rm u}$ are treated as a perturbation, and are further assumed to contain only nonlinear terms and to be invariant under time inversion (e.g., their Taylor expansions begin with the second order and do not contain odd powers of the time derivatives $\dot{x}_{{\rm l}}$, $\dot{x}_{\rm u}$). The coefficients $\omega_{\rm l}>0$, and $\omega_{\rm u}>0$ are the eigenfrequencies of the two oscillators.

To study the most relevant resonant effects, we concentrate on the case when $\omega_{{\rm u}}/\omega_{\rm l}$ is close to 3:2. We chose this resonance because it is the most prominent one evident in the QPO data (Abramowicz et al. 2003a; Török et al. 2008). The degree of closeness to the rational ratio is expressed by the detuning parameter $\sigma\equiv 2\omega_{\rm u}- 3\omega_{\rm l}$.

Our analysis is applicable when the amplitudes of oscillations and the detuning parameter are small, and are such that $a_{\rm l}\sim a_{\rm u}\sim\epsilon\ll 1$ and $\sigma\sim\epsilon^2$, respectively. In that case, perturbation techniques can be used to find approximate solutions of Eqs. (1) and (2). Using the method of multiple scales (e.g., Nayfeh & Mook 1979), we find the lowest-order real displacements in the form:

$\displaystyle x_{\rm l}(t) = \Re\left[A_{\rm l}(t){\rm e}^{{\rm i}\omega_{\rm l... ... x_{\rm u}(t) = \Re\left[A_{\rm u}(t){\rm e}^{{\rm i}\omega_{\rm u}t}\right]\!.$     (3)

The higher-order terms add only higher harmonics to the quasiperiodic signal described by these solutions. The main difference with respect to the solutions of a linear system are that the complex amplitudes

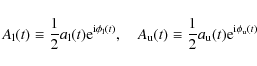\begin{displaymath}A_{\rm l}(t)\equiv\frac{1}{2}a_{\rm l}(t){\rm e}^{{\rm i}\phi... ...)\equiv\frac{1}{2}a_{\rm u}(t){\rm e}^{{\rm i}\phi_{\rm u}(t)} \end{displaymath} (4)

depend on time. We refer to the true frequencies of the solution, $\omega_{\rm l}^\star$ and $\omega_{\rm u}^\star$, as the ``observed frequencies''. They are shifted with respect to the eigenfrequencies by the corrections $\Delta\omega_{\rm l}=\dot{\phi}_{\rm l}$ and $\Delta\omega_{\rm u}=\dot{\phi}_{\rm u}$.

We assume energy conservation, so that the two real amplitudes may be parameterized using the fractional energy $\xi(t)$:

\begin{displaymath}a_{\rm l}^2=\xi E, \quad a_{\rm u}^2=(1-\xi)\frac{E}{\nu}, \quad 0\leq\xi\leq1, \end{displaymath} (5)

where $E\equiv a_{\rm l}^2+\nu a_{\rm u}^2$ is the total dimensionless energy and $\nu$ is a constant that depends on the properties of the system (Horák & Karas 2006). We introduce the phase function $\gamma(t)$ as

\begin{displaymath}\gamma\equiv2\phi_{\rm u}-3\phi_{\rm l}+\sigma t. \end{displaymath} (6)

The difference $2\omega_{\rm u}^\star - 3\omega_{\rm l}^\star$ expressed using the frequency corrections is

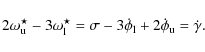\begin{displaymath}2\omega_{\rm u}^\star - 3\omega_{\rm l}^\star = \sigma - 3\dot{\phi}_{\rm l}+ 2\dot{\phi}_{\rm u}= \dot{\gamma}. \end{displaymath} (7)

Hence, the observed frequencies are commensurable whenever $\dot{\gamma}=0$, even if the eigenfrequencies are not exactly so (the deviation is proportional to $\epsilon^{2}$).

The dynamics of the system is then governed by the two first-order ordinary differential equations

 
                                       $\displaystyle \dot{\xi}$ = $\displaystyle \frac{1}{8}\beta\omega_{\rm u}(1-\xi)(\xi E)^{3/2}\sin\gamma,$ (8)
$\displaystyle \dot{\gamma}$ = $\displaystyle \sigma + \frac{1}{4}~\omega_{\rm u}E~ \Big[\mu_{\rm l}~\xi + \fra... ...u_{\rm u}}{\nu}(1-\xi) +\frac{1}{4}~ \beta(3-5\xi)(\xi E)^{1/2}\cos\gamma\Big],$ (9)

where $\beta $, $\mu_{\rm u}$, and $\mu_{\rm l}$ are as yet unspecified dimensionless constants characterizing a given system.

The values of the system parameters follow directly from the coefficients of the Taylor expansions of the functions $f_{\rm l}$ and $f_{\rm u}$ and depend on the particular physical model. For example, Rebusco (2004) studied small nonlinear, epicyclic oscillations in nearly geodesic orbits of test particles in Schwarzschild spacetime using the method of multiple scales. Horák & Karas (2006) generalized the approach of Rebusco (2004) to motion in an arbitrary axisymmetric, gravitational field. In both works, the radial and vertical oscillations of the particles were governed by equations of the form of Eqs. (1) and (2), e.g., Eqs. (14) and (15) in Horák & Karas (2006). The latter work contains explicit formulae for the constants $\beta $, $\mu_{\rm u}$ and $\mu_{\rm l}$ in terms of derivatives of the effective potential (see the relations after their Eq. (68)). In addition, a general form of Eqs. (1) and (2) is suitable for studying resonance phenomena in different physical conditions. Horák (2008) examined the nonlinear interaction between two epicyclic modes of a slender accretion torus; Eq. (6) in his paper represents a particular example of the general equations discussed here.

Both $\xi(t)$ and $\gamma(t)$ are slowly varying functions of time, which describe the slow modulation of amplitudes and phases during the oscillations. The amplitude modulation occurs on the characteristic timescale $t_{\rm mod}\equiv\epsilon^{-3}t_{\rm osc}$, with $t_{\rm osc}\equiv\omega_{\rm u}^{-1}$ being the characteristic timescale of the oscillations. The two amplitudes are anti-correlated, and the variations in $\xi $ correspond to an exchange of energy between the modes that keeps the total energy of the oscillations, E, constant. Since the oscillations are nonlinear, the observed frequencies are modulated periodically, reflecting the modulation of the amplitudes. In the context of QPOs, this process was discussed by Horák et al. (2004) in relation to the correlations between the QPO frequencies and the phase of the normal-branch oscillations (NBOs) Yu et al. (2001).

 \begin{figure} \par\includegraphics[width=8.7cm]{0740fig1.eps} \end{figure} Figure 1:

Regions where a resonance is present (resonance ``tongues'') in the plane of the eigenfrequency ratio and the total energy of oscillations. Each point in the plane corresponds to one single $(\gamma ,\xi )$-disk and different regions to different topologies of these disks (see Fig. 2). Regions (A), (B) and (C) correspond to zero, one, and two fixed points in the $(\gamma ,\xi )$-disk. The parameters of the system are given in the text.
Open with DEXTER

 \begin{figure} \par\mbox{\includegraphics[width=5.5cm]{0740fig2a.eps} \hspace*{8... ...eps} \hspace*{8mm} \includegraphics[width=5.5cm]{0740fig2c.eps} } \end{figure} Figure 2:

Three possible types of topologies of the $(\gamma ,\xi )$-disk denoted in Fig. 1 as A, B, and C ( left, middle and right, respectively). The polar angle and the distance from the origin represent the phase function $\gamma $ and the fractional energy $\xi $, respectively. The values of the total energy and detuning parameter corresponding to these examples are $(\sigma /\omega _{\rm u}, E) = (0.005, 0.1)$, (0.025, 0.1), and (0.02, 0.1). Each curve corresponds to a solution of the governing Eqs. (8) and (9). The disks corresponding to $(\sigma ,E)$ from the resonance tongues contain both the librating (white regions), and circulating (shaded regions) trajectories. The fixed points $P_\pm $ correspond to a saddle point or extrema of the integral of motion $F(\xi ,\gamma )$.
Open with DEXTER

The time evolution of the system can be studied directly from Eqs. (8) and (9) or with the aid of another integral of motion

$\displaystyle F = \xi\left[-\frac{8\sigma}{E}+\mu_{\rm l}~\xi+\frac{\mu_{\rm u}}{\nu}(2-\xi) +\beta(1-\xi)(\xi E)^{1/2}\cos\gamma\right].$     (10)

Different solutions trace different curves of $F(\gamma,\xi)={\rm constant}$ in the $(\gamma ,\xi )$-disk. Depending on the values of the parameters $\beta $, $\mu_{\rm l}$, $\mu_{\rm u}$, E, and $\sigma $, there may exist zero, one or two fixed points in this disk, each representing strictly periodic oscillations of the system. They correspond to oscillations whose amplitudes are not modulated and whose phases $\phi_{\rm l}(t)$ and $\phi_{\rm u}(t)$ are linear functions of time that adjust the frequencies of oscillations to the exact 3:2 ratio. The fixed points are either extrema or saddles of the functions $F(\xi ,\gamma )$ and their positions in the $(\gamma ,\xi )$-disk are given by the conditions $\dot{\xi}=\dot{\gamma}=0$ imposed on Eqs. (8) and (9). Generally, their $\gamma $-coordinate equals $k\pi$ with k being an integer.

The number of fixed points in the $(\gamma ,\xi )$-disk depends on the energy E and on the detuning parameter $\sigma $. For a fixed value of $\omega_{\rm u}$, the latter quantity is given by the ratio of the eigenfrequencies, $\mathcal{R}\equiv\omega_{\rm u}/\omega_{\rm l}$. Hence, it is possible to indicate regions in the $(\mathcal{R},E)$ plane differing in the number of fixed points. Figure 1 shows these regions for the system described by the fiducial set of parameters, $\beta=\mu_{{\rm l}}=\mu_{\rm u}=1$, and $\nu=9/4$.

Some examples of the three possible topologies of the $(\gamma ,\xi )$-disk are given in Fig. 2. All of them contain circulating trajectories for which $\gamma(t)$ monotonically increases or decreases in the full range (e.g., $0\leq\gamma<2\pi$). The ratio of observed frequencies can be expressed (to an accuracy of up to $\epsilon^3$) as

\begin{displaymath}\mathcal{R}^\star\equiv\frac{\omega_{\rm u}^\star}{\omega_{\r... ...{3}{2}\left(1+\frac{\dot{\gamma}}{2\omega_{\rm u}}\right)\cdot \end{displaymath} (11)

Hence, this ratio is always larger or smaller than 3/2, if the system evolves along the circulating trajectories with increasing or decreasing $\gamma $, respectively.

Closer to the resonance, the $(\gamma ,\xi )$-disks in addition contain a fixed point that corresponds to an extremum of the function $F(\gamma,\xi)$. This point is always surrounded by librating orbits with two turning points where $\dot{\gamma}$ changes its sign. When the system follows these trajectories, the observed frequency ratio oscillates around 3:2 . The regions of librating and circulating orbits are divided by a separatrix. When the $(\gamma ,\xi )$-disk contains two fixed points, the second point is a saddle point, in which the trajectory crosses itself. Consequently, it takes an infinite amount of time for the system to reach the saddle point from any other point on the separatrix.

3 Slow passage through the resonance

We consider the case when the eigenfrequencies and couplings vary slowly and the system gradually passes through the resonance. We concentrate on the part of this process in which the eigenfrequencies are close to the rational 3:2 ratio. We assume that the total relative variations in the eigenfrequencies are small (of the order of $\epsilon^{2}$), and the timescale for these variations, T, is much longer than any other timescale connected to the nonlinear oscillations (in particular $T\gg t_{~{\rm mod}}$).

In general, the oscillations of the system are the solutions to Eqs. (1) and (2), where $\omega_{{\rm l}}$ and $\omega_{\rm u}$, as well as the nonlinear functions $f_{\rm l}$ and $f_{\rm u}$, are known functions that depend explicitly on time. Since the characteristic timescale of the process T is much longer than $t_{~{\rm mod}}$, the only change to Eqs. (8), (9) is that the eigenfrequencies $\omega_{{\rm l}}$ and $\omega_{\rm u}$ and the coefficients $\beta $, $\mu_{\rm l}$, $\mu_{\rm u}$, and $\nu$ become slow functions of time. Close to the resonance, the oscillations are most sensitive to the change in the detuning parameter $\sigma(t)\equiv2\omega_{\rm u}(t)-3\omega_{{\rm l}}(t)$, while they are practically unaffected by small changes in the other quantities. This is because the coefficients of the terms (other than $\sigma $) in Eqs. (8) and (9) are always multiplied by small quantities (of the order of $\sim$ $\epsilon^{2}$ and $\sim$ $\epsilon^3$). We do not consider the ``singular'' case, when the two eigenfrequencies are nearly correlated and $\omega_{\rm u}\approx 1.5\omega_{\rm l}$. Since the characteristic timescale of passage through resonance is taken to be far longer than that of the resonant modulation, we may neglect time derivatives of $\sigma $ and E in the evolution Eqs. (8) and (9) that describe the evolution of the system on the timescale $t_{~{\rm mod}}$.

As the system passes through the resonance, the topology of the $(\gamma ,\xi )$-disk gradually changes. The system trajectory $[\gamma(t),\xi(t)]$ does not strictly follow the curves $F(\gamma,\xi)={\rm const.}$ because the ratio $\sigma/E\sim1$ changes significantly. Both quantities are of the order of $\epsilon^{2}$ and the change in the total energy E is negligible because the relative change in $\nu$ is proportional to $\epsilon^{2}$. Accordingly, in the following, we assume that $\nu={\rm const.}$

 \begin{figure} \par\mbox{\includegraphics[width=7cm]{0740fig3a.eps} \hspace*{1cm} \includegraphics[width=9cm]{0740fig3b.eps} } \end{figure} Figure 3:

Behavior of the resonant oscillations of the system undergoing a slow secular change of its eigenfrequencies. The detuning parameter $\sigma $ increases linearly with time so that the system gradually passes through the resonance. The left panel shows the trajectory of the system projected into the $(\gamma ,\xi )$-disk. The right panel shows behavior of the amplitude difference, $\delta a=a_{\rm l}-a_{\rm u}$, (measured in arbitrary units) as a function of the ratio the observed frequencies, $\mathcal{R}^\star=\omega_{\rm u}^\star/\omega_{\rm l}^\star$. Because of the slow changes in the eigenfrequencies, the energy exchange between modes is not exactly symmetric and the total energy is redistributed between the modes when the system passed the resonance.
Open with DEXTER

 \begin{figure} \par\mbox{\includegraphics[width=7cm]{0740fig4a.eps} \hspace*{1cm} \includegraphics[width=9cm]{0740fig4b.eps} } \end{figure} Figure 4:

Example of a trajectory with a frequency-locking episode. Left: trajectory projected onto the $(\gamma ,\xi )$-disk. frequency locking corresponds to the redistribution of the energy when the system is trapped in the region of the librating orbits. Right: the frequency-locking effect in the plot showing ratio of the observed frequencies versus eigenfrequency ratio.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=17.6cm]{0740fig5.eps} \end{figure} Figure 5:

Energy exchange during the forward transition through the 3:2 resonance (e.g., from the lower to the higher eigenfrequency ratios). $\xi _{\rm i}$ and $\xi _{\rm f}$ are the fractional energy in the lower oscillation mode before and after the transition. Left: dependence on the initial condition (different symbols denote different initial phases, $\gamma _{\rm i}=0,\pi /2$ and $\pi $) for $\beta =5$. Right: dependence on the value of the parameter $\beta $ (the initial phase is $\gamma _{\rm i}=0$). The branches corresponding to solutions with (denoted by ``FL'') and without the frequency-locking period are clearly separated. In this plot, $\xi _{\rm i}$ is sampled uniformly - an indication of the probability of finding the system in a ``frequency-locked'' solution is given by the relative number of points on the FL branch.
Open with DEXTER

The general effect of the resonance transition is illustrated by the example shown in Fig. 3. The eigenfrequencies vary at a constant rate, $\sigma(t) = \sigma_{\rm i} + \dot{\sigma}~t$. The left panel shows the evolution of the oscillations in the $(\gamma ,\xi )$-disk, and the right panel shows the observable quantities (i.e., the ratio of observed frequencies $\mathcal{R}^\star$ versus the amplitude difference $\delta a=a_{\rm l}-a_{\rm u}$). These figures are for $\sigma_{\rm i} = -0.1\omega_{\rm u}$, and $\dot{\sigma} = 3\times10^{-5}\omega_{\rm u}^2$, where $\omega_{\rm u}$ is the upper frequency in the exact resonance. The system is described by $\beta=-\mu_{\rm l}=\mu_{\rm u}=5$ and $\nu=9/4$, and the initial conditions are $\xi_{\rm i}\equiv\xi(0)=0.5$, and $\gamma_{\rm i}\equiv\gamma(0)=0$. The total energy is fixed at E=0.1. We also tried different rates of passage and different initial conditions.

In all cases the behavior of the system is qualitatively similar: the initial value of the detuning parameter corresponds to a point $(\sigma_{\rm i}, E)$ outside the resonance tongue. Hence, the $(\gamma ,\xi )$-disk initially contains only circulating orbits. One of them is closely followed by the system (the outer ``circles'' in the left panel of Fig. 3). The $\xi $-coordinate oscillates slightly in correspondence to a weak energy exchange between the modes. As the system approaches resonance, the magnitude of these oscillations increases gradually. The system then enters into the resonance tongue and the topology of the $(\gamma ,\xi )$-disk suddenly changes as the librating trajectories appear. When the trajectory of the system crosses the separatrix and enters the region of librating trajectories, the energy exchange becomes asymmetric i.e., the inflow of the energy into one of the modes exceeds the outflow. The system may escape from this region passing the separatrix again before it completes a single orbit (as in Fig. 3) or it can be trapped in this region for a longer time. A trapping in the region of librating orbits is accompanied by several changes in the sign of $\dot{\gamma}$, and therefore by changes in the direction of the orbit in the $(\gamma ,\xi )$-disk. The ratio $\mathcal{R}^\star$ of the observed frequencies oscillates around 1.5 (as follows from Eq. (11)). When the system leaves the resonance tongues and moves farther away, the energy exchange between modes becomes more symmetric and less apparent. The final fractional energy $\xi _{\rm f}$ after the passage is generally different from the initial one $\xi _{\rm i}$: the energy is redistributed due to the resonance.

We note that the behavior of the amplitudes with respect to the frequency ratio as shown in the right panel of Fig. 3, is similar to that reported for several atoll sources (Török 2008).

An example of a trajectory trapped in the region of the librating orbits is shown in Fig. 4. The parameters of the solution are $\sigma_0 = -0.2\omega_{\rm u}$, $\dot{\sigma} = 4\times10^{-5}\omega_{\rm u}^2$, $\beta=\mu_{\rm l}=-\mu_{\rm u}=5$, and $\nu=9/4$. The initial conditions are $\xi_{\rm i}=0.9$, $\gamma _{\rm i}=0$, and the total energy is E=0.1. Obviously, the nonlinearities adjust the observed frequencies so that their ratio oscillates about the resonance value 3:2 during the trapping period.

We examined the stability of this process against changes in the initial conditions and other parameters characterizing the passage through the resonance. The effects of changing the initial conditions are summarized in the left panel of Fig. 5. Again, the parameters of the system were set to be the values $\beta=-\mu_{\rm l}=\mu_{\rm u}=5$, and $\nu=9/4$, and the initial detuning parameter and the rate of change were defined to be $\sigma_{~0} = -0.1\omega_{\rm u}$, and $\dot{\sigma} = 3\times10^{-5}\omega_{\rm u}^2$, respectively. The solutions trapped in the librating regions that partake for some time in an episode of what could be termed ``frequency-locking'' are clearly separated from the others. These solutions are quite common for small $\xi _{\rm i}$. In this case, they are accompanied by significant amounts of exchanged energy. As the initial fractional energy $\xi _{\rm i}$ increases, they become rather exceptional.

Although different for the solutions with and without frequency-locking, the $\xi _{\rm i}$- $\xi _{\rm f}$ dependence is fairly independent of the initial phase function $\gamma _{\rm i}$, as can be seen from the left panel of Fig. 5, where the solutions for different $\gamma _{\rm i}$ are indicated by different symbols. Similarly, we also checked that the rate of the transition $\dot{\sigma}$ has no significant influence on the resulting $\xi_{~{\rm i}}$- $\xi_{~{\rm f}}$ plot.

The right panel of Fig. 5 illustrates the effect of changing the value of the parameter $\beta $. The redistribution of energy in the solutions without the ``frequency-locking'' period becomes more pronounced as the value of $\beta $ increases. In addition, the solution with the ``frequency-locking'' period become more frequent (see Table 1). The value $\beta=0$ corresponds to the case, in which there is no resonant coupling between the two oscillations, and $\xi_{\rm i}=\xi_{\rm f}$. Of course, there are no ``frequency-locked'' solutions in this case.

The dependence of the results on the remaining parameters could be discussed in a similar way; however, it can be shown that for sufficiently slow transitions of the resonance the entire dynamics depends only on a single parameter, $\hat{\beta} = \beta\sqrt{E}/(\mu_{\rm l}- \mu_{\rm u}/\nu)$. Therefore, one does not expect any qualitatively new behavior as the other parameters are changed.

Table 1:   Occurrence rate of solution with frequency-locking period in sets of 200 solutions for different values of $\gamma _{\rm i}$ and $\beta $. In each set the initial value $\xi _{\rm i}$ is uniformly distributed between 0 and 1, while the other parameters are kept constant.

4 Discussion and conclusions

If the twin kHz QPOs in neutron stars correspond to two physical oscillators that have a nonlinear coupling, the two QPOs may exhibit resonance phenomena when the QPO frequencies are close to a ratio of two small integer numbers. Among the most characteristic observable imprints of the internal resonance are: (i) exchange of energy between the oscillations; (ii) equality of the quality factors of oscillations; and (iii) locking of the frequency ratio of oscillations. Our work was devoted to the mathematics of the first and third phenomena.

Some models of QPOs, which may support an internal resonance of the type described in this work were described in Sect. 1. In this work, we explored only the 3:2 resonance, which is one of the most prominent in the data (Abramowicz et al. 2003a; Török et al. 2008). The examination of other resonances may be completed in an analogous way.

Assuming a slow (secular) change of the eigenfrequencies of the two coupled oscillators, we demonstrated that the energy is redistributed between the two oscillators when the system passes through a resonance. This effect is evident in the change in the sign of the amplitude difference when the ratio of the eigenfrequencies ratio crosses a rational value, such as 3:2. This result is in qualitative agreement with the observations for some neutron stars (Török 2008).

A class of solutions exhibits a time interval during which a frequency-locking of the two oscillations occurs. This corresponds to small oscillations of the true frequencies around the ratio 3:2 while the system drifts over a (wider) range of eigenfrequency ratios (Fig. 4).

Acknowledgements
This work was started at the Göteborg University and continued at MPA Garching. J.H. is grateful to Prof. Chengmin Zhang for useful discussions and acknowledges support of the grants GAËCR 205/07/0052 and GACR 205/06/P415, P.R. is supported by the Pappalardo Fellowship at MIT and M.A.A. was supported by the Polish Ministry of Education grant N203 009 31/1466 and grant MSM4781305903, W.K. acknowledges partial support through grant 1P03D00530 and G.T. was supported by the grant MSM4781305903.

References

All Tables

Table 1:   Occurrence rate of solution with frequency-locking period in sets of 200 solutions for different values of $\gamma _{\rm i}$ and $\beta $. In each set the initial value $\xi _{\rm i}$ is uniformly distributed between 0 and 1, while the other parameters are kept constant.

All Figures

  \begin{figure} \par\includegraphics[width=8.7cm]{0740fig1.eps} \end{figure} Figure 1:

Regions where a resonance is present (resonance ``tongues'') in the plane of the eigenfrequency ratio and the total energy of oscillations. Each point in the plane corresponds to one single $(\gamma ,\xi )$-disk and different regions to different topologies of these disks (see Fig. 2). Regions (A), (B) and (C) correspond to zero, one, and two fixed points in the $(\gamma ,\xi )$-disk. The parameters of the system are given in the text.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=5.5cm]{0740fig2a.eps} \hspace*{8... ...eps} \hspace*{8mm} \includegraphics[width=5.5cm]{0740fig2c.eps} } \end{figure} Figure 2:

Three possible types of topologies of the $(\gamma ,\xi )$-disk denoted in Fig. 1 as A, B, and C ( left, middle and right, respectively). The polar angle and the distance from the origin represent the phase function $\gamma $ and the fractional energy $\xi $, respectively. The values of the total energy and detuning parameter corresponding to these examples are $(\sigma /\omega _{\rm u}, E) = (0.005, 0.1)$, (0.025, 0.1), and (0.02, 0.1). Each curve corresponds to a solution of the governing Eqs. (8) and (9). The disks corresponding to $(\sigma ,E)$ from the resonance tongues contain both the librating (white regions), and circulating (shaded regions) trajectories. The fixed points $P_\pm $ correspond to a saddle point or extrema of the integral of motion $F(\xi ,\gamma )$.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=7cm]{0740fig3a.eps} \hspace*{1cm} \includegraphics[width=9cm]{0740fig3b.eps} } \end{figure} Figure 3:

Behavior of the resonant oscillations of the system undergoing a slow secular change of its eigenfrequencies. The detuning parameter $\sigma $ increases linearly with time so that the system gradually passes through the resonance. The left panel shows the trajectory of the system projected into the $(\gamma ,\xi )$-disk. The right panel shows behavior of the amplitude difference, $\delta a=a_{\rm l}-a_{\rm u}$, (measured in arbitrary units) as a function of the ratio the observed frequencies, $\mathcal{R}^\star=\omega_{\rm u}^\star/\omega_{\rm l}^\star$. Because of the slow changes in the eigenfrequencies, the energy exchange between modes is not exactly symmetric and the total energy is redistributed between the modes when the system passed the resonance.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=7cm]{0740fig4a.eps} \hspace*{1cm} \includegraphics[width=9cm]{0740fig4b.eps} } \end{figure} Figure 4:

Example of a trajectory with a frequency-locking episode. Left: trajectory projected onto the $(\gamma ,\xi )$-disk. frequency locking corresponds to the redistribution of the energy when the system is trapped in the region of the librating orbits. Right: the frequency-locking effect in the plot showing ratio of the observed frequencies versus eigenfrequency ratio.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.6cm]{0740fig5.eps} \end{figure} Figure 5:

Energy exchange during the forward transition through the 3:2 resonance (e.g., from the lower to the higher eigenfrequency ratios). $\xi _{\rm i}$ and $\xi _{\rm f}$ are the fractional energy in the lower oscillation mode before and after the transition. Left: dependence on the initial condition (different symbols denote different initial phases, $\gamma _{\rm i}=0,\pi /2$ and $\pi $) for $\beta =5$. Right: dependence on the value of the parameter $\beta $ (the initial phase is $\gamma _{\rm i}=0$). The branches corresponding to solutions with (denoted by ``FL'') and without the frequency-locking period are clearly separated. In this plot, $\xi _{\rm i}$ is sampled uniformly - an indication of the probability of finding the system in a ``frequency-locked'' solution is given by the relative number of points on the FL branch.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.