| Issue |
A&A
Volume 499, Number 1, May III 2009
|
|
|---|---|---|
| Page(s) | 137 - 148 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200810945 | |
| Published online | 25 March 2009 | |
Photometric and polarimetric clues to the circumstellar
environment of RY Lupi![[*]](/icons/foot_motif.png)
N. Manset1 - P. Bastien2 - F. Ménard3 - C. Bertout4 - A. Le Van Suu5 - L. Boivin2
1 - Canada-France-Hawaii Telescope Corporation, 65-1238 Mamalahoa
Hwy Kamuela HI 96743, USA
2 - Département de physique and Observatoire du Mont Mégantic,
Université de Montréal, Montréal QC, Canada
3 - Laboratoire d'Astrophysique de Grenoble, UMR UJF-CNRS 5571,
Observatoire de Grenoble, Université Joseph Fourier, BP 53, 38041
Grenoble Cedex 9, France
4 - Institut d'Astrophysique, 98bis Bd. Arago, 75014 Paris, France
5 - CPPM - Centre de Physique des Particules de Marseille, CNRS/IN2P3,
Université de la Méditerranée Aix-Marseille II, 163 Avenue de
Luminy, Case 907, 3288 Marseille Cedex 9, France
Received 10 September 2008 / Accepted 10 February 2009
Abstract
Aims. We investigate the stellar and circumstellar properties of the bright southern T Tauri star RY Lup, a G-type star showing type III variability.
Methods. We report simultaneous BV polarimetric and UBV photometric observations obtained during 12 consecutive nights on the 1.0 m and 50 cm telescopes of the European Southern Observatory at La Silla. We compare these data to models.
Results. The polarization is high (![]() 3.0%) when the star is faint and red (
3.0%) when the star is faint and red (
![]() ,
,
![]() ), and it is low (
), and it is low (![]() 0.5%) when it is bright and bluer (
0.5%) when it is bright and bluer (
![]() ,
,
![]() ). The photometric and polarimetric variations share a common period of 3.75 d. Irregular light variations, larger at shorter wavelengths, are also superposed on the cyclic variations and may be due to processes different than the one producing the periodic variations. The linear polarization is produced by dust scattering in an asymmetric (flat) circumstellar envelope. The photometric and polarimetric variations can be explained with an almost edge-on circumstellar disk that is warped close to the star, where it interacts with the star's magnetosphere. The inhomogeneous disk matter contained in the warp corotates with the star and partially occults it during part of the rotation period, which explains the dips in luminosity and the accompanying increase in polarization. All the information available on RY Lup is consistent with a system comprising a G8 star surrounded by an edge-on disk, and we find that the mass of RY Lup is
). The photometric and polarimetric variations share a common period of 3.75 d. Irregular light variations, larger at shorter wavelengths, are also superposed on the cyclic variations and may be due to processes different than the one producing the periodic variations. The linear polarization is produced by dust scattering in an asymmetric (flat) circumstellar envelope. The photometric and polarimetric variations can be explained with an almost edge-on circumstellar disk that is warped close to the star, where it interacts with the star's magnetosphere. The inhomogeneous disk matter contained in the warp corotates with the star and partially occults it during part of the rotation period, which explains the dips in luminosity and the accompanying increase in polarization. All the information available on RY Lup is consistent with a system comprising a G8 star surrounded by an edge-on disk, and we find that the mass of RY Lup is
![]() ,
while its age is
,
while its age is
![]() .
.
Key words: stars: pre-main sequence - stars: variables: general - stars: circumstellar matter - polarization - methods: observational
1 Introduction
Solar-type young stellar objects (T Tauri stars; TTSs herafter) display light variations of up to a few magnitudes on many timescales at all wavelengths. Herbst et al. (1994) have identified three main physical processes at work in these objects: (a) magnetic activity, (b) accretion power, and (c) variable extinction caused by occultation of the stellar surface by circumstellar matter. These authors define three types of photometric variability.
- Type I:
- Rotational modulation caused by cold magnetic spots. These are most easily detectable in the weak emission lines T Tauri stars (WTTSs). The maximum amplitude that can be attributed to cold magnetic spots is about 0.8 mag in V and 0.5 mag in I.
- Types II and IIp:
- Variability caused by cold and hot spots. Type II variations are either irregular or periodic, in which case they are called type IIp, and occur only in classical T Tauri stars (CTTSs).
- Type III:
- Variable stellar obscuration by circumstellar dust. Also called UX Ori type variability, this type occurs in some TTSs but is mainly observed in higher mass Herbig Ae/Be stars (HAEBESs). Type III variability is characterized by large amplitude light variations in stars with no evident veiling or effective temperature variations. Type III variables often fluctuate around their high-luminosity state, while sometimes fading suddenly by several magnitudes before recovering their previous luminosity on a timescale of days, and the fading episodes are often cyclic. That the degree of linear polarization increases as the star becomes faint is a major argument supporting the idea that variable obscuration is responsible for the stars fading. For more details, see Ménard & Bertout (1999).
The TTS RY Lupi (=HBC 252 = HIP 78317) is located in the Lupus
T association at
![]() ,
,
![]() .
The marginally
significant Hipparcos parallax of
.
The marginally
significant Hipparcos parallax of
![]() mas (Perryman et al. 1997) indicates a distance of 108
+48-25 pc. The
distance estimated by Bertout et al. (1999) for the Lupus 1,
3, and 4 clouds (147
+42-27 pc) includes the individual parallax
of RY Lupi but also better constrained values for a few other stars, and
therefore appears somewhat more reliable. It is also more in line with
previously derived distance estimates for that starforming region (see
for example Alves & Franco 2006; and Franco 2002).
mas (Perryman et al. 1997) indicates a distance of 108
+48-25 pc. The
distance estimated by Bertout et al. (1999) for the Lupus 1,
3, and 4 clouds (147
+42-27 pc) includes the individual parallax
of RY Lupi but also better constrained values for a few other stars, and
therefore appears somewhat more reliable. It is also more in line with
previously derived distance estimates for that starforming region (see
for example Alves & Franco 2006; and Franco 2002).
There are several estimates of RY Lup's spectral type, which was
determined as K1:ea V (Li) by Herbig (1977) and as K4 by
Appenzeller et al. (1983). Based on the latter
spectral type and their own photometric data, Hughes et al. (1994) deduced a mass range
![]() and and an age range
and and an age range
![]() for the star. From an extended set of spectroscopic data obtained
over several years, Gahm et al. (1989) concluded that the
spectral type of RY Lup is G8 IV-V with an uncertainty of one spectral
subclass. They also found that the type does not change as the star
becomes fainter. In contrast to many CTTSs with rich emission-line spectra,
line emission in RY Lup is usually restricted to H
for the star. From an extended set of spectroscopic data obtained
over several years, Gahm et al. (1989) concluded that the
spectral type of RY Lup is G8 IV-V with an uncertainty of one spectral
subclass. They also found that the type does not change as the star
becomes fainter. In contrast to many CTTSs with rich emission-line spectra,
line emission in RY Lup is usually restricted to H![]() ,
and sometimes
this line is not even seen in emission (Appenzeller et al. 1983). However, the H
,
and sometimes
this line is not even seen in emission (Appenzeller et al. 1983). However, the H![]() line goes in
emission when the star gets fainter (Evans et al. 1982; Liseau
et al. 1987; Hutchinson et al. 1989).
line goes in
emission when the star gets fainter (Evans et al. 1982; Liseau
et al. 1987; Hutchinson et al. 1989).
The spectral energy distribution of RY Lup shows a sizable infrared
excess, as well as modest UV excess (Evans et al. 1982; Gahm
et al. 1989). The photometric variability of the star was
discovered by Woods on Harvard plates in 1921 (Hoffmeister
1958), and the star was classified as a typical RW Aur star on
the basis of its lightcurve (Hoffmeister 1949). From a
long-term study of the optical photometry of the star, Gahm et al. (1989) report (a) significant photometric variations on timescales of hours, (b) a constant variability with a 3.75 d period over ![]() 52 years, and (c) a decline in the mean and maximum
photometric magnitudes over decades. Other investigators derived
slightly different periods for the photometric variability: 3.6 d
(Boesgaard 1984; Hutchinson et al. 1989), 3.67 d
(Hoffmeister 1958), and 3.9 d (Bouvier et al. 1986).
52 years, and (c) a decline in the mean and maximum
photometric magnitudes over decades. Other investigators derived
slightly different periods for the photometric variability: 3.6 d
(Boesgaard 1984; Hutchinson et al. 1989), 3.67 d
(Hoffmeister 1958), and 3.9 d (Bouvier et al. 1986).
The photometric behavior of RY Lup is typical of type III variability. The star gets redder as it gets fainter (Evans et al. 1982; Liseau et al. 1987; Hutchinson et al. 1989; Covino et al. 1992), and the amplitude of the variations also decreases with wavelength. Furthermore, Liseau et al. (1987) and Gahm et al. (1989) report color flips in B-V, where the color changes by one magnitude in less than 20 h from an extremely blue to an extremely red color. The infrared photometric properties of RY Lup were investigated by Glass & Penston (1974), who report a lightcurve of type I0.6s and an emission class I, based on Herbig & Rao's (1972) notation.
The intrinsic position angle of T-Tauri-star polarization is generally a
function of both wavelength and time, i.e.,
![]() (Bastien 1981); see also Bastien
(1988a) for a review of young-stellar-object polarization
properties, and RY Lup is a good example of this behavior (Bastien
1985). These authors also noticed remarkably large and rapid
variations in both polarization and position angle in RY Lup. Drissen et al. (1989) have confirmed RY Lup's variable
polarization. Their data did not show any periodicity but displayed a
correlation in the sense that the polarization is higher when the star
is fainter.
(Bastien 1981); see also Bastien
(1988a) for a review of young-stellar-object polarization
properties, and RY Lup is a good example of this behavior (Bastien
1985). These authors also noticed remarkably large and rapid
variations in both polarization and position angle in RY Lup. Drissen et al. (1989) have confirmed RY Lup's variable
polarization. Their data did not show any periodicity but displayed a
correlation in the sense that the polarization is higher when the star
is fainter.
Bastien (1982, 1985, 1988a) compiled
all the polarimetric and photometric (both visual and photoelectric)
data available in the literature on T Tauri stars and did not find any
correlation between the polarization, UBVRI photometry, and equivalent
widths of emission lines. The polarization is, however, well-correlated
with IR photometric data. Simultaneous photometry and polarimetry of
RY Lup was reported by Hutchinson et al. (1994), who find
that the polarization increases as the star gets redder and fainter, and
![]() also changes. Finally, we note that no circular polarization
was seen by Hutchinson et al. (1994), although Yudin & Evans
(1998) detected it at the
also changes. Finally, we note that no circular polarization
was seen by Hutchinson et al. (1994), although Yudin & Evans
(1998) detected it at the ![]() level.
level.
The paper is organized as follows. We present our observations in Sect. 2, followed by an analysis of the photometric and polarimetric data in Sect. 3. A discussion of possible mechanisms for the explanation of the photometric and polarimetric variations is presented together with a polarimetric model and the derived properties of RY Lup in Sect. 4. Our conclusions follow.
2 Observations
Simultaneous photometric and polarimetric observations were carried out
on the 50 cm and 1.0 m telescopes, respectively, of the European
Southern Observatory (ESO) at La Silla from 1982 February 12 to
24, using the ESO photometer and polarimeter![]() . Standard UBV filters were used for the photometric
observations. The polarimetric bandpasses approximate the BV bands
and are defined by the following central wavelengths and bandwidths:
4300 Å (1000 Å) and 5250 Å (500 Å). Data were reduced with the
standard ESO data reduction programs.
. Standard UBV filters were used for the photometric
observations. The polarimetric bandpasses approximate the BV bands
and are defined by the following central wavelengths and bandwidths:
4300 Å (1000 Å) and 5250 Å (500 Å). Data were reduced with the
standard ESO data reduction programs.
During the same observing period, we also observed every
night![]() primary photometric
standard stars and two comparison stars within 1
primary photometric
standard stars and two comparison stars within 1![]() from RY Lup,
HD 14224 and HD 14262. The photometric data for RY Lup are listed in Table 6. In the following, we also make use of
UBVRI data obtained with the same ESO 50 cm telescope in 1983
June-August by Bouvier et al. (1988).
from RY Lup,
HD 14224 and HD 14262. The photometric data for RY Lup are listed in Table 6. In the following, we also make use of
UBVRI data obtained with the same ESO 50 cm telescope in 1983
June-August by Bouvier et al. (1988).
Concerning the polarimetric observations, standard polarized and unpolarized stars were observed throughout the observing run. The instrumental polarization was estimated to be <0.05%, and was therefore neglected. The polarization data are given in Tables 7 and 8, where one finds the Julian date JD-2 400 000.0, the polarization and its error, the equatorial position angle and its error, and the phase (see below) in Col. 1 through 6.
The photometric and polarimetric data obtained over the 12 consecutive nights are presented as a function of the Julian date in
Fig. 1. Large-amplitude variations in both
photometric and polarimetric data are clear. These amplitudes are
typically 1.2, 0.25, and 0.37 mag, in V, B-V, and U-B,
respectively, and 2.3%, 48![]() ,
1.8%, 47
,
1.8%, 47![]() ,
for the polarization
level and positions angle at 4300 Å and 5250 Å, respectively. The
extreme values are even higher. However, the most striking feature of
the data is that, when the star is bright the polarization is low and
when the polarization is high, the star is fainter and also redder.
,
for the polarization
level and positions angle at 4300 Å and 5250 Å, respectively. The
extreme values are even higher. However, the most striking feature of
the data is that, when the star is bright the polarization is low and
when the polarization is high, the star is fainter and also redder.
![\begin{figure}
\par\includegraphics[width=8cm]{0945fg01.ps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg21.png) |
Figure 1: Photometry and polarimetry (observed polarization, i.e. intrinsic + interstellar) of RY Lup at 4300 Å and 5250 Å as a function of the Julian date. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg02.eps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg22.png) |
Figure 2: Observed V magnitudes of RY Lupi from 1977 to 1990. |
| Open with DEXTER | |
3 Analysis of observations
3.1 Period search
A period was searched for in our data sets using a very simple sinusoid fit. Periods between 0.1 and 12 days were considered. All data were taken into account when looking for a period: the polarization and position angles at 4300 Å and 5250 Å, as well as the UBV and UBVRI data. The 1982 and 1983 photometric data were searched independently; i.e., it was not assumed that the phase was conserved from 1982 to 1983.
We derived an average period of 3.74+0.20-0.18 days. The errors indicated are the standard deviations of the best frequencies. This value is in agreement with the value of 3.75 days found by Gahm et al. (1989) from a compilation of data for the past 52 years. It also agrees with the value derived above for the photometric observations ranging from 1977 to 1990.
![\begin{figure}
\par\includegraphics[width=8cm]{0945fg03.eps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg23.png) |
Figure 3: Bottom panel: histogram of observed V magnitudes from 1977 to 1990. Top panel: the cumulative distribution of V observations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg04.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg24.png) |
Figure 4: Same data as in Fig. 2, but phase-folded with a 3.75 d period. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{0945fg05.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg25.png) |
Figure 5: Photometry and polarimetry (observed polarization, i.e. intrinsic + interstellar) of RY Lup at 4300 Å and 5250 Å as a function of phase, calculated with a period of 3.75 d. The open circles are data points repeated for clarity. |
| Open with DEXTER | |
To compare our observations to the photometric variability of RY Lupi on longer timescales, we added to our own measurements the optical photometric data gathered by Gahm et al. (1993a) and Herbst et al. (1994) for the period extending from the late 1970s to 1990. Figure 2 displays the 622 V-measurements contained in the database and Fig. 3 shows how they are distributed in half-magnitude intervals. There is less than a 10% chance of observing RY Lupi within 0.5 mag of its brightest state in V, but a 60% chance of observing it in a state brighter than V=11.5 mag. The star is fainter than V=12.5 about 10% of the time. The data shown in Fig. 2 present cyclical variations with a period of 3.75 d, based on a CLEANed periodogram analysis (Baisch & Bokelmann 1999) of the V data and Monte Carlo simulations showing that the probability for the derived period to be due to chance is less than 0.1%. No other peak in the periodogram reaches this significance level. Figure 4 shows that the derived period does not account for the full variability of the star. Obviously, there are additional, random light variations that complicate the photometric behavior of RY Lup.
The 3.75 d-period was used, along with an arbitrary epoch of JD = 2 445 000.0, to compute the phase diagrams presented in the rest of this paper. The photometric and polarimetric data are presented together as a function of the orbital phase in Fig. 5.
3.2 Photometric observations
The color-magnitude diagrams of the photometric data are shown in Fig. 6. It is immediately obvious that RY Lup gets redder as it gets fainter as noted by previous investigators. The so-called blueing effect (i.e., when a star goes from getting redder to getting bluer as it continues to get fainter; cf. Evans et al. 1982, Hutchinson et al. 1987, Gahm et al. 1993b) is not seen in our data, but this is hardly surprising since this effect has only been observed in RY Lup for Vmagnitudes fainter than about 12.0, a magnitude that our data barely reach.
The color-magnitude graphs also show that the B-V vs. V relationship is much tighter than the U-B vs. V one; there is more scatter in the U-B color as the star gets fainter. The B-V vs. V diagram has a slope of 6.1. The U-B vs. V upper envelope has a slope of 7.2, whereas the lower envelope has a slope of 2.1. Variations are not monotonic, and go back and forth.
The photometry does not show systematic trends as a function of time. As the V magnitude goes up or down, colors can go either way. One interesting feature is that for the 2 photometric minima, there is more scatter in U-B, but not in B-V, but that is in part due to the low accuracy of U measurements when the star is faint.
| |
Figure 6: V magnitude as a function of U-B and B-V colors. |
| Open with DEXTER | |
3.3 Polarimetric observations
Generally, polarimetric observations include both intrinsic polarization
produced at the target and interstellar (IS) polarization. The Heiles
(2000) polarization catalog, which contains polarimetric
observations for more than 9000 stars, was used to estimate the
interstellar polarization in the vicinity of RY Lup by selecting 6 stars
located within 35 pc and 15![]() of it. We assumed that RY Lup's
distance is 150 pc (Bertout et al. 1999) and that the visual
extinction is
of it. We assumed that RY Lup's
distance is 150 pc (Bertout et al. 1999) and that the visual
extinction is
![]() (see our calculation of
(see our calculation of ![]() in
Sect. 4). The distance interval
chosen, 35 pc, comes from the average of the error bars
+42-27on the distance found by Bertout et al. (1999). The map of IS
polarization is presented in
Fig. 7. The IS distance-weighted polarization
calculated by averaging the polarization of the 6 stars is 0.44%
in
Sect. 4). The distance interval
chosen, 35 pc, comes from the average of the error bars
+42-27on the distance found by Bertout et al. (1999). The map of IS
polarization is presented in
Fig. 7. The IS distance-weighted polarization
calculated by averaging the polarization of the 6 stars is 0.44% ![]() 0.20% in the V band, with a distance-weighted equatorial average
position angle of
0.20% in the V band, with a distance-weighted equatorial average
position angle of ![]()
![]() .
See Manset & Bastien
(2002) for more details about our averaging procedure.
.
See Manset & Bastien
(2002) for more details about our averaging procedure.
![\begin{figure}
\includegraphics[width=9cm]{0945fg07.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg31.png) |
Figure 7:
Map of the interstellar polarization in the vicinity of
RY Lup. The computed average interstellar polarization for RY Lup is
shown at the position of the hexagon. Stars used to determine the
average IS polarization are drawn with larger symbols than other stars,
which are either outside the 15 |
| Open with DEXTER | |
If one chooses different distances or distance intervals, e.g.,
110 ![]() 35 pc (8 stars), 120
35 pc (8 stars), 120 ![]() 35 pc (9 stars), 150
35 pc (9 stars), 150 ![]() 35
pc (6 stars),
and 150
35
pc (6 stars),
and 150 ![]() 75 pc (14 stars), the results
are similar those given above. For example, 150
75 pc (14 stars), the results
are similar those given above. For example, 150 ![]() 75 pc yields an
interstellar polarization of 0.55%
75 pc yields an
interstellar polarization of 0.55% ![]() 0.16% and at a position angle
of 39
0.16% and at a position angle
of 39 ![]() 10
10![]() .
Therefore we can conclude
that the derived IS polarization is robust.
.
Therefore we can conclude
that the derived IS polarization is robust.
As seen in Tables 7 and 8, RY Lup's
observed weighted average polarization is 0.92% at 134![]() at
4300 Å (N=31), and 0.84% at 139
at
4300 Å (N=31), and 0.84% at 139![]() at 5250 Å (N=29). These
levels of polarization are higher than the IS polarization and indicate
the presence of an intrinsic polarization component in RY Lup's
measurements. The IS position angle is also different than RY Lup's,
which provides another clue for the presence of intrinsic polarization.
at 5250 Å (N=29). These
levels of polarization are higher than the IS polarization and indicate
the presence of an intrinsic polarization component in RY Lup's
measurements. The IS position angle is also different than RY Lup's,
which provides another clue for the presence of intrinsic polarization.
Using the above estimate of the IS polarization in the V band and
Serkowski's law for IS polarization (Serkowski et al. 1975), we derived the IS polarization value for the 2 observed
wavelengths. We assumed that
![]() Å for
Serkowski's law (a typical value) and that the position angle of the IS
polarization is constant as a function of wavelength. After subtracting
this estimated IS polarization from the observed one, we found that
the average values of intrinsic polarization for RY Lup were 1.30% at
position angle 130
Å for
Serkowski's law (a typical value) and that the position angle of the IS
polarization is constant as a function of wavelength. After subtracting
this estimated IS polarization from the observed one, we found that
the average values of intrinsic polarization for RY Lup were 1.30% at
position angle 130![]() at wavelength 4300 Å, and 1.22% at position
angle 133
at wavelength 4300 Å, and 1.22% at position
angle 133![]() at wavelength 5250 Å. RY Lup's intrinsic polarization
is thus high, which suggests that RY Lup's circumstellar matter is
distributed in a disk rather than in a spherical shell.
at wavelength 5250 Å. RY Lup's intrinsic polarization
is thus high, which suggests that RY Lup's circumstellar matter is
distributed in a disk rather than in a spherical shell.
If RY Lup's disk is comparable to other CTTS disks, it is likely to
be very optically thick (Ménard & Bertout 1999). Therefore, since
the intrinsic polarization is oriented in direction ![]() 130
130![]() and the polarization is parallel to the scattering plane (the equatorial
plane of the circumstellar disk), we predict that RY Lup's disk's
equatorial plane is oriented in direction
and the polarization is parallel to the scattering plane (the equatorial
plane of the circumstellar disk), we predict that RY Lup's disk's
equatorial plane is oriented in direction ![]() 130
130![]() .
In
contrast, an optically thin disk would be oriented at
.
In
contrast, an optically thin disk would be oriented at ![]() 40
40![]() .
RY Lup has been observed extensively with WFPC2 and adaptive
optics on HST, and no disk was detected (Stapelfeldt, private
communication).
.
RY Lup has been observed extensively with WFPC2 and adaptive
optics on HST, and no disk was detected (Stapelfeldt, private
communication).
We also note that polarimetric variations have a higher amplitude in the
blue at 4300 Å than in the green at 5250 Å. The observed position
angle varies by ![]() 45
45![]() at both wavelengths. The polarization
and position angle at 4300 Å are correlated with the polarization and
position angle at 5250 Å; see Fig. 8, where data
obtained within 63 min in both filters are plotted. The correlation
seen in position angles between the two filters is a consequence of the
fact that the intrinsic polarization variations are significantly larger
than the value of the IS polarization.
at both wavelengths. The polarization
and position angle at 4300 Å are correlated with the polarization and
position angle at 5250 Å; see Fig. 8, where data
obtained within 63 min in both filters are plotted. The correlation
seen in position angles between the two filters is a consequence of the
fact that the intrinsic polarization variations are significantly larger
than the value of the IS polarization.
![\begin{figure}
\par\includegraphics[width=6cm]{0945fg08.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg33.png) |
Figure 8: Quasi-simultaneous polarimetric data at 4300 Å and 5250 Å. Each point represents data obtained within 63 min of each other. The straight lines show the 1:1 correspondence. |
| Open with DEXTER | |
When plotting the polarimetric data in the Q-U plane, one finds that
our observations trace an ellipse, spending more time around
![]() (see Figs. 9 and
10). The parameters of the fitted ellipses are given in
Table 1. The variations are periodic with a period of 3.75 d,
with second harmonics and even higher harmonics present as will be
discussed in Sect. 4.2. The axis of both ellipses
(Figs. 9 and
10) is compatible with the orientation of the position
angle of the intrinsic polarization obtained by subtracting the IS
polarization.
(see Figs. 9 and
10). The parameters of the fitted ellipses are given in
Table 1. The variations are periodic with a period of 3.75 d,
with second harmonics and even higher harmonics present as will be
discussed in Sect. 4.2. The axis of both ellipses
(Figs. 9 and
10) is compatible with the orientation of the position
angle of the intrinsic polarization obtained by subtracting the IS
polarization.
We finally note that polarimetric data presented by Drissen et al. (1986) are much more erratic than seen here and do not display any periodic variations, using periods of 3.75 d or 7.5 d. On the other hand, the few data points presented by Bastien (1985) seem to show a maximum in polarization around phase 0.0, when using the same epoch and period of 3.75 d, which is compatible with the behavior reported here (see Fig. 5).
Figure 11 shows the photometric and 4300 Å polarimetric data obtained within 29 min (0.02 JD) of one another. When RY Lup is faint, its polarization is maximum at both wavelengths, with no delay in time between them. The polarization is correlated with the magnitude and the colors. There is no correlation between the position angle and the photometric data. The 5250 Å polarimetric data show a qualitatively similar behavior.
4 Discussion
As briefly explained in the introduction, the main causes of light variability in TTSs are the presence of cold and/or hot spots on the stellar surface (with related episodes of magnetic flaring and variable accretion) and variable obscuration of the star by circumstellar matter. A few other sources of variability could perhaps explain RY Lup's behavior, such as pulsations and binarity. We discuss all these possibilities in turn.
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg09.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg35.png) |
Figure 9: Polarimetric data in the QU plane, at 4300 Å. The ellipse is a fit to the data. Four orbital phases are indicated by open circles. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg10.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg36.png) |
Figure 10: Polarimetric data in the QU plane, at 5250 Å. The ellipse is a fit to the data. Four orbital phases are indicated by open circles. |
| Open with DEXTER | |
4.1 Possible mechanisms for the photometric and polarimetric variations
Stellar pulsations cannot explain the data satisfactorily. If the pulsations were radial, i.e., spherically symmetric, then no changes in polarization would be expected. If the pulsations were non-radial, then many periods with differing amplitudes would be expected, leading to more complicated light and polarization variations than the observations show. Furthermore, T Tauri stars are located too far from the instability strip in the HR diagram, and the theory of pulsating variables (e.g. Cox 1980) predicts a period that is about 2 h shorter than the 3.75 d observed period. Gahm et al. (1989) also ruled out pulsations related to the deuterium-burning phase.
Table 1: Ellipses parameters in the (Q, U) plane.
There is currently no observational support for RY Lup being a binary system with a 3.75 d period. There is no evidence of a companion in the spectrum of RY Lup, and the phase of the light variations is not conserved rigorously. Even though RY Lup's polarization variations could be interpreted as that of a binary (Manset & Bastien 2000, 2001), the observations cited in this paragraph do not appear to be compatible with this hypothesis.
![\begin{figure}
\par\includegraphics[width=12cm]{0945fg11.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg37.png) |
Figure 11: Quasi-simultaneous photometry and polarimetry (intrinsic +interstellar) of RY Lup at 4300 Å. Each point represents data obtained within 29 min of one another. |
| Open with DEXTER | |
The presence of large spots on the surface of rotating stars was
proposed by Hoffmeister (1965) as a mechanism to explain the
cyclic variations observed in stars like RY Lup. However, the
presence of magnetic or accretion spots cannot explain the wavelength
dependence of the observed photometric variations, nor does it explain
the H![]() line variations and the infrared excess of RY Lup, a
conclusion also reached by Liseau et al. (1987), Hutchinson et al. (1989), and Gahm et al. (1989). If magnetic or
accretion spots were present on the stellar surface, they would affect
the colors and spectral type, which are not observed to change when the
star's brightness changes.
line variations and the infrared excess of RY Lup, a
conclusion also reached by Liseau et al. (1987), Hutchinson et al. (1989), and Gahm et al. (1989). If magnetic or
accretion spots were present on the stellar surface, they would affect
the colors and spectral type, which are not observed to change when the
star's brightness changes.
Bastien & Landstreet (1979) have found that most of the
polarization in TTSs arises in extended circumstellar dust envelopes
outside the gas-emitting regions. The presence of dust around RY Lup is
evident from the observed polarization and especially its variable
wavelength dependence (Bastien 1985) and also from its
near-infrared excess and its detection at far-infrared wavelengths by
IRAS (Beichman et al. 1985). The existence of intrinsic
polarization in RY Lup thus qualitatively agrees with the hypothesis of
variable circumstellar extinction by dusty clouds orbiting the star. As
far as the photometry is concerned, the reddening appears consistent
with obscuration by interstellar grains with R=3.1 during the small
amplitude variations. On the other hand, the deep minima (that did not
occur during our observing run) seem to be associated with extinction by
larger grains having
![]() (Evans et al.1982; Hutchinson
et al. 1989).
(Evans et al.1982; Hutchinson
et al. 1989).
Since the polarization position angle ![]() changes in time, a model
with a circumstellar cloud passing right in front of the star (on the
observer's line of sight) would not work; in that case, the position
angle is not expected to change. According to Hutchinson et al. (1994), the relationship between the white light
polarization and the V magnitude is too steep compared to expectations
(see Grinin et al. 1991) and cannot be explained by the
occultation of an unpolarized source. Indeed, if dusty blobs orbiting
around the star were responsible for the light and polarimetric
variations, they would produce a polarization vector that describes a
double loop in the (Q, U) plane during one photometric period, as can be
seen from the simple orbiting dust blob model by Bastien
(1981). Such behavior is not compatible with our
observations.
changes in time, a model
with a circumstellar cloud passing right in front of the star (on the
observer's line of sight) would not work; in that case, the position
angle is not expected to change. According to Hutchinson et al. (1994), the relationship between the white light
polarization and the V magnitude is too steep compared to expectations
(see Grinin et al. 1991) and cannot be explained by the
occultation of an unpolarized source. Indeed, if dusty blobs orbiting
around the star were responsible for the light and polarimetric
variations, they would produce a polarization vector that describes a
double loop in the (Q, U) plane during one photometric period, as can be
seen from the simple orbiting dust blob model by Bastien
(1981). Such behavior is not compatible with our
observations.
However, in the case of binary stars embedded in circumstellar dusty envelopes, Manset & Bastien (2000, 2001) have found that several effects (eccentric orbits, variable absorption effects (pre- and post-scattering factors), the scattering functions of dust grains, and asymmetric envelopes) can cause single harmonic variations. Indeed, we see in Sect. 4.2 that RY Lup shows two peaks in polarization, with the one around phase 0.6 much weaker than the other one at phase 0.0. Therefore, various effects could explain why RY Lup's polarimetric variations do not trace a double loop in the (Q, U) plane.
It is however clear that a photopolarimetric model, such as the one developed for AA Tau (Bouvier et al. 1999; Ménard et al. 2003; O'Sullivan et al. 2005) with a warped disk resulting from the interaction between a disk and an inclined magnetosphere, explains the photometric and polarimetric observations of RY Lup quantitatively. The low-mass TTS AA Tau exhibits a roughly constant level of brightness, interrupted by quasi-periodic dips of over 1 mag, with an increase in polarization when the star is faint; i.e., it displays similar behavior to that of RY Lup.
The observed color variability of RY Lup (Sect. 3.2) can be explained easily by assuming that an accretion column and its accompanying accretion spot, both hot and not completely occulted by the disk, come in and out of view as proposed for AA Tau by Bouvier et al. (2003). We note in passing that Gahm et al. (1993b) proposed a similar idea for explaining the color variations of RY Lup. In the O'Sullivan et al. (2005) simulations, a Gaussian-shaped warp passing in front of AA Tau produces a 1 mag. drop in the photometry with a 0.4-0.6% increase in polarization, and the dip in photometry is slightly more pronounced in the blue than in the red. RY Lup dims by about 1 mag in V while its polarization increase by more than 2%. For the warped disk to occult the star, the inclination of the disk must be high, and in the case of RY Lup, which displays more pronounced polarimetric variations, it should be higher than for AA Tau. We examine in the following whether a simple model aiming at reproducing the polarimetry only supports these assumptions.
Table 2: Coefficients of the 4th order fit to the polarimetric data.
![\begin{figure}
\par\includegraphics[width=11.5cm]{0945fg12.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg75.png) |
Figure 12: Polarimetry of RY Lup at 4300 Å as a function of phase, calculated with a period of 3.75 d. The line represents the order 4 Fourier fit. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm]{0945fg13.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg76.png) |
Figure 13: Polarimetry of RY Lup at 5250 Å as a function of phase, calculated with a period of 3.75 d. The line represents the order 4 Fourier fit. |
| Open with DEXTER | |
4.2 A polarization model
It is customary when analyzing the polarization data of spectroscopic binaries
to fit the data with a very general Fourier series, e.g.,
![]()
![]()
where
![]() ,
with
,
with ![]() the orbital phase (see for example
Manset & Bastien 2002, 2003). Even for the case of
RY Lup, which is not a binary, it is useful to adopt the same
representation because it is quite general.
the orbital phase (see for example
Manset & Bastien 2002, 2003). Even for the case of
RY Lup, which is not a binary, it is useful to adopt the same
representation because it is quite general.
The results of the fourth order fit for RY Lup are given in
Table 2 and plotted along with the polarization as a
function of phase in Figs. 12 and
13. The coefficients of
the Fourier fit higher than second order (in 2l) are not
negligible. Including terms up to the fourth order reduces the
normalized ![]() of the fit (see Table 3), especially at
4300 Å. We note the two peaks in polarization around phases 0.0 and 0.6
at both wavelengths.
of the fit (see Table 3), especially at
4300 Å. We note the two peaks in polarization around phases 0.0 and 0.6
at both wavelengths.
For rotating astrophysical systems, Milgrom (1979) presented a formalism that allows one to compute the linear polarization produced by single Rayleigh scattering of unpolarized radiation in a system with arbitrary distributions of scatterers, absorbers, and radiation field. General relations between system properties and observable quantities can be derived. In particular, the inclination of the system can be obtained for systems in which the optical depth for absorption from any scatterer to infinity, along the line of sight, is independent of the phase (i.e., if absorption can be neglected).
Similar methods have been developed by Rudy & Kemp (1978) and Brown et al. (1978, hereafter BME) in the case of binary stars. For the analysis and interpretation of polarization data from binaries, see Bastien (1988b) and Manset (2005).
Even though RY Lup is not a binary, its polarimetric variations are very
similar to such systems. We therefore used both methods, Milgrom's and
BME's, to estimate the inclination angle of the system. Both approaches
only assume single scattering. This means that we are restricted to
small grains (![]() 0.08
0.08 ![]() m) distributed in an optically thin region
(
m) distributed in an optically thin region
(
![]() )
around RY Lup. The assumption of single scattering is,
however, over-simplistic, as it is not consistent with the achromatic
extinction.
)
around RY Lup. The assumption of single scattering is,
however, over-simplistic, as it is not consistent with the achromatic
extinction.
Milgrom's theory tells us that each set of four coefficients qi and ui for a given order in l will yield an ellipse in the (Q, U)-plane. Figures 9 and 10 present the data in the Stokes parameters (Q, U)-plane, along with an ellipse fit to the data. The ellipse's parameters are given in Table 1. If one makes the additional assumption that the extinction from any scatterer to the observer is independent of phase, then the inclination of the rotation axis of the system can be determined independently for the first and second order terms in lfrom the canonical relations given by Milgrom (1979).
The inclination found using both models, both wavelengths, and the first
2 orders are presented in Table 4. The value for the orbital
inclination should not be a function of the wavelength of observation,
but is different for the Milgrom method at 4300 Å, whereas the 3 other
Milgrom values agree with each other and give an average of 85.6![]()
![]() 3
3![]() .
The BME values for a given wavelength agree with one
another, but the average inclination for the first order, 125.8
.
The BME values for a given wavelength agree with one
another, but the average inclination for the first order, 125.8![]() ,
differs from the value obtained from the second order, 95.9
,
differs from the value obtained from the second order, 95.9![]() .
The
difference between first and second order inclination values could stem
from the fact that the system is not axially symmetric (e.g., a warp
explains the data) and that first and second order coefficients may have
different sensitivities to the non-axial density distribution. Since
both orders contribute to the polarimetric variations, there is no
reason to favor one value over the other. However, the Milgrom
average value of 85.6
.
The
difference between first and second order inclination values could stem
from the fact that the system is not axially symmetric (e.g., a warp
explains the data) and that first and second order coefficients may have
different sensitivities to the non-axial density distribution. Since
both orders contribute to the polarimetric variations, there is no
reason to favor one value over the other. However, the Milgrom
average value of 85.6![]() points to an almost edge-on geometry, and
suggests that the second order BME inclination, 95.9
points to an almost edge-on geometry, and
suggests that the second order BME inclination, 95.9![]() ,
is
correct. If the orientation of the inclination (i.e., if the
rotation axis is pointing toward or away from the observer) is
ambiguous, the values 85.6
,
is
correct. If the orientation of the inclination (i.e., if the
rotation axis is pointing toward or away from the observer) is
ambiguous, the values 85.6![]() and 95.9
and 95.9![]() are actually equivalent,
and
are actually equivalent,
and ![]() 5
5![]() from an edge-on geometry.
from an edge-on geometry.
We therefore conclude from our polarimetric observations that RY Lup's geometry is very close to edge-on. A model comprising a warped disk producing variable extinction because it is seen almost edge-on thus appears to be able to explain the data.
4.3 Derived properties of RY Lup
In the following we demonstrate that the period of 3.75 days found in the data is compatible with the rotation period of a G8 pre-main sequence star seen at a high inclination angle and derive the stellar parameters for RY Lup under this assumption. We conclude that the matter responsible for the periodic partial occultation of the star is corotating with the star.
To deduce the stellar parameters from the photometric and
spectroscopic properties of RY Lup, we must compute its
photospheric luminosity
![]() .
Because both accretion and disk
emission may contribute to the luminosity of young stellar objects, one
must choose the photometric band that is least influenced by
non-stellar emission to estimate the photospheric luminosity.
Several methods for doing this have been proposed in the past. For
example, Strom et al. (1989) normalized a blackbody with
temperature equal to the stellar effective temperature
.
Because both accretion and disk
emission may contribute to the luminosity of young stellar objects, one
must choose the photometric band that is least influenced by
non-stellar emission to estimate the photospheric luminosity.
Several methods for doing this have been proposed in the past. For
example, Strom et al. (1989) normalized a blackbody with
temperature equal to the stellar effective temperature
![]() to
the R-filter flux, while Kenyon & Hartmann (1995) used the flux
in the J-filter and a suitable bolometric correction to derive the
photospheric luminosity of a large sample of Taurus stars. However, as
Cieza et al. (2005) re-discovered recently
to
the R-filter flux, while Kenyon & Hartmann (1995) used the flux
in the J-filter and a suitable bolometric correction to derive the
photospheric luminosity of a large sample of Taurus stars. However, as
Cieza et al. (2005) re-discovered recently![]() , the disk emission
of accreting stars contributes significantly to the J-flux, so that
the photospheric luminosities derived by Hartmann and Kenyon for
CTTSs are systematically overestimated.
, the disk emission
of accreting stars contributes significantly to the J-flux, so that
the photospheric luminosities derived by Hartmann and Kenyon for
CTTSs are systematically overestimated.
RY Lup displays a moderate UV excess and a sizable infrared excess, so it is plausible that part of its variability can be attributed to accretion. As recommended by Cieza et al. (2005) we therefore use the observed flux in I and the relevant bolometric correction here (using the standard values given by Kenyon & Hartmann 1995; for a G8 star) to derive the photospheric luminosity of RY Lup. An additional complication stems from the wide variability range of RY Lup, since we must determine the magnitude within this range that corresponds to the emission from the clean photosphere.
Table 3:
![]() values for the Fourier fit.
values for the Fourier fit.
Table 4: Orbital inclinations found using the Milgrom and BME models.
![\begin{figure}
\par\includegraphics[width=8.8cm]{0945fg14.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg88.png) |
Figure 14: Correlation between B and B-V as derived from the full RY Lupi data set (filled circles). The solid line shows how a star moves in the diagram when it suffers a 1 magnitude extinction change. |
| Open with DEXTER | |
We note here that the two main mechanisms that can be invoked for
explaining the light variability of RY Lup, i.e., disk
accretion and the occultation of the central star, act in opposite
directions; accretion increases the V-luminosity, while
occultation due to dust clouds decreases it. Also, the B and Vfluxes are correlated in accretion events (e.g., Bertout et al.
1988), while we expect some de-correlation of these fluxes in
occultation events, due to the combined effects of absorption
(resulting in a B-V increase) and scattering (which produces a
decrease in B-V). As illustrated in Fig. 14, the RY Lupi
V vs. B-V scatter diagram displays a correlation between
B and B-V when the star is brightest, while the scatter
increases and the star's color becomes bluer when it becomes faint.
One might be tempted to attribute the V variations around maximum
light (
![]() )
to variable accretion, but one
notices that they occur along the direction expected from a change
in extinction. It thus appears that the full variability of RY Lupi
in B and V is likely caused by changes in the extinction caused
by the disk matter and that its photospheric brightness corresponds
to the largest observed flux in the optical filters. That there are
no obvious manifestations of accretion in the optical photometry of
RY Lupi can probably be attributed to the low contrast between
photospheric emission and accretion spot emission that is expected
for G and earlier spectral types.
)
to variable accretion, but one
notices that they occur along the direction expected from a change
in extinction. It thus appears that the full variability of RY Lupi
in B and V is likely caused by changes in the extinction caused
by the disk matter and that its photospheric brightness corresponds
to the largest observed flux in the optical filters. That there are
no obvious manifestations of accretion in the optical photometry of
RY Lupi can probably be attributed to the low contrast between
photospheric emission and accretion spot emission that is expected
for G and earlier spectral types.
We recall in passing that, as seen in Sect. 3, the
probability of observing RY Lupi in the V range
11.0-11.5 is
0.36 and the probability of observing the star in a brighter (dimmer)
state is 0.23 (0.41). From Fig. 14, and from the extinction of
RY Lupi at maximum light being ![]() 0.5 mag (see below), we
conclude that the extinction in front of the star is lower than 1.5
magnitude during about 59% of the observing time or, equivalently,
during the same fraction of the rotation period.
0.5 mag (see below), we
conclude that the extinction in front of the star is lower than 1.5
magnitude during about 59% of the observing time or, equivalently,
during the same fraction of the rotation period.
Table 5: Properties of RY Lupi derived assuming two different distances and their associated uncertainties.
Table 6: Photometric data for RY Lup.
Coming back to the photospheric flux, we use the average value of the
brightest V measurements as a representative estimate. We take
V =
10.34, V-I = 1.08. From there, and assuming a spectral type G8, we find
![]() .
We then derive photospheric luminosities from the I-flux,
assuming two different distances 147
+42-27 pc (Bertout et al. 1999) and 108
+48-25 pc (Perryman et al. 1997) and deduce masses, stellar radii, and ages of RY Lupi
for the average and extrema distance values from the Siess et al. (2000) evolutionary tracks. These results are summarized in
Table 5. As seen there, the nominal parallax value of
RY Lupi as given in the Hipparcos catalog is incompatible with a
position on the pre-main sequence track of a G8 star; the minimum
distance leading to a luminosity compatible with that track is 120 pc.
.
We then derive photospheric luminosities from the I-flux,
assuming two different distances 147
+42-27 pc (Bertout et al. 1999) and 108
+48-25 pc (Perryman et al. 1997) and deduce masses, stellar radii, and ages of RY Lupi
for the average and extrema distance values from the Siess et al. (2000) evolutionary tracks. These results are summarized in
Table 5. As seen there, the nominal parallax value of
RY Lupi as given in the Hipparcos catalog is incompatible with a
position on the pre-main sequence track of a G8 star; the minimum
distance leading to a luminosity compatible with that track is 120 pc.
Since we now have an estimated range of values for the stellar
radius, we can use the relation
| (1) |
to derive the stellar inclination angle. Using the values
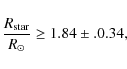 |
(2) |
where the error bars reflect the uncertainty on
It has been argued in the previous sections that stellar spots cannot be
responsible for the observed simultaneous photometric and polarimetric
variations and that the matter responsible for these variations is very
likely associated with the disk itself. For the stellar mass given
above, the Keplerian radius for a period of 3.75 days is ![]() 6.5
6.5
![]() .
We therefore have two possible scenarios. The disk material
that is responsible for occulting the star could be located at the
Keplerian radius by chance (since there is no obvious physical reason
it should be located precisely there) or it could be corotating with
the star because it is located at the disk edge and trapped by the
stellar magnetosphere, in analogy with the case of AA Tau. With no
information on the magnetic-field strength of RY Lupi, it is impossible
to derive a precise magnetospheric radius, but a range of a few stellar
radii is usually assumed for typical CTTSs with kGauss magnetic field
strengths, so that this second possibility appears plausible.
.
We therefore have two possible scenarios. The disk material
that is responsible for occulting the star could be located at the
Keplerian radius by chance (since there is no obvious physical reason
it should be located precisely there) or it could be corotating with
the star because it is located at the disk edge and trapped by the
stellar magnetosphere, in analogy with the case of AA Tau. With no
information on the magnetic-field strength of RY Lupi, it is impossible
to derive a precise magnetospheric radius, but a range of a few stellar
radii is usually assumed for typical CTTSs with kGauss magnetic field
strengths, so that this second possibility appears plausible.
Table 7: Polarimetric data for RY Lup at 4300 Å.
Table 8: Polarimetric data for RY Lup at 5250 Å.
5 Conclusions
RY Lup is a T Tauri star with a 60% chance of being observed in a state brighter than V=11.5 mag. Our re-analysis of 622 photometric measurements obtained in the V band from the late 1970s to 1990 also shows that there is less than a 10% chance of observing RY Lupi within 0.5 magnitude of its brightest state in V, and the star is fainter than V=12.5 about 10% of the time.
From our BV polarimetric and UBV photometric data obtained simultaneously during 12 consecutive nights, we conclude the following.
- There are large amplitude photometric variations
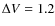 mag,
mag,
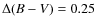 mag, and
mag, and
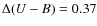 mag.
mag.
- There are large amplitude variations for the observed polarization at
4300 Å,
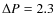 %,
%,
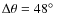 ,
and at 5250 Å,
1.8%, and 47
,
and at 5250 Å,
1.8%, and 47 .
.
- When RY Lup is bright, a lower polarization is observed; and when the polarization is high, the star is fainter and also redder.
- A period search on all our data yielded a period of 3.74+0.20-0.18 days.
- After subtracting an estimate of the IS polarization, we find that
RY Lup's intrinsic polarization is high: 1.30% at 130
 at 4300 Å,
and 1.22% at 133
at 4300 Å,
and 1.22% at 133 at 5250 Å.
at 5250 Å.
- Polarimetric variations have a slightly higher amplitude in the blue at
4300 Å than in the green at 5250 Å. The observed position angle varies by
 45
45 at both wavelengths.
at both wavelengths.
- The polarization and position angle at 4300 Å are correlated with the polarization and position angle at 5250 Å.
Acknowledgements
We are grateful to R. Lamontagne, A. F. Moffat, and L. Drissen for useful discussions. Special thanks go to G. Hutchinson for making his data available before publication and for sharing his enthusiasm on this star. This work was supported by the Sonderforschungsbereih 131-Radioastronomie and by the Natural Sciences and Engineering Research Counil of Canada.
References
- Alves, F. O., & Franco, G. A. P. 2006, MNRAS, 366, 238 [NASA ADS]
- Appenzeller, I., Jankovics, I., & Krautter, J. 1983, A&AS, 53, 291 [NASA ADS] (In the text)
- Baisch, S., & Bokelmann, G. H. R. 1999, Computers & Geosciences, 25, 739 [NASA ADS] [CrossRef]
- Bastien, P. 1981, A&A, 94, 294 [NASA ADS] (In the text)
- Bastien, P. 1982, A&AS, 48, 153 [NASA ADS], 513 (In the text)
- Bastien, P. 1985, ApJS, 59, 277 [NASA ADS] [CrossRef] (In the text)
- Bastien, P. 1988a, in Polarized radiation of circumstellar origin, ed. G. V. Coyne, A. F. J. Moffat, S. Tapia, A. M. Magalhães, R. E. Schulte-Ladbeck, & D. T. Wickramasinghe (Vatican City State/Tucson: AZ Vatican Observatory/University of Arizona Press), 541 (In the text)
- Bastien, P. 1988b, in Polarized radiation of circumstellar origin, ed. G. V. Coyne, A. F. J. Moffat, S. Tapia, A. M. Magalhães, R. E. Schulte-Ladbeck, & D. T. Wickramasinghe (Vatican City State/Tucson: AZ Vatican Observatory/University of Arizona Press), 595 (In the text)
- Bastien, P., & Landstreet, J. 1979, ApJ, 229, L137 [NASA ADS] [CrossRef] (In the text)
- Beichmann, C. A., Neugebauer, G., Habing, H. J., et al. 1985, IRAS Catalogs and Atlases (In the text)
- Bertout, C., Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef]
- Bertout, C., Robichon, N., & Arenou, F. 1999, A&A, 352, 574 [NASA ADS] (In the text)
- Boesgaard, A. M. 1984, AJ, 89, 1635 [NASA ADS] [CrossRef] (In the text)
- Bouvier, J., Bertout, C., & Bouchet, P. 1986, A&A, 158, 149 [NASA ADS] (In the text)
- Bouvier, J., Bertout, C., & Bouchet, P. 1988, A&AS 75, 1 (In the text)
- Bouvier, J., Chelli, A., Allain, S. et al. 1999, A&A, 349, 619 [NASA ADS] (In the text)
- Bouvier, J, Grankin, K. N., Alencar, S. H. P., et al. 2003, A&A, 409, 169 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brown, J. C., McLean, I. S., & Emslie, A. 1978, A&A, 68, 415 [NASA ADS] (In the text)
- Cieza, L. A., Kessler-Silacci, J. E., Jaffe, D. T., et al. 2005, ApJ, 635, 422 [NASA ADS] [CrossRef] (In the text)
- Comeron, F., in Handbook of Star Forming Regions, ASP Conf. Ser., in preparation
- Covino, E., Terranegra, L., Franchini, M., et al. 1992, A&AS, 94, 273 [NASA ADS] (In the text)
- Cox, J. P. 1980, Theory of Stellar Pulsations (Princeton: Princeton University Press), 10 (In the text)
- Drissen, L., Lamontagne, R., Moffat, A. F. J., et al. 1986, ApJ, 304, 188 [NASA ADS] [CrossRef] (In the text)
- Drissen, L., Bastien, P., & St-Louis, N. 1989, AJ, 97, 814 [NASA ADS] [CrossRef] (In the text)
- Evans, A., Bode, M. F., Whittet, D. C.B, et al. 1982, MNRAS, 199, 37 [NASA ADS] (In the text)
- Franco, G. A. P. 2002, MNRAS, 331, 474 [NASA ADS] [CrossRef]
- Gahm, G. F., Fischerström, C., Liseau, R., et al. 1989, A&A, 211, 115 [NASA ADS] (In the text)
- Gahm, G. F., Gullbring, E., Fischerström, et al. 1993a, A&AS, 100, 371 [NASA ADS] (In the text)
- Gahm, G. F., Liseau, R., Gullbring, E., et al. 1993b, A&A, 279, 477 [NASA ADS] (In the text)
- Glass, I. S., & Penston, M. V. 1974, MNRAS, 167, 237 [NASA ADS] (In the text)
- Grinin, V. P., Kiselev, N. N., Chernova, G. P., et al. 1991, Ap&SS, 186, 283 [NASA ADS] [CrossRef] (In the text)
- Heiles, C. 2000, AJ, 119, 923 [NASA ADS] [CrossRef] (In the text)
- Herbig, G. H. 1977, ApJ, 214, 747 [NASA ADS] [CrossRef] (In the text)
- Herbig, G. H., & Kameswara Rao, N. 1972, ApJ, 174, 401 [NASA ADS] [CrossRef] (In the text)
- Herbst, W., Herbst, D. K., Grossman, E. J., & Weinstein, D. 1994, AJ, 108, 1906 [NASA ADS] [CrossRef] (In the text)
- Hoffmeister, C. 1949, Astron. Nachr., 278, 24 [NASA ADS] [CrossRef] (In the text)
- Hoffmeister, C. 1958, Veröff. Sternw. Sonneberg, 3, 340 [NASA ADS] (In the text)
- Hoffmeister, C. 1965, Veröff. Sonneberg, 6, 97 [NASA ADS] (In the text)
- Hughes, J., Hartigan, P., Krautter, J., et al. 1994, AJ, 108, 1071 [NASA ADS] [CrossRef] (In the text)
- Hutchinson, M. G., Evans, A., Davies, J., et al. 1987, n Circumstellar Matter, ed. I. Appenzeller, & C. Hordan (Dordrecht: Reidel), Proc. IAU Symp., 122, 109 (In the text)
- Hutchinson, M. G., Evans, A., Davies, J. K., et al. 1989, MNRAS, 237, 683 [NASA ADS] (In the text)
- Hutchinson, M. G., Albinson, J. S., Barrett, P., et al. 1994, A&A, 285, 883 [NASA ADS] (In the text)
- Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] (In the text)
- Liseau, R., Lindroos, K. P., & Fischerström, C. 1987, A&A, 183, 274 [NASA ADS] (In the text)
- Manset, N. 2005, in Polarimetry of Binary Stars, Astronomical Polarimetry - Current Status and Future Directions, ASP Conf. Ser. 343, 389 (In the text)
- Manset, N., & Bastien, P. 2000, AJ, 120, 413 [NASA ADS] [CrossRef] (In the text)
- Manset, N., & Bastien, P. 2001, AJ, 122, 2692 [NASA ADS] [CrossRef] (In the text)
- Manset, N., & Bastien, P. 2002, AJ, 124, 1089 [NASA ADS] [CrossRef] (In the text)
- Manset, N., & Bastien, P. 2003, AJ, 125, 3274 [NASA ADS] [CrossRef]
- Ménard, F., & Bertout, C. 1999, in The Origin of Stars and Planetary Systems, NATO ASIC Proc., 540, 341
- Ménard, F., Bouvier, J., Dougados, C., et al. 2003, A&A, 409, 163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Milgrom, M. 1979, A&A, 76, 338 [NASA ADS] (In the text)
- O'Sullivan, M., Truss, M., Walker, C., et al. 2005, MNRAS, 358, 632 [NASA ADS] [CrossRef] (In the text)
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, 49 [NASA ADS] (In the text)
- Rudy, R. J., & Kemp, J. C. 1976, ApJ, 207, L125 [NASA ADS] [CrossRef] (In the text)
- Serkowski, K., Mathewson, D. L., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] (In the text)
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] (In the text)
- Strom, K. M., Strom, S. E., Edwards, S., et al. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] (In the text)
- Yudin, R. V., & Evans, A. 1998, A&AS, 131, 401 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... RY Lupi
![[*]](/icons/foot_motif.png)
- Based on observations collected at the European Southern Observatory in La Silla, Chile.
- ... polarimeter
![[*]](/icons/foot_motif.png)
- The instruments were decommissionned long ago. Information and technical specifications are available directly from ESO upon request. See http://www.eso.org/sci/facilities/lasilla/instruments/ for more details.
- ...
night
![[*]](/icons/foot_motif.png)
- Except 1982 February 14-15 (UT).
- ... recently
![[*]](/icons/foot_motif.png)
- The contribution of the disk to the J flux of CTTSs had been noted in earlier works, e.g., Bertout et al. (1988).
All Tables
Table 1: Ellipses parameters in the (Q, U) plane.
Table 2: Coefficients of the 4th order fit to the polarimetric data.
Table 3:
![]() values for the Fourier fit.
values for the Fourier fit.
Table 4: Orbital inclinations found using the Milgrom and BME models.
Table 5: Properties of RY Lupi derived assuming two different distances and their associated uncertainties.
Table 6: Photometric data for RY Lup.
Table 7: Polarimetric data for RY Lup at 4300 Å.
Table 8: Polarimetric data for RY Lup at 5250 Å.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm]{0945fg01.ps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg21.png) |
Figure 1: Photometry and polarimetry (observed polarization, i.e. intrinsic + interstellar) of RY Lup at 4300 Å and 5250 Å as a function of the Julian date. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg02.eps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg22.png) |
Figure 2: Observed V magnitudes of RY Lupi from 1977 to 1990. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{0945fg03.eps}
\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg23.png) |
Figure 3: Bottom panel: histogram of observed V magnitudes from 1977 to 1990. Top panel: the cumulative distribution of V observations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg04.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg24.png) |
Figure 4: Same data as in Fig. 2, but phase-folded with a 3.75 d period. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{0945fg05.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg25.png) |
Figure 5: Photometry and polarimetry (observed polarization, i.e. intrinsic + interstellar) of RY Lup at 4300 Å and 5250 Å as a function of phase, calculated with a period of 3.75 d. The open circles are data points repeated for clarity. |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: V magnitude as a function of U-B and B-V colors. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm]{0945fg07.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg31.png) |
Figure 7:
Map of the interstellar polarization in the vicinity of
RY Lup. The computed average interstellar polarization for RY Lup is
shown at the position of the hexagon. Stars used to determine the
average IS polarization are drawn with larger symbols than other stars,
which are either outside the 15 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm]{0945fg08.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg33.png) |
Figure 8: Quasi-simultaneous polarimetric data at 4300 Å and 5250 Å. Each point represents data obtained within 63 min of each other. The straight lines show the 1:1 correspondence. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg09.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg35.png) |
Figure 9: Polarimetric data in the QU plane, at 4300 Å. The ellipse is a fit to the data. Four orbital phases are indicated by open circles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0945fg10.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg36.png) |
Figure 10: Polarimetric data in the QU plane, at 5250 Å. The ellipse is a fit to the data. Four orbital phases are indicated by open circles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{0945fg11.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg37.png) |
Figure 11: Quasi-simultaneous photometry and polarimetry (intrinsic +interstellar) of RY Lup at 4300 Å. Each point represents data obtained within 29 min of one another. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm]{0945fg12.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg75.png) |
Figure 12: Polarimetry of RY Lup at 4300 Å as a function of phase, calculated with a period of 3.75 d. The line represents the order 4 Fourier fit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm]{0945fg13.ps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg76.png) |
Figure 13: Polarimetry of RY Lup at 5250 Å as a function of phase, calculated with a period of 3.75 d. The line represents the order 4 Fourier fit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{0945fg14.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10945-08/Timg88.png) |
Figure 14: Correlation between B and B-V as derived from the full RY Lupi data set (filled circles). The solid line shows how a star moves in the diagram when it suffers a 1 magnitude extinction change. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


