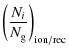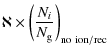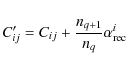EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 498 / No 3 (May II 2009) A&A, 498 3 (2009) 915-929 Full HTML
Free Access
Issue
A&A
Volume 498, Number 3, May II 2009
Page(s) 915 - 929
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/200911712
Published online 19 March 2009

CHIANTI - an atomic database for emission lines

IX. Ionization rates, recombination rates, ionization equilibria for the elements hydrogen through zinc and updated atomic data

K. P. Dere1 - E. Landi2 - P. R. Young3 - G. Del Zanna4 - M. Landini5 - H. E. Mason6

1 - Department of Computational and Data Sciences, George Mason University, 4400 University Dr., Fairfax VA, 22030, USA
2 - Artep, Inc. Ellicott City, MD, 21042; and Naval Research Laboratory, 4555 Overlook Ave. SW, Washington DC 20375-5320, USA
3 - George Mason University, 4400 University Dr., Fairfax VA, 22030, USA and Naval Research Laboratory, 4555 Overlook Ave. SW, Washington DC 20375-5320, USA
4 - Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
5 - Dipartmento di Astronomia e Scienza dello Spazio, Universitá di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy
6 - Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK

Received 23 January 2009 / Accepted 8 March 2009

Abstract
Aims. The goal of the CHIANTI atomic database is to provide a set of atomic data for the interpretation of astrophysical spectra emitted by collisionally dominated, high temperature, optically thin sources.
Methods. A complete set of ground level ionization and recombination rate coefficients has been assembled for all atoms and ions of the elements of H through Zn and inserted into the latest version of the CHIANTI database, CHIANTI 6. Ionization rate coefficients are taken from the recent work of Dere (2007, A&A, 466, 771) and recombination rates from a variety of sources in the literature. These new rate coefficients have allowed the calculation of a new set of ionization equilibria and radiative loss rate coefficients. For some ions, such as Fe
Results. viii And Fe
Conclusions. ix , there are significant differences from previous calculations. In addition, existing atomic parameters have been revised and new atomic parameters inserted into the database.
Arg5. For each ion in the CHIANTI database, elemental abundances, ionization potentials, atomic energy levels, radiative rates, electron and proton collisional rate coefficients, ionization and recombination rate coefficients, and collisional ionization equilibrium populations are provided. In addition, parameters for the calculation of the continuum due to bremsstrahlung, radiative recombination and two-photon decay are provided. A suite of programs written in the Interactive Data Language (IDL) are available to calculate line and continuum emissivities and other properties. All data and programs are freely available at http://wwwsolar.nrl.navy.mil/chianti

Key words: atomic data - atomic processes - radiation mechanisms: thermal - plasmas

1 Introduction

The goal of the CHIANTI atomic database for astrophysical spectroscopy is to provide an assessed set of atomic parameters to calculate the radiative output of hot, optically-thin, collisionally-dominated plasmas. The first release of CHIANTI occurred in 1996 (Dere et al. 1997) and was recently updated in 2005 (Landi et al. 2006). The focus of the current release is to include ionization and recombination rate coefficients. Improvements in CHIANTI 6.0 also include improved data sets of many ions already in the database, data for new ions, and new and updated software.

There are a number of conventions that are used throughout the paper. We abbreviate version X.Y of the CHIANTI database as CHIANTI X.Y throughout the following text. Temperatures are given in Kelvin. We refer to values of the excitation collision strength averaged over a Maxwellian velocity distribution as the effective collision strength. The CHIANTI database includes various files for each ion. For example, for C IV, the file containing the energy level information is c_5.elvlc and the file containing the radiative information is c_4.wgfa. These are referred to simply as the elvlc file etc. For each ion, a consistent energy level numbering scheme is maintained.

2 Ionization rate coefficients

Recently Dere (2007) provided a complete set of ground-level ionization rate coefficients for all ions of the elements hydrogen through zinc. These rates were obtained by the integration of ionization cross sections over a Maxwellian velocity distribution. For neutral and singly ionized ions, the cross sections were largely obtained by fits to laboratory measurements. The extrapolation of these fits to an infinite velocity domain was made possible by the development of an ionization scaling law similar to those developed by Burgess & Tully (1992) for collisional excitation. For more highly ionized species, the cross sections were often calculated with the Flexible Atomic Code (FAC) Gu (2003b,2002). These calculations took into account the processes of both direct ionization and excitation-autoionization and were compared with laboratory measurements and other calculations when available. Cross sections for many of these measurements were obtained from the Atomic and Molecular Research Center of the National Institute for Fusion Science (https://dbshino.nifs.ac.jp/). On average, the adopted cross sections reproduce the measured cross sections to an accuracy of 13%. We note that, for example, the ionization rate of Fe IV here refers to the process where an incident electron ionizes the Fe IV ion to produce Fe V.

Mattioli et al. (2007) have produced an updated set of ionization cross-sections and rate coefficients and find reasonable agreement with the rates of Dere (2007).

3 Recombination rate coefficients

Recombination takes place through the processes of radiative and dielectronic recombination. Most authors calculate the total recombination rate coefficient by summing the rate coefficients for radiative recombination and dielectronic recombination. Nahar and colleagues (Nahar & Pradhan 1992) have used a unified treatment of total electron ion recombination to determine the recombination rates for a number of ions. However, Pindzola et al. (1992) find that the interference between the dielectronic and radiative processes is small. We note that, for example, the recombination rate of Fe IV here refers to the process where an incident electron recombines with the Fe IV ion to produce Fe III.

3.1 Radiative recombination

For radiative recombination onto the completely-ionized through sodium-isoelectronic sequences, the ground state coefficients of Badnell (2006c) are included. For P II and Ca III, the radiative recombination coefficients of Wane & Aymar (1987) are used. For other isoelectronic sequences, the radiative recombination rates are taken from Aldrovandi & Péquinot (1973) and Aldrovandi & Pequignot (1976) for the elements Si and S and from Woods et al. (1981) for Fe. Aldrovandi & Péquinot (1974) provide radiative recombination coefficients for the ions Al II,III, P III, Cl II-VIII, Ar II-IX, and Ca II. For this work the Aldrovandi & Péquinot (1974) rates have been fit with the 4 parameter formula of Verner & Ferland (1996) except where this fit fails to reproduce any one of the data points by less than 6%. In this case the 6 parameter formula of Gu (2003b) was used. Other values for Ar, Ca and Ni are taken from Shull & Van Steenberg (1982) who interpolated the rates of Aldrovandi & Péquinot (1973) and Woods et al. (1981); Aldrovandi & Pequignot (1976). Further interpolations were performed by Landini & Monsignori Fossi (1990) and Landini & Monsignori Fossi (1991) for F, Al, P, Cl, K, Ti, Cr, Mn, and Co and these values are also included here. The rate coefficients for Cu and Zn were obtained from Mazzitelli & Mattioli (2002). The radiative recombination rate coefficients for Sc and V have been interpolated here.

3.2 Dielectronic recombination

3.2.1 H through Mg isoelectronic sequences

Badnell and colleagues, as outlined by Badnell et al. (2003), have used the AUTOSTRUCTURE program to calculate dielectronic coefficients for a number of ions. Rate coefficients for ground state dielectronic recombination are taken from Badnell (2006a) for hydrogen-like ions, from Bautista & Badnell (2007) for helium-like ions, from Colgan et al. (2004) for lithium-like ions, from Colgan et al. (2003) for the beryllium-like ions, Altun et al. (2005) for the boron-like ions, from Zatsarinny et al. (2005b) for carbon-like ions, Mitnik & Badnell (2004) for nitrogen-like ions, Zatsarinny et al. (2005a) for oxygen-like ions, Zatsarinny et al. (2006) for fluorine-like ions, Zatsarinny et al. (2004) for neon-like ions, Altun et al. (2006) for sodium-like ions, and Altun et al. (2007) for magnesium-like ions. This set of calculations provide a coherent set of dielectronic recombination rates and we have adopted them as a standard by which to assess the validity of other calculations.

3.2.2 Al through Ar isoelectronic sequences

For ions in the aluminum and higher isoelectronic sequences, calculations of the dielectronic recombination rates are not always available. Recently, Badnell (2006b) has provided dielectronic recombination rates for the ions Fe IX-XIV and Schmidt et al. (2008) for the ion Fe VIII. In a series of papers, Jacobs and co-workers calculated dielectronic recombinations rates for a number of the astrophysically abundant elements. These include Si (Jacobs et al. 1977a), S (Jacobs et al. 1979), Ca and Ni (Jacobs et al. 1980), and Fe (Jacobs et al. 1977b). It should be noted that the rates tabulated for Fe are the sum of the radiative and dielectronic recombination rates. Woods et al. (1981,1982a) have fit these rates for Fe and Shull & Van Steenberg (1982); Woods et al. (1982b) have fit these rates for C, N, O, Ne, Mg, Si, S, Ca and Ni. In addition, Shull & Van Steenberg (1982) has interpolated these rates for Ar. The parameters of the analytical fits for the combined data set are tabulated by Shull & Van Steenberg (1982). In general, there is good agreement between the rates of Jacobs and co-workers and those of Badnell and co-workers.

Mazzotta et al. (1998) has provided a set of dielectronic recombination rate coefficients for the ions magnesium through nickel. Their rates are collected from the work of Shull & Van Steenberg (1982), Landini & Monsignori Fossi (1990,1991), and Mattioli (1988). Other rates were calculated by means of the Burgess general formula (Burgess 1965). For ions in isoelectronic sequences up to the Mn-like, Mazzotta et al. (1998) then renormalized their rates to the work of Arnaud & Raymond (1992). Consequently, the reconstruction of the rates of Mazzotta et al. (1998) is problematical.

For ions in the aluminum through argon isoelectronic sequences, there are a reasonable number of calculations with which to compile a set of dielectronic recombination rates. For these sequences, we have used the rates of Badnell and co-workers for the Fe ions. For ions of Si, S, Ar, Ca and Ni we have included the rates of Woods et al. (1981) and Shull & Van Steenberg (1982) which are based on the Jacobs et al. calculations. For the ions of P, Cl, K, Ti, Cr, Mn and Co we have used the rates of Landini & Monsignori Fossi (1991) who interpolated the rates of Woods et al. (1981) and Shull & Van Steenberg (1982). For the ions of Sc and V, we have used the rates of Mazzotta et al. (1998) but, as noted above, it is not always clear how these rates were determined. The rate coefficients for Cu and Zn were obtained from Mazzitelli & Mattioli (2002).

One exception to these selections is for S III. The rates of Nahar & Pradhan (1995) are in good agreement with those of Jacobs et al. (1979) and provide a good description of the rate over a large temperature range.

3.2.3 K through Mn isoelectronic sequences

The number of reliable calculations of dielectronic recombination rates for ions in these isoelectronic sequences is quite limited. They are available for Ca II (Jacobs et al. 1980), Fe II (Nahar et al. 1997), Fe III (Nahar 1997), Fe IV (Nahar 1996), Fe V (Nahar et al. 1998), Fe VI (Nahar & Bautista 1999) and Ni III Nahar & Bautista (2001). In addition, the rate coefficients of Mazzitelli & Mattioli (2002) are available for Cu and Zn. Many rates rely on the Burgess general formula (GF) (Burgess 1965) but it is not clear how accurately it can be applied to these complex ions. Arnaud & Raymond (1992) suggest that these latter rates for the Fe ions can be made more accurate by normalizing them to the rates of Hahn (1989). Our own experience with the dielectronic recombination rates of Hahn (2002) is that they are often very different from the detailed calculations of Badnell and Jacobs and co-workers for a number of elements and ions. Lacking real criteria to assess these rates, our choices for these are somewhat arbitrary and described below.

K isoelectronic sequence

For Ca II, the rates of Shull & Van Steenberg (1982) which are based on the calculations of Jacobs et al. (1980), are included. For Ni X, the rates of Shull & Van Steenberg (1982) are also included but it is likely that these are based on the Burgess GF and are not particularly reliable. For the elements P, Cl, K, Ti, Cr, Mn and Co we have used the rates of Landini & Monsignori Fossi (1991). We have included the rates of Mazzotta et al. (1998) for the elements Sc and V and the rates of Mazzitelli & Mattioli (2002) for Cu and Zn.

Ca through Mn isoelectronic sequences

Here, all of the rates are from Mazzotta et al. (1998) except for Fe II-VI and Ni III which are taken from Nahar and co-workers, as referenced above, and for Cu and Zn which are taken from Mazzitelli & Mattioli (2002).

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig1.eps} \end{figure} Figure 1:

Ionization equilibria for Fe I-IX. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig2.eps} \end{figure} Figure 2:

Ionization equilibria for Fe IX-XVII. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER

4 Ionization equilibria

Under the conditions of coronal equilibrium, the ionization state of a plasma is determined by the balance between ionization and recombination processes. Using the ionization and recombination rate coefficients previously discussed, we have calculated the ionization equilibria of all ions of all elements from hydrogen through zinc for a range of temperatures from 104 to 109 K. A number of sets of ionization equilibria calculations are currently available. These include those by Jordan (1969,1970), Summers (1974), Jacobs et al. (1977b,1979,1977a,1980); Jacobs (1985), Shull & Van Steenberg (1982), Arnaud & Rothenflug (1985), Landini & Monsignori Fossi (1991), Arnaud & Raymond (1992), Mazzotta et al. (1998), Mazzitelli & Mattioli (2002), Bryans et al. (2006) and Bryans et al. (2009). These various calculations have used new or updated values of the ionization or recombination rate coefficients. In previous versions of CHIANTI, the calculations of Mazzotta et al. (1998) have been the default specified for using the IDL procedures and we compare our calculations with these. The ionization calculations of Bryans et al. (2006) and Bryans et al. (2009) are now included with the CHIANTI 6 database.

For many ions, there are often significant differences for the neutrals and first ionization stage ions. For the neutrals, Mazzotta et al. (1998) uses the ionization rates of Arnaud & Rothenflug (1985) and Arnaud & Raymond (1992), for which references are not provided. Consequently, it is not possible to assess the origin of the differences. Otherwise, for the elements H through Ca, the differences between the two calculations are minor.

In Figs. 1-4, our present ionization equilibrium calculations for iron are displayed, together with those of Mazzotta et al. (1998). In general, the differences are not large but there are a few cases where there is noticeable disagreement. In Fig. 1 the ionization equilibria for Fe II, III, V, VI, VIII AND IX show considerable differences. For the ions Fe X-XXI, the temperatures at which the current maximum ion fraction is found is typically a factor of 0. to 0.1 higher in $\log~T$ with the most common value being 0.05 in $\log~T$. For higher stages of ionization, the differences are small. Perhaps the greatest differences of significance are with the ions Fe VIII and Fe IX.

For other elements, there are often several ions with notable differences. In general, the differences between our ionization equilibria and those of Mazzotta et al. (1998) must be attributed to the combined effect of updated ionization and recombination rates. It would be useful to the user of these data to examine them for the particular ions in which they are interested.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig3.eps} \end{figure} Figure 3:

Ionization equilibria for Fe XVII-XXIV. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER

5 New atomic data for the hydrogen isoelectronic sequence

5.1 Recombination in hydrogen-like systems

The data included in CHIANTI 5.2 for recombination into excited levels of H-like ions were taken from Mewe et al. (1985), who provided the analytical formulae and the parameters to calculate the recombination rates for the np [2 P ] doublets with n=2 to 5. However, Mewe et al. (1985) treated recombination into the [2 P ] doublets using LS coupling; in our implementation we neglected to split the Mewe et al. (1985) values according to the statistical weights of the fine-structure levels in each doublet. This inaccuracy has been corrected in the present version.

5.2 C VI

For H-like C, we have replaced the previous collision strengths with those calculated with the R-matrix codes by Ballance et al. (2003) who include all levels up to n=5. The fine structure collision strengths have been obtained assuming a distribution according to statistical weights. Only excitations from the 1s and 2s levels are retained.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig4.eps} \end{figure} Figure 4:

Ionization equilibria for Fe XXIV-XXVII. Full line - current calculations, dashed line = Mazzotta et al. (1998), whose calculations only extend to 108 K.
Open with DEXTER
A-values have been obtained from a standard SUPERSTRUCTURE calculation that included all levels up to n=5. The A-values replace the previous ones, due to Wiese et al. (1996). There is general agreement, to within a few percent. However the new model includes more transitions than the previous one. We continue to use the A-values from the 2s level of Parpia & Johnson (1982). Fine-structure values for electron and proton impact excitation within the n=2 levels are obtained from the close-coupling calculation of Zygelman & Dalgarno (1987). The new model predicts an increased emissivity (14%) for the 1s [2 S 1/2]-2p [2 P 1/2] transition at 33.74 Å.

5.3 O VIII

The previous CHIANTI model contained collision strengths obtained from an interpolation of the R-matrix calculations of Aggarwal & Kingston (1991). We have replaced them with those calculated with the R-matrix codes by Ballance et al. (2003) that included all levels up to n=5. The fine structure collision strengths have been obtained assuming a distribution according to statistical weights. Only excitations from the 1s and 2s levels are retained.

A-values have been obtained from a standard SUPERSTRUCTURE calculation that also included all levels up to n=5. The A-values replace the previous ones, due to Wiese et al. (1996). There is general agreement, to within a few percent, however the new model includes more transitions than the previous one.

We continue to use the A-values from the 2s level of Parpia & Johnson (1982). The new model ion provides emissivities for the stronger spectral lines in close agreement (within 20%) with the previous ones.

6 New atomic data for the helium isoelectronic sequence

6.1 Recombination in helium-like systems

Recombination to excited levels and cascades from excited levels following recombination are important contributions to the level population balance in He-like ions. In the present version of CHIANTI we have improved both the approach and the data for taking these processes into account.

6.1.1 CHIANTI 5 limitations

In CHIANTI 5, ionization and recombination effects were included in an approximate way in the calculation of the level populations of the H-like and He-like sequences and of Fe XVII-XXIII. In fact, collisional excitation was assumed to take place from the ground level only. Under this approximation, the effects of ionization and recombination could be included as a correction to the level populations calculated without these two processes, as

             $\displaystyle {\left({N_{i} \over N_{\rm g}}\right)}_{\rm ion/rec}$ = $\displaystyle \aleph \times {\left({N_{i} \over N_{\rm g}}\right)}_{\rm no~ion/rec}$  
$\displaystyle \aleph$ = $\displaystyle 1 + {{n_{\rm q-1}\alpha_{\rm ion} + n_{\rm q+1}\alpha_{\rm rec}}\over{n_{\rm q}C_{\rm g\to i}}}$ (1)

where $N_i/N_{\rm g}$ are the level populations of level i relative to the ground level g, $\alpha_{\rm ion}$ and $\alpha_{\rm rec}$ are the total ionization and recombination rates (including cascades) to level i, nq-1, nq+1 are the fractional abundances of the ionizing and recombining ions, respectively, and nq is the fractional abundance of the ion whose populations are being calculated. For He-like ions, only recombination was considered. For each level, the $\alpha_{\rm rec}$ rate included both direct recombination into the level, as well as cascades following recombination into a higher energy level. Landi et al. (2006) discussed that such approach provides accurate results at densities lower than a critical density $N_{\rm cr}$ beyond which metastable levels begin to provide significant contribution to collisional excitation, so that their approach no longer holds. Approximate values of $N_{\rm cr}$ are 1010 cm-3 for C V, 1010.5 cm-3 for N VI, 1011 cm-3 for O VII, 1012 cm-3 for Ne IX, 1013 cm-3 for Mg IX, and higher for higher values of nuclear charge.

In CHIANTI 6, we have revisited recombination for the He-like sequence for two reasons. First, the $N_{\rm cr}$ value of He-like ions was low enough to depart from the Landi et al. (2006) approach at densities comparable to, or lower than densities of many astrophysical sources and, second, the data that were used for the n=2 levels were not suited for this approach. In fact, CHIANTI 5 data for n=2 levels consisted of recombination rates that included direct recombination to each n=2 level, and cascades following recombinations to levels with $n \geq 3$, where n is the principal quantum number. Thus, those data were missing the cascades following recombination onto the n=2 levels, and hence underestimated the recombination coefficient in Eq. (1). This effect was significant for the 1s2s 3S1 level.

6.1.2 New approach

In CHIANTI 6 we have corrected both problems. We have used the approach of Gabriel & Jordan (1973), by modifying the definition of the collision excitation rate coefficient from the ground level to the levels 1s2s 3S1, 1s2p 3P0,1,2 and 1s2p 1P1. The new collision excitation rate coefficient is defined as

\begin{displaymath}C'_{ij} = C_{ij} + {{n_{ q+1}}\over{n_q}} \alpha_{\rm rec}^i \end{displaymath} (2)

where $\alpha_{\rm rec}^i$ is the total recombination rate to level i including cascades following recombination to all levels with $n \geq 3$. This approach is valid at any density because it takes into account recombination explicitly.

6.1.3 New recombination data

Recombination data for C V, N VI, O VII, Ne IX, Mg XI and Si XIII were changed to adopt the more recent and complete calculations of Porquet & Dubau (2000) for all the ions in the 1s2s and 1s2p configurations. Porquet & Dubau (2000) included both radiative and dielectronic recombination including cascades from levels of configurations with principal quantum number $n \geq 3$.

Recombination data for the other He-like ions (S, Ar, Ca, Ni) have been retained from CHIANTI 5.2. These rates were also taken from Mewe et al. (1985); those for the 1s2p 3P triplet suffered from the same problem described in the H-like sequence discussion; we corrected the rates for the 1s2p 3P triplet from the same problem described in the H-like sequence discussion.

A typographical error was also corrected in the recombination rates file of Fe XXV.

6.2 Ne IX

Chen et al. (2006) has recently performed a large-scale calculation of Ne IX. They included all the lowest 15 configurations of this ion, up to 1s5g, for a total of 49 fine-structure levels. Experimental energies were taken from version 3 of the NIST database (Ralchenko et al. 2007), with the exception of the 2s2p 3P levels whose energies come from Chen et al. (2006).

Theoretical energy levels, radiative transition rates and electron excitation rate coefficients were taken from Chen et al. (2006). The only exception are the radiative transition rates for transitions 1-2 and 1-6, which were taken from the experimental values of Träbert et al. (1999) and Lin et al. (1977), respectively. Electron impact excitation was treated using a fully relativistic close-coupling code, employing the Dirac R-Matrix method on an atomic structure model calculated with the multi-configuration Dirac-Fock method. Resonances and channel coupling effects were both taken into account and significant resonant structure neglected in previous studies was included. Effective collision strengths were provided by the authors in the $5.0 \leq \log T \leq 8.0$ temperature range.

6.3 C V, N VI, O VII, Mg XI, Si XIII

The hydrogenic radiative transition rates for decays originating from levels of the n=2 and n=3 configurations used in CHIANTI 5.2 were replaced by the values calculated by Porquet & Dubau (2000).

6.4 S XV

The collision strengths for the levels up to n=3 of Zhang & Sampson (1987) have been replaced with those of Kimura et al. (2000), calculated with a Dirac-R-Matrix code. Kimura et al. (2000) provide effective collision strengths in the temperature range 106-107.6. The new data produce differences in the emissivities of the 1s2 1S0-1s 2p 3P1,2 and 1s2 1S0-1s 2s 3S1 transitions of less than 10%.

6.5 Ar XVII

Whiteford et al. (2001) used a 31 level intermediate-coupling, frame-transformation, R-matrix calculation that included resonance effects and radiation damping, to obtain collision strengths for all levels up to n=4 and these are included in the current database. They estimate their effective collision strengths to be accurate to within 20% between temperatures of $3 \times 10^5$ and $3 \times 10^8$ K. The collision strengths for the n=5 levels obtained from Zhang & Sampson (1987) are retained as well as the radiative data. The new data show negligible differences in the emissivities of the n=2 lines, and differences with 20% for the transitions from higher levels.

6.6 Ca XIX

The effective collision strengths for the levels up to n=3 of Zhang & Sampson (1987) have been replaced with the Dirac-R-Matrix collision strengths of Kimura et al. (2000), which are provided in the range $2.5\times 10^6$-108 K. The new collision strengths result in differences of up to 20% in the emissivity of the 1s2 1S0-1s 2s 3S1 transition, and differences of about 10% in the forbidden lines and in the 1s2-1s 3p transition.

6.7 Fe XXV

The collision strengths of Zhang & Sampson (1987) were replaced with those of Whiteford et al. (2001). The new data were obtained from a 49 level (up to n=5) intermediate-coupling, frame-transformation, R-matrix calculation that included resonance effects and radiation damping. Whiteford et al. (2001) estimate their effective collision strengths to be accurate to within 20% between temperatures of 106 and 109 K. The new data produce slightly increased (up to 10%) intensities in the n=3,4 lines.

7 New atomic data for the beryllium isoelectronic sequence

The CHIANTI atomic model for Mg IX, Si XI, S XIII, Ar XV and Ca XVII has been expanded from 46 to 92 levels by including the extensive calculations of Bhatia and Landi (for references, see below). In all cases the configurations included are 2s2, 2s2p, 2p2, 2l3l', 2l4l' and 2s5l' with l=s,p and l'=s,p,d. The authors provided theoretical energy levels, A-values and oscillator strengths for all levels and possible transitions within the adopted atomic model. Electron impact excitation rate coefficients were calculated in the Distorted Wave approximation with the UCL suite of codes (Eissner 1998; Eissner et al. 1974). Collision strengths were given for all transitions involving the lowest 4 levels in the atomic model (2s2 1S0 and 2s2p 3P1,2,3), since these are the only significant levels for collisional excitation. R-Matrix effective collision strengths for transitions within the 2s2, 2s2p, and 2p2 configurations available in the literature and in CHIANTI 5 were retained, to ensure that the effects of resonant excitation were taken into account.

7.1 N IV

The N IV CHIANTI model consists of all 20 levels for the six configurations 2s2, 2s2p, 2p2 and 2s3l (l=s,p,d). Since CHIANTI 1, the radiative decay rates for N IV were from an unpublished calculation of one of the authors (Young) using the SSTRUCT code. These have now been replaced with the calculations of Tachiev & Froese Fischer (1999). Eleven forbidden transitions that help depopulate levels in excited configurations have been retained from the Young calculation, since Tachiev & Froese Fischer (1999) did not provide rates for these transitions. Ten transitions have A-values different from the previous calculation by more than 30%. At $N_{\rm e} = 10^{10}~{\rm cm}^{-3}$ and $\log~T = 5.1$, three of the levels show differences in level populations of >10% due to the new radiative data.

The effective collision strengths from Ramsbottom et al. (1994) for transitions amongst the 2s2, 2s2p and 2p2 configurations have been re-fitted with nine point splines, in order to improve the fidelity of the fits at low temperatures. In particular, the new fits now reproduce the original data to within 1.2% over the temperature range $3.2 \le \log T \le 5.5$. The extension to lower temperatures is important for modeling photoionized plasmas.

7.2 Mg IX

The Mg IX data of Bhatia & Landi (2007a) are used for CHIANTI 6. They collected experimental energy levels for the majority of the 2l3l' levels and for many 2l4l' and 2l5l' levels. The energies have been taken from Edlén (1983), Kelly (1987), Hoory et al. (1970) and Version 3.0 of the NIST database (Ralchenko et al. 2007); multiple energy values from different sources were averaged together.

Oscillator strengths and A-values were calculated for all possible transitions among the 92 fine-structure levels; their values compared favorably with earlier calculations and measured lifetimes. Collision strengths were calculated for five values of the incident electron energy (25, 50, 75, 100 and 125 Ry) for transitions involving the n=3,4,5 levels. The R-Matrix effective collision strengths of Keenan et al. (1986) were used for the n=2 transitions in place of the Bhatia & Landi (2007a) results to take into account resonant excitation important in the $5.2 \leq \log T \leq 6.8$ temperature range.

7.3 Si XI

Bhatia & Landi (2007b) published a complete dataset for Si XI that is used here. They assembled experimental energy levels from a variety of sources: Edlén (1983), Acton et al. (1985), Hoory et al. (1970), the NIST database (Ralchenko et al. 2007), Tondello (1969), Brandt et al. (1988) and Khardi et al. (1994). Multiple entries from different sources were averaged together.

A-values and oscillator strengths were calculated for all possible transitions between the 92 fine-structure levels. Collision strengths were calculated for five values of the incident electron energy (35, 70, 105, 140 and 175 Ry). The effective collision strengths for transitions among the 2s2, 2s2p, and 2p2 levels were taken from the R-Matrix calculations of Berrington et al. (1985), and are accurate in the $5.4 \leq \log T \leq 7.0$ temperature range.

7.4 S XIII

Landi & Bhatia (2008) calculated the complete S XIII dataset adopted in the present CHIANTI 6. They collected the experimental energy levels from Edlén (1983,1985), Fawcett & Hayes (1987), Goldsmith et al. (1974), Lepson et al. (2005), Fawcett et al. (1970), Khardi et al. (1994) and Version 3 of the NIST database (Ralchenko et al. 2007) that we use here.

Collision strengths were calculated at five incident electron energies (45, 90, 135, 180 and 225 Ry) for transitions between n=2 configurations and the n=3,4,5 configurations. For transitions within the n=2 levels we used the R-Matrix effective collision strengths of Keenan (1988) calculated for the $5.6 \leq \log T \leq 7.2$ temperature range.

7.5 Ar XV

The data for Ar XV used in CHIANTI 6 are provided by Bhatia & Landi (2008). Experimental energy levels come from Edlén (1983,1985), Khardi et al. (1994), and Lepson et al. (2003), although all these measurements concerned only n=3 levels and no experimental energy is available for the n=4,5 levels. A-values and oscillator strengths were provided for all possible transitions within the 92 fine-structure levels.

Collision strengths for collisional excitation from the four lowest levels were given by Bhatia & Landi (2008) at five incident electron energies: 60, 120, 180, 240 and 300 Ry. For transitions within the n=2 configurations the R-Matrix effective collision strengths of Keenan (1988) in the $5.7 \leq \log T \leq 7.3$ temperature range are included.

7.6 Ca XVII

Landi & Bhatia (2009a) provide the Ca XVII data set that we use here. They also reviewed the experimental energies available for this ion from Edlén (1983,1985), Fawcett & Hayes (1975), and McKenzie & Landecker (1982). Experimental energies, used for CHIANTI 6, were available only for the n=2,3 levels and none were available for the n=4,5 levels.

Collision strengths were provided at five different values of the incident electron energies (75, 112.5, 150, 187.5 and 225 Ry). The R-Matrix effective collision strengths from Dufton et al. (1983), which include the n=2 levels, have been used in place of the Landi & Bhatia (2009a) results to take into account the effects of resonances; these are provided in the $6.4 \leq \log T \leq 7.2$ temperature range.

7.7 Ni XXV

Chidichimo et al. (2003) calculated effective collision strengths for Ni XXV using the R-Matrix approximation together with the Intermediate Frame Coupling Transformation. They provided data for all the transitions within the n=2 complex (corresponding to the lowest 10 levels) and for five additional transitions of interest, namely 2s2 1S0-2s3p 1,3P1, 2s2p 3P1-2s3d 3D2, and 2s2p 1P1-2s3s 1S0, 1D2. Chidichimo et al. (2003) provide effective collision strengths calculated in the $6.3 \leq \log T(K) \leq 8.3$ temperature range in $\Delta \log T=0.2$ steps.

Recently, Landi & Bhatia (2009b) developed a complete set of energy levels, A-values and collision strengths for Ni XXV. Experimental energies are available only for the n=2,3 levels; the values for the n=2 levels come from Edlén (1983), with the exception of the 2p2 3P levels whose energy was corrected by Edlén (1985). The energies for the n=3 levels were taken from the measurements of Boiko et al. (1977); more details can be found in Landi & Bhatia (2009b).

Collision strengths for transitions involving the n=3,4,5 levels were provided at five different values of the incident electron energies (150, 225, 300, 375 and 450 Ry), while those involving the n=2 levels included values calculated at two additional lower energies: 50 and 100 Ry. The Landi & Bhatia (2008c) collision strengths is based on the Distorted Wave approximation. A-values and oscillator strengths were provided by Landi & Bhatia (2009b) for all possible transitions within the atomic model.

The current Ni XXV dataset includes all of the atomic data developed by Landi & Bhatia (2009b) except for those transitions where the R-Matrix collision strengths of Chidichimo et al. (2003) are available.

8 New atomic data for the boron isoelectronic sequence

8.1 O IV

The 2s2 2p 4P1/2-2p3 4S3/2 collision strength was missing from the original CHIANTI 1 release. Including this transition increases the population of the upper 2p3 4S3/2 level by around 50%, with negligible effects on other level populations.

The collision strength fits for transitions amongst the first 10 levels of the O IV model have been revised to improve the low temperature coverage. In particular the fits now reproduce the original data to within 1.2% over the range $3.2 \le \log T \le 5.5$.

8.2 Ne VI

In earlier versions of CHIANTI, the A-value for the ground transition ( $^2{\rm P}_{1/2}$- $^2{\rm P}_{3/2}$) was missing. This transition has now been added with the A-value from Tachiev & Froese Fischer (2000). The transition has negligible effect for studies of UV transitions in electron-ionized plasmas, but is significant for low temperature, photoionized plasmas.

8.3 Al IX

The radiative decay rate for the ground $^2{\rm P}_{1/2}$- $^2{\rm P}_{3/2}$transition of Al IX has been replaced by the value from Tachiev & Froese Fischer (2000) that is factor of 2.7 greater. The new value is consistent with the neighboring magnesium and silicon ions in the isoelectronic sequence.

9 New atomic data for the carbon isoelectronic sequence

9.1 O III

The upsilon values for the $^3{\rm P}_1$- $^3{\rm P}_2$ transition was found to be a factor 3 lower than those from the original source paper (Lennon & Burke 1994). The data were re-fit and replaced in the CHIANTI database.

The A-values for the ground configuration have been updated with the values of Tachiev & Froese Fischer (2001), except for the 2-4 and 3-4 transitions for which the previous data of Storey & Zeippen (2000) are retained.

9.2 Ne V

The A-values for the ground $^3{\rm P}_0$- $^3{\rm P}_1$ and $^3{\rm P}_0$- $^1{\rm D}_2$ transitions were not correctly replaced in the previous version of CHIANTI (Landi et al. 2006). The Galavis et al. (1997) values have been added and are factors 0.76 and 0.36 lower than the CHIANTI 5 values. Otherwise, the Ne V model remains the same.

9.3 Mg VII

The previous model of Mg VII consisted of electron collision and radiative data from Bhatia & Doschek (1995). The data used for the ground configuration transitions have been reassessed following the identification of a number of Mg VII forbidden lines in the HST/STIS spectrum of the symbiotic star AG Draconis (Young et al. 2006). The Bhatia & Doschek (1995) collision calculation was performed in the Distorted Wave approximation and thus resonance effects, that are particularly important for forbidden transitions, are missing.

Two R-matrix calculations for Mg VII are available in the literature: Aggarwal (1984b,a) and Lennon & Burke (1994). The latter are the more sophisticated but effective collision strengths are only calculated for the temperature range $3.0 \le \log T \le 5.0$ - lower than the temperature of maximum abundance of Mg VII in an electron-ionized plasma, $\log~T = 5.8$. The Aggarwal calculations cover a larger temperature region, from $5 \times 10^3$ to $5\times 10^7$ K. It was decided to merge the two data-sets, and the method is as follows.

The Aggarwal (1984b,a) effective collision strengths were recomputed onto a temperature grid of $5.0 \le \log ~T\le 7.6$ in 0.2 dex intervals using spline fits. These values were then multiplied by a scale factor determined by the ratio of the Lennon & Burke (1994) collision strengths to the Aggarwal (1984b,a) collision strengths at $\log~T = 5.0$. For the 10 transitions amongst the ground configuration levels, the scale factor varied from 0.82 to 1.19. Merging the Lennon & Burke (1994) collision strengths with the scaled Aggarwal (1984b,a) collision strengths led to sets of upsilons defined over the range $3.0\le\log~T\le 7.6$ in 0.2 dex intervals.

The merged upsilons were fit with 9 point splines (Young et al. 2003), but accurate fits could only be obtained for the reduced temperature range $3.8 \le \log T \le 6.2$ for which the fits are accurate to $\le$1.20%.

All ground configurations A-values have been replaced with the data from Galavis et al. (1997), except for the 3P1-1D2 and 3P2-1D2 transitions for which the data of Storey & Zeippen (2000) have been retained. Energies for the 3P1, 3P2 and 1D2 levels in the ground configuration have been derived from infrared and ultraviolet astrophysical spectra, using the values from Kelly & Lacy (1995), Feuchtgruber et al. (1997) and Young et al. (2006).

9.4 Si IX

All ground configuration A-values were replaced with the data from Galavis et al. (1997).

10 New atomic data for the nitrogen isoelectronic sequence

10.1 O II

The effective collision strengths for the ground $2{\rm s}^2 2{\rm p}^3$configuration of O II have been replaced with the results of Pradhan et al. (2006). The previous data came from McLaughlin & Bell (1994) and an unpublished calculation of Bhatia. McLaughlin & Bell (1994) only provided collision strengths for transitions between LS terms, which were split according to their statistical weights. The Bhatia data were used for the fine structure transitions $^2{\rm D}_{5/2}$- $^2{\rm D}_{3/2}$and $^2{\rm P}_{3/2}$- $^2{\rm P}_{1/2}$ within the ground configuration. Dere et al. (1997) noted that, for transitions common to both the McLaughlin & Bell (1994) and Bhatia data-sets, there were some large differences. The new Pradhan et al. (2006) calculations are around 40-50% and 75% lower for the 2D5/2-2D3/2 and 2P3/2-2P1/2 transitions, respectively. The Pradhan et al. (2006) and McLaughlin & Bell (1994) data-sets agree to within 15% except for the 2D3/2-2P1/2 transition for which the Pradhan et al. (2006) data are around 30% lower.

The Pradhan et al. (2006) effective collision strengths are tabulated at six temperatures between 1000 and 25 000 K and were fit with 5 point splines that reproduce the original data to an accuracy of $\le$0.61%. The energy level and radiative data files remain unchanged, except that levels 4 and 5 have been swapped to reflect the level ordering of Pradhan et al. (2006).

10.2 Fe XX

The new model ion is largely based on the Iron Project R-matrix calculations of Witthoeft et al. (2007a), and includes 302 fine-structure levels of Fe XX arising from the 2s22p3, 2s2p4, 2p5, 2s2 2p2 3l, 2s 2p3 3l and 2s2 2p2 4l configurations. Resonant enhancement included in the R-matrix calculations provide a better estimate of the collision strengths at lower temperatures. The new model ion includes all 45 451 transitions of the n=4 calculation, with A-values calculated with AUTOSTRUCTURE and observed energies as from the previous CHIANTI model. The n=5 levels are based on the CHIANTI 5.2 model.

11 New atomic data for the oxygen isoelectronic sequence

11.1 Si VII

The observed energy levels of the n=2 configurations of Si VII from Ralchenko et al. (2007) have been replaced with the values of Edlén (1983). This change improves the agreement between CHIANTI wavelengths and values from Hinode/EIS. All the other data for Si VII are unchanged from the previous version.

12 New atomic data for the fluorine isoelectronic sequence

The data for the F-like ions Si VI, S VIII, Ar X, Ca XII, Ni XX have been replaced by the large-scale calculations of Witthoeft et al. (2007b). The CHIANTI model for these ions grows from three levels (113 in the case of Ni XX) to 195 levels for all ions. Witthoeft et al. (2007b) used an automated parallelized version of an R-Matrix code that allowed to carry out calculations along the isoelectronic sequence using the Intermediate Coupling Frame Transformation method with the same atomic model for all ions. Only the energy mesh of the collision strengths was varied along the isoelectronic sequence to ensure accurate resolution of the resonances. The configurations included by Witthoeft et al. (2007b) are 2s2 2p5, 2s2p6, 2s2 2p43l, 2s2p53l, and 2s2 2p44l' with l=s,p,d and l'=s,p,d,f for a total of 195 fine-structure levels. Witthoeft et al. (2007b) provide a complete dataset of energy levels, A-values and effective collision strengths for all levels and transitions for the adopted atomic model. The temperatures for which the effective collision strengths are calculated changes from ion to ion.

The exclusion of the 2s2p5 4l' configurations from the calculations decreases their accuracy for transitions to and among the 2s2p5 3l, and 2s2 2p4 4l' levels because certain resonances are left out. For elements with $Z \leq 12$, the accuracies are sufficiently degraded that we only include the astrophysically most abundant ions with $Z \geq 14$. Ions with $Z \leq 14$ will be included in the next release of CHIANTI.

The n=3,4 levels included by Witthoeft et al. (2007b) allow predictions of large numbers of $n=3 \to 2$ transitions in the X-ray and EUV wavelength ranges as well as UV transitions among the n=3 and n=4 levels. These transitions generate spectral lines previously neglected by spectral codes that have been observed from laboratory, solar and astrophysical plasmas (i.e. Acton et al. 1985; Curdt et al. 2004) and that have diagnostic applications to the measurement of plasma temperature, emission measure and element abundances.

12.1 Na III

In previous versions of CHIANTI the A-values for Na III were obtained by interpolation from neighboring ions on the isoelectronic sequence. These have now been replaced by the values of Froese Fischer & Tachiev (2004). The values for the allowed 2PJ-2S1/2 transition are very close to the earlier values, but the new 2P1/2-2P3/2 A-value is a factor 3.2 greater with the new data.

12.2 Si VI

Experimental energy levels for Si VI come from Edlén (1983) for the n=2 levels and Artru & Brillet (1977) for the n=3 levels. The effective collision strengths are given at temperatures in the $3.9 \leq \log T \leq 7.7$ range but, in order to obtain a satisfactory 9-point spline fit to these data, we have used only the subset of data ranging from $\log T = 4.5$ to $\log T = 7.1$. This range includes all temperatures at which the abundance of Si VI is significant in collision-dominated astrophysical plasmas.

12.3 S VIII

The experimental energy levels for the n=2 levels are taken from Edlén (1983), while those for the n=3 levels come from Fawcett & Hayes (1987) and Bengtsson et al. (1993). The effective collision strengths were published by Witthoeft et al. (2007b) for the $4.1\leq \log T \leq 8.1$ temperature range but we used them only in the $4.5 \leq \log T \leq 7.3$ range to improve the fit of the original data in the range where S VIII has significant fractional abundance.

12.4 Ar X

Experimental energies for the n=2 levels come from Edlén (1983), while those for the n=3 levels come from Lepson et al. (2003), Fawcett et al. (1971), Bengtsson et al. (1994) and Connerade et al. (1971). Effective collision strengths were calculated in the $4.3 \leq \log T \leq 8.3$ temperature range but we only used those in the $4.9 \leq \log T \leq 7.0$ range to provide a better fit at no loss in the accuracy of the data we used.

12.5 Ca XII

The experimental energies of Edlén (1983) were used for the n=2 levels, while the n=3 values come from Feldman et al. (1973). Effective collision strengths were calculated in the $4.5 \leq \log T \leq 8.5$ range but we only used those in the $4.9 \leq \log T \leq 7.9$ range to improve the fit.

12.6 Fe XVIII

The new model ion is largely based on the Iron Project R-matrix calculations of Witthoeft et al. (2006). Previous calculations largely underestimated the intensities of some spectral lines, most notably the 2s2 2p4 3s $\to$ 2s2 2p5 transitions. These are some of the strongest lines in the X-ray spectra of plasmas at temperatures $T \simeq 5$ MK and are important for temperature-diagnostics. The new data largely resolve long-standing discrepancies (factors of 2-3) between previous calculations and a wide range of laboratory and astrophysical observations. Del Zanna (2006) performed a benchmark study on Fe XVIII based on these new collision strengths and revised line identifications and observed energies. We adopt here the observed energies and A-values developed by Del Zanna (2006) together with the collision strengths of Witthoeft et al. (2006). The model ion includes the 2p5, 2s2p6, 2p43l, 2s 2p53l, 2p63l, 2p44l, 2s2p54l, and 2p64l configurations for a total of 279 fine-structure levels and 33 355 transitions. The atomic data for the n=5 levels is retained from CHIANTI 5.

12.7 Ni XX

The experimental energies of Edlén (1983) were adopted for the n=2levels while those of Gordon et al. (1980), Landi & Phillips (2005) and Gu et al. (2007) were used for the n=3 levels. Effective collision strengths were provided in the $4.9 \leq \log T \leq 8.9$ temperature range but we used them only in the $5.5 \leq \log T \leq 7.9$ to improve the accuracy of the 9-point spline fit.

13 New atomic data for the sodium isoelectronic sequence

13.1 Mg II

The CHIANTI model for Mg II has been unchanged since Version 1 (Dere et al. 1997). Collision strengths had been obtained privately from an unpublished calculation of Sampson that was an extension of calculations presented in Sampson et al. (1990). Comparisons with the more recent calculation of Sigut & Pradhan (1995) revealed large differences for the 3s 2S-3p 3P transition, e.g., the Sampson effective collision strength at 10 000 K is 37.8, while that from Sigut & Pradhan (1995) is 16.9. The earlier calculation of Mendoza (1983) gave a collision strength of 16.5 at the same temperature. On account of this problem, the Mg II model has been re-assessed and revised.

The new model consists of 13 levels belonging to the 2p63l(l=s,p,d), 2p64l (l=s,p,d,f) and 2p6 5s configurations. Effective collision strengths are from Sigut & Pradhan (1995) with LS collision strengths involving s states split according to their statistical weights. All collision strengths have been fit with 5 point splines. A-values and oscillator strengths are from an unpublished calculation of Froese Fischer[*]. This calculation gives A-values for all levels up to and including the 4f states. For the 5s state, the oscillator strengths of Sigut & Pradhan (1995) are used to derive A-values for the 3p-5s and 4p-5s transitions making use of observed energies. Observed energy levels are taken from Version 3.1.3 of the NIST Atomic Spectra Database.

The most significant feature of the new model is that the strong 3s-3p doublet at 2796 and 2803 Å is now predicted to be around a factor 2 lower than in the previous CHIANTI versions.

14 New atomic data for the magnesium isoelectronic sequence

14.1 Ar VII

The energy levels and the wavelengths for Ar VII have been updated and expanded using the experimental measurements of Phillips & Parker (1941). The energies of the triplet levels of Ar VII have been calculated relative to the ground level by using the wavelength of the 3s2 1S0-3s3p 3P1 transition reported in the SUMER solar disk atlas (877.92 Å, Curdt et al. 2001). Additional energies have been taken from Version 3 of the NIST database (Ralchenko et al. 2007). The new energies improve the Ar VII wavelengths at around 1000 Å.

14.2 Fe XV, Ni XVII

The experimental values of the radiative decay rates for the 3s2 1S0-3s3p 3P1 from Träbert et al. (1988) replaces the theoretical values available in CHIANTI 5.2. The new value for Fe XV is less than 5% different from the value in CHIANTI 5.2, but for Ni XVII the new value is 3.5 times larger.

15 New atomic data for the aluminum isoelectronic sequence

15.1 Fe XIV, Ni XVI

The A-values for the 3s23p 2P3/2-3s3p2 4P5/2 transitions of these two ions have been replaced with the experimental values measured by Träbert et al. (1988). The differences from the values in CHIANTI 5.2 are less than 5% for Fe XIV and a factor $\simeq$1.5 for Ni XVI.

16 New atomic data for the silicon isoelectronic sequence

16.1 Cl IV, Ar V, K VI

Collisional data for transitions amongst the five ground levels of these ions are available from Galavis et al. (1995). Effective collision strengths are tabulated at 11 temperatures over the range $3.0 \le \log T \le 5.0$ and these were fit with 9 point splines to within 0.59%. Radiative data for Cl IV and K VI were taken from Mendoza & Zeippen (1982) and for Ar V they are from Biemont & Bromage (1983). Observed energy values in each case are from Version 3.0.3 of the online NIST database.

17 New atomic data for the phosphorus isoelectronic sequence

17.1 Ni XIV

The atomic data and transition rates for Ni XIV have been taken from the calculations of Landi & Bhatia (2009c) who provide the only complete, self-consistent set of atomic data available in the literature.

The atomic model included the lowest 143 fine-structure levels, belonging to the 3s2 3p3, 3s3p4, 3s23p2 3d, 3s3p3 3d, 3p5 and 3s2 3p3d2 configurations. Experimental energies were taken from several sources: Feldman & Doschek (2007), Shirai et al. (2000), Sugar et al. (1991), Smitt et al. (1976), Borges et al. (2005) and Fawcett & Hayes (1972). Theoretical energy levels, radiative transition rates, oscillator strengths, and electron-ion collision strengths were calculated using the Flexible Atomic Code (Gu 2003a). A-values and oscillator strengths were calculated for all transitions among the 143 levels in the atomic model. In the calculations, all configurations belonging to the n=3 complex were included to provide a comprehensive and accurate target description.

Collision strengths were calculated using the Distorted Wave approximation at six values of the incident electron energy: 0.112, 8.07, 21.3, 43.4, 80.3 and 141.8 Ry above the threshold of each transition. These data lack the contribution of resonances, which is important at low temperatures and can affect line emissivities and intensity ratios; Landi & Bhatia (2009c) discuss the effects of considering only direct excitation.

This data set allows us to calculate, for the first time, line emissivities of several transitions observed in solar spectra that provide line intensity ratios that can be used for density diagnostics of active region plasmas.

18 New atomic data for the sulphur isoelectronic sequence

18.1 Ar III, Ca V

Ar III and Ca V are new additions to CHIANTI, and the models consist of the five levels of the ground 3s23p4 configuration. Effective collision strengths are from Galavis et al. (1995) who tabulate values over the temperature range $3.0\le \log~T\le 5.0$ at 0.2 dex intervals. Nine point spline fits were performed on the data, and these reproduce the original data to within 0.38%. The most recent A-value calculations for the forbidden transitions of Ca V are from Mendoza (1983) and Biémont & Hansen (1986) which agree to within 15%. We simply choose to use the Biémont & Hansen (1986) calculations for CHIANTI. Observed energy values are taken from Version 3.0.3 of the online NIST database.

18.2 Cr IX, Mn X

The atomic model adopted for Cr IX and Mn X includes the 48 fine-structure levels in the 3s2 3p4, 3s3p5, 3p6 and 3s2 3p3 3d configurations. Experimental energy levels have been taken from Smitt et al. (1976) and Shirai et al. (2000) but they are available only for the lowest two configurations and for a handful of 3s2 3p3 3d levels.

Theoretical energy levels, A-values and oscillator strengths, and electron collision strengths have been calculated by Landi & Young (2009) using the FAC code. A-values and oscillator strengths were provided for all possible transitions between the levels of the model, and collision strengths were calculated using the Distorted Wave approximation for six values of the incident electron energy above the threshold of each transition: 0.03, 4.05, 10.8, 21.9, 40.6, and 71.7 (Cr IX) and 0.035, 4.4, 11.7, 23.8, 44.0 and 77.7 (Mn X). Transitions from these ions provide a few lines visible in the solar transition region (e.g Young & Landi 2009) spectrum and are suitable for emission measure and electron density diagnostics.

18.3 Fe XI

Of the 38 levels belonging to the 3s23p33d configuration of Fe XI, 26 did not have experimental energies in the previous CHIANTI model. An additional experimental energy has been added for the (2D)3P0 level following the identification of the emission line at 189.00 Å in solar spectra by Keenan et al. (2005). The energy for the level has been derived by one of the authors (Young) by measuring the wavelengths of the lines at 189.00 and 189.13 Å in a solar active spectrum from the Hinode/EIS instrument. The lines represent decays of the 3s23p33d 3P0 and 3P1 levels to the 3P1 level in the ground configuration. By converting the measured wavelengths to energies and adding the difference to the known 3s23p33d 3P1 energy, an energy of 541 760 cm-1 was derived for the 3P0level.

For transitions from the remaining 25 levels in the 3s23p33d configuration, the wavelengths are derived from the theoretical energies of Bhatia & Doschek (1996). The energies for these levels have now been revised, and the wavelengths updated. For levels that belong to a multiplet that has one or more levels with experimental energies, the theoretical energy separations have been used to derive revised theoretical energies from the experimental energies. Otherwise, the theoretical energies have been revised by averaging the difference between the theoretical and experimental energies of levels with the same parent term. In both cases the updated theoretical energies should be more accurate than those previously used. The CHIANTI wavelengths for those lines emitted from the levels with no experimental energies have been updated. Note that updated energy levels are provided in the CHIANTI elvlc file in the fifth and sixth energy columns of the file.

19 New atomic data for the chlorine isoelectronic sequence

19.1 Cr VIII, Mn IX

Cr VIII and Mn IX are new entries in the CHIANTI database, and complete sets of data have been calculated for the first time by Landi & Young (2009). Their atomic models include the 31 fine-structure levels belonging to the 3s23p5, 3p6 and 3s23p43d configurations. The energy levels are taken from Smitt et al. (1976) and Shirai et al. (2000) for both ions. Theoretical energy levels, A-values and oscillator strengths, and electron collision strengths were calculated by Landi & Young (2009) using FAC. A-values and oscillator strengths were provided for all possible transitions between the levels of the model, and collision strengths were calculated using the Distorted Wave approximation for six values of the incident electron energy above the threshold: 0.025, 3.2, 8.4, 17.2, 31.8, and 56.3 (Cr VIII) and 0.025, 3.5, 9.2, 18.7, 34.7 and 61.3 (Mn IX).

This dataset represents the first ever published in the literature and it allows the identification and diagnostic use of several lines that have been observed in the solar transition region (Young & Landi 2009).

20 New atomic data for the argon isoelectronic sequence

20.1 Cr VII, Mn VIII

The atomic model for both these ions includes the lowest 13 fine-structure levels belonging to the 3s23p6 and 3s23p53d configurations. The Cr VII experimental energy levels are taken from Ekberg (1976) while those for Mn VIII come from Smitt & Svensson (1983).

Landi & Young (2009) used the FAC code to calculate theoretical energy levels, A-values, oscillator strengths, and electron collision strengths for all transitions in the atomic model; collision strengths were calculated using the Distorted Wave approximation for six values of the incident electron energy above the threshold 0.02, 3.2, 8.4, 17.2, 31.8, and 56.2 (Cr VII) and 0.02, 3.5, 9.2, 18.7, 34.7, and 61.3 (Mn VIII).

These calculations are the first available in the literature and allow the inclusion of the strong 3p6 1S0-3s23p5 3d 1P1 allowed line, observed in solar spectra (Young & Landi 2009) in the determination of the plasma emission measure as a function of temperature.

20.2 Fe IX

Young (2009) has identified four new Fe IX transitions from spectra from the Hinode/EIS instrument. These yield four new observed energy levels for Fe IX which have been added to the CHIANTI energy level file, and the wavelengths in the CHIANTI radiative data file have been updated. Three of the levels belong to the 3s23p43d2 configuration which previously had no experimental energy levels. We have thus used the average difference between the theoretical and observed energies for these newly-identified levels to scale all of the remaining 3s23p43d2 levels. This should lead to more accurate wavelengths for these lines in CHIANTI.

20.3 Ni XI

Ni XI lines have been observed in the past both in solar and stellar spectra, and yet atomic data for this ion have been calculated only recently. In CHIANTI 6 we have included the calculations of Aggarwal & Keenan (2007,2008), that allow the prediction of line intensities for the lowest 17 fine-structure levels, belonging to the 3s23p6, 3s23p5 3d and 3s3p6 3d configurations. They used the GRASP code (Dyall et al. 1989; Grant et al. 1980) to calculate energy levels, A-values and oscillator strengths for a large number of configurations, and the fully relativistic DARC code (Norrington & Grant 2009) to calculate collision strengths including resonant excitation.

We retained only the 17 lowest levels among those made available by the authors (Norrington & Grant 2009) as these allow the prediction of the emission of the lines observed from astrophysical sources. The authors provide effective collision strengths at temperatures in the $5.0 \leq \log T \leq 7.0$ temperature range.

21 New atomic data for the potassium isoelectronic sequence

21.1 Fe VIII

New Fe VIII line identifications have been made by Young & Landi (2009) based on comparisons of the CHIANTI atomic model of Fe VIII and spectra from the Hinode/EIS instrument. Five new experimental energies are available for the 3p53d2(3F) 4D and 3p53d2(1G) 2G multiplets and these have been added to the CHIANTI energy level file. The CHIANTI wavelength file has also been updated using these new energies. The emission lines are found between 206 and 258 Å.

22 Element abundances

In the CHIANTI software a number of the routines require the input of element abundances to derive, e.g., synthetic spectra and contribution functions. Several sets of abundances are provided, including the solar coronal abundances of Feldman et al. (1992), the ``hybrid'' solar abundances of Fludra & Schmelz (1999), and the cosmic abundances of Allen (1973). Solar photosphere abundances are used as the default abundance set, and in the previous version of CHIANTI they were taken from Grevesse & Sauval (1998). Since this work, the photospheric abundances have been the subject of intense debate following the revision of the carbon and oxygen abundances by Asplund and co-workers (Asplund et al. 2005,2004). These elements now have a lower abundance than in the tabulation of Grevesse & Sauval (1998), as much as 46% lower in the case of oxygen, with the changes largely resulting from the application of 3D model atmospheres to the interpretation of photospheric absorption lines instead of 1D models. Since solar photospheric abundances are a vital reference point for many fields in astronomy the new abundances have caused a re-assessment of many previous works. The most dramatic has been in the study of the solar interior, where models had previously been in excellent agreement with the precise helioseismic measurements of parameters such as the sound speed profile. Oxygen is the dominant contributor to opacity in the region just below the convection zone, and the revised abundance significantly affected the solar structure in this region, breaking the excellent agreement with measurements.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig5.eps} \end{figure} Figure 5:

Radiative loss rate for coronal abundances ( upper curve) and photospheric abundances ( lower curve).
Open with DEXTER

Table 1:   Radiative loss rates as a function of temperature.

The crucial role of oxygen in the solar interior models has led to a number of different measurements and re-analyses of oxygen lines and photospheric models (e.g., Meléndez & Asplund 2008; Caffau et al. 2008; Centeno & Socas-Navarro 2008, and references therein) leading to oxygen abundances ranging between the value given in Grevesse & Sauval (1998) and that given in Grevesse et al. (2007). This makes it difficult for a project such as CHIANTI which seeks to provide a single set of reference abundances for users. Our solution is to retain the original Grevesse & Sauval (1998) abundances as the default for the CHIANTI software, and to provide the Grevesse et al. (2007) abundances as an option that can be selected by the user.

Although the change in the oxygen abundance is the most significant in the Grevesse et al. (2007) tabulation, it is also to be noted that the neon and argon abundances have changed by a similar amount. This is on account of the fact that neither of these elements can be measured in the solar photosphere, and so they have usually been measured relative to oxygen by other means (spectroscopy of the solar upper atmosphere, solar energetic particle measurements).

CHIANTI users are encouraged to bear in mind the ongoing debate over solar photospheric abundances and to assess the impact on their analyses.

23 Radiative loss rates

The radiative loss rate plays an important role in the energy balance of coronal plasmas. The total radiative loss rate per unit emission measure ( $\int n_{\rm e} N_{\rm H} {\rm d}V$) has been calculated with the ionization equilibria discussed in Sect. 4. The loss rate includes the processes of bremsstrahlung, radiative recombination, line radiation and two-photon radiation. An electron density of 109 cm-3 was used and two sets of elemental abundances - the coronal abundances of Feldman et al. (1992) and the photospheric abundances of Grevesse & Sauval (1998). The values of the radiative loss rate are shown in Fig. 5 and in Table 1.

The most recent calculation of radiative loss rates are those of Colgan et al. (2008); Landi & Landini (1999). Landi & Landini (1999) used the Arcetri spectral code and the CHIANTI 2 database. Their Fig. 1 shows calculations at a density of 1010 cm-3 for the coronal abundances used here (Feldman et al. 1992) and the ionization equilibria of Arnaud & Rothenflug (1985) and Arnaud & Raymond (1992). A comparison shows that the calculations of Landi & Landini (1999) are very similar to our current values. The major differences are at $8 \times 10 ^6$ K where the current loss rate is a factor of 1.7 higher and at $1.6 \times 10 ^4$ K where the current loss rate is a factor of 1.7 less than the values of Landi & Landini (1999). The differences at the higher temperature is primarily due to the fact that CHIANTI 2 did not include transitions for the hydrogen-like and helium-like ions. The differences at the lower temperature are probably due to differences in the way the Arcetri code and CHIANTI calculate the radiative losses due to the continuum.

There are significant differences between the calculations of Colgan et al. (2008) and those of both Landi & Landini (1999) and our current values. Detailed comparisons with Colgan et al. (2008) are not possible as none of the atomic data used in the authors' radiative loss calculation were published. However we note that for most ions radiative losses are dominated by a small number of strong fine structure transitions in low-lying configurations, and so modeling these transitions with accurate atomic data is crucial to deriving accurate radiative loss estimates. Colgan et al. (2008) treated entire configurations as single levels in their calculations with no fine structure included, and no attempt was made by the authors to assess the accuracy of their approach for the dominant low-lying configurations. Within CHIANTI fine structure levels are used for every ion and the most accurate atomic data for transitions between these levels are chosen following assessments of the best available data in the literature. We are thus confident in the accuracy of the CHIANTI radiative losses for the ion models used in the database.

24 New IDL procedures

The parameters that are necessary to calculate ionization cross sections and rate coefficients, recombination rate coefficients and ionization equilibria are now included in the CHIANTI database. Accordingly, new Interactive Data Language (IDL) functions ioniz_cross, ioniz_rate, recomb_rate and make_ioneq_all are also provided.

ioniz_cross
returns the ionization cross section for a specified ion and electron energy in eV.
ioniz_rate
returns the ionization rate coefficient for a specified ion and temperature in K.
recomb_rate
returns the recombination rate coefficient for a specified ion and temperature in K
make_ioneq_all
creates a new ionization equilibrium file for all ions of all elements from H through Zn as a function of the specified temperature in K.

25 Summary

In this paper we have used the ionization rates of Dere (2007) and a revised set of recombination rates to provide an updated set of ionization equilibria for all elements from H through Zn. The resulting ionization equilibria are not radically different from those of Mazzotta et al. (1998). The most notable differences are for the ions Fe VIII and Fe IX. Atomic data for ions new to the CHIANTI database have been included. Atomic data for many ions in previously versions of CHIANTI have also been updated. Radiative loss rates for solar coronal and photospheric abundances have been calculated with the CHIANTI 6 database. New IDL procedures have been provided to allow the calculation of ionization and recombination processes.

Acknowledgements

This research has made use of NASA's Astrophysics Data System. Support for this work has been provided by the NASA SR&T and LWS programs. The work of E. Landi is supported by the NNG06EA14I, NNH06CD24C and other NASA grants. The work of H. Mason and G. Del Zanna is supported by the Science and Technology Facilities Council.

References

Footnotes

... Fischer[*]
Data available from http://www.vuse.vanderbilt.edu/~cff/mchf_collection.html

All Tables

Table 1:   Radiative loss rates as a function of temperature.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig1.eps} \end{figure} Figure 1:

Ionization equilibria for Fe I-IX. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig2.eps} \end{figure} Figure 2:

Ionization equilibria for Fe IX-XVII. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig3.eps} \end{figure} Figure 3:

Ionization equilibria for Fe XVII-XXIV. Full line - current calculations, dashed line = Mazzotta et al. (1998).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig4.eps} \end{figure} Figure 4:

Ionization equilibria for Fe XXIV-XXVII. Full line - current calculations, dashed line = Mazzotta et al. (1998), whose calculations only extend to 108 K.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1712fig5.eps} \end{figure} Figure 5:

Radiative loss rate for coronal abundances ( upper curve) and photospheric abundances ( lower curve).
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.