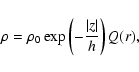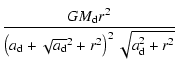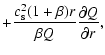Formation of gaseous arms in barred galaxies with dynamically important magnetic field: 3D MHD simulations

B. Kulesza-Żydzik; K. Kulpa-Dybeł; K. Otmianowska-Mazur; G. Kowal; M. Soida

doi:10.1051/0004-6361/200911635

Free Access

Issue		A&A Volume 498, Number 2, May I 2009


Page(s)		L21 - L24
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200911635
Published online		08 April 2009

LETTER TO THE EDITOR

Formation of gaseous arms in barred galaxies with dynamically important magnetic field: 3D MHD simulations

B. Kulesza-Zydzik¹ - K. Kulpa-Dybe $\l$ ¹ - K. Otmianowska-Mazur¹ - G. Kowal^1,2 - M. Soida¹

1 - Astronomical Observatory, Jagiellonian University, ul Orla 171, 30-244 Kraków, Poland
2 - Department of Astronomy, University of Wisconsin, 475 North Charter Street, Madison, WI 53706, USA

Received 9 January 2009 / Accepted 16 March 2009

Abstract
Aims. We present results of three-dimensional nonlinear MHD simulations of a large-scale magnetic field and its evolution inside a barred galaxy with the back reaction of the magnetic field on the gas. The model does not consider the dynamo process. To compare our modeling results with observations, we construct maps of the high-frequency (Faraday-rotation-free) polarized radio emission on the basis of simulated magnetic fields. The model accounts for the effects of projection and the limited resolution of real observations.
Methods. We performed 3D MHD numerical simulations of barred galaxies and polarization maps.
Results. The main result is that the modeled magnetic field configurations resemble maps of the polarized intensity observed in barred galaxies. They exhibit polarization vectors along the bar and arms forming coherent structures similar to the observed ones. In the paper, we also explain the previously unsolved issue of discrepancy between the velocity and magnetic field configurations in this type of galaxies. The dynamical influence of the bar causes gas to form spiral waves that travel outwards. Each gaseous spiral arm is accompanied by a magnetic counterpart, which separates and survives in the inter-arm region. Because of a strong compression, shear of non-axisymmetric bar flows and differential rotation, the total energy of modeled magnetic field grows constantly, while the azimuthal flux grows slightly until $0.05~\rm Gyr$ and then saturates.

Key words: magnetohydrodynamics (MHD) - galaxies: ISM - galaxies: magnetic fields

1 Introduction

A non-axisymmetric gravitational potential of the bar in barred galaxies influences strongly the dynamics of stars and the interstellar medium (ISM), including its magnetic field. The radio polarization observations of barred galaxies (e.g., Beck et al. 2005) show that the magnetic field topology is far more complicated than the gaseous component would indicate. No physical process responsible for such a complexity has been found so far. The radio maps of twenty barred galaxies were presented in Beck et al. (1999,2002,2005) and Harnett et al. (2004). The main observed features of two of the most spectacular galaxies NGC 1097 and NGC 1365 (Beck et al. 2005) can be summarized as follows:

the polarized emission (PI) forms ridges coinciding with dust lanes along leading edges of the bar in the central region of galaxy;
the pitch angles of B-vectors vary rapidly in the bar region when located upstream from dust lanes, producing a depolarization valley in the telescope beam;
the ridges of vanishing polarized intensity are observed in the shear shock areas;
in the outer disk, the polarization vectors form a spiral pattern with the maximum of emission along the spiral arms but in the inter-arm regions.

The issue of magnetic field evolution in barred galaxies was analyzed in several papers (see Moss et al. 1998,2001,2007,1999; Otmianowska-Mazur et al. 1997,2002). In Moss et al. (2007), three-dimensional (3D) calculations were applied to study the process of magnetic field dynamo and gas evolution under the influence of a bar potential. Moreover, they prepared the global synthetic polarization maps to compare them directly with the NGC 1365 radio observations. Even though all of the input parameters have been studied varying each inturn failed to reproduce a configuration of polarization vectors similar to that observed. The idea of magnetic arms between the gaseous counterparts was also studied by Rohde et al. (1998) using 3D MHD dynamo simulations. The authors applied a non-uniform distribution of magnetic diffusivity with its higher values in spiral arms and lower in the inter-arm region. This arrangement was related to the presence of higher turbulent motions in the spiral arms due to the presence of star-forming activity there. The assumption of higher magnetic diffusion in spiral arms, no matter how reasonable, has never been confirmed by observations. The authors found that it was possible to obtain magnetic arms in the inter-arm region in the case of resonance of the density pattern speed and a magnetic drift velocity, thus not for all galaxies. Our nonlinear model of magnetic field evolution in barred galaxies, which takes into account the back reaction of magnetic field on the gas, offers an opportunity to understand the relationship between the large-scale magnetic and gas velocity fields.

Our previous 3D simulations (Otmianowska-Mazur et al. 2002) concerning the large-scale magnetic field evolution in barred galaxies applied the evolution in velocity fields predicted by the N-body sticky-particle simulations at that time. It was impossible to introduce either the back-reaction of magnetic field on the gas component or the physical mechanism of gaseous spiral waves on the magnetic field structure. In the present paper, we study the nonlinear evolution of the gas and magnetic field in a barred galaxy. Our 3D calculations are carried out with the use of a MHD code written by Kowal (2008). We do not include the dynamo process in our MHD equations. The gravitational potential originating in stars in the form of the bar, halo, and bulge is modeled analytically. The magnetic field of galaxies is usually studied using polarized radio-continuum observations, yielding the magnetic field configuration integrated along the line of sight projected onto the sky plane and convolved to a certain radio telescope beam. Since our models contain full three-dimensional magnetic field structures, we analyze them by simulating the polarization maps and comparing these maps directly with observations.

2 Methods

2.1 The initial conditions and input parameters

We investigate the evolution of a barred galaxy solving the resistive MHD equations (Landau & Lifshitz 1998). We apply an isothermal equation of state $p_{\rm gas} = \rho c_{\rm s}^2$ , where $c_{\rm s}=5$ km s^-1 is a constant isothermal speed of sound. In our model, we assume that the initial gas density distribution is of the form:

$\begin{displaymath} \rho = \rho_0\exp\left(-\frac{\vert z\vert}{h}\right)Q(r), \end{displaymath}$

(1)

where $\rho_0=1$ H $~\rm cm^{-3}$ is the initial gas density of the neutral hydrogen in the galactic mid-plane, $h=0.3~\rm kpc$ is the gas scale-height, and function Q(r)is the truncation factor that reduces the density to small values at $r>R_{\rm max}$ , $R_{\rm max}=9$ kpc being the galaxy radius. We assume the azimuthal initial magnetic field configuration (B_z=0, B_r=0, $B_{\varphi}(z,r)$ ). Its distribution depends strictly on the gas density distribution via the condition $\beta=\frac{p_{\rm gas}}{p_{\rm mag}}$ , where $\beta=10.0$ at the beginning (determining the initial value of magnetic field to be $B_0=1.0~ \mu\rm G$ in the galactic mid-plane). We use the turbulent diffusion coefficient for the interstellar gas $\eta=3\times 10^{25}~~\rm cm^2~\rm s^{-1}$ (Lesch 1993).

The gravitational potential of stars is introduced analytically. Our galaxy is initially composed of three components: the large and massive halo, the central bulge and the rotating disk of stars. The circular speed of the gas is:

$\displaystyle V_{\rm rot}^2$	=	$\displaystyle \frac{G M_{\rm d} r^2}{\left(a_{\rm d}+\sqrt{a_{\rm d}}^2+r^2\right)^2 \sqrt{a_{\rm d}^2+r^2}}$
		$\displaystyle +GM_{\rm b}\left(r^2+a_{\rm b}^2\right)^{-3/ 2}+GM_{\rm h}\left(r^2+a_{\rm h}^2\right)^{-3 / 2}$
		$\displaystyle + \frac{c_{\rm s}^{2}(1+\beta) r}{\beta Q} \frac{\partial Q}{\partial r} ,$	(2)

where $M_{\rm d}=10^{10}~ M_\odot$ is the mass of the disk of stars, $a_{\rm d}=0.2$ kpc is its characteristic scale-length, and both $M_{\rm b}=10^{10}~ M_\odot$ , and $a_{\rm b}=2$ kpc refer to the bulge and $M_{\rm h}=10^{11}~ M_\odot$ , and $a_{\rm h}=20$ kpc refer to the halo. The bar component grows gradually in time (from $t_{\rm beg}=0.1~\rm Gyr$ to $t_{\rm end}=0.4~\rm Gyr$ ), changing the gravitational potential of the galaxy. The bar potential is described by the second-order Ferrers ellipsoid (Ferrers 1877) with semi-axes $a=4~\rm kpc$ , $b=2~\rm kpc$ , and $c=2~\rm kpc$ . To conserve the total mass of the galaxy, we reduce the bulge mass, such that $M_{\rm bar}(t)+M_{\rm b}(t)=M$ , where M is constant during the calculations. The bar angular velocity $\Omega_{\rm bar}$ is set to be $30~\rm km~\rm s^{-1}~\rm kpc^{-1}$ . This determines the value of the corotation radius to be $R_{\rm cor}=4.46~\rm kpc$ .

We use a higher-order shock-capturing Godunov-type scheme based on the essentially non-oscillatory (ENO) spacial reconstruction, a Harten-Lax-van-Leer (HLL) approximate Riemann-solver and Runge-Kutta (RK) time integration (e.g. Del Zanna et al. 2003) to solve isothermal non-ideal MHD equations. We evolve the induction equation using the constrained transport (CT) method (Evans & Hawley 1988) to ensure that magnetic field divergence vanishes everywhere at all times.

The computational domain extends from $-10~\rm kpc$ to $10~\rm kpc$ in the x and y directions, and from $-2.5~\rm kpc$ to $2.5~\rm kpc$ in the z direction with the grid size n_x=n_y=512, n_z=129.

2.2 Stokes parameters

To compare our results with observed properties of barred galaxies, we constructed synthetic radio-polarization maps (face on) at selected time steps. We calculated the maps by integrating Stokes parameters of the synchrotron emissivities I, Q, and U along the line of sight and finally convolving them with an assumed Gaussian beam. As a result, we generated polarization maps of the intensity and the angle of polarization B-vectors. We assumed that the distribution of relativistic electrons change radially and vertically as Gaussian functions. The truncation radius and scale height were respectively equal to 9 kpc and 1 kpc. The adopted intrinsic polarization degree of synchrotron emission is $70\%$ and the energy spectral index of the relativistic electrons $\gamma$ is 2.8.

3 Results

3.1 Velocity structures and magnetic field amplification

Figure 1 shows the gas density distribution (grey-scale plot) and velocity field (in a reference frame corotating with the bar) in the galactic mid-plane at time $t=0.64~\rm Gyr$ . The bar's major axis is inclined by $20\hbox{$^\circ$ }$ to the x-axis. The high density regions appearing from the innermost region of the galaxy indicate the leading edge of the bar. Density enhancements are visible at the ends of the bar and in the spiral arms generated in the galactic disk. The bar strongly disturbs the gas velocity field. Rapid variations in the velocity vector direction can be seen in the innermost region of the bar. The gas flows out of the center just before it passes the shock, and then turns back toward the center along the leading edge of the bar. Gas motions generate shocks that strongly influence the magnetic field structure. The bar is gradually introduced to the model from $t_{\rm beg}=0.1~\rm Gyr$ to $t_{\rm end}=0.4~\rm Gyr$ . During this time, as we can see in Fig. 2, the mean value of the $B_\phi$ flux in the galactic mid-plane increases slightly and then saturates. No significant enhancement in the $B_\phi$ flux can be seen. The total magnetic field energy (B²) increases as the galaxy evolves, because of an increase in the magnetic field complexity, which is in turn the result of a complex velocity field global structure. In our model, the most significant part of the growth in the magnetic field energy originates in the combined effects of shearing motions and compression present in the innermost bar region.

$\begin{figure} \par {\includegraphics[width=7.5cm]{1635fig1.ps} }\end{figure}$	Figure 1: Velocity field in the rest frame of the bar (vectors) and the gas density distribution (grey-scale, dark means high values of density) along the z=0 plane at time $t=0.64~\rm Gyr$ .
Open with DEXTER

3.2 The polarization maps

Figure 3 shows the distributions of polarization angle (vectors) and polarized intensity (contours) superimposed on the column density (grey-scale) at time t=0.64 Gyr. To illustrate the evolution of the magnetic field configuration in our model, we present results for three crucial time steps: 0.3 Gyr (Fig. 3 left), 0.46 Gyr (Fig. 3 in the middle), and 0.64 Gyr (Fig. 3 right). As mentioned above, in the beginning the modeled barred galaxy is in magneto-hydrostatic equilibrium. After almost one and a half rotation periods ( $t_1=0.30~\rm Gyr$ ), the density distribution diverges significantly from its initial form. In the inner part of the disk, where the bar is present, we find the highest gaseous density and magnetic field intensity regions.

The compression of both the gas and magnetic field is also visible in the outer part of the disk in the form of spiral arms. All of these gaseous structures are created by the dynamical influence of the non-axisymmetric gravitational potential of the bar. This potential also changes the initial azimuthal configuration of the magnetic field. First, the magnetic field follows the gas distribution, as can easily be seen for time step $t_1=0.30~\rm Gyr$ in Fig. 3 (left), where the magnetic field strength maxima are aligned with the gaseous ones. However, at later time-steps, the magnetic arms begin to detach themselves from the gaseous spirals and drift into the inter-arm regions preserving similar to the gaseous arms pitch angles (see $t_2=0.46~\rm Gyr$ Fig. 3, middle). At $t_3=0.64~\rm Gyr$ (Fig. 3, right), we can observe that our magnetic arms are distributed between density wave structures. The magnetic arms do not corotate with gaseous spiral structure, but they follow the general gas motion in the disk, which has a slightly lower angular velocity. The last map (Fig. 3, right) also shows the depolarization regions present in the bar. They are the effect of so-called beam depolarization, where magnetic field lines both along the bar and in the inter-arm regions converge with large angles within small, one-beam-size areas. Similar results were also obtained by Otmianowska-Mazur et al. (2002).

$\begin{figure} \par\includegraphics[width=7.5cm]{1635fig2.ps} \end{figure}$	Figure 2: Time dependence of the total magnetic field energy B² (solid line) and the mean $B_\phi$ flux in the galactic mid-plane (dashed). The third plot (dotted) presents the total magnetic field energy without taking into account the innermost bar region. All values are normalized to their initial values.
Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[width=5.2cm]{1635fig3.eps}\includegrap... ...5.2cm]{1635fig4.eps}\includegraphics[width=5.2cm]{1635fig5.eps} } \end{figure}$

Figure 3:

Face-on polarization maps at $\lambda=6.2~\rm cm$ at selected times steps ( $0.3~\rm Gyr$ left, $0.46~\rm Gyr$ middle, $0.64~\rm Gyr$ right): polarized intensity (contours), polarization angle (vectors) and column density (grey-scale). All maps have been smoothed down to the resolution $40\hbox {$^{\prime \prime }$ }$ . The black color represents the regions with the highest density.

Open with DEXTER

3.3 Magnetic pitch angles

To analyze and compare the pitch angles of the magnetic and gaseous arms, we project our results onto the polar coordinate space of azimuthal angle in the disk and $\ln(r)$ , where r is the galactocentric distance. In this case, the logarithmic spiral is represented by a straight line inclined by its pitch angle. The grey plot of the gas density (integrated along the line of sight) and superimposed contours of polarized intensity and B-vectors at a time $0.64~\rm Gyr$ are shown in Fig. 4. The values of the pitch angle of the magnetic arms are similar to those of the gaseous ones, i.e., they are of order of $5\hbox{$^\circ$ }$ . We also estimated the mean pitch angle (averaged over the azimuthal angle and radius in the plane of galaxy) to be $3\hbox{$^\circ$ }$ . Since we do not apply dynamo effects, the aforementioned pitch angle values are rather low, slightly smaller than usually observed in spiral galaxies (see Beck 1993). However, between the radii $r=4.1~\rm kpc$ and $r=4.5~\rm kpc$ , the mean pitch angles are much higher and reach $24\hbox{$^\circ$ }$ .

In the inner part of the disk (between the bar and spiral arms), the B-vectors of the polarized intensity change their pitch angles rapidly (Fig. 4, see $\phi$ around 100 and 300, and $\ln r$ between 2.2 and 3.2). This is caused by the strong flow of the gas between the end of the bar and the magnetic spiral arms, which produces valleys of depolarization within a telescope beam. This bears some resemblance to the observations of NGC 1356 (Beck et al. 2005) and NGC 3627 (Soida et al. 2001), even though we applied different rotation curves.

4 Discussion and conclusions

For the first time, we have simulated the evolution of large-scale galactic magnetic fields in barred galaxies using 3D MHD nonlinear numerical simulations without a dynamo process. The physical processes modeled and observed in our simulations can be summarized as follows. First, the dynamical influence of the bar causes the gas to form spiral waves. Later on, both the shear and compression in the arms cause the magnetic arms to be aligned with the gaseous structures. Since the pattern of the gaseous spiral arms travels faster than the disk itself, especially beyond the corotation radius, the gaseous structures move further out, while the magnetic arms remain in the interarm regions. This results in the magnetic and spiral arms having similar pitch angles.

We found that:

1.: Magnetic arms develop inside the gaseous ones, but gradually diverge away from the desnity waves. The magnetic arms are consequently shifted toward the interarm regions, in qualitative agreement with observations.
2.: The above effect is also responsible for prducing the depolarized valleys in the bar region, which also agrees with observations.
3.: The magnetic pitch angles of the synthetic magnetic arms are similar to the pitch angles measured in spiral gaseous structures, which also agrees with observations.

This process could also be responsibile for the shifting of the magnetic arms to the interarm regions in spiral galaxies.

$\begin{figure} \par {\includegraphics[width=8.8cm]{1635fig6.eps} } \end{figure}$	Figure 4: The distribution of polarized intensity and B-vector orientation superimposed on the gas density at $\lambda=6.2~\rm cm$ in the frame of azimuthal angle in the disk and the logarithm of distance from the center. The map has been convolved to the resolution $40\hbox {$^{\prime \prime }$ }$ .
Open with DEXTER

Acknowledgements

The authors express their gratitude to R. Beck and M. Urbanik for helpful comments. This work was supported by Polish Ministry of Science and Higher Education through grants: 92/N-ASTROSIM/2008/0 and 3033/B/H03/2008/35. Presented computations have been performed on the GALERA supercomputer in TASK Academic Computer Centre in Gdansk.

References

Beck, R., 1993, in The Cosmic Dynamo, ed. F. Krause, K.-H. Rädler, & G. Rüdiger (Dordrecht: Kluwer), IAU Symp., 157, 283 (In the text)
Beck, R., Ehle, M., Shoutenkov, V., et al. 1999, Nature, 397, 324 [NASA ADS] [CrossRef]
Beck, R., Shoutenkov, V., Ehle, M., et al. 2002, A&A, 391, 83 [NASA ADS] [CrossRef] [EDP Sciences]
Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Del Zanna, L., Bucciantini, N., & Londrillo, P. 2003, A&A, 400, 397 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [NASA ADS] [CrossRef] (In the text)
Ferrers, N. M. 1877, Quart. J. Pure Appl. Math., 14, 1 (In the text)
Harnett, J., Ehle, M., Fletcher, A., et al. 2004, A&A, 421, 571 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kowal, G. 2008, in prep.
Landau, L. D., & Lifshitz, E. M. 1984, Eloectrodynamics of Continuous Media (Oxford: Pergamon) (In the text)
Lesch, H. 1993, in The Cosmic Dynamo, ed. F. Krause, K.-H. Rädler, & G. Rüdiger (Dordrecht: Kluwer), IAU Symp., 157, 395 (In the text)
Moss, D., Korpi, M., Rautiainen, P., & Salo, H. 1998, A&A, 329, 895 [NASA ADS]
Moss, D., Rautiainen, P., & Salo, H. 1999, MNRAS, 303, 125 [NASA ADS] [CrossRef]
Moss, D., Shukurov, A., Sokoloff, D., Beck, R., & Fletcher, A. 2001, A&A, 380, 55 [NASA ADS] [CrossRef] [EDP Sciences]
Moss, D., Snodin, A., Englmaier, P., et al. 2007, A&A, 465, 157 [NASA ADS] [CrossRef] [EDP Sciences]
Otmianowska-Mazur, K., von Linden, S., Lesch, H., & Skupniewicz, G. 1997, A&A, 323, 56 [NASA ADS]
Otmianowska-Mazur, K., Elstner, D., Soida, M., & Urbanik, M. 2002, A&A, 384, 48 [NASA ADS] [CrossRef] [EDP Sciences]
Rohde, R., Elstner, D., & Rudiger, G. 1998, A&A, 329, 911 [NASA ADS] (In the text)
Soida, M., Urbanik, M., Beck, R., Wielebinski, R., & Balkowski, C. 2001, A&A, 378, 40 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

All Figures

$\begin{figure} \par {\includegraphics[width=7.5cm]{1635fig1.ps} }\end{figure}$	Figure 1: Velocity field in the rest frame of the bar (vectors) and the gas density distribution (grey-scale, dark means high values of density) along the z=0 plane at time $t=0.64~\rm Gyr$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm]{1635fig2.ps} \end{figure}$	Figure 2: Time dependence of the total magnetic field energy B² (solid line) and the mean $B_\phi$ flux in the galactic mid-plane (dashed). The third plot (dotted) presents the total magnetic field energy without taking into account the innermost bar region. All values are normalized to their initial values.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=5.2cm]{1635fig3.eps}\includegrap... ...5.2cm]{1635fig4.eps}\includegraphics[width=5.2cm]{1635fig5.eps} } \end{figure}$	Figure 3: Face-on polarization maps at $\lambda=6.2~\rm cm$ at selected times steps ( $0.3~\rm Gyr$ left, $0.46~\rm Gyr$ middle, $0.64~\rm Gyr$ right): polarized intensity (contours), polarization angle (vectors) and column density (grey-scale). All maps have been smoothed down to the resolution $40\hbox {$^{\prime \prime }$ }$ . The black color represents the regions with the highest density.
Open with DEXTER
In the text

$\begin{figure} \par {\includegraphics[width=8.8cm]{1635fig6.eps} } \end{figure}$	Figure 4: The distribution of polarized intensity and B-vector orientation superimposed on the gas density at $\lambda=6.2~\rm cm$ in the frame of azimuthal angle in the disk and the logarithm of distance from the center. The map has been convolved to the resolution $40\hbox {$^{\prime \prime }$ }$ .
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.