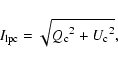| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 591 - 599 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200811210 | |
| Published online | 11 March 2009 | |
Full Stokes polarimetric observations with a single-dish radio telescope
E. Cenacchi1,![]() - A. Kraus1 - A. Orfei2 - K.-H. Mack2
- A. Kraus1 - A. Orfei2 - K.-H. Mack2
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - Istituto di Radioastronomia, INAF, via P. Gobetti 101, 40129 Bologna, Italy
Received 22 October 2008 / Accepted 22 January 2009
Abstract
Context. The study of the linear and circular polarization in AGN allows one to gain detailed information about the properties of the magnetic fields in these objects. However, the observation of circular polarization (CP) with single-dish radio telescopes, in particular, is usually difficult because of the expected weak signal. Measurements of CP are normally derived as (small) differences between two large numbers (left hand circular, LHC, and right hand circular, RHC), and an accurate calibration is absolutely necessary.
Aims. We attempt to improve the calibration accuracy by including the Stokes parameter V in the common single-dish polarimetric measurements, thus allowing a full Stokes study of the source under examination.
Methods. By completing a detailed study, up to 2nd order, of the Müller matrix elements in terms of cross-talk components, we are able to reach the accuracy necessary to study circular polarization.
Results. The new calibration method was applied to data taken at the 100-m Effelsberg radio telescope during regular test observations of extragalactic sources at 2.8, 3.6, 6, and 11 cm. The D-terms in phase and amplitude appear stable with time and the few known values of circular polarization were reproduced.
Conclusions. Whenever a classical receiver and a multiplying polarimeter are available, we demonstrate that the proposed calibration scheme allows one to include Stokes V in standard single-dish polarimetric observations as the difference between two native circular outputs.
Key words: polarization - radio continuum: galaxies - techniques: polarimetric - methods: observational
1 Introduction
The study of circular polarization (CP) and accurate multi-frequency observations of linear polarization (LP) provide probes of AGN magnetic field properties. Spectral information, CP and LP, can be used to constrain the low energy end of the relativistic particle distribution (Beckert 2003), derive the magnetic field order, strength, and geometry (Gabuzda 2006), and infer the particle content of the AGN jets (Wardle et al. 1998). To date, several studies of CP from AGN have been carried out with interferometers: ATCA at 5 GHz (Rayner et al. 2000), VLBA at 5.0 GHz and 15.0 GHz (Homan & Wardle 1999), and the VLA at 8.4 GHz (Bower et al. 2002). On the other hand, for instance the Michigan 26-metre radio telescope at 4.8 GHz and 8.0 GHz (Aller et al. 2003) has been used to perform single-dish CP observations.
Stokes V, which measures CP by means of the ratio V/I, has often been discarded from polarimetric observation strategies and calibrations, due to its typically low value, and there has been a strong preference for radio-astronomical receivers to provide circularly polarized output, since this configuration enables the efficient measurement of Stokes I, Q, and U.
When a single-dish telescope delivers two opposite circular outputs, it is relatively easy to retrieve information about Stokes I (sum of the outputs) as well as Q and U (cross-correlation of the outputs), but the estimate of Stokes V (difference of the outputs) can be severely contaminated by the receiver internal noise and gain fluctuations, and by small intrinsic asymmetries in the receiver channels structure (e.g., differences in cables lengths and/or internal gains, unwanted internal reflections). Some of these effects produce a small percentage of the contamination present between the signals from the left and the right channel (D-terms), in amplitude and phase.
To retrieve the information provided by Stokes V in the single-dish polarimetric observations, the most common receiving architecture has been examined. A full Stokes calibration scheme has been derived by identifying at each step the possible contamination that may be introduced by the devices used in the receiving chain, along with the dependence of the
![]() Müller matrix elements on the D-terms, to 2nd order. This result has been applied to several observations carried out at the Effelsberg 100-m telescope.
Müller matrix elements on the D-terms, to 2nd order. This result has been applied to several observations carried out at the Effelsberg 100-m telescope.
The application of an accurate
![]() Müller matrix to the observed raw data offers the possibility of performing multi-frequency full Stokes observations of the sources, providing a complete description of their polarization spectra.
Müller matrix to the observed raw data offers the possibility of performing multi-frequency full Stokes observations of the sources, providing a complete description of their polarization spectra.
2 Basics of polarimetry
2.1 Polarized waves
By focusing on the electric field only (the magnetic field can always be derived from
![]() ), a wave that is travelling along the z-axis with complex amplitude
), a wave that is travelling along the z-axis with complex amplitude
![]() can always be decomposed into two components, one along the x-axis and one along the y-axis, as follows:
can always be decomposed into two components, one along the x-axis and one along the y-axis, as follows:
where
Polarization is a phenomenon that can occur in transversal waves, and is described by the ``trace'' left by a wave passing through a plane perpendicular to the propagation direction. A clearly defined polarization state (linear, circular, elliptical, also called ``mode'') can be recognized in all cases where a constant relation between Ex and Ey and
![]() and
and
![]() exists and reflects the existence of ordered motion in the electric vector.
exists and reflects the existence of ordered motion in the electric vector.
Any polarized wave can be considered to consist of two linearly polarized waves, as shown in Eq. (1), but any pair of orthogonally polarized waves (e.g., left circular/right circular, left elliptical/right elliptical with axis at 90![]() ,
etc.) can be used as a basis for describing a polarization state. Typically the most convenient choices are the polarizations to which the telescope outputs respond.
,
etc.) can be used as a basis for describing a polarization state. Typically the most convenient choices are the polarizations to which the telescope outputs respond.
2.2 Jones vector and Müller matrix in the LR circular representation
The polarization properties of the radiation can be described using various vectors. The Jones vector describes the information related to amplitude and phase of the observed signal components, and thus is the preferred vector when describing mathematically the receiver internal devices. The Stokes vector reflects the relation between the signal components, and defines the overall polarization of the signal, and thus is the most suitable choice when describing the source physical characteristics.
The Jones and Stokes vectors carry the same information and are linked by a set of transformation equations. As a rule of thumb, the basis of the transformation should be chosen according to the polarization of the output signal of the telescope under examination. The following equations are related to the circular LR frame, which we adopted in this paper following Kraus (1986) and Heiles (2002).
The Jones vector, ![]() ,
and the Stokes vector,
,
and the Stokes vector, ![]() ,
are defined as follows
,
are defined as follows
where the asterisk stands for complex conjugate and
The Müller matrix relates the polarimetric properties of the source, i.e. the Stokes parameters, to the measurements from the polarimeter at the telescope. Hence, it describes the instrument polarization characteristics. An ideal instrument that measures Stokes parameters perfectly, would be characterized by a unitary Müller matrix
![]()
where
When handling linear polarization, the polarization angle is measured with respect to some instrumental zeropoint, usually related to a reference direction on the celestial sphere. During the source tracking, the reference system of an alt-azimuth mounted telescope rotates with respect to the source, that is, the parallactic angle of the sources (and consequently its polarization angle) rotates during the observation. Following Turlo et al. (1985), the time-dependent rotation component
B of the Müller matrix can be extracted and applied separately from the instrumental component of the Müller matrix, and
T is assumed to be constant with time. The overall Müller matrix can then be expressed as
M = TB, where
B is the rotation matrix of a linear rotating system (rotation of ![]() )
)
3 Application to a single-dish observation
McKinnon (1992) and Hamaker et al. (1996) published major works on how to manage polarimetry with a radio interferometer, and Johnston (2002) adapted their study to single-dish antennas equipped with linear dipoles. Nowadays, telescopes are commonly equipped with scalar feeds and hybrid or waveguide elements that supply circularly polarized outputs. In the following, we describe, step by step, how this instrumentation can affect, in terms of instrumental polarization, the measurement of the incoming radiation. A typical receiving chain is sketched in Fig. 1. In Table 1, we summarize our notation.
Table 1: Summary of the adopted notation.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{1210fig1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11210-08/Timg54.gif) |
Figure 1:
Receiver sketch. The block diagram shows the main parts of a typical radio-astronomical receiver: the scalar feed, sensitive to all the polarization states; the directional coupler, which couples the linearly polarized noise diode signal with the source radiation; the polarizer, which transforms the signal into the circularly polarized representations; the OMT, which splits the orthogonally polarized signals (polarizer and OMT are sometime realized as a single device); the low noise amplifiers (LNA); the down-conversion parts, represented here in a single block (labeled ``conversions''); the total power detectors (TP); the two multipliers, here shown as a single device, which take as input the LHC and RHC channels to give out Stokes Q, and the LHC and the 90 |
| Open with DEXTER | |
3.1 The antenna
The targets of single-dish observations are typically point-like with respect to the antenna beam and the observables are the integrated Stokes parameters and the full Stokes spectra of the source. The local CP and LP can be observed only by resolving the source with interferometric techniques, and are averaged, and often cancelled, when the source is not spatially resolved (beam depolarization).
An ideal rotationally symmetric telescope does not change the state of polarization of the incident radiation, although radiation with circular polarization changes its state every time it is reflected, due the changes in the direction of propagation (see McGuire & Chipman, 1994).
The first deviation from the ideal case is due to the blockage by the subreflector and its supporting structure. The radiation scattering causes a cross-polarization effect, both in amplitude and phase, which can be reduced significantly by adopting an appropriate structure design. Coupling the antenna with corrugated horns or dual mode horns with circularly symmetric patterns offers cross-polarization efficiencies closer to 1.
The parabolic shape is usually optimized at a specific elevation, typically around 45![]() .
When the antenna observes far from this value, its shape deviates from the original parabola (and the symmetry could be broken), unless it is equipped with some correction mechanism that compensates the gravitational deformations (active surfaces or homology). As an example of the deformation involved, Table 2 lists the deviation from the best-fit model of the parabola for a typical dish without compensating techniques.
.
When the antenna observes far from this value, its shape deviates from the original parabola (and the symmetry could be broken), unless it is equipped with some correction mechanism that compensates the gravitational deformations (active surfaces or homology). As an example of the deformation involved, Table 2 lists the deviation from the best-fit model of the parabola for a typical dish without compensating techniques.
Table 2: Deviation from the best fit parabolic surface.
3.2 The feed
The feed is used to obtain a Gaussian beam pattern and converts the electromagnetic field from propagating in free space to propagating in a waveguide. The most common type, coupled with Cassegrain and Gregorian antennas, is a conical corrugated horn (often called ``scalar feed''), because it provides a Gaussian beam profile and is characterized by negligible cross-polarization. Unlike linear dipoles or helical antennas, the scalar feed usually does not have a single defined polarization mode, since it can support linear, circular, and dual polarization, depending on its design and the electronic devices that are coupled with it. A typical scalar feed provides a single output: some additional devices are needed to divide it into the polarized components.
A lack of symmetry in the feed conical shape could produce some polarization aberrations. As an example of the deviation from the ideal feed shape, the typical mechanical accuracy is 0.02 mm to 0.03 mm. This corresponds, at 6 cm (nearly 600 mm of diameter, in secondary focus) to a non-circularity between 0.003% and 0.005%.
For off-axis feeds (multibeam or focal plane receivers that permanently hosts several different feeds), the rotational symmetry is broken. As a result, a certain amount of instrumental polarization enters and increases the polarized signal ![]() ,
and the antenna patterns of the two orthogonal polarization channels of the receiver differ (beam squint). The result is a constant pointing offset between the two opposite beams that depends on the distance of the feed from the optical axis (Fiebig et al. 1991).
,
and the antenna patterns of the two orthogonal polarization channels of the receiver differ (beam squint). The result is a constant pointing offset between the two opposite beams that depends on the distance of the feed from the optical axis (Fiebig et al. 1991).
3.3 The directional coupler for calibration
A radio-astronomical receiver is affected by a certain amount of gain instability, due to electronic noise added by each component, thus two measurements of an identical power source could yield slightly different voltage values. To stabilize this fluctuation, an internal noise of known temperature (Tcal) is added to the astronomical signal using a directional coupler. This calibration signal is linearly polarized and injected into the receiver at a known polarization angle. The Tcal is also used to convert the measured voltage into kelvin.
The value of Tcal is usually known to an accuracy of 3% to 5% over a wide bandwidth (e.g., 500 MHz for the 6 cm receiver at the Effelsberg telescope).
A typical value of the stability is 0.01 dB/K, which should be interpreted as a Tcal variation of 0.2% per 1 K variation in the receiver room temperature (which usually remains constant). Assuming a Tcal nominal value of 2 K and a thermal excursion inside the room of ![]() 5 K, a value of (
5 K, a value of (
![]() ) K is obtained.
) K is obtained.
3.4 The polarizer and the ortho-mode transducer (OMT)
The polarizer and the OMT divide the signal into two orthogonal circular polarized components. This process is imperfect and some fraction of one component can affect the other component. This effect is known as ``cross-talk'' and is quantified by the so called ``D-terms'' (values <1% are usually considered good).
The ensemble of feed, polarizer and OMT is completely analogous to a pair of circularly polarized feeds, although the instrumental effects on the polarization measurements differ.
At this point in the receiving chain, the following can be expected:
- Antenna: the non-perfect rotational symmetry can cause diattenuation and birefringent effects (that is, some instrumental polarization and some conversion between the components Q, U, V). For circular polarization, a change in sign must be expected at each reflection. These effects are usually cancelled by appropriate technical equipment (active surface, appropriate cabling to compensate the change in sign) and by a calibration that compensates possible residual components (e.g., antenna gain curve as a function of elevation);
- Feed: small mechanical imperfections cause additional diattenuation and birefringent effects; however at low frequencies this should be a negligible contribution, since, e.g., at 6 cm, the imperfections are typically of the order of 0.01%;
- Directional coupler: the phase of the transmitted signal is not constant over the bandwidth, typically causing an additional cross-polarization;
- Polarizer and OMT: a small part of the left circularly polarized signal could enter the right circularly polarized signal, and vice versa. This could heavily affect the V measurement, while the effect on I, Q and U should be negligible;
- LNA: a small fraction of the received radiation is reflected back to the previous components due to inevitable impedance mismatches, an effect called non-zero return loss. Once this spurious signal passes through the polarizer, it faces the directional coupler and is reflected back again. The two reflections added to a passage through the polarizer transform the circular polarization into its orthogonal polarization. This leads to a spurious exchange of radiation between the left and right-hand channels.
3.5 The down-conversion
After the OMT, the two circularly polarized signals are amplified and down-converted (that is, the signal frequency is lowered). The ``conversion box'' can be considered linear (some deviation appears for strong sources) but could introduce some polarization aberration: some small difference in the signal path length could alter the phase difference between the two components, and the amplitude could also be slightly modified. The signal, after the front-end according to Conway & Kronberg (1969) and McKinnon (1992), is then (see Table 1 for the adopted notation)
where
Table 3: Raw measurements of all Stokes parameters for unpolarized sources.
The receiver architecture usually offers narrow bandwidths (some tenths of MHz) at low frequencies (![]() 3 GHz) and wider bandwidths (some hundreds of MHz, few thousands in some new generation receivers) at higher frequency (>3 GHz). It can be shown that under these circumstances the bandwidth depolarization factor (see Gardner & Whiteoak 1966), which affects LP and is defined as the ratio of the observed degree of linear polarization to the emitted one, is negligible for typical extragalactic sources (a typical Rotation Measure of 50 rad/m2 infers a depolarization factor of amost 1 at both 2.5 GHz over a 100 MHz band, and at 5 GHz over a 500 MHz band).
3 GHz) and wider bandwidths (some hundreds of MHz, few thousands in some new generation receivers) at higher frequency (>3 GHz). It can be shown that under these circumstances the bandwidth depolarization factor (see Gardner & Whiteoak 1966), which affects LP and is defined as the ratio of the observed degree of linear polarization to the emitted one, is negligible for typical extragalactic sources (a typical Rotation Measure of 50 rad/m2 infers a depolarization factor of amost 1 at both 2.5 GHz over a 100 MHz band, and at 5 GHz over a 500 MHz band).
4 Correction of observations using the instrumental Müller matrix, T
After the down-conversion, the signals are sent to the devices that perform the measurements by implementing Eqs. (4). Typical devices are square law detectors (which obtain the flux densities from the left and right channels) and multiplying polarimeters (which supply Q and U, through a 90![]() shift of
shift of ![]() or
or ![]() ). In Appendix A, the calibration procedure is described (the complete calculations are presented in Cenacchi (2009, Ph.D. Thesis, in prep.)).
). In Appendix A, the calibration procedure is described (the complete calculations are presented in Cenacchi (2009, Ph.D. Thesis, in prep.)).
4.1 Effects on the measurements
The instrumental Müller matrix elements contain information about the amount of contamination among the four Stokes parameters, due to spurious, unwanted, conversions occurring inside the receiver. The conversion of Q, U, and V into I is typically negligible, the conversion of I and V into Q and U represents a small but still significant corruption, and the conversion of I, Q, and U into V can completely overwhelm the result of the measurement, leading to the impossibility of disentangling the instrumental contribution from the intrinsic V value. This is clearly apparent when studying completely unpolarized (thermal) sources.
As an example, Table 3 lists the Stokes values measured in November 2007 during a test observation with the Effelsberg 100-m telescope at 6 cm, of two planetary nebulae. Being thermal sources, they are expected to be unpolarized. The sources were observed with five-beam-wide on-the-fly cross-scans centred on the source. The Q and U values were inferred directly from the multiplying polarimeter. The V value was estimated to be the difference between the left and right channels, after those were corrected separately for pointing (to compensate for the beam squint) and gain curve. The cross-scan technique intrinsically removes possible differences between the internal channel noise (![]() 1 K for the Effelsberg telescope at 6 cm).
1 K for the Effelsberg telescope at 6 cm).
The measured Q, U and V values, from unpolarized sources, are understood to be due to contamination from Stokes I, that is, from a small net exchange in amplitude and phase between the left and right channels that, despite the multiplication and correction for pointing and gain, still produces a spurious significant LP and CP detection.
Appendix B contains the definition of each element of the Müller matrix.
4.2 How to apply the D-term calibration
In the following, the polarimetric calibration strategy, used to derive the Müller matrix and the errors of its elements, is described.
4.2.1 Derivation of the Müller matrix
The proposed calibration scheme is based completely on observations of astronomical calibration sources, each observation schedule including a fully unpolarized source (Q=U=V=0) and a highly linearly polarized source (for which one does not require V=0 K). The left and right channels must be corrected separately for pointing and gain curve. The raw V value can then be estimated to be the difference in the measured results. The right and left opacity correction can be applied to the channels, and the raw I can be derived as the sum of the right and left temperatures. The raw Q and U originate in the multiplying polarimeter.
By observing one or more unpolarized sources whose flux density is known, Eq. (6) is simplified as follows
where t11, t21, t31 and t41 are given in Eqs. (B.1). These four matrix elements involve the parameters
The polarization angle of the internal noise signal,
![]() is known (either from technical specifications or from previous measurements) and the remaining five quantities can be solved from six measurements of the calibrators (four Stokes parameters measurements of the unpolarized source and Stokes Q and U measurements of the linearly polarized calibrator).
is known (either from technical specifications or from previous measurements) and the remaining five quantities can be solved from six measurements of the calibrators (four Stokes parameters measurements of the unpolarized source and Stokes Q and U measurements of the linearly polarized calibrator).
Table 4: Observed Stokes parameters for NGC 7027 at 6 cm.
Table 5: Observed circular polarization, before and after applying the D-term calibration.
Once the D-terms, in amplitudes and phases, are determined, all terms of T can be calculated, since they depend on only these parameters. By applying this procedure, it is unnecessary to assume the V value of the linearly polarized calibrator.
4.2.2 Measurement of the errors
We define the uncertainties in
![]() ,
and
,
and ![]() of the calibrator(s) to be
of the calibrator(s) to be
![]() ,
and
,
and ![]() ,
respectively, which implies that the corresponding uncertainty in the matrix elements are
,
respectively, which implies that the corresponding uncertainty in the matrix elements are
Because of the non-linearity of the equations involved, it is impossible to propagate these errors by estimating the cross-terms, into the complete instrumental Müller matrix. It is however possible, by comparing the mathematical definitions of the matrix elements, to use the results given by Eqs. (10) to establish an upper limit to the remaining errors, e.g., it is clear from their definition that the errors in m11 and m14 must be similar. By applying similar qualitative considerations, the complete error matrix can be estimated to be
The intrinsic Stokes vector can then be obtained by inverting T, propagating step-by-step the errors
Finally, after
5 Observed results
5.1 Instrumental terms
During the year 2007, several observations were completed at the 100-m Effelsberg telescope to test the new sub-reflector. Part of this testing time was also used to check the full Stokes polarimetric calibration. A selected sample of 43 sources (39 extragalactic sources, 2 planetary nebulae, 2 planets) were observed at monthly intervals at 6 cm. Subsequently, some observations at 11 cm, 3.6 cm and 2.8 cm were also completed.
The Stokes parameters measurement listed in Table 4 for the planetary nebula NGC 7027 also yielded the following instrumental terms (averaged over time, and standard deviations)
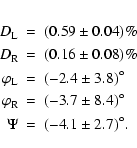
These values agree with the receiver technical specifications. The measured amplitudes also agree with the EVN measurements. The definition of the D-term phase in the interferometry processing is quite obscure, and it is therefore unclear whether the results differ or not.
Table 6: Repeated observations of circular polarization, in percentage, from a sample of sources, during 2007.
Table 7: Observed linear polarization, in percentage, from a sample of sources measured at 6 cm at Effelsberg during 2007.
Table 8: Observed polarization angle, in degrees, from a sample of sources measured at 6 cm at Effelsberg during 2007.
5.2 Circular polarization
We used our D-term calibration to search for CP in 19 AGNs with improved sensitivity over previous observations at Effelsberg.
Table 5 lists a comparison at 6 cm between the raw circular polarization and the values obtained after the calibration, using NGC 7027 as an unpolarized calibrator and 3C 286 as a strongly polarized calibrator. The data were observed in November 2007.
After the D-term calibration, the second planetary nebula, NGC 6572, appears circularly unpolarized as expected. Significant amounts of CP were detected in the two known CP sources 0743-006 and 1519-273 at levels consistent with published levels (0743-006:
![]() %, Aller et al. (2003) and
%, Aller et al. (2003) and
![]() %, Homan et al. (2001), both adopting the circular RL frame and for 1519-273:
%, Homan et al. (2001), both adopting the circular RL frame and for 1519-273:
![]() % (Aller et al. 2003)). In the Effelsberg measurement of 1519-273, the source appeared unpolarized from the raw values, but the D-term calibration revealed a level of CP in good agreement with the values reported in the literature. The Effelsberg measurement of the weakly circularly polarized source 3C 279 also shows a level of CP close to that published (
% (Aller et al. 2003)). In the Effelsberg measurement of 1519-273, the source appeared unpolarized from the raw values, but the D-term calibration revealed a level of CP in good agreement with the values reported in the literature. The Effelsberg measurement of the weakly circularly polarized source 3C 279 also shows a level of CP close to that published (
![]() %, Aller et al. 2003).
%, Aller et al. 2003).
Time variability in CP and changes of sign are common (Aller et al. 2003), and 1519-273 is the most stable CP source identified so far. Table 6 shows a list of CP values derived in 2007. Our detections also confirm the stability of the CP level of 1519-273.
5.3 Linear polarization
The proposed calibration scheme maintains the same reliability in the calibration of linear polarization as that reported by Turlo et al. (1985) based on a
![]() Müller matrix. Our method also measures Stokes V, the D-terms, and the complete set of errors.
Müller matrix. Our method also measures Stokes V, the D-terms, and the complete set of errors.
The traditional polarization calibration assumes that a Müller matrix is unaffected by errors, whereas the scheme that we propose also includes error propagation during the matrix inversion and its application; the error estimates are then intrinsically higher than those obtained with the standard procedure. Tables 7 and 8 compare the standard and new calibration schemes, when measuring linear polarization.
The linear polarization values obtained are consistent with those obtained with the standard method.
6 Conclusions
We have proposed a calibration procedure based on a 4The mathematical interpretation of the Müller matrix elements offers the possibility of deriving the instrumental polarimetric characteristics of the telescope (D-terms, in amplitude and phase) directly from the observation, allowing direct comparison with the technical specifications defined by the engineers.
The proposed procedure is valid for all single-dish telescopes equipped with a receiving architecture consisting of a standard receiver, two total power detectors for the two circularly polarized channels, and a multiplying polarimeter (one of the most common solutions available nowadays), and can be applied at any observed frequency.
Acknowledgements
This research was supported by the EU Framework 6 Marie Curie Early Stage Training programme under contract number MEST-CT-2005-19669 ``ESTRELA''. This work is based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. Effelsberg D-terms, coming from EVN measurements at 6 cm, were kindly given us by S. Bernhart. Thanks to A. Roy for the careful review, the detailed suggestions and the language corrections. Thanks to J. P. Hamaker, who refereed the paper, for the interesting comments. Finally, it must be mentioned that this paper has been written under the constant and quiet supervision of someone extremely young.
Appendix A: The backend and derivation of the measured Stokes parameters
In the following, the average symbol
![]() is omitted, and the subscript s represents the source and subscript c the calibration-noise diode.
is omitted, and the subscript s represents the source and subscript c the calibration-noise diode.
A.1 Total power detectors
In order to measure the total power in the right and left polarizations, measurements of
![]() and
and
![]() are performed. According to Eq. (8), by introducing the square law detector gain (the scalar quantity g) and recalling that
are performed. According to Eq. (8), by introducing the square law detector gain (the scalar quantity g) and recalling that
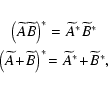
one obtains
Equation (A.1) can be expressed in terms of either the Stokes parameters or source linearly polarized flux
The Tcal is usually fully linearly polarized and characterized by Vc=0 K. This simplifies the corresponding calculations. By comparing the measured signal with that of the noise diode, the receiver gain fluctuations are removed. In addition, the Tcal calibration procedure calibrates the source strength measurements in terms of antenna temperatures, in kelvin. Discarding the terms of order
where
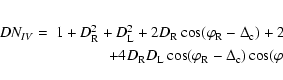
These two equations illustrate how the measured
A.2 Multiplying polarimeter
In order to measure the linear polarization components, ![]() and
and ![]() ,
the measurements
,
the measurements
![]() and
and
![]() are performed using a multiplying polarimeter. The multiplier outputs in the polarimeter are related to the incoming electric fields by
are performed using a multiplying polarimeter. The multiplier outputs in the polarimeter are related to the incoming electric fields by
where
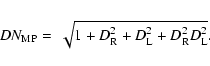
Equations (A.4) can be expressed in terms of Stokes parameters or in terms of linearly polarized flux density. By assuming that gQ = gU and
where
The Tcal is applied in an analogous way to Eqs. (A.2). The ratio of the
![]() value to the corresponding measured voltage infers the conversion factor K/V that should be applied to the on-source Q and U measurements
value to the corresponding measured voltage infers the conversion factor K/V that should be applied to the on-source Q and U measurements
Discarding the terms of order
where
![\begin{eqnarray*}DN_{\rm QU} = \left[1 + D_{\rm L}^2 + D_{\rm R}^2 + 2 D_{\rm L}...
...os \left( \Delta - \varphi_{\rm R} \right)\right]^{\frac{1}{2}}.
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa11210-08/img146.gif)
The channels Q and U could also be calibrated separately. In this case, in Eqs. (A.7) two different denominators, one for each channel, would be present.
Equations (A.3) and (A.7) infer all 16 elements of the Müller matrix in terms of D-terms, which are required to relate the measured to the true Stokes parameters.
Appendix B: Definitions of the matrix elements
From Eqs. (A.3), (A.7) and recalling the definition given in Eq. (5), the coefficients of the instrumental Müller matrix
T can be summarized as follows:
![]() Propagation of
Propagation of ![]() into
into ![]()
![]() Propagation of
Propagation of ![]() into
into ![]()
| t12 | = | ||
| (B.1b) |
![]() Propagation of
Propagation of ![]() into
into ![]()
| (B.1c) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{14}\!=\!\frac{1}{DN_{IV}}\left[D_{\rm R}^2 \!- \!D_{\rm ...
..._{\rm R} \cos (\varphi _{\rm R}\! - \!\Delta _{\rm c} )\right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img152.gif) |
(B.1d) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{21}=\frac{1}{DN_{\rm QU}}\left[D_{\rm L} \cos \left(\Psi...
... D_{\rm R} \cos \left(\Psi - \varphi _{\rm R} \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img153.gif) |
(B.1e) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{22}=\frac{1}{DN_{\rm QU}}\left[\cos \Psi + D_{\rm R} D_{\rm L} \cos \left(\Psi + \Phi \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img154.gif) |
(B.1f) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{23}=\frac{1}{DN_{\rm QU}}\left[\sin \Psi - D_{\rm R} D_{\rm L} \sin \left(\Psi + \Phi \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img155.gif) |
(B.1g) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{24}=\frac{1}{DN_{\rm QU}}\left[D_{\rm R} \cos \left(\Psi...
...- D_{\rm L} \cos \left(\Psi + \varphi _{\rm L} \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img156.gif) |
(B.1h) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{31}=\frac{1}{DN_{\rm QU}}\left[-D_{\rm L} \sin \left(\Ps...
...- D_{\rm R} \sin \left(\Psi - \varphi _{\rm R} \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img157.gif) |
(B.1i) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{32}=\frac{1}{DN_{\rm QU}}\left[-\sin \Psi - D_{\rm R} D_{\rm L} \sin \left(\Psi + \Phi \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img158.gif) |
(B.1j) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{33}=\frac{1}{DN_{\rm QU}}\left[\cos \Psi - D_{\rm R} D_{\rm L} \cos \left(\Psi + \Phi \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img159.gif) |
(B.1k) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{34}=\frac{1}{DN_{\rm QU}}\left[-D_{\rm R} \sin \left(\Ps...
...+ D_{\rm L} \sin \left(\Psi + \varphi _{\rm L} \right) \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img160.gif) |
(B.1l) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{41}=\frac{1}{DN_{IV}}\left[D_{\rm R} \cos (\varphi _{\rm...
...- D_{\rm L} \cos (\varphi _{\rm L} + \Delta _{\rm c} )\right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img161.gif) |
(B.1m) |
![]() Propagation of
Propagation of ![]() into
into ![]()
| (B.1n) |
![]() Propagation of
Propagation of ![]() into
into ![]()
| (B.1o) |
![]() Propagation of
Propagation of ![]() into
into ![]()
![\begin{displaymath}%
t_{44}=\frac{1}{DN_{IV}}\left[1 + D_{\rm R} \cos (\varphi _...
...+ D_{\rm L} \cos (\varphi _{\rm L} + \Delta _{\rm c} )\right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img164.gif) |
(B.1p) |
References
- Aller, H. D., Aller, M. F., & Plotkin, R. M. 2003, Ap&SS, 288, 17 [NASA ADS] [CrossRef] (In the text)
- Beckert, T. 2003, Ap&SS, 288, 123 [NASA ADS] [CrossRef] (In the text)
- Bower, G. C., Falcke, H., & Mellon, R. R. 2002, ApJ, 578, L103 [NASA ADS] [CrossRef] (In the text)
- Conway, R. G., & Kronberg, P. P. 1969, MNRAS, 142, 11 [NASA ADS] (In the text)
- Fiebig, D., Wohlleben, R., Prata, A., & Rusch, W. V. T. 1991, IEEE Trans. on Antennas and Propagation, 39, 774 [NASA ADS] [CrossRef] (In the text)
- Gabuzda, D. 2006, in Proc. of the 8th European VLBI Network Symp. (In the text)
- Gardner, F. F., & Whiteoak, J. B. 1966, ARA&A, 4, 245 [NASA ADS] [CrossRef] (In the text)
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Heiles, C. 2002, in Single-Dish Radio Astronomy: Techniques and Applications, ed. S. Stanimirovic, D. Altschuler, P. Goldsmith, & C. Salter, ASP Conf. Ser., 278, 131 (In the text)
- Homan, D. C., & Wardle, J. F. C. 1999, AJ, 118, 1942 [NASA ADS] [CrossRef] (In the text)
- Homan, D. C., Attridge, J. M., & Wardle, J. F. C. 2001, ApJ, 556, 113 [NASA ADS] [CrossRef] (In the text)
- Johnston, S. 2002, Publ. Astron. Soc. Aust., 19, 277 [NASA ADS] [CrossRef] (In the text)
- Kraus, J. D. 1986, Radioastronomy (Powell, Ohio: Cygnus-Quasar Books) (In the text)
- McGuire, Jr., J. P., & Chipman, R. A. 1994, Appl. Opt., 33, 5080 [NASA ADS] [CrossRef] (In the text)
- McKinnon, M. M. 1992, A&A, 260, 533 [NASA ADS] (In the text)
- Rayner, D. P., Norris, R. P., & Sault, R. J. 2000, MNRAS, 319, 484 [NASA ADS] [CrossRef] (In the text)
- Turlo, Z., Forkert, T., Sieber, W., & Wilson, W. 1985, A&A, 142, 181 [NASA ADS] (In the text)
- Wardle, J. F. C., Homan, D. C., Ojha, R., & Roberts, D. H. 1998, Nature, 395, 457 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
![[*]](/icons/foot_motif.gif)
- E. C. is a member of the International Max Planck Research School for Radio and Infrared Astronomy.
All Tables
Table 1: Summary of the adopted notation.
Table 2: Deviation from the best fit parabolic surface.
Table 3: Raw measurements of all Stokes parameters for unpolarized sources.
Table 4: Observed Stokes parameters for NGC 7027 at 6 cm.
Table 5: Observed circular polarization, before and after applying the D-term calibration.
Table 6: Repeated observations of circular polarization, in percentage, from a sample of sources, during 2007.
Table 7: Observed linear polarization, in percentage, from a sample of sources measured at 6 cm at Effelsberg during 2007.
Table 8: Observed polarization angle, in degrees, from a sample of sources measured at 6 cm at Effelsberg during 2007.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm,clip]{1210fig1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11210-08/Timg54.gif) |
Figure 1:
Receiver sketch. The block diagram shows the main parts of a typical radio-astronomical receiver: the scalar feed, sensitive to all the polarization states; the directional coupler, which couples the linearly polarized noise diode signal with the source radiation; the polarizer, which transforms the signal into the circularly polarized representations; the OMT, which splits the orthogonally polarized signals (polarizer and OMT are sometime realized as a single device); the low noise amplifiers (LNA); the down-conversion parts, represented here in a single block (labeled ``conversions''); the total power detectors (TP); the two multipliers, here shown as a single device, which take as input the LHC and RHC channels to give out Stokes Q, and the LHC and the 90 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
\vec{J}=\left[ \begin{array}{c}
\widetilde E_{\rm L} \\
\w...
...E_{\rm R} {\rm e}^{-{\rm i}\delta_{\rm R}}
\end{array}\right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img15.gif)
![\begin{displaymath}
\vec{S}=\left[ \begin{array}{c}
I \\
Q \\
U \\
V
\end{array} \right]
\end{displaymath}](/articles/aa/full_html/2009/17/aa11210-08/img16.gif)
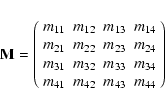
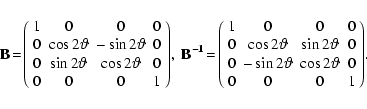
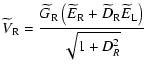
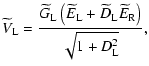
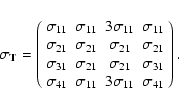
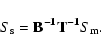
![$\displaystyle \widetilde V_{\rm R}\widetilde V_{\rm R}^* =\frac{g_2G_{\rm R}^2 ...
...rm R}^*+ \widetilde E_{\rm L}\widetilde E_{\rm R}^*\widetilde D_{\rm R} \right]$](/articles/aa/full_html/2009/17/aa11210-08/img101.gif)
![$\displaystyle \widetilde V_{\rm L}\widetilde V_{\rm L}^* =\frac{g_1G_{\rm L}^2 ...
...m L}^*+ \widetilde E_{\rm R}\widetilde E_{\rm L}^*\widetilde D_{\rm L} \right].$](/articles/aa/full_html/2009/17/aa11210-08/img102.gif)

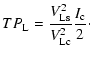
![$\displaystyle \widetilde V_{\rm R}\widetilde V_{\rm L}^* = \frac{\widetilde G_{...
...\rm R}\widetilde D_{\rm L}^* \widetilde E_{\rm L} \widetilde E_{\rm R}^*\right]$](/articles/aa/full_html/2009/17/aa11210-08/img126.gif)
![$\displaystyle \widetilde V_{\rm L}\widetilde V_{\rm R}^* = \frac{\widetilde G_{...
...m R}^* \widetilde D_{\rm L} \widetilde E_{\rm L}^* \widetilde E_{\rm R}\right],$](/articles/aa/full_html/2009/17/aa11210-08/img127.gif)