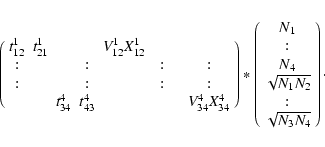| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 601 - 613 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200811083 | |
| Published online | 05 March 2009 | |
An integrated optics beam combiner for the second generation VLTI instruments
M. Benisty1 - J.-P. Berger1 - L. Jocou1 - P. Labeye2 - F. Malbet1 - K. Perraut1 - P. Kern1
1 - Laboratoire d'AstrOphysique de Grenoble (LAOG), 414 rue de la piscine, 38400 Saint-Martin d'Hères, France
2 -
CEA-LETI, Minatec, 17 rue des martyrs, 38054 Grenoble, France
Received 3 October 2008 / Accepted 28 January 2009
Abstract
Context. Recently, an increasing number of scientific publications making use of images obtained with near-infrared long-baseline interferometry have been produced. The technique has reached, at last, a technical maturity level that opens new avenues for numerous astrophysical topics requiring milli-arc-second model-independent imaging. The Very Large Telescope Interferometer (VLTI) will soon be equipped with instruments able to combine between four and six telescopes.
Aims. In the framework of the VLTI second generation instruments Gravity and VSI, we propose a new beam combining concept using integrated optics (IO) technologies with a novel ABCD-like fringe encoding scheme. Our goal is to demonstrate that IO-based combinations bring considerable advantages in terms of instrumental design and performance. We therefore aim at giving a full characterization of an IO beam combiner in order to establish its performance and check its compliance with the specifications of an imaging instrument.
Methods. For this purpose, prototype IO beam combiners have been manufactured and laboratory measurements were made in the H band with a dedicated testbed, simulating a four-telescope interferometer. We studied the beam combiners through the analysis of throughput, instrumental visibilities, phases and closure phases in wide band as well as with spectral dispersion. Study of the polarization properties was also carried out.
Results. We obtain competitive throughput (65%), high and stable instrumental contrasts (from 80% in wide band up to 100% ![]() 1% with spectral dispersion), stable but non-zero closure phases (e.g. 115
1% with spectral dispersion), stable but non-zero closure phases (e.g. 115![]()
![]() 2
2![]() )
which we attribute to internal optical path differences (OPD) that can be calibrated. We validate a new static and an achromatic phase shifting IO function close to the nominal 90
)
which we attribute to internal optical path differences (OPD) that can be calibrated. We validate a new static and an achromatic phase shifting IO function close to the nominal 90![]() value (e.g. 80
value (e.g. 80![]()
![]() 1
1![]() ). All these observables show limited chromaticity over the H band range.
). All these observables show limited chromaticity over the H band range.
Conclusions. Our results demonstrate that such ABCD-like beam combiners are particularly well suited for interferometric combination of multiple beams to achieve aperture synthesis imaging. This opens the way to extending this technique to all near infrared wavelengths and in particular, the K band.
Key words: instrumentation: interferometers
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{1083fig1.ps}\par\includegraphics[angle=180,width=10.9cm,clip]{1083fig2.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg7.gif) |
Figure 1:
Upper panel: theoretical design of the integrated optics 4-way beam combiner allowing pairwise combination and using phase-shifting devices to produce 4 outputs in quadrature. We refer to each output using the index m,l,k. mlk is the
|
| Open with DEXTER | |
1 Introduction
Optical long baseline interferometry offers a unique way to directly probe astrophysical environments with milli-arcsecond resolution. The study of stellar surfaces, evolved stars, young stars, our galactic center and the heart of active galactic nuclei require access to direct imaging. Until now, a large fraction of observations in the near infrared (NIR) were obtained with 2 to 3-telescope arrays, with little spatial frequency coverage (so-called uv coverage), restricting the astrophysical interpretation to a parametric one in most of the cases. However, discriminating between different successful scenarios of complex or rapidly-changing objects raises the need for images as model-independent as possible. This translates into the requirement to use as many telescopes as possible in order to fill the uv plane and allow an unambiguous image reconstruction. Until very recently, most of the images produced with optical long baseline interferometers had moderate complexity and therefore did not bring additional information with respect to parametric modelling. In our opinion, the complexity barrier where the reconstructed image adds meaningful scientific value to the astrophysical interpretation was recently passed by Monnier et al. (2007) and Zhao et al. (2008) using the MIRC instrument, an image plane 4-beam combiner using single mode fibers, at the CHARA interferometer (ten Brummelaar et al. 2005; Monnier et al. 2006b).
The Very Large Telescope Interferometer (VLTI, Haguenauer et al. 2008; Schöller 2007) will be equipped in 2012-2015 with two second-generation instruments: gravity (Eisenhauer et al. 2008) and VSI (Malbet et al. 2006,2008) which will be capable of exploiting the imaging capability of the array by combining four beams for the first and six for the second. The stringent requirements for these two instruments have triggered the interest in using integrated optics (IO) as a core technology for the beam combining function. The ability to integrate a singlemode circuit on a substrate, able to interfere all the beams offers numerous advantages both in terms of performance and ease of operation. Single-mode beam combiners provide natural modal filtering, which associated with proper photometric calibration has been shown to lead to accurate visibility measurements. The compactness of the chip allows the instrument footprint to be minimized and the thermal control to be optimized (further enhancing the calibration accuracy). No alignment is required, other than the injection in the input guides, even though the combination scheme is complex. Finally, this technology offers the flexibility to easily switch beam combiners to adapt to a particular situation (e.g. target, number of telescopes).
Since the initial proposition by Kern et al. (1996), LAOG and its industrial partner LETI/CEA have been developing the use of IO technology to interferometrically combine light beams in optical waveguides lying on a solid substrate of a few centimeter (Malbet et al. 1999; Berger et al. 2000; Kern et al. 1996). This instrumental research program has consisted in designing, fabricating and characterizing all the IO building blocks required to build an astronomical interferometric beam combiner. Several beam combining schemes have been implemented and tested. Some of them have led to successful on-sky demonstrations such as the VINCI/VLTI (2 telescopes) and IONIC3/IOTA (3 telescopes) instruments (Berger et al. 2003; LeBouquin et al. 2004; Kraus et al. 2005; Monnier et al. 2006a).
In the context of VLTI second-generation instrument studies, LeBouquin (2005) have studied the global efficiency of a great variety of IO beam combiners. This study has concluded that one of the most efficient ways to combine four beams (e.g. 4 UT or 4 AT) was to use a so-called ``pairwise static ABCD'' scheme (inspired by the visibility estimator of Shao & Staelin 1977). This IO circuit allows one to extract simultaneously four phase states of the coherent signal independently for each of the six baselines. We fabricated them (Labeye 2008), and in this paper, we present these new 4-beam combiners together with their complete laboratory characterization. They are probably the most sophisticated astronomical beam combiners built to date. The paper is organized as follow: in Sect. 2, the technology and the specific design of the beam combiners are described. In Sect. 3, we present the laboratory set up as well as the experimental procedure; the characterization results are given in Sect. 4 and discussed in Sect. 5.
2 The beam combiner: technology and design
Prior to fabrication, the IO circuit was designed and numerical computation simulating the propagation of an electromagnetic signal was carried out to determine the expected properties in terms of flux routing. Each IO function was checked and its throughput and flux distribution were optimized numerically. This step done, the simulation parameters were turned into technological parameters and a photolithographic mask was fabricated.
LETI uses a silica-on-silicon technology to fabricate IO circuits. This technological process requires several photolithographic steps to etch different layers. The beam combiners are made by depositing alternatively 3 doped silica layers on a silicon substrate. The second layer is etched to define channel waveguides and the other two layers constitute the optical cladding. For the first time, the etching technology allows us to completely isolate each waveguide from the others (Labeye et al. 2006). The produced beam combiners have been designed to operate in the atmospheric H band and more recently in the K band.
The so-called ``pairwise static ABCD'' beam combiner can be described as follows. Each beam combiner is designed to have 4 inputs and 24 outputs, allowing 6 interferometric pairwise
combinations, each one producing 4 phase-shifted outputs with a phase difference of 90![]() .
For each injected beam, the light propagates through waveguides and is split in three in a tricoupler (item (a) in Fig. 1) to enter the combining function (constituted of Y-junctions and couplers). The light is then divided in two in a Y junction that acts like a classical beamsplitter (item b), each beam later being combined in a coupler (item c) with a beam coming from another telescope. A coupler allows a controlled power transfer between one waveguide and another. As a consequence of energy conservation, each coupler has two outputs in phase opposition. In only one of these four arms, there is a phase-shifting device designed to change the phase of the propagating beam by 90
.
For each injected beam, the light propagates through waveguides and is split in three in a tricoupler (item (a) in Fig. 1) to enter the combining function (constituted of Y-junctions and couplers). The light is then divided in two in a Y junction that acts like a classical beamsplitter (item b), each beam later being combined in a coupler (item c) with a beam coming from another telescope. A coupler allows a controlled power transfer between one waveguide and another. As a consequence of energy conservation, each coupler has two outputs in phase opposition. In only one of these four arms, there is a phase-shifting device designed to change the phase of the propagating beam by 90![]() (Fig. 2). This leads to four output beams, two of them being in phase opposition with an additional phase-shift of 90
(Fig. 2). This leads to four output beams, two of them being in phase opposition with an additional phase-shift of 90![]() with respect to the other two (e.g.
with respect to the other two (e.g.
![]() and
and
![]() ;
;
![]() and
and
![]() ,
following Fig. 2). The phase-shifting function is based on the variation of the
effective index (i.e. index seen by the fundamental mode propagating into the waveguide) with the waveguide diameter (Labeye 2008). To create a phase shift, enlarging one of
the two waveguides creates a difference in the effective index and leads to an optical
path difference between two parallel waveguides of the same physical length. In order to achieve an achromatic phase shift, the wavelength dependence is compensated by concatenating a few
waveguide segments of different diameters separated by tapers (i.e. adiabatic functions) to avoid any loss due to discontinuities (Fig. 3). Since the photometry is extracted from a linear combination of the interferometric signal itself, the beam combiners have no dedicated photometric channels. This allows us to efficiently use all photons for the interferometric combinations. By design, each interferometric pair simultaneously gives access to four phase states in quadrature (ABCD-like but without temporal modulation). These 4 measurements allow the visibility amplitude and phase to be retrieved using the ABCD method described in Colavita (1999). In practice, the departure from ideal quadrature
forbids the use of simple algorithms and leads us to consider a generalized algorithm capable of handling a realistic description of the beam combiner properties.
,
following Fig. 2). The phase-shifting function is based on the variation of the
effective index (i.e. index seen by the fundamental mode propagating into the waveguide) with the waveguide diameter (Labeye 2008). To create a phase shift, enlarging one of
the two waveguides creates a difference in the effective index and leads to an optical
path difference between two parallel waveguides of the same physical length. In order to achieve an achromatic phase shift, the wavelength dependence is compensated by concatenating a few
waveguide segments of different diameters separated by tapers (i.e. adiabatic functions) to avoid any loss due to discontinuities (Fig. 3). Since the photometry is extracted from a linear combination of the interferometric signal itself, the beam combiners have no dedicated photometric channels. This allows us to efficiently use all photons for the interferometric combinations. By design, each interferometric pair simultaneously gives access to four phase states in quadrature (ABCD-like but without temporal modulation). These 4 measurements allow the visibility amplitude and phase to be retrieved using the ABCD method described in Colavita (1999). In practice, the departure from ideal quadrature
forbids the use of simple algorithms and leads us to consider a generalized algorithm capable of handling a realistic description of the beam combiner properties.
Throughout the paper, the outputs are identified with the index m,l,k, such as mlk, where m,l are the interfering beams, and k=[1..4], the output for this combination (similarly, the A-C-B-D measurements of Fig. 2). The same nomenclature applies to functions. In the case of Y-junctions, we denote them using the index m,l to specify the beam combination to which they are related, with m corresponding to the actual beam that enters the Y-junction. The index k designates its two outputs. For example, Y121 and Y122 are the two outputs of the Y-junction that splits beam 1 in signals that will interfere with beam 2. Similarly, Y211 and Y212 are the outputs of the Y-junction that splits beam 2 into signals that will combine with beam 1. We use the same notation for the couplers, e.g. C241 and C242 are the outputs of the coupler corresponding to the combination of beam 2 and 4.
| |
Figure 2:
Details of the beam combining function: for each interferometric pair (e.g. [12]), one arm is shifted by 90 |
| Open with DEXTER | |
With this notation, the intensity recorded at the outputs of the combination of beams m, l can be written:
where Nm is the number of photons in the m beam and tmlk the total transmission of the k output for the ml beam pair. Vmlk is the instrumental contrast,
| |
Figure 3: Principle of the phase-shifting function: a variation of the optical path is induced by a differential change of the waveguide effective index due to a change in their width. The concatenation of carefully optimized portions of waveguides with controlled effective index allows to flatten the wavelength response. |
| Open with DEXTER | |
3 Laboratory set up
In this section, we present the aims of the experiments, our testbed as well as our operating mode for the data acquisition and processing.
3.1 Goals of the characterization
With such beam combiners, all the information about the coherence of the object is included in the way the 4 pixels are related to each other, including the instrumental contribution. This contribution has therefore to be known, i.e. fully calibrated.
The relationship between the measured fluxes on the pixels and the visibility amplitudes and phases of the object can be expressed with a matrix representing the behavior of the instrument. With an unresolved internal source (i.e.
![]() and
and
![]() )
and without piston (i.e. centered at zero OPD), Eq. (1) becomes:
)
and without piston (i.e. centered at zero OPD), Eq. (1) becomes:
with
ml1 and ml2 correspond to two outputs of the same coupler (the same is valid for outputs ml3 and ml4). Therefore, ideally, because energy is conserved at the output of a coupler the following relations should apply:
The overall behavior of the beam combiner can be generalized in a matrix. When considering all combinations, the matrix should then be constituted of similar blocks of a [4 ![]() 3] matrix with zero elsewhere. In reality, crossing terms appear both as incoherent and
coherent contributions, and the actual outgoing intensities should be described using a general matrix of 24
3] matrix with zero elsewhere. In reality, crossing terms appear both as incoherent and
coherent contributions, and the actual outgoing intensities should be described using a general matrix of 24 ![]() 10 terms:
10 terms:
This matrix, called the V2PM (visibility to pixel matrix), in accordance to previous work on multiaxial interferometers (Tatulli & LeBouquin 2006), completely characterizes the instrumental behavior of the beam combiner e.g. the transmission, the visibility, the phase relations and the parasite flux. The ultimate goal of such a study would be to precisely estimate and calibrate it (Lacour et al. 2008). However, it is out of the scope of such a paper to present and discuss a full characterization of the global beam combiner matrix. We prefer to focus on characterizing the individual tricoupler functions, Y-junctions, couplers and phase-shifting devices described by Eq. (3) as well as the global routing of the incoherent flux (so-called crosstalk) inside the beam combiner. As it will be seen later, the crosstalk terms (related to the crossing terms in Eq. (4)) are sufficiently small, which justifies this approach.
To reach this goal, we set up a laboratory testbed and tested the IO beam combiners through photometric and interferometric measurements to calibrate this instrumental matrix. The following quantities, as well as their dependence on wavelength, have been measured:
- 1.
- the so called ``normalized kappa matrix''
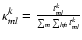 ;
;
- 2.
- instrumental contrast
Vkml;
- 3.
- instrumental phase shift between outputs,
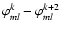 ,
with
,
with
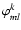 being the individual phase of the output signal mlk;
being the individual phase of the output signal mlk;
- 4.
- instrumental closure phase
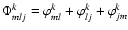 ;
;
3.2 Testbed description
We designed a dedicated interferometric testbed capable of simulating an 8 telescope interferometer (Jocou 2007). Figure 4 describes individual functions of the setup. The bench includes various items:
- (a)
- an object simulator that can reproduce a single star or a binary star with an adjustable flux ratio;
- (b)
- up to 8 optical devices simulating telescopes and coupling the light into single-mode polarization-maintaining fibers;
- (c)
- optical path compensation and modulation devices (delay lines of a few mm long);
- (d)
- an IO beam combiner;
- (e)
- a spectrometer;
- (f)
- a Wollaston prism to split the linear polarizations;
- (g)
- an infrared detector.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1083fig5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg33.gif) |
Figure 4: Schematic view of the laboratory testbed simulating the VLTI (see text for details). |
| Open with DEXTER | |
All laboratory tests were carried out in the H band with light sources of different coherence lengths. The object simulator can reproduce a single star as well as a binary star. In the latter case, its design is based on an optical setup that mimics a Michelson interferometer, but with a tilted mirror in one of its arm and with an unbalanced pathlength between the two arms. It produces two non-coherent luminous spots simulating a binary star, whose separation can be adjusted by tilting the mirrors. This setup will be used to characterize the dynamics of the testbed. The image is placed at the focal plane of a F/5 collimator to produce a
![]() diameter collimated beam. The wavefront is sampled by up to 8 telescopes that can be set to reproduce a replica of the VLTI entrance pupil. These telescopes are made up of an F/5 gradium lens feeding a polarization maintaining fiber and are placed in the collimated beam. Each telescope is mounted on an individual module with tip-tilt adjustments and a motorized translation stage (delay lines). Shutters are used to block the light of each telescope. The fibers, that have been equalized to limit differential effects (
diameter collimated beam. The wavefront is sampled by up to 8 telescopes that can be set to reproduce a replica of the VLTI entrance pupil. These telescopes are made up of an F/5 gradium lens feeding a polarization maintaining fiber and are placed in the collimated beam. Each telescope is mounted on an individual module with tip-tilt adjustments and a motorized translation stage (delay lines). Shutters are used to block the light of each telescope. The fibers, that have been equalized to limit differential effects (![]() = 1 mm), are gathered in a V-groove chip that feeds the IO beam combiner. A diffracting grating provides 15 spectral channels through the H band, while the Wollaston prism splits the linear polarization states to improve the instrumental transfer function. These two last elements, that can be placed and removed easily depending on the need, are located in an afocal mount with a magnification of 1. The detector is a near-infrared InGaAs PICNIC chip, with 40
= 1 mm), are gathered in a V-groove chip that feeds the IO beam combiner. A diffracting grating provides 15 spectral channels through the H band, while the Wollaston prism splits the linear polarization states to improve the instrumental transfer function. These two last elements, that can be placed and removed easily depending on the need, are located in an afocal mount with a magnification of 1. The detector is a near-infrared InGaAs PICNIC chip, with 40 ![]() m-large pixels. In the case of wide band measurements, each waveguide output is imaged on one single
pixel. Figure 5 is a detector image obtained when both the spectrograph and the Wollaston prism are used. It shows the 24 beam combiner outputs spectrally dispersed along the vertical direction. P1 and P2 correspond to the two linear polarization states.
m-large pixels. In the case of wide band measurements, each waveguide output is imaged on one single
pixel. Figure 5 is a detector image obtained when both the spectrograph and the Wollaston prism are used. It shows the 24 beam combiner outputs spectrally dispersed along the vertical direction. P1 and P2 correspond to the two linear polarization states.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1083fig6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg37.gif) |
Figure 5: A detector image of the 24 outputs, obtained when using the spectrograph and a Wollaston prism (splitting the two linear polarizations P1 and P2). The patterns are due to various non zero OPD for the different beam combinations. |
| Open with DEXTER | |
Table 1: Experimental protocol including photometric and interferometric measurements.
3.3 Data acquisition and processing
3.3.1 Protocol
The sequence of acquisitions performed to characterize the beam combiners consists of 6 steps that can be done with or without spectral dispersion (see Table 1). Step 1 is a background measurement with all shutters closed to prevent any light from propagating through the instrument. The 4 consecutive steps are measurements with only one beam at the time that give access to the flux splitting ratios in the couplers and tricouplers. Finally, Step 6 is the interferometric combination of all input beams. All measurements are repeated 1024 times.
The first 5 steps are used to validate the design in terms of photometry (light routing, transmission and splitting ratios, undesired flux, together with their wavelength dependence). Step 6 leads to the determination of the value, stability and chromaticity of instrumental contrasts and closure phases as well as of the phase relations between phase-shifted outputs, supposedly in quadrature. To get a complete and independent laboratory characterization of each output of the tested beam combiners, the interferometric measurements presented in this paper are obtained with OPD modulation and polarization splitting on a point-like source.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1083fig7.ps}\includegraphics[width=7.75cm,clip]{1083fig8.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg39.gif) |
Figure 6: Left: kappa matrix photometric coefficients obtained when the light is injected in one input at a time (F1..4) for Chip 1. The stars and squares show results obtained on two different days of experiments (called Day 1 and Day 3). Pixels from 1 to 24 are the 24 outputs of the beam combiner, identified as 121 to 344 in Table 2. Right: variation of the kappa matrix photometric coefficients with wavelength over the H band range, measured on Chip 2. The four panels correspond to the light injection in one input at the time (e.g. F1 for the injection in input 1). Inside each of them, among the 12 outputs illuminated, only 3 are plotted (in full, dashed, and dotted lines), corresponding to each combination cell. |
| Open with DEXTER | |
3.3.2 Data reduction
The data processing derives four quantities: the kappa matrix (i.e. the photometric contribution of each beam to the interferogram); the instrumental contrast; the phase-shift induced by the devices and the closure phases.
The kappa matrix is extracted from each individual set of data where only one input is illuminated (Table 1, Steps 2-5).
The instrumental contrast is computed using a classical visibility estimator on the interferograms to evaluate the coherence. This consists of estimating the envelope amplitude and calibrating for the photometric inbalance between the interfering beams. Since our experimental data are obtained with a SNR of ![]() 100, the use of such a simple estimator is appropriate.
100, the use of such a simple estimator is appropriate.
The phase-shift between two outputs is computed as the phase of the complex product of the Fourier spectra corresponding to the two signals. For two phase-shifted outputs related to the combination cell [ml] (written ml1 and ml3, i.e. outputs k=1
and k=3 respectively), it is calculated as follows:
![\begin{eqnarray*}\varphi_{ml}^{1}-\varphi_{ml}^{3} = \textrm{atan} \left(\frac{\...
...]}{\Re[F_{ml^{1}}(\nu_{ml,1})F_{ml^{3}}^{*}(\nu_{ml,3})]}\right)
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa11083-08/img40.gif)
where
The closure phase is measured using a triplet of telescopes i.e. from three pairwise combinations. It is calculated as the phase of the bispectrum, that is the complex product of the corresponding three Fourier spectra. Since each beam combination produces 4 phase-shifted output signals, there are 4 closure-phase signals per telescope triangle. For the telescope triangle [mln], the closure-phase derived from the output k can be written as:
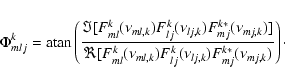
The closure phase is computed with the constraint that the frequencies respect the closure relation (e.g.
The methodology for data reduction with spectral dispersion is identical. From all illuminated pixels of the detector (in a case such as in Fig. 5), we measure interferograms from which we derive the chromatic behavior of instrumental quantities.
4 Results
In this section, we present the results of the laboratory experiments obtained on a point-like source, in terms of flux throughput and routing, instrumental contrasts, phase-shifts, and closure phases. The results correspond to two different IO chips manufactured in the same wafer (called Chip 1 and Chip 2 in all tables) in broad band, as well as with spectral dispersion for the second chip only.
For the latter experiment, we report in all tables the average values as well as the amplitude of the variation over the wavelength range (i.e.
![]() ,
for the instrumental quantity X). We refer to the latter as chromaticity in the text. Detailed studies that relate the performance to the IO design and simulations will be given in a following paper (Labeye et al. 2009, in prep.). All results are commented on in Sect. 5. The notations used in the tables and figures
are the same as defined in Sect. 2.
,
for the instrumental quantity X). We refer to the latter as chromaticity in the text. Detailed studies that relate the performance to the IO design and simulations will be given in a following paper (Labeye et al. 2009, in prep.). All results are commented on in Sect. 5. The notations used in the tables and figures
are the same as defined in Sect. 2.
4.1 Photometric measurements
Transmission:
when injecting 100 photons in one input, the transmission is the total number of photons detected at all outputs. The overall transmission budget includes the coupling efficiency from the telescope point spread function to the fiber, as well as the propagation losses inside the fibers and the IO chip transmission. The latter quantity is determined in broad band by using a fiber at each input and at each output, and the measured flux is normalized by a fiber-to-fiber transmission. The measurement gives about 65% in the H band for the transmission of the IO chip itself. The telescope-to-fiber coupling is ideallyTable 2: Kappa matrix photometric coefficients obtained when the light is injected only in the 4th input (F4). The first two lines correspond to the wide band experiments while the third gives the average value over wavelength, as well as the peak-to-valley amplitude over the wavelength range (chromaticity). Values are divided by 104. Bold numbers, preceded by a star, indicate the illuminated outputs.
Flux routing and individual IO functions:
for the following paragraphs, we use Step 1 to Step 5 (Table 1). Figure 6, left, gives the broad band photometric coefficients for the 24 beam combiner outputs obtained when shutters prevent three telescope beams from propagating through the chip. These coefficients are defined, for each pixel, by the ratio between the flux detected on one pixel and the sum of the flux on all outputs. As expected in such a case, 12 out of 24 pixels are illuminated. Two measurements taken on 2 different days are compared (stars and squared symbols) showing very small time variability. Table 2 gives an example of the averaged photometric coefficients for all 24 outputs, obtained when the light is injected in the 4th input.With the same experiments using spectral dispersion, one can derive their dependence on wavelength. Figure 6, right, gives their variation with wavelength over the spectral range. Table 2 also gives the chromaticity of photometric coefficients obtained when injecting in the 4th input.
To be more general, Table 3 gives measurements in all cases, i.e. when the light is injected in all 4 inputs, one at a time. We only provide the values corresponding to the outputs presenting the minimum and maximum chromaticity as well as the average chromaticity over the 12 signals. Because there is an important spread across the photometric coefficients values (see Table 2), the chromaticity is given with respect to the coefficient value obtained when averaging over the spectral band (i.e. divided by this value).
Table 3: Minimum, maximum and average of the photometric coefficients chromaticity among the 12 illuminated outputs from each injection.
Table 4: Tricoupler splitting ratio measured in wide band. The dispersion (rms) over 1024 measurements is 0.1%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{1083fig9.ps}\hspace*{2mm}
...
....ps}\hspace*{2mm}
\includegraphics[width=5.9cm,clip]{1083fig11.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg57.gif) |
Figure 7: Variation with wavelength of the tricoupler splitting ratio ( left) and of the Y-junctions ( middle, right). Middle: three Y-junction splitting ratios corresponding to the illumination in the first input (these Y-junctions are related to the [12], [13] and [14] combinations); Right: three Y-junctions splitting ratios obtained when injecting the light in the second input. For clarity, only one flux ratio coefficient (among 2 or 3) is plotted for each function. The error for each spectral channel is estimated from the dispersion over 1024 measurements and is smaller than the symbol sizes. The theoretical values of 33% for the tricoupler, and 50% for the Y-junctions, are given by the horizontal dashed line. Values for all functions are given in Tables 4 and 6. |
| Open with DEXTER | |
Table 5: Minimum, maximum and average chromaticity of tricoupler splitting ratio (among the three outputs of each tricoupler). T1 is the tricoupler corresponding to input 1.
From these coefficients, in both wide band and spectrally dispersed experiments, we determine the splitting ratio of the different optical functions (tricouplers, Y-junctions and couplers),
under the assumption that all functions are ideal (i.e. no photon loss;
![]() ,
with xi a splitting ratio coefficient). For the sake of clarity, for each Y-junction and coupler, only one value out of the two splitting ratio coefficients is given in the tables, since the second output is obviously its complementary to 100%.
,
with xi a splitting ratio coefficient). For the sake of clarity, for each Y-junction and coupler, only one value out of the two splitting ratio coefficients is given in the tables, since the second output is obviously its complementary to 100%.
Tricouplers:
Table 4 gives such values for the 4 tricoupler showing flux splitting ratios close to 33% for both chips, in wide band. The best flux separation is 33.7/33.4/32.8, for the three outputs, with a rms over 1024 measurements of 0.1%. These values are similar a few days later with a variation from 0.1% to 1.5%.
The results are comparable with the spectral dispersion. In this case, the closest splitting ratio from 33% is 32.9/31.4/35.6 ![]() 0.1%. Figure 7, left, presents the variation of the tricoupler splitting ratio with wavelength. Table 5 gives the minimum, maximum and average chromaticity of the tricoupler splitting ratio, among the 3 outputs of each of the four tricouplers of Chip 2.
0.1%. Figure 7, left, presents the variation of the tricoupler splitting ratio with wavelength. Table 5 gives the minimum, maximum and average chromaticity of the tricoupler splitting ratio, among the 3 outputs of each of the four tricouplers of Chip 2.
Table 6: Y-junction splitting ratio. The dispersion (rms) over 1024 measurements is 0.1%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
Y-junctions:
Table 6 gives the splitting ratio for the 12 Y-junctions. The values, measured in broad band, are close to 50%, with a 0.1%-dispersion over 1024 points. Variations are small from one day to another (2.9% maximum).With spectral dispersion, the splitting ratio are similar to the broad band measurements. Figure 7, middle and right, gives their wavelength-dependence. For clarity, only extreme behaviors are shown in the figure, with the smallest (middle plot) and greatest (right plot) variations over the H band. Out of the 12 Y-junctions, 10 show a maximum variation inferior to 9% over the spanned range of the H band, while 2 show a strong variation of about 26 and 28%. These two Y-junctions are the closest to the inputs (combination [23]). Over all the Y-junctions, the average chromaticity is 9.2%.
Table 7: Coupler splitting ratio. The dispersion (rms) over 1024 measurements is 0.2%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig12.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig13.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg59.gif) |
Figure 8: Variation of coupler splitting ratio with wavelength. Only one of the flux ratio coefficients is plotted, and extreme behaviors are given: left, when the light is injected in the first input; right, for an injection in the second input. The theoretical value of 50% is given by the horizontal dashed line. |
| Open with DEXTER | |
Couplers:
Table 7 gives the flux splitting ratio given by the 12 couplers, in broad band, showing asymmetric splitting, up to 61.5%/38.5%, similarly for the two beam combiners.With spectral dispersion, the obtained values are similar. The variation of the 12 coupler splitting ratio with wavelength is given in Fig. 8 (with only extreme behaviors). All couplers show low chromaticity, with an average maximum variation of about 5%, with minimum and maximum values of about 3 and 7%.
Finally, although, in theory, all functions are identical, we notice some slight variations from one another. In broad band, for Chip 1, the differences are up to 1.7%, 2.7% and 4%, for the tricouplers, Y-junctions and couplers, respectively, while for Chip 2, they are of 0.9%, 2.3%, and 2.6% for the same functions.
Table 8: Cross-talk flux (in %) determined when the light is injected in the 4 outputs successively. The two first lines report results obtained in broad band while the third line corresponds to the spectral dispersion case. Error bars are estimated from the dispersion (rms).
Cross-talk:
on the pixels where one should not detect any flux, the measured intensity gives the amount of undesired flux, i.e. cross-talk flux. It can be due to direct propagation into the substrate and to light leak at the X-junctions level, where waveguides are crossing. We estimate the cross-talk flux to be less than 1.2%Table 9: Instrumental contrasts (in %) obtained with wide band experiments (first two lines) and with spectral dispersion (third line) with a statistical error of 1%.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1083fig14.ps}\hspace*{2mm}
\includegraphics[width=6.6cm,clip]{1083fig15.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg60.gif) |
Figure 9: Left: an interferogram obtained with temporal OPD modulation with wide-band measurements. Right: the variation of instrumental contrasts with wavelength, for all four outputs of each beam pair. 100% contrasts are given by the horizontal dashed line. |
| Open with DEXTER | |
4.2 Interferometric measurements
Instrumental contrasts:
Fig. 9, left, shows an example of the interferograms obtained with Chip 1 in broad band. From these interferograms, we derive the instrumental contrasts after calibrating for the photometric inbalance between interfering beams. Table 9 gives the measured values, showing high contrast values. The minimum and maximum values are respectively of 95%
These results show a maximum variation of about 5% over a day timescale and 10% from one day to another. The measured contrasts on the four phase shifted outputs are only slightly different (on average 2%, up to 9%). The non-perfect linearity of our detector can lead to a bias of up to 5% in visibility. In the case of our experiments, this effect could not be reproduced and calibrated. Therefore, although the statistical errors can be very small (![]() 1%), an additional bias of 5% affects the contrast values.
1%), an additional bias of 5% affects the contrast values.
With spectral dispersion, the measured contrasts are very high (up to 100%) showing very small variations with wavelength (see Fig. 9, right). The maximum and minimum chromaticities, among all 24 outputs, are of 4.6% and 0.8% respectively, with an average of 2.3%.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig16.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig17.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg61.gif) |
Figure 10:
The phase-shifted interferograms recorded for the 4 outputs (full, dashed, dotted, dot-dashed lines) of the [34] beam pair are close to quadrature ( left). On
the contrary, the 4 outputs of the central combination [14] produce interferograms only slightly phase-shifted ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig18.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig19.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg62.gif) |
Figure 11:
Left: wavelength dependence of the phase-shifts for the outputs designed to be in quadrature, for all 6 pairwise combinations ([ml]). Error bars on each spectral point are of 1 |
| Open with DEXTER | |
Phase shifts:
Fig. 10 shows 4 phase-shifted interferograms in each panel, that correspond to the intensity of the 4 phase-shifted outputs for the interferometric couple [34]. These 4 outputs are in different phase states, as it can be seen, and in these specific examples, in the left panel, the phase-shift is close to the expected value of quadrature.
Table 10 gives the values of the phase-shifts obtained for the outputs designed to be in quadrature. For the first chip, on 5 of the 6 interferometric combinations, the phase shifts are close to the quadrature (from 78![]()
![]() 1
1![]() to 82
to 82![]()
![]() 1
1![]() ). For the sixth phase-shifting function, corresponding to the central [14] combination, the measurement gives about 26
). For the sixth phase-shifting function, corresponding to the central [14] combination, the measurement gives about 26![]()
![]() 1
1![]() .
The right panel of Fig. 10 corresponds to such a combination. The second chip gives different results, with phase shifts spanning a larger range of values (e.g. 62
.
The right panel of Fig. 10 corresponds to such a combination. The second chip gives different results, with phase shifts spanning a larger range of values (e.g. 62![]()
![]() 1
1![]() ;
88
;
88![]()
![]() 1
1![]() ). The function corresponding to the [14] combination still shows a much smaller value of about 33
). The function corresponding to the [14] combination still shows a much smaller value of about 33![]()
![]() 1.0
1.0![]() .
.
Over a timescale of half a day, measured phase shifts show variations of 1![]() at most, and from one day to another, a maximum variation of 3
at most, and from one day to another, a maximum variation of 3![]() .
.
With spectral dispersion, the obtained values for the phase shifts are similar. Figure 11 (left) and Table 10 show the wavelength dependence of the measured phase-shifts for the outputs expected to be in quadrature. The maximum chromaticity is of 13![]() (for the [23] combination, as for the Y-junctions) and the minimum is of 3.1
(for the [23] combination, as for the Y-junctions) and the minimum is of 3.1![]() .
Over all outputs, the average chromaticity is 5.6
.
Over all outputs, the average chromaticity is 5.6![]() .
.
Closure phases:
Table 11 gives a set of independent instrumental closure phases measured for the 4 phase shifted outputs of one telescope triangle, with spectral dispersion. The measured closure phases have non-zero values which means that the beam combiner functions themselves contribute to the phase budget. These terms can result from additional OPD originating in small length differences between waveguides or from the delay in reading the detector pixels. The phase relation between the various beam combiner outputs can be found again in the closure-phase values. In fact, the closure-phases differ by about 180Table 10:
Phase-shifts obtained with the wide band experiments (two first lines) with errors of 1.0![]() (the dispersion (rms) over half a day); The third line gives
the average values over the wavelength range.
(the dispersion (rms) over half a day); The third line gives
the average values over the wavelength range.
Figure 11 (right) and Table 11 give the variation of the instrumental closure phases with wavelength, in the case of one triangle of telescopes ([134]). The minimum variation over the wavelength range is of 18![]() while the maximum is of 30
while the maximum is of 30![]() .
.
Polarization:
the two linear polarization directions are perpendicular to each other following the symmetry axis of the chip itself (i.e. within the beam combiner plane (horizontal) and parallel to the light wavefront (vertical)). Such orientations are defined at the time of manufacturing the chip, and were confirmed by laboratory measurements.
In our study, disparities between measurements obtained on both linear polarization states were noticed. Contrasts and phase-shifts can be up to, respectively, 13% and 10![]() different, meaning that the two polarizations propagate differently. Also, for one polarization state, instrumental contrasts are higher than for the second one for all beam combiner outputs except for the ones related to the central phase shifting function ([14] combination). Similarly, phase shifts are closer to the quadrature for one polarization than the other for all outputs except the central ones (Table 12). Therefore, with respect to polarization, one phase shifting function has a different behavior than the 5 others.
different, meaning that the two polarizations propagate differently. Also, for one polarization state, instrumental contrasts are higher than for the second one for all beam combiner outputs except for the ones related to the central phase shifting function ([14] combination). Similarly, phase shifts are closer to the quadrature for one polarization than the other for all outputs except the central ones (Table 12). Therefore, with respect to polarization, one phase shifting function has a different behavior than the 5 others.
Table 11:
Closure-phase measurements for one independent triangle, for Chip 2
with spectral dispersion, as well as amplitude of the variation over the H band range. Statistical errors are of 2.5![]() .
.
In order to identify possible problems with instrumental polarization and to determine the best instrumental set-up to reduce the visibility loss due to birefringent fibers, a detailed study on a day timescale was done with three optical set-ups: the first one had polarizers before injection into the fibers and beam combination (i.e. before the telescope mounts); the second one had a Wollaston prism before imaging on the detector, after beam combination; and the third one had no polarization splitting.
We found that the instrumental contrasts can drop by 10 to 15% when no polarization splitting is done (Table 13). Slightly better contrasts (![]() 3%) were found when using
polarizers before beam combination rather than after with a Wollaston prism. When comparing stability for all configurations, no significant difference was found.
3%) were found when using
polarizers before beam combination rather than after with a Wollaston prism. When comparing stability for all configurations, no significant difference was found.
5 Discussion
The characterizations presented here shows that global properties of the designed beam combiners are very satisfactory for a first prototype. In this section, we discuss how departures from the ideal case might affect the performance.
Table 12:
Examples of phase-shifts (in degrees) measured in the two polarization states (P1, P2), for the 6 beam pairs. Statistical errors are of 1![]() .
.
Table 13: Contrasts and phase-shifts obtained when the splitting of polarizations is done before or after the combination, and when no splitting is achieved. Errors are statistical.
Photometry:
the transmission of the beam combiners directly impacts the instrument sensitivity and therefore, constrains the limiting magnitude. For these longest and most complex IO beam combiners tested today, a 65% transmission is satisfactory. An improved technology has allowed to reduce the losses with respect to previous beam combiners. For comparison, the IONIC3T/IOTA H band beam combiners that were made with the first technology and had only 3 Y-junctions and 3 couplers, presented a transmission of 60%. The gain comes essentially from improvement in propagation losses associated with a reduced beam combiner length.We show evidence for small crosstalk photon leaks that lead to unwanted flux in the combining cells. These potentially affect the photometry estimation and might introduce a small coherent contribution not revealed in this study. However the measured values for both chips are mostly inferior to 1% of the total flux and have contributions smaller than the typical error bars of the measurements. The origin of this effect has been identified as coming from imperfect fiber/IO coupling (in the experiment the fibers are not glued unlike in an actual instrument) and from flux coupling in the substrate that is partially guided. However, the latter contribution has been dramatically reduced thanks to new etching technology that allows each waveguide to be completely isolated from the others and to not waste flux (Labeye et al. 2006). As a matter of fact, our experiments using the old technology showed flux crosstalk of up to 8%.
The flux routing of the interfering beams, for each pair, needs to be as equal as possible,
although this is not a strong requirement. In fact, the instrumental visibility (and therefore the
SNR) decreases as the beam fluxes are unbalanced. For these beam combiners, the tricouplers equally split the flux in three (within the error bars), and the flux splitting ratios of the Y-junctions are satisfactory. On the contrary, the couplers can be as unbalanced as 60%/40% leading to a maximum contrast loss of 2%. These splitting ratios were estimated with the assumption of ideal functions, which actually present a small loss of a few ![]() (Labeye 2008). These unbalanced ratios are due to an error in the design, and new prototypes are being made with improved couplers. Globally, the agreement of the simulated data with the experiments is very satisfactory.
(Labeye 2008). These unbalanced ratios are due to an error in the design, and new prototypes are being made with improved couplers. Globally, the agreement of the simulated data with the experiments is very satisfactory.
Finally, the stability and repeatability of all observables are key elements to reach high dynamics. Photometric quantities are stable over a day timescale at the level of a percent, and are reproducible from one day to another with a maximum variation of 3%. We suspect that the absence of a glued interface between the fibers and IO beam combiners contributes to the small errors (except for the closure phases for which this effect is canceled out). However, for a first demonstration, the performances are good and the general flux routing is validated. The competitive transmission together with the capacity to use all photons for coherent combination lead to an overall high sensitivity for such 4-beam phase-shifting beam combiners.
Interferometry:
the instrumental contrast directly impacts the sensitivity of the instrument and should therefore be as high as possible. Here the beam combiners produce instrumental contrasts with values always above 80% in wide band, and reaching 100% with spectral dispersion. In broad band operation, the effects of differential dispersion due to unequal length of the fibers can lead to a contrast loss of up to 20% which explains the very high contrasts obtained with spectral dispersion. Statistically, the stability of the contrasts over a day timescale is good (from 1% to 4%) but the reproducibility of such measurements onto another day could not be validated due to the non-linearity of our detector. This affects the value with a bias of 5%, making our results only upper limits.
The phase shifting functions were initially designed to sample the coherence in four phase states in quadrature (the so called ABCD sampling). For the two tested beam combiners, the phase-shifting functions lead to 5 phase-shifts out of 6 in agreement with our expectations, while one of them (the central one corresponding to the [14] combination) is far from 90![]() .
We suspect an inhomogeneity in the constitution of the silicon substrate at the position of this phase shifting function. Of all 6 functions, this one is the most distant from the center of the beam combiner and is located next to the edge of the chip. This effect could explain the measurements obtained on both chips since they were located next to each other on the same wafer. This could also result from a relaxation of the stresses on the silica during the chip cut. An error in the design has been ruled out. This is the first time that these
functions have been tested and while still not completely controled, these results are encouraging and show that the use of phase shifting functions in IO beam combiners is promising. In addition, phase shifts are stable on a timescale of a day, within 1
.
We suspect an inhomogeneity in the constitution of the silicon substrate at the position of this phase shifting function. Of all 6 functions, this one is the most distant from the center of the beam combiner and is located next to the edge of the chip. This effect could explain the measurements obtained on both chips since they were located next to each other on the same wafer. This could also result from a relaxation of the stresses on the silica during the chip cut. An error in the design has been ruled out. This is the first time that these
functions have been tested and while still not completely controled, these results are encouraging and show that the use of phase shifting functions in IO beam combiners is promising. In addition, phase shifts are stable on a timescale of a day, within 1![]() and vary up to 3
and vary up to 3![]() from one day to another.
from one day to another.
The incidence of this departure from phase quadrature on the final complex visibility SNR estimation cannot be quantified without a proper calculation. It should be seen as a reduction in the instrumental response. In the limiting case where the phase shift is 0, one cannot retrieve unambiguously the complex visibility information. However since all but one phase shift have close to quadrature values, we believe this validates the concept.
Finally, the measured closure phases are not equal to zero. Specific phase contributions of each function, that result from non-perfectly symmetric pathways, are unknown. When observing a scientific target, calibrating with a point source (that is centro-symmetric and supposedly leads to a zero closure-phase) should allow us to remove the instrumental contribution. It should be expected that given the remarkable stability of such beam combiners (Berger et al. 2000) the instrumental response should be very well calibrated.
Chromaticity:
the importance of the chromaticity of the functions directly depends on the spectral resolution used in the instrument.
On all photometric coefficients, the average chromaticity can go from about 12% to 80%. Individual functions show varieties of chromaticity, with variations for tricouplers and Y-junctions from 3% to 28% while couplers can be considered as achromatic. The Y-junctions and couplers for the [23] combination are more chromatic than the others. More details will be given in a following paper (Labeye et al. 2009, in prep.). However photometric calibration in the presence of dispersion should solve this issue. With correction for photometric effects, the
obtained contrasts show very little chromaticity, with an average maximum variation of 4.6% over
the range of H band. Phase shifts show chromatic variations of 5.6![]() on average, the maximum
variation corresponding to the [23] combination as for individual functions. The closure phases
show strong variation with wavelength, up to 30
on average, the maximum
variation corresponding to the [23] combination as for individual functions. The closure phases
show strong variation with wavelength, up to 30![]() ,
which results in the sum of all chromatic
effects for the three telescopes in the closure relation.
,
which results in the sum of all chromatic
effects for the three telescopes in the closure relation.
We can anticipate that in cases where spectral resolution is low the effective wavelength might be affected and a proper wavelength calibration should be considered together with a proper stellar calibrator choice. In addition, in order to limit potential biases, particular care should be taken to specify the alignment accuracy between the beam combiner, spectrograph and detector pixels.
Polarization:
birefringence control is a critical part of a guided optics instrument. In our experiment, we used highly birefringent fibers which have a well defined polarization axis but, in turn, require specific care on how the polarization state is modified along the propagation.Our study first shows that all estimated quantities (photometry, instrumental contrast, phase shift, closure phase) can be different depending on the polarization state. We have shown in particular that the behavior of the central [14] combination is different from the other phase-shifting functions. This confirms the suspected marginal behavior of this combination, maybe originating from an inhomogeneity in the substrate for both chips.
Besides, our work showed that it is necessary to split the polarization states before or after the beam combinations, or to actively control the phase shift between the two linear states to avoid contrast loss. The use of birefringent fibers and waveguides forces the phase velocity of the two polarization states to be different and results in two shifted interferograms. When these two are superimposed, it leads to a single low contrast interferogram. In the case of a sensitive imaging instrument, splitting after the beam combination is recommended since the use of polarizers before the combination would lose half of the useful photons. As far as stability is concerned, without splitting, the differential phase shifting of the polarization states inside the beam combiner would lead to varying results. The new prototypes are being designed with special care given to this problem.
On-sky operating modes:
by allowing all the complex coherent factors to be measured in one single detector frame readout, these beam combiners offer two observational modes, depending on the stability of the fringes (i.e. on the atmospheric conditions or on the availability of a fringe tracker and its performance). If the fringes are stabilized to better than a fraction of the wavelength, a long coherent integration of the flux on each pixel is possible (i.e. coherencing mode), highly increasing the SNR compared to temporal encoding. Otherwise, by varying the OPD, one will access 4 phase-shifted interferograms on which to estimate the interferometric observables. The latter mode is also well suited for laboratory measurements and calibration.
Precision interferometry and data reduction:
we have shown that the described beam combiners present performance well suited for astronomical beam combination in a four telescope imaging interferometer. Our extensive laboratory characterization shows that on-sky performance, in terms of precision, should be comparable to what has been achieved with IONIC-VINCI/VLTI, IONIC3/IOTA or FLUOR/IOTA-CHARA. However, an interesting number of astrophysical problems will soon be more demanding (e.g. debris disk, hot Jupiter detection). In that case it is important to better characterize calibration issues and tackle all imperfections that could be introduced by the beam combiner. Such work is justified by the tremendous stability of the beam combiner that has been revealed by numerous industrial developments. Therefore, a proper calibration of the beam combiner should allow systematics biases to be removed. What we propose is to use the so-called ``visibility to pixel matrix'' calibration in order to carry out a global inversion of the matrix that links the measured intensities with the properties of the scientific object. Such a method, that will be detailed in a coming paper allows all instrumental contributions to be extracted. We briefly discuss here the philosophy of this data reduction. By developing the cosine, Eq. (1) can be written in such a way that instrumental terms are separated from the object contribution (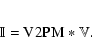
The complex visibility of the scientific source will be obtained by inverting the system. A full characterization of the V2PM matrix should be first done with internal calibration procedures. This method allows all instrumental effects to be included in a single matrix taking into account all crossing terms due to unideal behavior.
6 Conclusion
We have presented a laboratory characterization, in the H band, of an integrated optics beam combiner dedicated to the combination of a four telescope interferometer. It uses a novel ``pairwise static ABCD'' combination scheme which optimizes the extraction of coherence
information: visibility amplitudes, phases and closure phases. Our measurements show that, although complex, the flux routing inside the beam combiner is efficient and that the global throughput is
competitive (65%). In particular the comparison with simulated performance of several building block functions is very satisfactory. The instrumental contrasts are high (![]() 80%) and
stable showing maximum variations of a few
80%) and
stable showing maximum variations of a few ![]() within a day. The instrumental closure phases are different from zero but stable and probably caused by small internal optical path differences. The specificity of these beam combiners, which is to produce four phase shifted outputs to sample the coherence information (for each baseline) in one integration, has been validated. Finally, the global chromaticity of the beam combiner has required specific optimizations that are non-standard with respect to standard telecommunication IO functions. IO chips used in telecommunications are usually required to show a flat response on short bandpasses (
within a day. The instrumental closure phases are different from zero but stable and probably caused by small internal optical path differences. The specificity of these beam combiners, which is to produce four phase shifted outputs to sample the coherence information (for each baseline) in one integration, has been validated. Finally, the global chromaticity of the beam combiner has required specific optimizations that are non-standard with respect to standard telecommunication IO functions. IO chips used in telecommunications are usually required to show a flat response on short bandpasses (
![]()
![]() 20-30 nm) while here we have extended the couplers and tricouplers and phase shifter response to more than
20-30 nm) while here we have extended the couplers and tricouplers and phase shifter response to more than ![]() 150 nm around
150 nm around
![]() (Labeye 2008). These results on a first prototype validate the feasibility of a ``pairwise static ABCD'' combination scheme and its suitability for an interferometric imaging instrument.
(Labeye 2008). These results on a first prototype validate the feasibility of a ``pairwise static ABCD'' combination scheme and its suitability for an interferometric imaging instrument.
Most of technological building blocks are now defined. We are working on the definitive version that will be included inside Gravity and VSI. This will require a number of technological improvements and innovations. In particular, the phase-shifting function will be ameliorated to get closer to the nominal
![]() phase shift. The throughput will be improved with an optimized routing that will reduce the global propagation losses. We are currently extending the demonstration, using the same silica on silicon technology, to the K band, as required by Gravity and VSI. It is expected that, while less transmissive in this band, the short propagation distances inside the combiner will lead to acceptable global losses. Finally, we will explore how this combination concept can be extended to a six-way beam combiner and fit VSI requirements.
phase shift. The throughput will be improved with an optimized routing that will reduce the global propagation losses. We are currently extending the demonstration, using the same silica on silicon technology, to the K band, as required by Gravity and VSI. It is expected that, while less transmissive in this band, the short propagation distances inside the combiner will lead to acceptable global losses. Finally, we will explore how this combination concept can be extended to a six-way beam combiner and fit VSI requirements.
Acknowledgements
This work was financially supported by CNES, CNRS, ASHRA, Université Joseph Fourier and Agence Nationale de la Recherche grant ANR-06-BLAN-0421. We thank J.-B. Le Bouquin, and S. Lacour for fruitful discussions. We acknowledge the referee, Markus Schoeller, for his careful reading of the manuscript and for thoughtful suggestions that improved its clarity.
References
- Berger, J.-P., Benech, P., Schanen-Duport, I., et al. 2000, in Interferometry in Optical Astronomy, Proc. SPIE, 4006, 986
- Berger, J.-P., Haguenauer, P., Kern, P. Y., et al. 2003, in Interferometry for Optical Astronomy II, Proc. SPIE, 4838, 1099
- Berger, J.-P., Haguenauer, P., Kern, P., et al. 2008, in The Power of Optical/IR Interferometry, ed. A. Richichi, F. Delplancke, F. Paresce, & A. Chelli, 589
- Colavita, M. M. 1999, PASP, 111, 111 [NASA ADS] [CrossRef] (In the text)
- Eisenhauer, F., Perrin, G., Brandner, W., et al. 2008, in Proc. SPIE, 7013, 70132A (In the text)
- Haguenauer, P., Abuter, R., Alonso, J., et al. 2008, in Proc. SPIE, 7013, 70130C
- Jocou, L. 2007, Ph.D. Thesis, CNAM (In the text)
- Kern, P., Malbet, F., Schanen-Duport, I., & Benech, P. 1996, in Astrofib' 96: integrated optics for astronomical interferometry, ed. F. Kern, & P. Malbet (In the text)
- Kraus, S., Schloerb, F. P., Traub, W. A., et al. 2005, AJ, 130, 246 [NASA ADS] [CrossRef]
- Labeye, P. 2008, Ph.D. Thesis, Institut National Polytechnique de Grenoble (In the text)
- Labeye, P., Broquin, J.-E., Berger, J.-P., Kern, P., & Noel, P. 2006, in Silicon Photonics, Proc. SPIE., 6125, 161 (In the text)
- Lacour, S., Jocou, L., Moulin, T., et al. 2008, in Proc. SPIE, 7013, 701316 (In the text)
- LeBouquin, J. 2005, Ph.D. Thesis, Université Joseph Fourier - Grenoble I (In the text)
- LeBouquin, J. B., Rousselet-Perraut, K., Kern, P., et al. 2004, A&A, 3, 34
- Malbet, F., Kern, P., Schanen-Duport, I., et al. 1999, A&AS, 138, 135 [NASA ADS] [CrossRef] [EDP Sciences]
- Malbet, F., Kern, P. Y., Berger, J.-P., et al. 2006, in Advances in Stellar Interferometry, Proc. SPIE, 6268, 62680Y
- Malbet, F., Buscher, D., Weigelt, G., et al. 2008, Proc. SPIE, 7013, 701329
- Monnier, J. D., Berger, J.-P., Millan-Gabet, R., et al. 2006a, ApJ, 647, 444 [NASA ADS] [CrossRef]
- Monnier, J. D., Pedretti, E., Thureau, N., et al. 2006b, in Proc. SPIE, 6268, 62681
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] (In the text)
- Schöller, M. 2007, New Astron. Rev., 51, 628 [NASA ADS] [CrossRef]
- Shao, M., & Staelin, D. 1977, J. Opt. Soc. Am., 67, 81 [NASA ADS] (In the text)
- Tatulli, E., & LeBouquin, J.-B. 2006, MNRAS, 368, 1159 [NASA ADS] [CrossRef] (In the text)
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef]
- Zhao, M., Gies, D., Monnier, J. D., et al. 2008, ApJ, 684, L95 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Experimental protocol including photometric and interferometric measurements.
Table 2: Kappa matrix photometric coefficients obtained when the light is injected only in the 4th input (F4). The first two lines correspond to the wide band experiments while the third gives the average value over wavelength, as well as the peak-to-valley amplitude over the wavelength range (chromaticity). Values are divided by 104. Bold numbers, preceded by a star, indicate the illuminated outputs.
Table 3: Minimum, maximum and average of the photometric coefficients chromaticity among the 12 illuminated outputs from each injection.
Table 4: Tricoupler splitting ratio measured in wide band. The dispersion (rms) over 1024 measurements is 0.1%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
Table 5: Minimum, maximum and average chromaticity of tricoupler splitting ratio (among the three outputs of each tricoupler). T1 is the tricoupler corresponding to input 1.
Table 6: Y-junction splitting ratio. The dispersion (rms) over 1024 measurements is 0.1%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
Table 7: Coupler splitting ratio. The dispersion (rms) over 1024 measurements is 0.2%. The two first lines correspond to the wide band experiments while the third gives the average value and the variation amplitude over the wavelength range.
Table 8: Cross-talk flux (in %) determined when the light is injected in the 4 outputs successively. The two first lines report results obtained in broad band while the third line corresponds to the spectral dispersion case. Error bars are estimated from the dispersion (rms).
Table 9: Instrumental contrasts (in %) obtained with wide band experiments (first two lines) and with spectral dispersion (third line) with a statistical error of 1%.
Table 10:
Phase-shifts obtained with the wide band experiments (two first lines) with errors of 1.0![]() (the dispersion (rms) over half a day); The third line gives
the average values over the wavelength range.
(the dispersion (rms) over half a day); The third line gives
the average values over the wavelength range.
Table 11:
Closure-phase measurements for one independent triangle, for Chip 2
with spectral dispersion, as well as amplitude of the variation over the H band range. Statistical errors are of 2.5![]() .
.
Table 12:
Examples of phase-shifts (in degrees) measured in the two polarization states (P1, P2), for the 6 beam pairs. Statistical errors are of 1![]() .
.
Table 13: Contrasts and phase-shifts obtained when the splitting of polarizations is done before or after the combination, and when no splitting is achieved. Errors are statistical.
All Figures
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{1083fig1.ps}\par\includegraphics[angle=180,width=10.9cm,clip]{1083fig2.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg7.gif) |
Figure 1:
Upper panel: theoretical design of the integrated optics 4-way beam combiner allowing pairwise combination and using phase-shifting devices to produce 4 outputs in quadrature. We refer to each output using the index m,l,k. mlk is the
|
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Details of the beam combining function: for each interferometric pair (e.g. [12]), one arm is shifted by 90 |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Principle of the phase-shifting function: a variation of the optical path is induced by a differential change of the waveguide effective index due to a change in their width. The concatenation of carefully optimized portions of waveguides with controlled effective index allows to flatten the wavelength response. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1083fig5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg33.gif) |
Figure 4: Schematic view of the laboratory testbed simulating the VLTI (see text for details). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1083fig6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg37.gif) |
Figure 5: A detector image of the 24 outputs, obtained when using the spectrograph and a Wollaston prism (splitting the two linear polarizations P1 and P2). The patterns are due to various non zero OPD for the different beam combinations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1083fig7.ps}\includegraphics[width=7.75cm,clip]{1083fig8.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg39.gif) |
Figure 6: Left: kappa matrix photometric coefficients obtained when the light is injected in one input at a time (F1..4) for Chip 1. The stars and squares show results obtained on two different days of experiments (called Day 1 and Day 3). Pixels from 1 to 24 are the 24 outputs of the beam combiner, identified as 121 to 344 in Table 2. Right: variation of the kappa matrix photometric coefficients with wavelength over the H band range, measured on Chip 2. The four panels correspond to the light injection in one input at the time (e.g. F1 for the injection in input 1). Inside each of them, among the 12 outputs illuminated, only 3 are plotted (in full, dashed, and dotted lines), corresponding to each combination cell. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{1083fig9.ps}\hspace*{2mm}
...
....ps}\hspace*{2mm}
\includegraphics[width=5.9cm,clip]{1083fig11.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg57.gif) |
Figure 7: Variation with wavelength of the tricoupler splitting ratio ( left) and of the Y-junctions ( middle, right). Middle: three Y-junction splitting ratios corresponding to the illumination in the first input (these Y-junctions are related to the [12], [13] and [14] combinations); Right: three Y-junctions splitting ratios obtained when injecting the light in the second input. For clarity, only one flux ratio coefficient (among 2 or 3) is plotted for each function. The error for each spectral channel is estimated from the dispersion over 1024 measurements and is smaller than the symbol sizes. The theoretical values of 33% for the tricoupler, and 50% for the Y-junctions, are given by the horizontal dashed line. Values for all functions are given in Tables 4 and 6. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig12.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig13.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg59.gif) |
Figure 8: Variation of coupler splitting ratio with wavelength. Only one of the flux ratio coefficients is plotted, and extreme behaviors are given: left, when the light is injected in the first input; right, for an injection in the second input. The theoretical value of 50% is given by the horizontal dashed line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1083fig14.ps}\hspace*{2mm}
\includegraphics[width=6.6cm,clip]{1083fig15.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg60.gif) |
Figure 9: Left: an interferogram obtained with temporal OPD modulation with wide-band measurements. Right: the variation of instrumental contrasts with wavelength, for all four outputs of each beam pair. 100% contrasts are given by the horizontal dashed line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig16.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig17.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg61.gif) |
Figure 10:
The phase-shifted interferograms recorded for the 4 outputs (full, dashed, dotted, dot-dashed lines) of the [34] beam pair are close to quadrature ( left). On
the contrary, the 4 outputs of the central combination [14] produce interferograms only slightly phase-shifted ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1083fig18.ps}\hspace*{2mm}
\includegraphics[width=6.5cm,clip]{1083fig19.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa11083-08/Timg62.gif) |
Figure 11:
Left: wavelength dependence of the phase-shifts for the outputs designed to be in quadrature, for all 6 pairwise combinations ([ml]). Error bars on each spectral point are of 1 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



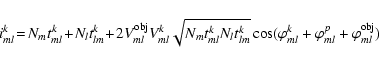
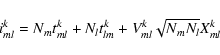
![$\displaystyle \left(
\begin{array}{c}
i_{ml}^{1}\\ [2mm]
i_{ml}^{2}\\ [2mm]
i...
...ay}{c}
N_{m} \\ [2mm]
N_{l} \\ [2mm]
\sqrt{N_{m}N_{l}} \\
\end{array}\right)$](/articles/aa/full_html/2009/17/aa11083-08/img23.gif)