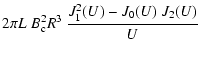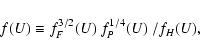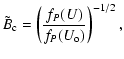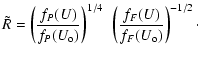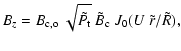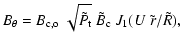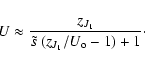| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 551 - 566 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200810971 | |
| Published online | 05 March 2009 | |
Causes and consequences of magnetic cloud expansion
P. Démoulin1 - S. Dasso2,3
1 - Observatoire de Paris, LESIA, UMR 8109 CNRS,
92195 Meudon Principal Cedex, France
2 -
Instituto de Astronomía y Física del Espacio, CONICET-UBA,
CC. 67, Suc. 28, 1428 Buenos Aires, Argentina
3 -
Departamento de Física, Facultad de Ciencias Exactas y
Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
Received 17 September 2008 / Accepted 23 February 2009
Abstract
Context. A magnetic cloud (MC) is a magnetic flux rope in the solar wind (SW), which, at 1 AU, is observed ![]() 2-5 days after its expulsion from the Sun. The associated solar eruption is observed as a coronal mass ejection (CME).
2-5 days after its expulsion from the Sun. The associated solar eruption is observed as a coronal mass ejection (CME).
Aims. Both the in situ observations of plasma velocity distribution and the increase in their size with solar distance demonstrate that MCs are strongly expanding structures. The aim of this work is to find the main causes of this expansion and to derive a model to explain the plasma velocity profiles typically observed inside MCs.
Methods. We model the flux rope evolution as a series of force-free field states with two extreme limits: (a) ideal magneto-hydrodynamics (MHD) and (b) minimization of the magnetic energy with conserved magnetic helicity. We consider cylindrical flux ropes to reduce the problem to the integration of ordinary differential equations. This allows us to explore a wide variety of magnetic fields at a broad range of distances to the Sun.
Results. We demonstrate that the rapid decrease in the total SW pressure with solar distance is the main driver of the flux-rope radial expansion. Other effects, such as the internal over-pressure, the radial distribution, and the amount of twist within the flux rope have a much weaker influence on the expansion. We demonstrate that any force-free flux rope will have a self-similar expansion if its total boundary pressure evolves as the inverse of its length to the fourth power. With the total pressure gradient observed in the SW, the radial expansion of flux ropes is close to self-similar with a nearly linear radial velocity profile across the flux rope, as observed. Moreover, we show that the expansion rate is proportional to the radius and to the global velocity away from the Sun.
Conclusions. The simple and universal law found for the radial expansion of flux ropes in the SW predicts the typical size, magnetic structure, and radial velocity of MCs at various solar distances.
Key words: Sun: coronal mass ejections (CMEs) - Sun: magnetic fields - interplanetary medium
1 Introduction
Interplanetary coronal mass ejections (ICMEs) are the manifestation of magnetized plasma structures ejected from the Sun as CMEs (e.g., Zurbuchen & Richardson 2006; Wimmer-Schweingruber et al. 2006). ICMEs are dynamic structures that move through and interact with the solar wind (SW). The size of an ICME drastically increases, typically by more than a 103 factor, during its travel from the Sun to the external heliosphere.
Magnetic clouds (MCs) are a particular subset of ICMEs that have a well-structured magnetic field. They are formed by twisted magnetic flux tubes, called flux ropes (e.g., Burlaga 1995). Though there is still no consensus, non-MC ICMEs are probably formed by magnetic structures similar to MCs. It is plausible that MCs are only observed when the spacecraft crosses the magnetic structure close to its center (Jian et al. 2006). The MC/ICME ratio increases from
![]() at solar maximum to
at solar maximum to
![]() at solar minimum (Cane & Richardson 2003). This evolution is most likely due to an observational selection effect since at solar maximum CMEs are launched from higher solar latitudes than at minimum, so a spacecraft located in the ecliptic more frequently crosses the periphery of the magnetic structure than at solar minimum (Richardson & Cane 2004). A secondary effect is that there are more interactions between ICMEs at solar maximum, so more distortion/reconnection of the magnetic structures is expected at solar maximum than minimum.
at solar minimum (Cane & Richardson 2003). This evolution is most likely due to an observational selection effect since at solar maximum CMEs are launched from higher solar latitudes than at minimum, so a spacecraft located in the ecliptic more frequently crosses the periphery of the magnetic structure than at solar minimum (Richardson & Cane 2004). A secondary effect is that there are more interactions between ICMEs at solar maximum, so more distortion/reconnection of the magnetic structures is expected at solar maximum than minimum.
The in situ measurements are limited to the spacecraft trajectory crossing the incoming ICME. Therefore, one needs to rely on modeling to derive the global magnetic structure from local measurements. This has restricted the analysis so far to MCs. Most of the magnetic models neglect the evolution of the magnetic field during the crossing time of the observed MC, and consider a flux rope locally invariant along its axis. These different approaches are reviewed by Riley et al. (2004), Dasso et al. (2005), Forbes et al. (2006), and briefly summarized below.
The magnetic field in MCs can be relatively well modeled by the so-called Lundquist model (Lundquist 1950), which considers a static and axially-symmetric linear force-free magnetic configuration (e.g., Burlaga 1988; Lepping et al. 1990; Lynch et al. 2003). Alternately, Farrugia et al. (1999) considered a cylindrical shape for the cloud cross-section and a non-linear force-free field, while Mulligan et al. (1999), Hidalgo et al. (2002), and Cid et al. (2002) have considered a cylindrical cloud with a finite plasma pressure. Elliptical models have also been developed with a linear force-free field (Vandas & Romashets 2003) and with a non-force free field (Hidalgo 2003). They are able to describe distortions of the magnetic structures due to the interaction with its environment.
The magnetic structure of MCs has also been analyzed by solving the magneto-static force balance as a Cauchy problem (e.g., Hu et al. 2005; Hu & Sonnerup 2002). The amount of distortion from circular cross section is variable in the MCs analyzed. Some MCs are significantly distorted (within the limit that a Cauchy problem is ill-posed, since it is sensitive to modifications of the boundary conditions, so that the results can be significantly affected by the temporal resolution and the range of the data used).
Inside MCs, and more generally inside ICMEs, the measured plasma velocity typically has a linear variation along the spacecraft trajectory. A much higher velocity is present in the front than in the back, indicating expansion. Burlaga & Behannon (1982) found consistency between the expansion speed estimated from in situ observations and the increase of their typical size, obtained from measurements with different spacecraft located between 2 and 4 AUs.
Self-similar models have been used to describe the expansion of flux ropes. Some consider only a radial expansion (e.g., Farrugia et al. 1993; Osherovich et al. 1993; Farrugia et al. 1997; Nakwacki et al. 2008), while others consider an isotropic expansion (e.g., Shimazu & Vandas 2002; Berdichevsky et al. 2003; Dasso et al. 2007). The main problem of the first group of models is that, even taking a force-free configuration at some point of the evolution, the only radial expansion implies the creation of strong unbalanced magnetic forces during the evolution. Then, the force-free state is singular in these models, happening only at one single time during the evolution, while observations show that MCs typically have a low-![]() plasma. A self-similar isotropic expansion does not change the force balance, so the second group of models are expected to be a better approximation. However, it is not obvious that the expansion could be isotropic since the magnetic force is anisotropic in a flux rope.
plasma. A self-similar isotropic expansion does not change the force balance, so the second group of models are expected to be a better approximation. However, it is not obvious that the expansion could be isotropic since the magnetic force is anisotropic in a flux rope.
Flux rope evolution has also been investigated with MHD simulations (Manchester et al. 2004; Chané et al. 2006; Cargill et al. 2000; Wu et al. 2007; Shen et al. 2007; Cargill & Schmidt 2002; Riley et al. 2003). A flux rope model is typically inserted in a SW model close to the Sun as an initial condition. Typically, these MHD simulations found that a flux rope, moving much faster than the surrounding SW, has its cross section flattened as it moves outward. Flattening is interpreted as two effects, one geometrical (spherical expansion) and the second due mainly to the dynamic pressure of the overtaken SW (Riley et al. 2003). The magnetic tension of the flux rope is not sufficient in these simulations to maintain an approximately circular cross section.
In present work we analyze the expansion of flux ropes in the SW with a complementary approach to the self-similar expansion models and to the MHD simulations cited above. Here we model the dynamical evolution of the flux rope as a moving boundary problem (see, e.g., Crank 1984), where the ``Stefan condition'' is provided by the pressure balance between the ambient solar wind and the MC boundary. Our approach is to keep only the main physical effects in order to derive, as well as we can, analytical results showing the effects of the main physical parameters. We assume a force-free evolution, and we will test how well the evolution could be considered as self-similar. The hypothesis and the main equations are derived in Sect. 2, with the scope to define the key variables of the evolution. The equations are solved in Sect. 3 for three very different types of flux rope. In Sect. 4, we use the known properties of the SW and our theoretical results to derive the expected and generic expansion of flux ropes in the SW. Then, we compare these results to the observed expansion of MCs and ICMEs. In Sect. 5 we analyze the evolution of flux ropes with the hypothesis of minimizing their magnetic energy with a preserved magnetic helicity; we show that under these dissipative conditions, flux ropes expand almost at the same rate as in ideal MHD. This further extends our main result, showing that the expansion of flux rope in the SW is mainly due to the decrease of the total SW pressure with solar distance. Finally, we summarize our results and conclude in Sect. 6.
| |
Figure 1: Schematic of a flux rope ejected from the Sun (the apex of the central field line is at a distance D from the Sun). The magnetic configuration of a magnetic cloud (MC) is well represented by an elongated twisted flux tube mostly anchored to the Sun. The schematic on the left shows the locally straight approximation used in this work (A color version is available in the electronic version). |
| Open with DEXTER | |
2 Equations for a force-free expanding flux rope
In this section we present a new model to describe the evolution of an expanding flux rope in the solar wind, deriving the complete set of its equations. Since MCs typically have a low-
2.1 Ideal MHD and force-free field evolution
This section describes the internal evolution of the flux rope. Its interaction with the surrounding SW is described in the next section.
The magnetic configuration of a MC is typically described by a flux rope ejected from the Sun (Fig. 1). When the flux rope is moving faster than the surrounding SW, plasma and magnetic field typically accumulate in front (in the so-called sheath region). With this forcing, magnetic reconnection is expected, and indeed evidence of reconnection occurrences have been found (Gosling et al. 2005; Dasso et al. 2007). The amount of reconnected flux is highly variable in MCs, depending at least on the SW field structures overtaken, the relative orientation of the SW and MC leading fields, and the difference between the SW and MC velocities. Below we neglect this interaction that will basically ``peal'' the flux rope so that a progressively less extended flux rope is moving in the SW. The surviving flux rope is indeed expected to expand following roughly the same law as the original one since the main driver of the expansion, the decrease of SW pressure with solar distance (see below), is basically the same.
The main driver of the flux rope expansion is the quasi-balance between forces inside and outside the rope during its travel in the solar wind. Below, we retain only the Lorentz force inside the flux rope, since the plasma ![]() is low in MCs (typically
is low in MCs (typically
![]() ,
with values ranging from less than
,
with values ranging from less than
![]() to a few times 0.1 (e.g., Burlaga & Behannon 1982; Wu & Lepping 2007; Feng et al. 2007; Lepping et al. 2003), so the plasma pressure has a weak contribution.
Other forces such as gravity are also negligible compared to the magnetic pressure gradient.
In the frame of the MC, the plasma velocity is typically smaller than the Alfvén velocity
(a few 100 km s-1, Burlaga & Behannon 1982), then the magnetic evolution can be described,
to first approximation, by a series of force-free equilibrium
(
to a few times 0.1 (e.g., Burlaga & Behannon 1982; Wu & Lepping 2007; Feng et al. 2007; Lepping et al. 2003), so the plasma pressure has a weak contribution.
Other forces such as gravity are also negligible compared to the magnetic pressure gradient.
In the frame of the MC, the plasma velocity is typically smaller than the Alfvén velocity
(a few 100 km s-1, Burlaga & Behannon 1982), then the magnetic evolution can be described,
to first approximation, by a series of force-free equilibrium
(
![]() ).
).
A MC typically has an elongated flux rope structure with a cross-section size much thinner than the curvature radius of its axis, so we approximate locally the magnetic field by a cylindrical field with a local invariance along its axis. We also simplify the problem by considering a circular cross section (Fig. 1). With these simplifications ![]() is described only by its axial, Bz(r), and azimuthal,
is described only by its axial, Bz(r), and azimuthal,
![]() ,
components; they are functions of the local radius r. The internal force balance is written as
,
components; they are functions of the local radius r. The internal force balance is written as
The flux rope evolution should then follow approximately the above force-free equilibrium during its evolution in the SW. We define the field
In this study we suppose an ideal MHD evolution (except in Sect. 5), so at all times there is the following elementary magnetic flux conservation
These equations relate ![]() to
to
![]() through the implicit expansion function
through the implicit expansion function
![]() .
.
2.2 Drivers of the evolution
In this section we describe the model for the evolution of the flux rope: first, its axial expansion, then its interaction with the surrounding SW. The apex of the flux rope axis is located at the variable distance D from the Sun, and it has a length L that increases with D (Fig. 1). We suppose that the axial expansion is uniform along and across the flux tube, so the local expansion rate
![]() is simply provided by the relative extension of the flux rope axis
is simply provided by the relative extension of the flux rope axis
where
Table 1: Definition of the main non-dimensional variables.
A second driver of the magnetic field evolution is the force balance with the surrounding SW.
As the total SW pressure decreases with solar distance (D) the flux rope expands and its internal pressure decreases accordingly, progressively reaching new states of quasi-equilibrium.
This balance of pressure, at the flux rope boundary r=R (flux rope radius), is simply written as
where
However, when a flux rope moves faster than the SW, a dynamic pressure, typically on the order of
![]() ,
is present in front of the flux rope (where
,
is present in front of the flux rope (where
![]() is the SW density and
is the SW density and
![]() is the relative velocity of the MC with respect to the SW). This dynamic pressure has a distribution around the flux rope that depends on the Mach number of the relative flow in pure hydrodynamic, and it is even more complex with a magnetized SW. Moreover, when the MC is moving significantly faster than the SW, a MHD shock is present in front of the flux rope. For a small fraction of MCs, typically those traveling in the fast solar wind with a comparable mean speed, both forward and reverse shocks are observed (e.g. Gosling et al. 1998). These shocks are associated with a jump in the total pressure. Each of the above complex interactions with
the SW are not isotropic around the flux rope and so they contribute to its deformation as present in MHD simulations (Sect. 1).
is the relative velocity of the MC with respect to the SW). This dynamic pressure has a distribution around the flux rope that depends on the Mach number of the relative flow in pure hydrodynamic, and it is even more complex with a magnetized SW. Moreover, when the MC is moving significantly faster than the SW, a MHD shock is present in front of the flux rope. For a small fraction of MCs, typically those traveling in the fast solar wind with a comparable mean speed, both forward and reverse shocks are observed (e.g. Gosling et al. 1998). These shocks are associated with a jump in the total pressure. Each of the above complex interactions with
the SW are not isotropic around the flux rope and so they contribute to its deformation as present in MHD simulations (Sect. 1).
We suppose below that the relative velocity of the flux rope with respect to the SW is sufficiently small, or equivalently that the magnetic tension is strong enough to neglect the deformation of the flux rope cross section, as well as the anisotropy of the total SW pressure around the flux rope. Then, at the boundary of the flux rope, defined by r=R, we write the pressure equilibrium as
where
While
![]() can be imposed as an external background pressure,
can be imposed as an external background pressure,
![]() can be written
as an explicit function of D only a posteriori, when the flux rope evolution is solved.
However, the non-dimensional factor
can be written
as an explicit function of D only a posteriori, when the flux rope evolution is solved.
However, the non-dimensional factor
![]() is typically in the interval between unity and several units (being larger for a stronger shock).
Moreover
is typically in the interval between unity and several units (being larger for a stronger shock).
Moreover
![]() is generally not expected to change drastically with D since it would require an important modification of the flux rope velocity, or of the SW properties at some distance D. In contrast,
is generally not expected to change drastically with D since it would require an important modification of the flux rope velocity, or of the SW properties at some distance D. In contrast,
![]() has a strong and systematic variation, typically
has a strong and systematic variation, typically
![]() (see Sect. 4.2).
For example, as the flux rope moves from 0.1 to 1 AU,
(see Sect. 4.2).
For example, as the flux rope moves from 0.1 to 1 AU, ![]() decreases by a factor
decreases by a factor
![]() well above any plausible variation of
well above any plausible variation of
![]() .
.
We define the non-dimensional function
![]() using the reference state (field
using the reference state (field
![]() when the flux rope is at the distance
when the flux rope is at the distance ![]() )
)
Formally,
2.3 Main equations of the evolution
In this section we write the above equations in a minimal format, decreasing both the number of equations and variables from five (Eqs. (1),
(2), (3), (4), (7)) and
![]() )
to two (Eq. (10), (11)) and B,r).
)
to two (Eq. (10), (11)) and B,r).
Since the magnetic field strength is present both in the force-free equation and the boundary equation (Eqs. (1), (7)), we keep B as one of the main unknown function.
From Eqs. ((2)-(4)), we derive
![]() and
and
![]() .
Then, both
.
Then, both
![]() and Bz can be written as a function of
and Bz can be written as a function of
![]() ,
r and the reference equilibrium by dividing previous equations by B. Thus, for example,
,
r and the reference equilibrium by dividing previous equations by B. Thus, for example,
where
The evolution of r is constrained by magnetic flux conservation. With Eq. (8) included in Eq. (2), we have
Since we suppose an ideal MHD evolution,
The boundary conditions of the system of Eqs. ((10), (11)) are
The force-free field evolution is described by a boundary-value problem coupling two first order differential Eqs. ((10), (11)); its solution provides
2.4 Reformulation of the equations
Since
![]() for any non-singular magnetic field, the system of Eqs. ((10), (11)) presents a weak singularity at
for any non-singular magnetic field, the system of Eqs. ((10), (11)) presents a weak singularity at
![]() (in both equations the numerator and denominator vanish). We define the
function
(in both equations the numerator and denominator vanish). We define the
function
![]() as
as
Equations ((10), (11)) rewrite as the non-singular equations
The field strength B is a decreasing function of
The evolution of B is driven by the modification of both the flux rope length, ![]() ,
and the
total pressure
,
and the
total pressure
![]() .
.
![]() is present only in Eqs. ((14), (15)) and
is present only in Eqs. ((14), (15)) and
![]() is present only in the boundary conditions (Eq. (12)). In order to group them in the equations,
we define a normalized field,
is present only in the boundary conditions (Eq. (12)). In order to group them in the equations,
we define a normalized field, ![]() ,
that has a fixed value at the boundary, r=R during the evolution (this fixed value is
,
that has a fixed value at the boundary, r=R during the evolution (this fixed value is
![]() ). We also define a normalized radius,
). We also define a normalized radius, ![]() ,
guided by the flux conservation (in order of magnitude). Then, we normalize both quantities to the reference field,
,
guided by the flux conservation (in order of magnitude). Then, we normalize both quantities to the reference field,
where
With the normalization (16), Eqs. ((14), (15)) are rewritten as
with
The boundary conditions are
The system of Eqs. ((17)-(20)) provides the evolution of ![]() and
and ![]() (and thus the size and the internal distribution of the magnetic field in the MC) while the flux rope travels in the solar wind. This system is numerically solved with a shooting method (Press et al. 1992, chap. 17) starting the integration at
(and thus the size and the internal distribution of the magnetic field in the MC) while the flux rope travels in the solar wind. This system is numerically solved with a shooting method (Press et al. 1992, chap. 17) starting the integration at
![]() from
from
![]() and
and
![]() .
An iteration on
.
An iteration on
![]() is realized so that
is realized so that
![]() converges to the boundary conditions (Eq. (20)).
converges to the boundary conditions (Eq. (20)).
The normalization defined by Eq. (16) is also applied to the field components to define
![]() .
Then, Eq. (8) is written as
.
Then, Eq. (8) is written as
and we have a similar equation for
2.5 General properties of the evolution
In the system of Eqs. ((17)-(20)), for a given reference field
![]() ,
,
![]() and
and ![]() are only functions of
are only functions of ![]() (so only of a combination of
(so only of a combination of ![]() and
and
![]() ).
We conclude that the normalized field
).
We conclude that the normalized field
![]() ,
as well as its components (Eq. (21)),
depends only on
,
as well as its components (Eq. (21)),
depends only on ![]() .
The explicit dependance of the field B(r) on
.
The explicit dependance of the field B(r) on
![]() is only present as a multiplicator factor: the field B(r) is deduced from
is only present as a multiplicator factor: the field B(r) is deduced from
![]() by multiplying the normalized field strength by
by multiplying the normalized field strength by
![]() and the normalized radial distance by
and the normalized radial distance by
![]() .
.
A typical reference magnetic field has an axial field dominating in the core of the flux rope, and an azimuthal field dominating at the periphery (recalling that a well behave field has
![]() ). As
). As ![]() increases to large values, Eq. (18) implies a smaller gradient
of
increases to large values, Eq. (18) implies a smaller gradient
of ![]() across the flux tube. This corresponds to a magnetic field having a smaller magnetic tension, so more dominated by its axial component (see Eq. (1)). So, as
across the flux tube. This corresponds to a magnetic field having a smaller magnetic tension, so more dominated by its axial component (see Eq. (1)). So, as ![]() increases,
the core expands more than its periphery, and the azimuthal field is compressed close
to the border of the flux rope (this is illustrated later for specific fields in Fig. 5). On the other hand, as
increases,
the core expands more than its periphery, and the azimuthal field is compressed close
to the border of the flux rope (this is illustrated later for specific fields in Fig. 5). On the other hand, as ![]() decreases to small values, the field strength has an increasing gradient provided by an increasing magnetic tension of the azimuthal field. So as
decreases to small values, the field strength has an increasing gradient provided by an increasing magnetic tension of the azimuthal field. So as ![]() decreases the magnetic field is increasing dominated by its azimuthal component in a larger fraction of the flux rope periphery.
decreases the magnetic field is increasing dominated by its azimuthal component in a larger fraction of the flux rope periphery.
In the particular case where the evolution with heliodistance of the length and pressure
satisfy
![]() ,
Eqs. ((17)-(20)) are satisfied with
,
Eqs. ((17)-(20)) are satisfied with
![]() and
and
![]() .
In this case the only evolution is a re-scaling of the radius by L and of the field
strength by L-2. So, when
.
In this case the only evolution is a re-scaling of the radius by L and of the field
strength by L-2. So, when
![]() , the evolution is simply an isotropic self-similar evolution regardless of the reference field.
, the evolution is simply an isotropic self-similar evolution regardless of the reference field.
For MCs in the SW, ![]() increases approximatively as the distance,
increases approximatively as the distance, ![]() ,
while
,
while
![]() decreases approximatively as
decreases approximatively as
![]() (see Sect. 4), so
(see Sect. 4), so
![]() .
With nP close to 4, any flux rope evolution is close to self-similar.
However, in the SW, typically,
.
With nP close to 4, any flux rope evolution is close to self-similar.
However, in the SW, typically,
![]() (see Sect. 4.2),
then
(see Sect. 4.2),
then
![]() has a moderate but still a significant evolution,
e.g. a factor
has a moderate but still a significant evolution,
e.g. a factor
![]() for an evolution between 0.1 and 10 AU. Then, in
the SW,
is the rope evolution close to a self-similar evolution or is there an important reorganization of the field inside the flux rope? How do the flux rope radius and the field strength change
with distance from the Sun? To answer these questions we need to solve the above equations for different reference fields
for an evolution between 0.1 and 10 AU. Then, in
the SW,
is the rope evolution close to a self-similar evolution or is there an important reorganization of the field inside the flux rope? How do the flux rope radius and the field strength change
with distance from the Sun? To answer these questions we need to solve the above equations for different reference fields
![]() .
.
3 Evolution of the normalized magnetic field
We consider below three examples of reference fields and follow their evolution with the
distance from the Sun. Generally, the spatial distribution of
![]() and
and
![]() ,
and their functional dependence with the radius, changes during the evolution.
The first two cases considered below are exceptions to this general behavior, and they can be solved analytically. This provides a deeper understanding of the flux rope evolution than with a numerical integration of the equations. The evolution of these two extremes cases are compared to the evolution of a reference field, the Lundquist's field, as it often provides a good fit to the observed magnetic field in MCs.
,
and their functional dependence with the radius, changes during the evolution.
The first two cases considered below are exceptions to this general behavior, and they can be solved analytically. This provides a deeper understanding of the flux rope evolution than with a numerical integration of the equations. The evolution of these two extremes cases are compared to the evolution of a reference field, the Lundquist's field, as it often provides a good fit to the observed magnetic field in MCs.
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.95\te...
...{
{\includegraphics[width=0.95\textwidth, clip=]{0971f2c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg148.gif) |
Figure 2:
Log-log plots of the normalized central magnetic field strength,
|
| Open with DEXTER | |
3.1 Uniformly twisted field
A uniformly twisted and non-linear force-free model (denoted GH, Gold & Hoyle 1960) is written as
The parameter Appl. Opt. describes both the spatial extension of the field and the amount of twist. To model a MC field, we consider this model up to the radius
In order to compare the results of different magnetic field configurations, we compute the ratio of the azimuthal to the axial flux
In this expression, we select the length L of the flux-rope portion to be
The evolution of a uniformly twisted flux rope is special since, apart from a change in magnitude, the spatial distribution of the twist cannot change due to radial expansion (nor due to axial expansion since we suppose a uniform expansion, Eq. (4)). Since the twist stays spatially uniformly distributed in the flux rope whatever is its evolution, then
![]() ,
with ``a'' being an unknown (to be determined). Including this
,
with ``a'' being an unknown (to be determined). Including this
![]() in Eq. (1) implies that the field is a GH's field, with only the freedom of modified parameters (called
in Eq. (1) implies that the field is a GH's field, with only the freedom of modified parameters (called
![]() ). This result is also directly shown by writing the ratio of Eqs. (18)
to (17). The terms in
). This result is also directly shown by writing the ratio of Eqs. (18)
to (17). The terms in
![]() simplify when a GH reference field (Eq. (22)) is inserted, and the equation can be directly integrated in
simplify when a GH reference field (Eq. (22)) is inserted, and the equation can be directly integrated in
![]() to write
to write
where
The solution of the evolution is completed by integration of Eq. (17) with Eqs. ((22), (24)) included. We find
This shows that the expansion of the full flux rope is in general not self-similar as
Equation (25) included in Eq. (24) provides ![]() in function of
in function of
![]() and allows us to impose the boundary condition on
and allows us to impose the boundary condition on ![]() (Eq. (20)), defining an equation for the central field strength
(Eq. (20)), defining an equation for the central field strength
![]() .
We find
.
We find
where we replace
The reference state has
![]() ,
then Eq. (26) is naturally satisfied with
,
then Eq. (26) is naturally satisfied with
![]() and
and
![]() for all
for all
![]() values. Since
values. Since
![]() ,
Equation (26) implies
,
Equation (26) implies
Deriving Eq. (26) with respect to
At the opposite limit, for decreasing ![]() values
values
![]() increases slightly less rapidly than
increases slightly less rapidly than
![]() (there is a correction depending on
(there is a correction depending on
![]() ). A simple approximation of
). A simple approximation of
![]() ,
with a relative error lower than 10%, for the ranges
,
with a relative error lower than 10%, for the ranges
![]() ,
,
![]() is
is
Equations ((27), (28)), as well as Fig. 2, show that
The normalized radius, ![]() ,
of the flux rope is found by setting
,
of the flux rope is found by setting
![]() in Eq. (25), or equivalently by setting
in Eq. (25), or equivalently by setting ![]() in Eq. (24) to its boundary value (Eq. (20)) and solving for
in Eq. (24) to its boundary value (Eq. (20)) and solving for
![]() .
The second way provides a more convenient equation for analysis,
.
The second way provides a more convenient equation for analysis,
A similar analysis of the behavior of
3.2 ``Split'' field
We consider in this section the theoretical field where
![]() and
and
![]() are separated in two different regions
are separated in two different regions
We simply refer to this magnetic field as ``SP'' below. This field is an extreme case where each component fully dominates in one region of the flux rope (in general, equilibriums have a gradual transition between a Bz dominated core to
a
![]() dominated periphery). The magnitude of
dominated periphery). The magnitude of
![]() for the limit
for the limit
![]() is selected to have an equilibrium (magnetic pressure balance with
is selected to have an equilibrium (magnetic pressure balance with
![]() ). Below we use the normalized parameter
). Below we use the normalized parameter
![]() .
.
The ratio of the azimuthal to the axial flux, defined as in Eq. (23), for this field is
Since the reference field (Eq. (30)) has only one non-null component in each region, the evolved field keeps this property (due to flux conservation). It implies a uniform Bz for
This equation has the same global structure than Eq. (26), then
It implies that the dependence of
The radial expansion of the field is found to be
1.25pt
implying a self-similar expansion of the core and a periphery strongly reduced in size as ![]() increases. The flux rope radius is simply
increases. The flux rope radius is simply
![]() .
This is a much simpler link to
.
This is a much simpler link to
![]() than for the GH field (Eq. (29)), while it has a similar dependence (Fig. 2).
than for the GH field (Eq. (29)), while it has a similar dependence (Fig. 2).
3.3 Linear force-free field
As an example of the general evolution of a flux rope field obtained by solving numerically Eqs. ((17), (18), (20)) we select the linear force-free model (Lundquist 1950) since it has shown good fits to various MC observations,
where J0 and J1 are the ordinary Bessel functions of order 0 and 1, respectively. This magnetic field is simply noted LU. The ratio of the azimuthal to the axial flux, defined as in Eq. (23), is
Fits of Eq. (35) to observed MCs typically implies
3.4 Comparison of the field evolutions
Below, we compare the evolution of the three fields defined in the above sections. Guided by the results on MCs, we compare the fields for
![]() (Fig. 2, left panels). We also show the case
(Fig. 2, left panels). We also show the case
![]() to illustrate an extreme case of very twisted flux ropes (not observed). Such an extreme case is selected for viewing purpose since the effect of
to illustrate an extreme case of very twisted flux ropes (not observed). Such an extreme case is selected for viewing purpose since the effect of
![]() is weak. We do not plot cases with
is weak. We do not plot cases with
![]() since they have an even lower dependence with
since they have an even lower dependence with ![]() ,
and all the fields have closer values of
,
and all the fields have closer values of
![]() and
and ![]() as
as
![]() decreases.
decreases.
As for the GH and SP fields (Eqs. (28), (33)),
![]() tends towards a fixed value for large value of
tends towards a fixed value for large value of ![]() for the LU field (Fig. 2, top panels). This corresponds to the case where the core field has expanded to fill most of the flux rope, so the central field
for the LU field (Fig. 2, top panels). This corresponds to the case where the core field has expanded to fill most of the flux rope, so the central field
![]() is almost equal to the field strength at the boundary. For
is almost equal to the field strength at the boundary. For
![]() ,
this limit is nearly the same for the three reference fields. In view of the strong differences in their twist distribution, we conclude that it is a general property for all field distributions found in MCs. Differences between the reference fields are only found for larger values of
,
this limit is nearly the same for the three reference fields. In view of the strong differences in their twist distribution, we conclude that it is a general property for all field distributions found in MCs. Differences between the reference fields are only found for larger values of
![]() .
For
.
For
![]() ,
the LU and SP results are still very close together (Fig. 2, right panels).
,
the LU and SP results are still very close together (Fig. 2, right panels).
A relatively strong variation of
![]() is present for small
is present for small ![]() values. This is because the region dominated by
values. This is because the region dominated by
![]() gets increasingly more extended compared to the core as
gets increasingly more extended compared to the core as ![]() becomes small. This implies an increasingly stronger variation of the field strength across the flux rope, then a central field less affected by the boundary field value, and so a larger
becomes small. This implies an increasingly stronger variation of the field strength across the flux rope, then a central field less affected by the boundary field value, and so a larger
![]() .
For
.
For
![]() ,
the GH and LU fields have very similar values of
,
the GH and LU fields have very similar values of
![]() ,
while the SP field has significant lower values (Fig. 2, top left panel).
,
while the SP field has significant lower values (Fig. 2, top left panel).
The results for ![]() are similar to the above results for
are similar to the above results for
![]() ,
with some minor differences that we do not describe (see Fig. 2, bottom panels). A main difference is the magnitude of the variations, with typically a factor 3 lower variation of
,
with some minor differences that we do not describe (see Fig. 2, bottom panels). A main difference is the magnitude of the variations, with typically a factor 3 lower variation of
![]() than of
than of
![]() .
.
While we consider three fields with very different twist profiles, the evolution of
![]() and
and ![]() are remarkably similar. This is obviously the case for a low ratio of the azimuthal to axial flux,
are remarkably similar. This is obviously the case for a low ratio of the azimuthal to axial flux,
![]() ,
since all the fields are dominated by their axial component and therefore these fields are similar. More interesting, this is approximately the case with
,
since all the fields are dominated by their axial component and therefore these fields are similar. More interesting, this is approximately the case with
![]() ,
a case typical of the values found in MCs. Even for the case of flux ropes much more twisted than MCs, the evolution of
,
a case typical of the values found in MCs. Even for the case of flux ropes much more twisted than MCs, the evolution of
![]() and
and ![]() are similar despite the very important differences in the field profiles (see Sect. 4.3 and Fig. 5).
are similar despite the very important differences in the field profiles (see Sect. 4.3 and Fig. 5).
We conclude that the evolution of
![]() and
and ![]() is weakly affected by the type of field profile. Moreover, the amplitude of the variation of
is weakly affected by the type of field profile. Moreover, the amplitude of the variation of
![]() and
and ![]() versus
versus ![]() remains moderate, especially for
remains moderate, especially for
![]() .
We compare this moderate evolution to the much stronger effect of
.
We compare this moderate evolution to the much stronger effect of
![]() in the field evolution in the next section.
in the field evolution in the next section.
4 Evolution of flux ropes in the solar wind
4.1 Flux rope length
The presence of counter-streaming suprathermal electrons in the SW is one of the primary signatures used to identify ICMEs (e.g., Gosling et al. 1987). It is also generally taken as an evidence that the corresponding field line is still rooted at both ends to the Sun since the solar corona is a reservoir of fast electrons (see e.g., Crooker & Horbury 2006; Wimmer-Schweingruber et al. 2006, for a review as well as possible caveats). Shodhan et al. (2000) found that periods of counter-streaming electrons are randomly distributed in 48 MCs observed near 1 AU, with a mean frequency of 59% of the MC duration. A very similar fraction, 55%, is found for 31 MCs observed at 5 AU indicating that a large fraction of a typical MC is still linked to the Sun (Crooker et al. 2004).
When the flux rope is attached to the Sun, the flux rope length, L, is mostly proportional to the distance, D, to the Sun (with only a weak correction depending on the evolution of the shape of the flux rope axis). When the flux rope becomes detached from the Sun, by reconnecting with the SW magnetic field, the evolution of L is more involved since torsional Alfvén waves are launched in the SW field. Here we simply suppose that the axial flux rope expansion evolves proportionally to its distance to the Sun. With the normalization to the reference field (Table 1) the coefficient of proportionality simplifies and the normalized length is simply
The implications of this assumption are relatively weak since
4.2 Solar wind total pressure
The total pressure in the SW, ![]() ,
has two main components: the plasma and the magnetic pressure.
,
has two main components: the plasma and the magnetic pressure.
Since the solar wind speed is radial and almost independent of solar distance, D, various
investigations found a plasma density decreasing as D-2 (e.g., Gazis et al. 2006; Issautier et al. 1998), in agreement with mass conservation. A wider variety of results are found for the electron temperature. The data are classically fit with a power-law
![]() .
nT is found to be typically in the range [0.3,1] (see Fig. 1 in Issautier et al. 1999). Recent estimations of nT are typically around 0.7, e.g.
.
nT is found to be typically in the range [0.3,1] (see Fig. 1 in Issautier et al. 1999). Recent estimations of nT are typically around 0.7, e.g.
![]() (Issautier et al. 1998) and
(Issautier et al. 1998) and
![]() (Gazis et al. 2006). The estimated values of nT are a function of the type of SW considered (slow/fast), of the removal or not of the ICMEs from the processed data, and of the range of distance considered. nT is typically observed to be lower in the fast SW and at larger D values, a tendency well reproduced by a kinetic collision-less SW model (Meyer-Vernet & Issautier 1998).
(Gazis et al. 2006). The estimated values of nT are a function of the type of SW considered (slow/fast), of the removal or not of the ICMEs from the processed data, and of the range of distance considered. nT is typically observed to be lower in the fast SW and at larger D values, a tendency well reproduced by a kinetic collision-less SW model (Meyer-Vernet & Issautier 1998).
The mean SW magnetic field is well described by the Parker model (Parker 1958) in most of the interplanetary space between 0.3 to 5 AU (Forsyth et al. 1996, and references therein).
Most of the observed deviations occur at high latitude where the Ulysses spacecraft found a slightly under wound magnetic field by
![]() ,
see Zurbuchen (2007) for a review. Then the SW magnetic field strength is approximately
,
see Zurbuchen (2007) for a review. Then the SW magnetic field strength is approximately
where
Following the above results, the total SW pressure is written in the undimensional form
where
Equation (39) provides the boundary condition, ![]() ,
for the flux rope expansion (Eq. (6)). In the above model,
,
for the flux rope expansion (Eq. (6)). In the above model,
![]() is a key function for the evolution of both the magnetic field strength, B, and the flux rope radius, R, (Eqs. (7), (16)). In Sect. 4.4, we compare the results of the model to studies of MCs/ICMEs that derived the evolution of both B and R with D from statistical analysis of a wide set of events observed at different D. All these studies fit the observed results with power law of D. Then, below we consider an approximation of Eq. (39) with a power law
is a key function for the evolution of both the magnetic field strength, B, and the flux rope radius, R, (Eqs. (7), (16)). In Sect. 4.4, we compare the results of the model to studies of MCs/ICMEs that derived the evolution of both B and R with D from statistical analysis of a wide set of events observed at different D. All these studies fit the observed results with power law of D. Then, below we consider an approximation of Eq. (39) with a power law
With this approach, we can also compare the above models to observations of expansion velocity measured at 1 AU (Sect. 4.5) if we derive the exponent nP at 1 AU.
The logarithmic derivative
![]() ,
called n, defines the local decrease of
,
called n, defines the local decrease of ![]() (i.e. a local approximation of
(i.e. a local approximation of ![]() is
is
![]() with nP=n). For
with nP=n). For
![]() ,
,
![]() since the radial component of the SW magnetic field provides the dominant pressure close to the Sun. At the opposite extreme, for
since the radial component of the SW magnetic field provides the dominant pressure close to the Sun. At the opposite extreme, for
![]() ,
,
![]() .
In between these two extremes, n varies between
.
In between these two extremes, n varies between
![]() to 2.5 for D varying from 0.3 to 3 AU.
to 2.5 for D varying from 0.3 to 3 AU.
At 1 AU, the radial and azimuthal magnetic field components are comparable in the slow SW present at low latitude (
![]() ). Then, the magnetic pressure alone implies
). Then, the magnetic pressure alone implies
![]() at 1 AU. The plasma pressure alone implies
at 1 AU. The plasma pressure alone implies
![]() with the recent results summarized above. Then, around 1 AU the value of n is weakly dependent on the plasma
with the recent results summarized above. Then, around 1 AU the value of n is weakly dependent on the plasma ![]() since the magnetic and plasma pressure provides similar n values. With
since the magnetic and plasma pressure provides similar n values. With
![]() ,
we get
,
we get
![]() for
for
![]() in the range [0.3,3]. Figure 3 shows that
in the range [0.3,3]. Figure 3 shows that
![]() (Eq. (40)), with nP = 2.8 is a good approximation of
(Eq. (40)), with nP = 2.8 is a good approximation of ![]() (Eq. (39)) within a relatively wide range of solar distances in the
slow SW. Finally, this value of n is only increased to
(Eq. (39)) within a relatively wide range of solar distances in the
slow SW. Finally, this value of n is only increased to
![]() for a fast SW (
for a fast SW (
![]() km s-1) and at high latitude (
km s-1) and at high latitude (
![]() ), so for
), so for
![]() ,
since the radial component of the magnetic field is then more dominant at 1 AU.
,
since the radial component of the magnetic field is then more dominant at 1 AU.
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.45\te...
...
{\includegraphics[width=0.45\textwidth, clip=]{0971f3bc.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg242.gif) |
Figure 3:
Log-log plots showing the evolution of the SW total pressure (Eq. (39)) normalized at 1 AU, and a power-law approximation (Eq. (40) with nP=2.8) as a function of the solar distance D
(in AU).
|
| Open with DEXTER | |
4.3 Expected evolution of flux ropes
With Eqs. ((37), (40)), (19) is rewritten as
With nP = 2.8,
More generally, with Eqs. (40), (16) implies
Figure 4 shows typical cases of observed MCs with
![]() .
All the three models considered above have a central field strength decreasing only slightly faster with solar distance than the
D-nP/2 scaling law. The radius of the flux rope increases with D slightly less than
D nP/4 since the correction to the scaling law is even smaller than for
.
All the three models considered above have a central field strength decreasing only slightly faster with solar distance than the
D-nP/2 scaling law. The radius of the flux rope increases with D slightly less than
D nP/4 since the correction to the scaling law is even smaller than for ![]() .
The slope difference becomes slightly more important as the flux rope becomes more twisted (larger
.
The slope difference becomes slightly more important as the flux rope becomes more twisted (larger
![]() ,
for example
,
for example
![]() in the right panels of Fig. 4).
in the right panels of Fig. 4).
The magnetic profile evolves with solar distance according to the results of Sect. 3. The core region expands more with increasing D than the periphery (panels of Bz and
![]() in Fig. 5 and panels
of
in Fig. 5 and panels
of
![]() in Fig. 6). This is because the SW total pressure does not decrease fast enough (less than D-4) to allow a true self-similar expansion of the flux rope. Indeed, the peripheral region is dominated by the azimuthal component. Its magnitude is mainly fixed by the total pressure
in Fig. 6). This is because the SW total pressure does not decrease fast enough (less than D-4) to allow a true self-similar expansion of the flux rope. Indeed, the peripheral region is dominated by the azimuthal component. Its magnitude is mainly fixed by the total pressure ![]() present in the surrounding SW. The extension in length,
present in the surrounding SW. The extension in length,
![]() ,
and the flux conservation restrict the radial expansion. As D increases, the field strength profile becomes flatter with the azimuthal component getting weaker than the axial component in most of the flux rope.
,
and the flux conservation restrict the radial expansion. As D increases, the field strength profile becomes flatter with the azimuthal component getting weaker than the axial component in most of the flux rope.
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.90\te...
...{
{\includegraphics[width=0.90\textwidth, clip=]{0971f4c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg254.gif) |
Figure 4:
Log-log plots of the central magnetic field strength, |
| Open with DEXTER | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=\textwi...
... }
}{
{\includegraphics[width=\textwidth, clip=]{0971f5c.eps} }
}
\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg256.gif) |
Figure 5:
Evolution of the field strength, B, the axial, Bz, and azimuthal,
|
| Open with DEXTER | |
4.4 Comparison to previous studies
We compare below our results with previous studies of MCs and ICMEs.Chen (1989) developed a toroidal model of a flux rope ejected from the Sun. The governing equations for the flux rope center and radius are deduced from MHD equations by approximately averaging the magnetic and plasma force over the flux rope cross section. Then, the deduced ordinary differential equations are solved starting from an initial unstable equilibrium in the corona. Chen (1996) extended the model to study the flux rope evolution in the interplanetary space using a SW model similar to the one described in Sect. 4.2. The initially stable flux rope in the corona is forced to erupt by imposing a strong increase of the azimuthal flux. However, while important for the physics of CMEs, the precise mechanism leading to the ejection should have a weak effect on the propagation of the interplanetary flux rope (for the same flux rope having the same global velocity).
The flux rope model of Chen (1996) keeps the inertial term and the plasma pressure in the internal dynamics while it only includes an approximate description of the magnetic forces. The model finally uses a spatial average of the force balance across the flux tube. Rather, we suppose that a force-free equilibrium is achieved at all times, and we analyze the internal force balance with several spatial profiles of the magnetic field. Despite these differences, the diameter of the flux rope has a similar dependence on the solar distance D (Table 2). This is so because the inertial term, the plasma pressure and the magnetic profile have only a weak effect on the diameter evolution. Most of the evolution is imposed by the dependence of
![]() in the surrounding SW.
in the surrounding SW.
Kumar & Rust (1996) developed a flux rope model based on the conservation of axial magnetic flux and magnetic helicity, supposing that the flux rope field stays linear force-free (see Sect. 5). They also analyzed a set of MCs previously fit to a LU field (see Sect. 3.3) by various authors.
Bothmer & Schwenn (1998) analyzed a set of
![]() MCs. The size S is defined by the product of the MC duration and the mean measured velocity (so they determine the apparent size of the MC along the spacecraft trajectory). Leitner et al. (2007) extended the analysis to 130 MCs, and they fit the magnetic field observations with the LU field (see Sect. 3.3), then they found the impact parameter and the orientation of the MC axis to estimate the diameter, d, of the MCs.
MCs. The size S is defined by the product of the MC duration and the mean measured velocity (so they determine the apparent size of the MC along the spacecraft trajectory). Leitner et al. (2007) extended the analysis to 130 MCs, and they fit the magnetic field observations with the LU field (see Sect. 3.3), then they found the impact parameter and the orientation of the MC axis to estimate the diameter, d, of the MCs.
In all these studies, the evolution of the MC radius (or size) is described by a power law,
![]() ,
in some range of distance, D, to the Sun. The above studies and ours agree on a larger exponent e in the internal heliosphere than outward. Indeed, the general tendency is
,
in some range of distance, D, to the Sun. The above studies and ours agree on a larger exponent e in the internal heliosphere than outward. Indeed, the general tendency is
![]() for D<1 AU, so that the expansion is close to self-similar, while
for D<1 AU, so that the expansion is close to self-similar, while
![]() for D>1 AU (Table 2). Around 1 AU, we find a power law exponent closer to the one of Leitner et al. when the full range of D is considered ([0.3, 7] AU).
for D>1 AU (Table 2). Around 1 AU, we find a power law exponent closer to the one of Leitner et al. when the full range of D is considered ([0.3, 7] AU).
Table 2: Summary of results on MCs and ICMEs.
We also compare our results with ICME studies (containing a subset of MCs). Liu et al. (2005) did a statistical study of about 220 ICMEs observed in situ from 0.3 to 5.4 AU. They combined two criteria to localize ICMEs: an enhanced alpha-to-proton density ratio (greater than 0.08) and a low proton temperature (lower than half the value expected in the solar wind with the same speed). Wang et al. (2005) did a similar analysis on a wider set of 600 possible ICMEs defined only by using the low temperature criteria. The size S is defined as for Bothmer & Schwenn (1998). These two similar studies have surprisingly different exponents for the power law fits (Table 2). Our result best agree with Wang et al. (2005), who found the same exponent as Leitner et al. (2007).
The same comparison is done for the magnetic field strength (with the exception of Chen (1996) who did not wrote this result). Our exponent is closer to the results of Leitner et al. (2007) within the inner heliosphere (while for the diameter, the agreement is best for the full range of D, Table 2). Our results are also compatible with both ICME studies within the uncertainties of the exponents (however, we do not compute a mean field, as for ICME studies).
We conclude that, taking into account the uncertainties, the field strength versus the distance predicted by our model is in good agreement with the observations. We also find that the relation for the flux rope diameter, and for the field strength, versus solar distance is not strictly a power-law (Fig. 4). This could be the main reason for the different results reported in Table 2 since the computed exponents dependent on the distribution of the analyzed events with solar distance in the different data sets.
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=\textwi...
... }
}{
{\includegraphics[width=\textwidth, clip=]{0971f6c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg280.gif) |
Figure 6:
Evolution of a flux rope for the three ideal-MHD cases shown in Fig. 5 (D = (0.1, 1, 10) AU in the top, middle,
bottom panels, respectively). r is the radial coordinate of the flux rope, with |
| Open with DEXTER | |
4.5 Expansion velocity
Since the time evolution of the flux rope is ideal we compute the plasma velocity by deriving
![]() with time, keeping
with time, keeping ![]() fixed (so following the same blob of plasma). With Eqs. ((16), (40)) we find
fixed (so following the same blob of plasma). With Eqs. ((16), (40)) we find
where
From the results of Sect. 3 and with ![]() written as a function of
written as a function of ![]() (Eq. (41)), we find that
(Eq. (41)), we find that
![]() is small compare to nP/4, so that the velocity inside the flux rope is approximately proportional to r (Fig. 6). A small correction to this is due to a weaker expansion of the flux-rope periphery (Sect. 4.3). This implies a smaller velocity there (than if the whole flux rope had a self-similar expansion).
is small compare to nP/4, so that the velocity inside the flux rope is approximately proportional to r (Fig. 6). A small correction to this is due to a weaker expansion of the flux-rope periphery (Sect. 4.3). This implies a smaller velocity there (than if the whole flux rope had a self-similar expansion).
The velocity profile becomes a linear function of r with increasing D since the dominated axial field region extends to a larger fraction of the flux rope (Fig. 5). Moreover, the expansion speed decreases with distance because r increases less rapidly than D. The expansion speed decreases by about a factor of two with a factor of ten increase in distance. Another effect to take into account for a wide range of D is the decrease of nP with D when the full
![]() is used (Eq. (39)), but here this weaker effect is not taken into account since we use Eq. (40) with nP=2.8. This effect is at most a factor of 2 from
is used (Eq. (39)), but here this weaker effect is not taken into account since we use Eq. (40) with nP=2.8. This effect is at most a factor of 2 from ![]() AU to
AU to ![]() AU) since
AU) since
![]() evolves at most from 4 close to the Sun to 2 at very large distances (Sect. 4.2).
evolves at most from 4 close to the Sun to 2 at very large distances (Sect. 4.2).
Next, it is remarkable that ``GH'' and ``LU'' fields have such similar velocities. Only the ``SP'' field, with its separation of field components into distinct regions, has a slightly different profile. We conclude that the velocity profiles measured in MCs are expected to be almost independent of the magnetic profile observed.
The magnitude of the expansion is directly proportional to the global velocity of the MC (![]() ), so that the results of Fig. 6 are scaled by
), so that the results of Fig. 6 are scaled by ![]() (Eq. (43)). In fact
(Eq. (43)). In fact ![]() has an even stronger effect on the observed velocity profiles since they are function of time, t, not of r, as follows. Let us just consider here the simplest case where the spacecraft crosses the center of the flux rope nose moving at a constant velocity
has an even stronger effect on the observed velocity profiles since they are function of time, t, not of r, as follows. Let us just consider here the simplest case where the spacecraft crosses the center of the flux rope nose moving at a constant velocity ![]() ,
then the position observed by the spacecraft is
,
then the position observed by the spacecraft is
![]() with
with ![]() being the time when the spacecraft crosses the flux rope center. Then, Eq. (43) rewritten in function of the observed time (t) is
being the time when the spacecraft crosses the flux rope center. Then, Eq. (43) rewritten in function of the observed time (t) is
This implies that the magnitude of the observed expansion velocity scales as
The generalization of the above results to all possible types of spacecraft/MC crossing can be derived following the same logic than as Démoulin et al. (2008). They consider self-similar expansion of a magnetic configurations with possible different expansion coefficients, l,m,n in three orthogonal directions (i.e., along the axial direction
![]() ,
and similar expressions in the x,y directions). Otherwise any orientation of the flux rope, any impact parameter and any radial motion of the flux rope away from the Sun can be selected. Redoing the analysis with the above flux ropes, we get the same equations for the velocity components at the spacecraft location, except that n=1 (from Eq. (37)) and
,
and similar expressions in the x,y directions). Otherwise any orientation of the flux rope, any impact parameter and any radial motion of the flux rope away from the Sun can be selected. Redoing the analysis with the above flux ropes, we get the same equations for the velocity components at the spacecraft location, except that n=1 (from Eq. (37)) and
![]() .
Then l,m are no longer constant across the flux rope. Still, nP/4 is the dominant term and only weak variations are present (Fig. 6, right panels). As expected from Figs. 2, 4, the core expands slightly more rapidly than the periphery of the flux rope.
.
Then l,m are no longer constant across the flux rope. Still, nP/4 is the dominant term and only weak variations are present (Fig. 6, right panels). As expected from Figs. 2, 4, the core expands slightly more rapidly than the periphery of the flux rope.
Finally, the above theoretical results on the expansion rate are compared to the expansion rate found in 26 typical MCs observed at 1 AU (Démoulin et al. 2008). They fit the observed main velocity component (anti-solar direction) with a linear function of time.
The observed slope,
![]() ,
normalized by
,
normalized by
![]() provides an estimation, called
provides an estimation, called ![]() ,
of the exponent l, since the MCs are observed close to their noses. They found
,
of the exponent l, since the MCs are observed close to their noses. They found
![]() .
This is indeed in close agreement with our theoretical expectations since we find
.
This is indeed in close agreement with our theoretical expectations since we find
![]() across all the theoretical flux ropes at 1 AU (Fig. 6, recalling that the ``SP'' case is far from observed MCs). We conclude that the expansion of MCs is dominantly controlled by the decrease of the total SW pressure with solar distance.
across all the theoretical flux ropes at 1 AU (Fig. 6, recalling that the ``SP'' case is far from observed MCs). We conclude that the expansion of MCs is dominantly controlled by the decrease of the total SW pressure with solar distance.
5 Evolution of flux ropes with energy minimization
In previous sections we have studied the evolution of flux ropes supposing an ideal MHD evolution, so preserving both the elementary axial and azimuthal magnetic fluxes. Here we investigate another extreme limit where the flux rope evolves with all the necessary reconnections to minimize its magnetic energy, keeping constant its magnetic helicity. The purpose is to check if the results of previous sections are robust enough. The true evolution of MCs is in between these two extreme limits.
5.1 Linear force-free state
In a resistive MHD evolution, for systems with low resistivity as the solar wind,
the magnetic field cannot relax to its absolute minimum energy since its magnetic helicity, H, is almost conserved (on a time-scale less than the global diffusion time-scale, that is typically many orders of magnitude above the evolution time scales, Matthaeus & Goldstein 1982; Berger 1984). If there is enough dissipation (e.g., via magnetic reconnection or turbulent dissipation) to remove all the free magnetic energy, the magnetic field relaxes to a linear force-free field (Taylor 1974). We assume such minimization of the magnetic energy under the constraint of a fixed H in present section (this is just an extreme possibility, we are not claiming that this energy minimization is fully achieved in MCs). This implies that the magnetic field stays a Lundquist's field in the flux rope (r<R)
where
Our approach is similar to the one of Kumar & Rust (1996). A main difference is that we do not set an external curl-free magnetic field around the flux rope. Indeed, in situ observations do not show evidence of this purely azimuthal field around MCs but rather the presence of the SW (with its variable magnetic field). This difference of treatment of the region outside the flux rope is at the primary differences between Kumar & Rust (1996) and our results (the scaling with solar distance, Table 2, as well as the evolution of the magnetic field profile, Fig. 5).
5.2 Formal solution of the evolution
The magnetic helicity contained in a cylindrical flux rope of length L is (Berger 1999)
where
with
We next suppose that there is no reconnection with the solar wind magnetic field. Then, the flux rope stays attached to the Sun, and the total axial magnetic flux, Fz is conserved, where Fz can be written as
If the flux rope partly reconnects with the overtaken solar wind magnetic field, being partially peeled, as observed in some cases (Dasso et al. 2006,2007), the present derivation could be applied only to the un-reconnected central part of the flux rope.
The pressure equilibrium at the boundary (Eq. (6)) is written as
There are three unknowns,
As in Sect. 2.4, the normalized field strength,
![]() ,
and
radius
,
and
radius ![]() only depends on
only depends on
![]() .
Defining the function f(U) as
.
Defining the function f(U) as
the solution of the system of Eqs. (50) is
![]() and R are obtained by replacing the above results
for
and R are obtained by replacing the above results
for
![]() and
and ![]() in Eq. (16).
in Eq. (16).
![\begin{figure}
\IfFileExists{color_figures.txt} {
{\includegraphics[width=0.47\t...
...
{\includegraphics[width=0.47\textwidth, clip=]{0971f7c.eps} }
}
\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg320.gif) |
Figure 7:
The evolution of
|
| Open with DEXTER | |
5.3 Evolution of flux ropes
As the flux rope gets farther from the Sun, its length L increases and the total pressure in the surrounding solar wind,for
We analyze first the evolution of U since it determines the spatial behavior of the field components. Two values of U are worth outlining. Let us call zJ0 and zJ1 the first zero of the Bessel functions J0 and J1, respectively. For U=zJ0 the axial field Bz vanishes (it frequently takes place near the observed flux rope boundary),
while for U=zJ1, the axial magnetic flux Fz vanishes (Eq. (48)). From the MC data fitted with the Lundquist field, the value of U is typically found to be around zJ0, while generally U<zJ1. Then, the range
![]() includes the observed MCs, and Fz(U) is a single-value and monotonically decreasing function of U. This implies that U stays in the same interval as
includes the observed MCs, and Fz(U) is a single-value and monotonically decreasing function of U. This implies that U stays in the same interval as ![]() to keep Fz preserved.
to keep Fz preserved.
The evolution of U is determined by the behavior of the function f(U) defined by Eq. (51). It is a monotonically decreasing function of U for
0<U<zJ1, with the limits
![]() for
for ![]() and
f(zJ1)=0. A simple approximation, only slightly underestimating f(U), is the function
and
f(zJ1)=0. A simple approximation, only slightly underestimating f(U), is the function
![]() .
Including this approximation in the first equation of (52), we get the approximate solution, plotted in Fig. 7,
.
Including this approximation in the first equation of (52), we get the approximate solution, plotted in Fig. 7,
In the SW case,
For ![]() decreasing below 1, the opposite behavior is present, i.e. the flux rope is more dominated by its azimuthal field for lower
decreasing below 1, the opposite behavior is present, i.e. the flux rope is more dominated by its azimuthal field for lower ![]() values. Then, we found the same behavior as with an ideal MHD evolution (Sect. 3.4). The limiting case, for
values. Then, we found the same behavior as with an ideal MHD evolution (Sect. 3.4). The limiting case, for ![]() small enough, is
small enough, is
![]() ,
resulting in a flux rope with a significant reverse Bz flux around the core field. Starting close to the Sun with this type of field, an evolution, that minimizes the energy, progressively removes the reverse Bz flux by reconnection to provide only an axial field, Bz, with a fixed sign within the flux rope (as often observed at and beyond 1 AU in MCs). Later, this relaxation continues and creates an increasingly flatter Bz profile, as well as a smaller
,
resulting in a flux rope with a significant reverse Bz flux around the core field. Starting close to the Sun with this type of field, an evolution, that minimizes the energy, progressively removes the reverse Bz flux by reconnection to provide only an axial field, Bz, with a fixed sign within the flux rope (as often observed at and beyond 1 AU in MCs). Later, this relaxation continues and creates an increasingly flatter Bz profile, as well as a smaller
![]() contribution to the field strength.
contribution to the field strength.
The evolution of
![]() is very limited in this energy minimization case (Fig. 2, top panels), mostly because the field stays a Lundquist's field and so lacks any significant difference between the field strength at the center and at the border of the flux rope. Then, most of the field strength evolution at the center is included in the
is very limited in this energy minimization case (Fig. 2, top panels), mostly because the field stays a Lundquist's field and so lacks any significant difference between the field strength at the center and at the border of the flux rope. Then, most of the field strength evolution at the center is included in the
![]() term (Eq. (16)). Indeed, from Eq. (52), we have
term (Eq. (16)). Indeed, from Eq. (52), we have
![]() ,
and at most only a change of a factor
,
and at most only a change of a factor
![]() is possible for
is possible for
![]() (compare to orders of magnitude for
(compare to orders of magnitude for
![]() ). Then the energy minimization case follows very well the simple scaling law
). Then the energy minimization case follows very well the simple scaling law
![]() (Fig. 4, top panels).
(Fig. 4, top panels).
The evolution of ![]() with
with ![]() is larger than with
is larger than with
![]() since
since ![]() involves not only fP(U), but also fF(U) that has a broader variation range.
involves not only fP(U), but also fF(U) that has a broader variation range.
![]() has a variation comparable to the ideal-MHD cases analyzed in Sect. 3 (Fig. 2, bottom panels).
has a variation comparable to the ideal-MHD cases analyzed in Sect. 3 (Fig. 2, bottom panels).
As for the ideal-MHD cases, the evolutions of both ![]() and R with the solar distance D are dominated by the
and R with the solar distance D are dominated by the
![]() contributions in Eq. (16). Indeed, Fig. 4 summarizes a broad range of evolutions ranging from ideal-MHD with very different twist profiles to a fully resistive evolution. The evolution of MCs is expected to be in between these cases, so their evolution of both
contributions in Eq. (16). Indeed, Fig. 4 summarizes a broad range of evolutions ranging from ideal-MHD with very different twist profiles to a fully resistive evolution. The evolution of MCs is expected to be in between these cases, so their evolution of both ![]() and R are expected to be mainly due to
and R are expected to be mainly due to
![]() .
The slight differences between the above models is not expected to appear in observations since these differences can easily be covered by other effects not considered here, such as the non-circular cross section of the flux rope, the dynamic SW pressure, the MC over-pressure, the jump of pressure at shocks, the reconnection with the SW, and the interaction with SW inhomogeneities (in particular overtaking flows).
.
The slight differences between the above models is not expected to appear in observations since these differences can easily be covered by other effects not considered here, such as the non-circular cross section of the flux rope, the dynamic SW pressure, the MC over-pressure, the jump of pressure at shocks, the reconnection with the SW, and the interaction with SW inhomogeneities (in particular overtaking flows).
6 Summary and conclusions
MCs are expanding flux ropes in the interplanetary space with very different expansion properties than the SW, as derived from the observed profiles of plasma velocity at fixed heliodistance, but also from the plasma density and field strength evolution with solar distance. Since the magnetic field energetically dominates the plasma in MCs, the difference in expansion between MC and SW is related to the special magnetic configuration of MCs. Several questions about the main physical mechanisms involved in their expansion remain unanswered in previous studies, e.g. how does their expansion depend on their magnetic configuration? Is an internal over-pressure needed to explain the observed expansion?
We investigate these problems by focusing on the main physical properties. As a local approximation for an elongated field configuration, we consider a straight cylindrical flux rope geometry. Since the plasma ![]() is low and the expansion velocity frequently is below the local Alfvén speed in most of the MC volume (Burlaga et al. 1982), we analyze the flux rope evolution as a series of force-free equilibria in pressure balance with the surrounding SW. We show that the presence of shocks or/and an internal over pressure only has a weak effect compared to the variation of the SW total pressure,
is low and the expansion velocity frequently is below the local Alfvén speed in most of the MC volume (Burlaga et al. 1982), we analyze the flux rope evolution as a series of force-free equilibria in pressure balance with the surrounding SW. We show that the presence of shocks or/and an internal over pressure only has a weak effect compared to the variation of the SW total pressure,
![]() ,
with solar distance D. We do not include the dynamic pressure of the SW (supposing that the MC and the SW travel at sufficiently comparable velocities). These simplifications permit us to tackle the problem analytically in some cases, and more generally by solving a system of ordinary differential equations (Eqs. (14)-(15)), allowing us a broad survey of the possible magnetic configurations and their evolution with solar distance.
,
with solar distance D. We do not include the dynamic pressure of the SW (supposing that the MC and the SW travel at sufficiently comparable velocities). These simplifications permit us to tackle the problem analytically in some cases, and more generally by solving a system of ordinary differential equations (Eqs. (14)-(15)), allowing us a broad survey of the possible magnetic configurations and their evolution with solar distance.
The main dependence of the field strength and radius is derived analytically in Sects. 3 and 5. We show that they mainly depend on the product
![]() ,
where L is the length of the flux rope and
,
where L is the length of the flux rope and ![]() is the total pressure in the SW. Then, flux ropes with a length evolving proportionally to
is the total pressure in the SW. Then, flux ropes with a length evolving proportionally to
![]() have a self-similar evolution independently of the structure of their magnetic field (i.e. field strength and spatial scales are simply multiplied by a global factor, function of
have a self-similar evolution independently of the structure of their magnetic field (i.e. field strength and spatial scales are simply multiplied by a global factor, function of
![]() ,
as D increases).
,
as D increases).
While a flux rope still attached to the Sun departs significantly from
![]() with the observed
with the observed
![]() dependence in the SW
dependence in the SW
![]() ,
we show that these flux ropes still have a nearly self-similar radial expansion. More precisely, their radius is mainly multiplied by
,
we show that these flux ropes still have a nearly self-similar radial expansion. More precisely, their radius is mainly multiplied by
![]() and their field strength by
and their field strength by
![]() as they travel away from the Sun (Sect. 3). This result is obtained after investigating the evolution of the several spatial distributions of magnetic field inside the flux rope. First, we analyze the ideal MHD evolution of a Lundquist's field, as well as extreme twist distributions (uniform or concentrated at the periphery of the flux rope, Sect. 4). Then, we consider the minimization of the magnetic energy with constant helicity (Sect. 5). The strongest departure from these laws, that still remains moderate, is obtained for flux ropes much more twisted than actually observed in MCs (Figs. 2, 4, right panels).
as they travel away from the Sun (Sect. 3). This result is obtained after investigating the evolution of the several spatial distributions of magnetic field inside the flux rope. First, we analyze the ideal MHD evolution of a Lundquist's field, as well as extreme twist distributions (uniform or concentrated at the periphery of the flux rope, Sect. 4). Then, we consider the minimization of the magnetic energy with constant helicity (Sect. 5). The strongest departure from these laws, that still remains moderate, is obtained for flux ropes much more twisted than actually observed in MCs (Figs. 2, 4, right panels).
For a flux rope environment given by a magnetized medium described by the Parker spiral of the SW, and values of plasma ![]() between 0.1 and 10, we found that the MC core expands slightly faster than its periphery with increasing D. This evolution is due to different constraints present on the axial field (dominant in the core) and on the azimuthal field (dominant at the periphery). This implies a flatter field strength profile with increasing D for both ideal and resistive evolutions. This is a plausible origin of the flattening tendency previously noticed in MCs observed at various solar distances (e.g., Burlaga et al. 1998).
between 0.1 and 10, we found that the MC core expands slightly faster than its periphery with increasing D. This evolution is due to different constraints present on the axial field (dominant in the core) and on the azimuthal field (dominant at the periphery). This implies a flatter field strength profile with increasing D for both ideal and resistive evolutions. This is a plausible origin of the flattening tendency previously noticed in MCs observed at various solar distances (e.g., Burlaga et al. 1998).
The expansion velocity is found to be almost proportional to the distance from the flux rope axis. While the expansion of the flux rope core (dominated by the axial field) is almost self-similar, the periphery (dominated by the azimuthal field) is expanding at a slightly lower rate for a typical twist value found in MCs. The velocity profile is almost the same for all the cases considered (varying the spatial distribution of the magnetic field and the dissipation law permitted in the MHD system). These results explain the origin of a nearly linear velocity profile observed generically in MCs.
Moreover, the expansion velocity rate found in the models described here is in full agreement with the values observed in MCs (Démoulin et al. 2008). Simulating the crossing of a MC orthogonally to its axis by a fixed spacecraft, we find a plasma velocity equal to
![]() ,
where t is the time (=0 at the
MC axis),
,
where t is the time (=0 at the
MC axis), ![]() is the velocity of the flux rope center, and l is an approximately constant coefficient (i.e. independent of the position within the flux rope and of the magnetic field configuration). We previously found the same functional form by analyzing a set of MCs observed at 1 AU (Démoulin et al. 2008). Furthermore, with a dependence of the SW total pressure as
is the velocity of the flux rope center, and l is an approximately constant coefficient (i.e. independent of the position within the flux rope and of the magnetic field configuration). We previously found the same functional form by analyzing a set of MCs observed at 1 AU (Démoulin et al. 2008). Furthermore, with a dependence of the SW total pressure as
![]() ,
we find
,
we find
![]() in present analysis. The typical decay of the SW pressure corresponds to
in present analysis. The typical decay of the SW pressure corresponds to
![]() ,
providing
,
providing
![]() ,
in agreement with our previous results
,
in agreement with our previous results
![]() in a set of MCs.
in a set of MCs.
The theoretical profile found,
![]() ,
also implies that the velocity profile observed in a MC by a spacecraft, with a given position in space, is strongly dependent on the mean velocity,
,
also implies that the velocity profile observed in a MC by a spacecraft, with a given position in space, is strongly dependent on the mean velocity, ![]() of the observed MC. Indeed, faster MCs need to expand faster to reach an approximate pressure balance with the surrounding SW at a given distance from the Sun. Also, bigger MCs have a larger velocity difference between their front and back simply because they are larger (and the expansion is almost self-similar). Our theoretical results further justify the use of a normalized expansion rate, rather than simply the difference between the front and back velocities, in order to quantify whether a MC is over-expanding or not.
of the observed MC. Indeed, faster MCs need to expand faster to reach an approximate pressure balance with the surrounding SW at a given distance from the Sun. Also, bigger MCs have a larger velocity difference between their front and back simply because they are larger (and the expansion is almost self-similar). Our theoretical results further justify the use of a normalized expansion rate, rather than simply the difference between the front and back velocities, in order to quantify whether a MC is over-expanding or not.
Finally, we found that the magnetic field strength evolves mostly as D-nP/2 and the MC radius as DnP/4. Both dependences predicted under general conditions by our model are in agreement with several statistical studies of MCs and ICMEs observed between 0.3 and 5 AU, taking into account the typical SW pressure dependence on solar distance.
We conclude that MCs and ICMEs are expanding magnetic structures mostly because they encounter a strongly decreasing total pressure in the surrounding SW as they travel away from the Sun. MCs are 3D expanding structures, with approximately a self-similar expansion along and across their axis, but with slightly different rate in these directions (in our model the expansion velocity across their axis is a factor
![]() lower than along their axis). This contrasts with the almost 2D expansion of the surrounding SW. The main differences between the typical expansion profiles of MCs and the SW are due to the different force balances involved. The MC expansion is the combined result of the internal magnetic force balance, its length extension and the pressure evolution at its boundary. However, the volume exponents are not so different in MCs and the SW (
lower than along their axis). This contrasts with the almost 2D expansion of the surrounding SW. The main differences between the typical expansion profiles of MCs and the SW are due to the different force balances involved. The MC expansion is the combined result of the internal magnetic force balance, its length extension and the pressure evolution at its boundary. However, the volume exponents are not so different in MCs and the SW (
![]() and
and
![]() ,
respectively). This implies, as observed, only a slightly more rapid decrease of the plasma density with solar distance in MCs than in the SW.
,
respectively). This implies, as observed, only a slightly more rapid decrease of the plasma density with solar distance in MCs than in the SW.
Acknowledgements
We thank Lidia van Driel-Gesztelyi and the referee for reading carefully, and, so improving the manuscript. The authors acknowledge financial support from ECOS-Sud through their cooperative science program (No. A08U01). This work was partially supported by the Argentinean grants: UBACyT X425, PICTs 2005-03-33370 and 2007-03-00856 (ANPCyT). S.D. is member of the Carrera del Investigador Científico, CONICET.
References
- Berdichevsky, D. B., Lepping, R. P., & Farrugia, C. J. 2003, Phys. Rev. E, 67, 036405 [NASA ADS] [CrossRef] (In the text)
- Berger, M. A. 1984, Geophys. Astrophys. Fluid. Dyn., 30, 79 [NASA ADS] [CrossRef]
- Berger, M. A. 1999, in Magnetic Helicity in Space and Laboratory Plasmas, 1 (In the text)
- Bothmer, V., & Schwenn, R. 1998, Annales Geophysicae, 16, 1 [NASA ADS] [CrossRef] (In the text)
- Burlaga, L. F. 1988, J. Geophys. Res., 93, 7217 [NASA ADS] [CrossRef] (In the text)
- Burlaga, L. F. 1995, Interplanetary magnetohydrodynamics (New York: Oxford University Press) (In the text)
- Burlaga, L. F., & Behannon, K. W. 1982, Sol. Phys., 81, 181 [NASA ADS] [CrossRef] (In the text)
- Burlaga, L. F., Klein, L., Sheeley, Jr., N. R., et al. 1982, Geophys. Res. Lett., 9, 1317 [NASA ADS] [CrossRef] (In the text)
- Burlaga, L., Fitzenreiter, R., Lepping, R., et al. 1998, J. Geophys. Res., 103, 277 [NASA ADS] [CrossRef] (In the text)
- Cane, H. V., & Richardson, I. G. 2003, J. Geophys. Res., 108, 1156 [CrossRef] (In the text)
- Cargill, P. J., & Schmidt, J. M. 2002, Annales Geophysicae, 20, 879 [NASA ADS]
- Cargill, P. J., Schmidt, J., Spicer, D. S., & Zalesak, S. T. 2000, J. Geophys. Res., 105, 7509 [NASA ADS] [CrossRef]
- Chané, E., Van der Holst, B., Jacobs, C., Poedts, S., & Kimpe, D. 2006, A&A, 447, 727 [NASA ADS] [CrossRef] [EDP Sciences]
- Chen, J. 1989, ApJ, 338, 453 [NASA ADS] [CrossRef] (In the text)
- Chen, J. 1996, J. Geophys. Res., 101, 27499 [NASA ADS] [CrossRef] (In the text)
- Cid, C., Hidalgo, M. A., Nieves-Chinchilla, T., Sequeiros, J., & Viñas, A. F. 2002, Sol. Phys., 207, 187 [NASA ADS] [CrossRef] (In the text)
- Crank, J. 1984, Free and moving boundary problems (New York: Oxford University Press) (In the text)
- Crooker, N. U., & Horbury, T. S. 2006, Space Sci. Rev., 123, 93109 [CrossRef]
- Crooker, N. U., Forsyth, R., Rees, A., Gosling, J. T., & Kahler, S. W. 2004, J. Geophys. Res., 109, A06110 [CrossRef] (In the text)
- Dasso, S., Mandrini, C. H., Démoulin, P., & Farrugia, C. J. 2003, J. Geophys. Res., 108, 1362 [CrossRef] (In the text)
- Dasso, S., Mandrini, C. H., Démoulin, P., Luoni, M. L., & Gulisano, A. M. 2005, Adv. Spa. Res., 35, 711 [NASA ADS] [CrossRef] (In the text)
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [NASA ADS] [CrossRef] [EDP Sciences]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] (In the text)
- Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [NASA ADS] [CrossRef] (In the text)
- Farrugia, C. J., Burlaga, L. F., Osherovich, V. A., et al. 1993, J. Geophys. Res., 98, 7621 [NASA ADS] [CrossRef] (In the text)
- Farrugia, C. J., Osherovich, V. A., & Burlaga, L. F. 1997, Annales Geophysicae, 15, 152 [NASA ADS] [CrossRef] (In the text)
- Farrugia, C. J., Janoo, L. A., Torbert, R. B., et al. 1999, in Solar Wind Nine, ed. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, AIP Conf. Proc., 471, 745 (In the text)
- Feng, H. Q., Wu, D. J., & Chao, J. K. 2007, J. Geophys. Res., 112, A02102 [CrossRef]
- Forbes, T. G., Linker, J. A., Chen, J., et al. 2006, Space Sci. Rev., 123, 251302 [CrossRef] (In the text)
- Forsyth, R. J., Balogh, A., Smith, E. J., Erdös, G., & McComas, D. J. 1996, J. Geophys. Res., 101, 395 [NASA ADS] [CrossRef] (In the text)
- Gazis, P. R., Balogh, A., Dalla, S., et al. 2006, Space Sci. Rev., 123, 417451 [CrossRef]
- Gold, T., & Hoyle, F. 1960, MNRAS, 120, 89 [NASA ADS] (In the text)
- Gosling, J. T., Baker, D. N., Bame, S. J., Feldman, W. C., & Zwickl, R. D. 1987, J. Geophys. Res., 92, 8519 [NASA ADS] [CrossRef], 8535 (In the text)
- Gosling, J. T., Riley, P., McComas, D. J., & Pizzo, V. J. 1998, J. Geophys. Res., 103, 1941 [NASA ADS] [CrossRef] (In the text)
- Gosling, J. T., Skoug, R. M., McComas, D. J., & Smith, C. W. 2005, J. Geophys. Res., 110, A01107 [CrossRef]
- Hidalgo, M. A. 2003, J. Geophys. Res., 108, 1320 [CrossRef] (In the text)
- Hidalgo, M. A., Cid, C., Vinas, A. F., & Sequeiros, J. 2002, J. Geophys. Res., 107, 1002 [CrossRef] (In the text)
- Hu, Q., & Sonnerup, B. U. Ö. 2002, J. Geophys. Res., 107, 1142 [CrossRef]
- Hu, Q., Smith, C. W., Ness, N. F., & Skoug, R. M. 2005, J. Geophys. Res., 110, A09S [CrossRef]03
- Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1998, J. Geophys. Res., 103, 1969 [NASA ADS] [CrossRef]
- Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1999, ed. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, AIP Conf. Ser., 471, 581 (In the text)
- Jian, L., Russell, C. T., Luhmann, J. G., & Skoug, R. M. 2006, Sol. Phys., 239, 393 [NASA ADS] [CrossRef] (In the text)
- Kumar, A., & Rust, D. M. 1996, J. Geophys. Res., 101, 15677 [NASA ADS] (In the text)
- Leitner, M., Farrugia, C. J., Möstl, C., et al. 2007, J. Geophys. Res., 112, A06113 [CrossRef] (In the text)
- Lepping, R. P., Burlaga, L. F., & Jones, J. A. 1990, J. Geophys. Res., 95, 11957 [NASA ADS] [CrossRef] (In the text)
- Lepping, R. P., Berdichevsky, D. B., Szabo, A., Arqueros, C., & Lazarus, A. J. 2003, Sol. Phys., 212, 425 [NASA ADS] [CrossRef]
- Liu, Y., Richardson, J. D., & Belcher, J. W. 2005, Planet. Space Sci., 53, 3 [NASA ADS] [CrossRef] (In the text)
- Liu, Y., Richardson, J. D., Belcher, J. W., et al. 2006, J. Geophys. Res., 111, A12S03
- Lundquist, S. 1950, Ark. Fys., 2, 361 (In the text)
- Lynch, B. J., Zurbuchen, T. H., Fisk, L. A., & Antiochos, S. K. 2003, J. Geophys. Res., 108, 1239 [CrossRef] (In the text)
- Manchester, W. B. I., Gombosi, T. I., Roussev, I., et al. 2004, J. Geophys. Res., 109, A02107 [CrossRef]
- Mandrini, C. H., Nakwacki, M., Attrill, G., et al. 2007, Sol. Phys., 244, 25 [NASA ADS] [CrossRef] (In the text)
- Matthaeus, W. H., & Goldstein, M. L. 1982, J. Geophys. Res., 87, 6011 [NASA ADS] [CrossRef]
- Meyer-Vernet, N., & Issautier, K. 1998, J. Geophys. Res., 103, 29705 [NASA ADS] [CrossRef] (In the text)
- Mulligan, T., Russell, C. T., Anderson, B. J., et al. 1999, in Solar Wind Nine, ed. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, AIP Conf. Proc., 471, 689 (In the text)
- Nakwacki, M., Dasso, S., Mandrini, C., & Demoulin, P. 2008, Journal of Atmospheric and Solar-Terrestrial Physics, 70, 1318 [NASA ADS] [CrossRef] (In the text)
- Osherovich, V. A., Farrugia, C. J., & Burlaga, L. F. 1993, J. Geophys. Res., 98, 13225 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1958, ApJ, 128, 664 [NASA ADS] [CrossRef] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes (Cambridge University Press) (In the text)
- Richardson, I. G., & Cane, H. V. 2004, J. Geophys. Res., 109, A09104 [CrossRef] (In the text)
- Riley, P., Linker, J. A., Mikic, Z., et al. 2003, J. Geophys. Res., 108, 1272 [CrossRef]
- Riley, P., Gosling, J. T., & Crooker, N. U. 2004, ApJ, 608, 1100 [NASA ADS] [CrossRef] (In the text)
- Shen, F., Feng, X., Wu, S. T., & Xiang, C. 2007, J. Geophys. Res., 112, A06109 [CrossRef]
- Shimazu, H., & Vandas, M. 2002, Earth, Planets, and Space, 54, 783 (In the text)
- Shodhan, S., Crooker, N. U., Kahler, S. W., et al. 2000, J. Geophys. Res., 105, 27261 [NASA ADS] [CrossRef] (In the text)
- Taylor, J. B. 1974, Phys. Rev. Lett., 33, 1139 [NASA ADS] [CrossRef] (In the text)
- Vandas, M., & Romashets, E. P. 2003, A&A, 398, 801 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wang, Y., Ye, P., Zhou, G., et al. 2005, Sol. Phys., 226, 337 [NASA ADS] [CrossRef] (In the text)
- Wimmer-Schweingruber, R. F., Crooker, N. U., Balogh, A., et al. 2006, Space Sci. Rev., 123, 177 [NASA ADS] [CrossRef]
- Wu, C.-C., & Lepping, R. P. 2007, Sol. Phys., 242, 159 [NASA ADS] [CrossRef]
- Wu, C.-C., Fry, C. D., Wu, S. T., Dryer, M., & Liou, K. 2007, J. Geophys. Res., 112, A09104 [CrossRef]
- Zurbuchen, T. H. 2007, ARA&A, 45, 297338 [CrossRef] (In the text)
- Zurbuchen, T. H., & Richardson, I. G. 2006, Space Sci. Rev., 123, 3143 [CrossRef]
All Tables
Table 1: Definition of the main non-dimensional variables.
Table 2: Summary of results on MCs and ICMEs.
All Figures
| |
Figure 1: Schematic of a flux rope ejected from the Sun (the apex of the central field line is at a distance D from the Sun). The magnetic configuration of a magnetic cloud (MC) is well represented by an elongated twisted flux tube mostly anchored to the Sun. The schematic on the left shows the locally straight approximation used in this work (A color version is available in the electronic version). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.95\te...
...{
{\includegraphics[width=0.95\textwidth, clip=]{0971f2c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg148.gif) |
Figure 2:
Log-log plots of the normalized central magnetic field strength,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.45\te...
...
{\includegraphics[width=0.45\textwidth, clip=]{0971f3bc.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg242.gif) |
Figure 3:
Log-log plots showing the evolution of the SW total pressure (Eq. (39)) normalized at 1 AU, and a power-law approximation (Eq. (40) with nP=2.8) as a function of the solar distance D
(in AU).
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=0.90\te...
...{
{\includegraphics[width=0.90\textwidth, clip=]{0971f4c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg254.gif) |
Figure 4:
Log-log plots of the central magnetic field strength, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=\textwi...
... }
}{
{\includegraphics[width=\textwidth, clip=]{0971f5c.eps} }
}
\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg256.gif) |
Figure 5:
Evolution of the field strength, B, the axial, Bz, and azimuthal,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt}{
{\includegraphics[width=\textwi...
... }
}{
{\includegraphics[width=\textwidth, clip=]{0971f6c.eps} }
}\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg280.gif) |
Figure 6:
Evolution of a flux rope for the three ideal-MHD cases shown in Fig. 5 (D = (0.1, 1, 10) AU in the top, middle,
bottom panels, respectively). r is the radial coordinate of the flux rope, with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\IfFileExists{color_figures.txt} {
{\includegraphics[width=0.47\t...
...
{\includegraphics[width=0.47\textwidth, clip=]{0971f7c.eps} }
}
\end{figure}](/articles/aa/full_html/2009/17/aa10971-08/Timg320.gif) |
Figure 7:
The evolution of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



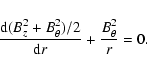
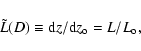
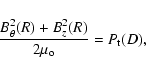
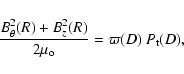
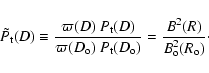
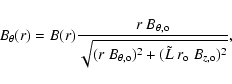
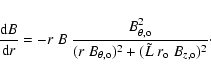
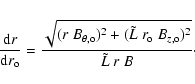
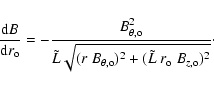
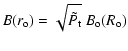
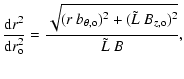
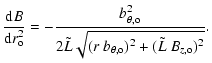
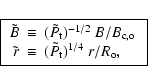
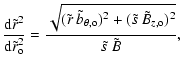
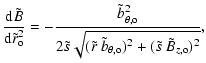
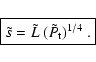
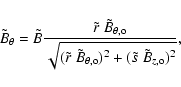
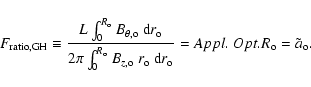
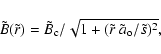
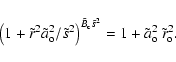
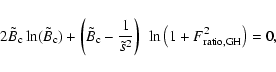
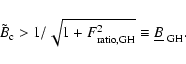
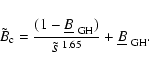
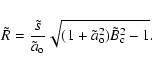
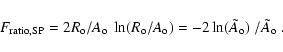
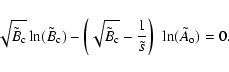
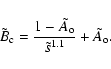
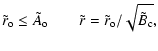
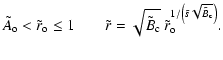
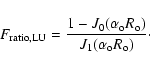
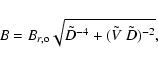
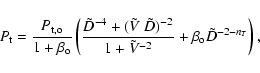
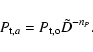
![\begin{displaymath}
v = \left. \frac{ {\rm d} r}{ {\rm d} t} \right\vert _{ r_{...
...{\rm o} }
+ \frac{n_P}{4} \right] ~\frac{V_{\rm c} ~r}{D} ,
\end{displaymath}](/articles/aa/full_html/2009/17/aa10971-08/img281.gif)
![\begin{displaymath}
v(t) = \left[ \left. \frac{ {\rm d} \ln \tilde{r} ( r_{\rm ...
...n_P}{4} \right] ~\frac{V_{\rm c} ^{2}~(t-t_{\rm c})}{D} \cdot
\end{displaymath}](/articles/aa/full_html/2009/17/aa10971-08/img289.gif)