| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 527 - 542 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200810786 | |
| Published online | 11 March 2009 | |
Calibration of Strömgren uvby-H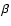 photometry for late-type stars
- a model atmosphere approach
photometry for late-type stars
- a model atmosphere approach![[*]](/icons/foot_motif.gif)
A. Önehag - B. Gustafsson - K. Eriksson - B. Edvardsson
Department of Physics and Astronomy, Uppsala Astonomical Observatory, Box 515, 751 20 Uppsala, Sweden
Received 11 August 2008 / Accepted 20 January 2009
Abstract
Context. The use of model atmospheres for deriving stellar fundamental parameters, such as
![]() ,
,
![]() ,
and [Fe/H], will increase as we find and explore extreme stellar populations where empirical calibrations are not yet available. Moreover, calibrations for upcoming large satellite missions of new spectrophotometric indices, similar to the uvby-H
,
and [Fe/H], will increase as we find and explore extreme stellar populations where empirical calibrations are not yet available. Moreover, calibrations for upcoming large satellite missions of new spectrophotometric indices, similar to the uvby-H![]() system, will be needed.
system, will be needed.
Aims. We aim to test the power of theoretical calibrations based on a new generation of MARCS models by comparisons with observational photomteric data.
Methods. We calculated synthetic uvby-H![]() colour indices from synthetic spectra. A sample of 367 field stars, as well as stars in globular clusters, is used for a direct comparison of the synthetic indices versus empirical data and for scrutinizing the possibilities of theoretical calibrations for temperature, metallicity, and gravity.
colour indices from synthetic spectra. A sample of 367 field stars, as well as stars in globular clusters, is used for a direct comparison of the synthetic indices versus empirical data and for scrutinizing the possibilities of theoretical calibrations for temperature, metallicity, and gravity.
Results. We show that the temperature sensitivity of the synthetic (b-y) colour is very close to its empirical counterpart, whereas the temperature scale based upon H![]() shows a slight offset. The theoretical metallicity sensitivity of the m1 index (and for G-type stars its combination with c1) is somewhat higher than the empirical one, based upon spectroscopic determinations. The gravity sensitivity of the synthetic c1 index shows satisfactory behaviour when compared to obervations of F stars. For stars cooler than the sun, a deviation is significant in the c1-(b-y) diagram. The theoretical calibrations of (b-y), (v-y), and c1 seem to work well for Pop II stars and lead to effective temperatures for globular cluster stars supporting recent claims that atomic diffusion occurs in stars near the turnoff point of NGC 6397.
shows a slight offset. The theoretical metallicity sensitivity of the m1 index (and for G-type stars its combination with c1) is somewhat higher than the empirical one, based upon spectroscopic determinations. The gravity sensitivity of the synthetic c1 index shows satisfactory behaviour when compared to obervations of F stars. For stars cooler than the sun, a deviation is significant in the c1-(b-y) diagram. The theoretical calibrations of (b-y), (v-y), and c1 seem to work well for Pop II stars and lead to effective temperatures for globular cluster stars supporting recent claims that atomic diffusion occurs in stars near the turnoff point of NGC 6397.
Conclusions. Synthetic colours of stellar atmospheres can indeed be used, in many cases, to derive reliable fundamental stellar parameters. The deviations seen when compared to observational data could be due to incomplete linelists but are possibly also due to the effects of assuming plane-parallell or spherical geometry and LTE.
Key words: stars: fundamental parameters - techniques: photometric - stars: atmospheres - stars: late-type
1 Introduction
The uvby photometric intermediate-band system of Strömgren (1963) and the H
Another development towards calibration of the systems also started early: the direct
calculation of
photometric indices by means of model atmospheres. Such theoretical calibrations were
attempted for early-type stars with relatively line-free spectra. For late
type stars, a statistical correction for the effects of spectral lines was made by Baschek
(1960) in his calibration of the Strömgren m index (a predecessor to m1). A first
systematic and detailed
calculation of uvby-H![]() indices for a grid of F and G dwarf model atmospheres was
published by Bell (1970), using scaled solar model atmospheres.
Bell
indices for a grid of F and G dwarf model atmospheres was
published by Bell (1970), using scaled solar model atmospheres.
Bell ![]() Parsons (1974)
calculated
Parsons (1974)
calculated
![]() colours for flux-constant model atmospheres of F and
G supergiants,
while Gustafsson
colours for flux-constant model atmospheres of F and
G supergiants,
while Gustafsson ![]() Bell (1979) produced theoretical colours in a number of systems,
including the uvby system, for a grid of giant-star model atmospheres.
Relya & Kurucz (1978) calculated
Bell (1979) produced theoretical colours in a number of systems,
including the uvby system, for a grid of giant-star model atmospheres.
Relya & Kurucz (1978) calculated
![]() and
and ![]() colours from early ATLAS models, and
discussed their shortcomings for late-type stars. uvby colours for new
sets of Kurucz models were published by
Lester et al. (1986).
Castelli
colours from early ATLAS models, and
discussed their shortcomings for late-type stars. uvby colours for new
sets of Kurucz models were published by
Lester et al. (1986).
Castelli ![]() Kurucz (2006) published H
Kurucz (2006) published H![]() indices. Sometimes, semiempirically
corrected fluxes from model
atmospheres have also been used for calibrations of Strömgren photometry, see e.g.
Lejeune et al. (1999) and Clem et al. (2004).
indices. Sometimes, semiempirically
corrected fluxes from model
atmospheres have also been used for calibrations of Strömgren photometry, see e.g.
Lejeune et al. (1999) and Clem et al. (2004).
The need for reliable calibrations of uvby-H![]() photometry has increased in the last
decade, not the least for estimating parameters of new and more ``exotic'' stars, such
as very metal-poor and super-metal-rich stars which are not found at great abundance in the
solar neighbourhood so that relatively complete sets of calibration stars cannot
easily be established. Furthermore, the preparation for the Gaia satellite includes a
careful analysis of the power of model atmospheres to provide a detailed astrophysical
calibration of the photometric system of the satellite. This analysis needs support
by a detailed test of the problems and possibilities to make a detailed theoretical
calibration of, e.g., the uvby-H
photometry has increased in the last
decade, not the least for estimating parameters of new and more ``exotic'' stars, such
as very metal-poor and super-metal-rich stars which are not found at great abundance in the
solar neighbourhood so that relatively complete sets of calibration stars cannot
easily be established. Furthermore, the preparation for the Gaia satellite includes a
careful analysis of the power of model atmospheres to provide a detailed astrophysical
calibration of the photometric system of the satellite. This analysis needs support
by a detailed test of the problems and possibilities to make a detailed theoretical
calibration of, e.g., the uvby-H![]() photometry.
photometry.
Subsequently, we shall present the theoretical models and colours
(Sects. 2 and 3). Stellar samples for empirical comparisons are discussed in
Sect. 4. Next, the
discussion will be focused on the determination of effective temperature, metallicity and
surface gravity of the stars, by discussing the
calibration of (b-y) and H![]() indices (Sect. 5, effective temperature),
of m1 (Sect. 6, metallicity) and c1
(Sect. 7, gravity) indices, devoting more limited interest to
``secondary'' effects such as the
metallicity sensitivity of (b-y) and c1, or the gravity sensitivity of m1.
In each section the results will be compared with empirical and
semi-empirical data and calibrations. Finally, in the last section some comments will be made on
the success and the problems of the theoretical calibrations, conclusions will
be drawn and recommendations given.
indices (Sect. 5, effective temperature),
of m1 (Sect. 6, metallicity) and c1
(Sect. 7, gravity) indices, devoting more limited interest to
``secondary'' effects such as the
metallicity sensitivity of (b-y) and c1, or the gravity sensitivity of m1.
In each section the results will be compared with empirical and
semi-empirical data and calibrations. Finally, in the last section some comments will be made on
the success and the problems of the theoretical calibrations, conclusions will
be drawn and recommendations given.
2 Model atmospheres and calculated spectra
The theoretical tools used in modelling the stellar colours are model stellar atmospheres and their calculated fluxes. These are based on extensive atomic and molecular data. Here, we shall briefly present the models and data used and refer to more complete descriptions.
2.1 Model atmospheres
The stellar atmosphere code MARCS (Gustafsson et al. 2008; http://marcs.astro.uu.se) was used to construct a grid of 168 theoretical 1D, flux constant, radiative + mixing-length convection, LTE models with fundamental atmospheric parameters as follows:Elemental abundances were adopted from Grevesse & Sauval (1998) except for the CNO abundances which were adopted following Asplund et al. (2005).
2.2 Synthetic spectrum calculations
In order to calculate synthetic spectra of sufficiently high resolution the Uppsala BSYN code was used with the MARCS models as input. The spectra were calculated within the wavelength limits of the Strömgren uvby filters with wavelength steps of 0.02 Å. The mictroturbulence parameter,
2.3 Line lists
We collected atomic line data from the Vienna Atomic Line Data Base, VALD (version I, Kupka et al. 1999). For hydrogen line data a version of the code HLINOP was used, and has been described by Barklem & Piskunov (2003). This code has been developed based on the original HLINOP by Peterson & Kurucz (see http://kurucz.harvard.edu). The hydrogen line profiles are calculated including Stark broadening, self-broadening, fine structure, radiative broadening, and Doppler broadening (both thermal and turbulent). The Stark broadening is calculated using the theory of Griem (1960 and subsequent papers) with corrections based on Vidal et al. (1973). Self-broadening is included following Barklem et al. (2000) for H
3 Colour index calculations
3.1 Filter profiles
To determine the theoretical m1, c1 and (b-y) indices, transmission profiles of the Strömgren uvby filters (Crawford & Barnes 1970, see Fig. 1) were multiplied with the calculated model stellar surface flux within the wavelength range of the filters: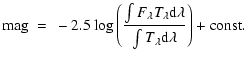 |
where
The H![]() index is defined (Crawford 1958) as the ratio of the flux measured through
a narrow and a wide profile, respectively, both centred around the H
index is defined (Crawford 1958) as the ratio of the flux measured through
a narrow and a wide profile, respectively, both centred around the H![]() line:
line:
 |
where
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f1.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg36.gif) |
Figure 1:
The uvby-H |
| Open with DEXTER | |
3.2 Transformation to the observational system
The frequent use of filter-profiles different from those that originally have defined the photomteric system needs some extra considerations. For the H
For the H![]() index, Crawford & Mander (1966) presented several filter systems,
of which we choose the (212, 214) filters as mentioned above.
Indices calculated by using this filter set, which are referred to as H
index, Crawford & Mander (1966) presented several filter systems,
of which we choose the (212, 214) filters as mentioned above.
Indices calculated by using this filter set, which are referred to as H![]() below,
should be transformed via a set of equations (CM66), in order to agree
with previous Crawford-Mander observations on their
standard system. The transformation for the (212, 214) filters
is described by the following two equations (CM66, Table III):
below,
should be transformed via a set of equations (CM66), in order to agree
with previous Crawford-Mander observations on their
standard system. The transformation for the (212, 214) filters
is described by the following two equations (CM66, Table III):
H
derived from a set of 45 and 35 bright stars, where H
The A0 star Vega clearly poses a number of problems for determining the zero-point of
the uvby and H![]() indices. It is known to be rapidly rotating, but with its axis close
to the line of sight (Gulliver et al. 1994;
Hill 2004).
Vega has also been regarded to show mild
indices. It is known to be rapidly rotating, but with its axis close
to the line of sight (Gulliver et al. 1994;
Hill 2004).
Vega has also been regarded to show mild ![]() Bootis star characteristics,
such as certain non-solar abundance ratios as well as dust emission in the IR
(see Gigas 1988;
Hill 1995; Ilijic et al. 1998;
Adelman & Gullliver 1990;
Heiter et al. 2002). However, these departures from
standard A0 stars, as well as standard model atmospheres, are thought to only lead to minor
modifications of its uvby-H
Bootis star characteristics,
such as certain non-solar abundance ratios as well as dust emission in the IR
(see Gigas 1988;
Hill 1995; Ilijic et al. 1998;
Adelman & Gullliver 1990;
Heiter et al. 2002). However, these departures from
standard A0 stars, as well as standard model atmospheres, are thought to only lead to minor
modifications of its uvby-H![]() indices (Paunzen et al. 2002). A more practical problem is
that neither of the two CM66 transformation equations from H
indices (Paunzen et al. 2002). A more practical problem is
that neither of the two CM66 transformation equations from H![]() to H
to H![]() will give a
fully satisfactory fit due to the fact that the index for Vega should be transformed
intermediately between the B star and the
A, F star sets. Several tests were performed which all pointed in the direction that
Vega should be transformed to the standard system via an equation somewhere in
between the B and the A, F transformations but with a heavier weight for the latter.
By using all listed A0 stars in Table II of CM66, a special transformation between
H
will give a
fully satisfactory fit due to the fact that the index for Vega should be transformed
intermediately between the B star and the
A, F star sets. Several tests were performed which all pointed in the direction that
Vega should be transformed to the standard system via an equation somewhere in
between the B and the A, F transformations but with a heavier weight for the latter.
By using all listed A0 stars in Table II of CM66, a special transformation between
H![]() and H
and H![]() for A0 dwarf stars was established,
as can be seen in Fig. 2.
The vertical line in the plot represents the observed H
for A0 dwarf stars was established,
as can be seen in Fig. 2.
The vertical line in the plot represents the observed H![]() value for Vega (Hauck & Mermilliod 1998).
However, the observed H
value for Vega (Hauck & Mermilliod 1998).
However, the observed H![]() value of Vega is not known.
In order to determine the zero point c in the transformation from calculated
(H
value of Vega is not known.
In order to determine the zero point c in the transformation from calculated
(H![]() )
to ``observed'' H
)
to ``observed'' H![]() values, H
values, H![]() = H
= H![]() + c,
we have therefore adopted an H
+ c,
we have therefore adopted an H![]() value for Vega derived from the A0 stars line
in Fig. 2, read off at the observed H
value for Vega derived from the A0 stars line
in Fig. 2, read off at the observed H![]() for the star.
After correction of the model H
for the star.
After correction of the model H![]() value to H
value to H![]() we have then calculated the model H
we have then calculated the model H![]() values by using the empirical
A, F-transformation relation as mentioned earlier.
values by using the empirical
A, F-transformation relation as mentioned earlier.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f2.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg43.gif) |
Figure 2:
H |
| Open with DEXTER | |
The transmission functions of the filters used by Olsen (1983, 1984)
and Schuster & Nissen (1988) depart from those on which the system
was originally based (Crawford 1966). Filter profiles representative for these
newer studies are given by Helt et al. (1987) and
Bessell (2005). In
particular, the more recent
v band is narrower, and its effective wavelength shifted by
about 25 Å towards the red. To test the effects of this, we have
calculated colours with the Helt et al. (1987) profiles as an
alternative to the Crawford set, and then applied the transformations as
given by Schuster & Nissen (1988) back to the standard system to mimic
the procedure of the observers. From this, we find changes of
the calculated values, amounting to typically 0.02 mag or less
in the m1 and c1 index values and only 0.002 in (b-y).
In particular, the changes in the
differential values measuring the sensitivity of m1 to metallicity
and of c1 to gravity are low,
in
![]() [Me/H] typically 0.003 and in
[Me/H] typically 0.003 and in
![]() typically 0.01. Such effects do not change our
conclusions in the present paper.
typically 0.01. Such effects do not change our
conclusions in the present paper.
3.3 Model colours
The model colours, with zero-point added using Vega observations, are supplemented the present paper electronically in tables containing the following information:
4 Comparison star samples
In order to test the reliability of our calculated colours, we selected a sample
of standard stars.
These were taken from various sources:
one subset with well determined spectroscopic parameters
was selected from The Bright Star Catalogue (Hoffleit & Warren 1995), another from
the uvby standard stars listed by Crawford & Barnes (1970), a third from
the list of metal-poor stars in Schuster & Nissen (1988), a fourth among stars that have been
observed by the Hubble-STIS spectrograph and a fifth from the stars listed in the study of Pop II stars by Jonsell et al. (2005). Altogether 367 stars were thus selected. The fundamental
parameters were taken from the sources listed, or from other sources given in the SIMBAD
catalogue and judged to have high quality. Complementary photometry
was also obtained from SIMBAD. Parameter determinations based on uvby-H![]() photometry were avoided as far as possible, since we aimed at testing calibrations based on
this photometric system relative to parameters
based on more fundamental methods. In practice, this usually means
effective temperatures based on the infrared flux method and gravities and metallicities based
on high-resolution spectroscopy.
The effective temperatures gathered from the Jonsell et al. (2005) sample are calculated
with the Alonso et al. (1996) calibration. These stars however, constitute less than 5% of our
total sample. In the case of multiple sources, i.e., stellar values listed in more than one
of our selected catalogues, a mean value was used.
The
photometry were avoided as far as possible, since we aimed at testing calibrations based on
this photometric system relative to parameters
based on more fundamental methods. In practice, this usually means
effective temperatures based on the infrared flux method and gravities and metallicities based
on high-resolution spectroscopy.
The effective temperatures gathered from the Jonsell et al. (2005) sample are calculated
with the Alonso et al. (1996) calibration. These stars however, constitute less than 5% of our
total sample. In the case of multiple sources, i.e., stellar values listed in more than one
of our selected catalogues, a mean value was used.
The
![]() indices of the standard stars were dereddened by means of the algorithm and
computer code of Hakkila (1997). For most of the stars, in particularly the dwarfs,
E(B-V) was less than
indices of the standard stars were dereddened by means of the algorithm and
computer code of Hakkila (1997). For most of the stars, in particularly the dwarfs,
E(B-V) was less than ![]() 0.01.
0.01.
Altogether, the standard stars span a volume in the parameter space ranging from 3900 K to
7850 K in
![]() ,
0.20 to 4.80 in
,
0.20 to 4.80 in ![]() (cgs units) and
-3.0 dex to 0.45 dex in
[Fe/H]. Data for the full standard sample is accessible
electronically from A&A as on-line material supplementing the present paper
and contains the following information: stellar coordinates, designation(s),
(cgs units) and
-3.0 dex to 0.45 dex in
[Fe/H]. Data for the full standard sample is accessible
electronically from A&A as on-line material supplementing the present paper
and contains the following information: stellar coordinates, designation(s),
![]() ,
,
![]() ,
[Fe/H], c0, m0, (b-y)0, H
,
[Fe/H], c0, m0, (b-y)0, H![]() ,
and source references.
As seen in Fig. 3 our standard sample satisfactorily covers the fundamental
parameter space, although one would need some more cool (
,
and source references.
As seen in Fig. 3 our standard sample satisfactorily covers the fundamental
parameter space, although one would need some more cool (
![]() )
and hot
(
)
and hot
(
![]() )
dwarf stars (
)
dwarf stars (
![]() ). For this purpose two complementary
homogeneous samples were tested; the stellar sample published by Casagrande
et al. (2006,
hereafter C06) and Valenti & Fischer (2005, hereafter VF05).
uvby colour indices for both samples were taken from Hauck & Mermilliod (1998).
These complimentary stellar samples cover the parameter spaces:
). For this purpose two complementary
homogeneous samples were tested; the stellar sample published by Casagrande
et al. (2006,
hereafter C06) and Valenti & Fischer (2005, hereafter VF05).
uvby colour indices for both samples were taken from Hauck & Mermilliod (1998).
These complimentary stellar samples cover the parameter spaces:
![]() ,
,
![]() and
and
![]() for the
VF05 sample and
for the
VF05 sample and
![]() ,
,
![]() and
and
![]() for the
C06 sample.
Despite that the lowest
for the
C06 sample.
Despite that the lowest ![]() values in the VF05 sample are characteristic of giants/sub-giants,
a majority (93%) of the VF05 stars are dwarfs with
values in the VF05 sample are characteristic of giants/sub-giants,
a majority (93%) of the VF05 stars are dwarfs with
![]() .
In the C06
sample all stars are
assumed to be dwarfs with
.
In the C06
sample all stars are
assumed to be dwarfs with
![]() .
A majority (85%) of the stars in the VF05 sample
are also metal-rich,
.
A majority (85%) of the stars in the VF05 sample
are also metal-rich,
![]() ,
whereas the C06 sample is evenly
distributed in metallicity. Likewise, the effective temperatures of the
C06 sample
(determined by the authors's new calibration of the infrared flux method) are evenly
distributed but the VF05 sample is biased towards higher temperatures,
,
whereas the C06 sample is evenly
distributed in metallicity. Likewise, the effective temperatures of the
C06 sample
(determined by the authors's new calibration of the infrared flux method) are evenly
distributed but the VF05 sample is biased towards higher temperatures,
![]() (74%). Among the stars in the standard sample, 18 and 72 are found in
the C06 and VF05 samples, respectively.
For the stars in the VF05 sample no significant trends of discrepacies for the
values given,
(74%). Among the stars in the standard sample, 18 and 72 are found in
the C06 and VF05 samples, respectively.
For the stars in the VF05 sample no significant trends of discrepacies for the
values given,
![]() ,
,
![]() and [Fe/H], were found. In the C06 sample
we find an overall difference in given
effective temperatures, growing for higher effective temperatures at
low metallicities (
and [Fe/H], were found. In the C06 sample
we find an overall difference in given
effective temperatures, growing for higher effective temperatures at
low metallicities (
![]() K at
K at
![]() K and
K and
![]() ).
).
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f3.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg63.gif) |
Figure 3:
Fundamental parameters, i.e.
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.2cm,angle=90]{0786f4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg64.gif) |
Figure 4:
The (b-y) colour index ( left) and H |
| Open with DEXTER | |
5 The effective-temperature calibration
Precise determinations of effective temperatures of stars are critical for a variety of reasons, not only for direct applications such as comparisons of isochrone calculations to observed colour-magnitude diagrams, but also in more indirect applications e.g. determinations of chemical abundances. Photometric indices play a critical role when determining the effective temperatures of stars. For stars located on the main sequence, model atmosphere calibrations of these indices may be particularly important since determinations of diameters are generally few and poor.
The Strömgren (b-y) index provides a sensitive
temperature measure for F, G and K stars. The H![]() index
is another frequently used criterion for deriving temperatures.
We study both indices here.
index
is another frequently used criterion for deriving temperatures.
We study both indices here.
In Fig. 4 (left) we explore the temperature sensitivity of the
theoretical (b-y) index for different metallicities.
As a comparison we also plot (b-y) for a set of Kurucz models
(Lester et al. 1986). We note that the indices, calculated with the different model sets,
more or less show the same behaviour although the models of Lester et al. are
systematically bluer at given
![]() .
In comparison with observed values for stars our synthetic indices show a satisfactory
temperature sensitivity over the full temperature range (4500-7000 K), see
Fig. 5.
.
In comparison with observed values for stars our synthetic indices show a satisfactory
temperature sensitivity over the full temperature range (4500-7000 K), see
Fig. 5.
In Fig. 4 (right) the H![]() index is plotted versus
effective temperature, together with the theoretical data of Castelli & Kurucz (2006).
For the warmer part of the temperature range we find no differences in sensitivity,
whereas for the cooler temperatures (5500 K) we note
that MARCS indices have a steeper gradient, thus lower H
index is plotted versus
effective temperature, together with the theoretical data of Castelli & Kurucz (2006).
For the warmer part of the temperature range we find no differences in sensitivity,
whereas for the cooler temperatures (5500 K) we note
that MARCS indices have a steeper gradient, thus lower H![]() values than those of
Castelli & Kurucz. Our steeper gradient tends to agree with observed stellar colours,
Fig. 6, which is probably due to improvements of the broadening
theory of H
values than those of
Castelli & Kurucz. Our steeper gradient tends to agree with observed stellar colours,
Fig. 6, which is probably due to improvements of the broadening
theory of H![]() .
.
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg65.gif) |
Figure 5:
Theoretical (b-y) values versus effective temperature for models with
different [Me/H] and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg66.gif) |
Figure 6:
Theoretical H |
| Open with DEXTER | |
5.1 Teff (b - y)
Several attempts (Alonso et al. 1996; Nordström et al. 2004; Ramírez & Meléndez 2005b; Holmberg et al. 2007) have been made to derive empirical calibrations for uvby-H
The result for dwarfs (
![]() )
are given numerically
in Appendix A.1 and can be seen in
Fig. 7 where we also merge our standard sample with the C06 sample
and plot temperatures for the individual stars derived from our theoretical calibration
equation.
The standard deviations for our calculated temperatures with respect
to literature values can be found in Table 1
A linear regression for the calculated temperatures of the two merged samples
is also shown in Fig. 7 and yields a dispersion
)
are given numerically
in Appendix A.1 and can be seen in
Fig. 7 where we also merge our standard sample with the C06 sample
and plot temperatures for the individual stars derived from our theoretical calibration
equation.
The standard deviations for our calculated temperatures with respect
to literature values can be found in Table 1
A linear regression for the calculated temperatures of the two merged samples
is also shown in Fig. 7 and yields a dispersion
![]() K. We note that our theoretical calibration gives higher
temperatures, as compared with literature values, by
K. We note that our theoretical calibration gives higher
temperatures, as compared with literature values, by ![]() 100 K for the cooler stars
(
100 K for the cooler stars
(
![]() < 5000 K) and tends to lead to lower temperatures (
< 5000 K) and tends to lead to lower temperatures (![]() 100-150 K)
than the values found in the literature for hotter stars (
100-150 K)
than the values found in the literature for hotter stars (
![]() > 6500 K).
Our calibration suggests lower temperatures than the
values listed in VF05 by 100-200 K for stars within the range of 5200-6300 K.
Below that our theoretical calibration gives systematically
> 6500 K).
Our calibration suggests lower temperatures than the
values listed in VF05 by 100-200 K for stars within the range of 5200-6300 K.
Below that our theoretical calibration gives systematically ![]() 100 K higher temperatures
for the VF05 stars, in accordance with the tendencies found also for the other comparison
samples. The standard deviation of the calculated temperatures for the
VF05 sample can be seen in Table 1.
100 K higher temperatures
for the VF05 stars, in accordance with the tendencies found also for the other comparison
samples. The standard deviation of the calculated temperatures for the
VF05 sample can be seen in Table 1.
If the choice of zero-point in our
calibration, based on Vega, is changed a systematic shift of the temperature scale
would result. We note that our calibraion suggests a solar (b-y) of 0.383, which may
be lower than Holmberg et al. (2006). A shift upwards by 0.02 dex would
correspond to a temperature shift ranging from +70 K at
![]() = 4500 K to
+200 K at
= 4500 K to
+200 K at
![]() = 6500 K.
= 6500 K.
It is also interesting to compare our results to previous empirical calibrations. The standard deviations of the calculated temperatures using four different empirical calibrations applied on our three comparison samples, are listed in Table 1. In order to illustrate the empirical trends the resultant linear regressions for the merged standard and C06 samples are shown in Fig. 7 (note the shifted scale by 1000 K).
The calibration results for giants (
![]() )
is presented in Appendix A.2 and shown in Fig. 8. The standard deviations
with respect to effective temperatures of the standard stars are shown in
Table 1 together with the standard deviations for the same sample when
using the A99 empirical calibration.
)
is presented in Appendix A.2 and shown in Fig. 8. The standard deviations
with respect to effective temperatures of the standard stars are shown in
Table 1 together with the standard deviations for the same sample when
using the A99 empirical calibration.
One should note, however, that these calibration equations, as well as the analogous ones derived for metallicities below, are not to be equals to the ones based on empirical data. We have derived them in order to test the models, not to determine precise parameters for the stars.
5.2 T
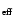 (H
(H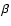 )
)
A theoretical temperature calibration for dwarfs
was also derived for the H
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f7.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg71.gif) |
Figure 7: Comparison of calibrations of (b-y) for dwarf stars with individual values for the standard stars and C06 plotted. The solid line represents a fit of the effective temperatures adopted for the stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperatures relative to empirical calibrations (Alonso et al. 1996; Holmberg et al. 2007; Ramírez & Meléndez 2005b) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
Table 1:
Standard deviations for
![]() and [Fe/H] derived
using models as compared with literature values of the different
comparison samples. See also Figs. 7-9 and
Figs. 13, 14.
and [Fe/H] derived
using models as compared with literature values of the different
comparison samples. See also Figs. 7-9 and
Figs. 13, 14.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f8.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg72.gif) |
Figure 8: Comparison of calibrations of (b-y) for giant stars with individual values for the standard stars plotted. The solid line represents a fit of the effective temperatures adopted for the standard stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperatures relative to empirical calibrations (Alonso et al. 1999; Ramírez & Meléndez 2005b) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f9.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg73.gif) |
Figure 9:
Comparison of calibrations of
|
| Open with DEXTER | |
5.3 T
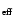 (b - y) vs. T
(b - y) vs. T
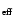 (H
(H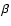 )
)
Now we compare the derived temperatures based on (b-y) and H
It is worth noting that the difference between the (b-y) and H![]() calibrations
responds in opposite directions to different gravities.
I.e., the temperature sensitivity
calibrations
responds in opposite directions to different gravities.
I.e., the temperature sensitivity
![]() decreases with increasing gravity for (b-y)
while it increases for
decreases with increasing gravity for (b-y)
while it increases for
![]() for H
for H![]() (see Fig. 4).
As is seen, these differences are also metallicity dependent, and tend to
vanish for low metallicities. However, for stars with known reddening and assuming
e.g. the metallicity to be known and relatively high, this may make it possible to
obtain a temperature and rough gravity classification from (b-y) and H
(see Fig. 4).
As is seen, these differences are also metallicity dependent, and tend to
vanish for low metallicities. However, for stars with known reddening and assuming
e.g. the metallicity to be known and relatively high, this may make it possible to
obtain a temperature and rough gravity classification from (b-y) and H![]() ,
only.
,
only.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f10.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg77.gif) |
Figure 10:
The effective temperatures calculated by the equations based on H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f11.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg78.gif) |
Figure 11: The m1 index versus (b-y) for MARCS and Lester et al. (1986, LGK) model atmospheres. Arrows show the effect of increasing the N abundances by a factor of 3. |
| Open with DEXTER | |
6 The metallicity calibration
The basic aim of
![]() was to measure the total intensity of the
metal lines in the v band. As was early appreciated by Strömgren, for late F and G stars of Pop I these lines are, however, to a considerable extent located on the flat
part of the Curve of Growth and are thus not very sensitive to metallicity, but
rather to microturbulence.
Moreover, for the hotter stars, the H
was to measure the total intensity of the
metal lines in the v band. As was early appreciated by Strömgren, for late F and G stars of Pop I these lines are, however, to a considerable extent located on the flat
part of the Curve of Growth and are thus not very sensitive to metallicity, but
rather to microturbulence.
Moreover, for the hotter stars, the H![]() line is strongly affecting the band, and for
stars later than G5, CN lines of the (0, 1) band in the Violet System are also significant.
Thus, the effects of the value of the mircroturbulence parameter, as well as of the
individual CNO abundances, e.g. due to dredge-up of CNO processed material
from the interior, must be taken into consideration. Certainly, m1 also varies with
effective temperature and, to a less degree, with surface gravity.
line is strongly affecting the band, and for
stars later than G5, CN lines of the (0, 1) band in the Violet System are also significant.
Thus, the effects of the value of the mircroturbulence parameter, as well as of the
individual CNO abundances, e.g. due to dredge-up of CNO processed material
from the interior, must be taken into consideration. Certainly, m1 also varies with
effective temperature and, to a less degree, with surface gravity.
The variation of the calculated m1 with (b-y) and metallicity
for the model atmospheres is shown in Fig. 11 and
compared with calculated indices by Lester et al. (1986).
As is seen, the index offers a good discrimination in metallicity except for
stars of Extreme Population II
for which it only works for the cooler end of the temperature interval. A
characteristic measure of the sensitivity of the index to overall metallicity is
![]() [Me/H])(b-y), where the subscript denotes that the sensitivity
is measured at a constant (b-y). This quantity, as measured for models with
[Me/H])(b-y), where the subscript denotes that the sensitivity
is measured at a constant (b-y). This quantity, as measured for models with
![]() and
and
![]() and 4.0, is given in Table 2.
and 4.0, is given in Table 2.
Table 2:
The metallicity sensitivity,
![]() [Me/H])(b-y), for
models with
[Me/H])(b-y), for
models with ![]() = 4.5 and 4.0.
= 4.5 and 4.0.
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f12.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg84.gif) |
Figure 12:
The m1 index versus (b-y) for MARCS models plotted together with
standard stars of different gravities in different panels
( |
| Open with DEXTER | |
We may compare the sensitivity of the m1 index with the empirical results. However, recent calibrations of the Strömgen photometry, e.g. by Holmberg et al. (2007), contain complex non-linear expressions in which all the indices are involved - in principle a reasonable approach since e.g. also the c1 index carries information on the metallicity. Since this metallicity dependence is, however, far from independent of that carried by the m1 index the terms in the calibration expressions involving c1 may well mask some of the dependence of m1 on metallicity. So, as we wish to understand the way m1 changes with metallicity, we have instead turned back to the earlier empirical calibrations like that of Nissen (1988), where the metallicity dependence of m1 was still treated separately.
Thus, Nissen (1988) finds
where
In order to further explore the properties of the calculated m1 indices we have plotted individual stars with fairly well-determined fundamental parameters, chosen from our standard sample in the m1-(b-y) diagram. As is seen in Fig. 12, these stars match the calculated indices relatively well, although there seems to be a tendency of the sensitivity of the m1 index to metallicity to be exaggerated by the model fluxes for the hotter stars. Also, it is clear from Fig. 12 that the metal-rich stars lie somewhat low, possibly suggesting that the zero-point of the m1 index as determined from Vega may be somewhat in error.
When studying the calculated indices of
Lester et al. (1986) in
Fig. 11
we find that they reproduce the observed sensitivity of the m1 index more successfully
than ours. However, these
authors have transformed their calculated colours to match a set of standard stars
and have thus scaled the amplitude of the m1 index by a correction factor to
fit the observations. This is the probable reason for the closer agreement of those
calculations with observations. We note that our line list is more complete, and that
our treatment of the hydrogen line broadening (affecting H![]() and thus the
v band) is more accurate.
and thus the
v band) is more accurate.
What is then the reason for our discrepancy for early F stars? We have compared the MARCS model fluxes with observed solar and stellar fluxes from ground-based and space observations (Edvardsson 2008; Edvardsson et al. 2008) and traced probably significant discrepancies in the region 4000 Å- 5000 Å, with empirical fluxes of the Sun and solar-type stars being somewhat smaller than model fluxes in the b band, while the blue-violet fluxes from HST/STIS of the more metal-poor stars are clearly in excess of the model fluxes in the violet-blue spectral region. These departures in both the b and v band may conspire to cause the discrepancy in calculated metallicity sensitivity. As discussed by Edvardsson et al. (2008), 3D model simulations suggest that these effects may be due to thermal inhomogeneities in the stellar atmospheres. Other systematic errors in the models, e.g. due to errors in opacities, line data and effects of departures from LTE are probably less significant.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f13.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg88.gif) |
Figure 13: The [Me/H] calibration for F stars from the standard sample and Casagrande et al. (2006, C06). The solid line represents a linear regression of the effective temperatures adopted for the stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperautres relative to empirical calibrations (Schuster & Nissen 1989; Holmberg et al. 2007; Ramírez & Meléndez 2005a) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
As a further test of our m1 indices we will now be guided by the
separate metallicity calibrations for F and G stars, respectively, by
Schuster & Nissen (1989, Eqs. (2) and (3), hereafter S&N89).
The derived F-star equation is based on the m1 and (b-y) index and for the
G-star equation the c1 index is also included. We shall attempt a calibration expression
based upon the form of these equations and using our theoretical colour grid.
The results, when applying this to the standard stars and the C06 sample, can be seen in
Figs. 13 and 14.
For F-stars we find standard deviations of derived [Me/H] values compared with literature values for the
standard-star sample as given in Table 1.
We note, that for the standard sample, our theoretical calibration tends to suggest lower metallicities than
the adopted values for a majority of the stars in the sample and increasing differences with
increasing metallicity so that the differences amount to typically 0.3 dex at
[Me/H] = 0.0. The overall trend might indicate a zero-point problem;
a shift of all stars by 0.130 dex gives a lower spread of the
calculated metallicities compared to adapted values,
![]() = 0.217.
This is however still not satisfactory in comparison with the empirical equations which
generally show less spread and imply higher metallicities (see
Table 1
and Fig. 13). A linear regression for the F-star calibration values to the adopted
values for the standard stars and the C06 sample is plotted in Fig. 13. The standard deviation
for this line fit is
= 0.217.
This is however still not satisfactory in comparison with the empirical equations which
generally show less spread and imply higher metallicities (see
Table 1
and Fig. 13). A linear regression for the F-star calibration values to the adopted
values for the standard stars and the C06 sample is plotted in Fig. 13. The standard deviation
for this line fit is ![]() = 0.172 dex.
When applying our calibration to the C06 sample we see the same indications as for the
standard sample, except for the lower metallicities, where the theoretical calibration
suggest somewhat lower metallicities (
= 0.172 dex.
When applying our calibration to the C06 sample we see the same indications as for the
standard sample, except for the lower metallicities, where the theoretical calibration
suggest somewhat lower metallicities (![]() 0.05 dex) than derived in C06.
However, the 13 F-stars in this sample are too few to
allow any definite conclusions.
When making use of the 266 F-stars in the VF sample and remembering that this sample
is highly biased towards metal-rich dwarf stars (
0.05 dex) than derived in C06.
However, the 13 F-stars in this sample are too few to
allow any definite conclusions.
When making use of the 266 F-stars in the VF sample and remembering that this sample
is highly biased towards metal-rich dwarf stars (
![]() and
and
![]() )
we
see the same trend as for the standard sample, i.e. our calibration suggests
lower metallicities than those given by VF05 (see also Table 1).
)
we
see the same trend as for the standard sample, i.e. our calibration suggests
lower metallicities than those given by VF05 (see also Table 1).
For the G-stars we find similar standard deviations for our standard sample with
respect to literature values, see Table 1.
There is an overall tendency that our
theoretical calibration implies lower metallicities than listed in the
literature for the metal-rich standard stars.
The increasing deviation with increasing metallicity is of the same order
as for the F-star calibration, i.e. ![]() 0.3 dex at [Me/H] = 0.0.
By adding 0.190 dex to all stars we would obtain a lower spread,
0.3 dex at [Me/H] = 0.0.
By adding 0.190 dex to all stars we would obtain a lower spread,
![]() = 0.181, which is of the same order as the deviation
shown by empirical equations (see Table 1).
A linear regression to the calculated metallicities for the standard sample and C06
is plotted as a solid line in the figure (
= 0.181, which is of the same order as the deviation
shown by empirical equations (see Table 1).
A linear regression to the calculated metallicities for the standard sample and C06
is plotted as a solid line in the figure (![]() = 0.200).
When using the 69 G-stars in the C06 sample, the result for the standard
sample is confirmed, the theoretical calibration suggests lower metallicities
for the higher metallicity range (
= 0.200).
When using the 69 G-stars in the C06 sample, the result for the standard
sample is confirmed, the theoretical calibration suggests lower metallicities
for the higher metallicity range (
![]() )
than listed in literature.
Applying the calibrations to the 694 G-stars in the VF05 sample, we obtain similar
results as for the C06 sample.
)
than listed in literature.
Applying the calibrations to the 694 G-stars in the VF05 sample, we obtain similar
results as for the C06 sample.
For comparison the metallicities of our three comparison samples are calculated with 3 different empirical calibrations. The resulting standard deviations with respect to literature values can be seen in Table 1 and linear regressions when applied to our standard sample and C06 can be seen in Figs. 13 and 14 for F-stars and G-stars, respectively.
We note in passing that Clem et al. (2004) also found discrepancies between their calculated m1 indices and observations. For their coolest models they had to apply upward corrections to their calculated m1 indices of 0.1-0.3 mag. Our m1 indices depart considerably less from observations but some upward corrections would be needed to fit the coolest stars in Fig. 12.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f14.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg96.gif) |
Figure 14: The [Me/H] calibration for G stars. For plot description see Fig. 13. Note that empirical calibrations of HNA07 and RM05 overlap and could therefore be difficult to distinguish. |
| Open with DEXTER | |
Table 3: The change in the uvby indices when the microturbulence parameter is increased.
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f15.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg104.gif) |
Figure 15:
The c1 index versus (b-y) for MARCS and
Lester et al. (1986, LGK)
model atmospheres with different |
| Open with DEXTER | |
The strong effects of microturbulence on the strengths of the dominating lines in the v band
makes it important to investigate whether this could be the reason for the mis-match of the
m1 index in the theoretical calibration. In Table 3 we examine the
effects of changing the microturbulence parameter ![]() .
The changes have been chosen
to be greater for the lower-gravity models to take the greater parameter values usually
obtained by spectroscopy for giants into account. We see that the effect of increasing
the microturbulence is generally greater for lower
.
The changes have been chosen
to be greater for the lower-gravity models to take the greater parameter values usually
obtained by spectroscopy for giants into account. We see that the effect of increasing
the microturbulence is generally greater for lower ![]() and lower temperatures, as
expected. When comparing to Fig. 12 we see that this effect
would indeed improve the situation by shifting the theoretical curves
and steepening the curves in the low
and lower temperatures, as
expected. When comparing to Fig. 12 we see that this effect
would indeed improve the situation by shifting the theoretical curves
and steepening the curves in the low
![]() end. Yet, the effects are considerably
smaller than those needed to eliminate the mis-match.
end. Yet, the effects are considerably
smaller than those needed to eliminate the mis-match.
Another circumstance which might have some significance as an explanation for the problems with the m1 sensitivity is the effect of lines from the (0, 1) band of the CN violet system in the v band. In particular for the cooler giant stars, which may be affected by the first dredge-up of CNO-processed material, the CN lines may become stronger due to this; even if the carbon abundances are reduced by CNO processing, the enhanced N abundance (to which C is converted) makes the CN lines stronger. Also the 13CN lines should be significantly enhanced due to the production of 13C and N by CNO processing. We have explored these effects by systematically increasing the N abundances by a factor of 3, keeping the C abundance constant. This should lead to an overestimate of the effect, except for possibly stars high-up on the giant branch. As indicated in Fig. 11 this only leads to some effects for the more metal-rich giant stars and is not the explanation for the mis-match discussed here.
7 Surface-gravity calibration
The
Analogously with our treatment of the metallicity dependence of the m1 index, we have measured the quantity
![]() at constant
(b-y) as a measure of the gravity sensitivity of c1. Again we
have to turn back to earlier calibrations to find corresponding direct
empirical measures. Thus, Schuster & Nissen (1989) have elaborated the methodology
of Crawford (1975, 1979) and write
at constant
(b-y) as a measure of the gravity sensitivity of c1. Again we
have to turn back to earlier calibrations to find corresponding direct
empirical measures. Thus, Schuster & Nissen (1989) have elaborated the methodology
of Crawford (1975, 1979) and write
where
![]() ,
(b-y)0 being the dereddened
(b-y), and
,
(b-y)0 being the dereddened
(b-y), and
![]() is the difference of a dereddened
c1 index and a standard sequence with
is the difference of a dereddened
c1 index and a standard sequence with
![]() at a given H
at a given H![]() .
From this one may estimate the empirical sensitivity
.
From this one may estimate the empirical sensitivity
![]() to be approximately
proportional to 2.5/f. We thus obtain the following empirical values of
(
to be approximately
proportional to 2.5/f. We thus obtain the following empirical values of
(
![]() )
for [Fe/H] = 0: (0.21;0.30),
(0.16; 0.40) and (0.15; 0.47). From Fig. 15 and
Table 4 we
measure the corresponding theoretical
)
for [Fe/H] = 0: (0.21;0.30),
(0.16; 0.40) and (0.15; 0.47). From Fig. 15 and
Table 4 we
measure the corresponding theoretical
![]() values to be 0.19, 0.08 and 0.02, respectively.
Thus, we find that the empirical gravity sensitivity of the c1 index is well
reproduced by the hotter models while it becomes underestimated for the cooler
ones. We have also compared the calculated c1 indices with the observed
ones for our standard stars and the C06 sample and find a good agreement for the
hotter stars (cf. Fig. 16) while for the cooler stars there
is a severe mismatch.
This is in itself not very remarkable - the total line blocking in the
ultraviolet spectra of the cooler stars is considerably greater than
values to be 0.19, 0.08 and 0.02, respectively.
Thus, we find that the empirical gravity sensitivity of the c1 index is well
reproduced by the hotter models while it becomes underestimated for the cooler
ones. We have also compared the calculated c1 indices with the observed
ones for our standard stars and the C06 sample and find a good agreement for the
hotter stars (cf. Fig. 16) while for the cooler stars there
is a severe mismatch.
This is in itself not very remarkable - the total line blocking in the
ultraviolet spectra of the cooler stars is considerably greater than ![]() ,
and it is to be expected that this will not be very accurately described by the
model spectra. The fluxes in the u and v bands are highly sensitive to other
parameters, such as microturbulence, and in particular CN abundance for the cooler giants,
and these are known to vary systematically with gravity. In fact, as is indicated by
arrows in Fig. 15, the CN line strengthening which is expected for the
red giants improves the fit to observed c1 indices for the red giant models considerably.
,
and it is to be expected that this will not be very accurately described by the
model spectra. The fluxes in the u and v bands are highly sensitive to other
parameters, such as microturbulence, and in particular CN abundance for the cooler giants,
and these are known to vary systematically with gravity. In fact, as is indicated by
arrows in Fig. 15, the CN line strengthening which is expected for the
red giants improves the fit to observed c1 indices for the red giant models considerably.
Clem et al. (2004) applied semiempirical corrections also to their calculated (u-v) and (v-b) colours in order to fit observations. The resulting effect on their c1 indices is typically less than 0.1 mag while we would need a downward correction of our c1 indices of about 0.2 mag for the coolest models to fit (cf. Fig. 16) the metal poor stars and even more for the metal-rich ones.
![\begin{figure}
\par\includegraphics[width=13cm,angle=90,clip]{0786f16.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg113.gif) |
Figure 16:
The c1 index versus (b-y) for MARCS models with different
[Me/H] and |
| Open with DEXTER | |
Table 4:
The sensitivity to surface gravity, (
![]() ,
for
models with [Me/H] = 0.5 and 0.0.
,
for
models with [Me/H] = 0.5 and 0.0.
In a recent article, Twarog et al. (2007) discuss the metallicity dependence of the
c1 index for disk stars ([Fe/H] ![]() -1.00) and conclude that the
metallicity sensitivity of the index generally has been underestimated. An interesting
test would therefore be to follow their recipe, i.e. divide our model grid into
three groups (hot, warm and cold), and check whether or not our synthetic colours
show the same behaviour. For the hot models (
(b-y) < 0.43) we find the same strong
metallicity dependence of the m1 index and the same lack of sensitivity of the
c1 index as is found by Twarog et al. For warm models (0.43
-1.00) and conclude that the
metallicity sensitivity of the index generally has been underestimated. An interesting
test would therefore be to follow their recipe, i.e. divide our model grid into
three groups (hot, warm and cold), and check whether or not our synthetic colours
show the same behaviour. For the hot models (
(b-y) < 0.43) we find the same strong
metallicity dependence of the m1 index and the same lack of sensitivity of the
c1 index as is found by Twarog et al. For warm models (0.43
![]() 0.50)
we do find, like Twarog et al., a strong c1 sensitivity to metallicity, but
likewise a relatively strong dependence of the m1 index in contrast to the result
of Twarog et al.
For cool stars (
0.50)
we do find, like Twarog et al., a strong c1 sensitivity to metallicity, but
likewise a relatively strong dependence of the m1 index in contrast to the result
of Twarog et al.
For cool stars (
![]() 0.50), we separate unevolved dwarfs from subgiants
and giants by making use of the defined LC (
0.50), we separate unevolved dwarfs from subgiants
and giants by making use of the defined LC (
![]() calibration in Twarog et al. The models
follow the same trends and LC separates the more metal-poor models ([Me/H] = -0.5 and -1.0)
but does not succed in separating the metal-rich ones ([Me/H]
calibration in Twarog et al. The models
follow the same trends and LC separates the more metal-poor models ([Me/H] = -0.5 and -1.0)
but does not succed in separating the metal-rich ones ([Me/H] ![]() ), as is
also found by Twarog et al.
It should however be noted that when applying the metallicity calibrations for hot and
warm stars as defined by Twarog et al. on our standard sample, we do not
reach any higher accuracy in reproducing the literature values of [Fe/H] than when
using e.g. S&N89.
), as is
also found by Twarog et al.
It should however be noted that when applying the metallicity calibrations for hot and
warm stars as defined by Twarog et al. on our standard sample, we do not
reach any higher accuracy in reproducing the literature values of [Fe/H] than when
using e.g. S&N89.
7.1 Applications
In the area of application of the uvby photometry, some particular questions have been of special interest to us: to which extent can the photometry be used for determining gravities and temperatures for metal-poor stars, and how sensitive is the synthetic c1 index to certain elements such as nitrogen.Following Clem et al. (2004), we shall test our model colours versus observed colours for globular clusters. Unlike the approach of Clem et al., our main emphasis lies on exploring the possibilities and shortcomings of our theoretical model colours sooner than correcting them semiempirically to establish new calibrations.
7.1.1 M92
As a check on the capabilities of the c1 index for determining gravities, we have tested the model
indices relative to the observed uvby photometry for the extreme Pop II globular cluster M92.
Adopting a metallicity of [Fe/H]= -2.22, a distance of 8.3 kpc, and a reddening of
E(B-V)=0.023
(Grundahl et al. 2000),
we have converted the observed y-(b-y) diagram of Grundahl et al. (private communication)
to the fundamental parameters along the evolutionary sequence past the turnoff point,
using Mv, (b-y),
![]() (determined by MARCS models) and assuming a mass
of 0.8
(determined by MARCS models) and assuming a mass
of 0.8 ![]() for the giants; c.f. the
for the giants; c.f. the
![]() values given in
Table 5. The bolometric corrections used were taken from VandenBerg & Clem (2003).
Next, we have calculated values for the uvby colours using MARCS models for these parameter
values, to compare with the directly observed dereddened indices for M92 stars, according
to Grundahl et al. As is seen in Table 5, the observed colours
are well reproduced by the models. We have also calculated the derivatives
values given in
Table 5. The bolometric corrections used were taken from VandenBerg & Clem (2003).
Next, we have calculated values for the uvby colours using MARCS models for these parameter
values, to compare with the directly observed dereddened indices for M92 stars, according
to Grundahl et al. As is seen in Table 5, the observed colours
are well reproduced by the models. We have also calculated the derivatives
![]() along the giant branch and find typical values ranging from -0.2 to -0.1, thus agreeing within 20% between the observations and the calculations. This
suggests that we can use the uvby system to estimate gravities for metal-poor giant
stars.
along the giant branch and find typical values ranging from -0.2 to -0.1, thus agreeing within 20% between the observations and the calculations. This
suggests that we can use the uvby system to estimate gravities for metal-poor giant
stars.
7.1.2 NGC 6397
As a second test, effective temperatures for stars in the metal-poor globular cluster NGC 6397 were derived. This is an application of current interest as Korn et al. (2007) have recently claimed that they have identified abundance trends between groups of cluster stars which they suggest are caused by atomic diffusion. Tracing abundance differences between different groups, at the turnoff, on the subgiant branch and on the lower and higher red-giant branch (TOP, SGB, lRGB, hRGB), requires well determined stellar parameters, and most importantly well measured effective temperature differences between the groups. Korn et al. derive effective temperatures with a photometric and spectroscopic approach and they find consistent temperatures.Table 5:
Observed and calculated colours for ![]() values along the sub-giant - giant branch
for M92 and MARCS, respectively. The tabulated colours are mean colour values of
stars close to the given fundamental parameters.
values along the sub-giant - giant branch
for M92 and MARCS, respectively. The tabulated colours are mean colour values of
stars close to the given fundamental parameters.
Table 6: Derived effective temperatures from empirical calibrations of photometry ((b-y) and (v-y)), and spectroscopy (Korn et al. 2007), as well as our theoretical calibration, for groups of stars in the metal-poor cluster NGC 6397. The temperatures are mean values for a number of stars/models in each group.
7.1.3 NGC 6752
In another test, the nitrogen sensitivity of of the c1 index was examined. In a recent paper, Yong et al. (2008), measure the nitrogen content of giants in the globular cluster NGC 6752 ([Fe/H]Table 7:
Calculated
![]() [N/Fe] for giant models as a
comparison to the observed
[N/Fe] for giant models as a
comparison to the observed ![]() sensitivity of NGC 6752
(Yong et al. 2008).
sensitivity of NGC 6752
(Yong et al. 2008).
8 Conclusions and recommendations
We have explored the possibilities and shortcomings of synthetic uvby-H![]() photometry
based on new MARCS model atmospheres. In general a good agreement with
empirical calibrations of this photometric system is found. However, a number of systematic
deviations between theory and observations also become apparent. The temperature
sensitivity of the (b-y) colour (i.e.
photometry
based on new MARCS model atmospheres. In general a good agreement with
empirical calibrations of this photometric system is found. However, a number of systematic
deviations between theory and observations also become apparent. The temperature
sensitivity of the (b-y) colour (i.e.
![]() )
seems marginally stronger for the calculated colours than
is found when using infrared flux method determinations of temperatures.
A similar, and even somewhat greater, difference occurs for temperatures based
on the H
)
seems marginally stronger for the calculated colours than
is found when using infrared flux method determinations of temperatures.
A similar, and even somewhat greater, difference occurs for temperatures based
on the H![]() index, when compared with the empirical scale.
The (b-y) calibration for Pop II stars supports Korn et al. (2007), who claim the signatures
of atomic diffusion in the metal-poor globular cluster NGC 6397.
index, when compared with the empirical scale.
The (b-y) calibration for Pop II stars supports Korn et al. (2007), who claim the signatures
of atomic diffusion in the metal-poor globular cluster NGC 6397.
For the metallicity index m1 the theoretical sensitivity
![]() [Me/H] is
somewhat stronger than the empirical one that is based on spectroscopic [Fe/H]-determinations.
For the gravity sensitivity of the c1 Balmer discontinuity measure, we find a reasonably
good agreement with observations for stars hotter than the Sun, where the Balmer discontinuity
is significant. Considerable problems remain for the cooler stars, although the model
calibration works well for Pop II giants.
[Me/H] is
somewhat stronger than the empirical one that is based on spectroscopic [Fe/H]-determinations.
For the gravity sensitivity of the c1 Balmer discontinuity measure, we find a reasonably
good agreement with observations for stars hotter than the Sun, where the Balmer discontinuity
is significant. Considerable problems remain for the cooler stars, although the model
calibration works well for Pop II giants.
One might ask whether these problems may be solved when even more detailed atomic and molecular line data become available to feed into model atmospheres. This is possible but it is also possible that thermal inhomogenities as generated by convection and possibly also non-LTE effects, contribute to the difference between synthetic and observed values of (b-y) and m1. Concerning the problems in reproducing the observed c1 indices of cooler stars, these may well be due to failures in line-data, although thermal inhomogeneities in the atmospheres may also here turn out to be the important effect. One should also realise that there are still residual problems associated with differences and uncertainties in the observed and adopted Strömgren passbands (Manfroid & Sterken 1987). The current study illustrates the problems in synthetic photometry in the visual wavelength regions. Continued efforts along such lines must be complemented with more detailed studies of the shortcoming of classical model atmospheres and the replacement of those, also in large-scale calibration efforts, by physically more realistic models.
Acknowledgements
Anders Eriksson is thanked for a major contribution at the startup of this project. Remo Collet is thanked for discussions on 3D model atmospheres and Mike Bessell, Ulrike Heiter, Johan Holmberg, Andreas Korn, Karin Lind, and the anonymous referee are thanked for valuable suggestions and comments on the manuscript. Ana García Pérez is thanked for the calculations of reddening.
Appendix A: Calibrations
In the following
A.1 Theoretical T
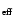 calibration for dwarf stars, (b - y) and H
calibration for dwarf stars, (b - y) and H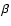
![\begin{eqnarray*}\Theta_{\rm eff}(b-y)_{\rm dwarf} & = & 0.415 + 1.313(b-y) - 0....
...b-y)\rm [Me/H] \\
& & - 0.003\rm [Me/H] - 0.006\rm [Me/H]^{2}.
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa10786-08/img128.gif)
The models, upon which the calibration is based, are selected to follow the restrictions given for the empirical equation (A96, Eq. (9). Restrictions adopted from Fig. 11a):
![\begin{eqnarray*}& &\Theta_{\rm eff}(\rm H\beta)_{\rm dwarf} =
28.60 - 19.79\r...
....422\rm H\beta\rm [Me/H] - 1.068\rm [Me/H] + 0.002\rm [Me/H]^{2}
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa10786-08/img133.gif)
In analogy with the theoretical calibration based on (b-y), the
limits determining which models to use, were set to be equal to the
ones for empirical calibration (A96, Eq. (10) and
its following applicable ranges):
![]() H
H
![]() for -0.5 < [Me/H]
for -0.5 < [Me/H] ![]() ;
;
![]() H
H
![]() for -1.5 < [Me/H]
for -1.5 < [Me/H] ![]() ;
;
![]() H
H
![]() for -2.5 < [Me/H]
for -2.5 < [Me/H] ![]() ;
;
![]() H
H
![]() for -3.5 < [Me/H]
for -3.5 < [Me/H] ![]() ;
;
![]() (set as a limit for dwarf stars).
(set as a limit for dwarf stars).
A.2 Theoretical T
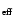 calibration for giants, (b - y)
calibration for giants, (b - y)
![\begin{eqnarray*}\Theta_{\rm eff}(b-y)_{\rm giant} & = &
a_{0} + a{_1}(b-y) + ...
...(b-y)\rm [Me/H] + \it a{_4}\rm [Me/H] + \it a{_5}\rm [Me/H]{^2}.
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa10786-08/img146.gif)
Here we deviate from the same restriction limits for the calibrations as presented in Alonso et al. (1999, Tables 2 and 3). New theoretical limits were set due to model restrictions:
A.3 Theoretical metallicity calibration for G-stars
The models, upon which the metallicity calibrations for G and F stars are based,
are selected to follow the restrictions given for the empirical equations
of S&N89, Eqs. (3) and (2), respectively. The G-stars limits cover the following
intervals:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (set as limit for
(set as limit for ![]() ).
).
![\begin{eqnarray*}& &{\rm [Me/H]}_{\rm G} = -2.796 + 39.21m_{1} - 88.97m^{2}_{1} ...
...) + \left[27.03m_{1} - 1.220c_{1} - 41.42m^{2}_{1}\right]c_{1} .
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa10786-08/img156.gif)
Table 8:
The derived coefficients for the theoretical calibration in the intervalls
I:
![]() ,
II:
,
II:
![]() &
&
![]() and III:
and III:
![]() &
&
![]() .
.
A.4 Theoretical metallicity calibration for F-stars
F-star limits are given by:![\begin{eqnarray*}\rm [Me/H]_{F} & = & 1.850 - 34.21m_{1} + 105.34m_{1}(b-y) \\
...
...\
& & \\
c_{3} & = & 0.4462 - 2.233(b-y) + 2.885(b-y)^{2} .
\end{eqnarray*}](/articles/aa/full_html/2009/17/aa10786-08/img162.gif)
References
- Adelman, S. J., & Gulliver, A. F. 1990, ApJ, 348, 712 [NASA ADS] [CrossRef] (In the text)
- Ali, A. W., & Griem, H. R. 1966, Phys. Rev., 144, 366 [NASA ADS] [CrossRef] (In the text)
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] (In the text)
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ardeberg, A., & Lindgren H. 1981, RMxA&A, 6, 173 [NASA ADS] (In the text)
- Asplund, M., Grevess, N., & Sauval, A. J. 2005, ASPC, 336, 25 [NASA ADS] (In the text)
- Barklem, P. S., & Piskunov, N. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray, Proc., IAU Symp., 210 (In the text)
- Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&A, 363, 1091 [NASA ADS] (In the text)
- Baschek, B. 1960, Z. Ap, 50, 296 [NASA ADS] (In the text)
- Bell, R. A. 1970, MNRAS, 148, 25 [NASA ADS] (In the text)
- Bell, R. A. 1971, MNRAS, 154, 343 [NASA ADS]
- Bell, R. A., & Parsons, S. B. 1974, MNSAS, 169, 71 (In the text)
- Bessell, M. S. 2005, A&ARv, 43, 293 [CrossRef] (In the text)
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] (In the text)
- Castelli, F., & Kurucz, R. L. 2006, A&A, 454, 333 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Christlieb, N., Gustafsson, B., Korn, A. J., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef]
- Clem, J. L., VandenBerg, D. A., Grundahl, F., & Bell, R. 2004, AJ, 127, 1227 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1958, ApJ, 128, 185 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1966, IAU Symp., 24, 170 [NASA ADS] (In the text)
- Crawford, D. L. 1975, AJ, 80, 955 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1979, AJ, 84, 1858 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Mander, J. 1966, AJ, 71, 114 [NASA ADS] [CrossRef]
- Crawford, D. L., & Barnes, J. V. 1970, AJ, 75 978 (In the text)
- Edvardsson, B. 2008, in A stellar journey, A symposium in celebration of Bengt Gustafsson's 65th birthday, Phys. Scr., in press (In the text)
- Edvardsson, B., Eriksson, K., Gustafsson, B., et al. 2008, A&A, in preparation
- Gigas, D. 1988, A&A, 192, 264 [NASA ADS] (In the text)
- Grevesse, N., & Sauval, A. J. 1998, SSRv, 85, 161 [NASA ADS] [CrossRef] (In the text)
- Griem, H. R. 1960, ApJ, 132, 883 [NASA ADS] [CrossRef] (In the text)
- Grundahl, F., VandenBerg, D. A., Bell, R. A., Andersen, M. I., & Stetson, P. B. 2000, AJ, 120, 1884 [NASA ADS] [CrossRef] (In the text)
- Gulliver, A. F., Hill, G., & Adelman, S. J. 1994, ApJ, 429, L81 [NASA ADS] [CrossRef] (In the text)
- Gustafsson, B., & Bell, R. A. 1979, A&A, 74, 313 [NASA ADS] (In the text)
- Gustafsson, B., & Nissen, P. E. 1972, A&A, 19, 291 [NASA ADS] (In the text)
- Gustafsson, B., Edvardsson, B., Eriksson, K., Jørgensen, U. G., & Plez, B. 2003, Conf. Ser., 288, 331 [NASA ADS]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hakkila, J., Myers, J. M., Stidham, B. J., & Hartmann, D. H. 1997, AJ, 114, 2043 [NASA ADS] [CrossRef] (In the text)
- Heiter, U., Weiss, W. W., & Paunzen, E. 2002, A&A, 381, 971 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Helt, B. E., Franco, G. A. P., & Florentin Nielsen, R. 1987, in ESO Workshop on the SN1987A, ed. I. J. Danziger, Garching, 89 (In the text)
- Hill, G. M. 1995, A&A, 294, 536 [NASA ADS] (In the text)
- Hill, G., Gulliver, A. F., & Adelman, S. J. 2004, IAU Symp., 224, 35 [NASA ADS] (In the text)
- Hoffleit, D., & Warren, W. H. Jr. 1995, VizieR On-line Data Catalog: V/50, SIMBAD (In the text)
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ilijic, S., Rosandic, M., Dominis, E., et al. 1998, CoSka, 27, 467 [NASA ADS] (In the text)
- Jonsell, K., Edvardsson, B., Gustafsson, B., et al. 2005, A&A, 440, 321 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] (In the text)
- Kupka, F., Piskunov, N. E., Ryabchikova, T. A., et al. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kurucz, R.L. 1995, Kurucz CD-ROM No.15, Cambridge, Mass., Smithsonian Astrophysical Observatory (In the text)
- Lester, J. B., Gray, R. O., & Kurucz, R. L. 1986, ApJS, 61, 509 [NASA ADS] [CrossRef] (In the text)
- Lejeune, T., Lastennet, E., Westera, P., & Buser, R. 1999, ASP Conf Proc., 192, 207 [NASA ADS] (In the text)
- Manfoid, J., & Sterken, C. 1987, A&AS, 71, 539 [NASA ADS]
- Nissen, P. E. 1970, A&A (In the text)
- Nissen, P. E. 1981, A&A, 97, 145 [NASA ADS] (In the text)
- Nissen, P. E. 1988, A&A, 199, 146 [NASA ADS] (In the text)
- Nissen, P. E., & Gustafsson, B. 1978, in Astronomical Papers Dedicated to Bengt Strömgren, Copenhagen, 43 (In the text)
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Olsen, E. H. 1983, A&AS, 54, 55 [NASA ADS] (In the text)
- Olsen, E. H. 1984, A&A, 57, 443 [NASA ADS] (In the text)
- Olsen, E. H. 1988, A&A, 189, 173 [NASA ADS] (In the text)
- Paunzen, E., Iliev, I. K., Kamp, I., et al. 2002, MNRAS, 336, 1030 [NASA ADS] [CrossRef] (In the text)
- Plez, B., Masseron, T., Van Eck, S., et al. 2008, ASP, Conf. Ser., in press (In the text)
- Querci, F., Querci, M., & Kunde, V. 1971, A&A, 31, 265 [NASA ADS] (In the text)
- Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 [NASA ADS] [CrossRef] (In the text)
- Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 [NASA ADS] [CrossRef] (In the text)
- Relyea, L. J., & Kurucz, R. L. 1978, ApJS 37, 45
- Schuster, W. J., & Nissen, P. E. 1988, A&AS, 73, 225 [NASA ADS] (In the text)
- Schuster, W. J., & Nissen, P. E. 1989, A&A, 221, 65 [NASA ADS] (In the text)
- Strömgren, B. 1963, QJRAS, 4, 8 [NASA ADS] (In the text)
- Strömgren, B. 1964, Astrophys. Norveg., 9, 333 [NASA ADS] (In the text)
- Strömgren, B. 1966, Ann. Rev. Astr. Ap., 4, 433 [NASA ADS] [CrossRef]
- Twarog, B. A., Vargas, L. C., & Anthony-Twarog, B. J. 2007, AJ, 134, 1777 [NASA ADS] [CrossRef] (In the text)
- VandenBerg, D. A., & Clem, J. L. 2003, AJ, 126, 778 [NASA ADS] [CrossRef] (In the text)
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] (In the text)
- Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37 [NASA ADS] [CrossRef] (In the text)
- Wallerstein, G. 1962, ApJS, 6, 407 [NASA ADS] [CrossRef] (In the text)
- Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008, ApJ, 684, 1159 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... approach
![[*]](/icons/foot_motif.gif)
- Model colours are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/498/527
All Tables
Table 1:
Standard deviations for
![]() and [Fe/H] derived
using models as compared with literature values of the different
comparison samples. See also Figs. 7-9 and
Figs. 13, 14.
and [Fe/H] derived
using models as compared with literature values of the different
comparison samples. See also Figs. 7-9 and
Figs. 13, 14.
Table 2:
The metallicity sensitivity,
![]() [Me/H])(b-y), for
models with
[Me/H])(b-y), for
models with ![]() = 4.5 and 4.0.
= 4.5 and 4.0.
Table 3: The change in the uvby indices when the microturbulence parameter is increased.
Table 4:
The sensitivity to surface gravity, (
![]() ,
for
models with [Me/H] = 0.5 and 0.0.
,
for
models with [Me/H] = 0.5 and 0.0.
Table 5:
Observed and calculated colours for ![]() values along the sub-giant - giant branch
for M92 and MARCS, respectively. The tabulated colours are mean colour values of
stars close to the given fundamental parameters.
values along the sub-giant - giant branch
for M92 and MARCS, respectively. The tabulated colours are mean colour values of
stars close to the given fundamental parameters.
Table 6: Derived effective temperatures from empirical calibrations of photometry ((b-y) and (v-y)), and spectroscopy (Korn et al. 2007), as well as our theoretical calibration, for groups of stars in the metal-poor cluster NGC 6397. The temperatures are mean values for a number of stars/models in each group.
Table 7:
Calculated
![]() [N/Fe] for giant models as a
comparison to the observed
[N/Fe] for giant models as a
comparison to the observed ![]() sensitivity of NGC 6752
(Yong et al. 2008).
sensitivity of NGC 6752
(Yong et al. 2008).
Table 8:
The derived coefficients for the theoretical calibration in the intervalls
I:
![]() ,
II:
,
II:
![]() &
&
![]() and III:
and III:
![]() &
&
![]() .
.
All Figures
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f1.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg36.gif) |
Figure 1:
The uvby-H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f2.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg43.gif) |
Figure 2:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f3.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg63.gif) |
Figure 3:
Fundamental parameters, i.e.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.2cm,angle=90]{0786f4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg64.gif) |
Figure 4:
The (b-y) colour index ( left) and H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg65.gif) |
Figure 5:
Theoretical (b-y) values versus effective temperature for models with
different [Me/H] and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg66.gif) |
Figure 6:
Theoretical H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f7.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg71.gif) |
Figure 7: Comparison of calibrations of (b-y) for dwarf stars with individual values for the standard stars and C06 plotted. The solid line represents a fit of the effective temperatures adopted for the stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperatures relative to empirical calibrations (Alonso et al. 1996; Holmberg et al. 2007; Ramírez & Meléndez 2005b) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f8.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg72.gif) |
Figure 8: Comparison of calibrations of (b-y) for giant stars with individual values for the standard stars plotted. The solid line represents a fit of the effective temperatures adopted for the standard stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperatures relative to empirical calibrations (Alonso et al. 1999; Ramírez & Meléndez 2005b) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f9.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg73.gif) |
Figure 9:
Comparison of calibrations of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f10.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg77.gif) |
Figure 10:
The effective temperatures calculated by the equations based on H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f11.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg78.gif) |
Figure 11: The m1 index versus (b-y) for MARCS and Lester et al. (1986, LGK) model atmospheres. Arrows show the effect of increasing the N abundances by a factor of 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f12.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg84.gif) |
Figure 12:
The m1 index versus (b-y) for MARCS models plotted together with
standard stars of different gravities in different panels
( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f13.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg88.gif) |
Figure 13: The [Me/H] calibration for F stars from the standard sample and Casagrande et al. (2006, C06). The solid line represents a linear regression of the effective temperatures adopted for the stars relative to the corresponding values obtained from the theoretical calibration. Below that (shaded area and right y-axis) corresponding linear regressions of the adopted effective temperautres relative to empirical calibrations (Schuster & Nissen 1989; Holmberg et al. 2007; Ramírez & Meléndez 2005a) are shown. The dotted line is a one-to-one line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=90]{0786f14.ps}}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg96.gif) |
Figure 14: The [Me/H] calibration for G stars. For plot description see Fig. 13. Note that empirical calibrations of HNA07 and RM05 overlap and could therefore be difficult to distinguish. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90]{0786f15.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg104.gif) |
Figure 15:
The c1 index versus (b-y) for MARCS and
Lester et al. (1986, LGK)
model atmospheres with different |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=90,clip]{0786f16.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10786-08/Timg113.gif) |
Figure 16:
The c1 index versus (b-y) for MARCS models with different
[Me/H] and |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


