| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 627 - 640 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200810698 | |
| Published online | 18 February 2009 | |
Spectroscopic binaries among Hipparcos M giants![[*]](/icons/foot_motif.gif) ,
,![[*]](/icons/foot_motif.gif)
I. Data, orbits, and intrinsic variations
B. Famaey1,![]() - D. Pourbaix1,
- D. Pourbaix1,![]() - A. Frankowski1,
- A. Frankowski1,![]() - S. Van Eck1,
- S. Van Eck1,![]() - M. Mayor2 - S. Udry2 - A. Jorissen1
- M. Mayor2 - S. Udry2 - A. Jorissen1
1 -
Institut d'Astronomie et d'Astrophysique, Université
libre de Bruxelles, Faculté des Sciences, CP 226, Boulevard du Triomphe, 1050
Bruxelles, Belgium
2 -
Observatoire de Genève, Université de Genève, 1290 Sauverny, Switzerland
Received 28 July 2008 / Accepted 19 December 2008
Abstract
Context. This paper is a follow-up on the vast effort to collect radial velocity data for stars belonging to the Hipparcos survey.
Aims. We aim at extending the orbital data available for binaries with M giant primaries. The data presented in this paper will be used in the companion papers of this series to (i) derive the binary frequency among M giants and compare it to that of K giants (Paper II); and (ii) analyse the eccentricity - period diagram and the mass-function distribution (Paper III).
Methods. Keplerian solutions are fitted to radial-velocity data. However, for several stars, no satisfactory solution could be found, even though the radial-velocity standard deviation is greater than the instrumental error, because M giants suffer from intrinsic radial-velocity variations due to pulsations. We show that these intrinsic radial-velocity variations can be linked with both the average spectral-line width and the photometric variability.
Results. We present an extensive collection of spectroscopic orbits for M giants with 12 new orbits, plus 17 from the literature. On top of these, 1 preliminary orbit yielded an approximate value for the eccentricity and the orbital period. Moreover, to illustrate how the large radial-velocity jitter present in Mira and semi-regular variables may easily be confused with orbital variations, we also present examples of pseudo-orbital variations (in S UMa, X Cnc, and possibly in HD 115 521, a former IAU radial-velocity standard). Because of this difficulty, M giants involving Mira variables were excluded from our monitored sample. We finally show that the majority of M giants detected as X-ray sources are actually binaries.
Conclusions. The data presented in this paper considerably increase the orbital data set for M giants, and will allow us to conduct a detailed analysis of the eccentricity - period diagram in a companion paper (Paper III).
Key words: stars: binaries: spectroscopic - stars: late-type - stars: AGB and post-AGB
1 Introduction
When a mass-losing M giant is present in a binary system, the interaction of the wind of the giant with the companion gives rise to photometric activity or spectroscopic symbiosis (like in symbiotic stars, in VV Cephei-like systems, or in low-mass X-ray binaries like V2116 Oph) that make the system very conspicuous even far away. However, if the M giant does not lose large amounts of mass, the binary nature of the star will not be as conspicuous. Combined with M giants often exhibiting pulsations that cause intrinsic velocity variations, thereby confusing the search for orbital variations, it explains why so few spectroscopic binaries involving M giants are known so far. Indeed, the Ninth Catalogue of Spectroscopic Binary Orbits (9; Pourbaix et al. 2004) contains 2746 entries (query in March 2007), among which only 32 systems involve M giants, and yet 21 of these are either well-known symbiotic systems or VV-Cephei-like systems.
Carquillat and collaborators have devoted a series of papers to spectroscopic binaries of spectral types F to M, but only 2 binaries with primaries of spectral type MIII were studied (Prieur et al. 2006; Carquillat & Ginestet 1996). Previously, Stephenson (1967) provided a list of 7 systems with composite spectra involving an M star. But it is the paper by Hinkle et al. (2002) that, to the best of our knowledge, has so far provided the most extensive list of spectroscopic binaries involving non-symbiotic M giants.
With the present paper, we start a series devoted to a detailed study of the properties of spectroscopic binaries involving an MIII primary. The number of such binaries with known orbital elements has nearly doubled, as a result of our observing campaign of an extensive sample of M giants, drawn from the Hipparcos Catalogue, for which CORAVEL radial velocities have been obtained in a systematic way (Udry et al. 1997). The main driver behind this large database lies, of course, with the stellar kinematics in our Galaxy. And indeed the kinematical properties of the present sample of M giants have been fully analysed by Famaey et al. (2005, 2008). But this large data set may also be used to search for binaries.
The present paper presents the radial-velocity data (Sect. 2) and orbital elements (Sect. 4) of the newly-discovered spectroscopic binaries, for which a satisfactory orbit could be obtained. It also discusses the intrinsic variations sometimes mimicking orbital variations (Sect. 3). The list of new orbital elements is complemented with an exhaustive list of orbital elements for non-symbiotic M giants drawn from the literature (Table 8). In Paper II (Frankowski et al. 2009), we will use the observational information gathered in this paper to derive the frequency of spectroscopic binaries among M giants, and compare it with that of K giants. Paper III (Jorissen et al. 2009) will then present an in-depth analysis of the eccentricity-period diagram for M giants.
2 Radial-velocity data
The basic sample of M giants
is drawn from the Hipparcos survey stars
(identified by flag ``S'' in field H68 of the Hipparcos
catalogue; ESA 1997).
These M giants were extracted from the Hipparcos survey stars on the basis of the
spectral type provided in the Hipparcos catalogue and of the absolute
magnitude
MHp < 4 computed from the Hipparcos parallax and
Hp magnitude. Mira stars or supergiants of luminosity class I (when
explicitly mentioned in the spectral classification) were not included
in the sample (notably because of the confusion that their envelope
pulsation may cause on the radial-velocity variations). This first
sample (defined here as sample I) contains 771
M giants with declinations greater than ![]() and corresponds
to the sample of northern M giants analysed in Famaey et al. (2005),
to which 65 M giants with declinations between 0 and
and corresponds
to the sample of northern M giants analysed in Famaey et al. (2005),
to which 65 M giants with declinations between 0 and ![]() have been added.
Two radial-velocity measurements, spanning at least one year, have been obtained with the CORAVEL spectrovelocimeter (Baranne et al. 1979) for all stars of sample I,
as part of a monitoring programme targeting
all Hipparcos survey stars later than about F (Udry et al. 1997).
Note that 22 objects of the sample of Famaey et al. (2005) are not present in sample I because they had only one radial
velocity measurement, making them unsuitable for
binarity analysis. Famaey's sample was also screened for other irregularities, such as
wrong Hipparcos spectral type or mistaken identity
have been added.
Two radial-velocity measurements, spanning at least one year, have been obtained with the CORAVEL spectrovelocimeter (Baranne et al. 1979) for all stars of sample I,
as part of a monitoring programme targeting
all Hipparcos survey stars later than about F (Udry et al. 1997).
Note that 22 objects of the sample of Famaey et al. (2005) are not present in sample I because they had only one radial
velocity measurement, making them unsuitable for
binarity analysis. Famaey's sample was also screened for other irregularities, such as
wrong Hipparcos spectral type or mistaken identity![]() .
Extrinsic S stars were removed from the sample as well.
.
Extrinsic S stars were removed from the sample as well.
Subsamples of sample I have been subject to more intensive observing campaigns. Every third star from this sample has received a denser coverage,
with (mostly) 4 instead of 2 measurements (7 stars received only
3 measurements), to achieve a better
binary detection rate: this subsample of sample I is defined as sample II.
Figure 1 displays the histograms of
![]() (the number of measurements per star),
(the number of measurements per star),
![]() (average uncertainty of one measurement), and
(average uncertainty of one measurement), and ![]() (time spanned by the measurements of a given star) for the 254 stars of sample II.
(time spanned by the measurements of a given star) for the 254 stars of sample II.
![\begin{figure}
\par\includegraphics[width=8.5cm]{10698f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg15.gif) |
Figure 1:
Histograms of the number of measurements per star (
|
| Open with DEXTER | |
Table 1: The four observing campaigns defining the four (sub)samples of Hipparcos M giants.
Furthermore, 35 stars
from sample II, suspected of being binaries (i.e., with
a radial-velocity standard deviation
![]() km s-1 at the end of the observing campaign of sample II)
have been monitored with the ELODIE spectrograph (Baranne et al. 1996) at the Haute-Provence Observatory to derive their orbital elements. They make up sample III.
At the end of the ELODIE monitoring, a late measurement was obtained
for 157 stars from sample II with
km s-1 at the end of the observing campaign of sample II)
have been monitored with the ELODIE spectrograph (Baranne et al. 1996) at the Haute-Provence Observatory to derive their orbital elements. They make up sample III.
At the end of the ELODIE monitoring, a late measurement was obtained
for 157 stars from sample II with
![]() km s-1 (this
selection being mainly based on right ascension), in order to detect binaries with very long orbital periods. These constitute sample IV. A summary of the properties of these four samples is presented in Table 1.
km s-1 (this
selection being mainly based on right ascension), in order to detect binaries with very long orbital periods. These constitute sample IV. A summary of the properties of these four samples is presented in Table 1.
The CORAVEL data were put on the ELODIE radial-velocity
system to ensure homogeneity (Udry et al. 1999b). The
uncertainty
![]() of one radial-velocity measurement is
approximately 0.3 km s-1 for CORAVEL measurements, but is better for
ELODIE measurements. With the ELODIE single-fibre mode used during the
present observing campaigns, it may be as good as 50 m s-1(Baranne et al. 1996). It was not measured in a systematic way; however, to fix the ideas, an accuracy of 0.2 km s-1 has been associated with the ELODIE measurements in the data files.
of one radial-velocity measurement is
approximately 0.3 km s-1 for CORAVEL measurements, but is better for
ELODIE measurements. With the ELODIE single-fibre mode used during the
present observing campaigns, it may be as good as 50 m s-1(Baranne et al. 1996). It was not measured in a systematic way; however, to fix the ideas, an accuracy of 0.2 km s-1 has been associated with the ELODIE measurements in the data files.
The data for sample I (average velocity, radial-velocity standard
deviation, and binarity flag) may be found in Table A.1![]() (Cols. 24-26) of Famaey et al. (2005).
A similar table, merging CORAVEL and ELODIE data, is given in
Table 2 for sample II, which also provides the binarity diagnostics (according to the rules that will be specified in
Sect. 3.1).
Individual radial-velocity measurements for the 35 stars of sample III
are given in Table 3. Roger Griffin has kindly provided us with supplementary measurements for HD 182 190 and HD 220 088 that allowed us to compute an orbit for these two stars. These measurements were performed with his Cambridge spectrovelocimeter and are listed in Table 3, with the label ``CAM''. To put them on the ELODIE system, an offset of -0.8 km s-1 has been applied.
(Cols. 24-26) of Famaey et al. (2005).
A similar table, merging CORAVEL and ELODIE data, is given in
Table 2 for sample II, which also provides the binarity diagnostics (according to the rules that will be specified in
Sect. 3.1).
Individual radial-velocity measurements for the 35 stars of sample III
are given in Table 3. Roger Griffin has kindly provided us with supplementary measurements for HD 182 190 and HD 220 088 that allowed us to compute an orbit for these two stars. These measurements were performed with his Cambridge spectrovelocimeter and are listed in Table 3, with the label ``CAM''. To put them on the ELODIE system, an offset of -0.8 km s-1 has been applied.
Table 2: The first five lines of the list of stars from sample II. The full table is only available electronically at the CDS.
Table 3: The individual radial-velocity measurements for the 35 stars of sample III. The full table is available electronically from the CDS, Strasbourg.
3 Binaries, intrinsic radial-velocity jitter, and pseudo-orbits caused by pulsation
![\begin{figure}
\par\includegraphics[width=9cm]{10698f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg26.gif) |
Figure 2:
The radial-velocity
standard deviation
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10698f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg27.gif) |
Figure 3: The radial-velocity standard deviation (corrected for the instrumental error) as a function of the standard deviation on the Hipparcos Hp magnitude. Symbols are the same as in Fig. 2, except that large circles identify stars detected as X-ray sources by the ROSAT All-Sky Survey, following Hünsch et al. (1998). The dotted line represents the trend between radial-velocity and photometric variability reported by Hinkle et al. (1997). This is not a dividing line like the one plotted in Fig. 2. |
| Open with DEXTER | |
3.1 Binarity diagnostic
The search for spectroscopic binaries (SBs) among M giants is made
difficult by the bulk mass motion existing in the atmospheres of these
stars (all M giants being variable to some extent;
e.g. Jorissen et al. 1997; Soszynski et al. 2004; Eyer & Grenon 1997), since such motion triggers
some intrinsic radial-velocity jitter![]() (e.g.,
Udry et al. 1998; Hinkle et al. 2002). This intrinsic jitter amounts to nearly
1.5 km s-1 in the coolest (non-Mira) M giants
(e.g.,
Udry et al. 1998; Hinkle et al. 2002). This intrinsic jitter amounts to nearly
1.5 km s-1 in the coolest (non-Mira) M giants![]() (Fig. 2), so the detection of SBs cannot rely
solely on a
(Fig. 2), so the detection of SBs cannot rely
solely on a ![]() test comparing the radial-velocity standard
deviation
test comparing the radial-velocity standard
deviation
![]() to the average instrumental error
to the average instrumental error
![]() .
In the following, we denote by
.
In the following, we denote by
![]() the radial-velocity
standard deviation corrected for the average
instrumental error
the radial-velocity
standard deviation corrected for the average
instrumental error
![]() ,
i.e.
,
i.e.
![]() .
.
In a first step, to flag a star as a binary in samples II, III, and IV,
we therefore rely solely on the visual examination of the
radial-velocity variations, and whether or not it is possible to obtain a meaningful orbital solution.
The binarity diagnostic is then complemented by two criteria, described
in detail in Sects. 3.1.1 and 3.1.2:
(i) the location of the star in a diagram
![]() (Fig. 2),
where
(Fig. 2),
where ![]() denotes the intrinsic width of spectral lines
(Sect. 3.1.1); and (ii) its
location in a diagram
denotes the intrinsic width of spectral lines
(Sect. 3.1.1); and (ii) its
location in a diagram
![]() (Fig. 3),
where
(Fig. 3),
where
![]() is the standard deviation of the Hipparcos
magnitude (Sect. 3.1.2).
The final binarity diagnostic for all stars from sample III (and for
stars from sample IV, which are SB or suspected SB)
is listed in Table 4 according to the following categories:
is the standard deviation of the Hipparcos
magnitude (Sect. 3.1.2).
The final binarity diagnostic for all stars from sample III (and for
stars from sample IV, which are SB or suspected SB)
is listed in Table 4 according to the following categories:
- a
- ``ORB'': a satisfactory orbit could be computed (see Fig. 4);
- b
- ``ORB:'': the orbit is preliminary, because the number of data points or the time coverage are not large enough, or two different solutions are possible (see Fig. 4);
- c
- ``SB'': the star is a spectroscopic binary, but there are not enough data points to even compute a preliminary orbit (see Fig. 5);
- d
- ``SB?'': the star is suspected to be a binary (see Fig. 6), even though it falls close to the dividing line in the
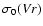 -
-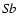 diagram (see Sect. 3.1.1 and Fig. 2);
diagram (see Sect. 3.1.1 and Fig. 2);
- e
- ``SB/jitter?'' : it is not clear whether the radial velocity variations are of intrinsic or extrinsic nature (see Fig. 7): the star falls close to the dividing line in the
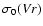 -
-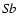 diagram (Fig. 2).
diagram (Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.8cm]{10698f4-1.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg36.gif) |
Figure 4: Radial-velocity data points for the spectroscopic binaries, along with their orbital solution. The solution marked as ``ORB:'' is not very well constrained and hence preliminary. All panels span a Vr range of 30 km s-1. Error bars on the individual measurements (of the order of 0.2 km s-1) are too small to be seen. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{10698f4-2.ps}\par\vspace*{2mm}
\includegraphics[width=8.4cm]{10698f4-3.ps}\par
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg37.gif) |
Figure 4: continued. |
| Open with DEXTER | |
Table 4: Binarity and photometric-variability diagnostics for stars from sample III (as well as binaries or suspected binaries from sample IV).
3.1.1 Intrinsic width of spectral lines
We note that the parameter ![]() ,
measuring the intrinsic width
of spectral lines, provides useful guidance in distinguishing radial-velocity
jitter from orbital motion.
This parameter is defined as
,
measuring the intrinsic width
of spectral lines, provides useful guidance in distinguishing radial-velocity
jitter from orbital motion.
This parameter is defined as
![]() ,
where s is
the standard deviation of a Gaussian fitted to the CORAVEL cross-correlation
dip (see Baranne et al. 1979) and s0 the instrumental width (7 km s-1 for CORAVEL at the Haute-Provence Observatory;
for details see Van Eck & Jorissen 2000; Jorissen & Mayor 1988, also Paper II).
Indeed, Fig. 2 reveals that stars for
which no orbital solution could be found (open squares) have
radial-velocity standard deviations that increase
as
,
where s is
the standard deviation of a Gaussian fitted to the CORAVEL cross-correlation
dip (see Baranne et al. 1979) and s0 the instrumental width (7 km s-1 for CORAVEL at the Haute-Provence Observatory;
for details see Van Eck & Jorissen 2000; Jorissen & Mayor 1988, also Paper II).
Indeed, Fig. 2 reveals that stars for
which no orbital solution could be found (open squares) have
radial-velocity standard deviations that increase
as ![]() increases. In Paper II, we will show that
increases. In Paper II, we will show that ![]() correlates closely
with the stellar radius. We thus foresee that radial-velocity
variations in stars falling well below the dashed line in
Fig. 2 are most likely of intrinsic (rather than
orbital) origin. Of course, binaries with an orbit seen almost face
on, or with a long period, or insufficiently sampled, may also fall
below the dashed line.
Let us stress that the slope of this dividing line in Fig. 2 can be influenced by both the number of radial-velocity data points for a given object and the total number of objects in the sample (see Sect. 2.1 of Paper II).
correlates closely
with the stellar radius. We thus foresee that radial-velocity
variations in stars falling well below the dashed line in
Fig. 2 are most likely of intrinsic (rather than
orbital) origin. Of course, binaries with an orbit seen almost face
on, or with a long period, or insufficiently sampled, may also fall
below the dashed line.
Let us stress that the slope of this dividing line in Fig. 2 can be influenced by both the number of radial-velocity data points for a given object and the total number of objects in the sample (see Sect. 2.1 of Paper II).
Examples of radial-velocity variations for such stars from sample III, falling below the dividing line in Fig. 2, are plotted in Fig. 8, and it is clear that no orbital solution can be found for them. On the other hand, stars along the dashed line, whose velocity variations are plotted in Fig. 7, could either be SB or exhibit radial-velocity jitter. These 10 stars are listed in Table 4c.
On the other hand, among stars from samples III and IV, for which 5 or more measurements have been made, 22 certain spectroscopic binaries have been found, as listed in Table 4a. Of those, only 3 (HD 89 758, HD 108 907, and HD 132 813) were previously known to be spectroscopic binaries, and a new satisfactory orbit could be computed for 12 of them (with the help of supplementary data points from the Cambridge spectrovelocimeter for HD 182 190 and HD 220 088; see Table 3). The orbital elements are presented in Sect. 4. The radial-velocity data points of the binary stars are displayed in Fig. 4 for those binaries with an orbit available (labelled in Table 4 as ORB or, for preliminary solutions, ORB:), and in Fig. 5 for the SBs without orbits. On top of the firm binaries, 5 stars were identified whose radial-velocity variations are very likely orbital (listed in Table 4b and displayed in Fig. 6).
3.1.2 Photometric variability
Although Mira stars have been excluded from our sample, some
semi-regular variables are nevertheless present. Both classes
of variables often exhibit pseudo-orbital
variations caused by
shock waves associated with the envelope pulsation (Hatzes & Cochran 1998; Hekker et al. 2008; Wood 2000; Derekas et al. 2006; Udry et al. 1998; Soszynski 2007; Setiawan et al. 2004; Hinkle et al. 2002).
For semi-regular variables,
Hinkle et al. (2002) obtain semi-amplitudes K between 1.6 and
3.1 km s-1, whereas for Miras the semi-amplitudes may reach 20 km s-1 in
the most extreme cases (Alvarez et al. 2001). In terms of standard
deviations, these values become 1.1, 1.7, and 14 km s-1, respectively
(remember that for sinusoidal variations,
![]() ). Semi-regular and Mira variables may thus be expected to
exhibit
). Semi-regular and Mira variables may thus be expected to
exhibit
![]() values anywhere in the range of 1 to about
14 km s-1.
values anywhere in the range of 1 to about
14 km s-1.
Moreover, the radial-velocity curves of these stars may often be fitted by a Keplerian orbit with a period of a few hundred days (Udry et al. 1998; Wood et al. 2004; Lebzelter et al. 2005; Hinkle et al. 2002). However, it happens that this Keplerian solution fits the data for 4 to 10 cycles, and then becomes invalid. Two illuminating examples of this kind of behaviour are discussed in the Appendix for stars that do not belong to the samples considered in this paper (the Mira S star S UMa and the semiregular carbon star X Cnc). If the time span of the radial-velocity monitoring is not long enough (i.e., shorter than the 4 to 10 cycles mentioned above), the inadequacy of the Keplerian solution may not be noticed, thus leading to the erroneous suspicion of binarity.
It is therefore very important to check that the Keplerian
solutions proposed in Sect. 4 hereafter are valid, by eliminating
the possibility that they have an intrinsic origin, as often observed
for Mira and semi-regular variables. For this purpose, we collected
from the literature the photometric
properties of all the stars listed in
Table 4 (including those flagged as having
``radial-velocity jitter'', among which we should expect to find a large
fraction of photometric variables). We searched the
Hipparcos Variability Annex, which has the advantage of being an
unbiased information source containing all our stars. The results are plotted in
Fig. 3 (
![]() -
-
![]() diagram), and
listed in Table 4. As we can see, all stars
flagged as spectroscopic binaries (Fig. 3), have
much larger radial-velocity standard deviations than expected from the relation between radial velocity and photometric variability for single stars (as reported by Hinkle et al. 1997). We also see that this relation exhibits some scatter (Fig. 3), and that stars flagged as ``SB/jitter?'' define a rough dividing curve between intrinsic and extrinsic radial velocity variations in the
diagram), and
listed in Table 4. As we can see, all stars
flagged as spectroscopic binaries (Fig. 3), have
much larger radial-velocity standard deviations than expected from the relation between radial velocity and photometric variability for single stars (as reported by Hinkle et al. 1997). We also see that this relation exhibits some scatter (Fig. 3), and that stars flagged as ``SB/jitter?'' define a rough dividing curve between intrinsic and extrinsic radial velocity variations in the
![]() -
-
![]() diagram.
diagram.
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg44.gif) |
Figure 5: Radial-velocity data points for the spectroscopic binaries with no orbit available yet. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg45.gif) |
Figure 6: Radial-velocity data points for the suspected spectroscopic binaries. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-6.ps} \includegraphics[width=9cm]{10698f4-7.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg46.gif) |
Figure 7: Radial-velocity variations for stars falling close to the dividing line between jitter and orbital motion in Fig. 2, for which the nature of the the radial-velocity variations is unclear. The vertical scale spans 10 km s-1 in all cases. They are denoted by crosses in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-8.ps} \includegraphics[width=9cm]{10698f4-9.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg47.gif) |
Figure 8: Examples of radial-velocity variations for stars (referred to by their HD number, as listed in each panel) falling close to the dividing line between jitter and orbital motion in Fig. 2, with a radial-velocity jitter most likely of intrinsic nature. They are denoted by open squares in Figs. 2 and 3. |
| Open with DEXTER | |
In the column ``Var'' of Table 4, we see that almost all stars later than M3 are semi-regular (SR) variables, as expected. It
is very clear that the fraction of SR variables with
![]() mag increases among stars with (or suspected of having)
radial-velocity jitter. A specific case (HD 114 961, marked as a suspected binary ``SB?'' in Table 4) will be discussed in
Sect. 3.3.
Such stars are not very numerous among the ones flagged as
SB. Therefore, one can be confident that all
the stars flagged as SB in Table 4a are indeed
binaries. Only two among those are semi-regular
variables with large photometric amplitudes (i.e.,
HD 16 058 = 15 Tri and HD 132 813 = RR UMi), and there are
good arguments in favour of their binary nature. HD 16 058 is a newly
flagged spectroscopic binary, but it is an X-ray source. As we show in
Sect. 3.2, X-ray detection in M giants is a strong
indication of binarity. The binary nature of HD 132 813 has already been
claimed by Dettmar & Gieseking (1983) and Batten & Fletcher (1986), who obtained consistent orbital
parameters (Table 8). Our recent radial-velocity
measurements are consistent with these orbital parameters (see
Fig. 9), thus clearly demonstrating the binary nature
of HD 132 813 from the stability of the Keplerian solution.
mag increases among stars with (or suspected of having)
radial-velocity jitter. A specific case (HD 114 961, marked as a suspected binary ``SB?'' in Table 4) will be discussed in
Sect. 3.3.
Such stars are not very numerous among the ones flagged as
SB. Therefore, one can be confident that all
the stars flagged as SB in Table 4a are indeed
binaries. Only two among those are semi-regular
variables with large photometric amplitudes (i.e.,
HD 16 058 = 15 Tri and HD 132 813 = RR UMi), and there are
good arguments in favour of their binary nature. HD 16 058 is a newly
flagged spectroscopic binary, but it is an X-ray source. As we show in
Sect. 3.2, X-ray detection in M giants is a strong
indication of binarity. The binary nature of HD 132 813 has already been
claimed by Dettmar & Gieseking (1983) and Batten & Fletcher (1986), who obtained consistent orbital
parameters (Table 8). Our recent radial-velocity
measurements are consistent with these orbital parameters (see
Fig. 9), thus clearly demonstrating the binary nature
of HD 132 813 from the stability of the Keplerian solution.
![\begin{figure}
\par\includegraphics[width=9cm]{10698f5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg49.gif) |
Figure 9: Orbit from Batten & Fletcher (1986) for HD 132 813. Overplotted are our new data points, consistent with this orbit from the literature, obtained about two decades ago. |
| Open with DEXTER | |
3.2 X-ray emission as binarity diagnostic
X-rays are normally not observed in single M giants lying to the right of the so-called dividing line, an almost vertical boundary in the HR diagram separating stars with hot coronae emitting X-rays (to the left) from stars with high mass loss (to the right), which are normally not X-ray emitters (Hünsch et al. 1998). Since X-rays may be generated by several physical processes in a binary system, their detection in an M giant is a strong argument in favour of its binary nature. First, X-rays may be produced at the shocks resulting from the collision of streams in the complex flow pattern associated with wind accretion in a detached binary system involving an AGB star (Theuns et al. 1996; Mastrodemos & Morris 1998; Jahanara et al. 2005; Theuns & Jorissen 1993). Second, X-rays are generated when the gravitational energy of the M giant wind falling in the potential well of the companion star is converted into radiative energy when hitting the stellar surface. The accretion luminosity will either be radiated away in the form of hard X-rays if the infalling matter is optically thin; or if that matter is optically thick, half will be converted into thermal energy and half will be radiated away in the form of blackbody radiation (according to the virial theorem).
A search for X-ray sources among M giants is therefore an efficient way of finding binary systems. The ROSAT all-sky survey of X-ray sources detected only 11 out of 482 M giants of luminosity classes I to III from the Bright Star Catalogue (Hünsch et al. 1998). They are listed in Table 5, along with a comment regarding the binary nature. These few detections justify using radial-velocity variations to detect binaries among M giants in our paper.
Table 5:
Properties of the 11 M giants detected as X-ray sources by the ROSAT
all-sky survey (following Hünsch et al. 1998), where for three stars, the X-ray source is offset by more than 1![]() from the M giant optical position.
from the M giant optical position.
It may be seen from Table 5 that, in most cases, the
M giants detected as X-ray sources are flagged as binaries (4 from the
present work, 1 from the literature, and 1 symbiotic). In three cases (HD 62 898, HD 132 813, and HD 155 035),
the X-ray source is offset by more than 1![]() from the optical
position of the giant, which casts doubts on the M giant being the
source of the X-rays (see Hünsch et al. 1998, for details).
In two other cases, there is a
visual G-type companion, where X-rays may arise from
coronal emission. Thus only HD 130 144 and HD 150 450 have no
satisfactory explanation for the
origin of the X-rays. In Fig. 3, it is HD 130 144 that
appears amidst the non-binary M giants.
from the optical
position of the giant, which casts doubts on the M giant being the
source of the X-rays (see Hünsch et al. 1998, for details).
In two other cases, there is a
visual G-type companion, where X-rays may arise from
coronal emission. Thus only HD 130 144 and HD 150 450 have no
satisfactory explanation for the
origin of the X-rays. In Fig. 3, it is HD 130 144 that
appears amidst the non-binary M giants.
3.3 Special cases
3.3.1 HD 114 961
Since semi-regular and Mira variables may be expected to exhibit
![]() values anywhere in the range from 1 to about 14 km s-1, the value
values anywhere in the range from 1 to about 14 km s-1, the value
![]() km s-1 observed for the
semi-regular variable HD 114 961 (SW Vir) in sample II is not incompatible with
intrinsic variations (although we flagged it as a suspected binary; indeed, HD 114 961 is the triangle in
Fig. 2 with the largest
km s-1 observed for the
semi-regular variable HD 114 961 (SW Vir) in sample II is not incompatible with
intrinsic variations (although we flagged it as a suspected binary; indeed, HD 114 961 is the triangle in
Fig. 2 with the largest
![]() for
for
![]() km s-1).
Let us note, however, that the radial-velocity data available for this star are unfortunately too scarce to infer any periodicity, so no firm conclusion can be reached at this point regarding the intrinsic or orbital origin of the large radial-velocity scatter exhibited by SW Vir.
km s-1).
Let us note, however, that the radial-velocity data available for this star are unfortunately too scarce to infer any periodicity, so no firm conclusion can be reached at this point regarding the intrinsic or orbital origin of the large radial-velocity scatter exhibited by SW Vir.
3.3.2 HD 115 521
HD 115 521 is an interesting case, similar to those discussed in the appendix. It belongs to sample I (and therefore does not appear in
Table 4 since it has only been measured twice in our observing campaign), but being a radial-velocity
standard star till the 1990s (Udry et al. 1999a), it was measured very
frequently and turned out in the first place to be variable with a small amplitude
(
![]() km s-1) and a period around 500 d
(Duquennoy & Mayor 1991). The 127 measurements are listed in Table 6, only available
electronically at the CDS, Strasbourg.
Later on, variations on a much longer time scale became apparent, exceeding the
measurements' time span of
6358 d. The orbital period therefore cannot be determined with good
accuracy. Moreover, owing to this insufficient sampling of the orbital cycle, the value adopted for the orbital period strongly influences the value derived for the eccentricity.
Table 7 lists the (pseudo-)orbital elements used
to draw the radial-velocity curve of Fig. 10. The high
uncertainties on the elements of the long-period orbit
should serve as a reminder that these
elements are very uncertain. Only lower bounds to the orbital period
and the eccentricity are therefore listed in
Table 8.
km s-1) and a period around 500 d
(Duquennoy & Mayor 1991). The 127 measurements are listed in Table 6, only available
electronically at the CDS, Strasbourg.
Later on, variations on a much longer time scale became apparent, exceeding the
measurements' time span of
6358 d. The orbital period therefore cannot be determined with good
accuracy. Moreover, owing to this insufficient sampling of the orbital cycle, the value adopted for the orbital period strongly influences the value derived for the eccentricity.
Table 7 lists the (pseudo-)orbital elements used
to draw the radial-velocity curve of Fig. 10. The high
uncertainties on the elements of the long-period orbit
should serve as a reminder that these
elements are very uncertain. Only lower bounds to the orbital period
and the eccentricity are therefore listed in
Table 8.
Table 6: The 127 radial-velocity measurements for HD 115 521. The table, only available at the CDS, Strasbourg, lists the Julian Date, the radial velocity, and the corresponding error.
Table 7: Orbital elements for the system HD 115 521. It is not certain, however, that the short-period variations (A+a) are due to an orbital motion (see text). The long period orbit is not well-constrained.
The properties of the short-period variations would imply
a rather low mass for the companion: assuming a mass of
1.3 ![]() for the giant, the minimum mass for the companion is
0.054
for the giant, the minimum mass for the companion is
0.054 ![]() ,
corresponding to a brown dwarf.
It is not entirely clear whether the short-period variations are
indeed due to an orbital motion, for several reasons. First, as for
S UMa and X Cnc discussed in the Appendix, the data deviate from the Keplerian
solution after a dozen cycles, and this is very clearly seen in
Fig. 10, where the first data points do not fall on the
solution defined by later measurements.
Second, with
,
corresponding to a brown dwarf.
It is not entirely clear whether the short-period variations are
indeed due to an orbital motion, for several reasons. First, as for
S UMa and X Cnc discussed in the Appendix, the data deviate from the Keplerian
solution after a dozen cycles, and this is very clearly seen in
Fig. 10, where the first data points do not fall on the
solution defined by later measurements.
Second, with
![]() and K =
1.2 km s-1 (Table 7),
the short-period variations of HD 115 521 fall on the
and K =
1.2 km s-1 (Table 7),
the short-period variations of HD 115 521 fall on the
![]() (K being the semi-amplitude of the radial-velocity variations)
relationship as defined by Hekker et al. (2008) for K giants
(K being the semi-amplitude of the radial-velocity variations)
relationship as defined by Hekker et al. (2008) for K giants![]() . The
existence of this relation between the amplitude of the
radial-velocity variations and an intrinsic property of stars like the
surface gravity hints at an intrinsic origin of such
radial-velocity variations. The relation
. The
existence of this relation between the amplitude of the
radial-velocity variations and an intrinsic property of stars like the
surface gravity hints at an intrinsic origin of such
radial-velocity variations. The relation
![]() found by Hekker et al. (2008) among K giants (initially
suggested by Hatzes & Cochran 1998) continues in the domain of
M giants, as we discuss in Paper II, where it is shown that the
radial-velocity standard deviation correlates with the CORAVEL
parameter
found by Hekker et al. (2008) among K giants (initially
suggested by Hatzes & Cochran 1998) continues in the domain of
M giants, as we discuss in Paper II, where it is shown that the
radial-velocity standard deviation correlates with the CORAVEL
parameter ![]() (measuring the spectral line width), which is in turn
a good measure of the stellar radius (see Figs. 1 and 3 of
Paper II).
(measuring the spectral line width), which is in turn
a good measure of the stellar radius (see Figs. 1 and 3 of
Paper II).
However, if the shorter-period radial-velocity variations are intrinsic, then one expects photometric variations with a period of 475 d; unfortunately, we could not find any mention of them, in either the Catalogue of Suspected Variable Stars, where HD 115 521 is entry NSV 6173, or in the Hipparcos Photometry Annex, or in the ASAS Catalogue of Variable Stars (Pojmanski 2002).
![\begin{figure}
\par\includegraphics[width=9cm]{10698f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg80.gif) |
Figure 10: The radial-velocity measurements of the former radial-velocity standard HD 115 521. Short-term variations with a period of 475 d are superimposed on variations with a much longer time scale. The solid curve is obtained by adopting P = 29208 d and e = 0.87 for the long-period orbit. |
| Open with DEXTER | |
4 Orbital elements of newly-discovered binaries
The complete set of orbital elements for the 12 newly discovered binaries are listed in Table 8. Figure 11 presents the phase diagrams for those firm orbital solutions. The second part of Table 8 provides a preliminary period and eccentricity for the binary with not enough data points to derive meaningful orbital solutions. For the sake of completeness, the last part of Table 8 collects periods, eccentricities, and mass functions for (non-symbiotic) M giants available in the literature, or kindly communicated by R. Griffin. This combined data set will be used in Paper III to discuss general properties (like the eccentricity-period diagram) of systems involving M giant primaries. It must be stressed that Table 8 includes orbits neither for symbiotics nor for VV-Cephei-like systems (VV Cep, AZ Cas, etc.). A list of orbital elements for the former may be found in Belczynski et al. (2000) and Mikoajewska (2003). Mikoajewska (2007) and Fekel et al. (2007) provide references for the most recent symbiotic orbits.
![\begin{figure*}
\par\includegraphics[width=8cm]{10698f7-1.ps}
\includegraphics...
...th=8cm]{10698f7-2.ps}
\includegraphics[width=8cm]{10698f7-3.ps}
\end{figure*}](/articles/aa/full_html/2009/17/aa10698-08/Timg81.gif) |
Figure 11: Orbital phase diagrams for the orbital solutions, according to the solutions listed in Table 8. |
| Open with DEXTER | |
Table 8: An extensive list of orbital elements for (non-symbiotic) M giants.
![\begin{figure}
\par\includegraphics[width=9cm]{10698f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg194.gif) |
Figure 12: Top panel: radial-velocity curve for HD 108 907 (4 Dra), an M giant with a hot compact companion, merging 57 data points from the Cambridge, Victoria, and CORAVEL spectrovelocimeters listed in Reimers et al. (1988) (open symbols) and the 15 data points from this paper (filled symbols). Bottom panel: phase diagram for the orbital solution merging these two data sets. |
| Open with DEXTER | |
For HD 108 907 (4 Dra = CQ Dra), Table 8 lists three orbital solutions.
The first entry is obtained with our own CORAVEL and ELODIE data alone. The
second entry is a solution computed by Reimers et al. (1988), based on their
57 recent data points plus 14 much older ones. The third orbit has been
computed by merging our 15 data points with the 57 Cambridge/CORAVEL/Victoria data points from Reimers et al. (1988), and
this combined solution is presented in Fig. 12. This
system is of special interest, since
Reimers (1985) and Reimers et al. (1988) argued
that the companion of the red giant is a cataclysmic
variable, because International Ultraviolet Explorer spectra
revealed a steep rise shortward of 140 nm along with broad lines (full widths
of 1000 km s-1) of highly excited species like He II and C IV.
That conclusion has been challenged, however, by more recent studies
(Wheatley et al. 2003; Skopal 2005b,a) based on ROSAT X-ray
observations. They conclude instead that the
companion is a single WD
accreting from the wind of its red giant companion, as in normal
symbiotic systems.
The residual radial-velocity jitter of 0.6 km s-1 (listed as ![]() (O-C) in Table 8) appears normal for a star with
(O-C) in Table 8) appears normal for a star with
![]() km s-1, as seen from Fig. 2.
km s-1, as seen from Fig. 2.
Acknowledgements
The authors have the pleasure of thanking Roger Griffin for his generous donation of unpublished RV measurements for HD 182 190 and HD 220 088, which made it possible to compute their orbits. We are also indebted for his permission to quote in Table 8 several of his new orbits of M giants prior to their publication and for his helpful comments on the manuscript of this paper. We thank the referee, F. Fekel, whose comments greatly improved the paper, and in particular stimulated the addition of Fig. 3. This work has been partly funded by an Action de recherche concertée (ARC) from the Direction générale de l'Enseignement non obligatoire et de la Recherche scientifique - Direction de la recherche scientifique - Communauté française de Belgique.
Appendix A: Pseudo-orbits among Mira and semiregular variables
This Appendix presents two cases of (suspected) pseudo-orbital variations exhibited by Mira and semi-regular variables. These stars do not belong to the samples studied earlier in this paper.
A.1 HD 110 813
HD 110 813 (S UMa) is a Mira S star with a light cycle of 225.9 d (as listed in the General Catalogue of Variable Stars - GCVS; the analysis below shows that a period of 222 d seems more appropriate), and was considered a spectroscopic binary of period
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA1-1.eps} \includegraphics[width=9cm]{10698fA1-2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg197.gif) |
Figure A.1: Top panel: radial-velocity curve for HD 110 813, a Mira S star with a pulsation period of 225.9 d (according to GCVS) and a pseudo-orbital period of 576 d. Bottom panel: same for the carbon star HD 76 221, a semi-regular variable with a pulsation period of about 195 d (according to GCVS), and a pseudo-orbital period of 530 d. For both stars, the last measurements become discrepant with the (pseudo-)orbital solution computed from earlier data points. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg198.gif) |
Figure A.2:
Top panel: Stellingwerf's
|
| Open with DEXTER | |
Table A.1: Pseudo-orbital solutions for the Mira S star HD 110 813 (S UMa) and the semi-regular carbon star HD 76 221 (X Cnc), based on the complete data set but the last two points (see Table A.2).
Table A.2: Radial velocities for HD 76 221 and HD 110 813.
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg217.gif) |
Figure A.3:
Top panel: same as Fig. A.2 for the carbon star
HD 76 221,
for all data points but the last
two (outliers). The solid vertical line marks the frequency of the
pseudo-orbital variation and the dot-dashed line the frequency of
light variations. The harmonics 1/3, 1/2, 3/4, and 3/2 of the pulsation
frequency 1/195 =
|
| Open with DEXTER | |
Figure A.1 shows the radial-velocity curve of S UMa and
a (pseudo-)orbital solution based on 17 measurements (from 1987.946 to
2002.464 or JD 2447141.743 to JD 2452444.403;
Tables A.1 and A.2). This pseudo-orbit is slightly
different from the one found by Udry et al. (1998). Although the
radial-velocity data could be fitted with a period of 576 d for 10 cycles,
the last
two measurements (JD 2452824.356 and JD 2453048.562)
deviate markedly from this solution. The radial-velocity variations
cannot therefore be ascribed to orbital motion. In any case, a
system with such a short orbital period cannot be detached. Using the
period-radius relationship for Mira stars pulsating in the fundamental
mode (van Leeuwen et al. 1997), a radius of 258 ![]() is inferred from
the 222-d period, assuming a mass of 1.5
is inferred from
the 222-d period, assuming a mass of 1.5 ![]() .
Adopting a mass of
1
.
Adopting a mass of
1 ![]() for the companion, for the Roche radius to be larger than the
stellar radius requires an orbital period of at least 1130 d, which is
inconsistent with the observed value of 576 d.
for the companion, for the Roche radius to be larger than the
stellar radius requires an orbital period of at least 1130 d, which is
inconsistent with the observed value of 576 d.
What then is the origin of this 576 d period? The Stellingwerf
(phase-dispersion minimisation) ![]() statistics
(Stellingwerf 1978) are shown in Fig. A.2,
constructed from all datapoints but the last two outliers. It
shows that all the prominent peaks are combinations of the Mira frequency
f1 = 1/222 d-1 and of the yearly frequency
f2 = 1/365.25 d-1, or harmonics of f1. In particular the 576 d period may be identified with the frequency f1 - f2.
This finding, along with the previous result for the
minimum period allowed by the Roche radius, definitely denies the
reality of the binary nature of HD 110 813.
Alvarez et al. (2001) have shown that S UMa exhibits an asymmetric
cross-correlation dip, as usual among Mira variables. Asymmetric profiles observed in Mira variables are often associated with radial-velocity variations,
which indeed mimick an orbital motion (see also Hinkle et al. 2002).
statistics
(Stellingwerf 1978) are shown in Fig. A.2,
constructed from all datapoints but the last two outliers. It
shows that all the prominent peaks are combinations of the Mira frequency
f1 = 1/222 d-1 and of the yearly frequency
f2 = 1/365.25 d-1, or harmonics of f1. In particular the 576 d period may be identified with the frequency f1 - f2.
This finding, along with the previous result for the
minimum period allowed by the Roche radius, definitely denies the
reality of the binary nature of HD 110 813.
Alvarez et al. (2001) have shown that S UMa exhibits an asymmetric
cross-correlation dip, as usual among Mira variables. Asymmetric profiles observed in Mira variables are often associated with radial-velocity variations,
which indeed mimick an orbital motion (see also Hinkle et al. 2002).
A.2 HD 76 221
The semiregular carbon star HD 76 221 (X Cnc) behaves similarly to HD 110 813 (Udry et al. 1998): a satisfactory (pseudo-)orbital solution with a period of 530 d (Table A.1) could be found with the first 13 data points, but is not confirmed by the last two data points (bottom panel of Fig. A.1). The phase-dispersion minimisation statistics (Fig. A.3, based on the first 13 data points) reveals several harmonics of the 195 d photometric period, but this time, the 530-d periodicity of the radial velocities does not seem to be one of these. This 530-d-signal may be yet another example of the long secondary periods (of unknown origin) found by Houk (1963) (see also Hinkle et al. 2002) among SR variables, since the ranges of periods, mass functions, and semi-amplitudes found by Hinkle et al. (2002) (and listed in Table A.1) all match the values for HD 76 221. Only the eccentricity does not conform to the Hinkle et al. range (0.32-0.37, with one case at 0.08). Soszynski (2007) also notes that the long secondary periods sometimes undergo phase shifts; however, we do not find it very plausible that these photometric and spectroscopic phase shifts have the same physical origin. The phase shifts in the light-curve are attributed by Soszynski (2007) to dust clouds in the vicinity of a companion, whereas the phase shifts in radial velocity preclude the orbital nature of the radial velocity variations.
References
- Alvarez, R., Jorissen, A., Plez, B., et al. 2001, A&A, 379, 305 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baranne, A., Mayor, M., & Poncet, J. L. 1979, Vistas in Astronomy, 23, 279 [NASA ADS] [CrossRef] (In the text)
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Batten, A. H., & Fletcher, J. M. 1986, PASP, 98, 647 [NASA ADS] [CrossRef] (In the text)
- Belczynski, K., Mikoajewska, J., Munari, U., Ivison, R. J., & Friedjung, M. 2000, A&AS, 146, 407 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bessell, M. S., & Wood, P. R. 1984, PASP, 96, 247 [NASA ADS] [CrossRef]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS]
- Carquillat, N., & Ginestet, J. M. 1996, A&AS, 117, 445 [NASA ADS] [CrossRef] [EDP Sciences]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences]
- Derekas, A., Kiss, L. L., Bedding, T. R., et al. 2006, ApJ, 650, L55 [NASA ADS] [CrossRef]
- Dettmar, R.-J., & Gieseking, F. 1983, A&AS, 54, 541 [NASA ADS] (In the text)
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] (In the text)
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA (In the text)
- Eyer, L., & Grenon, M. 1997, in Hipparcos - Venice '97, ed. R. M. Bonnet, E. Høg, P. L. Bernacca, L. Emiliani, A. Blaauw, C. Turon, J. Kovalevsky, L. Lindegren, H. Hassan, M. Bouffard, B. Strim, D. Heger, M. A. C. Perryman, & L. Woltjer, ESA Special Publication, 402, 467
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Famaey, B., Siebert, A., & Jorissen, A. 2008, A&A, 483, 453 [NASA ADS] [CrossRef] [EDP Sciences]
- Fekel, F. C., Hinkle, K. H., Joyce, R. R., Wood, P. R., & Lebzelter, T. 2007, AJ, 133, 17 [NASA ADS] [CrossRef] (In the text)
- Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences]
- Frankowski, A., Famaey, B., Van Eck, S., et al. 2009, A&A, 498, 479 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II) (In the text)
- Griffin, R. F. 1979, The Observatory, 99, 198 [NASA ADS]
- Griffin, R. F. 1983, The Observatory, 103, 56 [NASA ADS]
- Griffin, R. F. 1990, The Observatory, 110, 85 [NASA ADS]
- Griffin, R. F. 2008, The Observatory, submitted
- Gunn, J. E., & Griffin, R. F. 1979, AJ, 84, 752 [NASA ADS] [CrossRef]
- Hatzes, A. P., & Cochran, W. D. 1998, in Cool Stars, Stellar Systems, and the Sun, ed. R. A. Donahue, & J. A. Bookbinder, ASP Conf. Ser., 154, 311
- Hekker, S., Snellen, I. A. G., Aerts, C., et al. 2008, A&A, 480, 215 [NASA ADS] [CrossRef] [EDP Sciences]
- Hinkle, K. H., Lebzelter, T., & Scharlach, W. W. G. 1997, AJ, 114, 2686 [NASA ADS] [CrossRef] (In the text)
- Hinkle, K., Lebzelter, T., Joyce, R., & Fekel, F. 2002, ApJ, 123, 1002 [NASA ADS] (In the text)
- Houk, N. 1963, AJ, 68, 253 [NASA ADS] [CrossRef] (In the text)
- Hünsch, M., Schmitt, J. H. M. M., Schröder, K., & Zickgraf, F. 1998, A&A, 330, 225 [NASA ADS] (In the text)
- Jackson, E. S., Shane, W. W., & Lynds, B. T. 1957, ApJ, 125, 712 [NASA ADS] [CrossRef]
- Jahanara, B., Mitsumoto, M., Oka, K., et al. 2005, A&A, 441, 589 [NASA ADS] [CrossRef] [EDP Sciences]
- Jorissen, A., & Mayor, M. 1988, A&A, 198, 187 [NASA ADS]
- Jorissen, A., Mowlavi, N., Sterken, C., & Manfroid, J. 1997, A&A, 324, 578 [NASA ADS]
- Jorissen, A., Frankowski, A., Famaey, B., & Van Eck, S. 2009, A&A, 498, 489 [NASA ADS] [CrossRef] [EDP Sciences] (Paper III) (In the text)
- Lebzelter, T., Hinkle, K. H., Wood, P. R., Joyce, R. R., & Fekel, F. C. 2005, A&A, 431, 623 [NASA ADS] [CrossRef] [EDP Sciences]
- Lucke, P. B., & Mayor, M. 1982, A&A, 105, 318 [NASA ADS]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef]
- Luyten, W. J. 1936, ApJ, 84, 85 [NASA ADS] [CrossRef]
- Mastrodemos, N., & Morris, M. 1998, ApJ, 497, 303 [NASA ADS] [CrossRef]
- Mayor, M., Benz, W., Imbert, M., et al. 1984, A&A, 134, 118 [NASA ADS]
- McLaughlin, D. B., & van Dijke, S. E. A. 1944, ApJ, 100, 63 [NASA ADS] [CrossRef]
- Mikoajewska, J. 2003, in Symbiotic stars probing stellar evolution, ed. R. L. M. Corradi, J. Mikoajewska, & T. J. Mahoney, San Francisco, Astron. Soc. Pacific Conf. Ser., 303, 9 (In the text)
- Mikoajewska, J. 2007, Baltic Astron., 16, 1 [NASA ADS] (In the text)
- Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] (In the text)
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Prieur, J.-L., Carquillat, J.-M., & Griffin, R. F. 2006, Astron. Nachr., 327, 686 [NASA ADS] [CrossRef]
- Reimers, D. 1985, A&A, 142, L16 [NASA ADS] (In the text)
- Reimers, D., & Schroeder, K.-P. 1983, A&A, 124, 241 [NASA ADS]
- Reimers, D., Griffin, R. F., & Brown, A. 1988, A&A, 193, 180 [NASA ADS] (In the text)
- Samus, N. N. 1997, Informational Bulletin on Variable Stars, 4501, 1
- Setiawan, J., Pasquini, L., da Silva, L., et al. 2004, A&A, 421, 241 [NASA ADS] [CrossRef] [EDP Sciences]
- Skopal, A. 2005a, in The Astrophysics of Cataclysmic Variables and Related Objects, ed. J.-M. Hameury, & J.-P. Lasota, San Francisco, ASP Conf. Ser., 330, 463
- Skopal, A. 2005b, A&A, 440, 995 [NASA ADS] [CrossRef] [EDP Sciences]
- Soszynski, I. 2007, ApJ, 660, 1486 [NASA ADS] [CrossRef]
- Soszynski, I., Udalski, A., Kubiak, M., et al. 2004, Acta Astron., 54, 129 [NASA ADS]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] (In the text)
- Stephenson, C. B. 1967, PASP, 79, 363 [NASA ADS] [CrossRef] (In the text)
- Theuns, T., & Jorissen, A. 1993, MNRAS, 265, 946 [NASA ADS]
- Theuns, T., Boffin, H. M. J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS]
- Tokovinin, A. A. 1997, A&AS, 124, 75 [NASA ADS] [CrossRef] [EDP Sciences]
- Udry, S., Jorissen, A., Mayor, M., & Van Eck, S. 1998, A&AS, 131, 25 [NASA ADS] [CrossRef] [EDP Sciences]
- Udry, S., Mayor, M., Andersen, J., et al. 1997, in Hipparcos - Venice '97 ed. M. Perryman (ESA SP-402), ESA, Noordwijk, 693 (In the text)
- Udry, S., Mayor, M., Maurice, E., et al. 1999a, in Precise Stellar Radial Velocities, ed. J. B. Hearnshaw, & C. D. Scarfe, San Francisco, ASP Conf. Ser., 170, 383 (In the text)
- Udry, S., Mayor, M., & Queloz, D. 1999b, in Precise Stellar Radial San Francisco, ed. J. B. Hearnshaw, & C. D. Scarfe, Velocities, ASP Conf. Ser., 170, 367 (In the text)
- Van Eck, S., & Jorissen, A. 2000, A&A, 360, 196 [NASA ADS]
- van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Yudin, B. 1997, MNRAS, 287, 955 [NASA ADS] (In the text)
- Verhoelst, T., van Aarle, E., & Acke, B. 2007, A&A, 470, L21 [NASA ADS] [CrossRef] [EDP Sciences]
- Welty, A. D., & Wade, R. A. 1995, AJ, 109, 326 [NASA ADS] [CrossRef]
- Wheatley, P. J., Mukai, K., & de Martino, D. 2003, MNRAS, 346, 855 [NASA ADS] [CrossRef]
- Wood, P. R. 2000, PASA, 17, 18 [NASA ADS]
- Wood, P. R., Olivier, E. A., & Kawaler, S. D. 2004, ApJ, 604, 800 [NASA ADS] [CrossRef]
Footnotes
- ... giants
![[*]](/icons/foot_motif.gif)
- Based on observations carried out at the Swiss telescope installed at the Observatoire de Haute Provence (OHP, France), and at the 1.93-m OHP telescope.
- ...
![[*]](/icons/foot_motif.gif)
![[*]](/icons/foot_motif.gif)
- Full Tables 2, 3, and Table 6 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/498/627
- ...
![[*]](/icons/foot_motif.gif)
- Postdoctoral Researcher, FNRS, Belgium.
- ...
![[*]](/icons/foot_motif.gif)
- Research Associate, FNRS, Belgium.
- ...
![[*]](/icons/foot_motif.gif)
- Postdoctoral Researcher, FNRS, Belgium. Currently at Department of Physics, Technion-Israel Institute of Technology, Haifa 32000, Israel.
- ... identity
![[*]](/icons/foot_motif.gif)
- The only mistake found in Famaey et al. (2005) was the star HIP 26 247 = RR Cam = BD + 72
 275, which was wrongly assigned radial velocity
measurements from the binary star J275 in the Hyades cluster. The
former star should therefore be discarded from the CORAVEL sample.
275, which was wrongly assigned radial velocity
measurements from the binary star J275 in the Hyades cluster. The
former star should therefore be discarded from the CORAVEL sample.
- ... Table A.1
![[*]](/icons/foot_motif.gif)
- As a result of the confusion between HIP 26 247 and a binary star (see footnote 1), the star HIP 26 247 is erroneously flagged as a binary in that table.
- ... jitter
![[*]](/icons/foot_motif.gif)
- A term introduced by Gunn & Griffin (1979) in this context.
- ... M giants
![[*]](/icons/foot_motif.gif)
- Mayor et al. (1984) have shown that stars located at the tip of the giant branch in the globular
cluster 47 Tuc have a jitter of
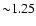 km s-1, while the jitter
reduces to 0.27 km s-1 for 1 mag-fainter stars. This trend goes further
down the red-giant branch, as shown with much higher accuracy levels
by Setiawan et al. (2004) and da Silva et al. (2006).
km s-1, while the jitter
reduces to 0.27 km s-1 for 1 mag-fainter stars. This trend goes further
down the red-giant branch, as shown with much higher accuracy levels
by Setiawan et al. (2004) and da Silva et al. (2006).
- ... K giants
![[*]](/icons/foot_motif.gif)
- The gravity estimate is
obtained as follows. From V = 4.80 and the 2MASS value K = 0.47,
one derives
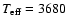 K and
BCK = 2.74, from the
V-K calibrations of Bessell & Wood (1984) and
Bessell et al. (1998). The maximum-likelihood distance of
Famaey et al. (2005) (
K and
BCK = 2.74, from the
V-K calibrations of Bessell & Wood (1984) and
Bessell et al. (1998). The maximum-likelihood distance of
Famaey et al. (2005) (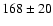 pc) then yields
pc) then yields
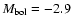 ,
and a radius of 84
,
and a radius of 84 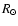 from the Stefan-Boltzmann relationship
between luminosity,
from the Stefan-Boltzmann relationship
between luminosity,
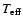 and radius. Adopting a mass of
1.3
and radius. Adopting a mass of
1.3 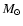 then yields a gravity of
then yields a gravity of
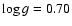 .
.
All Tables
Table 1: The four observing campaigns defining the four (sub)samples of Hipparcos M giants.
Table 2: The first five lines of the list of stars from sample II. The full table is only available electronically at the CDS.
Table 3: The individual radial-velocity measurements for the 35 stars of sample III. The full table is available electronically from the CDS, Strasbourg.
Table 4: Binarity and photometric-variability diagnostics for stars from sample III (as well as binaries or suspected binaries from sample IV).
Table 5:
Properties of the 11 M giants detected as X-ray sources by the ROSAT
all-sky survey (following Hünsch et al. 1998), where for three stars, the X-ray source is offset by more than 1![]() from the M giant optical position.
Table 6:
The 127 radial-velocity measurements for HD 115 521. The table, only available at the CDS, Strasbourg, lists the Julian Date, the radial velocity, and the corresponding error.
from the M giant optical position.
Table 6:
The 127 radial-velocity measurements for HD 115 521. The table, only available at the CDS, Strasbourg, lists the Julian Date, the radial velocity, and the corresponding error.
Table 7: Orbital elements for the system HD 115 521. It is not certain, however, that the short-period variations (A+a) are due to an orbital motion (see text). The long period orbit is not well-constrained.
Table 8: An extensive list of orbital elements for (non-symbiotic) M giants.
Table A.1: Pseudo-orbital solutions for the Mira S star HD 110 813 (S UMa) and the semi-regular carbon star HD 76 221 (X Cnc), based on the complete data set but the last two points (see Table A.2).
Table A.2: Radial velocities for HD 76 221 and HD 110 813.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm]{10698f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg15.gif) |
Figure 1:
Histograms of the number of measurements per star (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg26.gif) |
Figure 2:
The radial-velocity
standard deviation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10698f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg27.gif) |
Figure 3: The radial-velocity standard deviation (corrected for the instrumental error) as a function of the standard deviation on the Hipparcos Hp magnitude. Symbols are the same as in Fig. 2, except that large circles identify stars detected as X-ray sources by the ROSAT All-Sky Survey, following Hünsch et al. (1998). The dotted line represents the trend between radial-velocity and photometric variability reported by Hinkle et al. (1997). This is not a dividing line like the one plotted in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10698f4-1.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg36.gif) |
Figure 4: Radial-velocity data points for the spectroscopic binaries, along with their orbital solution. The solution marked as ``ORB:'' is not very well constrained and hence preliminary. All panels span a Vr range of 30 km s-1. Error bars on the individual measurements (of the order of 0.2 km s-1) are too small to be seen. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{10698f4-2.ps}\par\vspace*{2mm}
\includegraphics[width=8.4cm]{10698f4-3.ps}\par
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg37.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg44.gif) |
Figure 5: Radial-velocity data points for the spectroscopic binaries with no orbit available yet. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg45.gif) |
Figure 6: Radial-velocity data points for the suspected spectroscopic binaries. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-6.ps} \includegraphics[width=9cm]{10698f4-7.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg46.gif) |
Figure 7: Radial-velocity variations for stars falling close to the dividing line between jitter and orbital motion in Fig. 2, for which the nature of the the radial-velocity variations is unclear. The vertical scale spans 10 km s-1 in all cases. They are denoted by crosses in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f4-8.ps} \includegraphics[width=9cm]{10698f4-9.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg47.gif) |
Figure 8: Examples of radial-velocity variations for stars (referred to by their HD number, as listed in each panel) falling close to the dividing line between jitter and orbital motion in Fig. 2, with a radial-velocity jitter most likely of intrinsic nature. They are denoted by open squares in Figs. 2 and 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg49.gif) |
Figure 9: Orbit from Batten & Fletcher (1986) for HD 132 813. Overplotted are our new data points, consistent with this orbit from the literature, obtained about two decades ago. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg80.gif) |
Figure 10: The radial-velocity measurements of the former radial-velocity standard HD 115 521. Short-term variations with a period of 475 d are superimposed on variations with a much longer time scale. The solid curve is obtained by adopting P = 29208 d and e = 0.87 for the long-period orbit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[width=8cm]{10698f7-1.ps}
\includegraphics...
...th=8cm]{10698f7-2.ps}
\includegraphics[width=8cm]{10698f7-3.ps}
\end{figure*}](/articles/aa/full_html/2009/17/aa10698-08/Timg81.gif) |
Figure 11: Orbital phase diagrams for the orbital solutions, according to the solutions listed in Table 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg194.gif) |
Figure 12: Top panel: radial-velocity curve for HD 108 907 (4 Dra), an M giant with a hot compact companion, merging 57 data points from the Cambridge, Victoria, and CORAVEL spectrovelocimeters listed in Reimers et al. (1988) (open symbols) and the 15 data points from this paper (filled symbols). Bottom panel: phase diagram for the orbital solution merging these two data sets. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA1-1.eps} \includegraphics[width=9cm]{10698fA1-2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg197.gif) |
Figure A.1: Top panel: radial-velocity curve for HD 110 813, a Mira S star with a pulsation period of 225.9 d (according to GCVS) and a pseudo-orbital period of 576 d. Bottom panel: same for the carbon star HD 76 221, a semi-regular variable with a pulsation period of about 195 d (according to GCVS), and a pseudo-orbital period of 530 d. For both stars, the last measurements become discrepant with the (pseudo-)orbital solution computed from earlier data points. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg198.gif) |
Figure A.2:
Top panel: Stellingwerf's
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10698fA3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10698-08/Timg217.gif) |
Figure A.3:
Top panel: same as Fig. A.2 for the carbon star
HD 76 221,
for all data points but the last
two (outliers). The solid vertical line marks the frequency of the
pseudo-orbital variation and the dot-dashed line the frequency of
light variations. The harmonics 1/3, 1/2, 3/4, and 3/2 of the pulsation
frequency 1/195 =
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


