| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 379 - 397 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810569 | |
| Published online | 05 March 2009 | |
The VIMOS VLT Deep Survey
Evolution of the major merger rate since z  1 from
spectroscopically confirmed galaxy pairs
1 from
spectroscopically confirmed galaxy pairs![[*]](/icons/foot_motif.gif)
L. de Ravel1 - O. Le Fèvre1 - L. Tresse1 - D. Bottini2 - B. Garilli2 - V. Le Brun1 - D. Maccagni2 - R. Scaramella4,13 - M. Scodeggio2 - G. Vettolani4 - A. Zanichelli4 - C. Adami1 - S. Arnouts23,1 - S. Bardelli3 - M. Bolzonella3 - A. Cappi3 - S. Charlot8,10 - P. Ciliegi3 - T. Contini7 - S. Foucaud21 - P. Franzetti2 - I. Gavignaud12 - L. Guzzo9 - O. Ilbert20 - A. Iovino9 - F. Lamareille7 - H. J. McCracken10,11 - B. Marano6 - C. Marinoni18 - A. Mazure1 - B. Meneux22,24 - R. Merighi3 - S. Paltani15,16 - R. Pellò7 - A. Pollo1,17 - L. Pozzetti3 - M. Radovich5 - D. Vergani2 - G. Zamorani3 - E. Zucca3 - M. Bondi4 - A. Bongiorno22 - J. Brinchmann19 - O. Cucciati9,14 - S. de la Torre1 - L. Gregorini4 - P. Memeo2 - E. Perez-Montero7 - Y. Mellier10,11 - P. Merluzzi5 - S. Temporin9
1 - Laboratoire d'Astrophysique de Marseille, UMR 6110 CNRS-Université de Provence, BP8, 13376 Marseille Cedex 12, France
2 -
IASF - INAF, via Bassini 15, 20133, Milano, Italy
3 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127, Bologna, Italy
4 -
IRA - INAF, via Gobetti 101, 40129, Bologna, Italy
5 -
INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131, Napoli, Italy
6 -
Università di Bologna, Dipartimento di Astronomia, via Ranzani 1, 40127, Bologna, Italy
7 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 avenue E. Belin, 31400 Toulouse, France
8 -
Max Planck Institut für Astrophysik, 85741 Garching, Germany
9 -
INAF - Osservatorio Astronomico di Brera, via Brera 28, 20021 Milan, Italy
10 -
Institut d'Astrophysique de Paris, UMR 7095, 98 bis Bvd Arago, 75014 Paris, France
11 -
Observatoire de Paris, LERMA, 61 avenue de l'Observatoire, 75014 Paris, France
12 -
Astrophysical Institute Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
13 -
INAF - Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
14 -
Universitá di Milano-Bicocca, Dipartimento di Fisica, Piazza delle Scienze 3, 20126 Milano, Italy
15 -
Integral Science Data Centre, Ch. d'Écogia 16, 1290 Versoix, Switzerland
16 -
Geneva Observatory, Ch. des Maillettes 51, 1290 Sauverny, Switzerland
17 -
The Andrzej Soltan Institute for Nuclear Studies, ul. Hoza 69, 00-681 Warsaw, Poland
18 -
Centre de Physique Théorique, UMR 6207 CNRS-Université de Provence, 13288 Marseille, France
19 -
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
20 -
Institute for Astronomy, 2680 Woodlawn Dr., University of Hawaii, Honolulu, Hawaii, 96822, USA
21 -
School of Physics & Astronomy, University of Nottingham, University Park, Nottingham NG72RD, UK
22 -
Max Planck Institut für Extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching bei München, Germany
23 -
Canada France Hawaii Telescope corporation, Mamalahoa Hwy, Kamuela, HI-96743, USA
24 -
Universitätssternwarte München, Scheinerstrasse 1, 81679 München, Germany
Received 11 July 2008 / Accepted 31 January 2009
Abstract
Context. The rate at which galaxies grow via successive mergers is a key element in understanding the main phases of galaxy evolution.
Aims. We measure the evolution of the fraction of galaxies in pairs and the merging rate since redshift ![]() assuming a (
assuming a (
![]() ,
,
![]() and
and
![]() )
cosmology.
)
cosmology.
Methods. From the VIMOS VLT Deep Survey we use a sample of 6464 galaxies with
![]() to identify 314 pairs of galaxies, each member with a secure spectroscopic redshift, which are close in both projected separation and in velocity.
to identify 314 pairs of galaxies, each member with a secure spectroscopic redshift, which are close in both projected separation and in velocity.
Results. We estimate that at ![]() ,
10.9
,
10.9 ![]()
![]() of galaxies with
of galaxies with
![]() (Q=1.11) are in pairs with separations
(Q=1.11) are in pairs with separations
![]() ,
,
![]() km s-1, and with
km s-1, and with
![]() ,
significantly larger than 3.8
,
significantly larger than 3.8 ![]()
![]() at
at
![]() ;
thus, the pair fraction evolves as (1+z)m with m = 4.73
;
thus, the pair fraction evolves as (1+z)m with m = 4.73 ![]() 2.01. For bright galaxies with
2.01. For bright galaxies with
![]() ,
the pair fraction is higher and its evolution with redshift is flatter with m=1.50
,
the pair fraction is higher and its evolution with redshift is flatter with m=1.50 ![]() 0.76, a property also observed for galaxies with increasing stellar masses. Early-type pairs (dry mergers) increase their relative fraction from
0.76, a property also observed for galaxies with increasing stellar masses. Early-type pairs (dry mergers) increase their relative fraction from ![]() at
at
![]() to
to ![]() at
at
![]() .
The star formation rate traced by the rest-frame [OII] EW increases by 26
.
The star formation rate traced by the rest-frame [OII] EW increases by 26 ![]()
![]() for pairs with the smallest separation
for pairs with the smallest separation
![]() .
Following published prescriptions to derive merger timescales, we find that the merger rate of
.
Following published prescriptions to derive merger timescales, we find that the merger rate of
![]() galaxies evolves as
galaxies evolves as
![]()
![]() 10-4
10-4 ![]()
![]() .
.
Conclusions. The merger rate of galaxies with
![]() has significantly evolved since
has significantly evolved since ![]() and is strongly dependent on the luminosity or stellar mass of galaxies. The major merger rate increases more rapidly with redshift for galaxies with fainter luminosities or stellar mass, while the evolution of the merger rate for bright or massive galaxies is slower, indicating that the slow evolution reported for the brightest galaxies is not universal. The merger rate is also strongly dependent on the spectral type of galaxies involved. Late-type mergers were more frequent in the past, while early-type mergers are more frequent today, contributing to the rise in the local density of early-type galaxies. About
and is strongly dependent on the luminosity or stellar mass of galaxies. The major merger rate increases more rapidly with redshift for galaxies with fainter luminosities or stellar mass, while the evolution of the merger rate for bright or massive galaxies is slower, indicating that the slow evolution reported for the brightest galaxies is not universal. The merger rate is also strongly dependent on the spectral type of galaxies involved. Late-type mergers were more frequent in the past, while early-type mergers are more frequent today, contributing to the rise in the local density of early-type galaxies. About ![]() of the stellar mass in present day galaxies with
of the stellar mass in present day galaxies with
![]() has been accreted through major merging events since z = 1. This indicates that major mergers have contributed significantly to the growth in stellar mass density of bright galaxies over the last half of the life of the Universe.
has been accreted through major merging events since z = 1. This indicates that major mergers have contributed significantly to the growth in stellar mass density of bright galaxies over the last half of the life of the Universe.
Key words: galaxies: evolution - galaxies: interactions - galaxies: formation
1 Introduction
In the current hierarchical structure formation paradigm, mass assembly in galaxies proceeds via a process of coalescence between increasingly more massive dark matter halos. This halo merging tree history can be quantified by a halo merger rate, measuring the growth of mass per average mass in a representative volume of the Universe. However, these models do not directly predict a growth of galaxy mass via mergers (Moore et al. 2001), and the actual contribution of mergers to the evolution of galaxies remains poorly predicted.
Merging two galaxies is potentially a very powerful process. It is possible that during major merger events, i.e. mergers where the two components have more or less the same mass, disks could be transformed into spheroidals, as predicted using detailed simulations (Combes 2004; Mihos & Hernquist 1996; Conselice et al. 2006). It is also expected that major merger events profoundly modify the spectrophotometric properties of the galaxies involved, for instance triggering a burst of star formation (e.g. Patton et al. 2005). Galaxies in the process of merging have been observed, however the contribution of this process to the evolution of the global galaxy population is not yet precisely constrained. Indirect evidence for merging is also inferred from other galaxy properties like the luminosity or mass function. The luminosity of the red bulge dominated population of galaxies is seen to increase since ![]() ,
part of which could be produced by mergers (Ilbert et al. 2006). It seems possible that the increase in the density of intermediate mass early-type galaxies since
,
part of which could be produced by mergers (Ilbert et al. 2006). It seems possible that the increase in the density of intermediate mass early-type galaxies since ![]() may be happening at the expense of late-type galaxies involved in merging events (Tresse et al. 2007). Merging is therefore potentially a very important physical phenomenon which could drive the evolution of galaxies along cosmic time. The average numbers of merger events needed to build a typical M* galaxy, the contribution of mergers to the mass growth of galaxies, or the identification of a prefered time in the life of the Universe when mergers were more frequent, are all important elements to help towards our understanding of galaxy evolution. It is then crucial to quantify the contribution of merging to the evolution process and its impact on important quantities like the cosmic star formation rate (e.g. Bouwens et al. 2006; Tresse et al. 2007; Woods et al. 2006) or the global stellar mass density (e.g. Arnouts et al. 2007; Bundy et al. 2005; Pozzetti et al. 2007).
may be happening at the expense of late-type galaxies involved in merging events (Tresse et al. 2007). Merging is therefore potentially a very important physical phenomenon which could drive the evolution of galaxies along cosmic time. The average numbers of merger events needed to build a typical M* galaxy, the contribution of mergers to the mass growth of galaxies, or the identification of a prefered time in the life of the Universe when mergers were more frequent, are all important elements to help towards our understanding of galaxy evolution. It is then crucial to quantify the contribution of merging to the evolution process and its impact on important quantities like the cosmic star formation rate (e.g. Bouwens et al. 2006; Tresse et al. 2007; Woods et al. 2006) or the global stellar mass density (e.g. Arnouts et al. 2007; Bundy et al. 2005; Pozzetti et al. 2007).
To estimate the contribution of mergers to the formation and evolution of galaxies is not a trivial task. In the nearby Universe merger events can be identified a posteriori from perturbed morphologies, wisps, tails, and other peculiar signatures seen at low surface brightness. Only recently volume complete measurements of the merger rate in the nearby Universe have become available. In the Millennium catalogue, especially tailored to a volume complete identification
of merging events, de Propris et al. (2007) use the relative velocity measured from spectroscopic redshifts to confirm true galaxy pairs in the process of merging. They find
that the merger fraction is 2% at a mean redshift of 0.06, refining earlier estimates based on pair fraction (Patton et al. 2000, 2002). At higher redshifts, searching for evidence for past mergers becomes increasingly difficult, because the residual signatures of mergers often have a too low surface brightness. At redshifts ![]() ,
it is therefore easier to search for ``a priori mergers'', encounters that are likely to lead to a merger event, rather than to look for
``a posteriori'' signs of past mergers. When two galaxies are close together in space, and depending on their relative velocities, gravity is acting to bring them closer in a bound system that will merge. A measure of the merging frequency is then to count galaxy pairs with a separation and velocity difference such as they are likely to be gravitationally bound and destined to merge. By selecting pairs of galaxies with similar magnitudes and hence approximately with similar masses, one can focus on major merger events. They are able to significantly contribute to the mass assembly,
to modify morphologies, as well as to significantly alter the star and gas content of the incoming galaxies. Assuming that a dynamically bound system of two galaxies will most likely evolve into one more massive galaxy, one can then derive the merger rate from the pair count. A major
uncertainty of this estimator is the timescale upon which a merger will be completed. N-body simulations are then used to provide reasonable estimates of the merger timescales (Conselice et al. 2006; Kitzbichler & White 2008).
,
it is therefore easier to search for ``a priori mergers'', encounters that are likely to lead to a merger event, rather than to look for
``a posteriori'' signs of past mergers. When two galaxies are close together in space, and depending on their relative velocities, gravity is acting to bring them closer in a bound system that will merge. A measure of the merging frequency is then to count galaxy pairs with a separation and velocity difference such as they are likely to be gravitationally bound and destined to merge. By selecting pairs of galaxies with similar magnitudes and hence approximately with similar masses, one can focus on major merger events. They are able to significantly contribute to the mass assembly,
to modify morphologies, as well as to significantly alter the star and gas content of the incoming galaxies. Assuming that a dynamically bound system of two galaxies will most likely evolve into one more massive galaxy, one can then derive the merger rate from the pair count. A major
uncertainty of this estimator is the timescale upon which a merger will be completed. N-body simulations are then used to provide reasonable estimates of the merger timescales (Conselice et al. 2006; Kitzbichler & White 2008).
Cold dark matter simulations show that the evolution of the dark matter halos merger rate follows a power law
![]() where
where
![]() is the local value, and m parameterizes the evolution. While some simulations predict that m should have
is the local value, and m parameterizes the evolution. While some simulations predict that m should have
![]() (Gottl¨øber 2001), measuring m directly from galaxy samples is an important step to understand the evolution of galaxies. Many observational attempts have been carried out to track the evolution of the merger rate as a function of redshift (e.g. Burkey et al. 1994; Carlberg et al. 1994; Yee & Ellingson 1994; Patton et al. 1997; Le Fèvre et al. 2000; Patton et al. 2000, 2002; Conselice et al. 2003; Lin et al. 2004; Kartaltepe et al. 2007a,b; Lin et al. 2008; Lotz et al. 2008; Kampczyk et al. 2007). Despite this, m remains poorly constrained with
(Gottl¨øber 2001), measuring m directly from galaxy samples is an important step to understand the evolution of galaxies. Many observational attempts have been carried out to track the evolution of the merger rate as a function of redshift (e.g. Burkey et al. 1994; Carlberg et al. 1994; Yee & Ellingson 1994; Patton et al. 1997; Le Fèvre et al. 2000; Patton et al. 2000, 2002; Conselice et al. 2003; Lin et al. 2004; Kartaltepe et al. 2007a,b; Lin et al. 2008; Lotz et al. 2008; Kampczyk et al. 2007). Despite this, m remains poorly constrained with
![]() ,
meaning either no evolution of the merger rate with cosmic time, or a strong evolution. Part of this large range of values can be understood as coming from the different criteria used to identify merger candidates, or the photometric band used to identify pairs (Bundy et al. 2005). Furthermore, comparing measurements at low and high redshifts from different surveys is complicated due to the different selection functions used. At redshifts z>0.3, most pair counts so far have been performed from a measurement of the number of pairs observed on deep images, with either a photometric redshift of the galaxies (e.g. Conselice et al. 2003; Lotz et al. 2008), or a spectroscopic redshift of one of the galaxies in the pair (e.g. Patton et al. 1997; Le Fèvre et al. 2000).
The effect of contamination by galaxies projected along the line of sight producing false pairs is then estimated from galaxy counts, and the observed pair fraction is corrected to get an estimate of the true pair fraction. As redshift increases, projection effects become increasingly important making it difficult to estimate the true pair fraction, creating a fondamental uncertainty in the measurement of m. At
,
meaning either no evolution of the merger rate with cosmic time, or a strong evolution. Part of this large range of values can be understood as coming from the different criteria used to identify merger candidates, or the photometric band used to identify pairs (Bundy et al. 2005). Furthermore, comparing measurements at low and high redshifts from different surveys is complicated due to the different selection functions used. At redshifts z>0.3, most pair counts so far have been performed from a measurement of the number of pairs observed on deep images, with either a photometric redshift of the galaxies (e.g. Conselice et al. 2003; Lotz et al. 2008), or a spectroscopic redshift of one of the galaxies in the pair (e.g. Patton et al. 1997; Le Fèvre et al. 2000).
The effect of contamination by galaxies projected along the line of sight producing false pairs is then estimated from galaxy counts, and the observed pair fraction is corrected to get an estimate of the true pair fraction. As redshift increases, projection effects become increasingly important making it difficult to estimate the true pair fraction, creating a fondamental uncertainty in the measurement of m. At ![]() a galaxy with a luminosity L* has a 40% probability of having a galaxy with a similar magnitude but at a different redshift projected within an apparent radius of
a galaxy with a luminosity L* has a 40% probability of having a galaxy with a similar magnitude but at a different redshift projected within an apparent radius of
![]() (Le Fèvre et al. 2000).
(Le Fèvre et al. 2000).
To overcome these limitations, the most secure method to identify a physical pair of galaxies is to obtain a velocity measurement of each galaxy in the pair, enabling us to identify pairs of galaxies which are most likely to be gravitationaily bound. Only recently samples with spectroscopic redshifts for both galaxies in a pair are becoming available (Lin et al. 2007, 2008). In this paper we use for the first time a complete redshift survey to ![]() and as faint as
and as faint as
![]() to securely identify pairs with both galaxies having a
spectroscopic redshift. We use the VIMOS VLT Deep Survey (VVDS) (Le Fèvre et al. 2005a), to search for galaxy pairs and to derive the pair fraction and the merger rate evolution. We present the galaxy sample and the methodology to build a pair sample in Sect. 2, we derive the pair fraction evolution in Sect. 3, and we examine the spectrophotometric properties of galaxies in pairs in Sect. 4. We compute the merger rate in Sect. 5. We evaluate the fraction of the stellar mass involved in mergers since
to securely identify pairs with both galaxies having a
spectroscopic redshift. We use the VIMOS VLT Deep Survey (VVDS) (Le Fèvre et al. 2005a), to search for galaxy pairs and to derive the pair fraction and the merger rate evolution. We present the galaxy sample and the methodology to build a pair sample in Sect. 2, we derive the pair fraction evolution in Sect. 3, and we examine the spectrophotometric properties of galaxies in pairs in Sect. 4. We compute the merger rate in Sect. 5. We evaluate the fraction of the stellar mass involved in mergers since ![]() in Sect. 6, and conclude in Sect. 7. We adopt a
in Sect. 6, and conclude in Sect. 7. We adopt a
![]() ,
,
![]() and
and
![]() cosmology throughout this work and magnitudes are given in the AB system.
cosmology throughout this work and magnitudes are given in the AB system.
2 Identification of galaxy pairs
2.1 VVDS overview
We use the deep sample from the VIMOS VLT Deep Survey on the 0216-04 field. Data have been obtained with the Visible Multi Object Spectrograph (VIMOS) on the ESO-VLT UT3 (Le Fèvre et al. 2004). A total of 9842 objects have been observed in the VVDS-Deep field over a total area of ![]()
![]() ,
selected solely on the basis of apparent magnitude
,
selected solely on the basis of apparent magnitude
![]() .
The mean redshift of the sample is z=0.76. The velocity measurement of each galaxy redshift has an accuracy of
.
The mean redshift of the sample is z=0.76. The velocity measurement of each galaxy redshift has an accuracy of ![]()
![]() (Le Fèvre 2005a). A strategy of multiple spectrograph passes has been used (Bottini et al. 2005), defining areas where targets have been randomly selected in four separate observations, and another area where two independent observations have been performed, leading to an effective random sampling of the galaxy population of respectively
(Le Fèvre 2005a). A strategy of multiple spectrograph passes has been used (Bottini et al. 2005), defining areas where targets have been randomly selected in four separate observations, and another area where two independent observations have been performed, leading to an effective random sampling of the galaxy population of respectively ![]() 35% and
35% and ![]() 20% for each of these two areas (with respectively
20% for each of these two areas (with respectively
![]() and
and
![]() ). We use a catalogue which contains 6464 objects in an effective area of
). We use a catalogue which contains 6464 objects in an effective area of ![]()
![]() ,
using only the most secure redshifts, i.e. quality flags 2-4 and 9 for primary targets and 22-24 and 29 for secondary targets. Flags 2-4 correspond to redshifts measured with a confidence level of 80%, 95% and 100%, respectively, and flag 9 indicates spectra with a single emission line
(see Le Fèvre et al. 2005a, for details).
,
using only the most secure redshifts, i.e. quality flags 2-4 and 9 for primary targets and 22-24 and 29 for secondary targets. Flags 2-4 correspond to redshifts measured with a confidence level of 80%, 95% and 100%, respectively, and flag 9 indicates spectra with a single emission line
(see Le Fèvre et al. 2005a, for details).
2.2 Selection of pairs in the VVDS
We have identified pairs in two ways. First, we searched in the main VVDS catalogue to find pairs of galaxies close in separation perpendicular to the plane of the sky using the angular distance at the redshift of the pair, and close in velocity along the line of sight as derived from the redshift measurements. Secondly, we visually examined the 2D spectra to identify secondary objects close to a primary VVDS target which escaped the automated spectra detection algorithm (Scodeggio et al. 2005) because their angular proximity to the main target along the slit creates
a blend of the two spectra at the faint isophotes used for detection. We looked for evidence of 2 continuum traces next to each other, with a clear separation of the object profiles along the
slit. The 1D spectrum of the companion was then extracted and its redshift measured
using the cross-correlation with templates as done for the main VVDS sample, and was assigned a flag 3X, with X following the flag nomenclature of the survey as described in Sect. 2.1. We then search in the parent VVDS imaging catalogue for the object responsible for the secondary trace, providing its sky coordinates, the magnitudes and colors. If the photometric catalogue did not identify the companion also because of blending, ugri and z images from the CFHTLS
(http://www.cfht.hawaii.edu/Science/CFHLS/) were examined and the multi-band photometry of the companion was performed using flux extraction in image areas isolating the object. This process concerned mainly objects with separations
![]() arcsec.
arcsec.
Our final catalogue contains all primary target galaxies with secure redshift measurements (flags 2-4, 9) and
![]() (6287 objects), all secondary target galaxies identified by the automated spectra extraction program (flags 22-24, 29) (160 objects) and all the companions identified through our visual examination of 2D spectra (flags 32-34, 39) (17 objects).
(6287 objects), all secondary target galaxies identified by the automated spectra extraction program (flags 22-24, 29) (160 objects) and all the companions identified through our visual examination of 2D spectra (flags 32-34, 39) (17 objects).
To create the pair catalogue, we first compute two quantities: the projected separation ![]() and the line-of-sight velocity difference
and the line-of-sight velocity difference ![]() .
For a pair of galaxies with redshift zi and zj and an angular separation
.
For a pair of galaxies with redshift zi and zj and an angular separation ![]() these parameters are given by:
these parameters are given by:
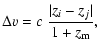 |
(1) |
where
The
![]() selection of the VVDS implies that galaxies in the sample have an absolute magnitude
selection of the VVDS implies that galaxies in the sample have an absolute magnitude
![]() at z = 1. We are missing pairs for which one member of the pair is fainter than this limit, for which we need to apply a completeness correction as described in Sect. 2.4. From the luminosity function of the complete VVDS sample, we know that the characteristic luminosity M* in B-band evolves with redshift as
at z = 1. We are missing pairs for which one member of the pair is fainter than this limit, for which we need to apply a completeness correction as described in Sect. 2.4. From the luminosity function of the complete VVDS sample, we know that the characteristic luminosity M* in B-band evolves with redshift as
![]() (Ilbert et al. 2005). We have therefore applied a magnitude evolution
MB = -18 - Q(z) to our absolute magnitude cutoff when looking for pairs (see Fig. 1).
(Ilbert et al. 2005). We have therefore applied a magnitude evolution
MB = -18 - Q(z) to our absolute magnitude cutoff when looking for pairs (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg82.gif) |
Figure 1:
Absolute B band magnitude distribution versus redshift of the primary galaxies in a pair with
|
| Open with DEXTER | |
2.3 The VVDS pair catalogue
Using Eq. (1), we have identified 702 simple pairs and 190 triplets with
![]() and
and
![]() .
To select major mergers, we have imposed an absolute magnitude difference between the two members of a pair in the B band of
.
To select major mergers, we have imposed an absolute magnitude difference between the two members of a pair in the B band of
![]() mag (see Fig. 2). On the left panel of Fig. 3 we present the number of pairs with
mag (see Fig. 2). On the left panel of Fig. 3 we present the number of pairs with
![]() and
and
![]() as a function of
as a function of ![]() and on the right panel, the number of pairs with
and on the right panel, the number of pairs with
![]() and
and
![]() as a function of
as a function of ![]() .
.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10569f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg86.gif) |
Figure 2:
The line-of-sight velocity difference |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{10569f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg88.gif) |
Figure 3:
Left: number of pairs as a function of
|
| Open with DEXTER | |
The two-point correlation function ![]() describes the excess probability of finding a galaxy at distance r from a galaxy selected at random over that expected in a uniform, random distribution. This function is usually parametrised by a power law with correlation length r0:
describes the excess probability of finding a galaxy at distance r from a galaxy selected at random over that expected in a uniform, random distribution. This function is usually parametrised by a power law with correlation length r0:
![]() .
Integration over this function yields a number of pairs that varies as
.
Integration over this function yields a number of pairs that varies as
![]() (Patton et al. 2002). Using the mean slope
(Patton et al. 2002). Using the mean slope
![]() of the correlation function found in the VVDS (Le Fèvre et al. 2005b), we expect an increase of the number of pairs
of the correlation function found in the VVDS (Le Fèvre et al. 2005b), we expect an increase of the number of pairs ![]()
![]() .
This is in good agreement with our pair counts which gives a slope of
.
This is in good agreement with our pair counts which gives a slope of ![]() 1.24 as shown in the left panel of Fig. 3.
1.24 as shown in the left panel of Fig. 3.
We identify the number of pairs as a function of separations
![]() and
and
![]() in Table 1. For
in Table 1. For
![]() ,
,
![]() and imposing at least one of the pair members to have
and imposing at least one of the pair members to have
![]() ,
we have a total of 36 pairs. The fraction of close pairs added by visual examination of the
2D spectra is
,
we have a total of 36 pairs. The fraction of close pairs added by visual examination of the
2D spectra is ![]() 10% for pairs with a projected separation of less than 2 arcsec.
10% for pairs with a projected separation of less than 2 arcsec.
We give the list of all 36 pairs with
![]() ,
,
![]() ,
,
![]() and
and
![]() in Table 2 and we display the images and spectra of each of these pairs in Fig. 4.
in Table 2 and we display the images and spectra of each of these pairs in Fig. 4.
2.4 Accounting for selection effects
To compute the total number of true pairs, we need to correct for three basic effects imposed by the VVDS selection function:
- 1.
- the limiting magnitude
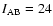 which imposes a loss of faint companions when we search for major mergers with
which imposes a loss of faint companions when we search for major mergers with
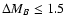 ;
;
- 2.
- the spatial sampling rate and the spectroscopic success rate in measuring redshifts;
- 3.
- the loss of pairs at small separations because of the ground based seeing limitation of the observations.
Table 1:
Number of pairs with
![]() and
MB < -18 - Q(z). In brackets the number of triplets is given.
and
MB < -18 - Q(z). In brackets the number of triplets is given.
Table 2:
List of the 36 spectroscopic pairs with
![]() ,
,
![]() and
and
![]() mag selected in the bright
mag selected in the bright
![]() sample. Id numbers beginning with ``p'' are manually extracted. Pair numbers can be use to retrieve reduced images and spectra in Fig. 4. RA(2000) and Dec(2000) are given for the first galaxy.
sample. Id numbers beginning with ``p'' are manually extracted. Pair numbers can be use to retrieve reduced images and spectra in Fig. 4. RA(2000) and Dec(2000) are given for the first galaxy.
The spectroscopic targets have been selected on the only basis of magnitude criterion
![]() .
Therefore, we miss companions which have an absolute magnitude fainter than imposed by the
.
Therefore, we miss companions which have an absolute magnitude fainter than imposed by the
![]() cutoff and the
cutoff and the
![]() mag difference, artificially lowering the number of pairs. To take this into account, we compute for each galaxy a weight
mag difference, artificially lowering the number of pairs. To take this into account, we compute for each galaxy a weight
![]() using the ratio between the comoving number densities above and below the magnitude cutoff (Ilbert et al. 2005). For each galaxy, we derive
using the ratio between the comoving number densities above and below the magnitude cutoff (Ilbert et al. 2005). For each galaxy, we derive
![]() which corresponds to the maximum absolute magnitude when searching for a companion and
which corresponds to the maximum absolute magnitude when searching for a companion and
![]() which corresponds to the survey limit I=24 in the absolute B band at the given galaxy redshift. We then assign a weight for each galaxy:
which corresponds to the survey limit I=24 in the absolute B band at the given galaxy redshift. We then assign a weight for each galaxy:
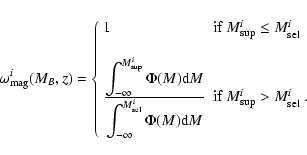
We combine these weights in each pair k as
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4a.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg111.gif) |
Figure 4:
Images (6'' |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4b.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg112.gif) |
Figure 4: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4c.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg113.gif) |
Figure 4: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4d.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg114.gif) |
Figure 4: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4e.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg115.gif) |
Figure 4: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4f.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg116.gif) |
Figure 4: continued. |
| Open with DEXTER | |
Since 25% of the field has been spectroscopicaly observed and the redshifts are not measured with 100% certainty, we must correct for the VVDS sampling rate and redshift success rate. These have been very well constrained (see Ilbert et al. 2005) resulting in the target sampling rate (TSR) and the spectroscopic success rate (SSR) computed as a function of redshift. The SSR has been assumed independent of the galaxy type, as demonstrated to be true up to ![]() in Zucca et al. (2006). We therefore introduce the weight
in Zucca et al. (2006). We therefore introduce the weight
![]() .
For each galaxy, we have information on its redshift, its apparent magnitude
.
For each galaxy, we have information on its redshift, its apparent magnitude
![]() ,
its spectroscopic flag and its spatial flag (whether the galaxy is on the field with four passes or two passes). We derive the completness weight as follows:
,
its spectroscopic flag and its spatial flag (whether the galaxy is on the field with four passes or two passes). We derive the completness weight as follows:
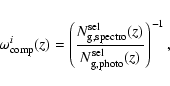
where
The last correction we need to apply results from the observations which have been performed
under a typical ground based seeing of 1 arcsec. We correct for the increasing incompleteness
to target both components of close pairs as the separation between them decreases. Assuming a clustered distribution of galaxies, the number of galaxy pairs should be a monotonically decreasing function of the pair separation. However, pairs are under-counted for separations
![]() arcsec because of the seeing effects.
arcsec because of the seeing effects.
We derive the ratio ![]() between the observed pair count in the spectroscopic catalogue, Nzz, over the observed pair count in the photometric catalogue,
between the observed pair count in the spectroscopic catalogue, Nzz, over the observed pair count in the photometric catalogue,
![]() ,
as a function of the angular separation (see Fig. 5). We apply a weight
,
as a function of the angular separation (see Fig. 5). We apply a weight
![]() on each pair k using the ratio:
on each pair k using the ratio:
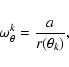
where the mean ratio a is the probability of randomly selecting a pair, obtained at large separations. This ratio is close to the squared mean target sampling rate (
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f5.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg134.gif) |
Figure 5: Spectroscopic completeness as a function the angular pair separations. The line is the fit used to derive the mean correcting factor a which corresponds roughly to the square of the completeness. |
| Open with DEXTER | |
The corrected number of galaxies
![]() in each redshift bin is then:
in each redshift bin is then:
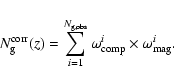 |
(2) |
The total number of pairs
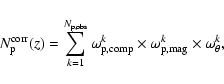 |
(3) |
where
3 Evolution of the pair fraction with redshift
3.1 Pair fraction evolution using VVDS data
We give the total number of identified pairs as a function of the two separation criteria in Table 1 for the adopted
![]() mag difference. We use Eqs. (2) and (3) to compute the pair
fraction
mag difference. We use Eqs. (2) and (3) to compute the pair
fraction
![]() in each redshift bin as follows:
in each redshift bin as follows:
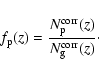 |
(4) |
Table 3 gives values of
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg144.gif) |
Figure 6:
Evolution of the pair fraction as a function of redshift for different sets of
|
| Open with DEXTER | |
Figure 6 shows the evolution of the pair fraction of galaxies with
![]() ,
30, 50,
,
30, 50,
![]() ,
,
![]() and
and
![]() .
A total of
.
A total of ![]() 10.86
10.86 ![]()
![]() of galaxies with
of galaxies with
![]() and
and
![]() are in close pairs at
are in close pairs at
![]() compared to
compared to ![]() 3.76
3.76 ![]()
![]() at
at
![]() .
This leads to
.
This leads to
![]()
![]()
![]() .
The fraction of galaxies brighter than
MB = -18 - Q(z) in pairs increases significantly with redshift.
.
The fraction of galaxies brighter than
MB = -18 - Q(z) in pairs increases significantly with redshift.
We have investigated the dependency of the pair fraction on the pair separation. Increasing the separation of the two members of a pair both in ![]() and
and ![]() ,
the index m varies from 4.73
,
the index m varies from 4.73 ![]() 2.01 to 2.45
2.01 to 2.45 ![]() 0.11 when separations increase from
0.11 when separations increase from
![]() to
to
![]() .
.
Interestingly, we find a strong dependency on the limiting absolute magnitude of the galaxies in the pairs. Table 3 gives the pair fractions for different redshift,
![]() and
and
![]() using the
using the
![]() VVDS sample and Table 4 gives the best fit values of m and
VVDS sample and Table 4 gives the best fit values of m and
![]() .
For
.
For
![]() and
and
![]() ,
m decreases from m=4.73
,
m decreases from m=4.73 ![]() 2.01 in the complete faint sample to m=3.07
2.01 in the complete faint sample to m=3.07 ![]() 1.68 for the bright sample with
1.68 for the bright sample with
![]() ,
implying a weaker evolution. This trend is seen for any separation from (
,
implying a weaker evolution. This trend is seen for any separation from (
![]() ,
,
![]() )
to (
)
to (
![]() ,
,
![]() ). Here, we show that the pair fraction evolves faster for fainter samples. We will come back to this property in Sect. 7.
). Here, we show that the pair fraction evolves faster for fainter samples. We will come back to this property in Sect. 7.
Table 3:
Pair fraction (in %) for different sets of separations and redshift, with
![]() (faint sample) and with
(faint sample) and with
![]() (bright sample) using VVDS data. (See Sect. 3.1.)
(bright sample) using VVDS data. (See Sect. 3.1.)
Table 4:
Best fits parameters for m and
![]() of major mergers as a function of the dynamical parameters in the faint
of major mergers as a function of the dynamical parameters in the faint
![]() sample and in the bright
sample and in the bright
![]() one.
one.
3.2 Constraints combining low redshift pair fraction with VVDS estimates
To better constrain the evolutionary parameters, the comparison of high redshift data to the local value of the pair fraction is
important. Patton et al. (2000) derived the pair fraction in a sample of 5426 galaxies in the SSRS2 redshift survey. Using close (
![]() )
dynamical (
)
dynamical (
![]() )
pairs, they found
)
pairs, they found
![]()
![]()
![]() at z = 0.015. We also compare our data to results from the CNOC2 Redshift survey (Patton et al. 2002) for the same magnitude selection but for a higher mean redshift:
at z = 0.015. We also compare our data to results from the CNOC2 Redshift survey (Patton et al. 2002) for the same magnitude selection but for a higher mean redshift:
![]()
![]()
![]() at z = 0.3.
at z = 0.3.
de Propris et al. (2007) derived measurements of the pair fraction using galaxy asymmetry and pair proximity to measure galaxy merger fractions for a volume limited sample of 3184 galaxies with
![]() and
and
![]() drawn from the Millennium Galaxy Catalogue. They found a pair fraction of 4.1
drawn from the Millennium Galaxy Catalogue. They found a pair fraction of 4.1 ![]()
![]() for galaxies with
for galaxies with
![]() .
.
Combining these values with our brighter sample (
![]() ), we estimate m = 1.50
), we estimate m = 1.50 ![]() 0.76 and
0.76 and
![]()
![]() 0.52. Here, we show that the fainter the galaxy sample is, the faster is the evolution of the pair fraction.
0.52. Here, we show that the fainter the galaxy sample is, the faster is the evolution of the pair fraction.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f7.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg282.gif) |
Figure 7:
Evolution of the pair fraction as a function of redshift adding SSRS2 (open diamond), CNOC2 (open circle) and MGC (open square) low redshift points to VVDS measurements (filled diamonds) for
|
| Open with DEXTER | |
Figure 7 shows the best fit when combining these pair fraction measurements with our brightest sample.
3.3 Influence of stellar mass on the pair fraction
To identify if the evolution of the pair fraction is also dependent on the stellar mass of the galaxies (as a proxy for total mass), we applied exactly the same method as we used for the luminosity in Sect. 3.1 but on a mass selected sample instead. Using masses derived in the VVDS and the evolution of the characteristic stellar mass,
M*star, as described in Pozzetti et al. (2007), we define a stellar-mass selected sample volume complete up to redshift ![]() 1 (using an evolution parameter
1 (using an evolution parameter
![]()
![]() z to reproduce the evolution of
z to reproduce the evolution of
![]() ). Stellar masses are derived using a Bruzual & Charlot (2003) model and allowing bursts on top of a smooth star formation history. We applied the same corrections described in Sect. 2.4 by replacing the luminosity function by the mass function.
). Stellar masses are derived using a Bruzual & Charlot (2003) model and allowing bursts on top of a smooth star formation history. We applied the same corrections described in Sect. 2.4 by replacing the luminosity function by the mass function.
We define a major pair via the ratio M1/M2 of stellar masses, and select pairs with
![]() corresponding roughly to a luminosity selected sample with
corresponding roughly to a luminosity selected sample with
![]() mag.
mag.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg287.gif) |
Figure 8:
The three sub-samples defined to study the influence of the mass on the pair fraction using pairs with
|
| Open with DEXTER | |
We divided our sample in different sub-samples: one with
![]() (106 pairs), one with
(106 pairs), one with
![]() (77 pairs) and one with
(77 pairs) and one with
![]() (37 pairs) with separations
(37 pairs) with separations
![]() and increasing the projected separation to
and increasing the projected separation to
![]() for better statistics, as shown in Fig. 8. Figure 9 shows the evolution of the pair fraction in those different mass sub-samples. For low mass galaxies with
for better statistics, as shown in Fig. 8. Figure 9 shows the evolution of the pair fraction in those different mass sub-samples. For low mass galaxies with
![]() ,
m = 3.13
,
m = 3.13 ![]() 1.54 and
1.54 and
![]()
![]() 3.42. For intermediate mass galaxies with
3.42. For intermediate mass galaxies with
![]() ,
m = 2.04
,
m = 2.04 ![]() 1.65 and
1.65 and
![]()
![]() 6.81. For massive galaxies with
6.81. For massive galaxies with
![]() ,
m = 0.52
,
m = 0.52 ![]() 2.07 and
2.07 and
![]()
![]() 19.5. We see a flatter evolution as we select more massive galaxies. It is therefore apparent that intermediate or low mass galaxies are responsible for most of the evolution of the pair fraction and merger rate.
19.5. We see a flatter evolution as we select more massive galaxies. It is therefore apparent that intermediate or low mass galaxies are responsible for most of the evolution of the pair fraction and merger rate.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f9.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg293.gif) |
Figure 9:
Evolution of the pair fraction for different sub-samples with different stellar mass limits
|
| Open with DEXTER | |
Table 5: Spectral types of pairs for the less and the most massive selected samples. Fractions are given in brackets.
4 Physical properties of galaxy pairs
4.1 Spectro-photometric properties
One of the expected effects of a merging or close interaction of galaxies is an increase
in the star formation rate of the system. We evaluate here if our sample of pairs has a stronger star formation rate than the global population by studying the rest-frame
![]() equivalent widths (EW) as a function of projected separation within a given
equivalent widths (EW) as a function of projected separation within a given
![]() (
(
![]() ).
).
![]() were derived using the platefit software (Lamareille et al. 2006), which performs a continuum fit to the observed spectra using template fitting. It enables an unbiased measurement of the intensities of absorption and emission
lines. For each pair, we produced the mean
were derived using the platefit software (Lamareille et al. 2006), which performs a continuum fit to the observed spectra using template fitting. It enables an unbiased measurement of the intensities of absorption and emission
lines. For each pair, we produced the mean
![]() by summing the individual
by summing the individual
![]() of each galaxy, assuming
of each galaxy, assuming
![]() if the line is not detected. Using only galaxies for which the
if the line is not detected. Using only galaxies for which the ![]() line has been detected, the mean
line has been detected, the mean
![]() is larger, on average, for the closest pairs with
is larger, on average, for the closest pairs with
![]()
![]() 4.35 for
4.35 for
![]() ,
,
![]()
![]() 3.78 for
3.78 for
![]() ,
and
,
and
![]()
![]() 3.12 for
3.12 for
![]() indicating a 25.9
indicating a 25.9 ![]()
![]() increase in
increase in
![]() at small separations (see Fig. 10). We perform the same estimation also using galaxies for which the
at small separations (see Fig. 10). We perform the same estimation also using galaxies for which the ![]() line has not been detected (
line has not been detected (
![]() ). Both samples show an increase of the mean
). Both samples show an increase of the mean
![]() at small projected separations, extending to higher redshifts results of Woods et al. (2006) in the local CFA2 sample. We conclude that star formation is enhanced in close merging systems at the mean redshift
at small projected separations, extending to higher redshifts results of Woods et al. (2006) in the local CFA2 sample. We conclude that star formation is enhanced in close merging systems at the mean redshift
![]() = 0.76 of our sample.
= 0.76 of our sample.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f10.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg314.gif) |
Figure 10:
Mean
|
| Open with DEXTER | |
4.2 Spectral types of galaxies in pairs
In this section, we compare the spectral properties of galaxies in dynamical pairs with field galaxies. For each galaxy in the VVDS, the spectral type has been derived on the basis of the template fitting of the rest-frame multi-![]() photometry (Zucca et al. 2006). Galaxies were classified as type 1 (E/S0), type 2 (Early spiral), type 3 (Late spiral) and type 4 (Irregular). Therefore, for each pair, we know the spectral types of both the primary galaxy and its companion(s).
photometry (Zucca et al. 2006). Galaxies were classified as type 1 (E/S0), type 2 (Early spiral), type 3 (Late spiral) and type 4 (Irregular). Therefore, for each pair, we know the spectral types of both the primary galaxy and its companion(s).
We have investigated which galaxy types are involved in a pair as cosmic time evolves. We classified each pair with a flag (X-X) where X is the spectral type of each pair member. For instance ``dry mergers'' with the merging of two early-type galaxies are classified as type (1-1). We consider
all the permutations between these four types. We classify as ``early-type'' pairs, those with flags (1-1), (1-2) and (2-2), late-type pairs the pairs with flags (3-3), (3-4), and (4-4), and mixed type pairs those with flags (1-3), (1-4), (2-3), and (2-4). Table 6 gives the fraction of these different classes in the
![]() pair sample. The fraction of pairs involving only E/SO galaxies increases from
pair sample. The fraction of pairs involving only E/SO galaxies increases from ![]() at
at ![]() to
to ![]() at
at ![]() ,
the fraction of pairs involving at least one E/SO increases from
,
the fraction of pairs involving at least one E/SO increases from ![]() at
at ![]() to
to ![]() at
at ![]() ,
while the vast majority of pairs involving at least one late-spiral or Irr galaxy represents a fraction decreasing from
,
while the vast majority of pairs involving at least one late-spiral or Irr galaxy represents a fraction decreasing from ![]() at
at ![]() to
to ![]() at
at ![]() .
.
Table 6:
Fraction of pairs vs. the spectral classes of each galaxy in the pair for redshift
![]() and
and
![]() .
Pairs with
MB < -18 - Q(z) and
.
Pairs with
MB < -18 - Q(z) and
![]() are considered (202 pairs in total).
are considered (202 pairs in total).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f11.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg328.gif) |
Figure 11: Fraction of early-type and late-type galaxies in the underlying selected sample brighter than MB = -18 - Q(z) (filled squares) and in the underlying selected sample brighter than MB = -18.77 - Q(z) (empty squares) as a function of redshift. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f12.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg329.gif) |
Figure 12: Fraction of early- (circles), mixed- (diamonds) and late-type (squares) pairs in the selected sample brighter than MB = -18 - Q(z) as a function of redshift. |
| Open with DEXTER | |
Figure 11 shows the evolution of the fraction of early-type, and late-type
galaxies in two different samples: one brighter than
MB = -18 - Q(z) (faint sample) and one brighter than
MB = -18.77 - Q(z) (bright sample). In the faint sample, the population is dominated by late-type galaxies at all redshifts. In the bright sample, late-type galaxies dominate between ![]() and
and ![]() ,
and early-type galaxies become dominant between
,
and early-type galaxies become dominant between ![]() and
and ![]() .
Early-type galaxies represent only one third of the sample at
.
Early-type galaxies represent only one third of the sample at ![]() ,
but about two thirds at
,
but about two thirds at ![]() .
Figure 12 shows the fraction of early, mixed and late-type pairs with
.
Figure 12 shows the fraction of early, mixed and late-type pairs with
![]() as a function of redshift. At
as a function of redshift. At
![]() ,
,
![]() (
(![]() )
of these pairs are early(late) type pairs whereas at
)
of these pairs are early(late) type pairs whereas at
![]() ,
,
![]() (
(![]() )
of these pairs are early(late) type pairs following the same trend as the underlying sample of galaxies.
)
of these pairs are early(late) type pairs following the same trend as the underlying sample of galaxies.
Figure 13 shows the pair fraction as a function of redshift, for
3 classes of pair types compared to the global pair fraction: two early-type galaxies, one early and one late component, two late-types, using a sample with
![]() .
The early-type pair fraction evolves slowly with redshift with m=1.44
.
The early-type pair fraction evolves slowly with redshift with m=1.44 ![]() 0.93. On the contrary, the late-early and late type pair fractions evolve strongly with redshift, with m=5.16
0.93. On the contrary, the late-early and late type pair fractions evolve strongly with redshift, with m=5.16 ![]() 2.56 and m=4.74
2.56 and m=4.74 ![]() 0.81 respectively.
0.81 respectively.
Table 5 gives the distributions of pairs as a function of the stellar mass selection and spectral types of the pairs. The
![]() sub-sample is dominated by late-type pairs (50%) while the
sub-sample is dominated by late-type pairs (50%) while the
![]() sub-sample is dominated by early-type pairs (59.5%) (see Sect. 4.2). We conclude that most of the pair fraction evolution is coming from lower mass late-type or mixed-type pairs.
sub-sample is dominated by early-type pairs (59.5%) (see Sect. 4.2). We conclude that most of the pair fraction evolution is coming from lower mass late-type or mixed-type pairs.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f13.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg337.gif) |
Figure 13:
Evolution of the global pair fraction in the faint sample (
|
| Open with DEXTER | |
5 Evolution of the merger rate
Knowing the pair fraction, we derive the merger rate i.e. the number of mergers per unit time and per comoving volume. This rate can be expressed as
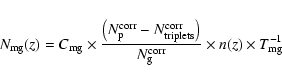 |
(5) |
where
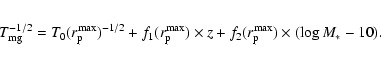
We computed T0, f1 and f2 for
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f14.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg346.gif) |
Figure 14:
Evolution with redshift of the merging time-scale in Gyr as a function of
|
| Open with DEXTER | |
The time-scales are found to be higher than the standard assumption that half of the pairs with
![]() undergo a merger in half a Giga-year (Patton et al. 2000, 2002; Lin et al. 2004). Using the Kitzblicher and White (2008) prescription, we find that even for the closest pairs the merging time-scale is 1.5 times higher than assumptions previously used in the literature.
undergo a merger in half a Giga-year (Patton et al. 2000, 2002; Lin et al. 2004). Using the Kitzblicher and White (2008) prescription, we find that even for the closest pairs the merging time-scale is 1.5 times higher than assumptions previously used in the literature.
Table 7:
Merger rate values for different sets of parameters and redshifts in units of 10-4 mergers
![]() for the bright sample(
for the bright sample(
![]() )
for galaxies with
)
for galaxies with
![]() .
.
The merger rate should be an ``absolute value'', independent of
![]() and
and ![]() since we take into account the merging time-scales corresponding to different pair separations. To check that the merger rate does not depend on the adopted value of
since we take into account the merging time-scales corresponding to different pair separations. To check that the merger rate does not depend on the adopted value of
![]() and
and ![]() ,
we have computed the merger rate for different sets of
,
we have computed the merger rate for different sets of
![]() with
with
![]() ;
results are presented in Table 7, and plotted in Fig. 15. The merger rate values are in good agreement, both in slope and normalization, for different sets of projected separations. This is a good indication of the robustness of the method. In the following, we use values of the merger rate with
;
results are presented in Table 7, and plotted in Fig. 15. The merger rate values are in good agreement, both in slope and normalization, for different sets of projected separations. This is a good indication of the robustness of the method. In the following, we use values of the merger rate with
![]() for better statistics, when necessary. The merger rate increases from
for better statistics, when necessary. The merger rate increases from ![]() 12.3
12.3 ![]() 10-4 to
10-4 to ![]() 19.4
19.4 ![]() 10-4 mergers
10-4 mergers
![]() from z=0.5 to z=0.9. The merger rate evolves as
from z=0.5 to z=0.9. The merger rate evolves as
![]()
![]()
![]() with
with
![]()
![]() 0.77 and
0.77 and
![]()
![]() 10-4. Table 8 lists the values of the parameters
10-4. Table 8 lists the values of the parameters
![]() and
and
![]() for different sets of separations and we plot in Fig. 15 the evolution of the merger rate for
for different sets of separations and we plot in Fig. 15 the evolution of the merger rate for
![]() ,
30, 50, 100
,
30, 50, 100
![]() and
and
![]() .
.
Using this merger rate evolution parametrisation, we estimate the fraction of present day galaxies
![]() that have undergone one major merger (Patton et al. 2002) since
that have undergone one major merger (Patton et al. 2002) since ![]() .
.
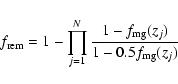 |
(6) |
where zj corresponds to a lookback time of
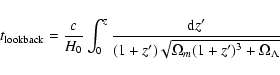 |
(7) |
based on a mean merging time-scale of 0.75 Gyr (corresponding to
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f15.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg398.gif) |
Figure 15:
Evolution of the
MB < -18 - Q(z) galaxy merger rate for different sets of
|
| Open with DEXTER | |
We have also computed the merger rate for two different luminosities using pairs with
![]() .
A similar trend to the pair fraction is observed: for galaxies with
.
A similar trend to the pair fraction is observed: for galaxies with
![]() ,
we find
,
we find
![]()
![]() 0.77, while for brighter galaxies with
0.77, while for brighter galaxies with
![]() we find
we find
![]()
![]() 1.83 using only VVDS data. For the same limiting magnitude and using the merger rate measured by de Propris et al. (2007) to constrain the low redshift end,
1.83 using only VVDS data. For the same limiting magnitude and using the merger rate measured by de Propris et al. (2007) to constrain the low redshift end,
![]()
![]() 0.44.
0.44.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f16.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg401.gif) |
Figure 16:
Evolution of the merger rate for different luminosity ranges. For the brightest sample (
|
| Open with DEXTER | |
Similarly, we have computed the merger rate for different mass selected samples as defined in Sect. 3.3 using
![]() .
For the less massive sample (
.
For the less massive sample (
![]() ),
),
![]()
![]() 1.57 with
1.57 with
![]()
![]() 10-4 mergers
10-4 mergers
![]() ,
while for the intermediate sample (
,
while for the intermediate sample (
![]() ),
),
![]()
![]() 1.67 with
1.67 with
![]() =
=
![]()
![]() 10-4 mergers
10-4 mergers
![]() ,
as shown in Fig. 17.
,
as shown in Fig. 17.
Table 8:
Best fit parameters of
![]() and
and
![]() for major mergers as a function of the dynamical parameters for the faint sample and for galaxies with
for major mergers as a function of the dynamical parameters for the faint sample and for galaxies with
![]() .
.
We see a change in the evolution of the merger rate as we go to the highest masses. First, the number of less massive merging events (
![]() )
is greater than the number of high mass merging events (
)
is greater than the number of high mass merging events (
![]() ). Then we see a flattening of the evolution of the merger rate as we go to higher mass galaxies, confirming that the evolution of the major merger rate is mainly due to the less massive galaxy population.
). Then we see a flattening of the evolution of the merger rate as we go to higher mass galaxies, confirming that the evolution of the major merger rate is mainly due to the less massive galaxy population.
6 Stellar mass involved in mergers
We estimate the fraction of the total stellar mass involved in a merger process,
fM*(z), since ![]() as a function of redshift as
as a function of redshift as
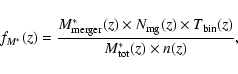 |
(8) |
where n(z) is the comoving number density of galaxies,
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f17.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg440.gif) |
Figure 17:
Evolution of the merger rate for different mass ranges using
|
| Open with DEXTER | |
7 Summary and discussion
Our results can be summarized as follows:
- (i)
- We find that
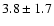 ,
,
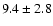 ,
and
,
and
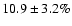 of galaxies with
MB(z) < -18 - Q(z) at
of galaxies with
MB(z) < -18 - Q(z) at
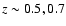 and 0.9 respectively, are in pairs of galaxies with luminosities
and 0.9 respectively, are in pairs of galaxies with luminosities
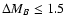 and separations less than
and separations less than
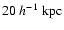 .
.
- (ii)
- The evolution of the pair fraction with redshift is strongly dependent on the absolute luminosity or stellar mass of the brighter galaxy in the pair: it evolves more slowly for brighter or more massive galaxies than for faint galaxies. Using the VVDS alone, the pair fraction of galaxies with
MB(z) < -18 -Q(z) is found to strongly evolve with redshift as
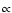 (1+z)m with m=4.46
(1+z)m with m=4.46 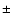 0.81 for separations of
0.81 for separations of
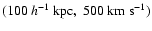 ,
while for brighter galaxies with
MB(z) < -18.77 -Q(z), we find a slower evolution with m=3.18
,
while for brighter galaxies with
MB(z) < -18.77 -Q(z), we find a slower evolution with m=3.18 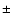 1.34. Combining VVDS data with low redshift measurements from de Propris et al. (2007), Patton et al. (2000, 2002), and taking
1.34. Combining VVDS data with low redshift measurements from de Propris et al. (2007), Patton et al. (2000, 2002), and taking
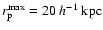 ,
we similarly find m=1.50
,
we similarly find m=1.50 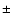 0.76 for bright galaxies with
0.76 for bright galaxies with
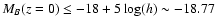 and m=4.73
and m=4.73 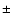 2.01 for the fainter
2.01 for the fainter
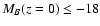 sample. In addition, the evolution of the pair fraction is found to be stronger with m = 3.13
sample. In addition, the evolution of the pair fraction is found to be stronger with m = 3.13 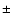 1.54 for less massive galaxies with
1.54 for less massive galaxies with
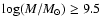 ,
than for more massive galaxies with
,
than for more massive galaxies with
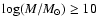 for which we find m = 2.04
for which we find m = 2.04 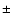 1.65. Low mass pairs are therefore contributing more to the evolution of the pair fraction than high mass pairs.
1.65. Low mass pairs are therefore contributing more to the evolution of the pair fraction than high mass pairs.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f18.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg446.gif)
Figure 18: The fraction of stellar mass density involved in a merger process since
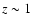 as a function of redshift for different mass selected sub-samples.
as a function of redshift for different mass selected sub-samples.Open with DEXTER - (iii)
- The star formation rate of close pairs is enhanced at separations
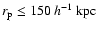 .
We find that the mean
.
We find that the mean
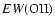 in close pairs is larger by 26
in close pairs is larger by 26 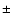
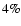 than the one derived for galaxies with greater separations.
than the one derived for galaxies with greater separations.
- (iv)
- The evolution of the pair fraction is stronger for late-type pairs with
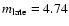
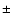 0.81, than for early-type pairs with
0.81, than for early-type pairs with
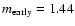
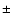 0.93. Late-type pairs are therefore contributing significantly more to the observed evolution of the pair fraction than early-type pairs in our
0.93. Late-type pairs are therefore contributing significantly more to the observed evolution of the pair fraction than early-type pairs in our
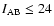 sample.
sample.
- (v)
- Using the merging timescale from Kitzbichler & White (2008), we find that the merger rate increases from
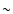 12.3
12.3 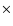 10-4 to
10-4 to 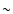 19.4
19.4 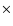 10-4 mergers
10-4 mergers
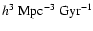 from z=0.5 to z=0.9. The merger rate of galaxies with
MB(z) < -18 -Q(z) evolves as
from z=0.5 to z=0.9. The merger rate of galaxies with
MB(z) < -18 -Q(z) evolves as
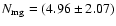
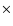 10-4
10-4 
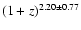 .
Similarly to the pair fraction, we find that the merger rate evolves faster for fainter or less massive galaxies, with
.
Similarly to the pair fraction, we find that the merger rate evolves faster for fainter or less massive galaxies, with
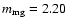
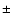 0.77 and 2.38
0.77 and 2.38 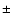 1.57 respectively, than for brighter or more massive galaxies with
1.57 respectively, than for brighter or more massive galaxies with
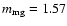
 0.44 and 1.27
0.44 and 1.27 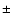 1.67 respectively. The merger rate is evolving more strongly for late-type mergers than for early-type mergers.
1.67 respectively. The merger rate is evolving more strongly for late-type mergers than for early-type mergers.
The dependency of the merger rate and its evolution on luminosity or stellar mass is indeed a prediction from the latest simulations using advanced semi-analytic models as described in Kitzbichler & White (2008). At the limiting magnitudes or stellar masses of our sample, Kitzbichler & White (2008) predict that the merger rate decreases and evolves more slowly for galaxy samples with increasing luminosity or stellar mass, similar to the trend observed in our sample.
The star formation rate is significantly enhanced in merging pairs with a net star formation increase of ![]()
![]() for these galaxies. Nevertheless, it accounts for only
for these galaxies. Nevertheless, it accounts for only ![]() to
to ![]() of the global galaxy population from redshift
of the global galaxy population from redshift ![]() to
to ![]() which is not sufficient to counteract the strong fading of the global star formation rate observed since
which is not sufficient to counteract the strong fading of the global star formation rate observed since ![]() .
This may indicate that the gas reservoir of massive and intermediate mass galaxies has already been depleted at redshifts
.
This may indicate that the gas reservoir of massive and intermediate mass galaxies has already been depleted at redshifts ![]() ,
in agreement with their observed peak in star formation at
,
in agreement with their observed peak in star formation at ![]() (e.g. Tresse et al. 2007). It is then apparent that the decreasing SFR since
(e.g. Tresse et al. 2007). It is then apparent that the decreasing SFR since
![]() is regulated by other physical processes like gas availability in the intergalactic medium, or feedback.
is regulated by other physical processes like gas availability in the intergalactic medium, or feedback.
Major merging events are largely dominated by pairs of late or mixed type galaxies, but while early-type mergers represent about ![]() of the merging events of bright galaxies at
of the merging events of bright galaxies at ![]() ,
they become approximately
,
they become approximately ![]() of all mergers at
of all mergers at
![]() ,
which is in good agreement with previous results on dry mergers (e.g. Lin et al. 2008). This indicates that major mergers are efficient in lowering the number density of intermediate mass late-type galaxies to build up more early-type galaxies. We confirm that merging is one of the important physical processes driving galaxy evolution, with the observed galaxy merger rate undoubtedly closely linked to the hierarchical build up of dark matter galaxy halos, with a rapid mass accretion phase of massive halos since
,
which is in good agreement with previous results on dry mergers (e.g. Lin et al. 2008). This indicates that major mergers are efficient in lowering the number density of intermediate mass late-type galaxies to build up more early-type galaxies. We confirm that merging is one of the important physical processes driving galaxy evolution, with the observed galaxy merger rate undoubtedly closely linked to the hierarchical build up of dark matter galaxy halos, with a rapid mass accretion phase of massive halos since ![]() (Abbas et al. 2008). Our finding that
(Abbas et al. 2008). Our finding that ![]()
![]() of the
stellar mass in present day massive galaxies has experienced a major merger since
of the
stellar mass in present day massive galaxies has experienced a major merger since ![]() is an indication that major mergers have been significantly contributing to the observed evolution of the stellar mass density since
is an indication that major mergers have been significantly contributing to the observed evolution of the stellar mass density since ![]() (Bundy et al. 2005; Arnouts et al. 2007).
(Bundy et al. 2005; Arnouts et al. 2007).
Acknowledgements
We are thankful to Simon White for forwarding us a preprint of the Kitzbichler & White (2008) work ahead of publication. This research has been developed within the framework of the VVDS consortium. This work has been partially supported by the CNRS-INSU and its Programme National de Cosmologie (France), and by Italian Ministry (MIUR) grants COFIN2000 (MM02037133) and COFIN2003 (No. 2003020150) and by INAF grants (PRIN-INAF 2005). The VLT-VIMOS observations have been carried out on guaranteed time (GTO) allocated by the European Southern Observatory (ESO) to the VIRMOS consortium, under a contractual agreement between the Centre National de la Recherche Scientifique of France, heading a consortium of French and Italian institutes, and ESO, to design, manufacture and test the VIMOS instrument. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
References
- Abbas, U., de la Torre, S., Le Fèvre, O., et al. 2008, submitted (In the text)
- Allam, S. S., Tucker, D. L., SDSS Collaboration 2004, AAS, 204, 4312 [NASA ADS]
- Allam, S. S., Tucker, D. L., Gee, P., Loh, Y., & Puerari, I. 2005, AAS, 207, 2504 [NASA ADS]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baker, N. 1966, in Stellar Evolution, ed. R. F. Stein, & A. G. W. Cameron (New York: Plenum), 333
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] (In the text)
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., & Franx, M. 2006, ApJ, 653, 53 [NASA ADS] [CrossRef] (In the text)
- Bridge, C., Carlberg, R., McCarthy, P., & Patton, D. 2005, JRASC, 99, 134 [NASA ADS]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
- Bundy, K., Ellis, R. S., & Conselice, C. J. 2005, ApJ, 625, 621 [NASA ADS] [CrossRef] (In the text)
- Burkey, J. M., Keel, W. C., Windhorst, R. A., & Franklin, B. E. 1994, ApJ, 429, 13 [NASA ADS] [CrossRef] (In the text)
- Carlberg, R. G. 1991, ApJ, 375, 429 [NASA ADS] [CrossRef]
- Carlberg, R. G., Pritchet, C. J., & Infante, L. 1994, ApJ, 435, 540 [NASA ADS] [CrossRef] (In the text)
- Carlberg, R. G., Cohen, J. G., Patton, D. R., et al. 2000, ApJ, 532, L1 [NASA ADS] [CrossRef]
- Combes, F. 2004, ASSL, 319, 57 [NASA ADS] (In the text)
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] (In the text)
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] (In the text)
- de Propris, R., Liske, J., Driver, S. P., Allen, P. D., & Cross, N. J. G. 2005, AJ, 130, 1516 [NASA ADS] [CrossRef]
- de Propris, R., Conselice, C. J., Liske, J., et al. 2007, ApJ, 666, 212 [NASA ADS] [CrossRef] (In the text)
- Domingue, D., & Xu, C. K. 2005, AAS, 207, 17911 [NASA ADS]
- Gottl¨øber, S., Klypin, A., & Kravtsov, A. V. 2001, AJ, 546, 223 [NASA ADS] [CrossRef]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kartaltepe, J. S., Sanders, D. B., Scoville, N. Z., et al. 2007a, ApJS, 172, 320 [NASA ADS] [CrossRef] (In the text)
- Kartaltepe, J. S., Sanders, D. B., Scoville, N. Z., & Capak, P. 2007b, AAS, 210, 3906 [NASA ADS]
- Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS [arXiv:0804.1965] (In the text)
- Kampczyk, P., Lilly, S. J., Carollo, C. M., et al. 2007, ApJS, 172, 329 [NASA ADS] [CrossRef] (In the text)
- Khochfar, S., & Burkert, A. 2001, ApJ, 561, 517 [NASA ADS] [CrossRef]
- Lamareille, F., Contini, T., Le Borgne, J.-F., et al. 2006, A&A, 448, 893 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lavery, R. J., Remijan, A., Charmandaris, V., Hayes, R. D., & Ring, A. A. 2004, AJ, 612, 679 [NASA ADS] [CrossRef]
- Le Fèvre, O., Abraham, R., Lilly, S. J., et al. 2000, MNRAS, 311, 565 [NASA ADS] [CrossRef] (In the text)
- Le Fèvre, O., et al. 2004, ASSL, 301, 7 [NASA ADS] (In the text)
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005a, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Le Fèvre, O., Guzzo, L., Meneux, B., et al. 2005b, A&A, 439, 877 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lin, L., Koo, D. C., Willmer, C. N. A., et al. 2004, ApJ, 617, L9 [NASA ADS] [CrossRef] (In the text)
- Lin, L., Koo, D. C., Weiner, B. J., et al. 2007, ApJ, 660, 51 [NASA ADS] [CrossRef] (In the text)
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] (In the text)
- Lotz, J. M., Davis, M., Faber, S. M., et al. 2008, ApJ, in press (In the text)
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] (In the text)
- Moore, B., Calcáneo-Roldán, C., Stadel, J., et al. 2001, Phys. Rev., 64, 3508 (In the text)
- Patton, D. R., & Atfield, J. E. 2008, ApJ, in press (In the text)
- Patton, D. R., Pritchet, C. J., Yee, H. K. C., Ellingson, E., & Carlberg, R. G. 1997, ApJ, 475, 29 [NASA ADS] [CrossRef] (In the text)
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] (In the text)
- Patton, D. R., Pritchet, C. J., Carlberg, R. G., et al. 2002, ApJ, 565, 208 [NASA ADS] [CrossRef] (In the text)
- Patton, D. R., Grant, J. K., Simard, L., et al. 2005, AJ, 130, 2043 [NASA ADS] [CrossRef] (In the text)
- Pollo, A., Meneux, B., Guzzo, L., et al. 2005, A&A, 439, 887 [NASA ADS] [CrossRef] [EDP Sciences]
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] (In the text)
- Tresse, L., Ilbert, O., Zucca, E., et al. 2007, A&A, 472, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woods, D. F., Geller, M. J., & Barton, E. J. 2006, AJ, 132, 197 [NASA ADS] [CrossRef] (In the text)
- Yee, H. K. C., & Ellingson, E. 1994, AJ, 445, 37 (In the text)
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... pairs
![[*]](/icons/foot_motif.gif)
- based on observations obtained with the European Southern Observatory Telescopes at the Paranal Observatory, under programs 072.A-0586 and 073.A-0647.
All Tables
Table 1:
Number of pairs with
![]() and
MB < -18 - Q(z). In brackets the number of triplets is given.
and
MB < -18 - Q(z). In brackets the number of triplets is given.
Table 2:
List of the 36 spectroscopic pairs with
![]() ,
,
![]() and
and
![]() mag selected in the bright
mag selected in the bright
![]() sample. Id numbers beginning with ``p'' are manually extracted. Pair numbers can be use to retrieve reduced images and spectra in Fig. 4. RA(2000) and Dec(2000) are given for the first galaxy.
sample. Id numbers beginning with ``p'' are manually extracted. Pair numbers can be use to retrieve reduced images and spectra in Fig. 4. RA(2000) and Dec(2000) are given for the first galaxy.
Table 3:
Pair fraction (in %) for different sets of separations and redshift, with
![]() (faint sample) and with
(faint sample) and with
![]() (bright sample) using VVDS data. (See Sect. 3.1.)
(bright sample) using VVDS data. (See Sect. 3.1.)
Table 4:
Best fits parameters for m and
![]() of major mergers as a function of the dynamical parameters in the faint
of major mergers as a function of the dynamical parameters in the faint
![]() sample and in the bright
sample and in the bright
![]() one.
one.
Table 5: Spectral types of pairs for the less and the most massive selected samples. Fractions are given in brackets.
Table 6:
Fraction of pairs vs. the spectral classes of each galaxy in the pair for redshift
![]() and
and
![]() .
Pairs with
MB < -18 - Q(z) and
.
Pairs with
MB < -18 - Q(z) and
![]() are considered (202 pairs in total).
are considered (202 pairs in total).
Table 7:
Merger rate values for different sets of parameters and redshifts in units of 10-4 mergers
![]() for the bright sample(
for the bright sample(
![]() )
for galaxies with
)
for galaxies with
![]() .
.
Table 8:
Best fit parameters of
![]() and
and
![]() for major mergers as a function of the dynamical parameters for the faint sample and for galaxies with
for major mergers as a function of the dynamical parameters for the faint sample and for galaxies with
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg82.gif) |
Figure 1:
Absolute B band magnitude distribution versus redshift of the primary galaxies in a pair with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10569f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg86.gif) |
Figure 2:
The line-of-sight velocity difference |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{10569f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg88.gif) |
Figure 3:
Left: number of pairs as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4a.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg111.gif) |
Figure 4:
Images (6'' |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4b.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg112.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4c.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg113.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4d.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg114.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0569-4e.eps} %\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg115.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0569-4f.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg116.gif) |
Figure 4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f5.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg134.gif) |
Figure 5: Spectroscopic completeness as a function the angular pair separations. The line is the fit used to derive the mean correcting factor a which corresponds roughly to the square of the completeness. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg144.gif) |
Figure 6:
Evolution of the pair fraction as a function of redshift for different sets of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f7.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg282.gif) |
Figure 7:
Evolution of the pair fraction as a function of redshift adding SSRS2 (open diamond), CNOC2 (open circle) and MGC (open square) low redshift points to VVDS measurements (filled diamonds) for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg287.gif) |
Figure 8:
The three sub-samples defined to study the influence of the mass on the pair fraction using pairs with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f9.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg293.gif) |
Figure 9:
Evolution of the pair fraction for different sub-samples with different stellar mass limits
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f10.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg314.gif) |
Figure 10:
Mean
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f11.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg328.gif) |
Figure 11: Fraction of early-type and late-type galaxies in the underlying selected sample brighter than MB = -18 - Q(z) (filled squares) and in the underlying selected sample brighter than MB = -18.77 - Q(z) (empty squares) as a function of redshift. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f12.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg329.gif) |
Figure 12: Fraction of early- (circles), mixed- (diamonds) and late-type (squares) pairs in the selected sample brighter than MB = -18 - Q(z) as a function of redshift. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f13.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg337.gif) |
Figure 13:
Evolution of the global pair fraction in the faint sample (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f14.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg346.gif) |
Figure 14:
Evolution with redshift of the merging time-scale in Gyr as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f15.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg398.gif) |
Figure 15:
Evolution of the
MB < -18 - Q(z) galaxy merger rate for different sets of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f16.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg401.gif) |
Figure 16:
Evolution of the merger rate for different luminosity ranges. For the brightest sample (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f17.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg440.gif) |
Figure 17:
Evolution of the merger rate for different mass ranges using
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10569f18.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10569-08/Timg446.gif) |
Figure 18:
The fraction of stellar mass density involved in a merger process since |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


