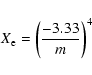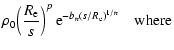| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 615 - 626 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200809965 | |
| Published online | 18 February 2009 | |
Total mass distributions of Sersic galaxies from photometry and central velocity dispersion
D. Chakrabarty1 - B. Jackson2
1 - School of Physics & Astronomy, University of Nottingham, Nottingham NG7 2RD, UK
2 -
Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
Received 14 April 2008 / Accepted 7 February 2009
Abstract
Aims. We develop a novel way of finding total mass density profiles in Sersic ellipticals, to about 3 times the major axis effective radius, using no other information other than what is typically available for distant galaxies, namely the observed surface brightness distribution and the central velocity dispersion ![]() .
.
Methods. The luminosity density profile of the observed galaxy is extracted by deprojecting the measured brightness distribution and scaling it by a fiduciary, step-function shaped, raw mass-to-light ratio profile (M/L). The resulting raw, discontinuous, total, 3-D mass density profile is then smoothed according to a proposed smoothing prescription. The parameters of this raw M/L are characterised by implementing the observables in a model-based study.
Results. The complete characterisation of the formalism is provided as a function of the measurements of the brightness distribution and ![]() .
The formalism, thus specified, is demonstrated to yield the mass density profiles of a suite of test galaxies and is successfully applied to extract the gravitational mass distribution in NGC 3379 and NGC 4499, out to about 3 effective radii.
.
The formalism, thus specified, is demonstrated to yield the mass density profiles of a suite of test galaxies and is successfully applied to extract the gravitational mass distribution in NGC 3379 and NGC 4499, out to about 3 effective radii.
Key words: methods: data analysis - galaxies: fundamental parameters
1 Introduction
Any evaluation of the total mass in distant galaxies is a struggle against the paucity of available observational evidence. Photometry is hardly enough to indicate the content of both the luminous as well as the dark matter, unless the functional dependence between luminosity content and dark mass is accessible. This is of course not the case; the existence of such a relation is itself uncertain, especially in early type galaxies. While kinematic information of tracers has often been advanced as indicators of mass distributions in galaxies, the implementation of such information is tricky, primarily because of the mass-anisotropy degeneracy. Thus, one often resorts to cleverly designed observational techniques and/or algorithms and formalisms which thrive even in light of the limited measurements. Examples of these include the Planetary Nebula Spectrograph (Romanowsky et al. 2004), the NMAGIC code (de Lorenzi et al. 2007) and CHASSIS (Chakrabarty & Saha 2001).
The X-ray emission from X-ray active systems can be analysed to offer insight into the gravitational mass distribution in the galaxy, under the assumption of hydrostatic equilibrium (O'Sullivan & Ponman 2004; Mahdavi et al. 2008; Fukazawa et al. 2006; Lemze et al. 2008; Humphrey et al. 2008; Zhang et al. 2007, to cite some recent work). However, what makes this method potentially unreliable is the lack of information about the distribution of the fraction of hot gas that is in hydrostatic equilibrium (Diehl & Statler 2007; Churazov et al. 2008).
Comparatively, a more stable route to mass distribution determination is via lensing measurements. However, the biggest shortcoming of mass determination from lensing measurements alone is the unavailability of the full three-dimensional mass distribution. To improve upon this, lensing data is often supplemented by dynamically obtained mass estimates (Bolton et al. 2008; Koopmans & Treu 2003; Czoske et al. 2008; Gavazzi et al. 2007).
However, there are questionable implementational problems involved in (parametric) dynamical mass determination, the chief of which are typically the mass-anisotropy degeneracy, binning-triggered instability of scant velocity dispersion data, reliance on the modelling of the stellar mass density and an even more fundamental worry caused by the assumption of one smooth parametric representation of the phase-space distribution function of the used tracer and by its relation to the phase-space density of the whole galaxy. This is of course in addition to the uncertainties in the mass distribution resulting from substituting the real geometry of the system by sphericity, as is typically done with all mass determination procedures. Above all, using tracer kinematics for mass determination (de Lorenzi et al. 2008; Douglas et al. 2007, etc.) is limited in applicability given the reliance on the size of the tracer kinematic data! Large data sets are of course hard to attain in systems that are not close by. Moreover, this method is unsuitable for fast evaluation of the mass distribution of individual galaxies that are members of a large sample, as for example, a galaxy obseved in a large survey.
On the contrary, it would be highly beneficial to design a method that is comparatively less data-intensive in that it demands only what is easily available from observations. We advance a methodology that provides total gravitational mass density distributions to about 3 effective radii, as compared to only 1 effective radius (Cappellari et al. 2006), in a fast and easy-to-implement fashion.
This advanced formalism is inspired by a trick that was
reported in Chakrabarty (2007, hereafter, Paper I). This trick
involves the exploitation of only photometry and the central velocity
dispersion measure (![]() )
in a galaxy, in order to generate the
total local mass-to-light ratio (M/L) profile to a distance that is
about thrice the semi-major axis effective radius. This cutoff
distance is described in details below. The prescription for
constructing this profile was provided in Paper I, though only for
a certain class of power-law galaxies. However, the exact nature of
this prescription is very much a function of the photometric class
that the galaxy belongs to. Thus, the formula reported in Paper I
cannot be invoked to shed light on the mass distribution in galaxies
that betray a different (and more ubiquitous) photometric class,
eg. ellipticals, the surface brightness of which can be fit by a
Sersic profile (Sersic 1968). This is precisely what is reported
in this paper.
)
in a galaxy, in order to generate the
total local mass-to-light ratio (M/L) profile to a distance that is
about thrice the semi-major axis effective radius. This cutoff
distance is described in details below. The prescription for
constructing this profile was provided in Paper I, though only for
a certain class of power-law galaxies. However, the exact nature of
this prescription is very much a function of the photometric class
that the galaxy belongs to. Thus, the formula reported in Paper I
cannot be invoked to shed light on the mass distribution in galaxies
that betray a different (and more ubiquitous) photometric class,
eg. ellipticals, the surface brightness of which can be fit by a
Sersic profile (Sersic 1968). This is precisely what is reported
in this paper.
This paper is arranged as follows: the basic framework of the suggested formalism is discussed in Sect. 2, followed by a note on the models that we use. The method used to obtain the sought functional forms is briefly mentioned in Sect. 4. Results obtained from our work are subsequently discussed in Sect. 5. Tests of the method are described in Sect. 6 while Sect. 7 deals with applications to real galaxies NGC 3379 and NGC 4494. The paper is rounded off with a section devoted to discussions of relevant points.
2 Formalism
The only Sersic model that was considered in Paper I did actually indicate that the mass estimation trick suggested for the power-law systems might be possible for Sersic galaxies too. Following this lead, as in Paper I, we first invoke a raw two-stepped M/L profile of the Sersic galaxy at hand, where it is the distribution of M/Lwith the major axis coordinate x, that is relevant. This raw M/Ldistribution is subsequently smoothed, (according to the smoothing prescription provided in Paper I and discussed below) to provide the real M/L distribution of the system, to a distance that is by definition, 3 times the major-axis effective radii for a Sersic galaxy with sersic index n=4 but is an approximation for the major-axis effective radius for all other values of n. The formal definition of this distance is given in Eq. (1) while the justification for our choice of this length scale is delineated in Sect. 8.4. Figure 1 represents a schematic diagram of this raw M/L profile against x.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9965.fig1.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg30.gif) |
Figure 1:
Schematic view of a raw M/L distribution
along the major axis coordinate x, for a model galaxy. The dashed
line marks the position of the jump radius
|
| Open with DEXTER | |
As can be appreciated from Fig. 1, the unprocessed
M/L profile is a two-stepped function that is characterised by three
free parameters, including the position of the step, or the jump
radius
![]() and the M/L amplitudes inside and outside
and the M/L amplitudes inside and outside
![]() .
The object of the current exercise is to fully characterise this
unprocessed M/L profile, so that upon smoothing, the final, total,
local M/L distribution over x is retrieved. This final form of the
M/L distribution is significantly different from the discontinuous,
2-stepped, raw M/L that we initially choose to work with. In fact,
the final form of the profile is smooth and the M/L values vary a
lot with x, sometimes abruptly, depending on the details of the
model galaxy. Figure 4 in Paper I represents a comparison of one such
raw M/L profile and the final smoothed M/L distribution that is
advanced as the representative M/L profile for the test system at
hand. In fact, later in Fig. 6, a raw M/L(exemplified in Fig. 1) is compared to the true M/Ldistribution of the test galaxy under consideration - the difference
between the raw and final forms of the M/L profiles is clear in that
figure.
.
The object of the current exercise is to fully characterise this
unprocessed M/L profile, so that upon smoothing, the final, total,
local M/L distribution over x is retrieved. This final form of the
M/L distribution is significantly different from the discontinuous,
2-stepped, raw M/L that we initially choose to work with. In fact,
the final form of the profile is smooth and the M/L values vary a
lot with x, sometimes abruptly, depending on the details of the
model galaxy. Figure 4 in Paper I represents a comparison of one such
raw M/L profile and the final smoothed M/L distribution that is
advanced as the representative M/L profile for the test system at
hand. In fact, later in Fig. 6, a raw M/L(exemplified in Fig. 1) is compared to the true M/Ldistribution of the test galaxy under consideration - the difference
between the raw and final forms of the M/L profiles is clear in that
figure.
As in Paper I,
![]() is set equal to 3
is set equal to 3![]() ,
where
,
where
and m is the slope of the straight line that is fit to the plot of core-removed
The smoothing prescription used here is the same as in Paper I - we
smooth the raw total mass density profile by two successive
applications of a box filter of size corresponding to ![]() .
.
The amplitude of M/L(x) for
![]() is referred to as
is referred to as
![]() and that for
and that for
![]() it is
it is
![]() .
Now
that
.
Now
that
![]() has been pinned down by construction, we hope to get a
constraint on the available choices for
has been pinned down by construction, we hope to get a
constraint on the available choices for
![]() from the
central velocity dispersion (
from the
central velocity dispersion (![]() )
and also hope to identify a
functional dependence of
)
and also hope to identify a
functional dependence of
![]() on
on
![]() .
The
exact form of such a constraint or function is yet unknown but we
begin by expecting these to be defined in terms of the photometric
parameters that describe the surface brightness profile of the Sersic
galaxy under consideration, namely, the Sersic index n and
.
The
exact form of such a constraint or function is yet unknown but we
begin by expecting these to be defined in terms of the photometric
parameters that describe the surface brightness profile of the Sersic
galaxy under consideration, namely, the Sersic index n and ![]() that we have defined above (Eq. (1)). The central
brightness is not a free parameter since we normalise all luminosity
density profiles to a central value of 1000
that we have defined above (Eq. (1)). The central
brightness is not a free parameter since we normalise all luminosity
density profiles to a central value of 1000 ![]() pc-3. Thus, we want to find the function
pc-3. Thus, we want to find the function
![]() ,
where
,
where
| (2) |
The inspiration for the hypothesis that f depends on the photometric parameters is discussed below.
Given that by construction,
![]() is the uniform amplitude
of the raw M/L profile for
is the uniform amplitude
of the raw M/L profile for
![]() ,
we expect it to be related
to the ``central'' mass-to-light ratio of the galaxy, where by
``central'' is implied the distance at which the measurement of the
central velocity dispersion (
,
we expect it to be related
to the ``central'' mass-to-light ratio of the galaxy, where by
``central'' is implied the distance at which the measurement of the
central velocity dispersion (![]() )
is obtained (at x=x0, with
x0 typically less than
)
is obtained (at x=x0, with
x0 typically less than
![]() ). However, in a real system, the
true central M/L cannot be securely determined from the measurement
of
). However, in a real system, the
true central M/L cannot be securely determined from the measurement
of ![]() alone, owing to uncertainties about the validity of the
assumptions that are invoked, in order to translate knowledge of
alone, owing to uncertainties about the validity of the
assumptions that are invoked, in order to translate knowledge of
![]() to that of mass enclosed within x0 (using virial
theorem). Such uncertainties basically stem from the presence of
anisotropy in phase-space. In the mass modelling trick advanced in
Paper I, room is allowed for the accommodation of such uncertainties,
as long as the deviations from the assumptions used in the virial
estimate of mass are not atypically more than what has been observed
with real ellipticals (Padmanabhan et al. 2004); this is discussed in the
following paragraph.
to that of mass enclosed within x0 (using virial
theorem). Such uncertainties basically stem from the presence of
anisotropy in phase-space. In the mass modelling trick advanced in
Paper I, room is allowed for the accommodation of such uncertainties,
as long as the deviations from the assumptions used in the virial
estimate of mass are not atypically more than what has been observed
with real ellipticals (Padmanabhan et al. 2004); this is discussed in the
following paragraph.
In Paper I, the virial estimate of the central M/L, from ![]() was parametrised by
was parametrised by ![]() .
It was found that for a measured
.
It was found that for a measured
![]() ,
as long as
,
as long as
![]() lies within a range of values
(the details of this range correspond to the given
lies within a range of values
(the details of this range correspond to the given ![]() ),
compatibility between the predicted and known (model) mass density
distributions is ensured. In other words, for
),
compatibility between the predicted and known (model) mass density
distributions is ensured. In other words, for ![]() calculated from
a given
calculated from
a given ![]() ,
,
![]() can be safely chosen to belong to
a range of M/L values:
can be safely chosen to belong to
a range of M/L values:
![]() to
to
![]() .
Such positioning of
.
Such positioning of
![]() can be
checked by comparing the mass distributions recovered with
can be
checked by comparing the mass distributions recovered with
![]() and
and
![]() ,
for consistency. Here
,
for consistency. Here
![]() while
while
![]() is an unknown
function of the photometric parameters and
is an unknown
function of the photometric parameters and ![]() - say
- say
![]() ,
,
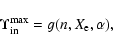 |
(3) |
where
Thus, there are two unknown functions that we wish to constrain:
![]() and
and
![]() .
These functions, when
known, will provide
.
These functions, when
known, will provide
![]() from
from
![]() which will
be known from
which will
be known from ![]() ,
(i.e.
,
(i.e. ![]() )
and the observed brightness
distribution of the galaxy. Once we know
)
and the observed brightness
distribution of the galaxy. Once we know
![]() from
from
![]() ,
we would then have fully characterised the raw M/Ldistribution over x. The smoothed out version of this raw M/Lprofile will then be advanced as the true M/L profile of the system
at hand. This in conjunction with the luminosity density distribution
will allow knowledge of the mass density distribution.
,
we would then have fully characterised the raw M/Ldistribution over x. The smoothed out version of this raw M/Lprofile will then be advanced as the true M/L profile of the system
at hand. This in conjunction with the luminosity density distribution
will allow knowledge of the mass density distribution.
We hope to recover the analytical forms of these two unknown functions
for Sersic galaxies to 3![]() ,
through an analysis of a sample of
model Sersic galaxy surface brightness profiles. Analytical fits are
sought to the data that is collated from the suite of models that we
work with, in order to recognise patterns, if any, that may show up in
the relations between the various quantities, in particular,
,
through an analysis of a sample of
model Sersic galaxy surface brightness profiles. Analytical fits are
sought to the data that is collated from the suite of models that we
work with, in order to recognise patterns, if any, that may show up in
the relations between the various quantities, in particular,
![]() and
and
![]() .
The
variation in these relations with changing models is then explored to
unravel the reliance of these relations on the photometric parameters.
.
The
variation in these relations with changing models is then explored to
unravel the reliance of these relations on the photometric parameters.
3 Models
We identify the relation between
![]() and
and
![]() in Sersic galaxies, by recognising (and then quantifying) the patterns
that emerge between these quantities, as diverse model galaxies are
scanned. To reminisce, Sersic galaxies are those, the surface
brightness profile I(R) of which can be approximated as:
in Sersic galaxies, by recognising (and then quantifying) the patterns
that emerge between these quantities, as diverse model galaxies are
scanned. To reminisce, Sersic galaxies are those, the surface
brightness profile I(R) of which can be approximated as:
![\begin{displaymath}I(R) = I_0\exp\left[-b_n(R/R_{\rm e})^{1/n}\right],
\end{displaymath}](/articles/aa/full_html/2009/17/aa09965-08/img48.gif) |
(4) |
where I0 is the central surface brightness,
Here, the equation for p is due to Lima Neto et al. (1999) and the ellipsoidal coordinate s is defined as
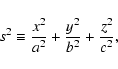 |
(6) |
for the axial ratios of a:b:c for the ellipsoidal system at hand. We use
As in Paper I, in our models, we assume oblateness and an inclination
of 90![]() ,
with a uniform projected axial ratio of 0.7; the work
of Padilla & Strauss (2008) corroborates such considerations of geometry and
ellipticity. Also, the model systems are assumed to be viewed in the
ACS z-band, at a distance of 17 Mpc. Though we recover the sought
functions for these chosen configurations, generalisations to other
systems will be suggested in Sects. 5.3 and 5.4.
,
with a uniform projected axial ratio of 0.7; the work
of Padilla & Strauss (2008) corroborates such considerations of geometry and
ellipticity. Also, the model systems are assumed to be viewed in the
ACS z-band, at a distance of 17 Mpc. Though we recover the sought
functions for these chosen configurations, generalisations to other
systems will be suggested in Sects. 5.3 and 5.4.
Actually Terzic & Sprague (2007) gives the more general 5-parameter mass
density model which describes Sersic galaxies with a core inside a
given break radius. However, we work with the simpler case of Sersic
galaxies that can be qualified by a 3-parameter model. In fact, we
constrict this further, by normalising the central luminosity density
![]() to 1000
to 1000 ![]() pc-3. Also, we look for the luminosity
distribution along the major axis. Thus, our models are distinguished
only by the Sersic index n and the
pc-3. Also, we look for the luminosity
distribution along the major axis. Thus, our models are distinguished
only by the Sersic index n and the ![]() defined in Eq. ( 1).
defined in Eq. ( 1).
![\begin{figure}
\par\includegraphics[width=16cm]{9965.fig2.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg58.gif) |
Figure 2:
Right panel: trends in
|
| Open with DEXTER | |
Models were formulated for Sersic indices n=3, 4, 5.3, 6, 7, 8 and 9
with ![]() of 726 pc, 1000 pc, 1400 pc, 2000 pc. While these models
were extensively explored to achieve the sought functions, we
investigated selected models with n lying in this range and higher
of 726 pc, 1000 pc, 1400 pc, 2000 pc. While these models
were extensively explored to achieve the sought functions, we
investigated selected models with n lying in this range and higher
![]() values. In particular, we are interested in models with Sersic
index
values. In particular, we are interested in models with Sersic
index ![]() 4, with larger
4, with larger ![]() .
Our viable models include galaxies
with n=3,
.
Our viable models include galaxies
with n=3,
![]() kpc and n=4,
kpc and n=4,
![]() kpc. Such an extended
size range holds special interest for the greater fraction of observed
ellipticals that correspond to this low n. Additionally, models with
other n were also found to work to
kpc. Such an extended
size range holds special interest for the greater fraction of observed
ellipticals that correspond to this low n. Additionally, models with
other n were also found to work to
![]() kpc. This choice of
models is supported by the results that
kpc. This choice of
models is supported by the results that
- In the nearby Virgo cluster, the ACSVCS survey (Ferrarese et al. 2006)
reports that nearly 90
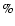 of the targetted early-type systems (Sersic
and cored-Sersic included) fall in the range of
of the targetted early-type systems (Sersic
and cored-Sersic included) fall in the range of
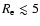 kpc
in the z-band (which is the waveband directly comparable to our
models). All the programme galaxies with
kpc
in the z-band (which is the waveband directly comparable to our
models). All the programme galaxies with ![$n\in[3,4]$](/articles/aa/full_html/2009/17/aa09965-08/img65.gif) were found to
have
were found to
have
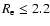 kpc while the single galaxy with
kpc while the single galaxy with 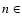 (4,5.3]
and
(4,5.3]
and
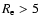 kpc, is not a Sersic galaxy but is a cored Sersic
system. Here, we remind ourselves that the reported effective radius
kpc, is not a Sersic galaxy but is a cored Sersic
system. Here, we remind ourselves that the reported effective radius
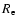 is really the geometric mean of the extent along the photometric
semi-axes. Thus, the extent along the semi-major axis is greater (by
about a factor of about 1.2, for an axial ratio of 0.7) than the
reported
is really the geometric mean of the extent along the photometric
semi-axes. Thus, the extent along the semi-major axis is greater (by
about a factor of about 1.2, for an axial ratio of 0.7) than the
reported 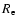 .
In other words, the surrogate for
.
In other words, the surrogate for 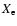 is about 1.2 times the values of
is about 1.2 times the values of 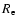 quoted earlier in this paragraph. Even when
this factor in taken into account, the range of our models covers the
programme galaxies of the ACSVCS.
quoted earlier in this paragraph. Even when
this factor in taken into account, the range of our models covers the
programme galaxies of the ACSVCS.
- Measurement of effective radius is waveband dependent
(Ko & Im 2005; Temi et al. 2008), so that for n=3 and 4, our limits on the
model
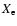 values in the z-band, are compatible with observations
(Trujillo et al. 2001; La Barbera et al. 2005; Ferrarese et al. 2006).
values in the z-band, are compatible with observations
(Trujillo et al. 2001; La Barbera et al. 2005; Ferrarese et al. 2006).
- At high redshifts, systems display evolution towards higher
compactness (Buitrago et al. 2008). Though this evolution is marked for
systems at z>1.7 (sample of Buitrago et al. 2008),
Ferreras et al. (2009) suggest a milder size evolution for the most
massive galaxies for
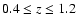 .
Thus, in the higher redshift
range that we propose our scheme to be most useful in, if anything,
the size range of our models would be more suitable.
.
Thus, in the higher redshift
range that we propose our scheme to be most useful in, if anything,
the size range of our models would be more suitable.
Sersic indices 2 or lower appeared not to be viable for the formalism to function, implying that this formalism is suitable only for elliptical systems (see Sect. 3). Sersic indices greater than 9 were not examined since such systems are very rare.
These luminosity density models, described by
Eq. (5) and the used values of n and ![]() ,
were
embedded in an NFW-type dark halo (Navarro et al. 1996) of mass density
,
were
embedded in an NFW-type dark halo (Navarro et al. 1996) of mass density
![]() ,
to give a total mass density of:
,
to give a total mass density of:
| (7) |
where by choice,
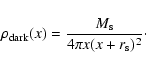 |
(8) |
Here
We ascribe ![]() 1-
1-![]() errors of about 10
errors of about 10![]() to the luminosity
density distributions that we generate and search for compatibility
between the model mass density distribution and the predicted one,
within these error bars.
to the luminosity
density distributions that we generate and search for compatibility
between the model mass density distribution and the predicted one,
within these error bars.
4 Method
Combinations of the parameters ![]() ,
,
![]() and
and
![]() that showed compatability with the known (model) mass
density profiles, up to 3
that showed compatability with the known (model) mass
density profiles, up to 3![]() ,
at the aforementioned four separate
,
at the aforementioned four separate
![]() coordinates, were searched for by our smoothing formalism
that is automated.
coordinates, were searched for by our smoothing formalism
that is automated.
We record the list of
![]() values that imply compatibility
for a chosen
values that imply compatibility
for a chosen ![]() (chosen typically in the range of 2 to 10). The
starting value of
(chosen typically in the range of 2 to 10). The
starting value of
![]() was typically about
was typically about ![]() while
the upper value was set as 3
while
the upper value was set as 3![]() ,
which was always sufficient to
find the whole range of
,
which was always sufficient to
find the whole range of
![]() values that correspond to
compatability. Similarly, we record the
values that correspond to
compatability. Similarly, we record the
![]() value
corresponding to a given
value
corresponding to a given
![]() .
.
The plots of
![]() and
and
![]() ,
as
functions of
,
as
functions of ![]() are monitored, with the aim of recognising the
analytical form of these functional dependences. Similarly, the plot
of
are monitored, with the aim of recognising the
analytical form of these functional dependences. Similarly, the plot
of
![]() as a function of
as a function of
![]() is analysed at
different n and
is analysed at
different n and ![]() ,
to identify
,
to identify
![]() .
.
5 Results
With ![]() held at 726 pc, as n is varied, the plots of
held at 726 pc, as n is varied, the plots of
![]() against
against ![]() are shown in the left panel of
Fig. 2 while the relation between
are shown in the left panel of
Fig. 2 while the relation between
![]() against
against
![]() is depicted for these models, in the right panel of
this figure.
is depicted for these models, in the right panel of
this figure.
5.1 Relation between
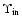 and
and 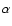
When the data collated from the different models is plotted it is
noted that while
![]() ,
the
,
the
![]() relation is well fit by a
quadratic function of
relation is well fit by a
quadratic function of
![]() .
This latter functional form has
only a weak bearing on the Sersic index n, though
.
This latter functional form has
only a weak bearing on the Sersic index n, though
![]() is found to increase slightly as n is
increased from 5.3 to 9. Thus, by denying this increased amplitude of
is found to increase slightly as n is
increased from 5.3 to 9. Thus, by denying this increased amplitude of
![]() with higher values of n, we merely
constrict the range of values from which
with higher values of n, we merely
constrict the range of values from which
![]() can be
chosen. Thus, our attempt at simplification of the sought functional
form preempts a small reduction in the applicability of our formalism
to more anisotropic galaxies than what is effectively allowed.
can be
chosen. Thus, our attempt at simplification of the sought functional
form preempts a small reduction in the applicability of our formalism
to more anisotropic galaxies than what is effectively allowed.
In Fig. 3, we present the values of
![]() at distinct values of
at distinct values of
![]() ,
for
different
,
for
different ![]() ,
and a single Sersic index of 5.3. The functional form
of the relation is recovered from our analysis, and this is
over-plotted on the data, in solid lines. This functional form is given by:
,
and a single Sersic index of 5.3. The functional form
of the relation is recovered from our analysis, and this is
over-plotted on the data, in solid lines. This functional form is given by:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9965.fig3.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg92.gif) |
Figure 3:
The values of
|
| Open with DEXTER | |
5.2 Relation between
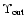 and
and
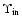
The data from the assorted models indicate that
![]() is
noted to fall exponentially with
is
noted to fall exponentially with
![]() ;
in fact, a good fit
to this relation is given by the following equation:
;
in fact, a good fit
to this relation is given by the following equation:
| (10) |
where
We advance the following formulae for ![]() ,
A0 and
,
A0 and ![]() :
:
These relations are valid for all model systems with
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{9965.fig4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg140.gif) |
Figure 4:
Trends in the three different parameters
that define the exponential fall-off of
|
| Open with DEXTER | |
5.3 Photometry in other wave-bands
It is always possible that the observed photometry is presented in a
wave-band different from the ACS z-band for which we predict the
above relations between the properties of the raw M/L, though the
z-band is in general a better choice for high redshift systems than
a bluer waveband. If the available photometry is in a band different
from z, (say the w-band), then the factor by which every value of
![]() and
and
![]() should be changed, is obtained
from the following considerations. We realise that if w is such that
a model galaxy is brighter in z than in the w-band, then the M/Lratio by which the inner and outer parts of the brightness profile in
z need to be scaled, are smaller than the same by which the profile
in w needs to be scaled. In fact, the value of
should be changed, is obtained
from the following considerations. We realise that if w is such that
a model galaxy is brighter in z than in the w-band, then the M/Lratio by which the inner and outer parts of the brightness profile in
z need to be scaled, are smaller than the same by which the profile
in w needs to be scaled. In fact, the value of
![]() corresponding to observations in w should be scaled by a factor of
corresponding to observations in w should be scaled by a factor of
![]() .
Here
.
Here
![]() is the solar
absolute magnitude in the w-band. In the ACS z-band
is the solar
absolute magnitude in the w-band. In the ACS z-band
![]() .
However, this transformation into the w-band is really an
approximation since we assume all the way that
.
However, this transformation into the w-band is really an
approximation since we assume all the way that ![]() is the same over
wavebands. This is not true (Ko & Im 2005; Temi et al. 2008).
is the same over
wavebands. This is not true (Ko & Im 2005; Temi et al. 2008).
5.4 Distance to the galaxy
It is important to enquire about the stability of the posited forms of
![]() and
and
![]() when the distance to a galaxy is
different from what has been used in the models, namely 17 Mpc
(approximate distance to Virgo). The only influence of the distance
D (in Mpc) to the observed galaxy is in affecting the luminosity
density distribution that is obtained be deprojecting the observed
surface brightness profile, through a term that is linear in
D-1. It is this luminosity density profile that is scaled by
when the distance to a galaxy is
different from what has been used in the models, namely 17 Mpc
(approximate distance to Virgo). The only influence of the distance
D (in Mpc) to the observed galaxy is in affecting the luminosity
density distribution that is obtained be deprojecting the observed
surface brightness profile, through a term that is linear in
D-1. It is this luminosity density profile that is scaled by
![]() and
and
![]() in the inner and outer parts of
the galaxy. Thus, if the galaxy is in reality further than 17 Mpc, the
implementation of the suggested M/L values would amount to an
overestimation of the luminosity density. To compensate for this, we
need to modulate the relevant
in the inner and outer parts of
the galaxy. Thus, if the galaxy is in reality further than 17 Mpc, the
implementation of the suggested M/L values would amount to an
overestimation of the luminosity density. To compensate for this, we
need to modulate the relevant
![]() and
and
![]() values
by the factor D/17.
values
by the factor D/17.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9965.fig5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg145.gif) |
Figure 5:
Figure to compare the predicted total mass density
distribution with x (in red) with the known (model) mass density
profile (in green), for the model described by n=3.5 and
|
| Open with DEXTER | |
6 Tests
In this section we discuss the testing of our advanced parametric
forms of
![]() (Eq. (9) with
inputs from 10, 11 and 12) and
(Eq. (9) with
inputs from 10, 11 and 12) and
![]() (Eq. (8)). The scheme is tested on models
that were excluded from the fitting exercise that resulted in our
identification of the forms of the functions f and g.
(Eq. (8)). The scheme is tested on models
that were excluded from the fitting exercise that resulted in our
identification of the forms of the functions f and g.
Figure 5 shows a comparison of the predicted and model
mass density profiles along the ![]() -axis for the model galaxy
that has a Sersic index of 3.5 and
-axis for the model galaxy
that has a Sersic index of 3.5 and
![]() pc.
pc. ![]() is set to
is set to
![]() k ms-1, averaged over a radius of about
k ms-1, averaged over a radius of about
![]() pc. For this system, we extract
pc. For this system, we extract
![]() and
and
![]() .
This
pair of
.
This
pair of
![]() values are used to scale the
luminosity density distribution for this model galaxy which is then
smoothed to offer a final mass density distribution along the major
axis. These
values are used to scale the
luminosity density distribution for this model galaxy which is then
smoothed to offer a final mass density distribution along the major
axis. These
![]() values imply a predicted
mass density distribution (in red in Fig. 5) that
tallies favourably with the model (in green in
Fig. 5).
values imply a predicted
mass density distribution (in red in Fig. 5) that
tallies favourably with the model (in green in
Fig. 5).
The predicted mass density distribution when compared to the luminosity density distribution offers the final or smoothed M/L which is shown in Fig. 6 to be significantly different from the raw M/L profile (in this black line).
However, this was the example of one given model galaxy, characterised
by a given central velocity dispersion. Tests were undertaken to
validate the relations predicted between the properties of the raw
M/L and the photometric parameters of model galaxies, across the
full range of ![]() .
The tests were carried out with model
galaxies with Sersic index of 4 and
.
The tests were carried out with model
galaxies with Sersic index of 4 and ![]() of 726 pc and 1400 pc. In
Fig. 7, we see the calculated
of 726 pc and 1400 pc. In
Fig. 7, we see the calculated
![]() value corresponding to a given
value corresponding to a given
![]() ,
for which
compatibility is noted between the known (model) and predicted total
mass density distributions, to 3
,
for which
compatibility is noted between the known (model) and predicted total
mass density distributions, to 3![]() .
Such
.
Such
![]() values
are shown in the two panels of this figure, in black dots.
values
are shown in the two panels of this figure, in black dots.
It is to be noted that these calculated values of
![]() very closely straddle (within errors of
very closely straddle (within errors of ![]() 5
5![]() )
the analytical
relationship between
)
the analytical
relationship between
![]() and
and
![]() that is
predicted in Eqs. (9)-(12), for given
that is
predicted in Eqs. (9)-(12), for given ![]() and n; in
this case for n=4,
and n; in
this case for n=4,
![]() pc (left) and n=4,
pc (left) and n=4,
![]() pc
(right). Thus, these tests offer confidence in the formalism that we
suggest.
pc
(right). Thus, these tests offer confidence in the formalism that we
suggest.
![\begin{figure}
\par\includegraphics[width=7.9cm]{9965.fig6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg152.gif) |
Figure 6:
Figure to compare the final total
(local) M/L distribution with the initially chosen raw M/L profile
(in broken lines), for the test galaxy the total mass of which is
presented in Fig. 5. The final M/L is presented
within 3 |
| Open with DEXTER | |
7 Applications
In this section, we check out the efficacy of the advanced scheme in
recovering gravitational mass density distribution of two elliptical
galaxies, NGC 4494 and NGC 3379, to 3![]() .
Our predicted mass
distributions are compared to independent dynamical mass models for
these systems.
.
Our predicted mass
distributions are compared to independent dynamical mass models for
these systems.
7.1 NGC 3379
NGC 3379 was reported by Romanowsky et al. (2004) and Douglas et al. (2007) to
contain very little dark matter on the basis of a Jeans equation
analysis of the kinematics of around 200 planetary nebulae (PNe) that
reside in the dark halo of this galaxy. An independent estimation of
the distribution of the total mass density of this galaxy was
performed by Chakrabarty (2009, submitted to AJ), by
implementing these PNe velocities in the Bayesian algorithm CHASSIS
(Chakrabarty $&$ Portegies Zwart 2005; Chakrabarty & Saha 2001). As acknowledged by Chakrabarty (2009),
these mass distributions from CHASSIS indicate somewhat higher masses
than the estimates of Douglas et al. (2007), owing to the
assumption of isotropy within CHASSIS. While details of such mass
estimation techniques are irrelevant to the current work, here we
present a comparison between the mass density profile obtained from
our formalism with the same obtained from CHASSIS. We also present a
comparison between the cumulative mass result M(r) via the quantity
defined as
![]() ,
where
,
where ![]() is referred to as the
circular velocity.
is referred to as the
circular velocity.
![\begin{figure}
{
$\begin{array}{c c}
\includegraphics[height=.3\textheight]{99...
... \includegraphics[height=.3\textheight]{9965.fig8.ps}\end{array}$ }
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg154.gif) |
Figure 7:
Comparison of model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.9cm]{9965.fig9.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg155.gif) |
Figure 8:
The radial distribution of the recovered
total mass density is depicted in black, on the left. On this is
superimposed the mass density profile obtained by implementing the
kinematic information of a sample of planetary nebulae in NGC 3379
(the same sample as used by Douglas et al. 2007), in the Bayesian
algorithm CHASSIS (Chakrabarty 2009, communicated to AJ). The
quantity |
| Open with DEXTER | |
Our predictions are based on the analysis of the photometry of
NGC 3379 in the B-band (Capaccioli et al. 1990) and the data for
projected central velocity dispersion, as given by
Statler & Smecker-Hane (1999). Using this
![]() data along the major axis of
the galaxy, (Table 1A of Statler & Smecker-Hane 1999), we get an
data along the major axis of
the galaxy, (Table 1A of Statler & Smecker-Hane 1999), we get an ![]() of
about 7.5. The photometry suggests an
of
about 7.5. The photometry suggests an ![]() of 2.2 kpc. Additionally,
we deproject the B-band surface brightness profile using the
Bayesian deprojection algorithm DOPING (Chakrabarty $&$ Ferraese 2008). We consider
NGC 3379 to be at a distance of 11 kpc, as in Douglas et al. (2007). Our
predicted values of (upper limit on)
of 2.2 kpc. Additionally,
we deproject the B-band surface brightness profile using the
Bayesian deprojection algorithm DOPING (Chakrabarty $&$ Ferraese 2008). We consider
NGC 3379 to be at a distance of 11 kpc, as in Douglas et al. (2007). Our
predicted values of (upper limit on)
![]() and
and
![]() ,
as modulated by differences in the wave-band of the
available photometry and distance to the system, are about 9.3 and 5.9.
,
as modulated by differences in the wave-band of the
available photometry and distance to the system, are about 9.3 and 5.9.
The resulting mass density distribution that we advance for NGC 3379
within 3![]() ,
is depicted in black on the left of
Fig. 8. This is compared to the mass model identified by
CHASSIS.
,
is depicted in black on the left of
Fig. 8. This is compared to the mass model identified by
CHASSIS. ![]() derived
from our calculated mass distribution, from the dynamical mass
modelling by CHASSIS and that reported by Douglas et al. (2007) are
represented in the right panel of Fig. 8.
derived
from our calculated mass distribution, from the dynamical mass
modelling by CHASSIS and that reported by Douglas et al. (2007) are
represented in the right panel of Fig. 8.
The comparison of the total mass density profile indicates the clear
trend for our predicted mass distribution to be on the lower side
compared to the gravitational matter density provided by CHASSIS. This
is only to be expected since CHASSIS in its current form, assumes
isotropy, which affects CHASSIS idiosyncratically to spuriously
enhance mass density, as acknowledged by Chakrabarty
(2009). Consequently, the ![]() profile advanced by our work is also
on the lower side of the profile that follows from CHASSIS, though our
result compares better with the result advanced by Douglas et al. (2007).
profile advanced by our work is also
on the lower side of the profile that follows from CHASSIS, though our
result compares better with the result advanced by Douglas et al. (2007).
![\begin{figure}
\par\includegraphics[width=13.9cm]{9965.fig10.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg157.gif) |
Figure 9: Figure to bring out the results for the galaxy NGC 4494. The left panel depicts a projection of the luminosity density distribution that we estimate for the galaxy (in black), compared to the V-band surface brightness data (in red). The total gravitational mass distribution of the galaxy is represented in the middle panel while the mass-to-light ratio on the V-band is shown on the right. |
| Open with DEXTER | |
7.2 NGC 4494
NGC 4494 is a nearby elliptical, the mass distribution of which to 7
effective radii has recently been presented by Napolitano et al. (2008). The
distance to this galaxy is given as 15.8 Mpc by Napolitano et al. (2008). The
V-band photometry of this galaxy is presented in Table A1 of
Napolitano et al. (2008). This surface brightness profile indicates an ![]() of
3.37 kpc and is deprojected, given the radial variation of the
projected eccentricity (assuming an oblate geometry and edge-on
viewing). The projection of such recovered luminosity
density distribution is shown in the left panel of
Fig. 9, compared to the surface brightness data of this
galaxy (in red). Napolitano et al. (2008) also cite the central velocity
dispersion of this system as 150 km s-1 (Paturel et al. 2003).
Considering this
of
3.37 kpc and is deprojected, given the radial variation of the
projected eccentricity (assuming an oblate geometry and edge-on
viewing). The projection of such recovered luminosity
density distribution is shown in the left panel of
Fig. 9, compared to the surface brightness data of this
galaxy (in red). Napolitano et al. (2008) also cite the central velocity
dispersion of this system as 150 km s-1 (Paturel et al. 2003).
Considering this
![]() to be the dispersion averaged over
to be the dispersion averaged over
![]() ,
where
,
where
![]() for this galaxy, we obtain an
for this galaxy, we obtain an ![]() of 2. Our predicted values of
of 2. Our predicted values of
![]() and
and
![]() are
about 2 and 0.121. These are used to characterise the raw M/L, which
when smoothed, gives rise to the total mass distribution that is shown
in the middle panel of Fig. 9.
are
about 2 and 0.121. These are used to characterise the raw M/L, which
when smoothed, gives rise to the total mass distribution that is shown
in the middle panel of Fig. 9.
The total M/L ratio of NGC 4494, in the V-band is shown on the
right panel of Fig. 9 while the enclosed gravitational
mass distribution is depicted in the middle panel. This is very
similar to the radial mass distribution of NGC 4494, within the inner
3![]() ,
as reported by Napolitano et al. (2008, their Fig. 13).
,
as reported by Napolitano et al. (2008, their Fig. 13).
8 Discussions and summary
We have presented a novel mechanism for estimating total mass density
profiles of elliptical galaxies that can be described by a Sersic-type
surface brightness distribution. This formalism uses nothing in excess
of what is typically available in the observational domain, namely,
photometry and the central velocity dispersion profile. This allows
the implementation of this scheme even for systems at high
redshifts. (Such an implementation of this scheme will be presented in
a future contribution - Chakrabarty ![]() Conselice, under
preparation). The advanced scheme uses the methodology presented in
Paper I, in the context of Sersic galaxies.
Conselice, under
preparation). The advanced scheme uses the methodology presented in
Paper I, in the context of Sersic galaxies.
To begin with, we generate a sample of luminosity density
distributions that project to Sersic brightness profiles, of assorted
values of n and ![]() .
These toy galaxies are then assigned various
values of the local central mass-to-light ratio (parametrised by
.
These toy galaxies are then assigned various
values of the local central mass-to-light ratio (parametrised by
![]() ). For each such configuration, we monitor the allowed range
of
). For each such configuration, we monitor the allowed range
of
![]() and the value of
and the value of
![]() that corresponds
to any such
that corresponds
to any such
![]() .
This pair of
.
This pair of
![]() values define the raw or unsmoothed
two-stepped local mass-to-light ratio distribution with x. The local
mass density distribution in the system (to 3
values define the raw or unsmoothed
two-stepped local mass-to-light ratio distribution with x. The local
mass density distribution in the system (to 3![]() )
is judged by
scaling the luminosity density profile by the raw M/L profile and
then smoothing the result by the prescribed smoothing routine (two
successive applications of a box filter of size corresponding to
)
is judged by
scaling the luminosity density profile by the raw M/L profile and
then smoothing the result by the prescribed smoothing routine (two
successive applications of a box filter of size corresponding to
![]() ).
).
The dependence of
![]() on
on
![]() is found to be
well approximated with an exponential decline that is described by
three free parameters, which are actually all functions of the model
characteristics, namely, n and
is found to be
well approximated with an exponential decline that is described by
three free parameters, which are actually all functions of the model
characteristics, namely, n and ![]() .
The dependence of these three
parameters on n and
.
The dependence of these three
parameters on n and ![]() are extracted from our model-based study
and analytical fits to these trends are presented. Such fits are noted
to be favourably represented by polynomials.
are extracted from our model-based study
and analytical fits to these trends are presented. Such fits are noted
to be favourably represented by polynomials.
The reliance of the band of the allowed values of
![]() on
on
![]() is also quantified as ranging from
is also quantified as ranging from ![]() to
to
![]() ,
where the form of the function
,
where the form of the function
![]() is also found to be polynomial
in nature.
is also found to be polynomial
in nature.
8.1 Deviation from predicted trends?
Even though the polynomial fits are found to do a good job for most
configurations, for certain models, the predictions appear incorrect
(by no more than 10![]() ), e.g.
), e.g. ![]() may be judged under-estimated for
n=8 and 9 for the configuration:
may be judged under-estimated for
n=8 and 9 for the configuration:
![]() pc. However, this should
be interpreted as erroneous recording of
pc. However, this should
be interpreted as erroneous recording of
![]() for these
for these
![]() values from our models, rather than a failure of our
predictions. Typically, such errors emanate from lack of refinement
in the step-sizes used in our work and is potentially amendable.
values from our models, rather than a failure of our
predictions. Typically, such errors emanate from lack of refinement
in the step-sizes used in our work and is potentially amendable.
8.2 Applicable to
As delineated in Sect. 3, the formalism that we
advance here, is applicable only to galaxies with Sersic indices ![]() .
It is only for such systems that the luminosity density
profile is steep enough, i.e. falls quickly enough to ensure that in
the ``outer'' parts of the system the luminous matter density is
completely overwhelmed by the dark matter density, so that the total
matter density is effectively a representation of the dark matter
distribution. Thus, changes in the central M/L or
.
It is only for such systems that the luminosity density
profile is steep enough, i.e. falls quickly enough to ensure that in
the ``outer'' parts of the system the luminous matter density is
completely overwhelmed by the dark matter density, so that the total
matter density is effectively a representation of the dark matter
distribution. Thus, changes in the central M/L or ![]() do not
affect the M/L in these ``outer'' parts. Now, to qualify ``outer'',
we state that this region corresponds to
do not
affect the M/L in these ``outer'' parts. Now, to qualify ``outer'',
we state that this region corresponds to
![]() .
This is anyway
true, only if the luminous matter fraction is not too small, in which
case, we need to settle for progressively lower M/L in the outer
parts, as
.
This is anyway
true, only if the luminous matter fraction is not too small, in which
case, we need to settle for progressively lower M/L in the outer
parts, as ![]() increases.
increases.
8.2.1 Effect of lowering Sersic Index
If however, the luminous density profile is too flat, (as for n <
3), the contribution of the luminous matter, to the total mass, is
significant, even in ``outer'' parts. In order to achieve similarly
shaped total mass profiles, the value of
![]() will need to
increase with increasing
will need to
increase with increasing ![]() .
Then, the exponential fall-off of
.
Then, the exponential fall-off of
![]() with
with
![]() will not be noted. Qualitatively
speaking, this is the reason why our formalism will not be valid for
galaxies with Sersic indices less than 3.
will not be noted. Qualitatively
speaking, this is the reason why our formalism will not be valid for
galaxies with Sersic indices less than 3.
8.2.2 Effect of increasing size
However, this increased flattening of the luminosity density profile can be attained even for- n=3 and
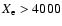 pc;
pc;
- n=4 and
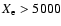 pc;
pc;
- n <3.
![\begin{figure}
\par\mbox{\includegraphics[height=7cm]{9965.fig11.ps} \includegraphics[height=7cm]{9965.fig12.ps} }\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg167.gif) |
Figure 10:
The left panel depicts the relation between
|
| Open with DEXTER | |
8.2.3 What the ranges mean
However, it is important to keep in mind that these ranges have been
ascertained on the basis of a discretised scanning of the parameters
n and ![]() ,
of our two-parameter galaxy models. Thus, when we say
that models with n<3 cannot be explained with the predicted
relationships between
,
of our two-parameter galaxy models. Thus, when we say
that models with n<3 cannot be explained with the predicted
relationships between
![]() ,
what
we really mean is that our experiments with a model with n=2indicated failure of adherence to these predicted trends. It is very
much possible that a model with an intermediate Sersic index can be
explained by our predictions, such as a galaxy with n=2.3, say. In
other words, the ranges of n and
,
what
we really mean is that our experiments with a model with n=2indicated failure of adherence to these predicted trends. It is very
much possible that a model with an intermediate Sersic index can be
explained by our predictions, such as a galaxy with n=2.3, say. In
other words, the ranges of n and ![]() described above owes, to our
dealing only with models ascribed the aforementioned discrete values
(values mentioned in Sect. 3). Consequently, the
ranges listed above are a conservative interpretation.
described above owes, to our
dealing only with models ascribed the aforementioned discrete values
(values mentioned in Sect. 3). Consequently, the
ranges listed above are a conservative interpretation.
The practical question to ask is, are these suggested ranges
compatible with real galaxies? As itemised in
Sect. 3, our choice is supported by the trends
observed for the Virgo cluster, within the ACS Virgo Cluster Survey,
in alliance with the predicted evolution towards greater
compactness in high-redshift systems (Ferreras et al. 2009). Furthermore,
keeping in mind that a waveband dependence of effective radius exists,
our model ![]() values in the z-band fall within limits indicated by
observations (Trujillo et al. 2001; La Barbera et al. 2005; Ferrarese et al. 2006).
values in the z-band fall within limits indicated by
observations (Trujillo et al. 2001; La Barbera et al. 2005; Ferrarese et al. 2006).
Additionally, we question the relevance of the upper limits on the effective radii at n=3 and 4, which are smaller than the range permitted for higher values of n. As far as the correlation between the shape parameter n and log of effective radius is concerned, it is well known that in general, half-light radius decreases with decreasing n (Trujillo et al. 2001; Boselli et al. 2008; Côté et al. 2008; Brown et al. 2003; Naab & Trujillo 2006). In fact, such a correlation is physical and is hinted at by the global relations between structural parameters; it is not merely a reflection of the fitting procedure (Trujillo et al. 2001).
8.2.4 Effect of model dark matter distribution
Of course, it could be perceived that such fate of the mass
distribution at
![]() would be dictated by the exact details of
the underlying dark matter distribution that defines the model
galaxy. Indeed, for the high values of n, the M/L at
would be dictated by the exact details of
the underlying dark matter distribution that defines the model
galaxy. Indeed, for the high values of n, the M/L at
![]() (
(
![]() )
is dictated by the details of the dark matter
distribution, but it is the smoothing of this raw M/L profile
that gives us the end product, namely the total local M/L ratio
profile of the galaxy upto the benchmark x of
)
is dictated by the details of the dark matter
distribution, but it is the smoothing of this raw M/L profile
that gives us the end product, namely the total local M/L ratio
profile of the galaxy upto the benchmark x of
![]() .
It is
precisely this smoothing procedure that brings into the final M/Lstructure, elements of the mass distribution in the inner
.
It is
precisely this smoothing procedure that brings into the final M/Lstructure, elements of the mass distribution in the inner
![]() in
the galaxy, as well as a relatively less significant signature of the
same that lies outside the radius upto which the distribution is
sought. The difference that smoothing makes to the raw M/L profile,
as distinguished from the final M/L profile, is clear in
Fig. 6.
in
the galaxy, as well as a relatively less significant signature of the
same that lies outside the radius upto which the distribution is
sought. The difference that smoothing makes to the raw M/L profile,
as distinguished from the final M/L profile, is clear in
Fig. 6.
Thus, given such (1) implementation of our smoothing procedure and
that (2) the jump radius in the raw M/L profile is itself
![]() ,
we
find that our experiments bear the fact that changing the mass scale
and length scale of the used NFW dark matter density distribution
across the wide ranges do not affect the mass
configuration for
,
we
find that our experiments bear the fact that changing the mass scale
and length scale of the used NFW dark matter density distribution
across the wide ranges do not affect the mass
configuration for
![]() ,
though further out in the galaxy, the
influence of changing the DM density distribution picks up
quickly. The consistency in the
,
though further out in the galaxy, the
influence of changing the DM density distribution picks up
quickly. The consistency in the
![]() relation, noted with changes in
relation, noted with changes in ![]() and
and ![]() is brought out in the
left panel of Fig. 10. The allowed ranges in
is brought out in the
left panel of Fig. 10. The allowed ranges in ![]() and
and
![]() are provided in the right panel of Fig. 10.
are provided in the right panel of Fig. 10.
8.2.5 Why choose NFW?
The modelling of the dark matter distribution in early type galaxies is obviously indirect and consequently difficult and unreliable. Ferreras et al. (2008) suggest a large scatter in the outer slope of the dark matter distributions that they recover for their targeted galaxies. Gavazzi et al. (2007) corroborate an NFW modelling of the dark haloes of their sample galaxies, suggesting that the total matter density tends to an overall isothermal form. Given this degree of uncertainty, it might be argued that there is not much sense in splitting hair to decide between an NFW and isothermal dark matter distributions, as long as the dark haloes that we probe in our analysis are compatible with observations or simulations.
This is indeed the case, when we compare our ranges of halo
characteristics (right panel of Fig. 10) to the suggestion
by Kleinheinrich et al. (2006) that the recovered range of virial masses of their
NFW model to be
![]()
![]() .
Such a mass range is compatible with the suggestion by Hoekstra et al. (2004) for a fiduciary galaxy of luminosity
LB=1010
.
Such a mass range is compatible with the suggestion by Hoekstra et al. (2004) for a fiduciary galaxy of luminosity
LB=1010
![]() that has an NFW profile (
that has an NFW profile (
![]() ,
as indicated by Fig. 4 in Hoekstra et al. 2004).
This mass range corresponds to a range of about 8 kpc to about 30 kpc
for
,
as indicated by Fig. 4 in Hoekstra et al. 2004).
This mass range corresponds to a range of about 8 kpc to about 30 kpc
for ![]() .
In fact, we cover these ranges in the runs, the results of
which are presented in Fig. 10, and also scan haloes of
lower masses. For various haloes defined within the red and black
quadrilaterals in Fig. 10, compatible
.
In fact, we cover these ranges in the runs, the results of
which are presented in Fig. 10, and also scan haloes of
lower masses. For various haloes defined within the red and black
quadrilaterals in Fig. 10, compatible
![]() relations were recovered.
relations were recovered.
This explains our choice of sticking with the NFW prescription for our
dark halo model. For reasons similar to what we explain above, we
suggest that upon smoothing, haloes of varying shapes but similar
masses within 3![]() are not expected to affect the mass distribution
within 3
are not expected to affect the mass distribution
within 3![]() in the massive ellipticals that we deal with in this
formalism.
in the massive ellipticals that we deal with in this
formalism.
Thus, we see that our methodology is valid, irrespective of selecting
haloes defined by widely different ![]() and
and ![]() values, (i.e. NFW
haloes defined by points inside the black and red quadrilaterals in
Fig. 10). This motivates us to choose to work with a
smaller subset of all the haloes explored in these runs; in particular,
we choose to work with haloes defined by the more massive half of the
values, (i.e. NFW
haloes defined by points inside the black and red quadrilaterals in
Fig. 10). This motivates us to choose to work with a
smaller subset of all the haloes explored in these runs; in particular,
we choose to work with haloes defined by the more massive half of the
![]() range that limits the red quadrilateral. This chosen
subset in the
range that limits the red quadrilateral. This chosen
subset in the
![]() space is bound by the green quadrilateral in
Fig. 10.
space is bound by the green quadrilateral in
Fig. 10.
8.2.6 Effect of model geometry
In addition to details of the DM distribution, we admit that the model structure does include the free parameters that describe the Sersic model of density distributions in general triaxial galaxies, as it ideally should, though this work has full potential of being extended into two-dimensions and include an axisymmetric description of the galaxy. Now, the triaxiality of the models needs to be defined in terms of a chosen geometry and intrinsic eccentricities - it is of course not possible to constrain such characteristics from observations alone.
In our models, these were fixed as oblateness with an axial ratio of 0.7. It is indeed possible that the unknown functions f and g that we attempt to constrain, harbour dependence on these intrinsic geometric factors. However, the preparatory assumptions involved in the deprojection of an observed brightness distribution, namely the underpinning of intrinsic geometry and viewing angle, are essentially unconstrained, unless the system is favourably inclined or flattened. In other words, the unknown in our modelling are the usual quantities that render deprojection non-unique.
As for the specification of the ellipticity in our models, a typical value has been adopted - Padilla & Strauss (2008) suggest an axial ratio distribution for a large sample of SDSS ellipticals, with a mode in the range of 0.6 to 0.8. Inspired by this, we use an axial ratio of 0.7 in our models. Again, the uncertainty in intrinsic ellipticity, cannot be known for a general observed galaxy. The quantification of the deprojection effects on the formulae provided above is possible, at least in a statistical sense, and it is envisaged that the same will be pursued in the future.
8.3 What if central super massive black holes?
The case of a central mass condensation in the system was dealt with in Paper I, in reference to the example of the galaxy M 87 - the recovered mass distribution of M 87 was demonstrated to be consistent with the same obtained from kinematical considerations. If independent measurements indicate an observed system to harbour a massive central mass condensation, then the scheme delineated in Paper I will be followed.
8.4 Why X instead of R
instead of R ?
?
The usage of ![]() instead of
instead of ![]() is preferred since
is preferred since ![]() as per
its definition here, as well as in Paper I, is derived solely from the
inputs to the methodology, namely the surface brightness profile along
the semi-major axis which we consider to be along the
as per
its definition here, as well as in Paper I, is derived solely from the
inputs to the methodology, namely the surface brightness profile along
the semi-major axis which we consider to be along the
![]() -axis. Thus, any changes to the shape of the brightness profile
will be directly reflected in a linear change in
-axis. Thus, any changes to the shape of the brightness profile
will be directly reflected in a linear change in ![]() but not
necessarily so in the half-light radius that is estimated from
isophotal analysis. In fact, here we use the same definition for
but not
necessarily so in the half-light radius that is estimated from
isophotal analysis. In fact, here we use the same definition for ![]() as in Paper I, (see Sect. 2).
as in Paper I, (see Sect. 2).
The usage of ![]() should not be cause for concern since
should not be cause for concern since ![]() is
merely one definition of the semi-major axis effective
radius and reduces to the conventional definition of the major-axis
effective radius for n=4
is
merely one definition of the semi-major axis effective
radius and reduces to the conventional definition of the major-axis
effective radius for n=4![]() . When an unknown
galaxy is being analysed within this formalism, its half-light radius
is just as much an unknown as is the
. When an unknown
galaxy is being analysed within this formalism, its half-light radius
is just as much an unknown as is the ![]() that we define here. Thus,
there is no loss of connection with observations by the implementation
of
that we define here. Thus,
there is no loss of connection with observations by the implementation
of ![]() .
.
8.5 Effect of choice of smoothing prescription
It merits mention that other choices for the smoothing
prescription and
![]() may also work, but here we concentrate on
the above mentioned configuration and the specification of
may also work, but here we concentrate on
the above mentioned configuration and the specification of
![]() and
and
![]() are accordingly unique to these
choices.
are accordingly unique to these
choices.
8.6 Effect of choice of estimation of central local M/L
In a similar context, it may be argued that the definition of ![]() that we use herein will leave an imprint. We equate
that we use herein will leave an imprint. We equate ![]() to the
central local M/L, inspired by this result that is achieved in
Paper I. Here the total gravitational mass found enclosed within the
radius x0 is M(x0) where M(x0) is linked to the 3-D velocity
dispersion at x0 via:
to the
central local M/L, inspired by this result that is achieved in
Paper I. Here the total gravitational mass found enclosed within the
radius x0 is M(x0) where M(x0) is linked to the 3-D velocity
dispersion at x0 via:
![]() .
Then, according
to our definition,
.
Then, according
to our definition, ![]() is given as the ratio of M(x0) and the
enclosed light within x0. For other definitions of
is given as the ratio of M(x0) and the
enclosed light within x0. For other definitions of ![]() ,
other ranges of
,
other ranges of
![]() will be valid (and therefore other
forms of dependences of
will be valid (and therefore other
forms of dependences of
![]() on
on
![]() ,
for the
same galaxy). Thus, the pairs of f and g functions that we advance
here, work for the used choice of the definition.
,
for the
same galaxy). Thus, the pairs of f and g functions that we advance
here, work for the used choice of the definition.
We would like to emphasise that the extraction of the exact value of
the mass enclosed within x0 (and therefore of ![]() ), from a
measurement of
), from a
measurement of ![]() , is not the point of this exercise;
uncertainties in this extraction do not undermine the advanced results
either, as long as the galaxy at hand is ``not too'' aspherical or
anisotropic at x0. Here we qualify ``not too'' as those
configurations for which we obtain consistent mass profiles using the
two extreme values of
, is not the point of this exercise;
uncertainties in this extraction do not undermine the advanced results
either, as long as the galaxy at hand is ``not too'' aspherical or
anisotropic at x0. Here we qualify ``not too'' as those
configurations for which we obtain consistent mass profiles using the
two extreme values of
![]() ,
that are allowed for the
extracted value of
,
that are allowed for the
extracted value of ![]() .
Thus, when the method fails, we know that
it does. As long as this aforementioned consistency is noted, choosing
.
Thus, when the method fails, we know that
it does. As long as this aforementioned consistency is noted, choosing
![]() from anywhere within the range corresponding to the
given
from anywhere within the range corresponding to the
given ![]() will lead to consistent total mass distributions within
3
will lead to consistent total mass distributions within
3![]() .
Additionally, this range is neither too constricted nor too
relaxed, as was discussed in Paper I.
.
Additionally, this range is neither too constricted nor too
relaxed, as was discussed in Paper I.
8.7 Comparatively better applicability
The presented device is based upon conclusions that are drawn from a
sample of model Sersic galaxies. This would naturally imply that the
success of this formalism is crucially dependant on the generality of
the models. In particular, we have discussed the ranges of n and
![]() for which our advanced results are true. We have also discussed
the effect of changing properties of the dark halo that we use in the
models and find the advanced scheme robust to such model parameter
variations.
for which our advanced results are true. We have also discussed
the effect of changing properties of the dark halo that we use in the
models and find the advanced scheme robust to such model parameter
variations.
In fact, the formalism presented above is unique in its scope and structure. Estimates of total mass distributions in distant elliptical systems are difficult and therefore rare; the formulae presented herein are therefore advantageous and could be treated as guides to decipher the total mass distribution of Sersic galaxies in large surveys.
Most importantly, the advanced methodology is successful within a severely constricted data domain, compared to any other scheme that aims to obtain mass distributions in elliptical galaxies. All that the advanced method demands in terms of data is what is typically available - surface brightness profile and a measure of central velocity dispersion. The undemanding nature of our method renders it applicable even at high redshifts. The simplicity of implementation of the input data is advantageous in that it allows for the scheme to be used in an automated way, to obtain mass distributions for large samples of galaxies. Tricks such as this and Nipoti et al. (2008) exploit the basic configuration within galaxies and offer novel ways for characterisation of distant systems.
Acknowledgements
D.C. is funded by a Royal Society Dorothy Hodgkin Fellowship. B.J. acknowledges the support of a University of Nottingham Summer Studentship. We thank Sebastian Foucaud for useful discussions that helped enrich the paper.
References
- Bolton, A. S., Treu, T., Koopmans, L. V. E., et al. 2008, ApJ, 684, 248 [NASA ADS] [CrossRef]
- Boselli, A., Boissier, S., Cortese, L., & Gavazzi, G. 2008, A&A, 489, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
- Brown, R. J. N., Forbes, D. A., Silva, D., et al. 2003, MNRAS, 341, 747 [NASA ADS] [CrossRef]
- Buitrago, F., Trujillo, I., Conselice, C. J., et al. 2008, ApJ, 687, L61 [NASA ADS] [CrossRef] (In the text)
- Capaccioli, M., Held, E. V., Lorenz, H., & Vietri, M. 1990, AJ, 99, 1813 [NASA ADS] [CrossRef] (In the text)
- Cappellari, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] (In the text)
- Chakrabarty, D., & Ferrarese, L. 2008, International Journal of Modern Physics D, as part of Proceedings for the 6th International Workshop on Data An alysis in Astronomy, Modelling and Simulations in Science, 17, 2 (In the text)
- Chakrabarty, D. 2007, MNRAS, 377, 30 [NASA ADS] [CrossRef] (In the text)
- Chakrabarty, D., & Portegies Zwart, S. 2004, ApJ, 128, 1046 [NASA ADS]
- Chakrabarty, D., & Saha, P. 2001, AJ, 557, 292 [CrossRef] (In the text)
- Churazov, E., Forman, W., Vikhlinin, A., et al. 2008, MNRAS, 388, 1062 [NASA ADS] [CrossRef]
- Côté, P., et al. 2008, IAU Symp., 245, 395 [NASA ADS]
- Czoske, O., Barnabè, M., Koopmans, L. V. E., Treu, T., & Bolton, A. S. 2008, MNRAS, 384, 987 [NASA ADS] [CrossRef]
- de Lorenzi, F., Gerhard, O., Saglia, R. P., et al. 2008, MNRAS, 385, 1729 [NASA ADS] [CrossRef]
- de Lorenzi, F., Debattista, V. P., Gerhard, O., & Sambhus, N. 2007, MNRAS, 376, 71 [NASA ADS] [CrossRef] (In the text)
- Diehl, S., & Statler, T. S. 2007, ApJ, 668, 150 [NASA ADS] [CrossRef]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef]
- Ferrarese, L., Côté, P., Blakeslee, J. P., et al. 2006, [arXiv:astro-ph/0612139] (In the text)
- Ferreras, I., Lisker, T., Pasquali, A., Khochfar, S., & Kaviraj, S. 2009, [arXiv:0901.4555] (In the text)
- Ferreras, I., Saha, P., Williams, L. L. R., & Burles, S. 2008, IAU Symp., 244, 206 [NASA ADS] (In the text)
- Mahdavi, A., Hoekstra, H., Babul, A., & Henry, J. P. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef]
- Fukazawa, Y., Botoya-Nonesa, J. G., Pu, J., Ohto, A., & Kawano, N. 2006, ApJ, 636, 698 [NASA ADS] [CrossRef]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef]
- Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] (In the text)
- Humphrey, P. J., Buote, D. A., Brighenti, F., Gebhardt, K., & Mathews, W. G. 2008, ApJ, 683, 161 [NASA ADS] [CrossRef]
- Kleinheinrich, M., et al. 2006, A&A, 455, 441 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ko, J., & Im, M. 2005, J. Korean Astronomical Society, 38, 149 [NASA ADS]
- Koopmans, L. V. E., & Treu, T. 2003, ApJ, 583, 606 [NASA ADS] [CrossRef]
- La Barbera, F., Covone, G., Busarello, G., et al. 2005, MNRAS, 358, 1116 [NASA ADS] [CrossRef]
- Lemze, D., Barkana, R., Broadhurst, T. J., & Rephaeli, Y. 2008, MNRAS, 386, 1092 [NASA ADS] [CrossRef]
- Lima Neto, G. B., Gerbal, D., & Márquez, I. 1999, MNRAS, 309, 481 [NASA ADS] [CrossRef]
- Mazure, A., & Capelato, H. V. 2002, A&A, 383, 384 [NASA ADS] [CrossRef] [EDP Sciences]
- Naab, T., & Trujillo, I. 2006, MNRAS, 369, 625 [NASA ADS] [CrossRef]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2008,[arXiv:0810.1291] (In the text)
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] (In the text)
- Nipoti, C., Treu, T., & Bolton, A. S. 2008, MNRAS, 390, 349 [NASA ADS] [CrossRef] (In the text)
- O'Sullivan, E., & Ponman, T. J. 2004, MNRAS, 354, 935 [NASA ADS] [CrossRef]
- Padilla, N. D., & Strauss, M. A. 2008, MNRAS, 388, 1321 [NASA ADS] (In the text)
- Padmanabhan, N., Seljak, U., Strauss, M. A., et al. 2004, New Astron., 9, 329 [NASA ADS] [CrossRef] (In the text)
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Prugniel, P., & Simien, F. 1997, A&A, 321, 111 [NASA ADS]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2004, Science, 301, 1696 [NASA ADS] [CrossRef] (In the text)
- Sersic, J. L. 1968, Cordoba, Argentina: Observatorio Astronomico (In the text)
- Statler, T. S., & Smecker-Hane, T. 1999, AJ, 117, 839 [NASA ADS] [CrossRef] (In the text)
- Temi, P., Brighenti, F., & Mathews, W. G. 2008, ApJ, 672, 244 [NASA ADS] [CrossRef]
- Terzic, B., & Graham, A. W. 2005, MNRAS, 362, 197 [NASA ADS] [CrossRef]
- Terzic, B., & Sprague, B. J. 2007, MNRAS, 377, 855 [NASA ADS] [CrossRef] (In the text)
- Trujillo, I., Asensio Ramos, A., Rubiño-Martín, J. A., et al. 2002, MNRAS, 333, 510 [NASA ADS] [CrossRef] (In the text)
- Trujillo, I., Graham, A. W., & Caon, N. 2001, MNRAS, 326, 869 [NASA ADS] [CrossRef]
- Zhang, Z., Xu, H., Wang, Y., et al. 2007, ApJ, 656, 805 [NASA ADS] [CrossRef]
Footnotes
- ...=4
![[*]](/icons/foot_motif.gif)
- Semi-major axis effective radius has been used before, for example by Naab & Trujillo (2006).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9965.fig1.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg30.gif) |
Figure 1:
Schematic view of a raw M/L distribution
along the major axis coordinate x, for a model galaxy. The dashed
line marks the position of the jump radius
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{9965.fig2.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg58.gif) |
Figure 2:
Right panel: trends in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9965.fig3.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg92.gif) |
Figure 3:
The values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{9965.fig4.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg140.gif) |
Figure 4:
Trends in the three different parameters
that define the exponential fall-off of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9965.fig5.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg145.gif) |
Figure 5:
Figure to compare the predicted total mass density
distribution with x (in red) with the known (model) mass density
profile (in green), for the model described by n=3.5 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm]{9965.fig6.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg152.gif) |
Figure 6:
Figure to compare the final total
(local) M/L distribution with the initially chosen raw M/L profile
(in broken lines), for the test galaxy the total mass of which is
presented in Fig. 5. The final M/L is presented
within 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
{
$\begin{array}{c c}
\includegraphics[height=.3\textheight]{99...
... \includegraphics[height=.3\textheight]{9965.fig8.ps}\end{array}$ }
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg154.gif) |
Figure 7:
Comparison of model
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.9cm]{9965.fig9.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg155.gif) |
Figure 8:
The radial distribution of the recovered
total mass density is depicted in black, on the left. On this is
superimposed the mass density profile obtained by implementing the
kinematic information of a sample of planetary nebulae in NGC 3379
(the same sample as used by Douglas et al. 2007), in the Bayesian
algorithm CHASSIS (Chakrabarty 2009, communicated to AJ). The
quantity |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.9cm]{9965.fig10.ps}
\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg157.gif) |
Figure 9: Figure to bring out the results for the galaxy NGC 4494. The left panel depicts a projection of the luminosity density distribution that we estimate for the galaxy (in black), compared to the V-band surface brightness data (in red). The total gravitational mass distribution of the galaxy is represented in the middle panel while the mass-to-light ratio on the V-band is shown on the right. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[height=7cm]{9965.fig11.ps} \includegraphics[height=7cm]{9965.fig12.ps} }\end{figure}](/articles/aa/full_html/2009/17/aa09965-08/Timg167.gif) |
Figure 10:
The left panel depicts the relation between
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.