| Issue |
A&A
Volume 498, Number 1, April IV 2009
|
|
|---|---|---|
| Page(s) | 127 - 138 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/20079063 | |
| Published online | 05 March 2009 | |
The dust condensation sequence in red supergiant stars
T. Verhoelst1,2,![]() - N. Van der Zypen1 - S. Hony3 - L. Decin1,
- N. Van der Zypen1 - S. Hony3 - L. Decin1,![]() - J. Cami4 - K. Eriksson5
- J. Cami4 - K. Eriksson5
1 - Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
2 - University of Manchester, Jodrell Bank Centre for Astrophysics, Manchester M13 9PL, UK
3 - Laboratoire AIM, CEA/DSM - CNRS - Université Paris Diderot, DAPNIA/SAp, 91191 Gif-sur-Yvette, France
4 - Physics and Astronomy Dept, University of Western Ontario,
London ON N6A 3K7, Canada
5 - Institute for Astronomy and Space Physics, Box 515, 75120
Uppsala, Sweden
Received 13 November 2007 / Accepted 31 December 2008
Abstract
Context. Red supergiant (RSG) stars exhibit significant mass loss by means of a slow, dense wind. They are often considered to be the more massive counterparts of Asymptotic Giant Branch (AGB) stars. While AGB mass loss is related to their strong pulsations, the RSG are often only weakly variable. This raises the question of whether their wind-driving mechanism and the dust composition of the wind are the same.
Aims. We study the conditions at the base of the wind by determining the dust composition of a sample of RSG. The dust composition is assumed to be sensitive to the density, temperature, and acceleration at the base of the wind. We compare the derived dust composition with the composition measured in AGB star winds.
Methods. We compile a sample of 27 RSG infrared spectra (ISO-SWS) and supplement these with photometric measurements to derive the full spectral energy distribution (SED). These data are modelled using a dust radiative-transfer code, taking into account the optical properties of the relevant candidate materials to search for correlations between mass-loss rate, density at the inner edge of the dust shell, and stellar parameters.
Results. We find strong correlations between the dust composition, mass-loss rate, and the stellar luminosity, roughly in agreement with the theoretical dust condensation sequence. We identify the need for a continuous (near-)IR dust opacity and tentatively propose amorphous carbon, and we note significant differences with AGB star winds in terms of the presence of PAHs, absence of ``the'' 13 ![]() m band, and a lack of strong water bands.
m band, and a lack of strong water bands.
Conclusions. Dust condensation in RSG is found to experience a freeze-out process that is similar to that in AGB stars. Together with the positive effect of the stellar luminosity on the mass-loss rate, this suggests that radiation pressure on dust grains is an important ingredient in the driving mechanism. Still, differences with AGB stars are manifold and thus the winds of RSG should be studied individually in further detail.
Key words: techniques: spectroscopic - stars: atmospheres - circumstellar matter - supergiants - stars: mass-loss - dust, extinction
1 Introduction
As stars of initial mass
![]() evolve off the main sequence and reach the core helium-burning phase, they become red supergiant (RSG) stars, the largest and most luminous of all stars (for a review on massive star observation and evolution, see Massey 2003). By means of their stellar wind and eventually, when they end their life, in a supernova explosion, they enrich the ISM with heavy elements and large amounts of kinetic energy, possibly triggering new star formation (Herbst & Assousa 1977; Gehrz 1989). The dusty stellar winds of RSG not only influence their evolution, but also complicate the determination of general properties such as the effective temperature and surface gravity, e.g. in terms of reddening,
which appears to differ from that in the ISM (Massey et al. 2005).
evolve off the main sequence and reach the core helium-burning phase, they become red supergiant (RSG) stars, the largest and most luminous of all stars (for a review on massive star observation and evolution, see Massey 2003). By means of their stellar wind and eventually, when they end their life, in a supernova explosion, they enrich the ISM with heavy elements and large amounts of kinetic energy, possibly triggering new star formation (Herbst & Assousa 1977; Gehrz 1989). The dusty stellar winds of RSG not only influence their evolution, but also complicate the determination of general properties such as the effective temperature and surface gravity, e.g. in terms of reddening,
which appears to differ from that in the ISM (Massey et al. 2005).
Most RSG are irregular variables with smaller amplitudes and higher effective temperatures than AGB stars. Moreover, they often exhibit significant chromospheric activity. These properties imply that they differ intrinsically from their lower-mass counterparts in which strong pulsations and cool molecular layers are understood to be crucial ingredients of the mass-loss mechanism (Hoefner et al. 1998, and further updates). Convection, rotation and/or chromospheric activity may instead be found to play an important role. For example, Josselin & Plez (2007) identified a correlation between mass-loss rate and the strength of the photospheric turbulence.
While the mechanism responsible for the initial levitation of the atmosphere may therefore differ between RSG and AGB stars, both types of stars are often used together in studies of the dust-condensation sequence and wind-driving mechanism (e.g. Matsuura et al. 2005; Dijkstra et al. 2005). Nevertheless, Speck et al. (2000) found differences in the dust composition of RSG and AGB stars, the former often exhibiting Ca-Al-rich silicates instead of magnesium silicates.
Combining a dust condensation sequence, e.g. the one presented by Tielens (1990), with conditions in an expanding stellar wind, one expects a process called ``freeze-out'', in which the sequence is not halted at an intermediate product when the wind density drops below the density required for the next step. This freeze-out has been tentatively observed in AGB stars (e.g. Heras & Hony 2005). If the dust condensation and the wind dynamics are similar for the RSG, one may also expect to observe incomplete dust condensation. We test this hypothesis by the analysis of all ISO-SWS spectra of RSG.
Table 1: Object designations and general characteristics. Star with their names printed in italic have luminosities which also allow an AGB star identification. The bolometric magnitudes were computed from the dereddened K band magnitudes, using the bolometric corrections of Levesque et al. (2005).
In Sect. 2, we present the construction of the sample and its main characteristics. Section 3 describes the reduction of the ISO-SWS spectra. In the following section, we discuss the details of our modelling strategy, including the photosphere models, dust components, radiative-transfer method, and model-fitting strategy. In Sect. 5.1, we analyse an ``average'' RSG dust spectrum to check for any major shortcomings in our modelling approach. The results for all individual sample stars are then summarised in Sect. 5.2, and the trends and correlations between the derived parameters are presented. The discrepancies between the models and observed spectra are studied in Sect. 6. We end with a discussion and our conclusions (Sect. 8).
2 The sample
The availability of an ISO-SWS spectrum is an essential ingredient to our research aims. Our first step was therefore the selection of all stars with spectral types M and K and luminosity classes I and II from the list of usable 2.4-45 ![]() m ISO-SWS spectra presented by Sloan et al. (2003). From this list of 41 stars, we removed the RV Tauri star R Sct since it is a Post-AGB object. The spectra of XX Per, IRC +60370 and WX Cas display signs of technical anomalies
and are also removed from our list. Distances were derived from the HIPPARCOS parallax measurement (Perryman et al. 1997) or from the assumed distances to the clusters containing our program stars (Humphreys 1978). For IRC+40427, no reliable distance estimate es
available. We assumed that it is a typical 2 kpc, which may in fact be too nearby, since the observed reddening is far stronger than the combined effect of this distance and its circumstellar shell (see Sect. 5.2). Since the strong reddening may also be a consequence of a non-spherical distribution of the circumstellar dust, we refrained from deriving a distance from the observed reddening.
m ISO-SWS spectra presented by Sloan et al. (2003). From this list of 41 stars, we removed the RV Tauri star R Sct since it is a Post-AGB object. The spectra of XX Per, IRC +60370 and WX Cas display signs of technical anomalies
and are also removed from our list. Distances were derived from the HIPPARCOS parallax measurement (Perryman et al. 1997) or from the assumed distances to the clusters containing our program stars (Humphreys 1978). For IRC+40427, no reliable distance estimate es
available. We assumed that it is a typical 2 kpc, which may in fact be too nearby, since the observed reddening is far stronger than the combined effect of this distance and its circumstellar shell (see Sect. 5.2). Since the strong reddening may also be a consequence of a non-spherical distribution of the circumstellar dust, we refrained from deriving a distance from the observed reddening.
Effective temperatures and bolometric corrections were estimated from the spectral type based on the relations found by Levesque et al. (2005). Comparison with the evolutionary tracks of Lejeune & Schaerer (2001) revealed 24 bona fide red supergiants, and 3 strong candidates![]() . VY CMa is an RSG experiencing extreme mass loss, which produces an optically thick circumstellar environment (CSE). The detailed analysis required to derive reliable dust-composition parameters for VY CMa is beyond the scope of this paper, and we refer to Harwit et al. (2001) for a study of its ISO-SWS spectrum.
. VY CMa is an RSG experiencing extreme mass loss, which produces an optically thick circumstellar environment (CSE). The detailed analysis required to derive reliable dust-composition parameters for VY CMa is beyond the scope of this paper, and we refer to Harwit et al. (2001) for a study of its ISO-SWS spectrum.
We use these 26 stars in our study. Their designations and main characteristics are presented in Table 1. The overlap with the samples of Sylvester et al. (1994), Speck et al. (2000), and Levesque et al. (2005) is 8, 11, and 14 stars, respectively.
Kraemer et al. (2002) present a classification of, amongst others, our sample stars on the basis of their photospheric and dust characteristics. Most stars are in the 2.SEa, 2.SEb, or 2.SEc classes, implying that they exhibit strong dust features from both silicates and alumina, and molecular bands in the photospheric part of the spectrum.
3 The observations
The Infrared Space Observatory Short Wavelength Spectrometer
(ISO-SWS Kessler et al. 1996) observations were performed in the AOT1
observing mode, resulting in a low-resolution full grating scan,
except for S Per, which was observed at full instrumental resolution
in the AOT06 mode. The observations were then processed using the SWS
interactive analysis product, IA (see de Graauw et al. 1996) using
calibration files and procedures equivalent to pipeline version 10.1. Further data processing consisted of extensive poor data removal and rebinning to a fixed wavelength resolution
(![]() /
/
![]() )
grid. The poor data removal takes advantage of the large amount of redundancy in the available spectral scans to identify cosmic hits, sudden changes in dark-current and other artifacts that cause the signal of a single or multiple detectors to diverge from the mean of the other spectral scans. To combine the different subband into one continuous spectrum from 2 to
45
)
grid. The poor data removal takes advantage of the large amount of redundancy in the available spectral scans to identify cosmic hits, sudden changes in dark-current and other artifacts that cause the signal of a single or multiple detectors to diverge from the mean of the other spectral scans. To combine the different subband into one continuous spectrum from 2 to
45 ![]() m, we applied scaling factors and offsets. In general, the match between the different subbands was good and the applied scaling/offsets were small compared to the flux-calibration
uncertainties with a few exceptions: Alpha Her and NR Vul display far larger differences between the various subbands than expected on the basis of the flux-calibration uncertainties alone. This is most likely due to mispointed observations. For these two observations, we use the
IRAS point-source fluxes as a guideline for splicing the spectrum. The RMS noise increases with increasing wavelength, in particular at
m, we applied scaling factors and offsets. In general, the match between the different subbands was good and the applied scaling/offsets were small compared to the flux-calibration
uncertainties with a few exceptions: Alpha Her and NR Vul display far larger differences between the various subbands than expected on the basis of the flux-calibration uncertainties alone. This is most likely due to mispointed observations. For these two observations, we use the
IRAS point-source fluxes as a guideline for splicing the spectrum. The RMS noise increases with increasing wavelength, in particular at
![]() m. The flux levels of our sample stars decline with wavelength, in particular if there is little or no dust excess. This causes some of the longest wavelength sections of the spectra to be noise-dominated. The worst example is HD 14580, as can be seen in Fig. 2. The noise-dominated parts are not used in the analysis.
m. The flux levels of our sample stars decline with wavelength, in particular if there is little or no dust excess. This causes some of the longest wavelength sections of the spectra to be noise-dominated. The worst example is HD 14580, as can be seen in Fig. 2. The noise-dominated parts are not used in the analysis.
Table 2: Dust species used in this study with their commonly-used name, their size, shape and the source of the optical constants. The size distribution is that derived by Mathis et al. (1977) and the cross section are computed in the CDE (Continuous Distribution of Ellipsoids) approximation.
For a proper estimation of the photospheric irradiation and underlying continuum, we prefer constructing a spectral energy distribution (SED) covering wavelengths from the UV to the far-IR. Optical photometry was presented by Johnson et al. (1966a), Johnson et al. (1966b), Mendoza (1967), Lee (1970), Cousins & Lagerweij (1971), Humphreys & Ney (1974), Wawrukiewicz & Lee (1974), Nicolet (1978), and Kharchenko (2001). Near-IR photometry is available for all of our sources from the 2MASS catalogue (Skrutskie et al. 2006) and the far-IR side of the SED can be studied with the IRAS observations, which are available for all but seven of our sources (Neugebauer et al. 1984).
Using interstellar-extinction estimates from either the model by Arenou et al. (1992) or from the observed extinction towards early-type stars in the corresponding clusters, we dereddened the photometric and spectroscopic data with the law presented by Cardelli et al. (1989),
extended toward longer wavelengths with the local ISM curve of Chiar & Tielens (2006), and by assuming
![]() (Massey et al. 2005).
(Massey et al. 2005).
4 Modelling
The focus of this study is to derive accurate dust masses and compositions. Therefore, several aspects of the complex RSG atmospheres are not taken into account and the following simplifications are made when constructing the radiative-transfer models: (1) all calculations are done in 1D-spherical geometry, which implies that we neglect inhomogeneities; (2) we do not take the chromosphere into account; (3) we do not include any extra-photospheric molecular layers; and (4) we assume that the mass loss is constant.
4.1 Photospheres
The stellar photospheres are represented by MARCS (edition 1998) models (Gustafsson et al. 2008) since these are specifically developed for cool stars, with an emphasis on molecular opacities and the effects of extended atmospheres, which do not allow us to use a plane-parallel approximation. They were computed in spherical geometry with solar abundances, a surface gravity![]() of
of
![]() ,
a microturbulent velocity
,
a microturbulent velocity
![]() km s-1, and temperatures ranging from 3000 to 4500 K. The effective temperatures were derived from the spectral type following the relations of Levesque et al. (2005).
km s-1, and temperatures ranging from 3000 to 4500 K. The effective temperatures were derived from the spectral type following the relations of Levesque et al. (2005).
4.2 Dust radiative transfer
The dust shell is modelled using the proprietary spherical radiative-transfer code MODUST (Bouwman 2001; Bouwman et al. 2000). Under the constraint of radiative equilibrium, this code solves the monochromatic radiative-transfer equation from UV/optical to millimetre wavelengths using a Feautrier-type solution method (Mihalas 1978; Feautrier 1964). The code allows us to include several different dust components of various grain sizes and shapes, each with its own temperature distribution.
4.3 Dust composition
We searched the literature for relevant dust species to include in our
study. Speck et al. (2000) identified melilite, alumina and olivines![]() in the RSG in their sample, but they did not require a 13
in the RSG in their sample, but they did not require a 13 ![]() m-carrier candidate such as Spinel because they did not detect this feature in their RSG spectra and neither do we (see Sect. 6). In their sample of AGB stars Heras & Hony (2005) found those species used by Speck et al. (2000) and also Mg0.1Fe0.9O, which has a feature at 19.5
m-carrier candidate such as Spinel because they did not detect this feature in their RSG spectra and neither do we (see Sect. 6). In their sample of AGB stars Heras & Hony (2005) found those species used by Speck et al. (2000) and also Mg0.1Fe0.9O, which has a feature at 19.5 ![]() m, outside the wavelength band observed by Speck et al. (2000). Cami (2002) used olivines, alumina, spinel, and Mg0.1Fe0.9O. For a discussion of the need for melilite instead of an iron-magnesium silicate in RSG, we refer to Speck et al. (2000), who presented a category of RSG 10 micron spectra with a peak position significantly to the red of that of olivines. Moreover, they showed an excellent agreement with a predicted melilite emission spectrum.
m, outside the wavelength band observed by Speck et al. (2000). Cami (2002) used olivines, alumina, spinel, and Mg0.1Fe0.9O. For a discussion of the need for melilite instead of an iron-magnesium silicate in RSG, we refer to Speck et al. (2000), who presented a category of RSG 10 micron spectra with a peak position significantly to the red of that of olivines. Moreover, they showed an excellent agreement with a predicted melilite emission spectrum.
From a theoretical point of view, a dust-formation scenario usually begins with TiO2 seeds, onto which first simple oxides such as Al2O3 and MgFeO grow. If the density and temperature conditions are suitable, then also melilite, and both olivines and pyroxenes with iron contents can condense onto the grains. The full condensation scheme consists of quite a few more dust species (e.g. Anorthite and Plagioclase), but no spectral signatures of these dust types have so far been detected in RSG.
The dust species used in this study and their relevant characteristics are presented in Table 2. The optical constants are obtained from the AIU Jena database![]() .
.
The RSG in this sample appear to be pure outflow sources, i.e. there
are no indications that they may be binary systems with stable,
circumbinary, dust disks: as shown in Fig. 2, there is
no strong discrepancy between the reddening and the IR excess, nor is
there any sign of processed, crystalline grains such as those seen
around some Post-AGB objects (e.g. Gielen et al. 2008) or in
protoplanetary disks (e.g. van Boekel et al. 2005). This implies that
grain growth beyond 0.1 ![]() m is unlikely (see e.g. Woitke & Niccolini 2005; Gail & Sedlmayr 1999). The absorption cross-sections can therefore be calculated in the Rayleigh limit, and an underlying grain
size distribution is only required to derive the dust masses. We use
the size distribution derived by Mathis et al. (1977) and compute the
cross-section for the approximation of a Continuous Distribution of
Ellipsoids (CDE, Bohren & Huffman 1983), since we found this to provide
closer agreement with the observations than the Mie approximation. More sophisticated treatments of grain sizes and shapes now exist, such as a Distribution of Hollow Spheres (DHS), but within the Rayleigh limit, CDE works very well (Min et al. 2005). We must point out that according to Höfner (2008), relaxing the restriction to the small particle limit in the modelling of AGB winds leads to a possible grain growth to 1
m is unlikely (see e.g. Woitke & Niccolini 2005; Gail & Sedlmayr 1999). The absorption cross-sections can therefore be calculated in the Rayleigh limit, and an underlying grain
size distribution is only required to derive the dust masses. We use
the size distribution derived by Mathis et al. (1977) and compute the
cross-section for the approximation of a Continuous Distribution of
Ellipsoids (CDE, Bohren & Huffman 1983), since we found this to provide
closer agreement with the observations than the Mie approximation. More sophisticated treatments of grain sizes and shapes now exist, such as a Distribution of Hollow Spheres (DHS), but within the Rayleigh limit, CDE works very well (Min et al. 2005). We must point out that according to Höfner (2008), relaxing the restriction to the small particle limit in the modelling of AGB winds leads to a possible grain growth to 1 ![]() m, which may also assist in the radiative driving of the wind.
m, which may also assist in the radiative driving of the wind.
An overview of the spectral features of these different dust species is shown in Fig. 1. An in-depth discussion of this figure is presented in Sect. 5.1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig1.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg25.gif) |
Figure 1:
The average of all dereddened observed dust spectra, each
normalized with its photospheric flux at 3.5 |
| Open with DEXTER | |
4.4 The strategy
The unknown angular scale of the central star is determined by scaling
the model to the ISO-SWS spectrum between 3.5 and 4.5 ![]() m since
these wavelengths are relatively free of dust and molecular
emission/absorption. This method allows us to bypass the uncertain
absolute luminosity and distance. The geometrical properties of the
dust shell are proportional to the stellar radius and thus their
angular scale is also now fixed. In the assumption of a continuous
wind, the outer radius of the dust shell cannot be determined from the
current modelling since the outer regions of the wind are too cold to
contribute to the Mid-IR spectrum. We therefore fix its value at
5000
m since
these wavelengths are relatively free of dust and molecular
emission/absorption. This method allows us to bypass the uncertain
absolute luminosity and distance. The geometrical properties of the
dust shell are proportional to the stellar radius and thus their
angular scale is also now fixed. In the assumption of a continuous
wind, the outer radius of the dust shell cannot be determined from the
current modelling since the outer regions of the wind are too cold to
contribute to the Mid-IR spectrum. We therefore fix its value at
5000 ![]() .
.
The mass-loss rate does depend on the assumed distance and luminosity. The initial model grid (central star + dust shell) is calculated for a typical luminosity of 10
![]() .
This model mass-loss rate
.
This model mass-loss rate
![]() is converted to a true
is converted to a true ![]() using the distances presented in Sect. 2 and the angular scale derived from the fitting (see also Sect. 5.2). The outflow velocity and dust-to-gas ratio are assumed to be 10 km s-1 and 0.01 respectively, both typical values for RSG. We note that these are uncertain to a factor of at least 2.
using the distances presented in Sect. 2 and the angular scale derived from the fitting (see also Sect. 5.2). The outflow velocity and dust-to-gas ratio are assumed to be 10 km s-1 and 0.01 respectively, both typical values for RSG. We note that these are uncertain to a factor of at least 2.
The parameters to be determined from the individual fitting of the spectra are the inner radius,
![]() ,
the mass-loss rate,
,
the mass-loss rate,
![]() ,
and the relative abundances of the different dust
species.
,
and the relative abundances of the different dust
species.
We refrain from completing a formal minimisation while determining the optimum dust-shell parameters. We instead determine the best-fit model by visual inspection, following a robust strategy. The reasons for doing so are twofold. 1) It is our aim to achieve, at the same
time, a good fit to the SED and the detailed IR-spectrum. This is essential because the circumstellar reddening places a strong constraint on the inner shell radius, which in turn determines the relative contribution of the individual dust species to the observed
features by means of their different temperatures. It is almost impossible to devise a good weighting scheme providing equal importance to the ![]() 10 photometric points and the thousands of
spectral points in the SWS spectra. In particular, since the uncertainties in the data vary considerably throughout the sample, this would imply adapting the weighting on a per-source basis. The only way of judging whether such a complicated weighting scheme operates reliably is visual inspection; 2) There are some spectral regions that may be poorly reproduced by a (in our opinion) suitable model. This is due to the presence of components in the observed spectra which are missing from the model, such as extended molecular layers (also known as MOLspheres) or PAHs. These regions and there importance can again only be identified by visual inspection.
10 photometric points and the thousands of
spectral points in the SWS spectra. In particular, since the uncertainties in the data vary considerably throughout the sample, this would imply adapting the weighting on a per-source basis. The only way of judging whether such a complicated weighting scheme operates reliably is visual inspection; 2) There are some spectral regions that may be poorly reproduced by a (in our opinion) suitable model. This is due to the presence of components in the observed spectra which are missing from the model, such as extended molecular layers (also known as MOLspheres) or PAHs. These regions and there importance can again only be identified by visual inspection.
The core of our strategy is an iteration of the following sequence:
- we estimate the dust mass-loss rate from the full SED and the observed
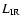 /
/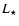
![[*]](/icons/foot_motif.gif) ;
;
- the relative abundances of melilite, olivine, and alumina are adjusted to reproduce the peak position of the 10
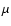 m feature, and the same is done for the 18
m feature, and the same is done for the 18 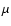 m feature peak position using olivine, melilite, and Mg0.1Fe0.9O;
m feature peak position using olivine, melilite, and Mg0.1Fe0.9O;
- when the peak positions of the features are well reproduced but not yet their strength, we vary the inner radius to adjust their relative strengths, and the mass-loss rate to alter the absolute emission levels. We also check that our model predicts the correct amount of circumstellar reddening.
5 Results
5.1 A continuum opacity source
In Fig. 1, we present an ``averaged'' RSG ISO-SWS spectrum, where each individual spectrum is dereddened with the appropriate value (final column in Table 1) and
normalized to the average flux between 3.5 and 4 ![]() m. We exclude RSG without significant mass loss. We also show models with envelopes containing only a single dust type.
m. We exclude RSG without significant mass loss. We also show models with envelopes containing only a single dust type.
It is striking to note in this figure that the observed excess appears to start already at 5 ![]() m, while the modelled dust features are all located beyond 8
m, while the modelled dust features are all located beyond 8 ![]() m. A related problem could be the slope of the photospheric (?) part of the modelled spectrum at 2.5-3
m. A related problem could be the slope of the photospheric (?) part of the modelled spectrum at 2.5-3 ![]() m.
m.
The excess around 6 ![]() m and the difference in slope around 3
m and the difference in slope around 3 ![]() m have been attributed to the presence of a MOLsphere, i.e. an extra-photospheric layer of molecular material
(e.g. Tsuji 2000), in which H2O especially would be the main source of excess emission and absorption. Individual lines of water in these MOLspheres have been detected (e.g. Jennings & Sada 1998) and the shells have been resolved by near and mid-IR interferometry (e.g. Ohnaka 2004; Perrin et al. 2005,2004). Verhoelst et al. (2006) argued that a purely molecular MOLsphere cannot explain the wavelength dependence of the opacity across the entire IR range in the case of RSG
m have been attributed to the presence of a MOLsphere, i.e. an extra-photospheric layer of molecular material
(e.g. Tsuji 2000), in which H2O especially would be the main source of excess emission and absorption. Individual lines of water in these MOLspheres have been detected (e.g. Jennings & Sada 1998) and the shells have been resolved by near and mid-IR interferometry (e.g. Ohnaka 2004; Perrin et al. 2005,2004). Verhoelst et al. (2006) argued that a purely molecular MOLsphere cannot explain the wavelength dependence of the opacity across the entire IR range in the case of RSG ![]() Ori, and they suggested alumina as additional mid-IR opacity source. However, this does not yet explain the observation made by Ryde et al. (2006) that water lines appear in absorption at 12
Ori, and they suggested alumina as additional mid-IR opacity source. However, this does not yet explain the observation made by Ryde et al. (2006) that water lines appear in absorption at 12 ![]() m in the spectra of
m in the spectra of ![]() Cep, while they are believed to generate an excess at 6
Cep, while they are believed to generate an excess at 6 ![]() m
m![]() in the same spectrum. Moreover, the excess around 6
in the same spectrum. Moreover, the excess around 6 ![]() m in the individual stars does not show any water lines in proportion to the excess with respect to the photospheric continuum.
m in the individual stars does not show any water lines in proportion to the excess with respect to the photospheric continuum.
Although extra-photospheric molecular material is clearly present, we propose that the peculiarities in the shape of the overall SED discussed here are due to a source of continuous opacity of a fairly cool temperature. Free-free emission from a chromosphere or ionised wind can be present in RSG (e.g. Harper et al. 2001), but since its source function has a temperature above that of the photosphere, it cannot explain the additional extinction towards the near-IR![]() . The colour temperature of the excess is therefore indicative of dust rather than free-free emission. We find that the inclusion of either metallic Fe, amorphous C, or micron-sized grains in the dust shell can explain the excess emission at 6
. The colour temperature of the excess is therefore indicative of dust rather than free-free emission. We find that the inclusion of either metallic Fe, amorphous C, or micron-sized grains in the dust shell can explain the excess emission at 6 ![]() m, the slope issue at 3
m, the slope issue at 3 ![]() m, and the additional extinction at near-IR wavelengths (see Sect. 5.2). The remaining residuals are due to molecular absorption, as expected from the presence of a cool MOLsphere.
m, and the additional extinction at near-IR wavelengths (see Sect. 5.2). The remaining residuals are due to molecular absorption, as expected from the presence of a cool MOLsphere.
The question of whether this missing dust species is metallic iron, micron-sized grains, or amorphous carbon, cannot be answered fully by the current analysis. The presence of metallic Fe in the CSE of VY CMa was postulated by Harwit et al. (2001) and is also used to explain the SEDs of OH/IR stars (Kemper et al. 2002). Moreover, metallic Fe is a product of the O-rich condensation sequence. Nevertheless, amorphous carbon is an equally interesting possibility, since it would be roughly 20 times as effective in accelerating the wind as Fe (see Table 1 in Woitke 2006). The occurence of pure carbon in an oxygen-rich CSE is plausible (Höfner & Andersen 2007), even more so in RSG where the chromospheric radiation field can be responsible for the dissociation of CO. For the amount of pure carbon required to explain the RSG spectra, we find that only of the order of 1% of the CO must be dissociated. This is well below the amountfound to be possible in theoretical models of M stars with chromospheres (Beck et al. 1992). More evidence for the presence of carbon that is not bound in CO, is the detection of PAH emission in four of our sources (Sect. 6.2.3). Papers discussing the possible presence of amorphous carbon in oxygen-rich outflows often dismiss the spectroscopic detection of its presence as impossible due to the lack of spectral features. Interestingly, we find here that, when studying the full SED, it is possible to detect continuous-opacity sources. Continuous opacity by micron-sized O-rich grains, playing a crucial role in the driving of the wind, has been proposed for AGB stars by Höfner (2008), but it is unclear whether this grain growth can also occur in RSG stars.
Table 3: The best fit model parameters.
Regardless of the origin of this continuum emission, it must be included in our modelling to ensure that reliable mass fractions are derived for the other dust species. We chose to include amorphous C, knowing that Fe would have a similar effect.
5.2 Models for all sample stars
Figures 2 and 3 present the observed SEDs and spectra, respectively, and the best-fit models, sorted by increasing dust luminosity or by decreasing photospheric temperature when no dust emission is present. The agreement is in general excellent. IRC +40427 appears to be far more reddened than our estimate of AV = 1.79, which suggests that it is located much further away than our default value of 2 kpc.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{9063fig2.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg39.gif) |
Figure 2:
The SEDs of all sample stars with their best-fit models (total spectrum in red dashes and non-reddened photospheric spectrum in bluedots). The photometric points are either the 7 Geneva filters or B and V in the Johnson system, J, H and Ks from 2mass and I12 and I25 from the IRAS mission. The dotted vertical line indicates 9.7 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{9063fig3.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg40.gif) |
Figure 3: The ISO-SWS spectra of all sample stars with their best-fit models (symbols and colours as in Fig. 2). |
| Open with DEXTER | |
The results for all 27 sample stars are summarized in Table 3. For 6 objects, the mass-loss rate is too low (
![]() yr-1) to enable a reliable determination of the dust composition. The distance- and luminosity-corrected mass-loss rate presented in Col. 9 is computed as
yr-1) to enable a reliable determination of the dust composition. The distance- and luminosity-corrected mass-loss rate presented in Col. 9 is computed as
![]() A (d/1 kpc)2, where
A (d/1 kpc)2, where
![]() is the mass-loss rate for an assumed luminosity of 10
is the mass-loss rate for an assumed luminosity of 10
![]() (the default value in our model grid), A is the scaling factor used to match the observed flux around 4
(the default value in our model grid), A is the scaling factor used to match the observed flux around 4 ![]() m, and d is the distance.
m, and d is the distance.
6 Analysis of the residuals
A general problem, especially for the higher mass-loss stars, is the
overprediction of the near-IR photometry. This corresponds to the need
for an extinction law of a higher RV. The dust already includes a
component with grey extinction properties (see Sect. 5.1),
but in our models it is located too far away from the central star to
provide sufficient extinction. Our model assumes the same inner radius
for all dust species, but the discrepancy observed here may indicate
that the continuous opacity source is located even closer to the base
of the wind, right above the photosphere. The detection of alumina
0.5 ![]() above the photosphere of Betelgeuse (Perrin et al. 2007; Verhoelst et al. 2006) indicates that dust condensation so close to the photosphere is possible.
above the photosphere of Betelgeuse (Perrin et al. 2007; Verhoelst et al. 2006) indicates that dust condensation so close to the photosphere is possible.
6.1 Molecular bands
The ISO spectra up to 8 ![]() m are dominated by photospheric and
possibly continuum dust emission. The observed spectral features
should therefore be mainly photospheric, molecular, absorption
bands. To search for evidence of the MOLsphere(s) discussed in
Sect. 5.1 or for shortcomings in our model atmospheres, we
compare the average normalized
m are dominated by photospheric and
possibly continuum dust emission. The observed spectral features
should therefore be mainly photospheric, molecular, absorption
bands. To search for evidence of the MOLsphere(s) discussed in
Sect. 5.1 or for shortcomings in our model atmospheres, we
compare the average normalized![]() residuals with
simulated molecular absorption bands in
Fig. 4. Although our models clearly reproduce the
observed spectra very well (most of the residuals do not reach a 5%
level), we detect strong additional absorption by CO and maybe also
some water and OH. The presence of the last two constituents can
probably be explained after some detailed fine tuning of the
atmosphere models. Cool CO also appears to be very abundant above the
photosphere, which is in line with a postulated crucial role in the
wind-driving mechanism. The fact that no massive MOLspheres containing
water are observed clearly sets the RSG apart from the AGB stars. This
finding supports our assumption (Sect. 5.1) that the excess
at 6
residuals with
simulated molecular absorption bands in
Fig. 4. Although our models clearly reproduce the
observed spectra very well (most of the residuals do not reach a 5%
level), we detect strong additional absorption by CO and maybe also
some water and OH. The presence of the last two constituents can
probably be explained after some detailed fine tuning of the
atmosphere models. Cool CO also appears to be very abundant above the
photosphere, which is in line with a postulated crucial role in the
wind-driving mechanism. The fact that no massive MOLspheres containing
water are observed clearly sets the RSG apart from the AGB stars. This
finding supports our assumption (Sect. 5.1) that the excess
at 6 ![]() m and the precise value of the spectral slope at
3.5
m and the precise value of the spectral slope at
3.5 ![]() m are due to some continuum emission source and not an
extra-photospheric water column.
m are due to some continuum emission source and not an
extra-photospheric water column.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig4.ps}\\ [4mm]
\includegraphics[width=8cm,clip]{9063fig5.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg44.gif) |
Figure 4: Upper panel: the average normalized residuals in the blue part of the ISO-SWS spectrum together with simulated molecular absorption bands. For more details on the computation of the molecular templates we refer to Cami (2002). Lower panel: the wavelength range of the residuals (black solid line) which is dust dominated. |
| Open with DEXTER | |
6.2 Residual dust features
The lower panel of Fig. 4 shows the average
residuals in the dust-dominated part of the spectrum. Many
discrepancies are clear: (1) a strong absorption band starting at
8 ![]() m and possibly extending to 12
m and possibly extending to 12 ![]() m, if we interpret the
emission bump at 9.7
m, if we interpret the
emission bump at 9.7 ![]() m as an underestimated olivine-dust
fraction; (2) a broad 13
m as an underestimated olivine-dust
fraction; (2) a broad 13 ![]() m feature; and (3) a broad, emission
feature at 18
m feature; and (3) a broad, emission
feature at 18 ![]() m. Concerning the first problem, a significant
SiO layer just above the photosphere, which deepens the absorption
band, could be present since such a layer is detected around
m. Concerning the first problem, a significant
SiO layer just above the photosphere, which deepens the absorption
band, could be present since such a layer is detected around
![]() Ori with MIDI interferometry by Perrin et al. (2007), although
the SiO bandhead does not correspond well to the observed residuals
around 8
Ori with MIDI interferometry by Perrin et al. (2007), although
the SiO bandhead does not correspond well to the observed residuals
around 8 ![]() m. The current dust model may also not yet contain the
correct silicate dust composition, shape, and grain size.
m. The current dust model may also not yet contain the
correct silicate dust composition, shape, and grain size.
6.2.1 A 13 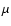 m feature?
m feature?
In their analysis, Speck et al. (2000) found that RSG usually do not
display the 13 ![]() m feature observed in AGB stars. After model
subtraction, we find in general a feature around 13
m feature observed in AGB stars. After model
subtraction, we find in general a feature around 13 ![]() m, although
it is much broader than that seen in the lower-mass counterparts. Only
a few selected targets exhibit the AGB-like 13
m, although
it is much broader than that seen in the lower-mass counterparts. Only
a few selected targets exhibit the AGB-like 13 ![]() m feature, but
these stars (SU Per and S Per) may differ in other respects as well: S Per is the only target in our sample exhibiting strong water bands,
and Speck et al. (2000) suggested that it is more similar to lower-mass
semi-regulars. The broad excess in the residual spectrum cannot be
isolated in any of the spectra prior to model subtraction. Therefore,
it cannot be identified positively as a component, but might be due to
some systematic problem with our models. The most likely systematic
effect causing such an discrepancy would be a lack of absorptivity in
a set of optical properties that we have used.
m feature, but
these stars (SU Per and S Per) may differ in other respects as well: S Per is the only target in our sample exhibiting strong water bands,
and Speck et al. (2000) suggested that it is more similar to lower-mass
semi-regulars. The broad excess in the residual spectrum cannot be
isolated in any of the spectra prior to model subtraction. Therefore,
it cannot be identified positively as a component, but might be due to
some systematic problem with our models. The most likely systematic
effect causing such an discrepancy would be a lack of absorptivity in
a set of optical properties that we have used.
6.2.2 The 18 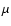 m feature
m feature
The 18 ![]() m feature observed in the residuals is most probably the
feature typically ascribed to the silicates generating the 9.7
m feature observed in the residuals is most probably the
feature typically ascribed to the silicates generating the 9.7 ![]() m
feature (the olivines). However, starting from laboratory-measured
optical constants, we find that it is impossible to reproduce this
peak position: it is either blue-shifted (olivines) or peaks toward
the red (melilite). The inclusion of either alumina or MgFeO causes
the model emission band to be centered on the observed
wavelength. However, this always causes a double-peaked band profile,
which is never observed. We note that this discrepancy is not unique
to the RSG but is also found in AGB stars with optically-thin dust
shells as studied by Heras & Hony (2005). This problem may be related to
that at 8
m
feature (the olivines). However, starting from laboratory-measured
optical constants, we find that it is impossible to reproduce this
peak position: it is either blue-shifted (olivines) or peaks toward
the red (melilite). The inclusion of either alumina or MgFeO causes
the model emission band to be centered on the observed
wavelength. However, this always causes a double-peaked band profile,
which is never observed. We note that this discrepancy is not unique
to the RSG but is also found in AGB stars with optically-thin dust
shells as studied by Heras & Hony (2005). This problem may be related to
that at 8 ![]() m.
m.
6.2.3 Detection of PAHs
As shown in Fig. 5, we clearly detect PAH emission bands
at 6.3, 7.6, 11.3, and 14.2 ![]() m in 3 stars: AD Per, IRC 40427,
and U Lac. RS Per exhibits a significant PAH feature only at
7.6
m in 3 stars: AD Per, IRC 40427,
and U Lac. RS Per exhibits a significant PAH feature only at
7.6 ![]() m. AD Per and IRC 40427 also display a feature at
12.7
m. AD Per and IRC 40427 also display a feature at
12.7 ![]() m. The PAHs in AD Per, RS Per, and IRC 40427 were
already detected by Sylvester et al. (1994,1998), who related
their presence to the dissociation of CO molecules by the UV radiation
field of the chromosphere, since no PAHs are detected in AGB stars. The diffuse ISM is known to exhibit PAH emission features but
we are confident that the bands observed here originate in the CSE of
the RSG, since 1) the observed bands are as strong in the UKIRT observations of Sylvester et al. (1994) as in our ISO-SWS observations, in spite of the different apertures; 2) the UKIRT observations used a chopping technique, which should remove a large fraction of an extended ISM feature; and 3) the relative band strenghts do not agree with those of the ISM, and in some cases, the 6.22
m. The PAHs in AD Per, RS Per, and IRC 40427 were
already detected by Sylvester et al. (1994,1998), who related
their presence to the dissociation of CO molecules by the UV radiation
field of the chromosphere, since no PAHs are detected in AGB stars. The diffuse ISM is known to exhibit PAH emission features but
we are confident that the bands observed here originate in the CSE of
the RSG, since 1) the observed bands are as strong in the UKIRT observations of Sylvester et al. (1994) as in our ISO-SWS observations, in spite of the different apertures; 2) the UKIRT observations used a chopping technique, which should remove a large fraction of an extended ISM feature; and 3) the relative band strenghts do not agree with those of the ISM, and in some cases, the 6.22 ![]() m feature is shifted to longer wavelengths.
m feature is shifted to longer wavelengths.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig6.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg45.gif) |
Figure 5:
The 5 to 15 |
| Open with DEXTER | |
Using the dust-shell models presented here, we are able to isolate the PAH emission features. This allows us to study the band shapes and strengths in a manner similar to Peeters (2002) and Hony et al. (2001). This analysis can yield important information about the structural properties of the PAH family and provide clues about their formation conditions. This analysis is left to a future study. Perusal of Fig. 5 already indicates that the PAH features in our sample span an interesting range in detected bands, band-strength ratios, and band shapes.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{9063fig7.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg47.gif) |
Figure 6:
Left panel: the correlation between mass-loss rate and the ratio of dust to photospheric luminosity. The slope is that of a linear fit, the Kendall values refer to the Kendall rank correlation value and its significance. The Kendall rank correlation
|
| Open with DEXTER | |
7 Analysis
7.1 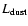 /
/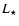 as a mass-loss rate indicator
as a mass-loss rate indicator
Column 10 presents the ratio of dust to photospheric luminosity. This ratio can be used as a distance-independent mass-loss indicator, which is non-trivial, since it must be checked that the variation of
![]() /
/![]() over the sample is due to different mass-loss rates and not only a difference in dust composition, e.g. the oxides tend to generate far less emission than the magnesium-rich silicates, for a similar dust mass. In the left hand panel of Fig. 6, we show our derived relation between
over the sample is due to different mass-loss rates and not only a difference in dust composition, e.g. the oxides tend to generate far less emission than the magnesium-rich silicates, for a similar dust mass. In the left hand panel of Fig. 6, we show our derived relation between
![]() /
/![]() and mass-loss rate, based on our modelling including the differences in dust composition. When assuming an identical luminosity for all stars, we find an almost one-to-one relation between mass-loss rate and dust-luminosity fraction. This shows that
and mass-loss rate, based on our modelling including the differences in dust composition. When assuming an identical luminosity for all stars, we find an almost one-to-one relation between mass-loss rate and dust-luminosity fraction. This shows that
![]() /
/![]() is a good mass-loss indicator. When correcting for distance and stellar luminosity, the relation is less steep. This is a consequence of the correlation between stellar luminosity and mass-loss rate discussed in the next section.
is a good mass-loss indicator. When correcting for distance and stellar luminosity, the relation is less steep. This is a consequence of the correlation between stellar luminosity and mass-loss rate discussed in the next section.
7.2 A correlation between mass-loss rate and stellar luminosity
The middle panel of Fig. 6 illustrates a
strong correlation between mass-loss rate and stellar luminosity and
also therefore with stellar mass. The best-fit linear relation is:
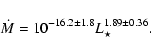
Since an increase in the mass-loss rate with luminosity, i.e. the size of the object, is expected just from scaling arguments, we also show the dust luminosity fraction as a function of stellar luminosity (right hand panel of Fig. 6 ). Interestingly, we find evidence for a more efficient wind-driving mechanism in the more luminous stars. The best-fit linear relation here is:
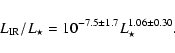
We also note that we do not find a significant trend between mass-loss rate and effective temperature.
7.3 Dust composition as a function of mass-loss rate
A purely empirical indication of the relation between mass-loss rate and dust composition can be obtained by simply plotting peak the position of the 10-![]() m complex versus dust luminosity. This is shown in the upper left panel of Fig. 7. With increasing mass-loss rate, the peak position shifts from 11 to 10
m complex versus dust luminosity. This is shown in the upper left panel of Fig. 7. With increasing mass-loss rate, the peak position shifts from 11 to 10 ![]() m. For intermediate values (e.g. BD+35 4077, see top right in Fig. 2), it is difficult to assign a single peak wavelength.
m. For intermediate values (e.g. BD+35 4077, see top right in Fig. 2), it is difficult to assign a single peak wavelength.
We search for correlations between dust composition and mass-loss rate based on our modelling and identify the following trends with increasing mass-loss rate:
- 1.
- the mass fraction of olivines increases;
- 2.
- the melilite content decreases;
- 3.
- the MgFeO content may decrease, but the Kendall test yields a low significance;
- 4.
- the carbon and alumina content don't show a clear trend.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{9063fig8.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg50.gif) |
Figure 7: Correlations between the different dust species and the mass-loss rate as traced by the dust luminosity (same analysis as in Fig. 6). |
| Open with DEXTER | |
8 Conclusions
We have analyzed the ISO-SWS spectra of 27 red supergiant stars, of which 21 show evidence of significant mass loss by a dusty wind. The measured properties of the winds around RSG share important characteristics with those around AGB stars with relatively low mass-loss rates: 1) the dust has a high fraction of ``simple'' dust species such as metal-oxides; 2) the winds have a relatively low abundance of silicates; and 3) the fraction of silicates correlates well with the mass-loss rate and/or the density and pressure at the base of the wind, as predicted by the canonical condensation sequence of Tielens (1990).
However, in some respects, RSG are not just the heavier twins of AGB stars: 1) they display molecular bands of only diatomic molecules (not H2O, CO2 or SO2); 2) the general slope of the SED from near-IR to mid-IR wavelengths can only be explained by the presence of a source of continuous opacity, which, in the case of RSG, could be due to amorphous carbon; and 3) PAHs are observed in 4 sources, suggesting a strong influence by the chromospheric radiation field.
Apart from the correlation observed by Josselin & Plez (2007) between photospheric turbulence strength and mass-loss rate, we also find that the stellar luminosity strengthens the wind.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig9.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg51.gif) |
Figure 8: Olivine content as a function of temperature and pressure at the inner edge of the dust shell. The lines represent regimes of constant mass-loss rate, as derived by Gail & Sedlmayr (1986). |
| Open with DEXTER | |
Although the correlations and detections presented in this paper are significant (in an approximate statistical sense), we are aware of possible 1) degeneracies between the fitting parameters; 2) biases due to our particular fitting strategy and model assumptions; and 3) biases due to our limited set of dust constituents.
Major progress will be possible in the near future by use of the 2nd generation VLTI instrumentation, in particular MATISSE (Lopez et al. 2006), which will allow the quasi-instanteneous imaging of many RSG from the near to mid-IR. This will allow us to determine the true spatial distribution of the different dust components.
Acknowledgements
The authors would like to thank the anonymous referee and T. Posch for many valuable comments, and C. Kemper for a careful reading of the manuscript. KE gratefully acknowledges support from the Swedish Research Council.
References
- Arenou, F., Grenon, M., & Gomez, A. 1992, A&A, 258, 104 [NASA ADS] (In the text)
- Beck, H. K. B., Gail, H.-P., Henkel, R., & Sedlmayr, E. 1992, A&A, 265, 626 [NASA ADS] (In the text)
- Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (New York: Wiley) (In the text)
- Bouwman, J. 2001, Ph.D. Thesis, University of Amsterdam
- Bouwman, J., de Koter, A., van den Ancker, M. E., & Waters, L. B. F. M. 2000, A&A, 360, 213 [NASA ADS]
- Cami, J. 2002, Ph.D. Thesis (University of Amsterdam) (In the text)
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Chiar, J. E., & Tielens, A. G. G. M. 2006, ApJ, 637, 774 [NASA ADS] [CrossRef] (In the text)
- Cousins, A. W. J., & Lagerweij, H. C. 1971, Monthly Notes of the Astronomical Society of South Africa, 30, 12 [NASA ADS] (In the text)
- de Graauw, T., Haser, L. N., Beintema, D. A., et al. 1996, A&A, 315, L49 [NASA ADS] (In the text)
- Dijkstra, C., Speck, A. K., Reid, R. B., & Abraham, P. 2005, ApJ, 633, L133 [NASA ADS] [CrossRef]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS]
- Feautrier, P. 1964, C.R. Acad. Sc. Paris, 258, 3189 [NASA ADS]
- Gail, H.-P., & Sedlmayr, E. 1986, A&A, 166, 225 [NASA ADS] (In the text)
- Gail, H.-P., & Sedlmayr, E. 1999, A&A, 347, 594 [NASA ADS]
- Gehrz, R. 1989, in Interstellar Dust, ed. L. J. Allamandola, & A. G. G. M. Tielens, IAU Symp., 135, 445
- Gielen, C., van Winckel, H., Min, M., Waters, L. B. F. M., & Lloyd Evans, T. 2008, A&A, 490, 725 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Harper, G. M., Brown, A., & Lim, J. 2001, ApJ, 551, 1073 [NASA ADS] [CrossRef] (In the text)
- Harwit, M., Malfait, K., Decin, L., et al. 2001, ApJ, 557, 844 [NASA ADS] [CrossRef] (In the text)
- Henning, T., & Stognienko, R. 1996, A&A, 311, 291 [NASA ADS]
- Henning, T., Begemann, B., Mutschke, H., & Dorschner, J. 1995, A&AS, 112, 143 [NASA ADS]
- Heras, A. M., & Hony, S. 2005, A&A, 439, 171 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Herbst, W., & Assousa, G. E. 1977, ApJ, 217, 473 [NASA ADS] [CrossRef]
- Hoefner, S., Jorgensen, U. G., Loidl, R., & Aringer, B. 1998, A&A, 340, 497 [NASA ADS] (In the text)
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Höfner, S., & Andersen, A. C. 2007, A&A, 465, L39 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hony, S., Van Kerckhoven, C., Peeters, E., et al. 2001, A&A, 370, 1030 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Humphreys, R. M. 1978, ApJS, 38, 309 [NASA ADS] [CrossRef] (In the text)
- Humphreys, R. M., & Ney, E. P. 1974, ApJ, 194, 623 [NASA ADS] [CrossRef] (In the text)
- Jaeger, C., Mutschke, H., Begemann, B., Dorschner, J., & Henning, T. 1994, A&A, 292, 641 [NASA ADS]
- Jennings, D. E., & Sada, P. V. 1998, Science, 279, 844 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewskj, W. Z. 1966a, Communications of the Lunar and Planetary Laboratory, 4, 99 [NASA ADS] (In the text)
- Johnson, H. L., Mendoza, V., & Eugenio, E. 1966b, Annales d'Astrophysique, 29, 525 [NASA ADS] (In the text)
- Josselin, E., & Plez, B. 2007, A&A, 469, 671 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kemper, F., de Koter, A., Waters, L. B. F. M., Bouwman, J., & Tielens, A. G. G. M. 2002, A&A, 384, 585 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] (In the text)
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] (In the text)
- Kholopov, P. N., Samus, N. N., Frolov, M. S., et al. 1998, in Combined General Catalogue of Variable Stars, 4.1 Ed (II/214A)
- Koike, C., Kaito, C., Yamamoto, T., et al. 1995, Icarus, 114, 203 [NASA ADS] [CrossRef]
- Kraemer, K. E., Sloan, G. C., Price, S. D., & Walker, H. J. 2002, ApJS, 140, 389 [NASA ADS] [CrossRef] (In the text)
- Lebzelter, T., Posch, T., Hinkle, K., Wood, P. R., & Bouwman, J. 2006, ApJ, 653, L145 [NASA ADS] [CrossRef]
- Lee, T. A. 1970, ApJ, 162, 217 [NASA ADS] [CrossRef] (In the text)
- Lejeune, T., & Schaerer, D. 2001, A&A, 366, 538 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] (In the text)
- Lopez, B., Wolf, S., Lagarde, S., et al. 2006, in Advances in Stellar Interferometry, ed. J. D. Monnier, M. Schöller, & W. C. Danchi, Proc. SPIE, 6268, 62680Z (In the text)
- Massey, P. 2003, ARA&A, 41, 15 [NASA ADS] [CrossRef] (In the text)
- Massey, P., Plez, B., Levesque, E. M., et al. 2005, ApJ, 634, 1286 [NASA ADS] [CrossRef] (In the text)
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] (In the text)
- Matsuura, M., Zijlstra, A. A., van Loon, J. T., et al. 2005, A&A, 434, 691 [NASA ADS] [CrossRef] [EDP Sciences]
- Mendoza, E. E. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 149 [NASA ADS] (In the text)
- Mihalas, D. 1978, Stellar atmospheres 2nd edn. (San Francisco: W. H. Freeman and Co.), 650
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mutschke, H., Begemann, B., Dorschner, J., et al. 1998, A&A, 333, 188 [NASA ADS]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [NASA ADS] [CrossRef] (In the text)
- Nicolet, B. 1978, A&AS, 34, 1 [NASA ADS] (In the text)
- Ohnaka, K. 2004, A&A, 424, 1011 [NASA ADS] [CrossRef] [EDP Sciences]
- Peeters, E. 2002, Ph.D. Thesis, Proefschrift, Rijksuniversiteit Groningen, 237 (In the text)
- Perrin, G., Ridgway, S. T., Mennesson, B., et al. 2004, A&A, 426, 279 [NASA ADS] [CrossRef] [EDP Sciences]
- Perrin, G., Ridgway, S. T., Verhoelst, T., et al. 2005, A&A, 436, 317 [NASA ADS] [CrossRef] [EDP Sciences]
- Perrin, G., Verhoelst, T., Ridgway, S. T., et al. 2007, A&A, 474, 599 [NASA ADS] [CrossRef] [EDP Sciences]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] (In the text)
- Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS]
- Ryde, N., Richter, M. J., Harper, G. M., Eriksson, K., & Lambert, D. L. 2006, ApJ, 645, 652 [NASA ADS] [CrossRef] (In the text)
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
- Sloan, G. C., Kraemer, K. E., Price, S. D., & Shipman, R. F. 2003, ApJS, 147, 379 [NASA ADS] [CrossRef] (In the text)
- Speck, A. K., Barlow, M. J., Sylvester, R. J., & Hofmeister, A. M. 2000, A&AS, 146, 437 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sylvester, R. J., Barlow, M. J., & Skinner, C. J. 1994, MNRAS, 266, 640 [NASA ADS] (In the text)
- Sylvester, R. J., Skinner, C. J., & Barlow, M. J. 1998, MNRAS, 301, 1083 [NASA ADS] [CrossRef]
- Tielens, A. G. G. M. 1990, in From Miras to Planetary Nebulae: Which Path for Stellar Evolution?, ed. M. O. Mennessier, & A. Omont, 186 (In the text)
- Tsuji, T. 2000, ApJ, 538, 801 [NASA ADS] [CrossRef] (In the text)
- van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Verhoelst, T., Decin, L., van Malderen, R., et al. 2006, A&A, 447, 311 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wawrukiewicz, A. S., & Lee, T. A. 1974, PASP, 86, 51 [NASA ADS] [CrossRef] (In the text)
- Woitke, P. 2006, A&A, 460, L9 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woitke, P., & Niccolini, G. 2005, A&A, 433, 1101 [NASA ADS] [CrossRef] [EDP Sciences]
Footnotes
- ...
![[*]](/icons/foot_motif.gif)
- Postdoctoral Fellow of the Fund for Scientific Research, Flanders.
- ... candidates
![[*]](/icons/foot_motif.gif)
- Stars removed from the list because they are either on the AGB or even on the RGB: T Cet, WX Cas, BD+59 594,
 Aur, HD 90586, RT Car, BC Cyg, CIT 11 and IRC+60370,
Aur, HD 90586, RT Car, BC Cyg, CIT 11 and IRC+60370,  Cap, S Pav and
Cap, S Pav and 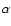 UMa.
UMa.
- ... gravity
![[*]](/icons/foot_motif.gif)
- Lower gravity models failed to converge at the lowest temperatures, which led us to adopt this value uniformly. The stellar mass of the models in this grid is only 1
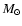 ,
but at the resolution of our set of observations, the differences with respect to higher-mass models would not be noticeable.
,
but at the resolution of our set of observations, the differences with respect to higher-mass models would not be noticeable.
- ... olivines
![[*]](/icons/foot_motif.gif)
- Remark that the term Olivine in principle refers to the crystalline form. Although the correct phrasing should be ``amorphous silicate with an olivine stoichiometry'', we refer to this material as Olivines, as is done in similar studies.
- ... database
![[*]](/icons/foot_motif.gif)
- http://www.astro.uni-jena.de/Laboratory/Database/databases.html
- ...
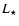
![[*]](/icons/foot_motif.gif)
-
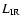 is calculated as the integration over
is calculated as the integration over
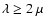 m of the final model spectrum minus the photospheric model and
m of the final model spectrum minus the photospheric model and  is calculated by integrating the photospheric model over all wavelengths.
is calculated by integrating the photospheric model over all wavelengths.
- ...
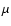 m
m![[*]](/icons/foot_motif.gif)
- The MOLspheres are found to be colder than the photospheric background, and generate excess emission only through their larger emitting surface.
- ... near-IR
![[*]](/icons/foot_motif.gif)
- We know that the near-IR is suffering additional extinction (as oppposed to less excess emission) from the fit of our photosphere models to the unreddened optical fluxes.
- ... normalized
![[*]](/icons/foot_motif.gif)
- Normalization of each observed
and model spectrum was performed by inverse scaling with the average
flux (
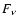 )
between 3.5 and 4
)
between 3.5 and 4 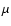 m. The spectra were then
subtracted, and the residuals calculated in this way averaged over the
sample.
m. The spectra were then
subtracted, and the residuals calculated in this way averaged over the
sample.
All Tables
Table 1: Object designations and general characteristics. Star with their names printed in italic have luminosities which also allow an AGB star identification. The bolometric magnitudes were computed from the dereddened K band magnitudes, using the bolometric corrections of Levesque et al. (2005).
Table 2: Dust species used in this study with their commonly-used name, their size, shape and the source of the optical constants. The size distribution is that derived by Mathis et al. (1977) and the cross section are computed in the CDE (Continuous Distribution of Ellipsoids) approximation.
Table 3: The best fit model parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig1.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg25.gif) |
Figure 1:
The average of all dereddened observed dust spectra, each
normalized with its photospheric flux at 3.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{9063fig2.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg39.gif) |
Figure 2:
The SEDs of all sample stars with their best-fit models (total spectrum in red dashes and non-reddened photospheric spectrum in bluedots). The photometric points are either the 7 Geneva filters or B and V in the Johnson system, J, H and Ks from 2mass and I12 and I25 from the IRAS mission. The dotted vertical line indicates 9.7 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{9063fig3.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg40.gif) |
Figure 3: The ISO-SWS spectra of all sample stars with their best-fit models (symbols and colours as in Fig. 2). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig4.ps}\\ [4mm]
\includegraphics[width=8cm,clip]{9063fig5.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg44.gif) |
Figure 4: Upper panel: the average normalized residuals in the blue part of the ISO-SWS spectrum together with simulated molecular absorption bands. For more details on the computation of the molecular templates we refer to Cami (2002). Lower panel: the wavelength range of the residuals (black solid line) which is dust dominated. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig6.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg45.gif) |
Figure 5:
The 5 to 15 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{9063fig7.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg47.gif) |
Figure 6:
Left panel: the correlation between mass-loss rate and the ratio of dust to photospheric luminosity. The slope is that of a linear fit, the Kendall values refer to the Kendall rank correlation value and its significance. The Kendall rank correlation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{9063fig8.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg50.gif) |
Figure 7: Correlations between the different dust species and the mass-loss rate as traced by the dust luminosity (same analysis as in Fig. 6). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9063fig9.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa9063-07/Timg51.gif) |
Figure 8: Olivine content as a function of temperature and pressure at the inner edge of the dust shell. The lines represent regimes of constant mass-loss rate, as derived by Gail & Sedlmayr (1986). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


