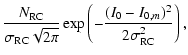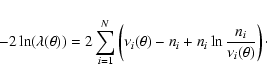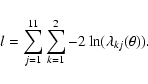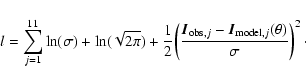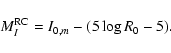Stellar populations in the Galactic bulge

E. Vanhollebeke; M. A. T. Groenewegen; L. Girardi

doi:10.1051/0004-6361/20078472

Home

All issues

Volume 498 / No 1 (April IV 2009)

A&A, 498 1 (2009) 95-107

Full HTML

Free Access

Issue		A&A Volume 498, Number 1, April IV 2009


Page(s)		95 - 107
Section		Galactic structure, stellar clusters, and populations
DOI		https://doi.org/10.1051/0004-6361/20078472
Published online		05 March 2009

Modelling the Galactic bulge with TRILEGAL

E. Vanhollebeke¹ - M. A. T. Groenewegen^2,1 - L. Girardi³

1 - Instituut voor Sterrenkunde, K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
2 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
3 - Padova Osservatorio Astronomia, Vicolo dell'Osservatorio 5, 35122 Padova, Italy

Received 13 August 2007 / Accepted 30 January 2009

Abstract
Aims. The aim of this paper is to study the characteristics of the stellar populations and the metallicity distribution in the Galactic bulge. We study the entire stellar population, but also retrieve information using only the red clump stars.
Methods. To study the characteristics of the stellar populations and the metallicity distribution in the Galactic bulge, we compared the output of the galaxy model TRILEGAL, which implements the Binney et al. (1997, MNRAS, 288, 365) bulge model, with observations from 2MASS and OGLE-II. A minimisation procedure has been set up to retrieve the best fitting model with different stellar populations and metallicity distributions.
Results. Using the TRILEGAL code we find that the best model resembling the characteristics of the Galactic bulge is a model with the distance to the Galactic centre $R_0 = 8.7\pm ^{0.57}_{0.43}$ kpc, the major axis ratios of the bar $1{:}\eta {:}\zeta = 1{:}0.68{\pm}_{0.19}^{0.05}\!\!{:} 0.31\pm_{0.04}^{0.06}$ , and the angle between the Sun-centre line and the bar $\phi = 15^\circ \pm _{12.7}^{13.3}$ . Using these parameters the best model is found for a burst of 8 Gyr, although it is almost indistinguishable from models with ages of 9 and 10 Gyr. The metallicity distribution found is consistent with metallicity distributions in the literature based on spectroscopic results.

Key words: Galaxy: bulge - Galaxy: structure - stars: distances - Galaxy: fundamental parameters - stars: Hertzsprung Russell (HR) and C-M diagrams

1 Introduction

The central part of our Milky Way Galaxy (MWG) consists of the Galactic bulge (GB), the central part of the halo, and the Galactic centre (GC). Over the years, several studies have tried to understand the characteristics of these parts of the MWG, for example about the formation history, the rate of star formation, the relations between different stellar components, and its kinematics (Wyse 1995).

Understanding the formation history of galactic spheroids (i.e. elliptical galaxies and the bulges of spiral galaxies) is crucial in understanding galaxy formation in general as these spheroids contain a large fraction of all stellar mass in the local universe (Zoccali et al. 2003, and references therein, hereafter ZRO2003). Because of its proximity, our GB is the spheroid for which the most information is accessible. Issues that can be addressed in the GB are, e.g., the initial mass function, the distribution of stellar ages, and the 3D structure. For more distant spheroids, this sort of information is only accessible by very indirect means based on the study of the integrated light.

Many different approaches exist to studying galaxy formation. Often galaxy models are used to study the entire content of a galactic component such as the bulge (Merrifield 2004; Freudenreich 1998; Robin et al. 2003; Dwek et al. 1995; Bissantz & Gerhard 2002; Binney et al. 1997), but studies of the same kinds of stars can also reveal a wealth of information. Examples of this are, e.g., the use of red clump stars (Nishiyama et al. 2006; Paczynski & Stanek 1998; Stanek et al. 1997; Rattenbury et al. 2007; Udalski 1998; Babusiaux & Gilmore 2005; López-Corredoira et al. 2007), RR Lyrae stars (Udalski 1998; Fernley et al. 1987; Feast 1997), masers (Reid et al. 1988; Sevenster et al. 1999), and Mira variables (Whitelock 1992; Groenewegen & Blommaert 2005). Our target is both to perform a calibration of the bulge geometry and to explore the distribution of ages that can be inferred from these data.

The paper is organised as follows. In Sect. 2 we give a resume on the models and parameters generally used to study the GB, the star formation rate, and the metallicity distribution of the GB. In Sect. 3 we give a brief introduction to the galaxy model used in this work. Section 4 is dedicated to the observational data used. Section 5 explains the method used and Sect. 6 discusses the results derived using this method. Section 7 discusses the results using the same method if only the red clump stars are used. In Sect. 8 we summarise and come to the conclusions.

2 The Galactic bulge

At the moment, it is still not clear whether one should draw a distinction between a triaxial central bulge and a bar component (Merrifield 2004). Sometimes the bulge is referred to as the bar (see e.g. Sevenster et al. 1999) and in other cases studies find a bar within the bulge (see e.g. Cabrera-Lavers et al. 2007; López-Corredoira et al. 2007). In this paper we will adopt the formalism described by Sevenster (1999): we will use the term Galactic bulge for the Galactic component seen in the general direction of $\vert\ell\vert \le 10\hbox{$^\circ$ }$ , we will use bar if we refer to the prolate or triaxial component of the GB.

This section gives a brief overview of recent studies proposing different models and parameters describing the GB. Also the possible star formation rate and age metallicity relations will be described.

2.1 Models describing the Galactic bulge and its bar

Many different geometries can be assumed for the GB. Oblate spheroidal models can be a good start, providing a first order estimate of the bulge luminosity and minor to major axis ratios (Dwek et al. 1995). As became clear over the past decades, there is a triaxial part, the bar, which needs a triaxial model. There are three types of triaxial models proposed: Gaussian-type functions, exponential-type functions, and power-law functions (see Dwek et al. 1995, and references therein). Dwek et al. (1995) find that the best model to fit the COBE/DIRBE data for the bulge is an exponential-type function with a modified spheroid included. Robin et al. (2003) use the same parameter set as Dwek et al. (1995) introduced to fit the bulge. They used a boxy Gaussian type function, but did not model the inner parts of the bulge. Binney et al. (1997) and also Bissantz & Gerhard (2002) used a truncated power-law to model the bulge. In this paper, we will use the Binney et al. (1997) formalism to model the number density of stars $f_{\rm bulge}$ , which is given by:

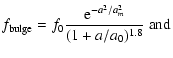$\displaystyle f_{\rm bulge} = f_0 \frac{{\rm e}^{-a^2/a_m^2}}{(1+a/a_0)^{1.8}} {\ \rm and}$			(1)
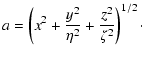$\displaystyle a = \left( x^2 + \frac{y^2}{\eta^2} + \frac{z^2}{\zeta^2}\right)^{1/2}\cdot$			(2)

In these formulae, a_m represents the scale length, a₀ the inner truncation length, and f₀ is the stellar density per kpc³ of the bulge. The axis-ratios of the bar are given by: $1{:}\eta{:}\zeta$ .

2.2 Parameters describing the Galactic bulge

Table 1: A not complete overview of recent values of parameters describing the GB, its bar and the distance to the GC.

The typical parameters needed to describe the GB (see previous section) are the scale length (a_m) and inner truncation length (a₀) of the bulge, the axis-ratios (1: $\eta$ : $\zeta$ ) of the bar, the angle between the Sun-centre line and the major axis of the bar ( $\phi$ ), and the scaling parameter (f₀). Of course also the Sun's distance to the Galactic centre (R₀) is an important parameter in this context.

One of the most studied types of stars in the GB are the red clump stars. The red clump stars are considered as standard candles to determine distances. They can also be used to estimate the axis ratios of the bulge and the angle $\phi$ . Using these red clump stars, values between 7.4 and 8.4 kpc for R₀ have been found (see e.g. Nishiyama et al. 2006; Paczynski & Stanek 1998; Udalski 1998; Babusiaux & Gilmore 2005). Values for $\phi$ derived from red clump stars are situated either around 20 $\hbox{$^\circ$ }$ or around 45 $^\circ$ (see e.g. Stanek et al. 1997, $\phi=20\hbox{$^\circ$ }{-} 30\hbox{$^\circ$ }$ ; Babusiaux & Gilmore 2005, $\phi = 22\hbox{$^\circ$ }\pm 5.5{\hbox{$^\circ$ }}$ ; and López-Corredoira et al. 2007, $\phi=43\hbox{$^\circ$ }$ ). Recent work on the red clump stars in the GB comes from Cabrera-Lavers et al. (2007) and Rattenbury et al. (2007). Cabrera-Lavers et al. (2007) claim two very different large-scale triaxial structures in the inner Galaxy. A first component is a long thin stellar bar ( $\vert b\vert<2\hbox{$^\circ$ }$ ) with a position angel of $43.0\hbox{$^\circ$ }\pm 1.8\hbox{$^\circ$ }$ . The second component is a distinct triaxial bulge that extends to at least $\vert b\vert\le 7.5\hbox{$^\circ$ }$ and has a position angle of $12.6\hbox{$^\circ$ }\pm 3.2\hbox{$^\circ$ }$ . Rattenbury et al. (2007) study the red clump stars observed with OGLE in the OGLE-II phase and find that the bar's major axis is oriented at 24 $^\circ$ -27 $^\circ$ to the Sun-Galactic centre line-of-sight.

Another kind of stars that is considered a standard candle are the RR Lyrae stars. Using these stars typical values for R₀ of $\sim$ 8.0 kpc have been found (see e.g. Udalski 1998; Fernley et al. 1987; Feast 1997).

Other types of stars that have been studied to characterise the GB are e.g. Mira variables (see e.g. Groenewegen & Blommaert 2005, R₀ = 8.8 kpc and $\phi=43\hbox{$^\circ$ }$ ; and Whitelock 1992, $1{:}\eta{:}\zeta = 1{:}0.25{:}0.25$ , $\phi=45\hbox{$^\circ$ }$ ); H₂O masers (Reid et al. 1988) see R₀ = 7.1 kpc, and OH/IR stars (Sevenster et al. 1999) (see a_m = 2500 pc and $\phi = 44\hbox{$^\circ$ }$ ).

Studying one type of star is not the only method to obtain information on the characteristics of the Galactic bulge and distance to the Galactic centre. Eisenhauer et al. (2003) and Eisenhauer et al. (2005) studied stars orbiting the central black hole and found values for R₀ of respectively $7.94 \pm 0.42$ kpc and $7.62 \pm 0.32$ kpc. Recently, Ghez et al. (2008) and Gillessen et al. (2009) used additional data to find, respectively, $8.0 \pm 0.4$ kpc and $8.33 \pm 0.35$ kpc. Also surveys like 2MASS and the surface brightness maps of COBE/DIRBE were used. Studies based on these databases find values for $\phi$ around 20 $^\circ$ (see e.g. López-Corredoira et al. 2005; Dwek et al. 1995; Binney et al. 1997; Bissantz & Gerhard 2002), scale lengths a_m between 1900 pc and 2800 pc (see e.g. Freudenreich 1998; Bissantz & Gerhard 2002; Binney et al. 1997), and an axis-ratio of 1:0.5-0.6:0.4 (López-Corredoira et al. 2005; Merrifield 2004), except Dwek et al. (1995) who find lower values for the axis-ratio (1:0.33:0.23). Robin et al. (2003) used HIPPARCOS data to model and retrieved axis-ratios of 1:0.27:0.27 and an angle $\phi$ of 11.1 $^\circ$ $\pm$ 0.7 $^\circ$ .

The Milky Way Galaxy consists not only of stars, there is also an amount of gas present. The location of H I gas in the galaxy (see Fig. 2 in Merrifield 2004) immediately reveals the non-axisymmetric distribution of the gas. This non-axisymmetric distribution can also be seen when one measures the velocities of the interstellar CO molecule (Dame et al. 2001). Using the distribution of the H I gas Merrifield (2004) retrieve an angle $\phi$ of 25 $^\circ$ .

Table 1 gives an overview of these studies and the parameters retrieved. Concerning the angle between the Sun-centre line and the bar $\phi$ , Table 1 clearly shows two groups of values: a low value around $20\hbox{$^\circ$ }$ and a higher value around $45\hbox{$^\circ$ }$ . According to Sevenster et al. (1999) the lower values found for $\phi$ arise when the longitude range used is too narrow or when low latitudes are excluded. Groenewegen & Blommaert (2005) point out that this could also be due to the fact that these studies trace different populations, which may be distributed differently.

2.3 Star formation rate and metallicity distribution

Besides the uncertainty in the literature on the parameters describing the GB geometry and its bar, the characteristics of the stars located in the GB are being debated.

Lately, studies show traces of an intermediate age population in the GB. Before, it was believed that the GB consisted only of an old population (more than 10 Gyr). Recent studies still reveal that the GB is dominated by this old population, but traces of a smaller intermediate age population can no longer be ignored.

Holtzman et al. (1993) studied a field in Baade's Window and concluded that, based on the luminosity function, there exist not only old stars in the GB, but also a significant, although unquantified, number of intermediate age stars (less than 10 Gyr). Ortolani et al. (1995) conclude that there is no age difference between the majority of bulge stars and the halo globular clusters and no more than ${\sim} 10\%$ of the bulge population can be represented by intermediate age stars (see also Ortolani et al. 2001, ZRO2003); Feltzing & Gilmore (2000) found no significant young stellar population in the GB, but emphasise that it is still possible to have an age range of several Gyr. van Loon et al. (2003, hereafter vLGO2003) found that in addition to the dominant old population ( ${\ge} 7$ Gyr), there is also an intermediate-age population ( ${\sim} 200$ Myr-7 Gyr) and possibly even younger ( ${\le} 200$ Myr) stars are found across the inner bulge (although the latter could be attributed to foreground stars). Concerning an intermediate age population, Groenewegen & Blommaert (2005) found that the Mira variables in the studied OGLE bulge fields have ages of a few Gyr. Also Uttenthaler et al. (2007) found some AGB stars that might be tracers of a younger population: some of their selected AGB stars in the GB show Technetium, which indicates that these AGB stars must originate from a younger population.

The detection of a metallicity spread or absence of it and the metallicity distribution reveals information on the formation history. During the last decade, there were several papers studying the metallicity in the GB. McWilliam & Rich (1994) obtained for 14 M giants in the GB high resolution spectroscopy. They found a mean metallicity of $\langle$ [Fe/H] $\rangle = -0.19 \pm 0.02$ . Sadler et al. (1996) studied K and M giants in Baade's Window and found a mean abundance of $\langle$ [Fe/H] $\rangle = -0.11 \pm 0.04$ . Feltzing & Gilmore (2000) studied HST images and found that the metallicity of the bulge is equal to that of the old disk and that there is only a marginal evidence for a central metallicity gradient. Also Ramírez et al. (2000) studied M giants in the GB. They found a mean metallicity $\langle$ [Fe/H] $\rangle = -0.21 \pm 0.30$ and no evidence for a metallicity gradient along the minor or major axes of the inner bulge (R < 560 pc). vLGO2003 found a mean metallicity [M/H] $\sim 0.5$ , but also stars with a metallicity of +0.5 and -2 are common, but not dominant. The old stars in the population ( ${\ge} 7$ Gyr) tend to have higher metallicities (see their Fig. 18). They propose that the metallicity distribution of the old stars might be bimodal: one component of super-solar metallicity and another of subsolar metallicity. ZRO2003 found that most of the bulge stars have a metallicity [M/H] between +0.1 and -0.6 with a peak at -0.1.

3 TRILEGAL

In this paper, we use the code TRILEGAL (TRIdimensional modeL of thE GALaxy, Girardi et al. 2005), a population synthesis code to simulate the stellar content towards any direction on the sky. In this paper the model will be used to compute colour-magnitude diagrams (CMD) towards the GB. This means that we simulate the photometric properties of stars located towards a given direction $(\ell,b)$ and complete down to a given limiting magnitude.

Figure 1 in Girardi et al. (2005) shows the general scheme of the TRILEGAL code. As is shown in their Fig. 1, the input to the model consists of four main elements:

a library of stellar evolutionary tracks. It is essentially composed of the Girardi et al. (2000) tracks with some updates at low metallicities (Girardi 2002, unpublished), and now complemented with the TP-AGB models by Marigo & Girardi (2007). These latter are expected to describe the TP-AGB phase with much more realistic lifetimes and luminosities than in the original Girardi et al. (2000) isochrones;
a library of synthetic spectra, which is used to compute bolometric corrections and extinction coefficients for the simulated stars. They are described in detail by Girardi et al. (2002);
the instrumental setup, describing the settings of the telescope to be used, e.g. filters, detectors, and the effective sky area to be simulated;
a detailed description of the Galaxy components, being the Galactic thin and thick disk, the Halo and the Bulge. For each component a Star Formation Rate (SFR), Age-Metallicity Relation (AMR), and space densities are assumed. These parameters are different for every Galaxy component, therefore the Galactic components are treated separately by the code. Also the Initial Mass Function (IMF) and interstellar absorption belong to this group of input parameters.

The TRILEGAL code itself performs a Monte Carlo simulation to generate stars in accordance with the input (see above). The SFR, AMR and IMF define a stars age, metallicity, and mass. An interpolation in the grids of evolutionary tracks results in the absolute photometry, which is then converted to apparent magnitudes based on the bolometric corrections, distance modulus, and extinction.

The output of the TRILEGAL code is a catalogue of stars that contains for each star the Galactic component in which they are located, stellar age, metallicity [M/H], initial mass, luminosity L, effective temperature $T_{\rm eff}$ , gravity g, distance modulus m-M₀, visual extinction A_V, core mass and the perfect photometric data in each of the wanted filters. To be able to compare the output in CMDs with observational data one has to perform some extra calculations which are not included in the TRILEGAL code such as adding photometric errors, saturation of the bright stars in real observations, and completeness.

A more detailed description of the TRILEGAL code and the parameters used concerning the disk and halo can be found in Girardi et al. (2005).

Extinction is calculated by the TRILEGAL code for each object separately based on the input A_V value and the distance modulus of the objects. Therefore, the extinction varies along the line-of-sight (see Girardi et al. 2005, for a more detailed description on the way the extinction is distributed). Some changes are made, however, to this part of the code with respect to Girardi et al. (2005). Not only can we now give the extinction value A_V as an input parameter to the code, but a spread on the A_V has also been used in this work. The extinction values and their sigma used can be found in Table 2 and are based on Sumi (2004).

An important point is that we have used TRILEGAL with the original filter curves provided for 2MASS (Skrutskie et al. 2006) and OGLE-II (Udalski et al. 1997), so simulating as far as possible the original photometric systems. The bolometric corrections for 2MASS have already been described in detail by Bonatto et al. (2004). Those for OGLE-II have been newly computed, and apart from being used in TRILEGAL have also been incorporated into the Padova database of isochrones. Extensive tables of bolometric corrections and isochrones in the OGLE-II system are now made available at the websites http://pleiadi.pd.astro.it/isoc_photsys.02 (static tables) and http://stev.oapd.inaf.it/cmd (interactive web form).

Furthermore, extinction coefficients in the several 2MASS and OGLE-II passbands have been computed for a G2V star using the Cardelli et al. (1989) extinction curve with R_V=3.1. The extinction coefficients turn out to be $A_{U_{\rm OGLE}}/A_V=1.524$ , $A_{B_{\rm OGLE}}/A_V=1.308$ , $A_{V_{\rm OGLE}}/A_V=1.021$ , $A_{I_{\rm OGLE}}/A_V=0.571$ , $A_{J_{\rm 2MASS}}/A_V=0.290$ , $A_{H_{\rm 2MASS}}/A_V=0.183$ , and $A_{K_{\rm s,2MASS}}/A_V=0.118$ .

These numbers would be suitable to simulate extinction in the nearby disk, but do not apply to a bulge with an anomalous ratio of total to selective extinction (see Udalski 2003). Since the reasons for such anomalous ratios are still not understood, one does not know really how to properly simulate extinction for the bulge. Our choice has been very pragmatic: we assume that the generalised Cardelli et al. (1989) extinction curve still applies, and just change its input R_V value until the mean R_VI=1.964 value for the bulge (Sumi 2004) is recovered. Therefore, we find that the anomalous extinction is reproduced with a R_V=2.4, which produces $A_{U_{\rm OGLE}}/A_V=1.715$ , $A_{B_{\rm OGLE}}/A_V=1.386$ , $A_{V_{\rm OGLE}}/A_V=1.017$ , $A_{I_{\rm OGLE}}/A_V=0.506$ , $A_{J_{\rm 2MASS}}/A_V=0.256$ , $A_{H_{\rm 2MASS}}/A_V=0.162$ , $A_{K_{\rm s,2MASS}}/A_V=0.101$ . These values are assumed in this work.

Table 2: Properties of the selected fields.

4 Observational data

4.1 Two micron all sky survey - 2MASS

The two micron all sky survey (2MASS) project is a collaboration between The University of Massachusetts and the Infrared Processing and Analysis Center (JPL/Caltech). The resulting 2MASS project made uniformly-calibrated observations of the entire sky (with a sky coverage of 99.998%) in the J (1.24 $\mu$ m), H (1.66 $\mu$ m) and $K_{\rm s}$ (2.16 $\mu$ m) near-infrared bands (Skrutskie et al. 2006).

In this paper, we will use the 2MASS Point Source Catalog (PSC), which contains astrometry and photometry in the three survey bandpasses for 470 992 970 sources. For every source, position, magnitude, astrometric and photometric uncertainties, and flags, indicating the quality of the source characterisations, are provided.

4.2 Optical gravitation lensing experiment - OGLE

The optical gravitational lensing experiment (OGLE) aims at detecting dark matter using micro lensing phenomena. Crowded regions are a suited place to conduct this survey. The Large Magellanic Cloud (LMC) was the first target in the second phase. Later on additional targets were added among 11 deg² in the GB.

In this paper, we will use data from Udalski et al. (2002) from OGLE-II who present the VI photometric maps of the GB as a natural by-product of large micro lensing surveys. These maps contain the mean VI-photometry and astrometry of about 30 million stars, covering about 11 deg² in different parts of the GB. Each field covers $14.2' \times 57'$ .

4.3 Selected fields

The fields selected to perform this study are shown in Table 2. The fields are chosen based on the OGLE fields from Udalski et al. (2002) and are as much as possible spread in longitude and latitude around the Galactic centre. The data from 2MASS has been downloaded according to the positions of the OGLE fields, using Gator on the IRSA web site (http://irsa.ipac.caltech.edu/).

5 Analysis

When calculating a set of models of any kind, one always needs an objective method to determine why one model is better than another. One also wants to know the error bars and/or confidence intervals for the derived parameters.

5.1 Method

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig01.eps} \end{figure}$	Figure 1: Example of the photometric errors of the $K_{\rm s}$ -band 2MASS data for field bul_sc40.
Open with DEXTER

The output of the TRILEGAL code consists of perfect photometric data (see Sect. 3). In order to be able to compare the output of the code with real observations, we need to add photometric errors to the output of TRILEGAL.

Both 2MASS and OGLE-II give individual errors on the observations. These individual errors are shown in Fig. 1 as an example for the 2MASS $K_{\rm s}$ -band data in field bul_sc40 in function of the $K_{\rm s}$ -band magnitude. Using this data a density profile has been generated: for each bin in $K_{\rm s}$ (size 0.1 mag) we calculated how likely it is for a star to have an error $\sigma_{K_{\rm s}}$ . Each bin in $\sigma_{K_{\rm s}}$ (size 0.01 mag) is then given a number between 0 and 1 representing the relative amount of stars in this bin with respect to all stars with a similar $K_{\rm s}$ -band magnitude. For each star in the output file of TRILEGAL a random number has been generated between 0 and 1. The assigned error is then the closest to $\sigma_{K_{\rm s}}$ with respect to the assigned density profile. This method has been used to generate photometric errors in all the observed magnitude bands from both 2MASS as OGLE-II for each field individually.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig02.eps} \end{figure}$

Figure 2:

$J - K_{\rm s}$ vs. $K_{\rm s}$ CMD for field bul_sc40. The figure on the left are the observations, the figure on the right is a model with R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The black dots in the model (right panel) are stars that originate from the disk, the dark blue dots originate from the halo and the red dots are bulge stars. This colour code will be used in all figures of this type. The light grey lines indicate the boxes used to compute the model with the observations.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig03.eps} \end{figure}$	Figure 3: Same figure and colour code as Fig. 2 for the same model but now for a V - I vs. I CMD. The additional box which is not seen in Fig. 2 is used to compare the red clump stars.
Open with DEXTER

With the observational data and the data calculated with TRILEGAL, CMDs have been constructed. For the 2MASS data these CMDs are in $J - K_{\rm s}$ vs. $K_{\rm s}$ (see Fig. 2), for the OGLE data the CMDs are V - I vs. I (see Fig. 3). To be able to compare a CMD constructed with observational data to a CMD constructed with modelled data, the CMDs have been divided into regions. For both the 2MASS data and OGLE data, we define a disk region and a bulge region in the dereddened CMDs as follows:

$\displaystyle K_{{\rm s},0} \le 12.2$	$\textstyle \rm {\ and\ }$	$\displaystyle (J - K_{\rm s})_0 \le 0.25 \rm {\ (for\ 2MASS\ disk)}$	(3)
$\displaystyle I_0 \le 14.1$	$\textstyle \rm {\ and\ }$	$\displaystyle (V - I)_0 \le 1.4 \rm {\ (for\ OGLE\ disk)}$	(4)
$\displaystyle K_{{\rm s},0} \le 10.7$	$\textstyle \rm {\ and\ }$	$\displaystyle K_{{\rm s},0} \ge -10.4 (J - K_{\rm s})_0 + 18.9$	(5)
		$\displaystyle \rm {\ (for\ 2MASS\ bulge)}$
$\displaystyle I_0 \le 12.4$	$\textstyle \rm {\ and\ }$	$\displaystyle I_0 \ge -8.2 (V - I)_0 + 24.0$	(6)
		$\displaystyle \rm {\ (for\ OGLE\ bulge).}$

For the OGLE data we defined additionally a clump region which contains the red clump stars, as $16.1 \le I_0 \le 12.6$ and $0.8 \le (V - I)_0 \le 1.8$ .

The regions are defined on a model with no extinction. Based on the assumed extinction for a field, these boxes are also reddened, in this way, these boxes include for every field the same part of the CMD. The boxes are defined in such a way that there is only a very small contamination of disk stars in the bulge region and the other way around. Therefore, if we want to study the bulge parameters, the only part of interest is the bulge region. The stars in the selected regions, are used to create histograms. All histograms were created in one magnitude ( $K_{\rm s}$ for 2MASS and I for OGLE) and not in the colours. The histograms for the disk and bulge region, which are probably not affected by incompleteness, are used to compare the number counts in each bin.

The histogram for the stars in the red clump region are not used for number counts, but to derive the red clump magnitude both from observations and modelled data. To derive the I_0,m magnitude for the red clump, the method described in Stanek & Garnavich (1998) has been used. This method fits a 2D polynomial to the underlying population, with on top of this a Gaussian function to determine the magnitude of the red clump. The formula is given by:

n(I₀) = a	+	b (I₀ - I_0,m) + c (I₀ - I_0,m)²
	+	$\displaystyle \frac{N_{\rm RC}}{\sigma_{\rm RC} \sqrt{2\pi}} \exp\left(-\frac{(I_0 - I_{0,m})^2}{2\sigma_{\rm RC}^2} \right),$	(7)

with the first tree terms corresponding to the underlying population with coefficients a, b, and c for the second degree polynomial. The last term refers to the red clump population itself, with parameters corresponding to a Gaussian fit: scaling factor $N_{\rm rc}$ , sigma $\sigma_{\rm RC}$ and peak of the observed red clump stars I_0,m. Figure 4 shows a fit using this method to the I-band observations in the bul_sc40 field. Using this fit to the red clump, we will compare the peak position of the red clump stars in the observations to the peak position of the red clump in the model. The expected magnitude of the red clump $M_I^{\rm RC}$ is often compared to the peak position in the magnitude distribution of the red clump in order to estimate the distance to these stars.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig04.eps} \end{figure}$	Figure 4: Example showing how the red clump stars are fitted using the method described by Stanek & Garnavich (1998). The black histogram are the stars selected from the ``red clump box'' in the V - I vs. I CMD and the grey line is the Gaussian fit with underlying second degree polynomial.
Open with DEXTER

5.2 Poisson distributed maximum likelihood

For the stars in the selected disk and bulge areas (see Figs. 2 and 3) the constructed histograms are used to compare number counts. The typical errors on the amount of stars in these histogram bins are Poisson errors ( ${\sim} \frac{1}{\sqrt n_i}$ with n_i the total amount of stars in bin i). Therefore the selected test to perform on these histogram is a log likelihood test for Poisson statistics (Eidelman et al. 2004):

$\begin{displaymath} -2\ln(\lambda(\theta)) = 2 \sum_{i=1}^N \left( \nu_i(\theta) - n_i + n_i \ln\frac{n_i}{\nu_i(\theta)} \right)\cdot \end{displaymath}$

(8)

In this formula $\theta$ is the set of unknown parameters one wants to derive, $n = (n_1,\ n_2,\ \ldots, n_N)$ is the data vector containing the observations with N the number of bins in a histogram. $\nu$ are the expected values, which are derived from the histograms of the modelled data and are therefore dependent on $\theta$ . When n_i = 0, the last term in Eq. (8) is set to zero.

For each field, there are 4 histograms (one for the disk region and one for the bulge region, both for the comparison with 2MASS and OGLE). When determining the parameters for the bulge, we only use the histograms based on the stars in the bulge boxes. This means that for each field, 2 histograms remain. Table 2 shows that we selected 11 fields. Including all this gives us a value l for each model, which we want to minimise:

$\begin{displaymath} l = \sum_{j=1}^{11} \sum_{k=1}^2 -2\ln(\lambda_{kj}(\theta)). \end{displaymath}$

(9)

5.3 Gaussian distributed log-likelihood

In addition to a box for the disk and bulge stars, Fig. 3 also shows a box in which the red clump stars are expected to be. Equation (7) is fitted to the number counts in this box, as illustrated in Fig. 4. The same is done for the model stars. The parameter of interest is the mean magnitude of the RC, $I_{\rm0,m}$ . When evaluating calculated models based on the position of the red clump, we cannot use the Poisson distributed maximum likelihood (see Sect. 5.2). In this case the errors are not Poisson distributed, but normal $N(0,\sigma^2)$ . To determine the appropriateness of a model concerning its position of the red clump, the log-likelihood function l can be used (Decin et al. 2007):

$\begin{displaymath} l = \sum_{j=1}^{11} \ln(\sigma) + \ln(\sqrt{2\pi}) + \frac{1... ...,j} - \vec{I}_{{\rm model},j}(\theta)}{\sigma}\right)^2\cdot } \end{displaymath}$

(10)

To find the best model, this equation needs to be minimised. As the standard deviation $\sigma$ we selected 0.025 mag, which is the half of the bin size used to construct the histograms containing the red clump stars (see also Sect. 6.3).

5.4 Minimisation procedure

The minimisation procedure used in this work is the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method (Broyden 1970; Goldfarb 1970; Shanno 1970; Fletcher 1970) which can be used to solve a non-linear optimisation problem. By analysing gradient vectors, the method constructs an approximated Hessian matrix allowing a quasi-Newton fitting method to move towards the minimum in parameter space. The parameters were normalised in the minimisation procedure so they have an equal influence on the choice of the next set of parameters.

To significantly decrease the amount of computing time, the simulations made during the minimisation runs, we adopt a shallower limiting magnitude, at I = 18. This does not influence our results as the stars fainter than this limit have no relevance to our analysis (see Sect. 5.1). Because these areas are chosen well above the completeness limits for both the 2MASS and OGLE data, we did not include completeness, again to speed up calculations.

The model calculations and minimisation procedure have been performed using Python. The program has been written as such that the 11 different fields, that need to be calculated to evaluate one model (see Sect. 4.3), were calculated simultaneously over 11 different CPU's. We could make use of 18 Dell PowerEdge PC's with a total of 54 processors of 3400 MHz, which makes it possible to evaluate about 5 models at the same time. In total we evaluated ${\sim} 10^5$ models in a time span of about a year.

5.5 Uncertainties on the model parameters

As explained by Decin et al. (2007) the log-likelihood function can be used to estimate the uncertainties on the model parameters. A model with a likelihood value l is equally good as the best model if $\min(l) + N_{\rm crit} > l$ . These critical values $N_{\rm crit}$ follow a $\chi^2_p$ -distribution with p the degrees of freedom (Decin et al. 2007; Eidelman et al. 2004). A table with these values for $p \in [1,20]$ can be found in Decin et al. (2007, and references therein).

6 Results

Table 3: Overview of the different models described in the text.

The SFR and AMR chosen to start the minimisation process with are based on ZRO2003 and are shown in Fig. 5. The left figure shows a bulge formed by a single star burst about 10 Gyr ago and the right figure indicates that the majority of the stars have a metallicity slightly lower than solar ( $Z_\odot = 0.019$ ).

The start values for the minimisation procedure have been chosen in accordance with Binney et al. (1997, see also Table 1#: R₀ = 8.0 kpc, a_m = 1.9 kpc, a₀ = 100 pc, $\eta = 0.60$ , $\zeta = 0.40$ , $\phi = 20\hbox {$^\circ $ }$ , and f₀ = 624.0. The output of this minimisation procedure is a model with following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.69$ , $\zeta = 0.30$ , $\phi = 20\hbox {$^\circ $ }$ , and f₀ = 422.3 (see also Table 3, model 1).

The constructed histograms for this model are shown for field bul_sc40 in Fig. 6. As mentioned in Sect. 5.1 we only used the histograms constructed with the I and $K_{\rm s}$ magnitude to compare the model with the observations. The histograms in V - I and $J - K_{\rm s}$ illustrate the fit between the model and the data for the colours. The minimisation procedure uses only the stars in the bulge box. The stars in the disk box were used prior to the minimisation process to set the scale parameter for the disk stars and to check the contamination of disk and halo objects in the ``bulge box''. For field bul_sc40 adopting the same model as in Fig. 6, we find that out of a total of 2731 objects in the bulge box for the 2MASS data only 127 originate from the disk and halo. Concerning the 2110 objects in the bulge box for the OGLE data, only 105 originate from the disk and halo. Since this is already a very modest fraction (about 5% for both CMDs), possible errors in our representation of the disk and halo geometry are expected to have a negligible impact on the star counts inside the bulge box.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig05.eps} \end{figure}$	Figure 5: The left figure shows the SFR normalised to 1 and the right figure shows the metallicity distribution normalised to 1 (based on ZRO2003).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig06.eps} \end{figure}$

Figure 6:

Histograms showing the distribution of selected bulge stars for field bul_sc40. The black line represents the observations, the red line the model. The left panel shows the 2MASS data, the right panel the OGLE data. The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.69$ , $\zeta = 0.30$ , $\phi = 20\hbox {$^\circ $ }$ , and f₀ = 422.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003.

Open with DEXTER

Figure 6 shows the distribution of stars for the observations and the model for the selected bulge stars for field bul_sc40. Also for all the other fields this model overestimates the amount of bulge stars in the 2MASS data and underestimates the amount of bulge stars in the OGLE data, therefore this model can still be improved, but not by adapting the parameters already in the minimisation procedure.

6.1 Varying the metallicity distribution

One of the parameters not in the minimisation procedure is the metallicity. The metallicity distribution in ZRO2003, which has been used for the previous model calculations, is based on photometric results and is slightly less metal-rich in comparison with metallicity distributions derived from spectroscopic results from e.g. McWilliam & Rich (1994), Sadler et al. (1996), and Ramìrez et al. (2000; see Fig. 14 in ZRO2003). Therefore, we shifted the metallicity distribution towards a more metal-rich population. Already when we shift [Fe/H] with 0.1 dex our fit improves (see model 2 in Table 3). The metallicity distribution has been shifted with +0.1, +0.2, +0.3, +0.4, and +0.5 dex (see respectively models 2, 4, 6, 8, and 10 in Table 3). We obtained the best fit with a shift of +0.3 dex for [Fe/H]. New minimisation procedures have been set up using these shifted metallicity distributions in order to test the effect of the change in metallicity distribution on the derived parameters. The minimisation procedure was started from the result of the previous minimisation process (see model 1 in Table 3). The results are listed in Table 3 (see models 3, 5, 7, 9, and 11). Reminimising the models revealed no differences concerning the metallicity distribution shift, again the best results are found using a shifted metallicity distribution of +0.3 dex with respect to ZRO2003. Concerning the parameters describing the geometry of the bulge and its bar, only $\phi$ and f₀ change. These changes are small and fall within the expected error bars (see Sect. 6.3). Figure 14 in ZRO2003 shows that a shift with 0.3 dex in [Fe/H] is consistent with the noticed differences between the metallicity distribution they derived and metallicity distributions derived based on spectroscopy. In fact, Zoccali et al. (2008) have recently rederived the bulge metallicity distribution, based on high resolution spectroscopy for a large sample. They find metallicities systematically higher than in ZRO03 by about 0.2 dex, which is perfectly in line with what we obtain in this paper.

6.2 Varying the age distribution

The star formation rate is also a input to the model (see Sect 2.3). Therefore we also tested other SFR's. First we start with shifting the star burst to a different age in steps of 1 Gyr from a star burst 7 Gyr ago to a star burst 13 Gyr ago. Table 3 gives an overview of these models when no new minimisation procedure is started (see models 12, 14, 16, 18, 20, and 22). Amongst these models, there is no better model than model 7. When a minimisation procedure is set up, using the different age distributions and the parameters describing the geometry as derived in model 7 as start values, we find models 13, 15, 17, 19, 21, and 23 (see Table 3). Three of these models are equally good based on $l_{\rm bulge}$ : model 15 with a star burst of 8 Gyr is the so-called best model, but models 17 (star burst of 9 Gyr ago) and 7 (star burst 10 Gyr ago) are equally good and one cannot distinguish between these three models. Concerning the parameters describing the geometry, the differences seen between these three models, fall within the expected error bars (see Sect. 6.3).

Changing the age of the star burst is not the only possibility to alter the SFR. Section 2.3 describes that most likely there are also intermediate age stars in the GB and maybe also some younger stars. In order to check these possibilities, we used the SFR given in vLGO2003 (see their Fig. 28). The metallicity distribution used is the metallicity distribution of ZRO2003 shifted with 0.3 dex. Young stars as well as intermediate age stars are included in the SFR by vLGO2003. To check the possibility of an intermediate age population on top of the dominant old population, the age distribution of vLGO2003 has been used, but without the stars younger than 0.1 Gyr and a SFR without the stars younger than 1 Gyr. The metallicity distribution used in these scenarios is again the shifted distribution found by ZRO2003. The results are again shown in Table 3.

Model 24 in Table 3 shows that we do not get a significantly better fit if we use the SFR by vLGO2003 and the shifted metallicity distribution by ZRO2003. Because the SFR has changed drastic, and therefore also the colour distribution of the stars in the resulting models, a new minimisation procedure is necessary to check if no better model can be found using the SFR by vLGO2003. The previous best model found (model 15), has been chosen to start the minimisation procedure with. This resulted in the following model: R₀ = 10.7 kpc, a_m = 3.1 kpc, a₀ = 86 pc, $\eta = 0.73$ , $\zeta = 0.30$ , $\phi = 8\hbox{$^\circ$ }$ , and f₀ = 455.0 (model 25 in Table 3). All parameters except R₀ and f₀fall within the expected error bars of the best model with a star burst of 10 Gyr as SFR (see Sect. 6.3). The differences seen between R₀ and f₀ are huge and do not fall within the previously defined error bars. $l_{\rm bulge}$ Additionally, shows that this model is not significantly better than model 15.

Also for the two SFR's including only intermediate age stars based on the SFR by vLGO2003 a new minimisation procedure was set up. Using the SFR by vLGO2003 for stars older than 0.1 Gyr, the minimisation procedure ended with the following model: R₀ = 9.3 kpc, a_m = 2.8 kpc, a₀ = 92 pc, $\eta = 0.66$ , $\zeta = 0.30$ , $\phi = 17\hbox{$^\circ$ }$ , and f₀ = 394.0. All parameters found using this SFR are within the error bars derived on model 15 (see Sect. 6.3). Using the SFR for stars older than 1 Gyr, the minimisation procedure ended with the same model: R₀ = 9.3 kpc, a_m = 2.8 kpc, a₀ = 92 pc, $\eta = 0.66$ , $\zeta = 0.30$ , $\phi = 17\hbox{$^\circ$ }$ , and f₀ = 394.0, which then of course falls also within the error bars of model 15. Based on $l_{\rm bulge}$ , these two later models are not as good as model 15.

6.3 Error bars

To derive the error bars on these model parameters, we used the method described in Sect. 5.5. For each parameter we explored the parameter space around the value found by the minimisation procedure and rounded the found parameters within the found error bars. All models that fall within the critical value of $N_{\rm crit} = 14.07$ from our model are equally good. This results in the following error bars for model 7: $R_0=8.6\pm^{0.15}_{0.10}$ kpc, $a_m=2.7\pm^{0.04}_{0.08}$ kpc, $a_0=97\pm^{1.1}_{3.5}$ pc, $\eta=0.68\pm^{0.01}_{0.07}$ , $\zeta=0.30\pm^{0.01}_{0.01}$ , $\phi=14\hbox{$^\circ$ }\pm^{5.6}_{9.6}$ , and $f_0 = 427.3\pm^{10.8}_{25.7}$ .

These error bars have been used in the previous section to determine whether parameters between different models fall within the same range. As model 15 was found to be the best model, we also calculated the error bars for this model. We obtain: $R_0=8.7\pm^{0.57}_{0.42}$ kpc, $a_m=2.5\pm^{1.73}_{0.13}$ kpc, $a_0=95\pm^{7.5}_{12.8}$ pc, $\eta=0.68\pm^{0.04}_{0.19}$ , $\zeta=0.31\pm^{0.06}_{0.04}$ , $\phi=15\pm^{13.3}_{12.7}$ , and $f_0=406.0\pm^{40.4}_{167.3}$ . The error bars on this model are somewhat larger than the error bars found for model 7.

Based on the outcome of the minimisation procedures, the error bars on the determination of the magnitude of the red clump stars in the I-band have been determined. This resulted in an average error of 0.03 mag which is consistent with the chosen value in Eq. (10).

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig07.eps} \end{figure}$

Figure 7:

Histograms showing the distribution of selected bulge stars for field bul_sc40. The black line represents the observations, the red line the model. The upper panels shows the 2MASS data, the lower panels the OGLE data. The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003 but shifted with 0.3 dex. (This figure is also available in electronic form, showing histograms for all the modelled fields.)

Open with DEXTER

$\begin{figure} \par\includegraphics[width=16.4cm,clip]{8472fig08.eps} \end{figure}$

Figure 8:

Histograms showing the distribution of selected bulge stars for all the modelled fields. The black line is the histogram for the observational data, the red line represents the model. For each field there are four panels, the first two panels shows the 2MASS data (one for star counts in $J - K_{\rm s}$ and one for the star counts in $K_{\rm s}$ . The other two panels show the star counts for the OGLE data (V - I and I). The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003 but shifted with 0.3 dex.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{8472fig09.eps} \end{figure}$	Figure 8: continued.
Open with DEXTER

7 Red clump stars

The red clump stars can be used as a distance indicator as well as an estimator to the angle $\phi$ between the bar and the Sun-centre line (see also Sect. 2.2). Using the red clump stars, a new minimisation procedure as described in Sect. 5.4 was set up. In this scenario, there are only two variable parameters: R₀ and $\phi$ , the other parameters have been kept constant (a_m = 2.6 kpc, a₀ = 95 pc, $\eta = 0.68$ , $\zeta = 0.31$ , and f₀ = 406.0). An age of 8 Gyr and a metallicity distribution based on ZRO2003 and shifted with 0.3 dex has been used (which is consistent with the best model found, 15). The minimisation process started with R₀ = 8.7 kpc and $\phi = 14\hbox {$^\circ $ }$ and ended with R₀ = 8.7 pc and $\phi = 26.7\hbox{$^\circ$ }$ . This model is also listed in Table .

Using the method to derive error bars on these parameters, with $N_{\rm crit} = 5.99$ , the following error bars were calculated: $R_0 = 8.7\pm^{0.62}_{0.54}$ kpc and $\phi = 26.7\hbox{$^\circ$ }\pm^{4.5}_{26.7}$ . Therefore the model derived based on the red clump stars for R₀ and $\phi$ falls within the previously defined error bars for the model derived on the stars located in the bulge box. Although this model has a smaller $l_{\rm bulge}$ and $l_{\rm RC}$ , it is not significantly better than the previous found best model (see model 15 in Table 3.)

In Sect. 6 other SFR's have been tested (see Table 3). Also for these other models, we compared the red clump stars. Based on the red clump stars, Table 3 shows that the models with a star burst of 10 Gyr as SFR but with shifted metallicity distributions are equally good, except for model 7 which has a significantly worse $l_{\rm RC}$ . There is based on the critical value $N_{\rm crit}$ no difference between these models. Concerning the models with a SFR based on vLGO2003 the comparison with the red clump stars shows that our fit could not be improved adapting this SFR.

The results of this minimisation, and in particular the R₀value, are clearly associated to the set of stellar models that we used. Models with a different absolute magnitude of the red clump, for instance, would lead to a different GC distance. Girardi et al. (1998) and Girardi & Salaris (2001) claim the set of stellar models we are using (Girardi et al. 2000) do reproduce the very accurate $M_I^{\rm RC}$ value derived from Hipparcos; however their claims are tight to the specific choice of SFR (from Rocha-Pinto et al. 2000b) and AMR (from Rocha-Pinto et al. 2000a) employed in modelling the Solar Neighbourhood. Future revisions of these functions may lead to different results.

Several other works have already tried to access the bulge orientation and GC distance using red clump stars, employing different data, extinction corrections, and assumptions about the intrinsic magnitude difference between the local (Hipparcos) and the bulge red clump (i.e. the population correction, $\Delta M_\lambda^{\rm RC}=M_\lambda^{\rm RC}({\rm Hipp}) - M_\lambda^{\rm RC}({\rm galaxy})$ ). From the entries in Table 1, one notices that our best R₀ value agrees with the distance determinations to the bulge from Paczynski & Stanek (1998) and Stanek & Garnavich (1998), which were also derived from I-band data from OGLE. However, these are significantly larger than those derived from Babusiaux & Gilmore (2005) and Nishiyama et al. (2006) using near-infrared data.

In order to allow any future comparison between our R₀ determination and those from other authors, we provide below a representative value of the absolute red clump magnitude of our models.

Since TRILEGAL simulates the entire population along a given line-of-sight, our simulated LFs for the red clump box include effects like the dispersion in the distances of bulge stars, geometrical factors, and the contamination by disk and halo stars. As a consequence, our effective $M_I^{\rm RC}$ values do vary slightly from region to region even though the bulge stellar population which is being simulated is everywhere the same. Moreover, the Galactic centre line-of-sight has not been simulated, and a representative value of $M_I^{\rm RC}$ has to be inferred from the values distributed across the bulge. Figure 9 shows the observed peak positions of the red clump, I_0,m as a function of longitude $\ell$ . These peak positions are corrected for extinction using the extinction values given in Table 2. The full line is a linear least squares fit through these peak positions and is given by $I_{0,m} = (14.502 \pm 0.018) + (-0.029 \pm 0.03)\ell$ . Therefore the peak position I_0,m in the GC ( $\ell=0$ ) is given by $14.502\pm0.018$ . This is related to the absolute red clump magnitude by

$\begin{displaymath} M_I^{\rm RC} = I_{0,m} - (5 \log R_0 - 5). \end{displaymath}$

(11)

Using the distance to the GC $R_0=8.7\pm^{0.57}_{0.42}$ kpc derived from our minimisation procedures for an age of 8 Gyr, and the peak position I_0,m inferred for the GC, this equation gives $M_I^{\rm RC} = -0.196\pm^{0.143}_{0.106}$ . This value is consistent with the $M_I^{\rm RC} = -0.185\pm0.016$ used by Paczynski & Stanek (1998), and with the $M_I^{\rm RC} = -0.23\pm0.03$ used by Stanek & Garnavich (1998), in their GC distance determinations. The value is also consistent with the recent determination of $M_I^{\rm RC} = -0.22\pm0.03$ by Groenewegen (2008) from an analysis based on the revised Hipparcos parallaxes. This explains why their distance determinations are consistent with ours despite the quite different methods employed.

On the other hand, our preferred R₀ value disagrees with the Babusiaux & Gilmore (2005) and Nishiyama et al. (2006) distance determinations based on near-infrared data for the red clump. These works find R₀ values close to 7.5 kpc, which means a disagreement at the level of 0.3 mag in distance modulus. The origin of this discrepancy is not understood at the moment.

It is worth remarking that our favoured R₀ value of 8.7 kpc comes from both the red clump and the bulge box, the latter consisting mainly of upper-RGB and TP-AGB stars. These stellar groups are quite independent in their photometric properties. Our R₀ value is also consistent with the determinations based on the RR Lyrae and Mira variables. Although it disagrees with with the BH geometrical distance derived from Eisenhauer et al. (2005,2003) it does agree with the recent determination by Ghez et al. (2008).

8 Summary and conclusions

In this paper we have studied the characteristics of the Galactic bulge based on CMD comparisons between OGLE and 2MASS data an the results from the galactic model TRILEGAL (Girardi et al. 2005). Several star formation rates and metallicity distributions have been tested. Over all these different SFR's and metallicity distributions the model parameters give within the error bars the same results except for the angle $\phi$ between the Sun-centre line and the Bar. Concerning the other parameters we found a distance to the Galactic centre $R_0 = 8.7\pm ^{0.57}_{0.43}$ kpc, a scale length for the Bulge a_m of $2.5\pm^{1.73}_{0.16}$ kpc, an inner truncation length for the Bulge a₀ of $95\pm^{7.5}_{12.8}$ pc, and a scaling factor $f_0=406.0\pm^{40.4}_{167.3}$ . Concerning the characteristics of the Bar, we found the ratio of the major axis to be $1 {:} 0.68\pm_{0.05}^{0.19} {:} 0.31\pm_{0.06}^{0.04}$ and an angle $\phi$ of $15\hbox{$^\circ$ }\pm_{13.3}^{12.7}$ . The largest scatter in the found model parameters is found for the angle $\phi$ . Nevertheless the found values are all rather small and around $15{-}20\hbox{$^\circ$ }$ . The present best model of the bulge will be provided as the default in the interactive web interface to TRILEGAL (http://stev.oapd.inaf.it/trilegal).

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig10.eps} \end{figure}$	Figure 9: Peak positions I₀ of the red clump stars corrected for extinction in function of the longitude $\ell$ .
Open with DEXTER

If we compare our results to the results found in the literature and listed in Table 1 our parameters fall within the listed range of parameters except for the axial ratio $\eta$ . Concerning the distance to the GC, our value resembles the values found by Paczynski & Stanek (1998) based on red clump stars and Groenewegen & Blommaert (2005) based on Mira variables. Our results disagree with e.g. Udalski (1998) based on red clump stars in the GB. If we compute the mean observed magnitude I₀ from the distance modulus listed in Udalski (1998) using $M_I^{\rm RC}$ from Stanek & Garnavich (1998) as they did, than this is consistent with the observed mean magnitude we derived in this work. The other two studies deriving the distance to the GC based on red clump stars which are inconsistent with this work are Babusiaux & Gilmore (2005) and Nishiyama et al. (2006). These two studies are consistent with each other and use a very similar method: both define an ``extinction-free'' magnitude. It is not exactly clear why the results of these methods are not consistent with our results. As these studies are performed using K-band observations, we can not compare the expected magnitude as we could do for Udalski (1998). For the scale length of the bulge, we found the same value as Freudenreich (1998) and similar values as Sevenster et al. (1999) and Bissantz & Gerhard (2002). The inner truncation length for the Bulge is similar to the two values listed in Table 1 by Binney et al. (1997) and Bissantz & Gerhard (2002). The value $\eta$ we found is higher than the values found in the literature. Concerning the other ratio of the major axis $\zeta$ we found similar results as Whitelock (1992), Dwek et al. (1995), and Stanek et al. (1997). For the last parameter $\phi$ , we found values consistent with the group of studies finding lower values for $\phi$ (see e.g. Dwek et al. 1995; Babusiaux & Gilmore 2005; López-Corredoira et al. 2005; Merrifield 2004; Robin et al. 2003; Stanek et al. 1997; Rattenbury et al. 2007; Bissantz & Gerhard 2002; Binney et al. 1997). As already mentioned by Groenewegen & Blommaert (2005) the different results found in the literature with respect to the angle between the bar and the Sun-centre line (see e.g. our results in contrast to Whitelock 1992; Groenewegen & Blommaert 2005; López-Corredoira et al. 2007; Sevenster et al. 1999) could originate from a different spatial distribution of the stellar population these studies trace.

We also tested different star formation rates and metallicity distributions. A model with a star burst of 8 Gyr based on ZRO2003 gave the best results together with a metallicity distribution also based on ZRO2003 but shifted by 0.3 dex, although we could find no clear discrepancy between this model and the models with a star burst 10 Gyr ago could be found. We could not improve our fits including intermediate and/or young stars if we compared both the stars we selected in the defined bulge box and the red clump stars. Therefore we conclude that based on 2MASS and OGLE data comparisons with the TRILEGAL model we find best results for a population of 8 Gyr. Nevertheless it is still possible that there are also intermediate age stars located in the GB, although we could not trace them using our described method (see e.g. Uttenthaler et al. 2007; Groenewegen & Blommaert 2005).

Using the peak positions of the red clump stars and the distance to the Galactic centre retrieved by our minimisation procedures, we found that $M_I^{\rm RC} = -0.170 \pm_{0.066}^{0.069}$ . This value is consistent with recent values found in the literature, although it resembles best the values found by Girardi & Salaris (2001) using red clump stars in the solar neighbourhood ( $M_I^{\rm RC} = -0.171$ ) or using red clump stars in Baade's Window if $\alpha$ -enhancement is taken into account ( $M_I^{\rm RC} = -0.161$ ).

Acknowledgements

E.V. would like to thank the system administration group of the Institute for Astronomy in Leuven and in special E. Broeders for the helpful discussions with respect to the implementation of the described minimisation algorithms. L.G. acknowledges partial support by the University of Padova (Progetto di Ricerca di Ateneo CPDA052212). This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

Babusiaux, C., & Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef]
Binney, J., Gerhard, O., & Spergel, D. 1997, MNRAS, 288, 365 [NASA ADS]
Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef]
Bonatto, C., Bica, E., & Girardi, L. 2004, A&A, 415, 571 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Broyden, C. G. 1970, Journal of the Institute of Mathematics and Its Applications, 6, 76
Cabrera-Lavers, A., Hammersley, P. L., González-Fernández, C., et al. 2007, A&A, 465, 825 [NASA ADS] [CrossRef] [EDP Sciences]
Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] (In the text)
Decin, L., Hony, S., de Koter, A., et al. 2007, A&A, 475, 233 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [NASA ADS] [CrossRef]
Eidelman, S., Hayes, K., Olive, K., et al. 2004, Phys. Lett. B, 592 (In the text)
Eisenhauer, F., Schödel, R., Genzel, R., et al. 2003, ApJ, 597, L121 [NASA ADS] [CrossRef] (In the text)
Eisenhauer, F., Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef] (In the text)
Feast, M. W. 1997, MNRAS, 284, 761 [NASA ADS]
Feltzing, S., & Gilmore, G. 2000, A&A, 355, 949 [NASA ADS] (In the text)
Fernley, J. A., Jameson, R. F., Longmore, A. J., Watson, F. G., & Wesselink, T. 1987, MNRAS, 226, 927 [NASA ADS]
Fletcher, R. 1970, Comput. J., 13, 317 [CrossRef]
Freudenreich, H. T. 1998, ApJ, 492, 495 [NASA ADS] [CrossRef]
Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] (In the text)
Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] (In the text)
Girardi, L., & Salaris, M. 2001, MNRAS, 323, 109 [NASA ADS] [CrossRef] (In the text)
Girardi, L., Groenewegen, M. A. T., Weiss, A., & Salaris, M. 1998, MNRAS, 301, 149 [NASA ADS] [CrossRef] (In the text)
Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Goldfarb, D. 1970, Mathematics of Computation, 24, 23 [CrossRef] http://links.jstor.org/sici?sici=0025-5718D
Groenewegen, M. A. T., & Blommaert, J. A. D. L. 2005, A&A, 443, 143 [NASA ADS] [CrossRef] [EDP Sciences]
Groenewegen, M. A. T. 2008, A&A, 488, 835 (In the text)
Holtzman, J. A., Light, R. M., Baum, W. A., et al. 1993, AJ, 106, 1826 [NASA ADS] [CrossRef] (In the text)
López-Corredoira, M., Cabrera-Lavers, A., & Gerhard, O. E. 2005, A&A, 439, 107 [NASA ADS] [CrossRef] [EDP Sciences]
López-Corredoira, M., Cabrera-Lavers, A., Mahoney, T. J., et al. 2007, AJ, 133, 154 [NASA ADS] [CrossRef]
Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] (In the text)
Merrifield, M. R. 2004, in Milky Way Surveys: The Structure and Evolution of our Galaxy, ed. D. Clemens, R. Shah, & T. Brainerd, ASP Conf. Ser., 317, 289
Nishiyama, S., Nagata, T., Sato, S., et al. 2006, ApJ, 647, 1093 [NASA ADS] [CrossRef]
Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] (In the text)
Ortolani, S., Barbuy, B., Bica, E., et al. 2001, A&A, 376, 878 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Paczynski, B., & Stanek, K. Z. 1998, ApJ, 494, L219 [NASA ADS] [CrossRef]
Ramírez, S. V., Stephens, A. W., Frogel, J. A., & DePoy, D. L. 2000, AJ, 120, 833 [NASA ADS] [CrossRef] (In the text)
Rattenbury, N. J., Mao, S., Sumi, T., & Smith, M. C. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef]
Reid, M. J., Schneps, M. H., Moran, J. M., et al. 1988, ApJ, 330, 809 [NASA ADS] [CrossRef] (In the text)
Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences]
Rocha-Pinto, H. J., Maciel, W. J., Scalo, J., & Flynn, C. 2000a, A&A, 358, 850 [NASA ADS] (In the text)
Rocha-Pinto, H. J., Scalo, J., Maciel, W. J., & Flynn, C. 2000b, A&A, 358, 869 [NASA ADS] (In the text)
Sadler, E. M., Rich, R. M., & Terndrup, D. M. 1996, AJ, 112, 171 [NASA ADS] [CrossRef] (In the text)
Sevenster, M. N. 1999, MNRAS, 310, 629 [NASA ADS] [CrossRef] (In the text)
Sevenster, M., Saha, P., Valls-Gabaud, D., & Fux, R. 1999, MNRAS, 307, 584 [NASA ADS] [CrossRef] (In the text)
Shanno, D. F. 1970, Mathematics of Computation, 24, 647 [CrossRef] http://links.jstor.org/sici?sici=0025-5718F
Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
Stanek, K. Z., & Garnavich, P. M. 1998, ApJ, 503, L131 [NASA ADS] [CrossRef] (In the text)
Stanek, K. Z., Udalski, A., Szymanski, M., et al. 1997, ApJ, 477, 163 [NASA ADS] [CrossRef]
Sumi, T. 2004, MNRAS, 349, 193 [NASA ADS] [CrossRef] (In the text)
Udalski, A. 1998, Acta Astron., 48, 113 [NASA ADS]
Udalski, A. 2003, ApJ, 590, 284 [NASA ADS] [CrossRef] (In the text)
Udalski, A., Kubiak, M., & Szymanski, M. 1997, Acta Astron., 47, 319 [NASA ADS] (In the text)
Udalski, A., Szymanski, M., Kubiak, M., et al. 2002, Acta Astron., 52, 217 [NASA ADS] (In the text)
Uttenthaler, S., Hron, J., Lebzelter, T., et al. 2007, A&A, 463, 251 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
van Loon, J. T., Gilmore, G. F., Omont, A., et al. 2003, MNRAS, 338, 857 [NASA ADS] [CrossRef] (In the text)
Whitelock, P. 1992, in Variable Stars and Galaxies, in honor of M. W. Feast on his retirement, ed. B. Warner, ASP Conf. Ser., 30, 11
Wyse, R. F. G. 1995, in Stellar Populations, ed. P. C. van der Kruit, & G. Gilmore, IAU Symp., 164, 133 (In the text)
Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

Footnotes

... systems: Our experience is that the simulation of the 2MASS photometric system presents zero-point offsets of just a few 0.01 mag. Zero-point errors of similar magnitude are just expected in synthetic photometry applied to present-day libraries of synthetic spectra, and are also likely present in our simulations of the OGLE-II system.
... determinations: We recall that their $M_I^{\rm RC}$ values were derived from the Hipparcos sample of red clump stars with good parallax measurements, without applying any population correction between the Hipparcos and bulge samples. Girardi & Salaris (2001, their Table 4) estimated that this correction is smaller than 0.1 mag.

All Tables

Table 1: A not complete overview of recent values of parameters describing the GB, its bar and the distance to the GC.

Table 2: Properties of the selected fields.

Table 3: Overview of the different models described in the text.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig01.eps} \end{figure}$	Figure 1: Example of the photometric errors of the $K_{\rm s}$ -band 2MASS data for field bul_sc40.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig02.eps} \end{figure}$	Figure 2: $J - K_{\rm s}$ vs. $K_{\rm s}$ CMD for field bul_sc40. The figure on the left are the observations, the figure on the right is a model with R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The black dots in the model (right panel) are stars that originate from the disk, the dark blue dots originate from the halo and the red dots are bulge stars. This colour code will be used in all figures of this type. The light grey lines indicate the boxes used to compute the model with the observations.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig03.eps} \end{figure}$	Figure 3: Same figure and colour code as Fig. 2 for the same model but now for a V - I vs. I CMD. The additional box which is not seen in Fig. 2 is used to compare the red clump stars.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig04.eps} \end{figure}$	Figure 4: Example showing how the red clump stars are fitted using the method described by Stanek & Garnavich (1998). The black histogram are the stars selected from the ``red clump box'' in the V - I vs. I CMD and the grey line is the Gaussian fit with underlying second degree polynomial.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig05.eps} \end{figure}$	Figure 5: The left figure shows the SFR normalised to 1 and the right figure shows the metallicity distribution normalised to 1 (based on ZRO2003).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig06.eps} \end{figure}$	Figure 6: Histograms showing the distribution of selected bulge stars for field bul_sc40. The black line represents the observations, the red line the model. The left panel shows the 2MASS data, the right panel the OGLE data. The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.69$ , $\zeta = 0.30$ , $\phi = 20\hbox {$^\circ $ }$ , and f₀ = 422.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig07.eps} \end{figure}$	Figure 7: Histograms showing the distribution of selected bulge stars for field bul_sc40. The black line represents the observations, the red line the model. The upper panels shows the 2MASS data, the lower panels the OGLE data. The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003 but shifted with 0.3 dex. (This figure is also available in electronic form, showing histograms for all the modelled fields.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=16.4cm,clip]{8472fig08.eps} \end{figure}$	Figure 8: Histograms showing the distribution of selected bulge stars for all the modelled fields. The black line is the histogram for the observational data, the red line represents the model. For each field there are four panels, the first two panels shows the 2MASS data (one for star counts in $J - K_{\rm s}$ and one for the star counts in $K_{\rm s}$ . The other two panels show the star counts for the OGLE data (V - I and I). The model has the following parameters: R₀ = 8.6 kpc, a_m = 2.7 kpc, a₀ = 97 pc, $\eta = 0.68$ , $\zeta = 0.30$ , $\phi = 14\hbox {$^\circ $ }$ , and f₀ = 427.3. The star formation rate is a 10 Gyr burst and the metallicity distribution is based on ZRO2003 but shifted with 0.3 dex.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=16.5cm,clip]{8472fig09.eps} \end{figure}$	Figure 8: continued.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8472fig10.eps} \end{figure}$	Figure 9: Peak positions I₀ of the red clump stars corrected for extinction in function of the longitude $\ell$ .
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.