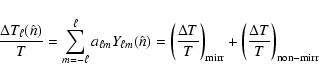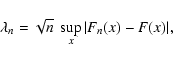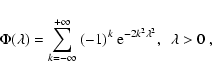| Issue |
A&A
Volume 498, Number 1, April IV 2009
|
|
|---|---|---|
| Page(s) | L1 - L3 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200911795 | |
| Published online | 25 March 2009 | |
LETTER TO THE EDITOR
Plane-mirroring anomaly in the cosmic microwave background maps
V. G. Gurzadyan1 - T. Ghahramanyan1 - A. L. Kashin1 - H. G. Khachatryan1 - A. A. Kocharyan1,2 - H. Kuloghlian1 - D. Vetrugno3 - G. Yegorian1
1 - Yerevan Physics Institute and Yerevan State University, Yerevan, Armenia
2 - School of Mathematical Sciences, Monash University, Clayton, Australia
3 - University of Lecce, Lecce, Italy
Received 5 February 2009 / Accepted 16 March 2009
Abstract
The plane-mirror symmetry previously noticed in the Cosmic Microwave Background (CMB)
temperature anisotropy maps of Wilkinson Microwave Anisotropy Probe is shown to possess
certain anomalous properties. The degree of the randomness determined by the Kolmogorov stochasticity parameter in both symmetry regions appears to have identical values which, however, essentially differ from the corresponding values for other sky regions. If the mirroring were of cosmological origin, this would imply either additional randomizing properties in those directions of the Universe or their different line-of-sight depth. This analysis also provides a way to test the hypothesis of a link between the nature of dark energy and inhomogeneities.
Key words: cosmic microwave background
1 Introduction
A signature of hidden plane-mirror symmetry in the CMB maps has been found in the Wilkinson Microwave Anisotropy Probe's (WMAP) temperature maps (Gurzadyan et al. 2007b). This is one of the non-Gaussianities among others reported for CMB properties (e.g. de Oliveira-Costa et al. 2004; Copi et al. 2007; Schwarz et al. 2004; Eriksen et al. 2004, 2007; Cruz et al. 2005, 2009; Gurzadyan et al. 2005, 2007; Morales & Saez 2008).
The symmetry revealed by the inhomogeneities in the distribution of the excursion sets
was shown to have the highest significance at low multipoles 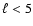 ,
while the effect quickly disappears at higher multipoles (Gurzadyan et al. 2008). This effect was studied in WMAP's 94 GHz W-band maps; the foreground-reduced maps (http://lambda.gsfc.nasa.gov/product/map/current/)
showed the negligible role of Galactic contamination.
,
while the effect quickly disappears at higher multipoles (Gurzadyan et al. 2008). This effect was studied in WMAP's 94 GHz W-band maps; the foreground-reduced maps (http://lambda.gsfc.nasa.gov/product/map/current/)
showed the negligible role of Galactic contamination.
We now use another descriptor to probe the properties of the mirror symmetry regions, the Kolmogorov stochasticity parameter (Kolmogorov 1933; Arnold 2008a,b), which describes the degree of randomness of number sequences from dynamical systems or number theory that can be applied to CMB data. As a result, a map of the degree of randomness of the CMB can be created which shows regions of high and low randomness (Gurzadyan et al. 2008; Gurzadyan et al. 2009). Among the high randomness regions is for example the Cold Spot, a southern non-Gaussian anomaly (see Cruz et al. 2009).
Applying the Kolmogorov parameter to the mirror symmetry regions, we found that
both areas within 3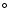 radius have coinciding values of randomness, but
that the value is different from those of other equal size regions.
This indicates either the existence of an extra randomizing factor in the
directions of the mirror symmetry centers or different spatial depth scales in those directions.
radius have coinciding values of randomness, but
that the value is different from those of other equal size regions.
This indicates either the existence of an extra randomizing factor in the
directions of the mirror symmetry centers or different spatial depth scales in those directions.
2 Mirror symmetry regions
Mirroring symmetry has been revealed in WMAP's 3-year, and then in the 5-year 94 GHz
W-band maps (Hinshaw et al. 2008). This band has the highest resolution,
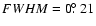 ,
and the least contamination by the Galactic synchrotron background.
,
and the least contamination by the Galactic synchrotron background.
The role of the Galactic disk was minimized via exclusion of the equatorial belt
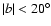 ,
and as mentioned, the foreground-reduced maps were used to confirm the negligible contribution of the dust.
,
and as mentioned, the foreground-reduced maps were used to confirm the negligible contribution of the dust.
The distribution of the excursion sets at the temperature interval within
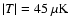 was shown to be concentrated around almost antipodal centers (Gurzadyan et al. 2007b)
was shown to be concentrated around almost antipodal centers (Gurzadyan et al. 2007b)
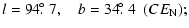 |
|||
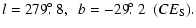 |
The locations of
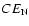 and
and
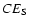 are not special with respect to the
positions of the sum of the multipole vectors up to
are not special with respect to the
positions of the sum of the multipole vectors up to 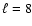 (the modulus of the vectors weighted by
(the modulus of the vectors weighted by
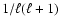 ), or,
for example, to the Cold Spot (Cruz et al. 2005). The positions are close
to those of the Maxwellian vectors of multipole
), or,
for example, to the Cold Spot (Cruz et al. 2005). The positions are close
to those of the Maxwellian vectors of multipole 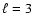 ,
and drift towards the equator at
higher temperature intervals.
,
and drift towards the equator at
higher temperature intervals.
The mirroring was studied in the context of the topology of the Universe
for a multipole dependence (Starobinsky 1993), i.e.
where on the right hand side the first mirrored term can dominate at low multipoles, while the second, non-mirrored term becomes the main one at higher multipoles.
Partial mirroring given by Eq. (1) does not necessarily imply the dominance of multipoles with 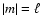 ,
i.e. planarity, since in the first term on the right hand side of Eq. (1) all
,
i.e. planarity, since in the first term on the right hand side of Eq. (1) all
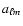 with an even value of
with an even value of 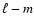 may be non-zero.
may be non-zero.
WMAP5 maps show stronger mirroring at low multipoles, i.e.
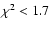 for
for 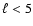 ,
with monotonic weakening at higher multipoles:
,
with monotonic weakening at higher multipoles:
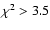 at
at 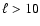 (Gurzadyan et al. 2008).
(Gurzadyan et al. 2008).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1795fig1.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11795-09/Timg22.gif) |
Figure 1: Map of the degree of randomness (Kolmogorov map) for CMB WMAP's data with indicated mirror symmetry centers. |
| Open with DEXTER | |
3 Kolmogorov's stochasticity parameter and the symmetry regions
Considering the CMB maps as sequences of numbers indicating the pixelized temperature, one can represent the sky distribution of the Kolmogorov stochasticity parameter (Gurzadyan & Kocharyan 2008).
Kolmogorov's statistic and parameter are defined (Kolmogorov 1933; Arnold 2008a) for n independent numbers
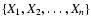 of the random variable X ordered in an increasing manner
of the random variable X ordered in an increasing manner
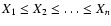 .
The cumulative distribution function (CDF) of X is
.
The cumulative distribution function (CDF) of X is
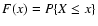 .
The stochasticity parameter
.
The stochasticity parameter 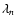 is defined by the limit (Kolmogorov 1933)
is defined by the limit (Kolmogorov 1933)
where the empirical distribution function Fn(x) is
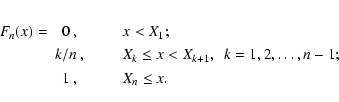
For any continuous CDF F the convergence is uniform for
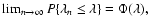 where
where
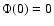 ,
and independent of F (Kolmogorov 1933).
,
and independent of F (Kolmogorov 1933).
The values of the function 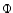 for Gaussian CDF estimated for the mirroring regions of radius 3
for Gaussian CDF estimated for the mirroring regions of radius 3 centered on
centered on
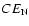 and
and
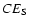 (Fig. 1) are given in Table 1. For comparison the values for equal size regions but situated at two other antipodes (i.e. shifted by 180
(Fig. 1) are given in Table 1. For comparison the values for equal size regions but situated at two other antipodes (i.e. shifted by 180 )
as well as for two intermediate regions are also represented.
)
as well as for two intermediate regions are also represented.
Table 1:
Mean values for
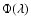 for the mirroring (1 and 2, boldface) and 4 other regions.
for the mirroring (1 and 2, boldface) and 4 other regions.
The situation with region 4 is indicative: its mean
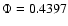 is decreased
to the value given in the Table when the data of a single pixel with high randomness (0.7) situated there are cancelled. Instead, the randomness for the mirroring regions is stable
with respect to analogical pixel elimination or shifts. Figure 2 represents the variation of
is decreased
to the value given in the Table when the data of a single pixel with high randomness (0.7) situated there are cancelled. Instead, the randomness for the mirroring regions is stable
with respect to analogical pixel elimination or shifts. Figure 2 represents the variation of 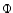 vs the radius, where the difference between the mirroring regions and the others is also seen.
vs the radius, where the difference between the mirroring regions and the others is also seen.
This shows that the regions centered at
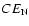 and
and
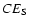 possess large scale randomness of a degree equal to each other but 3-5 times higher and of different behavior than those for typical regions of the sky.
possess large scale randomness of a degree equal to each other but 3-5 times higher and of different behavior than those for typical regions of the sky.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1795fig2.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11795-09/Timg37.gif) |
Figure 2:
The degree of randomness |
| Open with DEXTER | |
4 Discussion
Figure 1 shows the sky map of the distribution of the degree of randomness of the CMB,
as discussed above. The centers of the mirror symmetry are shown, which are distinguished by higher values of Kolmogorov's parameter (randomness) than other regions; this can be followed even in Fig. 1 due to the domination of high- structures in the vicinity of the symmetry centers.
structures in the vicinity of the symmetry centers.
Thus we see enhanced randomness in the mirrored regions; either the randomizing effect is not isotropic and is dominant over those directions, or the line-of-sight depth is greater in those directions. Among the cosmological randomizing mechanisms can be the inhomogeneous matter distribution in the Universe, i.e. when the voids due to their hyperbolic, diverging lensing properties can cause randomization of the temperature distribution in the CMB maps (Gurzadyan & Kocharyan 2009). The voids, including those of large scale, are among the discussed reasons also for the Cold Spot, (see Inoue & Silk 2007; Das & Spergel 2008). If the mirroring symmetry were of cosmological nature, it could be a result of a combination of topological and of the integrated Sachs-Wolfe effects (Zeldovich 1973; Sokolov & Schwartsman 1975; Sokolov & Starobinsky 1975; Zeldovich & Starobinsky 1984; Kofman & Starobinsky 1985; Starobinsky 1993; de Oliveira-Costa et al. 1996).
There have been attempts to link the nature of the dark energy with light propagation effects (lensing) due to inhomogeneities (see Mattsson 2007; Wiltshire 2008; Biswas & Notari 2008; Larena et al. 2008). Our analysis provides a way to test such a link, namely, if the inhomogeneities, i.e. the voids, are causing the randomization in the CMB, then the dark energy evolution vs redshift and the corresponding Hubble diagram have to differ in the plane-mirroring directions with respect to other directions.
Thus, with Kolmogorov's stochasticity parameter one has another indicator which supports the anomalous symmetry in CMB maps and acts as a quantitative descriptor of underlying effects.
Acknowledgements
We are grateful to A. A. Starobinsky for valuable discussions and the referee for helpful comments.
References
- Arnold, V. 2008a, Nonlinearity, 21, T109 [NASA ADS] [CrossRef] (In the text)
- Arnold, V. I. 2008b, ICTP/2008/001, Trieste
- Biswas, T., & Notari, A. 2008, JCAP, 06, 021 [NASA ADS] (In the text)
- Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2007, Phys. Rev. D, 75, 023507 [NASA ADS] [CrossRef] (In the text)
- Cruz, M., Martinez-Gonzalez, E., Vielva, P., & Cayon, L. 2005, MNRAS, 356, 29 [NASA ADS] [CrossRef] (In the text)
- Cruz, M., Martinez-Gonzalez, E., & Vielva, P. [arXiv:0901.1986] (In the text)
- Das, S., & Spergel, D. N. 2008 [arXiv:0809.4704] (In the text)
- Eriksen, H., Banday, A. J., Gorski, K. M., & Lilje, P. B. 2004, ApJ, 612, 633 [NASA ADS] [CrossRef] (In the text)
- Eriksen, H. K., Banday, A. J., Górski, K. M., et al. 2007, ApJ, 660, L81 [NASA ADS] [CrossRef] (In the text)
- Gurzadyan, V. G., & Kocharyan, A. A. 2008, A&A, 492, L33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gurzadyan, V. G., & Kocharyan, A. A. 2009, A&A, 493, L61 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gurzadyan, V. G., de Bernardis, P., & de Troia, G. 2005, Mod. Phys. Lett. A, 20, 813 [NASA ADS] [CrossRef] (In the text)
- Gurzadyan, V. G., Bianco, C. L., Kashin, A. L., et al. 2007a, Phys. Lett. A, 363, 121 [NASA ADS] [CrossRef] (In the text)
- Gurzadyan, V. G., Starobinsky, A. A., Kashin, A. L., et al. 2007b, Mod. Phys. Lett. A, 22, 2955 [NASA ADS] [CrossRef] (In the text)
- Gurzadyan, V. G., Starobinsky, A. A., Ghahramanyan, T., et al. 2008, A&A, 490, 929 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gurzadyan, V. G., Allahverdyan, A. E., et al. 2009, A&A, in press [arXiv:0811.2832] (In the text)
- Hinshaw, G., J. L. Weiland, J. L., et al. 2008 [arXiv:0803.0732] (In the text)
- Inoue, K. T., & Silk, J. 2007, ApJ, 664, 650 [NASA ADS] [CrossRef] (In the text)
- Kofman, L. A., & Starobinsky, A. A. 1985, Sov. Astron. Lett., 11, 271 [NASA ADS]
- Kolmogorov, A. N. 1933, G. Ist. Ital. Attuari, 4, 83 (In the text)
- Larena, J., Alimi, J.-M., Buchert, Thomas, K., et al. 2008 [arXiv:0808.1161] (In the text)
- Mattsson, T. 2007 [arXiv:0711.4264] (In the text)
- Morales, J. A., & Saez, D. [arXiv:0802.1042] (In the text)
- de Oliveira-Costa, A., Smoot, G. F., & Starobinsky, A. A. 1996, ApJ, 468, 457 [NASA ADS] [CrossRef] (In the text)
- de Oliveira-Costa, A., Tegmark, M., Zaldarriaga, M., & Hamilton, A. 2004, Phys. Rev. D, 69, 063516 [NASA ADS] [CrossRef] (In the text)
- Schwarz, D. J., Starkman, G. D., Huterer, D., & Copi, C. J. 2004, Phys. Rev. Lett., 93, 221301 [NASA ADS] [CrossRef] (In the text)
- Sokolov, D. D., & Schwartsman, V. F. 1975, Sov. Phys. - JETP, 39, 196 [NASA ADS] (In the text)
- Sokolov, D. D., & Starobinsky, A. A. 1975, Sov. Astron., 19, 629 [NASA ADS] (In the text)
- Starobinsky, A. A. 1993, JETP Lett., 57, 622 [NASA ADS] (In the text)
- Wiltshire, D. L. 2008, Int. J. Mod. Phys. D, 17, 641 [NASA ADS] [CrossRef] (In the text)
- Zeldovich, Ya. B. 1973, Comm. Astroph. Space Phys., 5, 169 [NASA ADS] (In the text)
- Zeldovich, Ya. B., & Starobinsky, A. A. 1984, Sov. Astron. Lett., 10, 135 [NASA ADS] (In the text)
All Tables
Table 1:
Mean values for
![]() for the mirroring (1 and 2, boldface) and 4 other regions.
for the mirroring (1 and 2, boldface) and 4 other regions.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1795fig1.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11795-09/Timg22.gif) |
Figure 1: Map of the degree of randomness (Kolmogorov map) for CMB WMAP's data with indicated mirror symmetry centers. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1795fig2.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11795-09/Timg37.gif) |
Figure 2:
The degree of randomness |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.