| Issue |
A&A
Volume 498, Number 1, April IV 2009
|
|
|---|---|---|
| Page(s) | 37 - 47 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200811366 | |
| Published online | 11 March 2009 | |
Keck spectroscopic survey of strongly lensed galaxies in Abell 1703: further evidence of a relaxed, unimodal cluster
J. Richard1,2,![]() - L. Pei2 - M. Limousin3,4 - E. Jullo5 - J. P. Kneib5
- L. Pei2 - M. Limousin3,4 - E. Jullo5 - J. P. Kneib5
1 - Durham University, Physics and Astronomy Department, South Road, Durham DH1 3LE, UK
2 - Caltech Astronomy, MC105-24, Pasadena, CA 91125, USA
3 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 57 avenue d'Azereix, 65000 Tarbes, France
4 - Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Marie Vej 30, 2100 Copenhagen, Denmark
5 - Laboratoire d'Astrophysique de Marseille, OAMP, CNRS-Université Aix-Marseille, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
Received 17 November 2008 / Accepted 30 January 2009
Abstract
Context. Strong gravitational lensing is a unique tool that can be used to accurately model the inner mass distribution of massive galaxy clusters. In particular, clusters with large Einstein radii provide a wealth of multiply imaged systems in the cluster core. Measuring the redshift of these multiple images provides strong constraints for precisely determining the shape of the central dark matter profile.
Aims. This paper presents a spectroscopic survey of strongly lensed galaxies in the massive cluster lens Abell 1703, which displays a large Einstein radius (28
![]() at z=2.8) and numerous strongly-lensed systems including a central ring-like configuration.
at z=2.8) and numerous strongly-lensed systems including a central ring-like configuration.
Methods. We used the LRIS spectrograph on Keck to target multiple images and lensed galaxy candidates, and used the measured spectroscopic redshifts to constrain the mass distribution of the cluster using a parametric model.
Results. The spectroscopic data enable us to measure accurate redshifts for 7 sources at z>2 , all of which are in good agreement with their photometric redshifts. We update the identification of multiply imaged systems by discovering 3 new systems and identifying a radial counter image. We also report the discovery of a remarkably bright ![]() 3.6 L* i-band dropout at z=5.827 in our mask and it is only moderately magnified by the cluster (
3.6 L* i-band dropout at z=5.827 in our mask and it is only moderately magnified by the cluster (
![]() ). The improved parametric mass model, including 16 multiple systems with 10 spectroscopic redshifts, further constrains the smooth cluster-scale mass distribution with a generalized NFW profile of best-fit logarithmic slope
). The improved parametric mass model, including 16 multiple systems with 10 spectroscopic redshifts, further constrains the smooth cluster-scale mass distribution with a generalized NFW profile of best-fit logarithmic slope
![]() ,
concentration
,
concentration
![]() and scale radius
and scale radius
![]() kpc. The overall rms in the image plane is 1.3
kpc. The overall rms in the image plane is 1.3
![]() .
.
Conclusions. Our strong-lensing model allows us to predict a large-scale shear signal that is consistent with weak-lensing measurements inferred from Subaru data out to 4 Mpc h-1. Also considering the strong-lensing modeling requires a single dark matter clump, this suggests that Abell 1703 is a relaxed, unimodal cluster. This unique cluster could be probed further using deep X-ray, SZ, and dynamics analysis for a detailed study of the physics in a relaxed cluster.
Key words: galaxies : high-redshift - galaxies: distances and redshifts - galaxies: clusters: individual: Abell 1703 - gravitational lensing
1 Introduction
Massive galaxy clusters with large Einstein radii (
![]()
![]() )
offer a wealth of information about their central mass distribution by displaying large numbers of multiple images in their strong-lensing regions. The most striking case is the cluster Abell 1689, with
)
offer a wealth of information about their central mass distribution by displaying large numbers of multiple images in their strong-lensing regions. The most striking case is the cluster Abell 1689, with
![]()
![]() (Limousin et al. 2007; Broadhurst et al. 2005), which holds the largest number of
strong lensing constraints in a single field. This gives an opportunity to map inner-mass profiles to a high level of precision. Parametric cluster-lens mass models have been widely used (Smith et al. 2005; Kneib et al. 1996; Richard et al. 2007), but accurate redshift information is necessary
to construct accurate mass models and obtain their fiducial parameters.
Only one redshift of a set of multiple images enables us to estimate the absolute total mass within the Einstein radius. Adding many more redshifts allows us to measure the full central mass profile accurately. Even though photometric redshifts offer an acceptable level of precision for such modeling (Broadhurst et al. 2005; Bradac et al. 2008), spectroscopic redshifts are the most reliable way to confirm the identifications and find new multiply-imaged systems. Lowering the redshift error on the multiple systems with spectroscopy has another tool, because one can use strong-lensing to constrain the cosmological parameters w and
(Limousin et al. 2007; Broadhurst et al. 2005), which holds the largest number of
strong lensing constraints in a single field. This gives an opportunity to map inner-mass profiles to a high level of precision. Parametric cluster-lens mass models have been widely used (Smith et al. 2005; Kneib et al. 1996; Richard et al. 2007), but accurate redshift information is necessary
to construct accurate mass models and obtain their fiducial parameters.
Only one redshift of a set of multiple images enables us to estimate the absolute total mass within the Einstein radius. Adding many more redshifts allows us to measure the full central mass profile accurately. Even though photometric redshifts offer an acceptable level of precision for such modeling (Broadhurst et al. 2005; Bradac et al. 2008), spectroscopic redshifts are the most reliable way to confirm the identifications and find new multiply-imaged systems. Lowering the redshift error on the multiple systems with spectroscopy has another tool, because one can use strong-lensing to constrain the cosmological parameters w and
![]() based on purely geometrical considerations (Golse et al. 2002; Link & Pierce 1998).
based on purely geometrical considerations (Golse et al. 2002; Link & Pierce 1998).
On the theoretical side, Broadhurst & Barkana (2008) have compared the measured lensing parameters for a sample of clusters with large ![]() to predictions from the standard
to predictions from the standard ![]() CDM cosmology, and report a 4-
CDM cosmology, and report a 4-![]() discrepancy in the existence of such large
discrepancy in the existence of such large ![]() for the corresponding virial mass. Their result, based on a sample of massive halos derived from the Millennium simulation, includes a full treatment of the projection effects, which strongly bias this sample towards alignments of the triaxial dark-matter halos along the line of sight.
This bias is also pointed out by Oguri & Blandford (2009), who investigated a full-sky Monte-Carlo realizations of massive clusters. They show that, although the population of clusters with large Einstein radii is scarce, it is possible to find Einstein radii as large as 50
for the corresponding virial mass. Their result, based on a sample of massive halos derived from the Millennium simulation, includes a full treatment of the projection effects, which strongly bias this sample towards alignments of the triaxial dark-matter halos along the line of sight.
This bias is also pointed out by Oguri & Blandford (2009), who investigated a full-sky Monte-Carlo realizations of massive clusters. They show that, although the population of clusters with large Einstein radii is scarce, it is possible to find Einstein radii as large as 50
![]() in the whole sky, under the assumptions of a WMAP5 cosmology. The main difference beween Broadhurst & Barkana (2008) and Oguri & Blandford (2009) is that the latter treats the sample as a whole-sky survey, which is far more representative of the observed population than the Millennium simulation, which only covers a small volume of
in the whole sky, under the assumptions of a WMAP5 cosmology. The main difference beween Broadhurst & Barkana (2008) and Oguri & Blandford (2009) is that the latter treats the sample as a whole-sky survey, which is far more representative of the observed population than the Millennium simulation, which only covers a small volume of ![]() 5000 Mpc3. This undermines any disagreement between the presence of large
5000 Mpc3. This undermines any disagreement between the presence of large ![]() and
and ![]() -CDM.
-CDM.
Among the clusters with large ![]() ,
we have started to study the mass distribution of
Abell 1703, in Limousin et al. (2008), hereafter L08. This is one of the richest clusters discovered in the Sloan Digital Sky Survey (SDSS), and it shows strong gravitational lensing (Hennawi et al. 2008). In this previous work, we identified 13 systems forming highly-magnified
multiple images, including a central ring. Based on the spectroscopic redshift of this central feature and photometric redshifts for the remaining images, all the lensing systems have been reproduced by a single NFW (Navarro et al. 1997) profile for the dark matter, making Abell 1703 relatively simpler than other bimodal lensing clusters (e.g. Elíasdóttir et al. 2007 for Abell 2218; Richard et al. 2007 for Abell 68; Verdugo et al. 2007 for MS2053). We therefore decided to use it as a more reliable probe for comparing the results of strong and weak-lensing measurements in clusters with large Einstein radii from Broadhurst et al. (2008).
,
we have started to study the mass distribution of
Abell 1703, in Limousin et al. (2008), hereafter L08. This is one of the richest clusters discovered in the Sloan Digital Sky Survey (SDSS), and it shows strong gravitational lensing (Hennawi et al. 2008). In this previous work, we identified 13 systems forming highly-magnified
multiple images, including a central ring. Based on the spectroscopic redshift of this central feature and photometric redshifts for the remaining images, all the lensing systems have been reproduced by a single NFW (Navarro et al. 1997) profile for the dark matter, making Abell 1703 relatively simpler than other bimodal lensing clusters (e.g. Elíasdóttir et al. 2007 for Abell 2218; Richard et al. 2007 for Abell 68; Verdugo et al. 2007 for MS2053). We therefore decided to use it as a more reliable probe for comparing the results of strong and weak-lensing measurements in clusters with large Einstein radii from Broadhurst et al. (2008).
We present in this paper results from a spectroscopic survey conducted at Keck using the LRIS instrument, aiming at confirming the photometric redshifts, multiple images identification, and precisely constraining the mass distribution in Abell 1703. We obtained new spectroscopic redshift measurements for most of the systems identified by L08 (10 out of 13), in good agreement with their
corresponding photometric redshifts. We also report an exceptionally bright i-band dropout at ![]() ,
forming a magnified single image close to the region of multiple images. We further identify three new systems of multiple images and constrain the lensing model, as well as comparing the weak-lensing extrapolation of our model to the recently measured weak-lensing profile of Broadhurst et al. (2008).
,
forming a magnified single image close to the region of multiple images. We further identify three new systems of multiple images and constrain the lensing model, as well as comparing the weak-lensing extrapolation of our model to the recently measured weak-lensing profile of Broadhurst et al. (2008).
We present the observations and data reduction of the spectroscopic data in Sect. 2. Section 3 gives the redshift measurements, spectra, and the main results from the mass modeling. We discuss these results in Sect. 4. Throughout the paper, we used a standard ![]() -CDM model with
-CDM model with
![]() ,
,
![]() ,
and H0=70 km s-1 Mpc -1, whenever necessary. In this cosmology, 1
,
and H0=70 km s-1 Mpc -1, whenever necessary. In this cosmology, 1
![]() on the sky is equivalent to a physical distance of 4.244 kpc at the redshift z = 0.28 of the cluster. All magnitudes are quoted in the AB system.
on the sky is equivalent to a physical distance of 4.244 kpc at the redshift z = 0.28 of the cluster. All magnitudes are quoted in the AB system.
2 Observations
2.1 Imaging and photometric redshifts
The current study is based on the same imaging data as described in L08, based on Hubble Space Telescope and Subaru observations of Abell 1703 covering broad-band filters from B to H. These images were previously used to derive photometric redshifts with the software Hyperz (Bolzonella et al. 2000). We briefly summarize the characteristic parameters, central wavelength, and depth, of these images in Table 1.
2.2 Keck spectroscopy
We used the Low Resolution Imager and Spectrograph (LRIS, Oke et al. 1995) on the Keck telescope to perform multi-slit observations of the Abell 1703 cluster field. We designed a multi-slit mask containing 32 slits of 1.0
![]() width to include as many of the multiple systems previously identified in L08 as possible, with a few tilted slits following the geometry of long arcs (Fig. 1). In the case of fainter or less reliable identifications, independent images of the same system were observed in separate slits. Additional slits in the mask included new multiple systems candidates, cluster members, and background galaxies as estimated
through their photometric redshifts.
width to include as many of the multiple systems previously identified in L08 as possible, with a few tilted slits following the geometry of long arcs (Fig. 1). In the case of fainter or less reliable identifications, independent images of the same system were observed in separate slits. Additional slits in the mask included new multiple systems candidates, cluster members, and background galaxies as estimated
through their photometric redshifts.
Table 1: Summary of the broad-band images used for the photometry.
![\begin{figure}
\par\includegraphics[height=13.5cm,angle=0]{1366fig1.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg19.gif) |
Figure 1: ACS color image of Abell 1703 (combination of the HST filters F450W, F606W and F850LP), showing the location of all the multiply-imaged systems included in this study. The white cross at the center of the image marks the location of the brightest cluster galaxy, which has been subtracted for clarity. The dashed line outlines the limit of the region where we expect multiple images up to z=6. The systems presented in L08 are shown in white, and the new systems presented in this work are shown in red. Squares identify the multiple images with spectroscopic redshifts.The green triangle located to the lower right marks the location of the i-band dropout presented in Sect. 3.2. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=3.3cm]{1366fig2a.eps}\hspace*{2m...
...s}\hspace*{2mm}
\includegraphics[width=5.3cm]{1366fig2x.eps} }
\par
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg20.gif) |
Figure 2: BVI ACS color image close-up on individual z>0.5 sources in the LRIS mask with the location of the slit, and corresponding extracted spectra. The i-band dropout (23, see Sect. 3.2) is presented separately in Fig. 4. |
| Open with DEXTER | |
![\begin{figure}
\mbox{\includegraphics[width=3.3cm]{1366fig3a.eps}\hspace*{2mm}
\...
...o.eps}\hspace*{2mm}
\includegraphics[width=5.3cm]{1366fig3p.eps} }\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg21.gif) |
Figure 3: Continuation of Fig. 2. |
| Open with DEXTER | |
The LRIS instrument was set up with a 6800 Å dichroic isolating the blue arm, with a 300-line/mm grism blazed at 5000 ![]() ,
from the red arm, with a 600-line/mm grating blazed at 7500 Å. This ensures a high throughput over the wavelength range 3500 to 9500 Å and good spectral resolution in the red to resolve skylines as well as
,
from the red arm, with a 600-line/mm grating blazed at 7500 Å. This ensures a high throughput over the wavelength range 3500 to 9500 Å and good spectral resolution in the red to resolve skylines as well as
![]() emission line doublets
in the redshift range 0.85-1.40. This instrument setup is also well-matched with the photometric redshift estimates of the targeted sources. We obtained 2 h of exposure time on 2008 May 10 in photometric conditions and very good seeing (0.7
emission line doublets
in the redshift range 0.85-1.40. This instrument setup is also well-matched with the photometric redshift estimates of the targeted sources. We obtained 2 h of exposure time on 2008 May 10 in photometric conditions and very good seeing (0.7
![]() ).
).
2.3 Data reduction and redshift measurements
Data reduction of the spectra was performed using the Python version of the Kelson (2003) reduction scripts, which offer the advantage of processing the images in their distorted framework. This helps to reduce noise correlations, in particular for the case of tilted slits. We performed standard reduction steps for bias removal, flat-field correction, wavelength calibration, sky subtraction, and cosmic-ray rejection, and used observations of the standard star BD+33-2642 obtained on the same night to derive the flux calibration.
Close-ups on the targets and extracted spectra are presented in Figs. 2 and 3. We measured the redshift for 33 sources in the entire LRIS mask. The spectra show either Lyman-![]() (in absorption or emission) with additional ultraviolet absorption lines in the blue part or a resolved doublet of
(in absorption or emission) with additional ultraviolet absorption lines in the blue part or a resolved doublet of
![]() )
in the red part of the spectrum. In two multiple systems (10/11 and 16), we observed these images in multiple slits: redshift measurements were obtained by identifying significant absorption lines after stacking the relevant
exposures. For each spectrum, the average redshift value is obtained from the peaks of the main spectral features identified, while the corresponding error is taken from the spectral dispersion. Additional uncertainties generated by the accuracy of the relative and absolute wavelength calibrations, about 1.1 and 1.5 Å, respectively, were quadratically added to yield the final redshift errors. A confidence class
)
in the red part of the spectrum. In two multiple systems (10/11 and 16), we observed these images in multiple slits: redshift measurements were obtained by identifying significant absorption lines after stacking the relevant
exposures. For each spectrum, the average redshift value is obtained from the peaks of the main spectral features identified, while the corresponding error is taken from the spectral dispersion. Additional uncertainties generated by the accuracy of the relative and absolute wavelength calibrations, about 1.1 and 1.5 Å, respectively, were quadratically added to yield the final redshift errors. A confidence class
![]() ,
ranging from 1 to 4, was assigned to
each measurement according to the prescription of Le Fevre et al. (1995), which corresponds to a probability level for a correct identification of 50%, 75%, 95%, and 100%, respectively. A specific value of 9 is used when only a single secure spectral feature is seen in emission.
,
ranging from 1 to 4, was assigned to
each measurement according to the prescription of Le Fevre et al. (1995), which corresponds to a probability level for a correct identification of 50%, 75%, 95%, and 100%, respectively. A specific value of 9 is used when only a single secure spectral feature is seen in emission.
Table 2: Overview of the sources included in the LRIS mask.
Table 2 summarizes the redshift measurements
![]() ,
confidence class
,
confidence class
![]() and the spectral features used to derive the redshift for all
objects detected in the LRIS mask, including those additional targets serendipitously falling into the slits. For the majority of sources located within the ACS
field of view, we report the corresponding photometric redshift
and the spectral features used to derive the redshift for all
objects detected in the LRIS mask, including those additional targets serendipitously falling into the slits. For the majority of sources located within the ACS
field of view, we report the corresponding photometric redshift
![]() in the same table. We find good agreement between individual
in the same table. We find good agreement between individual
![]() and
and
![]() values, with a typical error
values, with a typical error
![]() or
or
![]() and no catastrophic measurements. This strong consistency mainly stems from the use of space-based images of very similar PSF size, together with ground-based near-infrared images obtained with MOIRCS in excellent seeing
conditions (0.4
and no catastrophic measurements. This strong consistency mainly stems from the use of space-based images of very similar PSF size, together with ground-based near-infrared images obtained with MOIRCS in excellent seeing
conditions (0.4
![]() ).
).
Table 3: Location and redshift estimate of three new multiply-image systems, as well as the radial feature (10.4) associated with the giant arc (systems 10 and 11).
3 Results
3.1 Multiple images redshifts and identifications
Figure 1 presents a color image of the central region of Abell 1703, combining the B, V, and Z ACS filters, where we marked in white the location of the 11 multiply imaged sources identified in our previous work (L08). Our spectroscopic data enabled us to measure the redshifts for the following 8 systems (displayed as white squares in Fig. 1):
- system 1 at z=0.8889 forms a very highly magnified ring-shaped configuration with 4 images close to the BCG and a less-magnified 5th image to the south west. Although its redshift was previously derived in L08, we obtained a new spectrum with the same mask in much better conditions;
- system 3 at z=3.277 is located to the north of the BCG, with 3 images: 2 bright merging images and a fainter counter-image to the west;
- systems 4/5 at z=1.9082 are two individual regions identified in the same source, which forms a cusp configuration of 3 images;
- system 6 at z=2.360 is a similar configuration as systems 4/5, but closer to the center of the cluster;
- system 7 at z=2.983 is again a cusp configuration like systems 4/5, but farther from the center of the cluster;
- systems 10/11 at z=2.627 are two individual regions identified in the giant tangential arc to the south east of the BCG. A fainter counter-image is located to the west. The new mass model presented here enabled us to associate the radial feature reported in L08, very close to the BCG (next to the ring configuration of system 1) to be a 4th image (10.4) associated with this arc;
- system 15 at z=2.355 is a typical Einstein-cross configuration of 4 images surrounding the BCG. We note that systems 6 (z=2.360) and 15 (z=2.355) have similar redshifts and are therefore very close to one another in the source plane, with a projected separation of
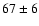 kpc;
kpc;
- system 16 at z=2.810 is another Einstein-cross configuration located at a slightly higher redshift, but found very close to system 15 in the image plane due to projection effects.
Apart from system 1, all the other systems are located in the redshift range 1.9<z<3.3. Using the new spectroscopic redshifts into the mass model (see Sect. 3.3), we have computed the predicted region of multiple images for a redshift z=6 (Fig. 1). As we expect all the multiple images present in the HST optical bands to lie within this region, we use it to update our systematic search for multiple images based on the photometric redshift catalog.
We find three additional systems complementing the list presented in L08. We display them in Fig. 1 and report the corresponding positions and photometric redshifts in Table 3:
- system 12 is again a typical cusp configuration of 3 images located to the north and ``following'' the nearby systems 4/5, 7, 8 and 9;
- systems 13 and 14 are two other Einstein-cross configurations of 4 images surrounding the BCG. System 14 is located near systems 15 and 16 in the image plane, while system 13 is closer to the cluster center.
3.2 Spectroscopy of a remarkably bright i-dropout
One of the sources in the LRIS mask, identified as 23 in the spectroscopic catalog (Table 2), deserves particular attention. Located to the south west of the cluster center (green triangle in Fig. 1), it has been selected for its very red
![]() color and bright
color and bright
![]() ,
while undetected blueward of the i band in the other deep ACS images. The NICMOS and MOIRCS photometry
,
while undetected blueward of the i band in the other deep ACS images. The NICMOS and MOIRCS photometry
![]() and
and
![]() further constrain its spectral energy distribution to be compatible with a photometric redshift
further constrain its spectral energy distribution to be compatible with a photometric redshift
![]() (Fig. 4, top and middle panels), and the i-z color make it a very strong i-dropout photometric candidate according to the Bouwens et al. (2006)
selection criterion.
(Fig. 4, top and middle panels), and the i-z color make it a very strong i-dropout photometric candidate according to the Bouwens et al. (2006)
selection criterion.
The LRIS spectrum for this object covers the wavelength range 3800-9230 Å,
corresponding to
2.12< z<6.59 for Lyman-![]() .
We detect a 5
.
We detect a 5![]() -significant emission line
at
-significant emission line
at
![]() Å (Fig. 4, lower panel), with an integrated flux
Å (Fig. 4, lower panel), with an integrated flux
![]() erg s-1 cm-2, and an observed equivalent width W>50 Å when assuming a 5
erg s-1 cm-2, and an observed equivalent width W>50 Å when assuming a 5![]() upper limit on the underlying continuum. This line is slightly resolved in the spectral direction, with a possibly asymmetric profile. To estimate this asymmetry, we used the weighted skewness statistics Sw, which is based on the third momentum of the flux distribution fi (seen as an array of size N) and was used as a selection criterion for Lyman-
upper limit on the underlying continuum. This line is slightly resolved in the spectral direction, with a possibly asymmetric profile. To estimate this asymmetry, we used the weighted skewness statistics Sw, which is based on the third momentum of the flux distribution fi (seen as an array of size N) and was used as a selection criterion for Lyman-![]() emitters (LAEs, Kashikawa et al. 2006). The value of Sw, measured in Angstroms, is defined as
emitters (LAEs, Kashikawa et al. 2006). The value of Sw, measured in Angstroms, is defined as
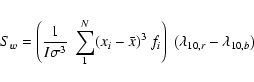 |
(1) |
where (xi) and (fi) are the arrays of coordinates and fluxes, of size N,
At this redshift, we compute a magnification factor and associated error
![]() mag, derived with the improved strong lensing model (see Sect. 3.3.2). We note that, although this object is a single image, it is located very close to the region of strong lensing, allowing an accurate estimate of the magnification with our model.
mag, derived with the improved strong lensing model (see Sect. 3.3.2). We note that, although this object is a single image, it is located very close to the region of strong lensing, allowing an accurate estimate of the magnification with our model.
After correcting for this magnification, the source is both magnified and intrinsically
bright (
![]() ), as there are only 9 of such sources at
), as there are only 9 of such sources at ![]() brighter than
z=25.5 AB found in the UDF, HUDF and GOODS fieds (Bouwens et al. 2006). This object is similar in redshift and intrinsic magnitude to the spectroscopically confirmed i-dropouts by Stanway et al. (2004) at z=5.78 and z=5.83, or the slightly magnified object at z=5.515
found in the cluster RDCS1252.9-292 (Dow-Hygelund et al. 2005). Based on the latest constraints of the luminosity function at
brighter than
z=25.5 AB found in the UDF, HUDF and GOODS fieds (Bouwens et al. 2006). This object is similar in redshift and intrinsic magnitude to the spectroscopically confirmed i-dropouts by Stanway et al. (2004) at z=5.78 and z=5.83, or the slightly magnified object at z=5.515
found in the cluster RDCS1252.9-292 (Dow-Hygelund et al. 2005). Based on the latest constraints of the luminosity function at ![]() (Bouwens et al. 2008), the unlensed magnitude
corresponds to an 3.6 L* galaxy. We also note that the very red i-z=2.9 color is much redder than for any of the 9 dropouts with z<25.5 from Bouwens et al. (2006),
detected in both the i and z bands, and where the reddest color was found to be i-z=2.4. Thanks to the magnification and the combination of filters at this redshift, the i-z color allows the average depression factor
(Bouwens et al. 2008), the unlensed magnitude
corresponds to an 3.6 L* galaxy. We also note that the very red i-z=2.9 color is much redder than for any of the 9 dropouts with z<25.5 from Bouwens et al. (2006),
detected in both the i and z bands, and where the reddest color was found to be i-z=2.4. Thanks to the magnification and the combination of filters at this redshift, the i-z color allows the average depression factor
![]() at
at ![]() to be measured, between the observed and intrinsic fluxes shortward of Lyman-
to be measured, between the observed and intrinsic fluxes shortward of Lyman-![]() ,
due to line blanketting. The corresponding value
,
due to line blanketting. The corresponding value
![]() is a lower limit, due to possible contamination of the red side of the line in the i band filter. This value is close (but slightly superior) to the predicted value at z=6 (
is a lower limit, due to possible contamination of the red side of the line in the i band filter. This value is close (but slightly superior) to the predicted value at z=6 (
![]() )
when following the Madau (1995) prescription.
)
when following the Madau (1995) prescription.
Although the current photometry does not allow deriving physical parameters
on this source (such as age, reddening, stellar mass), when probing the rest-frame UV at z=6 we can measure the UV spectral slope ![]() ,
defined as
,
defined as
![]() .
Using
the J-H=0.18 color, we derive
.
Using
the J-H=0.18 color, we derive
![]() ,
a value redder than a spectrum flat in
,
a value redder than a spectrum flat in ![]() (
(
![]() ), as can be seen in Fig. 4. Although this value is typical of Lyman-break galaxies at
), as can be seen in Fig. 4. Although this value is typical of Lyman-break galaxies at ![]() (
(
![]() ,
Adelberger & Steidel 2000), it is redder than for the sample of 27 i-dropouts studied by Stanway et al. (2005), who derived
,
Adelberger & Steidel 2000), it is redder than for the sample of 27 i-dropouts studied by Stanway et al. (2005), who derived
![]() based on J and H photometry, or the sample of lensed z-band dropouts presented in Richard et al. (2008).
The use of IRAC observations probing the longer wavelengths would allow us to understand whether this redder color stems from an old stellar population or an effect of reddening, similar to the work done by Egami et al. (2005) on a highly lensed galaxy at
based on J and H photometry, or the sample of lensed z-band dropouts presented in Richard et al. (2008).
The use of IRAC observations probing the longer wavelengths would allow us to understand whether this redder color stems from an old stellar population or an effect of reddening, similar to the work done by Egami et al. (2005) on a highly lensed galaxy at ![]() discovered in Abell 2218
(Kneib et al. 2004).
discovered in Abell 2218
(Kneib et al. 2004).
![\begin{figure}
\hspace*{3mm}\includegraphics[width=8cm]{1366fig4a.eps}\hspace*{3...
....3cm]{1366fig4c.eps}\includegraphics[width=5.3cm]{1366fig4d.eps} }\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg222.gif) |
Figure 4:
A bright i-dropout found in the field of Abell 1703. The top panel shows the individual detections in the ACS, NICMOS, and MOIRCS images. The object is resolved and elongated along the shear direction, with an angular size 0.45
|
| Open with DEXTER | |
3.3 Strong lensing
3.3.1 Modeling method
Our starting point in modeling the dark matter distribution in Abell 1703 is the mass model presented in details by L08, where we used the LENSTOOL![]() public software (Jullo et al. 2007) to constrain a parametric mass model with the identified multiple systems. The model is optimized through the new Bayesian Markov chain Monte-Carlo (hereafter MCMC) sampler, described in detail in Jullo et al. (2007). This process uses the observational constraints (positions of the multiply imaged systems) to optimize the parameters describing the mass distribution by matching the location of each image of a given system in the source plane.
public software (Jullo et al. 2007) to constrain a parametric mass model with the identified multiple systems. The model is optimized through the new Bayesian Markov chain Monte-Carlo (hereafter MCMC) sampler, described in detail in Jullo et al. (2007). This process uses the observational constraints (positions of the multiply imaged systems) to optimize the parameters describing the mass distribution by matching the location of each image of a given system in the source plane.
The contribution of the stellar mass from the central galaxy is parametrized by a Pseudo Isothermal Elliptical Mass Distribution (PIEMD) using the profile derived from the photometry. The PIEMD profile, which has been widely used for modeling cluster-scale (Smith et al. 2005)
and galaxy-scale (Natarajan et al. 1998) halos, assumes each dark matter clump can be parametrized
by a central position, ellipticity e![]() , position angle
, position angle ![]() ,
central velocity dispersion
,
central velocity dispersion ![]() ,
and two characteristic radii: a core and a cut radius. The total mass is proportional to
,
and two characteristic radii: a core and a cut radius. The total mass is proportional to
![]() .
.
Using this parametrization, the PIEMD mass density
![]() takes the form
takes the form
where x and y coordinates are oriented along the position angle
Table 4: Best-fit parameters used to model the mass distribution.
The cluster-scale dark-matter component is modeled with a generalized NFW (hereafter gNFW) profile
(Zhao 1996) including a central logarithmic slope ![]() :
:
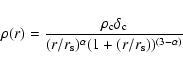 |
(3) |
where
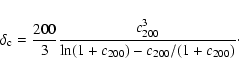 |
(4) |
Again, the spherical gNFW profile is generalized to an elliptical mass distribution using a relation similar to Eq. (2). A more detailed description of the implementation of the gNFW profile in lenstool is provided by Sand et al. (2008).
Individual cluster galaxies were added as small-scale PIEMD perturbers based on their photometry and shape parameters, using empirical scaling relations between their dynamical parameters (central velocity dispersion and scale radius) and their luminosity, assuming the Faber & Jackson (1976) relation and a constant mass-to-light ratio for each galaxy (see Covone et al. 2006 for more details). The same parameters of one particular cluster galaxy to the north (852) were optimized individually to reproduce the configuration of the surrounding systems 3, 7, 8, 9 and 12.
We replaced the photometric redshifts kept as free parameters in L08 by their spectroscopic equivalents for the 7 relevant sources (9 systems). The precision of the new model, which uses the same parametrization as L08, can be estimated using the rms of the location of multiple
images in the image plane, defined as
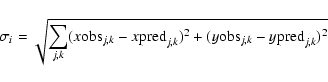 |
(5) |
where (xobsj,k, yobsj,k) and (xpredj,k, ypredj,k) are the observed and predicted locations of image j in system k, respectively. Using the exact same parametrization, we find a value of
We summarize the best-fit parameters of the new model in Table 4. In this table, the positions (x) and (y) of each clump are in arcsecs relative to the central galaxy
(RA = 13:15:05.276, Dec = +51:49:02.85) and oriented in WCS (north is up, east is left). Orientations ![]() are measured in degrees and ellipticities (e) of the potentials are given as 1-b/a, where a and b are the semi-major and semi-minor axis of the ellipse, respectively. The radius (r) refers to the scale radius
are measured in degrees and ellipticities (e) of the potentials are given as 1-b/a, where a and b are the semi-major and semi-minor axis of the ellipse, respectively. The radius (r) refers to the scale radius ![]() in the case of the gNFW profile, and the
in the case of the gNFW profile, and the
![]() radius in the case of the PIEMD profile (see L08 for details).
radius in the case of the PIEMD profile (see L08 for details).
The main gNFW component shows a concentration
c200=4.72+0.43-0.45, a scale radius
![]() kpc, and an inner slope
kpc, and an inner slope
![]() .
The geometrical parameters (center, orientation and ellipticity) are very similar to the ones measured on the cD
galaxy (see also Sect. 3.3.4 below). In comparison with the results from L08, the strongest variations in the best-fit parameters are found in the gNFW profile, which appears to be more concentrated (larger c200 and smaller scale radius
.
The geometrical parameters (center, orientation and ellipticity) are very similar to the ones measured on the cD
galaxy (see also Sect. 3.3.4 below). In comparison with the results from L08, the strongest variations in the best-fit parameters are found in the gNFW profile, which appears to be more concentrated (larger c200 and smaller scale radius ![]() ), but both results are compatible at the 3
), but both results are compatible at the 3![]() level. Adding the new constraints (spectroscopic redshifts, new multiple systems), while keeping the same model parametrization, did not reduce the uncertainty in the best-fit parameters, even if both models reproduce the constraints on the multiple images with a similar precision. This argues for a remaining degeneracy within the gNFW parameters, which cannot be completely disentangled by a mass model purely based on strong lensing.
level. Adding the new constraints (spectroscopic redshifts, new multiple systems), while keeping the same model parametrization, did not reduce the uncertainty in the best-fit parameters, even if both models reproduce the constraints on the multiple images with a similar precision. This argues for a remaining degeneracy within the gNFW parameters, which cannot be completely disentangled by a mass model purely based on strong lensing.
3.3.2 Redshift predictions and magnifications
One of the main benefits of the Bayesian approach is that the MCMC optimization provides a large number of models that sample the posterior probability-density function of all the parameters (Jullo et al. 2007). We can use these different realizations to estimate the average value and associated error for any given parameter or combination of parameters. In our case, we estimate the redshift and associated error for each of the new multiple systems 12, 13, and 14. These values are reported in Table 3. We also computed the magnification factors ![]() and associated error for every source in our LRIS mask (Table 2), as well as the other multiple systems (Table 3). The magnification factors range from 0.01-0.05 mag for single images to about 4.8 mag for the source 1.1.
and associated error for every source in our LRIS mask (Table 2), as well as the other multiple systems (Table 3). The magnification factors range from 0.01-0.05 mag for single images to about 4.8 mag for the source 1.1.
3.3.3 Weak-lensing predictions
Although solely based on strong lensing constraints out to 50
![]() (the region of multiple images), our mass model can be used to predict the tangential shear induced on background galaxies up to larger scales. The main observable with weak-lensing is the reduced shear
(the region of multiple images), our mass model can be used to predict the tangential shear induced on background galaxies up to larger scales. The main observable with weak-lensing is the reduced shear
![]() where
where ![]() is the gravitational shear and
is the gravitational shear and ![]() the convergence. In order to compare our predictions with weak-lensing observations of Abell 1703 with Subaru described by Broadhurst et al. (2008), we adopt the definion of the tangential reduced shear g+ from Umetsu & Broadhurst (2008), i.e. the projection of the shear perpendicularly to the direction of the cluster center (see also Medezinski et al. 2007).
the convergence. In order to compare our predictions with weak-lensing observations of Abell 1703 with Subaru described by Broadhurst et al. (2008), we adopt the definion of the tangential reduced shear g+ from Umetsu & Broadhurst (2008), i.e. the projection of the shear perpendicularly to the direction of the cluster center (see also Medezinski et al. 2007).
Using the MCMC realizations, we determine predictions for g+ and its associated 3-![]() error as a function of angular distance r from the center of the mass distribution, assuming a distribution of background sources at a fixed redshift
error as a function of angular distance r from the center of the mass distribution, assuming a distribution of background sources at a fixed redshift
![]() corresponding the the mean of the redshift distribution of sources in the observations from Broadhurst et al. (2008). Figure 5 presents these estimations against their weak-lensing measurements over the same range of r.
We find that our strong-lensing model represents a very good fit to the weak-lensing datapoints up to 4 Mpc h-1, with a
corresponding the the mean of the redshift distribution of sources in the observations from Broadhurst et al. (2008). Figure 5 presents these estimations against their weak-lensing measurements over the same range of r.
We find that our strong-lensing model represents a very good fit to the weak-lensing datapoints up to 4 Mpc h-1, with a ![]() of 4.1/7 = 0.58, even after extrapolating our mass model to a radial distance 20
of 4.1/7 = 0.58, even after extrapolating our mass model to a radial distance 20![]() larger than the region of strong lensing constraints. This argues again for the overall simplicity of the cluster, with a single NFW profile providing a good fit both for the strong-lensing and weak-lensing measurements.
larger than the region of strong lensing constraints. This argues again for the overall simplicity of the cluster, with a single NFW profile providing a good fit both for the strong-lensing and weak-lensing measurements.
![\begin{figure}
\par\includegraphics[height=8cm,angle=270]{1366fig5.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg256.gif) |
Figure 5:
Tangential reduced shear g+ predicted with the strong lensing model based on constraints in the central region (black error bar on top). The mean value and 3 |
| Open with DEXTER | |
3.3.4 Ellipticity of the mass distribution and Einstein radius
From the best-fit geometrical parameters found during the optimization of the mass model (Table 4), we notice a good agreement between the values for the ellipticity and position angle of the large scale gNFW profile (
![]() ,
,
![]() degrees) and the same parameters of the cD galaxy (
degrees) and the same parameters of the cD galaxy (
![]() ,
,
![]() 52 degrees) as measured with SExtractor
52 degrees) as measured with SExtractor![]() . This is not really surprising, as this correlation has previously been reported both in strong-lensing analysis (e.g. Gavazzi et al. 2003 in MS2137) and in X-ray observations (Hashimoto et al. 2008), as well as in numerical works (Dubinski 1998; Faltenbacher et al. 2005).
. This is not really surprising, as this correlation has previously been reported both in strong-lensing analysis (e.g. Gavazzi et al. 2003 in MS2137) and in X-ray observations (Hashimoto et al. 2008), as well as in numerical works (Dubinski 1998; Faltenbacher et al. 2005).
More generally, the total mass distribution of dark matter is the sum of this gNFW component and the various PIEMD profiles associated with the cluster galaxies, and the global ellipticity
![]() may have a different value. We use the convergence map
may have a different value. We use the convergence map ![]() (which shares an identical geometry with the mass distribution) to measure this ellipticity
(which shares an identical geometry with the mass distribution) to measure this ellipticity
![]() a posteriori by fitting elliptical contours with the IRAF routine ellipse. We keep
the center of the ellipses fixed at the peak of the mass map and let the ellipticity
a posteriori by fitting elliptical contours with the IRAF routine ellipse. We keep
the center of the ellipses fixed at the peak of the mass map and let the ellipticity
![]() and position angle
and position angle ![]() vary as free parameters with the semi major axis a. In the central region (a<15
vary as free parameters with the semi major axis a. In the central region (a<15
![]() ), we find a best-fit value
), we find a best-fit value
![]() (Fig. 6) dominated by the geometry of the cD and the gNFW profile. At larger distances
(Fig. 6) dominated by the geometry of the cD and the gNFW profile. At larger distances
![]() increases to reach a maximum of 0.4 at
increases to reach a maximum of 0.4 at ![]()
![]() (Fig. 6), is due to
an alignment of bright galaxies (as seen in projection) to the north west and the south east, therefore along a similar direction as
(Fig. 6), is due to
an alignment of bright galaxies (as seen in projection) to the north west and the south east, therefore along a similar direction as
![]() .
These galaxies contribute to increasing the value of
.
These galaxies contribute to increasing the value of
![]() compared to
compared to
![]() ,
this effect being significant on the mass distribution up to the edge of the ACS field of view. The same ellipticity is seen on the weak-lensing reconstructions performed by Broadhurst et al. (2008).
,
this effect being significant on the mass distribution up to the edge of the ACS field of view. The same ellipticity is seen on the weak-lensing reconstructions performed by Broadhurst et al. (2008).
We also computed the effective Einstein radius ![]() ,
defined as the radius rfrom the center of the cluster (located at the peak of the mass distribution) at which
,
defined as the radius rfrom the center of the cluster (located at the peak of the mass distribution) at which
![]() (Broadhurst & Barkana 2008). We measured the value and error on
(Broadhurst & Barkana 2008). We measured the value and error on ![]() for the redshift z=2.627 of the giant tangential arc (formed with the systems 10 and 11),
using the different MCMC realizations. We find
for the redshift z=2.627 of the giant tangential arc (formed with the systems 10 and 11),
using the different MCMC realizations. We find
![]() arcsec, a lower value than one would measure based on the simple distance of the giant arc (Fig. 6). This value is close but less than the estimate of 32
arcsec, a lower value than one would measure based on the simple distance of the giant arc (Fig. 6). This value is close but less than the estimate of 32
![]() given by Broadhurst & Barkana (2008), who mentions an agreement of
given by Broadhurst & Barkana (2008), who mentions an agreement of ![]() with the distance of the arc. This apparent discrepancy comes from the ellipticity of the mass distribution, as the giant arc is oriented along the major axis of the elliptical mass distribution. This ellipticity is now well-constrained by the large number
of spectroscopically confirmed multiple images presented here, making the new measurement of
with the distance of the arc. This apparent discrepancy comes from the ellipticity of the mass distribution, as the giant arc is oriented along the major axis of the elliptical mass distribution. This ellipticity is now well-constrained by the large number
of spectroscopically confirmed multiple images presented here, making the new measurement of ![]() more robust.
more robust.
We can use the same cumulative probability distribution
![]() as Broadhurst & Barkana (2008) to test the agreement of this new Einstein radius with the
as Broadhurst & Barkana (2008) to test the agreement of this new Einstein radius with the ![]() CDM Millennium simulation. This probability is computed from the distribution of concentrations at a given virial mass, accounting for the various biases arising from selecting a population of lensing clusters, as well as the projection effects. We find a higher probability P=20% (instead of 7.9%)
of agreement, making Abell 1703 less discrepant than the other mentioned clusters (Abell 1689, CL0024 and RXJ1347) for its virial mass. Together with the results from these 3 other clusters (P=8.5%, P=3.9%, and P=13%, respectively) the combined probability for these 4 clusters is 9e-5, or a 3.7
CDM Millennium simulation. This probability is computed from the distribution of concentrations at a given virial mass, accounting for the various biases arising from selecting a population of lensing clusters, as well as the projection effects. We find a higher probability P=20% (instead of 7.9%)
of agreement, making Abell 1703 less discrepant than the other mentioned clusters (Abell 1689, CL0024 and RXJ1347) for its virial mass. Together with the results from these 3 other clusters (P=8.5%, P=3.9%, and P=13%, respectively) the combined probability for these 4 clusters is 9e-5, or a 3.7![]() discrepancy. However, as mentioned earlier, there are few such clusters observed in the whole sky in comparison with the size of the Millennium Simulation, making it more plausible to reconcile the observations with whole-sky simulations.
discrepancy. However, as mentioned earlier, there are few such clusters observed in the whole sky in comparison with the size of the Millennium Simulation, making it more plausible to reconcile the observations with whole-sky simulations.
![\begin{figure}
\par\includegraphics[height=8cm,angle=0]{1366fig6.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg272.gif) |
Figure 6:
Convergence map distribution |
| Open with DEXTER | |
4 Abell 1703: a relaxed, unimodal cluster?
Our strong-lensing analysis using a simple NFW component for the large-scale dark matter distribution, after individual treatment of the central cD galaxy and small-scale mass distributions associated with the galaxy substructure in the cluster, is able to reproduce the large number of multiple images identified in Abell 1703. Even if the overall rms in the predicted location of the multiple images (1.3
![]() )
is still quite larger than the precision in astrometric measurements with HST (typically 0.1
)
is still quite larger than the precision in astrometric measurements with HST (typically 0.1
![]() ), we find no systematics as a function of the location of the multiples, which would argue for the need for secondary dark matter clumps. This was the case in the clusters Abell 2218 (Elíasdóttir et al. 2007) and Abell 68 (Richard et al. 2007), which show strong evidence of bimodality.
), we find no systematics as a function of the location of the multiples, which would argue for the need for secondary dark matter clumps. This was the case in the clusters Abell 2218 (Elíasdóttir et al. 2007) and Abell 68 (Richard et al. 2007), which show strong evidence of bimodality.
Furthermore, adding new spectroscopic measurements of 7 multiple sources has removed an identical number of free parameters (i.e., the redshifts of the sources) from the analysis presented in L08. However, we find no significant increase in the overall rms of the
multiple images compared to this previous work, under the same assumptions. In addition, the strongest variations in the best-fit parameters compared with the previous
values presented in L08 are found for the gNFW profile, but both results are compatible within the 3![]() confidence level. The remaining scatter in the positions of multiple images is very likely due to the small-scale substructure in the dark matter distribution, which is not included here apart from the visible cluster galaxies. One way to increase the complexity of this model would be to estimate small-scale deviations from the smooth mass distribution,
using adaptive-grid based models (Jullo et al. 2009, submitted).
confidence level. The remaining scatter in the positions of multiple images is very likely due to the small-scale substructure in the dark matter distribution, which is not included here apart from the visible cluster galaxies. One way to increase the complexity of this model would be to estimate small-scale deviations from the smooth mass distribution,
using adaptive-grid based models (Jullo et al. 2009, submitted).
Finally, the best-fit parameters of our strong-lensing analysis have been consistent with weak-lensing measurements. Our best-fit concentration parameter
c200=4.72+0.43-0.45, corresponding to
![]() with the second definition based on the virial radius
with the second definition based on the virial radius
![]() ,
is somewhat lower than the value derived by Broadhurst et al. (2008),
,
is somewhat lower than the value derived by Broadhurst et al. (2008),
![]() ,
but marginally compatible at 2.4
,
but marginally compatible at 2.4![]() level. Despite this lower concentration, the predicted shear profile provides an overall good fit to their observations, where the main difference is our smaller Einstein radius (which sets the location of the first datapoint in Fig. 5, as in Broadhurst et al. 2008), allowing for a shallower slope of the shear profile. We also note that the two shear measurements at large radii (where the signal gets weaker) are slightly lower than the predictions
(but consistent within their error bars). Together, these differences affect the best-fit concentration parameter. The new Einstein radius measurement should be
more reliable, since it is based on a larger number of multiple images at the center. There seems to be less discrepancy between our new strong-lensing NFW parameters and the weak-lensing measurements, as was the case for Abell 1689 (Limousin et al. 2007; Broadhurst et al. 2005).
level. Despite this lower concentration, the predicted shear profile provides an overall good fit to their observations, where the main difference is our smaller Einstein radius (which sets the location of the first datapoint in Fig. 5, as in Broadhurst et al. 2008), allowing for a shallower slope of the shear profile. We also note that the two shear measurements at large radii (where the signal gets weaker) are slightly lower than the predictions
(but consistent within their error bars). Together, these differences affect the best-fit concentration parameter. The new Einstein radius measurement should be
more reliable, since it is based on a larger number of multiple images at the center. There seems to be less discrepancy between our new strong-lensing NFW parameters and the weak-lensing measurements, as was the case for Abell 1689 (Limousin et al. 2007; Broadhurst et al. 2005).
Overall, we argue that these results provide further evidence that Abell 1703 is a relaxed cluster, as already suggested in L08. Follow-up X-ray observations of the cluster core should allow again this assumption to be confirmed, and would separate the X-ray gas component from the
dark matter in the mass distribution when doing the strong-lensing analysis, following the work by Bradac et al. (2008) for RXJ1347. Another independent measurement of the mass profile would be to study the dynamics of cluster galaxies up to large radii, giving another estimate of the virial radius and virial mass. Finally, we expect to find a larger sample of similar relaxed clusters from the ongoing LoCuSS survey (Zhang et al. 2008) of clusters with lower masses (as inferred from their X-ray luminosity) at ![]() .
By pursuing the same strong lensing analysis on this broader sample, we will probe a wider distribution of Einstein radii, ellipticities, and concentration parameters with less bias compared to available numerical simulations.
.
By pursuing the same strong lensing analysis on this broader sample, we will probe a wider distribution of Einstein radii, ellipticities, and concentration parameters with less bias compared to available numerical simulations.
Acknowledgements
We thank the anonymous referee for his/her helpful comments, and acknowledge useful discussions with Masamune Oguri, Carlos Frenk, and Mark Swinbank. J.R. acknowledges support from an European Union Marie-Curie Fellowship. M.L. acknowledges the Agence Nationale de la Recherche for its support, project number 06-BLAN-0067. The Dark Cosmology Center is funded by the Danish National Research Foundation. We thank the Danish Centre for Scientific Computing at the University of Copenhagen for providing a generous amount of time on its supercomputing facility. J.P.K. aknowledges the Centre National de la Recherche Scientifique for its support. The authors recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain.
References
- Adelberger, K. L., & Steidel, C. C. 2000, ApJ, 544, 218 [NASA ADS] [CrossRef] (In the text)
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] (In the text)
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., & Franx, M. 2006, ApJ, 653, 53 [NASA ADS] [CrossRef] (In the text)
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2008, ApJ, 686, 230 [NASA ADS] [CrossRef] (In the text)
- Bradac, M., Schrabback, T., Erben, T., et al. 2008, ApJ, 681, 187 [NASA ADS] [CrossRef]
- Broadhurst, T. J., & Barkana, R. 2008, MNRAS, 390, 1647 [NASA ADS] (In the text)
- Broadhurst, T., Benítez, N., Coe, D., et al. 2005, ApJ, 621, 53 [NASA ADS] [CrossRef]
- Broadhurst, T., Umetsu, K., Medezinski, E., Oguri, M., & Rephaeli, Y. 2008, ApJ, 685, L9 [NASA ADS] [CrossRef] (In the text)
- Covone, G., Kneib, J.-P., Soucail, G., et al. 2006, A&A, 456, 409 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dow-Hygelund, C. C., Holden, B. P., Bouwens, R. J., et al. 2005, ApJ, 630, L137 [NASA ADS] [CrossRef] (In the text)
- Dubinski, J. 1998, ApJ, 502, 141 [NASA ADS] [CrossRef]
- Egami, E., Kneib, J.-P., Rieke, G. H., et al. 2005, ApJ, 618, L5 [NASA ADS] [CrossRef] (In the text)
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007[arXiv:astro-ph/0710.5636] (In the text)
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] (In the text)
- Faltenbacher, A., Allgood, B., Gottlöber, S., Yepes, G., & Hoffman, Y. 2005, MNRAS, 362, 1099 [NASA ADS] [CrossRef]
- Gavazzi, R., Fort, B., Mellier, Y., Pelló, R., & Dantel-Fort, M. 2003, A&A, 403, 11 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Golse, G., Kneib, J.-P., & Soucail, G. 2002, A&A, 387, 788 [NASA ADS] [CrossRef] [EDP Sciences]
- Hashimoto, Y., Henry, J. P., & Boehringer, H. 2008, MNRAS, 390, 1562 [NASA ADS] (In the text)
- Hennawi, J. F., Gladders, M. D., Oguri, M., et al. 2008, AJ, 135, 664 [NASA ADS] [CrossRef] (In the text)
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [CrossRef] (In the text)
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [NASA ADS] [CrossRef] (In the text)
- Kelson, D. D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] (In the text)
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef]
- Kneib, J.-P., Ellis, R. S., Santos, M. R., & Richard, J. 2004, ApJ, 607, 697 [NASA ADS] [CrossRef] (In the text)
- Le Fevre, O., Crampton, D., Lilly, S. J., Hammer, F., & Tresse, L. 1995, ApJ, 455, 60 [NASA ADS] [CrossRef] (In the text)
- Limousin, M., Richard, J., Jullo, E., et al. 2007, ApJ, 668, 643 [NASA ADS] [CrossRef]
- Limousin, M., Richard, J., Kneib, J.-P., et al. 2008, A&A, 489, 23 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Link, R., & Pierce, M. J. 1998, ApJ, 502, 63 [NASA ADS] [CrossRef]
- Madau, P. 1995, ApJ, 441, 18 [NASA ADS] [CrossRef] (In the text)
- Medezinski, E., Broadhurst, T., Umetsu, K., et al. 2007, ApJ, 663, 717 [NASA ADS] [CrossRef] (In the text)
- Natarajan, P., Kneib, J.-P., Smail, I., & Ellis, R. S. 1998, ApJ, 499, 600 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
- Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] (In the text)
- Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [NASA ADS] [CrossRef] (In the text)
- Richard, J., Kneib, J.-P., Jullo, E., et al. 2007, ApJ, 662, 781 [NASA ADS] [CrossRef]
- Richard, J., Stark, D. P., Ellis, R. S., et al. 2008, ApJ, 685, 705 [NASA ADS] [CrossRef] (In the text)
- Sand, D. J., Treu, T., Ellis, R. S., Smith, G. P., & Kneib, J.-P. 2008, ApJ, 674, 711 [NASA ADS] [CrossRef] (In the text)
- Shimasaku, K., Kashikawa, N., Doi, M., et al. 2006, PASJ, 58, 313 [NASA ADS] (In the text)
- Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef]
- Stanway, E. R., Bunker, A. J., McMahon, R. G., et al. 2004, ApJ, 607, 704 [NASA ADS] [CrossRef] (In the text)
- Stanway, E. R., McMahon, R. G., & Bunker, A. J. 2005, MNRAS, 359, 1184 [NASA ADS] [CrossRef] (In the text)
- Umetsu, K., & Broadhurst, T. 2008, ApJ, 684, 177 [NASA ADS] [CrossRef] (In the text)
- Verdugo, T., de Diego, J. A., & Limousin, M. 2007, ApJ, 664, 702 [NASA ADS] [CrossRef] (In the text)
- Zhang, Y.-Y., Finoguenov, A., Böhringer, H., et al. 2008, A&A, 482, 451 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Zhao, H. 1996, MNRAS, 278, 488 [NASA ADS] (In the text)
Footnotes
- ...
![[*]](/icons/foot_motif.gif)
- Marie-Curie fellow.
- ... LENSTOOL
![[*]](/icons/foot_motif.gif)
- http://www.oamp.fr/cosmology/lenstool/
- ...e
![[*]](/icons/foot_motif.gif)
- We use here the definition e=1-b/a of the ellipticity, where a and b are the semi-major and semi-minor axis of the ellipse, respectively.
- ... SExtractor
![[*]](/icons/foot_motif.gif)
- The value of
 given in L08 had an error in its definition and we update it to the correct one.
given in L08 had an error in its definition and we update it to the correct one.
All Tables
Table 1: Summary of the broad-band images used for the photometry.
Table 2: Overview of the sources included in the LRIS mask.
Table 3: Location and redshift estimate of three new multiply-image systems, as well as the radial feature (10.4) associated with the giant arc (systems 10 and 11).
Table 4: Best-fit parameters used to model the mass distribution.
All Figures
![\begin{figure}
\par\includegraphics[height=13.5cm,angle=0]{1366fig1.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg19.gif) |
Figure 1: ACS color image of Abell 1703 (combination of the HST filters F450W, F606W and F850LP), showing the location of all the multiply-imaged systems included in this study. The white cross at the center of the image marks the location of the brightest cluster galaxy, which has been subtracted for clarity. The dashed line outlines the limit of the region where we expect multiple images up to z=6. The systems presented in L08 are shown in white, and the new systems presented in this work are shown in red. Squares identify the multiple images with spectroscopic redshifts.The green triangle located to the lower right marks the location of the i-band dropout presented in Sect. 3.2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=3.3cm]{1366fig2a.eps}\hspace*{2m...
...s}\hspace*{2mm}
\includegraphics[width=5.3cm]{1366fig2x.eps} }
\par
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg20.gif) |
Figure 2: BVI ACS color image close-up on individual z>0.5 sources in the LRIS mask with the location of the slit, and corresponding extracted spectra. The i-band dropout (23, see Sect. 3.2) is presented separately in Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=3.3cm]{1366fig3a.eps}\hspace*{2mm}
\...
...o.eps}\hspace*{2mm}
\includegraphics[width=5.3cm]{1366fig3p.eps} }\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg21.gif) |
Figure 3: Continuation of Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\hspace*{3mm}\includegraphics[width=8cm]{1366fig4a.eps}\hspace*{3...
....3cm]{1366fig4c.eps}\includegraphics[width=5.3cm]{1366fig4d.eps} }\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg222.gif) |
Figure 4:
A bright i-dropout found in the field of Abell 1703. The top panel shows the individual detections in the ACS, NICMOS, and MOIRCS images. The object is resolved and elongated along the shear direction, with an angular size 0.45
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8cm,angle=270]{1366fig5.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg256.gif) |
Figure 5:
Tangential reduced shear g+ predicted with the strong lensing model based on constraints in the central region (black error bar on top). The mean value and 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8cm,angle=0]{1366fig6.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11366-08/Timg272.gif) |
Figure 6:
Convergence map distribution |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\Sigma(x,y)=\frac{\sigma_0^2}{2G}\ \frac{r_{\rm cut}}{r_{\rm ...
...^2+\rho^2)^{1/2}}-\frac{1}{(r_{\rm cut}^2+\rho^2)^{1/2}}\Bigg]
\end{displaymath}](/articles/aa/full_html/2009/16/aa11366-08/img227.gif)