| Issue |
A&A
Volume 498, Number 1, April IV 2009
|
|
|---|---|---|
| Page(s) | 321 - 327 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200811036 | |
| Published online | 18 February 2009 | |
Phase closure nulling
Application to the spectroscopy of faint companions
A. Chelli - G. Duvert - F. Malbet - P. Kern
Laboratoire d'Astrophysique de Grenoble and Mariotti Center, UMR 5571 Université Joseph Fourier, BP 53, 38041 Grenoble Cedex 9, France
Received 25 September 2008 / Accepted 16 December 2008
Abstract
We provide a complete theory of the phase closure of
a binary system in which a small, feeble, and unresolved companion
acts as a perturbing parameter on the spatial frequency spectrum
of a dominant, bright, resolved source. We demonstrate that the
influence of the companion can be measured with precision by
measuring the phase closure of the system near the nulls of the
primary visibility function. In these regions of phase closure
nulling, frequency intervals always exist where the phase closure signature of
the companion is larger than any systematic error and can then
be measured. We show that this technique allows retrieval of many
astrophysically relevant properties of faint and close companions
such as flux, position, and in favorable cases,
spectrum. We conclude by a rapid study of the
potentialities of phase closure nulling observations with current
interferometers and explore the requirements for a new type of
dedicated instrument.
Key words: stars: fundamental parameters - stars: planetary systems - stars: binaries: close - stars: binaries: spectroscopic - instrumentation: interferometers - methods: observational
1 Introduction
A common feature of the observational problem posed by spectroscopic binaries, evolved stars companions, hot Jupiters, and extrasolar planets is the presence of a point-like source of low flux in the vicinity of a much larger and much brighter star. Indeed, it is the properties of the faint companion that are desired, and are the most difficult to acquire. Directly detecting the flux of an extrasolar planet and establishing its spectrum seems the most demanding task, to be fulfilled only by dedicated spatial missions (DARWIN: Cockell et al. 2008, and TPF-I: Lawson et al. 2008) using interferometry nulling techniques (Bracewell 1978).
Ground-based optical long baseline interferometers also have the capability of detecting extrasolar planets restricted to the case of a giant planet orbiting close to its parent star (Vannier et al. 2006), such as 51 Peg the first exoplanet to be unraveled by radial velocity techniques (Mayor & Queloz 1995). The principle consists in measuring interferograms in different spectral regions where the ratio between the planet photons and the stellar ones changes because of an emission line or an absorption line in the planet atmosphere. The position of the interferogram measured by the phase is directly related to the position of the photocenter of the star-planet system on the sky. The slight shift in the phase between two spectral regions is in principle measurable for bright extrasolar planets such as hot Jupiters.
Even when using color-differential techniques the phase measurement is plagued by the variation of the refractive index in air. This is why efforts are currently concentrated on using the phase closure, which corresponds to the sum of the phases measured in three connected baselines (see Sect. 2.4 for details). This technique allows the observer to remove any atmospheric perturbation or instrumental-based errors localized in each arm of the interferometer. This detection has not been performed yet because of instrumental biases and the need to decrease the photon noise even with large telescopes.
An important property of stars resolved by long baseline
interferometry is that the
coherence of the light decreases with increasing spatial frequencies
down to zero before increasing again following the well known behavior
of the Bessel functions. Michelson & Pease (1921) used this
property to measure the diameter of Betelgeuse for the first time.
Indeed, the visibility of a photosphere of uniform brightness
distribution over a circular disk is canceled out at the spatial
frequency
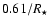 where
where 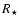 is the stellar angular radius.
Another property is that the phase of the visibility jumps by 180 degrees at each crossing of the Bessel function's zeros (hereafter
called visibility nulls or simply nulls). At each null, the coherent flux of
the star is canceled out, making it easier to detect a change in the phase
jump due to a faint close companion.
is the stellar angular radius.
Another property is that the phase of the visibility jumps by 180 degrees at each crossing of the Bessel function's zeros (hereafter
called visibility nulls or simply nulls). At each null, the coherent flux of
the star is canceled out, making it easier to detect a change in the phase
jump due to a faint close companion.
In this paper we demonstrate that, in precisely the restricted case of
the lobe crossing, the influence of even a very faint companion can be
measured with precision, and its spectrum can be obtained by measuring the phase
closure of the system near the nulls of the primary visibility
function. In these regions where the phase closure nulling of
the primary is effective, the phase closure signature of the secondary
stands out to a point where its basic properties (flux, position,
spectrum, etc.) can be measured. In a companion paper (Duvert et al. 2009),
this technique was used to detect the companion of the single-lined
spectroscopic binary 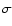 Puppis, at a few stellar
radii distance.
Puppis, at a few stellar
radii distance.
![\begin{figure}
\par\includegraphics[angle=-270,width=4.7cm,clip]{1036fig1.ps}\hs...
...*{1.2cm}
\includegraphics[angle=-270,width=4.7cm,clip]{1036fig3.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg13.gif) |
Figure 1:
Visibility for a star represented well by a uniform
brightness distribution over a disk of angular radius |
| Open with DEXTER | |
2 Description of the problem
2.1 Visibility of a stellar photosphere of uniform brightness
When observing a star with a multi-aperture interferometer, it is well known that one detects the amplitude of the visibility function (or the amplitude squared) and that this amplitude decreases with increasing spatial frequency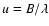 ,
where Bis the baseline and
,
where Bis the baseline and 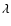 the wavelength. Thanks to the
Zernike-Van Cittert theorem, it can be shown that this visibility
function coincides with the Fourier transform of the spatial
energy distribution of the star; hence, for a star whose energy distribution
is well-represented by a uniform disk, the visibility function
is proportional to a Bessel function of the first order
the wavelength. Thanks to the
Zernike-Van Cittert theorem, it can be shown that this visibility
function coincides with the Fourier transform of the spatial
energy distribution of the star; hence, for a star whose energy distribution
is well-represented by a uniform disk, the visibility function
is proportional to a Bessel function of the first order
The visibility function is a complex number that, in this special case of a simple centro-symmetric brightness distribution, turns out to be real (i.e. the imaginary part is zero). It is often displayed by its amplitude and its phase (see Fig. 1).
The visibility becomes negative when the baseline is longer
than
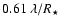 ,
corresponding to the first null, so
the phase suddenly changes from zero to
180 degrees (see right panel of Fig. 1). It becomes
positive again when crossing the second null, and so on.
,
corresponding to the first null, so
the phase suddenly changes from zero to
180 degrees (see right panel of Fig. 1). It becomes
positive again when crossing the second null, and so on.
2.2 Visibility of a resolved star with a faint companion
When an object is composed of two components, the object visibility function is the sum of the visibility function of the two components weighted by the fraction of flux of each component and a phase modulated by the apparent angular separation on the sky. If one adds a faint companion to the star of the previous section with a flux ratio r and separated from the star by s(assuming for sake of simplicity that the system orientation is parallel to the frequency axis), then the complex visibility of the system isIf the flux ratio r is small, the amplitude of the visibility function will be very slightly modified by the presence of the faint companion. The stronger effect occurs around visibility nulls of the primary, where the system visibility is no longer zero. At these locations, the visibility perturbation is equal to the flux ratio. This effect still remains weak and is beyond the performances of current interferometers as soon as the flux ratio is less than about 1%. However, besides the fact the companion is not detectable, studies around visibility nulls keep their interest for precise diameter and limb darkening measurements (Le Bouquin et al. 2008).
2.3 Phase changed by the faint companion
More interesting is the phase of the object visibility.
By definition, the tangent of the
phase of a complex number is equal to the ratio of its imaginary part
by its real part. Therefore we have
For small flux ratios and except for around nulls, the phase of the object is very close to 0 or 180 degrees, and may be approximated by
with n=0 if
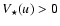 ,
and n=1 if
,
and n=1 if
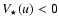 .
For
separations
.
For
separations 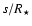 much greater than 1, it is quasi periodic, with a
pseudo period s-1.
much greater than 1, it is quasi periodic, with a
pseudo period s-1.
The phase is the result of two contributions: from the star
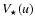 and from the companion
and from the companion
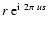 .
The
contribution of the star decreases as the
frequency increases and is even canceled at the nulls, while that of the
companion keeps constant as long as it is not resolved. Most of the
time, the companion produces a phase signature in the range
.
The
contribution of the star decreases as the
frequency increases and is even canceled at the nulls, while that of the
companion keeps constant as long as it is not resolved. Most of the
time, the companion produces a phase signature in the range
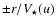 .
But more important,
around visibility nulls, in the frequency ranges for which
.
But more important,
around visibility nulls, in the frequency ranges for which
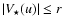 ,
this phase signature becomes significant, with an exact
value of
,
this phase signature becomes significant, with an exact
value of
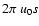 at the frequencies u0 of the nulls (
at the frequencies u0 of the nulls (
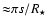 for the
first null), much greater than 180 degrees. It follows
that, as opposed to the visibility amplitude, even for small flux
ratios, frequency intervals always exist around nulls, where the
phase signature of the companion is larger than any systematic error
and can then be measured.
for the
first null), much greater than 180 degrees. It follows
that, as opposed to the visibility amplitude, even for small flux
ratios, frequency intervals always exist around nulls, where the
phase signature of the companion is larger than any systematic error
and can then be measured.
2.4 Phase closure of a resolved star with a faint companion
An interferometer formed by 3 telescopes transmits 3 frequency systems, u12, u23, and u13=u12+u23, associated with the 3 baselines, each characterized by a phase and a visibility. It provides one phase closure defined as the phase of the bispectrum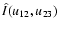 ,
with
,
with
where * denotes the complex conjugate, and
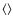 represents an ensemble
average. The phase closure has two important
properties: it is insensitive to atmospheric phase fluctuations, and
for a point source, it is equal to zero. Then, for an extended object,
it is given by
represents an ensemble
average. The phase closure has two important
properties: it is insensitive to atmospheric phase fluctuations, and
for a point source, it is equal to zero. Then, for an extended object,
it is given by
| (6) |
where
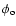 is the phase of the object spatial Fourier
transform.
is the phase of the object spatial Fourier
transform.
If the telescopes are aligned with baselines parallel to the direction
of the double system, the phase closure may be written
Figure 2 shows the expected phase closure, around the first visibility null, from a double system with a flux ratio of 1% and various separations. The system is observed with a spectral resolution of 1500, like the one available with the AMBER instrument at the VLTI (Petrov et al. 2007). Note the importance of the phase closure signature from the companion.
| |
Figure 2:
Phase closure modulo |
| Open with DEXTER | |
3 Phase closure nulling
In the case of a system formed by an extended uniform disk and a point source, the useful phase closure signal is the departure from 0 or 180 degrees. We have then clearly interest in selecting the working frequency interval at the highest frequencies, around visibility nulls at u=u0, where the phase closure signature of the companion is at its maximum. In these regions, there is always (as the stellar visibility crosses the zero) a frequency interval within which the useful signal is stronger than any systematic error, hence can be measured.Figure 3 shows the useful phase closure signal for various flux ratios and distances of 10, 100, and 1000 stellar radii. The horizontal lines correspond to a given systematic error of 0.1 degree. The frequency interval within which the useful signal is stronger than this error diminishes rapidly with the flux ratio, but is always present.
We propose using the regions around minima of visibility, where the
phase closure nulling of the primary is effective, and the
useful signal is over the limit
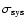 imposed by
systematic errors, to detect and to characterize faint
companions. By doing so, we do not cancel the stellar flux
as in classical nulling experiments (Bracewell 1978), but
we only cancel the stellar coherent flux. The main limiting noise will then be
the photon noise from the central star, as shown in Sect. 3.2.
imposed by
systematic errors, to detect and to characterize faint
companions. By doing so, we do not cancel the stellar flux
as in classical nulling experiments (Bracewell 1978), but
we only cancel the stellar coherent flux. The main limiting noise will then be
the photon noise from the central star, as shown in Sect. 3.2.
![\begin{figure}
\par\includegraphics[angle=-270,width=7.5cm,clip]{1036fig5.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg44.gif) |
Figure 3:
Absolute value of the useful phase closure signal of a double system
formed by a uniform disk and a point source as a function of the
highest frequency located around the first visibility null of the
primary. The spectral resolution is
|
| Open with DEXTER | |
3.1 Spectroscopy of close companions
The spectroscopy of close companions may be extracted from spectrally dispersed
phase closure measurements obtained with an
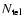 telescopes interferometer
(
telescopes interferometer
(
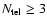 ). The baselines should be such that the longest one
corresponds to a null of the primary star in order to maximize the
useful signal. As an example, an interferometer with 3
telescopes and frequencies {
u23, u12, u13} in the ratio
1:2:3, allowing bootstrapping,
would be a very efficient system. The data consists of spectrally
dispersed phase closure measurements performed as a function of the
spatial frequency.
). The baselines should be such that the longest one
corresponds to a null of the primary star in order to maximize the
useful signal. As an example, an interferometer with 3
telescopes and frequencies {
u23, u12, u13} in the ratio
1:2:3, allowing bootstrapping,
would be a very efficient system. The data consists of spectrally
dispersed phase closure measurements performed as a function of the
spatial frequency.
The double system is characterized by 4 parameters: the stellar radius
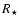 ,
the flux ratio r, the separation s, and the position
angle. The 4 parameters may be extracted from a
modeling of the phase closure variations as a function of both the spatial
frequency and the wavelength. The spectrum of the companion is then
obtained by multiplying the
flux ratio by the spectrum of the primary.
,
the flux ratio r, the separation s, and the position
angle. The 4 parameters may be extracted from a
modeling of the phase closure variations as a function of both the spatial
frequency and the wavelength. The spectrum of the companion is then
obtained by multiplying the
flux ratio by the spectrum of the primary.
3.2 Error analysis
We consider for simplicity an interferometer formed by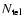 aligned telescopes in a non-redundant configuration. We also assume that
the direction of observation varies little during the
experiment so that the double system is characterized by only 3 parameters: the stellar angular radius
aligned telescopes in a non-redundant configuration. We also assume that
the direction of observation varies little during the
experiment so that the double system is characterized by only 3 parameters: the stellar angular radius 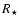 ,
the flux ratio r, and the
projected separation s along the direction of
observation. Spectrally dispersed phase closure
measurements are performed as a function of the spatial frequency and
then fitted, with a 3-parameter model.
,
the flux ratio r, and the
projected separation s along the direction of
observation. Spectrally dispersed phase closure
measurements are performed as a function of the spatial frequency and
then fitted, with a 3-parameter model.
The limiting noises in optical interferometry from the visible to the near infrared are the atmospheric noise, the photon noise from the source, and the detector readout noise. General expressions of the errors on the parameters of the double system are derived in Appendix A. In the photon noise regime, the errors reach their minimum values and then stay constant as soon as the working frequency domains cover at least one period s-1. For separations greater than a few stellar radii and working frequency intervals over s-1, the error on the flux ratio and that on the separation, with a 3-telescope interferometer, are given by
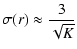 |
(8) | ||
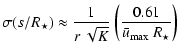 |
(9) |
where K is the total number of photoevents detected during the whole
observation and
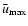 the average frequency of the
longest baseline.
the average frequency of the
longest baseline.
These formulae have been checked numerically through a rigorous error
analysis. They are valid everywhere, even around the nulls. Besides
the error
on the separation being inversely proportional to the maximum frequency,
the errors are independent of the working frequency domains. This
clearly reinforces the usefulness of observing around
visibility nulls, where the useful phase closure signal is dominant. The
error on the flux ratio only depends on the total number of collected
photoevents, while that on the distance is also inversely proportional
to the flux ratio. In the photon noise regime, both errors are
independent of the spectral
resolution
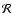 ,
as long as the spectral averaging is
performed over less than half a period 1/2 s, that is, when
,
as long as the spectral averaging is
performed over less than half a period 1/2 s, that is, when
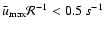 .
This condition provides a
maximum recoverable distance imposed by the spectral resolution of
.
This condition provides a
maximum recoverable distance imposed by the spectral resolution of
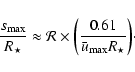 |
(10) |
The error on the flux of the companion is
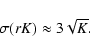 |
(11) |
The direct photometric detection of the companion would provide an error of
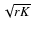 .
In terms of performances, the direct detection is
.
In terms of performances, the direct detection is
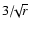 better than detection from phase
closure. However,
this is the price to pay because, to our knowledge, there is no other
direct method than the one we propose, which is capable of detecting stellar
companions within an Airy disk and at a distance from the hosting star
as small as a few stellar radii. Once the conditions above are
fulfilled, measuring the flux ratio for each spectral element at
resolution
better than detection from phase
closure. However,
this is the price to pay because, to our knowledge, there is no other
direct method than the one we propose, which is capable of detecting stellar
companions within an Airy disk and at a distance from the hosting star
as small as a few stellar radii. Once the conditions above are
fulfilled, measuring the flux ratio for each spectral element at
resolution
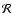 is an effective way to measure the
companion spectrum.
is an effective way to measure the
companion spectrum.
![\begin{figure}
\par\includegraphics[angle=-270,width=7.9cm,clip]{1036fig6.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg59.gif) |
Figure 4:
a) ( Top): error on the flux ratio of a double system from the closure
phase information of a 3-telescope interferometer. The signal is made by 900 phase
closure regularly sampled within the working frequency intervals,
and spectrally dispersed along 270 spectral channels, with a
spectral resolution of 1500. The experimental parameters are;
observing wavelength:
|
| Open with DEXTER | |
3.3 Performances
The mean error on the flux ratio in the H band at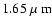 from a 3-telescope interferometer and an integration time of 3 h, obtained
by averaging all the spectral channels over an optical bandwidth of
from a 3-telescope interferometer and an integration time of 3 h, obtained
by averaging all the spectral channels over an optical bandwidth of
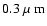 ,
is plotted in Fig. 4a. The upper
curves correspond to 3 telescopes of 2 m, 1% transmission, and a
Strehl ratio of 0.5. It roughly represents the present state of the
AMBER instrument on the VLTI with Auxiliary telescopes. The middle and
lower curves correspond
to telescopes of 2 m and 8 m, a transmission of 10%, and Strehl
ratios of 0.9 and 0.5, respectively (see the caption of
Fig. 4 for details).
,
is plotted in Fig. 4a. The upper
curves correspond to 3 telescopes of 2 m, 1% transmission, and a
Strehl ratio of 0.5. It roughly represents the present state of the
AMBER instrument on the VLTI with Auxiliary telescopes. The middle and
lower curves correspond
to telescopes of 2 m and 8 m, a transmission of 10%, and Strehl
ratios of 0.9 and 0.5, respectively (see the caption of
Fig. 4 for details).
If we assume a signal-to-noise ratio of 10 on the flux ratio for a positive detection, then the AMBER instrument with Auxiliary telescopes would allow detection of companions 104 fainter around second-magnitude stars and 103 fainter around five-magnitude stars. Spectroscopy would be possible from flux ratios of 10-4. Optimized interferometers with 10% transmission (Fig. 4, middle and bottom curves) would allow the detection of companions 104 fainter around 5 to 7 mag stars and 103 fainter around 8 to 10 mag stars. Spectroscopy would be possible from flux ratios of 10-5.
Figure 4b shows the baseline needed to resolve
the primary star, that is, to reach the first visibility null for late
dwarfs and giants. The horizontal line at 200 m corresponds to the
maximum baseline of the VLTI, which imposes maximum
H magnitudes of about 2.5 and 1.5 for M0 dwarves and giants,
respectively. Also the field of view of fiber-linked interferometers is limited to one Airy
disk 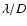 ,
where D is the telescope diameter. Given that the
baseline for reaching the first null is
,
where D is the telescope diameter. Given that the
baseline for reaching the first null is
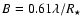 ,
it gives
a maximum recoverable separation of about B/D stellar radii,
which is 100 stellar radii on the VLTI with 2 m telescopes. A baseline
of 1000 m necessary for resolving a solar type star at a distance of 10 pc
would provide a field of 500 stellar radii.
,
it gives
a maximum recoverable separation of about B/D stellar radii,
which is 100 stellar radii on the VLTI with 2 m telescopes. A baseline
of 1000 m necessary for resolving a solar type star at a distance of 10 pc
would provide a field of 500 stellar radii.
As specified in Sect. 3.2, the minimum error is attained
in the photon noise regime when the
working frequency intervals cover at least one period s-1. This
implies, for the first null, a baseline variation 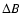 of
of
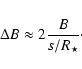 |
(12) |
At kilometric baselines, it represents a variation of 200 m for a distance of 10 stellar radii. The simplest way to achieve such variations is to use earth rotation with repositionable telescopes located at positions such that the baselines and orientations optimize the observing time around the nulls. However, the double system may also be characterized at the price of a lower signal-to-noise ratio, even if the working frequency intervals cover much less than a period. Indeed, the companion of the spectroscopic binary
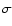 Puppis has been detected and characterized with only 3
snapshot observations of 5 min each; before, during and after the
null, using the spectral dimension to increase the frequency
coverage.
Puppis has been detected and characterized with only 3
snapshot observations of 5 min each; before, during and after the
null, using the spectral dimension to increase the frequency
coverage.
4 Discussion
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1036fig7.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg64.gif) |
Figure 5: Lower limit of the number of stars resolved at a given baseline in the J, H, and K bands. |
| Open with DEXTER | |
4.1 Science cases
We have demonstrated that a phase closure nulling experiment can bring astrophysically significant information on the close environment of resolved stars. Figure 5 shows the lower limit of the number of targets available to phase closure nulling experiments as a function of baseline length. The sample was obtained with the SearchCal utility (Bonneau et al. 2006) and is limited to the stars whose apparent diameter can be reliably estimated from parallax and (spectro)photometric measurements available at the CDS. The minimum number of targets available for current arrays like the VLTI is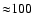 in K and
in K and
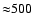 in J. The technique is not
limited to observing unbalanced binary systems but can also
address a broader range of topics. These topics may change either by
changing the nature of the resolved bright astrophysical target and/or
the off-axis accompanying astrophysical signal.
in J. The technique is not
limited to observing unbalanced binary systems but can also
address a broader range of topics. These topics may change either by
changing the nature of the resolved bright astrophysical target and/or
the off-axis accompanying astrophysical signal.
In star and planet formation, astronomers are interested in protoplanetary disks, which in general have the property of being centro-symmetric so that the phase closure signal is zero. Any perturbating signal located off-axis can then be detected by closure phase nulling: inhomogeneities on the disk surface, presence of a forming planetesimal, presence of a collimated jet of outflowing wind partially screened by the disk. It also applies to other science cases holding disk-like cataclysmic variables, active galactic nuclei, proplanetary nebulae, gaseous disk around hot stars. The case of exoplanets is of particular interest, but the various kind of binaries must not be forgotten involving young, main sequence, or evolved stars and even the case of merging binaries.
In a future where interferometry is sensitive to fainter targets, a possible application of this technique is the detection of the gravitational images due to a massive gravitational lens spatially resolved. In the following sections, we restrict ourselves to the companion of evolved and main sequence stars.
4.1.1 Companions of evolved stars
Clearly the simplest observational case, already permitted with current interferometers, is the study of close companions to giant stars. The scientific interest is twofold: improving our knowledge of the masses of giant stars and detecting planetary systems around earlier type stars than the ones known to date. It is indeed customary to look for companions of stars of masses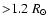 ,
not in their main-sequence phase,
where radial velocity measurements are rendered difficult by the
paucity of spectral lines (furthermore broadened by the rapid stellar
rotation), but in their giant, cooler phase. However, the detection of
substellar companions around giant stars using radial velocities has
always been problematic because the intrinsic pulsation of those stars
would mimic the signature of a close substellar companion, and radial
profiles can be altered by large, slowly rotating,
cool spots on the surface. Only a few detections have been reported
to date (Döllinger et al. 2007; Hatzes et al. 2005; Hatzes & Cochran 1998). The phase closure nulling would provide a
completely independent method of characterizing at least the closest
companions, and give the orbit needed to measure individual masses.
,
not in their main-sequence phase,
where radial velocity measurements are rendered difficult by the
paucity of spectral lines (furthermore broadened by the rapid stellar
rotation), but in their giant, cooler phase. However, the detection of
substellar companions around giant stars using radial velocities has
always been problematic because the intrinsic pulsation of those stars
would mimic the signature of a close substellar companion, and radial
profiles can be altered by large, slowly rotating,
cool spots on the surface. Only a few detections have been reported
to date (Döllinger et al. 2007; Hatzes et al. 2005; Hatzes & Cochran 1998). The phase closure nulling would provide a
completely independent method of characterizing at least the closest
companions, and give the orbit needed to measure individual masses.
We demonstrate this very possibility in a companion paper (Duvert et al. 2009), where we apply the phase closure nulling method for the detection of the close companion of the star Sigma Puppis and the characterization of this SB1 binary system.
4.1.2 Companions of main-sequence stars
These companions can range from brown dwarves (hereafter BDs) or hot Jupiters (HJs) to earth-like planets. With an expected flux ratio of a few 10-4 in the near infrared, brown dwarves could be detected with present-day telescope apertures at any distance from the star within the field-of-view permitted (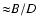 ). The
experiment could bring two new pieces of information: the mass of the BDs (by
solving the orbit) and the NIR spectrum, possibly different in close
binaries than the spectra of isolated BDs.
). The
experiment could bring two new pieces of information: the mass of the BDs (by
solving the orbit) and the NIR spectrum, possibly different in close
binaries than the spectra of isolated BDs.
A few HJs, thus very close to their star (
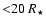 )
and
with temperatures of 1000-1500 K, will be detectable as well
with a flux ratio in the 10-4-10-3 range in K band and
longwards (see e.g. Fortney et al. 2008). A handful of HJs
have already been photometrically detected with the IRAC and MIPS
instruments of the Spitzer Space Telescope
(Charbonneau et al. 2005; Knutson et al. 2008) in transit
experiments. Phase closure nulling experiments in this case would
permit the NIR spectrum of the object, the orbit and thus
the mass to be obtained, without being restricted to transit objects. Phase closure
nulling experiments on dwarf stars with HJs would only be possible
today on a handful of them since
the baseline needed to null a Sun equivalent at 10 pc is
)
and
with temperatures of 1000-1500 K, will be detectable as well
with a flux ratio in the 10-4-10-3 range in K band and
longwards (see e.g. Fortney et al. 2008). A handful of HJs
have already been photometrically detected with the IRAC and MIPS
instruments of the Spitzer Space Telescope
(Charbonneau et al. 2005; Knutson et al. 2008) in transit
experiments. Phase closure nulling experiments in this case would
permit the NIR spectrum of the object, the orbit and thus
the mass to be obtained, without being restricted to transit objects. Phase closure
nulling experiments on dwarf stars with HJs would only be possible
today on a handful of them since
the baseline needed to null a Sun equivalent at 10 pc is
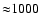 m at
m at
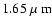 .
This restriction can be overcome in the near
future as fibered interferometers with kilometer baselines are
currently underway (Perrin et al. 2006).
.
This restriction can be overcome in the near
future as fibered interferometers with kilometer baselines are
currently underway (Perrin et al. 2006).
For any planetary companions still cooler and smaller than HJs, the flux
ratio between the star and the companion rapidly becomes forbidding
(>109) in the NIR and is manageable only longwards of
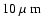 (see Fig. 2 in Traub & Jucks 2002). In the
N band, the above-mentioned constraint on the baseline length then becomes very
challenging (>104 m), and the
signal transmission on such distances would be quite impossible for
ground-based interferometers,
unless techniques like the parametric conversion to visible or NIR
wavelength, such as described in Del Rio et al. (2008), are used
before recombination.
(see Fig. 2 in Traub & Jucks 2002). In the
N band, the above-mentioned constraint on the baseline length then becomes very
challenging (>104 m), and the
signal transmission on such distances would be quite impossible for
ground-based interferometers,
unless techniques like the parametric conversion to visible or NIR
wavelength, such as described in Del Rio et al. (2008), are used
before recombination.
4.2 Towards a dedicated instrument
We have discussed the main properties of phase closure nulling: around each null of the visibility function of the star, a spatial frequency interval exists where the signal of a companion becomes stronger than any systematic error, hence potentially detectable. The errors on the companion detection, both in flux ratio and in position, depend roughly on the square root of the number of star photons detected, and the imageable region for a fiber-linked interferometer (the distance from the star where the companion's signature can be seen) is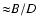 stellar radii. The need to be at a star null fixes
a minimum baseline length. The need to reach a given sensitivity for
the flux ratio implies either a given minimum size for the telescope
apertures, thus a maximum imageable area, or/and a given integration time.
The spectral resolution
stellar radii. The need to be at a star null fixes
a minimum baseline length. The need to reach a given sensitivity for
the flux ratio implies either a given minimum size for the telescope
apertures, thus a maximum imageable area, or/and a given integration time.
The spectral resolution
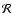 does not need to be very
high, typically
does not need to be very
high, typically
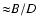 .
.
Today interferometers with baselines of a few hundred meters can already detect faint companions to the few closest giant stars using phase closure nulling. It seems possible to go further - and still use ground-based optical arrays - to characterize the faint companions, down to HJ masses, of the nearby main-sequence stars. This can be envisioned with an interferometer, that
- 1.
- reaches the first zero of a solar-type star at 10 pc in an infrared band - already kilometric baselines in H band;
- 2.
- has a spectral resolution of
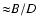 to enable detection of
companions up to
to enable detection of
companions up to
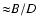 stellar radii. This is 500 for a 1000 m
baseline and 2 m-class telescopes;
stellar radii. This is 500 for a 1000 m
baseline and 2 m-class telescopes;
- 3.
- permits long integration times on the zero crossing thanks to earth rotation and repositionable telescopes;
- 4.
- has the highest attainable transmission: since our S/N only depends on the photon S/N of the primary, this should be as large as possible. Since we are only interested in phase closure that is a robust measurement insensitive to relay optics wavefront disturbance or atmosphere stability, the attention should go on improving the transmission of the relay optics, not their optical quality. This is best realized with fully integrated optics, fiber linking the foci of the telescopes at the primary focus.
- 5.
- uses a few detectors with low noise for the detection, such as a 4-pixel ABCD method. New developments (Rothman et al. 2007) seem to imply that such low-noise IR detectors can be available in a few years from now.
- 6.
- takes advantage of the new developments in integrated optics, permitting both beam recombination and spectrography, thus avoiding the losses at all the diopters of bulk optics used for beam transportation and in the spectrograph. Such a concept, derived from on-going developments for visible spectroscopy (Le Coarer et al. 2007) is under investigation (Kern et al. 2009) and can be envision on the sky in the coming few years.
5 Conclusion
We have introduced both the concept of phase closure nulling and its application in the detection of faint close companions to resolved stars, accuratly measuring their position and spectra. This concept is the only one to date to permit such direct detection inside an Airy disk. We developed the complete error analysis of the phase closure nulling, and show how this method permits ground-based interferometry to complement and, in favorable cases, compete with the direct detection methods considered for future space-borne experiments. We discussed a few science cases that would benefit from phase closure nulling experiments and sketched the requirements for a new type of interferometer dedicated to such studies.
Appendix A: Error calculation
A.1 Error on phase closure
The formal error on the phase closure, in the presence of photon noise and detector readout noise, was computed by Chelli (1989) and Tatulli & Chelli (2005). Neglecting the coupling between the photon noise and the detector noise and retaining the dominant terms, the variance of the phase closure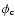 may be approximated by
may be approximated by
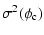 |
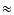 |
![$\displaystyle \frac{N_{\rm tel}^2}{2K} \times \biggl
[\frac{1}{\vert V(u_{12})\...
...}+\frac{1}{\vert V(
u_{23})\vert^2}+\frac{1}{\vert V(u_{13})\vert^2}
\biggr ] ~$](/articles/aa/full_html/2009/16/aa11036-08/img75.gif) |
|
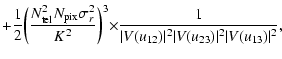 |
(A.1) |
where K is the total number of detected photoevents,
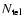 the number of
telescopes,
the number of
telescopes,
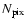 the number of pixels, and
the number of pixels, and
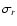 the detector readout noise. And
|V(u12)|,
|V(u23)|,
|V(u13)|, are the visibility amplitudes of the observed object.
the detector readout noise. And
|V(u12)|,
|V(u23)|,
|V(u13)|, are the visibility amplitudes of the observed object.
A.2 Error on the parameters of a double system
We want to estimate the errors on the parameters of a double system made of an extended uniform disk and a point source, from a least square fit of a set of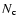 uncorrelated phase closure
measurements obtained with an interferometer formed by
uncorrelated phase closure
measurements obtained with an interferometer formed by
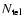 telescopes. For simplicity, we assume that the telescopes are aligned,
with a non redundant configuration, and that the direction of
observation varies little during the experiment and may be considered
constant. Under these conditions, the object is characterized by 3
parameters: the stellar angular radius
telescopes. For simplicity, we assume that the telescopes are aligned,
with a non redundant configuration, and that the direction of
observation varies little during the experiment and may be considered
constant. Under these conditions, the object is characterized by 3
parameters: the stellar angular radius 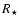 ,
the flux ratio r, and the
projected separation s along the direction of observation.
,
the flux ratio r, and the
projected separation s along the direction of observation.
The 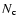 phase closures are sampled at frequencies
phase closures are sampled at frequencies
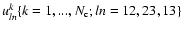 ,
in frequency intervals
,
in frequency intervals
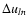 .
We define the
.
We define the 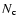 lines and 3 columns matrix
lines and 3 columns matrix
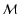 ,
of element mjk, by
,
of element mjk, by
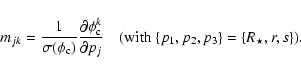 |
(A.2) |
The variances of the parameters are the diagonal elements of the matrix
![$[^t\mathcal{M}\times\mathcal{M}]^{-1}$](/articles/aa/full_html/2009/16/aa11036-08/img84.gif) .
Let us first
examamine the matrix
.
Let us first
examamine the matrix
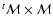 .
It is given by
.
It is given by
![$\displaystyle \left[\begin{array}{l@{~~~}c@{~~~}c}
\displaystyle \sum_{k} {\fra...
...2}\Bigl(\frac{\partial\phi_{\rm c}^k}{\partial{s}}\Bigr)^2}
\end{array}\right].$](/articles/aa/full_html/2009/16/aa11036-08/img86.gif) |
(A.3) |
We neglect now the detector noise (photon noise regime), and we assume that we are working outside the null regions, so that the phase closure may be approximated by Eq. (7). Each element of the matrix above is the sum of nine terms. There are two types of terms
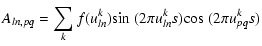 |
(A.4) | ||
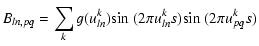 |
(A.5) |
where f(u) and g(u) are smoothly varying functions over the working frequency intervals
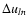 .
.
At last, we assume that the projected separation
s is larger than a few stellar radii and that the working frequency
intervals are larger than s-1, but smaller than the mean
frequencies:
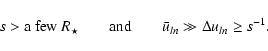 |
(A.6) |
Under these conditions, all the A terms are equal to zero and, given that
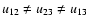 (non redundancy), the only non
null B terms are those for which
(non redundancy), the only non
null B terms are those for which
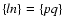 .
In addition,
.
In addition,
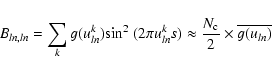 |
(A.7) |
where
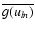 is the average value of g(uln) over
the working frequency interval
is the average value of g(uln) over
the working frequency interval
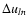 .
The matrix
.
The matrix
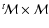 may then be written into
the form
may then be written into
the form
![$\displaystyle {}\!^t\mathcal{M}\times\mathcal{M} \approx
\frac{K}{N_{\rm tel}^2...
...[2mm]
0 & 0 & (2\pi \bar{u}_{\max} r)^2\overline{Z(R_\star)}
\end{array}\right]$](/articles/aa/full_html/2009/16/aa11036-08/img95.gif) |
(A.8) |
where K is the total number of photoevents detected during the whole observation and
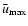 the average value of the highest
frequency.
the average value of the highest
frequency.
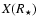 ,
,
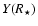 ,
and
,
and
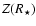 are given by
are given by
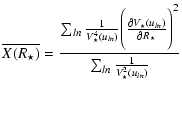 |
(A.9) | ||
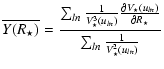 |
(A.10) | ||
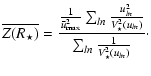 |
(A.11) |
The errors on the parameters of the system may now be computed. Inverting the matrix
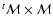 provides
provides
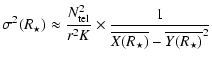 |
(A.12) | ||
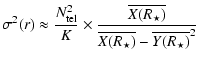 |
(A.13) | ||
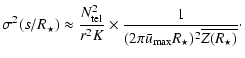 |
(A.14) |
Let us focus on the flux ratio and on the stellar separation. Numerical
calculations show that the quantities
![$\overline{X(R_\star)}/[\overline{X(R_\star)}-\overline{Y(R_\star)}^2]$](/articles/aa/full_html/2009/16/aa11036-08/img105.gif) and
and
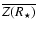 are fairly constant and
close to 1 in a wide range of experimental
conditions, even for observations performed around the nulls. Then,
in the photon noise regime, the
errors on the flux ratio and the separation may be fairly approximated
by
are fairly constant and
close to 1 in a wide range of experimental
conditions, even for observations performed around the nulls. Then,
in the photon noise regime, the
errors on the flux ratio and the separation may be fairly approximated
by
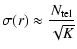 |
(A.15) | ||
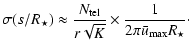 |
(A.16) |
Acknowledgements
This research has made use of the SearchCal service of the Jean-Marie Mariotti Centre, of the CDS Astronomical Databases SIMBAD and VIZIER, and of the NASA Astrophysics Data System Abstract Service.
References
- Benest, D., & Duvent, J. L. 1995, A&A, 299, 621 [NASA ADS]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences]
- Bracewell, R. N. 1978, Nature, 274, 780 [NASA ADS] [CrossRef] (In the text)
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef]
- Chelli, A. 1989, A&A, 225, 277 [NASA ADS]
- Del Rio, L., Ribiere, M., Delage, L., & Reynaud, F. 2008, Opt. Commun., 281, 2722 [NASA ADS] (In the text)
- Döllinger, M. P., Hatzes, A. P., Pasquini, L., et al. 2007, A&A, 472, 649 [NASA ADS] [CrossRef] [EDP Sciences]
- Duvert, G., Chelli, A., Malbet, F., & Kern, P. 2009, A&A, in press (In the text)
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] (In the text)
- Hatzes, A. P., & Cochran, W. D. 1998, MNRAS, 293, 469 [NASA ADS] [CrossRef]
- Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences]
- Kern, P., Le Coarer, E., & Benech, P. 2009, Opt. Express (In the text)
- Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef]
- Le Bouquin, J.-B., Bauvir, B., Haguenauer, P., et al. 2008, A&A, 481, 553 [NASA ADS] [CrossRef] [EDP Sciences]
- Le Coarer, E., Blaize, S., Benech, P., et al. 2007, Nature Photonics, 1, 473 [NASA ADS] [CrossRef] (In the text)
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] (In the text)
- Michelson, A. A., & Pease, F. G. 1921, ApJ, 53, 249 [NASA ADS] [CrossRef] (In the text)
- Perrin, G., Woillez, J., Lai, O., et al. 2006, Science, 311, 194 [NASA ADS] [CrossRef] (In the text)
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences]
- Rothman, J., Perrais, G., Destefanis, G., et al. 2007, in SPIE Conf. Ser., 6542 (In the text)
- Tatulli, E., & Chelli, A. 2005, J. Opt. Soc. Am. A, 22, 1589 [NASA ADS] [CrossRef] (In the text)
- Traub, W. A., & Jucks, K. W. 2002, A Possible Aeronomy of Extrasolar Terrestrial Planets (Atmospheres in the Solar System: Comparative Aeronomy), 369 (In the text)
- Vannier, M., Petrov, R. G., Lopez, B., & Millour, F. 2006, MNRAS, 367, 825 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... Centre
![[*]](/icons/foot_motif.gif)
- Available at http://jmmc.fr
All Figures
![\begin{figure}
\par\includegraphics[angle=-270,width=4.7cm,clip]{1036fig1.ps}\hs...
...*{1.2cm}
\includegraphics[angle=-270,width=4.7cm,clip]{1036fig3.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg13.gif) |
Figure 1:
Visibility for a star represented well by a uniform
brightness distribution over a disk of angular radius |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Phase closure modulo |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-270,width=7.5cm,clip]{1036fig5.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg44.gif) |
Figure 3:
Absolute value of the useful phase closure signal of a double system
formed by a uniform disk and a point source as a function of the
highest frequency located around the first visibility null of the
primary. The spectral resolution is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-270,width=7.9cm,clip]{1036fig6.ps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg59.gif) |
Figure 4:
a) ( Top): error on the flux ratio of a double system from the closure
phase information of a 3-telescope interferometer. The signal is made by 900 phase
closure regularly sampled within the working frequency intervals,
and spectrally dispersed along 270 spectral channels, with a
spectral resolution of 1500. The experimental parameters are;
observing wavelength:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1036fig7.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa11036-08/Timg64.gif) |
Figure 5: Lower limit of the number of stars resolved at a given baseline in the J, H, and K bands. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



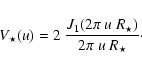
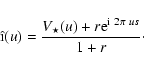
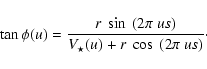
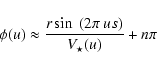
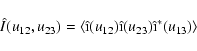
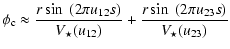
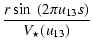
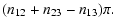
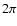 of a double system, formed by an extended
uniform disk and a point source, as a function of the
maximum reduced frequency. The spectral resolution is
of a double system, formed by an extended
uniform disk and a point source, as a function of the
maximum reduced frequency. The spectral resolution is
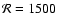 .
The 3 frequencies {
u23, u12, u13}
(see Eq. (
.
The 3 frequencies {
u23, u12, u13}
(see Eq. (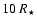 ,
,
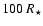 ,
and
,
and
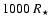 )
and
a flux ratio of 0.01. The signature of the secondary
source is dominant in the region around the minimum visibility
of the primary (near reduced frequency 0.61). The thin line with a 180 degree shift
at 0.61 corresponds to the phase closure of the primary alone.
)
and
a flux ratio of 0.01. The signature of the secondary
source is dominant in the region around the minimum visibility
of the primary (near reduced frequency 0.61). The thin line with a 180 degree shift
at 0.61 corresponds to the phase closure of the primary alone.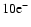 ;
32 pixels per frame. The calculations
took the photon noise and the
detector readout noise into account. Three cases were considered: 3 telescopes with diameter D=2 m, a Strehl ratio S=0.5, and 1% total
transmission (upper curve, this case corresponds roughly to the
present state of the AMBER experiment on the VLTI), D=2 m,
S=0.9 and 10% total transmission (middle curve), D=8 m,
S=0.5 and 10% transmission (lower curve). The broken lines
correspond to an integration time per frame of 12 s.
Represented are: Sirius with a possible M dwarf companion (
;
32 pixels per frame. The calculations
took the photon noise and the
detector readout noise into account. Three cases were considered: 3 telescopes with diameter D=2 m, a Strehl ratio S=0.5, and 1% total
transmission (upper curve, this case corresponds roughly to the
present state of the AMBER experiment on the VLTI), D=2 m,
S=0.9 and 10% total transmission (middle curve), D=8 m,
S=0.5 and 10% transmission (lower curve). The broken lines
correspond to an integration time per frame of 12 s.
Represented are: Sirius with a possible M dwarf companion (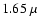 m, namely to reach
the first visibility null, for late dwarfs and giants. The
horizontal line at 200 m corresponds to the maximum baseline of the
VLTI.
m, namely to reach
the first visibility null, for late dwarfs and giants. The
horizontal line at 200 m corresponds to the maximum baseline of the
VLTI.