| Issue |
A&A
Volume 498, Number 1, April IV 2009
|
|
|---|---|---|
| Page(s) | 289 - 293 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200810867 | |
| Published online | 18 February 2009 | |
The size distribution of magnetic bright points derived from Hinode/SOT observations
D. Utz1 - A. Hanslmeier1 - C. Möstl1,2 - R. Muller3 - A. Veronig1 - H. Muthsam4
1 - IGAM/Institute of Physics, University of Graz, Universitätsplatz 5, 8010 Graz, Austria
2 - Space Research Institute, Austrian Academy of Sciences, Schmiedlstraße 6, 8042 Graz, Austria
3 - Laboratoire d'Astrophysique de Toulouse et Tarbes, UMR 5572, CNRS et Université Paul Sabatier Toulouse 3, 57 avenue d'Azereix, 65000 Tarbes, France
4 - Institute of Mathematics, University of Vienna, Nordbergstraße 15, 1090 Wien, Austria
Received 27 August 2008 / Accepted 14 January 2009
Abstract
Context. Magnetic bright points (MBPs) are small-scale magnetic features in the solar photosphere. They may be a possible source of coronal heating by rapid footpoint motions that cause magnetohydrodynamical waves. The number and size distribution are of vital importance in estimating the small scale-magnetic-field energy.
Aims. The size distribution of MBPs is derived for G-band images acquired by the Hinode/SOT instrument.
Methods. For identification purposes, a new automated segmentation and identification algorithm was developed.
Results. For a sampling of 0.108 arcsec/pixel, we derived a mean diameter of
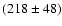 km for the MBPs. For the full resolved data set with a sampling of 0.054 arcsec/pixel, the size distribution shifted to a mean diameter of
km for the MBPs. For the full resolved data set with a sampling of 0.054 arcsec/pixel, the size distribution shifted to a mean diameter of
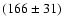 km. The determined diameters are consistent with earlier published values. The shift is most probably due to the different spatial sampling.
km. The determined diameters are consistent with earlier published values. The shift is most probably due to the different spatial sampling.
Conclusions. We conclude that the smallest magnetic elements in the solar photosphere cannot yet be resolved by G-band observations. The influence of discretisation effects (sampling) has also not yet been investigated sufficiently.
Key words: Sun: photosphere - magnetic fields - techniques: image processing
1 Introduction
Magnetic bright points (MBPs) are small-scale magnetic features in the solar photosphere that are important for understanding solar magnetism. In addition, these features play a crucial role in solar physics in two ways. First of all, they can generate MHD waves that can contribute to the coronal heating problem, and secondly they can store magnetic energy.
To complete more robust statistical analyses and derive the parameters of MBPs, an automated algorithm must be developed to identify the interesting features. Manually operated (e.g., Muller & Keil 1983) or semy manually operated (e.g., Möstl et al. 2006) algorithms are impractical for processing significantly large data sets. Although a few automated identification algorithms exist (e.g., Sobotka et al. 1993; Bovelet & Wiehr 2007) more identification methods used in previous works were semi-automated (see e.g., Möstl et al. 2006), i.e., the features must be identified manually and are then tracked automatically. This method is quite time-consuming and can be subjective, and a more efficient and objective method of identification and feature tracking is therefore required. Different approaches to automated algorithms exist. Some authors attempted applying Fourier-filtering techniques prior to identifying MBPs by given thresholds. Others developed single level (of brightness) identification algorithms. An automated algorithm is also required for analysing long time series such as those obtained from the Hinode mission and reduces the uncertainty. The uncertainty can be reduced in two ways. Firstly, the statistical uncertainty decreases with the increasing size of data sets. Secondly, results derived by an automated algorithm do not depend on the user but rather on a specific parameter set. A further advantage would be the reproducibility of the results. Therefore, we developed an automated identification algorithm similar to the so-called MLT 4 algorithm of Bovelet & Wiehr (2007), which was originally developed for investigatng granulation patterns and later adapted to investigations of MBPs. Our algorithm is dedicated to MBP research. Our approach, the resulting algorithm, and our results derived so far, are outlined in this paper.
This paper is the first in a series of articles dealing with Magnetic Bright Points in the solar photosphere. Here, we concentrate on the developed identification algorithm.
2 Data
We used two data sets of the SOT (solar optical telescope; for a description see e.g., Suematsu et al. 2008; Ichimoto et al. 2004) an instrument onboard the Hinode mission (e.g., see Kosugi et al. 2007) built in cooperation between NAOJ (national astronomical observatory Japan) and Lookhead Martin corporation. The SOT has a 50 cm primary mirror, which limits the spatial resolution by diffraction to be about 0.2 arcsec.
For our analysis two data sets of G-band images (here the contrast of MBPs is increased, compared to white-light images) close to disc centre were used. Data set I had a field of view (FOV) of 55.8 arcsec by 111.6 arcsec with a spatial sampling of 0.108 arcsec/pixel. The complete time series consisted of 645 G-band images. Data set II had a FOV of 27.7 arcsec by 27.7 arcsec with a spatial sampling of 0.054 arcsec/pixel and consisted of 756 exposures.
Both data sets were fully
calibrated and reduced by Hinode standard data-reduction algorithms
distributed under Solar SoftWare (SSW)![]() .
.
| |
Figure 1: Left: full-size Hinode/SOT exposure of data set II. The image has a size of about 27 by 27 arcsec. Middle: a zoomed part of this image is shown (size 130 by 130 pixels equal to be about 6 by 6 arcsec). Right: another zoom in (31 by 31 pixels) which corresponds to be about 1.7 by 1.7 arcsec or about 1200 by 1200 km is displayed. One sees that the MBPs are very grainy (not smooth) structures. |
| Open with DEXTER | |
3 Algorithm
The largest problem in identifying MBPs correctly with an automated algorithm is their small size (see the example Fig. 1) since some pixel noise always exists in the images that can be misinterpreted by an automated algorithm as small features. Furthermore, the small size has a significant influence on derived parameters such as areas or velocities. Several characteristics of MBPs can be used by a detection algorithm:
- brightness (MBPs are brighter than their immediate vicinity);
- brightness gradient (MBPs should have a large brightness gradient);
- size of features (MBPs are very small-scale features).
Therefore, we have to derive the size of the features, which requires a segmentation algorithm. Since there will be some oversegmentation, the size of the features alone will be insufficient to ensure that the identified feature is truly a MBP. We therefore require an algorithm for size detection (segmentation), which also uses the information about the brightness and brightness gradient. The developed algorithm consists of three major processing steps:
- segmentation step;
- clean-up step;
- identification step.
| |
Figure 2: Illustration of the segmentation algorithm. From top left to bottom right, every 40th segmentation step is shown. The image used here for illustration is a subimage of one Hinode/SOT exposure, showing a field of view of 10.8 arcsec by 10.8 arcsec. |
| Open with DEXTER | |
When the algorithm finishs, the original image has transformed into a segmented image. Each of the features can then be accessed and analysed. At this stage, the segmentation algorithm may also oversegment some features i.e., the segmentation process may have split single features if they possess several brightness maxima.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{0867fig3.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg7.gif) |
Figure 3: Left top figure shows the original image (spatial sampling of 0.108 arcsec/pixel). Several bright points could be seen. Next, the segmented image is shown before the application of the clean-up algorithm. Followed by the image of the segments after application of the clean-up algorithm. On the left bottom side, the false color image is plotted with the derived feature borders. The middle bottom panel shows the image and the pixels identified as Bright Points (without application of a clean up). Finally, the identified features after application of the clean-up algorithm are plotted. |
| Open with DEXTER | |
The clean up algorithm is applied to reduce the oversegmentation of single features. There are basically three processes that produce oversegmentation:
- pixel noise;
- cosmic rays and particle hits;
- granular brightenings.
The difference between the brightest pixel and the brightest border pixel of a feature was calculated. If this value is smaller than a certain threshold value, the feature is most probably an oversegmented element on top of a granular feature (i.e., a granular brightening). However, it could also be a bright point on the edge of a granule and a second difference (between brightest pixel and mean border brightness) is therefore calculated. If the segmented feature is a MBP or a bright granular border, this difference should be large, since the mean border brightness of the MBP should be small (most border pixels lie in the dark intergranular region; only a few connect the MBP to the granule). If this derived value is below a second threshold, the feature will be merged with the element that has the brightest bordering pixel. The result of this process can be seen in Fig. 3.
The final step (before analysis) is the identification of the MBPs, when the size of each image segment was calculated. We must first define ``size'' appropriately. The simplest idea would be to take all of the pixels of a feature segment into account. This is problematic, since a feature quite often extends continuously into the intergranular region, and therefore the derived size would be far too large (a visualisation of this can be seen in Fig. 4). In most studies, the size was defined by considering all pixels exceeding a certain brightness level. A disadvantage of this approach is missing fainter MBPs, i.e., all of the features that are bright relative to their vicinity but not sufficiently bright to exceed this criterion. Our definition conflicts with these definitions. We consider all pixels in a segment that have brightnesses between an upper and lower boundary. The upper boundary is given by the brightest pixel in the segment. The lower boundary is given by the upper boundary minus a threshold parameter (set in the program). The brightest pixel in a segment has, for example, a value a factor of 1.5 above the mean photospheric intensity and the brightness threshold is set to be 30%. All of the pixels of brightness between a factor of 1.5 to 1.2 of the segment are taken into account in calculating the size. MBPs can be described by flux tubes. The inner part should be homogenously bright, and on the outside the MBPs should be surrounded by dark intergranular matter. This produces a significant brightness gradient in a small transition region between the intergranular and MBP region. In our case, this transition region is not taken into account for the size determination. Because of the steep intensity gradient, slight variations in the selected brightness threshold do not correspond to significant differences in the derived sizes (changing the parameter by 30 percent changes the derived sizes by about 10 percent). Finally, the correct elements are selected on the basis of their sizes. Each feature that does not exceed a certain upper cut-off size is regarded to be a MBP. In our case, these values were 10 and 25 pixels, respectively (see also Fig. 5). Information about these features, such as brightness, size, position, and image number (equal to time), are recorded separately. Finally, important parameters such as the size distribution or the number density of MBPs in the Field of View (FOV) are calculated.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig4.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg8.gif) |
Figure 4: Demonstration of the size determination. Top: A 31 by 31 pixels zoom in detail of an image is shown. Second row: the segment of the image which belongs to the MBP feature (I left, II middle, III right) is displayed. If all of the segment pixels would be taken into account for the size of the MBP, the derived area would too large. Bottom row: the pixels actually taken into account for the size calculation. |
| Open with DEXTER | |
4 Results
The size distribution was determined by deriving the area of each
MBP in pixels. The size criterion was chosen in such a way that
only the brightest pixels of the MBPs were taken into account for
size derivation. The threshold was set to be 30% of the mean
photospheric intensity. This value was chosen because the automated processed images had then the closest agreement when compared to visually identified and processed ones. The derived area was then transformed into a
circle of equal area.
The size distribution obtained from data set I
(sampling of 0.108
 per pixel), follows a normal
distribution with the fit parameters
per pixel), follows a normal
distribution with the fit parameters
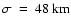 (standard deviation) and
(standard deviation) and
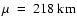 (mean value). This size
distribution incorporates in total
52 628 measurements of MBP sizes in 645 G-band time-series images. The size distribution derived for data set II (sampling of 0.054
(mean value). This size
distribution incorporates in total
52 628 measurements of MBP sizes in 645 G-band time-series images. The size distribution derived for data set II (sampling of 0.054
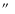 per pixel), also follows a normal
distribution but with different fitting parameters of
per pixel), also follows a normal
distribution but with different fitting parameters of
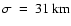 and
and
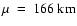 .
In this case,
7891 single MBP size measurements were obtained for 756 G-band time-series images. The ratio of the
number of measurements in both data sets I and II (of about 7) corresponds to the difference in FOV
(27
.
In this case,
7891 single MBP size measurements were obtained for 756 G-band time-series images. The ratio of the
number of measurements in both data sets I and II (of about 7) corresponds to the difference in FOV
(27
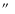 by 27
by 27
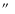 to 55
to 55
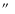 by 111
by 111
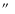 ). Despite the lower number of detected MBPs, the data set of higher spatial resolution is more reliable because it is ``closer'' to the true size distribution due to its smaller pixel size. Both
distributions are shown in Fig. 5. It is
obvious that the distribution is shifted to smaller values.
). Despite the lower number of detected MBPs, the data set of higher spatial resolution is more reliable because it is ``closer'' to the true size distribution due to its smaller pixel size. Both
distributions are shown in Fig. 5. It is
obvious that the distribution is shifted to smaller values.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig5.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg14.gif) |
Figure 5:
MBP size distributions for both data sets and their fitted normal distributions.
Data set I displayed in solid line (spatial sampling of 0.108 arcsec/pixel). Data set II displayed in dashed line (sampling rate of 0.054 arcsec/pixel). Fit parameters of data set I are 218 |
| Open with DEXTER | |
Since the algorithm has problems in differentiating between large MBPs and small granules, we could only derive sizes of up to 280 km and 220 km, respectively.
The shift in the two size distributions is most likely caused by the change in the sampling resolution (changed from 0.108 arcsec/pixel to 0.054 arcsec/pixel). We checked this by artificially decreasing the sampling resolution of data set II and then applied our algorithm again using the same set of parameters. The result can be seen in Fig. 6. For the artificially lower resolved data set (which corresponds to a lower spatial sampling), we found values of about (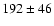 )
km that agree with the above presented Fig. 5. The degradation in sampling was achieved by summing the intensity values of four neighbouring pixels to derive that of the new single pixel.
)
km that agree with the above presented Fig. 5. The degradation in sampling was achieved by summing the intensity values of four neighbouring pixels to derive that of the new single pixel.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig6.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg16.gif) |
Figure 6:
The size distribution of data set II together with the size distribution derived after decreasing the spatial sampling artificially. Original fitting parameters: 166 |
| Open with DEXTER | |
We now examine the effects of discretisation. The size distribution found for data set II (166 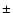 31 km) is similar to that of
Wiehr et al. (2004). Their work was based on data from the 1
m Swedish Solar Telescope (SST) on La Palma with a sampling of 0.041
31 km) is similar to that of
Wiehr et al. (2004). Their work was based on data from the 1
m Swedish Solar Telescope (SST) on La Palma with a sampling of 0.041
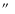 per pixel. They derived most frequently a diameter of 160
per pixel. They derived most frequently a diameter of 160 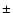 20 km. We consider the shift and change in our size distribution with sampling to be due to an undersampling of the features. This means that the algorithm derives sizes that are larger than in reality.
The sizes could not only be overestimated but also
underestimated, if a feature is only recognised partly. This is due to an averaging effect during the discretisation. Every pixel value represents the average brightness of the corresponding true surface area on the sun. For small features (occupying a few pixels), this effect can lead to the feature being completely missed, particularly when the MBPs are considered to be located in the dark intergranular region. Therefore, small bright elements would be averaged with dark intergranular areas, and the features would not longer be identified as a bright element. This process produces the shift in the distribution to larger sizes in the case of lower sampling (Fig. 5). If there is a certain probability of deriving values that are too large or too small, a not so well sampled distribution will become broader. This is because more values will be redistributed from the center into the wings of the distribution than vice versa. We therefore conclude that the sampling has a high influence
on the observed parameters of small-scale features, which we already demonstrated above (Figs. 5 and 6). We conclude that the size
distribution will converge to the true distribution, when not only the true diffraction limit improves but also the spatial sampling is increased.
20 km. We consider the shift and change in our size distribution with sampling to be due to an undersampling of the features. This means that the algorithm derives sizes that are larger than in reality.
The sizes could not only be overestimated but also
underestimated, if a feature is only recognised partly. This is due to an averaging effect during the discretisation. Every pixel value represents the average brightness of the corresponding true surface area on the sun. For small features (occupying a few pixels), this effect can lead to the feature being completely missed, particularly when the MBPs are considered to be located in the dark intergranular region. Therefore, small bright elements would be averaged with dark intergranular areas, and the features would not longer be identified as a bright element. This process produces the shift in the distribution to larger sizes in the case of lower sampling (Fig. 5). If there is a certain probability of deriving values that are too large or too small, a not so well sampled distribution will become broader. This is because more values will be redistributed from the center into the wings of the distribution than vice versa. We therefore conclude that the sampling has a high influence
on the observed parameters of small-scale features, which we already demonstrated above (Figs. 5 and 6). We conclude that the size
distribution will converge to the true distribution, when not only the true diffraction limit improves but also the spatial sampling is increased.
Sizes around and below the theoretical resolution limit (in our case of between 140 km and 160 km) have to be doubted because these regions could normally never be resolved. Sizes found below the theoretical resolution limit are most probably due to uncertainties (e.g. pixel noise, and algorithm artefacts). To deal with oversegmentation, the detected elements must have at least a defined minimum difference between their brightest pixels and their mean border pixels. When sizes become smaller and smaller, we reach a regime where the brightest pixel is also a border pixel of the feature (below 9 pixels this is always true). If the pixel brightness increases, the mean border brightness of the entire feature increases. Therefore, the brightest pixel in the feature must be considerably brighter to maintain the brightness threshold criteria. This behavior is illustrated in Figs. 7 and 8. We conclude that this effect steepens the decrease in the size distribution from the maximum to smaller sizes. The left branch of the distribution is in all the cases below the theoretical resolution limit of the telescope. Our investigation suggests that there is most probably no (or at least no strong) brightness/size relation at all (in the accessible range down to about 140 km), as stated before by Berger et al. (1995).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0867fig7.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg17.gif) |
Figure 7: The relative number and brightness excess (to the mean photospheric brightness) versus the size of the features in pixel is shown. Only values right of the vertical line at 13 pixels (diffraction limit) should be relied on. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0867fig8.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg18.gif) |
Figure 8: The number versus brightness excess distribution shifts to higher brightness excesses, when the detected feature sizes decrease. |
| Open with DEXTER | |
5 Conclusion
In this article, we have described our new pattern recognition and automated identification algorithm for MBPs in the solar photosphere. We have demonstrated the potential of our algorithm and showed first results of the algorithm applied to data obtained from Hinode/SOT. The derived size distribution of the MBPs depends strongly on the achieved resolution. Therefore, we suppose that the spatial resolution of Hinode/SOT is insufficient to resolve the smallest elements in the photosphere and that higher resolution images are needed such as those obtained by the 1 m Swedish solar telescope (SST) on La Palma/Spain. Nevertheless the results agree well with earlier published values and we are confident that our algorithm is suitable for analysing not only static parameters such as size distributions but also dynamical characteristics such as velocities and lifetimes. Insight into the sampling problem could be gained by computer simulations. In the future, it will be an important task to derive size distributions with computer-simulation algorithms and compare them with observational data to derive a more robust understanding of errors arising in the sampling processes.
We emphasise that the influence of discretisation is of course not only unique to MBPs but a general problem for other investigations (dealing with similar sampled data) as well. Therefore, this effect should be considered and investigated in more detail.
Acknowledgements
We are grateful to the Hinode team for the possibility to use their data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway). This work was supported by FWF Fonds zur Förderung wissenschaftlicher Forschung grant: P20762. D.U. and A.H. are grateful to the ÖAD Österreichischer Austauschdienst for financing a scientific stay at the Pic du Midi Observatory. R.M. is grateful to the Ministère des Affaires Étrangères et Européennes, for financing a stay at the University of Graz. We want to thank the anonymous referee for his remarks and comments, which helped us to improve the outcome of this work.
References
- Berger, T. E., Schrijver, C. J., Shine, R. A., et al. 1995, ApJ, 454, 531 [NASA ADS] [CrossRef] (In the text)
- Bovelet, B., & Wiehr, E. 2007, Sol. Phys., 109 (In the text)
- Ichimoto, K., Tsuneta, S., Suematsu, Y., et al. 2004, in Optical, Infrared, and Millimeter Space Telescopes, ed. J. C. Mather, Proc. SPIE, 5487, 1142
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] (In the text)
- Möstl, C., Hanslmeier, A., Sobotka, M., Puschmann, K., & Muthsam, H. J. 2006, Sol. Phys., 237, 13 [NASA ADS] [CrossRef] (In the text)
- Muller, R., & Keil, S. L. 1983, Sol. Phys., 87, 243 [NASA ADS] [CrossRef] (In the text)
- Sobotka, M., Bonet, J. A., & Vazquez, M. 1993, ApJ, 415, 832 [NASA ADS] [CrossRef] (In the text)
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 26
- Wiehr, E., Bovelet, B., & Hirzberger, J. 2004, A&A, 422, L63 [NASA ADS] [CrossRef] [EDP Sciences]
Footnotes
- ... (SSW)
![[*]](/icons/foot_motif.gif)
- The software package can be obtained via the webpage: http://msslxr.mssl.ucl.ac.uk:8080/SolarB/AnalysisSoftware.jsp
All Figures
| |
Figure 1: Left: full-size Hinode/SOT exposure of data set II. The image has a size of about 27 by 27 arcsec. Middle: a zoomed part of this image is shown (size 130 by 130 pixels equal to be about 6 by 6 arcsec). Right: another zoom in (31 by 31 pixels) which corresponds to be about 1.7 by 1.7 arcsec or about 1200 by 1200 km is displayed. One sees that the MBPs are very grainy (not smooth) structures. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Illustration of the segmentation algorithm. From top left to bottom right, every 40th segmentation step is shown. The image used here for illustration is a subimage of one Hinode/SOT exposure, showing a field of view of 10.8 arcsec by 10.8 arcsec. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{0867fig3.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg7.gif) |
Figure 3: Left top figure shows the original image (spatial sampling of 0.108 arcsec/pixel). Several bright points could be seen. Next, the segmented image is shown before the application of the clean-up algorithm. Followed by the image of the segments after application of the clean-up algorithm. On the left bottom side, the false color image is plotted with the derived feature borders. The middle bottom panel shows the image and the pixels identified as Bright Points (without application of a clean up). Finally, the identified features after application of the clean-up algorithm are plotted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig4.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg8.gif) |
Figure 4: Demonstration of the size determination. Top: A 31 by 31 pixels zoom in detail of an image is shown. Second row: the segment of the image which belongs to the MBP feature (I left, II middle, III right) is displayed. If all of the segment pixels would be taken into account for the size of the MBP, the derived area would too large. Bottom row: the pixels actually taken into account for the size calculation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig5.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg14.gif) |
Figure 5:
MBP size distributions for both data sets and their fitted normal distributions.
Data set I displayed in solid line (spatial sampling of 0.108 arcsec/pixel). Data set II displayed in dashed line (sampling rate of 0.054 arcsec/pixel). Fit parameters of data set I are 218 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0867fig6.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg16.gif) |
Figure 6:
The size distribution of data set II together with the size distribution derived after decreasing the spatial sampling artificially. Original fitting parameters: 166 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0867fig7.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg17.gif) |
Figure 7: The relative number and brightness excess (to the mean photospheric brightness) versus the size of the features in pixel is shown. Only values right of the vertical line at 13 pixels (diffraction limit) should be relied on. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0867fig8.eps}
\end{figure}](/articles/aa/full_html/2009/16/aa10867-08/Timg18.gif) |
Figure 8: The number versus brightness excess distribution shifts to higher brightness excesses, when the detected feature sizes decrease. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


