| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 773 - 787 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200811471 | |
| Published online | 18 February 2009 | |
Modeling the chemical evolution of a collapsing prestellar core in two spatial dimensions![[*]](/icons/foot_motif.png)
R. J. van Weeren1 - C. Brinch1,2 - M. R. Hogerheijde1
1 - Leiden Observatory, Leiden University,
PO Box 9513, 2300 RA Leiden, The Netherlands
2 -
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 4 December 2008 / Accepted 9 February 2009
Abstract
Context. The physical conditions in a collapsing cloud can be traced by observations of molecular lines. To correctly interpret these observations the abundance distributions of the observed species need to be derived. The chemistry in a collapsing molecular cloud is not in a steady state as the density and temperature evolve. We therefore need to follow chemical reactions, both in the gas phase and on dust grains, as well as gas-grain interactions, to predict the abundance distributions.
Aims. Our aim is to model the abundances of molecules, in the gas phase and on grain mantles in the form of ice, from prestellar core collapse to disk formation. We want to investigate the need for grain surface reactions and compare our results with observed abundances, column densities, and ice-mantle compositions.
Methods. We use a 2-dimensional hydrodynamical simulation as a physical model from which we take the density, temperature, and the flow of the gas. Trace particles, moving along with the gas, are used to follow the chemistry during prestellar core collapse and disk formation. We calculated abundance profiles and column densities for various species. The evolution of these abundances and the composition of ices on grain mantles were compared to observations and we tested the influence of grain surface reactions on the abundances of species. We also investigated the initial abundances to be adopted in more detailed modeling of protoplanetary disks by following the chemical evolution of trace particles accreting onto the disk.
Results. Fractional abundances of HCO+, N2H+, H2CO, HC3N, and CH3OH from our model with grain surface reactions provide a good match to observations, while abundances of CO, CS, SO, HCN, and HNC show better agreement without grain surface reactions. The observed mantle composition of dust grains is best reproduced when we include surface reactions. The initial chemical abundances to be used for detailed modeling of a protoplanetary disk are found to be different from those in dark interstellar clouds. Ices with a binding energy lower than about 1200 K sublimate before accreting onto the disk, while those with a higher binding energy do not.
Key words: astrochemistry - hydrodynamics - stars: formation - ISM: molecules - ISM: clouds
1 Introduction
Star and planet formation can be studied through emission lines of molecules in the gas phase and from absorption lines of ices on dust grains. In star-forming regions, the chemistry is not in steady state as the physical conditions change throughout the process (Lee et al. 2004). The chemical processes in star-forming regions are still far from understood and give rise to a large number of different molecular species (e.g., Cazaux et al. 2003). In particular, our knowledge about gas-dust interactions and the chemical reactions on grains surfaces is still very limited. However, we need to understand these processes if we want to correctly asses the physical conditions in star-forming regions and follow the chemical evolution from cold molecular cores towards stars and planetary systems.
Previous studies of the chemical evolution during star formation have (mainly) focused on prestellar core formation and contraction (e.g., Aikawa et al. 2005). Freeze-out of neutral species is an important process in these dark clouds resulting in chemical differentiation. This has been observed in numerous prestellar cores and dark clouds, e.g., Tafalla et al. (2002); Pagani et al. (2005). These authors found that CO and sulfur-bearing species (e.g., CS, SO) deplete at larger radii (lower densities) while NH3 and N2H+ deplete at significantly higher number densities of
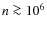 cm-3.
cm-3.
Rodgers & Charnley (2003) modeled chemical abundances in the envelopes surrounding newborn stars gradually heated by the embedded protostar and Lee et al. (2004) followed the chemical evolution during the collapse of a Bonnor-Ebert sphere. Generally, they find a phase of depletion followed by sublimation due to the rising temperature in the envelope of the protostar. Different species sublimate at different radii from the central protostar due to differences in the binding energies of species onto dust grain mantles. These studies used one-dimensional time-evolving models for the density and temperature distribution. By following fluid elements or massless trace particles moving along with the radially in-falling gas, abundances could be derived as function of distance from the protostar. No surface reactions were included in both of these simulations. Garrod & Herbst (2006) presented a model for hot cores which included surface reactions. However, the underlying physical model was relatively simple: consisting of a phase of free-fall isothermal collapse and a phase of gradual heating of the gas and dust by a central Young Stellar Object (YSO). Aikawa et al. (2008) used the same chemical model as Garrod & Herbst (2006) but adopted the results of a one-dimensional radiation-hydrodynamics calculation as the physical model of the core. They found that organic species were mainly formed on grain surfaces at temperatures of 20-40 K. These organic species then sublimated into the gas phase as the gas entered the inner hot (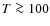 K) region surrounding the protostar.
K) region surrounding the protostar.
Separate studies have focused on the chemical evolution in static 2-dimensional protoplanetary disks (e.g., Aikawa et al. 1996,1997; Aikawa & Herbst 2001). In the cooler midplane of the disk various molecules freeze-out again and accumulate in ice mantles. Due to the strong radiation field from the protostar ion-molecule reactions become important in the upper disk layers and above (e.g., Jonkheid et al. 2004; van Dishoeck & Hogerheijde 1999; van Dishoeck et al. 1998).
Jørgensen et al. (2002) derived CO abundances, using Monte Carlo line radiative transfer modeling, for a sample of 18 low-mass protostars and prestellar cores. An increase in the CO abundance from Class 0 to Class I objects was observed (classification according to Adams et al. 1987; Lada 1987; Andre et al. 1993). Class I objects showed almost normal cosmic fractional CO abundances (
![]() ,
with
,
with
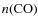 and
and
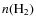 the number densities of CO and H2 respectively), while for Class 0 objects the abundances were almost an order of magnitude lower. Jørgensen et al. (2005a,2004) expanded on this work and constrained the abundances for a range of species in the envelopes of the same 18 objects. They found various trends for the abundances of species as function of envelope mass, reflecting the fact that the chemistry is not in steady state during prestellar core collapse. In general, it is thought that the envelopes of Class I objects have a lower density and higher temperature than Class 0 objects. When the temperature rises in the region surrounding the protostar this leads to the return of species, like CO, by sublimation to the gas phase. At the same time, further out in the envelope the abundances also increase as the freeze-out timescale gets longer due to a lower density.
The picture emerging from these and other observations is that freeze-out and desorption are important processes for the evolution of chemical abundances from Class 0 to Class I objects.
the number densities of CO and H2 respectively), while for Class 0 objects the abundances were almost an order of magnitude lower. Jørgensen et al. (2005a,2004) expanded on this work and constrained the abundances for a range of species in the envelopes of the same 18 objects. They found various trends for the abundances of species as function of envelope mass, reflecting the fact that the chemistry is not in steady state during prestellar core collapse. In general, it is thought that the envelopes of Class I objects have a lower density and higher temperature than Class 0 objects. When the temperature rises in the region surrounding the protostar this leads to the return of species, like CO, by sublimation to the gas phase. At the same time, further out in the envelope the abundances also increase as the freeze-out timescale gets longer due to a lower density.
The picture emerging from these and other observations is that freeze-out and desorption are important processes for the evolution of chemical abundances from Class 0 to Class I objects.
Molecular lines of depleted species in Class 0 and Class I objects can be accounted for with ``drop''-abundance profiles, Jørgensen et al. (2005b). In the inner and outer regions of the envelope there is no depletion (due to a high temperature, low density respectively), whereas at intermediate distances there is a drop in the abundance due to freeze-out. HCO+ shows a clear relationship with CO, while N2H+ abundances remain almost constant in the envelopes. Both of these effects can be explained by the formation and destruction channels of these species which both involve CO. CH3OH abundances for the same sample of 18 objects from Jørgensen et al. require in some cases abundance jumps in the inner regions. H2CO abundances were best fitted with ``drop''-abundance profiles, although an inner jump for H2CO could not be ruled out for most sources. Abundances of complex species like CH3OH are not directly affected by the longer freeze-out timescales in the envelope because of their high binding energies. These species can only return (in large amounts) to the gas phase by grain destruction mechanism (e.g., in shocks) or by sublimation if the temperature is high enough (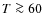 K, depending on the species).
K, depending on the species).
The composition of ices on grain mantles is also of interest. Grain mantles provide surfaces where species can meet and react (e.g., Allen & Robinson 1977). Abundances of certain species, a typical example is CH3OH, can increase dramatically when compared to their formation in the gas phase (e.g., Garrod et al. 2007). Also, the mantle composition has an effect on the binding energy of species onto grains and thus couples to the gas-grain interactions and gas phase chemistry. Modeled ice fractions can be compared to the observed ice mantle compositions in order to constrain which surface reactions take place.
The evolution of chemical abundances during prestellar core collapse may also provide us with a so called ``chemical clock''. It is still unclear wether such a clock exists. For example the use of sulfur-bearing species as a chemical clock was investigated by Buckle & Fuller (2003), but no definitive conclusion has been reached. Modeled abundances can in principle also be used to constrain hydrodynamical models of star formation if the chemistry is well enough understood. For example, high gas phase abundances of complex species formed on grain mantles, require the temperature to be at least higher than the sublimation temperatures of these species.
In Brinch et al. (2008b), from now on called Paper I, we followed for the first time the 2-dimensional time evolution of the CO abundance during prestellar core collapse and disk formation. A 2-dimensional hydrodynamical simulation was used to track the temperature, density, and follow particle motions. We also modeled line profiles for CO and its isotopologue C18O using the line excitation and radiative transfer code RATRAN (Hogerheijde & van der Tak 2000). In particular, the anti-correlation of the fractional CO abundance with envelope mass was reproduced. However, only a simple model for calculating the CO abundance was used. In this second paper we present a method for modeling the full chemical evolution of a collapsing prestellar core in more than one dimension. We replace the model for CO freeze-out/sublimation by a gas phase chemical network which also includes gas-grain interactions and grain surface reactions. This is necessary in order to derive the abundances of species which are more strongly influenced by gas phase or grain surface reactions. We apply this method to a collapsing one-solar mass rotating prestellar core with the physical conditions given by the 2-dimensional hydrodynamical simulation from Paper I.
Apart from the reasons mentioned above there are several important motivations for this work. First, with the upcoming higher resolution (<
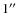 )
observations of ALMA it becomes important to extend the chemical modeling towards two and three dimensions as one-dimensional radial abundance distributions will no longer provide a good description of the observations. The resulting abundance distributions from our model can then be used in line excitation and radiative transfer codes to provide spatially resolved line profiles over the envelope and disk surrounding protostellar objects. This is needed to correctly derive the physical conditions around protostellar objects, such as the velocity field (Brinch et al. 2008a).
)
observations of ALMA it becomes important to extend the chemical modeling towards two and three dimensions as one-dimensional radial abundance distributions will no longer provide a good description of the observations. The resulting abundance distributions from our model can then be used in line excitation and radiative transfer codes to provide spatially resolved line profiles over the envelope and disk surrounding protostellar objects. This is needed to correctly derive the physical conditions around protostellar objects, such as the velocity field (Brinch et al. 2008a).
Second, our modeling also provides important constraints for the initial abundances of species to be adopted in more detailed disk modeling (e.g., Pavlyuchenkov et al. 2007; Semenov et al. 2006,2004) as in our simulation we can track the chemical evolution of gas and ice accreting onto the disk (see Sect. 5).
The method presented in this paper for modeling the chemical abundances is generally applicable and does not depend on the particular hydrodynamical simulation we have used. Our method can also handle one-dimensional as well as 3-dimensional hydrodynamical simulations as long as values for the density, temperature, velocity field, and the radiation field are provided.
The layout of this paper is as follows. In Sect. 2 we shortly summarize the hydrodynamical simulation we use as input for our chemistry. We also present the chemical network to compute the gas phase abundances and ice composition. In Sect. 3 we describe our method to couple the output from the hydrodynamical simulation to the chemistry. In Sect. 4 we present our results and compare them with observations. This is followed by a discussion and conclusions in Sects. 5 and 6.
2 Model
2.1 Physical model: a 2-dimensional hydrodynamical simulation
We use the same physical model of a collapsing prestellar core as in Paper I. The grid-based 2-dimensional simulation is described by Yorke & Bodenheimer (1999). The simulation consists of multiple nested grids in order to sample areas with higher spatial resolution, e.g., the inner disk. The smallest scales correspond to
 7 AU. The central cell is treated as a sink cell into which mass and angular momentum can flow (Boss & Black 1982). The Poisson equation for the gravitational potential is solved according to Black & Bodenheimer (1975). For the hydrodynamics and radiation transport, the scheme from Ròzyczka (1985) is taken. Artificial viscosity is included for shocks. The scheme from Laughlin & Bodenheimer (1994) is used for modeling angular momentum transport.
7 AU. The central cell is treated as a sink cell into which mass and angular momentum can flow (Boss & Black 1982). The Poisson equation for the gravitational potential is solved according to Black & Bodenheimer (1975). For the hydrodynamics and radiation transport, the scheme from Ròzyczka (1985) is taken. Artificial viscosity is included for shocks. The scheme from Laughlin & Bodenheimer (1994) is used for modeling angular momentum transport.
The initial conditions we adopt correspond to the J-model of Yorke & Bodenheimer (1999): a 1 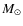 isothermal sphere (a temperature of
10 K for both the gas and dust) with an initial radius of 6667 AU and a power law density profile with a slope of -2. The isothermal sphere was given a solid body rotational perturbation of 10-13 s-1. For this set of initial conditions the free-fall time (
isothermal sphere (a temperature of
10 K for both the gas and dust) with an initial radius of 6667 AU and a power law density profile with a slope of -2. The isothermal sphere was given a solid body rotational perturbation of 10-13 s-1. For this set of initial conditions the free-fall time (
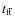 )
is
)
is
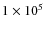 yr. The simulation runs from t = 0 to t = 2.5
yr. The simulation runs from t = 0 to t = 2.5
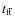 .
.
2.2 Chemical model
2.2.1 Gas phase chemistry
For computing the time-evolution of abundances of various species we make use of the UMIST 2007 database
2.2.2 Gas-grain interactions
We extend the gas phase chemical network with gas-grain interactions: freeze-out and desorption rates are calculated explicitly for each neutral species (e.g., Bergin et al. 1995). Species frozen out create ice mantles on the dust grains. The depletion (freeze-out) rate,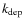 ,
for neutral species can be written as
,
for neutral species can be written as
with a the mean grain radius,
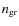 the grain number density. The sticking coefficient S is a function of
the grain number density. The sticking coefficient S is a function of
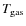 and
and
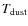 ,
depends on the species accreting, the velocity of the gas, the interaction energy between the grain surface and the gas species, and the excitation of the phonon spectrum of the grain. We ignore most of these complications and adopt a sticking probability of unity, except for atomic hydrogen for which S is described by a function of
,
depends on the species accreting, the velocity of the gas, the interaction energy between the grain surface and the gas species, and the excitation of the phonon spectrum of the grain. We ignore most of these complications and adopt a sticking probability of unity, except for atomic hydrogen for which S is described by a function of
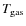 and
and
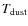 (Tielens 2005). Past studies have also considered lower values for the sticking coefficients (e.g., Aikawa et al. 1996). Lower limits for the sticking coefficients for CO, O2, and N2 at
(Tielens 2005). Past studies have also considered lower values for the sticking coefficients (e.g., Aikawa et al. 1996). Lower limits for the sticking coefficients for CO, O2, and N2 at
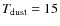 K were measured by Bisschop et al. (2006); Acharyya et al. (2007). The reported values were 0.9, 0.85, and 0.87 respectively, with a typical error of 0.05, so sticking coefficients which are significantly lower than unity do not seem to be justified, except at higher temperatures of
K were measured by Bisschop et al. (2006); Acharyya et al. (2007). The reported values were 0.9, 0.85, and 0.87 respectively, with a typical error of 0.05, so sticking coefficients which are significantly lower than unity do not seem to be justified, except at higher temperatures of
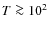 K. Temperatures in our model are generally lower than this value so we choose not to lower the sticking coefficients. We take a ``standard'' mean grain radius of
0.1
K. Temperatures in our model are generally lower than this value so we choose not to lower the sticking coefficients. We take a ``standard'' mean grain radius of
0.1 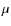 m, and a grain abundance of
m, and a grain abundance of
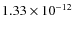 relative to
relative to
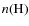 the number density of atomic hydrogen, and
the number density of atomic hydrogen, and
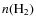 the number density of molecular hydrogen.
the number density of molecular hydrogen.
Table 1: The initial abundances.
When a species (X) freezes out it becomes bound. The values for the binding energy,
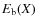 ,
onto the surface are uncertain. Just a few have been measured in laboratories, examples are CO, N2, O2 (see also Collings et al. 2004). The binding energies depend on the type of grain mantle (e.g., bare SiO2, CO ice, H2O ice, etc.). To complicate things even further, grain mantles are mixtures of ices and evolve with time. Following Lee et al. (2004), binding energies of a bare SiO2 mantle are used as a starting point (Hasegawa & Herbst 1993; Hasegawa et al. 1992, and references therein). The binding energies onto an H2O mantle (polar) and onto a CO mantle (a-polar) are greater and smaller than that of a SiO2 mantle by factors of 1.47 and 0.82, respectively. Note that these ratios are just rough estimates and could vary between species. Here we adopt CO mantle binding energies following Aikawa et al. (1996), i.e., we multiply the binding energies by a factor of 0.82. For some species no binding energies were found in the literature. For species which are chemically similar to species with binding energies given,
,
onto the surface are uncertain. Just a few have been measured in laboratories, examples are CO, N2, O2 (see also Collings et al. 2004). The binding energies depend on the type of grain mantle (e.g., bare SiO2, CO ice, H2O ice, etc.). To complicate things even further, grain mantles are mixtures of ices and evolve with time. Following Lee et al. (2004), binding energies of a bare SiO2 mantle are used as a starting point (Hasegawa & Herbst 1993; Hasegawa et al. 1992, and references therein). The binding energies onto an H2O mantle (polar) and onto a CO mantle (a-polar) are greater and smaller than that of a SiO2 mantle by factors of 1.47 and 0.82, respectively. Note that these ratios are just rough estimates and could vary between species. Here we adopt CO mantle binding energies following Aikawa et al. (1996), i.e., we multiply the binding energies by a factor of 0.82. For some species no binding energies were found in the literature. For species which are chemically similar to species with binding energies given,
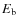 is interpolated. Otherwise
is interpolated. Otherwise
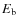 is estimated as
is estimated as
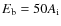 ,
with
,
with
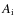 the atomic weight (Wiebe et al. 2003) and
the atomic weight (Wiebe et al. 2003) and
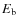 in units of Kelvin.
in units of Kelvin.
Species can be removed from grain mantles by various mechanisms. It is not completely clear yet which mechanisms operate and under what conditions, but at least thermal desorption (sublimation) is thought to be the most important one in protostellar environments.
The thermal desorption rate,
 ,
can be written as
,
can be written as
with
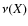 the vibrational frequency of X in its binding site, and
the vibrational frequency of X in its binding site, and
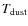 the dust temperature. The vibrational frequency is the characteristic timescale for a species to acquire sufficient energy through thermal fluctuations in order to sublimate. With the harmonic oscillator approximation, the vibrational frequency of X in its binding site is given by
the dust temperature. The vibrational frequency is the characteristic timescale for a species to acquire sufficient energy through thermal fluctuations in order to sublimate. With the harmonic oscillator approximation, the vibrational frequency of X in its binding site is given by
with
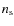 is the surface density of adsorption sites on a grain. The value of
is the surface density of adsorption sites on a grain. The value of
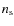 is estimated to be
is estimated to be 
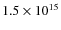 cm-2 (Hasegawa et al. 1992).
cm-2 (Hasegawa et al. 1992).
A second desorption mechanism which is taken into account is cosmic ray induced desorption. This mechanism was first proposed by Watson & Salpeter (1972). Energetic nuclei might eject molecules from grain surfaces by either raising the temperature of the entire grain or by spot heating near the impact site. Cosmic ray heating is dominated by heavy ions because they deposit much more energy compared to lighter more abundant energetic nuclei. It is important in cold molecular cores as the temperatures there are too low for thermal desorption. The formulation of Hasegawa & Herbst (1993) is used to calculate the cosmic ray desorption rate
2.2.3 Dissociative recombination on grain surfaces
Under normal conditions inside a molecular cloud, most grains will be negatively charged (Umebayashi & Nakano 1980). It is assumed that when a positive ion collides with a grain it will undergo dissociative recombination, with the same branching ratio as a dissociative recombination reaction in the gas phase. The products of these reactions return to the gas phase immediately. After the positive ion and the grain surface have been neutralized, an electron will stick immediately to the grain surface restoring its negative charge. If we assume that all grains have a negative charge then positive ions will collide more often with grains than their neutral counterparts. For single ionized species the collision rate is enhanced by a factor
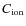 .
The rate coefficient for a dissociative recombination on a grain surface is then written as
.
The rate coefficient for a dissociative recombination on a grain surface is then written as
with
and a and
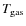 in cgs units (Umebayashi & Nakano 1980; Rawlings et al. 1992). The sticking coefficient for all ions is taken unity. The summation in Eq. (5) is over all possible recombination channels for a single ion; the quantity
in cgs units (Umebayashi & Nakano 1980; Rawlings et al. 1992). The sticking coefficient for all ions is taken unity. The summation in Eq. (5) is over all possible recombination channels for a single ion; the quantity
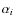 denotes the probability for a particular channel (branching ratio).
denotes the probability for a particular channel (branching ratio).
2.2.4 Grain surface chemistry
Chemical reactions between species on grain surfaces can be of considerable importance: for example the formation of H2 on grain mantles is the dominant mechanism to form H2. For other possible grain surface reactions the situation is less clear but abundances of some species are hard to explain without surface reactions as the gas phase production is too low to account for the observed abundances (see also Herbst 2005). We have extended the gas phase chemical network by grain surface reactions using the approach of Hasegawa et al. (1992). Two reactants wander over the surface of a dust grain until they find each other and (possibly) react. This wandering/diffusion can either happen by thermal hopping over energy barriers or by quantum mechanical tunneling (only efficient for light species). The diffusion rate of species i is given by the largest of the thermal hopping or tunneling rate
| (7) |
![\begin{displaymath}t_{i,{\rm quantum}} = \nu(X)^{-1}\exp\left[(2a/\hbar)(2 m(X) E_{{\rm B}})^{1/2}\right]
.
\end{displaymath}](/articles/aa/full_html/2009/15/aa11471-08/img48.png) |
(8) |
For the energy barrier against diffusion,
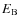 ,
we take a value of 30% of the binding energy, i.e.,
,
we take a value of 30% of the binding energy, i.e.,
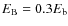 (Hasegawa et al. 1992). The reaction rate between two species i and j is given by
(Hasegawa et al. 1992). The reaction rate between two species i and j is given by
with
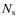 the number of surface sites on a grain (
the number of surface sites on a grain ( 106),
106),
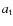 the tunneling barrier (1 Å),
the tunneling barrier (1 Å), 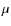 the reduced mass, and
the reduced mass, and 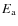 the activation energy for the reaction. For most reactions
the activation energy for the reaction. For most reactions
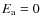 so that
so that
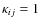 .
The set of surface reactions was taken from Hasegawa & Herbst (1993); Hasegawa et al. (1992), model N(4200 K). This set of reactions was complimented by that of Caselli et al. (2002), but including only the non-deuterated species. Activation energies for some specific reactions taken were: 2500 K for
.
The set of surface reactions was taken from Hasegawa & Herbst (1993); Hasegawa et al. (1992), model N(4200 K). This set of reactions was complimented by that of Caselli et al. (2002), but including only the non-deuterated species. Activation energies for some specific reactions taken were: 2500 K for
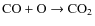 we took 1000 K (d'Hendecourt et al. 1985).
we took 1000 K (d'Hendecourt et al. 1985).
The surface rates were altered according to Stantcheva et al. (2001) and Caselli et al. (2002) in order to cope with the discrete aspects of grain surface chemistry. This so called ``modified rate approach'' has been tested against a more detailed stochastic method by Stantcheva & Herbst (2004) and shows reasonable agreement with it. In short, we compare the reaction rate coefficient (Eq. (9)) with that of the accretion and desorption rates. If the reaction rate is the smallest amongst the three the rate is not altered. In all other cases, the diffusion rate is replaced by the larger of the accretion and desorption rates. The net effect is to slow down the reactions which include at least one light species (i.e., atomic hydrogen). While not entirely correct, stochastic methods are still not available for large chemical networks and it is at least preferable the use the ``modified rate approach'' instead of the ordinary surface reaction rates.
3 Method
![\begin{figure}
\par\includegraphics[trim =0.3cm 0cm -0.3cm 0cm,width=8.5cm]{1471fi1}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg62.png) |
Figure 1:
Distribution of trace particles at t= 2.5
|
| Open with DEXTER | |
We integrate our initial abundances (Table 1) for 105 yr using typical conditions for a dense interstellar medium (ISM):
n = 104 cm-3,
![]() K, and an extinction corresponding to
K, and an extinction corresponding to
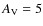 .
For this integration time, the gas phase abundances and grain mantle composition show a good match with observed abundances and ice-compositions in dark molecular clouds. The updated abundances then serve as starting abundances for the chemical simulation of the collapsing core. Before the actual collapse we also take a static core configuration into account which lasts
.
For this integration time, the gas phase abundances and grain mantle composition show a good match with observed abundances and ice-compositions in dark molecular clouds. The updated abundances then serve as starting abundances for the chemical simulation of the collapsing core. Before the actual collapse we also take a static core configuration into account which lasts
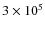 yr (i.e., one dynamical timescale and roughly the lifetime of a prestellar core). The abundances are then further integrated corresponding to this static configuration, but now with the temperature and density given by the first snapshot (t = 0) of the hydrodynamical simulation. This approach is similar to that of Aikawa et al. (2008). For direct cosmic-ray ionization reactions and cosmic-ray-induced photo-reactions we use the UMIST 2007 ionization rate
yr (i.e., one dynamical timescale and roughly the lifetime of a prestellar core). The abundances are then further integrated corresponding to this static configuration, but now with the temperature and density given by the first snapshot (t = 0) of the hydrodynamical simulation. This approach is similar to that of Aikawa et al. (2008). For direct cosmic-ray ionization reactions and cosmic-ray-induced photo-reactions we use the UMIST 2007 ionization rate  of
of
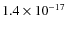 s-1 for H2. For the photodissociation reactions we also use the rates as given by the UMIST 2007 database, corresponding to a standard unshielded interstellar ultraviolet radiation field of about
108 photons cm-2 s-1 between 6 and 13.6 eV.
For the extinction we take a constant value of
s-1 for H2. For the photodissociation reactions we also use the rates as given by the UMIST 2007 database, corresponding to a standard unshielded interstellar ultraviolet radiation field of about
108 photons cm-2 s-1 between 6 and 13.6 eV.
For the extinction we take a constant value of
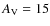 throughout the core during the whole simulation which implies that the UV-radiation field has little effect on the chemistry. The cosmic ray ionization rate is left unaltered.
throughout the core during the whole simulation which implies that the UV-radiation field has little effect on the chemistry. The cosmic ray ionization rate is left unaltered.
The output of the hydrodynamical simulation serves as an input for the physical conditions needed in the chemistry. As in Paper I, we populate the computational domain of the first snapshot (t = 0) with trace particles, see Fig. 1. The particles have no interaction with each other or the medium. The dynamics of these trace particles is discussed in Paper I. Instead of solving for the CO abundance only (using a very simple scheme), we compute abundances using a full set of chemical reactions (including gas-grain interactions and surface reactions).
For each trace particle we solve the following differential equations for the gas phase fractional abundance x(i), and surface fractional abundance xs(i) for species i
with Klj the gas phase reaction rates between species l and j and kij the grain surface reaction rate between species i and j. In both equations the first and second terms correspond to the gas phase formation and destruction of the species respectively. The last two terms correspond to the depletion and desorption processes. Since the particles move with the flow of the gas the absolute abundances evolve according to the molecular hydrogen density
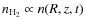 .
The set of differential equations is solved using DLSODE (Radhakrishnan & Hindmarsh 1993). Thus, for a single trace particle the calculation goes as follows: a trace particle starts at a position
(R0,z0) within the core with the abundances found from our initial calculations. Rate coefficients (Klj and kij) are calculated using the density and temperature at that position. The abundances in this trace particle (fluid element) are updated by integrating the differential equations of our chemical network (Eqs. (10)
and (11)). The integration time is equal to the time between two neighboring snapshots of the hydrodynamical simulation. The position of the trace particle is then updated, with the velocities given by our 2-dimensional hydrodynamical model. This process is repeated until the end of the simulation (
.
The set of differential equations is solved using DLSODE (Radhakrishnan & Hindmarsh 1993). Thus, for a single trace particle the calculation goes as follows: a trace particle starts at a position
(R0,z0) within the core with the abundances found from our initial calculations. Rate coefficients (Klj and kij) are calculated using the density and temperature at that position. The abundances in this trace particle (fluid element) are updated by integrating the differential equations of our chemical network (Eqs. (10)
and (11)). The integration time is equal to the time between two neighboring snapshots of the hydrodynamical simulation. The position of the trace particle is then updated, with the velocities given by our 2-dimensional hydrodynamical model. This process is repeated until the end of the simulation ( 2100 snapshots) or when the particle falls onto the protostar. We then proceed with the next trace particle.
2100 snapshots) or when the particle falls onto the protostar. We then proceed with the next trace particle.
We limit the number of particles to about 700 in order to carry out the computations in a reasonable amount of time. The trajectories of these 700 trace particles are a subset of that followed in Paper I. Out of
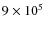 particles, 700 are chosen such that at particular time steps (t = 0.0, 0.5, 1.5, and 2.5
particles, 700 are chosen such that at particular time steps (t = 0.0, 0.5, 1.5, and 2.5
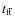 )
these particles are well distributed spatially throughout the core with respect to the varying physical conditions (i.e., the density of the particles increases radially inwards to properly sample the inner regions). We thus follow 4 different subsets of about 700 particles each. The particles move with the flow of the gas so they are irregularly distributed with respect to their locations (R,z). Therefore a mesh of triangles is constructed with data points (corresponding to the positions of the particles) at the vertices of the triangles. The mesh of triangles defines a piecewise-planar interpolating function, and we can thus grid the abundances onto a regular 2-dimensional grid. The spatial resolution varies from
)
these particles are well distributed spatially throughout the core with respect to the varying physical conditions (i.e., the density of the particles increases radially inwards to properly sample the inner regions). We thus follow 4 different subsets of about 700 particles each. The particles move with the flow of the gas so they are irregularly distributed with respect to their locations (R,z). Therefore a mesh of triangles is constructed with data points (corresponding to the positions of the particles) at the vertices of the triangles. The mesh of triangles defines a piecewise-planar interpolating function, and we can thus grid the abundances onto a regular 2-dimensional grid. The spatial resolution varies from  20 AU in the core center to
20 AU in the core center to  500 AU in the outer envelope.
500 AU in the outer envelope.
In order to asses the effects of grain surface reactions on the abundances of species we run the same simulation again but without the grain surface reactions, referred to as Model G. The model which includes grain surface reaction we will refer to as Model S.
4 Results
4.1 Abundance profiles & column densities
![\begin{figure}
\par\includegraphics[trim =0.3cm 0cm -0.3cm 0cm,width=8.5cm]{1471fi2}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg75.png) |
Figure 2:
Distribution of CO throughout the core at four different times during the simulation for Model S. The black contour shows the outline of the disk. The disk is defined as the region where
|
| Open with DEXTER | |
 500 AU. At the later stages CO freezes out again in the disk due to the increase in density in this region. Qualitatively the results are similar to that in Paper I, but the total CO abundance of
500 AU. At the later stages CO freezes out again in the disk due to the increase in density in this region. Qualitatively the results are similar to that in Paper I, but the total CO abundance of
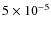 is lower than the cosmic abundance of
is lower than the cosmic abundance of
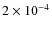 used in Paper I . This is due to the fact that CO ice on grain mantles efficiently transforms into other species (e.g., CO2 and CH3OH) by grain surface reactions, so the amount of depletion seems higher. Model G has a higher CO abundance (
used in Paper I . This is due to the fact that CO ice on grain mantles efficiently transforms into other species (e.g., CO2 and CH3OH) by grain surface reactions, so the amount of depletion seems higher. Model G has a higher CO abundance ( 10-4, similar to that in Paper I), because no surface conversion of CO takes place, but apart from this scaling the abundance distribution looks like that in
Fig. 2.
10-4, similar to that in Paper I), because no surface conversion of CO takes place, but apart from this scaling the abundance distribution looks like that in
Fig. 2.
For other neutral species the pattern is similar, gas-grain interactions determine to a large extent the abundance evolution of species during prestellar core collapse. We start with a high level of depletion (several orders of magnitude locally), and when the temperature rises in the center a sublimated zone develops. In the outer parts of the envelope the density drops, resulting in the increase of the gas phase abundances of species with a relatively low binding energy. Within the disk, species with a low binding energy freeze-out again. Species with a higher binding energy (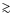 1200 K) are able to enter the disk without sublimating. Gas accretes onto the disk around
1200 K) are able to enter the disk without sublimating. Gas accretes onto the disk around  500 AU (at the centrifugal radius) well outside the sublimation fronts for these species. Some ices (e.g., H2O and CH3OH) in the disk are thus (partly, as they are also being produced within the disk) of primordial origin. The abundances of charged species are determined by the balance between destruction and formation. Parent species, and/or destructors often have gas-grain interactions so the abundances of charged species are influenced by gas-grain interactions indirectly. The 2-dimensional abundance distributions for various species are included in the online Appendices A (Model S) and B (Model G).
500 AU (at the centrifugal radius) well outside the sublimation fronts for these species. Some ices (e.g., H2O and CH3OH) in the disk are thus (partly, as they are also being produced within the disk) of primordial origin. The abundances of charged species are determined by the balance between destruction and formation. Parent species, and/or destructors often have gas-grain interactions so the abundances of charged species are influenced by gas-grain interactions indirectly. The 2-dimensional abundance distributions for various species are included in the online Appendices A (Model S) and B (Model G).
![\begin{figure}
\par\includegraphics[trim =0.cm 0cm -0.cm 0cm, width=8.5cm]{1471fi3}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg79.png) |
Figure 3:
Model S. The radial abundances through the disk (R,z=0) at four different times during the simulation. The line styles corresponding to different species are indicated in the top right panel at t = 0.5
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[trim = 0.0cm 0cm -0.0cm 0cm, width=8.5cm]{1471fi4}
\par\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg80.png) |
Figure 4: Model S. The radial abundances through the disk (R,z=0) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
Abundances of various species as function of radius (R,z=0) are shown in Figs. 3 and 4. Abundances perpendicular to the disk plane (R=0,z) are shown in Figs. 5 and 6. We have chosen to show only the results for Model S as we will discuss the differences with Model G in the next sections (with respect to global envelope abundances). The radial profiles, cutting through the disk midplane, are difficult to compare with previous work due to the fact that the one-dimensional models do not include rotation and hence do not form a disk. We can compare the abundance profiles perpendicular to the disk plane with that of Lee et al. (2004) and Aikawa et al. (2008). The underlying physical models and chemical networks differ so that a one-to-one comparison of the results is not possible, instead we will try to identify differences or similar patterns in the abundance profiles.
![\begin{figure}
\par\includegraphics[trim =0.cm 0cm -0.cm 0cm, width=8.5cm]{1471fi5}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg81.png) |
Figure 5: Model S. The abundances perpendicular to the disk (R=0,z) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[trim =0.0cm 0cm -0.0cm 0cm, width=8.5cm]{1471fi6}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg82.png) |
Figure 6: Model S. The abundances perpendicular to the disk (R=0,z) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
We can see various abundance fluctuations for species especially at smaller radii
( 1000 AU) or near their sublimation front. In particular, species often show changes in the abundances near the CO front, indicating that their formation or destruction is dependent on the CO abundance, as was also noted by Lee et al. (2004). For example the HCO+ abundance increases near the CO sublimation front, while the N2H+ abundance slightly decreases. Further inwards the abundances of these two species change again due to other gas phase reactions. Compared to Aikawa et al. (2008), the NH3 abundance shows a smaller increase at its sublimation front, about one order of magnitude compared to three orders of magnitude. This is caused by our lower binding energy of 887 K compared to 5534 K. We have chosen the lower value for the binding energy as we assume that the dust grains have an a-polar CO-mantle. This value may be correct at low temperatures (
1000 AU) or near their sublimation front. In particular, species often show changes in the abundances near the CO front, indicating that their formation or destruction is dependent on the CO abundance, as was also noted by Lee et al. (2004). For example the HCO+ abundance increases near the CO sublimation front, while the N2H+ abundance slightly decreases. Further inwards the abundances of these two species change again due to other gas phase reactions. Compared to Aikawa et al. (2008), the NH3 abundance shows a smaller increase at its sublimation front, about one order of magnitude compared to three orders of magnitude. This is caused by our lower binding energy of 887 K compared to 5534 K. We have chosen the lower value for the binding energy as we assume that the dust grains have an a-polar CO-mantle. This value may be correct at low temperatures ( K), but could be higher in the inner regions as most of the CO mantle has sublimated and we are left with a mantle consisting mostly of H2O ice. The CS abundances are two orders of magnitude lower then Aikawa et al. (2008), while for HCN they are higher by about the same amount. The HCO+, N2H+, and H2CO abundances are similar. Note that when we compare the results for Model G there is better agreement for some species, in particular for HCN and CS. The difference between Model S and G will be discussed in the next sections.
K), but could be higher in the inner regions as most of the CO mantle has sublimated and we are left with a mantle consisting mostly of H2O ice. The CS abundances are two orders of magnitude lower then Aikawa et al. (2008), while for HCN they are higher by about the same amount. The HCO+, N2H+, and H2CO abundances are similar. Note that when we compare the results for Model G there is better agreement for some species, in particular for HCN and CS. The difference between Model S and G will be discussed in the next sections.
![\begin{figure}
\par\includegraphics[width=8.6cm]{1471fi7}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg85.png) |
Figure 7:
Column densities for various gas phase species at four different times during the simulation, t = 0 (solid lines), t = 0.5
|
| Open with DEXTER | |
Compared to Lee et al. (2004), CS, HCN, H2CO, and NH3 abundance fluctuations are smaller, in particular at small radii and near sublimation fronts. As argued by Aikawa et al. (2008), these large fluctuations could arise from the fact that the number of species ( 80) and chemical reactions (
80) and chemical reactions ( 800) are significantly lower compared to our network. In a small reaction network, the sudden change of the abundance of one species may easily change the abundance of other species. In larger networks, there are more species included in the formation and destruction channels of a particular species so a sudden change in the abundance of one species does not necessarily propagate towards other species.
800) are significantly lower compared to our network. In a small reaction network, the sudden change of the abundance of one species may easily change the abundance of other species. In larger networks, there are more species included in the formation and destruction channels of a particular species so a sudden change in the abundance of one species does not necessarily propagate towards other species.
We have calculated vertically integrated column densities for various species, (
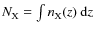 ), which are shown in Fig. 7. At t = 0, these species show flat profiles within
), which are shown in Fig. 7. At t = 0, these species show flat profiles within  1000 AU. After the collapse neutral species show an increase in the column density at the sublimation front. For HCO+, there is an increase around 300 AU (at t = 1.5 and 2.5
1000 AU. After the collapse neutral species show an increase in the column density at the sublimation front. For HCO+, there is an increase around 300 AU (at t = 1.5 and 2.5
 )
but further inwards the column density decreases again and remains flat. For N2H+ the situation is similar. CN shows relatively large variations in its column density inwards of
)
but further inwards the column density decreases again and remains flat. For N2H+ the situation is similar. CN shows relatively large variations in its column density inwards of  200 AU.
The column densities from Aikawa et al. (2003,2005,2001) can be compared to our first snapshot (t = 0). The results are comparable for most species, flat profiles towards the core center and slightly dropping for
200 AU.
The column densities from Aikawa et al. (2003,2005,2001) can be compared to our first snapshot (t = 0). The results are comparable for most species, flat profiles towards the core center and slightly dropping for
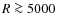 AU. Detailed comparison is not possible as our underlying physical model is rather different. Column densities in the disk increase about three to four orders of magnitude as in Aikawa et al. (1996); Aikawa & Herbst (2001); Aikawa et al. (2002) but are higher overall due to our massive disk of 0.4
AU. Detailed comparison is not possible as our underlying physical model is rather different. Column densities in the disk increase about three to four orders of magnitude as in Aikawa et al. (1996); Aikawa & Herbst (2001); Aikawa et al. (2002) but are higher overall due to our massive disk of 0.4 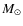 .
.
4.2 Comparison with observations of envelope abundances
Jørgensen et al. (2005a,2004,2002) presented a sample of abundances of various species in the envelopes of Class 0 and Class I objects, and in a few prestellar cores. Abundances were derived using observed line intensities and Monte Carlo radiative transfer modeling. In Paper I, our CO abundances show the same trend as Jørgensen et al. (2002), i.e., a rising CO abundance for a decreasing envelope mass. The global envelope abundance of a species in the simulation excludes the disk. The envelope is defined as the region where
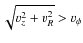 ,
with
,
with 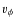 the rotational velocity. The abundance is calculated by dividing the total number of molecules of a species in the envelope by the total number H2 molecules in the envelope. We will now discuss the results for CO and the other species which were present in the sample of Jørgensen et al. We have also included the results from Model G, which does not include grain surface reactions. By comparing the results of Model G and S we can determine the influence of surface reactions on the abundances.
the rotational velocity. The abundance is calculated by dividing the total number of molecules of a species in the envelope by the total number H2 molecules in the envelope. We will now discuss the results for CO and the other species which were present in the sample of Jørgensen et al. We have also included the results from Model G, which does not include grain surface reactions. By comparing the results of Model G and S we can determine the influence of surface reactions on the abundances.
4.2.1 CO
The modeled CO abundances as function of envelope mass are shown in
Fig. 8. The abundance increases from
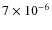 to
to
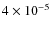 ,
for Model S. Overall the CO abundance is lower by about a factor of 10 compared to Model 3 in Paper I (including cosmic ray desorption and with
,
for Model S. Overall the CO abundance is lower by about a factor of 10 compared to Model 3 in Paper I (including cosmic ray desorption and with
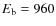 K). Some of the Carbon (and Oxygen) ends up in other species than CO. In particular, CO on grain surfaces is transformed efficiently towards CO2, H2CO, CH3OH and other species. If the grain surface reactions are slowed down, we will get a better match to the observations. In fact, CO2 ice and H2CO (gas) abundances are slightly overproduced in our simulation. The results of the simulation without grain surface reactions, Model G, are very similar to that in Paper I. This confirms that the CO abundance is mostly determined by gas-grain interactions and grain surface reactions, and not by the gas phase chemistry during prestellar core collapse.
K). Some of the Carbon (and Oxygen) ends up in other species than CO. In particular, CO on grain surfaces is transformed efficiently towards CO2, H2CO, CH3OH and other species. If the grain surface reactions are slowed down, we will get a better match to the observations. In fact, CO2 ice and H2CO (gas) abundances are slightly overproduced in our simulation. The results of the simulation without grain surface reactions, Model G, are very similar to that in Paper I. This confirms that the CO abundance is mostly determined by gas-grain interactions and grain surface reactions, and not by the gas phase chemistry during prestellar core collapse.
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8cm]{1471fi8}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg92.png) |
Figure 8:
Global envelope abundances of CO versus envelope mass. The bullets ``'' connected by solid lines are for Model S, which includes grain surface reactions. The bullets connected by dashed lines are for Model G without grain surface chemistry. Data for various objects from Jørgensen et al. (2004,2002) are overplotted. Class I objects are indicated by `` |
| Open with DEXTER | |
4.2.2 HCO+
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8cm]{1471fi9}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg93.png) |
Figure 9: Global envelope abundances of HCO+ versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
Before collapse, the HCO+ abundance decreases radially inwards. This is caused by freeze-out of its parent molecules (mainly CO) and by dissociative recombination of HCO+ (on grain surfaces). Within the sublimation front HCO+ shows a decrease in its abundance at smaller radii because of a lower H3+ abundance. In Fig. 9 we have plotted
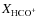 against envelope mass for 18 objects from Jørgensen et al. (2004). Our evolution of the HCO+ abundances agrees quite well with the observations, increasing from 10-9 to 10-8, indicating its chemistry is relatively well understood. The model without grain surface reactions shows a somewhat steeper evolution but overall is very similar, which also shows that the HCO+ abundance is not greatly influenced by grain surface reactions.
against envelope mass for 18 objects from Jørgensen et al. (2004). Our evolution of the HCO+ abundances agrees quite well with the observations, increasing from 10-9 to 10-8, indicating its chemistry is relatively well understood. The model without grain surface reactions shows a somewhat steeper evolution but overall is very similar, which also shows that the HCO+ abundance is not greatly influenced by grain surface reactions.
4.2.3 N2H+
The main formation mechanism for N2H+ (Jørgensen et al. 2004) is:
The main destruction mechanisms are:
The N2H+ abundances decrease radially inwards before collapse. This is caused by freeze-out of its parent molecules (mainly N2) and dissociative recombination of N2H+ (on grain surfaces). At t=0, the N2H+ abundance drops slower inwards than the CO abundance. Within the CO sublimation front, N2H+ is destroyed by CO, at later stages this happens throughout the envelope. The low H3+ abundance in the center also slows down N2H+ production. However, in the envelope the net abundance slightly rises due to a decreasing density. Model G shows lower abundances (also noted by Aikawa et al. 2003) and steeper evolution, both in disagreement with the observations. The higher abundances of about a factor two in the model with surface reactions are the result of the lower CO abundance in combination with the effects of grain surface formation of N2 and subsequent desorption of this parent molecule to the gas phase. We conclude that the model with grain surface reactions gives better results for N2H+.
![\begin{figure}
\par\includegraphics[trim =0cm 0 0 0cm,width=8.5cm]{1471fi10}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg100.png) |
Figure 10: Global envelope abundances of N2H+ versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
4.2.4 CS and SO
The sulfur-bearing species CS and SO show relatively low abundances of 10-11 - 10-10 during the simulation. These molecules are heavily depleted before collapse due to relatively high binding energies of 1780 K for both species. The abundances of both species increase by about an order of magnitude during the collapse due to the lower density (outer envelope) and higher temperature (center). For SO, in the center a spherical central sublimated zone develops (t = 0.5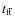 )
with an abundance of
)
with an abundance of

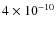 .
Above the midplane of the disk at a radius of
.
Above the midplane of the disk at a radius of  200 AU the abundance rises towards
200 AU the abundance rises towards 
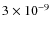 .
For CS the pattern is similar, an abundance of
.
For CS the pattern is similar, an abundance of
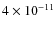 in the center at t = 0.5
in the center at t = 0.5
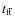 ,
the abundance peaks around t = 1.5
,
the abundance peaks around t = 1.5
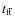 at
at
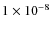 ,
above and within the disk at
,
above and within the disk at 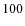 AU.
The enhancement is however too localized to have a major influence on the global envelope abundances. Observed global abundances are more then an order of magnitude higher and the abundances for Model G agree with the observations. This difference could be caused by grain surfaces reactions converting both species towards other species. If we would lower the rates for these reactions surface abundances of CS and SO increase, and as a result gas phase abundances should increase as well. The increase or decrease in the abundances of other species, linked to reaction networks of CS and SO, could also have an effect. Abundances of both species can also be increased by the impact of outflows which processes the gas (e.g., Bachiller & Perez Gutierrez 1997). As outflows are not included we could underestimate the abundances.
AU.
The enhancement is however too localized to have a major influence on the global envelope abundances. Observed global abundances are more then an order of magnitude higher and the abundances for Model G agree with the observations. This difference could be caused by grain surfaces reactions converting both species towards other species. If we would lower the rates for these reactions surface abundances of CS and SO increase, and as a result gas phase abundances should increase as well. The increase or decrease in the abundances of other species, linked to reaction networks of CS and SO, could also have an effect. Abundances of both species can also be increased by the impact of outflows which processes the gas (e.g., Bachiller & Perez Gutierrez 1997). As outflows are not included we could underestimate the abundances.
It has been suggested that sulfur-bearing species might provide a chemical clock (e.g., Ruffle et al. 1999). In the case of low mass protostars this was further investigated by Buckle & Fuller (2003). The chemical clock works as follows: large amounts of H2S are released from grain mantles by the rising temperature in the inner envelope. H2S is converted via several reactions steps into SO and SO2 on
timescales of
104 - 105 years. The abundances of these species drop at later times as they are converted into CS, H2CS, and OCS. Model S shows such a trend, at later times the SO abundance slightly drops and the CS abundance continues to increase. By comparing the abundances of species like CS, SO, SO2, H2S, and H2CS the timescale since the release of H2S can hopefully be constrained. Buckle & Fuller (2003) found that to reproduce the observed abundances the initial H2S abundance should be
>10-8. They did not compute the initial abundance of H2S. Instead, they estimated the abundance from observed gas phase and ice abundances, since no grain surface chemistry was included in their model. In our simulation the surface abundance of H2S is 
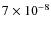 before collapse in agreement with their estimates that X
before collapse in agreement with their estimates that X
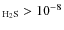 ,
although the abundance is on the low side. However, observed abundances of SO (Jørgensen et al. 2004) do not confirm the picture described above, i.e., they did not find systematically higher SO abundances for Class 0 objects compared to Class I objects. We do also not see such an effect in our model without grain surface reactions. More observations of various sulfur-bearing species are needed to determine if they could be used as a chemical clock.
,
although the abundance is on the low side. However, observed abundances of SO (Jørgensen et al. 2004) do not confirm the picture described above, i.e., they did not find systematically higher SO abundances for Class 0 objects compared to Class I objects. We do also not see such an effect in our model without grain surface reactions. More observations of various sulfur-bearing species are needed to determine if they could be used as a chemical clock.
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi11}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg108.png) |
Figure 11: Global envelope abundances of CS versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi12}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg109.png) |
Figure 12: Global envelope abundances of SO versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
4.2.5 HCN, HNC and CN
HCN and HNC abundances observed by Jørgensen et al. (2004) do not show a clear correlation with envelope mass. CN abundances increase with decreasing envelope mass. This trend for CN is also apparent in our simulation, although abundances are an order of magnitude too high compared to the observations.
CN abundances are too low by one order of magnitude for our model without grain surface reactions. HCN and HNC abundances are very similar and vary from
10-8 - 10-7. Initially, abundances rise, at 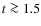
 the abundances remain more or less constant. HCN abundances are an order of magnitude too high, HNC abundances around two orders of magnitude. Both are produced in the gas phase but also by grain surface reactions.
the abundances remain more or less constant. HCN abundances are an order of magnitude too high, HNC abundances around two orders of magnitude. Both are produced in the gas phase but also by grain surface reactions.
The gas phase production of HCN, HNC, and CN depends on the abundance of nitrogen-bearing species. Several critical reactions involving nitrogen-bearing species have large uncertainties in the rate coefficients, caused by the lack of theoretical or experimental verification of the existence of reaction barriers (e.g., Flower et al. 2006). Furthermore, the elemental C:O abundance ratio as well as the
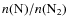 ratio has an effect on the nitrogen-bearing chemistry as was shown by these authors. Another important aspect is the sticking coefficient of atomic nitrogen and oxygen. Flower et al. (2006) and Akyilmaz et al. (2007) found that sticking coefficients lower than unity for these species could explain the relatively high abundances of N2H+ and NH3 in the gas phase when other molecules, such as CO, have already been frozen out. We conclude that the surface rates involving the production of HCN, HNC, and CN should probably be decreased, but that the uncertainties in the gas phase nitrogen-bearing chemistry may also have caused our abundances to differ from the observed values.
ratio has an effect on the nitrogen-bearing chemistry as was shown by these authors. Another important aspect is the sticking coefficient of atomic nitrogen and oxygen. Flower et al. (2006) and Akyilmaz et al. (2007) found that sticking coefficients lower than unity for these species could explain the relatively high abundances of N2H+ and NH3 in the gas phase when other molecules, such as CO, have already been frozen out. We conclude that the surface rates involving the production of HCN, HNC, and CN should probably be decreased, but that the uncertainties in the gas phase nitrogen-bearing chemistry may also have caused our abundances to differ from the observed values.
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi13}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg112.png) |
Figure 13: Global envelope abundances of HCN versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi14}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg113.png) |
Figure 14: Global envelope abundances of HNC versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi15}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg114.png) |
Figure 15: Global envelope abundances of CN versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
4.2.6 HC3N
Our modeled HC3N abundances provide a relatively good match to observed values, rising from 10-10 to 10-9. Without surface reactions, abundances drop by about two orders of magnitude. Some chemical models predict an increase in the abundance when the amount of depletion of other gas phase species (like CO) is high (e.g., Caselli et al. 1998; Hirahara et al. 1992; Ruffle et al. 1997). Observed abundances do not show such a trend as does our model, in fact our model predicts slightly higher abundances with decreasing envelope mass due to sublimation of HC3N from grain mantles and lower freeze-out rates. Jørgensen et al. (2004) mention the possibility (amongst others) that the UV (ultraviolet) radiation from the central protostar could also lead to such a trend. Our results do not support this explanation as we have not included the UV radiation from the central star. In fact, HC3N produced on grain surfaces and subsequently released to the gas phase could produce the observed values. ![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi16}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg115.png) |
Figure 16: Global envelope abundances of HC3N versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
4.2.7 H2CO and CH3OH
Observed H2CO abundances (Jørgensen et al. 2005a) show a clear anti-correlation with the envelope mass. H2CO freezes out at high densities and low temperatures. Sublimation takes places as the temperature rises in the inner regions and the freeze-out rate drops as the density in the envelope decreases. Our modeled abundances confirm this picture. The model without grain surface reactions produces abundances about an order of magnitude lower.
Our modeled CH3OH abundances show large variations, in the prestellar core observed gas phase abundances are very low ( 10-12 - 10-11) because of the large binding energy. Due to the rising temperature and subsequent sublimation, the CH3OH abundance quickly increases in the center, at later times the abundance drops again. The model without surface reactions fails to reproduce the observed abundances by about three to four orders of magnitude. Most of the CH3OH is produced by grain surface reactions, where CO is converted via several steps towards CH3OH which then sublimates into the gas phase. It is also believed that CH3OH abundances and to a lesser extend H2CO are influenced by other processes such as the impact of outflows (e.g., Bachiller & Perez Gutierrez 1997). CH3OH was only observed towards a handful of objects by Jørgensen et al. (2004). This makes comparison with models difficult. At least modeled abundances are roughly within the range of observed values. Increasing the number of objects with CH3OH abundances (or with tighter upper limits) would be helpful to further constrain the CH3OH production mechanism(s).
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi17}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg116.png) |
Figure 17: Global envelope abundances of H2CO versus envelope mass. Data for various objects from Jørgensen et al. (2005a) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
4.3 Ice composition
The ice composition of grain mantles can be derived from observations of infrared absorption bands against a continuum. In dense molecular clouds ices are observed against background stars (e.g., Whittet et al. 2007; Knez et al. 2005; Bergin et al. 2005; Nummelin et al. 2001). For Class 0, Class I, and Class II objects the protostar itself provides the continuum against which we can observe ice absorption features. H2O ice is the most abundant ice-component followed by either CO or CO2. Other ices also exist but the abundances are generally lower. The H2O abundance on grains is a few times 10-4 and its abundance is relatively stable because the binding energy is high (we have adopted 4674 K). Therefore the abundances of the various ices are often expressed as percentage of H2O. In Model S the fractional H2O ice abundance varies between
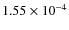 and
and
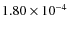 outside a radius of
outside a radius of  100 AU, in agreement with observed values (Schutte et al. 1999; Gibb et al. 2000, and references therein)
100 AU, in agreement with observed values (Schutte et al. 1999; Gibb et al. 2000, and references therein)
The grain mantles in Class 0 objects have similar ice compositions as those in cold molecular clouds, although a small amount of thermal processing seems to have taken place for a number of sources, e.g., Gerakines et al. (1999); Gibb et al. (2004). In Class I objects evidence is found for further processing of ices and complex molecule formation e.g, Zasowski et al. (2007); Alexander et al. (2003); Keane et al. (2001); Boogert et al. (2004); Gibb et al. (2004); Ehrenfreund et al. (1998); Watson et al. (2004). Class II objects have heated the remaining envelope and outer layers of the disk above the sublimation temperature of ices. Although, in some edge-on objects ice are observed, probably arising from the cold midplane of the disk (e.g., Pontoppidan et al. 2005).
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi18}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg119.png) |
Figure 18:
Global envelope abundances of CH3OH versus envelope mass. Data for various objects from Schöier et al. (2002); Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. Other data points indicated are the abundances fitted with ``drop''-abundance profiles, with ``+'' the abundance in the inner region and `` |
| Open with DEXTER | |
The vertically integrated column densities for various ices (Model S) are shown in Fig. 19.
![\begin{figure}
\par\includegraphics[trim =0.3cm 0 -0.3cm 0cm, width=8.8cm]{1471fi19}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg120.png) |
Figure 19:
Column densities of various ices at four different times during the simulation, t = 0 (solid lines), t = 0.5
|
| Open with DEXTER | |
We compare the modeled ice fractions at four different times during the simulation (t = 0, 0.5, 1.5, and 2.5
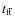 )
to observed values towards the field star Elias 16 (in the vicinity of the dense core TMC-1), the low-mass protostar Elias 29, and a sample of Class I/II objects from Zasowski et al. (2007). The abundances are given relative to H2O and are averaged over the envelope (which does not include the disk). We have also included the ice composition within the disk, at a distance of 500 AU, just outside the CO sublimation front. Model G severely underproduces various ices like CH3OH, CO2, H2O and H2CO. This is explained by the fact that surface reactions are the dominant production mechanisms for these species. Sublimation of these ices then also leads to a higher gas phase abundance. Most of the CH4 ice is located within the disk in Model S where the density is high. For model G, the CH4 ice fraction is higher in the envelope. Surface reactions are thus not required to form a significant amount of CH4. Below we further discuss the results from Model S for several species.
)
to observed values towards the field star Elias 16 (in the vicinity of the dense core TMC-1), the low-mass protostar Elias 29, and a sample of Class I/II objects from Zasowski et al. (2007). The abundances are given relative to H2O and are averaged over the envelope (which does not include the disk). We have also included the ice composition within the disk, at a distance of 500 AU, just outside the CO sublimation front. Model G severely underproduces various ices like CH3OH, CO2, H2O and H2CO. This is explained by the fact that surface reactions are the dominant production mechanisms for these species. Sublimation of these ices then also leads to a higher gas phase abundance. Most of the CH4 ice is located within the disk in Model S where the density is high. For model G, the CH4 ice fraction is higher in the envelope. Surface reactions are thus not required to form a significant amount of CH4. Below we further discuss the results from Model S for several species.
Modeled CO ice abundances are in rough agreement with observed values. Within the prestellar core the CO ice fraction is on the low side with a value of 14% while the CO2 fraction of 47% is quite high. Although, values of 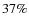 and
and 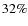 were reported by Boogert et al. (2004) towards B5 IRS 1 and HH 46 IRS. The CH3OH ice fraction of about 5% is in agreement with the observations given the large scatter, the same is true for H2CO. Our modeled SO2 ice fraction (
were reported by Boogert et al. (2004) towards B5 IRS 1 and HH 46 IRS. The CH3OH ice fraction of about 5% is in agreement with the observations given the large scatter, the same is true for H2CO. Our modeled SO2 ice fraction (
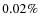 )
is on the low side, but its identification is uncertain. The NH3 ice fraction (
)
is on the low side, but its identification is uncertain. The NH3 ice fraction (
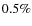 )
is low, observations indicate higher fractions of about
)
is low, observations indicate higher fractions of about 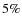 ,
but the NH3 identifications are also somewhat uncertain. A higher binding energy as in Aikawa et al. (2008) would increase its fraction. As has been mentioned in Sect. 4.2.5 the large uncertainties in the gas phase nitrogen-bearing chemistry may also have affected the NH3 ice abundance. During the collapse the fraction of CO ice decreases from 15 to 5%, the fraction of CO2 ice also decreases, from 47 to 30%. The CH3OH fraction stays more or less constant while the H2CO ice fraction increases from 1 to 4%. The decrease in the CO ice fraction is also being observed (as discussed above) and is the results of its low binding energy and the conversion into other more complex species. Slowing down the surface reaction
,
but the NH3 identifications are also somewhat uncertain. A higher binding energy as in Aikawa et al. (2008) would increase its fraction. As has been mentioned in Sect. 4.2.5 the large uncertainties in the gas phase nitrogen-bearing chemistry may also have affected the NH3 ice abundance. During the collapse the fraction of CO ice decreases from 15 to 5%, the fraction of CO2 ice also decreases, from 47 to 30%. The CH3OH fraction stays more or less constant while the H2CO ice fraction increases from 1 to 4%. The decrease in the CO ice fraction is also being observed (as discussed above) and is the results of its low binding energy and the conversion into other more complex species. Slowing down the surface reaction
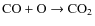 by increasing the activation energy of 1000 K somewhat would produce less CO2 and increase the CO ice fraction. An alternative would be to increase the barrier against diffusion (
by increasing the activation energy of 1000 K somewhat would produce less CO2 and increase the CO ice fraction. An alternative would be to increase the barrier against diffusion (
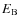 )
which should also slow down CO2 production, as well as the production of other ices.
)
which should also slow down CO2 production, as well as the production of other ices.
Table 2: Grain mantle compositions.
5 Discussion
When we compare our gas phase abundances and ice compositions to observations, it seems that the surface reaction rates are somewhat too high. First we slightly overproduce the amount of CO2 compared to CO. Our ratio of CO2 to CO is about three while observations often show ratios of about one to two. Also the H2CO gas phase abundances are a little high. Furthermore species like HCN, HNC are overproduced by quite some amount, although uncertainties in the nitrogen-bearing chemistry might also have influenced these results. To slow down the surface rates several options exist. First, the binding energy (
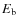 )
of atomic hydrogen could be increased which would slow down surface hydrogenation reactions. We have taken a fast diffusion rate for atomic hydrogen (
)
of atomic hydrogen could be increased which would slow down surface hydrogenation reactions. We have taken a fast diffusion rate for atomic hydrogen (
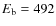 )
so it could be that we have to increase its binding energy to slow down the diffusion rate (see Ruffle & Herbst 2000). Another option is to increase the barrier against diffusion
)
so it could be that we have to increase its binding energy to slow down the diffusion rate (see Ruffle & Herbst 2000). Another option is to increase the barrier against diffusion
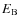 for all surface reactions (e.g.,
for all surface reactions (e.g.,
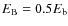 ).
For certain reactions it is also possible to increase the activation energy (
).
For certain reactions it is also possible to increase the activation energy (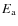 ). Although, this will not help slowing down the HCN and HNC production as there are are no activation energies involved in the production of these species but for the oxidation reaction of CO leading to CO2 this would be an option. As a first step, lowering the diffusion rate for atomic hydrogen and increasing the energy barrier against diffusion will be the best option.
). Although, this will not help slowing down the HCN and HNC production as there are are no activation energies involved in the production of these species but for the oxidation reaction of CO leading to CO2 this would be an option. As a first step, lowering the diffusion rate for atomic hydrogen and increasing the energy barrier against diffusion will be the best option.
The underproduction of CS and SO (Model S) is not completely understood. Although CS and SO are transformed by surface reactions this should not have a very large effect on the abundances as most of those surface reactions do not involve H atoms and are therefore quite slow. Reduced gas phase abundances of CO (and other species) could result in a different gas phase chemistry leading to the decrease of parent species for CS and SO production. More work is needed to further investigate this effect.
In our simulation we have taken a constant value for the extinction (
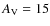 )
throughout the collapsing prestellar core. This is a good approximation during the initial phases of the collapse
(
)
throughout the collapsing prestellar core. This is a good approximation during the initial phases of the collapse
(
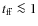 ). Only at the outer edges of the core the results could change significantly due to the presence of the interstellar radiation field combined with lower values for the extinction. We are mainly interested in the central regions of the core and have only plotted our results for
). Only at the outer edges of the core the results could change significantly due to the presence of the interstellar radiation field combined with lower values for the extinction. We are mainly interested in the central regions of the core and have only plotted our results for
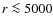 AU. Prestellar cores can also be shielded by several magnitudes of external extinction, for example if they are embedded within a larger dark molecular cloud. Our simulation can therefore be described as the chemical modeling of an externally shielded collapsing core. At
AU. Prestellar cores can also be shielded by several magnitudes of external extinction, for example if they are embedded within a larger dark molecular cloud. Our simulation can therefore be described as the chemical modeling of an externally shielded collapsing core. At
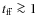 the extinction in the region above the midplane of the disk drops below
the extinction in the region above the midplane of the disk drops below
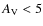 so that photo-dissociation and ion-molecule reactions become important. The importance of these reactions is increased by the stronger radiation field from the central protostar. However, the overall effect on the global abundances of species is reduced as most of the mass is located within the shielded disk where the extinction is large (
so that photo-dissociation and ion-molecule reactions become important. The importance of these reactions is increased by the stronger radiation field from the central protostar. However, the overall effect on the global abundances of species is reduced as most of the mass is located within the shielded disk where the extinction is large (
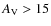 ), even at the closest distance to the protostar of
), even at the closest distance to the protostar of  7 AU within the simulation.
7 AU within the simulation.
To include the effect of the radiation field the extinction should be calculated at every position within the core. From the density given by the hydrodynamical simulation we could in principle derive the amount of extinction using the relation
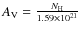
 ,
with
,
with
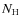 the column density of hydrogen nuclei between the protostar and the point of interest. However, in practice this is more complicated as a significant amount of extinction arises from regions close to the protostar within 7 AU, beyond the resolution of our simulation where we do not have information on the density distribution. The dust destruction radius is located roughly at 2000 K (Duschl et al. 1996)
the column density of hydrogen nuclei between the protostar and the point of interest. However, in practice this is more complicated as a significant amount of extinction arises from regions close to the protostar within 7 AU, beyond the resolution of our simulation where we do not have information on the density distribution. The dust destruction radius is located roughly at 2000 K (Duschl et al. 1996)  0.1 AU from the protostar which sets an upper limit on the resolution needed to derive the amount of extinction. By increasing the resolution of the hydrodynamical simulation this can be satisfied. As a first approximation for the intrinsic strength of radiation field, we could take the luminosity from the protostar given by the hydrodynamical simulation. The protostar luminosity is based on the mass accretion rate plus a central core luminosity. Including these effects can be a starting point for future work.
Our hydrodynamical simulation has a simplified radiative transfer, this may have resulted in deviations in the gas and dust temperature compared to more realistic simulations. Jonkheid et al. (2004) presented a model which calculated the gas and dust temperature as well as the chemistry in the surface layers of a flaring protoplanetary disk. The heating rate of the gas was controlled by UV radiation and the gas cooling by line emission of various species and by collisions with dust grain. They found that the gas temperature exceeds the dust temperature, in the part of the disk that is optically thin to UV radiation, by up to several hundreds of Kelvin. In the optically thick part of the disk the gas temperature was found to be well coupled to the dust temperature. In our hydrodynamical simulation the dust isotherms are more spherical compared to the results in Jonkheid et al. (2004). Small changes in the dust temperature can have an important effect on the sublimation rate as it is exponentially dependent on the dust temperature. Therefore accurate dust temperatures are important for calculating the position of the sublimation front if the binding energies of the species are known. Observations of the position of sublimation fronts of various species could be a sensitive tracer of the dust temperature. The very high gas temperatures found above the disk also have an effect on the gas phase chemistry. Although Jonkheid et al. (2004) reported that effect was small. However, their chemical network was rather limited and no gas-grain interactions were included. A temperature increase from 60 to 550 K in the upper disk layers (at R = 150 AU and
0.1 AU from the protostar which sets an upper limit on the resolution needed to derive the amount of extinction. By increasing the resolution of the hydrodynamical simulation this can be satisfied. As a first approximation for the intrinsic strength of radiation field, we could take the luminosity from the protostar given by the hydrodynamical simulation. The protostar luminosity is based on the mass accretion rate plus a central core luminosity. Including these effects can be a starting point for future work.
Our hydrodynamical simulation has a simplified radiative transfer, this may have resulted in deviations in the gas and dust temperature compared to more realistic simulations. Jonkheid et al. (2004) presented a model which calculated the gas and dust temperature as well as the chemistry in the surface layers of a flaring protoplanetary disk. The heating rate of the gas was controlled by UV radiation and the gas cooling by line emission of various species and by collisions with dust grain. They found that the gas temperature exceeds the dust temperature, in the part of the disk that is optically thin to UV radiation, by up to several hundreds of Kelvin. In the optically thick part of the disk the gas temperature was found to be well coupled to the dust temperature. In our hydrodynamical simulation the dust isotherms are more spherical compared to the results in Jonkheid et al. (2004). Small changes in the dust temperature can have an important effect on the sublimation rate as it is exponentially dependent on the dust temperature. Therefore accurate dust temperatures are important for calculating the position of the sublimation front if the binding energies of the species are known. Observations of the position of sublimation fronts of various species could be a sensitive tracer of the dust temperature. The very high gas temperatures found above the disk also have an effect on the gas phase chemistry. Although Jonkheid et al. (2004) reported that effect was small. However, their chemical network was rather limited and no gas-grain interactions were included. A temperature increase from 60 to 550 K in the upper disk layers (at R = 150 AU and  AU) will increase the freeze-out rate by a factor of
AU) will increase the freeze-out rate by a factor of
 3, although this may be compensated by a lower sticking coefficient
3, although this may be compensated by a lower sticking coefficient  .
X-rays from the central protostar also have an effect on the chemistry as shown by Stäuber et al. (2005). Abundances of some species were found to be enhanced by 2-3 orders of magnitude. Due to smaller cross sections, X-rays penetrate further into the disk and envelope and therefore affect the chemistry on larger scales (
.
X-rays from the central protostar also have an effect on the chemistry as shown by Stäuber et al. (2005). Abundances of some species were found to be enhanced by 2-3 orders of magnitude. Due to smaller cross sections, X-rays penetrate further into the disk and envelope and therefore affect the chemistry on larger scales ( 1000 AU) than the UV radiation field (
1000 AU) than the UV radiation field ( 400 AU, Stäuber et al. 2004). Eventually the chemistry needs to be coupled to the radiative transfer (e.g., van Zadelhoff et al. 2003) for the modeling to be self consistent and correctly address this issues.
400 AU, Stäuber et al. 2004). Eventually the chemistry needs to be coupled to the radiative transfer (e.g., van Zadelhoff et al. 2003) for the modeling to be self consistent and correctly address this issues.
In our model we can follow the chemical composition of gas accreting onto the disk. Gas does not directly accrete onto the disk but flows around the disk upwards (see Fig. 20) before entering the disk around the centrifugal radius (see also Paper I). This has important implications for the chemistry as the gas is more exposed to UV and X-ray radiation from the central protostar before entering the disk. The dust temperature at the centrifugal radius of the disk sets a sublimation temperature for ices accreting onto the disk. The result is that ices with a low binding energy (
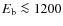 K) sublimate before entering the disk while ices with a high binding energy (
K) sublimate before entering the disk while ices with a high binding energy (
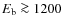 K) are able to enter the disk. The strong UV radiation field may also cause photodesorption of ices. Recently, Öberg et al. (2007) determined high yields for CO photodesorption in laboratory experiments. In our simulation at t = 2.5
K) are able to enter the disk. The strong UV radiation field may also cause photodesorption of ices. Recently, Öberg et al. (2007) determined high yields for CO photodesorption in laboratory experiments. In our simulation at t = 2.5
 ,
most of the CO ice (
,
most of the CO ice (
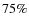 )
is not able to accrete onto the disk, as the sublimation front lies just outside of the centrifugal radius (at
)
is not able to accrete onto the disk, as the sublimation front lies just outside of the centrifugal radius (at  500 AU), while H2CO ice can enter the disk without sublimating, see Fig. 20. By following the chemical evolution of gas accreting onto the disk we can derive the initial abundances to be adopted in more detailed modeling of the chemistry within the disk. For example Semenov et al. (2004) took as initial abundances those computed in a dark cloud (out of which the disk eventually forms). However, the initial abundances are different from those in dark clouds as some chemical processing has already taken place before the gas enters the disk. Using the correct initial abundances might improve the results of those models.
500 AU), while H2CO ice can enter the disk without sublimating, see Fig. 20. By following the chemical evolution of gas accreting onto the disk we can derive the initial abundances to be adopted in more detailed modeling of the chemistry within the disk. For example Semenov et al. (2004) took as initial abundances those computed in a dark cloud (out of which the disk eventually forms). However, the initial abundances are different from those in dark clouds as some chemical processing has already taken place before the gas enters the disk. Using the correct initial abundances might improve the results of those models.
![\begin{figure}
\par\includegraphics[trim =0.5cm 0cm -0.5cm 0cm,width=9cm]{1471fi20}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg144.png) |
Figure 20:
Left: abundances as function of time for a single trace particle which accretes onto the disk. At
|
| Open with DEXTER | |
We have chosen a standard dust grain radius of 0.1 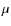 m for our simulation to compare our results with previous work (e.g., Aikawa et al. 2008). This is an oversimplification as grains are expected to grow to larger sizes under the conditions in the simulation, especially within the disk. The main effect of grain growth will be a decrease in the depletion rate as the total grain surface area decreases. The lower depletion rates also have an effect on the nitrogen-bearing chemistry as was shown by Flower et al. (2006). An approach might be to use the more sophisticated treatment by Flower et al. (2005), following the coagulation of the grains simultaneously with the chemical evolution of the medium. This is, however, beyond the scope of this paper.
m for our simulation to compare our results with previous work (e.g., Aikawa et al. 2008). This is an oversimplification as grains are expected to grow to larger sizes under the conditions in the simulation, especially within the disk. The main effect of grain growth will be a decrease in the depletion rate as the total grain surface area decreases. The lower depletion rates also have an effect on the nitrogen-bearing chemistry as was shown by Flower et al. (2006). An approach might be to use the more sophisticated treatment by Flower et al. (2005), following the coagulation of the grains simultaneously with the chemical evolution of the medium. This is, however, beyond the scope of this paper.
6 Conclusions
We have modeled the chemical abundances during prestellar core collapse and have compared the global evolution of these abundances with observations. We have used trace particles, moving with the flow of the gas as given by a 2-dimensional hydrodynamics simulation, to derive the chemical evolution of the collapsing core.
Gas-grain interactions determine to a large extent the abundance evolution of species during prestellar core collapse. Before collapse, most species are depleted due to freeze-out onto dust grains. When the temperature rises in the center a sublimated zone develops. At the same time in the outer parts of the envelope the density drops, which lowers the freeze-out rate resulting in an increase in the gas phase abundance of species with a relatively low binding energy. Within the disk, species with a low binding energy freeze-out again, species with a higher binding energy are able to enter the disk without sublimating. The abundances of charged species are mostly determined by the balance between destruction and formation. Parent species, or destructors often have gas-grain interactions so the abundance of charged species is still influenced by gas-grain interactions, although in an indirect way.
We conclude that grain surface reactions are important for the formation of some species, in particular for CH3OH, CO2, H2O and H2CO. Without surface reactions most of the ice is in the form of CO, and the relative fraction of other ices is much lower than observed. An example is CH3OH where the ice fraction for Model G is lower by more than 5 orders of magnitude. Gas phase abundances of species likes CH3OH and H2CO are also too low without surface reactions when we compare global envelope abundances with observations. So we confirm that surface reactions are important for the production of some species. CH4 is produced quite efficiently in the gas phase. Only at high densities within the disk CH4 is produced more efficiently by grain surface reactions. Abundances are higher in the envelope if we do not include surface reactions. It could be that some CH4 is transformed in Model S towards CH3 and C2H2 by surface reactions. CS and SO abundances show a better match to observations if no surface reactions are included.
Our method provides important information on the initial abundances of species to be adopted in chemical modeling of protoplanetary disks. The initial abundances are often derived from chemical models of dark molecular clouds. However, as we have shown, significant chemical processing of the gas and the grain mantles occurs before accretion onto the disk. For example ices with a low binding energy (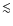 1200 K) are not able to enter the disk, while those with a higher binding energy are able to directly accrete onto the disk. Also gas accreting onto the disk (coming from
1200 K) are not able to enter the disk, while those with a higher binding energy are able to directly accrete onto the disk. Also gas accreting onto the disk (coming from
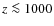 AU) may be temporally exposed to the strong radiation field from the central protostar, especially at the later stages of the collapse when
AU) may be temporally exposed to the strong radiation field from the central protostar, especially at the later stages of the collapse when 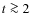
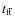 .
This is caused by the upward motion of gas around the disk, representing a bow shock feature. The gas then accretes above the midplane, roughly at the position of the centrifugal radius onto the disk.
.
This is caused by the upward motion of gas around the disk, representing a bow shock feature. The gas then accretes above the midplane, roughly at the position of the centrifugal radius onto the disk.
The method we have presented for modeling the chemical abundances is generally applicable to other hydrodynamical simulations. Although, modeling the chemical evolution is computationally expensive it can be parallelized easily as the trace particles have no interaction with each other. This can be used to extend the modeling to higher spatial resolution (from the 20 AU we have used) and towards three dimensions. This will allow us to probe the chemical evolution in the planet forming zone in greater detail. Including the effects of the UV radiation and X-rays is important in the later stages (
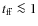 )
of the collapse, especially for the upper disk layers and the envelope.
)
of the collapse, especially for the upper disk layers and the envelope.
Finally, modeling line profiles with RATRAN and comparing them to observations may provide more information on the physical conditions during prestellar core collapse.
From an observational point of view, increasing the sample of objects with modeled envelope masses and abundances, will help to test chemical models. In particular, more CH3OH observations as well as those from sulfur bearing species are needed. This will also help to find species which could be used as chemical clocks. Second, laboratory experiments of grain surface reactions may further help to constrain the surface reaction and diffusion rates.
Acknowledgements
We would like to thank the anonymous referee for useful comments. CB is partially supported by the European Commission through the FP6 - Marie Curie Early Stage Researcher Training programme. The research of M.R.H. is supported through a VIDI grant from the Netherlands Organization fro Scientific Research.
References
- Acharyya, K., Fuchs, G. W., Fraser, H. J., van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 466, 1005 [NASA ADS] [CrossRef] [EDP Sciences]
- Adams, F. C., Lada, C. J., & Shu, F. H. 1987, ApJ, 312, 788 [NASA ADS] [CrossRef]
- Aikawa, Y., & Herbst, E. 2001, A&A, 371, 1107 [NASA ADS] [CrossRef] [EDP Sciences]
- Aikawa, Y., Miyama, S. M., Nakano, T., & Umebayashi, T. 1996, ApJ, 467, 684 [NASA ADS] [CrossRef]
- Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L51 [NASA ADS] [CrossRef]
- Aikawa, Y., Ohashi, N., Inutsuka, S.-I., Herbst, E., & Takakuwa, S. 2001, ApJ, 552, 639 [NASA ADS] [CrossRef]
- Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences]
- Aikawa, Y., Ohashi, N., & Herbst, E. 2003, ApJ, 593, 906 [NASA ADS] [CrossRef]
- Aikawa, Y., Herbst, E., Roberts, H., & Caselli, P. 2005, ApJ, 620, 330 [NASA ADS] [CrossRef] (In the text)
- Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] (In the text)
- Akyilmaz, M., Flower, D. R., Hily-Blant, P., Pineau Des Forêts, G., & Walmsley, C. M. 2007, A&A, 462, 221 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Alexander, R. D., Casali, M. M., André, P., Persi, P., & Eiroa, C. 2003, A&A, 401, 613 [NASA ADS] [CrossRef] [EDP Sciences]
- Allen, M., & Robinson, G. W. 1977, ApJ, 212, 396 [NASA ADS] [CrossRef] (In the text)
- Andre, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef]
- Bachiller, R., & Perez Gutierrez, M. 1997, ApJ, 487, L93 [NASA ADS] [CrossRef] (In the text)
- Bergin, E. A., Langer, W. D., & Goldsmith, P. F. 1995, ApJ, 441, 222 [NASA ADS] [CrossRef] (In the text)
- Bergin, E. A., Melnick, G. J., Gerakines, P. A., Neufeld, D. A., & Whittet, D. C. B. 2005, ApJ, 627, L33 [NASA ADS] [CrossRef]
- Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297 [NASA ADS] [CrossRef] [EDP Sciences]
- Black, D. C., & Bodenheimer, P. 1975, ApJ, 199, 619 [NASA ADS] [CrossRef] (In the text)
- Boogert, A. C. A., & Ehrenfreund, P. 2004, in Astrophysics of Dust, ed. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 547
- Boogert, A. C. A., Pontoppidan, K. M., Lahuis, F., et al. 2004, ApJS, 154, 359 [NASA ADS] [CrossRef]
- Boss, A. P., & Black, D. C. 1982, ApJ, 258, 270 [NASA ADS] [CrossRef] (In the text)
- Brinch, C., Hogerheijde, M. R., & Richling, S. 2008a, A&A, 489, 607 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brinch, C., van Weeren, R. J., & Hogerheijde, M. R. 2008b, A&A, 489, 617 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Buckle, J. V., & Fuller, G. A. 2003, A&A, 399, 567 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [NASA ADS] [CrossRef]
- Caselli, P., Stantcheva, T., Shalabiea, O., Shematovich, V. I., & Herbst, E. 2002, Planet. Space Sci., 50, 1257 [NASA ADS] [CrossRef]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] (In the text)
- Chang, Q., Cuppen, H. M., & Herbst, E. 2007, A&A, 469, 973 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chiar, J. E., Adamson, A. J., Kerr, T. H., & Whittet, D. C. B. 1995, ApJ, 455, 234 [NASA ADS] [CrossRef]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] (In the text)
- d'Hendecourt, L. B., Allamandola, L. J., & Greenberg, J. M. 1985, A&A, 152, 130 [NASA ADS] (In the text)
- Duschl, W. J., Gail, H.-P., & Tscharnuter, W. M. 1996, A&A, 312, 624 [NASA ADS] (In the text)
- Ehrenfreund, P., Dartois, E., Demyk, K., & D'Hendecourt, L. 1998, A&A, 339, L17 [NASA ADS]
- Ehrenfreund, P., & Schutte, W. A. 2000, in From Molecular Clouds to Planetary, ed. Y. C. Minh, & E. F. van Dishoeck, IAU Symp., 197, 135
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2005, A&A, 436, 933 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gerakines, P. A., Whittet, D. C. B., Ehrenfreund, P., et al. 1999, ApJ, 522, 357 [NASA ADS] [CrossRef]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [NASA ADS] [CrossRef]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef]
- Herbst, E. 2005, in ESA SP, 577, ed. A. Wilson, 205 (In the text)
- Hirahara, Y., Suzuki, H., Yamamoto, S., et al. 1992, ApJ, 394, 539 [NASA ADS] [CrossRef]
- Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] (In the text)
- Jonkheid, B., Faas, F. G. A., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 428, 511 [NASA ADS] [CrossRef] [EDP Sciences]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2005a, A&A, 437, 501 [NASA ADS] [CrossRef] [EDP Sciences]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2005b, A&A, 435, 177 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Keane, J. V., Tielens, A. G. G. M., Boogert, A. C. A., Schutte, W. A., & Whittet, D. C. B. 2001, A&A, 376, 254 [NASA ADS] [CrossRef] [EDP Sciences]
- Knez, C., Boogert, A. C. A., Pontoppidan, K. M., et al. 2005, ApJ, 635, L145 [NASA ADS] [CrossRef]
- Lada, C. J. 1987, in Star Forming Regions, ed. M. Peimbert, & J. Jugaku, IAU Symp., 115, 1
- Laughlin, G., & Bodenheimer, P. 1994, ApJ, 436, 335 [NASA ADS] [CrossRef] (In the text)
- Lee, J.-E., Bergin, E. A., & Evans, II, N. J. 2004, ApJ, 617, 360 [NASA ADS] [CrossRef] (In the text)
- Nummelin, A., Whittet, D. C. B., Gibb, E. L., Gerakines, P. A., & Chiar, J. E. 2001, ApJ, 558, 185 [NASA ADS] [CrossRef]
- Öberg, K. I., Fuchs, G. W., Awad, Z., et al. 2007, ApJ, 662, L23 [NASA ADS] [CrossRef] (In the text)
- Pagani, L., Pardo, J.-R., Apponi, A. J., Bacmann, A., & Cabrit, S. 2005, A&A, 429, 181 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Palumbo, M. E., Geballe, T. R., & Tielens, A. G. G. M. 1997, ApJ, 479, 839 [NASA ADS] [CrossRef]
- Pavlyuchenkov, Y., Semenov, D., Henning, T., et al. 2007, ApJ, 669, 1262 [NASA ADS] [CrossRef]
- Pontoppidan, K. M., Dullemond, C. P., van Dishoeck, E. F., et al. 2005, ApJ, 622, 463 [NASA ADS] [CrossRef] (In the text)
- Radhakrishnan, K., & Hindmarsh, A. C. 1993, in LLNL report UCRL-ID-113855 (In the text)
- Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., & Williams, D. A. 1992, MNRAS, 255, 471 [NASA ADS]
- Rodgers, S. D., & Charnley, S. B. 2003, ApJ, 585, 355 [NASA ADS] [CrossRef] (In the text)
- Ròzyczka, M. 1985, A&A, 143, 59 [NASA ADS] (In the text)
- Ruffle, D. P., & Herbst, E. 2000, MNRAS, 319, 837 [NASA ADS] [CrossRef] (In the text)
- Ruffle, D. P., Hartquist, T. W., Taylor, S. D., & Williams, D. A. 1997, MNRAS, 291, 235 [NASA ADS]
- Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [NASA ADS] [CrossRef] (In the text)
- Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002, A&A, 390, 1001 [NASA ADS] [CrossRef] [EDP Sciences]
- Schutte, W. A., Boogert, A. C. A., Tielens, A. G. G. M., et al. 1999, A&A, 343, 966 [NASA ADS]
- Semenov, D., Wiebe, D., & Henning, T. 2004, A&A, 417, 93 [NASA ADS] [CrossRef] [EDP Sciences]
- Semenov, D., Wiebe, D., & Henning, T. 2006, ApJ, 647, L57 [NASA ADS] [CrossRef]
- Stantcheva, T., & Herbst, E. 2004, A&A, 423, 241 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stantcheva, T., Caselli, P., & Herbst, E. 2001, A&A, 375, 673 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., Jørgensen, J. K., & Benz, A. O. 2004, A&A, 425, 577 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., & Benz, A. O. 2005, A&A, 440, 949 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] (In the text)
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium, ed. A. G. G. M. Tielens (Cambridge, UK: Cambridge University Press) (In the text)
- Umebayashi, T., & Nakano, T. 1980, PASJ, 32, 405 [NASA ADS] (In the text)
- van Dishoeck, E. F., & Hogerheijde, M. R. 1999, in NATO ASIC Proc. 540, The Origin of Stars and Planetary Systems, ed. C. J. Lada, & N. D. Kylafis, 97
- van Dishoeck, E. F., Helmich, F. P., Schutte, W. A., et al. 1998, in Star Formation with the Infrared Space Observatory, ed. J. Yun, & L. Liseau, ASP Conf. Ser., 132, 54
- van Zadelhoff, G.-J., Aikawa, Y., Hogerheijde, M. R., & van Dishoeck, E. F. 2003, A&A, 397, 789 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Watson, W. D., & Salpeter, E. E. 1972, ApJ, 174, 321 [NASA ADS] [CrossRef] (In the text)
- Watson, D. M., Kemper, F., Calvet, N., et al. 2004, ApJS, 154, 391 [NASA ADS] [CrossRef]
- Whittet, D. C. B., Shenoy, S. S., Bergin, E. A., et al. 2007, ApJ, 655, 332 [NASA ADS] [CrossRef]
- Wiebe, D., Semenov, D., & Henning, T. 2003, A&A, 399, 197 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Yorke, H. W., & Bodenheimer, P. 1999, ApJ, 525, 330 [NASA ADS] [CrossRef] (In the text)
- Zasowski, G., Markwick-Kemper, F., Watson, D. M., et al. 2007, ArXiv e-prints, 712
- Ziurys, L. M., Apponi, A. J., & Phillips, T. G. 1994, ApJ, 433, 729 [NASA ADS] [CrossRef]
Online Material
Appendix A: 2-Dimensional abundances including grain surface chemistry
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi21}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg147.png) |
Figure A.1:
Distribution of HCO+ throughout the core at four different times during the simulation for Model S. The black contour shows the outline of the disk. The disk is defined as the region where
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi22}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg148.png) |
Figure A.2: Same as for Fig. A.1 but for N2H+. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi23}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg149.png) |
Figure A.3: Same as for Fig. A.1 but for CS. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi24}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg150.png) |
Figure A.4: Same as for Fig. A.1 but for SO. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi25}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg151.png) |
Figure A.5: Same as for Fig. A.1 but for HCN. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi26}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg152.png) |
Figure A.6: Same as for Fig. A.1 but for HNC. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi27}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg153.png) |
Figure A.7: Same as for Fig. A.1 but for CN. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi28}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg154.png) |
Figure A.8: Same as for Fig. A.1 but for HC3N. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi29}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg155.png) |
Figure A.9: Same as for Fig. A.1 but for H2CO. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi30}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg156.png) |
Figure A.10: Same as for Fig. A.1 but for CH3OH. |
| Open with DEXTER | |
Appendix B: 2-Dimensional abundances without grain surface chemistry
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi31}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg157.png) |
Figure B.1: Distribution of CO throughout the core at four different times during the simulation for Model G. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi32}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg158.png) |
Figure B.2: Same as for Fig. B.1 but for HCO+. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi33}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg159.png) |
Figure B.3: Same as for Fig. B.1 but for N2H+. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi34}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg160.png) |
Figure B.4: Same as for Fig. B.1 but for CS. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi35}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg161.png) |
Figure B.5: Same as for Fig. B.1 but for SO. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi36}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg162.png) |
Figure B.6: Same as for Fig. B.1 but for HCN. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi37}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg163.png) |
Figure B.7: Same as for Fig. B.1 but for HNC. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi38}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg164.png) |
Figure B.8: Same as for Fig. B.1 but for CN. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi39}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg165.png) |
Figure B.9: Same as for Fig. B.1 but for HC3N. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi40}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg166.png) |
Figure B.10: Same as for Fig. B.1 but for H2CO. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi41}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg167.png) |
Figure B.11: Same as for Fig. B.1 but for CH3OH. |
| Open with DEXTER | |
Footnotes
- ... dimensions
![[*]](/icons/foot_motif.png)
- Appendices are only available in electronic form at http://www.aanda.org
- ... database
![[*]](/icons/foot_motif.png)
- http://www.udfa.net
All Tables
Table 1: The initial abundances.
Table 2: Grain mantle compositions.
All Figures
![\begin{figure}
\par\includegraphics[trim =0.3cm 0cm -0.3cm 0cm,width=8.5cm]{1471fi1}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg62.png) |
Figure 1:
Distribution of trace particles at t= 2.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.3cm 0cm -0.3cm 0cm,width=8.5cm]{1471fi2}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg75.png) |
Figure 2:
Distribution of CO throughout the core at four different times during the simulation for Model S. The black contour shows the outline of the disk. The disk is defined as the region where
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.cm 0cm -0.cm 0cm, width=8.5cm]{1471fi3}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg79.png) |
Figure 3:
Model S. The radial abundances through the disk (R,z=0) at four different times during the simulation. The line styles corresponding to different species are indicated in the top right panel at t = 0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim = 0.0cm 0cm -0.0cm 0cm, width=8.5cm]{1471fi4}
\par\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg80.png) |
Figure 4: Model S. The radial abundances through the disk (R,z=0) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.cm 0cm -0.cm 0cm, width=8.5cm]{1471fi5}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg81.png) |
Figure 5: Model S. The abundances perpendicular to the disk (R=0,z) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.0cm 0cm -0.0cm 0cm, width=8.5cm]{1471fi6}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg82.png) |
Figure 6: Model S. The abundances perpendicular to the disk (R=0,z) at four different times during the simulation. Labeling of species as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{1471fi7}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg85.png) |
Figure 7:
Column densities for various gas phase species at four different times during the simulation, t = 0 (solid lines), t = 0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8cm]{1471fi8}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg92.png) |
Figure 8:
Global envelope abundances of CO versus envelope mass. The bullets ``'' connected by solid lines are for Model S, which includes grain surface reactions. The bullets connected by dashed lines are for Model G without grain surface chemistry. Data for various objects from Jørgensen et al. (2004,2002) are overplotted. Class I objects are indicated by `` |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8cm]{1471fi9}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg93.png) |
Figure 9: Global envelope abundances of HCO+ versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0cm 0 0 0cm,width=8.5cm]{1471fi10}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg100.png) |
Figure 10: Global envelope abundances of N2H+ versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi11}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg108.png) |
Figure 11: Global envelope abundances of CS versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi12}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg109.png) |
Figure 12: Global envelope abundances of SO versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi13}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg112.png) |
Figure 13: Global envelope abundances of HCN versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi14}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg113.png) |
Figure 14: Global envelope abundances of HNC versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi15}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg114.png) |
Figure 15: Global envelope abundances of CN versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi16}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg115.png) |
Figure 16: Global envelope abundances of HC3N versus envelope mass. Data for various objects from Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi17}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg116.png) |
Figure 17: Global envelope abundances of H2CO versus envelope mass. Data for various objects from Jørgensen et al. (2005a) are overplotted. Symbols and line styles are defined in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi18}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg119.png) |
Figure 18:
Global envelope abundances of CH3OH versus envelope mass. Data for various objects from Schöier et al. (2002); Jørgensen et al. (2004) are overplotted. Symbols and line styles are defined in Fig. 8. Other data points indicated are the abundances fitted with ``drop''-abundance profiles, with ``+'' the abundance in the inner region and `` |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.3cm 0 -0.3cm 0cm, width=8.8cm]{1471fi19}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg120.png) |
Figure 19:
Column densities of various ices at four different times during the simulation, t = 0 (solid lines), t = 0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[trim =0.5cm 0cm -0.5cm 0cm,width=9cm]{1471fi20}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg144.png) |
Figure 20:
Left: abundances as function of time for a single trace particle which accretes onto the disk. At
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi21}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg147.png) |
Figure A.1:
Distribution of HCO+ throughout the core at four different times during the simulation for Model S. The black contour shows the outline of the disk. The disk is defined as the region where
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi22}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg148.png) |
Figure A.2: Same as for Fig. A.1 but for N2H+. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi23}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg149.png) |
Figure A.3: Same as for Fig. A.1 but for CS. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi24}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg150.png) |
Figure A.4: Same as for Fig. A.1 but for SO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi25}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg151.png) |
Figure A.5: Same as for Fig. A.1 but for HCN. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi26}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg152.png) |
Figure A.6: Same as for Fig. A.1 but for HNC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi27}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg153.png) |
Figure A.7: Same as for Fig. A.1 but for CN. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi28}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg154.png) |
Figure A.8: Same as for Fig. A.1 but for HC3N. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi29}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg155.png) |
Figure A.9: Same as for Fig. A.1 but for H2CO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi30}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg156.png) |
Figure A.10: Same as for Fig. A.1 but for CH3OH. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi31}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg157.png) |
Figure B.1: Distribution of CO throughout the core at four different times during the simulation for Model G. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi32}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg158.png) |
Figure B.2: Same as for Fig. B.1 but for HCO+. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi33}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg159.png) |
Figure B.3: Same as for Fig. B.1 but for N2H+. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi34}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg160.png) |
Figure B.4: Same as for Fig. B.1 but for CS. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi35}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg161.png) |
Figure B.5: Same as for Fig. B.1 but for SO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi36}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg162.png) |
Figure B.6: Same as for Fig. B.1 but for HCN. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi37}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg163.png) |
Figure B.7: Same as for Fig. B.1 but for HNC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi38}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg164.png) |
Figure B.8: Same as for Fig. B.1 but for CN. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi39}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg165.png) |
Figure B.9: Same as for Fig. B.1 but for HC3N. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width= 8.5cm]{1471fi40}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg166.png) |
Figure B.10: Same as for Fig. B.1 but for H2CO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[trim =0 0 0 0cm,width=8.5cm]{1471fi41}
\end{figure}](/articles/aa/full_html/2009/15/aa11471-08/Timg167.png) |
Figure B.11: Same as for Fig. B.1 but for CH3OH. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



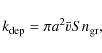
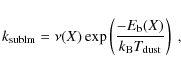
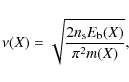
![\begin{displaymath}
k_{{\rm cr}} = 3.16 \times 10^{-19} \nu(X) \exp\left(\frac{-E_{{\rm b}}(X)}{k_{{\rm B}} \cdot 70 \mbox{ [K]}}\right) \cdot
\end{displaymath}](/articles/aa/full_html/2009/15/aa11471-08/img42.png)
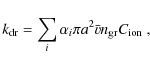
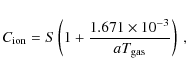
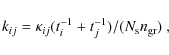
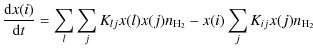
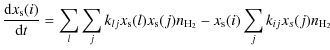
 ,
with
,
with  '', Class 0 objects by ``
'', Class 0 objects by ``
 '', and prestellar cores by ``
'', and prestellar cores by ``
 ''.
''.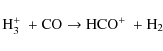
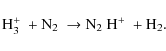
 '' that in the outer region of the envelope.
'' that in the outer region of the envelope. 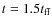 the conditions for the trace particle are roughly that of the dark ISM, T = 10 K and
n = 104 cm-3. Right: trace particle trajectory, the position of the particle at different times is indicated in the figure. The acceleration of the particle as well as the upward motion around the disk are visible before the particle accretes onto the disk.
the conditions for the trace particle are roughly that of the dark ISM, T = 10 K and
n = 104 cm-3. Right: trace particle trajectory, the position of the particle at different times is indicated in the figure. The acceleration of the particle as well as the upward motion around the disk are visible before the particle accretes onto the disk.