| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 743 - 753 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200811255 | |
| Published online | 24 February 2009 | |
A robust morphological classification of high-redshift galaxies using support vector machines on seeing limited images
II. Quantifying morphological k-correction in the COSMOS field at 1 < 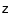 < 2:
Ks band vs. I band
< 2:
Ks band vs. I band![[*]](/icons/foot_motif.png)
M. Huertas-Company1,3 - L. Tasca2 - D. Rouan1 - D. Pelat4 - J. P. Kneib2 - O. Le Fèvre2 - P. Capak7 - J. Kartaltepe8 - A. Koekemoer10 - H. J. McCracken5 - M. Salvato6 - D. B. Sanders8 - C. Willott9
1 - LESIA-Paris Observatory, 5 place Jules Janssen, 92195 Meudon, France
2 -
LAM, CNRS-Université de Provence,
38 rue Frédric Joliot-Curie, 13388 Marseille Cedex 13, France
3 -
IAA-C/ Camino Bajo de Huétor, 50 - 18008 Granada, Spain
4 -
LUTH-Paris Observatory,
5 place Jules Janssen, 92195 Meudon, France
5 -
IAP, CNRS-Université Pierre et Marie Curie,
98 boulevard Arago, 75014 Paris, France
6 -
Caltech, Pasadena, CA 91125, 105-24 Caltech, Pasadena, CA 91125, USA
7 -
Spitzer Science Center, 314-6 Caltech, Pasadena, CA 91125,105-24 Caltech, Pasadena, CA 91125, USA
8 -
Institute for Astronomy, 2680 Woodlawn Drive, University of Hawaii, Honolulu, HI 96822, USA
9 -
Physics Department, University of Ottawa, 150 Louis Pasteur, MacDonald Hall, Ottawa, ON K1N 6N5, Canada
10 -
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218, USA
Received 30 October 2008 / Accepted 14 February 2009
Abstract
Context. Morphology is the most accessible tracer of galaxies physical structure, but its interpretation in the framework of galaxy evolution still remains problematic. Its quantification at high redshift requires deep high-angular resolution imaging, which is why space data (HST) are usually employed. At z>1, the HST visible cameras however probe the UV flux, which is dominated by the emission of young stars, which could bias the estimated morphologies towards late-type systems.
Aims. In this paper we quantify the effects of this morphological k-correction at 1<z<2 by comparing morphologies measured in the K and I-bands in the COSMOS area. The Ks-band data indeed have the advantage of probing old stellar populations in the rest frame for z<2, enabling determination of galaxy morphological types unaffected by recent star formation.
Methods. In Paper I we presented a new non-parametric method of quantifying morphologies of galaxies on seeing-limited images based on support vector machines. Here we use this method to classify  50 000 Ks selected galaxies in the COSMOS area observed with WIRCam at CFHT. We use a 10-dimensional volume, including 5 morphological parameters, and other characteristics of galaxies such as luminosity and redshift. The obtained classification is used to investigate the redshift distributions and number counts per morphological type up to
50 000 Ks selected galaxies in the COSMOS area observed with WIRCam at CFHT. We use a 10-dimensional volume, including 5 morphological parameters, and other characteristics of galaxies such as luminosity and redshift. The obtained classification is used to investigate the redshift distributions and number counts per morphological type up to 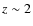 and to compare them to the results obtained with HST/ACS in the I-band on the same objects. We associate to every galaxy with
and to compare them to the results obtained with HST/ACS in the I-band on the same objects. We associate to every galaxy with
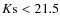 and z<2 a probability between 0 and 1 of being late-type or early-type. We use this value to assess the accuracy of our classification as a function of physical parameters of the galaxy and to correct for classification errors.
and z<2 a probability between 0 and 1 of being late-type or early-type. We use this value to assess the accuracy of our classification as a function of physical parameters of the galaxy and to correct for classification errors.
Results. The classification is found to be reliable up to 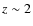 .
The mean probability is
.
The mean probability is 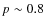 .
It decreases with redshift and with size, especially for the early-type population, but remains above
.
It decreases with redshift and with size, especially for the early-type population, but remains above 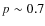 .
The classification globally agrees with the one obtained using HST/ACS for z<1. Above
.
The classification globally agrees with the one obtained using HST/ACS for z<1. Above 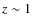 ,
the I-band classification tends to find less early-type galaxies than the Ks-band one by a factor
,
the I-band classification tends to find less early-type galaxies than the Ks-band one by a factor 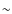 1.5, which might be a consequence of morphological k-correction effects.
1.5, which might be a consequence of morphological k-correction effects.
Conclusions. We argue therefore that studies based on I-band HST/ACS classifications at z>1 could be underestimating the elliptical population. Using our method in a
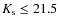 magnitude-limited sample, we observe that the fraction of the early-type population is (
magnitude-limited sample, we observe that the fraction of the early-type population is (
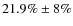 )
at
)
at
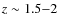 and (
and (
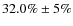 )
at the present time. We will discuss the evolution of the fraction of galaxies in types from volume-limited samples in a forthcoming paper.
)
at the present time. We will discuss the evolution of the fraction of galaxies in types from volume-limited samples in a forthcoming paper.
Key words: galaxies: fundamental parameters - galaxies: high-redshift
1 Introduction
In the local Universe, the distribution of galaxies is bimodal, primarily reflecting a relationship between color and morphology. On the one hand the spiral-like galaxies are gas-rich, form stars and are supported by the rotation of their stars and on the other hand the elliptical-like galaxies are gas-poor, do not form stars anymore and are supported by the velocity dispersion of the stars. This is the so-called elliptical-spiral Hubble sequence. A fundamental question in observational cosmology is how this bimodality appears throughout the history of the Universe. Classical approaches to tackle this question consist in studying the evolution of the luminosity (e.g. Ilbert et al. 2006b), the star-forming rate or the mass assembly (e.g. Bundy et al. 2006; Arnouts et al. 2007) for different morphological types. For that purpose, large samples of galaxies are required with a robust estimate of distances, luminosities and morphological types.
However, the difficulty in quantifying morphology of high-redshift objects with a few simple, reliable measurements is still a major obstacle. The dependence on angular resolution and wavelength in fact turns the interpretation in terms of evolution difficult. To overcome these difficulties, astronomers have found alternative solutions such as classifying galaxies by spectral type (Madgwick et al. 2002) or by spectro-photometric type (Zucca et al. 2006). However, direct interpretation of these results in the framework of galaxy evolution is not straightforward since galaxies move from one spectral class to another by a passive evolution of their stellar populations. A classification based on structural parameters is less sensitive to the star formation history, hence more robust to follow similar galaxies at different redshifts.
In the visible, progress over the last ten years have come in particular from the Hubble deep fields (HDF) observed with the Hubble Space Telescope. They brought observational evidence that galaxy evolution is differentiated with respect to morphological type and that a large fraction of distant galaxies have peculiar morphologies that do not fit
into the elliptical-spiral Hubble sequence (Ilbert et al. 2006b; Wolf et al. 2003; Brinchmann et al. 1998). There is some evidence indeed that most of the stellar mass assembly occurs around
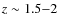 (e.g. Abraham et al. 2007). A better understanding of the physical processes that lead to the present Hubble sequence should come therefore from observations in this redshift range. In this context, near infrared observations are particularly important because the Ks-band flux at
(e.g. Abraham et al. 2007). A better understanding of the physical processes that lead to the present Hubble sequence should come therefore from observations in this redshift range. In this context, near infrared observations are particularly important because the Ks-band flux at 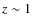 is less dependent on the recent history of star formation, hich peaks in the rest-frame UV and thus gives a galaxy type from the distribution of old stars, more closely related to the underlying total mass than optical observations. A number of Ks-band surveys have being carried out using ground-based telescopes with different spatial coverages and limiting magnitudes (e.g. Gardner et al. 1993; McCracken et al. 2000b; Maihara et al. 2001). In all cases the morphological information is poor because of the seeing-limited spatial resolution. Some morphological analyses have been performed using NICMOS on HST which is the only space instrument available in this wavelength range. All the results are on small areas involving a few tens of galaxies (e.g. Saracco et al. 2008; Conselice & GNS Team 2007) or in clusters (e.g. Zirm et al. 2008) but there are no extensive morphological classifications of field galaxies.
is less dependent on the recent history of star formation, hich peaks in the rest-frame UV and thus gives a galaxy type from the distribution of old stars, more closely related to the underlying total mass than optical observations. A number of Ks-band surveys have being carried out using ground-based telescopes with different spatial coverages and limiting magnitudes (e.g. Gardner et al. 1993; McCracken et al. 2000b; Maihara et al. 2001). In all cases the morphological information is poor because of the seeing-limited spatial resolution. Some morphological analyses have been performed using NICMOS on HST which is the only space instrument available in this wavelength range. All the results are on small areas involving a few tens of galaxies (e.g. Saracco et al. 2008; Conselice & GNS Team 2007) or in clusters (e.g. Zirm et al. 2008) but there are no extensive morphological classifications of field galaxies.
In Huertas-Company et al. (2008, hereafter Paper I) we proposed therefore a generalization of the non-parametric morphological classification methods that uses an unlimited number of dimensions and non-linear separators, enabling us to use all the information brought by the different morphological parameters simultaneously. We showed that when applied to seeing limited data it reduces errors by more than a factor 2 compared to classical non-parametric methods, leading to a mean accuracy of  80% of correct classifications.
80% of correct classifications.
In this paper, we use this method to quantify the morphologies of  50 000 galaxies based on structural parameters measured in the near infrared. Galaxies are observed in the COSMOS field with WIRCam at CFHT in Ks-band. We perform basic statistics such as redhisft and magnitude counts per morphological type and compare them to the ones obtained on the same objects using HST/ACS imaging (I-band) in order to quantify morphological k-correction effects. This classification is intended as a framework for future studies of the evolution of counts, luminosities, luminosity densities, correlation function for each morphological type over several redshift bins.
50 000 galaxies based on structural parameters measured in the near infrared. Galaxies are observed in the COSMOS field with WIRCam at CFHT in Ks-band. We perform basic statistics such as redhisft and magnitude counts per morphological type and compare them to the ones obtained on the same objects using HST/ACS imaging (I-band) in order to quantify morphological k-correction effects. This classification is intended as a framework for future studies of the evolution of counts, luminosities, luminosity densities, correlation function for each morphological type over several redshift bins.
The paper proceeds as follows: the data set and the sample selection are presented in the next section. In Sect. 3 we describe the technique used to quantify morphologies. In Sect. 4, we analyze the results of the classification and show the first statistics. We finally compare the results with the ones obtained with HST/ACS in Sect. 5 and discuss the effects of morphological k-correction.
We use the following cosmological parameters throughout the paper:
![]() and
and
![]() and the AB system for magnitudes.
and the AB system for magnitudes.
2 The data
2.1 Description
The Ks-band data were taken with WIRCam (Thibault et al. 2003) installed at CFHT in the near infrared 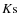 band (
band (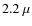 m). The observed area is 2.65 deg2 and is centered in the COSMOS field (Scoville & COSMOS Team 2005). Images are reduced with the Terapix
pipeline
m). The observed area is 2.65 deg2 and is centered in the COSMOS field (Scoville & COSMOS Team 2005). Images are reduced with the Terapix
pipeline![]() and have a pixel scale of
0.15
and have a pixel scale of
0.15
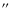 with a mean FWHM of 0.7
with a mean FWHM of 0.7
 .
Figure 1 shows a cutout of the final reduced image. Data are complete up to
.
Figure 1 shows a cutout of the final reduced image. Data are complete up to
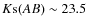 .
A more detailed description of the data set can be found in McCracken et al. (2008, in preparation).
.
A more detailed description of the data set can be found in McCracken et al. (2008, in preparation).
The I-band data used in Sect. 5 are part of the COSMOS HST/ACS field (Koekemoer et al. 2007). The data set consists of a contiguous 1.64 deg2 field covering the entire COSMOS field. The Advanced Camera for Surveys (ACS) together with the F814W filter (``Broad I'') were employed.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg26.png) |
Figure 1:
|
| Open with DEXTER | |
2.2 Building the Ks-band catalog
2.2.1 Detection and cleaning
All objects having a  signal above sky, over four contiguous pixels
are detected using SEXTRACTOR (Bertin & Arnouts 1996). We then performed a
cleaning task in order to separate galaxies from stars and spurious
detections. This was made using the SEXTRACTOR MU_MAX and
MAG_AUTO parameters that give the peak surface brightness above the background
and the Kron-like elliptical aperture magnitude, respectively. The distribution
of objects in this parameter space clearly defines three regions that separate extended sources from point-like or non-resolved sources and from spurious detections. In this
separation scheme, objects with very faint magnitude and high peak
surface brightness are considered as false detections.
The final reduced tiles have several strips where the noise is considerably higher than in the other regions of the image. Therefore, objects that fall in these regions were masked. Furthermore a mask was also applied to the objects that are too close to bright stars (
signal above sky, over four contiguous pixels
are detected using SEXTRACTOR (Bertin & Arnouts 1996). We then performed a
cleaning task in order to separate galaxies from stars and spurious
detections. This was made using the SEXTRACTOR MU_MAX and
MAG_AUTO parameters that give the peak surface brightness above the background
and the Kron-like elliptical aperture magnitude, respectively. The distribution
of objects in this parameter space clearly defines three regions that separate extended sources from point-like or non-resolved sources and from spurious detections. In this
separation scheme, objects with very faint magnitude and high peak
surface brightness are considered as false detections.
The final reduced tiles have several strips where the noise is considerably higher than in the other regions of the image. Therefore, objects that fall in these regions were masked. Furthermore a mask was also applied to the objects that are too close to bright stars (
 ). The final area after having applied the mask is 2.08 deg2.
We finally obtain, after cleaning and masking, 282 122 non-spurious sources over the whole field.
). The final area after having applied the mask is 2.08 deg2.
We finally obtain, after cleaning and masking, 282 122 non-spurious sources over the whole field.
2.2.2 Star/galaxy separation
In order to select galaxies from the total K-selected photometric sample, we have used a number of photometric parameters to remove candidate stars, as described below. Some of the parameters that can be used are: (i) the CLASS_STAR parameter given by SEXTRACTOR providing the ``stellarity-index'' for each object, (ii) the MU_CLASS, i.e. the position in the MU_MAX-MAG_AUTO plane described above, reliable up to
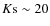 (iii) the
(iii) the 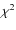 of the SED fitting carried out during the photometric redshift estimate (Ilbert et al. 2006a), with templates SEDs of both stars and galaxies.
of the SED fitting carried out during the photometric redshift estimate (Ilbert et al. 2006a), with templates SEDs of both stars and galaxies.
We decided to use a combination of these criteria. For objects brighter than
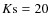 ,
we selected as stars objects having a
,
we selected as stars objects having a
![]() and a photometric redshift lower than 0.05 or a stellar spectral class from the SED fitting in addition to the MU_CLASS parameter. For objects with
and a photometric redshift lower than 0.05 or a stellar spectral class from the SED fitting in addition to the MU_CLASS parameter. For objects with
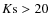 the MU_CLASS parameter was not used and the spectral class was only used when available. The final sample consists in 27 343 point-like sources and 254 779 galaxies.
the MU_CLASS parameter was not used and the spectral class was only used when available. The final sample consists in 27 343 point-like sources and 254 779 galaxies.
2.2.3 The photometric redshift catalog
Photometric redshifts are computed in Ilbert et al. (2009) using a 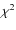 template-fitting method. They are computed with 30 broad, intermediate, and narrow bands covering the UV (GALEX), visible-NIR (SUBARU, CFHT, UKIRT and NOAO) and mid-IR (Spitzer/IRAC). Measurement were calibrated with large spectroscopic samples from VLT-VIMOS and Keck-DEIMOS. Comparison of the derived photo-z with 4148 spectroscopic redshifts (
template-fitting method. They are computed with 30 broad, intermediate, and narrow bands covering the UV (GALEX), visible-NIR (SUBARU, CFHT, UKIRT and NOAO) and mid-IR (Spitzer/IRAC). Measurement were calibrated with large spectroscopic samples from VLT-VIMOS and Keck-DEIMOS. Comparison of the derived photo-z with 4148 spectroscopic redshifts (
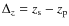 )
indicates a dispersion of
)
indicates a dispersion of
![]() at
iAB<22.5. For more details on how the redshifts are computed, please see Ilbert et al. (2009).
at
iAB<22.5. For more details on how the redshifts are computed, please see Ilbert et al. (2009).
Our final catalog has 198 684 objects with realiable photometric redshift measurements.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1255fig2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg36.png) |
Figure 2:
Redshift distribution for the 44 089 analyzed galaxies. Error bars are calculated using Poisson |
| Open with DEXTER | |
2.2.4 The morphological catalog
The morphological analysis is made in a subsample of the initial catalog: first we select only the galaxies which have a measured photometric redshift. Then we cut the catalog to
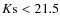 and
and
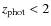 .
This decision is based in a visual inspection; objects fainter than 21.5 have a S/N per pixel lower than 5, so we decided not to include them in the morphological study. Simulations of those objects in fact show that the morphological classifications obtained are highly contaminated. Photometric redshift above
.
This decision is based in a visual inspection; objects fainter than 21.5 have a S/N per pixel lower than 5, so we decided not to include them in the morphological study. Simulations of those objects in fact show that the morphological classifications obtained are highly contaminated. Photometric redshift above 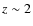 are not reliable enough according to Ilbert et al. (2009). This selection results in a final morphological catalog of 44 089 galaxies. Figure 2 shows the redshift distribution of the final catalog.
are not reliable enough according to Ilbert et al. (2009). This selection results in a final morphological catalog of 44 089 galaxies. Figure 2 shows the redshift distribution of the final catalog.
In order to verify precisely whether the sample is complete for all the morphological types and to quantify the selection effects, we generated 5000 fake galaxies with exponential (Freeman 1970) and de Vaucouleurs profiles (de Vaucouleurs 1948) of different morphological types (bulge fraction uniformly distributed between 0 and 1) and with galaxy sizes uniformly distributed between 0
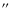 and 1.5
and 1.5
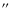 and dropped them in the real background images. We then tried to detect them with SEXTRACTOR. Results are shown in Fig. 3. As we can see, the sample is complete for all the bulge fraction values up to our magnitude limit (
and dropped them in the real background images. We then tried to detect them with SEXTRACTOR. Results are shown in Fig. 3. As we can see, the sample is complete for all the bulge fraction values up to our magnitude limit (
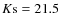 ). We also looked at the completeness as a function of size. We generated for that purpose pure bulge and pure disk profiles with different sizes and detect them with SEXTRACTOR (Fig. 4). As expected bulges are detected up to fainter magnitudes, however the sample is complete up to
). We also looked at the completeness as a function of size. We generated for that purpose pure bulge and pure disk profiles with different sizes and detect them with SEXTRACTOR (Fig. 4). As expected bulges are detected up to fainter magnitudes, however the sample is complete up to
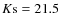 for both bulges and disks for sizes ranging from 0
for both bulges and disks for sizes ranging from 0
 to 1.5
to 1.5
 .
.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1255fig3.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg39.png) |
Figure 3: Completeness for extended sources as a function of the bulge fraction (B/T) as assessed from a mock sample of 5000 galaxies dropped in the field images. |
| Open with DEXTER | |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=6.5cm,clip]{1255fig4a.ps}...
...par\subfigure[]{\includegraphics[width=6.5cm,clip]{1255fig4b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg40.png) |
Figure 4:
Completeness as a function of size for simulated disks a) and bulges b) as assessed from a mock sample of 5000 galaxies dropped in the field images. The size is represented by the disk scale length for disks ( |
| Open with DEXTER | |
3 Morphology
Galaxies in the catalog have been separated into two main morphological types (late-type and early-type) using the free available code galSVM![]() (Huertas-Company et al. 2007). By late-type we mean spiral and irregular galaxies and early-type galaxies include elliptical and lenticular types. galSVM is a non-parametric N-dimensional code based on support vector machines (SVM) that uses a training set built from a local visually classified sample.
The employed procedure can be summarized in 4 main steps (see Paper I for more details):
(Huertas-Company et al. 2007). By late-type we mean spiral and irregular galaxies and early-type galaxies include elliptical and lenticular types. galSVM is a non-parametric N-dimensional code based on support vector machines (SVM) that uses a training set built from a local visually classified sample.
The employed procedure can be summarized in 4 main steps (see Paper I for more details):
- 1.
- Build a training set: we select a nearby visually classified sample at wavelengths corresponding to the rest-frame of the high redshift sample to be analyzed. In our case, we want to simulate Ks-band observations. We used therefore an SDSS local sample observed in the i and z bands which roughly corresponds to the rest-frame wavelengths between
 and
and 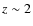 for Ks-band observations. We then move the sample to the proper redshift and image quality and drop it in the real background.
for Ks-band observations. We then move the sample to the proper redshift and image quality and drop it in the real background.
- 2.
- Measure a set of morphological parameters on the sample.
- 3.
- Train a support vector based learning machine with a fraction of the simulated sample and use the other fraction to test and estimate errors.
- 4.
- Classify real data with the trained machine and correct for possible systematic errors detected in the testing step.
3.1 The training sample
The most important step in obtaining the morphology with a non-parametric method is to correctly calibrate the volume filled by the data in the multi-dimensional space. This is a critical step since it will determine the decision regions that will be used to perform the classification. Indeed, galaxy morphology derivation depends on the physical properties of the galaxy (luminosity, redshift, wavelength) and on the observing conditions (background level, resolution). A suitable calibration set should consequently reproduce closely all the properties of the sample to be analyzed. One classical approach consists in visually classifying a fraction of the sample and use it as a training set to optimize boundaries (Menanteau et al. 2006,1999). However this is not possible for seeing limited data where the resolution is too low to enable a reliable visual classification. Here, we then decide to simulate the high redshift sample from a visually classified local catalog, selected in the rest-frame color of the high redshift sample. This has three main advantages: first, it is less affected by K-correction effects, second it does not introduce any modeling effect, since the used galaxies are real and finally, the training set is built to reproduce the observing conditions and physical properties of the sample to be analyzed, but it is classified safely on well-resolved images, so it does not need to have a specially high resolution.
Table 1:
Accuracy of the classifications based on the test sample for a 10 parameters SVM training (C, A, G, Ell, S, M20, C2, SB, z, mag) as a function of probability. The table shows the fraction of correct classifications when a probability bin
![$[P_{\min},P_{\max}]$](/articles/aa/full_html/2009/15/aa11255-08/img41.png) is considered. Numbers between brackets give the number of objects per bin. Top: early-type galaxies, bottom: late-type galaxies.
is considered. Numbers between brackets give the number of objects per bin. Top: early-type galaxies, bottom: late-type galaxies.
We use a catalog of 1319 objects from the Sloan Digital Sky Survey observed in two photometric bands (z and i) and visually classified (Tasca & White 2005). As explained in Paper I, for every galaxy stamp we first generate a random pair of (magnitude, redshift) values with a probability distribution that matches the real magnitude and redshift distribution of the sample to be simulated and then we proceed in four steps: a) removal of foreground stars, b) degradation of the resolution according to a 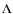 CDM cosmology, c) binning to reach the desired pixel scale and d) dropping in a real background image.
CDM cosmology, c) binning to reach the desired pixel scale and d) dropping in a real background image.
The photometric band (z or i) used to create the galaxy depends on the associated redshift. We choose the one that is closer to the rest-frame band at this given z.
We did not take into account any variation of the PSF within the field for performing the simulations. We in fact expect this variation to be small and consequently not to induce strong changes in the morphology since the analyzed galaxies are significantly larger than the PSF.
Among all the simulated objects, 450 were used as training and the remaining 869 as test.
![\begin{figure}
\par\mbox{\subfigure[]{\includegraphics[width=6.3cm,clip]{1255fig...
...}
\subfigure[]{\includegraphics[width=6.3cm,clip]{1255fig5f.ps} }}\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg45.png) |
Figure 5: Bi-dimensional maps of the mean probabilities for different redshift, magnitude and size bins of the real sample. The size is represented by the half light radius as measured by SExtractor. The plots show the mean probability distribution as a function of a single parameter. Error bars show the dispersion of the probability distribution. On the left column we show the probability maps for early-type objects and on the right the maps for late-type objects. The black cells indicate that there are no objects in the considered bin. |
| Open with DEXTER | |
3.2 Classification procedure
We use 450 simulated galaxies as training sample. The morphological mixing is fixed to 50/50, i.e. 50% of early-type galaxies and 50% of late-type. Even if this is not a realistic distribution it is required to minimize the errors in the SVM classification. The classification is made in a 10-D volume with a Radial Basis Function Kernel (see Paper I for more details). The measured parameters include 6 morphological parameters: Asymmetry, Concentration (Conselice et al. 2000; and Abraham et al. 1996, definitions), Gini (Abraham et al. 2003), M20 (Lotz et al. 2004), Smoothness (Conselice et al. 2003), a distance parameter (photometric redshift), a shape parameter (elongation), 2 luminosity parameters (surface brightness and magnitude). See Paper I for details on how these parameters are calculated.
In Paper I we show, thanks to the test sample, that increasing the number of parameters of the classification never results in a degeneracy that decreases the accuracy. We realized however that when dealing with the real sample, some parameters might produce a bias if they are not realistic. This is the case of the magnitude. Indeed when doing the simulations we use the same magnitude distribution for early and late-type galaxies. This creates an artificial excess of early-type galaxies at faint magnitudes in the simulated sample that is not seen in the real world. Therefore if the magnitude is used as input parameter for the classification the number of early-type galaxies are overestimated. To avoid this bias we proceed in 2 steps: first we make a 9-D classification (without the magnitude) and then we use the measured magnitude distribution per morphological type to generate a new simulated sample with this magnitude distribution. We use this second sample to make the final 10-D classification.
3.3 The output catalog
Classical support vector classifiers only predict class label (i.e. early-type or late-type) but not probability information. Recently some authors (Wu et al. 2004; Platt 2000) have proposed different methods to estimate a posteriori probability, i.e. given k classes of data, for any 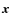 the goal is to estimate
the goal is to estimate
![]() .
The free available package libSVM (Chang & Lin 2001) implements the method described in Wu et al. (2004). Therefore we added this new feature to our classification output:
we associate to every galaxy in the morphological catalog, a class label and a probability of belonging to the given class. Since we are dealing with a 2-class problem, the probability p(galaxy = early-type) = 1 - p(galaxy = late-type). In the following, we use this parameter to assess the accuracy of our classification.
.
The free available package libSVM (Chang & Lin 2001) implements the method described in Wu et al. (2004). Therefore we added this new feature to our classification output:
we associate to every galaxy in the morphological catalog, a class label and a probability of belonging to the given class. Since we are dealing with a 2-class problem, the probability p(galaxy = early-type) = 1 - p(galaxy = late-type). In the following, we use this parameter to assess the accuracy of our classification.
![\begin{figure}
\par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{1255fig6a...
...} }
\subfigure[]{\includegraphics[width=6cm,clip]{1255fig6f.ps} }}\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg48.png) |
Figure 6:
Sample completeness as a function of redshift. Left column are early-type galaxies and right column late-type. a-d) size b-e) redshift and c-f) magnitude for different probability cuts. Dotted line: galaxies with p>0.6, dashed line: galaxies with p>0.7, dashed-dotted line: galaxies with p>0.8 and dashed line with three dots: galaxies with p>0.9. Error bars are calculated using Poisson |
| Open with DEXTER | |
3.4 Accuracy
As shown in Paper I, one of the main advantages of the employed method is that the reliability of the classifications can be quantified using a test sample simulated in the same way as the training one.
Here we use the probability as the main estimator. We first looked at the evolution of the correct classifications as a function of different probability thresholds. Results are shown in Table 1. As we can see, there is a clear correlation between the probability threshold and the number of correct identifications: the accuracy clearly increases when the considered probability is higher. If we select only objects with a probability between 0.5 and 0.6 the mean accuracy is only around 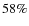 .
However, objects with probabilities greater than 0.8 are classified with nearly
.
However, objects with probabilities greater than 0.8 are classified with nearly 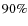 accuracy. The contamination is around
accuracy. The contamination is around 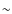 20% for the whole sample (p>0.5).
20% for the whole sample (p>0.5).
This relations between the probability parameter and the success rate enable the use of the probability as an estimate of the classification accuracy as a function of physical parameters of the galaxies directly on the real sample. We decided to represent 2D maps of the mean probability values (Fig. 5) for different magnitude, redshift and size bins. We observe several interesting trends:
- Globally, late-type galaxies have higher probabilities for all redshift, magnitude and size values. This indicates that late-type objects are easily isolated. It is probably a consequence of the ellipticity parameter, used in the classification procedure. Indeed, objects with high ellipticity are identified as late-type galaxies with high probability so that the mean probability increases.
- As expected there is a clear trend with size for both morphological types, small objects (
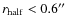 )
have lower probabilities (
)
have lower probabilities (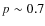 )
while large ones (
)
while large ones (
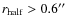 )
have higher values (p>0.8) (Figs. 5c, d).
)
have higher values (p>0.8) (Figs. 5c, d).
- There is also a trend with redshift, especially for early-type objects: below
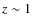 the mean probability is around
the mean probability is around 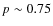 and it decreases to
and it decreases to 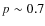 for z>1. The number of galaxies with low probability (
for z>1. The number of galaxies with low probability (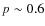 )
also increases (Figs. 5a, b).
)
also increases (Figs. 5a, b).
- Finally, the magnitude is also important for determining the quality of the classification. Above
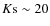 the mean probability for early-type objects is around
the mean probability for early-type objects is around 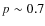 (Figs. 5a, e). Interestingly, this trend does not appear for the late-type population (Figs. 5b, f). This is probably a consequence of the way the training sample is built (Sect. 3.2): at faint magnitudes, the number of early-type galaxies is low so the machine tends to find late-type galaxies with higher probability.
(Figs. 5a, e). Interestingly, this trend does not appear for the late-type population (Figs. 5b, f). This is probably a consequence of the way the training sample is built (Sect. 3.2): at faint magnitudes, the number of early-type galaxies is low so the machine tends to find late-type galaxies with higher probability.
To answer this question we selected objects with 4 probability thresholds (p>0.6, p>0.7, p>0.8 and p>0.9) and examined the completeness of the selected sample as a function of the magnitude, the redshift, the size and the morphological type. Figure 6 shows the results. If no biases were introduced all the lines should be flat (i.e. ``we keep all the galaxies in the same way''). We observe in Fig. 6 that this is not the case. This is seen in particular when looking at the completeness as a function of size and morphological type: large objects are preferred as expected and early-type objects are more penalized.
Therefore a sample selected by performing a probablity cut should not be used for global statistical analysis. It can be used however to select particular class of objects for which a very good accuracy is needed. In the next section we show however a way of using the information brought by probabilities for statistical purposes.
3.4.1 Best estimator
Considering that we have N galaxies with a probability pk of being in class A (e.g. early-type or late-type), we can define two functions to estimate the number of objects in a given class.
The first one (hereafter counts estimator) uses a function
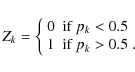
Then the number of objects in class A is simply:
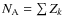 .
Objects with a probability greater than 0.5 of belonging to a given class are simply added. With this estimator we consider therefore in the same way a galaxy with p=0.51 and one with p=0.99; it is just added to the corresponding class and the probability is ignored.
.
Objects with a probability greater than 0.5 of belonging to a given class are simply added. With this estimator we consider therefore in the same way a galaxy with p=0.51 and one with p=0.99; it is just added to the corresponding class and the probability is ignored.
The second one (hereafter probability estimator) tries to make use of the information contained in the probability parameter. It has been shown in the previous section that galaxies with higher probabilities have lower classification errors. However making arbitrary probability cuts introduces biases in the global statistics in the sense that not all the objects are removed uniformly. It would be interesting therefore to find a way of using the information contained in this parameter without introducing biases. For that purpose, we define a random variable

Then we can estimate the number of objects in class A as the mathematical expectation of this variable:
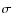 error on the number as the square root of the variance of the variable:
error on the number as the square root of the variance of the variable:
Therefore, the larger the number of galaxies with probability values close to 0.5, the more the differences between the two estimators will be important. As a matter of fact, if all the probabilities are equal to one, both estimators give the same results whereas if all the probabilities are equal to 0.5, the probability estimator gives half the value of the count estimator. In this sense the comparison of the results furnished by the two estimators is a kind of measure of the classification accuracy.
3.4.2 Errors due to the training set
The estimator presented above takes into account the information brought by the probability parameter to estimate at best the number of galaxies of each morphological type and correct from misclassifications. However, there is another source of error which has to be considered. It is related to the training set itself. Indeed, even if the training sample is built to reproduce at best the parameters of the real one it can contain errors or there can exist galaxies which are not well represented in the parameter space. In order to estimate these errors, we performed Monte Carlo simulations: we randomly removed elements from the training sample and generated therefore multiple training samples with fewer galaxies. We then used these samples to train different machines and classify the real sample. The generated samples have similar properties than the original one but do not fill the parameter space in the same way. They can be used consequently to estimate the effect in the final classification of missing objects in the parameter space. The differences found in the classifications are then employed to estimate a kind of confidence region of our classification scheme in the following sections.
4 Results and discussion
4.1 Global statistics
We find 33291(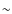 75%) late-type galaxies and 10798 (
75%) late-type galaxies and 10798 (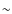 25%) early-type galaxies with the counts estimator and
25%) early-type galaxies with the counts estimator and
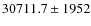 (
(
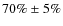 )
and
)
and
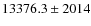 (
(
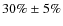 )
early-type galaxies with the probability estimator. In the next sections we try to locate more precisely the differences.
)
early-type galaxies with the probability estimator. In the next sections we try to locate more precisely the differences.
4.2 Number counts
Figure 7 shows the number counts per morphological type using the two estimators described above. As expected, early-type objects dominate the bright end of the magnitude distribution while late-type objects are more frequent at the faint-end. The effect of using the probability estimator is seen clearly in the faint elliptical population (
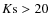 ). In particular the number of faint early-type galaxies increases when using the probability estimator. This reflects that at faint magnitudes early-type galaxies are classified with lower probabilities as seen from the 2D maps (Fig. 5). The use of the probability parameter in performing the counts enables to correct for the classification errors by adding galaxies that fell in the late-type class but had a significant probability of being elliptical.
). In particular the number of faint early-type galaxies increases when using the probability estimator. This reflects that at faint magnitudes early-type galaxies are classified with lower probabilities as seen from the 2D maps (Fig. 5). The use of the probability parameter in performing the counts enables to correct for the classification errors by adding galaxies that fell in the late-type class but had a significant probability of being elliptical.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg66.png) |
Figure 7:
Number counts per morphological type for the 44 089 analyzed galaxies. The solid line shows the results obtained with the probability estimator; the line width indicates the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig8.ps} \end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg67.png) |
Figure 8:
Redshift distribution per morphological type for the 44 089 analyzed galaxies. The solid line shows the results obtained with the probability estimator; the line width indicates |
| Open with DEXTER | |
4.3 Morphological evolution
Figure 8 shows the morphological mixing evolution up to 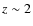 .
Both estimators reveal an increase of the early type fraction from
.
Both estimators reveal an increase of the early type fraction from 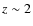 ,
however the effect is less important when taking into account the probability. In fact, with the probability estimator we find
,
however the effect is less important when taking into account the probability. In fact, with the probability estimator we find
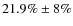 early-type objects at
early-type objects at 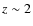 while the local fraction is
while the local fraction is
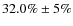 .
The counts estimator predicts a fraction of
.
The counts estimator predicts a fraction of 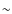 15% at
15% at 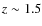 .
Considering the probability helps therefore to correct from the incompleteness of the early-type population at high z due to the lower probability values.
.
Considering the probability helps therefore to correct from the incompleteness of the early-type population at high z due to the lower probability values.
This variation in the early-type population is a well-known effect which has been detected using rest-frame morphologies from HST (e.g. Cassata et al. 2005; Brinchmann et al. 1998) and probably reflects the building-up of the red sequence from late-type systems. It could be argued however that this effect was a consequence of morphological k-correction since at higher redshifts we probe the UV galaxy emission, i.e. young stellar populations. The fact that we still observe this trend with NIR data (which probe older stellar populations) seems to point that this is a real effect and not a morphological k-correction effect. It is important to point out that the fraction found here at 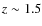 is significantly higher than the one obtained in Cassata et al. (2005); Arnouts et al. (2007) or Abraham et al. (2007). This short evolution could be explained by a selection effect. The K<21.5 selected sample does not probe the same galaxy populations at
is significantly higher than the one obtained in Cassata et al. (2005); Arnouts et al. (2007) or Abraham et al. (2007). This short evolution could be explained by a selection effect. The K<21.5 selected sample does not probe the same galaxy populations at 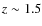 and
and 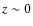 :
at
:
at 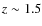 ,
only the high mass end of the K-band luminosity function is sampled whereas at
,
only the high mass end of the K-band luminosity function is sampled whereas at 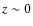 ,
the LF is sampled over several magnitudes. This will be investigated in a forthcoming paper in which we will use stellar mass estimates to build a volume limited sample. In this paper we want to focus on the morphological k-correction effects and for that purpose a magnitude-limited sample is enough. The following sections are therefore focused on this important point.
,
the LF is sampled over several magnitudes. This will be investigated in a forthcoming paper in which we will use stellar mass estimates to build a volume limited sample. In this paper we want to focus on the morphological k-correction effects and for that purpose a magnitude-limited sample is enough. The following sections are therefore focused on this important point.
5 Investigating the morphological k-correction effect
In the previous section, we have obtained a morphological classification from NIR imaging. A crucial point is to understand the differences (if there are some) between morphologies quantified in the visible and the ones computed here. We perform for that purpose a match between the Ks selected morphological catalog and the morphologies measured from HST/ACS data (I-band) in an independent way.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1255fig9.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg70.png) |
Figure 9: One-to-one comparison of the ACS and WIRCam classifications as a function of redshift. Red line: mean probability for a galaxy classified as early-type in the K-band to be classified as early-type in the I-band (HST). Blue line: mean probability for a galaxy classified as late-type in the K-band to be classified as late-type in the I-band. Error bars show the dispersion of the probability distribution. |
| Open with DEXTER | |
For the classification of the I-band sample we use a similar method as for the K-band sample: we train a 5-D support vector machine (gini, concentration, asymmetry and ellipticity). As shown in Paper I, this is largely enough for a well-resolved sample like the ACS one. Since ACS galaxies are better resolved than WIRCam ones, the training sample is not built from an SDSS sample but by visually classifying 500 real ACS galaxies. The way the visual classification is performed is fully described in Tasca et al. (2008, in preparation).
We match 32 171 objects of our K-selected sample. The remaining objects were too faint in the ACS data (I>24) to perform reliable morphological classifications. The global morphological mixing from HST/ACS data is in good agreement with the one obtained with WIRCam for the same objects: 9163 (I-band), 10458.8 (Ks-band) early-type galaxies and 25002 (I-band), 23706.2 (Ks-band) late-type galaxies respectively. However, where are the differences localized precisely?
5.1 One-to-one comparison
Figure 9 shows the mean probability for a galaxy classified as early (late) in the Ks-band to be classified as early (late) in the I-band as a function of redshift.
We observe, that globally, there is no ambiguity in the identification of late-type objects. A galaxy which is found to be late-type in the Ks-band is also a late-type system in the I-band with a probability around 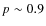 up to
up to 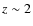 .
.
For early-type objects, there is clear trend with redshift: below 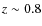 a galaxy classified as early-type in the Ks-band has a probability of
a galaxy classified as early-type in the Ks-band has a probability of 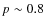 of being early-type in the I-band. Above
of being early-type in the I-band. Above 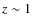 the discrepancies between the two classifications become higher and an elliptical galaxy is classified as early in both classifications only with a probability of
the discrepancies between the two classifications become higher and an elliptical galaxy is classified as early in both classifications only with a probability of 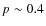 .
Above
.
Above 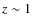 the I-band filter starts to probe the UV flux and therefore the obtained morphology is determined from young stars whereas the Ks-band filter stills probe the visible spectra of the galaxy. We are thus probably seeing a k-correction effect: late-type objects are identified in the same way since their stellar populations are younger whereas for early-type objects the ambiguity is higher and a fraction of objects tend to move to later morphological types.
the I-band filter starts to probe the UV flux and therefore the obtained morphology is determined from young stars whereas the Ks-band filter stills probe the visible spectra of the galaxy. We are thus probably seeing a k-correction effect: late-type objects are identified in the same way since their stellar populations are younger whereas for early-type objects the ambiguity is higher and a fraction of objects tend to move to later morphological types.
What are then the differences of morphologically selecting a sample in the Ks-band or in the I-band above 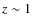 ?
?
5.2 Comparing redshift distributions
Figure 10 shows the redshift distributions obtained from both classifications. The distributions for late-type objects present small differences as expected from the comparison performed in the previous section. Notice however that in the lowest redshift bin, the two classification find different values. This is probably a consequence of classification errors since very big galaxies are not well represented in the training. A Kolmogorov-Smirnov test (KS-test) reveals that the two functions arise from the same statistic with 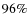 confidence.
The early-type redshift distributions present more differences, as expected from the comparisons of the previous section, in particular above
confidence.
The early-type redshift distributions present more differences, as expected from the comparisons of the previous section, in particular above 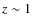 .
The match between the two distributions as computed from the KS-test is high at z<1 (
.
The match between the two distributions as computed from the KS-test is high at z<1 (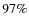 )
but clearly decreases above
)
but clearly decreases above 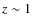 (
(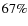 ). Interestingly, the I-band estimate goes out of the confidence region at z>1. We find in particular an excess of early-type galaxies by a factor
). Interestingly, the I-band estimate goes out of the confidence region at z>1. We find in particular an excess of early-type galaxies by a factor 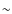 1.5 in the Ks-band when compared to the I-band. Above
1.5 in the Ks-band when compared to the I-band. Above 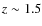 the number of objects is small and the uncertainties high. Even if at
the number of objects is small and the uncertainties high. Even if at 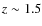 ,
the Ks-band classification is less accurate (Sect. 3.4), the difference is significant after taking into account most of the classification errors. The differences are probably due to morphological k-correction effects. It seems therefore that a morphological classification based on HST/ACS I-band data at those redshifts tends to under-estimate the elliptical population. Nevertheless, these results have to be confirmed with a more precise study of the early-type population at
,
the Ks-band classification is less accurate (Sect. 3.4), the difference is significant after taking into account most of the classification errors. The differences are probably due to morphological k-correction effects. It seems therefore that a morphological classification based on HST/ACS I-band data at those redshifts tends to under-estimate the elliptical population. Nevertheless, these results have to be confirmed with a more precise study of the early-type population at 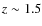 by studying their star forming histories and mass distributions. Another possible explanation for this result is the relative sizes of the PSFs between the two datasets: a typical galaxy in the ACS images has about fifty times more
resolution elements across it than the K-band data (since the
PSF sizes are 0.1
by studying their star forming histories and mass distributions. Another possible explanation for this result is the relative sizes of the PSFs between the two datasets: a typical galaxy in the ACS images has about fifty times more
resolution elements across it than the K-band data (since the
PSF sizes are 0.1
 vs. 0.7
vs. 0.7
 ), so the K-band
data are better at pulling out lower surface brightness faint
envelopes, which might be missed in the ACS data because the pixels
are too small and there is too much noise. A test of this would be
to convolve the ACS data to a PSF that
matches the K-band data. We are planning this task in a forthcoming paper.
), so the K-band
data are better at pulling out lower surface brightness faint
envelopes, which might be missed in the ACS data because the pixels
are too small and there is too much noise. A test of this would be
to convolve the ACS data to a PSF that
matches the K-band data. We are planning this task in a forthcoming paper.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1255fig10.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg77.png) |
Figure 10:
Redshift distribution per morphological type for the same 32 171 Ks-selected galaxies observed in the I-band and in the Ks-band. Red and pink lines are WIRCam and ACS early-type objects respectively and blue and violet lines are WIRCam and ACS late-type. The line width is the |
| Open with DEXTER | |
6 Summary and conclusions
We have presented a morphological classification in two main morphological types of 44 089 galaxies within the COSMOS field from seeing limited near-infrared imaging. Morphologies are estimated with the non-parametric N-dimensional code galSVM using a 10 dimensional volume and non-linear boundaries.
The final output catalog includes for every galaxy, a class label (early or late) and a probability of belonging to the class. The probability is proved to be highly correlated with the success rate and can therefore be used to assess the accuracy of the classifications.
This classification method has been used to obtain the number counts and the redshift distribution per morphological type up to 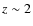 and to compare the results with the ones obtained from HST/ACS imaging on 32 171 galaxies in order to quantify morphological k-correction effects.
and to compare the results with the ones obtained from HST/ACS imaging on 32 171 galaxies in order to quantify morphological k-correction effects.
Our main conclusions are hereafter summarized:
Concerning the reliability of our morphological classification:
- 1.
- According to the simulated test sample, the average success rate is
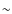 80% for the whole sample for both morphological classes, leading to
80% for the whole sample for both morphological classes, leading to 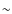 20% contaminations (i.e. fraction of failures).
20% contaminations (i.e. fraction of failures).
- 2.
- The probability parameter which results from the classification procedure is a good estimator of the reliability of the classifications since it is highly correlated with the success rate. Objects with probabilities greater than 0.8 are identified with nearly
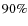 of confidence.
of confidence.
- 3.
- The study of the probability distributions as a function of the magnitude, the size and the redshift of the galaxies reveals that the most difficult class to isolate are faint (
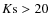 ), small (
), small (
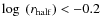 )
early-type objects above
)
early-type objects above 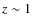 .
However, even for this class of objects, the average probability is around
.
However, even for this class of objects, the average probability is around 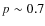 .
.
- 4.
- We also showed that selection based on a probability threshold does lead to a biased sample towards late-type systems. We proposed however a way of integrating the information brought by the probability parameter to perform statistical analysis.
- 5.
- Errors due the training sample dominate the error source.
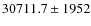 (
(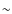
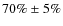 )
late-type galaxies and
)
late-type galaxies and
 (
(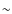
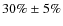 )
early-type galaxies. There are
)
early-type galaxies. There are 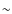
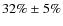 early-type galaxies at z<0.4 in our sample whereas the fraction at
early-type galaxies at z<0.4 in our sample whereas the fraction at 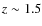 is
is
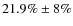 .
This effect persists even after correcting for classification errors using the probability parameter. The measurement qualitatively confirms the trend observed in previous studies as a
consequence of a progressive building up of the red sequence from late-type objects
(e.g. Abraham et al. 2007; Arnouts et al. 2007). We will investigate the evolution of the fraction in types defined with our method, and using a volume limited sample rather than a magnitude
limited sample, in a forthcoming paper.
.
This effect persists even after correcting for classification errors using the probability parameter. The measurement qualitatively confirms the trend observed in previous studies as a
consequence of a progressive building up of the red sequence from late-type objects
(e.g. Abraham et al. 2007; Arnouts et al. 2007). We will investigate the evolution of the fraction in types defined with our method, and using a volume limited sample rather than a magnitude
limited sample, in a forthcoming paper.
The comparison of the morphologies with the ones obtained obtained with HST/ACS in the I-band for 32 171 objects reveals several interesting trends:
- 1.
- The global morphological mixings are globally consistent. We find 9163 early-type galaxies and 25 002 late-type galaxies in the I-band and 10458 early-type for 23706 late-type galaxies in the Ks-band.
- 2.
- A galaxy classified as late-type in the I-band has a mean probability of
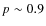 of being classified as late-type in the Ks-band.
of being classified as late-type in the Ks-band.
- 3.
- The match between the two photometric bands for early-type galaxies depends on redshift: below
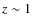 ,
an early-type galaxy in the I-band has a probability of
,
an early-type galaxy in the I-band has a probability of 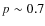 of being early-type in the Ks-band. Above this redshift, where the HST cameras are probing the UV flux, the probability decreases and reaches
of being early-type in the Ks-band. Above this redshift, where the HST cameras are probing the UV flux, the probability decreases and reaches 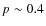 at
at 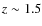 .
.
- 4.
- The comparison of the redshift distributions reveals also a redshift dependence: below
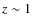 the two redshift distributions match quite well. The Kolmogorov-Smirnoff test gives a probability of match of p=0.97.
Above
the two redshift distributions match quite well. The Kolmogorov-Smirnoff test gives a probability of match of p=0.97.
Above 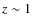 ,
the I-band classification tends to find less early-type galaxies than the Ks-band one by a factor
,
the I-band classification tends to find less early-type galaxies than the Ks-band one by a factor 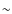 1.5. This probably reflects a morphological k-correction effect. Therefore, studies based on HST classifications at those redshifts could underestimate the elliptical population.
1.5. This probably reflects a morphological k-correction effect. Therefore, studies based on HST classifications at those redshifts could underestimate the elliptical population.
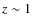 from I-band ACS data
is about 19%, increasing to 31% at
from I-band ACS data
is about 19%, increasing to 31% at
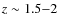 .
From our K-band data we estimate that the fraction
of early-type galaxies has increased by 10%
between z=1.5 and z=0, a further confirmation
of the gradual build up of the elliptical galaxy
population at the expense of late-type galaxies.
The Ks-band classification performed here is intended
as a framework for future studies of the evolution of
counts, luminosities, luminosity densities and correlation
function for each morphological type over several
redshift bins on a volume limited sample.
.
From our K-band data we estimate that the fraction
of early-type galaxies has increased by 10%
between z=1.5 and z=0, a further confirmation
of the gradual build up of the elliptical galaxy
population at the expense of late-type galaxies.
The Ks-band classification performed here is intended
as a framework for future studies of the evolution of
counts, luminosities, luminosity densities and correlation
function for each morphological type over several
redshift bins on a volume limited sample.
Acknowledgements
The authors want to thank the anonymous referee for his useful suggestions that clearly improved the paper. This work is part of a big collaboration, we would like to thank as well all the people who contributed somehow to this paper, specially with the data reduction (H. Aussel, D. Thompson, O. Ilbert).
References
- Abraham, R., van den Bergh, S., Glazebrook, K., et al. 1996, ApJS, 107, 1 [NASA ADS] [CrossRef] (In the text)
- Abraham, R. G., van den Bergh, S., & Nair, P. 2003, ApJ, 588, 218 [NASA ADS] [CrossRef] (In the text)
- Abraham, R. G., Nair, P., McCarthy, P. J., et al. 2007, ApJ, 669, 184 [NASA ADS] [CrossRef] (In the text)
- Arnouts, S., Walcher, C. J., Le Fevre, O., et al. 2007, ArXiv e-prints, 705
- Baker, A. J., Davies, R. I., Lehnert, M. D., et al. 2003, A&A, 406, 593 [NASA ADS] [CrossRef] [EDP Sciences]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brinchmann, J., Abraham, R., Schade, D., et al. 1998, ApJ, 499, 112 [NASA ADS] [CrossRef]
- Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef]
- Cassata, P., Cimatti, A., Franceschini, A., et al. 2005, MNRAS, 357, 903 [NASA ADS] [CrossRef]
- Chang, C.-C., & Lin, C.-J. 2001, LIBSVM: a library for support vector machines, software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm (In the text)
- Conselice, C., & GNS Team 2007, in Amer. Astron. Soc. Meet. Abstr., 211
- Conselice, C. J., Bershady, M. A., & Jangren, A. 2000, ApJ, 529, 886 [NASA ADS] [CrossRef] (In the text)
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] (In the text)
- Cresci, G., Davies, R. I., Baker, A. J., et al. 2006, A&A, 458, 385 [NASA ADS] [CrossRef] [EDP Sciences]
- de Vaucouleurs, G. 1948, Annales d'Astrophysique, 11, 247 [NASA ADS] (In the text)
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] (In the text)
- Gardner, J. P., Cowie, L. L., & Wainscoat, R. J. 1993, ApJ, 415, L9 [NASA ADS] [CrossRef]
- Huertas-Company, M., Rouan, D., Soucail, G., et al. 2007, A&A, 468, 937 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Huertas-Company, M., Rouan, D., Tasca, L., Soucail, G., & Le Fèvre, O. 2008, A&A, 478, 971 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006a, ArXiv Astrophysics e-prints (In the text)
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006b, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] (In the text)
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] (In the text)
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] (In the text)
- Madgwick, D. S., Lahav, O., Baldry, I. K., et al. 2002, MNRAS, 333, 133 [NASA ADS] [CrossRef] (In the text)
- Maihara, T., Iwamuro, F., Tanabe, H., et al. 2001, PASJ, 53, 25 [NASA ADS]
- McCracken, H. J., Metcalfe, N., Shanks, T. et al. 2000a, MNRAS, 311, 707 [NASA ADS] [CrossRef]
- McCracken, H. J., Metcalfe, N., Shanks, T., et al.. 2000b, MNRAS, 311, 707 [NASA ADS] [CrossRef]
- Menanteau, F., Ellis, R. S., Abraham, R. G., Barger, A. J., & Cowie, L. L. 1999, MNRAS, 309, 208 [NASA ADS] [CrossRef]
- Menanteau, F., Ford, H. C., Motta, V., et al. 2006, AJ, 131, 208 [NASA ADS] [CrossRef]
- Platt, J. 2000, Advances in Large Margin Classifiers
- Saracco, P., Longhetti, M., Andreon, S., & Mignano, A. 2008, ArXiv e-prints, 801
- Scoville, N. Z., & COSMOS Team. 2005, in BAAS, 1309 (In the text)
- Tasca, L., & White, S. 2005, [arXiv:astro-ph/0507249] (In the text)
- Thibault, S., Cui, Q., Poirier, M., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, ed. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841 (In the text)
- Wolf, C., Meisenheimer, K., Rix, H.-W., et al. 2003, A&A, 401, 73 [NASA ADS] [CrossRef] [EDP Sciences]
- Wu, T. F., J., L. C., & C., W. R. 2004, J. Machine Learning Res., 5, 975
- Zirm, A. W., Stanford, S. A., Postman, M., et al. 2008, ArXiv e-prints, 802 (In the text)
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ...I band
![[*]](/icons/foot_motif.png)
- Based on observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii.
- ...
pipeline
![[*]](/icons/foot_motif.png)
- http://terapix.iap.fr
- ... galSVM
![[*]](/icons/foot_motif.png)
- http://www.lesia.obspm.fr/~huertas/galsvm.html
All Tables
Table 1:
Accuracy of the classifications based on the test sample for a 10 parameters SVM training (C, A, G, Ell, S, M20, C2, SB, z, mag) as a function of probability. The table shows the fraction of correct classifications when a probability bin
![]() is considered. Numbers between brackets give the number of objects per bin. Top: early-type galaxies, bottom: late-type galaxies.
is considered. Numbers between brackets give the number of objects per bin. Top: early-type galaxies, bottom: late-type galaxies.
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg26.png) |
Figure 1:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1255fig2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg36.png) |
Figure 2:
Redshift distribution for the 44 089 analyzed galaxies. Error bars are calculated using Poisson |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1255fig3.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg39.png) |
Figure 3: Completeness for extended sources as a function of the bulge fraction (B/T) as assessed from a mock sample of 5000 galaxies dropped in the field images. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=6.5cm,clip]{1255fig4a.ps}...
...par\subfigure[]{\includegraphics[width=6.5cm,clip]{1255fig4b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg40.png) |
Figure 4:
Completeness as a function of size for simulated disks a) and bulges b) as assessed from a mock sample of 5000 galaxies dropped in the field images. The size is represented by the disk scale length for disks ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\subfigure[]{\includegraphics[width=6.3cm,clip]{1255fig...
...}
\subfigure[]{\includegraphics[width=6.3cm,clip]{1255fig5f.ps} }}\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg45.png) |
Figure 5: Bi-dimensional maps of the mean probabilities for different redshift, magnitude and size bins of the real sample. The size is represented by the half light radius as measured by SExtractor. The plots show the mean probability distribution as a function of a single parameter. Error bars show the dispersion of the probability distribution. On the left column we show the probability maps for early-type objects and on the right the maps for late-type objects. The black cells indicate that there are no objects in the considered bin. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{1255fig6a...
...} }
\subfigure[]{\includegraphics[width=6cm,clip]{1255fig6f.ps} }}\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg48.png) |
Figure 6:
Sample completeness as a function of redshift. Left column are early-type galaxies and right column late-type. a-d) size b-e) redshift and c-f) magnitude for different probability cuts. Dotted line: galaxies with p>0.6, dashed line: galaxies with p>0.7, dashed-dotted line: galaxies with p>0.8 and dashed line with three dots: galaxies with p>0.9. Error bars are calculated using Poisson |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg66.png) |
Figure 7:
Number counts per morphological type for the 44 089 analyzed galaxies. The solid line shows the results obtained with the probability estimator; the line width indicates the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1255fig8.ps} \end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg67.png) |
Figure 8:
Redshift distribution per morphological type for the 44 089 analyzed galaxies. The solid line shows the results obtained with the probability estimator; the line width indicates |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1255fig9.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg70.png) |
Figure 9: One-to-one comparison of the ACS and WIRCam classifications as a function of redshift. Red line: mean probability for a galaxy classified as early-type in the K-band to be classified as early-type in the I-band (HST). Blue line: mean probability for a galaxy classified as late-type in the K-band to be classified as late-type in the I-band. Error bars show the dispersion of the probability distribution. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1255fig10.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa11255-08/Timg77.png) |
Figure 10:
Redshift distribution per morphological type for the same 32 171 Ks-selected galaxies observed in the I-band and in the Ks-band. Red and pink lines are WIRCam and ACS early-type objects respectively and blue and violet lines are WIRCam and ACS late-type. The line width is the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



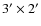 cutout of the observed area. Yellow circles are stars, magenta circles are masked objects, blue circles are galaxies and red circles are galaxies with computed morphology (see text for details).
cutout of the observed area. Yellow circles are stars, magenta circles are masked objects, blue circles are galaxies and red circles are galaxies with computed morphology (see text for details).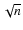 statistics.
statistics.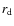 )
and by the bulge effective radius (
)
and by the bulge effective radius (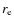 )
for bulges.
)
for bulges.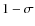 confidence band estimated from the probability distribution and the dashed region is the confidence region deduced from Monte Carlo simulations of the training sample (see text for details). The dashed line shows the results obtained with the counts estimator. Red lines stand for early-type galaxies and blue lines for late-type. Error bars are calculated using Poisson
confidence band estimated from the probability distribution and the dashed region is the confidence region deduced from Monte Carlo simulations of the training sample (see text for details). The dashed line shows the results obtained with the counts estimator. Red lines stand for early-type galaxies and blue lines for late-type. Error bars are calculated using Poisson