| Issue |
A&A
Volume 497, Number 2, April II 2009
|
|
|---|---|---|
| Page(s) | 487 - 495 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811105 | |
| Published online | 05 March 2009 | |
The close Be star companion of  Cephei
Cephei
H. E. Wheelwright1 - R. D. Oudmaijer1 - R. S. Schnerr2
1 - The School of Physics and Astronomy, EC Stoner Building, The University of Leeds, Leeds LS2 9JT, UK
2 - Institute for Solar Physics, Royal Swedish Academy of Sciences, Albanova University Centre, 10691 Stockholm, Sweden
Received 7 October 2008 / Accepted 16 February 2009
Abstract
Context. The prototype of the  Cephei class of pulsating stars,
Cephei class of pulsating stars,  Cep, rotates relatively slowly, and yet displays episodic H
Cep, rotates relatively slowly, and yet displays episodic H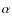 emission. Such behaviour is typical of a rapidly rotating, classical Be star. For some time this posed a contradiction to our understanding of the Be phenomena as rapid rotation is thought to be a prerequisite for the characteristic emission phases of Be stars. Recent work has demonstrated that the H
emission. Such behaviour is typical of a rapidly rotating, classical Be star. For some time this posed a contradiction to our understanding of the Be phenomena as rapid rotation is thought to be a prerequisite for the characteristic emission phases of Be stars. Recent work has demonstrated that the H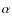 emission is in fact due to a close companion (separation
emission is in fact due to a close companion (separation 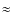
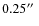 )
of the star. This resolves the apparent enigma if this close companion is indeed a classical Be star, as has been proposed.
)
of the star. This resolves the apparent enigma if this close companion is indeed a classical Be star, as has been proposed.
Aims. We aim to test the hypothesis that this close companion is a valid Be star by determining properties such as its spectral type and 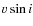 .
.
Methods. We employed the technique of spectroastrometry to investigate the close binary system. Using the spectroastrometric signatures observed, we split the composite binary spectra into its constituent spectra in the B band (4200-5000 Å) and R band (6200-7000 Å).
Results. The spectroastrometrically split spectra allow us to estimate spectral types of the binary components. We find that the primary of the close binary system has a spectral type of B2III and the secondary a spectral type of B5Ve. From the relationship between mass and spectral type, we determine the masses of the binary components to be
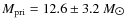 and
and
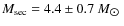 respectively. The spectroastrometric data allow some constraint on the orbit, and we suggest a moderate revision to the previously determined orbit. We confirm that the primary of the system is a slow rotator (
respectively. The spectroastrometric data allow some constraint on the orbit, and we suggest a moderate revision to the previously determined orbit. We confirm that the primary of the system is a slow rotator (
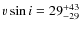 km s-1), while the secondary rotates significantly faster, at a
km s-1), while the secondary rotates significantly faster, at a
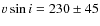 km s-1
km s-1
Conclusions. We show that the close companion to the  Cephei primary is certainly a valid classical Be star. It has a spectral type of B5Ve and is a relatively fast rotator. We confirm that the
Cephei primary is certainly a valid classical Be star. It has a spectral type of B5Ve and is a relatively fast rotator. We confirm that the  Cephei system does not contradict our current understanding of classical Be stars.
Cephei system does not contradict our current understanding of classical Be stars.
Key words: binaries: close - binaries: general - stars: emission-line, Be - stars: individual:
 Cephei
Cephei
1 Introduction
The well-studied object (Obj) Cephei(Obj) is a massive, pulsating star with a spectral type of early B (Hoffleit & Warren 1995). The star is the prototype of a class of early B type giants and subgiants that exhibit rapid radial velocity, photometric and line profile variations
due to pulsations (Sterken & Jerzykiewicz 1993).
Cephei(Obj) is a massive, pulsating star with a spectral type of early B (Hoffleit & Warren 1995). The star is the prototype of a class of early B type giants and subgiants that exhibit rapid radial velocity, photometric and line profile variations
due to pulsations (Sterken & Jerzykiewicz 1993).  Cep lies at a distance of
Cep lies at a distance of
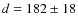 pc and has a visual magnitude of 3.2 (Perryman & ESA 1997). Donati et al. (2001) estimate that the star
has a bolometric magnitude of
pc and has a visual magnitude of 3.2 (Perryman & ESA 1997). Donati et al. (2001) estimate that the star
has a bolometric magnitude of
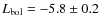 and a radius of
and a radius of
 .
Evolutionary tracks suggest that the star's mass is
.
Evolutionary tracks suggest that the star's mass is
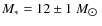 and that its age is approximately 12 Myr (Donati et al. 2001). As such it seems to be a fairly typical
and that its age is approximately 12 Myr (Donati et al. 2001). As such it seems to be a fairly typical  Cep star, as might be expected from the prototype of the class (Stankov & Handler 2005).
Cep star, as might be expected from the prototype of the class (Stankov & Handler 2005).
In fact,
 Cep is a tertiary system. A visual companion
lies at a distance of 13.4
Cep is a tertiary system. A visual companion
lies at a distance of 13.4
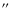 from the primary (Heintz 1978). The primary also has a closer, spectroscopic companion at a separation of approximately 0.25
from the primary (Heintz 1978). The primary also has a closer, spectroscopic companion at a separation of approximately 0.25
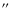 (Gezari et al. 1972). Hereafter, we refer to this star as the close companion and the primary of the system as
(Gezari et al. 1972). Hereafter, we refer to this star as the close companion and the primary of the system as  Cep. Little is known about the close companion. Measurements of the brightness difference between the primary and the close companion range from 5.0 mag to 1.8 mag
(Gezari et al. 1972; Balega et al. 2002). Catanzaro (2008) indirectly estimated the
Cep. Little is known about the close companion. Measurements of the brightness difference between the primary and the close companion range from 5.0 mag to 1.8 mag
(Gezari et al. 1972; Balega et al. 2002). Catanzaro (2008) indirectly estimated the 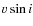 of the close companion to be
of the close companion to be 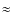 230 km s-1 and Pigulski & Boratyn (1992) estimated its mass to be
230 km s-1 and Pigulski & Boratyn (1992) estimated its mass to be 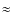
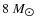 .
However, using the same orbital parameters but with a slightly reduced period Donati et al. (2001) conclude the secondary has a mass of
.
However, using the same orbital parameters but with a slightly reduced period Donati et al. (2001) conclude the secondary has a mass of
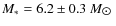 .
.
H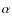 emission emanating from
emission emanating from 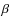 Cep was first reported by
Karpov (1932), and has since been found both absent and present
with a recurring timescale of approximately a decade
(Wilson & Seddon 1956; Kaper & Mathias 1995; Pan'ko & Tarasov 1997; Neiner et al. 2001). Such
episodic emission is typical of a classical Be star. However,
Cep was first reported by
Karpov (1932), and has since been found both absent and present
with a recurring timescale of approximately a decade
(Wilson & Seddon 1956; Kaper & Mathias 1995; Pan'ko & Tarasov 1997; Neiner et al. 2001). Such
episodic emission is typical of a classical Be star. However, 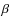 Cep is a slow rotator with a rotational period of 12 days and a
Cep is a slow rotator with a rotational period of 12 days and a 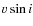 of approximately 25 km s-1(Telting et al. 1997; Henrichs et al. 2000). Be stars are typically rapid
rotators rotating at up to 80% of their break-up velocity
(Porter & Rivinius 2003). As this rapid rotation is thought to be
integral to the H
of approximately 25 km s-1(Telting et al. 1997; Henrichs et al. 2000). Be stars are typically rapid
rotators rotating at up to 80% of their break-up velocity
(Porter & Rivinius 2003). As this rapid rotation is thought to be
integral to the H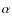 emission of Be stars, the H
emission of Be stars, the H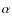 emission of
emission of 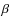 Cep is not consistent with the classical Be paradigm. Donati et al. (2001) proposed that the Be behaviour of the star is due to a magnetically confined wind leading
to shocks in the equatorial region (
Cep is not consistent with the classical Be paradigm. Donati et al. (2001) proposed that the Be behaviour of the star is due to a magnetically confined wind leading
to shocks in the equatorial region (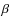 Cep does possess
an oblique magnetic field). However, if this were the case, the
H
Cep does possess
an oblique magnetic field). However, if this were the case, the
H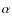 emission would be modulated by the rotation of the
star, and it is not (Schnerr et al. 2006). Thus the source of the
H
emission would be modulated by the rotation of the
star, and it is not (Schnerr et al. 2006). Thus the source of the
H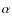 emission has posed a conundrum to our current
understanding of Be stars.
emission has posed a conundrum to our current
understanding of Be stars.
This enigma has been resolved by Schnerr et al. (2006), who used the
technique of spectroastrometry to show the H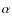 emission is in fact due to the close companion to
emission is in fact due to the close companion to 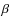 Cep. This
companion may well be a classical Be star and if this is the case the
contradictory nature of the system to current Be paradigms is
negated. Schnerr et al. (2006) used spectra in the R band about
H
Cep. This
companion may well be a classical Be star and if this is the case the
contradictory nature of the system to current Be paradigms is
negated. Schnerr et al. (2006) used spectra in the R band about
H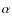 .
Here we use spectroastrometry to probe the blue
region of the companion's spectrum to test the hypothesis that the
close companion is a classical Be star.
.
Here we use spectroastrometry to probe the blue
region of the companion's spectrum to test the hypothesis that the
close companion is a classical Be star.
Spectroastrometry is a technique which utilises the spatial information present in a longslit spectrum. The information is contained in the spatial profile of the spectrum, specifically in the photocentre centroid and the spectral profile's width. Changes in the flux distribution as a function of wavelength are manifest by changes in the centroid and width of the spectrum. An unresolved binary system with one star dominating the flux at an emission line is revealed by a centroidal displacement towards the dominating star over this line. Conversely, if one star of the system has a strong absorption line in its spectrum the centroid of the spectral profile will shift to the other star over this line. Such signatures can be detected with high precision, of the order of 1 mas or less (Oudmaijer et al. 2008). Therefore this is a powerful technique with which to detect and study close binary systems, as shown by Baines et al. (2006).
The spectroastrometric signature of an unresolved binary system
contains information on the distribution of the flux emanating from
the system. Thus spectroastrometry can be not only be used to detect
binary systems, it can also deconvolve the observed spectrum into the
individual spectra of its components. Here we use this technique to
disentangle the spectra of the close 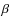 Cep binary components to investigate the properties of the close companion.
Cep binary components to investigate the properties of the close companion.
This paper is structured as follows: in Sect. 2 the details of the observations are presented, in Sect. 3 we present our spectroastrometric results, in Sect. 4 we discuss the spectra splitting methods and in Sect. 5 we present the results of splitting the spectra. A discussion and interpretation of the results follows in Sect. 6 and finally in Sect. 7 we summarise our findings.
2 Observations and data reduction
2.1 Observations
The data presented here were obtained using the 4.2 m William Herschel
Telescope (WHT) with the Intermediate Dispersion Spectrograph and Imaging System (ISIS) spectrograph. The data were obtained on the 7th of October 2006. Spectra of the 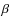 Cep system in the B (4200-5000 Å) and R (6200-6900 Å) bands were taken simultaneously using the dichoric slide of
ISIS. The slit width was to set to 5
Cep system in the B (4200-5000 Å) and R (6200-6900 Å) bands were taken simultaneously using the dichoric slide of
ISIS. The slit width was to set to 5
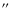 .
The R1200 and B1200
gratings were used and the resolving power of the spectrograph was
approximately 3800 (measured from telluric lines). The Marconi2 and
EEV12 CCDs were used on the red and blue arm respectively, each with a
pixel size of 13.5
.
The R1200 and B1200
gratings were used and the resolving power of the spectrograph was
approximately 3800 (measured from telluric lines). The Marconi2 and
EEV12 CCDs were used on the red and blue arm respectively, each with a
pixel size of 13.5
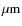 .
This resulted in angular pixel
scales of 0.20
.
This resulted in angular pixel
scales of 0.20
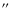 in the blue and 0.22
in the blue and 0.22
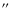 in the red region. As the average seeing during our observations was 1.27
in the red region. As the average seeing during our observations was 1.27
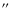 the spectral profile was well sampled, which is a requirement for accurate spectroastrometry (Bailey 1998).
the spectral profile was well sampled, which is a requirement for accurate spectroastrometry (Bailey 1998).
The data were gathered as part of wider study of binary systems. A
wide slit (5'') was used to ensure all the light from a given system entered the slit, despite the effect this had on the spectral resolution. Multiple spectra were taken at the following position angles (PA) on the sky: 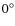 ,
,
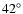 ,
,
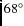 ,
,
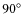 ,
,
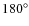 and
and
 .
Data were taken at a PA of
.
Data were taken at a PA of
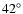 and
and
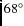 as Schnerr et al. (2006) suggested the binary was orientated at
as Schnerr et al. (2006) suggested the binary was orientated at 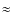
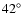 .
Dispersion calibration arcs were made using CuNe and CuAr lamps.
.
Dispersion calibration arcs were made using CuNe and CuAr lamps.
2.2 Data reduction
Data reduction was conducted using the Image Reduction and Analysis
Facility (IRAF)![]() and routines
written in Interactive Data Language (IDL). Flat field and bias frames
were combined and the averaged flat field was then normalised. The raw
data were then corrected using the averaged bias frame and the
normalised average flat frame. Saturated exposures were discarded. The
total intensity longslit spectra were then extracted from the
corrected data in a standard fashion. Wavelength calibration was
conducted using the arc spectra taken after the science observations
at a position angle of
and routines
written in Interactive Data Language (IDL). Flat field and bias frames
were combined and the averaged flat field was then normalised. The raw
data were then corrected using the averaged bias frame and the
normalised average flat frame. Saturated exposures were discarded. The
total intensity longslit spectra were then extracted from the
corrected data in a standard fashion. Wavelength calibration was
conducted using the arc spectra taken after the science observations
at a position angle of
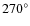 .
.
Spectroastrometry was performed by fitting Gaussian profiles to the spatial profile of the longslit spectra at each dispersion pixel. Spurious fits (for example due to cosmic rays) were identified and discarded, allowing the routine to fit the spectral profile. This resulted in a positional spectrum - the centroid of the Gaussian as a function of wavelength - and a FWHM (Full-Width-at-Half-Maximum) spectrum - the FWHM as a function of wavelength. The continuum position exhibited a general trend across the CCD chip (of the order of 10 pixels). This was removed by fitting a low order polynomial to the continuum regions of the spectrum. This set the continuum position of the centroid to zero. Spot checks were used to ensure line effects were not fit by the function.
A correction for slight changes in the dispersion was determined by cross correlating individual intensity spectra, and was then applied to the associated intensity, positional and FWHM spectra. This was to ensure slight changes in wavelength (due to flexure of the spectrograph) did not introduce spurious signatures when spectra obtained at differing position angles were combined. All intensity, positional and FWHM spectra at a given position angle were then combined to make an average spectrum for each position angle.
![\begin{figure}
\par\includegraphics[scale=0.75,clip]{1105fig1a.eps}\\
\includegraphics[scale=0.75,clip]{1105fig1b.eps}\\\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg46.png) |
Figure 1:
The average spectra of |
| Open with DEXTER | |
The average positional spectra for anti-parallel position angles were
combined to form the average North-South (NS) and East-West (EW)
positional spectra, i.e.: (
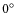 -
-
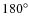 )/2 and
(
)/2 and
(
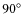 -
-
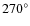 )/2. This procedure eliminates
instrumental artifacts as real signatures rotate by
)/2. This procedure eliminates
instrumental artifacts as real signatures rotate by
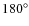 when viewed at the anti-parallel position angle while
artifacts remain at a constant orientation. However, in some of the
data a signature was noted at only one position angle. Subtraction of
the two anti-parallel spectra would not remove this effect but
clearly it is also an artifact. Thus all average position spectra
were assessed visually to exclude features only present at a single
position angle. Signatures in data taken at position angles with no
anti-parallel counterpart were judged real if they exhibited
qualitative similarity to signatures at a similar position angle that
were judged real. The FWHM spectra at opposite position angles were
visually inspected to search for artifacts. Features present in data
taken at only one position angle were classified as an artifact and
discarded. FWHM spectra at anti-parallel position angles were combined to make an average NS or EW FWHM spectrum.
when viewed at the anti-parallel position angle while
artifacts remain at a constant orientation. However, in some of the
data a signature was noted at only one position angle. Subtraction of
the two anti-parallel spectra would not remove this effect but
clearly it is also an artifact. Thus all average position spectra
were assessed visually to exclude features only present at a single
position angle. Signatures in data taken at position angles with no
anti-parallel counterpart were judged real if they exhibited
qualitative similarity to signatures at a similar position angle that
were judged real. The FWHM spectra at opposite position angles were
visually inspected to search for artifacts. Features present in data
taken at only one position angle were classified as an artifact and
discarded. FWHM spectra at anti-parallel position angles were combined to make an average NS or EW FWHM spectrum.
![\begin{figure}
\par\includegraphics[scale=0.3]{1105fig2a.eps}\hspace*{2mm}
\inc...
...fig2b.eps}\hspace*{2mm}
\includegraphics[scale=0.3]{1105fig2c.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg49.png) |
Figure 2:
The spectroastrometric signature of the close |
| Open with DEXTER | |
3 Results: The spectroastrometric signatures observed
3.1 The spectrum of  Cep
Cep
In Fig. 1 we present the average spectra observed in
both the B and R range. H can be
seen in absorption with a small double peaked emission profile, with
the blue peak just rising above the continuum level. The hydrogen
Balmer line profiles are also presented in the top panels of
Fig. 2. No emission is noticeable in the H
can be
seen in absorption with a small double peaked emission profile, with
the blue peak just rising above the continuum level. The hydrogen
Balmer line profiles are also presented in the top panels of
Fig. 2. No emission is noticeable in the H and H
and H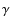 lines. Besides
lines. Besides
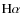 other
prominent lines in the red region are He I at
other
prominent lines in the red region are He I at 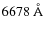 and a Diffuse Interstellar Band (DIB) at
and a Diffuse Interstellar Band (DIB) at 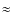 6280 Å. In the blue region many more absorption lines are present, most
prominent of which are the lines due to H I and He I. The
numerous weaker and narrow lines present are primarily due to O II, Si II, Si III and other ionised metals such as C II and N II.
6280 Å. In the blue region many more absorption lines are present, most
prominent of which are the lines due to H I and He I. The
numerous weaker and narrow lines present are primarily due to O II, Si II, Si III and other ionised metals such as C II and N II.
3.2 The spectroastrometric results
The spectroastrometric signatures of the close  Cep
binary system over the three principle hydrogen Balmer lines are
presented in Fig. 2. For each line we present:
the intensity profile and the centroidal signature and change in the
FWHM of the longslit spectra over these lines in the NS and EW
directions. The photocentre of the spectral profile shifts to the
North and East and the FWHM increases over these lines. This means we
clearly detect the close binary system - something not trivial in
seeing conditions of greater than 1
Cep
binary system over the three principle hydrogen Balmer lines are
presented in Fig. 2. For each line we present:
the intensity profile and the centroidal signature and change in the
FWHM of the longslit spectra over these lines in the NS and EW
directions. The photocentre of the spectral profile shifts to the
North and East and the FWHM increases over these lines. This means we
clearly detect the close binary system - something not trivial in
seeing conditions of greater than 1
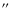 .
The signature is most
prominent over the
.
The signature is most
prominent over the
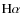 line while small and consistent
features can be noted across H
line while small and consistent
features can be noted across H and
and
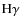 .
The spectroastrometric signature observed over the emission
component of the H
.
The spectroastrometric signature observed over the emission
component of the H profile implies that the source of
the emission lies to the North-East (NE) and the emission profile is
intrinsically broader than the absorption profile. This confirms the
result of Schnerr et al. (2006), i.e. the H
profile implies that the source of
the emission lies to the North-East (NE) and the emission profile is
intrinsically broader than the absorption profile. This confirms the
result of Schnerr et al. (2006), i.e. the H emission
is emanating from the companion in the NE and not the primary.
emission
is emanating from the companion in the NE and not the primary.
![\begin{figure}
\par\includegraphics[scale=0.25]{1105fig3a.eps}\includegraphics[s...
...0.25]{1105fig3b.eps}\includegraphics[scale=0.25]{1105fig3c.eps}\\\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg51.png) |
Figure 3:
XY plots of the spectroastrometric signature of the close |
| Open with DEXTER | |
Across the
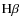 and H
and H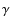 lines the
positional excursions occur in the same direction as over H
lines the
positional excursions occur in the same direction as over H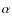 .
As these signatures take place across an absorption line
this indicates that the South-West (SW) component of the system
``dominates'' the absorption profile. In addition narrow positional
excursions to the NE and FWHM increases can be seen over the lines
seen alongside H
.
As these signatures take place across an absorption line
this indicates that the South-West (SW) component of the system
``dominates'' the absorption profile. In addition narrow positional
excursions to the NE and FWHM increases can be seen over the lines
seen alongside H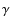 (primarily O II
lines). This indicates that these lines are associated with the SW
component of the system, the primary. These data highlight the
exquisite sensitivity of spectroastrometry to changes in the flux
distribution. Changes in the photocentre of the order of 5 mas or less are detected. The noise in the positional spectra is typically of the order of 1 mas.
(primarily O II
lines). This indicates that these lines are associated with the SW
component of the system, the primary. These data highlight the
exquisite sensitivity of spectroastrometry to changes in the flux
distribution. Changes in the photocentre of the order of 5 mas or less are detected. The noise in the positional spectra is typically of the order of 1 mas.
The ``XY plots'' (NS against EW excursions) of the  Cep
system are presented in Fig. 3. The XY plots trace a
straight line to the North and East - the direction in which the
source of the H
Cep
system are presented in Fig. 3. The XY plots trace a
straight line to the North and East - the direction in which the
source of the H emission lies. The position angle of
the binary is determined from a simple least-squares fit to the data, and is
in general consistent across the different lines (
emission lies. The position angle of
the binary is determined from a simple least-squares fit to the data, and is
in general consistent across the different lines (
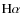 :
:
 ,
,
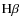 :
:
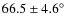 &
&
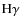 :
:
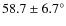 ). However, the H
). However, the H position angle is not
consistent with the H
position angle is not
consistent with the H data. The H
data. The H and
H
and
H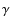 lines were associated with much weaker positional
excursions and as such these position angles are more uncertain than
the position angle derived from the H
lines were associated with much weaker positional
excursions and as such these position angles are more uncertain than
the position angle derived from the H data.
data.
4 Splitting the spectra
Two approaches were used to split entangled/composite binary spectra. The first approach was pioneered by Bailey (1998). This method utilises the fact that the changes in the flux ratio of a binary system lead to positional displacements of the photocentre. The movement of the photocentre across a given wavelength is proportional to the component separation and the component flux ratio at the particular wavelength. This centroid movement takes place about the continuum position, which is determined by the continuum brightness ratio of the two components. Therefore if the separation and the continuum flux ratio of the two components are known the intensity spectra and positional spectra observed can used to disentangle the individual fluxes of the two components.
The second approach, that of Porter et al. (2004), does not require
any prior knowledge of the binary system. This method not only
deconvolves spectra, it also estimates the separation of the two
binary components. This method is based upon numerical simulations of
point source binary systems performed by Porter et al. (2004). Porter et al. (2004) determined the dependence of the spectroastrometric signature of a given binary on the system's
properties. Using the relationships established by these simulations
one can use the three spectroastrometric observables (the centroid,
total flux and width at a given
 ), with knowledge of
the seeing, to recover the individual fluxes of the binary components. For a full description of the method see Porter et al. (2004).
), with knowledge of
the seeing, to recover the individual fluxes of the binary components. For a full description of the method see Porter et al. (2004).
![\begin{figure}
\par\includegraphics[scale=1]{1105fig4.ps}
\par\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg57.png) |
Figure 4:
The red spectrum of the close |
| Open with DEXTER | |
We have used both methods for two reasons. Firstly there are certain
limitations to the method of Porter et al. (2004). We found accurate
knowledge of the seeing was essential, something not trivial in this
case. To test the reliability of the method of Porter et al. (2004) we
applied this method on simulated data. It was found that with accurate
knowledge of the seeing this method consistently returned the
separation of the two point sources and their respective fluxes, to
within an error of 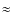 10% or better. However, when
adopting the minimum FWHM as an estimate of the seeing (which is
actually an upper limit) the method can under estimate the
separation. While we expect this effect to be small we treat our
estimate of
10% or better. However, when
adopting the minimum FWHM as an estimate of the seeing (which is
actually an upper limit) the method can under estimate the
separation. While we expect this effect to be small we treat our
estimate of
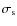 with caution and use the method of
Bailey (1998) as a consistency check.
with caution and use the method of
Bailey (1998) as a consistency check.
Secondly, we do not just use the method of Bailey (1998) as although we can find literature values for the difference in brightness of the two components and their separation, none are certain. The difference in magnitude reported ranges from 1.8 to 5.0 (Gezari et al. 1972; Balega et al. 2002) while the separation changes slowly due to the motion of the binary system. The orbit has been determined by Pigulski & Boratyn (1992). However this orbit is not consistent with our results and those of Schnerr et al. (2006) (see Sect. 6.2). Therefore, we do not use the orbital parameters of Pigulski & Boratyn (1992) to estimate the position of the secondary. Thus we used each method as a consistency check upon the other.
4.1 The method of Bailey (1998)
The method of Bailey (1998) uses two
spectroastrometric observables (centroidal excursions and the
total flux observed) and two inputs (binary projected separation and
difference in brightness). Three values for the difference in
brightness between the binary components were taken from the
literature: 1.82 mag at
 Å, a
rough average value of 3.4 mag around 5500 Å and 5 mag at 5000 Å (Gezari et al. 1972; Balega et al. 2002; Hartkopf et al. 2001). Distances in
the literature between the primary and the secondary range from
Å, a
rough average value of 3.4 mag around 5500 Å and 5 mag at 5000 Å (Gezari et al. 1972; Balega et al. 2002; Hartkopf et al. 2001). Distances in
the literature between the primary and the secondary range from
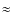
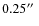 to 0.04
to 0.04
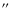 .
The most recent
observation of the system was in 1998, and thus the position of the
secondary in 2006 is uncertain.
.
The most recent
observation of the system was in 1998, and thus the position of the
secondary in 2006 is uncertain.
![\begin{figure}
\par\includegraphics[scale=1]{1105fig5.ps}
\par\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg60.png) |
Figure 5:
The blue spectrum of the close |
| Open with DEXTER | |
We used a range of distances (0.05
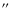 to 0.25
to 0.25
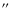 )
with each of
the magnitude differences listed above, and evaluated the results
based on the following criteria. Any input parameters
leading to negative flux in the secondary spectra were immediately
disregarded. Also situations where absorption lines in the primary
were mirrored by an emission line in the secondary spectra were
considered unlikely.
)
with each of
the magnitude differences listed above, and evaluated the results
based on the following criteria. Any input parameters
leading to negative flux in the secondary spectra were immediately
disregarded. Also situations where absorption lines in the primary
were mirrored by an emission line in the secondary spectra were
considered unlikely.
![\begin{figure}
\par\includegraphics[scale=1]{1105fig6.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg62.png) |
Figure 6:
The red spectrum of the close |
| Open with DEXTER | |
In the red region a brightness difference of 5 mag was
discarded as it resulted in secondary spectra with negative flux. A
difference in brightness of 3.4 mag was discounted as this led
to secondary spectra with He I 6678 Å in emission, an
uncommon occurrence in field stars. Using 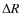 of 1.8 with a
range of separations did not result in a significant constraint upon
the separation of the two components. A separation of 0.05
of 1.8 with a
range of separations did not result in a significant constraint upon
the separation of the two components. A separation of 0.05
 was
discarded as this resulted in He I emission in the secondary
spectrum. Separations of 0.1
was
discarded as this resulted in He I emission in the secondary
spectrum. Separations of 0.1
 to 0.15
to 0.15
 resulted in a
secondary spectrum devoid of any He I 6678 Å feature while separations of 0.20
resulted in a
secondary spectrum devoid of any He I 6678 Å feature while separations of 0.20
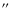 and 0.25
and 0.25
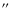 led to a secondary spectra with a He I 6678 Å absorption
feature. If the secondary is a mid B type star the presence of
He I 6678 Å is to be expected, but the absence of a
He I feature is consistent with a late type B star. Both
spectral types are possible and thus the binary separation is not
constrained beyond the range 0.05
led to a secondary spectra with a He I 6678 Å absorption
feature. If the secondary is a mid B type star the presence of
He I 6678 Å is to be expected, but the absence of a
He I feature is consistent with a late type B star. Both
spectral types are possible and thus the binary separation is not
constrained beyond the range 0.05
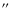 and 0.25
and 0.25
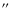 .
.
In Fig. 4 we present the average red spectra of
the close  Cep binary system, split using the method of
Bailey (1998), a brightness difference of 1.8 mag and
separations of 0.05'', 0.15'' and 0.25''. It is evident that the H
Cep binary system, split using the method of
Bailey (1998), a brightness difference of 1.8 mag and
separations of 0.05'', 0.15'' and 0.25''. It is evident that the H emission is associated with the secondary. The double peaked H
emission is associated with the secondary. The double peaked H emission profile is typical of rapidly rotating classical Be stars.
emission profile is typical of rapidly rotating classical Be stars.
When splitting the blue spectra differences in brightness between the
two binary components of 5.0 and 3.4 were discarded due to similar
arguments as presented above. Thus it appears the brightness
difference between the two binary components in the B band is
approximately 1.8 mag, as in the R band. In Fig. 5 we present the spectra obtained with this value of 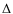 B and a separation of 0.20
B and a separation of 0.20
 .
The many
narrow absorption lines present in the composite spectrum
(O II, Si III etc.) are clearly associated with the
primary spectrum. Also evident is that the He I absorption
lines are weaker in the secondary spectrum than in the primary
spectrum. The secondary spectra obtained using smaller separations
were judged to be of dubious validity as they exhibited many emission
features coincident with absorption features in the primary
spectrum.
.
The many
narrow absorption lines present in the composite spectrum
(O II, Si III etc.) are clearly associated with the
primary spectrum. Also evident is that the He I absorption
lines are weaker in the secondary spectrum than in the primary
spectrum. The secondary spectra obtained using smaller separations
were judged to be of dubious validity as they exhibited many emission
features coincident with absorption features in the primary
spectrum.
4.2 The method of Porter et al. (2004)
The model of Porter et al. (2004) is based on a constant
convolving function, yet a change in focus along the chip length led
to a change in the width of the flux distribution. To negate this
difficulty the 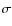 distribution was normalised via a
polynomial fit to remove changes not due to the binary system. The
mean seeing was estimated from the minimum of the now flattened FWHM
spectrum. However, this estimate of the seeing is an upper
estimate. Simulating a binary system with a separation of 0.20
distribution was normalised via a
polynomial fit to remove changes not due to the binary system. The
mean seeing was estimated from the minimum of the now flattened FWHM
spectrum. However, this estimate of the seeing is an upper
estimate. Simulating a binary system with a separation of 0.20
 and a difference in brightness of 1.8 mag we found the minimum
FWHM may over estimate the seeing by 0.02 pixels. Thus we
subtracted this from our estimate of the seeing using the FWHM
minimum.
and a difference in brightness of 1.8 mag we found the minimum
FWHM may over estimate the seeing by 0.02 pixels. Thus we
subtracted this from our estimate of the seeing using the FWHM
minimum.
In Fig. 6 we present the red spectrum of the  Cep system split using the method of Porter et al. (2004). The spectrum exhibits a close similarity to the
spectrum obtained using the method of Bailey (1998) and similar parameters as those output by the method of Porter et al. (2004).
Cep system split using the method of Porter et al. (2004). The spectrum exhibits a close similarity to the
spectrum obtained using the method of Bailey (1998) and similar parameters as those output by the method of Porter et al. (2004).
Applying the method of Porter et al. (2004) to the blue spectra did not result in separated spectra, as the model did not converge upon the most likely separation. This could be due to a lack of prominent features in the position spectra. The precision of the blue position spectra was no worse than that in the red spectra (of the order of 1 mas). However, the positional offsets in the blue region are much smaller than in those in the red region as the flux difference in the blue region is less pronounced than that over the H line.
line.
5 Results: the separated spectra
5.1 The spectral types of the binary components
The spectral type of  Cep has been estimated to be both
B1 and B2 while the luminosity class of the star has been reported to
be III, IV and V
(Morgan et al. 1955; Lesh 1968; Morel et al. 2006; Morgan et al. 1943). These spectral
classifications refer to the total light of the system. As we have
disentangled the spectra of the binary components we can now
spectrally type each component separately. The spectrum of the binary
system has also been designated `e & v' where e refers to the
emission nature and v the variability of the spectrum. We assume the
that the primary is responsible for the variability of the spectrum
due to its pulsating nature. To determine the spectral type of
the binary components we use the spectra that were separated with the
method of Bailey (1998), a brightness difference of 1.8 mag and a separation of 0.2''.
Cep has been estimated to be both
B1 and B2 while the luminosity class of the star has been reported to
be III, IV and V
(Morgan et al. 1955; Lesh 1968; Morel et al. 2006; Morgan et al. 1943). These spectral
classifications refer to the total light of the system. As we have
disentangled the spectra of the binary components we can now
spectrally type each component separately. The spectrum of the binary
system has also been designated `e & v' where e refers to the
emission nature and v the variability of the spectrum. We assume the
that the primary is responsible for the variability of the spectrum
due to its pulsating nature. To determine the spectral type of
the binary components we use the spectra that were separated with the
method of Bailey (1998), a brightness difference of 1.8 mag and a separation of 0.2''.
The presence of He I absorption in the red spectrum of the
primary indicates a B type star. The equivalent widths of the
H and He I absorption features suggest that
the primary is an early B (1-3) type star, with a luminosity class of IV or III. In the blue region the primary spectrum exhibits prominent
H I absorption lines (
and He I absorption features suggest that
the primary is an early B (1-3) type star, with a luminosity class of IV or III. In the blue region the primary spectrum exhibits prominent
H I absorption lines (
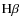 and
and
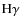 )
alongside He I absorption lines, which indicates a B type
star. The relatively strong He I lines and comparatively weak
H I lines indicate that the primary is an early B type star
(i.e. B0 to B2). Additional features in the primary spectrum include
absorption lines due to He I, O II, Si III,
C II, C III and N II, lines which are also
suggestive of an early B type star. No He II lines are
present, implying the star has a spectral type later than O9. The
ratio of the He I 4471
)
alongside He I absorption lines, which indicates a B type
star. The relatively strong He I lines and comparatively weak
H I lines indicate that the primary is an early B type star
(i.e. B0 to B2). Additional features in the primary spectrum include
absorption lines due to He I, O II, Si III,
C II, C III and N II, lines which are also
suggestive of an early B type star. No He II lines are
present, implying the star has a spectral type later than O9. The
ratio of the He I 4471 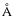 /Mg II 4481
/Mg II 4481
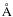 lines indicate the star is an early B type star, most
probably B2. To determine the luminosity class of the star the ratios
of the O II 4415 Å& 4417 Å to
He I 4387 Å and O II 4348 Å to
H
lines indicate the star is an early B type star, most
probably B2. To determine the luminosity class of the star the ratios
of the O II 4415 Å& 4417 Å to
He I 4387 Å and O II 4348 Å to
H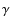 lines were used. The strength of the O II
lines indicates that the primary's luminosity class is most probably III.
lines were used. The strength of the O II
lines indicates that the primary's luminosity class is most probably III.
To summarise, the spectral type of the primary was determined to be B2III. The uncertainty associated with this conclusion is approximately one spectral subtype.
The most prominent feature in the red spectrum of the secondary is
that of the H emission. The H
emission. The H emission
extends approximately
emission
extends approximately 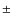 400 km s-1 from
the rest wavelength of H
400 km s-1 from
the rest wavelength of H ,
as also found by
Schnerr et al. (2006). A Gaussian fit to the
,
as also found by
Schnerr et al. (2006). A Gaussian fit to the
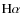 emission profile results in a value for the FWHM of the profile of
emission profile results in a value for the FWHM of the profile of
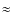 500 km s-1. This width is typical of a
rapidly rotating Be star. A He I 6678 Å absorption feature is present, although weak, with an equivalent width of
500 km s-1. This width is typical of a
rapidly rotating Be star. A He I 6678 Å absorption feature is present, although weak, with an equivalent width of 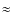 0.25 Å. This places an upper limit on the spectral type of about B4/B5.
0.25 Å. This places an upper limit on the spectral type of about B4/B5.
The secondary spectrum in the blue does not display the many narrow
absorption features due to O II and Si III the primary
does. Thus there is no reason to suspect it is not a dwarf star. The
spectrum of the secondary in the blue region exhibits absorption lines
due to H I (
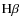 and
and
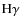 )
and
He I (i.e. 4388, 4471 Å). This is indicative of a
B type star. The He I lines are weaker than than those in the
spectrum of the primary (equivalent widths are approximately 15%
less) which suggests the secondary is of a later spectral type than
the primary. This is to be expected as it is less bright. In contrast,
the H I lines in the secondary are of a similar strength to
those in the primary, indicating an early B type star. However, as the
secondary shows emission in H
)
and
He I (i.e. 4388, 4471 Å). This is indicative of a
B type star. The He I lines are weaker than than those in the
spectrum of the primary (equivalent widths are approximately 15%
less) which suggests the secondary is of a later spectral type than
the primary. This is to be expected as it is less bright. In contrast,
the H I lines in the secondary are of a similar strength to
those in the primary, indicating an early B type star. However, as the
secondary shows emission in H it is possible there is
some emission in H
it is possible there is
some emission in H and H
and H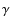 which ``fills
in'' the absorption profile of the secondary. Concentrating on the
strength of the He I lines, and the ratio of He I/Mg II (4471/4481 Å) lines, we conclude the most likely spectral type of the secondary is B5.
which ``fills
in'' the absorption profile of the secondary. Concentrating on the
strength of the He I lines, and the ratio of He I/Mg II (4471/4481 Å) lines, we conclude the most likely spectral type of the secondary is B5.
Therefore the spectral type of the secondary is determined to be B5Ve. The uncertainty in this spectral typing is again approximately one spectral subtype.
In determining the spectral type of the secondary we assume
that all the flux observed emanates directly from the star in question
and the spectral features observed are purely photospheric in their
origin. To asses the possible flux contribution from circumstellar
material we use the NIR study of Dougherty et al. (1991). In most cases
mid type Be stars were found to have a small V-J excess, the average
(V-J) excess of a B5Ve star according to Dougherty et al. (1991) is only
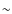 6% of the stellar continuum. In addition the continuum excess
falls off very sharply with decreasing wavelengths. Therefore we
expect the continuum excess due to any circumstellar material to be
negligible at optical wavelengths. Regarding emission lines there may
well be unresolved H I lines in the secondary spectrum
therefore we do not rely on the strength of the H I lines to
determine the spectral type of the secondary. There may also be some
emission component in the He I lines. However, in a study of
more than 100 Be stars over a period of 10 years Chauville et al. (2001)
did not observe any Be star with net He I 4471 Å emission. Therefore, in light of the above comments, we assume that the He I lines observed are photospheric in origin.
6% of the stellar continuum. In addition the continuum excess
falls off very sharply with decreasing wavelengths. Therefore we
expect the continuum excess due to any circumstellar material to be
negligible at optical wavelengths. Regarding emission lines there may
well be unresolved H I lines in the secondary spectrum
therefore we do not rely on the strength of the H I lines to
determine the spectral type of the secondary. There may also be some
emission component in the He I lines. However, in a study of
more than 100 Be stars over a period of 10 years Chauville et al. (2001)
did not observe any Be star with net He I 4471 Å emission. Therefore, in light of the above comments, we assume that the He I lines observed are photospheric in origin.
5.2 The mass ratio of the close binary system
Taking the spectral type of the primary to be B2III and that of the
secondary to be B5V and using the tabulated values of Landolt et al. (1982)
and Harmanec (1988) we obtain values for the masses of
the components of the system of
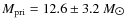 and
and
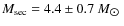 respectively. Uncertainties were estimated by allowing an uncertainty
in the spectral types of one subtype. The mass ratio of the system is
determined to be
respectively. Uncertainties were estimated by allowing an uncertainty
in the spectral types of one subtype. The mass ratio of the system is
determined to be
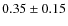 .
.
5.3 The v sin i of the individual binary components
Using the separated spectra the 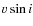 values of each component of
the binary system can be estimated. A rotational profile was
constructed for a variety of
values of each component of
the binary system can be estimated. A rotational profile was
constructed for a variety of 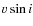 values: from 1 to 550 km s-1 in steps of 1 km s-1. The rotation profile was then convolved with synthetic spectra constructed
using ATLAS9 and SYNTHE (Kurucz 1993)
values: from 1 to 550 km s-1 in steps of 1 km s-1. The rotation profile was then convolved with synthetic spectra constructed
using ATLAS9 and SYNTHE (Kurucz 1993)![]() . Following the
convolution of the rotational profile and the synthetic spectra the
resultant spectra were broadened by convolution with a Gaussian
function to match the spectral resolution. The rotationally broadened
profile of the He I 4471 Å line was then compared
with the observed profile using a simple
. Following the
convolution of the rotational profile and the synthetic spectra the
resultant spectra were broadened by convolution with a Gaussian
function to match the spectral resolution. The rotationally broadened
profile of the He I 4471 Å line was then compared
with the observed profile using a simple 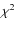 test.
test.
For the primary synthetic spectra were constructed using values of
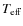 of 23 000 K, 24 000 K and 25 000 K and
of 23 000 K, 24 000 K and 25 000 K and 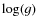 of 3.8.
These values were based on the values determined by
Catanzaro (2008) and the spectral type determined previously. To
simulate the spectrum of the secondary synthetic spectra were
constructed using values of
of 3.8.
These values were based on the values determined by
Catanzaro (2008) and the spectral type determined previously. To
simulate the spectrum of the secondary synthetic spectra were
constructed using values of
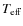 of 14 000 K, 15 000 K,
16 000 K and 17 000 K and
of 14 000 K, 15 000 K,
16 000 K and 17 000 K and 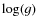 of 4.1. These values are based on a
B5 type dwarf star on the Main Sequence
(Harmanec 1988). The range of temperatures used reflects
the uncertainty in the spectral typing. A micro-turbulence of 2 km s-1 was used in the synthetic spectra
generation, and when constructing the rotational profiles a
limb-darkening coefficient of 0.6 was assumed.
of 4.1. These values are based on a
B5 type dwarf star on the Main Sequence
(Harmanec 1988). The range of temperatures used reflects
the uncertainty in the spectral typing. A micro-turbulence of 2 km s-1 was used in the synthetic spectra
generation, and when constructing the rotational profiles a
limb-darkening coefficient of 0.6 was assumed.
![\begin{figure}
\par\includegraphics[scale=0.3,clip]{1105fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg77.png) |
Figure 7:
A comparison between the spectroastrometrically separated He I 4471 Å profiles and the best fit rotationally broadened synthetic profiles. The solid line represents the He I line of the primary and secondary spectra respectively, the short-long dashed line the best fit primary synthetic spectrum (
|
| Open with DEXTER | |
The best fit 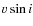 values obtained are dependent upon the value
of
values obtained are dependent upon the value
of
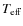 used to generate the synthetic spectrum. This is
because the depth of the He I line increases towards earlier
types. With the previous spectral typing an error in
used to generate the synthetic spectrum. This is
because the depth of the He I line increases towards earlier
types. With the previous spectral typing an error in
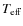 of
of 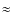 1000 K possible. However, the input
1000 K possible. However, the input
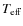 does not effect the width of the convolved profile. Thus the most likely value of
does not effect the width of the convolved profile. Thus the most likely value of
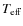 is the one for which the
rotationally broadened synthetic spectrum matches not only the height but also the width of the observed profile at a given value of
is the one for which the
rotationally broadened synthetic spectrum matches not only the height but also the width of the observed profile at a given value of 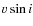 (i.e. that associated with the smallest
(i.e. that associated with the smallest 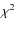 ). This effect is illustrated in Fig. 7 by plotting the best fit
rotationally broadened profiles at 15 000 K and 17 000 K over the secondary profile. The best fit at 15 000 K fails to fit the width and depth of the observed profile, which was reflected in the
large value for the minimum
). This effect is illustrated in Fig. 7 by plotting the best fit
rotationally broadened profiles at 15 000 K and 17 000 K over the secondary profile. The best fit at 15 000 K fails to fit the width and depth of the observed profile, which was reflected in the
large value for the minimum 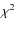 at this temperature. The best fit
at this temperature. The best fit 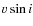 values were lower for lower values of
values were lower for lower values of
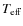 and ranged from
and ranged from
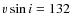 km s-1 at
km s-1 at
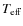 of 14 000 K to
of 14 000 K to
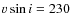 km s-1 at
km s-1 at
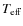 of 17 000 K. The lowest
of 17 000 K. The lowest
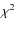 values were obtained with a
values were obtained with a
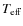 of 24 000 K in
the case of the primary and 17 000 K in the case of the secondary. We
determine that the primary has a
of 24 000 K in
the case of the primary and 17 000 K in the case of the secondary. We
determine that the primary has a 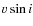 of
29+43-29 km s-1 and the secondary has a
of
29+43-29 km s-1 and the secondary has a 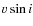 of
of
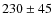 km s-1. The uncertainties in these values were determined from the change in
km s-1. The uncertainties in these values were determined from the change in 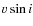 of the synthetic spectra which led to an increase in the
of the synthetic spectra which led to an increase in the 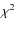 of the fit of 1. We note that the secondary profile was best fit using a B4 star profile (
of the fit of 1. We note that the secondary profile was best fit using a B4 star profile (
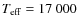 K), rather than a B5 profile. This is consistent with an uncertainty of 1 subtype in the spectral type of the secondary.
K), rather than a B5 profile. This is consistent with an uncertainty of 1 subtype in the spectral type of the secondary.
6 Discussion
6.1 The v sin i of the individual binary components
The 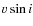 of the primary is consistent with literature values of
around 25 km s-1 (Telting et al. 1997), although it is
imprecise. This imprecision is due to the use of a relatively wide
slit resulting in an instrumental profile with a FWHM of
of the primary is consistent with literature values of
around 25 km s-1 (Telting et al. 1997), although it is
imprecise. This imprecision is due to the use of a relatively wide
slit resulting in an instrumental profile with a FWHM of 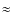 70 km s-1. The
70 km s-1. The 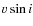 value for the secondary is similarly imprecise. However, it is clear that the
secondary does rotate substantially faster than the primary, in agreement with the estimate of
value for the secondary is similarly imprecise. However, it is clear that the
secondary does rotate substantially faster than the primary, in agreement with the estimate of 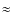 230 km s-1 of Catanzaro (2008).
230 km s-1 of Catanzaro (2008).
Given the spectral type of the secondary it's critical velocity is
approximately 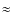 430 km s-1 (Townsend et al. 2004). It is suggested that the orbit of the
430 km s-1 (Townsend et al. 2004). It is suggested that the orbit of the  Cep system is seen almost edge on (Pigulski & Boratyn 1992, see also Sect. 6.2). If the stars rotate in the plane of the orbit, which is not necessarily the case, then the above
Cep system is seen almost edge on (Pigulski & Boratyn 1992, see also Sect. 6.2). If the stars rotate in the plane of the orbit, which is not necessarily the case, then the above 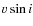 values are the intrinsic rotation velocities of the stars. In this case the rotational velocity of the secondary is 45-65% of its critical velocity. This rotation may not be consistent with the hypothesis that the secondary is a classical Be star.
values are the intrinsic rotation velocities of the stars. In this case the rotational velocity of the secondary is 45-65% of its critical velocity. This rotation may not be consistent with the hypothesis that the secondary is a classical Be star.
Whether or not all Be stars rotate at their break-up velocity
is currently a matter or some debate, with arguments both for
(Townsend et al. 2004) and against (Cranmer 2005) this
scenario. However, it is generally accepted that all Be stars rotate
at a substantial fraction of their break-up velocity. To prove
the secondary is rotating at/near its critical velocity we need an
independent determination of its inclination, which is far from
trivial. In addition even if i was constrained, this 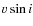 measurement would not be conclusive. It has been shown the method used
here to determine
measurement would not be conclusive. It has been shown the method used
here to determine 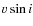 returns a lower limit as it does not
account for gravity darkening (Townsend et al. 2004). However, the
secondary is shown to be rotating relatively fast, even at the
lower limit of
returns a lower limit as it does not
account for gravity darkening (Townsend et al. 2004). However, the
secondary is shown to be rotating relatively fast, even at the
lower limit of
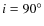 ,
and it may be rotating at a substantial fraction of its break-up velocity. This is essentially consistent with the finding of Porter (1996) who demonstrated Be stars intrinsically rotate at approximately 70% of their break-up velocity (using a similar technique to estimate
,
and it may be rotating at a substantial fraction of its break-up velocity. This is essentially consistent with the finding of Porter (1996) who demonstrated Be stars intrinsically rotate at approximately 70% of their break-up velocity (using a similar technique to estimate 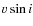 ). Therefore it is indeed likely the secondary is a classical Be star.
). Therefore it is indeed likely the secondary is a classical Be star.
6.2 The orbit of 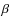 Cephei
Cephei
The orbit of the close companion to 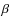 Cep has been
determined by Pigulski & Boratyn (1992). However, both the results
presented here and by Schnerr et al. (2006) suggest a revision of the
orbital parameters is required. According to the orbit of Pigulski & Boratyn (1992) the companion to
Cep has been
determined by Pigulski & Boratyn (1992). However, both the results
presented here and by Schnerr et al. (2006) suggest a revision of the
orbital parameters is required. According to the orbit of Pigulski & Boratyn (1992) the companion to 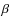 Cep should have been to the SW of the primary in 2006. The data presented here, and by Schnerr et al. (2006) are not consistent with this prediction. As the spectroastrometric data proves the H
Cep should have been to the SW of the primary in 2006. The data presented here, and by Schnerr et al. (2006) are not consistent with this prediction. As the spectroastrometric data proves the H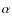 emission is emanating from the close companion, the data place the companion to the NE of the primary in 2006.
emission is emanating from the close companion, the data place the companion to the NE of the primary in 2006.
Here we investigate whether a slight change of orbital parameters can
result in an orbit consistent with observations. It was found the data
allow a straight line fit, which implies that the system is viewed at
a very high inclination, i.e. 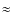
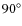 .
From a
least-squared fit to the data we obtain a value for the position angle
of the line of nodes to be
.
From a
least-squared fit to the data we obtain a value for the position angle
of the line of nodes to be
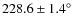 .
We took
the date of 1914.6 as our reference periastron, as did
Pigulski & Boratyn (1992). For the period of the orbit we considered the
suggestion of Hadrava & Harmanec (1996) that the system was
approaching periastron in 1996. This period of 81.4 years differs from
the value used by Pigulski & Boratyn (1992) but is within 3
.
We took
the date of 1914.6 as our reference periastron, as did
Pigulski & Boratyn (1992). For the period of the orbit we considered the
suggestion of Hadrava & Harmanec (1996) that the system was
approaching periastron in 1996. This period of 81.4 years differs from
the value used by Pigulski & Boratyn (1992) but is within 3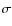 of their value. The semi-major axis of the orbit was estimated via
Kepler's third law, the above period and the total mass of the
system. With the data at our disposal constraining e and
of their value. The semi-major axis of the orbit was estimated via
Kepler's third law, the above period and the total mass of the
system. With the data at our disposal constraining e and  is difficult. We set e at 0.6 and investigated what value of
is difficult. We set e at 0.6 and investigated what value of  was required to fit the observational data, given the
parameters determined above. We found a value of
was required to fit the observational data, given the
parameters determined above. We found a value of  of
of
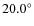 fit the data well (see Fig. 8).
fit the data well (see Fig. 8).
The final orbital parameters used were:
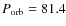 yr, e=0.60,
T0=1914.6,
yr, e=0.60,
T0=1914.6,
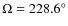 ,
,
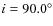 ,
a=0.25'' and
,
a=0.25'' and
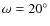 .
Most parameters are within 3
.
Most parameters are within 3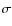 of the values of (Pigulski & Boratyn 1992). The orbit is consistent with
previous speckle interferometric observations of the system and our
spectroastrometrically determined position of the
secondary. Admittedly, systems are rarely observed at an inclination
of exactly
of the values of (Pigulski & Boratyn 1992). The orbit is consistent with
previous speckle interferometric observations of the system and our
spectroastrometrically determined position of the
secondary. Admittedly, systems are rarely observed at an inclination
of exactly
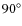 .
Changing the inclination by up to a
few degrees does little to qualitatively change the picture. Provided
.
Changing the inclination by up to a
few degrees does little to qualitatively change the picture. Provided  is revised in light of any inclination changes, a consistent fit to the data is achieved when i is changed by a few
degrees (see Fig. 8). We stress such an orbit is only illustrative, and more observations are needed to fully constrain all the orbital parameters. However, we successfully demonstrate a slight revision of the orbital parameters of Pigulski & Boratyn (1992) is all that
is required to obtain an orbit consistent with observations.
is revised in light of any inclination changes, a consistent fit to the data is achieved when i is changed by a few
degrees (see Fig. 8). We stress such an orbit is only illustrative, and more observations are needed to fully constrain all the orbital parameters. However, we successfully demonstrate a slight revision of the orbital parameters of Pigulski & Boratyn (1992) is all that
is required to obtain an orbit consistent with observations.
![\begin{figure}
\par\includegraphics[scale=0.3]{1105fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg92.png) |
Figure 8:
A possible relative orbit of the companion of the close |
| Open with DEXTER | |
7 Conclusions
In this paper we have studied the close binary system of 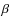 Cep utilising the novel approach of splitting the binary spectra using spectroastrometry. Disentangling the composite
binary spectrum allows us to determine key properties of each
component. We find that the H
Cep utilising the novel approach of splitting the binary spectra using spectroastrometry. Disentangling the composite
binary spectrum allows us to determine key properties of each
component. We find that the H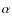 emission of the system
is due to the close secondary, as shown by Schnerr et al. (2006). Splitting the convolved spectrum and assessing the spectral type of each component we find that the companion is a
dwarf star with a spectral type of B5. We also find it may rotate at a substantial fraction of its critical velocity, with a lower limit of
emission of the system
is due to the close secondary, as shown by Schnerr et al. (2006). Splitting the convolved spectrum and assessing the spectral type of each component we find that the companion is a
dwarf star with a spectral type of B5. We also find it may rotate at a substantial fraction of its critical velocity, with a lower limit of
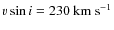 corresponding to
corresponding to
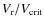 of 53%.
of 53%.
The secondary's estimated mass and 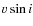 fall within the range of
typical values for classical Be stars. Thus we consider it highly
likely the secondary is indeed such a star. Therefore we have not only
confirmed the result of Schnerr et al. (2006) but we validate their
suggestion that the secondary could be a classical Be star. In which
case the H
fall within the range of
typical values for classical Be stars. Thus we consider it highly
likely the secondary is indeed such a star. Therefore we have not only
confirmed the result of Schnerr et al. (2006) but we validate their
suggestion that the secondary could be a classical Be star. In which
case the H emission is thought to be due to gaseous
equatorial material ejected from the star by a combination of rapid
rotation and some other phenomena, e.g. non-radial pulsation
(Porter & Rivinius 2003). As the H
emission is thought to be due to gaseous
equatorial material ejected from the star by a combination of rapid
rotation and some other phenomena, e.g. non-radial pulsation
(Porter & Rivinius 2003). As the H emission is
shown to originate from a star where the standard Be paradigm applies
the
emission is
shown to originate from a star where the standard Be paradigm applies
the  Cep system does not pose any contradictions to the
current understanding of either
Cep system does not pose any contradictions to the
current understanding of either  Cep stars or classical Be stars.
Cep stars or classical Be stars.
Acknowledgements
The William Herschel Telescope is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofosica de Canarias. R.D.O. is grateful for the support from the Leverhulme Trust for awarding a Research Fellowship. H.E.W gratefully acknowledges a PhD studentship from the Science and Technology Facilities Council of the United Kingdom (STFC). The authors wish to thank an anonymous referee for a careful reading of the manuscript and insightful comments which helped improve the paper.
References
- Bailey, J. A. 1998, in Optical Astronomical Instrumentation, ed. S. D'Odorico, Proc. SPIE, 3355, 932 In the text
- Baines, D., Oudmaijer, R. D., Porter, J. M., & Pozzo, M. 2006, MNRAS, 367, 737 In the text
- Balega, I. I., Balega, Y. Y., Hofmann, K.-H., et al. 2002, A&A, 385, 87 In the text
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, 20P
- Catanzaro, G. 2008, MNRAS, 387, 759 In the text
- Chauville, J., Zorec, J., Ballereau, D., et al. 2001, A&A, 378, 861 In the text
- Cranmer, S. R. 2005, ApJ, 634, 585 In the text
- Donati, J.-F., Wade, G. A., Babel, J., et al. 2001, MNRAS, 326, 1265 In the text
- Dougherty, S. M., Taylor, A. R., & Clark, T. A. 1991, AJ, 102, 1753 In the text
- Gezari, D. Y., Labeyrie, A., & Stachnik, R. V. 1972, ApJ, 173, L1 In the text
- Hadrava, P., & Harmanec, P. 1996, A&A, 315, L401 In the text
- Harmanec, P. 1988, Bull. astr. Inst. Czechosl, 39, 329 In the text
- Hartkopf, W. I., McAlister, H. A., & Mason, B. D. 2001, AJ, 122, 3480 In the text
- Heintz, W. D. 1978, Geophysics and Astrophysics Monographs, 15 In the text
- Henrichs, H. F., de Jong, J. A., Donati, J.-F., et al. 2000, in The Be Phenomenon in Early-Type Stars, ed. M. A. Smith, H. F. Henrichs, & J. Fabregat, ASP Conf. Ser., 214, IAU Colloq. 175, 324 In the text
- Hoffleit, D., & Warren, Jr., W. H. 1995, VizieR Online Data Catalog, 5050, 0 In the text
- Kaper, L., & Mathias, P. 1995, in Astrophysical Applications of Stellar Pulsation, ed. J. Matthews, ASP Conf. Ser. 83, IAU Colloq., 155, 295 In the text
- Karpov, B. G. 1932, Lick Observatory Bulletin, 16, 159 In the text
- Kurucz, R. L. 1993, CD-ROM 13, http://kurucz.harvard.edu In the text
- Landolt, H. H., Börnstein, R., Hellwege, K. H., et al. 1982, Numerical data and functional relationships in science and technology: New series, Group IV, A&A and Space Research, Vol 2, A&A, sub volume b, Stars and Star Clusters (Berlin: Springer) In the text
- Lesh, J. R. 1968, ApJs, 17, 371 In the text
- Morel, T., Butler, K., Aerts, C., Neiner, C., & Briquet, M. 2006, A&A, 457, 651 In the text
- Morgan, W. W., Keenan, P. C., & Kellman, E. 1943, An atlas of stellar spectra, with an outline of spectral classification (Chicago, Ill., The University of Chicago Press) In the text
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, ApJs, 2, 41 In the text
- Neiner, C., Henrichs, H., Geers, V., & Donati, J.-F. 2001, IAU Circ., 7651, 3 In the text
- Oudmaijer, R., Parr, A., Baines, D., & Porter, J. 2008, A&A, 489, 627 In the text
- Pan'ko, E. A., & Tarasov, A. E. 1997, Astron. Lett., 23, 545 In the text
- Perryman, M. A. C., & ESA, 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ed. M. A. C. Perryman, & ESA, ESA SP, 1200 In the text
- Pigulski, A., & Boratyn, D. A. 1992, A&A, 253, 178 In the text
- Porter, J. M. 1996, MNRAS, 280, L31 In the text
- Porter, J. M., & Rivinius, T. 2003, PASP, 115, 1153 In the text
- Porter, J. M., Oudmaijer, R. D., & Baines, D. 2004, A&A, 428, 327 In the text
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93
- Schnerr, R. S., Henrichs, H. F., Oudmaijer, R. D., & Telting, J. H. 2006, A&A, 459, L21 In the text
- Stankov, A., & Handler, G. 2005, ApJs, 158, 193 In the text
- Sterken, C., & Jerzykiewicz, M. 1993, Space Sci. Rev., 62, 95 In the text
- Telting, J. H., Aerts, C., & Mathias, P. 1997, A&A, 322, 493 In the text
- Townsend, R. H. D., Owocki, S. P., & Howarth, I. D. 2004, MNRAS, 350, 189 In the text
- Wilson, R., & Seddon, H. 1956, The Observatory, 76, 145 In the text
Footnotes
- ... (IRAF)
![[*]](/icons/foot_motif.png)
- IRAF: written and supported by the IRAF programming group at the National Optical Astronomy Observatories (NOAO) in Tuscon Arizona (http://iraf.noao.edu/).
- ...(Kurucz 1993)
![[*]](/icons/foot_motif.png)
- We used the GNU Linux port of ATLAS9 and SYNTHE developed by Sbordone et al. (2004). For the initial atmospheric models we used the grid of models by Castelli & Kurucz (2003).
All Figures
![\begin{figure}
\par\includegraphics[scale=0.75,clip]{1105fig1a.eps}\\
\includegraphics[scale=0.75,clip]{1105fig1b.eps}\\\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg46.png) |
Figure 1:
The average spectra of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.3]{1105fig2a.eps}\hspace*{2mm}
\inc...
...fig2b.eps}\hspace*{2mm}
\includegraphics[scale=0.3]{1105fig2c.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg49.png) |
Figure 2:
The spectroastrometric signature of the close |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.25]{1105fig3a.eps}\includegraphics[s...
...0.25]{1105fig3b.eps}\includegraphics[scale=0.25]{1105fig3c.eps}\\\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg51.png) |
Figure 3:
XY plots of the spectroastrometric signature of the close |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=1]{1105fig4.ps}
\par\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg57.png) |
Figure 4:
The red spectrum of the close |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=1]{1105fig5.ps}
\par\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg60.png) |
Figure 5:
The blue spectrum of the close |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=1]{1105fig6.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg62.png) |
Figure 6:
The red spectrum of the close |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.3,clip]{1105fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg77.png) |
Figure 7:
A comparison between the spectroastrometrically separated He I 4471 Å profiles and the best fit rotationally broadened synthetic profiles. The solid line represents the He I line of the primary and secondary spectra respectively, the short-long dashed line the best fit primary synthetic spectrum (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.3]{1105fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11105-08/Timg92.png) |
Figure 8:
A possible relative orbit of the companion of the close |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



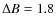 and
d = 0.20''. In the top left the wavelength range is reduced and centred on
and
d = 0.20''. In the top left the wavelength range is reduced and centred on
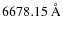 profile. The determined values for the separation and brightness difference were
profile. The determined values for the separation and brightness difference were
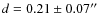 and
and
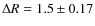 .
.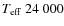 K,
K, 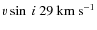 ), the short-dashed line the best fit secondary synthetic spectrum at a
), the short-dashed line the best fit secondary synthetic spectrum at a
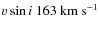 )
and the long dashed line is the best fit secondary synthetic spectrum at a
)
and the long dashed line is the best fit secondary synthetic spectrum at a
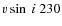
 ).
). and
and  .
The average uncertainty in the data was approximately 0.015'' in each direction.
.
The average uncertainty in the data was approximately 0.015'' in each direction.