| Issue |
A&A
Volume 497, Number 2, April II 2009
|
|
|---|---|---|
| Page(s) | 497 - 509 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200810904 | |
| Published online | 05 March 2009 | |
A new implementation of the infrared flux method using the
2MASS catalogue![[*]](/icons/foot_motif.png)
J. I. González Hernández1,![]() - P. Bonifacio1,2,
- P. Bonifacio1,2,![]()
1 - GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, Place
Jules Janssen, 92190
Meudon, France
2 -
Istituto Nazionale di Astrofisica - Osservatorio Astronomico di
Trieste, via Tiepolo 11, 34143 Trieste, Italy
Received 3 September 2008 / Accepted 15 January 2009
Abstract
Context. The effective temperature scale of FGK stars, especially at the lowest metallicities remains a major problem in the chemical abundance analysis of metal-poor stars.
Aims. We present a new implementation of the infrared flux method (IRFM) using the 2MASS catalogue.
Methods. We computed the theoretical quantities in the 2MASS
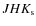 filters by integrating theoretical fluxes computed from ATLAS models, and compare them directly with the observed 2MASS
filters by integrating theoretical fluxes computed from ATLAS models, and compare them directly with the observed 2MASS
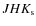 magnitudes. This is the main difference between our implementation of the IRFM and that of Ramírez & Meléndez (2005, ApJ, 626, 446, hereafter RM05), since to introduce new stars at the lowest metallicities they transform the 2MASS
magnitudes. This is the main difference between our implementation of the IRFM and that of Ramírez & Meléndez (2005, ApJ, 626, 446, hereafter RM05), since to introduce new stars at the lowest metallicities they transform the 2MASS
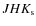 magnitudes into the TCS photometric system. We merge in our sample the stars from Alonso et al. (1996, A&AS, 117, 227, hereafter AAM96; 1999, A&AS, 139, 335, hereafter AAM99), and other studies to appropriately cover a wide range of metallicities, ending up with 555 dwarf and subgiant field stars and 264 giant field stars. We derived a new bolometric flux calibration using the available Johnson-Cousins
magnitudes into the TCS photometric system. We merge in our sample the stars from Alonso et al. (1996, A&AS, 117, 227, hereafter AAM96; 1999, A&AS, 139, 335, hereafter AAM99), and other studies to appropriately cover a wide range of metallicities, ending up with 555 dwarf and subgiant field stars and 264 giant field stars. We derived a new bolometric flux calibration using the available Johnson-Cousins
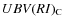 and the 2MASS
and the 2MASS
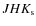 photometry. We also computed new
photometry. We also computed new
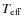 versus colour empirical calibrations using our extended sample of stars.
versus colour empirical calibrations using our extended sample of stars.
Results. We derived effectives temperatures for almost all the stars in the AAM96 and AAM99 samples and find that our scales of temperature are hotter by 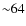 K (
K (
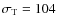 K, N=332 dwarfs) and
K, N=332 dwarfs) and 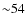 K with a
K with a
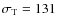 K (N=202 giants). The same comparison with the sample of RM05 for stars with [Fe/H] <-2.5 provides a difference of
K (N=202 giants). The same comparison with the sample of RM05 for stars with [Fe/H] <-2.5 provides a difference of 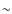 -87 K (
-87 K (
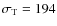 K, N=12 dwarf stars) and
K, N=12 dwarf stars) and 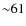 K (
K (
 K, N=18 giant stars).
K, N=18 giant stars).
Conclusions. Our temperature scale is slightly hotter than that of AAM96 and RM05 for metal-rich dwarf stars but cooler than that of RM05 for metal-poor dwarfs. We have performed an fully self-consistent IRFM in the 2MASS photometric system. For those who wish to use 2MASS photometry and colour-temperature calibrations to derive effective temperatures, especially for metal-poor stars, we recommend our calibrations over others available in the literature. In our implementation we avoid the transformation of the 2MASS
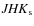 magnitudes to a different photometric system and thus fully exploit the excellent internal consistency of the 2MASS photometric system.
magnitudes to a different photometric system and thus fully exploit the excellent internal consistency of the 2MASS photometric system.
Key words: infrared: stars - stars: abundances - stars: atmospheres - stars: fundamental parameters
1 Introduction
The effective temperature is a function of the bolometric flux and the
angular diameter according to the equation
where
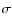 is the Stefan-Boltzmann constant,
is the Stefan-Boltzmann constant,
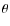 the angular diameter, and
the angular diameter, and
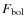 the bolometric
flux measured on the surface of the Earth. However, direct
measure of angular diameters is restricted to relatively few
stars, especially for dwarf stars. Kervella et al. (2008, interferometry,2004) and Brown et al. (2001, transit observations) have directly measured the
angular diameters of bright stars. Only recently, Baines et al. (2008) have
used the CHARA interferometric array to provide measurements of
angular diameters of
the bolometric
flux measured on the surface of the Earth. However, direct
measure of angular diameters is restricted to relatively few
stars, especially for dwarf stars. Kervella et al. (2008, interferometry,2004) and Brown et al. (2001, transit observations) have directly measured the
angular diameters of bright stars. Only recently, Baines et al. (2008) have
used the CHARA interferometric array to provide measurements of
angular diameters of 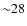 dwarf and subgiant stars, although all
of them have metallicities [Fe/H] >-0.5.
dwarf and subgiant stars, although all
of them have metallicities [Fe/H] >-0.5.
A semi-direct method of temperature determination is one that
makes use of Eq. (1) but relies on model atmospheres,
rather than on a direct measure of the angular diameter.
The infra red flux method (hereafter IRFM; Blackwell et al. 1990, and references therein) is especially
adequate for determining the effective temperature of F, G and K stars.
The IRFM was first introduced by Blackwell & Shallis (1977) who proposed simultaneously determining
the effective temperature and the angular diameter of a star. The
basic idea is to use the monochromatic flux in the infrared since it is
mainly dependent on the angular diameter but is approximately
dependent only on the first power of
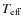 ,
whereas the
integrated flux strongly depends on the temperature (proportional
to
,
whereas the
integrated flux strongly depends on the temperature (proportional
to
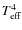 ).
).
Popular indirect methods for deriving effective temperatures are the excitation equilibrium of Fe I lines (e.g. Santos et al. 2004,2005) and on fitting Balmer lines (e.g. Barklem et al. 2002; Fuhrmann et al. 1994,1993). Temperatures based on Fe I excitation equilibrium depend on the model assumptions, such as non-LTE effects, especially in metal-poor stars (see Shchukina & Trujillo Bueno 2001; Thévenin & Idiart 1999). Recently, Barklem (2007) has also raised concerns about possible non-LTE effects on the wings of Balmer lines. Both excitation equilibria (Asplund 2005) and Balmer lines (Ludwig et al. 2009, in prep.) are also sensitive to granulation effects. This makes such methods strongly model-dependent, which is an undesirable feature. However, temperatures derived from Balmer lines and Fe I excitation equilibria have the considerable advantage of being reddening independent.
One of the motivations of this work is to investigate the trend of Li abundances towards low metallicities ([Fe/H] < -2.5), using our own implementation of the IRFM. (Bonifacio et al. 2007) investigated the Spite plateau at the lowest metallicities (down to [Fe/H] = -3.3) and found marginal evidence that there could be an increased scatter or even a sharp drop in the Li abundance at these low metallicities. Determination of the baryonic density from the fluctuations in the cosmic microwave background (CMB) by the WMAP satellite (Spergel et al. 2003,2007) implies a primordial Li abundance, which is at least a factor of 3-4 larger than observed on the Spite plateau, creating a conflict with the traditional interpretation of the plateau (Spite & Spite 1982b,a). This discrepancy would be even greater if the drop in the Li abundance versus metallicity were to be confirmed (see Sbordone et al. 2008, in prep.).
One decade ago, Bonifacio & Molaro (1997) determined Li abundances using the
IRFM temperatures of Alonso et al. (1996a). They investigated the different
Li abundance trends found with different temperature scales.
In particular, the temperatures of Ryan et al. (1996), which are based on
the IRFM implementation of Magain (1987), are cooler than the IRFM
temperatures of Alonso et al. (1996a), provided
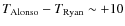 K at [Fe/H]
K at [Fe/H]
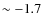 and
and
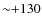 K at [Fe/H]
K at [Fe/H] 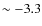 .
From this, Bonifacio & Molaro (1997) concluded that the presence or absence of
trends in lithium abundance with
.
From this, Bonifacio & Molaro (1997) concluded that the presence or absence of
trends in lithium abundance with
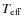 is strongly dependent on the
temperature scale adopted.
is strongly dependent on the
temperature scale adopted.
Meléndez & Ramírez (2004) applied their own IRFM implementation
(Ramírez & Meléndez 2005a) to deriving the effective temperature and Li abundances
for a sample of stars similar to that of Ryan et al. (1996). They find
individual temperature differences of up to 400-500 K
for the some stars with metallicity below -3.0 dex.
More recently, Bonifacio et al. (2007) have compared the temperatures
obtained from
 profiles to other temperature indicators,
among them those from the IRFM-based colour-temperature calibrations
of (Ramírez & Meléndez 2005a) and Alonso et al. (1996b).
When a reddening based on the Schlegel et al. (1998) maps is adopted, from the
profiles to other temperature indicators,
among them those from the IRFM-based colour-temperature calibrations
of (Ramírez & Meléndez 2005a) and Alonso et al. (1996b).
When a reddening based on the Schlegel et al. (1998) maps is adopted, from the
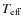 :(V-K) calibration of Alonso et al. (1996b), the mean
difference
:(V-K) calibration of Alonso et al. (1996b), the mean
difference
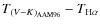 is only 8 K with
a standard deviation of 100 K. However, if we use the
is only 8 K with
a standard deviation of 100 K. However, if we use the
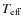 :(V-K)calibration of Ramírez & Meléndez (2005b), this mean difference is
:(V-K)calibration of Ramírez & Meléndez (2005b), this mean difference is
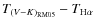 of 265 K, with a standard
deviation of 122 K.
of 265 K, with a standard
deviation of 122 K.
Ramírez & Meléndez (2005a) add as calibrators a small sample of
metal-poor stars mainly from Christlieb et al. (2004) and Cayrel et al. (2004),
and a larger sample of metal-rich stars from Santos et al. (2004) to the
original sample of Alonso et al. (1996a), and computed new
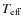 -colour
calibrations.
Since the majority of calibrators shared by the two
samples, this large difference (
-colour
calibrations.
Since the majority of calibrators shared by the two
samples, this large difference ( K)
between the calibrations of Ramírez & Meléndez (2005a) and Alonso et al. (1996b) at low
metallicity is a priori unexpected.
One could argue that the models used by the two groups
are not exactly the same, however they must be very similar
(ATLAS 9 models with the same ODFs and microturbulent velocity).
Since the IRFM is only weakly dependent on
the models adopted, as shown by the results of Casagrande et al. (2006),
who used both ATLAS and MARCS models, it seems unlikely that
this difference is rooted in the different models.
We suggest instead that this is because Ramírez & Meléndez (2005a) use
2MASS
K)
between the calibrations of Ramírez & Meléndez (2005a) and Alonso et al. (1996b) at low
metallicity is a priori unexpected.
One could argue that the models used by the two groups
are not exactly the same, however they must be very similar
(ATLAS 9 models with the same ODFs and microturbulent velocity).
Since the IRFM is only weakly dependent on
the models adopted, as shown by the results of Casagrande et al. (2006),
who used both ATLAS and MARCS models, it seems unlikely that
this difference is rooted in the different models.
We suggest instead that this is because Ramírez & Meléndez (2005a) use
2MASS![]()
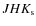 magnitudes for
the low metallicity calibrators; such magnitudes were then transformed
into the TCS system to merge them with the homogeneous
set of TCS photometry of Alonso et al. (1996a).
The errors in the transformation between the 2MASS and the
TCS systems are then added to the photometric error and may have
undesired effects on the final calibration.
We have no way to prove that this is indeed the case; however,
to circumvent such problems in this paper, we propose a new
implementation of the IRFM, including the stars from Alonso et al. (1996a,1999a) and Ramírez & Meléndez (2005a), but using the 2MASS photometry for all
calibrators rather than a mixture of 2MASS and TCS.
The 2MASS magnitudes are probably not as accurate
as the careful TCS photometry of Alonso et al. (1996a),
but the internal consistency of the 2MASS
photometry is very high, about 1-2% (Cutri et al. 2003).
magnitudes for
the low metallicity calibrators; such magnitudes were then transformed
into the TCS system to merge them with the homogeneous
set of TCS photometry of Alonso et al. (1996a).
The errors in the transformation between the 2MASS and the
TCS systems are then added to the photometric error and may have
undesired effects on the final calibration.
We have no way to prove that this is indeed the case; however,
to circumvent such problems in this paper, we propose a new
implementation of the IRFM, including the stars from Alonso et al. (1996a,1999a) and Ramírez & Meléndez (2005a), but using the 2MASS photometry for all
calibrators rather than a mixture of 2MASS and TCS.
The 2MASS magnitudes are probably not as accurate
as the careful TCS photometry of Alonso et al. (1996a),
but the internal consistency of the 2MASS
photometry is very high, about 1-2% (Cutri et al. 2003).
2 Implementation of the IRFM
The IRFM (Blackwell et al. 1990) evaluates the quotient between the bolometric
flux,
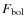 ,
and the monochromatic flux at a chosen infrared
wavelength,
,
and the monochromatic flux at a chosen infrared
wavelength,
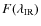 ,
both measured at the surface of the
earth, as an indicator of the
,
both measured at the surface of the
earth, as an indicator of the
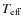 .
This quotient is the so-called
observational R-factor,
.
This quotient is the so-called
observational R-factor,
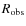 .
The theoretical counterpart
derived from models,
.
The theoretical counterpart
derived from models,
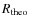 ,
is obtained as the quotient
between the integrated flux,
,
is obtained as the quotient
between the integrated flux, 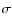
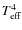 ,
and the monochromatic
flux at
,
and the monochromatic
flux at
 ,
,
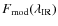 ,
at the
surface of the star. Thus the basic equation of the IRFM is
,
at the
surface of the star. Thus the basic equation of the IRFM is
 |
= | ![$\displaystyle \frac{F_{\rm bol}}{F(\lambda_{\rm IR})}=\frac{\sigma
T_{\rm eff}^4}{F_{\rm mod}(\lambda_{\rm IR}{\rm ,}T_{\rm eff}{\rm ,[Fe/H]}, \log g)}$](/articles/aa/full_html/2009/14/aa10904-08/img55.png) |
|
| = | ![$\displaystyle R_{\rm theo}(\lambda_{\rm IR}{\rm ,}T_{\rm eff}{\rm ,[Fe/H]}, \log g)$](/articles/aa/full_html/2009/14/aa10904-08/img56.png) |
(2) |
where the dependence of models on metallicity, surface gravity, and
 is explicitly taken into account. The monochromatic
fluxes are obtained by applying the relation
is explicitly taken into account. The monochromatic
fluxes are obtained by applying the relation
![\begin{displaymath}F(\lambda_{\rm IR})=q(\lambda_{\rm IR}{\rm ,}T_{\rm eff}{\rm
...
... cal}(\lambda_{\rm IR})10^{-0.4(m_\star-m_{\rm
cal})}\right ]
\end{displaymath}](/articles/aa/full_html/2009/14/aa10904-08/img57.png) |
(3) |
where
 is the magnitude of the target star,
and
is the magnitude of the target star,
and
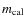 and
and
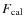 are, respectively, the
magnitudes and the absolute monochromatic fluxes of the calibrator
star (see Table 1 and Sect. 5). The q-factor,
usually
are, respectively, the
magnitudes and the absolute monochromatic fluxes of the calibrator
star (see Table 1 and Sect. 5). The q-factor,
usually  ,
is a dimensionless factor that corrects the effect of the
different curvature of the flux distribution across the filter
window (see Alonso et al. 1996a,1999a,1994, for more details). We have
used the definition of Alonso et al. (1996a) for the computations of the
q-factors (see Sect. 5).
,
is a dimensionless factor that corrects the effect of the
different curvature of the flux distribution across the filter
window (see Alonso et al. 1996a,1999a,1994, for more details). We have
used the definition of Alonso et al. (1996a) for the computations of the
q-factors (see Sect. 5).
Table 1: Monochromatic Fluxes for Vega from the calibrated ATLAS 9 flux.
By merging the previous two equations we can separate the
observational and model inputs as
The synthetic magnitudes, the q- and R-factors, necessary for implementing of the IRFM were computed from the ATLAS theoretical fluxes of Castelli & Kurucz (2003)
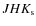 filters.
We used the fluxes in the ranges 3500 K <
filters.
We used the fluxes in the ranges 3500 K <
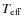 <7500 K,
0.0<
<7500 K,
0.0<  <5.0, and -4< [Fe/H] <+0.5, and
for metal-poor models with [Fe/H]
<5.0, and -4< [Fe/H] <+0.5, and
for metal-poor models with [Fe/H] 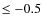 ,
we used
the fluxes computed from the
,
we used
the fluxes computed from the 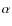 -enhanced models.
We derived a new calibration of the bolometric flux in the 2MASS
photometric system (see Sect. 6).
-enhanced models.
We derived a new calibration of the bolometric flux in the 2MASS
photometric system (see Sect. 6).
3 Online data available at the CDS
Several tables are available at the CDS![]() . We provide eight
tables containing the q- and R-factors computed as indicated in
Sects. 2 and 5 for metallicities in the
range [-4, 0.5], temperatures in the range [3500, 50 000], and gravities
in the range [0, 5]. Within these tables, we also put the
theoretical colour V-K and magnitudes JHKs in the 2MASS system for
each atmospheric model. These theoretical colour and magnitudes, which
are not used in this work, were normalised to
Vega assuming
. We provide eight
tables containing the q- and R-factors computed as indicated in
Sects. 2 and 5 for metallicities in the
range [-4, 0.5], temperatures in the range [3500, 50 000], and gravities
in the range [0, 5]. Within these tables, we also put the
theoretical colour V-K and magnitudes JHKs in the 2MASS system for
each atmospheric model. These theoretical colour and magnitudes, which
are not used in this work, were normalised to
Vega assuming
 .
If the user wants to use a different
zero point for Vega, it is trivial to add it to
our theoretical magnitudes. In addition, eight
tables containing the A-factors and BX-B coefficients
for the same set of models are also available at the CDS,
needed for the bolometric flux calibration (see Sect. 6).
At the CDS, we also provide two tables, with 555 dwarf
stars and with 264 giant stars, containing the photometric
data and reddenings used in this paper, stellar parameters and metallicity, bolometric fluxes
and IRFM temperatures for all the stars in our samples (see
Sects. 4.1 and 4.2).
.
If the user wants to use a different
zero point for Vega, it is trivial to add it to
our theoretical magnitudes. In addition, eight
tables containing the A-factors and BX-B coefficients
for the same set of models are also available at the CDS,
needed for the bolometric flux calibration (see Sect. 6).
At the CDS, we also provide two tables, with 555 dwarf
stars and with 264 giant stars, containing the photometric
data and reddenings used in this paper, stellar parameters and metallicity, bolometric fluxes
and IRFM temperatures for all the stars in our samples (see
Sects. 4.1 and 4.2).
4 Sample, observational data, and stellar parameters
4.1 Photometric data
Our sample includes almost all the stars in Alonso et al. (1996a,1999a)
with available photometric data in the final release of the 2MASS
catalogue (Skrutskie et al. 2006) and with photometric accuracy
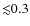 mag, for temperature determinations. We adopted this rather high
tolerance because giant stars of Alonso et al. (1999a) are relatively bright and
usually the 2MASS photometric accuracy is very low for these stars.
However, to improve the precision of the bolometric flux
and
mag, for temperature determinations. We adopted this rather high
tolerance because giant stars of Alonso et al. (1999a) are relatively bright and
usually the 2MASS photometric accuracy is very low for these stars.
However, to improve the precision of the bolometric flux
and
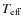 :colour-[Fe/H] calibrations significantly, we decided to
further lower the accuracy limit down to
:colour-[Fe/H] calibrations significantly, we decided to
further lower the accuracy limit down to
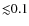 mag (see
Sects. 6 and 9). Therefore, stars with
2MASS photometric errors >0.1 mag were only used for the purpose of
deriving effective temperatures and they are provided as online data
at the CDS.
mag (see
Sects. 6 and 9). Therefore, stars with
2MASS photometric errors >0.1 mag were only used for the purpose of
deriving effective temperatures and they are provided as online data
at the CDS.
We adopted the same
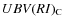 photometric data as used by
Ramírez & Meléndez (2005b,a), which were kindly provided by
Ramírez & Meléndez (private communication). These data
were extracted from the General Catalogue of Photometric Data
(Mermilliod et al. 1997, GCPD).
For those stars of the Alonso et al. (1996a,1999a) samples without Vdata in the GCPD these magnitudes were obtained from Simbad
photometric data as used by
Ramírez & Meléndez (2005b,a), which were kindly provided by
Ramírez & Meléndez (private communication). These data
were extracted from the General Catalogue of Photometric Data
(Mermilliod et al. 1997, GCPD).
For those stars of the Alonso et al. (1996a,1999a) samples without Vdata in the GCPD these magnitudes were obtained from Simbad![]() , and were later used to derive
bolometric fluxes and IRFM temperatures.
, and were later used to derive
bolometric fluxes and IRFM temperatures.
4.2 Metallicity and surface gravity
For our sample of stars from (Alonso et al. 1996a,1999a), we adopted the surface gravities and metallicities provided by Ramírez & Meléndez (private communication) which mostly use the mean values of those reported in Cayrel de Strobel et al. (2001).
We completed our sample of dwarfs and subgiants with the metal-rich and metal-poor stars already included in the sample of Ramírez & Meléndez (2005a). The metal-rich sample mostly contains planet-host stars and the comparison sample from Santos et al. (2004), but we also added to our sample the stars with [Fe/H] >-2 from Casagrande et al. (2006). We completed the sample with extremely metal-poor dwarfs from Bonifacio et al. (2007), Christlieb et al. (2004), and Barklem et al. (2005). For these stars, we adopted the same surface gravity and metallicity as published in the above papers.
Our sample of giants contains the stars in Alonso et al. (1999a), plus the metal-poor stars from Ramírez & Meléndez (2005a). This includes stars from the ``First Stars'' project (Cayrel et al. 2004; Spite et al. 2005), and we adopted the surface gravity and metallicity for these stars as provided in these papers.
The errors on surface gravity and metallicity for all dwarf, subgiant,
and giant stars were assumed to be
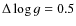 dex and
dex and
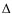 [Fe/H] =0.1. The average systematic errors due to a
different metallicity (by +0.1 dex) and a different surface gravity
(by +0.5 dex) are 13 K and 11 K, respectively, for dwarfs, and
11 K and 28 K for giants. These errors were estimated by
quadratically adding the errors on effective temperature from each
band and calculating the average over all stars in both samples.
[Fe/H] =0.1. The average systematic errors due to a
different metallicity (by +0.1 dex) and a different surface gravity
(by +0.5 dex) are 13 K and 11 K, respectively, for dwarfs, and
11 K and 28 K for giants. These errors were estimated by
quadratically adding the errors on effective temperature from each
band and calculating the average over all stars in both samples.
4.3 Reddening corrections
The extinction in each photometric band, Ai, as determined
using the relation
Ai=RiE(B-V), where Ri is given by the
coefficients provided in (McCall 2004). Reddening
corrections, E(B-V), were adopted from Ramírez &
Meléndez (private communication). For the metal-rich stars of Casagrande et al. (2006) and
the extremely metal-poor dwarfs of Bonifacio et al. (2007) and Christlieb et al. (2004),
reddening corrections were derived
from the maps of Schlegel et al. (1998). The E(B-V) from the maps is
appropriate for objects outside the dust layer, which is confined to
the Galactic disc. For objects which are within the dust layer
the map estimate should be corrected by a factor
![$[1-\exp(-\vert d\sin
b\vert/h)]$](/articles/aa/full_html/2009/14/aa10904-08/img75.png) ,
where d is the distance of the star,
b its galactic latitude and h the scale height of the
dust layer (see, e.g. Bonifacio et al. 2000b).
For this purpose we used the parallaxes
provided by Simbad (which come mainly from the Hipparcos
catalogue Perryman et al. 1997) and assumed
a scale height of the dust layer of 125 pc.
Bonifacio et al. (2000a) note that, when the maps of Schlegel et al. (1998)
provide reddenings larger than 0.1 mag, they
overestimate the reddening with respect to other
indicators, and proposed a simple formula
for correcting the reddening from the maps.
We make use of formula (1) of Bonifacio et al. (2000a)
to correct the reddenings derived
from the maps of Schlegel et al. (1998).
,
where d is the distance of the star,
b its galactic latitude and h the scale height of the
dust layer (see, e.g. Bonifacio et al. 2000b).
For this purpose we used the parallaxes
provided by Simbad (which come mainly from the Hipparcos
catalogue Perryman et al. 1997) and assumed
a scale height of the dust layer of 125 pc.
Bonifacio et al. (2000a) note that, when the maps of Schlegel et al. (1998)
provide reddenings larger than 0.1 mag, they
overestimate the reddening with respect to other
indicators, and proposed a simple formula
for correcting the reddening from the maps.
We make use of formula (1) of Bonifacio et al. (2000a)
to correct the reddenings derived
from the maps of Schlegel et al. (1998).
5 Photometric zero points and absolute flux calibrations for use with the IRFM
Equation (4) is what needs to be implemented practically to derive IRFM temperatures. The quantities on the lefthand side are observed quantities while those on the righthand side are theoretical quantities. One is immediately faced with a series of choices
- 1.
- the magnitude of the standard star (
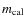 );
);
- 2.
- the monochromatic flux of the standard star (
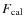 );
);
- 3.
- the zero point for q;
- 4.
- the zero point for
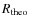 .
.
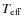 = 9400,
= 9400,  = 3.9, a
metallicity of -0.5, and a microturbulent velocity of 0
= 3.9, a
metallicity of -0.5, and a microturbulent velocity of 0
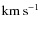 .
Such a spectrum is not available in tabular form, we could
indeed recompute it, however using such a spectrum to zero
our theoretical quantities would mean using a spectrum that is
computed from a model inconsistent with the
rest of the theoretical grid.
Furthermore, as we shall see in Sect. 6,
we will also need the absolute fluxes in other bands to
derive a calibration for the bolometric flux.
The natural choice is to use the corresponding theoretical
magnitudes of Bessell et al. (1998) transformed into the 2MASS system.
These magnitudes rely on the model for Vega, proposed by Castelli & Kurucz (1994),
consistent with the grid of Castelli & Kurucz (2003) that we are using.
A possible solution is to follow what was done by Casagrande et al. (2006),
who in fact used two different calibrations for optical and IR
magnitudes.
Inspection of Eq. (4) suggests another solution:
use the same spectrum of the standard star to calibrate all bands.
In this way any error in the calibration will cancel out
when computing the flux ratio on the lefthand side of
Eq. (4). However, to have a good absolute calibration,
one also needs accurate observed or derived 2MASS magnitudes of the
standard star Vega, which is quite difficult to obtain.
We decided to adopt as 2MASS magnitudes of Vega those provided by
McCall (2004, see Sect. 6#.
This theoretical spectrum
should also be used to define the zero point of q and
.
Such a spectrum is not available in tabular form, we could
indeed recompute it, however using such a spectrum to zero
our theoretical quantities would mean using a spectrum that is
computed from a model inconsistent with the
rest of the theoretical grid.
Furthermore, as we shall see in Sect. 6,
we will also need the absolute fluxes in other bands to
derive a calibration for the bolometric flux.
The natural choice is to use the corresponding theoretical
magnitudes of Bessell et al. (1998) transformed into the 2MASS system.
These magnitudes rely on the model for Vega, proposed by Castelli & Kurucz (1994),
consistent with the grid of Castelli & Kurucz (2003) that we are using.
A possible solution is to follow what was done by Casagrande et al. (2006),
who in fact used two different calibrations for optical and IR
magnitudes.
Inspection of Eq. (4) suggests another solution:
use the same spectrum of the standard star to calibrate all bands.
In this way any error in the calibration will cancel out
when computing the flux ratio on the lefthand side of
Eq. (4). However, to have a good absolute calibration,
one also needs accurate observed or derived 2MASS magnitudes of the
standard star Vega, which is quite difficult to obtain.
We decided to adopt as 2MASS magnitudes of Vega those provided by
McCall (2004, see Sect. 6#.
This theoretical spectrum
should also be used to define the zero point of q and
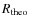 for the standard star,
in order to have a fully self-consistent IRFM.
for the standard star,
in order to have a fully self-consistent IRFM.
![\begin{figure}
\par\includegraphics[width=9cm]{10904f1.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg78.png) |
Figure 1:
Spectral energy distribution of the ATLAS model of Vega
(
|
| Open with DEXTER | |
Throughout this work we adopt the theoretical flux of Vega of
Castelli & Kurucz (1994)![]() ,
which has been calibrated to absolute flux, at Earth, using
the value recommended by Hayes (1985,
,
which has been calibrated to absolute flux, at Earth, using
the value recommended by Hayes (1985, 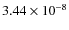 erg s-1 cm-2 nm-1).
This spectrum is used to define the zero point of the q factor
and the monochromatic fluxes, at the isophotal wavelengths of the
2MASS filters, listed in Table 1 are used in our
implementation of Eq. (4).
As noted by Casagrande et al. (2006), such a calibrated
spectrum differs to the one used by Cohen et al. (1992) and
adopted by Cohen et al. (2003) to define the absolute
flux calibration of the 2MASS magnitudes. In Fig. 1
we display the calibrated spectrum of Vega in comparison with the
adopted monochromatic fluxes of Cohen et al. (2003). The difference is
small when comparing them with the continuum flux of our ATLAS 9
model of Vega at the same infrared wavelenghts.
We stress that, for the purpose of consistent
IRFM temperatures, we are not all that interested in having
accurate monochromatic fluxes, but instead accurate
ratios of bolometric fluxes to monochromatic fluxes. However, it
should be noted that the adopted observed magnitudes for Vega are
perhaps the source of uncertainty in a given temperature scale
based on the IRFM.
erg s-1 cm-2 nm-1).
This spectrum is used to define the zero point of the q factor
and the monochromatic fluxes, at the isophotal wavelengths of the
2MASS filters, listed in Table 1 are used in our
implementation of Eq. (4).
As noted by Casagrande et al. (2006), such a calibrated
spectrum differs to the one used by Cohen et al. (1992) and
adopted by Cohen et al. (2003) to define the absolute
flux calibration of the 2MASS magnitudes. In Fig. 1
we display the calibrated spectrum of Vega in comparison with the
adopted monochromatic fluxes of Cohen et al. (2003). The difference is
small when comparing them with the continuum flux of our ATLAS 9
model of Vega at the same infrared wavelenghts.
We stress that, for the purpose of consistent
IRFM temperatures, we are not all that interested in having
accurate monochromatic fluxes, but instead accurate
ratios of bolometric fluxes to monochromatic fluxes. However, it
should be noted that the adopted observed magnitudes for Vega are
perhaps the source of uncertainty in a given temperature scale
based on the IRFM.
We adopted an error of 1 per cent on the monochromatic flux of each band for the determination of effective temperatures. The average systematic errors due to this uncertainty are 44 K and 46 K for dwarfs and giants, respectively. These errors were estimated by adding the errors quadratically on temperature from each band and calculating the average over all stars in both samples.
6 Bolometric fluxes
One of the fundamental observational quantities for applying the IRFM is
the bolometric flux. The bolometric flux is not readily available for
any given star, but Blackwell & Petford (1991) suggested that one could use a relation
of the type
![$F_{\rm bol} = 10^{-0.4m}\phi(X,{\rm [Fe/H]})$](/articles/aa/full_html/2009/14/aa10904-08/img80.png) ,
where m is a suitable broad band colour and
X a colour index. Such a calibration has
been derived by Alonso et al. (1995) using the
K magnitude and the V-K colour (Johnson system); Casagrande et al. (2006) have derived
several similar calibrations for different
choices of m and the colour index.
In an initial attempt we tried to use the Alonso et al. (1995) calibration for
this purpose,
which provided satisfactory results;
however, the referees have correctly pointed out that,
in doing so, we were forced to transform
our (
,
where m is a suitable broad band colour and
X a colour index. Such a calibration has
been derived by Alonso et al. (1995) using the
K magnitude and the V-K colour (Johnson system); Casagrande et al. (2006) have derived
several similar calibrations for different
choices of m and the colour index.
In an initial attempt we tried to use the Alonso et al. (1995) calibration for
this purpose,
which provided satisfactory results;
however, the referees have correctly pointed out that,
in doing so, we were forced to transform
our (
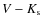 )
colour into Johnson's system,
thus losing the internal consistency
of the 2MASS system. Furthermore, we had to apply the Alonso et al. (1995) calibration outside its formal range of applicability,
for very metal-poor stars. The calibration of Alonso et al. (1995)
only had two stars at [Fe/H] = -3.2 and -2.9 and the rest with
[Fe/H] >-2.6. A similar extrapolation problem would apply
if we had used any of the calibrations derived by Casagrande et al. (2006), which
were derived for stars with [Fe/H] >-1.9.
We therefore decided to derive a new calibration that makes use of
the
)
colour into Johnson's system,
thus losing the internal consistency
of the 2MASS system. Furthermore, we had to apply the Alonso et al. (1995) calibration outside its formal range of applicability,
for very metal-poor stars. The calibration of Alonso et al. (1995)
only had two stars at [Fe/H] = -3.2 and -2.9 and the rest with
[Fe/H] >-2.6. A similar extrapolation problem would apply
if we had used any of the calibrations derived by Casagrande et al. (2006), which
were derived for stars with [Fe/H] >-1.9.
We therefore decided to derive a new calibration that makes use of
the 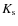 magnitude and the 2MASS-based (
magnitude and the 2MASS-based (
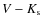 )
colour
and covers the metallicity range appropriate to our sample of stars.
)
colour
and covers the metallicity range appropriate to our sample of stars.
We adopt an approach similar to that of Alonso et al. (1995)
and Casagrande et al. (2006), with a slight difference.
The above authors use a set of effective wavelengths
and monochromatic fluxes for Vega in order to define
the integrated flux within each broad band from the
photometry and the magnitudes of Vega.
From the definition of magnitude follows
where m is any photometric band. Provided then that the integrated flux of Vega in any given band is known, the integrated flux for the target star may be simply derived from its measured magnitude and the magnitude of Vega. In Table 3 we provide our adopted integrated magnitudes for Vega for the bands we are interested in, and
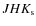 refer to the 2MASS colours.
These integrated magnitudes were derived
by integrating the filter response
functions of Bessell (1990) for the optical bands
and Cohen et al. (2003) for the 2MASS bands,
over the theoretical flux of Vega.
Consistently, the magnitudes for Vega were taken
from McCall (2004), which gives the model magnitudes of Bessell et al. (1998)
for the optical bands. This author
calculates the 2MASS magnitudes of Vega using the
IR absolute monochromatic fluxes from Cohen et al. (2003), which are
in fact quite similar to our adopted absolute monochromatic fluxes
from the calibrated model of Vega (see Fig. 1).
Initially we were going to adopt the magnitudes of Vega equal to zero
in the 2MASS bands, but when we
derived the IRFM temperatures, our scale of temperatures was
refer to the 2MASS colours.
These integrated magnitudes were derived
by integrating the filter response
functions of Bessell (1990) for the optical bands
and Cohen et al. (2003) for the 2MASS bands,
over the theoretical flux of Vega.
Consistently, the magnitudes for Vega were taken
from McCall (2004), which gives the model magnitudes of Bessell et al. (1998)
for the optical bands. This author
calculates the 2MASS magnitudes of Vega using the
IR absolute monochromatic fluxes from Cohen et al. (2003), which are
in fact quite similar to our adopted absolute monochromatic fluxes
from the calibrated model of Vega (see Fig. 1).
Initially we were going to adopt the magnitudes of Vega equal to zero
in the 2MASS bands, but when we
derived the IRFM temperatures, our scale of temperatures was
 K hotter than that of Alonso et al. (1996a), which we think is
the best implementation of the IRFM available in the literature due to
its internal consistency in the whole range of metallicities from -3.0
to 0.5. By adopting the magnitudes of Vega given by McCall (2004),
this difference is reduced to
K hotter than that of Alonso et al. (1996a), which we think is
the best implementation of the IRFM available in the literature due to
its internal consistency in the whole range of metallicities from -3.0
to 0.5. By adopting the magnitudes of Vega given by McCall (2004),
this difference is reduced to 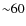 K, which we consider more
appropriate (see Sect. 8.1).
In addition, the remarks on zero points of Sect. 5 also apply
here. This choice guarantees that any error in the absolute
calibration of bolometric fluxes and monchromatic fluxes will cancel
out in Eq. (4).
K, which we consider more
appropriate (see Sect. 8.1).
In addition, the remarks on zero points of Sect. 5 also apply
here. This choice guarantees that any error in the absolute
calibration of bolometric fluxes and monchromatic fluxes will cancel
out in Eq. (4).
From Eq. (5) and the data in Table 3 for any star for which photometry in several bands is available, one may computed the total flux measured at Earth in the given bands. From this value, the bolometric flux can be obtained by using model data.
In practice the stars we decided to use to derive the bolometric flux calibrations fall into one of four groups:
- 1.
- stars with full
 data;
data;
- 2.
- stars with
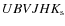 data;
data;
- 3.
- stars with
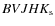 data;
data;
- 4.
- stars with
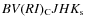 data.
data.
For each group one may compute
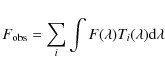 |
(6) |
where the sum is extended to all the available bands and
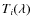 is the response function of the
i
is the response function of the
i band, the integrals must be considered extended
from 0 to infinity, formally, although in practise the response
function of each filter vanishes outside a finite interval
and numerically one stops integrating outside this interval.
One can then use the models to compute the correction
band, the integrals must be considered extended
from 0 to infinity, formally, although in practise the response
function of each filter vanishes outside a finite interval
and numerically one stops integrating outside this interval.
One can then use the models to compute the correction
where A is a function of
 ,
,
 and [Fe/H].
Obviously a different A has to be computed for
any given set of available bands. The A factors
for the different band combinations we have used are
given in machine readable form at the CDS (see Sect. 3)
with different subscripts 1 to 4 corresponding to the different
band combinations.
This is again slightly different from what
was done by Alonso et al. (1995) or Casagrande et al. (2006),
who used the monochromatic fluxes at the effective wavelengths
of each band to approximate the spectral energy distribution
of the star and integrated this approximate energy distribution
over the whole interval. We only make use of integrated fluxes, which
are related to the observed magnitudes through Eq. (5)
and of the fluxes and magnitudes of Vega given in
Table 3.
and [Fe/H].
Obviously a different A has to be computed for
any given set of available bands. The A factors
for the different band combinations we have used are
given in machine readable form at the CDS (see Sect. 3)
with different subscripts 1 to 4 corresponding to the different
band combinations.
This is again slightly different from what
was done by Alonso et al. (1995) or Casagrande et al. (2006),
who used the monochromatic fluxes at the effective wavelengths
of each band to approximate the spectral energy distribution
of the star and integrated this approximate energy distribution
over the whole interval. We only make use of integrated fluxes, which
are related to the observed magnitudes through Eq. (5)
and of the fluxes and magnitudes of Vega given in
Table 3.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f2.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg93.png) |
Figure 2:
Left: empirical calibration |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f3.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg94.png) |
Figure 3: The same as Fig. 2, but for giants. |
| Open with DEXTER | |
While the 2MASS magnitudes are provided by the catalogue, it is
customary for the optical bands to provide the V magnitude and the
colours U-B, B-V, V-R, V-I.
While for the bands B to I it is straightforward to
obtain the magnitude (e.g.
R = V-(V-R)), some caution
must be exerted for the U band, for which the atmospheric
extinction is strongly varying across the band and establishes the UV
cut-off. In fact, this band has proved to be the most difficult
to standardize. Bessell (1990) provides a response curve
UX in which the atmospheric extinction is folded in
and gives the curves BX and B for the B band.
The former is to be used to compute the synthetic photometry
of the (U-B) colour, while the latter is to be used
to compute the synthetic (B-V) colour.
For the stars to be used in our bolometric flux calibration
we define the U magnitude
| U = (U-B) + V +(B-V) + (BX-B) | (8) |
where V, (U-B), and (B-V) are the observed magnitude and colours of the star, and (BX-B)is derived from the theoretical models with the requirement that it must be equal to zero for Vega. The colours (BX-B) are given in the online data at the CDS (see Sect. 3).
The bolometric flux of each star was determined as in
Alonso et al. (1995). We first determined the fluxes of each band by applying
Eq. (5) from the observed magnitudes of the star. Then
we derived the bolometric flux,
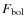 ,
using the
Eq. (7). Thus the temperature
,
using the
Eq. (7). Thus the temperature
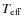 was then
determined using the IRFM that combines
was then
determined using the IRFM that combines
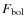 and the
monochromatic fluxes at IR wavelengths. This new value for the
effective temperature may re-enter in Eq. (7)
to derive a new
value for
and the
monochromatic fluxes at IR wavelengths. This new value for the
effective temperature may re-enter in Eq. (7)
to derive a new
value for
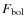 ,
and so on. This iterative procedure converges
quickly towards a final
,
and so on. This iterative procedure converges
quickly towards a final
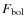 .
In each iteration, the factors
A and BX-B were determined using a trilinear interpolation within
the grid for the corresponding
.
In each iteration, the factors
A and BX-B were determined using a trilinear interpolation within
the grid for the corresponding
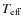 ,
,
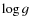 ,
and [Fe/H] of the star.
We considered the errors on the IRFM
,
and [Fe/H] of the star.
We considered the errors on the IRFM
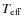 due to uncertainties
on the adopted absolute calibration of the 2MASS photometric system,
and the errors on the magnitudes
due to uncertainties
on the adopted absolute calibration of the 2MASS photometric system,
and the errors on the magnitudes
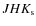
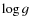 ,
and [Fe/H].
,
and [Fe/H].
We derived relations between bolometric fluxes and colours,
taking also the effects of metallicity into account.
We adopted the same fitting formula as adopted by
Casagrande et al. (2006)
where the
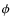 is derived as
is derived as
![$\phi(V-m,{\rm [Fe/H]})=
F_{\rm bol}/10^{-0.4m}$](/articles/aa/full_html/2009/14/aa10904-08/img97.png) , X=V-m represents the J,H,
, X=V-m represents the J,H,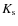 magnitudes, and ai
(i=0,...,6) are the coefficients of the fit. We
iterate the fitting procedure by discarding the points more than
2.5
magnitudes, and ai
(i=0,...,6) are the coefficients of the fit. We
iterate the fitting procedure by discarding the points more than
2.5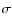 from the mean fit. We also tried other fitting formulae
such as that of Alonso et al. (1995), but they led to similar results. This
has been extensively tested by Casagrande et al. (2006), who also give fits using
optical bands.
from the mean fit. We also tried other fitting formulae
such as that of Alonso et al. (1995), but they led to similar results. This
has been extensively tested by Casagrande et al. (2006), who also give fits using
optical bands.
Table 2:
Coefficients and range of applicability of the
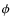 :(V-m)-[Fe/H] calibrations.
:(V-m)-[Fe/H] calibrations.
Table 3: Adopted absolute integrated fluxes and magnitudes for Vega.
For dwarf stars, we selected all the stars of group 1) from the sample
of Alonso et al. (1996a) and Ramírez & Meléndez (2005a) with uncertainties in the
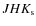 magnitudes less than 0.1 at all metallicities. We
added the stars of group 4) from the sample of Casagrande et al. (2006) with the
same restrictions and we completed the sample with stars of
groups 2) and 3) with [Fe/H] <-2. We only added metal-poor stars to
give more weight to the metal-rich stars of groups 1) and 4);
otherwise, we would end up with including all dwarf stars and the fit
would be dominated by the greater number of stars of group 3).
magnitudes less than 0.1 at all metallicities. We
added the stars of group 4) from the sample of Casagrande et al. (2006) with the
same restrictions and we completed the sample with stars of
groups 2) and 3) with [Fe/H] <-2. We only added metal-poor stars to
give more weight to the metal-rich stars of groups 1) and 4);
otherwise, we would end up with including all dwarf stars and the fit
would be dominated by the greater number of stars of group 3).
For giant stars, we applied the same restrictions but the number of
stars with Alonso et al. (1996a) and Ramírez & Meléndez (2005a) of groups 1) and 4) was
very small (only 10 stars in group 1) and 26 in group 4) with
uncertainties in the
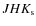 magnitudes less than 0.1), so we
decided to include all the stars of groups 2) and 3).
magnitudes less than 0.1), so we
decided to include all the stars of groups 2) and 3).
In Figs. 2 and 3 we
display the polynomial fits that represent the empirical
calibrations 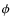 versus colours and metallicity. The coefficients
of these calibrations are given in Table 2, together
with the remaining number of stars after the 2.5
versus colours and metallicity. The coefficients
of these calibrations are given in Table 2, together
with the remaining number of stars after the 2.5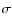 clipping and
the rms of the fit,
clipping and
the rms of the fit,
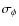 .
These calibrations show
similar behaviours to those of Alonso et al. (1995) and Alonso et al. (1999a), at
least in the metallicity range from -3 to 0.
.
These calibrations show
similar behaviours to those of Alonso et al. (1995) and Alonso et al. (1999a), at
least in the metallicity range from -3 to 0.
Table 4: Comparison with other temperature scales.
7 IRFM temperatures and angular diameters
To determine effective temperatures we need to apply
Eq. (4). The bolometric fluxes are estimated using
the empirical calibration
![$F_{\rm bol,cal} = 10^{-0.4K_{\rm s}}\phi(V-K_{\rm s},{\rm [Fe/H]})$](/articles/aa/full_html/2009/14/aa10904-08/img105.png) given
in Table 2 and the 2MASS
given
in Table 2 and the 2MASS 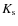 and
Johnson V magnitudes. The q- and R-factors are determined from an
initial guess of the temperature of the star,
and
Johnson V magnitudes. The q- and R-factors are determined from an
initial guess of the temperature of the star,
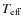 0, by
trilinear interpolation in the grid, using the surface gravity
and metallicity of the star.
Then, we determine a new value for the temperature by comparing the
theoretical bolometric flux,
0, by
trilinear interpolation in the grid, using the surface gravity
and metallicity of the star.
Then, we determine a new value for the temperature by comparing the
theoretical bolometric flux,
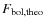 ,
derived from the
previous determination of
,
derived from the
previous determination of
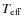 and the bolometric flux,
and the bolometric flux,
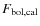 ,
using the expression:
,
using the expression:
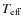
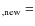
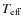
![$_{\rm ,old}[F_{\rm bol,cal}/F_{\rm
Bol,theo}]^{1/4}$](/articles/aa/full_html/2009/14/aa10904-08/img109.png) .
We again derive the q- and R-factors for
.
We again derive the q- and R-factors for
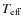
 and repeat this process iteratively until
|
and repeat this process iteratively until
|
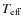
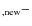
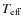
 K.
K.
The final temperature of the star is determined as the average of the
three temperatures extracted from each of 2MASS filters weighted with the
inverse of their individual errors (see Alonso et al. 1996a). The error
on the weighted mean is computed as
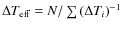 where
where
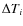 are the errors of the temperatures from
the individual filters (i=J, H,
are the errors of the temperatures from
the individual filters (i=J, H, 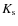 )
and N=3 is the number
of available temperatures.
These errors
)
and N=3 is the number
of available temperatures.
These errors
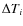 account for the photometric errors of the observed
account for the photometric errors of the observed
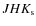 and
V magnitudes, the error on the adopted absolute calibration for the
2MASS photometric system, and the uncertainties on surface gravity and
metallicity. To estimate
and
V magnitudes, the error on the adopted absolute calibration for the
2MASS photometric system, and the uncertainties on surface gravity and
metallicity. To estimate
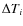 ,
we just add all
the individual errors of the i band quadratically.
,
we just add all
the individual errors of the i band quadratically.
The angular diameters have been calculated from
Eq. (1) with the derived IRFM temperatures and
bolometric fluxes. Their errors were estimated by propagating a mean
error of 1.3% in the bolometric fluxes and the errors on
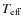 .
.
8 Comparison with other temperature scales
In this section, we compare our temperature scale with other
temperature determinations based on different implementations of the
IRFM (Casagrande et al. 2006; Ramírez & Meléndez 2005a; Alonso et al. 1999a,1996b), on the excitation equilibrium
of Fe I lines (Santos et al. 2004), and on the fitting of Balmer line
profiles (Barklem et al. 2002; Bonifacio et al. 2007). In Table 4 we gather the
mean differences between our temperatures and those of different
samples,
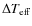 ,
together with the standard deviation
(scatter) around the mean,
,
together with the standard deviation
(scatter) around the mean,
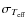 .
.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f4.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg115.png) |
Figure 4:
Comparison of our temperature scale with that of
Alonso et al. (1996a,1999a). The dashed-dotted line indicates the average
temperature difference and dashed lines the standard deviation,
|
| Open with DEXTER | |
8.1 Alonso et al. sample
The updated temperatures do not differ significantly from those of
Alonso et al. (1996a,1999a). Our temperature scale is
hotter than that of Alonso et al. (1996a,1999a) for both dwarfs and giants.
We find an average
difference
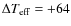 K with a
K with a
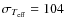 K (N=332 dwarfs) and
K (N=332 dwarfs) and
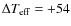 K with a
K with a
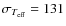 K (N=202 giants). This
translates into a mean
K (N=202 giants). This
translates into a mean
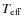 difference of
difference of
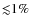 .
Although not negligible, such differences are within the error bars
of the current temperature determinations, although the scatter,
.
Although not negligible, such differences are within the error bars
of the current temperature determinations, although the scatter,
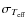 ,
seems to be quite large.
The different bolometric flux calibration, photometric data and
absolute flux calibration might be responsible for this small
difference between the two temperature scales.
Casagrande et al. (2006) checked that using the absolute calibration of
Alonso et al. (1995) and if using the TCS filters, their calibration and that
of Ramírez & Meléndez (2005a) agree within 20 K. However, to do
this exercise they had to transform the 2MASS magnitudes into the TCS
system, so their conclusions may be affected by these
transformations.
,
seems to be quite large.
The different bolometric flux calibration, photometric data and
absolute flux calibration might be responsible for this small
difference between the two temperature scales.
Casagrande et al. (2006) checked that using the absolute calibration of
Alonso et al. (1995) and if using the TCS filters, their calibration and that
of Ramírez & Meléndez (2005a) agree within 20 K. However, to do
this exercise they had to transform the 2MASS magnitudes into the TCS
system, so their conclusions may be affected by these
transformations.
Even if we select subsamples of
different mean metallicity, the
differences remain very small (see Table 4).
In conclusion, in the whole metallicity range, the systematic
difference between our temperature scale and that of
Alonso et al. (1996a,1999a) in dwarfs and giants is positive but smaller
than +65 K, which is in fact less that the average of the
individual uncertainties in our calibration (
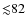 K for
dwarfs and
K for
dwarfs and
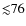 K for giants).
K for giants).
8.2 Ramírez & Meléndez sample
Ramírez & Meléndez (2005a) extend the sample of stars of Alonso et al. (1996a,1999a)
with metal-rich stars from Santos et al. (2004) and very metal-poor stars
from Christlieb et al. (2004) and Cayrel et al. (2004).
We determined effective temperatures for the
calibrators of Ramírez & Meléndez (2005a) using our implementation of the
IRFM. Our temperature scale is on average hotter than that of
Ramírez & Meléndez (2005a) by about
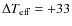 K
(
K
(
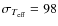 K, N=84 dwarfs) and
K, N=84 dwarfs) and
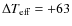 K
(
K
(
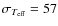 K, N=25 giants). This difference
might be partially related to the use of different absolute
calibration as we stated in Sect. 8.1.
K, N=25 giants). This difference
might be partially related to the use of different absolute
calibration as we stated in Sect. 8.1.
Among giants, we find minor differences when we look at the most
metal-poor and metal-rich stars in the sample (see
Table 4).
However, this behaviour changes when we inspect the dwarf stars.
While for metal-rich dwarfs we
find
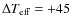 K (
K (
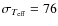 K,
N=69 dwarfs with [Fe/H] > -0.5), for metal-poor dwarfs we find
our temperature scale to be cooler:
K,
N=69 dwarfs with [Fe/H] > -0.5), for metal-poor dwarfs we find
our temperature scale to be cooler:
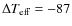 K (
K (
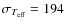 K,
N=12 dwarfs with [Fe/H] < -2.5).
We believe that this difference is mainly due to the photometric
transformations between the 2MASS and the TCS systems that
Ramírez & Meléndez (2005a) need to perform in order to derive the IRFM
temperatures.
K,
N=12 dwarfs with [Fe/H] < -2.5).
We believe that this difference is mainly due to the photometric
transformations between the 2MASS and the TCS systems that
Ramírez & Meléndez (2005a) need to perform in order to derive the IRFM
temperatures.
8.3 Casagrande et al. sample
Casagrande et al. (2006) propose a new IRFM using multiband
photometry. They derive empirical effective temperature and
bolometric flux calibration for G and K dwarfs stars in the
range -1.87 < [Fe/H] <0.34. They use
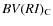 Johnson-Cousins photometry and
Johnson-Cousins photometry and
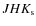 2MASS photometry.
We applied our implementation to estimating the
2MASS photometry.
We applied our implementation to estimating the
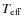 of stars in
their sample and find our temperature scale only slightly cooler
by
of stars in
their sample and find our temperature scale only slightly cooler
by
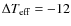 K (
K (
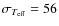 K,
N=101 dwarfs). For these stars, we estimated the reddening
corrections from the maps of dust of Schlegel et al. (1998),
corrected as described in Sect. 4.3. In
Table 4, we also compare our temperature scale with
that of Casagrande et al. (2006) by arbitrarily adopting the reddening
corrections E(B-V)=0 for all the stars, under the assumption that
all these stars are nearby and should not show any reddening at
all. We find
K,
N=101 dwarfs). For these stars, we estimated the reddening
corrections from the maps of dust of Schlegel et al. (1998),
corrected as described in Sect. 4.3. In
Table 4, we also compare our temperature scale with
that of Casagrande et al. (2006) by arbitrarily adopting the reddening
corrections E(B-V)=0 for all the stars, under the assumption that
all these stars are nearby and should not show any reddening at
all. We find
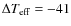 K (
K (
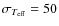 K,
N=101 dwarfs), i.e. temperatures 29 K cooler on average.
This systematic
difference is well within our error budget, so we decided to use these
reddening corrections to be consistent with other new stars included
in the sample for which we need to estimate the reddening corrections
as the dwarf stars from Bonifacio et al. (2007, see Sect. 8.6).
K,
N=101 dwarfs), i.e. temperatures 29 K cooler on average.
This systematic
difference is well within our error budget, so we decided to use these
reddening corrections to be consistent with other new stars included
in the sample for which we need to estimate the reddening corrections
as the dwarf stars from Bonifacio et al. (2007, see Sect. 8.6).
8.4 Santos et al. sample
Santos et al. (2004) have carried out a detailed spectroscopic analysis of
planet-host stars and a comparison sample of stars without known
planets. Their effective temperatures are based on the
excitation equilibrium of the Fe I lines. Our
temperature scale is only slightly hotter than that of Santos et al. (2004)
with
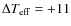 K (
K (
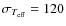 K,
N=133 dwarfs), although with a large scatter. As in the
previous section, we also derived the reddening corrections from the
Schlegel et al. (1998) dust maps, corrected as described
in Sect. 4.3. In Table 4, we also show
the comparison with E(B-V)=0.
K,
N=133 dwarfs), although with a large scatter. As in the
previous section, we also derived the reddening corrections from the
Schlegel et al. (1998) dust maps, corrected as described
in Sect. 4.3. In Table 4, we also show
the comparison with E(B-V)=0.
8.5 Cayrel et al. sample
Cayrel et al. (2004) present UVES spectroscopic observations of very
metal-poor giant stars. They derived
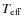 using the
using the
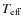 :colour-[Fe/H] calibrations of Alonso et al. (1999b).
Our
:colour-[Fe/H] calibrations of Alonso et al. (1999b).
Our
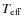 scale is hotter by
scale is hotter by
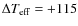 K (
K (
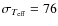 K, N=34 giants with [Fe/H] <-2.5);
however, that part of this difference
stems from the different choice made for the reddening.
Here we adopted the reddening from the dust maps of Schlegel et al. (1998),
corrected as described in Sect. 4.3, whereas
Cayrel et al. (2004) instead used the Burstein & Heiles (1982) maps. The
different choice in
reddening accounts for a difference of
K, N=34 giants with [Fe/H] <-2.5);
however, that part of this difference
stems from the different choice made for the reddening.
Here we adopted the reddening from the dust maps of Schlegel et al. (1998),
corrected as described in Sect. 4.3, whereas
Cayrel et al. (2004) instead used the Burstein & Heiles (1982) maps. The
different choice in
reddening accounts for a difference of
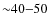 K, on average
(Cayrel et al. 2004). The remaining 75 K reflect the difference
between our calibration and that of Alonso et al. (1999b).
Unsurprisingly, this is, essentially, the same as
what was found for giant stars with [Fe/H] <-2.5 in
Sect. 8.1 (see Table 4).
K, on average
(Cayrel et al. 2004). The remaining 75 K reflect the difference
between our calibration and that of Alonso et al. (1999b).
Unsurprisingly, this is, essentially, the same as
what was found for giant stars with [Fe/H] <-2.5 in
Sect. 8.1 (see Table 4).
8.6 Bonifacio et al. sample
Bonifacio et al. (2007) present high quality spectroscopic data
of a sample of extremely metal-poor dwarf stars.
They derived the effective temperatures
by fitting the wings of the
 line. We derived
the effective temperatures of these stars using the 2MASS
line. We derived
the effective temperatures of these stars using the 2MASS
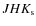 magnitudes and reddenings from Schlegel et al. (1998), corrected
as described in Sect. 4.3. Our effective
temperatures are significantly hotter than those derived from the
Balmer lines,
magnitudes and reddenings from Schlegel et al. (1998), corrected
as described in Sect. 4.3. Our effective
temperatures are significantly hotter than those derived from the
Balmer lines,
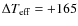 K (
K (
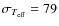 K, N=16 dwarfs with [Fe/H] <-2.5). The
difference between the temperatures derived from
K, N=16 dwarfs with [Fe/H] <-2.5). The
difference between the temperatures derived from
 ,
and those
derived by using the colour V-K in the calibrations of
Ramírez & Meléndez (2005b) is roughly
,
and those
derived by using the colour V-K in the calibrations of
Ramírez & Meléndez (2005b) is roughly 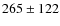 K. This
K. This 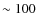 K
difference may be partially explained by our comparison with the
temperature scale of Ramírez & Meléndez (2005a) with
K
difference may be partially explained by our comparison with the
temperature scale of Ramírez & Meléndez (2005a) with
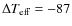 K
(see Sect. 8.2). This has an impact on the Li abundances
in extremely metal-poor stars down to [Fe/H] =-4(see Sbordone et al. 2008, in prep.), because the IRFM temperatures would
provide higher Li abundances at the lowest metallicities, whereas
K
(see Sect. 8.2). This has an impact on the Li abundances
in extremely metal-poor stars down to [Fe/H] =-4(see Sbordone et al. 2008, in prep.), because the IRFM temperatures would
provide higher Li abundances at the lowest metallicities, whereas
 temperatures seem to show a slowly decreasing trend in Li
towards lower metallicities.
temperatures seem to show a slowly decreasing trend in Li
towards lower metallicities.
Bonifacio et al. (2007) use the theory of Barklem et al. (2000) to describe the self-broadening of Balmer lines. For the same sample of stars, Bonifacio et al. (2003) instead use the Ali & Griem (1965,1966) theory and derived effective temperatures which were on average 150 K hotter, thus in substantial agreement with our IRFM temperatures.
8.7 Christlieb et al. sample
Christlieb et al. (2004) present the Hamburg/ESO R-process Enhanced Star survey
(HERES) with the aim of searching for very metal-poor stars
([Fe/H] <-2.5) with r-process elements enhanced. We selected those
stars with available B-V and V photometry in Christlieb et al. (2004) and
took the stellar parameters from Barklem et al. (2005). The effective
temperatures were estimated by averaging the resulting
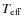 from the
different
from the
different
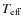 :colour-[Fe/H] calibrations of Alonso et al. (1996b) and
Alonso et al. (1999b). They followed the prescription described by
Sivarani et al. (2004). Our
:colour-[Fe/H] calibrations of Alonso et al. (1996b) and
Alonso et al. (1999b). They followed the prescription described by
Sivarani et al. (2004). Our
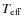 scale is significantly hotter by
scale is significantly hotter by
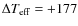 K (
K (
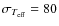 K, N=8 dwarfs with -3.1 [Fe/H] <-1.6) and
K, N=8 dwarfs with -3.1 [Fe/H] <-1.6) and
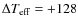 K (
K (
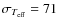 K, N=22 giants
with -3.4 [Fe/H] <-2.6). This difference probably comes from the
different adopted reddenings and the difference between our
temperature scale and that of Alonso et al. (1996a) and Alonso et al. (1999a).
K, N=22 giants
with -3.4 [Fe/H] <-2.6). This difference probably comes from the
different adopted reddenings and the difference between our
temperature scale and that of Alonso et al. (1996a) and Alonso et al. (1999a).
8.8 Barklem et al. sample
Balmer-line profile fitting in principle allows a very precise
determination of stellar effective temperature for cool stars.
Barklem et al. (2002) claim an accuracy of the temperature
determinations of 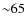 K for solar metallicity stars but for
[Fe/H]
K for solar metallicity stars but for
[Fe/H]  of
of 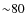 and [Fe/H]
and [Fe/H] 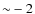 of
of
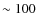 K.
Uncertainties in the theory of self-broadening,
deviations from LTE and granulation effects add
to the systematic error budget of Balmer-line based
effective temperatures.
We compared our temperature scale with that of Barklem et al. (2002).
Our temperatures are
hotter by
K.
Uncertainties in the theory of self-broadening,
deviations from LTE and granulation effects add
to the systematic error budget of Balmer-line based
effective temperatures.
We compared our temperature scale with that of Barklem et al. (2002).
Our temperatures are
hotter by
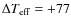 K (
K (
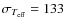 K,
N=23 dwarfs with [Fe/H] >-2.5). However, for metal-rich dwarfs with
[Fe/H] >-0.5, this difference drops to
K,
N=23 dwarfs with [Fe/H] >-2.5). However, for metal-rich dwarfs with
[Fe/H] >-0.5, this difference drops to
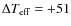 K
(
K
(
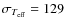 K, N=16 dwarfs with [Fe/H] >-0.5). The
average difference between the two temperature scales remains within
the uncertainties on the temperature determinations, although the
standard deviation is large.
K, N=16 dwarfs with [Fe/H] >-0.5). The
average difference between the two temperature scales remains within
the uncertainties on the temperature determinations, although the
standard deviation is large.
9 T
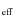 :colour-[Fe/H] calibrations
:colour-[Fe/H] calibrations
We derived relations between
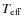 and colours, also taking
the effects of metallicity into account.
We adopted the same fitting formula that was adopted by
Alonso et al. (1999b,1996b), Ramírez & Meléndez (2005b), and Casagrande et al. (2006)
and colours, also taking
the effects of metallicity into account.
We adopted the same fitting formula that was adopted by
Alonso et al. (1999b,1996b), Ramírez & Meléndez (2005b), and Casagrande et al. (2006)
where
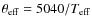 , X
represents the colour, and bi
(i=0,...,5) are the coefficients of
the fit. We iterate the fitting procedure by discarding the points
more than 2.5
, X
represents the colour, and bi
(i=0,...,5) are the coefficients of
the fit. We iterate the fitting procedure by discarding the points
more than 2.5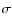 from the mean fit. All our calibrations were
adequately tested by removing some terms and/or adding higher order
terms in either X and [Fe/H]. We verified that neither removing
terms nor introducing higher order terms improves the
accuracy of the fit significantly. Therefore we adopted
Eq. (10).
from the mean fit. All our calibrations were
adequately tested by removing some terms and/or adding higher order
terms in either X and [Fe/H]. We verified that neither removing
terms nor introducing higher order terms improves the
accuracy of the fit significantly. Therefore we adopted
Eq. (10).
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{10904f5.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg159.png) |
Figure 5:
Left: empirical calibration
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{10904f6.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg160.png) |
Figure 6:
The same as Fig. 5, but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f7.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg161.png) |
Figure 7: The same as Fig. 5, but for giants. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f8.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg162.png) |
Figure 8:
The same as Fig. 5, but for
|
| Open with DEXTER | |
In Figs. 5-8,
we display the polynomial fits which represent the empirical
calibrations
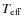 versus colours and metallicity. We discarded all
the stars with uncertainties in the
versus colours and metallicity. We discarded all
the stars with uncertainties in the
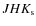 magnitudes greater
than 0.1. The coefficient of
these calibrations are given in Table 5, along
with the remaining number of stars
after the 2.5
magnitudes greater
than 0.1. The coefficient of
these calibrations are given in Table 5, along
with the remaining number of stars
after the 2.5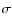 clipping and the rms of the fit,
clipping and the rms of the fit,
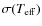 .
Normally, the number of iterations were fewer
than 20. Our polynomial fits of the colour B-V usually have similar
rms. than those provided by Ramírez & Meléndez (2005b). We should point out the
small number of giant stars with metallicities [Fe/H] >-1.5, because
most of the giant stars in the sample of Alonso et al. (1999a) are very
bright objects, hence with poor-quality 2MASS
.
Normally, the number of iterations were fewer
than 20. Our polynomial fits of the colour B-V usually have similar
rms. than those provided by Ramírez & Meléndez (2005b). We should point out the
small number of giant stars with metallicities [Fe/H] >-1.5, because
most of the giant stars in the sample of Alonso et al. (1999a) are very
bright objects, hence with poor-quality 2MASS
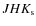 magnitudes. For dwarf stars, our empirical calibrations of V-R and
V-I have smaller rms than those of Ramírez & Meléndez (2005b). For giant
stars, the calibration of V-R shows a greater rms than in
Ramírez & Meléndez (2005b), probably due to the small number of stars in our sample.
magnitudes. For dwarf stars, our empirical calibrations of V-R and
V-I have smaller rms than those of Ramírez & Meléndez (2005b). For giant
stars, the calibration of V-R shows a greater rms than in
Ramírez & Meléndez (2005b), probably due to the small number of stars in our sample.
Table 5:
Coefficients and range of applicability of the
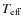 :colour-[Fe/H] calibrations.
:colour-[Fe/H] calibrations.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10904f9.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg166.png) |
Figure 9:
Comparison between the angular diameters
from Baines et al. (2008),
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10904f10.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg167.png) |
Figure 10: Same as Fig. 9, but for giants. |
| Open with DEXTER | |
On the other hand, our empirical calibrations of the colours V-J,
V-H, and
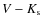 have a smaller rms than those presented
by Ramírez & Meléndez (2005b).
For giants, our fits are more accurate although our sample contains
slightly fewer giant stars than the sample of Ramírez & Meléndez (2005b).
have a smaller rms than those presented
by Ramírez & Meléndez (2005b).
For giants, our fits are more accurate although our sample contains
slightly fewer giant stars than the sample of Ramírez & Meléndez (2005b).
10 Angular diameters
The IRFM was developed to provide the
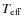 and
and 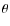 simultaneously from observed and theoretical data. One fundamental
test to the IRFM is thus the comparison with measured angular
diameters.
Ramírez & Meléndez (2005a) compare their results with measured angular diameters
from Richichi & Percheron (2002) and Kervella et al. (2004) for giant and dwarf stars,
respectively. These stars are too bright for the 2MASS
catalogue, making the 2MASS
simultaneously from observed and theoretical data. One fundamental
test to the IRFM is thus the comparison with measured angular
diameters.
Ramírez & Meléndez (2005a) compare their results with measured angular diameters
from Richichi & Percheron (2002) and Kervella et al. (2004) for giant and dwarf stars,
respectively. These stars are too bright for the 2MASS
catalogue, making the 2MASS
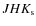 magnitudes very
uncertain. However, Baines et al. (2008) have recently presented new
measurements of angular diameters using the Center for High Angular
Resolution Astronomy (CHARA) Array, a six-element Y-shaped
interferometric array. We searched for the
magnitudes very
uncertain. However, Baines et al. (2008) have recently presented new
measurements of angular diameters using the Center for High Angular
Resolution Astronomy (CHARA) Array, a six-element Y-shaped
interferometric array. We searched for the
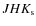 magnitudes of
the stars reported in Baines et al. (2008) and the results are presented in
Figs. 9 and 10. The stellar parameters were
adopted from Baines et al. (2008), and the metallicities were extracted from
Santos et al. (2004) and from Cayrel de Strobel et al. (2001). However, for same cases,
especially for giant stars, we did not find any available
metallicity determination, so we decided to adopt [Fe/H] =0.
The V magnitudes were extracted from the GCPD (Mermilliod et al. 1997), and
in those cases where no value was found, we took the V magnitude as
given in the SIMBAD catalogue.
One can compare our IRFM angular diameters,
magnitudes of
the stars reported in Baines et al. (2008) and the results are presented in
Figs. 9 and 10. The stellar parameters were
adopted from Baines et al. (2008), and the metallicities were extracted from
Santos et al. (2004) and from Cayrel de Strobel et al. (2001). However, for same cases,
especially for giant stars, we did not find any available
metallicity determination, so we decided to adopt [Fe/H] =0.
The V magnitudes were extracted from the GCPD (Mermilliod et al. 1997), and
in those cases where no value was found, we took the V magnitude as
given in the SIMBAD catalogue.
One can compare our IRFM angular diameters,
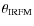 ,
with the direct measurements,
,
with the direct measurements,
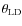 .
For dwarf stars, the average difference,
.
For dwarf stars, the average difference,
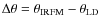 is 0.002 with a standard deviation
is 0.002 with a standard deviation
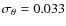 (N=22 stars).
We can also derive a direct temperature,
(N=22 stars).
We can also derive a direct temperature,
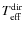 ,
from
,
from
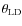 and the bolometric flux, determined from our
bolometric flux calibration, by using Eq. (1). The
previous comparison between angular diameters thus translates into a
temperature difference,
and the bolometric flux, determined from our
bolometric flux calibration, by using Eq. (1). The
previous comparison between angular diameters thus translates into a
temperature difference,
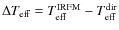 ,
of -32 with
,
of -32 with
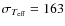 (N=22 stars).
For giants, the number of stars with relatively accurate
(N=22 stars).
For giants, the number of stars with relatively accurate
 data is low. The sample of Baines et al. (2008) contains only six giant stars.
For these stars, we find
data is low. The sample of Baines et al. (2008) contains only six giant stars.
For these stars, we find
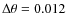 with a
with a
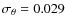 which translates into
which translates into
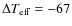 with a
with a
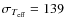 .
These results are also given in Table 4 in comparison
with other temperature determinations.
Our new implementation of the IRFM provides
good results when comparing with direct measurements of angular
diameters.
The absence of any trend with metallicity in the
residuals shown in Fig. 9 over almost
1 dex in metallicity is very encouraging.
This suggests that the model atmospheres
correctly model the variation of fluxes with metallicity.
Since the metal-rich range is the most difficult for
modelling the opacity, it is reasonable to
expect that the models are also reliable
at low metallicity.
In other words, we do not expect that our temperature
scale has spurious trends with metallicity due
to inadequate modelling of the stellar atmospheres.
.
These results are also given in Table 4 in comparison
with other temperature determinations.
Our new implementation of the IRFM provides
good results when comparing with direct measurements of angular
diameters.
The absence of any trend with metallicity in the
residuals shown in Fig. 9 over almost
1 dex in metallicity is very encouraging.
This suggests that the model atmospheres
correctly model the variation of fluxes with metallicity.
Since the metal-rich range is the most difficult for
modelling the opacity, it is reasonable to
expect that the models are also reliable
at low metallicity.
In other words, we do not expect that our temperature
scale has spurious trends with metallicity due
to inadequate modelling of the stellar atmospheres.
11 Summary
We have made use of the IRFM to determine effective temperatures
of 555 dwarf and subgiant field stars and of 264 giant field stars.
Our implementation of the IRFM uses the 2MASS photometric system as a
reference system to perform all the calculations. We derived a
bolometric flux calibration down to metallicities of [Fe/H] =-3.5
for dwarfs and -4.0 for giants, as a function of the 2MASS
magnitude, m, and the colour, V-m. We computed theoretical
magnitudes by integrating the ATLAS models in the 2MASS
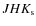 filters.
filters.
Our temperature scale is hotter than that of Alonso et al. (1996a,1999a) by
 K (
K (
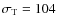 K, N=332 dwarfs) and
K, N=332 dwarfs) and
 K (
K (
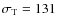 K, N=202 giants). Similar
results are found when comparing with Ramírez & Meléndez (2005a). However,
interestingly, for dwarfs stars with [Fe/H] <-2.5, the
comparison with the sample of Ramírez & Meléndez (2005a) provides a difference of
K, N=202 giants). Similar
results are found when comparing with Ramírez & Meléndez (2005a). However,
interestingly, for dwarfs stars with [Fe/H] <-2.5, the
comparison with the sample of Ramírez & Meléndez (2005a) provides a difference of
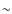 -87 K (
-87 K (
 K, N=12 dwarfs).
We believe this difference is related to Ramírez & Meléndez (2005a)
transforming the 2MASS
K, N=12 dwarfs).
We believe this difference is related to Ramírez & Meléndez (2005a)
transforming the 2MASS
 magnitudes to the TCS photometric
system to derive bolometric fluxes and effective temperatures
for their calibrators at the lowest metallicities, whereas we
determine the bolometric fluxes and effective temperatures in the
2MASS photometric system.
magnitudes to the TCS photometric
system to derive bolometric fluxes and effective temperatures
for their calibrators at the lowest metallicities, whereas we
determine the bolometric fluxes and effective temperatures in the
2MASS photometric system.
Our
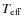 are hotter than those estimated using
are hotter than those estimated using 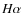 line profiles
by
line profiles
by
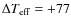 K (Barklem et al. 2002,
K (Barklem et al. 2002,
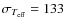 K, N=23 dwarfs with [Fe/H] >-2.5) and
K, N=23 dwarfs with [Fe/H] >-2.5) and
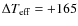 K (Bonifacio et al. 2007,
K (Bonifacio et al. 2007,
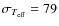 K, N=16 dwarfs with [Fe/H] <-2.5).
This result has implications for the Li abundances for very
metal-poor stars down to [Fe/H] =-4. Higher temperatures provide
higher Li abundances; therefore, the drop of the Li abundances
towards lower metallicities will cancel out, and the Li abundances
would remain in a plateau.
K, N=16 dwarfs with [Fe/H] <-2.5).
This result has implications for the Li abundances for very
metal-poor stars down to [Fe/H] =-4. Higher temperatures provide
higher Li abundances; therefore, the drop of the Li abundances
towards lower metallicities will cancel out, and the Li abundances
would remain in a plateau.
We derived
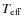 versus colour empirical calibrations,
which are compatible with those presented by
Alonso et al. (1999b,1996b), Ramírez & Meléndez (2005b), Casagrande et al. (2006),
within the quoted errors.
For those who wish to use 2MASS photometry to estimate effective
temperatures for a wide range of metallicities, we recommend
our calibration, which were derived within
the 2MASS system, rather than the others, which are either
based on different systems or on hybrid systems.
Our calibrations exploit the excellent internal consistency
of the 2MASS photometry and should provide accurate
temperatures in a relative sense.
In an absolute sense, our calibrations are of the same
quality as the other calibrations.
versus colour empirical calibrations,
which are compatible with those presented by
Alonso et al. (1999b,1996b), Ramírez & Meléndez (2005b), Casagrande et al. (2006),
within the quoted errors.
For those who wish to use 2MASS photometry to estimate effective
temperatures for a wide range of metallicities, we recommend
our calibration, which were derived within
the 2MASS system, rather than the others, which are either
based on different systems or on hybrid systems.
Our calibrations exploit the excellent internal consistency
of the 2MASS photometry and should provide accurate
temperatures in a relative sense.
In an absolute sense, our calibrations are of the same
quality as the other calibrations.
A comparison of IRFM angular diameters with interferometric measurements of angular diameters from Baines et al. (2008) provides good agreement for both dwarf and giant stars. This gives us confidence that our new implementation of the IRFM is reasonable.
Acknowledgements
We are very grateful to Ivan Ramírez & Jorge Meléndez for kindly providing us with the photometric data that they collected in 2005 for dwarf and giant stars of Alonso et al. We acknowledge support from the EU contract MEXT-CT-2004-014265 (CIFIST). This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France.
References
- Ali, A. W., & Griem, H. R. 1965, Phys. Rev., 140, 1044 In the text
- Ali, A. W., & Griem, H. R. 1966, Phys. Rev., 144, 366 In the text
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1994, A&A, 282, 684 In the text
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1995, A&A, 297, 197 In the text
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996a, A&AS, 117, 227 In the text
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996b, A&A, 313, 873 In the text
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999a, A&AS, 139, 335 In the text
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999b, A&AS, 140, 261 In the text
- Asplund, M. 2005, ARA&A, 43, 481 In the text
- Baines, E. K., McAlister, H. A., Brummelaar, T. A. T., et al. 2008, ApJ, 682, 577 In the text
- Barklem, P. S. 2007, A&A, 466, 327 In the text
- Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&A, 363, 1091 In the text
- Barklem, P. S., Stempels, H. C., Allende Prieto, C., et al. 2002, A&A, 385, 951 In the text
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 In the text
- Bessell, M. S. 1990, PASP, 102, 1181 In the text
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 In the text
- Blackwell, D. E., & Petford, A. D. 1991, A&A, 250, 459 In the text
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 In the text
- Blackwell, D. E., Petford, A. D., Arribas, S., Haddock, D. J., & Selby, M. J. 1990, A&A, 232, 396 In the text
- Bonifacio, P., & Molaro, P. 1997, MNRAS, 285, 847 In the text
- Bonifacio, P., Monai, S., & Beers, T. C. 2000a, AJ, 120, 2065 In the text
- Bonifacio, P., Caffau, E., & Molaro, P. 2000b, A&AS, 145, 473 In the text
- Bonifacio, P., et al. 2003, Elemental
Abundances in Old Stars
and Damped Lyman-
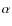 Systems, 25th meeting of the IAU, Joint
Discussion 15, 22 July 2003, Sydney, Australia, ed. P. E. Nissen,
M. Pettini,
O. Engvold
(San Francisco, CA: ASP),
Highlights of Astronomy, 13, 581
In the text
Systems, 25th meeting of the IAU, Joint
Discussion 15, 22 July 2003, Sydney, Australia, ed. P. E. Nissen,
M. Pettini,
O. Engvold
(San Francisco, CA: ASP),
Highlights of Astronomy, 13, 581
In the text
- Bonifacio, P., Molaro, P., & Sivarani, T. 2007, A&A, 462, 851 In the text
- Brown, T. M., Charbonneau, D., Gilliland, R. L., Noyes, R. W., & Burrows, A. 2001, ApJ, 552, 699 In the text
- Burstein D., & Heiles C., 1982, AJ, 87, 1165 In the text
- Castelli, F., & Kurucz, R. L. 1994, A&A, 281, 817 In the text
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp. 210, A20P [arXiv:astro-ph/0405087v1] In the text
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 In the text
- Cayrel de Strobel, G., Soubiran, C., & Ralite, N. 2001, A&A, 373, 159 In the text
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 In the text
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 In the text
- Christlieb, N., Beers, T. C., Barklem, P. S., et al. 2004, A&A, 428, 1027 In the text
- Cutri, R. M., et al. 2003, The IRSA 2MASS All-Sky Point Source Catalog, NASA/IPAC Infrared Science Archive, http://www.ipac.caltech.edu/2mass/releases/allsky/doc/explsup.html In the text
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 In the text
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 In the text
- Hayes, D. S. 1985, Calibration of Fundamental Stellar Quantities, 111, 225 In the text
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 In the text
- Kervella, P., Mérand, A., Pichon, B., et al. 2008, A&A, 488, 667 In the text
- Kurucz, R. L. 1993, ATLAS9 Stellar Atmospheres
Programs and 2
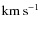 Grid, CD-ROM No. 13, Smithsonian Astrophysical Observatory,
Cambridge, MA, USA.
Grid, CD-ROM No. 13, Smithsonian Astrophysical Observatory,
Cambridge, MA, USA.
- Ludwig, H.-G., Behara, N. T., Steffen, M., & Bonifacio, P. 2009, A&A, in preparation In the text
- Magain, P. 1987, A&A, 181, 323 In the text
- McCall, M. L. 2004, AJ, 128, 2144 In the text
- Meléndez, J., & Ramírez, I. 2004, ApJ, 615, L33 In the text
- Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 In the text
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 In the text
- Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 In the text
- Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 In the text
- Richichi, A., & Percheron, I. 2002, A&A, 386, 492 In the text
- Ryan, S. G., Beers, T. C., Deliyannis, C. P., & Thorburn, J. A. 1996, ApJ, 458, 543 In the text
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 In the text
- Santos, N. C., Israelian, G., Mayor, M., et al. 2005, A&A, 437, 1127 In the text
- Sbordone et al. 2008, A&A, in preparation In the text
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 In the text
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 In the text
- Shchukina, N. G., Trujillo Bueno, J., & Asplund, M. 2005, ApJ, 618, 939
- Sivarani, T., Bonifacio, P., Molaro, P., et al. 2004, A&A, 413, 1073 In the text
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 In the text
- Spergel, D. N., Bean, R., & Doré, O. Å. 2003, ApJS, 148, 175 In the text
- Spergel, D. N., Verde, L., & Peiris, H. V. Å. 2007, ApJS, 170, 377 In the text
- Spite, M., & Spite, F. 1982, Nature, 297, 483 In the text
- Spite, F., & Spite, M. 1982, A&A, 115, 357 In the text
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 In the text
- Thévenin, F., & Idiart, T. P. 1999, ApJ, 521, 753 In the text
Footnotes
- ... catalogue
![[*]](/icons/foot_motif.png)
- Tables as described in Sect. 3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/497/497
- ...
![[*]](/icons/foot_motif.png)
- Cosmological Impact of the First STars (CIFIST) Marie Curie Excellence Team.
- ...
2MASS
![[*]](/icons/foot_motif.png)
- The 2MASS catalogue can be accessed at http://www.ipac.caltech.edu/2mass/.
- ...Castelli & Kurucz (2003)
![[*]](/icons/foot_motif.png)
- http://wwwuser.oats.inaf.it/castelli/grids.html
- ... CDS
![[*]](/icons/foot_motif.png)
- http://cdsweb.u-strasbg.fr/
- ... Simbad
![[*]](/icons/foot_motif.png)
- http://simbad.u-strasbg.fr/simbad/.
- ...Castelli & Kurucz (1994)
![[*]](/icons/foot_motif.png)
- http://wwwuser.oats.inaf.it/castelli/vega/fm05t9550g395k2odfnew.dat
All Tables
Table 1: Monochromatic Fluxes for Vega from the calibrated ATLAS 9 flux.
Table 2:
Coefficients and range of applicability of the
![]() :(V-m)-[Fe/H] calibrations.
:(V-m)-[Fe/H] calibrations.
Table 3: Adopted absolute integrated fluxes and magnitudes for Vega.
Table 4: Comparison with other temperature scales.
Table 5:
Coefficients and range of applicability of the
![]() :colour-[Fe/H] calibrations.
:colour-[Fe/H] calibrations.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{10904f1.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg78.png) |
Figure 1:
Spectral energy distribution of the ATLAS model of Vega
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f2.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg93.png) |
Figure 2:
Left: empirical calibration |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f3.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg94.png) |
Figure 3: The same as Fig. 2, but for giants. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f4.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg115.png) |
Figure 4:
Comparison of our temperature scale with that of
Alonso et al. (1996a,1999a). The dashed-dotted line indicates the average
temperature difference and dashed lines the standard deviation,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{10904f5.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg159.png) |
Figure 5:
Left: empirical calibration
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{10904f6.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg160.png) |
Figure 6:
The same as Fig. 5, but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f7.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg161.png) |
Figure 7: The same as Fig. 5, but for giants. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{10904f8.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg162.png) |
Figure 8:
The same as Fig. 5, but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10904f9.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg166.png) |
Figure 9:
Comparison between the angular diameters
from Baines et al. (2008),
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10904f10.ps}
\end{figure}](/articles/aa/full_html/2009/14/aa10904-08/Timg167.png) |
Figure 10: Same as Fig. 9, but for giants. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




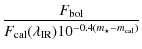
![$\displaystyle q(\lambda_{\rm IR}{\rm ,}T_{\rm eff}{\rm ,[Fe/H]}, \log g)$](/articles/aa/full_html/2009/14/aa10904-08/img64.png)

![$\displaystyle R_{\rm theo}(\lambda_{\rm IR}{\rm ,}T_{\rm eff}{\rm ,[Fe/H]}, \log g).$](/articles/aa/full_html/2009/14/aa10904-08/img66.png)
 )
in the infrared. The solid and dashed-dotted lines
represent the intensity and continuum flux, respectively. The filled
circles are the monochromatic fluxes adopted by
)
in the infrared. The solid and dashed-dotted lines
represent the intensity and continuum flux, respectively. The filled
circles are the monochromatic fluxes adopted by 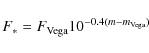
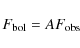
 -[Fe/H]
for dwarfs in the metallicity bins
-[Fe/H]
for dwarfs in the metallicity bins
![$-0.5 < [{\rm Fe}/{\rm H}] \le 0.5$](/articles/aa/full_html/2009/14/aa10904-08/img8.png) (filled circles),
(filled circles),
![$-1.5 < [{\rm Fe}/{\rm H}] \le -0.5$](/articles/aa/full_html/2009/14/aa10904-08/img9.png) ( open circles),
( open circles),
![$-2.5 < [{\rm Fe}/{\rm H}] \le -1.5$](/articles/aa/full_html/2009/14/aa10904-08/img10.png) ( triangles), and
( triangles), and
![$[{\rm Fe}/{\rm H}] \le -2.5$](/articles/aa/full_html/2009/14/aa10904-08/img11.png) ( diamonds). The lines
correspond to our calibration for
( diamonds). The lines
correspond to our calibration for
![$[{\rm Fe}/{\rm H}]=0$](/articles/aa/full_html/2009/14/aa10904-08/img12.png) ( solid
line), -1.0 ( dotted line), -2.0 ( dashed line), -3.0
( dotted-dashed line). Right: residuals of the fit
(
( solid
line), -1.0 ( dotted line), -2.0 ( dashed line), -3.0
( dotted-dashed line). Right: residuals of the fit
(
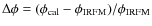 )
as a function
of
)
as a function
of
![$\displaystyle \phi(X,{\rm [Fe/H]}) = a_0 + a_1 X + a_2 X^2 + a_3 X^3
+a_4 X {\rm [Fe/H]} + a_5 {\rm [Fe/H]} + a_6 {\rm [Fe/H]}^2$](/articles/aa/full_html/2009/14/aa10904-08/img96.png)
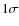 ,
from the average (see text).
,
from the average (see text).![\begin{displaymath}\theta_{\rm eff}\!=\!b_0 + b_1 X + b_2 X^2 + b_3 X {\rm [Fe/H]} + b_4 {\rm [Fe/H]} + b_5
{\rm [Fe/H]}^2~
\end{displaymath}](/articles/aa/full_html/2009/14/aa10904-08/img156.png)
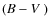 -[Fe/H] for
dwarfs in the metallicity bins
-[Fe/H] for
dwarfs in the metallicity bins
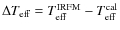 )
as a function
of (B-V).
)
as a function
of (B-V).
 ,
are also shown containing the uncertainties of both
,
are also shown containing the uncertainties of both