| Issue |
A&A
Volume 497, Number 2, April II 2009
|
|
|---|---|---|
| Page(s) | 325 - 334 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200810781 | |
| Published online | 24 February 2009 | |
Non-thermal emission from microquasar/ISM interaction
P. Bordas1 - V. Bosch-Ramon2 - J. M. Paredes1 - M. Perucho3
1 - Departament d'Astronomia i Meteorologia and Institut de Ciències del Cosmos (ICC), Universitat de Barcelona (UB/IEEC), Martí i Franquès 1, 08028 Barcelona, Spain
2 - Max Planck Institut für Kernphysik, Saupfercheckweg 1, Heidelberg 69117, Germany
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received 11 August 2008 / Accepted 11 December 2008
Abstract
Context. The interaction of microquasar jets with their environment can produce non-thermal radiation as in the case of extragalactic outflows impacting on their surroundings. Significant observational evidence of jet/medium interaction in galactic microquasars has been collected in the past few years, although little theoretical work has been done regarding the resulting non-thermal emission.
Aims. In this work, we investigate the non-thermal emission produced in the interaction between microquasar jets and their environment, and the physical conditions for its production.
Methods. We developed an analytical model based on those successfully applied to extragalactic sources. The jet is taken to be a supersonic and mildly relativistic hydrodynamical outflow. We focus on the jet/shocked medium structure in its adiabatic phase, and assume that it grows in a self-similar way. We calculate the fluxes and spectra of the radiation produced via synchrotron, inverse Compton, and relativistic bremsstrahlung processes by electrons accelerated in strong shocks. A hydrodynamical simulation is also performed to investigate further the jet interaction with the environment and check the physical parameters used in the analytical model.
Results. For reasonable values of the magnetic field, and using typical values of the external matter density, the non-thermal particles could produce significant amounts of radiation at different wavelengths, although they do not cool primarily radiatively, but by adiabatic losses. The physical conditions of the analytical jet/medium interaction model are consistent with those found in the hydrodynamical simulation.
Conclusions. Microquasar jet termination regions could be detectable at radio wavelengths for current instruments sensitive to  arcminute scales. At X-ray energies, the expected luminosities are moderate, although the emitter is more compact than the radio one. The source may be detectable by XMM-Newton or Chandra, with 1-10 arcsec of angular resolution. The radiation at gamma-ray energies may be within the detection limits of the next generation of satellite and ground-based instruments.
arcminute scales. At X-ray energies, the expected luminosities are moderate, although the emitter is more compact than the radio one. The source may be detectable by XMM-Newton or Chandra, with 1-10 arcsec of angular resolution. The radiation at gamma-ray energies may be within the detection limits of the next generation of satellite and ground-based instruments.
Key words: ISM: jets and outflows - X-rays: binaries - radiation mechanisms: non-thermal
1 Introduction
Microquasars (MQ) are radio-emitting X-ray binaries (REXB) that display relativistic ejections (Mirabel & Rodríguez 1999). The binary system is formed by a compact object, a neutron star or a black hole, and a normal (non-degenerate) star. The relativistic ejections may be transient or persistent (Ribó 2005), with duty cycles of jet activity that vary from source to source. The steady jets are formed during the so-called Low/Hard state (Fender et al. 2001), and are expected to be only mildly relativistic (Gallo et al. 2003). Presently, about 15 MQs are known in the Milky Way (Paredes 2005), although some authors have proposed that many if not all REXBs could be MQs (e.g. Fender 2004). Thus, the true number of MQs in our galaxy could be significantly higher.
MQs are regarded as scaled-down versions of distant quasars since they exhibit many of the characteristics in common with extragalactic sources. They serve as suitable scenarios for understanding a number of processes, such as mass accretion onto the compact object or jet formation and evolution, on timescales inaccessible in the case of quasars. In analogy with radio-loud quasars, which have jets impacting onto the intracluster medium, one may also expect to find radiative signatures due to strong shocks in the termination regions of MQ jets. Hot spots and double-lobe morphologies are common features of the powerful extragalactic FRII sources (Faranoff & Riley 1974), in which a variety of large-scale non-thermal structures are evident at radio wavelengths. In the case of MQs, evidence of jet interaction with the interstellar medium (ISM) are not numerous, partially due to the relatively small number of known sources. Nevertheless, hints or evidence of these interactions have been observed, at different wavelengths, in SS 433 (Zealey et al. 1980), 1E 1740.7-2942 (Mirabel et al. 1992), XTE J1550-564 (Corbel et al. 2002), Cygnus X-3 (Heindl et al. 2003), Cygnus X-1 (Martí et al. 1996; Gallo et al. 2005), GRS 1915+105 (Kaiser et al. 2004), H1743-322 (Corbel et al. 2005), LS I +61 303 (Paredes et al. 2007a), and Circinus X-1 (Tudose et al. 2006), although little theoretical work has been completed regarding the hydrodynamics of the interaction, or the resulting non-thermal emission (e.g. Aharonian & Atoyan 1998; Velázquez & Raga 2000; Heinz & Sunyaev 2002; Bosch-Ramon et al. 2005; Perucho & Bosch-Ramon 2008).
MQ ejections can transport significant amounts of kinetic energy and momentum far from the binary system. The product of the age of the source and its jet kinetic power,
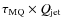 ,
can be as high as 1012 s
,
can be as high as 1012 s
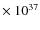 -1039 erg s
-1039 erg s
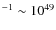 -1051 erg (see. e.g., Cygnus X-1, Gallo et al. 2005; SS 433, Zealey et al. 1980). MQ jet termination regions could produce significant fluxes if they were at distances of few kpc. It could well be that MQs were associated, by their interaction with their surrounding medium, with some of the extended non-thermal radio sources detected in the Galaxy of unknown origin (e.g., Paredes et al. 2007b).
-1051 erg (see. e.g., Cygnus X-1, Gallo et al. 2005; SS 433, Zealey et al. 1980). MQ jet termination regions could produce significant fluxes if they were at distances of few kpc. It could well be that MQs were associated, by their interaction with their surrounding medium, with some of the extended non-thermal radio sources detected in the Galaxy of unknown origin (e.g., Paredes et al. 2007b).
In this work, we investigate whether a typical MQ fulfills the conditions to be detectable when interacting with the surrounding external gas. We adopt some reasonable assumptions for the MQ power and age, and the density of the ISM, as well as for the non-thermal energy and magnetic field equipartition fraction in the interaction regions. We study the case of a high-mass system to observe the role of a massive and hot companion. In the case of a low-mass system, the radiation field of the companion star and therefore the inverse Compton (IC) contribution would be much lower.
This paper is organized as follows. In Sect. 2, we present an analytical interaction model to characterize the three shocked zones; for each region, we study the main properties of the non-thermal emitters, and establish the physical conditions and geometry. In Sect. 3, we calculate the total emission produced by synchrotron, relativistic bremsstrahlung, and IC processes for the different set of parameters used in the model. We carried out hydrodynamical simulations to study in more detail the jet evolution when interacting with the ambient medium. These simulations allow us also to test and enforce the validity of the assumptions of the analytical model. This is achieved in Sect. 4. The details of the hydrodynamical simulations can be found in Appendix A. Finally, in Sect. 5 we discuss the obtained results, providing detectability predictions at different energy bands.
2 Model description
We use a model adapted from those applied to extragalactic sources to investigate the interactions of MQ jets with their environment. Falle (1991) and Kaiser & Alexander (1997) developed an analytical model in which self-similarity was used to characterize the evolution of the jet/medium interaction structures in radio galaxies. We closely followed their work, including minor modifications necessary in appling the model in the MQ context.
We consider twin conical jets emerging from the central source in opposite directions. The ejecta begin to decelerate when the mass of the swept-up external gas becomes similar to the mass carried by the jet. Two shocks are formed at the jet tip: a forward shock (the bow-shock) propagating into the ISM and a reverse shock directed inwards into the jet material. Matter crossing the reverse shock inflates the cocoon, which protects the jet from disruption due to turbulent gas entrainment. A reconfinement shock is also formed in the jet at the point where its pressure equals that of the cocoon.
In our scenario, the shocks are assumed to be strong. The density and pressure of the shocked material are calculated using the Rankine-Hugoniot conditions for a strong shock at each front. We note that since the conditions in the shocked regions evolve with time, all related physical variables will also vary with time. Therefore, the non-thermal particle population is calculated by considering the time dependence of the radiative and adiabatic losses (see Sect. 2.3). Given that all the considered shocks are weakly relativistic, we adopt an adiabatic index
 .
We assume the presence of a randomly oriented magnetic field B in the downstream regions, derived by assuming the magnetic energy density to be
.
We assume the presence of a randomly oriented magnetic field B in the downstream regions, derived by assuming the magnetic energy density to be  10% (
10% (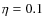 )
of the thermal energy density. In each shock region, the fraction of kinetic luminosity transferred into non-thermal particles is assumed to be 1% (
)
of the thermal energy density. In each shock region, the fraction of kinetic luminosity transferred into non-thermal particles is assumed to be 1% ( ).
).
2.1 The properties of the three emitting zones
We focus our study on three separated emitting zones. The first zone, the shell region, corresponds to the ISM material swept-up by the bow-shock. The second, the cocoon region, corresponds to the material of the jet crossing the reverse shock. The third zone accounts for the shocked jet material after crossing the conical reconfinement shock. A sketch of the model is shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0781fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg18.png) |
Figure 1:
Scheme of the model (not to scale) representing the three different zones. The central binary system is located at the center. Two jets emerge from it and extent outwards until they are effectively decelerated at a distance of |
| Open with DEXTER | |
2.1.1 Bow-shock
We are interested in the case in which the bow-shock can accelerate particles, and we concentrate on its adiabatic
phase (see Sedov 1959), which implies that the inertia of the medium must be large enough to take a significant fraction of the energy and momentum from the jet. Although in the extragalactic context the non-thermal radio emission is understood to originate solely from the shocked jet material in the cocoon, we explore the possibility of having also a contribution from the shocked ISM material. After the interaction structures have reached a characteristic length-scale
![$l_{\rm0}=[Q_{\rm jet}^{2}/\rho_{\rm ISM}^{2}c^{6}(\Gamma_{\rm jet}-1)^3]^{1/4}$](/articles/aa/full_html/2009/14/aa10781-08/img19.png) ,
where
,
where
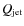 is the jet power,
is the jet power,
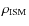 is the ISM mass density,
is the ISM mass density,
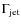 is the jet bulk Lorentz factor and c is the speed of light, the equations for the length and velocity of the bow-shock at a given source age
is the jet bulk Lorentz factor and c is the speed of light, the equations for the length and velocity of the bow-shock at a given source age
 are (see Falle 1991 and Kaiser & Alexander 1997):
are (see Falle 1991 and Kaiser & Alexander 1997):
 |
(1) |
and
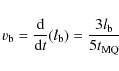 |
(2) |
respectively. The dimensionless constant
 depends on the adiabatic index of the jet material and the geometry of the bow-shock. The pressure in the shell can be calculated to be
depends on the adiabatic index of the jet material and the geometry of the bow-shock. The pressure in the shell can be calculated to be
 .
.
To determine the radius of the bow-shock, 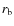 ,
we assume a self-similar relationship between its length and width given by
,
we assume a self-similar relationship between its length and width given by
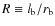 ,
which can vary from source to source in the range
,
which can vary from source to source in the range
![$R\in [2-3]$](/articles/aa/full_html/2009/14/aa10781-08/img30.png) (see Leahy et al. 1989; Kaiser et al. 2004; Perucho & Martí 2007). Here, we use a fiducial value of R=3 (similar to the value from our simulations; see Appendix A). We assume a plane shock and do not consider in detail the precise geometry of the bow-shock. Nevertheless, we need to know the accelerator size to compute the maximum energies the particles can reach, as well as estimate the emitter size required in providing the surface brightness of the source. For the bow-shock, both the accelerator and the emitter size are taken to be
(see Leahy et al. 1989; Kaiser et al. 2004; Perucho & Martí 2007). Here, we use a fiducial value of R=3 (similar to the value from our simulations; see Appendix A). We assume a plane shock and do not consider in detail the precise geometry of the bow-shock. Nevertheless, we need to know the accelerator size to compute the maximum energies the particles can reach, as well as estimate the emitter size required in providing the surface brightness of the source. For the bow-shock, both the accelerator and the emitter size are taken to be 
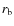 .
The mass density and the pressure, which was assumed to equal that of the cocoon, were taken to be homogeneous in the entire shell. Since the bow-shock velocity evolves with time, the mass density and the pressure vary as well. Therefore, the magnetic energy density also varies with time. Finally, the radiation field energy density depends on
.
The mass density and the pressure, which was assumed to equal that of the cocoon, were taken to be homogeneous in the entire shell. Since the bow-shock velocity evolves with time, the mass density and the pressure vary as well. Therefore, the magnetic energy density also varies with time. Finally, the radiation field energy density depends on  ,
,
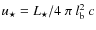 (where
(where 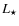 is the companion luminosity).
is the companion luminosity).
2.1.2 Cocoon
The cocoon is filled with jet material that crosses the reverse shock. A contact discontinuity separates the cocoon and the shell region materials. We do not consider the mixing of the gas of both zones that could occur due to Kevin-Helmholtz and/or Rayleigh-Taylor instabilities.
The cocoon pressure is assumed to equal that of the other side of the contact discontinuity at any time,
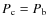 .
Given the strong compression of the ISM gas in the shell zone, the length and the width of the cocoon are taken to be also
.
Given the strong compression of the ISM gas in the shell zone, the length and the width of the cocoon are taken to be also 
 and
and 
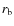 ,
respectively. For the accelerator size and the reverse shock, we adopt the constant jet width after the reconfinement point (see below). The pressure and mass density of the material can be taken as homogeneous for the entire cocoon to first order approximation. The homogeneity assumption comes from the fact that the cocoon material is expected to be subsonic. Both pressure and mass density will depend on the time evolution of the reverse shock velocity, like the magnetic and radiation fields, in the same way as for the shell.
,
respectively. For the accelerator size and the reverse shock, we adopt the constant jet width after the reconfinement point (see below). The pressure and mass density of the material can be taken as homogeneous for the entire cocoon to first order approximation. The homogeneity assumption comes from the fact that the cocoon material is expected to be subsonic. Both pressure and mass density will depend on the time evolution of the reverse shock velocity, like the magnetic and radiation fields, in the same way as for the shell.
2.1.3 Reconfinement region
The conical jet emergig initially from the central engine has an opening angle
 rad, where z is the distance to the injection point and r is the jet radius. Given the pressure exerted by the surrounding cocoon, the jet radius becomes approximately constant at
rad, where z is the distance to the injection point and r is the jet radius. Given the pressure exerted by the surrounding cocoon, the jet radius becomes approximately constant at
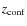 ,
the distance at which the lateral jet pressure becomes similar to the cocoon one. Following Kaiser & Alexander (1997), we obtain the following radius for the reconfined jet:
,
the distance at which the lateral jet pressure becomes similar to the cocoon one. Following Kaiser & Alexander (1997), we obtain the following radius for the reconfined jet:
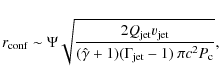 |
(3) |
where
 is the adiabatic index of the cocoon material and
is the adiabatic index of the cocoon material and
 is the jet velocity. (for a recent semi-analytical treatment of reconfinement shocks, see Nalewajko & Sikora 2008). After injection downstream, the shocked material continues to move almost at the jet velocity. The normal component of the reconfinement shock velocity, i.e., that affected by a discontinuity, is much smaller than
is the jet velocity. (for a recent semi-analytical treatment of reconfinement shocks, see Nalewajko & Sikora 2008). After injection downstream, the shocked material continues to move almost at the jet velocity. The normal component of the reconfinement shock velocity, i.e., that affected by a discontinuity, is much smaller than
 .
The jet retains most of its thrust and remains supersonic until it is braked at the reverse shock. From the reconfinement point, the jet roughly keeps a constant radius. We neglect further recollimation shocks that may occur (see Appendix A).
.
The jet retains most of its thrust and remains supersonic until it is braked at the reverse shock. From the reconfinement point, the jet roughly keeps a constant radius. We neglect further recollimation shocks that may occur (see Appendix A).
The size of the accelerator is taken to be the width of the jet at the recollimation shock,
 .
Once accelerated, relativistic particles are advected approximately to the jet velocity, and propagate to the reverse shock. The length of the emitter, assumed to be one-dimensional, is therefore taken to be
.
Once accelerated, relativistic particles are advected approximately to the jet velocity, and propagate to the reverse shock. The length of the emitter, assumed to be one-dimensional, is therefore taken to be 
 ,
since
,
since
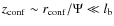 .
The magnetic field in the reconfinement region is derived as in the other interaction zones. The radiation density, however, gradually decays from
.
The magnetic field in the reconfinement region is derived as in the other interaction zones. The radiation density, however, gradually decays from
 to
to  as the inverse square of the distance to the companion star. The density and the pressure are considered to remain roughly constant after the reconfinement point since the jet radius is constant beyond
as the inverse square of the distance to the companion star. The density and the pressure are considered to remain roughly constant after the reconfinement point since the jet radius is constant beyond
 .
.
2.2 The non-thermal particle populations
The theory of diffusive shock acceleration in the linear regime for non-relativistic velocities predicts a power-law index of 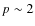 for the injected particle spectrum in strong shocks (e.g. Drury 1983). We assume this value for the non-thermal particle spectra injected at the reconfinement, reverse and bow-shock fronts, i.e.
N(E)=K E-2. As noted above, the normalization constant K is taken such that
for the injected particle spectrum in strong shocks (e.g. Drury 1983). We assume this value for the non-thermal particle spectra injected at the reconfinement, reverse and bow-shock fronts, i.e.
N(E)=K E-2. As noted above, the normalization constant K is taken such that  1% of the kinetic power flowing in the jets is converted into non-thermal energy in the post-shock region immediately after each shock. We note that the radiation luminosities scale linearly with this non-thermal fraction.
1% of the kinetic power flowing in the jets is converted into non-thermal energy in the post-shock region immediately after each shock. We note that the radiation luminosities scale linearly with this non-thermal fraction.
The maximum energies of the relativistic particles,
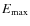 ,
are calculated at any source age by equating the energy gain to the different cooling processes. When radiative cooling is ineffective, the maximum energy is constrained by the Hillas limit (Hillas 1984), i.e. the particle gyroradius,
,
are calculated at any source age by equating the energy gain to the different cooling processes. When radiative cooling is ineffective, the maximum energy is constrained by the Hillas limit (Hillas 1984), i.e. the particle gyroradius, 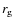 ,
equals the accelerator size. We have adopted Bohm diffusion (
,
equals the accelerator size. We have adopted Bohm diffusion (
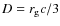 )
and the magnetic field in each shocked region, to calculate the rate at which particles gain energy (e.g. Protheroe 1999):
)
and the magnetic field in each shocked region, to calculate the rate at which particles gain energy (e.g. Protheroe 1999):
![\begin{displaymath}\dot{E}_{\rm accel}(t)\approx (3/20)~[v_{\rm s}(t)/c]^2 {\rm e}~B(t)~c .
\end{displaymath}](/articles/aa/full_html/2009/14/aa10781-08/img45.png) |
(4) |
Focusing hereafter on electrons, the particle energy distribution is computed by taking into account radiative (synchrotron, relativistic bremsstrahlung and IC emission; see, e.g., Blumenthal & Gould 1970) and adiabatic losses during the lifetime of the source. As highlighted by Blundell et al. (2000) in their study of extragalactic double radio sources, the spectral aging of the non-thermal populations depends on the evolution of the physical conditions in each region, in particular the expansion velocities and magnetic fields for each interaction zone. At each time, the conditions for the radiative and adiabatic losses vary. The non-thermal particle distribution at a given source age
 must therefore be computed by adding the differently evolved contributions of the particles injected previously at the shock fronts all along the source lifetime until reaching
must therefore be computed by adding the differently evolved contributions of the particles injected previously at the shock fronts all along the source lifetime until reaching
 .
.
For the synchrotron losses, we use the magnetic field considered above for each interaction region. Relativistic bremsstrahlung is calculated accounting for the densities in the downstream regions. To compute IC losses, we consider the dominant radiation field from the companion, an OB star with luminosity
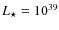 erg s-1. Adiabatic losses,
erg s-1. Adiabatic losses,
![$\dot{E}~(t)~=~[v(t)~/~r~(t)]~E$](/articles/aa/full_html/2009/14/aa10781-08/img47.png) ,
are computed from the size of the emitters r(t) and the expansion velocity v(t). In the downstream region, after the reconfinement shock, there is no expansion since the jet radius keeps roughly constant. In the case of the shell region, the expansion velocity is
,
are computed from the size of the emitters r(t) and the expansion velocity v(t). In the downstream region, after the reconfinement shock, there is no expansion since the jet radius keeps roughly constant. In the case of the shell region, the expansion velocity is 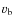 ,
and for the cocoon, it is
,
and for the cocoon, it is 
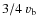 (Landau & Lifshitz 1987).
(Landau & Lifshitz 1987).
As noted above, the electron population properties, the adiabatic coefficient, and the magnetic and radiation fields are taken homogeneous in the bow-shock and cocoon regions. A study of the detailed spatial structure of the magnetic field, pressure, and mass density at each interaction region is beyond the scope of this work. For the electrons injected at the reconfinement shock, we compute their evolution by assuming a one-dimensional emitter, the jet, with a stellar radiation density that decays as  1/z2.
1/z2.
The list of the parameters remaining constant in our analytic model are presented in Table 1.
Table 1: List of the parameters which remain with a constant value in the analytic model.
Given  and the evolved electron distribution in each emitting region, and accounting for the mentioned radiation mechanisms, we computed the SEDs in each zone, as is presented in the next section.
and the evolved electron distribution in each emitting region, and accounting for the mentioned radiation mechanisms, we computed the SEDs in each zone, as is presented in the next section.
3 Model results
We studied how the computed SEDs are affected by variations in the source age,
 ,
the jet kinetic power,
,
the jet kinetic power,
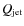 ,
and the ISM density,
,
and the ISM density,
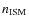 .
In Figs. 2 to 5 we display the SEDs for the shell (top), cocoon (middle), and jet reconfinement (bottom) regions. The contribution of only one jet interacting with the ISM is accounted. The complete set of parameter values required in different cases to obtain the particle evolution and subsequent emission are presented in Table 2.
.
In Figs. 2 to 5 we display the SEDs for the shell (top), cocoon (middle), and jet reconfinement (bottom) regions. The contribution of only one jet interacting with the ISM is accounted. The complete set of parameter values required in different cases to obtain the particle evolution and subsequent emission are presented in Table 2.
Synchrotron emission from the three interaction zones is the channel by means of which the highest radiation output is obtained, at bolometric luminosities that can be as high as  1033 erg s-1 for powerful sources (see Figs. 4 and 5). At high and very high energies, IC emission is the dominant process in the cocoon and reconfinement regions, reaching luminosities of
1033 erg s-1 for powerful sources (see Figs. 4 and 5). At high and very high energies, IC emission is the dominant process in the cocoon and reconfinement regions, reaching luminosities of  1030 erg s-1, while in the shell zone, relativistic bremsstrahlung dominates in this energy range, at luminosities of
1030 erg s-1, while in the shell zone, relativistic bremsstrahlung dominates in this energy range, at luminosities of  1032 erg s-1. Notable differences are found in the reported SEDs while varying the source age
1032 erg s-1. Notable differences are found in the reported SEDs while varying the source age
 from 104 to 105 yr. For older sources, the interaction zones are located at larger distances from the companion star, its radiation energy density
from 104 to 105 yr. For older sources, the interaction zones are located at larger distances from the companion star, its radiation energy density 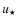 decreases, and the IC contribution becomes slightly lower, although particle aging leads to higher emission at lower energies in the shell and cocoon regions. Relativistic bremsstrahlung in the shell zone is strongly affected by the source age, due to a particle accumulation effect, generating luminosities a factor of
decreases, and the IC contribution becomes slightly lower, although particle aging leads to higher emission at lower energies in the shell and cocoon regions. Relativistic bremsstrahlung in the shell zone is strongly affected by the source age, due to a particle accumulation effect, generating luminosities a factor of  10 higher for old sources. For the ambient medium density, higher values of
10 higher for old sources. For the ambient medium density, higher values of
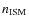 make the jet to be braked at shorter distances from the central engine. The interaction regions are then influenced by a higher radiation energy density from the companion star, and the IC emission is enhanced accordingly. The relativistic Bremsstrahlung emission in the shell zone is also higher for denser mediums, since the luminosity is proportional to the target ion field density,
make the jet to be braked at shorter distances from the central engine. The interaction regions are then influenced by a higher radiation energy density from the companion star, and the IC emission is enhanced accordingly. The relativistic Bremsstrahlung emission in the shell zone is also higher for denser mediums, since the luminosity is proportional to the target ion field density,
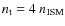 .
Finally, we note that in our model all the non-thermal luminosities are proportional to
.
Finally, we note that in our model all the non-thermal luminosities are proportional to
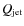 .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg57.png) |
Figure 2:
Derived SEDs for the shell ( top), cocoon ( middle), and jet reconfinement ( bottom) regions taking the values for the jet power
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg58.png) |
Figure 3:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg59.png) |
Figure 4:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg60.png) |
Figure 5:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
3.1 Emission from the shell region
Under the acceleration conditions in this region, the maximum energies
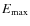 of electrons for the different cases range 2-10 TeV, being always limited by synchrotron losses. Synchrotron emission is also the dominant radiative channel, peaking at higher frequencies for higher
of electrons for the different cases range 2-10 TeV, being always limited by synchrotron losses. Synchrotron emission is also the dominant radiative channel, peaking at higher frequencies for higher  .
The electron energy distribution has an energy break,
.
The electron energy distribution has an energy break,  ,
at which the radiative cooling timescale and the age of the source are the same. The value of
,
at which the radiative cooling timescale and the age of the source are the same. The value of  varies depending on the physical conditions: older sources render smaller
varies depending on the physical conditions: older sources render smaller  ,
since particles have cooled by means of synchrotron radiation for a longer time; higher densities yield lower
,
since particles have cooled by means of synchrotron radiation for a longer time; higher densities yield lower  ,
due to shorter
,
due to shorter  and therefore higher B and synchrotron cooling. Higher jet powers enhances B as well, reducing
and therefore higher B and synchrotron cooling. Higher jet powers enhances B as well, reducing  again (this discussion about
again (this discussion about  is also valid for the other interaction regions). The energy break is manifested in the synchrotron spectrum at frequencies in the range
is also valid for the other interaction regions). The energy break is manifested in the synchrotron spectrum at frequencies in the range  1014-1016 Hz. Given the long synchrotron cooling timescales
1014-1016 Hz. Given the long synchrotron cooling timescales
 s (
B-4=B/10-4 G) compared with the age of the source
s (
B-4=B/10-4 G) compared with the age of the source  1012 s, only the highest energy band of the particle spectrum has reached its steady state. The synchrotron luminosities reach values of
1012 s, only the highest energy band of the particle spectrum has reached its steady state. The synchrotron luminosities reach values of  1033 erg s-1 (see Figs. 4 and 5). The relativistic bremsstrahlung has a strong dependence on the density, follows the energy distribution of electrons, and can reach luminosities of
1033 erg s-1 (see Figs. 4 and 5). The relativistic bremsstrahlung has a strong dependence on the density, follows the energy distribution of electrons, and can reach luminosities of  1032 erg s-1 in the 1 MeV-10 GeV range (see Fig. 5). The IC luminosities are well below the synchrotron ones in all of the studied cases.
1032 erg s-1 in the 1 MeV-10 GeV range (see Fig. 5). The IC luminosities are well below the synchrotron ones in all of the studied cases.
3.2 Emission from the cocoon
Electrons can reach energies of about
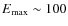 TeV, being limited by escape losses.
Synchrotron emission, again the dominant radiative channel, extends up to hard X-rays in the cocoon, with luminosities reaching up to
TeV, being limited by escape losses.
Synchrotron emission, again the dominant radiative channel, extends up to hard X-rays in the cocoon, with luminosities reaching up to  1033 erg s-1 (see Fig. 5) depending on the different parameter values. As in the shell region, the IC luminosities are well below the synchrotron ones. Otherwise, due to the low densities in the cocoon, relativistic bremsstrahlung is negligible in this zone.
1033 erg s-1 (see Fig. 5) depending on the different parameter values. As in the shell region, the IC luminosities are well below the synchrotron ones. Otherwise, due to the low densities in the cocoon, relativistic bremsstrahlung is negligible in this zone.
3.3 Emission from the jet reconfinement region
The size of the accelerator (Hillas 1984) places a limit of  10 TeV on the maximum energies that electrons can acquire at the reconfinement shock. An increase in both the synchrotron and the IC emissivities is found for denser mediums, in which case
10 TeV on the maximum energies that electrons can acquire at the reconfinement shock. An increase in both the synchrotron and the IC emissivities is found for denser mediums, in which case 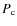 is higher yielding shorter
is higher yielding shorter
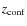 ,
which determines the magnetic and radiation field energy densities. The synchrotron luminosity is similar to that of the IC for weak jets, whereas it is well above it for powerful jets, where luminosities
,
which determines the magnetic and radiation field energy densities. The synchrotron luminosity is similar to that of the IC for weak jets, whereas it is well above it for powerful jets, where luminosities  1032 erg s-1 are obtained (see Figs. 4 and 5). This is due to the stronger dependence of the synchrotron emission on the jet power. The stellar radiation field enhances the IC contribution when the set of parameters cause
1032 erg s-1 are obtained (see Figs. 4 and 5). This is due to the stronger dependence of the synchrotron emission on the jet power. The stellar radiation field enhances the IC contribution when the set of parameters cause
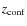 to be shorter. As in the cocoon region, the relativistic bremsstrahlung contribution is negligible.
to be shorter. As in the cocoon region, the relativistic bremsstrahlung contribution is negligible.
4 Hydrodynamical simulations vs analytical model
We performed hydrodynamical simulations to study further the interaction of MQ jets with their surroundings (see Appendix for details). The values of
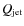 ,
,
 ,
and
,
and
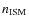 adopted in the hydrodynamical simulations are similar to those assumed in the analytical model, so we can check the main physical quantities used in computing the non-thermal emission. The pressure evolution with simulation time has been computed for the shell and cocoon regions. We show also a fit of their evolution performed to check their values up to
adopted in the hydrodynamical simulations are similar to those assumed in the analytical model, so we can check the main physical quantities used in computing the non-thermal emission. The pressure evolution with simulation time has been computed for the shell and cocoon regions. We show also a fit of their evolution performed to check their values up to
 yr. From an initial value of
yr. From an initial value of 
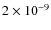 erg cm-3, the cocoon pressure smoothly reaches
erg cm-3, the cocoon pressure smoothly reaches 
 erg cm-3 at
erg cm-3 at
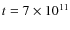 s. The shell behaves similarly, as expected, with a final pressure of
s. The shell behaves similarly, as expected, with a final pressure of 
 erg cm-3. These values are in reasonable agreement with those found in the analytical model, being in the range
erg cm-3. These values are in reasonable agreement with those found in the analytical model, being in the range
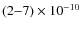 erg cm-3. Concerning the mass densities,
erg cm-3. Concerning the mass densities,
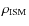 stabilizes at
stabilizes at 
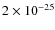 g cm-3 and
g cm-3 and
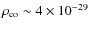 g cm-3 for the shell and the cocoon regions, respectively. These values are again similar to those found in the analytical treatment. On the other hand, the geometry of the emitting structures is related to the self-similar ratio R. In the analytical model, we use R=3. We find this value to be in accordance with the results of the numerical simulations, which yield a value of between 2.5 and 2.7. Finally, we note that in our model only a strong shock at the reconfinement point is assumed, and no additional shocks are considered along the jet. Otherwise, the hydrodynamical simulations demonstrate the existence of several conical shocks that develop in the jet when its pressure falls to that of the surrounding cocoon (see Fig. A.1). Therefore, the non-thermal emission presented in Figs. 2-5 for the reconfinement region, with only one strong shock and an acceleration efficiency of
g cm-3 for the shell and the cocoon regions, respectively. These values are again similar to those found in the analytical treatment. On the other hand, the geometry of the emitting structures is related to the self-similar ratio R. In the analytical model, we use R=3. We find this value to be in accordance with the results of the numerical simulations, which yield a value of between 2.5 and 2.7. Finally, we note that in our model only a strong shock at the reconfinement point is assumed, and no additional shocks are considered along the jet. Otherwise, the hydrodynamical simulations demonstrate the existence of several conical shocks that develop in the jet when its pressure falls to that of the surrounding cocoon (see Fig. A.1). Therefore, the non-thermal emission presented in Figs. 2-5 for the reconfinement region, with only one strong shock and an acceleration efficiency of  ,
should be taken as a rough approximation of the true situation.
,
should be taken as a rough approximation of the true situation.
Table 2:
Parameter values adopted to compute the SEDs for the three emitting zones .
.
5 Discussion
We have explored whether non-thermal emission can be expected from the bow-shock, the cocoon and the reconfinement regions in the interaction of MQ jets with their environment. In the extragalactic framework, non-thermal radiation is supposed to originate only in the cocoon as extended radio emission, as well as locally in the hot spots at the jet tips. Although the shell of shocked ambient material plays an important role in the analytical models describing the growth of FR II galaxies (Blandford et al. 1974; Scheuer 1974), no radio emission is usually assumed to be produced there (see, however, Rudnick et al. 1980). In our model, the bow-shock velocity is still large enough to accelerate particles, so it is important to compute the expected non-thermal emission also from this region. Our results show a contribution from this zone that is comparable to that of the cocoon and higher than that coming from the reconfinement region. The geometry of the interaction structures, however, difficult to disentangle the emission from the cocoon and the bow-shock region since they could appear cospatial in the plane of the sky. Relativistic bremsstrahlung would favour a shell origin of the emission.
The highest radiation output within the studied set of parameters corresponds to the case:
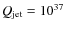 erg s-1,
erg s-1,
 yr and
yr and
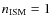 cm-3. For an emitting source located at 3 kpc, this would imply a flux density of
cm-3. For an emitting source located at 3 kpc, this would imply a flux density of  150 mJy at 5 GHz. The emitting size would be of a few arcminutes, since the electron cooling timescale is longer than the source lifetime and electrons can fill the entire cocoon/shell structures. Considering this angular extension and a radio telescope beam size of 10'', radio emission at a level of
150 mJy at 5 GHz. The emitting size would be of a few arcminutes, since the electron cooling timescale is longer than the source lifetime and electrons can fill the entire cocoon/shell structures. Considering this angular extension and a radio telescope beam size of 10'', radio emission at a level of  1 mJy beam-1 is expected. At X-ray energies, we measure a bolometric flux for the range 1-10 keV of
1 mJy beam-1 is expected. At X-ray energies, we measure a bolometric flux for the range 1-10 keV of
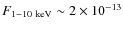 erg s-1 cm-2. The electrons emitting in X-rays by synchrotron have short timescales, and the emitter size cannot be significantly larger than the accelerator itself. Although the X-rays produced in the shell by relativistic bremsstrahlung are expected to be quite diluted, the X-rays from the cocoon would originate in a relatively small region close to the reverse shock, and could be detectable by XMM-Newton and Chandra on scales of a few arcseconds. In the gamma-ray domain, the flux between 100 MeV and 100 GeV is
erg s-1 cm-2. The electrons emitting in X-rays by synchrotron have short timescales, and the emitter size cannot be significantly larger than the accelerator itself. Although the X-rays produced in the shell by relativistic bremsstrahlung are expected to be quite diluted, the X-rays from the cocoon would originate in a relatively small region close to the reverse shock, and could be detectable by XMM-Newton and Chandra on scales of a few arcseconds. In the gamma-ray domain, the flux between 100 MeV and 100 GeV is
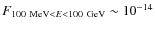 erg s-1 cm-2, while the integrated flux above 100 GeV is
erg s-1 cm-2, while the integrated flux above 100 GeV is
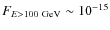 erg s-1 cm-2. These values are too low to be detectable with available Cherenkov telescopes. Taking into account the rough linearity between
erg s-1 cm-2. These values are too low to be detectable with available Cherenkov telescopes. Taking into account the rough linearity between
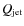 ,
,
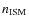 ,
,
 ,
,
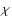 and d-2 and the gamma-ray fluxes obtained, sources with higher values of these quantities than used here may render the MQ jet termination regions detectable by present Cherenkov telescopes. For the weakest jets, i.e, lowest ISM densities and youngest sources adopted in our model (
and d-2 and the gamma-ray fluxes obtained, sources with higher values of these quantities than used here may render the MQ jet termination regions detectable by present Cherenkov telescopes. For the weakest jets, i.e, lowest ISM densities and youngest sources adopted in our model (
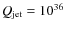 erg s-1,
erg s-1,
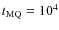 yr and
yr and
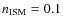 cm-3), the fluxes are strongly suppressed. In the radio band, the specific flux is
cm-3), the fluxes are strongly suppressed. In the radio band, the specific flux is
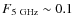 mJy beam-1; the integrated flux at X-rays in this case is
mJy beam-1; the integrated flux at X-rays in this case is
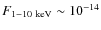 erg s-1 cm-2, and at gamma-rays
erg s-1 cm-2, and at gamma-rays
 erg s-1 cm-2 and
erg s-1 cm-2 and
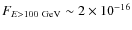 erg s-1 cm-2.
erg s-1 cm-2.
We note that the fluxes presented above depend strongly on the non-thermal luminosity fraction 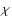 .
In the present model we adopted a quite conservative value of
.
In the present model we adopted a quite conservative value of  .
For a source able to accelerate particles with a higher efficiency at the interaction shock fronts, the expected non-thermal fluxes would be enhanced by a factor (
.
For a source able to accelerate particles with a higher efficiency at the interaction shock fronts, the expected non-thermal fluxes would be enhanced by a factor (
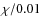 ).
).
The non-thermal emission from the interaction regions in MQs exhibits characteristic features that can be distinguished from emission originated in the central binary system. First of all, the interaction structures are localized at distances of up to  1020 cm. The lifetime of electrons radiating at high and very high energies is relatively short and the emission region should therefore be localized close to the accelerator (but far away from the central system). Regarding radio emission, synchrotron cooling times are expected to be longer than the source lifetime,
1020 cm. The lifetime of electrons radiating at high and very high energies is relatively short and the emission region should therefore be localized close to the accelerator (but far away from the central system). Regarding radio emission, synchrotron cooling times are expected to be longer than the source lifetime,
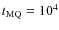 -105 yr. The cocoon and bow-shock emitting regions would be expected to form a kind of radio nebula around the central system, and the flux densities at the level shown above would then originate in a quite extended source.
-105 yr. The cocoon and bow-shock emitting regions would be expected to form a kind of radio nebula around the central system, and the flux densities at the level shown above would then originate in a quite extended source.
The detection of non-thermal emission from the interaction zones would be proof that efficient acceleration of particles to relativistic energies is occuring far away from the central binary system. The averaged kinetic power carried away in the jets could be more tightly constrained, eventually showing that it can be much higher than that inferred directly from observations of the inner jet emission alone (Gallo et al. 2005; Heinz 2002)
Despite our focus on the non-thermal emission from the MQ jet termination regions, thermal bremsstrahlung emission should be expected from the shell. Although the shocks considered here are still adiabatic, a non-negligible fraction of the jet kinetic luminosity of up to a few percent may be radiated by means of thermal bremsstrahlung. For bow-shock velocities of 107 cm s-1, the thermal emission would peak in UV-soft X-ray, energy band, which is strongly affected by absorption in the ISM. Observations of the thermal radiation in radio and optical from the interaction structures were used to extract information about the shell physical conditions (e.g. Cygnus X-1, studied by Gallo et al. 2005 and Russell et al. 2007).
The role of accelerated protons in the shocks deserves a few words, since it may be relevant to specific situations. Given the conditions in the strong shocks that we consider, relativistic protons may reach energies of about 100 TeV; for shell densities  1 cm-3, the accelerated protons have lifetimes of about 1015 s. To reach the gamma-ray fluxes detectable for the present generation of satellite-borne and ground-based gamma-ray instruments above
1 cm-3, the accelerated protons have lifetimes of about 1015 s. To reach the gamma-ray fluxes detectable for the present generation of satellite-borne and ground-based gamma-ray instruments above  100 GeV, of
100 GeV, of  10-13 erg cm-2 s-1, the energy in non-thermal protons stored in the shell should be as high as
10-13 erg cm-2 s-1, the energy in non-thermal protons stored in the shell should be as high as  1048 erg at distances of a few kpc. For a source age of
1048 erg at distances of a few kpc. For a source age of
 yr, the required injected power in relativistic protons should be about
yr, the required injected power in relativistic protons should be about 
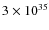 erg s-1, thus implying that moderate levels of hadronic emission from MQ jet termination regions may be eventually detected from powerful jets, i.e.
erg s-1, thus implying that moderate levels of hadronic emission from MQ jet termination regions may be eventually detected from powerful jets, i.e.
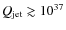 erg s-1.
erg s-1.
The reason why some MQs exhibit non-thermal emission from the jet/ISM interaction regions, but in other cases this emission remains undetected, is still unclear. In the context of our model, we can study the effects of varying the set of parameters defining the source and their environment, and predict some cases in which the interaction structures may or may not be detectable. First of all, the energy input injected into the medium should be sufficiently high, and there may exist strong differences in the jet kinetic power from source to source. In addition, it could also be the case that the density of the surrounding medium is so low that the shell and the cocoon become too large and their radiation too diluted to be detectable (see, for instance, Heinz 2002). MQ jets could also be disrupted at some source age, as found in FR I galaxies. If this happened within a time far shorter than the MQ lifetime, the probability of detecting a cocoon/shell structure in the MQ surroundings would be smaller (although the detection of some other kind of structures is not excluded). On the other hand, some sources may be too far, or the non-thermal fraction too small, to detect significant emission from the interaction regions.
The evolution of the pressure, mass density, velocities, and the Mach number predicted by the analytical model are in good agreement with those found in the hydrodynamical simulations for the shell and the cocoon regions. Otherwise, these simulations indicate that several conical shocks may be present within the jet as a consequence of pressure adjustments with the surrounding cocoon, instead of the one strong shock adopted in the analytical treatment. Finally, the length and width of the structures in the model and those found in the numerical simulations are also similar, with a constant ratio 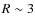 in both cases, implying that the physical assumptions used in the analytical treatment are valid to first order.
in both cases, implying that the physical assumptions used in the analytical treatment are valid to first order.
The results of this work show that the surroundings of some MQs could be extended non-thermal emitters from radio to gamma-rays. In addition, from a comparison with observations, the magnetic field and the particle acceleration efficiency in the jet/ISM interaction regions can be constrained, providing an insight into the physics of these interaction structures. Although the adopted model is rather simple, it is interesting to note that it already accounts for cases when the sources should remain undetectable and cases in which radiation could be detected.
Acknowledgements
The authors acknowledge support by the Spanish DGI of MEC under grant AYA2007-6803407171-C03-01, as well as partial support by the European Regional Development Fund (ERDF/FEDER). P.B. was supported by the DGI of MEC (Spain) under fellowship BES-2005-7234. V.B.-R. gratefully acknowledges support from the Alexander von Humboldt Foundation. M.P. acknowledges support from a postdoctoral fellowship of the Generalitat Valenciana (Beca Postdoctoral d'Excellència), a Max-Planck-Institut postdoctoral fellowship and by the Spanish MEC and the European Fund for Regional Development through grants AYA2007-67627-C03-01 and AYA2007-67752-C03-02.
Appendix A: Hydrodynamical simulations
![\begin{figure}
\par\includegraphics[width=8cm]{0781fig6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg148.png) |
Figure A.1:
Pressure along the jet axis as a function of distance from its injection point, at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{0781fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg149.png) |
Figure A.2:
Evolution of the self-similar parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg150.png) |
Figure A.3:
Mass density ( top) and pressure ( bottom) maps resulting from hydrodynamical simulations. The simulations were performed using
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig9.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg151.png) |
Figure A.4: Lorentz factor ( top) and Mach number ( bottom) maps resulting from hydrodynamical simulations. The adopted parameters are the same as those of Fig. A.3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig10.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg152.png) |
Figure A.5: Pressure ( left) and mass density ( right) evolution in the shell ( top) and cocoon ( bottom) regions as a function of time. A fitting of the results is also shown for both variables (dotted line). This fit serves to estimate the simulation values at longer times. This extrapolation is strictly valid only if an homogeneous external medium and a constant injection energy rate are assumed. |
| Open with DEXTER | |
The simulation was performed to check the physical values adopted in the analytical model. We used a two-dimensional finite-difference code based on a high-resolution shock-capturing scheme, which solves the equations of relativistic hydrodynamics written in conservation form. This code is an upgrade of the code described in Martí et al. (1997) (see Perucho et al. 2005). The simulation was carried out by two dual-core processors in the Max-Planck-Institut für Radioastronomie.
The numerical grid of the simulation is formed by 320 cells in the radial direction and 2400 cells in the axial direction in a uniform region, of physical dimensions
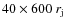 .
An expanded grid with 320 cells in the transversal direction, brings the boundary from
.
An expanded grid with 320 cells in the transversal direction, brings the boundary from
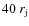 to
to
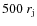 ,
whereas an extended grid in the axial direction, consisting of 440 extra cells, spans the grid axially from
,
whereas an extended grid in the axial direction, consisting of 440 extra cells, spans the grid axially from
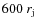 to
to
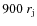 .
The enlargement of the grid is necessary to ensure that the boundary conditions are sufficiently distant from the region of interest, and to avoid numerical reflection of waves at the boundaries affecting our results. The conditions at the boundaries are reflection on the jet axis and at the side where the jet is injected, simulating the presence of the counter-jet cocoon, appart from the injection point where inflow conditions are used. Finally, outflow conditions in the outer axial and radial boundaries are used.
.
The enlargement of the grid is necessary to ensure that the boundary conditions are sufficiently distant from the region of interest, and to avoid numerical reflection of waves at the boundaries affecting our results. The conditions at the boundaries are reflection on the jet axis and at the side where the jet is injected, simulating the presence of the counter-jet cocoon, appart from the injection point where inflow conditions are used. Finally, outflow conditions in the outer axial and radial boundaries are used.
The numerical resolution in the uniform grid is thus 8 cells/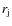 in the radial direction and 4 cells/
in the radial direction and 4 cells/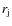 in the axial direction. The low resolution used is justified by the fact that we are interested in the macroscopic features of the jet and backflow, but not in mixing and turbulence, allowing far less time-consuming simulations. All the physical variables are scaled to the units of the code, which are the jet radius r, the rest-mass density of the ambient medium
in the axial direction. The low resolution used is justified by the fact that we are interested in the macroscopic features of the jet and backflow, but not in mixing and turbulence, allowing far less time-consuming simulations. All the physical variables are scaled to the units of the code, which are the jet radius r, the rest-mass density of the ambient medium
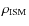 ,
and the speed of light c.
,
and the speed of light c.
The jet is injected in the grid at a distance of 1018 cm from the compact object, and its initial radius is taken to be
r0=1017 cm. The time unit of the code is thus equivalent to 
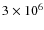 s, which is derived using the radius of the jet at injection and the speed of light (r0/c). Both the jet and the ambient medium are considered to be formed by a non-relativistic gas with adiabatic exponent
s, which is derived using the radius of the jet at injection and the speed of light (r0/c). Both the jet and the ambient medium are considered to be formed by a non-relativistic gas with adiabatic exponent
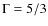 .
The number density in the ambient medium is
.
The number density in the ambient medium is
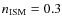 cm-3 and the temperature is T=100 K. The role of the temperature is irrelevant to our context. The velocity of the jet at injection is 0.6 c, its number density
cm-3 and the temperature is T=100 K. The role of the temperature is irrelevant to our context. The velocity of the jet at injection is 0.6 c, its number density
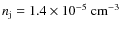 ,
and temperature
,
and temperature
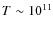 K (which corresponds to a sound speed
K (which corresponds to a sound speed 
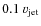 ). These parameter values result in a jet power
). These parameter values result in a jet power
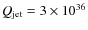 erg s-1. Figures A.3 and A.4 show the velocity, Mach number, mass density and pressure maps derived by the numerical simulations. The upper (lower) panels in Fig. A.5 show the evolution of the pressure and the mass density with simulation time for the shell (cocoon) region. The self-similar parameter R reaches a value of between 2.5 and 2.7 at the end of the simulations, as can be seen in Fig. A.2.
erg s-1. Figures A.3 and A.4 show the velocity, Mach number, mass density and pressure maps derived by the numerical simulations. The upper (lower) panels in Fig. A.5 show the evolution of the pressure and the mass density with simulation time for the shell (cocoon) region. The self-similar parameter R reaches a value of between 2.5 and 2.7 at the end of the simulations, as can be seen in Fig. A.2.
At the time the simulation is stopped, after evolving 
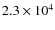 yr, the bow-shock moves at a speed
yr, the bow-shock moves at a speed 
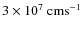 ,
and has reached a distance
,
and has reached a distance 
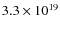 cm. Initially, the jet expands, accelerating and cooling, due to its initial overpressure. When the flow becomes underpressured with respect to the ambient medium, a first reconfinement shock is generated close to the injection point at
cm. Initially, the jet expands, accelerating and cooling, due to its initial overpressure. When the flow becomes underpressured with respect to the ambient medium, a first reconfinement shock is generated close to the injection point at
 cm. The fluid then again becomes overpressured when passing through the shock and this process is repeated several times around pressure equilibrium with the external medium. The subsequent shocks produced by these oscillations around equilibrium are stronger than the first, suggesting some coupling with a pinching Kelvin-Helmholtz instability. The jet is supersonic at injection, with Mach number
cm. The fluid then again becomes overpressured when passing through the shock and this process is repeated several times around pressure equilibrium with the external medium. The subsequent shocks produced by these oscillations around equilibrium are stronger than the first, suggesting some coupling with a pinching Kelvin-Helmholtz instability. The jet is supersonic at injection, with Mach number
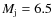 on axis, before the first reconfinement shock. After this shock, the Mach number oscillates around the initial value and decreases, with slight increases in the expansion regions, until the head of the jet. Here, transonic and subsonic velocities result from the increase in temperature and decrease in velocity, as the flow crosses the reverse shock. The cocoon and the shell material are still in high overpressure with respect to the ambient medium by the end of the simulation, by a factor >104. The gas that forms the cocoon is initially fast and slightly supersonic, with velocities up to
on axis, before the first reconfinement shock. After this shock, the Mach number oscillates around the initial value and decreases, with slight increases in the expansion regions, until the head of the jet. Here, transonic and subsonic velocities result from the increase in temperature and decrease in velocity, as the flow crosses the reverse shock. The cocoon and the shell material are still in high overpressure with respect to the ambient medium by the end of the simulation, by a factor >104. The gas that forms the cocoon is initially fast and slightly supersonic, with velocities up to
 and Mach numbers up to 2, close to the head of the jet. Farther downstream, the backflow becomes slower and subsonic, with velocities
and Mach numbers up to 2, close to the head of the jet. Farther downstream, the backflow becomes slower and subsonic, with velocities
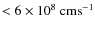 .
.
References
- Aharonian, F. A., & Atoyan, A. M. 1998, NewAR, 42, 579 In the text
- Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 In the text
- Blundell, K. M., & Rawlings, S. 2000, AJ, 119, 1111 In the text
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 In the text
- Bosch-Ramon, V., Aharonian, F. A., & Paredes, J. M. 2005, A&A, 432, 609 In the text
- Corbel, S., Kaaret, P., Fender, R. P., et al. 2004, ApJ, 617, 1272 In the text
- Corbel, S., & Fender, R. P. 2002, ApJ, 573, L35 In the text
- Drury, L. 1983, SSRv, 36, 57 In the text
- Falle, S. A. E. G. 1991, MNRAS, 250, 851 In the text
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167P, 31 In the text
- Fender, R. P. 2001, MNRAS, 322, 31 In the text
- Fender, R. P. 2004, in Compact Stellar X-ray Sources, eds. W. H. G. Lewin, & M. van der Klis (Cambridge Univ. Press) In the text
- Gallo, E., Fender, R. P., Kaiser, C., Russell, D., et al. 2005, Nature, 436, 819 In the text
- Gallo, E., Fender, R. P., & Pooley, G. G. 2003, MNRAS, 344, 60 In the text
- Heindl, W. A., Tomsick, J. A., Wijnands, R., & Smith, D. M. 2003, ApJ, 588, L97 In the text
- Heinz, S. 2002, A&A, 388, L40 In the text
- Heinz, S. 2006, ApJ, 636, 316 In the text
- Heinz, S., & Sunyaev, R. 2002, A&A, 390, 751 In the text
- Hillas, A. M. 1984, ARA&A, 22, 425 In the text
- Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 In the text
- Kaiser, C. R., Gunn, K. F., Brocksopp, C., & Sokoloski, J. L. 2004, ApJ, 612, 332 In the text
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics, 2nd English Edn (Oxford: Pergamon) In the text
- Leahy, J. P., Muxlow, T. W. B., & Stephens, P. W. 1989, MNRAS, 239, 401 In the text
- Martí, J., Rodriguez, L. F., Mirabel, I. F., & Paredes, J. M. 1996, A&A, 306, 449 In the text
- Martí, J. M., Müller, E., Font, J. A., Ibáñez, J. M., & Marquina, A. 1997, ApJ, 479, 151 In the text
- Mirabel, F., Rodriguez, L. F., Cordier, B., Paul, J., & Lebrun, F. 1992, Nature, 358, 215 In the text
- Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409 In the text
- Nalewajko, K., & Sikora, M. 2008, MNRAS, 392, 1205 In the text
- Paredes J. M. 2005, in High Energy Gamma-Ray Astronomy: 2nd International Symposium, eds. F. A. Aharonian, H. J. Völk, & D. Horns. AIP Conf. Proc., 745, 93 In the text
- Paredes, J. M., Ribó, M., Bosch-Ramon, V., et al. 2007a, ApJ, 664, L39 In the text In the text
- Paredes, J. M., Martí, J., Ishwara-Chandra, C. H., & Bosch-Ramon, V. 2007b, ApJ, 654, L135
- Perucho, M., & Bosch-Ramon, V. 2008, A&A, 482, 917 In the text
- Perucho, M., & Martí, J. M. 2007, MNRAS 382, 526 In the text
- Perucho, M., Martí, J. M., & Hanasz, M. 2005, A&A, 443, 863 In the text
- Protheroe, R. J. 1999, ADP-AT-98-9 [arXiv:astro-ph/9812055] In the text
- Ribó, M. 2005, ASPC, 340, 269 In the text
- Rudnick, L. 1988, ApJ, 325, 189 In the text
- Russell, D. M., Fender, R. P., Gallo, E., & Kaiser, C. R., MNRAS, 376, 1341 In the text
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 In the text
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) In the text
- Tudose, V., Fender, R. P., Kaiser, C. R., et al. 2006, MNRAS, 372, 417 In the text
- Velázquez, P. F., & Raga, A. C. 2000, A&A, 362, 780 In the text
- Zealey, W. J., Dopita, M. A., & Malin, D. F. 1980, MNRAS, 192, 731 In the text
All Tables
Table 1: List of the parameters which remain with a constant value in the analytic model.
Table 2:
Parameter values adopted to compute the SEDs for the three emitting zones![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0781fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg18.png) |
Figure 1:
Scheme of the model (not to scale) representing the three different zones. The central binary system is located at the center. Two jets emerge from it and extent outwards until they are effectively decelerated at a distance of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg57.png) |
Figure 2:
Derived SEDs for the shell ( top), cocoon ( middle), and jet reconfinement ( bottom) regions taking the values for the jet power
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg58.png) |
Figure 3:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg59.png) |
Figure 4:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0781fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg60.png) |
Figure 5:
Same as in Fig. 2 but taking
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{0781fig6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg148.png) |
Figure A.1:
Pressure along the jet axis as a function of distance from its injection point, at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{0781fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg149.png) |
Figure A.2:
Evolution of the self-similar parameter
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg150.png) |
Figure A.3:
Mass density ( top) and pressure ( bottom) maps resulting from hydrodynamical simulations. The simulations were performed using
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig9.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg151.png) |
Figure A.4: Lorentz factor ( top) and Mach number ( bottom) maps resulting from hydrodynamical simulations. The adopted parameters are the same as those of Fig. A.3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{0781fig10.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10781-08/Timg152.png) |
Figure A.5: Pressure ( left) and mass density ( right) evolution in the shell ( top) and cocoon ( bottom) regions as a function of time. A fitting of the results is also shown for both variables (dotted line). This fit serves to estimate the simulation values at longer times. This extrapolation is strictly valid only if an homogeneous external medium and a constant injection energy rate are assumed. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



 as a function of time. After the pronounced initial increase, R remains between 2.5 and 2.7 for most of the simulated time.
as a function of time. After the pronounced initial increase, R remains between 2.5 and 2.7 for most of the simulated time.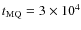 yr and
yr and