| Issue |
A&A
Volume 497, Number 2, April II 2009
|
|
|---|---|---|
| Page(s) | 525 - 535 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200810777 | |
| Published online | 05 March 2009 | |
Upward propagating high-frequency Alfvén waves as identified from dynamic wave-like spicules observed by SOT on Hinode
J.-S. He1,2 - C.-Y. Tu1 - E. Marsch2 - L.-J. Guo1 - S. Yao1 - H. Tian1,2
1 - Department of Geophysics, Peking University, Beijing, PR China
2 - Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany
Received 10 August 2008 / Accepted 6 February 2009
Abstract
Aims. We identify high-frequency Alfvén waves propagating upward in the solar chromosphere and transition region from observation by Solar Optical Telescope (SOT) onboard Hinode.
Methods. The spicule shape is enhanced through application of a normal radial gradient filter and an un-sharp mask on the images taken by SOT. The displaced position of the spicule is at each height obtained by tracing the maximum intensity after image processing. The dominant wave period is obtained by the FFT method applied to the time variations of the displaced position at a certain height. The phase speed is estimated with the help of a cross-correlation analysis of two temporal sequences of the displaced positions at two heights along the spicule.
Results. We find in four cases that the spicules are modulated by high-frequency (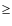 0.02 Hz) transverse fluctuations. Such fluctuations are suggested to be Alfvén waves that propagate upward along the spicules with phase speed ranges from 50 to 150 km s-1. Three of the modulated spicules show clear wave-like shapes with short wavelengths less than 8 Mm.
0.02 Hz) transverse fluctuations. Such fluctuations are suggested to be Alfvén waves that propagate upward along the spicules with phase speed ranges from 50 to 150 km s-1. Three of the modulated spicules show clear wave-like shapes with short wavelengths less than 8 Mm.
Conclusions. Our work identified directly upward propagation of Alfvén waves in the solar chromosphere and transition region. In addition to the recently reported Alfvén waves with very long wavelength and wave period, we find here four examples of Alfvén waves with shorter wavelengths and periods. These findings shed new light on the wave origin and on coronal and solar-wind heating.
Key words: waves - Sun: chromosphere - Sun: transition region - Sun: solar wind
1 Introduction
Upward propagating Alfvén waves are generally assumed to exist in the lower solar atmosphere and exploited in theoretical models for heating of the corona and solar wind acceleration (see, e.g., the reviews by Tu & Marsch 1995; Hollweg & Isenberg 2002). The models may basically be divided into two kinds. One kind of model assumes high-frequency Alfvén waves with the cyclotron damping mechanism (e.g., He et al. 2008; Axford et al. 1999; Tu & Marsch 1997,2001; Marsch & Tu 1997). The other kind of model assumes low-frequency Alfvén waves which are subject to a nonlinear damping mechanism (e.g., Matthaeus et al. 1999; Suzuki & Inutsuka 2005; Cranmer et al. 2007; Hollweg 2000). However, until recently it was difficult to identify directly the properties of Alfvén waves in the solar atmosphere from optical observations.
An indirect piece of evidence of the existence of Alfvén waves or turbulence is the extraordinary, besides the thermal motion effect, Doppler broadening of emission lines when observed on the disk (see the review by Wilhelm et al. 2007) and off the solar limb (e.g., Tu et al. 1998). The existence of Alfvén waves in the coronal plasma has been recently reported by Tomczyk et al. (2007), a result which is based on cross-correlation analysis of Fe XIII (1074.7 nm) Line-of-Sight (LOS) Doppler velocity time series. That Alfvén waves exist in the chromosphere has been recently revealed by De Pontieu et al. (2007a), with the evidence coming from the transverse oscillation of spicules as observed in Ca II H (3968 Å) by SOT (Tsuneta et al. 2008) onboard Hinode (Kosugi et al. 2007). In the work of De Pontieu et al. (2007a), Alfvén waves are thought to permeate the entire chromosphere, as inferred from the ubiquity of spicule oscillations, and the velocity amplitude of the oscillation is estimated to be on the order of 10 to 25 km s-1, and periods range from 100 to 500 s. It was suggested that the spectrum of the generated Alfvén waves includes signals of both the photospheric 5-min p-modes and chromospheric 3-min oscillations, and that these results strongly support coronal heating models that are based on the dissipation of low-frequency waves.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg3.png) |
Figure 1:
Left panel: processed image obtained by SOT in Ca II H (3968 Å) at t0 = 11:40:29 UT. The red dotted box indicates the position of the spicule. The blue line is used to represent the skeleton of the spicule shape,
D0(t0; y), which appears wave-like. Three blue short lines indicate the locations on the spicule where its displacement is further analyzed, i.e. Point-I, Point-II and Point-III. The dashed green line is the center longitudinal axis of the red dotted box. Middle panel: profile of the defined spicule intensity
|
| Open with DEXTER | |
De Pontieu et al. (2007a) found that the distribution of measured transverse displacements of 94 observed spicules agrees well with the distribution derived from a Monte Carlo simulation in which spicules carry low-frequency Alfvén waves with periods randomly chosen from a uniform
distribution between 150 and 350 s and velocity amplitudes from a Gaussian distribution around
20 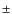 5 km s-1. The wavelength for their low-frequency Alfvén waves is reported to be generally in excess of the lengths of the field-tracing spicules, and the wavelength lower limit on the order of 20 Mm is compatible with the value resulting from multiplication of the phase speeds (50-200 km s-1) with the long wave periods (100-500 s). However, Alfvén waves with short periods less than 50 s and short wavelength less than 10 Mm have not yet been detected and studied from spicule dynamics. De Pontieu et al. (2007a) also reported the transverse displacement propagation with a phase speed on the order of 100-200 km s-1. However, it was not mentioned in their paper whether the propagating transverse displacement oscillates, like previously discussed 94 displacement oscillations just at a special height above the solar limb. De Pontieu et al. (2007a) modeled a mix of upward and downward propagating Alfvén waves on a spicule and compared the modeling result with the dynamics of one observed spicule. However, they did not show directly whether the Alfvén waves are propagating upward, downward or are a superposition of both.
5 km s-1. The wavelength for their low-frequency Alfvén waves is reported to be generally in excess of the lengths of the field-tracing spicules, and the wavelength lower limit on the order of 20 Mm is compatible with the value resulting from multiplication of the phase speeds (50-200 km s-1) with the long wave periods (100-500 s). However, Alfvén waves with short periods less than 50 s and short wavelength less than 10 Mm have not yet been detected and studied from spicule dynamics. De Pontieu et al. (2007a) also reported the transverse displacement propagation with a phase speed on the order of 100-200 km s-1. However, it was not mentioned in their paper whether the propagating transverse displacement oscillates, like previously discussed 94 displacement oscillations just at a special height above the solar limb. De Pontieu et al. (2007a) modeled a mix of upward and downward propagating Alfvén waves on a spicule and compared the modeling result with the dynamics of one observed spicule. However, they did not show directly whether the Alfvén waves are propagating upward, downward or are a superposition of both.
In this paper, we present four cases showing upward propagating Alfvén waves identified from dynamic spicules observed by SOT on Hinode in Ca II H (3968 Å). The wavelengths and periods of these waves are shorter than the ones previously reported. The wavelengths of Alfvén waves in our study are short enough to modulate the spicules such that they are looking wave-like. The periods of the wave in our study are short enough to be less than the time the spicules are visible. We speculate that the chromospheric waves identified here are generated by magnetic reconnection, and are at a frequency susceptible to cyclotron damping in the outer corona - a candidate mechanism for solar wind heating (e.g., Tu & Marsch 1997).
2 Observations and data analysis
The dataset used here of image sequences in the Ca II H (3968 Å) wavelength range was obtained by Hinode/SOT from 11:29:32 to 11:49:50 UT on 19 March 2007. During this period, SOT was looking at the southern polar region. The cadence for the image sequence is 4.8 s. The spatial pixel size is 0.054''. Such high temporal and spatial resolution allows us to observe the refined structure and dynamics of spicules in the polar region, which is a precondition to analyze an Alfvén wave carried by the spicule.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0777fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg5.png) |
Figure 2: From left through middle to right: profiles of D0(t, y) for Point-I, Point-II and Point-III, respectively, which are located at three heights marked with three blue short perpendicular slits listed from bottom to top in the left panel of Fig. 1. |
| Open with DEXTER | |
The SOT standard program ``fg_prep.pro'' is used to reduce the images by removing dark current and
other camera artifacts. The jitter of the images introduced by the spacecraft is mostly removed by
the correlation tracker system on SOT with trivial jitter of
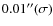 remaining in the
co-aligned time series (Shimizu et al. 2008). The time series have a slow pointing drift, with an
average speed component of
remaining in the
co-aligned time series (Shimizu et al. 2008). The time series have a slow pointing drift, with an
average speed component of 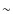 0.017''/min toward the north as identified from the solar
limb slow drift in the original time series. This slow drift speed component is eliminated before
studying the spicule dynamics. While the slow drift component tangential to the solar limb, which
cannot be identified from the dynamically evolving time series, is left to be eliminated by
subtracting the averaged linear transverse motion from the spicule dynamics in the following
analysis. The dataset, after taking into account the above effects, is ready to measure the
high-frequency displacement oscillation with amplitude being not less than 0.05''. We take two
steps of image processing in order to enhance the spicules for the convenience of further analysis.
In the first step, the normal radial gradient filtering (NRGF) technique (Morgan et al. 2006) is
implemented to filter the background radiation intensity, which fades away gradually along the
radius. The purpose of NRGF is to enhance the structures in the off-limb region as compared with
the structures on the solar disk. In the second step, the un-sharp mask technique (with ``gradient''
being the second-order gradient) (Koutchmy & Koutchmy 1989) is applied to remove the diffuse strong
radiation intensity in the off-limb region. Thus the spicule outline becomes clearer after
application of the un-sharp mask.
0.017''/min toward the north as identified from the solar
limb slow drift in the original time series. This slow drift speed component is eliminated before
studying the spicule dynamics. While the slow drift component tangential to the solar limb, which
cannot be identified from the dynamically evolving time series, is left to be eliminated by
subtracting the averaged linear transverse motion from the spicule dynamics in the following
analysis. The dataset, after taking into account the above effects, is ready to measure the
high-frequency displacement oscillation with amplitude being not less than 0.05''. We take two
steps of image processing in order to enhance the spicules for the convenience of further analysis.
In the first step, the normal radial gradient filtering (NRGF) technique (Morgan et al. 2006) is
implemented to filter the background radiation intensity, which fades away gradually along the
radius. The purpose of NRGF is to enhance the structures in the off-limb region as compared with
the structures on the solar disk. In the second step, the un-sharp mask technique (with ``gradient''
being the second-order gradient) (Koutchmy & Koutchmy 1989) is applied to remove the diffuse strong
radiation intensity in the off-limb region. Thus the spicule outline becomes clearer after
application of the un-sharp mask.
We then select four spicules to analyze their shapes and dynamics. A long slit with a certain
width, which is generally parallel to the spicule, is placed in the image sequences, see the left
panel in Fig. 1 for the first case of spicule at the time (t0 = 11:40:29 UT). Such
slit is used to record the intensity distribution (after the image processing) along and across the
spicule, I(x, y), where x is the transverse coordinate in the slit, and y is the longitudinal
coordinate. The area of the slit is divided into M 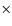 N pixels, where M is the number of
columns (the number of pixels in the transverse coordinate) and N is the number of rows (the
number of pixels in the longitudinal coordinate). The transverse and longitudinal side lengths of
the pixel,
N pixels, where M is the number of
columns (the number of pixels in the transverse coordinate) and N is the number of rows (the
number of pixels in the longitudinal coordinate). The transverse and longitudinal side lengths of
the pixel, 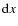 and
and 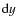 ,
are both set as 0.054''. The spicule intensity of the displaced point in the nth row on the spicule at the time t0,
,
are both set as 0.054''. The spicule intensity of the displaced point in the nth row on the spicule at the time t0,
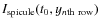 ,
is assigned with the mean of the intensity of the pixels having an intensity in the top 20 percent of the M pixels in the nth row.
,
is assigned with the mean of the intensity of the pixels having an intensity in the top 20 percent of the M pixels in the nth row.
The intensity distribution along the spicule,
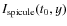 ,
is shown in the middle
panel of Fig. 1. The transverse position of the displaced point in the nth row on
the spicule at the time t0,
,
is shown in the middle
panel of Fig. 1. The transverse position of the displaced point in the nth row on
the spicule at the time t0,
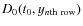 ,
is set with mean position of the M pixels with square intensity of every pixel as the weight. The transverse position obtained in this way has a sub-pixel resolution (<0.054''). Thus, a transverse position profile as a function of the longitudinal coordinate of the slit,
D0(t0, y), can be obtained and is illustrated as a blue line in the left panel of Fig. 1, which appears wave-like relative to the central longitudinal axis of the long slit shown as a green dashed line in the figure. The spicule may be inclined off the longitudinal axis of the fixed slit during its evolution. The spatially oblique trend of the spicule at the time t, Dt(y), is a linear-fitting result of D0(t; y) at the time t. We subtract Dt(y) from D0(t; y), and obtain a modified displacement spatial profile at the time t, which is defined as D1(t; y). We illustrate
D1(t0, y) in the right panel of Fig. 1. As can be seen in Fig. 1, the spicule appears wave-like in shape with a wavelength of
,
is set with mean position of the M pixels with square intensity of every pixel as the weight. The transverse position obtained in this way has a sub-pixel resolution (<0.054''). Thus, a transverse position profile as a function of the longitudinal coordinate of the slit,
D0(t0, y), can be obtained and is illustrated as a blue line in the left panel of Fig. 1, which appears wave-like relative to the central longitudinal axis of the long slit shown as a green dashed line in the figure. The spicule may be inclined off the longitudinal axis of the fixed slit during its evolution. The spatially oblique trend of the spicule at the time t, Dt(y), is a linear-fitting result of D0(t; y) at the time t. We subtract Dt(y) from D0(t; y), and obtain a modified displacement spatial profile at the time t, which is defined as D1(t; y). We illustrate
D1(t0, y) in the right panel of Fig. 1. As can be seen in Fig. 1, the spicule appears wave-like in shape with a wavelength of  2100 km (3'') and displacement amplitude of
2100 km (3'') and displacement amplitude of  70 km (0.10'') at that time (t0 = 11:40:29 UT).
70 km (0.10'') at that time (t0 = 11:40:29 UT).
Figure 2 shows three temporal sequences of displacements, D0(t; y1), D0(t; y2), and D0(t; y3), for Point-I, Point-II and Point-III on the spicule, where y1, y2 and y3 are the longitudinal coordinates in the long slit and equal to 3'', 3.5'', 4.5'', respectively. In Fig. 2, we find that points on the spicule oscillate along with the time, in addition to the average linear transverse motion across the central longitudinal axis of the long slit. Such average linear transverse motion of the point may be caused by the apparent turning of the spicule toward the photosphere or by long period waves acting on the spicule. The average linear transverse motion velocities for these three points from bottom to top are 3.1, 4.3 and 5.8 km s-1, respectively.
The linear transverse motion of the displaced point at the height y, Dy(t), is a linear-fitting result of D0(t; y) at the height y. We subtract Dy(t) from D0(t; y), and consider only the pure temporal oscillation at the height y, which we define as D2(t; y). The upper panel of Fig. 3 shows the oscillation sequence for Point-II at the height of y2,
D2(t; y2), which can be fitted with a sinusoidal curve. FFT analysis is used to calculate the power spectrum density (PSD) shown in the lower panel of Fig. 3. It is found that the PSD has a maximum at the frequency of 0.021 Hz, which corresponds to a period of 48 s. This period is shorter than the lower limit of the period range for Alfvén waves carried by the spicules as reported by De Pontieu et al. (2007a). The displacement amplitude for the oscillation is estimated to be 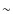 36 km (0.05'') near the image pixel scale, and the velocity amplitude is estimated to be
36 km (0.05'') near the image pixel scale, and the velocity amplitude is estimated to be 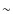 4.7 km s-1. This velocity amplitude is smaller than the range from 10 to 25 km s-1, given by De Pontieu et al. (2007a).
4.7 km s-1. This velocity amplitude is smaller than the range from 10 to 25 km s-1, given by De Pontieu et al. (2007a).
![\begin{figure}
\par\includegraphics[width=6.5cm]{0777fig3.eps}\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg14.png) |
Figure 3: Upper panel: Black line means the D2(t; y2) for Point-II. Red line is the fitting result with a sine function. Lower panel: Power spectrum density (PSD) of D2(t; y2) obtained with the FFT method. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg15.png) |
Figure 4: Upper left panel: D2(t; y1) for Point-I (black line) and its sin-fit result (red line). Upper right panel: D2(t; y2) for Point-II (black line) and its sin-fit result (red line). Lower left panel: cross power spectrum density (CPSD) for the oscillations of Point-I and Point-II. Lower right panel: Correlation coefficient as a function of time lag between the oscillations of Point-I and Point-II. |
| Open with DEXTER | |
We carry out the cross-correlation analysis of two oscillation sequences for two of the three
points,
D2(t, y1) and
D2(t, y2), in order to judge the propagation direction of the
oscillation as well as to estimate the phase speed. The upper left and upper right panels of
Fig. 4 display the oscillation sequences for Point-I and Point-II, respectively. These two oscillations have a maximum cross power spectrum density (CPSD) at a frequency of 0.031 Hz, see the lower left panel of Fig. 4. The correlation coefficient between oscillations of Point-I and Point-II as a function of the time lag can be obtained by applying inverse-FFT method to the CPSD profile, and is plotted in the lower right panel of Fig. 4. The correlation coefficient has a maximum value at the time lag of 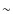 5 s showing that the oscillation for Point-II has a time lag of
5 s showing that the oscillation for Point-II has a time lag of 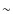 5 s relative to the oscillation for Point-I, which indicates that the Alfvén wave propagates upwards with a phase speed of
5 s relative to the oscillation for Point-I, which indicates that the Alfvén wave propagates upwards with a phase speed of 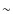 75 km s-1 along the spicule. Please note that the phase speed may be larger than 75 km s-1 since we can not distinguish a time lag shorter than 5 s, the interval between two exposures.
75 km s-1 along the spicule. Please note that the phase speed may be larger than 75 km s-1 since we can not distinguish a time lag shorter than 5 s, the interval between two exposures.
The upward propagation result is further confirmed in Fig. 5, by carrying out another cross-correlation analysis of D2(t; y2) and D2(t; y3), the oscillation sequences for Point-II and Point-III. It is found in the lower left panel of Fig. 5 that these two oscillations have a maximum CPSD at a frequency of 0.021 Hz. As is shown in the lower right panel of Fig. 5, the correlation coefficient profile has a maximum at the time lag of 5 s, the phase speed in the section between Point-II and Point-III is thus estimated to be 150 km s-1.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg16.png) |
Figure 5: Upper left panel: D2(t; y2) for Point-II (black line) and its sin-fit result (red line). Upper right panel: D2(t; y3) for Point-III (black line) and its sin-fit result (red line). Lower left panel: cross power spectrum density (CPSD) for the oscillations of Point-II and Point-III. Lower right panel: correlation coefficient as a function of time lag between the oscillations of Point-II and Point-III. |
| Open with DEXTER | |
Three other cases with Alfvén waves propagating upward along the spicules are also analyzed in this paper. Here we give a brief introduction to these three cases in the main text. For more detailed illustrations, please see the supplemental materials in Appendix A. In the second case, the oscillation period of the Alfvén wave is estimated to be 37 s corresponding to a frequency of 0.027 Hz. The amplitude of oscillating displacement is about 0.05'', and the velocity amplitude is about 6.1 km s-1. The Alfvén wave carried by this spicule is also found to propagate upward with a phase speed range between 59 and 117 km s-1. The second spicule appears in wave-like shape with an apparent wavelength of 5800 km at 11:41:31 UT. In the third case, the displacement oscillation sequences appear to have a period of 45 s with three displacement humps in a time range of 100 s. The displacement amplitudes are so large to reach 0.2'', a value higher than the displacement amplitudes in the former two cases of Alfvén waves, which may be related with the apparent surge-up of materials at the foot of this spicule and its large inclination. The Alfvén wave propagates upward along this spicule with a phase speed of about 73 km s-1. There is no clear wave-like shape appearing on the third spicule. In the fourth case, the displacements oscillate with a period of 50 s, and are greatly diminished from more than 0.1'' to less than 0.1'' after one period, which may indicate the damping of the Alfvén wave or the passing of an Alfvén wave packet. The Alfvén wave propagates upward along the fourth spicule with a phase speed range from 109 to 145 km s-1. The fourth spicule has a wave-like shape with an apparent wavelength of 5075 km at 11:49:11 UT. The second and the fourth spicules are visible at larger heights than the first and third spicules, and the lower sections of them are indiscernible. In Table 1, we list the characteristics of these four spicules with high-frequency Alfvén waves propagating upward on them.
Table 1: Characteristics of four cases of spicule dynamics with Alfvén waves propagating upward along them a.
3 Summary and discussion
We have found and analyzed four cases of dynamic spicules showing high-frequency transverse
displacement oscillations with time-lagged phases at greater heights, which suggests a modulation
of spicules by upward propagating high-frequency Alfvén waves. These Alfvén waves fluctuate
at high frequencies (>
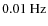 ), and propagate upward with phase speeds in the range between 50 and 150 km s-1. The maximum apparent transverse velocities are estimated to be 4.7, 6.1, 18.1, and 20.8 km s-1, derived by using an expression of
), and propagate upward with phase speeds in the range between 50 and 150 km s-1. The maximum apparent transverse velocities are estimated to be 4.7, 6.1, 18.1, and 20.8 km s-1, derived by using an expression of
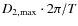 ,
where
,
where
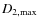 is the maximum transverse displacement and T is the wave period, which are compatible, respectively, with the values estimated directly from the time variations of the transverse displacements. The relatively smaller apparent velocity amplitudes for the Alfvén waves on the first and second spicules may be caused by the projection effect. They are still discernable after the elimination of jitter and slow drift on the image time series as well as the large-amplitude low-frequency transverse motion of the spicule.
is the maximum transverse displacement and T is the wave period, which are compatible, respectively, with the values estimated directly from the time variations of the transverse displacements. The relatively smaller apparent velocity amplitudes for the Alfvén waves on the first and second spicules may be caused by the projection effect. They are still discernable after the elimination of jitter and slow drift on the image time series as well as the large-amplitude low-frequency transverse motion of the spicule.
The dynamics of the third spicule shows an obvious surge-up at the foot, and the spicule is highly inclined, which may explain the observed large transverse velocity amplitude of Alfvén wave on it. The fourth spicule may be modulated by an Alfvén wave packet, and thus experiences a sequence of transverse oscillation with amplitude being large at the beginning and decreasing soon after one period. Damping of the Alfvén waves may be another possibility for the decrease of their velocity amplitudes. The heights above the limb in the projected plane for the four spicules, where we studied the transverse displacement oscillation, are maximally located at 4.4, 5.8, 1.5, and 7.3 Mm, respectively. We did not check observationally if these high-frequency waves exist in more extended spicule structures, say above 10 Mm. However, from theoretical consideration, it appears that for high-frequency waves it may be easier to propagate outward without reflection. We do not see noticeable growth or drop in wave displacement amplitude on the first three spicules except for the dynamics of the fourth spicule, which shows a growth in amplitude with increasing height and a damping in amplitude with increasing time at the same height.
To our knowledge, this is the first observation of an upward propagating Alfvén wave with a
frequency higher than 0.01 Hz in the chromosphere and transition region. The Alfvén waves
with a period of 50 s may be damped by cyclotron resonance at about 60 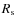 ,
which is the
mechanism used in models for the solar wind heating (Tu & Marsch 1997; Marsch & Tu 1997). Such high-frequency
Alfvén wave may undergo some damping in the corona if the nonlinear transverse cascade
(Cranmer & van Ballegooijen 2005) or the mode conversion to slow magneto-acoustic shock (Suzuki & Inutsuka 2005)
actually take place. However, the turbulence cascading in the solar corona may be weak
(Tu & Marsch 1997), therefore it is possible these waves will not be dissipated quickly within
60
,
which is the
mechanism used in models for the solar wind heating (Tu & Marsch 1997; Marsch & Tu 1997). Such high-frequency
Alfvén wave may undergo some damping in the corona if the nonlinear transverse cascade
(Cranmer & van Ballegooijen 2005) or the mode conversion to slow magneto-acoustic shock (Suzuki & Inutsuka 2005)
actually take place. However, the turbulence cascading in the solar corona may be weak
(Tu & Marsch 1997), therefore it is possible these waves will not be dissipated quickly within
60 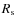 .
The question as to how such waves are dissipated is still open. The velocity
amplitude reported here is less than the mean velocity amplitude used in the model by Tu & Marsch (1997). This smallness is natural, since the former has a narrow frequency band, which is
embedded in the wide frequency band of the latter, and moreover the observation involves a projection effect. Due to the lack of three dimensional imaging of the dynamic wave-like spicules,
we only consider, in a plane perpendicular to the LOS, the distance between points as well as the
displacements of the points. This consideration may underestimate to some extent the phase speed
and velocity amplitude of the Alfvén wave, accordingly. To accurately calculate the properties
of Alfvén wave, imaging of the spicule from many more visual angles is required.
.
The question as to how such waves are dissipated is still open. The velocity
amplitude reported here is less than the mean velocity amplitude used in the model by Tu & Marsch (1997). This smallness is natural, since the former has a narrow frequency band, which is
embedded in the wide frequency band of the latter, and moreover the observation involves a projection effect. Due to the lack of three dimensional imaging of the dynamic wave-like spicules,
we only consider, in a plane perpendicular to the LOS, the distance between points as well as the
displacements of the points. This consideration may underestimate to some extent the phase speed
and velocity amplitude of the Alfvén wave, accordingly. To accurately calculate the properties
of Alfvén wave, imaging of the spicule from many more visual angles is required.
At present, there are three possible mechanisms to generate the Alfvén waves, of which horizontal random walk on the photosphere of the foot-point (van Ballegooijen et al. 1998) of a field line and photospheric 5-min oscillation as well as chromospheric 3-min oscillation (supporting Online Materials in De Pontieu et al. 2007a) are both considered to be responsible for the low-frequency Alfvén waves, while the third mechanism namely small-scale magnetic reconnection is expected to excite the high-frequency Afvén waves as suggested by Axford et al. (1999). However, up to now, there is still a lack of direct observational connection between the three possible mechanisms and the observed waves. The Alfvén waves with the short wavelength and period discussed in this paper may originate from magnetic reconnection, whereas the low-frequency Alfvén waves reported by De Pontieu et al. (2007a) were argued to be caused by the 5-min p-mode and 3-min chromospheric oscillation. These mechanisms may be related with the spicule dynamics which is found to consist of two types: type-I spicules that are probably driven by shock wave and have lifetimes of 3-7 min, and type-II spicules that are probably driven by magnetic reconnection and have lifetimes of 10-150 s (De Pontieu et al. 2007b).
The wave fluctuation on the spicule may be called the fast ``kink'' mode wave, if the spicule can
be described as a stable flux tube in the non-uniform medium. The ``kink'' mode wave will finally
evolve into Alfvén wave after its propagation upward into the more homogeneous medium
(Cranmer et al. 2007). The apparent thicknesses of the spicules we studied are wider than 120 km,
corresponding to the diffraction limit of SOT in 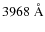 .
It is possible that such spicules may
contain some very fine threads thinner than 120 km. These possibly existent threads seem to be
affected by the same wave fluctuation and show consistent dynamics. It seems difficult for these
thin threads to mimic the observed high-frequency dynamic behavior if they were moving out of phase
in low-frequency large-amplitude oscillations, because they would then spin together and separate
from time to time, and so finally destruct the spicule.
.
It is possible that such spicules may
contain some very fine threads thinner than 120 km. These possibly existent threads seem to be
affected by the same wave fluctuation and show consistent dynamics. It seems difficult for these
thin threads to mimic the observed high-frequency dynamic behavior if they were moving out of phase
in low-frequency large-amplitude oscillations, because they would then spin together and separate
from time to time, and so finally destruct the spicule.
In this paper, we only presented four examples of upward propagating Alfvén waves along the spicules. These four examples show that high-frequency Alfvén waves do exist in the lower solar atmosphere. However it is not easy to pick out more spicules satisfying the analysis requirements from our dataset, since spicules rarely exist individually without overlapping or interacting with other spicules, and since very few spicules can be visible for a time only as long as two wave periods. Because of the limitation of the observational conditions, we cannot judge how much energy they can carry. To explore experimentally how much energy the high-frequency waves may contain, and to see if they can contribute to the corona heating and wind acceleration is a new task suggested by this study. A statistical study of the upward propagating Alfvén waves carried by more spicules is needed in the future work, in order to give a quantitative estimate of the energy flux carried by these waves.
Acknowledgements
Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway). SOT onboard Hinode was developed jointly by NAOJ, LMSAL, ISAS/JAXA, NASA, HAO and MELCO. We thank the SOT team for making their data public available on the internet. This work at Peking University is supported by the National Natural Science Foundation of China under Contract Nos. 40874090 and 40336053 and the Beijing Education Project XK100010404. He Jiansen's work is also supported by ``China Postdoctoral Science Foundation funded project''.
Appendix A: Another three cases for upward propagation of Alfvén waves
In this Appendix, we show another three cases of upward-propagating Alfvén waves. The figure formats in these three cases are similar to those in the first case. Several key characteristics (wave period, phase speed, and velocity amplitude) for the Alfvén waves on these three spicules are listed in Table 1. Please note that the number of clear cases found in our analyzed dataset is rather limited.
![\begin{figure}
\par\includegraphics[width=12.9cm,clip]{FigA1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg26.png) |
Figure A.1: The spatial profiles of intensity and displacement of the spicule at t0 = 11:41:31 UT for Case-2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{FigA2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg27.png) |
Figure A.2: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-2. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=11.5cm,clip]{FigA3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg28.png) |
Figure A.3: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y2) for Point-II for Case-2. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=11.5cm,clip]{FigA4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg29.png) |
Figure A.4: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{FigA5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg30.png) |
Figure A.5: The spatial profiles of intensity and displacement of the spicule at t0 = 11:33:56 UT for Case-3. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=13cm,clip]{FigA6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg31.png) |
Figure A.6: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-3. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{FigA7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg32.png) |
Figure A.7: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y2) for Point-II for Case-3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{FigA8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg33.png) |
Figure A.8: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-3. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{FigA9.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg34.png) |
Figure A.9: The spatial profiles of intensity and displacement of the spicule at t0 = 11:49:11 UT for Case-4. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=13cm,clip]{FigA10.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg35.png) |
Figure A.10: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-4. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{FigA11.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg36.png) |
Figure A.11: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y3) for Point-III for Case-4. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=13.3cm,clip]{FigA12.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg37.png) |
Figure A.12: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-4. |
| Open with DEXTER | |
References
- Axford, W. I., McKenzie, J. F., Sukhorukova, G. V., et al. 1999, Space Sci. Rev., 87, 25 In the text
- Cranmer, S. R., & van Ballegooijen, A. A. 2005, ApJS, 156, 265 In the text
- Cranmer, S. R., van Ballegooijen, A. A., & Edgar, R. J. 2007, ApJS, 171, 520 In the text
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007a, Science, 318, 1574 In the text
- De Pontieu, B., McIntosh, S., Hansteen, V. H., et al. 2007b, PASJ, 59, 655 In the text
- He, J.-S., Tu, C.-Y., & Marsch, E. 2008, Sol. Phys., 250, 147 In the text
- Hollweg, J. V. 2000, J. Geophys. Res., 105, 15699 In the text
- Hollweg, J. V., & Isenberg, P. A. 2002, J. Geophys. Res., 107, 1147 In the text
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 In the text
- Koutchmy, O., & Koutchmy, S. 1989, in High spatial resolution solar observations, ed. O. von der Luehe, 217 In the text
- Marsch, E., & Tu, C.-Y. 1997, Sol. Phys., 176, 87 In the text
- Matthaeus, W. H., Zank, G. P., Oughton, S., Mullan, D. J., & Dmitruk, P. 1999, ApJ, 523, L93 In the text
- Morgan, H., Habbal, S. R., & Woo, R. 2006, Sol. Phys., 236, 263 In the text
- Shimizu, T., Nagata, S., Tsuneta, S., et al. 2008, Sol. Phys., 249, 221 In the text
- Suzuki, T. K., & Inutsuka, S.-I. 2005, ApJ, 632, L49 In the text
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 In the text
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 In the text
- Tu, C.-Y., & Marsch, E. 1995, Space Sci. Rev., 73, 1 In the text
- Tu, C.-Y., & Marsch, E. 1997, Sol. Phys., 171, 363 In the text
- Tu, C.-Y., & Marsch, E. 2001, J. Geophys. Res., 106, 8233 In the text
- Tu, C.-Y., Marsch, E., Wilhelm, K., & Curdt, W. 1998, ApJ, 503, 475 In the text
- van Ballegooijen, A. A., Nisenson, P., Noyes, R. W., et al. 1998, ApJ, 509, 435 In the text
- Wilhelm, K., Marsch, E., Dwivedi, B. N., & Feldman, U. 2007, Space Sci. Rev., 133, 103 In the text
All Tables
Table 1: Characteristics of four cases of spicule dynamics with Alfvén waves propagating upward along them a.
All Figures
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg3.png) |
Figure 1:
Left panel: processed image obtained by SOT in Ca II H (3968 Å) at t0 = 11:40:29 UT. The red dotted box indicates the position of the spicule. The blue line is used to represent the skeleton of the spicule shape,
D0(t0; y), which appears wave-like. Three blue short lines indicate the locations on the spicule where its displacement is further analyzed, i.e. Point-I, Point-II and Point-III. The dashed green line is the center longitudinal axis of the red dotted box. Middle panel: profile of the defined spicule intensity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0777fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg5.png) |
Figure 2: From left through middle to right: profiles of D0(t, y) for Point-I, Point-II and Point-III, respectively, which are located at three heights marked with three blue short perpendicular slits listed from bottom to top in the left panel of Fig. 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm]{0777fig3.eps}\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg14.png) |
Figure 3: Upper panel: Black line means the D2(t; y2) for Point-II. Red line is the fitting result with a sine function. Lower panel: Power spectrum density (PSD) of D2(t; y2) obtained with the FFT method. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg15.png) |
Figure 4: Upper left panel: D2(t; y1) for Point-I (black line) and its sin-fit result (red line). Upper right panel: D2(t; y2) for Point-II (black line) and its sin-fit result (red line). Lower left panel: cross power spectrum density (CPSD) for the oscillations of Point-I and Point-II. Lower right panel: Correlation coefficient as a function of time lag between the oscillations of Point-I and Point-II. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0777fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg16.png) |
Figure 5: Upper left panel: D2(t; y2) for Point-II (black line) and its sin-fit result (red line). Upper right panel: D2(t; y3) for Point-III (black line) and its sin-fit result (red line). Lower left panel: cross power spectrum density (CPSD) for the oscillations of Point-II and Point-III. Lower right panel: correlation coefficient as a function of time lag between the oscillations of Point-II and Point-III. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.9cm,clip]{FigA1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg26.png) |
Figure A.1: The spatial profiles of intensity and displacement of the spicule at t0 = 11:41:31 UT for Case-2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{FigA2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg27.png) |
Figure A.2: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=11.5cm,clip]{FigA3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg28.png) |
Figure A.3: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y2) for Point-II for Case-2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=11.5cm,clip]{FigA4.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg29.png) |
Figure A.4: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{FigA5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg30.png) |
Figure A.5: The spatial profiles of intensity and displacement of the spicule at t0 = 11:33:56 UT for Case-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=13cm,clip]{FigA6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg31.png) |
Figure A.6: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{FigA7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg32.png) |
Figure A.7: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y2) for Point-II for Case-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{FigA8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg33.png) |
Figure A.8: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{FigA9.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg34.png) |
Figure A.9: The spatial profiles of intensity and displacement of the spicule at t0 = 11:49:11 UT for Case-4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=13cm,clip]{FigA10.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg35.png) |
Figure A.10: Profiles of D0(t; y) for Point-I, Point-II, and Point-III on the spicule for Case-4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{FigA11.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg36.png) |
Figure A.11: Correlation analysis result between D2(t; y1) for Point-I and D2(t; y3) for Point-III for Case-4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=13.3cm,clip]{FigA12.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa10777-08/Timg37.png) |
Figure A.12: Correlation analysis result between D2(t; y2) for Point-II and D2(t; y3) for Point-III for Case-4. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



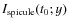 .
Right panel: profile of the spicule displacement
D1(t0; y).
.
Right panel: profile of the spicule displacement
D1(t0; y).