| Issue |
A&A
Volume 497, Number 1, April I 2009
|
|
|---|---|---|
| Page(s) | 209 - 242 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811382 | |
| Published online | 09 February 2009 | |
Parallaxes and proper motions for 20 open clusters as based on the new Hipparcos catalogue
F. van Leeuwen
Institute of Astronomy, Madingley Road, Cambridge, UK
Received 19 November 2008 / Accepted 2 February 2009
Abstract
Context. A new reduction of the astrometric data as produced by the Hipparcos mission has been published, claiming that the accuracies for nearly all stars brighter than magnitude
![]() are improved, by up to a factor 4, compared to the original catalogue. As correlations between the underlying abscissa residuals have also been reduced by more than an order of magnitude to an insignificant level, our ability to determine reliable parallaxes and proper motions for open clusters should be improved.
are improved, by up to a factor 4, compared to the original catalogue. As correlations between the underlying abscissa residuals have also been reduced by more than an order of magnitude to an insignificant level, our ability to determine reliable parallaxes and proper motions for open clusters should be improved.
Aims. The new Hipparcos astrometric catalogue is used to derive mean parallax and proper motion estimates for 20 open clusters. The HR-diagrams of the nearest clusters are compared and combined to provide future input to sets of observational isochrones.
Methods. Three different methods are applied, according to the proximity of the cluster, to compensate, where needed, for projection effects, spread in position along the line of sight, and the internal velocity dispersion of the cluster stars.
Results. The new parallaxes have accuracies between 2 and 2.5 times higher than what had been derived from the original Hipparcos catalogue. At least two to three groups of clusters, mostly of similar ages, are observed to each occupy their own specific space in the HR diagram. A significant discrepancy in distance moduli from those obtained with isochrone-based main-sequence fitting remains, in particular for one of these groups, containing the Pleiades, NGC 2516, and Blanco 1. The difference in absolute magnitudes between this group and one containing the Hyades and Praesepe clusters appears to be correlated with systematic differences in the Strömgren
![]() index between those groups. The same dependency has been known to exist for a long time, and is again confirmed by the Hipparcos data, in variations in absolute magnitudes for field stars of the same effective temperature.
index between those groups. The same dependency has been known to exist for a long time, and is again confirmed by the Hipparcos data, in variations in absolute magnitudes for field stars of the same effective temperature.
Conclusions. The positions of the cluster HR diagrams are consistent within different groups of clusters shown for example by the near-perfect alignment of the sequences for the Hyades and Praesepe, for Coma Ber and UMa, and for the Pleiades, NGC 2516, and Blanco 1. The groups are mutually consistent when systematic differences in
![]() are taken into account, where the effect of these differences on the absolute magnitudes has been calibrated using field-star observations.
are taken into account, where the effect of these differences on the absolute magnitudes has been calibrated using field-star observations.
Key words: methods: data analysis - astrometry - Hertzsprung-Russell (HR) and C-M diagrams - open clusters and associations: general - stars: distances
1 Introduction
The data accumulated by the Hipparcos mission allowed for the determination of large numbers of accurate absolute-parallax measurements for nearby stars (van Leeuwen 2007b; Perryman et al. 1997; ESA 1997). The new reduction (van Leeuwen 2007a) (VL7B from hereon), for example, provides some 27 000 stars with parallaxes known to better than 10 per cent, and over 10 000 known to better than 5 per cent. One of the many things learnt from this mission is the relatively large intrinsic spread in luminosities, even among stars which appear very similar in spectral type and photometric colour indices. An examination of G8V and K0V stars, for example, showed an intrinsic dispersion of 0.4 in absolute magnitudes for stars of the same colour index B-V (VL7B). A smaller, but still very significant, level of spread in absolute magnitudes is also observed for stars which were selected by Nicolet (1981) to be very similar in colour indices within the Geneva photometric system, the so-called photometric boxes (VL7B). Such a spread contrasts markedly with the very narrow main sequences observed for the best-studied and nearest open clusters, the Hyades (Perryman et al. 1998; Madsen et al. 2002), Pleiades (van Leeuwen et al. 1986; Mitchell & Johnson 1957) and Praesepe (Crawford & Barnes 1969a). The ability to superimpose the HR diagrams of such clusters on the HR diagram of the nearby stars, using parallax-based distance moduli rather than isochrone fitting, could provide quantitative information on some of the dependencies that cause the observed spread among the absolute magnitudes of apparently very similar field stars. Predictions on those dependencies are available from theoretical isochrones as based on a combination of models of stellar structure, stellar evolution and stellar atmospheres. However, observational evidence is required to test and eventually validate such models. The possibility of doing so has been hampered by the difficulty to determine with sufficient accuracy the parallaxes of star clusters. Even with the release of the Hipparcos data in 1997, some questions were left, most noticeably because of correlations between the errors on the underlying data from which the astrometric parameters for the clusters had been obtained. Doubts have in particular been raised on the effect that small areas of the sky with concentrations of bright stars may have locally on the measured parallaxes.
The new Hipparcos reduction has improved this situation in two ways: the error-correlation level on the underlying data has been reduced to an insignificant level, and the formal accuracies for most stars, and in particular the brighter stars, have been significantly improved. Both of these improvements have been made possible through a detailed study of the satellite dynamics and incorporating the findings of that study in the reconstruction of the along-scan attitude, which provides the reference frame for all the Hipparcos astrometric measurements. A potential weakening of the overall rigidity of the reconstructed catalogue. which may be caused by small areas with many bright stars, has also been dealt with. This so-called ``connectivity'' issue has been explained further in VL7B and van Leeuwen (2007b) (VL7V from hereupon). Given these improvements in both formal errors and overall reliability of the data, a renewed analysis of cluster parallaxes seemed very needed, not least as an apparent discrepancy for the Pleiades parallax as determined from the Hipparcos data has been used on several occasions to allegedly demonstrate errors in that catalogue (Pinsonneault et al. 1998; Soderblom et al. 2005; Pan et al. 2004; Southworth et al. 2005; Zwahlen et al. 2004; Soderblom et al. 1998). The reasons used in those papers to explain the Hipparcos results should be unreliable for the Pleiades cluster, such as error correlations and poor connectivity, have been eliminated by the new reduction (VL7B, VL7V).
For the open clusters studied here we make a few basic assumptions. The first is that all cluster-member stars share the same space motion, have the same age and originate from the same chemical composition ``cloud''. The stars are bound to the cluster, which means they will have a small internal dispersion in their velocities, decreasing towards the halo of the cluster. However, in particular the older clusters also tend to be surrounded by a wider halo of escaped former cluster members, which can complicate membership determinations. Furthermore, some of the youngest clusters can not easily be distinguished from fairly accidental concentrations in OB associations, and may not always be bound. However, in all cases the assumption of a shared overall velocity and distance has been applied.
The determination of astrometric parameters for clusters poses different problems as well as possibilities depending on the distance of the cluster. For the nearest cluster, the Hyades, the group is effectively three-dimensionally resolved, while its proximity causes it to cover a relatively large area (about 35 degrees diameter) on the sky. This creates the possibility of using the proper motions of individual cluster members to resolve the cluster along the line of sight. Intermediate-distance clusters can not be resolved this way, but astrometric studies still need to take into account projection effects on the proper motions, and a dispersion along the line of sight in the parallaxes of the individual cluster members. In defining the membership and determining the mean proper motion, the internal velocity dispersion also has to be taken into account, though this will often not be available as an independent measurement. Beyond about 250 pc, the dispersion of the parallaxes resulting from the finite size of the cluster becomes small with respect to formal errors on the measured parallaxes of the individual stars, and the same applies to the proper motion accuracies and the contribution from the internal velocity dispersion. The stars in these clusters can be treated as all having effectively the same parallax and proper motion, which can then be derived directly from a combined solution of the underlying data. This is the combined-abscissae method that was first presented by van Leeuwen & Evans (1998), and applied for all clusters by van Leeuwen (1999a) and Robichon et al. (1999). In those studies, however, the emphasis was on compensating for the error correlations in the underlying data, as well as in the proper combination of the two data streams that were used to create the old catalogue. These complications no longer apply when using of the new catalogue to derive astrometric parameters for open clusters.
This paper has been organized as follows. Section 2 presents a summary of the data, with particular emphasis on its use in deriving star-cluster astrometric parameters. Section 3 reviews briefly attempts made by Makarov (2002,2003) of applying corrections to the original Hipparcos astrometric data in the context of cluster-parallax determinations. Section 4 presents the different techniques applied to clusters at different distances. Section 5 presents an overview of other, isochrone independent distance modulus determinations for open clusters, and in particular introduces Hipparcos data to determine accuracies of these methods. This is followed by Sect. 6, where the results for individual clusters within 250 pc are presented, and Sect. 7 for clusters between 250 and 500 pc. In Sect. 8 the new set of distance moduli as derived from the parallaxes is compared with a range of earlier determinations, and the HR-diagram positions of cluster main sequences as obtained through ground-based photometry are compared. Section 9 briefly summarizes the space velocities of the clusters as derived from the new parallax and proper motion data. Finally, Sect. 10 presents conclusions from the current study.
2 The Hipparcos data
This section provides a summary of those aspects of the Hipparcos data that are of direct relevance to determining astrometric parameters for open clusters. For a more detailed description of the reductions that led to the new catalogue the reader is referred to VL7B, while VL7V provides a report on the validation tests applied to the data in the new catalogue.
The Hipparcos data originate from two fields of view, separated by a basic angle of 58 degrees, approximately scanning the sky along great circles. The transiting images seen through the two fields of view were projected on the same focal plane. The Hipparcos astrometric data have been derived from transit times over a modulating grid in this focal plane. Through the reconstruction of the along-scan attitude, these transit times are translated to scan phases. In the original reductions these scan phases are projected and measured on a reference great circle, with one such circle defined for each orbit (10.6 h period) of the satellite. The abscissae provided thus refer to a mean over all observations of a star over that period of time. These observations will therefore generally contain the combined information from between one and 8 transits of the field of view. In the new reduction the abscissae provided refer to individual field of view transits and are measured relative to the instantaneous scan direction. This allows for an improved recognition of faulty measurements, which usually are specific to just one field-of-view transit, and the ability to correct for small-scale grid distortions as a function of the across-scan coordinate.
With respect to the data presented in the first catalogue (ESA 1997), a number of very significant changes and overall improvements have been made. All improvements stem form the way the along-scan attitude is modelled, and how dynamic peculiarities of the satellite motion have been taken into account. There were two peculiarities in the satellite motion that were known but the extent and effect of which had been underestimated in the original reductions: (1) hits by very small particles, causing rotation-rate discontinuities, and (2) discrete satellite-non-rigidity events due to temperature changes affecting at least one of the solar panel mountings, causing so-called ``scan-phase discontinuities''. In the original reductions by the two consortia, FAST (Kovalevsky et al. 1992) and NDAC (Lindegren et al. 1992), these events were left mostly unrecognized and effectively smoothed over. This caused locally strongly correlated errors in the reference frame as created by the along-scan attitude reconstruction, as well as a non-Gaussian noise added to the abscissa measurements. The consequences of this ``smoothing over'' were made worse still by the use of the great-circle reduction method (van der Marel & Petersen 1992; van der Marel 1988), which referred all measurements over a 10.6 h period to projections on a single reference great circle. This was initially needed in order to deal with the relatively large errors (compared to the Hipparcos target accuracies) on the a priori astrometry provided by the Hipparcos Input Catalogue (ESA 1992; Turon et al. 1992). The great-circle reduction process caused multiple replication of local attitude errors. The effects of a local scan-phase discontinuity could therefore be felt at many different positions on the reference great circle, all separated by an integer number times the basic angle between the two fields of view. A further and more detailed analysis of these effects can be found in van Leeuwen & Evans (1998), van Leeuwen (2005a) and VL7B.
![\begin{figure}
\par\includegraphics[width=8.9cm]{11382f01.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg22.gif) |
Figure 1:
Top: Abscissa-error correlation level ( |
| Open with DEXTER | |
In the new reductions the peculiarities in the dynamics of the satellite have been incorporated fully in the attitude model (van Leeuwen & Fantino 2003). The great-circle reduction process has been replaced by a global iterative solution, similar to what is planned for the Gaia mission (O'Mullane et al. 2007). The iterations are between the reconstruction of the along-scan attitude and the construction of the star catalogue, both using the abscissa residuals as input data. A calibrated set of instrument parameters provides the link between the two systems. The result is a reduction in the overall noise level for the reconstructed along-scan attitude by about a factor five, and a reduction of the abscissa-error correlations by at least an order of magnitude. In the new reduction, the error-correlation level for field-transit abscissae has been examined by VL7V (Fig. 1). Even for relatively bright stars, correlation levels stay in all but the most extreme cases well below 0.1. To see how these error correlations may accumulate to correlated errors in the astrometric parameters of neighbouring stars, the coincidence factor has been introduced (van Leeuwen 1999b). Considering the scan of a single field of view as contained within a single full rotation of the satellite, the coincidence factor determines how often the measurements of two stars are contained within the same scan, as a fraction of the total number of scans for each star. This fraction drops rapidly as a function of the separation of the stars on the sky, as can be seen in the lower graph of Fig. 1. Any correlations between astrometric parameters for neighbouring stars would have to be the result of the combined effects of the abscissa-error correlations and the coincidence fraction. Given the low level of the correlations and the small range of the coincidence factors, no significant level of correlation is expected for the astrometric parameters of neighbouring stars in the new reduction. Similarly, a comparison between the new and the old reduction exposes the correlations in the astrometric parameters for the old reduction. Following these correlations as iterations for the new solution proceeded showed how gradually the memory of the old solution was lost (Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.9cm]{11382f02.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg23.gif) |
Figure 2:
Correlations ( |
| Open with DEXTER | |
The reduction of about a factor five in the noise level on the reconstructed along-scan attitude leads to a significant improvement in the formal errors on the parallax determinations for the brighter stars. In the published catalogue these accuracies were set by the reconstructed-attitude noise, while in the new reduction they are limited by primarily the photon noise on the abscissa data. For some of the brightest stars, this has resulted in accuracy improvements by up to a factor five. Also the reliability of the formal errors is much improved, as the errors on the field-of-view transit data can be directly related to the integrated photon count of the underlying measurements. Small corrections to the formal errors were derived and applied according to the across-scan position of a transit in the field of view, and the colour index of the star, in particular affecting the very red stars. Altogether, the new reduction provides a significant improvement in accuracy as well as overall reliability of the Hipparcos astrometric data, all of which should benefit the determination of astrometric parameters for open clusters.
3 Corrected Hipparcos data?
At this point it is worth noting the work done by Valeri Makarov on trying to remove the correlated errors caused by problems in the attitude modelling from the abscissa residuals as presented in the 1997 reduction (Makarov 2002,2006,2003). This correction was based on an idea first presented by van Leeuwen (1999b), which mainly focussed on the issue of connectivity between the two fields of view, and how this can be affected by the presence of locally dense groups of bright stars. The idea is that if such a group, like the core of the Pleiades cluster, is dominating the information for the attitude reconstruction, then if the astrometric data for this group of stars contains systematic errors, these errors would also reflect in the abscissa measurements for stars measured simultaneously with the Pleiades stars, but in the other field of view. By then examining the abscissa residuals of such measurements, one may be able to detect these systematic errors in, say, the Pleiades field. A simple test on the abscissa residuals of stars that shared some measurements this way with the Pleiades showed, however, that the unit weight standard deviation of the residuals for coinciding measurements was in fact slightly smaller than for the non-coinciding measurements (van Leeuwen 1999b). In other words, there is no signal contained in those residuals. The reason that Makarov was still able to produce a different parallax for the Pleiades cluster based on such data is that the coinciding stars tend to be much fainter than the Pleiades stars, and add substantial amounts of photon noise to the ``corrected'' data. The actual correction factor and other criteria as used by Makarov were quite arbitrary (see also van Leeuwen 2005b), and, combined with the photon noise contributions, could be adjusted to provide an expected result. The new reduction has taken care of the attitude modelling effects Makarov was trying to adjust, and it has done so in the only correct way, i.e. by re-analysing in detail the satellite dynamics and implementing this in an iterative solution. The results from the new reduction therefore effectively supersede the earlier results obtained by Makarov, even when these appear to give a ``more correct'' (that is, as expected by some) result.
4 Techniques for determining the astrometric parameters
In this section we look at techniques used to extract astrometric parameters for open clusters under different conditions of observing. First a set of exact relations is derived, followed by a first-order approximation, and finally the combined-abscissae method, as used for distant clusters, is recalled.
4.1 Exact solution
We define a fiducial reference point which we associate with the centre of
the cluster. Its position vector with respect to the Sun is defined as ![]() ,
which can be expressed in, for example, equatorial coordinates as:
,
which can be expressed in, for example, equatorial coordinates as:
![\begin{displaymath}\vec{R} = R \cdot \left[\begin{array}{r}\cos\alpha\cos\delta\\ \sin\alpha\cos\delta\\ \sin\delta\\ \end{array}\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img25.gif) |
(1) |
Similarly, the velocity vector
where the coefficients on the right relate to the observed radial velocity
Here
What we are interested in is how the proper motions for cluster members
will vary as a result of position in the cluster. For this purpose we include Eq. (3) in Eq. (2) and invert it to give
where the index ``i'' has been added to indicate reference to different positions in the cluster, with i=0 being the values for the assumed cluster centre. We now write Eqs. (2) and (3) as
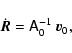 |
(5) |
where
which fully describes the relation between the observed components of the space velocity as a function of position on the sky and distance of the star.
4.2 Convergent point
The velocity vector of the cluster points to a position referred to as the
convergent point:
![\begin{displaymath}\dot{\vec{R}} = \dot{R}\left[\begin{array}{l}\cos\alpha_{\rm ...
...os\delta_{\rm c} \\
\sin\delta_{\rm c}\\
\end{array}\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img42.gif) |
(7) |
The common cluster-velocity components of all cluster member proper motions point towards this convergent point. The position of the convergent point depends on the actual velocity vector, of which one component, the radial velocity, is measured directly, and the other component, the proper motion, is scaled with the parallax of the cluster. Therefore, its determination on the sky allows for a measurement of the cluster distance. This is the traditional method used for determining the distance of the Hyades cluster. With the accuracies available in the Hipparcos data, this is no longer the best method available for the Hyades, but still the same effects can be put to use in different ways, to learn about the spatial distribution in the cluster.
Equation (4) can be rotated such that the proper motion is aligned with the direction of the convergent point, by multiplying it left and right by the matrix
![\begin{displaymath}\left[\begin{array}{rrr} 1 & 0 & 0 \\ 0 & \cos\psi & \sin\psi \\ 0 & -\sin\psi
& \cos\psi \\
\end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img43.gif) |
(8) |
where
4.3 First-order approximation
For clusters more distant than the Hyades, the differences between the stellar
coordinates and those of the cluster centre are sufficiently small to be
approximated in the relevant trigonometric functions. Thus, we develop
the matrix
![]() in Eq. (6) as
in Eq. (6) as
where
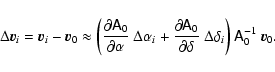 |
(10) |
The two matrix products give
![\begin{displaymath}\frac{\partial\ensuremath{\mathsf{A}} _0}{\partial\alpha}~\en...
...\sin\delta_0 \\
0 & -\sin\delta_0 & 0 \\
\end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img50.gif) |
(11) |
and
![\begin{displaymath}\frac{\partial\ensuremath{\mathsf{A}} _0}{\partial\delta}~\en...
...
0 & \phantom{-}0 & 0 \\
-1 & 0 & 0 \\
\end{array}\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img51.gif) |
(12) |
The first-order corrections for the proper motions and radial velocities of cluster members as a function of position on the sky are thus given by
where
Using
When the proper motion is large and the cluster is relatively nearby, the first term on the right will create an additional proper motion dispersion along the direction of the cluster proper motion. This effect is referred to as the relative secular parallax (van Leeuwen 1983). In the extreme case of the Hyades cluster, the proper motions can provide precise measurements of
When combining the astrometric data of different cluster members, the
formal errors and parameter correlations need to be taken properly into
account. There are additional noise contributions to the proper motions
from the internal velocity dispersion and to the parallaxes from the
finite size of the cluster. The main catalogue for the new reduction
provides for each solution the upper triangular matrix
![]() with which the astrometric parameters are to be multiplied when combining
data from different stars. This multiplication normalizes the errors on
the parameters. In fact, the inverse of the matrix
with which the astrometric parameters are to be multiplied when combining
data from different stars. This multiplication normalizes the errors on
the parameters. In fact, the inverse of the matrix
![]() is a
square root of the noise variance matrix
is a
square root of the noise variance matrix
![]() :
:
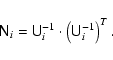 |
(16) |
To this we have to add the ``cosmic'' noise contributions from the parallax and proper motion dispersions. The parallax dispersion is derived from the typical positional spread of stars in an open cluster, for which a value of
Thus, as a cluster becomes more distant, this effect rapidly looses significance. Even for the Pleiades the effect is small, at about
The additional noise on the proper motions originates from the internal
velocity dispersion, which has a typical value of
![]() km s-1 in the cluster centre, and the relative
secular parallax, for which the contributions are described by
Eq. (15). In detail, both contributions depend on the
projected distance from the cluster centre, reflecting the space density
distribution of the cluster. In a cluster like the Pleiades both effects
are of order 1 mas s-1, but for most other clusters the effects are
smaller to much smaller. The contribution to the noise matrix for the
parallax and proper motion measurements as due to the actual distance of
a cluster star is given by
km s-1 in the cluster centre, and the relative
secular parallax, for which the contributions are described by
Eq. (15). In detail, both contributions depend on the
projected distance from the cluster centre, reflecting the space density
distribution of the cluster. In a cluster like the Pleiades both effects
are of order 1 mas s-1, but for most other clusters the effects are
smaller to much smaller. The contribution to the noise matrix for the
parallax and proper motion measurements as due to the actual distance of
a cluster star is given by
![\begin{displaymath}\ensuremath{\mathsf{N}} _{\rm p} = \left[\begin{array}{rrr}\s...
...gl(\frac{\mu_{\delta,0}}{\varpi_0}\bigr)^2
\end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img72.gif) |
(18) |
where
![\begin{displaymath}\ensuremath{\mathsf{N}} _{\rm q} = \left[\begin{array}{rrr} 0...
...& 0 \\
0 & 0 & \sigma_{\mu,{\rm q}}^2 \\
\end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img74.gif) |
(19) |
where
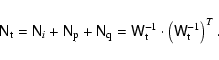 |
(20) |
Multiplication by the upper-triangular matrix
4.4 Distant clusters
For distant clusters, where the formal errors on the proper motions and parallaxes of the individual members are significantly larger than the corrections described above, the cluster parameters may be derived from a combined analysis of the abscissa residuals for the member stars. Thus, we repeat the astrometric parameter solutions for the cluster stars, but now solve for a single proper motion and parallax for all cluster members.
In order to make this common-parameter solution possible, the abscissa
residuals for stars involved need to be re-calculated, to provide residuals
relative to a chosen reference parallax and proper motion, which can be
seen as the first estimate of the cluster parallax and proper motion.
The abscissa residual for observation ``j'' of star ``i'' as provided
in the epoch astrometry file in VL7B is represented by
![]() .
A vector
.
A vector ![]() represents the cluster parallax and
proper motion, and similarly
represents the cluster parallax and
proper motion, and similarly
![]() the reference values for the cluster.
The corrected abscissa residuals are then given by
the reference values for the cluster.
The corrected abscissa residuals are then given by
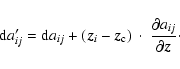 |
(21) |
The initial choice for
5 Some ground-based distance modulus or parallax determination methods, independent of isochrone fitting
In this section three methods that have been used for isochrone-independent cluster-distance determinations are reviewed by incorporating the new Hipparcos data. Some of the methods described below derived or used relations between observed parameters (generally photometric colour indices) and physical parameters of the observed stars, using stars with ground-based parallaxes, or open clusters and their assumed distances, for calibration. The uncertainty has been in distinguishing the error contributions from the calibration objects (such as the measured parallax) from the cosmic noise on such calibrations. The independent absolute parallaxes obtained from the Hipparcos data allow for an assessment of these noise levels.
5.1 Crawford's calibrations of the Strömgren photometric system
Here an overview is presented on a set of calibrations that have been (and are still) used for luminosity calibrations based on Strömgen photometry. A more recent calibration (but still pre-Hipparcos) is also available (Jordi et al. 1997), but concerns more the calibration of relations between specific indices, and recognizes that there are significant uncertainties in empirical photometric luminosity calibrations. First calibrations incorporating the Hipparcos data have been presented by Domingo & Figueras (1999) for late A-type stars and Jordi et al. (2002) on preliminary results for F, late A and B type stars.
The empirical calibration of absolute magnitudes through observations in the Strömgen photometric system by Crawford was done in three stages, on the F type stars using the Pleiades, ![]() Per and Coma Ber for establishing calibration slopes, and nearby stars with ground-based parallaxes for zero-point determination (Crawford 1975), on the B-type stars (Crawford 1978) and A type stars (Crawford 1979) using distances of the Pleiades and
Per and Coma Ber for establishing calibration slopes, and nearby stars with ground-based parallaxes for zero-point determination (Crawford 1975), on the B-type stars (Crawford 1978) and A type stars (Crawford 1979) using distances of the Pleiades and ![]() Per as determined through the F-star calibration. Thus, ultimately, the zero point of the calibration of the system rests on the ground-based parallaxes of 17 nearby F-type stars, while the slopes has been determined by means of the combined data from open cluster stars.
Per as determined through the F-star calibration. Thus, ultimately, the zero point of the calibration of the system rests on the ground-based parallaxes of 17 nearby F-type stars, while the slopes has been determined by means of the combined data from open cluster stars.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f03.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg82.gif) |
Figure 3: A comparison between the ground-based parallax values as used by Crawford (1975) and parallaxes for the same stars as obtained from the new Hipparcos reduction. The comparison shows a systematic difference of 3.4 mas and a noise on the ground-based parallaxes of 10 mas. |
| Open with DEXTER | |
As the ground-based parallaxes used by Crawford had relatively large errors, he applied a Lutz-Kelker correction (Lutz & Kelker 1973) to compensate for the bias in the derived distance moduli and thus the absolute magnitudes. Such corrections are provided for 48 of the 51 stars. Using the new Hipparcos parallaxes, the Lutz-Kelker correction is not needed, as parallax errors are for nearly all stars below 1 per cent. The direct comparison between the parallaxes (Fig. 3) shows a systematic difference of
![]() mas, and a noise level on this selection of ground-based parallaxes of 10.3 mas. Very similar results were obtained by Jordi et al. (2002) based on the 1997 reduction of the Hipparcos data. There it was also shown that the mean offset for the nearest stars, as used by Crawford, the correction was still larger, at -5 mas. A comparison between the absolute magnitudes as given by Crawford before (
mas, and a noise level on this selection of ground-based parallaxes of 10.3 mas. Very similar results were obtained by Jordi et al. (2002) based on the 1997 reduction of the Hipparcos data. There it was also shown that the mean offset for the nearest stars, as used by Crawford, the correction was still larger, at -5 mas. A comparison between the absolute magnitudes as given by Crawford before (
![]() )
and after the Lutz-Kelker correction (
)
and after the Lutz-Kelker correction (
![]() )
and those derived using the new Hipparcos parallaxes (
)
and those derived using the new Hipparcos parallaxes (
![]() )
gives the following results:
)
gives the following results:
| (22) |
where in the first solution the noise level was determined as 0.29, and in the second solution as 0.31 mag. The offset in the first solution is caused entirely by the systematic differences of 3.4 mas between the ground-based and Hipparcos parallaxes. After applying the correction for the systematic offset in the ground-based parallaxes, the observed difference is a (rounding-off) residual of
where
and a nominal distance modulus for the Pleiades of
In the solution to Eq. (23) also dependencies on
![]() and cross terms of
and cross terms of
![]() and
and
![]() were tested, but the result was not significant. The parameter
were tested, but the result was not significant. The parameter
![]() is correlated with abundance variations (Crawford 1975; Gustafsson & Nissen 1972; Nissen 1970b,a), which suggests that such variations are not a significant contribution in the remaining spread in absolute magnitudes.
is correlated with abundance variations (Crawford 1975; Gustafsson & Nissen 1972; Nissen 1970b,a), which suggests that such variations are not a significant contribution in the remaining spread in absolute magnitudes.
Table 1:
Comparison between absolute magnitude calibrations for different mean values of
![]() .
.
Table 1 shows the results of applying Eq. (24) to the mean ![]() values derived by Crawford for the five intervals he used for his analysis. The
values derived by Crawford for the five intervals he used for his analysis. The
![]() values derived from the new analysis differ by up to 0.14 mag from the values derived by Crawford for
values derived from the new analysis differ by up to 0.14 mag from the values derived by Crawford for
![]() .
.
Conclusions on the Crawford calibrations are the following. The systematic errors on the ground-based parallaxes for the calibration stars were partly offset by the Lutz-Kelker correction, which by itself does not seem to do any good to the data. The Crawford calibration can, as a result be offset by up to 0.14 mag. However, the remaining noise level for the calibration standards is much larger than what would be caused by measurement inaccuracies. It may be partly caused by duplicity, in which case the zero point of the calibration is also affected. When deriving distances of individual objects or star clusters using this calibration, this noise needs to be accounted for in the final accuracy figure until it can be quantified and related to independent observed parameters. For the calibrations of the A and B stars there are now available large numbers of calibration stars with well determined parallaxes, which should replace the current extrapolation based on the F stars and cluster distances derived therefrom. This concept is further evaluated in Sect. A. For the current paper the important aspect is the difference between the determination precision, usually quoted as accuracy, for the cluster-distance determinations, and the actual accuracy, which also takes into account the observed cosmic spread intrinsic to the calibration relation.
5.2 Photometric boxes in the Geneva photometric system
The method of the photometric boxes is based on the hypothesis that if two stars have nearly the same colours or derived parameters, then they will also have nearly the same physical and atmospheric properties (Creze et al. 1980; Nicolet 1981). This was applied by Nicolet (1981) to photometric data in the Geneva system for determining the distance moduli of 43 open clusters. The comparisons in the boxes were done directly between stars with ground-based parallax determinations and cluster stars, always sharing the same boxes. The accuracies for these parallaxes were still a major factor in these calculations, which can now be eliminated by substituting those data with the Hipparcos results. What can be measured is the difference in apparent magnitude between cluster members and parallax stars sharing the same photometric boxes. In the original solution two compatible noise sources had to be accounted for, the uncertainty of the measured parallaxes and the uncertainty in the hypothesis stated above. Using the Hipparcos parallaxes, the uncertainty in the hypothesis dominates fully. Nicolet estimated this to be at a level of 0.3 mag.
Table 2: Data from Nicolet (1981) for the cluster NGC 752.
The detailed data for one cluster, NGC 752, are provided by Nicolet (1981). They are partly reproduced here in Table 2, together with the new parallax data. Based on these data, an estimate of the distance modulus for the cluster can be obtained:
| (25) |
where
The photometric boxes method could be explored further though. Using the now much more extensive volume of photometric data and the Hipparcos parallax information for many of these stars should allow for a much closer examination of the differential effects within these boxes, and the way these may be related to luminosity variations. This in turn could lead the way to an improved photometric calibration of distance moduli for distant star clusters.
5.3 Differential parallax determinations with the MAP
![\begin{figure}
\par\includegraphics[width=9cm]{11382f04.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg145.gif) |
Figure 4: Differences between MAP-based and Hipparcos parallaxes for 71 stars. The error bars contain the contributions of the formal errors on the Hipparcos parallaxes and the precisions as given for the MAP data. |
| Open with DEXTER | |
Before starting the analysis of the Hipparcos data for the open clusters, it is worthwhile to investigate the results obtained with differential (small-field) parallax measurements, in particular those obtained with the multichannel astrometric photometer (MAP) (see for example Gatewood et al. 1990) and Hubble Space Telescope, both of which use the same techniques to calibrate from measured relative to estimated absolute parallaxes. Of particular interest are those results obtained before the release of the Hipparcos catalogue, as these provide the most likely measurements not biassed by an assumed outcome. A comparison of this kind was done by Gatewood et al. (1998) using the first release of the Hipparcos catalogue, where it was noticed that an additional noise component was present, but the origin and amplitude was not specified. Ground-based parallax measurements obtained mostly with the MAP were found for a total of 71 stars that have also data entries in the new Hipparcos catalogue. The errors as given for those measurements are explained by Gatewood as being precision rather than accuracy, and this becomes quite clear when examining the statistics of the differences with the Hipparcos measurements, shown in Fig. 4. Without adding absolute-calibration noise, the weighted mean of the differences and associated standard deviation are given by
| (26) | |||
| (27) |
With correct weights, the expected value for the standard deviation equals 1.0. Adding a noise contribution to account for calibration uncertainties to the precision reduces the unit-weight standard deviation. A value close to 1.0 is reached when adding a calibration noise of 2.37 mas:
| (28) | |||
| (29) | |||
| (30) |
The added noise should be regarded as an average over the studies included here, and may well vary significantly depending on sources available for calibration. However, it seems unlikely that these parallaxes will have absolute accuracies any better than at best 1.5 to 2.0 mas. The source of this calibration uncertainty is likely the generally small number of calibration stars available and the large intrinsic spread in absolute magnitudes within either an interval in colour index or a spectral class. For the present paper, these results are important when comparing the Hipparcos results with MAP-based parallax determinations for the same clusters.
6 Nine clusters and a moving group within 250 pc
In this section the results for clusters within 250 pc are presented. In order
of derived distance, these are the UMa moving group, the Hyades, Coma Ber, Pleiades, IC 2602, IC 2391, ![]() Per, Praesepe, NGC 2451 and Blanco 1. NGC 2451, however, does not correspond to the group of stars that was originally given this designation (Röser & Bastian 1994). The cluster identified as Cr 359, assigned by Loktin & Matkin (1994) a distance within the same range, has been rejected, as it does not show from the Hipparcos data in either proper motion or distribution on the sky (see also Robichon et al. 1999). The indications within the Hipparcos data for the existence of a cluster at 170 pc in Ophiuchus, as suggested by Mamajek (2006), are too weak.
Per, Praesepe, NGC 2451 and Blanco 1. NGC 2451, however, does not correspond to the group of stars that was originally given this designation (Röser & Bastian 1994). The cluster identified as Cr 359, assigned by Loktin & Matkin (1994) a distance within the same range, has been rejected, as it does not show from the Hipparcos data in either proper motion or distribution on the sky (see also Robichon et al. 1999). The indications within the Hipparcos data for the existence of a cluster at 170 pc in Ophiuchus, as suggested by Mamajek (2006), are too weak.
In all cases where HR diagrams are presented, mean reddening corrections for the clusters have been applied according to what appears from the consulted literature to be a reliable estimate. In all cases these corrections are small. No individual corrections for the differential reddening in the Pleiades and ![]() Per, or to data of individual field stars, have been applied. Corrections for metallicity variations have not been applied. For the small variations shown by the clusters examined here, there is no observational confirmation of significant luminosity variations with varying metallicity (see further Sect. A).
Per, or to data of individual field stars, have been applied. Corrections for metallicity variations have not been applied. For the small variations shown by the clusters examined here, there is no observational confirmation of significant luminosity variations with varying metallicity (see further Sect. A).
6.1 The Hyades
A major study of the Hyades cluster as based on the first Hipparcos catalogue was presented by Perryman et al. (1998), and further studies based on the same data by Madsen et al. (2000), Madsen et al. (2001) and de Bruijne et al. (2001). Differences between the results of these studies show one of the problems associated with most open-cluster studies, the statistical variations in results due to the relatively small number of member stars available, further complicated by uncertainties of membership. Combined with different selection criteria, results can look sometimes even significantly different. A major complication for the Hyades cluster, as well as other similar clusters, is the apparent presence of a halo of stars ``evaporated'' from the cluster. These can easily disturb estimates of the distance, space velocity and internal velocity dispersion of a cluster.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11382f05.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg151.gif) |
Figure 5:
Reduced proper motions in the selection field for the Hyades
cluster. In this diagram, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11382f06.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg152.gif) |
Figure 6: Map of the selected 150 Hyades stars, showing the current positions (points to the right of each line) and those extrapolated by 100 000 years (left-side points). |
| Open with DEXTER | |
Based on the new reduction the Hyades cluster membership was reassessed, and
similarly the internal dispersion in the proper motions as a function of the
projected distance to the ``centre'' of the cluster, where it should be
understood that in a loosely bound, and not very rich cluster like the Hyades,
the centre is not very well defined. The position of the projected centre was assumed to be (in the ICRS)
| (31) | |||
| (32) |
The catalogue has been searched for potential Hyades members within a radius of
| (33) |
or between 31.6 and 61.7 pc distance from the Sun. The chosen limits imply that a complete sphere with radius 15 pc around the assumed cluster centre is covered. A total of 270 stars were thus selected. The reduced proper motions of the selected stars were then examined for further membership selection. The reduced proper motions (Fig. 5) describe the observed proper motions as the components towards, and perpendicular to, the convergent point of the cluster, and corrected for the angular separation from the convergent point (Sect. 4.2) (see also van Altena 1966). Based on the reduced proper motions 150 stars were selected as probable members (one additional star, HIP 20895, was rejected based on a comparison between the measured parallax and the kinematic distance). Figure 6 shows these stars and their extrapolated displacements over the next 100 000 years that would result from the observed proper motions. The mean space velocity relative to the Sun for the selected stars has been derived from the observed parallaxes and proper motions only, applying Eq. (4) in a least-squares solution, and is found to be
![\begin{displaymath}\dot{\vec{R}} = \left[\begin{array}{r}-5.99 \\ 44.73 \\ 4.93 ...
...0.25 \\
0.61 \\
0.14 \\
\end{array}\right]~{\rm km~s}^{-1},
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img157.gif) |
(34) |
with a unit-weight standard deviation of 1.86. The latter is a clear indication that the observed proper motions are significantly affected by internal motions. As a result, the formal errors on the proper motions are insufficient for representing their actual noise level. The formal errors on the input data to the solution do include the errors on the measured parallaxes.
![\begin{figure}
\par\includegraphics[width=9cm]{11382f07.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg158.gif) |
Figure 7: Comparison between the formal errors on the distance moduli for the Hyades stars as measured directly through parallaxes (dots) and as derived from the space velocity and the observed proper motions (crosses). |
| Open with DEXTER | |
The space velocity, together with the observed proper motions and their
covariances can be used to derive, by means of Eq. (6), the
kinematic (relative) parallaxes for the cluster members. The advantage of
this for the Hyades cluster stems from the relatively large proper motion,
combined with small formal errors, and can clearly be seen when comparing
the error estimates on distance moduli derived from the measured and kinematic
parallaxes (Fig. 7).
The mean parallax of the selected stars was calculated from the kinematic
parallax estimates, and after projecting their distances onto the
line-of-sight for the cluster centre, to avoid any (though quite small)
projection-induced bias. The value thus obtained is
where the first error shows the standard deviation, representing the spread of stars in the cluster. The formal errors on the measurements hardly contribute to this value, being overall much smaller. The second error in Eq. (35) gives the error on the mean. Thus, based on the error on the mean, the weighted mean distance of the 150 plausible Hyades members selected here is
![\begin{figure}
\par\includegraphics[width=8cm]{11382f08.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg163.gif) |
Figure 8: The Hyades HR diagram for 150 probable members, using distance moduli for individual stars as based on kinematically derivedparallaxes. |
| Open with DEXTER | |
For the current study, the most important result is the position and shape of the Hyades HR diagram, representing an observed isochrone for stars of a specific age and chemical composition. The comparison between the diagrams as derived using the observed or the kinematic parallaxes has been shown on various previous occasions (de Bruijne et al. 2001; Madsen et al. 2000; Madsen 1999) and VL7B, so here is shown only the diagram using the distance moduli for individual stars as based on their kinematic parallaxes (Fig. 8). Clear from this figure is the narrow and well-defined main sequence, as well as the scattering of double stars up to 0.75 mag above it.
6.2 Coma Ber and UMa
![\begin{figure}
\par\includegraphics[width=13cm]{11382f09.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg164.gif) |
Figure 9:
A tangential projection of the distribution on the sky for
members of the clusters Coma Ber ( top left), Pleiades ( top right),
Praesepe ( bottom left) and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm]{11382f10.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg166.gif) |
Figure 10:
The distribution of the parallaxes against their formal errors for
the clusters Coma Ber ( top left), Pleiades ( top right), Praesepe ( bottom left)
and |
| Open with DEXTER | |
Coma Ber is a sparse cluster at high galactic latitude, considered older than the Pleiades and younger than the Hyades and Praesepe. Crawford & Barnes (1969b) derived a distance modulus of 4.5 for this cluster, and showed in the same paper the results for a small number of members of the core of the UMa moving group, which have characteristics very similar to the Coma Ber cluster. For this group a distance modulus of 1.8 is stated. Both distance determinations used the calibrations of the parameters c1 and ![]() as presented by Strömgren (1966). That calibration is in fact based on the one presented by Fernie (1965), who used open cluster data for which distances had been derived from on UBV photometry by Johnson et al. (1961). Among those clusters was Coma Ber, for which a distance modulus of 4.5 was given. All distances given in that paper were tied-in to a distance of 40 pc for the Hyades, which we now know should be 16 per cent larger, at 46.45 pc. It is therefore reasonable to assume that the distance and distance-moduli estimates based on this material may have been underestimated. It would in fact be more surprising if they were correct.
as presented by Strömgren (1966). That calibration is in fact based on the one presented by Fernie (1965), who used open cluster data for which distances had been derived from on UBV photometry by Johnson et al. (1961). Among those clusters was Coma Ber, for which a distance modulus of 4.5 was given. All distances given in that paper were tied-in to a distance of 40 pc for the Hyades, which we now know should be 16 per cent larger, at 46.45 pc. It is therefore reasonable to assume that the distance and distance-moduli estimates based on this material may have been underestimated. It would in fact be more surprising if they were correct.
There are few independent distance determinations for Coma Ber. Based on the so-called photometric boxes in the Geneva photometric system, and thereby effectively calibrating the cluster distance on ground-based parallaxes of nearby stars, Nicolet (1981) derived a distance modulus of
![]() .
A differential parallax determination by Gatewood (1995) gave a value of
.
A differential parallax determination by Gatewood (1995) gave a value of
![]() for the distance modulus. This is an internal error, and considering the discussion in Sect. 5.3, an error of the order of 0.3 to 0.4 mag for the absolute value may be more realistic. Based on UBV photometry, Cameron (1985) derived a distance modulus of 4.65, while a more recent photometric distance determination by Pinsonneault et al. (1998) gave a value of
for the distance modulus. This is an internal error, and considering the discussion in Sect. 5.3, an error of the order of 0.3 to 0.4 mag for the absolute value may be more realistic. Based on UBV photometry, Cameron (1985) derived a distance modulus of 4.65, while a more recent photometric distance determination by Pinsonneault et al. (1998) gave a value of
![]() .
The parallax determinations using the first release of the Hipparcos data gave values of
.
The parallax determinations using the first release of the Hipparcos data gave values of
![]() (Robichon et al. 1999) and
(Robichon et al. 1999) and
![]() (van Leeuwen 1999a).
(van Leeuwen 1999a).
Table 3: Summary of distance modulus determinations for the Pleiades over the past 30 years.
Eight members of the UMa group were analyzed for the present paper, with individual parallax accuracies in the new Hipparcos reduction between 0.14 and 0.41 mas, or relative errors between 0.35 and 1.0 per cent. The selected stars are from the list of Crawford & Barnes (1969b) (only those with single five-parameter astrometric solutions), including HD 113139 (HIP 63504). The average distance modulus for these stars as derived from the new Hipparcos catalogue is
![]() ,
placing this group about 10 per cent further away than was derived by Crawford & Barnes (1969b). The main reason for including these stars in the present paper and in connection with the Coma Ber cluster is the similarity in age between the two groups. The UMa stars are not examined with the cluster-analysis tools shown in Sect. 4, but rather as individual stars, taking full advantage of the high relative accuracies of the individual parallaxes.
,
placing this group about 10 per cent further away than was derived by Crawford & Barnes (1969b). The main reason for including these stars in the present paper and in connection with the Coma Ber cluster is the similarity in age between the two groups. The UMa stars are not examined with the cluster-analysis tools shown in Sect. 4, but rather as individual stars, taking full advantage of the high relative accuracies of the individual parallaxes.
A selection of 27 cluster members has been used for determining the parallax and proper motion of the Coma Ber cluster. There may be two or three more possible members of Coma Ber in the Hipparcos catalogue, but these deviate either in proper motion or in parallax by more than what could be expected from the formal errors. Excluding these stars had only an insignificant effect on the final results. Deriving the astrometric parameters for this, as well as the remaining clusters in this section, has been done through an examination of the astrometric parameters as provided for the individual member stars in the new catalogue. The proper motions have been corrected for the differential projection effects described by Eq. (13), using a radial velocity as specified in Table 5, -1.2 km s-1. The cluster members are spread sparsely over an area with a diameter of about 7.5 degrees on the sky (Fig. 9). Data correlations therefore did not play a major role when the parallax was derived using the 1997 catalogue, and it is thus not surprising that the results from the new reduction confirm and significantly strengthen the original findings by van Leeuwen (1999a) and Robichon et al. (1999). The distribution of the parallaxes and their formal errors is shown in Fig. 10. The summary data for Coma Ber are presented in Table 4. The parallax for Coma Ber is
determined as
![]() mas, which implies a distance modulus of
mas, which implies a distance modulus of
![]() .
Thus, the same increase of 10 per cent in distance as observed for the UMa group with respect to the determinations by Crawford & Barnes (1969b). Considering the calibration noise for ground-based differential parallaxes as determined in Sect. 5.3, the Hipparcos value is in good agreement with the determination by Gatewood (1995). There is a good agreement, too, with the values derived by Nicolet (1981) and Cameron (1985). The only marginally significant disagreement is with the determination by Pinsonneault et al. (1998), which differs by 3.4
.
Thus, the same increase of 10 per cent in distance as observed for the UMa group with respect to the determinations by Crawford & Barnes (1969b). Considering the calibration noise for ground-based differential parallaxes as determined in Sect. 5.3, the Hipparcos value is in good agreement with the determination by Gatewood (1995). There is a good agreement, too, with the values derived by Nicolet (1981) and Cameron (1985). The only marginally significant disagreement is with the determination by Pinsonneault et al. (1998), which differs by 3.4![]() .
The HR-diagram for Coma Ber is shown in Fig. 11 together with the results for the UMa stars and those obtained earlier for the Hyades cluster. At the parallaxes determined here, the HR diagrams of Coma Ber and the UMa group accurately overlap, but are slightly sub-luminous (0.15 mag.) with respect to the Hyades.
.
The HR-diagram for Coma Ber is shown in Fig. 11 together with the results for the UMa stars and those obtained earlier for the Hyades cluster. At the parallaxes determined here, the HR diagrams of Coma Ber and the UMa group accurately overlap, but are slightly sub-luminous (0.15 mag.) with respect to the Hyades.
Table 4: Summary data for 8 clusters within 250 pc.
![\begin{figure}
\par\includegraphics[width=17.8cm]{11382f11.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg183.gif) |
Figure 11: The HR diagrams for Coma Ber ( left), Pleiades ( centre) and Praesepe ( right), shown as full dots in each diagram. The Hyades stars are shown in the background as open circles. In addition. The Coma Ber diagram also shows the UMa stars (crosses), the Pleiades diagram shows the Coma Ber stars as crosses, and similarly for the Pleiades stars are shown in the Praesepe diagram. |
| Open with DEXTER | |
6.3 The Pleiades
More than any other result from the Hipparcos mission, the parallax estimate for the Pleiades cluster has been causing controversy (Valls-Gabaud 2007; Stello & Nissen 2001; van Leeuwen 1999b; Narayanan & Gould 1999; Pinsonneault et al. 1998; An et al. 2007; Percival et al. 2005,2003; van Leeuwen 2005b; Pan et al. 2004; van Leeuwen 1999a; Southworth et al. 2005; Robichon et al. 1999). In many ways this has been highly beneficial, as it has stimulated research projects on the Pleiades. In total there have been at least 15 attempts to determine the parallax or distance modulus of the Pleiades since the publication of the Hipparcos data in 1997. It has also been one of many reasons to continue with a further detailed analysis of the Hipparcos data. With the results of a wide range of studies now available, including the new Hipparcos determination, the solution may not as yet have been identified, but the discrepancy between different approaches has become clearer, and will undoubtedly be resolved in the near future. As has been announced on a few earlier occasions (van Leeuwen 2008), the new reduction of the Hipparcos data did not change significantly earlier estimates for the cluster parallax.
The Pleiades cluster covers an area on the sky of about 9 to 10 degrees in
diameter (van Leeuwen 1980,1983), which is, contrary to statements made by An et al. (2007), much larger than the error-correlation scale length for the 1997 Hipparcos catalogue (van Leeuwen 1999b). In that area, the Hipparcos catalogue contains about 57 members of the cluster, but only 53 of these can be used for determining the cluster parallax. The parallax determinations for the remaining 4 stars may be disturbed by duplicity or orbital motion. Figure 9 shows the distribution on the sky of the selected stars. The distribution of parallax measurements and their formal errors is shown in Fig. 10, with respect to the measured parallax of
![]() mas (distance modulus
mas (distance modulus
![]() ), as an internally consistent distribution of data points. In the new reduction, these data points are essentially uncorrelated (VL7B, VL7V). From the examination of the parallax zero point in the new catalogue (VL7V), there is no reason to suspect that all parallaxes in the catalogue are offset by anything more than the offset-detection limit of about 0.1 mas.
), as an internally consistent distribution of data points. In the new reduction, these data points are essentially uncorrelated (VL7B, VL7V). From the examination of the parallax zero point in the new catalogue (VL7V), there is no reason to suspect that all parallaxes in the catalogue are offset by anything more than the offset-detection limit of about 0.1 mas.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f12.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg186.gif) |
Figure 12:
Distribution of determinations (since 1997) for the Pleiades distance modulus and its standard error (other than those directly derived from the Hipparcos data). The distribution of the data points strongly suggests the presence of correlations between the different measurements. The central line represents the mean value of 5.63, the black diagonal lines on either side the 1 |
| Open with DEXTER | |
A comparison between the Pleiades parallax determination as presented above and some of the many determinations presented in the literature over the past 30 years looks, at first sight at least, alarming. Table 3 gives a summary for those not-Hipparcos-based observations. A couple of determinations have been left out on purpose: by Gatewood et al. (1990) (superseded by Gatewood et al. 2000); by Makarov (2002) (superseded by van Leeuwen 2007a, and by the present paper); by Fox Machado et al. (2006) and by Cameron (1985), where no formal error is given; and by Chen (1999), which contained serious flaws in the methods used (see also Robichon et al. 1999). The remaining papers do not provide independent observations either, which becomes clear when examining their spread with respect to the quoted errors. Taking only those determinations published after the publication of the Hipparcos data in 1997 (as shown in Fig. 12), the weighted mean and standard deviation for 11 observations are determined as 5.63 and 0.58 respectively. The latter value should be close to 1.0 instead. When applying a more realistic formal error to the differential parallax measurements, as described in Sect. 5.3, the uncertainties on the distance-modulus determinations by Gatewood et al. (2000) and Soderblom et al. (2005) are likely to be seriously underestimated (finding exactly the ``expected value'' does not mean that the standard deviation associated with the measuremnent is small), which would further lower the unit-weight standard deviation for the these observations.
Of the external measurements, those based on photometry only do not constitute independent measurements of the distance modulus, but rather a fitting to a set of models. Completely independent determinations are needed to verify these models. There are only four sets of such observations available:
- 1.
- the convergent point determination by Narayanan & Gould (1999), which has a high error associated with it (see also van Leeuwen 2005b; Lindegren et al. 2000);
- 2.
- the differential parallax measurements, for which the uncertainties in the calibration to absolute values have been seriously underestimated;
- 3.
- one binary system with radial velocity measurements and an astrometric orbit by Zwahlen et al. (2004);
- 4.
- the Hipparcos-data based parallax, derived from the measurements of 53 cluster members spread over some 50 square degrees on the sky.
It has been stated by Soderblom et al. (1998), and re-iterated by Stello & Nissen (2001) and An et al. (2007), that at the parallax found from the Hipparcos data for the Pleiades cluster, the cluster members will occupy an area of the HR diagram in which no field stars, or more specifically no field stars that are assumed to be young, are found. This is not the case, as field stars contained in the Hipparcos catalogue are observed in the area occupied by the Pleiades. This is shown in Fig. 13, where the Pleiades are compared with the data for field stars with parallax accuracies better than 7 per cent. For those stars reddening corrections tend to be very small. At all areas covered by the Pleiades HR diagram field stars are also found. A detailed study of those stars occupying the same region would be of interest.
There are additional problems in the comparison with the active solar-type stars in Soderblom et al. (1998). The first is that this type of activity as observed in the Pleiades is restricted to stars of spectral type later than about K2 to K3 (van Leeuwen & Alphenaar 1982; van Leeuwen et al. 1987). Observing similar activity among the more massive solar-type stars indicates an age for those stars considerably lower than the Pleiades age. They would therefore be expected to be found in or near star-forming regions, most likely as members of OB associations. However, most of these stars are not linked to clusters or associations. As a consequence, they do not have an independently assessed age. The ``young'' ages assigned to these stars is almost entirely based on interpretation of their activity (Soderblom et al. 1998).
The difference between the distance moduli of the Hyades and the Pleiades does not require an explanation in terms of metallicity. As is shown in Appendix A, the observed differences in luminosity, when accepting the Hipparcos-based parallaxes, are reflected in systematic differences in the photometric indices B-U and Strömgren c1 for F-type stars in the same way as what is observed for a large sample of field stars.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f13.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg187.gif) |
Figure 13: The HR diagram for the Pleiades (full dots) superimposed on the HR diagram for field stars with parallax accuracies better than 7 per cent. The distance modulus applied is the value of 5.40 mag derived in the present study, and the applied reddening is E(B-V)=0.04. |
| Open with DEXTER | |
The summary data for the Pleiades are shown in Table 4, and a comparison between the HR diagrams of the Pleiades, Coma Ber and the Hyades is presented in Fig. 11. Clearly visible in this figure is the difference in slope of the HR diagram for the Hyades and the Pleiades over the colour range 0.0 to 0.5 in B-V.
6.4 Praesepe
The Hipparcos data for Praesepe is relatively poor due to the closeness of the
cluster to the ecliptic plane. Membership is not a major problem for this cluster. Figure 9 shows a the map of the 24 Praesepe members included in the Hipparcos catalogue. The area covered by the cluster is about 4
![]() 5 in diameter. The parallax measurements for the selected stars are shown in Fig. 10. The accumulated information on the cluster can be found in Table 4. The distance modulus as derived from the new Hipparcos reduction is, at
5 in diameter. The parallax measurements for the selected stars are shown in Fig. 10. The accumulated information on the cluster can be found in Table 4. The distance modulus as derived from the new Hipparcos reduction is, at
![]() effectively identical to one determined by An et al. (2007) (
effectively identical to one determined by An et al. (2007) (
![]() )
and fully consistent with the value derived by Percival et al. (2003) (
)
and fully consistent with the value derived by Percival et al. (2003) (
![]() ,
using (V-I)C data). It is larger, but not significantly, than the value of 6.15 derived by Cameron (1985) from UBV data, and the value of
,
using (V-I)C data). It is larger, but not significantly, than the value of 6.15 derived by Cameron (1985) from UBV data, and the value of
![]() derived by Nicolet (1981) using photometric boxes. Also within the same range is the value derived from differential parallax measurements by (Gatewood & de Jonge 1994),
derived by Nicolet (1981) using photometric boxes. Also within the same range is the value derived from differential parallax measurements by (Gatewood & de Jonge 1994),
![]() .
These results, in a way, mostly reflect the very strong similarity between the Hyades and Praesepe clusters. As shown in Fig. 11, the HR diagrams of the two clusters closely overlap when distance moduli are determined using the Hipparcos astrometric data. This is as expected, given the difference of 3.03 mag in distance modulus, as derived from the parallax measurements, between the Hyades and Praesepe. This is very close to the value of 3.0 which has been used in the past to determine photometrically the distance of the Praesepe cluster with respect to the Hyades (see for example Upgren et al. 1979).
.
These results, in a way, mostly reflect the very strong similarity between the Hyades and Praesepe clusters. As shown in Fig. 11, the HR diagrams of the two clusters closely overlap when distance moduli are determined using the Hipparcos astrometric data. This is as expected, given the difference of 3.03 mag in distance modulus, as derived from the parallax measurements, between the Hyades and Praesepe. This is very close to the value of 3.0 which has been used in the past to determine photometrically the distance of the Praesepe cluster with respect to the Hyades (see for example Upgren et al. 1979).
6.5 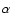 Per
Per
In its distribution on the sky (Fig. 9), ![]() Per resembles more a small remnant of an OB association than a bound open cluster. Still there is a very clear clustering in proper motion space (Fig. 14) and a well-defined HR diagram for the stars selected on proper motions. The Hipparcos catalogue contains 50 stars for which the membership is probable to very likely, providing a well-defined proper motion and parallax for the group (see
Table 4). The radial velocity for this cluster was taken from Petrie & Heard (1969) as -1.6 km s-1, which is based on the measurements of 77 stars in the field of the cluster. One star should be noted here in particular, HD 22192 (HIP 16826,
Per resembles more a small remnant of an OB association than a bound open cluster. Still there is a very clear clustering in proper motion space (Fig. 14) and a well-defined HR diagram for the stars selected on proper motions. The Hipparcos catalogue contains 50 stars for which the membership is probable to very likely, providing a well-defined proper motion and parallax for the group (see
Table 4). The radial velocity for this cluster was taken from Petrie & Heard (1969) as -1.6 km s-1, which is based on the measurements of 77 stars in the field of the cluster. One star should be noted here in particular, HD 22192 (HIP 16826, ![]() Per), which was considered as a non member by Petrie & Heard (1969), and also as a possible non-member by Abt (1978), but which star is found to have a well determined proper motion and parallax that are very close to the mean cluster values, and which therefore has been considered as a high-probability member in this study. The observed spread in the radial velocities of this star as reported by Petrie & Heard (1969) is larger than would be expected on the basis of the errors assigned to the 10 individual observations. In addition, the mean value quoted for the radial velocity of this star indicates that a straight (not weighted) mean was used, in which case the radial velocity found is
Per), which was considered as a non member by Petrie & Heard (1969), and also as a possible non-member by Abt (1978), but which star is found to have a well determined proper motion and parallax that are very close to the mean cluster values, and which therefore has been considered as a high-probability member in this study. The observed spread in the radial velocities of this star as reported by Petrie & Heard (1969) is larger than would be expected on the basis of the errors assigned to the 10 individual observations. In addition, the mean value quoted for the radial velocity of this star indicates that a straight (not weighted) mean was used, in which case the radial velocity found is
![]() km s-1. For the weighted mean a value of
km s-1. For the weighted mean a value of
![]() km s-1 is found, which is fully within the range of the mean
cluster radial velocity. It is unclear how Petrie & Heard (1969) found an
error on the mean of 1.7 km s-1 for what appears to be the un-weighted
mean. But why pay all this attention to one star? As a member of the
km s-1 is found, which is fully within the range of the mean
cluster radial velocity. It is unclear how Petrie & Heard (1969) found an
error on the mean of 1.7 km s-1 for what appears to be the un-weighted
mean. But why pay all this attention to one star? As a member of the
![]() Per cluster it is its brightest B star by more than 0.5 mag, and as such it can play an important role in the determination of the age of this system. The distribution of radial velocities indicates in addition that it could be an orbiting binary star.
Per cluster it is its brightest B star by more than 0.5 mag, and as such it can play an important role in the determination of the age of this system. The distribution of radial velocities indicates in addition that it could be an orbiting binary star.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11382f14.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg196.gif) |
Figure 14:
Distribution of the proper motions for the selected member stars
in the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm]{11382f15.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg202.gif) |
Figure 15:
The HR diagram for: ( left) the |
| Open with DEXTER | |
6.6 IC 2391 and IC 2602
The Southern Hemisphere clusters IC 2391 and IC 2602 are sometimes described as being like the Pleiades, though a little younger, and less populous. IC 2602 is embedded in the Scorpio-Centaurus OB association (Bertiau 1958; de Zeeuw et al. 1999). An extensive photometric and astrometric study by Braes (1962,1961) defined probable membership and derived a distance estimate of 150 pc (distance modulus 5.88). A combined UBV photometric and spectroscopic study at the same time by Whiteoak (1961) gave a distance of 155 pc (distance modulus 5.95), using measurements for 40 probable and 29 possible cluster members. Based on ubvy photometry for 33 stars, Hill & Perry (1969) determined a distance modulus of
![]() ,
and Nicolet (1981), using photometric boxes to connect the distance determination directly to stars with measured parallaxes, derived a distance modulus of
,
and Nicolet (1981), using photometric boxes to connect the distance determination directly to stars with measured parallaxes, derived a distance modulus of
![]() .
Finally, Pinsonneault et al. (1998) reported a distance modulus of 6.02 based on main-sequence fitting.
.
Finally, Pinsonneault et al. (1998) reported a distance modulus of 6.02 based on main-sequence fitting.
The proper motion and photometric study of IC 2391 by Hogg (1960) identified 21 stars as likely members and derived a distance of ![]() pc, from a distance modulus of
pc, from a distance modulus of
![]() .
Measurements in ubvy and
.
Measurements in ubvy and
![]() for 25 cluster members were obtained by Perry & Hill (1969), from which was derived a distance modulus of
for 25 cluster members were obtained by Perry & Hill (1969), from which was derived a distance modulus of
![]() .
They also derived a mean distance modulus of 5.90 for earlier determinations. Nicolet (1981) determined a distance modulus pf
.
They also derived a mean distance modulus of 5.90 for earlier determinations. Nicolet (1981) determined a distance modulus pf
![]() based on the photometric boxes. Maitzen & Catalano (1986) conducted a study of CP2 stars in IC 2391. It is interesting to note that four stars identified as cluster members in that study were found not to be so, based on their proper motions, though the parallaxes of these stars are close to the parallax for IC 2391. These stars are HD 74195 (HIP 42536), HD 74762 (HIP 42829), HD 74665 (HIP 42767) and HD 75202 (HIP 43071). Finally, Pinsonneault et al. (1998) derived a distance modulus for IC 2391 of 5.99, based on main-sequence fitting to theoretical isochrones.
based on the photometric boxes. Maitzen & Catalano (1986) conducted a study of CP2 stars in IC 2391. It is interesting to note that four stars identified as cluster members in that study were found not to be so, based on their proper motions, though the parallaxes of these stars are close to the parallax for IC 2391. These stars are HD 74195 (HIP 42536), HD 74762 (HIP 42829), HD 74665 (HIP 42767) and HD 75202 (HIP 43071). Finally, Pinsonneault et al. (1998) derived a distance modulus for IC 2391 of 5.99, based on main-sequence fitting to theoretical isochrones.
With 11 (IC 2391) and 15 (IC 2602) members in the Hipparcos catalogue respectively, they provide well determined parallax and proper motion estimates in the new reduction (Fig. 16). The distance moduli as derived for these two clusters from their parallax measurements are
![]() (IC 2391) and
(IC 2391) and
![]() (IC 2602), the summary data are presented in Table 4. The distributions of the member stars are shown in Fig. 17. Figure 15 shows the HR diagrams of IC 2391 and IC 2602 in comparison with the diagram for the Pleiades. The positions of the sequences for the three young clusters coincide well, in the same way as the sequences for the older clusters UMa and Coma Ber (Sect. 6.2) and those of the much older Hyades and Praesepe clusters. With the improvement by a factor two in formal errors on the
parallaxes for the Pleiades, IC 2391 and IC 2602 (with respect to the 1997
catalogue), this agreement is more substantial now than it was ever before.
Just as for the Pleiades cluster, the parallax-based distance moduli for IC 2391 and IC 2602 are found to be systematically smaller than has been estimated from main sequence fitting, where values of 5.99 and 6.02 were reported by
Pinsonneault et al. (1998) for IC 2391 and IC 2602 respectively. A distance modulus
of 6.02 would imply a parallax of 6.25 mas, which, in view of
Fig. 16 appears rather unlikely.
(IC 2602), the summary data are presented in Table 4. The distributions of the member stars are shown in Fig. 17. Figure 15 shows the HR diagrams of IC 2391 and IC 2602 in comparison with the diagram for the Pleiades. The positions of the sequences for the three young clusters coincide well, in the same way as the sequences for the older clusters UMa and Coma Ber (Sect. 6.2) and those of the much older Hyades and Praesepe clusters. With the improvement by a factor two in formal errors on the
parallaxes for the Pleiades, IC 2391 and IC 2602 (with respect to the 1997
catalogue), this agreement is more substantial now than it was ever before.
Just as for the Pleiades cluster, the parallax-based distance moduli for IC 2391 and IC 2602 are found to be systematically smaller than has been estimated from main sequence fitting, where values of 5.99 and 6.02 were reported by
Pinsonneault et al. (1998) for IC 2391 and IC 2602 respectively. A distance modulus
of 6.02 would imply a parallax of 6.25 mas, which, in view of
Fig. 16 appears rather unlikely.
6.7 Blanco 1 ( Scl)
Scl)
The cluster Blanco 1 has in the past been referred to as the ![]() Scl cluster, after the bright star considered to be a cluster member (de Epstein & Epstein 1985; Westerlund et al. 1988; Perry et al. 1978; Eggen 1970). The proper motion and parallax (at
Scl cluster, after the bright star considered to be a cluster member (de Epstein & Epstein 1985; Westerlund et al. 1988; Perry et al. 1978; Eggen 1970). The proper motion and parallax (at
![]() mas) measured by Hipparcos, however, clearly indicate that this star is not a cluster member. A suspicion that this star might not be a cluster member was already earlier expressed by Westerlund et al. (1988). Also confirmed as a non-member is HD 225119 (HIP 291), based on both proper motion and parallax, while the remaining three B star members identified by Westerlund et al. (1988) are all confirmed. As this cluster can now no longer be associated with
mas) measured by Hipparcos, however, clearly indicate that this star is not a cluster member. A suspicion that this star might not be a cluster member was already earlier expressed by Westerlund et al. (1988). Also confirmed as a non-member is HD 225119 (HIP 291), based on both proper motion and parallax, while the remaining three B star members identified by Westerlund et al. (1988) are all confirmed. As this cluster can now no longer be associated with ![]() Scl, it will be referred to as Blanco 1, after its discoverer (Blanco 1949). In previous studies of this system, the similarity between its member stars and those of the Pleiades cluster has been noticed repeatedly.
Scl, it will be referred to as Blanco 1, after its discoverer (Blanco 1949). In previous studies of this system, the similarity between its member stars and those of the Pleiades cluster has been noticed repeatedly.
Based on the proper motions in the cluster area, 13 stars were ultimately selected as probable cluster members. A map of those stars can be seen in Fig. 17. The astrometric parameters derived from the Hipparcos data are presented in Table 4. The distribution of the parallaxes and their formal errors for the member stars is shown in Fig. 16.
6.8 NGC 2451
The cluster referred to here as NGC 2451 identifies with what has been called
the Puppis Moving Group (PMG) by Röser & Bastian (1994), and by others as
NGC 2451a. The reason for this is, that this cluster does not identify with
the group of stars to which originally the name NGC 2451 was assigned. That
group of stars are mainly in the background for the PMG, at about twice the
distance, and only very few of those stars belong to the PMG.
The PMG is of approximately the same age as IC 2391 and IC 2602. Membership
determination for this cluster has in the past been somewhat problematic
(see for example Levato & Malaroda 1975a; Maitzen & Catalano 1986), and it has been
suggested that there are in fact two clusters sharing nearly the same line-of-sight (Röser & Bastian 1994), although the existence of the second, more distant cluster, is still uncertain (Baumgardt 1998). An example of the problems surrounding this cluster is the list of spectral types for 24 stars in NGC 2451 by Levato & Malaroda (1975a). When incorporating the Hipparcos data, only 4 of these stars are confirmed as cluster members, 8 stars are definitely not members, while 12 stars are not included in the Hipparcos catalogue. Among the non-members is the K5 IIa star HD 63032 (HIP 37819), which was still considered a certain member by Levato & Malaroda (1975a), but which has also been recognized as non-member by Röser & Bastian (1994). This star had been used in the past as an indicator of the age of NGC 2451. Its proper motion, at
![]() mas yr-1 and parallax at
mas yr-1 and parallax at
![]() mas well separates this star from the cluster. The non members in the field of NGC 2451 as contained in the Hipparcos catalogue do not show common parallax and proper motion values that would indicate membership of a second cluster behind NGC 2451. But with the second cluster at possibly twice the distance there may be very few if any actual members of it included in the Hipparcos catalogue. It should be noted that the PPM proper motions as used by Röser & Bastian (1994) are significantly offset in declination, by about 6 to 8 mas yr-1 from the Hipparcos data. The formal internal errors of about 3 mas yr-1 assigned to the PPM proper motions appear to be correct.
mas well separates this star from the cluster. The non members in the field of NGC 2451 as contained in the Hipparcos catalogue do not show common parallax and proper motion values that would indicate membership of a second cluster behind NGC 2451. But with the second cluster at possibly twice the distance there may be very few if any actual members of it included in the Hipparcos catalogue. It should be noted that the PPM proper motions as used by Röser & Bastian (1994) are significantly offset in declination, by about 6 to 8 mas yr-1 from the Hipparcos data. The formal internal errors of about 3 mas yr-1 assigned to the PPM proper motions appear to be correct.
![\begin{figure}
\par\includegraphics[width=14cm]{11382f16.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg214.gif) |
Figure 16:
The distribution of the parallaxes against their formal errors for
the IC 2391 ( top left), IC 2602 ( bottom left), Blanco 1 ( top right) and NGC 2451 ( bottom right) members in the Hipparcos catalogue. The central vertical line represents the mean parallax of each cluster, as presented in Table 4. The black lines on either side show the 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm]{11382f17.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg215.gif) |
Figure 17: A tangential projection of the distribution on the sky for members of the clusters IC 2391 ( top left), IC 2602 ( bottom left), Blanco 1 ( top right) and NGC 2451 ( bottom right). The coordinates are in radians, relative to the assumed cluster centre. |
| Open with DEXTER | |
The Hipparcos catalogue contains data for 14 stars that can be identified as
probable members of NGC 2451 as based on their proper motions and parallaxes.
The combined parallax data for these stars is shown in Fig. 16.
The mean parallax for the 14 selected stars is
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() .
This is very close to the result obtained by fitting to theoretical isochrones by Platais et al. (2001), who give a distance modulus of 6.35 or 6.38, depending on the models used. However, it was noted that the model isochrones showed shapes different from that of the observation, which means that slightly different answers can be obtained when changing the weights of the stars contributing to the isochrone fit. The summary data for NGC 2451 are given in Table 4. The HR diagram for the cluster
is shown in Fig. 15 together with the data for Blanco 1 and the Pleiades. The HR diagrams of all three clusters appear to coincide
well when applying the astrometrically derived distance moduli.
.
This is very close to the result obtained by fitting to theoretical isochrones by Platais et al. (2001), who give a distance modulus of 6.35 or 6.38, depending on the models used. However, it was noted that the model isochrones showed shapes different from that of the observation, which means that slightly different answers can be obtained when changing the weights of the stars contributing to the isochrone fit. The summary data for NGC 2451 are given in Table 4. The HR diagram for the cluster
is shown in Fig. 15 together with the data for Blanco 1 and the Pleiades. The HR diagrams of all three clusters appear to coincide
well when applying the astrometrically derived distance moduli.
7 Clusters between 250 and 500 pc
The astrometric parameters derived for clusters between 250 and 500 pc are generally less secure, as membership of individual stars can be doubtful, and generally few stars are contained in the Hipparcos catalogue. The clusters selected here are all well established, but do suffer, within the Hipparcos catalogue, from low numbers of (sometimes doubtful) members. A reasonably reliable set of astrometric parameters has been obtained for the following clusters: NGC 6475, NGC 7092, NGC 2516, NGC 2232, IC 4665, NGC 6633, Collinder 140, Trumpler 10, NGC 2422, NGC 3532 and NGC 2547. NGC 2264 is also described, but uncertainties in member identification do not allow for conclusions on its existence and astrometric parameters. The results for these clusters are presented in the sections below, including reference to other distance determinations for the same systems and comparisons with the results for nearby clusters of approximately the same age. All cluster solutions have followed the "combined abscissae" model as described in Sect. 4.4. A comparison was also made for NGC 6475 with the method used for the for the more nearby clusters as described in Sect. 4.3. The observed differences were well below the significance level.
![\begin{figure}
\par\includegraphics[width=16cm]{11382f18.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg218.gif) |
Figure 18: The HR-diagram positions of the stars used in the astrometric solutions to NGC 2516 and NGC 2422 (each compared with the Pleiades, open symbols), and NGC 6475 (compared with the Pleiades, open symbols, and Coma Ber, crosses). |
| Open with DEXTER | |
7.1 NGC 6475 (M7)
NGC 6475 is a well populated cluster, which, with at an estimated age of 200 to 260 Myr, is older than the Pleiades but younger than UMa and Coma Ber (Patenaude 1978). Membership has been determined in the past through both proper motions (Constantine et al. 1969) and radial velocities by Buscombe & Kennedy (1968) and Zentelis (1983) for the brighter, and Gieseking (1985) for the fainter potential members. A spectral study was done by Abt (1975) for the brightest members, and combined with UBV photometry by Loden (1984). Photometric studies in ![]() were done by Snowden (1976), Loden et al. (1980) and Nissen (1988). Recent distance modulus estimates have varied from
were done by Snowden (1976), Loden et al. (1980) and Nissen (1988). Recent distance modulus estimates have varied from
![]() (Nicolet 1981) to 7.01 (Nissen 1988) and 7.08 (Pinsonneault et al. 1998), where the latter is an apparent distance modulus. The reddening of the cluster was determined by Nissen (1988) as
(Nicolet 1981) to 7.01 (Nissen 1988) and 7.08 (Pinsonneault et al. 1998), where the latter is an apparent distance modulus. The reddening of the cluster was determined by Nissen (1988) as
![]() ,
equivalent to
,
equivalent to
![]() in E(B-V). Pinsonneault et al. (1998) use a value of
E(B-V)=0.06.
in E(B-V). Pinsonneault et al. (1998) use a value of
E(B-V)=0.06.
Within the Hipparcos catalogue 17 to 22 stars can be identified as probable members based on their proper motions. They cover an area of about 3.5 degrees in diameter, which is similar, considering the difference in distance, to the area covered by, for example, the Pleiades cluster. For the solution made here 20 stars were finally selected. Solutions with slightly different selections did not produce significantly different results. In particular restricting the extent of the cluster to a 2 degrees diameter only changed the parallax from
![]() to
to
![]() .
In all aspects the solution to the astrometric parameters of the cluster appears healthy, with only one rejected abscissa measurement out of 1328 in total used. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades and Coma Ber.
.
In all aspects the solution to the astrometric parameters of the cluster appears healthy, with only one rejected abscissa measurement out of 1328 in total used. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades and Coma Ber.
7.2 NGC 7092 (M 39)
A proper motion study by Ebbighausen (1940) and radial velocities by Trumpler (1928) established this group as a cluster with a radial velocity of -14 km s-1, and served as the main membership criterion for the following decades. The individual data for the latter study do not appear to have been published, but some derived information was presented by Eggen (1951), who also determined a photometric parallax of 4.5 mas. Another early photometric study of M 39 was presented by Mävers (1940), and covers an area of about 1.6 degrees diameter down to photographic magnitude 13. Based on a UBV photometric study, Johnson (1953) determined a distance modulus of ![]() ,
equivalent to a parallax of 3.6 mas. Around the same time, Weaver (1953) presented spectra and photoelectric magnitudes for some 30 potential cluster members. Meadows (1961) established that for the brightest members of M 39 the rotational velocities are much like those of field stars of the same spectral types, a study continued and extended to radial velocities and a search for binary stars in the cluster by Abt & Sanders (1973). A few more radial velocities of M 39 members were presented by Geyer & Nelles (1985). Using H
,
equivalent to a parallax of 3.6 mas. Around the same time, Weaver (1953) presented spectra and photoelectric magnitudes for some 30 potential cluster members. Meadows (1961) established that for the brightest members of M 39 the rotational velocities are much like those of field stars of the same spectral types, a study continued and extended to radial velocities and a search for binary stars in the cluster by Abt & Sanders (1973). A few more radial velocities of M 39 members were presented by Geyer & Nelles (1985). Using H![]() photometry calibrated to the Crawford (1973) relations, Kilkenny et al. (1975) derived individual distance moduli estimates for the brighter stars in the field, and determined, using UBV photometry and the zero-age main sequence by Blaauw (1963), a distance modulus of
photometry calibrated to the Crawford (1973) relations, Kilkenny et al. (1975) derived individual distance moduli estimates for the brighter stars in the field, and determined, using UBV photometry and the zero-age main sequence by Blaauw (1963), a distance modulus of
![]() ,
as well as a reddening of
,
as well as a reddening of
![]() .
.
A new proper motion study by McNamara & Sanders (1977) seemed to indicate a rather low abundance of fainter stars in the cluster. From a total of 1710 stars studied, only 30 brighter stars were found to be probable members, and most of those are at
(B-V)<0.3. A distance modulus of 7.12 was determined by fitting to the Johnson (1957) calibration sequence, for which a reddening of 0.02 was assumed. The apparent sparsity of fainter members may have been caused by a magnitude equation in the proper motions, as it was contradicted later by Platais (1984) in his proper motion study of the cluster (see also Platais 1994). This study was based on more homogeneous plate material. In it, 43 new (faint) candidate members were identified. The first distance-modulus determination that was at least indirectly based on parallax measurements (Nicolet 1981) provided a value of
![]() ,
equivalent to a parallax of 3.2 mas. A UBV photometric study by Mohan & Sagar (1985) based the distance modulus estimate of
,
equivalent to a parallax of 3.2 mas. A UBV photometric study by Mohan & Sagar (1985) based the distance modulus estimate of ![]() on a comparison with the zero-age main sequence as given by Schmidt-Kaler in (Voigt 1965), and estimated the age of the cluster to be between 200 and 400 Myr. The interstellar reddening has been determined for the cluster by Manteiga et al. (1991), based on IR photometry, at
E(B-V)=0.01. These authors put the age of M 39 to be between 240 and 480 Myr. Finally, Robichon et al. (1999) derived the parallax and distance modulus of M 39 from the first release of the Hipparcos data as
on a comparison with the zero-age main sequence as given by Schmidt-Kaler in (Voigt 1965), and estimated the age of the cluster to be between 200 and 400 Myr. The interstellar reddening has been determined for the cluster by Manteiga et al. (1991), based on IR photometry, at
E(B-V)=0.01. These authors put the age of M 39 to be between 240 and 480 Myr. Finally, Robichon et al. (1999) derived the parallax and distance modulus of M 39 from the first release of the Hipparcos data as
![]() mas and
mas and
![]() mag. respectively.
mag. respectively.
The new solution, based on 7 member stars, gives a parallax of
![]() and therefore a distance modulus of
and therefore a distance modulus of
![]() ,
based on the abscissa residuals for 903 field-of view transits, of which only one was rejected. The standard deviation for the astrometric solution is, at 1.03, close to the expected value. The proper motion of this cluster is relatively large, which eases the member selection. Based on its proper motion, the brightest star in the field, HIP 106346 (HD 205210) has been excluded from the solution. It appears not to be a cluster member, with also its parallax outside the
,
based on the abscissa residuals for 903 field-of view transits, of which only one was rejected. The standard deviation for the astrometric solution is, at 1.03, close to the expected value. The proper motion of this cluster is relatively large, which eases the member selection. Based on its proper motion, the brightest star in the field, HIP 106346 (HD 205210) has been excluded from the solution. It appears not to be a cluster member, with also its parallax outside the ![]() area. Including this star in the solution brings the parallax down to
area. Including this star in the solution brings the parallax down to
![]() mas (a distance modulus of
mas (a distance modulus of
![]() ), which demonstrates how sensitive these solutions can be to the selection of cluster members. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for the Praesepe and Coma Ber.
), which demonstrates how sensitive these solutions can be to the selection of cluster members. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for the Praesepe and Coma Ber.
7.3 NGC 2516
NGC 2516 has been described as a large and rich cluster. A study by Cox (1955) provided the first reliable magnitudes and colours in the region of NGC 2516. From these data, Cox derived a distance estimate of ![]() pc, and a reddening of
E(B-V)=0.11. A spectroscopic study of cluster members by Abt & Morgan (1969) showed a rich variety of peculiar stars to be present in the cluster. Dachs (1970) obtained UBV photometry for 70 stars in cluster, and derived a distance of
pc, and a reddening of
E(B-V)=0.11. A spectroscopic study of cluster members by Abt & Morgan (1969) showed a rich variety of peculiar stars to be present in the cluster. Dachs (1970) obtained UBV photometry for 70 stars in cluster, and derived a distance of ![]() pc (parallax of 2.7 mas) and a reddening of
E(B-V)=0.09. Dachs noted the presence of three evolved stars, and compared the cluster in age and content with the Pleiades, concluding that it is more than twice as rich. A similar study, but partially extended with measurements in RI and
pc (parallax of 2.7 mas) and a reddening of
E(B-V)=0.09. Dachs noted the presence of three evolved stars, and compared the cluster in age and content with the Pleiades, concluding that it is more than twice as rich. A similar study, but partially extended with measurements in RI and
![]() was presented by Feinstein et al. (1973). In it, the distance of the cluster was estimated at
was presented by Feinstein et al. (1973). In it, the distance of the cluster was estimated at
![]() pc, and the reddening at
E(B-V)=0.12. The age of the cluster was estimated at 60 Myr. Snowden (1975), using
pc, and the reddening at
E(B-V)=0.12. The age of the cluster was estimated at 60 Myr. Snowden (1975), using ![]() photometry, estimated the age of the cluster more than twice higher, at 135 Myr, and re-emphasized its similarity with the Pleiades and IC 2602. The reddening was estimated at
E(b-y)=0.088. Based on Geneva photometry, Nicolet (1981) derived a distance modulus of
photometry, estimated the age of the cluster more than twice higher, at 135 Myr, and re-emphasized its similarity with the Pleiades and IC 2602. The reddening was estimated at
E(b-y)=0.088. Based on Geneva photometry, Nicolet (1981) derived a distance modulus of
![]() ,
equivalent to a distance of
,
equivalent to a distance of ![]() pc, or a parallax of 2.3 mas. A study of the cluster in Walraven VBLUW photometry by
Verschoor & van Genderen (1983) showed a reddening of the cluster by
pc, or a parallax of 2.3 mas. A study of the cluster in Walraven VBLUW photometry by
Verschoor & van Genderen (1983) showed a reddening of the cluster by
![]() ,
with a spread among individual cluster members at 0.043 mag. The distance modulus of the cluster was derived as
,
with a spread among individual cluster members at 0.043 mag. The distance modulus of the cluster was derived as
![]() through a comparison with a ZAMS derived by The et al. (1980), which had been derived, through a transformation between photometric systems, from Johnson (1966). Based on Geneva photometric measurements for 67 stars, Cameron (1985) determined a distance modulus of 7.88 and a reddening of 0.12. A UBV study by Dachs & Kabus (1989) of 486 stars in the vicinity of the cluster indicated the presence of 362 cluster members in the sample. A distance modulus of
through a comparison with a ZAMS derived by The et al. (1980), which had been derived, through a transformation between photometric systems, from Johnson (1966). Based on Geneva photometric measurements for 67 stars, Cameron (1985) determined a distance modulus of 7.88 and a reddening of 0.12. A UBV study by Dachs & Kabus (1989) of 486 stars in the vicinity of the cluster indicated the presence of 362 cluster members in the sample. A distance modulus of
![]() and a reddening of 0.12 were derived. Spectroscopic observations for 36 bright stars in the cluster by González & Lapasset (2000) showed a radial velocity of
and a reddening of 0.12 were derived. Spectroscopic observations for 36 bright stars in the cluster by González & Lapasset (2000) showed a radial velocity of
![]() km s-1. A CCD UBVI photometric study by Sung et al. (2002) provided a distance modulus of
km s-1. A CCD UBVI photometric study by Sung et al. (2002) provided a distance modulus of
![]() and reddening of
and reddening of
![]() through comparisons with theoretical isochrones. The age was determined as 160 Myr.
through comparisons with theoretical isochrones. The age was determined as 160 Myr.
Dachs & Kabus (1989) identified cluster members till at least 30' from the cluster centre. Within this range, 11 stars are found in the Hipparcos catalogue that very closely share the same proper motion (Fig. 19); a further three stars showed similar but not sufficiently coinciding proper motions, and were not used as cluster members. The cluster proper motion and parallax have been estimated by means of the 1166 abscissa residuals of the selected stars, giving a value for the parallax of
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() .
As for the Pleiades, a shorter distance than was expected from the pre-Hipparcos estimates is found. It may be worth noting too that by extending the search radius to 1.3 degrees, 8 more stars are found that closely share the proper motion and distribution of parallaxes of the 11 selected cluster members. Scaled to the distance of the Pleiades, the radius of 1.3 degrees in NGC 2516 is equivalent to a radius of 3.7 degrees. Members of the Pleiades cluster are known at least up to 4 to 5 degrees from the cluster centre (van Leeuwen et al. 1986). Including those stars in the cluster-parallax and proper motion determination gives a solution with very similar statistics as obtained with the initial selection, and a value for the parallax of
.
As for the Pleiades, a shorter distance than was expected from the pre-Hipparcos estimates is found. It may be worth noting too that by extending the search radius to 1.3 degrees, 8 more stars are found that closely share the proper motion and distribution of parallaxes of the 11 selected cluster members. Scaled to the distance of the Pleiades, the radius of 1.3 degrees in NGC 2516 is equivalent to a radius of 3.7 degrees. Members of the Pleiades cluster are known at least up to 4 to 5 degrees from the cluster centre (van Leeuwen et al. 1986). Including those stars in the cluster-parallax and proper motion determination gives a solution with very similar statistics as obtained with the initial selection, and a value for the parallax of
![]() mas instead (distance modulus at
mas instead (distance modulus at
![]() ). Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades.
). Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades.
7.4 NGC 2232
The information on this cluster comes predominantly from Clariá (1972), who measured 43 stars in its vicinity in UBV and 22 in H![]() .
From these data Clariá derived a distance for the cluster of 360 pc, equivalent to a distance modulus of 7.78 and a parallax of 2.8 mas. The eight brightest stars in the list of cluster members by Clariá are included in the Hipparcos catalogue. They do not cluster as well in proper motion as could be expected for a cluster at 360 pc, and two stars in particular, HD 45153 (HIP 30580) and HD 45975 (HIP 31011) stand out in both proper motion and parallax. These stars have been excluded from determining the astrometric parameters of the cluster. The combined abscissa residuals for the six remaining stars give a cluster parallax of
.
From these data Clariá derived a distance for the cluster of 360 pc, equivalent to a distance modulus of 7.78 and a parallax of 2.8 mas. The eight brightest stars in the list of cluster members by Clariá are included in the Hipparcos catalogue. They do not cluster as well in proper motion as could be expected for a cluster at 360 pc, and two stars in particular, HD 45153 (HIP 30580) and HD 45975 (HIP 31011) stand out in both proper motion and parallax. These stars have been excluded from determining the astrometric parameters of the cluster. The combined abscissa residuals for the six remaining stars give a cluster parallax of
![]() mas. Of the 522 residuals used, 2 were rejected. Including the two stars identified above as possible non-members puts the parallax at
mas. Of the 522 residuals used, 2 were rejected. Including the two stars identified above as possible non-members puts the parallax at
![]() mas, and increases the standard deviation of the solution from 0.96 to 1.04. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and
mas, and increases the standard deviation of the solution from 0.96 to 1.04. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and ![]() Per.
Per.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f19.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg253.gif) |
Figure 19: Proper motion distribution of the stars identified as probable members of NGC 2516 in the Hipparcos catalogue. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm]{11382f20.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg254.gif) |
Figure 20: The HR-diagram positions of the stars used in the astrometric solutions to NGC 3532 and NGC 7092 (each compared with Coma Ber, crosses, and Praesepe, open circles), and NGC 6633 (compared with the Praesepe, open circles). |
| Open with DEXTER | |
7.5 IC 4665
Next to areas of the Pleiades and Praesepe clusters, the area of IC 4665 was one of the standard regions in the Johnson and Morgan UBV photometric system (Johnson 1954). A study by Hogg & Kron (1955) in UBV identified the cluster as somewhat younger than the Pleiades, at a parallax of about 2.3 mas (distance modulus of 8.2) and a reddening of
E(B-V)=0.10 to 0.18, based on a selection of 18 probable members. The membership selection was at least partly supported by the proper motion study of the cluster by Vasilevskis (1955), though this study was of limited accuracy. The cluster main sequence was shown very clearly in a photographic photometry study by McCarthy & O'Sullivan (1969), which incorporated further astrometric studies by Vasilevskis. Three studies in the early 70 s significantly refined the information available on IC 4665, through astrometric data (Sanders & van Altena 1972), photometry in ![]() (Crawford & Barnes 1972) and spectral classifications (Abt & Levato 1975). Crawford & Barnes (1972) derived a distance modulus of 7.5, and a reddening of
(Crawford & Barnes 1972) and spectral classifications (Abt & Levato 1975). Crawford & Barnes (1972) derived a distance modulus of 7.5, and a reddening of
![]() ,
where the error refers to the spread over individual cluster members. The proper motion of the cluster is quite small, and as a result there is increasing confusion between members and non-members for the fainter stars, which shows clearly from the HR diagrams of possible members by Sanders & van Altena (1972). Based on data obtained in the Geneva photometric system, Nicolet (1981) derived a distance modulus of
,
where the error refers to the spread over individual cluster members. The proper motion of the cluster is quite small, and as a result there is increasing confusion between members and non-members for the fainter stars, which shows clearly from the HR diagrams of possible members by Sanders & van Altena (1972). Based on data obtained in the Geneva photometric system, Nicolet (1981) derived a distance modulus of
![]() ,
equivalent to a parallax of 2.6 mas. Geyer & Nelles (1985) determined the radial velocity of the cluster as
,
equivalent to a parallax of 2.6 mas. Geyer & Nelles (1985) determined the radial velocity of the cluster as
![]() ,
based on data for 5 stars. Prosser (1993) combined existing and new astrometric, photometric and spectroscopic data for the cluster and identified numerous new candidate members. The age of the cluster was estimated to be between 30 Myr and the age of the Pleiades. The radial velocity of the cluster was determined by Prosser & Giampapa (1994) at about -13 km s-1.
,
based on data for 5 stars. Prosser (1993) combined existing and new astrometric, photometric and spectroscopic data for the cluster and identified numerous new candidate members. The age of the cluster was estimated to be between 30 Myr and the age of the Pleiades. The radial velocity of the cluster was determined by Prosser & Giampapa (1994) at about -13 km s-1.
The Hipparcos catalogue contains 6 or 7 stars that can be identified as probable members of the cluster. Four of these are contained in the astrometric study by Sanders & van Altena (1972), and identified as probable members in their discussion: S110 (HIP 86954), S115 (HIP 86960), S159 (HIP 87002) and S181 (HIP 87032). One star can be identified in (Vasilevskis 1955) as K 32 (HIP 86805), indicated as a possible member. Two more stars are just outside the areas covered by these studies, HIP 86993 and HIP 87592. The mean parallax as derived from 856 field transit abscissa residuals for these 7 stars is
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() .
There were no rejected observations. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 22, in comparison with similar data for the Pleiades, NGC 2451 and
.
There were no rejected observations. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 22, in comparison with similar data for the Pleiades, NGC 2451 and ![]() Per.
Per.
7.6 NGC 6633
A UBV photometric study of NGC 6633 by Hiltner et al. (1958) showed it to be similar in age to Praesepe, and subject to an interstellar reddening of
E(B-V)=0.17. They also derived a distance modulus of
![]() ,
equivalent to a parallax of 3.2 mas. A proper motion study covering 207 stars down to photographic magnitude 13.5 in an area of
,
equivalent to a parallax of 3.2 mas. A proper motion study covering 207 stars down to photographic magnitude 13.5 in an area of
![]() centred on the cluster was presented by Vasilevskis et al. (1958), and identified some 90 potential cluster members. A study by Sanders (1973) improved this still further, with 497 stars measured and 113 possible members. The problem faced by both these studies is the small size of the proper motions, which makes distinction from background stars difficult. The radial velocity for one of the giant members of the cluster was determined at -22.0 km s-1 by Wallerstein et al. (1963), and later by Geyer & Nelles (1985) at
centred on the cluster was presented by Vasilevskis et al. (1958), and identified some 90 potential cluster members. A study by Sanders (1973) improved this still further, with 497 stars measured and 113 possible members. The problem faced by both these studies is the small size of the proper motions, which makes distinction from background stars difficult. The radial velocity for one of the giant members of the cluster was determined at -22.0 km s-1 by Wallerstein et al. (1963), and later by Geyer & Nelles (1985) at
![]() .
Photometric measurements in
.
Photometric measurements in ![]() for 37 stars were obtained by Schmidt (1976), who noted a slightly variable extinction with an average value of
E(b-y)=0.124, and determined a distance modulus of 7.71, using the calibration by Crawford (1973). A study by Levato & Abt (1977) determined spectral classifications for the brightest cluster members identified in the studies referred to above. Based on Geneva photometric measurements, Nicolet (1981) determined a distance modulus of
for 37 stars were obtained by Schmidt (1976), who noted a slightly variable extinction with an average value of
E(b-y)=0.124, and determined a distance modulus of 7.71, using the calibration by Crawford (1973). A study by Levato & Abt (1977) determined spectral classifications for the brightest cluster members identified in the studies referred to above. Based on Geneva photometric measurements, Nicolet (1981) determined a distance modulus of
![]() ,
while using UBV photometry by Hiltner et al. (1958), Cameron (1985) derived a distance modulus of 7.63 and a reddening of
,
while using UBV photometry by Hiltner et al. (1958), Cameron (1985) derived a distance modulus of 7.63 and a reddening of
![]() ,
based on 39 members. Distance fitting was done with respect to the ZAMS as defined by Schmidt-Kaler in Voigt (1965). Based on the first release of the Hipparcos data, Robichon et al. (1999) determined a parallax of
,
based on 39 members. Distance fitting was done with respect to the ZAMS as defined by Schmidt-Kaler in Voigt (1965). Based on the first release of the Hipparcos data, Robichon et al. (1999) determined a parallax of
![]() mas, using data for 4 stars.
mas, using data for 4 stars.
In the new solution, the abscissa residuals of 917 field-of-view transits for 6 stars was used, from which a parallax of
![]() mas was derived, equivalent to a distance modulus of
mas was derived, equivalent to a distance modulus of
![]() .
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for Praesepe.
.
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for Praesepe.
Table 5: Summary data for the distant clusters as derived from combined-abscissae fitting.
7.7 Collinder 140
A combined photometric and spectroscopic study of Collinder 140 was presented by Clariá & Rosenzweig (1978), who derived a distance modulus of 7.78 (equivalent to a distance of 360 pc), reddening of
E(B-V)=0.05, and age of 21 to 23 Myr. From a UBV photometric study, Williams (1978) placed the cluster at ![]() pc and at an age of 40 Myr, and very little reddening, at
pc and at an age of 40 Myr, and very little reddening, at
![]() .
A spectroscopic study by Fitzgerald et al. (1980) derived a distance of
.
A spectroscopic study by Fitzgerald et al. (1980) derived a distance of ![]() pc, a reddening of
E(B-V)=0.04, and age of
pc, a reddening of
E(B-V)=0.04, and age of ![]() Myr. In his UBV photometric study of 38 clusters, Cameron (1985) determined a distance modulus of 7.96 (distance 391 pc) and reddening of
E(B-V)=0.06.
Myr. In his UBV photometric study of 38 clusters, Cameron (1985) determined a distance modulus of 7.96 (distance 391 pc) and reddening of
E(B-V)=0.06.
The distribution of proper motions and parallaxes in the region of Collinder 140 in the new Hipparcos catalogue shows the presence of 9 probable cluster members, for which the parallax, as derived from the 1413 individual field transits, is
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() .
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and
.
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and ![]() Per.
Per.
7.8 Trumpler 10
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11382f21.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg290.gif) |
Figure 21:
The HR-diagram positions of the stars used in the astrometric solutions to Collinder 140, NGC 2232 and Trumpler 10 (each compared with |
| Open with DEXTER | |
Trumpler 10 is a not very well studied, fairly young cluster. Lyngå (1960) did a UBV photometric study in the region of the cluster, measuring some 29 stars, for which a further analysis was provided by Lyngå (1962), who derived an age estimate of 30 to 60 Myr. Spectroscopic types in the cluster were determined by Levato & Malaroda (1975b), who gave an estimate of the cluster distance of ![]() pc, equivalent to a distance modulus of 8.22, and reddening at
pc, equivalent to a distance modulus of 8.22, and reddening at
![]() .
A proper motion study by Stock (1984) seemed to throw some doubt on the existence of the cluster, but the proper motions in this study were not of sufficient accuracy to recognize it.
.
A proper motion study by Stock (1984) seemed to throw some doubt on the existence of the cluster, but the proper motions in this study were not of sufficient accuracy to recognize it.
A search for potential cluster members in the region of Trumpler 10 identified 12 likely cluster members, with a mean parallax of
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() ,
close to the earlier ground-based estimate. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and
,
close to the earlier ground-based estimate. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 21, in comparison with similar data for NGC 2451 and ![]() Per.
Per.
7.9 NGC 2422 (M47)
The only two proper motion studies on this cluster are by van Schewick (1966) and Ishmukhamedov (1966), neither of which is easily accessible and played much of role in further investigations of this cluster. A UBV photometric study was presented by Smyth & Nandy (1962), and a spectroscopic study by Dworetsky (1975). Nicolet (1981) determined a distance modulus of
![]() using Geneva photometry. An extensive study of the cluster in
using Geneva photometry. An extensive study of the cluster in ![]() was carried out by Rojo Arellano et al. (1997), who determined a distance of
was carried out by Rojo Arellano et al. (1997), who determined a distance of
![]() (distance modulus 8.36) and a reddening of
(distance modulus 8.36) and a reddening of
![]() .
The age was estimated at 100 Myr. Analysis of the first release of the Hipparcos data by Robichon et al. (1999) showed a parallax of
.
The age was estimated at 100 Myr. Analysis of the first release of the Hipparcos data by Robichon et al. (1999) showed a parallax of
![]() .
A CCD-photometry study in UBVRI by Prisinzano et al. (2003) was used to study the luminosity and mass functions of the cluster.
.
A CCD-photometry study in UBVRI by Prisinzano et al. (2003) was used to study the luminosity and mass functions of the cluster.
The Hipparcos catalogue contains at least 7 stars that are probable cluster members. The abscissa residuals for the 879 field transits of these stars show a cluster parallax of
![]() mas, equivalent to a distance modulus of
mas, equivalent to a distance modulus of
![]() .
There were no rejected observations. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades.
.
There were no rejected observations. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 18, in comparison with similar data for the Pleiades.
7.10 NGC 3532
This rich open cluster was studied in photometry and astrometry by Koelbloed (1959), who derived a distance of ![]() pc (a distance modulus of 8.2), a very small amount of reddening (
E(B-V)=0.01), and age of 100 Myr. Further proper motions were obtained in an extensive study by King (1978), who identified 382 likely members in a field of about 1 degree square, down to photographic magnitude 11.0. A UBV photometric study of 183 stars in the region of the cluster by Fernandez & Salgado (1980) indicated a slightly larger distance of
pc (a distance modulus of 8.2), a very small amount of reddening (
E(B-V)=0.01), and age of 100 Myr. Further proper motions were obtained in an extensive study by King (1978), who identified 382 likely members in a field of about 1 degree square, down to photographic magnitude 11.0. A UBV photometric study of 183 stars in the region of the cluster by Fernandez & Salgado (1980) indicated a slightly larger distance of ![]() pc (a distance modulus of
pc (a distance modulus of
![]() )
and age of 200 Myr. Gieseking (1981) determined a radial velocity of 4.2 km s-1 for the cluster, and identified and measured a number of spectroscopic binaries contained in it. The larger distance and higher age seemed to be confirmed by
)
and age of 200 Myr. Gieseking (1981) determined a radial velocity of 4.2 km s-1 for the cluster, and identified and measured a number of spectroscopic binaries contained in it. The larger distance and higher age seemed to be confirmed by ![]() observations of 33 stars by Eggen (1981), who derived a distance modulus of
observations of 33 stars by Eggen (1981), who derived a distance modulus of
![]() ,
a reddening of
,
a reddening of
![]() ,
and age of 350 Myr. A somewhat smaller distance modulus of
,
and age of 350 Myr. A somewhat smaller distance modulus of
![]() was derived by Nicolet (1981) (distance 456 pc). Using photometric observations of 14 cluster stars in UBV and
was derived by Nicolet (1981) (distance 456 pc). Using photometric observations of 14 cluster stars in UBV and ![]() ,
Johansson (1981) derived a distance modulus of
,
Johansson (1981) derived a distance modulus of
![]() ,
and a reddening of
,
and a reddening of
![]() .
Further photometric observations for 68 stars, this time in UBVRI, were obtained by Wizinowich & Garrison (1982). This study showed some of the systematic differences that exist between different implementations of the same photometric system. Observations in UBV and DDO of 12 red giants in the cluster by Clariá & Lapasset (1988) showed a mean reddening of
.
Further photometric observations for 68 stars, this time in UBVRI, were obtained by Wizinowich & Garrison (1982). This study showed some of the systematic differences that exist between different implementations of the same photometric system. Observations in UBV and DDO of 12 red giants in the cluster by Clariá & Lapasset (1988) showed a mean reddening of
![]() .
In their analysis of the first release of the Hipparcos data, Robichon et al. (1999) derived a parallax of
.
In their analysis of the first release of the Hipparcos data, Robichon et al. (1999) derived a parallax of
![]() mas for the cluster, equivalent to a distance modulus of
mas for the cluster, equivalent to a distance modulus of
![]() .
.
In the new reduction of the Hipparcos data, 6 stars can be identified as very probable cluster members, having closely the same proper motion. Based on the 685 field-transit measurements for these stars, a cluster parallax of
![]() mas is derived, equivalent to a distance modulus of
mas is derived, equivalent to a distance modulus of
![]() .
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for Praesepe and Coma Ber.
.
Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 20, in comparison with similar data for Praesepe and Coma Ber.
7.11 NGC 2547
![\begin{figure}
\par\includegraphics[width=9cm]{11382f22.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg314.gif) |
Figure 22:
The HR-diagram positions of the stars used in the astrometric solutions to NGC 2547 and IC 4665 (each compared with Pleiades, open symbols and |
| Open with DEXTER | |
Photometric and astrometric studies of NGC 2547 were presented by Fernie (1960,1959), from which he derived an estimated distance of 360 pc (distance modulus 7.8) and reddening of
E(B-V)=0.03. Nicolet (1981) used Geneva photometry to derive a distance modulus of
![]() (distance 440 pc). Photoelectric data in UBV for 118 stars, and H
(distance 440 pc). Photoelectric data in UBV for 118 stars, and H![]() for 23 stars in the region of NGC 2547 were obtained by Clariá (1982), from which was derived a mean distance of 450 pc (distance modulus 8.3), a reddening of
for 23 stars in the region of NGC 2547 were obtained by Clariá (1982), from which was derived a mean distance of 450 pc (distance modulus 8.3), a reddening of
![]() and age of 57 Myr. Based on UBV data, Cameron (1985) derived a distance modulus of 8.1 and reddening of
E(B-V)=0.05. Analysis of the first release of the Hipparcos data by Robichon et al. (1999) showed a parallax of
and age of 57 Myr. Based on UBV data, Cameron (1985) derived a distance modulus of 8.1 and reddening of
E(B-V)=0.05. Analysis of the first release of the Hipparcos data by Robichon et al. (1999) showed a parallax of
![]() .
A BVI CCD study by Naylor et al. (2002) gave a distance modulus between 8.00 and 8.15, and age between 20 and 35 Myr.
.
A BVI CCD study by Naylor et al. (2002) gave a distance modulus between 8.00 and 8.15, and age between 20 and 35 Myr.
Eight stars were identified in the Hipparcos catalogue as probable cluster members based on their distribution of proper motions. The cluster parallax of
![]() (distance modulus
(distance modulus
![]() )
was derived from the abscissa residuals of the 1022 field transits of these stars. There were 2 data points rejected. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 22, in comparison with similar data for the Pleiades, NGC 2451 and
)
was derived from the abscissa residuals of the 1022 field transits of these stars. There were 2 data points rejected. Details of the solution are shown in Table 5. The HR-diagram positions of the stars used in the astrometric solution are shown in Fig. 22, in comparison with similar data for the Pleiades, NGC 2451 and ![]() Per.
Per.
7.12 NGC 2264
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f23.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg320.gif) |
Figure 23: Proper motions for nine stars in the field of NGC 2264. Data points indicates with a larger central dot represent the five stars selected as probable members based on a combination of proper motions, parallaxes and apparent magnitudes. |
| Open with DEXTER | |
NGC 2264 is an extremely young cluster, which, probably for that reason, has been studied well. An extensive photometric survey in UBV was presented by Walker (1956), who identified the lower main sequence to lie above the expected locus when comparing his data with the ``standard main sequence'' of Johnson & Morgan (1953), to which the data were fitted for the B stars. A distance modulus of 9.50 was derived this way, based on which it was concluded that stars of spectral types later than A0 were situated above the main sequence. A proper motion study by Vasilevskis et al. (1965) identified 140 stars with membership probabilities greater than 0.5 among 245 stars brighter than photographic magnitude 13, in a
![]() field centred on the cluster. A strongly variable reddening for the cluster stars was reported by Young (1978), possibly related to the molecular cloud associated with the cluster (Crutcher et al. 1978), though much less variation was indicated by the spectroscopic study of Barry et al. (1979) and the UBVRI photometric study of Mendoza V. & Gomez (1980). Nicolet (1981) determined a distance modulus of
field centred on the cluster. A strongly variable reddening for the cluster stars was reported by Young (1978), possibly related to the molecular cloud associated with the cluster (Crutcher et al. 1978), though much less variation was indicated by the spectroscopic study of Barry et al. (1979) and the UBVRI photometric study of Mendoza V. & Gomez (1980). Nicolet (1981) determined a distance modulus of
![]() ,
equivalent to a parallax of 1.2 mas. the radial velocity for the cluster was determined by Liu et al. (1989) as
,
equivalent to a parallax of 1.2 mas. the radial velocity for the cluster was determined by Liu et al. (1989) as ![]() km s-1, based on observations of 12 early-type cluster members. Using a combination of photometric and spectroscopic data, Perez et al. (1987) derived a distance modulus of
km s-1, based on observations of 12 early-type cluster members. Using a combination of photometric and spectroscopic data, Perez et al. (1987) derived a distance modulus of
![]() through a comparison with the main sequence as defined by Schmidt-Kaler in Schaifers et al. (1982).
through a comparison with the main sequence as defined by Schmidt-Kaler in Schaifers et al. (1982).
Table 6: Data on stars selected in the NGC 2264 field.
The Hipparcos catalogue contains at least 4 stars classified by Vasilevskis et al. (1965) as highly probable members (see Table 6). In addition, the catalogue contains the brightest star in the field, S Mon, which has a proper motion very similar to the four stars mentioned above. A little outside the field studied by Vasilevskis et al. (1965), four more stars can be identified to share the same proper motion, and are within the same range of parallax values. Details on all these stars are provided in Table 6, while their proper motions are shown in Fig. 23. Taking the data for all 9 stars together, a parallax of
![]() mas is obtained, which is why this cluster became included in the initial selection of clusters within 500 pc. This solution shows, however, a relatively large standard deviation of 1.4, and also the combined positions of the selected stars in the HR diagram look suspicious. The stars that seem to contribute most to the large standard deviation are three in the south of the field and S Mon, for which parallaxes near 3.5 mas are found. Eliminating these, a parallax of
mas is obtained, which is why this cluster became included in the initial selection of clusters within 500 pc. This solution shows, however, a relatively large standard deviation of 1.4, and also the combined positions of the selected stars in the HR diagram look suspicious. The stars that seem to contribute most to the large standard deviation are three in the south of the field and S Mon, for which parallaxes near 3.5 mas are found. Eliminating these, a parallax of
![]() mas is found (from the abscissae solution), and a standard deviation of 1.01. Of the 375 abscissae used, one was rejected in iterations. Given its uncertainty in the parallax determination as well as the final value, the data for this cluster have not been included in Table 5. They have been included in the discussion here to show the vulnerability of these solutions to more distant clusters to member selection criteria.
mas is found (from the abscissae solution), and a standard deviation of 1.01. Of the 375 abscissae used, one was rejected in iterations. Given its uncertainty in the parallax determination as well as the final value, the data for this cluster have not been included in Table 5. They have been included in the discussion here to show the vulnerability of these solutions to more distant clusters to member selection criteria.
8 Discussion
One of the aims of this study is to provide for nearby clusters distance moduli that are determined completely independent from main-sequence fitting or other types of photometric calibration. Ultimately, when combined with homogeneous photometry for more extensive selections of cluster members, those data can provide a set of observational isochrones, to be compared both qualitatively and quantitatively with theoretical isochrones. A first, but very limited, combination with photometric data from the Hipparcos catalogue already shows some interesting relations as well as systematic differences. More extensive comparisons can be made when combining the cluster parallaxes with, for example, ![]() or Geneva photometry, which is available for many of the clusters discussed above (Mermilliod 1995).
or Geneva photometry, which is available for many of the clusters discussed above (Mermilliod 1995).
8.1 Distance modulus and parallax comparisons
In this section the distance moduli as have been determined in various studies over the past 50 years are examined with respect to the new Hipparcos examinations. The comparisons are done as a function of cluster age, reflecting any systematic errors in the calibration sequences used. The ages used come from the catalogue by Kharchenko et al. (2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f24.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg329.gif) |
Figure 24:
Differences in distance moduli between values derived by Johnson (1957) and the new Hipparcos reduction ( bottom graph) and similarly ( middle graph) for the data for the |
| Open with DEXTER | |
The calibration of the ZAMS by Johnson (1957) has made a large impact, direct as well as indirect, on distance calibrations of open clusters for about half a century. It was built on three assumptions, the distance of the Hyades, assumed to be 40 pc (compared to the current estimate of
![]() pc), an area in the UBV colour-magnitude diagram (
0.55<B-V<0.85) where the Pleiades and Hyades would share the same locus, and a connection between NGC 2362 and the Pleiades around (B-V)=0, which was based on a theoretical evolutionary correction for the magnitudes based on studies by Tayler (1954,1956). None of these assumptions could be verified at the time, as it is only by means of accurate parallaxes that such verification is made possible. Johnson estimated the uncertainty on the distance moduli determined this way to be of order 0.2 mag. The distance moduli derived by Johnson played an important role in the early distance moduli determination through
pc), an area in the UBV colour-magnitude diagram (
0.55<B-V<0.85) where the Pleiades and Hyades would share the same locus, and a connection between NGC 2362 and the Pleiades around (B-V)=0, which was based on a theoretical evolutionary correction for the magnitudes based on studies by Tayler (1954,1956). None of these assumptions could be verified at the time, as it is only by means of accurate parallaxes that such verification is made possible. Johnson estimated the uncertainty on the distance moduli determined this way to be of order 0.2 mag. The distance moduli derived by Johnson played an important role in the early distance moduli determination through ![]() photometry (Crawford & Barnes 1969a; Crawford & Perry 1966; Crawford & Barnes 1972). Figure 24 shows the observed differences between distance moduli for clusters based on these calibrations and the new Hipparcos determination. The distance of the Hyades as used by Johnson (1957) was underestimated by 15 per cent, resulting in errors of around 0.3 mag in the distance estimates for similar clusters, such as Praesepe. The assumption Johnson made about the coincidence of the Pleiades and the Hyades is not supported by the Hipparcos data. In the
photometry (Crawford & Barnes 1969a; Crawford & Perry 1966; Crawford & Barnes 1972). Figure 24 shows the observed differences between distance moduli for clusters based on these calibrations and the new Hipparcos determination. The distance of the Hyades as used by Johnson (1957) was underestimated by 15 per cent, resulting in errors of around 0.3 mag in the distance estimates for similar clusters, such as Praesepe. The assumption Johnson made about the coincidence of the Pleiades and the Hyades is not supported by the Hipparcos data. In the ![]() photometry it would not be supported either if systematic differences in c1 are taken into account. The details of the connection between the Pleiades and the youngest open clusters, as implemented by Johnson, are also in need of adjustment.
photometry it would not be supported either if systematic differences in c1 are taken into account. The details of the connection between the Pleiades and the youngest open clusters, as implemented by Johnson, are also in need of adjustment.
The ZAMS definition by Johnson (1957) played also an important role in the ZAMS as presented by Schmidt-Kaler in Voigt (1965). This was used by Cameron (1985) for the distance modulus determination of 38 open clusters. As can be observed in Fig. 24, the same systematic differences are observed as for the Johnson and Crawford calibrations.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f25.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg330.gif) |
Figure 25: Distance modulus differences. Bottom: between Becker & Fenkart (1971) and Hipparcos for 15 clusters. Error bars represent Hipparcos determinations only. Middle: between Nicolet (1981) and the new reduction for 13 clusters. The error bars represent the combined errors from the two determinations. Top: between Loktin & Matkin (1994) and the new reduction for 15 clusters. The error bars represent the Hipparcos determinations only. |
| Open with DEXTER | |
The cluster distance determinations by Becker & Fenkart (1971) are at least partly still based on the initial calibrations by Johnson (1957), but with some modifications that affect mainly the young clusters. These modifications, based on incorporating the (B-U) data, appear to have led to a systematic overestimate of the distances of clusters with ages less than about 100 Myr.
A comparison with the distance moduli as determined by Nicolet (1981) (Sect. 5) provides a test on whether, for example, stars in young clusters are of the same luminosity as field stars when found in the same photometric boxes, or whether there are systematic differences, possibly related to age. The comparison, shown in Fig. 25, seems to indicate a systematic overestimate of distance moduli as obtained through the photometric boxes for young clusters, by 0.1 to 0.4 mag, while the older clusters are not significantly offset. One may conclude that the random field stars with ground-based parallaxes as used by Nicolet more resemble the older than the younger cluster stars in luminosity at the same colours. However, the volume of stars with accurate parallax data now available could be used to check in much more detail what the actual luminosity variations of stars sharing photometric boxes are, before drawing any further conclusions.
Clear systematic differences can be seen in Fig. 25 for the comparison with the distance modulus determinations by Loktin & Matkin (1994). These determinations are based (Loktin & Matkin 1990) on theoretical isochrones by Mermilliod & Maeder (1986), Hejlesen (1980) and (), describing evolutionary models for different ranges of age and mass. The systematic differences that can be seen in Fig. 25 are likely to be a reflection of the offsets in the those models, and the way these affect clusters of different ages.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f26.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg331.gif) |
Figure 26: Distance modulus differences. Bottom: between Robichon et al. (1999) and Hipparcos for 17 clusters. Error bars represent the old Hipparcos determinations only. Top: between Kharchenko et al. (2005) and the new reduction for 19 clusters. The error bars represent the new Hipparcos reduction only. |
| Open with DEXTER | |
An entirely different kind of comparison is that of the current determinations with those based on the first Hipparcos data release. Here the differences for the nearby clusters are small, though the errors have been reduced by about a factor two. For the more distant clusters the membership selection often becomes the critical parameter. This is most clearly demonstrated by IC 4765, for which a parallax based on 7 member stars was presented by Robichon et al. (1999), but for which there is no solution in the current paper. The more accurate proper motions in the area of this cluster in the new catalogue show only three possible members, all of which appear to be red giants. The general agreement for the nearby clusters between the current results and those derived using the 1997 catalogue is not entirely surprising. It relates to the size of the fields covered by most of these clusters compared to the radius within which correlations in the abscissa residuals were able to accumulate to correlations in astrometric parameters for neighbouring stars. Such accumulations have been shown to be only effective over distances of less than 1.5 degrees. For the Pleiades stars, spread over 8 degrees diameter on the sky, there were correlations for the brightest stars in the cluster centre, but all other stars remained largely unaffected.
A comparison with the catalogue of Kharchenko et al. (2005) was also made, but here conclusions are difficult to draw, as in particular for the range of clusters discussed here their methods of distance determination (based amongst others on results by Robichon et al. 1999) varied. What is clear from the comparison is that the distance moduli by presented by Kharchenko et al. (2005) for the current selection of clusters are on average too large by about 0.15 mag.
In general, for many of the distance calibrations referred to above the same issue applied. Distance calibrations were presented as accurate, while not considering the inaccuracies and remaining noise levels of the actual calibration model itself. While a lot of attention was paid to exact reddening corrections, and sometimes metallicity variations, the most basic of errors as well as noise contribution, in the reference ZAMS, was generally not considered as a contribution to the final accuracies. Calibrations depended for a long time, directly or indirectly, on Johnson (1957), which itself was based on a distance estimate of the Hyades that was short by 15 per cent, an unverified assumption on the relation between the Pleiades and Hyades main sequences, and a very early estimate of the evolutionary luminosity effects on B stars. It is only now, when distances can be measured with completely independent methods, that the limitations of these assumptions are exposed and can be corrected for.
8.2 HR diagram comparisons
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11382f27.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg332.gif) |
Figure 27: The composite HR diagrams for groups 1 & 2 (left)and group 3 (right). Symbols on the left: Hyades, closed circles; Praesepe, open circles; UMa, closed triangles; Coma Ber, open triangles; NGC 7092, crosses. Symbols on the right: Pleiades, closed circles; Blanco 1, open circles; NGC 2516, crosses. |
| Open with DEXTER | |
When examining the composite HR diagram of the clusters a few distinct groups appear, for which the distributions of stars largely coincide in colour-magnitude and colour-colour diagrams. Photometric data in the ![]() and Geneva systems was extracted from WEBDA
and Geneva systems was extracted from WEBDA![]() to further examine these groups. Additional photometry for UMa stars was obtained from Rufener (1988) and Hauck & Mermilliod (1998). In most cases field stars had to be removed from the selected data, but this was only done when a cluster main sequence could be clearly recognized. Clusters for which this was not possible have been left out. For the Hyades only stars were selected for which a kinematic parallax had been determined based on the new Hipparcos reduction, as described in Sect. 6.1. Thus, individual parallaxes were available for the selected stars. Directly measured individual parallaxes were used for the UMa stars.
to further examine these groups. Additional photometry for UMa stars was obtained from Rufener (1988) and Hauck & Mermilliod (1998). In most cases field stars had to be removed from the selected data, but this was only done when a cluster main sequence could be clearly recognized. Clusters for which this was not possible have been left out. For the Hyades only stars were selected for which a kinematic parallax had been determined based on the new Hipparcos reduction, as described in Sect. 6.1. Thus, individual parallaxes were available for the selected stars. Directly measured individual parallaxes were used for the UMa stars.
The (provisional) groups contain the following clusters for which more extensive photometry is available:
- 1.
- the Hyades and Praesepe;
- 2.
- Coma Ber, UMa and NGC 7092;
- 3.
- Pleiades, Blanco 1 and NGC 2516;
- 4.
 Per, NGC 2451, IC 4665, IC 2391, IC 2602 and NGC 6475.
Per, NGC 2451, IC 4665, IC 2391, IC 2602 and NGC 6475.
- as was noted earlier, the Hyades and Praesepe data very closely overlap, and together form a very narrow sequence;
- the Coma Ber and UMa main sequences also overlap closely, and are sub luminous with respect to Hyades and Praesepe;
- NGC 7092 appears to follow Coma Ber and UMa for 0.1<(B2-V1)<0.3;
- increases in luminosity are observed for Hyades and Praesepe stars relative to Coma Ber and UMa for (B2-V1)<0.2;
- increases in luminosity are observed for Coma Ber and UMa stars relative to NGC 7092 for (B2-V1)<0.0.
![\begin{figure}
\par\includegraphics[width=8cm]{11382f28.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg334.gif) |
Figure 28: The composite diagram for clusters in group 4 (see text). |
| Open with DEXTER | |
The clusters in group 4 are mostly young to very young, except for NGC 6475. In the region
0.15<(B2-V1)<0.45 the sequence fits well with the Coma Ber and UMa sequence, and is offset by about 0.15 mag from the group-1 sequence (Fig. 28). For values of
(B2-V1)<-0.1 the sequences of group 3 and 4 coincide. One complication with the group-4 sequence is the lack of well-studied actual clusters. The sequence for ![]() Per shows more variation than is observed for Pleiades, Hyades and Praesepe, while the clusters IC 2639 and IC 2602 are relatively sparse.
Per shows more variation than is observed for Pleiades, Hyades and Praesepe, while the clusters IC 2639 and IC 2602 are relatively sparse.
8.3 The Strömgren c0 index for F-type stars
The c0 index (c1 corrected for reddening) in the Strömgren photometry was shown by Crawford (1975) to be related to luminosity and surface gravity variations for F-type stars (see also Sect. 5.1).
Variations in c0 at a given value of ![]() or b-y are given by
or b-y are given by
![]() ,
i.e. c0 relative to the calibration relation given in Crawford (1975) (see also Fig. 30). This is the relation described in Sect. 5.1 by Eq. (24). It is further evaluated in the Appendix, Sect. A. The difference in the
,
i.e. c0 relative to the calibration relation given in Crawford (1975) (see also Fig. 30). This is the relation described in Sect. 5.1 by Eq. (24). It is further evaluated in the Appendix, Sect. A. The difference in the
![]() values for the Hyades and Praesepe with respect to, for example, the Pleiades, has been attributed in the past to increased helium abundances (Dobson 1990; Nissen 1988) (see also Crawford & Barnes 1969a), although isochrone fitting by An et al. (2007) seems to suggest that this is not the case. It has been known for nearly half a century and has been referred to in the past as the Hyades anomaly. It is most clearly observed in the (U-B) index, which is a measure of the Balmer jump for early-type stars. The significant difference in the Geneva (U-B) index for the clusters in group 1 and group 3 can be seen in Fig. 29. The Strömgren c0 index is closely related to the (U-B) index.
values for the Hyades and Praesepe with respect to, for example, the Pleiades, has been attributed in the past to increased helium abundances (Dobson 1990; Nissen 1988) (see also Crawford & Barnes 1969a), although isochrone fitting by An et al. (2007) seems to suggest that this is not the case. It has been known for nearly half a century and has been referred to in the past as the Hyades anomaly. It is most clearly observed in the (U-B) index, which is a measure of the Balmer jump for early-type stars. The significant difference in the Geneva (U-B) index for the clusters in group 1 and group 3 can be seen in Fig. 29. The Strömgren c0 index is closely related to the (U-B) index.
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382f29.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg335.gif) |
Figure 29: The U-B versus B2-V2 diagram in the Geneva photometry. The red dots represent data points in the Hyades and Praesepe clusters, the crosses for data from the Pleiades, Blanco 1 and NGC 2516. Some of the Pleiades points are offset because of localised differential reddening in the cluster. The difference in loci for the two groups of clusters is known as the Hyades anomaly. |
| Open with DEXTER | |
A comparison between the c0 versus b-y diagrams for clusters in the Pleiades and Hyades groups by Nissen (1988) showed that the systematic difference in c0 values between those clusters is about 0.033 to 0.04. Following Eq. (A.7), this would correspond to an expected difference of 0.3 to 0.4 in absolute magnitude, which is close to what is observed in the HR diagram for F stars in these clusters when using the Hipparcos parallax-based distance moduli. It is in this context also interesting to note that Nissen (1988) determined the difference between the true distance moduli, i.e. corrected for the c0 effects, for the Pleiades and Hyades as 1.96 (which would imply a distance of 114 pc for the Pleiades), compared to
![]() determined by means of the Hipparcos data and 2.33 as derived from isochrone fitting (An et al. 2007). In a way, by calibrating their isochrones on the Hyades main sequence, An et al. (2007) have turned the ``Hyades anomaly'' into a ``Pleiades anomaly''. An extensive discussion on how the Hyades anomaly may be related to the differences in parallax and isochrone-based cluster distance determinations was presented by Mermilliod et al. (1997).
determined by means of the Hipparcos data and 2.33 as derived from isochrone fitting (An et al. 2007). In a way, by calibrating their isochrones on the Hyades main sequence, An et al. (2007) have turned the ``Hyades anomaly'' into a ``Pleiades anomaly''. An extensive discussion on how the Hyades anomaly may be related to the differences in parallax and isochrone-based cluster distance determinations was presented by Mermilliod et al. (1997).
A systematic difference of 0.033 to 0.04 in c0 values would indicate, following Eq. (A.10), a lower surface gravity for the Hyades F stars by approximately 0.1, but that is also the noise level on that calibration, i.e. the same ![]() values can be observed for
values can be observed for
![]() values that differ by 0.03 to 0.04. An explanation of the magnitude difference as due to metallicity variations would require an unrealistic, and also not observed, difference in the values for
values that differ by 0.03 to 0.04. An explanation of the magnitude difference as due to metallicity variations would require an unrealistic, and also not observed, difference in the values for
![]() of around 0.15.
of around 0.15.
It is not clear why Stello & Nissen (2001) made no reference to the c0 index differences, as discussed earlier by Nissen (1988), in their discussion on the Strömgren photometry and the Hipparcos parallax measurement for the Pleiades. From a purely observational point of view, a much smaller difference in absolute magnitudes between the Pleiades and Hyades stars (the result of a larger difference in distance moduli), as suggested by fits on theoretical isochrones, would be more difficult to explain, as this would contradict the general trend which can be clearly observed between the parameters
![]() and
and
![]() for F-type field stars (Fig. A.3). A similar conclusion of internal observational consistency for the Hipparcos cluster parallaxes was reached by Grenon (2002), based on comparisons of K stars in the Hyades, Pleiades and Praesepe clusters.
for F-type field stars (Fig. A.3). A similar conclusion of internal observational consistency for the Hipparcos cluster parallaxes was reached by Grenon (2002), based on comparisons of K stars in the Hyades, Pleiades and Praesepe clusters.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11382f30.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg338.gif) |
Figure 30:
Comparison of the c1 ( top) and m1 ( bottom) versus
|
| Open with DEXTER | |
The relations used here show significant noise levels, and their applications do not provide exact results, they are merely an indication of trends and provide estimates of the effects differences in certain parameters may have. A comparison of F stars in the Hyades, Coma Ber and Pleiades clusters, for example, shows that the overall differences in c1 are in the same direction and at about the same amplitude as would be expected from the observed differences in the absolute magnitudes (Fig. 30), but it is difficult to assess whether there is not only a qualitative, but also a full quantitative agreement.
9 Space velocities
![\begin{figure}
\par\includegraphics[width=8.5cm]{11382f31.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg339.gif) |
Figure 31: Distribution of the velocities of 20 clusters and 8 UMa stars within the galactic plane, compared with the velocity distribution of A and F stars within 125 pc. The UMa stars form a small clump, and there are a few other coincidences in space velocity. The solar motion has not been subtracted. |
| Open with DEXTER | |
For general reference, the positions and space velocities for all 20 clusters and the individual UMa stars have been derived in galactic coordinates:
and its derivative
where
The most striking of velocity coincidences is between the Hyades and Praesepe, which, within the accuracy of the measurements, have identical u and v velocities. Considering that these two clusters are also very similar in photometric aspects, it seems reasonable to assume a common origin, which would then also explain their very similar age and chemical composition.
There are no such striking coincidences between the UMa stars and Coma Ber, though both groups are somewhat anomalous in the distribution of velocities or positions. There is some similarity between the Pleiades and NGC 2516, but Blanco 1 does not seem to fit.
Table 7: Positions and velocities of 20 clusters in the galactic reference frame.
10 Conclusions
The new reduction has eliminated problems in the Hipparcos astrometric data that were caused by peculiarities in the satellite dynamics and an occasional potential weakness in connectivity between the two fields of view. These were also issues raised by (Makarov 2002,2006,2003), but these effects can not be eliminated at the intermediate-data level, as had been shown already when the idea of such corrections was first presented by van Leeuwen (1999b). The new reduction dealt with these attitude problems there where they occurred (in the along-scan attitude reconstruction process) rather than with the indirect and diffuse effects they had on great-circle abscissa residuals. The attitude reconstruction is the only place in which they can be (and now have been) identified and corrected for. With also the connectivity issue having been addressed and tested in the new reduction, the current set of cluster parallax and proper motion values should not only be more precise, but also more accurate.
Differences between isochrone-fitting and parallax-based distance moduli for open clusters are not limited to the Pleiades, they are found to be systematic. The differences are observed between groups of clusters that show similar characteristics in for example the c0 and U-B indices for F-type stars, and could therefore be related to systematic surface gravity differences. A closer examination of field star data confirms that such variations are correlated to differences in absolute magnitudes, though not in a simple one-to-one relation. Differences are also observed between the Hyades and Praesepe group and Coma Ber and UMa, where none of the old ``Hipparcos problems'' ever applied, as concentrations of stars in these clusters are not dense enough. The notion that the parallax values for all these clusters have to be wrong because they do not fit the results obtained by traditional main sequence fitting, or the distance measurement for a single binary star in the cluster, such as expressed by Trimble et al. (2006), gives the impression that reduced data has to confirm theoretical models to be acceptable as results, rather than that those data are judged upon the merits of the observations they have been derived from, and the quality of the data reductions. The Pleiades story over the past ten years has shown a number of examples where poor results, sometimes even based on flawed methods, were accepted (and quoted) without reservation, simply because they confirmed expectations. In this context it is worth while recalling a statement made by Crawford (1973) in his Survey Lecture at the IAU General Assembly in 1970: In many cases, theory can help us observers quite a lot. We would be lost, or at least inefficient, without theory to guide us. However, we must be extremely careful not to force-fit or to let pre-conceived ideas mess us up. We are measuring observed parameters, and these we relate, or calibrate, to physical parameters.
Acknowledgements
Discussions with various colleagues over the past couple of years have contributed to this paper, in particular with Robin Catchpole, Derek Jones, and Simon Hodgkin. Carme Jordi, Mike Irwin, Bob Carswell, Jan Lub, Anthony Brown and George Wallerstein read earlier drafts and provided much appreciated comments and suggestions.
Appendix A: Provisional (re-)calibration of Strömgren indices
The currently available volume of information available on F stars (parallaxes, photometric and spectroscopic data), allows for a much more detailed calibration of the Strömgren photometric indices with absolute magnitudes, metallicities, and spectroscopically determined effective temperatures and surface gravity values. Presented here are the provisional results of a more extensive study currently in preparation. It has been included here in order to see how the observed systematic differences in colour indices and absolute magnitudes can be related to physical parameters as calibrated from nearby field stars.
The photometric data have been extracted from the ![]() catalogue by Hauck & Mermilliod (1998,1997). The spectroscopic data has been extracted from Cayrel de Strobel et al. (2001). For this exploratory exercize the data for multiple entries in the latter catalogue were simply averaged. The facilities of the Vizier
catalogue by Hauck & Mermilliod (1998,1997). The spectroscopic data has been extracted from Cayrel de Strobel et al. (2001). For this exploratory exercize the data for multiple entries in the latter catalogue were simply averaged. The facilities of the Vizier![]() web page were used to extract samples of F stars, which were later further ``cleaned'' from luminosity class I and II stars and binaries. Only data with Hipparcos parallax determinations better than 10 per cent were kept, and all stars fainter than apparent magnitude about 10 were left out. This criterion is only approximate, as close to the limit a specific star may be fainter in one catalogue, and still just bright enough in another.
web page were used to extract samples of F stars, which were later further ``cleaned'' from luminosity class I and II stars and binaries. Only data with Hipparcos parallax determinations better than 10 per cent were kept, and all stars fainter than apparent magnitude about 10 were left out. This criterion is only approximate, as close to the limit a specific star may be fainter in one catalogue, and still just bright enough in another.
The first calibration done was a more detailed repeat of the luminosity calibrations of (Crawford 1975). This involved two linked calibrations, namely between absolute v magnitude (in what follows, v is always assumed to be corrected for the parallax-based distance modulus) and b-y, which determined ![]() values, and between the observed values of c1 and
values, and between the observed values of c1 and
![]() as a function of
as a function of ![]() .
The iterations use what is observed in the data, and was also implemented by Crawford, that stars occupying the lower boundary in the v versus b-y diagram also occupy the lower envelope in the c1 versus
.
The iterations use what is observed in the data, and was also implemented by Crawford, that stars occupying the lower boundary in the v versus b-y diagram also occupy the lower envelope in the c1 versus
![]() diagram. Thus, the following relations were obtained, using only stars with
diagram. Thus, the following relations were obtained, using only stars with
![]() values less than 0.02:
values less than 0.02:
| (A.1) |
where the standard deviation was found to be 0.27 mag. The range in b-y covered is 0.21 to 0.43. The values of
| c1 | = | ||
| (A.2) |
with a standard deviation of 0.029 mag. This relation is shown in Fig. A.1 for four different values of
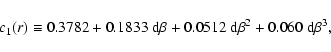 |
(A.3) |
and
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11382fA1.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg433.gif) |
Figure A.1:
The relation between
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA2.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg434.gif) |
Figure A.2:
The relation between
|
| Open with DEXTER | |
For determining the
![]() values the reference function as presented by Crawford (1975) is used, which accurately fits a second-order polynomial
values the reference function as presented by Crawford (1975) is used, which accurately fits a second-order polynomial
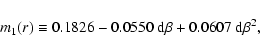 |
(A.4) |
where the standard deviation with respect to the discrete points defined by Crawford is 0.0005 mag (Fig. A.2). As was done above for
For completeness also the relation between b-y,
![]() ,
,
![]() and
and
![]() has been derived:
has been derived:
| b-y | = | ||
| (A.5) |
with a standard deviation of 0.014 mag. To compare with Crawford's original calibration, which was expressed in
| b-y | = | ||
| (A.6) |
The main differences with respect to Crawford's original calibration are in the higher order terms, which are less well determined for the much smaller volume of data that was available to Crawford at the time of the calibration.
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA3.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg445.gif) |
Figure A.3:
Calibration of |
| Open with DEXTER | |
The calibration in terms of absolute magnitudes has been done for ![]() as a function of
as a function of
![]() ,
,
![]() and
and
![]() :
:
with a standard deviation of 0.34 mag. Important here is that we are now able to recognize the effect of variation in the metallicity index
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA4.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg450.gif) |
Figure A.4:
The relation between
|
| Open with DEXTER | |
Spectroscopic data for 271 F dwarfs with ![]() photometry were selected from Cayrel de Strobel et al. (2001). For each star also spectroscopically determined effective temperatures and surface gravity values are provided, allowing for a direct comparison between these physical parameters and the Strömgren indices. The first of those relations is between
photometry were selected from Cayrel de Strobel et al. (2001). For each star also spectroscopically determined effective temperatures and surface gravity values are provided, allowing for a direct comparison between these physical parameters and the Strömgren indices. The first of those relations is between
![]() and the
and the
![]() :
:
| (A.8) |
with a dispersion of 69 K. Thus, the stars examined here would range in temperature from
The situation for the calibration of
![]() as a function of
as a function of
![]() is less simple due to the dependence on
is less simple due to the dependence on
![]() and the uneven distribution and relatively small number of calibration points. The relation used in the final fit is as follows
and the uneven distribution and relatively small number of calibration points. The relation used in the final fit is as follows
| (A.9) |
with a standard deviation of 0.10. The data and the calibration are shown in Fig. A.4. These results are in general agreement with similar calibrations presented by Crawford (1975) and Gustafsson & Nissen (1972).
![\begin{figure}\par\includegraphics[width=8.4cm]{11382fA5.eps}\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg456.gif) |
Figure A.5:
The relation between
|
| Open with DEXTER | |
with a standard deviation of 0.10. It is noted, however, that for the later-type stars more data points are found with significant disagreement between the
In general, when applying any of the above relations the standard deviation of the fit should be used as a measure of the uncertainty in the result obtained.
References
- Abt, H. A. 1975, PASP, 87, 417 [NASA ADS] [CrossRef] (In the text)
- Abt, H. A. 1978, PASP, 90, 692 [NASA ADS] [CrossRef] (In the text)
- Abt, H. A., & Morgan, W. W. 1969, AJ, 74, 813 [NASA ADS] [CrossRef] (In the text)
- Abt, H. A., & Sanders, W. L. 1973, ApJ, 186, 177 [NASA ADS] [CrossRef] (In the text)
- Abt, H. A., & Levato, H. 1975, PASP, 87, 849 [NASA ADS] [CrossRef] (In the text)
- An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef]
- Barry, D. C., Cromwell, R. H., & Schoolman, S. A. 1979, ApJS, 41, 119 [NASA ADS] [CrossRef] (In the text)
- Baumgardt, H. 1998, A&A, 340, 402 [NASA ADS] (In the text)
- Becker, W., & Fenkart, R. 1971, A&AS, 4, 241 [NASA ADS] (In the text)
- Bertiau, F. C. 1958, ApJ, 128, 533 [NASA ADS] [CrossRef]
- Blaauw, A. 1963, The Calibration of Luminosity Criteria (University of Chicago Press, Chicago), 383 (In the text)
- Blanco, V. M. 1949, PASP, 61, 183 [NASA ADS] [CrossRef] (In the text)
- Braes, L. L. E. 1961, Monthly Notes of the Astronomical Society of South Africa, 20, 7 [NASA ADS]
- Braes, L. L. E. 1962, Bull. Astron. Inst. Netherlands, 16, 297 [NASA ADS]
- Buscombe, W., & Kennedy, P. M. 1968, MNRAS, 139, 215 [NASA ADS] (In the text)
- Cameron, L. M. 1985, A&A, 147, 39 [NASA ADS] (In the text)
- Cayrel de Strobel, G., Soubiran, C., & Ralite, N. 2001, A&A, 373, 159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chen, B. 1999, A&A, 344, 494 [NASA ADS] (In the text)
- Clariá, J. J. 1972, A&A, 19, 303 [NASA ADS] (In the text)
- Clariá, J. J. 1982, A&AS, 47, 323 [NASA ADS] (In the text)
- Clariá, J. J., & Rosenzweig, P. 1978, AJ, 83, 278 [NASA ADS] [CrossRef] (In the text)
- Clariá, J. J., & Lapasset, E. 1988, MNRAS, 235, 1129 [NASA ADS] (In the text)
- Constantine, S. M., Harris, B. J., & Nikoloff, I. 1969, Proc. Astron. Soc. Aus., 1, 207 [NASA ADS] (In the text)
- Cox, A. N. 1955, ApJ, 121, 628 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1973, in Problems of Calibration of Absolute Magnitudes and Temperature of Stars, ed. B. Hauck, & B. E. Westerlund, IAU Symp., 54, 93 (In the text)
- Crawford, D. L. 1975, AJ, 80, 955 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1978, AJ, 83, 48 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L. 1979, AJ, 84, 1858 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Perry, C. L. 1966, AJ, 71, 206 [NASA ADS] [CrossRef]
- Crawford, D. L., & Barnes, J. V. 1969a, AJ, 74, 818 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Barnes, J. V. 1969b, AJ, 74, 407 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Barnes, J. V. 1972, AJ, 77, 862 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Barnes, J. V. 1974, AJ, 79, 687 [NASA ADS] [CrossRef] (In the text)
- Crawford, D. L., & Perry, C. L. 1976, AJ, 81, 419 [NASA ADS] [CrossRef] (In the text)
- Creze, M., Turon Lacarrieu, C., Golay, M., & Mandwewala, N. 1980, A&A, 85, 311 [NASA ADS]
- Crutcher, R. M., Hartkopf, W. I., & Giguere, P. T. 1978, ApJ, 226, 839 [NASA ADS] [CrossRef] (In the text)
- Dachs, J. 1970, A&A, 5, 312 [NASA ADS] (In the text)
- Dachs, J., & Kabus, H. 1989, A&AS, 78, 25 [NASA ADS] (In the text)
- Dambis, A. K. 1999, Astron. Lett., 25, 7 [NASA ADS] (In the text)
- de Bruijne, J. H. J., Hoogerwerf, R., & de Zeeuw, P. T. 2001, A&A, 367, 111 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- de Epstein, A. E. A., & Epstein, I. 1985, AJ, 90, 1211 [NASA ADS] [CrossRef]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef]
- Dobson, A. K. 1990, PASP, 102, 88 [NASA ADS] [CrossRef]
- Domingo, A., & Figueras, F. 1999, A&A, 343, 446 [NASA ADS] (In the text)
- Dworetsky, M. M. 1975, AJ, 80, 131 [NASA ADS] [CrossRef] (In the text)
- Ebbighausen, E. G. 1939, ApJ, 89, 431 [NASA ADS] [CrossRef]
- Ebbighausen, E. G. 1940, ApJ, 92, 434 [NASA ADS] [CrossRef] (In the text)
- Eggen, O. J. 1951, ApJ, 113, 657 [NASA ADS] [CrossRef] (In the text)
- Eggen, O. J. 1970, ApJ, 161, 159 [NASA ADS] [CrossRef]
- Eggen, O. J. 1981, ApJ, 246, 817 [NASA ADS] [CrossRef] (In the text)
- ESA 1992, The Hipparcos Input Catalogue, SP No. 1136 (ESA)
- ESA 1997, The Hipparcos and Tycho Catalogues, SP No. 1200 (ESA)
- Feinstein, A., Marraco, H. G., & Mirabel, I. 1973, A&AS, 9, 233 [NASA ADS] (In the text)
- Fernandez, J. A., & Salgado, C. W. 1980, A&AS, 39, 11 [NASA ADS] (In the text)
- Fernie, J. D. 1959, Monthly Notes of the Astron. Soc. S. Afr., 18, 57 [NASA ADS]
- Fernie, J. D. 1960, Monthly Notes of the Astron. Soc. S. Afr., 19, 120 [NASA ADS]
- Fernie, J. D. 1965, AJ, 70, 575 [NASA ADS] [CrossRef] (In the text)
- Fitzgerald, M. P., Miller, M., & Harris, G. L. H. 1980, MNRAS, 191, 95 [NASA ADS] (In the text)
- Fox Machado, L., Pérez Hernández, F., Suárez, J. C., Michel, E., & Lebreton, Y. 2006, Mem. Soc. Astron. Ital., 77, 455 [NASA ADS] (In the text)
- Gatewood, G. 1995, ApJ, 445, 712 [NASA ADS] [CrossRef] (In the text)
- Gatewood, G., & de Jonge, J. K. 1994, ApJ, 428, 166 [NASA ADS] [CrossRef] (In the text)
- Gatewood, G., Castelaz, M., Han, I., et al. 1990, ApJ, 364, 114 [NASA ADS] [CrossRef] (In the text)
- Gatewood, G., Kiewiet de Jonge, J., & Persinger, T. 1998, AJ, 116, 1501 [NASA ADS] [CrossRef] (In the text)
- Gatewood, G., de Jonge, J. K., & Han, I. 2000, ApJ, 533, 938 [NASA ADS] [CrossRef] (In the text)
- Geyer, E. H., & Nelles, B. 1985, A&AS, 62, 301 [NASA ADS] (In the text)
- Giannuzzi, M. A. 1995, A&A, 293, 360 [NASA ADS]
- Gieseking, F. 1981, A&A, 99, 155 [NASA ADS] (In the text)
- Gieseking, F. 1985, A&AS, 61, 75 [NASA ADS] (In the text)
- González, J. F., & Lapasset, E. 2000, AJ, 119, 2296 [NASA ADS] [CrossRef] (In the text)
- Grenon, M. 2002, Highlights of Astronomy, 12, 680 [NASA ADS] (In the text)
- Gustafsson, B., & Nissen, P. E. 1972, A&A, 19, 261 [NASA ADS]
- Hauck, B., & Mermilliod, M. 1997, VizieR Online Data Catalog, 2215, 0
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hejlesen, P. M. 1980, A&AS, 39, 347 [NASA ADS] (In the text)
- Hill, G., & Perry, C. L. 1969, AJ, 74, 1011 [NASA ADS] [CrossRef] (In the text)
- Hiltner, W. A., Iriarte, B., & Johnson, H. L. 1958, ApJ, 127, 539 [NASA ADS] [CrossRef] (In the text)
- Hogg, A. R. 1960, PASP, 72, 85 [NASA ADS] [CrossRef] (In the text)
- Hogg, A. R., & Kron, G. E. 1955, AJ, 60, 365 [NASA ADS] [CrossRef] (In the text)
- Ishmukhamedov, K. Z. 1966, Tsirkulyar Tashkentskoj Astronomicheskoj Observatorii, 346, 16 [NASA ADS] (In the text)
- Johansson, K. L. V. 1981, A&AS, 43, 421 [NASA ADS] (In the text)
- Johnson, H. L. 1953, ApJ, 117, 353 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L. 1954, ApJ, 119, 181 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L. 1957, ApJ, 126, 121 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L. 1966, ARA&A, 4, 193 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L., & Morgan, W. W. 1953, ApJ, 117, 313 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L., Hoag, A. A., Iriarte, B., Mitchell, R. I., & Hallam, K. L. 1961, Lowell Observatory Bulletin, 5, 133 [NASA ADS] (In the text)
- Jordi, C., Masana, E., Figueras, F., & Torra, J. 1997, A&AS, 123, 83 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jordi, C., Luri, X., Masana, E., et al. 2002, Highlights of Astronomy, 12, 684 [NASA ADS] (In the text)
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kilkenny, D., Hilditch, C. E. J., Hilditch, R. W., Hill, P. W., & Lynas-Gray, A. E. 1975, MNRAS, 172, 5P [NASA ADS] (In the text)
- King, D. S. 1978, J. Proc. R. Soc. N.S.W., 111, 1-12 = Sydney Obs. Pap. No. 79, 111, 1 (In the text)
- Koelbloed, D. 1959, Bull. Astron. Inst. Netherlands, 14, 265 [NASA ADS] (In the text)
- Kovalevsky, J., Falin, J. L., Pieplu, J. L., et al. 1992, A&A, 258, 7 [NASA ADS] (In the text)
- Levato, H., & Malaroda, S. 1975a, PASP, 87, 823 [NASA ADS] [CrossRef]
- Levato, H., & Malaroda, S. 1975b, PASP, 87, 173 [NASA ADS] [CrossRef] (In the text)
- Levato, H., & Abt, H. A. 1977, PASP, 89, 274 [NASA ADS] [CrossRef] (In the text)
- Lindegren, L., Hoeg, E., van Leeuwen, F., et al. 1992, A&A, 258, 18 [NASA ADS] (In the text)
- Lindegren, L., Madsen, S., & Dravins, D. 2000, A&A, 356, 1119 [NASA ADS]
- Liu, T., Janes, K. A., & Bania, T. M. 1989, AJ, 98, 626 [NASA ADS] [CrossRef] (In the text)
- Loden, K., Lindblad, P. O., Schober, J., & Urban, A. 1980, A&AS, 41, 85 [NASA ADS] (In the text)
- Loden, L. O. 1984, A&AS, 58, 595 [NASA ADS] (In the text)
- Loktin, A. V., & Matkin, N. V. 1990, SvA, 34, 571 [NASA ADS] (In the text)
- Loktin, A. V., & Matkin, N. V. 1994, A&A, Trans., 4, 153 (In the text)
- Lutz, T. E., & Kelker, D. E. 1973, PASP, 85, 573 [NASA ADS] [CrossRef] (In the text)
- Lyngå, G. 1960, Ark. Astron., 2, 379 [NASA ADS] (In the text)
- Lyngå, G. 1962, Ark. Astron., 3, 65 [NASA ADS] (In the text)
- Madsen, S. 1999, in Harmonizing Cosmic Distance Scales in a Post-HIPPARCOS Era, ed. D. Egret & A. Heck, Astron. Soc. Pac. Conf. Ser., 167, 78
- Madsen, S., Lindegren, L., & Dravins, D. 2000, in Stellar Clusters and Associations: Convection, Rotation, and Dynamos, ed. R. Pallavicini, G. Micela, & S. Sciortino, ASP Conf. Ser. 198, 137 (In the text)
- Madsen, S., Lindegren, L., & Dravins, D. 2001, in Dynamics of Star Clusters and the Milky Way, ed. S. Deiters, B. Fuchs, A. Just, R. Spurzem, & R. Wielen, ASP Conf. Ser., 228, 506 (In the text)
- Madsen, S., Dravins, D., & Lindegren, L. 2002, A&A, 381, 446 [NASA ADS] [CrossRef] [EDP Sciences]
- Maitzen, H. M., & Catalano, F. A. 1986, A&AS, 66, 37 [NASA ADS] (In the text)
- Makarov, V. 2002, AJ, 124, 3299 [NASA ADS] [CrossRef]
- Makarov, V. V. 2003, AJ, 126, 2408 [NASA ADS] [CrossRef]
- Makarov, V. V. 2006, AJ, 131, 2967 [NASA ADS] [CrossRef]
- Mamajek, E. E. 2006, AJ, 132, 2198 [NASA ADS] [CrossRef] (In the text)
- Manteiga, M., Martinez-Roger, C., Morales, C., & Sabau, L. 1991, A&AS, 87, 419 [NASA ADS] (In the text)
- Mävers, F.-W. 1940, Astron. Nachr., 270, 201 [NASA ADS] [CrossRef] (In the text)
- McCarthy, M. F., & O'Sullivan, S. 1969, Ric. Astron., 7, 483 (In the text)
- McNamara, B. J., & Sanders, W. L. 1977, A&AS, 30, 45 [NASA ADS] (In the text)
- Meadows, A. J. 1961, ApJ, 133, 907 [NASA ADS] [CrossRef] (In the text)
- Mendoza V., E. E., & Gomez, T. 1980, MNRAS, 190, 623 [NASA ADS] (In the text)
- Mermilliod, J.-C. 1995, in Information, On-Line Data in Astronomy, ed. D. Egret, & M. A. Albrecht, 127 (In the text)
- Mermilliod, J.-C., & Maeder, A. 1986, A&A, 158, 45 [NASA ADS] (In the text)
- Mermilliod, J.-C., Turon, C., Robichon, N., Arenou, F., & Lebreton, Y. 1997, in Hipparcos - Venice '97, ed. R. M. Bonnet, E. Høg, P. L. Bernacca, L. Emiliani, A. Blaauw, C. Turon, J. Kovalevsky, L. Lindegren, H. Hassan, M. Bouffard, B. Strim, D. Heger, M. A. C. Perryman, & L. Woltjer, ESA SP, 402, 643 (In the text)
- Mermilliod, J.-C., Platais, I., James, D. J., Grenon, M., & Cargile, P. A. 2008, A&A, 485, 95 [NASA ADS] [CrossRef] [EDP Sciences]
- Mitchell, R. I., & Johnson, H. L. 1957, ApJ, 125, 414 [NASA ADS] [CrossRef]
- Mohan, V., & Sagar, R. 1985, MNRAS, 213, 337 [NASA ADS] (In the text)
- Munari, U., Dallaporta, S., Siviero, A., et al. 2004, A&A, 418, L31 [NASA ADS] [CrossRef] [EDP Sciences]
- Narayanan, V. K., & Gould, A. 1999, ApJ, 523, 328 [NASA ADS] [CrossRef]
- Naylor, T., Totten, E. J., Jeffries, R. D., et al. 2002, MNRAS, 335, 291 [NASA ADS] [CrossRef] (In the text)
- Nicolet, B. 1981, A&A, 104, 185 [NASA ADS] (In the text)
- Nissen, P. E. 1970a, A&A, 8, 476 [NASA ADS]
- Nissen, P. E. 1970b, A&A, 6, 138 [NASA ADS]
- Nissen, P. E. 1988, A&A, 199, 146 [NASA ADS] (In the text)
- O'Mullane, W., Lammers, U., Bailer-Jones, C., et al. 2007, in Astronomical Data Analysis Software and Systems XVI, ed. R. A. Shaw, F. Hill, & D. J. Bell, Astron. Soc. Pac. Conf. Ser., 376, 99 (In the text)
- Pan, X., Shao, M., & Kulkarni, S. R. 2004, Nature, 427, 326 [NASA ADS] [CrossRef]
- Patenaude, M. 1978, A&A, 66, 225 [NASA ADS] (In the text)
- Percival, S. M., Salaris, M., & Kilkenny, D. 2003, A&A, 400, 541 [NASA ADS] [CrossRef] [EDP Sciences]
- Percival, S. M., Salaris, M., & Groenewegen, M. A. T. 2005, A&A, 429, 887 [NASA ADS] [CrossRef] [EDP Sciences]
- Perez, M. R., The, P. S., & Westerlund, B. E. 1987, PASP, 99, 1050 [NASA ADS] [CrossRef] (In the text)
- Perry, C. L., & Hill, G. 1969, AJ, 74, 899 [NASA ADS] [CrossRef] (In the text)
- Perry, C. L., Walter, D. K., & Crawford, D. L. 1978, PASP, 90, 81 [NASA ADS] [CrossRef]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS]
- Petrie, R. M., & Heard, J. F. 1969, Publications of the Dominion Astrophysical Observatory Victoria, 13, 329 [NASA ADS] (In the text)
- Pinsonneault, M. H., Stauffer, J., Soderblom, D. R., King, J. R., & Hanson, R. B. 1998, ApJ, 504, 170 [NASA ADS] [CrossRef]
- Pinsonneault, M. H., Terndrup, D. M., Hanson, R. B., & Stauffer, J. R. 2004, ApJ, 600, 946 [NASA ADS] [CrossRef] (In the text)
- Platais, I. 1994, Bulletin d'Information du Centre de Données Stellaires, 44, 9 [NASA ADS] (In the text)
- Platais, I., Kozhurina-Platais, V., Barnes, S., et al. 2001, AJ, 122, 1486 [NASA ADS] [CrossRef] (In the text)
- Platais, I. K. 1984, SvA Lett., 10, 84 [NASA ADS] (In the text)
- Prisinzano, L., Micela, G., Sciortino, S., & Favata, F. 2003, A&A, 404, 927 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Prosser, C. F. 1993, AJ, 105, 1441 [NASA ADS] [CrossRef] (In the text)
- Prosser, C. F., & Giampapa, M. S. 1994, AJ, 108, 964 [NASA ADS] [CrossRef] (In the text)
- Robichon, N., Arenou, F., Mermilliod, J. C., & Turon, C. 1999, A&A, 345, 471 [NASA ADS] (In the text)
- Rojo Arellano, E., Pena, J. H., & Gonzalez, D. 1997, A&AS, 123, 25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Röser, S., & Bastian, U. 1994, A&A, 285, 875 [NASA ADS] (In the text)
- Rufener, F. 1988, Catalogue of stars measured in the Geneva Observatory photometric system : 4 [NASA ADS] : 1988 (Sauverny: Observatoire de Geneve) (In the text)
- Sanders, W. L. 1973, A&AS, 9, 213 [NASA ADS] (In the text)
- Sanders, W. L., & van Altena, W. F. 1972, A&A, 17, 193 [NASA ADS] (In the text)
- Schaifers, K., Voigt, H. H., Landolt, H., Boernstein, R., & Hellwege, K. H. 1982, A&A, C: Interstellar Matter, Galaxy, Universe (Landolt-Boernstein: Numerical Data and functional Relationships in Science and Technology. New Series, Berlin: Springer) (In the text)
- Schmidt, E. G. 1976, PASP, 88, 63 [NASA ADS] [CrossRef] (In the text)
- Smyth, M. J., & Nandy, K. 1962, Publications of the Royal Observatory of Edinburgh, 3, 24 [NASA ADS] (In the text)
- Snowden, M. S. 1975, PASP, 87, 721 [NASA ADS] [CrossRef] (In the text)
- Snowden, M. S. 1976, PASP, 88, 174 [NASA ADS] [CrossRef] (In the text)
- Soderblom, D. R., King, J. R., Hanson, R. B., et al. 1998, ApJ, 504, 192 [NASA ADS] [CrossRef]
- Soderblom, D. R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [NASA ADS] [CrossRef]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2005, in Transits of Venus: New Views of the Solar System and Galaxy, ed. D. W. Kurtz, IAU Colloq., 196, 361
- Stello, D., & Nissen, P. E. 2001, A&A, 374, 105 [NASA ADS] [CrossRef] [EDP Sciences]
- Stock, J. 1984, Rev. Mex. Astron. Astrofis., 9, 127 [NASA ADS] (In the text)
- Strömgren, B. 1966, ARA&A, 4, 433 [NASA ADS] [CrossRef] (In the text)
- Sung, H., Bessell, M. S., Lee, B.-W., & Lee, S.-G. 2002, AJ, 123, 290 [NASA ADS] [CrossRef] (In the text)
- Tayler, R. J. 1954, ApJ, 120, 332 [NASA ADS] [CrossRef]
- Tayler, R. J. 1956, MNRAS, 116, 25 [NASA ADS]
- The, P. S., Bakker, R., & Antalova, A. 1980, A&AS, 41, 93 [NASA ADS] (In the text)
- Trimble, V., Aschwanden, M. J., & Hansen, C. J. 2006, PASP, 118, 947 [NASA ADS] [CrossRef] (In the text)
- Trumpler, R. 1928, PASP, 40, 265 [NASA ADS] [CrossRef] (In the text)
- Turon, C., Gomez, A., Crifo, F., et al. 1992, A&A, 258, 74 [NASA ADS]
- Upgren, A. R., Weis, E. W., & Deluca, E. E. 1979, AJ, 84, 1586 [NASA ADS] [CrossRef] (In the text)
- Valls-Gabaud, D. 2007, in IAU Symposium, ed. W. I. Hartkopf, E. F. Guinan, & P. Harmanec, IAU Symposium, Vol. 240, 281
- van Altena, W. F. 1966, AJ, 71, 482 [NASA ADS] [CrossRef] (In the text)
- van der Marel, H. 1988, Ph.D. Thesis, Technische Universiteit Delft
- van der Marel, H., & Petersen, C. S. 1992, A&A, 258, 60 [NASA ADS]
- van Leeuwen, F. 1980, in Star Formation, IAU Symp. 85, 157
- van Leeuwen, F. 1983, Ph.D. Thesis (In the text)
- van Leeuwen, F. 1999a, A&A, 341, L71 [NASA ADS] (In the text)
- van Leeuwen, F. 1999b, in Harmonizing cosmic distance scales in a post-Hipparcos era, ed. D. Egret, & A. Heck, 167 (PASPC), 52 (In the text)
- van Leeuwen, F. 2005a, A&A, 439, 805 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- van Leeuwen, F. 2005b, in Transits of Venus: New Views of the Solar System and Galaxy, IAU Colloq. 196, 347 (In the text)
- van Leeuwen, F. 2007a, Hipparcos, the new reduction of the raw data (Dordrecht: Springer) (In the text)
- van Leeuwen, F. 2007b, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences]
- van Leeuwen, F. 2008, in IAU Symp., 248, 82 (In the text)
- van Leeuwen, F., & Alphenaar, P. 1982, The Messenger, 28, 15 [NASA ADS]
- van Leeuwen, F., & Evans, D. W. 1998, A&A, 323, 157 (In the text)
- van Leeuwen, F., Alphenaar, P., & Brand, J. 1986, A&AS, 65, 309 [NASA ADS]
- van Leeuwen, F., Alphenaar, P., & Meys, J. J. M. 1987, A&AS, 67, 483 [NASA ADS]
- van Leeuwen, F., & Fantino, E. 2003, Space Sci. Rev., 108, 537 [NASA ADS] [CrossRef] (In the text)
- van Schewick, H. 1966, Veroeffentlichungen des Astronomisches Institute der Universitaet Bonn, 74, 1 [NASA ADS] (In the text)
- Vandenberg, D. A. 1985, ApJS, 58, 711 [NASA ADS] [CrossRef]
- Vasilevskis, S. 1955, AJ, 60, 384 [NASA ADS] [CrossRef] (In the text)
- Vasilevskis, S., Klemola, A., & Preston, G. 1958, AJ, 63, 387 [NASA ADS] [CrossRef] (In the text)
- Vasilevskis, S., Sanders, W. L., & Balz, A. G. A. 1965, AJ, 70, 797 [NASA ADS] [CrossRef] (In the text)
- Verschoor, J. N., & van Genderen, A. M. 1983, A&AS, 53, 419 [NASA ADS] (In the text)
- Voigt, H. H. 1965, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology - New Series Gruppe/Group 6 [NASA ADS] (Landolt-Bornstein) (In the text)
- Walker, M. F. 1956, ApJS, 2, 365 [NASA ADS] [CrossRef] (In the text)
- Wallerstein, G., Westbrooke, W., & Hannibal, D. 1963, PASP, 75, 522 [NASA ADS] [CrossRef] (In the text)
- Weaver, H. F. 1953, ApJ, 117, 366 [NASA ADS] [CrossRef] (In the text)
- Westerlund, B. E., Lundgren, K., Pettersson, B., Garnier, R., & Breysacher, J. 1988, A&AS, 76, 101 [NASA ADS]
- Whiteoak, J. B. 1961, MNRAS, 123, 245 [NASA ADS] (In the text)
- Williams, P. M. 1978, MNRAS, 183, 49 [NASA ADS] (In the text)
- Wizinowich, P., & Garrison, R. F. 1982, AJ, 87, 1390 [NASA ADS] [CrossRef] (In the text)
- Young, A. 1978, PASP, 90, 144 [NASA ADS] [CrossRef] (In the text)
- Zentelis, N. 1983, A&AS, 53, 445 [NASA ADS] (In the text)
- Zwahlen, N., North, P., Debernardi, Y., et al. 2004, A&A, 425, L45 [NASA ADS] [CrossRef] [EDP Sciences]
Footnotes
All Tables
Table 1:
Comparison between absolute magnitude calibrations for different mean values of
![]() .
.
Table 2: Data from Nicolet (1981) for the cluster NGC 752.
Table 3: Summary of distance modulus determinations for the Pleiades over the past 30 years.
Table 4: Summary data for 8 clusters within 250 pc.
Table 5: Summary data for the distant clusters as derived from combined-abscissae fitting.
Table 6: Data on stars selected in the NGC 2264 field.
Table 7: Positions and velocities of 20 clusters in the galactic reference frame.
All Figures
![\begin{figure}
\par\includegraphics[width=8.9cm]{11382f01.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg22.gif) |
Figure 1:
Top: Abscissa-error correlation level ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm]{11382f02.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg23.gif) |
Figure 2:
Correlations ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f03.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg82.gif) |
Figure 3: A comparison between the ground-based parallax values as used by Crawford (1975) and parallaxes for the same stars as obtained from the new Hipparcos reduction. The comparison shows a systematic difference of 3.4 mas and a noise on the ground-based parallaxes of 10 mas. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11382f04.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg145.gif) |
Figure 4: Differences between MAP-based and Hipparcos parallaxes for 71 stars. The error bars contain the contributions of the formal errors on the Hipparcos parallaxes and the precisions as given for the MAP data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11382f05.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg151.gif) |
Figure 5:
Reduced proper motions in the selection field for the Hyades
cluster. In this diagram, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11382f06.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg152.gif) |
Figure 6: Map of the selected 150 Hyades stars, showing the current positions (points to the right of each line) and those extrapolated by 100 000 years (left-side points). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11382f07.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg158.gif) |
Figure 7: Comparison between the formal errors on the distance moduli for the Hyades stars as measured directly through parallaxes (dots) and as derived from the space velocity and the observed proper motions (crosses). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f08.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg163.gif) |
Figure 8: The Hyades HR diagram for 150 probable members, using distance moduli for individual stars as based on kinematically derivedparallaxes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{11382f09.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg164.gif) |
Figure 9:
A tangential projection of the distribution on the sky for
members of the clusters Coma Ber ( top left), Pleiades ( top right),
Praesepe ( bottom left) and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{11382f10.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg166.gif) |
Figure 10:
The distribution of the parallaxes against their formal errors for
the clusters Coma Ber ( top left), Pleiades ( top right), Praesepe ( bottom left)
and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.8cm]{11382f11.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg183.gif) |
Figure 11: The HR diagrams for Coma Ber ( left), Pleiades ( centre) and Praesepe ( right), shown as full dots in each diagram. The Hyades stars are shown in the background as open circles. In addition. The Coma Ber diagram also shows the UMa stars (crosses), the Pleiades diagram shows the Coma Ber stars as crosses, and similarly for the Pleiades stars are shown in the Praesepe diagram. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f12.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg186.gif) |
Figure 12:
Distribution of determinations (since 1997) for the Pleiades distance modulus and its standard error (other than those directly derived from the Hipparcos data). The distribution of the data points strongly suggests the presence of correlations between the different measurements. The central line represents the mean value of 5.63, the black diagonal lines on either side the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f13.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg187.gif) |
Figure 13: The HR diagram for the Pleiades (full dots) superimposed on the HR diagram for field stars with parallax accuracies better than 7 per cent. The distance modulus applied is the value of 5.40 mag derived in the present study, and the applied reddening is E(B-V)=0.04. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11382f14.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg196.gif) |
Figure 14:
Distribution of the proper motions for the selected member stars
in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{11382f15.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg202.gif) |
Figure 15:
The HR diagram for: ( left) the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm]{11382f16.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg214.gif) |
Figure 16:
The distribution of the parallaxes against their formal errors for
the IC 2391 ( top left), IC 2602 ( bottom left), Blanco 1 ( top right) and NGC 2451 ( bottom right) members in the Hipparcos catalogue. The central vertical line represents the mean parallax of each cluster, as presented in Table 4. The black lines on either side show the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm]{11382f17.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg215.gif) |
Figure 17: A tangential projection of the distribution on the sky for members of the clusters IC 2391 ( top left), IC 2602 ( bottom left), Blanco 1 ( top right) and NGC 2451 ( bottom right). The coordinates are in radians, relative to the assumed cluster centre. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{11382f18.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg218.gif) |
Figure 18: The HR-diagram positions of the stars used in the astrometric solutions to NGC 2516 and NGC 2422 (each compared with the Pleiades, open symbols), and NGC 6475 (compared with the Pleiades, open symbols, and Coma Ber, crosses). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f19.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg253.gif) |
Figure 19: Proper motion distribution of the stars identified as probable members of NGC 2516 in the Hipparcos catalogue. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{11382f20.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg254.gif) |
Figure 20: The HR-diagram positions of the stars used in the astrometric solutions to NGC 3532 and NGC 7092 (each compared with Coma Ber, crosses, and Praesepe, open circles), and NGC 6633 (compared with the Praesepe, open circles). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11382f21.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg290.gif) |
Figure 21:
The HR-diagram positions of the stars used in the astrometric solutions to Collinder 140, NGC 2232 and Trumpler 10 (each compared with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11382f22.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg314.gif) |
Figure 22:
The HR-diagram positions of the stars used in the astrometric solutions to NGC 2547 and IC 4665 (each compared with Pleiades, open symbols and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f23.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg320.gif) |
Figure 23: Proper motions for nine stars in the field of NGC 2264. Data points indicates with a larger central dot represent the five stars selected as probable members based on a combination of proper motions, parallaxes and apparent magnitudes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f24.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg329.gif) |
Figure 24:
Differences in distance moduli between values derived by Johnson (1957) and the new Hipparcos reduction ( bottom graph) and similarly ( middle graph) for the data for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f25.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg330.gif) |
Figure 25: Distance modulus differences. Bottom: between Becker & Fenkart (1971) and Hipparcos for 15 clusters. Error bars represent Hipparcos determinations only. Middle: between Nicolet (1981) and the new reduction for 13 clusters. The error bars represent the combined errors from the two determinations. Top: between Loktin & Matkin (1994) and the new reduction for 15 clusters. The error bars represent the Hipparcos determinations only. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11382f26.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg331.gif) |
Figure 26: Distance modulus differences. Bottom: between Robichon et al. (1999) and Hipparcos for 17 clusters. Error bars represent the old Hipparcos determinations only. Top: between Kharchenko et al. (2005) and the new reduction for 19 clusters. The error bars represent the new Hipparcos reduction only. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11382f27.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg332.gif) |
Figure 27: The composite HR diagrams for groups 1 & 2 (left)and group 3 (right). Symbols on the left: Hyades, closed circles; Praesepe, open circles; UMa, closed triangles; Coma Ber, open triangles; NGC 7092, crosses. Symbols on the right: Pleiades, closed circles; Blanco 1, open circles; NGC 2516, crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11382f28.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg334.gif) |
Figure 28: The composite diagram for clusters in group 4 (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382f29.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg335.gif) |
Figure 29: The U-B versus B2-V2 diagram in the Geneva photometry. The red dots represent data points in the Hyades and Praesepe clusters, the crosses for data from the Pleiades, Blanco 1 and NGC 2516. Some of the Pleiades points are offset because of localised differential reddening in the cluster. The difference in loci for the two groups of clusters is known as the Hyades anomaly. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11382f30.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg338.gif) |
Figure 30:
Comparison of the c1 ( top) and m1 ( bottom) versus
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11382f31.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg339.gif) |
Figure 31: Distribution of the velocities of 20 clusters and 8 UMa stars within the galactic plane, compared with the velocity distribution of A and F stars within 125 pc. The UMa stars form a small clump, and there are a few other coincidences in space velocity. The solar motion has not been subtracted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11382fA1.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg433.gif) |
Figure A.1:
The relation between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA2.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg434.gif) |
Figure A.2:
The relation between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA3.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg445.gif) |
Figure A.3:
Calibration of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm]{11382fA4.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg450.gif) |
Figure A.4:
The relation between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.4cm]{11382fA5.eps}\end{figure}](/articles/aa/full_html/2009/13/aa11382-08/Timg456.gif) |
Figure A.5:
The relation between
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\dot{\vec{R}} = \left[\begin{array}{rrr}\cos\alpha\cos\delta ...
...ot{\alpha}\cos\delta \\
R~\dot{\delta}\\
\end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img27.gif)
![\begin{displaymath}\left[\begin{array}{l}V_{{\rm rad},i}\\
\kappa~\mu_{\alpha*,...
..._i & \cos\delta_i \\
\end{array}\right] ~\cdot~\dot{\vec{R}},
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img38.gif)
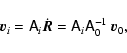
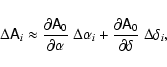
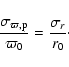
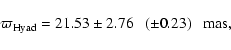
![\begin{displaymath}\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] = R\cdo...
... \cos l \cos b \\
\sin l \cos b \\ \sin b \end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img340.gif)
![\begin{displaymath}\left[\begin{array}{c} u \\
v \\
w
\end{array}\right] =
V_...
...r}\cos l \sin b \\ \sin l\sin b \\ -\cos b \end{array}\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa11382-08/img341.gif)