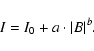The relationship between chromospheric emissions and magnetic field strength

M. Loukitcheva; S. K. Solanki; S. M. White

doi:10.1051/0004-6361/200811133

Free Access

Issue		A&A Volume 497, Number 1, April I 2009


Page(s)		273 - 285
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361/200811133
Published online		09 February 2009

The relationship between chromospheric emissions and magnetic field strength

M. Loukitcheva^1,2 - S. K. Solanki¹ - S. M. White³

1 - Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
2 - Astronomical Institute, St. Petersburg University, 198504 St. Petersburg, Russia
3 - Astronomy Department, University of Maryland, College Park, MD 20742, USA

Received 11 October 2008 / Accepted 28 January 2009

Abstract
Aims. We analyze observational data from 4 instruments to study the correlations between chromospheric emission, spanning the heights from the temperature minimum region to the middle chromosphere, and photospheric magnetic field.
Methods. The data consist of radio images at 3.5 mm from the Berkeley-Illinois-Maryland Array (BIMA), UV images at 1600 Å from TRACE, Ca II K-line filtergrams from BBSO, and MDI/SOHO longitudinal photospheric magnetograms. For the first time interferometric millimeter data with the highest currently available resolution are included in such an analysis. We determine various parameters of the intensity maps and correlate the intensities with each other and with the magnetic field.
Results. The chromospheric diagnostics studied here show a pronounced similarity in their brightness structures and map out the underlying photospheric magnetic field relatively well. We find a power law to be a good representation of the relationship between photospheric magnetic field and emission from chromospheric diagnostics at all wavelengths. The dependence of chromospheric brightness on magnetic field is found to be different for network and internetwork regions.

Key words: Sun: chromosphere - Sun: radio radiation - Sun: magnetic fields

1 Introduction

The solar chromosphere is known to be highly structured at different spatial scales and the range of chromospheric inhomogeneities is best revealed when observed at different wavelengths from the extreme ultraviolet to millimeter waves (see, e.g., Solanki 2004). Even far from activity complexes, in the quiet Sun magnetic field is generally believed to be responsible for chromospheric structuring. This is consistent with the strong correlation found between excess emission in the cores of the Ca II K and H resonance lines (the primary chromospheric diagnostic) and the presence and strength of quiet-Sun magnetic flux (e.g. Leighton 1959; Schrijver et al. 1989). Consequently, these resonance lines commonly serve as indicators of changes in the chromospheric structure related to global magnetic activity and heating of the outer atmosphere of the Sun and cool stars (Rutten & Uitenbroek 1991; Schrijver et al. 1989). In addition to the chromospheric emission related to the magnetic field, Schrijver (1987,1992) has suggested that part of the radiative flux from solar and stellar chromospheres, referred to as basal flux, has a nonmagnetic origin and is believed to stem from acoustic heating of the chromosphere (see, e.g. Rutten & Uitenbroek 1991).

Table 1: Overview of data taken on May 18, 2004.

The primary brightness patterns revealed in two-dimensional images obtained in the ionized calcium H and K lines include bright plages, chromospheric network located at the boundaries of supergranular cells, and bright points in the interior of the cells - internetwork grains or K2V bright points. Chromospheric network features are known to display a one-to-one spatial correspondence with regions of enhanced photospheric magnetic field (Skumanich et al. 1975; Sivaraman & Livingston 1982; Sivaraman et al. 2000; Nindos & Zirin 1998), while the (magnetic) origin of the internetwork grains is a controversial issue. From the analysis of simultaneous Kitt Peak Ca II K-line spectroheliograms and photospheric magnetic area scans, Sivaraman et al. (2000) showed the association of internetwork K2V bright points with magnetic features, confirming the earlier results of Sivaraman & Livingston (1982). However, from analysis of Ca II K-line and magnetic field data from the BBSO, Nindos & Zirin (1998) have found that not all internetwork bright points are associated with magnetic fields. The existence of 2 distinct classes of cell-interior grains, which differ in temporal behaviour and spatial motion and have a different origin, was revealed by observations with the Swedish Solar Telescope reported by Brandt et al. (1992), whereas Lites et al. (1999) found no obvious relation of the internetwork brightenings to the magnetic field, and Remling et al. (1996) concluded that they are a totally nonmagnetic phenomenon.

Quantitative studies of the relationship between magnetic field and the chromosphere (represented by the calcium K and H-lines), in both the active and quiet solar atmosphere, have been carried out by a number of authors (e.g. Skumanich et al. 1975; Rezaei et al. 2007; Harvey & White 1999; Schrijver et al. 1989; Ortiz & Rast 2005; Nindos & Zirin 1998). In the quiet-Sun chromosphere Skumanich et al. (1975) and Nindos & Zirin (1998) found a linear correlation between the K-line intensities and the absolute values of the magnetic field strength. Schrijver et al. (1989) extended this relationship to solar active regions and suggested that the relation between the K-line excess flux density (after the subtraction of the basal flux from the observed Ca II K-line flux) and the magnetic field flux density is best described by a power law with an exponent of about 0.6. Considering 4 types of brightness structures, which included active regions, decaying active regions, the enhanced network and quiet (weak) network, Harvey & White (1999) ascertained that in both active and quiet Sun the relation between the magnetic flux density and calcium residual intensity follows a power law with an exponent of 0.5. Ortiz & Rast (2005) cited a power-law exponent value of 0.66 for the quiet Sun, while Rezaei et al. (2007) obtained a lower exponent of 0.2 for locations in a quiet-Sun region, and higher values of 0.4-0.5 for network locations, depending on the magnetic field threshold value.

Rutten et al. (1991) found power-law relations between excess flux densities in stellar chromospheric lines with differing temperature responses, with the exponents increasing with increasing difference between their temperatures of formation. Relations between fluxes originating in the same atmospheric regime were found to be close to linear (i.e., having a power-law exponent of unity). For the quiet Sun the high degree of co-spatiality of the brightness features seen in the Ca II K line and the TRACE UV channels has been demonstrated by Rutten et al. (1999).

Almost all these studies have been limited to the visible and UV spectral range. An exception is the work of Lindsey & Jefferies (1991), who studied the cross-correlation statistics of the brightness variations in the submm (850 $\mu$ m) and Ca II K-line images. Their results are confined to the temperature minimum region and the heights of the low chromosphere. No detailed studies have compared millimeter emission, which originates from the middle chromosphere, with other chromospheric indicators. From observations at 350, 850 and 1200 $\mu$ m with the James Clerk Maxwell Telescope at a resolution of about 20 $^{\prime \prime }$ , Lindsey et al. (1995) reported submillimeter chromospheric brightness structures which resemble the supergranular network, although the resolution was marginal for such a study. Initial qualitative results of the comparison of chromospheric structure, identified in millimeter images obtained with BIMA at 3.5 mm with a resolution of about 10 $^{\prime \prime }$ , with calcium images from BBSO and line-of-sight photospheric magnetograms from SOHO/MDI were given in White et al. (2006).

In this paper we present an observational study of the relationships between the photospheric magnetic field and emission at different temperatures from chromospheric heights. We study the chromospheric observational data referring to the temperature minimum region (UV continuum at 1600 Å), low chromosphere (Ca II K line) and middle chromosphere (continuum at 3.5 mm). This is the first analysis of this type that includes millimeter observational data. Unfortunately, simultaneously recorded observational data on the chromospheric magnetic field suitable for such an analysis are unavailable. For this reason, we focus on the MDI/SOHO longitudinal photospheric magnetograms and study the dependence of the chromospheric intensity at different wavelengths on the photospheric magnetic field strength.

In Sects. 2 and 3 we describe the data and instruments used for the analysis and provide the details of the data reduction. In Sect. 4 the topography of the quiet chromosphere, chromospheric intensity distributions and cross-correlations between the magnetic field and chromospheric emission are presented. In Sect. 5 we summarize and discuss the results.

2 Observational data

We analyze observations from the Berkeley-Illinois-Maryland Array (BIMA) at 85 GHz ( $\lambda~=~3.5$ mm), Ca II K-line filtergrams from the Big Bear Solar Observatory (BBSO), UV images at 1600 Å from the Transition Region and Coronal Explorer (TRACE, Handy et al. 1999) and magnetograms from the Michelson Doppler Imager (MDI, Scherrer et al. 1995) on the Solar and Heliospheric Observatory (SOHO) satellite, obtained on May 18, 2004. The data consist of temporally resolved images of the measured intensities, which are given in Kelvin for millimeter data (see Sect. 2.1), in relative units for Ca II K-line and 1600 Å data (Sects. 2.2 and 2.3, respectively), and in Gauss for MDI photospheric magnetograms (Sect. 2.4). The overview of the data (including instruments, operating wavelengths, spatial resolution, cadence and image pixel size) used in the present study is given in Table 1.

2.1 BIMA observations at 3.5 mm

The 3.5 mm observations of a quiet-Sun area near the center of the disk were acquired with 9 BIMA antennae during the time interval 16:43-20:21 UT ( $\sim$ 3.5 h) when atmospheric phase conditions were good. The data were taken at a cadence of 10 s. The interferometer was in its most compact (``D'') configuration for these observations, providing a spatial resolution of order 12 $^{\prime \prime }$ within a 2 $^\prime$ field of view (FOV). The images were deconvolved using a maximum entropy method (MEM) and restored with a Gaussian beam. The details of the interferometric image restoration of the BIMA data, including description of the limitations imposed by the MEM deconvolution, are given in White et al. (2006). The final images were 128 pixels square, with a cell size of 3 $^{\prime \prime }$ and the flux in the inner 80 pixels of the FOV with the center at (-17 $^{\prime \prime }$ , 71 $^{\prime \prime }$ ) in heliocentric coordinates. All images were corrected for the primary beam response and flux units were converted to brightness temperatures for a 12 $^{\prime \prime }$ beam. Data within a 96 $^{\prime \prime }$ radius of the pointing center are used in the analysis below. The zero level in the BIMA image corresponds the coldest feature on the surface in the chromosphere that is optically thick at 3.5 mm wavelength. This should be at a temperature of order 6500-7000 K. The temperature fluctuations in the BIMA image represent direct temperature measurements above this minimum value on the optically thick surface in the chromosphere, ranging from 0 to 1100 K in the map for the entire 3.5 h period.

2.2 Ca II K line observations at 393.3 nm

The Ca II K-line observations were obtained with the 25-cm refractor of BBSO. A 5 h sequence of filtergrams in the core of the Ca II K-line (393.3 nm) with a bandpass of 0.6 Å was recorded by a KX-260 CCD camera, which has $512 \times 512$ pixels and a dynamic range of 14 bits. The exposure time was 250 ms, the cadence was 30 s, recorded field of view was $300\hbox{$^{\prime\prime}$ }\times 300\hbox{$^{\prime\prime}$ }\$ at a pixel size of 0.645 $^{\prime \prime }$ . The observations were taken under moderate to fair seeing conditions. The K-line data were preprocessed, which included calibration by dark and flat-field frames (Denker et al. 2001). The intensity scale of the images was equalized by setting the quiet-Sun integrated background intensity in all images to the same value. No absolute flux calibration was available for the data, hereafter we use the Ca II K-line intensities in arbitrary units. We note that the bandwidth of the calcium filter tuned to the line center was too large to separate the K-line peaks and thus the images obtained depict the structure of the solar chromosphere collected from a wide range of heights, but dominated by mid-chromospheric contributions, as sampled by the K2 peaks.

2.3 TRACE observations at 1600 Å

In parallel with the BIMA observations a total of 14 TRACE images with a cadence of 20 min were recorded at a wavelength of 1600 Å at full resolution (0.5 $^{\prime \prime }$ pixel size). The images were preprocessed, which included subtraction of the dark pedestal and current, as well as division by a corrected flat field. The data were normalized to the exposure time, giving data numbers per second (DN s^-1) with no absolute calibration. Both standard models of the quiet-Sun atmosphere such as FAL C (Fontenla et al. 1993) and non-LTE radiation hydrodynamic simulations such as those of Fossum & Carlsson (2005) place the disk-center radiation at 1600 Å in the temperature minimum region at a height of around 500 km above the photosphere (Handy et al. 1999; Fossum & Carlsson 2005; Krijger et al. 2001), although a contribution from 10⁵ K transition-region gas is also present due to the CIV Lines. In the quiet Sun this contribution is expected to be small (Krijger et al. 2001; Handy et al. 1998).

$\begin{figure} \par\includegraphics[angle=90,width=12.5cm,clip]{1133fig1.eps} \end{figure}$

Figure 1:

Portrait of the solar chromosphere averaged over 3.5 h at the center of the Sun's disk at 4 different wavelengths on May 18, 2004. From top left to bottom right: MDI longitudinal photospheric magnetogram (resolution of 4 $^{\prime \prime }$ ), TRACE 1600 Å image (resolution of 1 $^{\prime \prime }$ ), Ca II K-line center image from BBSO (resolution of 2-4 $^{\prime \prime }$ ) and BIMA image at 3.5 mm (resolution of 12 $^{\prime \prime }$ ). The images are created by averaging over the 3.5 h period of the BIMA observation. The details of the data units are given in Sect. 2. Dashed circles mark the 96 $^{\prime \prime }$ radius BIMA FOV where we regard fluxes to be reliable. X and Y axes are in arcsec from the disk center, which is located at (0,0).

Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=12.5cm,clip]{1133fig2.eps} \end{figure}$	Figure 2: The same as Fig. 1 plotted at the BIMA resolution of 12 $^{\prime \prime }$ . In the top left panel the absolute value of the MDI magnetogram is depicted. Overlays of contours of 3.5 mm emission at (30, 50, 70, 90, 95, 98)% of maximum brightness are overplotted in white.
Open with DEXTER

2.4 MDI magnetograms

One-minute cadence full-disk MDI magnetograms (spatial resolution of 4 $^{\prime \prime }$ , Scherrer et al. 1995) were selected for the 3.5 h BIMA observing period, which resulted in 188 images of the proxies of the photospheric magnetic field. The noise in the original 1-min MDI magnetograms is typically about 20 Gauss (Scherrer et al. 1995), which is comparable to the magnetic signal of quiet-Sun network features. By averaging in time over 24 consecutive individual magnetograms (30-min sequence) we reduced the noise to 4 Gauss. Averaging over the whole 3.5 h observing period (188 images) resulted in a level of the random noise of about 1.5 Gauss. Prior to averaging the influence of solar rotation on the time series was removed (see Sect. 3).

3 Data coalignment and reduction

We formed 4 observational data cubes I(x,y,t), which were subsequently aligned using a two-step procedure. The first step involved correction of differential solar rotation by using standard procedures of SolarSoftware in the IDL environment. All images were rotated to the fiducial time of 20:00 UT. In the second step the shift of the images was determined and applied by a 2D cross-correlation of each image of the sequence to the first image of the sequence.

After a sub-arcsecond accuracy was reached in the alignment of the data cubes we averaged the images in time over the whole observing period (16:43-20:20 UT) to obtain the mean (time-averaged) MDI magnetogram, Ca II K filtergram, TRACE 1600 Å image and BIMA image at 3.5 mm. Additionally we averaged over the uninterrupted sequence of images of good quality within the time interval 19:00-19:30 UT to check the stability of the large-scale quiet-Sun structures. We based our correlation analysis on the mean images to avoid the scatter introduced by the chromospheric oscillations within cell interiors and the chromospheric network. Consequently, by averaging the images we also suppress proper motions of the K-grains and of bright points in the network.

Finally, the full disk $B_{\Vert}$ MDI images were chosen as the coordinate reference against which all other mean images were co-aligned by using cross-correlation methods. Absolute values of the MDI magnetograms were formed prior to alignment. The remaining image displacements do not exceed 1 $^{\prime \prime }$ and we believe that they do not affect the results of our analysis. A 3.5 h time-averaged image of the BIMA FOV made at each of the 4 wavelength bands is shown in Fig. 1 at the original spatial resolution of each band.

The cross-correlation analysis between the chromospheric images and photospheric magnetograms was done both for the MDI magnetogram resolution (4 $^{\prime \prime }$ ) and for the resolution of the BIMA data (12 $^{\prime \prime }$ ). In the former case the Ca II K-line and TRACE 1600 Å images were rebinned to make the size of the pixels equal to that of the magnetograms. In the latter case we degraded all images to the resolution of the BIMA data prior to cross-correlating them. The shift between the BIMA images and the MDI magnetograms did not exceed 1 BIMA image pixel (<3 $^{\prime \prime }$ ). Figure 2 shows example time-averaged images at BIMA resolution.

4 Results

4.1 Mapping of chromospheric structure

$\begin{figure} \par\includegraphics[width=8cm,clip]{1133fig3.eps} \end{figure}$	Figure 3: Intensity distribution histograms over the 2-D quiet-Sun region near the disk center obtained, from top to bottom, in the TRACE 1600 Å channel, the Ca II K line and at 3.5 mm. In all three panels dotted curves depict log-normal fits.
Open with DEXTER

Figure 1 depicts the time-averaged quiet solar chromosphere at 3 different heights from the temperature minimum region (TRACE 1600 Å image) through the lower chromosphere (Ca II K-line filtergram) to the middle chromosphere (BIMA image at 3.5 mm) at the original resolution of the instruments (see Table 1) as well as the corresponding MDI/SOHO line-of-sight photospheric magnetogram. Since the QS region being analyzed lies near the disk center, the line-of-sight magnetic field, measured by MDI, can accurately be regarded as the vertical component of the magnetic field vector. Of particular interest is the relation of the BIMA image to the others. Visual inspection of Fig. 1 reveals strong morphological similarities between different chromospheric emissions and the photospheric magnetic field, most prominently on spatial scales of the enhanced magnetic flux and chromospheric network (brightenings in all 4 frames). In snapshot images (not plotted) brightenings appear not only at supergranular cell boundaries, but also within the cells. Averaged in time, bright network becomes more pronounced, while low-intensity short-lived internetwork bright points are significantly suppressed and eventually vanish with increased averaging. In general, use of time averages reduces differences between the 4 images due to the brightness variability of the structures.

The impression of a high degree of correlation of photospheric magnetograms (absolute value) with the Ca II K-line, 1600 Å and 3.5 mm images is confirmed quantitatively. Within a radius of 96 $^{\prime \prime }$ the linear correlation coefficient between the absolute magnetogram and calcium image is 0.75, while it is 0.63 between the magnetogram and emission at 1600 Å.

The degree of spatial agreement between the radio images and the other chromospheric diagnostics and the photospheric magnetic field is more clearly visible in maps degraded to the BIMA resolution of 12 $^{\prime \prime }$ , shown in Fig. 2 with radio contours overlaid on the other images at (30, 50, 70, 90, 95, 98)% of maximum mm brightness. The correlation coefficients between the mm image and the magnetogram are 0.56 (linear) and 0.72 (rank), while for the mm image and Ca II K-line image they are 0.65 and 0.69, respectively. At a resolution of 12 $^{\prime \prime }$ the magnetogram shows a higher correlation with the calcium and 1600 Å images than at 4 $^{\prime \prime }$ resolution, with the linear correlation coefficient being 0.82 and 0.74, respectively.

4.2 Histograms of chromospheric intensity distribution

With sufficiently good statistics the brightness histogram is expected to have a log-normal shape, comparable with a single population (Pauluhn et al. 2000). To test whether this is the case for the chromospheric intensities studied here we built intensity distribution histograms (observed frequency distribution normalized to unit area) for the selected 2D images at 1600 Å and 3.5 mm and fitted them with a single log-normal distribution function. Following Fontenla et al. (2007) histograms of the Ca II K intensity were fitted with a modified log-normal function having an additional parameter - an offset which represents line scattering of the photospheric background radiation. In Fig. 3 we show the derived histograms for the observed intensities at 1600 Å, in the Ca II K line and at 3.5 mm and their log-normal fits with solid and dotted curves respectively.

A log-normal with an offset provides a good fit to the observed Ca II K line intensity distribution, although the observed tail enhancement is slightly higher than that of the fitted log-normal (see central panel in Fig. 3). For the 1600 Å intensities the quality of the fit diminishes at low and high flux values and the departure from a log-normal form increases. Finally, due to a substantially higher noise level in the millimeter brightness data (and the smaller number of resolution elements available for the histogram) it is difficult to evaluate the quality of the log-normal fit for this dataset. On the whole, a tendency for bigger departures from a log-normal can be observed when spatial resolution is decreased. However, we cannot rule out the possibility that we are seeing the effects of different heating mechanisms in cell interiors and network lanes being manifested in the intensity distributions.

4.3 Relation between chromospheric emission and photospheric magnetic field

In order to study the relationship between the intensity of chromospheric bright features and the intensity of the associated magnetic elements, we computed scatter plots for the pairs of images. Firstly, we considered the pointwise (pixel-to-pixel) correlation globally in the field of view without regard to the location of the points. In Fig. 4 we show the resulting cross-correlation statistics of the brightness features in the time-averaged calcium image and the photospheric longitudinal magnetogram. The pixel intensity correlation is plotted in the main frame of the figure, with histograms of the calcium intensity in 4 subranges of the magnetic flux density superposed in the upper frame and of the magnetic field in 4 subranges of the calcium intensity to the right. We employed averaging over time to reduce the noise level in the scatter plots.

We searched for a quantitative relation between the quiet-Sun mean magnetic flux density (its absolute value) per pixel of 2 $^{\prime \prime }$ and Ca II K-line intensity, looking for the best least-squares fit among functions of 2 types: linear (i.e. a power law with unit exponent, Eq. (1), following Skumanich et al. 1975; Nindos & Zirin 1998) and a ``generalized'' power law (Eq. (2), following Schrijver et al. 1989)

$\begin{displaymath} I=I_{0}+a\cdot\vert B\vert \end{displaymath}$

(1)

$\begin{displaymath} I=I_{0}+a\cdot\vert B\vert^{b}. \end{displaymath}$

(2)

The item I₀ in Eqs. (1) and (2) denotes ``zero'' or ``basal'' flux, introduced by Schrijver (1987). For comparison with the results of Schrijver et al. (1989) and of others, who obtained a power law exponent of about 0.6 for active and quiet regions, we also calculated the best fit with the power-law exponent, b, fixed at 0.6. Fits to the data points and to binned values (averaged over all pixels within a narrow range of magnetic flux values) points (see central panel in Fig. 4) gave very similar results. Only data points with an absolute value of the magnetic flux exceeding the $1\sigma$ -noise level were considered for fitting.

In the same manner we studied the relationship between the observed UV intensity at 1600 Å and absolute magnetic flux density per 2 $^{\prime \prime }$ aperture, which is depicted in Fig. 5, and between intensity at 3.5 mm and absolute magnetic flux density per 12 $^{\prime \prime }$ aperture, plotted in Fig. 6. The decrease in range of $\langle B\rangle$ is due to the lower spatial resolution of mm data. In Table 2 we list the results of the function fitting to the data points for all 3 relationships investigated, and in particular we compare $\chi ^2$ values for 3 different fitting functions obtained for Poisson weighting and list the power law exponents obtained.

Table 2: Least-squares deviation, $\chi ^2$ , of the best fits to the relationships between the photospheric magnetic field and chromospheric emissions.

As seen from the scatter plots in Figs. 4-6 all three quantities, Ca II K-line, UV at 1600 Å and 3.5 mm emission, show a prominent non-linear dependence on photospheric magnetogram signal. This conclusion is confirmed by the best-fit curves plotted in Figs. 4-6 and by the $\chi ^2$ values listed in Table 2, which reach the smallest values for the fit in the form of a power law. The best-fit value of the power-law exponent is 0.31 for the relationship between the calcium intensity and the magnetic flux density, which lies between the high value of $0.6 \pm 0.1$ and 0.66 found by Schrijver et al. (1989) and Ortiz & Rast (2005) and the lower value of 0.2 obtained by Rezaei et al. (2007). For 1600 Å intensity vs. magnetic flux we obtain an exponent of 0.36. These results do not change if we use, e.g., 10-min or 30-min averages instead of the 3.5 h average used above. However, the scatter of the points at a given $\langle B\rangle$ decreases significantly with increasing averaging.

The relationships and density distributions that we determine nicely demonstrate that most of the data points in the quiet-Sun region are characterized by low magnetic flux and low chromospheric emission. In other words, the majority of data points lies in the lower left quarter of the scatter plot and ``anchors'' the relation. There are too few data points with high chromospheric emission and enhanced magnetic flux (greater than 100 G) to very reliably determine the form of the relation (see Figs. 4 and 5). The rather small $1\sigma$ error bars of the fitted exponents (last column of Table 2) are the formal errors returned by the fitting procedure and appear rather optimistic to us.

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig4.eps} \end{figure}$

Figure 4:

The Ca II K-line intensity vs. the absolute value of the magnetic flux density for a 2 $^{\prime \prime }$ pixel size. The images are averaged in time over 3.5 h. The vertical line at 1.5 G in the central panel represents the 1 $\sigma$ noise limit of the magnetogram signal. The fit results are represented by a solid curve for a power-law fit with free exponent, dotted curve for a power-law fit with the exponent fixed at 0.6 and dashed for a linear fit. The light grey solid curve outlines the Ca II K intensity binned in 70 intervals containing an equal number of points. Histograms on the left show the distribution of magnetic field strength in 4 subranges of the Ca II K-line flux. Histograms on top of the central panel depict the distribution of calcium intensity in 4 subranges of the magnetic flux. For each histogram the corresponding range of values considered is marked in the main figure: by horizontal solid lines for magnetic flux distributions and by vertical dotted lines for the Ca II K-line flux histograms. The numbers of counts, n, represented in the histograms are indicated.

Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig5.eps} \end{figure}$	Figure 5: The same as Fig. 4 for the TRACE 1600 Å flux at the 4 $^{\prime \prime }$ resolution of MDI.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig6.eps} \end{figure}$	Figure 6: The same as Fig. 4 for the brightness temperature at 3.5 mm at the BIMA resolution of 12 $^{\prime \prime }$ .
Open with DEXTER

Note that fitting of the data directly with a power law containing a zero flux item I₀, corresponding to emission from locations of zero magnetic flux (non-magnetic component) is similar to determining the zero point of chromospheric emission using the algorithm applied by Schrijver et al. (1989), according to which a range of test values of I₀ is subtracted from the observed flux I until the mean relationship $\Delta I=I-I_{0}=a\cdot\vert B\vert^{b}$ reaches its highest correlation by minimizing the perpendicular offsets between the excess flux and the fit. We have tried fitted the data using both algorithms and obtained similar zero flux values and power law exponents. To demonstrate the success of the algorithm, introduced by Schrijver et al. (1989), applied to the data analyzed here, we plot in Fig. 7 the excess Ca II K-line and 1600 Å fluxes after subtraction of the derived basal flux (listed in the Y-axis captions) and the corresponding power-law curves. These fits yield zero-flux values I₀ and power law exponents b very similar to those derived when fitting the observed fluxes directly with a function of the form $I=I_{0}+a\cdot\vert B\vert^{b}$ (listed in Table 2).

The plot of millimeter brightness vs. magnetic field strength displays a considerable scatter about the mean relation, which may have different causes (see Fig. 6). Pixels in the lower left corner with very low mm brightness can result from the underestimation of the mm flux due to the high noise in the snapshot images (White et al. 2006). Some of the peculiar pixels with intense mm brightness (in the upper left corner) are located above localized (small-scale) photospheric magnetic elements and near polarity changes. Therefore the corresponding magnetic flux almost vanishes when degrading the magnetogram to the BIMA resolution. Again, a power law gives a far better representation of the data than the linear curve. In this case, a rather low exponent of 0.20 is obtained.

4.4 Magnetogram signal thresholding experiment

In Figs. 4-6 the brightness shows signs of increasing more rapidly for smaller fields with $B \leq 30$ G. This may be saying that the chromospheric emission from weak-field regions (internetwork) has a different source than from stronger network fields. To study how the correlation depends on the magnetogram signal we have performed a thresholding experiment. We have successively fitted the relations between the chromospheric radiation and photospheric magnetic flux exceeding a number of threshold values (from 0 to 35 Gauss for correlation at the resolution of the photospheric magnetogram and from 0 to 20Gauss for the resolution of the mm images). In Figs. 8 and 9 we compare the resuting $\chi ^2$ values for linear and power law fits as a function of the B threshold value, plotted with triangle and diamond symbols, respectively. We also show the dependence of the fitted power-law exponent on the threshold value.

The power-law exponent of the fit to the calcium intensity grows with the imposed B threshold (see Fig. 8). The value of the power-law exponent of $\simeq$ 0.5 is reached both when we discard pixels with weak fields and consider only those pixels with magnetic flux exceeding $\simeq$ 20 G, and when we include all pixels in the fit (including those dominated by noise). The dependence of the power-law index on B threshold for the intensity at 1600 Å shows a different behaviour. It increases until it reaches a value of about 0.6. For magnetic flux density exceeding 13 G it starts to decrease rapidly for higher thresholds (Fig. 9b). The scatter of the points is so large that for these data it is not possible to clearly distinguish between linear and power-law fits. The sensitivity of the power law parameters to the B threshold is due to the small number of points at large $\langle B\rangle$ (see Fig. 5), which is due to the fact that the observations refer to the quiet Sun.

The scatter in the intensity at 3.5 mm is so large that its relationship with the magnetic flux density can be equally well fit by a linear or a power-law function. Also, the $\chi ^2$ values of the fits are large. However, according to the thresholding experiment for the correlation between the mm intensity and the magnetic flux (not plotted), a power law adequately fits the data for magnetic fields stronger than 3 G ( $\sim$ $1\sigma$ -noise level) and weaker than 15 G. For weak fields, the large scatter affects significantly the quality of the fit, while for fields stronger than 15 G there are insufficient data pixels for confident power-law fitting.

4.5 Discrimination between IN and NW emission. Separate flux analysis

Next we study the relations between the chromospheric emission and the magnetic flux separately for the areas representing cell interiors or internetwork (IN) and chromospheric network (NW). In other words, we tried to separate magnetically weak-field (IN locations) and strong-field (NW locations) components of the emission. To discriminate between IN and NW locations we employed a brightness threshold technique (see, e.g. Krijger et al. 2001). To this end we fitted the Ca II K-line intensity histogram constructed for the time-averaged intensity map by a double-Gaussian function, assuming that the intensity histogram is dominated by two main populations representing the IN and NW intensities (see Fig. 10). The resulting maxima of the single-Gaussian components were used as intensity thresholds to define respectively internetwork and network areas on the mean map. The resulting IN (black) and NW (white) binary masks are shown in the bottom panel of Fig. 10. The points belonging to neither of these categories are indicated by an intermediate shading.

We apply these binary masks to study the relationship between the photospheric magnetic field and IN/NW fluxes, respectively (see Figs. 11-13). Following the approach outlined in Sect. 4.3 we fitted the scatter plots with linear and power-law functions. For the areas selected to represent the network a power law provides the best fit to the data. In Table 3 we list the exponents from the best-fit power laws for the images at the resolution of the MDI magnetograms (4 $^{\prime \prime }$ ) and of the BIMA images (12 $^{\prime \prime }$ ). Below we discuss the results obtained for the 3.5 h image averages, but for comparison we list in Table 3 also those for the 0.5 h time-averages. For the calcium NW intensity, averaged in time over 3.5 h, the best-fit power-law exponent is 0.6, which is consistent with the value derived by Schrijver et al. (1989) for the Ca II K-line flux in an active region and by Harvey & White (1999) for the enhanced network. We note a big difference from the value we derived with no image segmentation (0.6 vs. 0.31, see Table 2), which means a stronger dependence of the network calcium intensity on the magnetic flux. At a resolution of 12 $^{\prime \prime }$ the best fit for the NW Ca II K-line flux is also provided by a power law. This time the power law exponent is 0.54, which is also in agreement with the results of Schrijver et al. (1989), who state that the mean dependence of the Ca II K-line excess flux on the magnetic flux density is more or less scale independent. Analysis of the network emission at 1600 Å gives similar results. The power-law exponent in the relationship between the NW intensity at 1600 Å and the magnetic flux density is $\simeq$ 0.5 at 4 $^{\prime \prime }$ resolution and 0.66 at 12 $^{\prime \prime }$ resolution (see Table 3). Finally, millimeter emission from the network regions as a function of the absolute value of the magnetic field is also best described by a power law (among the considered functions, see Fig. 13). In this case, however, exponents larger than unity are obtained and we regard this result with caution and do not include it in Table 3.

$\begin{figure} \par\includegraphics[width=7cm,clip]{1133fig7.eps} \end{figure}$	Figure 7: Log-log scatter plots for a) the Ca II K-line excess mean intensity (after the subtraction of the zero flux) and b) TRACE 1600 Å excess mean intensity vs. the absolute value of the magnetic flux density (for 2 $^{\prime \prime }$ pixel size). The solid lines represent the least-squares power-law fits to the data.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fig8.eps} \end{figure}$	Figure 8: Thresholding experiment for the CaII K-line flux vs. absolute value of the magnetic field: a) $\chi ^2$ and b) power law exponent as a function of the imposed B threshold. The vertical line represents the $1\sigma$ -noise level of the magnetogram signal.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fig9.eps} \end{figure}$	Figure 9: The same as in Fig. 7 for the TRACE 1600 Å flux.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{1133fi10.eps} \end{figure}$

Figure 10:

IN/NW definition. Upper panel: CaII K-line mean intensity image. Central panel: mean intensity histogram (thick solid), single-Gaussian profiles (dotted, dashed) from a double-Gaussian fit to the data points with vertical lines of the same type marking the location of the Gaussian maxima. Bottom panel: masks used for the definition of the internetwork (black) and network (white) areas.

Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi11.eps} \end{figure}$	Figure 11: Comparison of IN and NW emission averaged over 0.5 h: histograms of a) IN and c) NW magnetogram signal, b, d) Ca II K-line flux vs. absolute value of the IN and NW magnetic field, respectively. The solid vertical lines represent $1\sigma$ -noise of the magnetogram signal.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi12.eps} \end{figure}$	Figure 12: The same as in Fig. 11 for 1600 Å flux.
Open with DEXTER

The fact that chromospheric emission (be it from Ca II K, the 1600 Å range or 3.5 mm continuum) from the internetwork regions shows almost no dependence on the magnetogram signal (see upper panels of Figs. 11-13) is not really surprising given that the magnetogram values in the internetwork do not exceed 10 Gauss, with mean of 1.5 Gauss and 1.0 Gauss (for 0.5 h and 3.5 h time averages, respectively). Therefore, even after creation of 0.5 h averaged images, which reduces significantly the noise in the magnetograms, only about 3% of IN points display Bvalues exceeding the 1 $\sigma$ noise level (see left panels of Figs. 11 and 12). Even after averaging over 3.5 h, only 20% of IN locations have B values greater than 1 $\sigma$ -noise. Data that have been so heavily averaged are only of limited value to study the internetwork as IN features are commonly characterized by much shorter time scales. We also studied the internetwork emission using a less strict criterion to discriminate between the cell interiors and the cell boundaries. Points with the calcium intensity not exceeding the value corresponding to the intercept point of the two-Gaussian fit to the intensity histogram were selected to represent the IN mask. However, the use of this mask does not influence the results of the fit. Again, no dependence of IN chromospheric emission on the magnetogram signal was found. Consequently, the high level of noise in the MDI magnetograms used here (compared to the range of the B values in the internetwork regions) hinders a reliable study of the relation of internetwork chromospheric emission on magnetic field.

4.6 Chromospheric flux-flux relations

We studied flux-flux relationships by constructing scatter plots for chromospheric intensities. In this analysis excess fluxes for K-line and 1600 Å emission were considered, employing the basal fluxes derived earlier (see Sect. 4.3 and Fig. 7). For the mm intensity we included the zero flux as a parameter in the fitting power-law function. Next, using the $\chi ^2$ criterion we searched for the best linear and power law fits to these relationships. The scatter plots of intensity at 1600 Å vs. Ca II K-line intensity as well as Ca II K-line and 1600 Å vs. 3.5 mm intensity are depicted in Fig. 14 together with the best power-law and linear fits. For all three dependencies the curves depicting both fits are hardly distinguishable and the fits are of similar quality (see Fig. 14).

For the relation between K-line intensity and intensity at 1600 Å the power-law exponent is $\simeq$ 1, which implies that the relationship between the excess fluxes is close to linear at a resolution of 4 $^{\prime \prime }$ . The relationship between mm and calcium, as well as between mm and UV emissions at the resolution of the mm images, are both best described by power laws with the best-fit exponents of $\simeq$ 0.7, but as mentioned this exponent is rather uncertain since a linear function also represents the data well.

5 Discussion and conclusions

We have considered chromospheric disk-center, quiet-Sun emission at different wavelengths and its dependence on photospheric magnetogram signal, including, for the first time, observations at 3.5 mm. Maps in Ca II K core intensity, the TRACE 1600 Å channel, BIMA 3.5 mm brightness temperature and (unsigned) MDI magnetograms reveal clearly the same pattern, although at different spatial resolutions. At the resolution of 12 $^{\prime \prime }$ millimeter brightness resembles quiet-Sun time-averaged emission from other chromospheric heights, and demonstrates a dependence on the underlying magnetic field similar to that of the other chromospheric diagnostics.

The tightest relation between the chromospheric emission and photospheric magnetic field is displayed by the Ca II K line. At all wavelengths a power law gives a lower $\chi ^2$ than a linear fit, although for the 1600 Å radiation the difference is marginal. For Ca II K this result supports the conclusion reached by Schrijver et al. (1989), but based on active region data, and by Harvey & White (1999) for both active and quiet-Sun magnetic structures. For Ca II K Skumanich et al. (1975) and Nindos & Zirin (1998) found a linear dependence to be adequate. However, the linear dependencies were obtained after excluding weak fields (weaker than 25 G and 20 G, respectively) and for a magnetogram signal not exceeding 120 G and 50 G, respectively. In our study we included both weak fields exceeding $1\sigma$ -noise level of the magnetograms (1.5 or 4 G depending on the amount of averaging), and the highest values reached in the quiet-Sun data (about 230 G at MDI's spatial resolution). This suggests that the non-linearity of the relation found in this work is influenced mostly by weak chromospheric emission that reveals a strong dependence on magnetic fields. For instance, if we set a Bthreshold of 20 G we cannot distinguish between the quality of the linear and power-law fits for all chromospheric emissions analyzed here. Our conclusions agree with those presented by Rezaei et al. (2007), who found from the POLIS measurements at 1 $^{\prime \prime }$ resolution a clear non-linear increase of the calcium core flux with magnetic flux for values $B \leq 100$ G and a slow increase for higher values. They also demonstrated that the power-law exponent depends strongly on the value of the lower threshold.

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi13.eps} \end{figure}$	Figure 13: The same as in Fig. 11 for 3.5 mm brightness.
Open with DEXTER

Table 3: Dependence of the network emission on the magnetic flux: exponents of the power-law fits calculated for the images at 4 $^{\prime \prime }$ and 12 $^{\prime \prime }$ resolution, averaged over 3.5 h and 0.5 h

$\begin{figure} \par\includegraphics[width=8cm,clip]{1133fi14.eps} \end{figure}$	Figure 14: Scatter plots of chromospheric fluxes and their power-law fits (plotted as solid lines). For comparison we also plot linear fits as dotted lines. a) 1600 Å excess flux vs. CaII K-line excess flux, b) CaII K-line excess flux vs. 3.5 mm flux, and c) 1600 Å excess flux vs. 3.5 mm flux.
Open with DEXTER

The difference between the maximum magnetogram signal reached in our data and that in the data of Skumanich et al. (1975) and Nindos & Zirin (1998) may indicate either that their quiet-Sun regions are even quieter than the one we analyzed, or it may reflect differences in spatial resolution. One more difference between our analysis and the others is that we consider temporally averaged data rather than snapshot images. By using time-averaging we reduce significantly the scatter in the relationship and the noise in the magnetograms, which lead to more reliable power-law fits. By employing snapshot images we get more points in the scatter plots but due to higher magnetogram noise level the power-law exponent is even lower (and less reliable) than for the time-averaged images. One should also note the difference in the analysis techniques between this work and the others applied for building the scatter plots. In this work we employed pixel-to-pixel comparison of the images. However, the results of the fits are similar if we consider the binned chromospheric data averaged within a narrow range of magnetogram values. On the whole, from the data analyzed here we are able to confidently determine non-linear behaviour of 3 chromospheric magnetic-intensity relationships.

The exact power law exponents of the relations between the calcium core emission and the photospheric magnetic field differs from that found by Schrijver et al. (1989) (0.3 vs. 0.6) . This probably has to do with the smaller $\langle B\rangle$ range available in the quiet Sun, although it cannot be ruled out that the Ca II K intensity does not increase so rapidly in the quiet Sun as in active regions (see Solanki et al. 1991). To compare these explanations, we studied the dependence of the calcium emission on the magnetic flux in an active region close to disk center observed by the BBSO and MDI on 11.03.2004. The exponent obtained from a power-law fit for the AR emission is surprisingly low and similar to the QS values, being in the range 0.28-0.32, with the exact value depending somewhat on the criterion chosen to identify the AR pixels on the map. The use of a pixel size and a noise threshold similar to that of Schrijver et al. (1989) does not increase the value of the power-law exponent and it still differs from that of Schrijver et al. (1989) and Harvey & White (1999). The difference may have to do with the spectral range covered by the different observations.

The reduction in the power-law exponent as compared to the value derived by Schrijver et al. (1989) may be to a large extent the result of the inclusion of weak magnetic flux regions, which are systematically characterized by magnetogram field strengths that are smaller than the true values due to the presence of weak neutral lines with null line-of-sight component. Unfortunately, we cannot exclude the influence of these horizontal magnetic fields, which are missed by MDI observations. Such fields, partly seen in the internetwork regions by Hinode (e.g. Lites et al. 2007), are very likely small loops (Martínez González et al. 2007; Centeno et al. 2007) and may be due to a local dynamo (Vögler & Schüssler 2007; Schüssler & Vögler 2008). It is unclear if such low-lying loops really influence the structure of the higher-lying chromosphere. However, if they do contribute to the heating of those layers then this could explain the high chromospheric emission from many spatial locations associated with small magnetic fluxes in the MDI data (Fig. 7). Unresolved opposite magnetic polarities within the same individual MDI pixels have a similar effect. Both these effects together could explain the result that the power law exponent is lower when very quiet (low flux) pixels are included. Studies at higher spatial resolution and sensitivity are needed to test these hypotheses.

On the whole, chromospheric emission displays a rather different dependence on the network and internetwork magnetic field. The power-law exponents in the relation between the Ca II K-line intensity and the network magnetic flux are found to be similar to those obtained by Schrijver et al. (1989) for an active region and by Harvey & White (1999) for the quiet Sun network. The same conclusion holds for the relation between the UV emission at 1600 Å and magnetic flux in the network regions of the quiet Sun. For chromospheric fluxes at a resolution of 4 $^{\prime \prime }$ it was found that emission from the network entirely defines the trend for magnetic flux densities stronger than $\simeq$ 20 G. Our results for the calcium core emission remarkably confirm those of Rezaei et al. (2007), who obtained for the ensemble of quiet-Sun points a low value for the power-law exponent of $\simeq$ 0.2 (for snapshot images), while for the network emission from regions with $B \geq 20$ G the exponent reaches the value of 0.51 (and 0.45 for $B \geq 10$ G).

A considerable scatter about the mean relation between the millimeter flux at 3.5 mm and the magnetic flux density per 12 $^{\prime \prime }$ aperture makes a confident study of the mean trend difficult. Although the data strongly suggests that the dependence of the 3.5 mm brightness on magnetic field is non-linear and best described by a power law (among the functional forms considered here), but the sizeable scatter does not allow the exponents to be determined reliably. The best fit exponent depends strongly on the range of $\langle B\rangle$ considered.

In the internetwork regions almost no dependence of the Ca II K-line, UV at 1600 Å and 3.5 mm intensity on the magnetogram signal was found. Unfortunately, due to the very low B values in the internetwork, only a few percent of IN structures are associated with magnetogram signal exceeding the noise level. However, it should be noted that analysis of the cell interiors and their relation to the underlying magnetic field carried out in Rezaei et al. (2007) for Ca II H-line with lower noise and higher resolution has revealed similar results. This supports the idea that the role of magnetic field is negligible for bright internetwork grains (e.g. acoustic heating).

Correlation analysis performed for the quiet-Sun chromospheric emissions surprisingly revealed a linear relation between the Ca II K-line intensity and UV brightness at 1600 Å. According to Rutten et al. (1991), who claimed that the relations between the fluxes originating in the same atmospheric regimes are commonly close to linear, these chromospheric emissions are both generated in the chromospheric temperature regime from chromospheric ranges of heights. However, solar models place UV emission at 1600 Å in the temperature minimum region, while calcium emission is believed to be generated from heights more typical of the lower chromosphere. The power-law relations between calcium flux and 3.5 mm flux, as well as between 3.5 mm brightness and 1600 Å flux, suggest different temperatures of formation for these pairs of emissions, but as the power-law exponent do not differ much from unity we may assume that these emissions are still close in the heights of formation. However, the flux correlation analysis for the considered emissions and its conclusions should be treated with caution. Due to the very different temperature sensitivity of, on the one hand, UV and calcium intensity, and, on the other hand, 3.5 mm brightness, they represent different contributions from small (unresolved) hot magnetic features and cool weak-field regions within the same resolution element. In other words, in an inhomogeneous atmosphere the UV samples mainly the hot features, while the mm is composed of radiation from both. This could explain some of the difference in the behaviour of 1600 Å and Ca II K excess emission compared to mm emission, and, in particular, the large scatter in the flux-flux plots (Fig. 14).

Summarizing, clear spatial correlations found between photospheric magnetograms, the Ca II K-line, UV intensity at 1600 Å and 3.5 mm emission indicate that heating in the quiet-Sun lower and middle chromosphere maps out the underlying photospheric magnetic field rather well. Our results imply that at the chromospheric heights covered by the wavelengths investigated here we deal with the same heating mechanism. However, any mechanism that explains chromospheric heating must explain the relationship between chromospheric intensity excess and magnetic fields. In particular, it should validate both the dominating role of magnetic field in the chromospheric emission of the network and the absence of correlation between the internetwork emission and magnetic flux.

Of particular interest is the possibility of studying the middle chromosphere at the heights where mm emission originates, but because of very limited spatial resolution and insufficient sensitivity a detailed study like that cannot be conducted at present. In general, present data on both chromospheric emission and magnetic field are not sufficient to establish physical mechanisms that are acting at chromospheric heights leading to the observed brightness structures. In this respect, an extraordinarily powerful tool to study the thermal structure of the solar atmosphere from the temperature minimum region to the middle chromosphere will be provided by the Combined Array for Research in Millimeter-wave Astronomy (CARMA) and particularly by Atacama Large Millimeter Array (ALMA) as was demonstrated in Loukitcheva et al. (2008).

Acknowledgements

We thank H. Wang and V. Yurchyshyn for providing us with the data from the BBSO. We gratefully acknowledge the open-data policies of the NASA satellite TRACE and the ESA/NASA satellite SOHO and their instrument teams. We thank the referee, Charlie Lindsey, for his considerate and helpful comments. Millimeter-wavelength astronomy at the University of Maryland is supported by NSF grant AST-0540450. Solar research at the University of Maryland is supported by NASA grants NNX06-AC18G and NNX08-AQ48G. M. Loukitcheva acknowledges support from the Grant MK-1853.2007.2 of the Grant Council of the President of the Russian Federation.

References

Brandt, P. N., Rutten, R. J., Shine, R. A., & Trujillobueno, J. 1992, in Cool Stars, Stellar Systems, and the Sun, ed. M. S. Giampapa, & J. A. Bookbinder, ASP Conf. Ser., 26, 161 (In the text)
Centeno, R., Socas-Navarro, H., Lites, B., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef]
Denker, C., Yang, G., & Wang, H. 2001, Sol. Phys., 202, 63 [NASA ADS] [CrossRef] (In the text)
Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] (In the text)
Fontenla, J. M., Curdt, W., Avrett, E. H., & Harder, J. 2007, A&A, 468, 695 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Fossum, A., & Carlsson, M. 2005, ApJ, 625, 556 [NASA ADS] [CrossRef] (In the text)
Handy, B. N., Bruner, M. E., Tarbell, T. D., et al. 1998, Sol. Phys., 183, 29 [NASA ADS] [CrossRef]
Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] (In the text)
Harvey, K. L., & White, O. R. 1999, ApJ, 515, 812 [NASA ADS] [CrossRef]
Krijger, J. M., Rutten, R. J., Lites, B. W., et al. 2001, A&A, 379, 1052 [NASA ADS] [CrossRef] [EDP Sciences]
Leighton, R. B. 1959, ApJ, 130, 366 [NASA ADS] [CrossRef]
Lindsey, C., Kopp, G., Clark, T. A., & Watt, G. 1995, ApJ, 453, 511 [NASA ADS] [CrossRef] (In the text)
Lindsey, C. A., & Jefferies, J. T. 1991, ApJ, 383, 443 [NASA ADS] [CrossRef] (In the text)
Lites, B., Socas-Navarro, H., Kubo, M., et al. 2007, PASJ, 59, 571 (In the text)
Lites, B. W., Rutten, R. J., & Berger, T. E. 1999, ApJ, 517, 1013 [NASA ADS] [CrossRef] (In the text)
Loukitcheva, M. A., Solanki, S. K., & White, S. 2008, Ap&SS, 313, 197 [NASA ADS] [CrossRef] (In the text)
Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Solanki, S. K. 2007, A&A, 469, L39 [NASA ADS] [CrossRef] [EDP Sciences]
Nindos, A., & Zirin, H. 1998, Sol. Phys., 179, 253 [NASA ADS] [CrossRef]
Ortiz, A., & Rast, M. 2005, Mem. Soc. Astron. Ita., 76, 1018 [NASA ADS]
Pauluhn, A., Solanki, S. K., Rüedi, I., Landi, E., & Schühle, U. 2000, A&A, 362, 737 [NASA ADS] (In the text)
Remling, B., Deubner, F.-L., & Steffens, S. 1996, A&A, 316, 196 [NASA ADS] (In the text)
Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., & Schmidt, W. 2007, A&A, 466, 1131 [NASA ADS] [CrossRef] [EDP Sciences]
Rutten, R. J., & Uitenbroek, H. 1991, Sol. Phys., 134, 15 [NASA ADS] [CrossRef]
Rutten, R. G. M., Schrijver, C. J., Lemmens, A. F. P., & Zwaan, C. 1991, A&A, 252, 203 [NASA ADS] (In the text)
Rutten, R. J., de Pontieu, B., & Lites, B. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, ed. T. R. Rimmele, K. S. Balasubramaniam, & R. R. Radick, ASP Conf. Ser., 183, 383 (In the text)
Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [NASA ADS] [CrossRef] (In the text)
Schrijver, C. J. 1987, A&A, 172, 111 [NASA ADS]
Schrijver, C. J. 1992, A&A, 258, 507 [NASA ADS]
Schrijver, C. J., Cote, J., Zwaan, C., & Saar, S. H. 1989, ApJ, 337, 964 [NASA ADS] [CrossRef]
Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences]
Sivaraman, K. R., & Livingston, W. C. 1982, Sol. Phys., 80, 227 [NASA ADS] [CrossRef]
Sivaraman, K. R., Gupta, S. S., Livingston, W. C., et al. 2000, A&A, 363, 279 [NASA ADS]
Skumanich, A., Smythe, C., & Frazier, E. N. 1975, ApJ, 200, 747 [NASA ADS] [CrossRef]
Solanki, S. K. 2004, in Multi-Wavelength Investigations of Solar Activity, ed. A. V. Stepanov, E. E. Benevolenskaya, & A. G. Kosovichev, IAU Symp., 223, 195 (In the text)
Solanki, S. K., Steiner, O., & Uitenbroeck, H. 1991, A&A, 250, 220 [NASA ADS] (In the text)
Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences]
White, S. M., Loukitcheva, M., & Solanki, S. K. 2006, A&A, 456, 697 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

Footnotes

... magnetograms: lev1.8 data.

All Tables

Table 1: Overview of data taken on May 18, 2004.

Table 2: Least-squares deviation, $\chi ^2$ , of the best fits to the relationships between the photospheric magnetic field and chromospheric emissions.

All Figures

$\begin{figure} \par\includegraphics[angle=90,width=12.5cm,clip]{1133fig1.eps} \end{figure}$	Figure 1: Portrait of the solar chromosphere averaged over 3.5 h at the center of the Sun's disk at 4 different wavelengths on May 18, 2004. From top left to bottom right: MDI longitudinal photospheric magnetogram (resolution of 4 $^{\prime \prime }$ ), TRACE 1600 Å image (resolution of 1 $^{\prime \prime }$ ), Ca II K-line center image from BBSO (resolution of 2-4 $^{\prime \prime }$ ) and BIMA image at 3.5 mm (resolution of 12 $^{\prime \prime }$ ). The images are created by averaging over the 3.5 h period of the BIMA observation. The details of the data units are given in Sect. 2. Dashed circles mark the 96 $^{\prime \prime }$ radius BIMA FOV where we regard fluxes to be reliable. X and Y axes are in arcsec from the disk center, which is located at (0,0).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=12.5cm,clip]{1133fig2.eps} \end{figure}$	Figure 2: The same as Fig. 1 plotted at the BIMA resolution of 12 $^{\prime \prime }$ . In the top left panel the absolute value of the MDI magnetogram is depicted. Overlays of contours of 3.5 mm emission at (30, 50, 70, 90, 95, 98)% of maximum brightness are overplotted in white.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{1133fig3.eps} \end{figure}$	Figure 3: Intensity distribution histograms over the 2-D quiet-Sun region near the disk center obtained, from top to bottom, in the TRACE 1600 Å channel, the Ca II K line and at 3.5 mm. In all three panels dotted curves depict log-normal fits.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig4.eps} \end{figure}$	Figure 4: The Ca II K-line intensity vs. the absolute value of the magnetic flux density for a 2 $^{\prime \prime }$ pixel size. The images are averaged in time over 3.5 h. The vertical line at 1.5 G in the central panel represents the 1 $\sigma$ noise limit of the magnetogram signal. The fit results are represented by a solid curve for a power-law fit with free exponent, dotted curve for a power-law fit with the exponent fixed at 0.6 and dashed for a linear fit. The light grey solid curve outlines the Ca II K intensity binned in 70 intervals containing an equal number of points. Histograms on the left show the distribution of magnetic field strength in 4 subranges of the Ca II K-line flux. Histograms on top of the central panel depict the distribution of calcium intensity in 4 subranges of the magnetic flux. For each histogram the corresponding range of values considered is marked in the main figure: by horizontal solid lines for magnetic flux distributions and by vertical dotted lines for the Ca II K-line flux histograms. The numbers of counts, n, represented in the histograms are indicated.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig5.eps} \end{figure}$	Figure 5: The same as Fig. 4 for the TRACE 1600 Å flux at the 4 $^{\prime \prime }$ resolution of MDI.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{1133fig6.eps} \end{figure}$	Figure 6: The same as Fig. 4 for the brightness temperature at 3.5 mm at the BIMA resolution of 12 $^{\prime \prime }$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7cm,clip]{1133fig7.eps} \end{figure}$	Figure 7: Log-log scatter plots for a) the Ca II K-line excess mean intensity (after the subtraction of the zero flux) and b) TRACE 1600 Å excess mean intensity vs. the absolute value of the magnetic flux density (for 2 $^{\prime \prime }$ pixel size). The solid lines represent the least-squares power-law fits to the data.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fig8.eps} \end{figure}$	Figure 8: Thresholding experiment for the CaII K-line flux vs. absolute value of the magnetic field: a) $\chi ^2$ and b) power law exponent as a function of the imposed B threshold. The vertical line represents the $1\sigma$ -noise level of the magnetogram signal.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fig9.eps} \end{figure}$	Figure 9: The same as in Fig. 7 for the TRACE 1600 Å flux.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{1133fi10.eps} \end{figure}$	Figure 10: IN/NW definition. Upper panel: CaII K-line mean intensity image. Central panel: mean intensity histogram (thick solid), single-Gaussian profiles (dotted, dashed) from a double-Gaussian fit to the data points with vertical lines of the same type marking the location of the Gaussian maxima. Bottom panel: masks used for the definition of the internetwork (black) and network (white) areas.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi11.eps} \end{figure}$	Figure 11: Comparison of IN and NW emission averaged over 0.5 h: histograms of a) IN and c) NW magnetogram signal, b, d) Ca II K-line flux vs. absolute value of the IN and NW magnetic field, respectively. The solid vertical lines represent $1\sigma$ -noise of the magnetogram signal.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi12.eps} \end{figure}$	Figure 12: The same as in Fig. 11 for 1600 Å flux.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{1133fi13.eps} \end{figure}$	Figure 13: The same as in Fig. 11 for 3.5 mm brightness.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{1133fi14.eps} \end{figure}$	Figure 14: Scatter plots of chromospheric fluxes and their power-law fits (plotted as solid lines). For comparison we also plot linear fits as dotted lines. a) 1600 Å excess flux vs. CaII K-line excess flux, b) CaII K-line excess flux vs. 3.5 mm flux, and c) 1600 Å excess flux vs. 3.5 mm flux.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.