| Issue |
A&A
Volume 497, Number 1, April I 2009
|
|
|---|---|---|
| Page(s) | 1 - 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200809604 | |
| Published online | 09 February 2009 | |
Linear dynamics of weakly viscous accretion disks: a disk analog of Tollmien-Schlichting waves
O. M. Umurhan1,2,3 - G. Shaviv4,5
1 - Astronomy Unit, School of Mathematical Sciences, Queen Mary
University of London, London E1 4NS, UK
2 -
Department of Geophysics and Space Sciences, Tel-Aviv University,
Tel-Aviv, Israel
3 -
Astronomy Department,
City College of San Francisco, San Francisco, CA 94112, USA
4 -
Department of Physics, Technion-Israel Institute
of
Technology, 32 000 Haifa, Israel
5 -
Institute of Theoretical Astrophysics,
University of Heidelberg, 69120 Heidelberg, Germany
Received 19 February 2008 / Accepted 14 November 2008
Abstract
This paper discusses new perspectives and approaches to
the problem of disk dynamics
where, in this study, we focus on the
effects of the viscous instabilities influenced by
boundary effects.
The Boussinesq approximation of the viscous large shearing box
equations is analyzed in which the azimuthal length scale of the
disturbance is much larger than the radial and vertical scales.
We examine the stability of
a non-axisymmetric potential vorticity mode, i.e. a PV-anomaly.
in a configuration in which buoyant convection
and the strato-rotational instability do not to operate.
We consider a series of boundary conditions that show
the PV-anomaly to be unstable both on finite and semi-infinite radial domains.
We find these conditions lead to an instability that is the disk analog of
Tollmien-Schlichting waves. When the viscosity is weak, evidence of the instability
is most pronounced by the emergence of a vortex sheet at the critical layer
located away from the boundary where the instability is generated.
For some boundary conditions, a necessary criterion
for the onset of instability for vertical wavelengths
that are a sizable fraction of the layer's thickness and
when the viscosity is low is that
the appropriate Froude number of the flow be greater than one.
This instability persists if more realistic boundary conditions
are applied, although the criterion on the Froude number
is more complicated. The unstable waves studied here share qualitative
features to the instability seen in rotating Blasius boundary layers.
The implications of these results are discussed. An overall new strategy
for exploring and interpreting disk instability mechanisms
is also suggested.
Key words: instabilities - hydrodynamics - waves - stars: planetary systems: protoplanetary disks
1 Introduction
The magneto-rotational instability (Balbus 2003, MRI hereinafter) is generally considered to be the leading candidate explaining the source of enhanced transport observed for disk systems. Three conditions are required for its operation: the concurrent presence of rotation and shear, a primordial (no matter how small) magnetic field, and sufficient ionization of the fluid so that the gas is in the MHD regime. Consequently, it is natural to ask the question: what happens in an accretion disk if one or more of these conditions are not satisfied?
Supposing that there are disks in which the MRI or any other MHD (dynamo) mechanism is either weakly operating or entirely absent: what else can drive activity, possibly even leading to turbulence? Attempts to answer this question include, but are not limited to, defects in the Keplerian profile (Li et al. 2000), baroclinic instabilities (Klahr & Bodenheimer 2003; Johnson & Gammie 2005; Petersen et al. 2007a,2007b), transient growth and sustained subcritical dynamics (Richard & Zahn 1999; Iounnou & Kakouris 2000, Chagelishvili et al. 2003; Tevzadze et al. 2003; Yecko 2004; Umurhan & Regev 2004; Umurhan et al. 2006; Mukhopadhyay et al. 2004; Barranco & Marcus 2005; Lesur & Longaretti 2005; Lithwick 2007; and see the experiments of Richard 2001; and Ji et al. 2006) and, unsteady wave dynamics like the Papalouizou-Pringle instability (Papalouizou & Pringle 1984), hereinafter ``PPI'', and the strato-rotational instability (Dubrulle et al. 2005; Shalybkov & Rüdiger 2005; Umurhan 2006; Brandenburg & Rüdiger 2006), hereinafter ``SRI''. The majority of these recent investigations (excepting Yecko 2004; Afshordi et al. 2005) have focused on strictly inviscid processes. Indeed, the classical approach to such questions is to investigate processes that might lead to turbulent transport by first establishing a mechanism of linear instability from the vantage point of purely inviscid (or nearly inviscid) flow.
Since astrophysical fluids have some effective viscosity - however weak it may be - we pose the question: could a weakly viscous flow in a sheared and rotating environment undergo an intrinsically viscous type of linear instability that nonlinearly saturates with significant amplitude? A few previous studies have addressed this question. Kato (1978) demonstrated that if a fluid's viscosity is a function of the state of the fluid then a disk can experience pulsational dynamics in a way similar in quality to stellar pulsation like that in the theory of Cepheid variables. Hereafter we shall refer to this effect as the viscous pulsational instability (VPI). Latter & Ogilvie (2006) reexamined the VPI by studying how even axisymmetric f-modes, in a shearing sheet environment, create fluctuating stresses that explicitly draw energy from the shear which leads to overstability. Kleiber & Glatzel (1999) have shown that accretion tori (in this case, ones which have a constant specific angular momentum distribution) can be linearly unstable above a minimum Reynolds number. Dubrulle et al. (2005) and Shalybkov & Rüdiger (2005) also report that the growth rate of the SRI may be, under certain conditions, enhanced by viscosity.
Before proceeding we present some remarks concerning the nature of the fluid state to be studied as well as a discussion about boundary conditions and a proposed alternative way to consider their uses.
1.1 Viscous considerations
The non-commutative nature of the Navier-Stokes equations
in the limit of
![]() with the Euler equations
is a long standing fact (see the discussion in Schlichting & Gersten 2001,
p. 96-8).
For instance, viscous stresses do not necessarily vanish on
the boundaries of a viscous flow when the viscosity limits to zero.
In turn this implies that one may not
properly take the Navier Stokes equations and naïvely substitute zero viscosity
to reach the inviscid limit (Lions 1993; Joseph 2003).
Aside from the generic appearance of boundary layers,
other effects can appear when a weak viscosity is
included into problems of study. For example,
in the nearly inviscid shallow-water theory
of strong shear flows (Balmforth 1999),
normal-modes can emerge out of a continuous spectrum
when viscosity is introduced into the dynamics.
with the Euler equations
is a long standing fact (see the discussion in Schlichting & Gersten 2001,
p. 96-8).
For instance, viscous stresses do not necessarily vanish on
the boundaries of a viscous flow when the viscosity limits to zero.
In turn this implies that one may not
properly take the Navier Stokes equations and naïvely substitute zero viscosity
to reach the inviscid limit (Lions 1993; Joseph 2003).
Aside from the generic appearance of boundary layers,
other effects can appear when a weak viscosity is
included into problems of study. For example,
in the nearly inviscid shallow-water theory
of strong shear flows (Balmforth 1999),
normal-modes can emerge out of a continuous spectrum
when viscosity is introduced into the dynamics.
Another example of the subtleties inherent in viscous flow is the instability associated Tollmien-Schlichting waves (see discussion of T-S waves in Schlichting & Gersten 2001; and Schmid & Henningson 2000) - which are traveling waves appearing in wall-bounded flows that neither grow nor decay in the inviscid limit and become unstable when viscosity is included in the analysis (examples include plane Pouiselle-flow and Blasius boundary layers). Similar to the process discussed by Balmforth (1999), the traveling mode becomes unstable through the interaction of an inviscid normal mode and a viscous normal mode - the latter of which exists only as a member of the continuous spectrum in the inviscid limit (Baines et al. 1996). Far from being considered mathematical oddities, T-S waves appear to play a prominent role in the transition to turbulence in boundary-layer flows (for a recent summary see Drazin 1984). A situation studied which closely resembles the condition of an astrophysical disk is the modal and non-modal response of a rotating Blasius boundary layer (Yecko & Rossi 2004) in which instability is promoted when the azimuthal scale of a disturbance is longer than its vertical scale.
In a general sense, because the governing
equations are of a higher order in the viscous case,
a new space of
possible solutions emerges which are either absent or inactive in the inviscid case.
Our main query is therefore: if rotationally supported flows are (linearly) well-behaved
in the exactly inviscid limit but the viscous flow shows some type of
dynamically significant behaviour - even as the inviscid
limit is approached - then might it be misleading to test
stability only of exactly (Re = ![]() )
inviscid flows? Perhaps the
subtle nature of disks is linked to this feature.
That which best summarizes this perspective is the quote attributed
to the atmospheric dynamicist Eady where he is purported to
have said,
``It is not the process of linearization that limits insight. It is the nature
of the state we choose to linearize about'',
(Bayley et al. 1988).
)
inviscid flows? Perhaps the
subtle nature of disks is linked to this feature.
That which best summarizes this perspective is the quote attributed
to the atmospheric dynamicist Eady where he is purported to
have said,
``It is not the process of linearization that limits insight. It is the nature
of the state we choose to linearize about'',
(Bayley et al. 1988).
To prospect for an instability mechanism that might lead to sustained unsteady behavior by assuming a turbulent viscosity model a priori might seem contradictory at first. But, given the difference in behavior known to exist (in other problems) between nearly inviscid and exactly inviscid models it is therefore mandatory to clarify these differences within the context of an astrophysical disk too. A conjecture that such an investigation could address is the following. It is reasonable to suppose that disks are continuously fed with a turbulent flow field either by in-fall or some mass transfer processes. Could this turbulent flow field undergo a secondary transition into another dynamical state (possibly turbulence of a different stripe) due to the turbulently enhanced viscosity? Suggestions which hark on these lines of thought are found in Doering et al. (2000), Kersalé et al. (2004) and more directly in terms of secondary transitions induced by Ekmann flow as suggested in Lesur & Longaretti (2005). Overstability driven by material fluctuations in the turbulent stresses (i.e. the VPI, Kato 1978; and Latter & Ogilvie 2006) are also candidates for such secondary transitions.
1.2 Interpreting boundary conditions and their effects on dynamics
Much attention has been devoted to evaluating processes which are intrinisic in some way to the fluid - meaning to say that it is assumed that it is more valuable to study those mechanical processes which are minimally sensitive to the boundary conditions imposed and maximally ``emerging'' out of something essential about the fluid and its basic state. The MRI is an example of this as well as other more basic fluid dynamical instabilities such as the Rayleigh-Taylor and Rayleigh-Benard instabilities. We wonder if this approach to the question of disk turbulence may be self-limiting given that many fluid instabilities which lead to some form of turbulence in terrestrial flows are driven in large part by the boundary conditions of the system (e.g. T-S waves and turbulent transition). An alternative way is to view boundary conditions as a filter for certain solutions or as a tool to classify solutions. Kersalé et al. (2004) adopt a similar philosophy by studying the linear response of an incompressible fluid in a Taylor-Couette type of cylindrical flow subject to a variety of boundary conditions. Of course, the Taylor-Couette setup and the boundary conditions they test are not what one would expect in a terrestrial apparatus or experiment, however, if taken as a metaphor for a disk environment then this sort of exploration allows one to test, evaluate, understand and eventually categorize the dynamical response of a fluid as a function of differing boundary conditions.
The inviscid PPI and SRI are examples of linear instabilities
which come about
due to the imposition of arguably artificial boundary conditions on
inner and outer walls of a model disk system.
On the other hand, these results may be intepreted in terms of the Hayashi-Young
criterion for wave instability which states that a physically separated
wave pair may promote linear instability if the waves
counterpropagate with respect to each other
with
nearly the same wavespeed and if the waves have an action-at-distance
effect upon each other![]() (Hayashi & Young 1987;
and see also Sakai 1989; Baines & Mitsudera 1994).
Indeed Goldreich et al. (1985)
(Hayashi & Young 1987;
and see also Sakai 1989; Baines & Mitsudera 1994).
Indeed Goldreich et al. (1985)![]() point out that the PPI may be viewed
as a process resulting from the interaction of a pair of
edgewaves mutually interacting with each other across
a wave-evanescent region
point out that the PPI may be viewed
as a process resulting from the interaction of a pair of
edgewaves mutually interacting with each other across
a wave-evanescent region![]() .
The SRI may also be similarly rationalized (Umurhan 2008).
.
The SRI may also be similarly rationalized (Umurhan 2008).
Thus although the counterpropagating edgewaves responsible for the PPI and SRI are understood to result from the use of unrealistic boundary conditions, it is certainly not ruled out that the general counterpropagating wave mechanism could be at work in real disks. The linear instability of disks with two or more (potential) vorticity defects (e.g. Li et al. 2000) could be interpreted as an instance of this process.
1.3 An overview of the findings in this study
From
a systematic asymptotic scaling analysis we derive in Sect. 2 and
Appendix A
the equations appropriate to a box section of a viscous shearing
accretion disk (assuming an ![]() viscosity formalism) by exploiting the smallness
of the parameter
viscosity formalism) by exploiting the smallness
of the parameter
![]() which assesses the ratio
of the soundspeed to the rotation speed measured
at some radial point of a circumstellar disk.
We refer to this model as the Viscous Large Shearing Box (VLSB)
and these equations have appeared before (cf. Latter & Ogilvie 2006).
We are reminded
that while the velocity fluctuations in the shearing box
are an order
which assesses the ratio
of the soundspeed to the rotation speed measured
at some radial point of a circumstellar disk.
We refer to this model as the Viscous Large Shearing Box (VLSB)
and these equations have appeared before (cf. Latter & Ogilvie 2006).
We are reminded
that while the velocity fluctuations in the shearing box
are an order
![]() smaller than
prevailing rotational (``Keplerian'') velocities,
the steady accretion velocities implied by
the alpha viscosity model are
an order
smaller than
prevailing rotational (``Keplerian'') velocities,
the steady accretion velocities implied by
the alpha viscosity model are
an order
![]() smaller than the same disk rotational velocity.
smaller than the same disk rotational velocity.
We consider the fate of a non-axisymmetric potential vorticity disturbance (or simply ``PV-anomaly'') subject to varying boundary conditions. Accordingly, in Sects. 3 and 4 the VLSB are analyzed in the limit where the perturbation's azimuthal length scale is asymptotically larger than its radial and vertical scales (i.e. the quasi-hydrostatic semigeostrophic limit, Umurhan 2006, QHSG for short). Additionally we assume that the vertical component of gravity and entropy gradient are constants.
In Sect. 4.1 we formulate energy integrals of this reduced system in order to better understand what can contribute to destabilizing the PV-anomaly . The energy budget is characterized by a Reynolds-Orr type of equation whose sources and sinks are given by the energy which the PV-anomaly can extract from the shear, receive from the boundaries or lose due to dissipation.
In the spirit of Kersalé et al. (2004) we analyze the response of the PV-anomaly subject to a controlled array of boundary conditions. In discussing boundary conditions we refer to the boundary closest to central object as starside as opposed to the side furthest away from the object to which refer to as farside. We consider the dynamics as occurring on both a semi-infinite domain (farside at infinity) and on a finite domain. Below we summarize the main findings. Note that we have made sure to consider boundary conditions which filter out the SRI or PPI instabilities.
In Sect. 4.2 an asymptotic analysis is done for the limit where the scaled turbulent viscosity
parameter (defined in the text as ![]() )
is small.
We find instability
if the Froude number of the flow exceeds 1 for modestly large
vertical wavenumber.
Additionally, the PV-anomoly interacts with a critical layer of the
flow
creating a potential vorticity sheet sheet
whose radial extent is
)
is small.
We find instability
if the Froude number of the flow exceeds 1 for modestly large
vertical wavenumber.
Additionally, the PV-anomoly interacts with a critical layer of the
flow
creating a potential vorticity sheet sheet
whose radial extent is
![]() the size of
the vertical extent of the disk.
This analysis illustrates how an inviscid edgewave phenomenon (due to
the no-normal flow starside boundary condition) becomes unstable
when viscosity is included.
Most importantly
is that the instability is driven in part by the injection of
energy through the boundary.
the size of
the vertical extent of the disk.
This analysis illustrates how an inviscid edgewave phenomenon (due to
the no-normal flow starside boundary condition) becomes unstable
when viscosity is included.
Most importantly
is that the instability is driven in part by the injection of
energy through the boundary.
We consider in Sect. 4.3 finite domain disturbances of the PV-anomaly and let the viscosity parameter be an order 1 quantity. The fourth order normal mode problem requires us to appeal to numerical computational methods for solutions. We impose on the farside boundary that both the disturbance pressures and PV-anomalies vanish. At the starside boundary we require that there be no-normal flow there (as above). The remaining starside condition takes on four possibilities: (a) the flow is rigidly coupled at the wall; (b) the perturbations are stress-free; (c) the PV-anomaly is zero; (d) the PV-anomaly gradient is zero. The first two of these conditions are physically realistic. The latter two offer a means to consider the the effect of energy injection (or lack thereof) through the boundaries and to compare with the analytical analysis. For rigid and stress-free boundary conditions we see clear indications of a Tollmien-Schlichting type of instability, similar to the instability of rotating Blasius boundary layers (Yecko & Rossi 2004) and the energy budget of the disturbances show that this process does not draw upon energy across the boundaries.
2 Viscous Large Shearing Box and its QHSG approximation
In Appendix A we consider a box section of an ![]() -disk
centered about its midplane and at a distance R0 from the
central object. If the disk is cold, then it means that
the quantity defined by the ratio of the typical value
of the local midplane disk soundspeed, cs,
to the local Keplerian velocity, V0,
-disk
centered about its midplane and at a distance R0 from the
central object. If the disk is cold, then it means that
the quantity defined by the ratio of the typical value
of the local midplane disk soundspeed, cs,
to the local Keplerian velocity, V0,
is less than 1 by some substantial amount: protoplanetary disks, for example, are believed to have an
in which the total
entropy is defined by

and
All primed quantities are perturbations about the basic flow. The viscous stresses are
where
 |
(10) |
The above equations are non-dimensional. Time is scaled by the local rotation time of the box. All lengths are scaled according to a length
![\begin{displaymath}q \equiv
-\left[\frac{R}{\Omega}\left(\frac{\partial \Omega}{\partial
R}\right)\right]_{R_0}, \end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img39.gif) |
(11) |
in which
The steady state quantities are denoted with index b and in particular
we assume that pressure (pb) and density (![]() )
profiles satisfy the hydrostatic balance relationship
)
profiles satisfy the hydrostatic balance relationship
All corrections to this equations are of a higher order and ignored here. The expression responsible for the VPI can be identified as fluctuating viscosity parameter in (8), term
We call to attention that the accretion and
meridional velocities characterizing ![]() -disks (Kluzniak &
Kita 1999) do not appear
in the VLSB equation set (see Appendix A).
By definition, turbulent disks exhibit accretion
velocities as they are the natural consequence of equations
describing global dynamics. The shear velocities are in fact quite
complex as Kluzniak & Kita (1999) showed for the particular
case of an Shakura-Sunyaev type of
-disks (Kluzniak &
Kita 1999) do not appear
in the VLSB equation set (see Appendix A).
By definition, turbulent disks exhibit accretion
velocities as they are the natural consequence of equations
describing global dynamics. The shear velocities are in fact quite
complex as Kluzniak & Kita (1999) showed for the particular
case of an Shakura-Sunyaev type of ![]() -disk (Shakura & Sunyaev 1973). The radial
velocities in steady state are found to be sheared in the vertical
direction and, as well, there exists a vertical component to the
flow with both radial and vertical dependence (the meridional
flow). However the scaling arguments implemented to reach these
``shearing box'' equations, especially the relative scaling
relationships between the dynamical velocities and the accretion
scalings, show that the influence of the steady accretion rate
appears at higher orders in the expansion procedure. In other
words, dynamical perturbations on the scale of the box do not feel
the effects of steady accretion and meridional flow - they only
feel the effects of the steady Keplerian shear.
The scaling analysis also shows that
the
-disk (Shakura & Sunyaev 1973). The radial
velocities in steady state are found to be sheared in the vertical
direction and, as well, there exists a vertical component to the
flow with both radial and vertical dependence (the meridional
flow). However the scaling arguments implemented to reach these
``shearing box'' equations, especially the relative scaling
relationships between the dynamical velocities and the accretion
scalings, show that the influence of the steady accretion rate
appears at higher orders in the expansion procedure. In other
words, dynamical perturbations on the scale of the box do not feel
the effects of steady accretion and meridional flow - they only
feel the effects of the steady Keplerian shear.
The scaling analysis also shows that
the ![]() -viscosity (which is the driver of the accretion flow)
does influence the dynamics at these scales and is the reason why it
appears in these equations.
-viscosity (which is the driver of the accretion flow)
does influence the dynamics at these scales and is the reason why it
appears in these equations.
3 The quasi-hydrostatic semigeostrophic approximation of the VLSB equations
The equations of motion may be simplified for further analysis by implementing the quasi-hydrostatic semigeostrophic (QHSG) scaling arguments used in Umurhan (2006). The QHSG is useful in its ability to expose the essential mathematical features of the inviscid-SRI (Dubrulle et al. 2005; Umurhan 2006).
We suppose that the azimuthal scales of motion are much larger
than the radial or vertical scales. We measure this with the
small parameter ![]() .
In order to maintain
asymptotic validity we
assume the following orderings
.
In order to maintain
asymptotic validity we
assume the following orderings
| (13) |
Thus we suppose that the following operations upon dynamical quantities scale accordingly as

Then we suppose that the radial and vertical velocities are correspondingly smaller than the azimuthal velocities by this same scale, in other words
These scalings say then that

These scalings will make it easy to follow waves propagating with respect to the background Keplerian flow velocity. Therefore, the temporal dependence should also scale by the scaling appropriate to
Furthermore we say that the density, pressure (and by implication, the entropy) fluctuations are all order 1, that is
The new issue that must be addressed here is to suggest a scaling that brings in the viscous terms at the lowest non-trivial order. To this end setting
where we have introduced the basic state entropy ![]() and
its dynamically varying counterpart
and
its dynamically varying counterpart ![]() which are defined by
which are defined by
Only the azimuthal direction stress component survives at lowest order due to this scaling argument,
Although we have invoked scaling argments leading to the above sets of equations we have not formally rewritten all of the variables to signify these assumptions as it is our desire to preserve the transparency of the subsequent presentation. Note that effect responsible for the VPI survives this scaling argument as it appears in (20) as the term
4 Boussinesq simplification, assumptions and lLinearized dynamics
In Umurhan (2006) it was shown that the QHSG approximation of Boussinesq disk models recovers the linearized hydrodynamic behavior contained therein for concurrent small values of the azimuthal wavenumber and wavespeed. It was further demonstrated that the dynamics contained in the QHSG approximation of the LSB is faithfully represented if one considers instead the equivalent incompressible Boussinesq (Spiegel & Veronis 1960) version of QHSG approximated LSB equations. Applying this sequenced reasoning to the linearized version of (14-18) gives,
where we have dropped all primes from the velocity quantities
and explicitly set ![]() to its value of 1.
In the usual Boussinesq approximation,
density fluctuations are dynamically significant
when coupled to gravity. In these circumstances
to its value of 1.
In the usual Boussinesq approximation,
density fluctuations are dynamically significant
when coupled to gravity. In these circumstances ![]() is replaced by
is replaced by ![]() .
The non-dimensionalized temperature quantity
.
The non-dimensionalized temperature quantity ![]() and
its associated steady state temperature field Tb(z) are characterized
by the (linearized) conservation relation,
and
its associated steady state temperature field Tb(z) are characterized
by the (linearized) conservation relation,

For clarity we reexpress this thermal quantity in terms of
Throughout this study Nis taken to be real (buoyantly stable). The azimuthal stress is
![\begin{displaymath}\tilde N_y'
=\frac{2\alpha_1}{3}\left[\left(\partial_x^2
+\partial_z^2\right)v -
q\partial_x\Pi\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img78.gif) |
(27) |
The term that gives rise to the VPI appears in the above as
 |
(28) |
where the incompressibility condition was used in writing the first term on the RHS of this expression. Multiplying (25) by (2-q)/N2followed by operating on the result with
 |
(29) |
Adding these two equations together and making use of the relationships (22) and (24) yields the following single equation for
To showcase the elements in the above we have written

which is in general a function of the vertical coordinate zand vanishes on the symmetry axis driving the local Froude number to very large values. As we shall see,
implying that
In this asymptotic theory

corresponds to a the perturbed potential vorticity (Tevzadze et al. 2004; Umurhan 2006), also known as the potential vorticity anomaly (Hoskins et al. 1985) and also called vortensity in the astrophysical literature (e.g. Klahr & Bodenheimer 2003). Throughout the rest of this work we will interchangeably use the terms potential vorticity perturbation, potential vorticity disturbance and potential vorticity anomaly (i.e. PV-anomaly). The PV-anomaly Q relates to a vorticity pointing in the vertical direction.
We consider travelling wave normal mode solutions to (30):
the modes are assumed
to be
azimuthally periodic on scale Ly and vertically periodic
on scale Lz,
 |
(32) |
where the azimuthal wavevector k can be any positive number while the vertical wavevector
to be a wavenumber scaling of the viscous parameter. Thus the equation governing the structure function
The Froude-wavenumber is defined as
with the vertical velocity following from evaluating the incompressibility equation
at the boundary and using (34), i.e.
 |
(37) |
Finally, the perturbed potential vorticity is
4.1 Energy integrals
It is instructive to develop global energy integrals
as such quantities aid in developing an interpretation of
the results in the following sections. We restrict our attention
to the energetics associated with the QHSG-Boussinesq model set
(22-21) keeping in mind
the assumptions we made about vertical and azimuthal periodicity
and the constancy of N2.
The radial conditions are left arbitrary
and they will be dealt with accordingly in each of the subsequent subsections.
We proceed by defining the perturbation
thermomechanical energy density ![]() as
as

by multiplying (23) by w and (25) by
in which volume integrals are
integrated on volume ![]() with the volume element
with the volume element
![]() and where
the surface term is
and where
the surface term is
In writing
![\begin{displaymath}[f]^{x_{\rm out}}_0 \leftrightarrow f({x_{\rm out}}) - f(0),
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img115.gif)
where
The energy integral (38) is the Reynolds-Orr Equation
appropriate for this QHSG system.
The energy E is composed of the
baroclinic thermal term (![]()
![]() )
plus a kinetic energy
term (
)
plus a kinetic energy
term (![]() w2), however, the kinetic energy term contains only the
azimuthal velocity contribution because the vertical and
horizontal velocity contributions are small by comparison
in the scaled system of equations according to the QHSG
approximation of the original set (see Sect. 3 and Umurhan 2006,
for details). The term
w2), however, the kinetic energy term contains only the
azimuthal velocity contribution because the vertical and
horizontal velocity contributions are small by comparison
in the scaled system of equations according to the QHSG
approximation of the original set (see Sect. 3 and Umurhan 2006,
for details). The term
![]() represents the
integrated losses and is comprised of
viscous losses due to the azimuthal velocity since, by the same reasoning
as above, the corresponding losses due to vertical and radial velocities
(in the scaled system) are
negligible. The perturbed viscous stress term,
responsible for the VPI plays, a destabilizing role for
these PV-anomalies
as it appears in the above as the
the term
proportional to 2q|v|2.
The total external stresses on the system
is given by
represents the
integrated losses and is comprised of
viscous losses due to the azimuthal velocity since, by the same reasoning
as above, the corresponding losses due to vertical and radial velocities
(in the scaled system) are
negligible. The perturbed viscous stress term,
responsible for the VPI plays, a destabilizing role for
these PV-anomalies
as it appears in the above as the
the term
proportional to 2q|v|2.
The total external stresses on the system
is given by
![]() and is comprised of
the surface integrated body pressure and the surface
viscous stress - the latter of which is expressed only
with the tangential stress due to w. Finally
and is comprised of
the surface integrated body pressure and the surface
viscous stress - the latter of which is expressed only
with the tangential stress due to w. Finally
![]() is the Reynolds stress due to
the background shear state. This expression may
be interpreted as accounting for the amount of
energy perturbations extract from the background
shear state.
We note also
that inspection shows that
is the Reynolds stress due to
the background shear state. This expression may
be interpreted as accounting for the amount of
energy perturbations extract from the background
shear state.
We note also
that inspection shows that
![]() always, while
the remaining terms
always, while
the remaining terms
![]() and
and
![]() may be either positive
or negative given the state of the perturbed
flow or the boundary conditions employed.
may be either positive
or negative given the state of the perturbed
flow or the boundary conditions employed.
4.2 Asymptotic theory on a semi-infinite domain
The following assumptions are made in order to proceed analytically:
(i) the domain in the x direction lies between 0 and ![]() ,
thus
we have
,
thus
we have
![]() ;
(ii) we require that all quantities decay as
;
(ii) we require that all quantities decay as
![]() ;
(iii) there is no normal-flow at x=0 - this inner location is considered
starside as
it is closest to the central object;
(iv) the viscosity is weak but finite, hence, we assume that
;
(iii) there is no normal-flow at x=0 - this inner location is considered
starside as
it is closest to the central object;
(iv) the viscosity is weak but finite, hence, we assume that
![]()
![]() ;
(v) even though there is viscosity in the problem we impose no particular
stress condition at x=0 and let the fluid quantities
be dictated by what emerges in the interior
of the domain. This essentially means that flow stresses at
the starside are allowed to adjust according to the
dynamical response happening in the interior of the domain.
In practice it translates to only enforcing the no-normal flow
boundary condition
;
(v) even though there is viscosity in the problem we impose no particular
stress condition at x=0 and let the fluid quantities
be dictated by what emerges in the interior
of the domain. This essentially means that flow stresses at
the starside are allowed to adjust according to the
dynamical response happening in the interior of the domain.
In practice it translates to only enforcing the no-normal flow
boundary condition![]() .
.
4.2.1 Expansions and outer solution
We assume the following expansions well aware that this
is a singular perturbation calculation because of the presence of the critical
layer (see below). The solution for the wavespeed c is assumed of the form
| (41) |
and a similar series of the form
 |
(42) |
We know aposteriori that the critical layer will generate a solution proportional to
 |
(43) |
To this order the no-flow boundary condition at x=0 amounts to
The solution to this equation which decays as
where A0 is an arbitrary amplitude. Using this solution in boundary condition (44) amounts to selecting c0, which is
This says that the wavespeed is real and positive, which means in this case that there will be a critical layer in the domain, i.e. at
At
![]() we find the equation
we find the equation
| (47) |
Using (45) for ![]() and dividing the equation by c0-x we find
the more transparent form
and dividing the equation by c0-x we find
the more transparent form
 |
(48) |
In which we have defined the parameter
| (49) |
These expressions show, especially that for
![]() ,
that the solution begins to breakdown (i.e. break order)
when the quantity |x-c0| starts to approach 0. This divergence
must be controlled by considering a boundary layer calculation in and around the
critical layer. Note that since the vertical vorticity is proportional
to
,
that the solution begins to breakdown (i.e. break order)
when the quantity |x-c0| starts to approach 0. This divergence
must be controlled by considering a boundary layer calculation in and around the
critical layer. Note that since the vertical vorticity is proportional
to
![]() ,
the critical layer will appear as
a vortex sheet. The formal presentation of this solution, including the region of
validity and expression of the boundary conditions at this order is presented
in Sect. B.1.
,
the critical layer will appear as
a vortex sheet. The formal presentation of this solution, including the region of
validity and expression of the boundary conditions at this order is presented
in Sect. B.1.
4.2.2 Critical layer calculation, matching, and growth rate and analysis
As we demonstrated above, the solutions begin to breakdown in the vicinity of the critical layer which are those places where x-xc begins to get small. We must therefore reexamine (34) in this zone and to this end we define a new inner coordinate as |
(50) |
According to this new coordinate (34) is reexpressed as
We intorduce a series expansion for the solution to (51) by writing
The remainder of this calculation including the matching of the inner and outer solutions and the determination of the growth rate c1 has been relegated to Appendix B.2. We note that the term proportional to
The growth rate of this mode, i.e.
where we have restored the definition of
The instability emerges from the
inner boundary due to application of the no-normal flow condition
but it will be at the critical layer where evidence of it
appears in the form of a pronounced PV-anomaly.
The radial width of this vortex zone is proportional
to
![]() the size of the box and the amplitude will
be
the size of the box and the amplitude will
be
![]() times the leading order perturbation pressure field
(see the end of Appendix B.2). Restoring units and
recalling that the shearing-box has been scaled according to the
thermal scale height of the disk H , the radial
width of this vortex zone,
times the leading order perturbation pressure field
(see the end of Appendix B.2). Restoring units and
recalling that the shearing-box has been scaled according to the
thermal scale height of the disk H , the radial
width of this vortex zone, ![]() ,
is
,
is
Further analysis of these solutions together with the Reynolds-Orr Eq. (38) and the definitions (39-40) shows that to lowest order in Re-1
| (55) |
so that

A general evaluation of the Reynolds stress term
plus a correction which is
Let us reflect upon this for a moment: with these boundary conditions it is always the case that
4.3 Finite radial domain investigations
In this section we consider the normal-mode solutions
of (34) occurring on a finite radial domain
where
![]() .
All solutions
are computed numerically using a Newton-Raphson scheme on a Chebyshev
grid of anywhere from 33 to 129 points - higher
resolution is needed for smaller values of
.
All solutions
are computed numerically using a Newton-Raphson scheme on a Chebyshev
grid of anywhere from 33 to 129 points - higher
resolution is needed for smaller values of ![]() .
All numerically generated
solutions are normalized so that
.
All numerically generated
solutions are normalized so that
![]() .
Because
this is a fourth order system we must specify four boundary conditions.
In all
of the following calculations two of the boundary conditions
will be that
.
Because
this is a fourth order system we must specify four boundary conditions.
In all
of the following calculations two of the boundary conditions
will be that
 |
(58) |
in other words, that the pressure fluctuation and PV-anomaly are zero on the farside boundary. According to the normal-mode PV-anomaly,
| (59) |
For the remaining starside boundary we shall explore four different conditions enumerated in the corresponding subsections below. The most physically plausible viscous starside condition is to set to zero either the azimuthal velocity fluctuation or the azimuthal stress fluctuation. We have also considered zero PV-anomaly and zero PV-anomaly gradient conditions. Although these conditions are less physically realistic, they are simpler to interpret in terms of the energy arguments developed in previous sections.
4.3.1 Rigid and stress-free starside boundary
These conditions translate to requiringsince the zero-stress and rigid conditions implies that
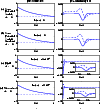 |
Figure 1:
A comparison of eigenfunctions for a variety of starside
boundary conditions. In all plots |
| Open with DEXTER | |
 |
Figure 2:
Like Fig. 1 except
|
| Open with DEXTER | |
4.3.2 Zero PV-anomaly
This boundary condition may be envisioned as the starside boundary
counteracting any tendency for the development of any PV-anomaly
there. Although this is somewhat artificial, we present here the
results of this investigation because these boundary conditions give solutions
that closely resemble those obtained for the calculation on the semi-infinite
domain calculation.
As in the semi-infinite domain calculation,
instability occurs
when
![]() ,
and it scales as
,
and it scales as ![]() for
for
![]() .
Inspection of the eigenfunctions in Fig. 1
for
.
Inspection of the eigenfunctions in Fig. 1
for
![]() ,
especially the profiles for
,
especially the profiles for ![]() ,
shows that (i) the perturbed potential
vorticity
is strongly localized in the critical
layers occurring where the real wavespeed approximately
equals the background flow speed; (ii) an additional boundary layer appears at
the starside boundary scaling like
,
shows that (i) the perturbed potential
vorticity
is strongly localized in the critical
layers occurring where the real wavespeed approximately
equals the background flow speed; (ii) an additional boundary layer appears at
the starside boundary scaling like ![]() and; (iii) the
vorticity in the critical layer follows the
and; (iii) the
vorticity in the critical layer follows the
![]() scaling determined
in the semi-infinite domain calculation.
We depict in Fig. 4a a contour plot of
growth rates as a function of both the Reynolds number and
the inverse of the Froude number,
scaling determined
in the semi-infinite domain calculation.
We depict in Fig. 4a a contour plot of
growth rates as a function of both the Reynolds number and
the inverse of the Froude number,
![]() for fixed values
of
for fixed values
of ![]() and k. The vertical axis may be understood
as representing a positive increase in the wave's speed
(see Eq. (46)). For the parameters depicted
in Fig. 4a (
and k. The vertical axis may be understood
as representing a positive increase in the wave's speed
(see Eq. (46)). For the parameters depicted
in Fig. 4a (
![]() ), instability sets in for
), instability sets in for
![]() .
.
4.3.3 Zero radial PV-anomaly gradient
Requiring no radial gradient of the PV-anomaly on the starside boundary
is arguably the least physically realistic but we include it here, as in
the previous section, because it best
reproduces
the asymptotic result of the semi-infinite domain calculation.
Like in the previous section, where ![]() is set to zero there,
there is instability when
is set to zero there,
there is instability when
![]() ,
a critical
layer emerges which also scales as
,
a critical
layer emerges which also scales as
![]() for small
values of
for small
values of ![]() .
However, the boundary layer appearing
near the starside boundary for the calculation
of Sect. 4.3.2 vanishes here. Finally, for small
values of
.
However, the boundary layer appearing
near the starside boundary for the calculation
of Sect. 4.3.2 vanishes here. Finally, for small
values of ![]() (i.e. Re-1) the Reynolds Orr
expression for these disturbances takes on the same leading
form as (56)
in Sect. 4.2; and this includes
the character of
(i.e. Re-1) the Reynolds Orr
expression for these disturbances takes on the same leading
form as (56)
in Sect. 4.2; and this includes
the character of
![]() .
We note that growth
rates here are nearly identical to the growth rates
determined in Sects. 4.3.2. Figure 4b
shows the landscape of instability (for
.
We note that growth
rates here are nearly identical to the growth rates
determined in Sects. 4.3.2. Figure 4b
shows the landscape of instability (for
![]() )
and we see that instability also sets in when
)
and we see that instability also sets in when
![]() (i.e. here for
(i.e. here for
![]() )
but that it is bounded above by a more complicated function of
Re.
We note that the critical layer becomes harder to distinguish
as viscosity (that is, Re-1 or
)
but that it is bounded above by a more complicated function of
Re.
We note that the critical layer becomes harder to distinguish
as viscosity (that is, Re-1 or ![]() )
is made larger.
)
is made larger.
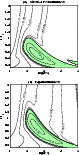 |
Figure 3:
Contours on the
|
| Open with DEXTER | |
 |
Figure 4: Same as Fig. 3 except: a) Zero PV-anomaly at x=0; b) Zero PV-anomaly gradient at x=0. |
| Open with DEXTER | |
5 Discussion and reflections
5.1 On the Tollmien Schlichting wave analogy
T-S waves appear in flows that are are wall-bounded at least on one
boundary. In the classic analysis done for Blasius boundary layers
(e.g. Schlichting & Gersten 2001) the instability is a
solution of the 2D Orr-Sommerfeld equation.
The mechanics leading to instability
is understood to arise
from the action of a purely viscous mode interacting with a nearly
inviscid mode (Baines et al. 1996). The global
velocity profiles set up are such that the relative phase between
the horizontal and (plate) normal-velocities promotes extraction of
energy from the shear which then leads to energetic growth (i.e.
![]() ).
The 3D instability studied here
shares some major similarities to classic T-S waves: (i) the equation
governing the dynamics of the potential vorticity modes (30)
has similar structure to the 2D Orr-Sommerfeld equation; (ii) the
instability emerges for both no-slip and free-slip boundary conditions
(but not limited to these).
What stands out in our minds is that, although
classical unstable T-S waves come about in a wide variety of
background flows excluding plane-Couette flow
(Baines et al. 1996; Schmid & Henningson 2000), the
instability here is present for a plane-Couette type of flow profile.
).
The 3D instability studied here
shares some major similarities to classic T-S waves: (i) the equation
governing the dynamics of the potential vorticity modes (30)
has similar structure to the 2D Orr-Sommerfeld equation; (ii) the
instability emerges for both no-slip and free-slip boundary conditions
(but not limited to these).
What stands out in our minds is that, although
classical unstable T-S waves come about in a wide variety of
background flows excluding plane-Couette flow
(Baines et al. 1996; Schmid & Henningson 2000), the
instability here is present for a plane-Couette type of flow profile.
The results here compare qualitatively to the results of rotating Blasius boundary layers. For example, Yecko & Rossi (2004) show that three dimensional modal instability preferentially emerges in anticylonic rotating Blasius flow when the vertical wavenumber of the disturbance is large in comparison to its streamwise (azimuthal) wavenumber (e.g. see Fig. 8b in Yecko & Rossi 2004). By comparison, the asymptotic scalings we have implemented spotlights dynamics characterized by these same spatial scale disparities. Thus despite the differences in the problems investigated between these two studies (i.e. the inclusion of gravity and entropy gradients and the differing base velocity profiles) the similarities in the circumstances for instability onset suggest that such processes may be more general in environments like disks - especially near the disk-star boundary.
5.2 On the assumed constancy of g and N
To make the analysis we have exposed here analytically possible we assumed that the vertical component of gravity and the Brunt-Väisälä to be constant with respect to the disk vertical coordinate, (31) which permits us to assume separable normal-mode solutions. On the other hand, real disks (including their small sections) are characterized by vertically varying values of g and N and this means that, in general, one cannot assume separable solutions in z and x, in particular
5.3 Relationship to the viscous pulsational instability
In an axisymmetric study of an shearing sheet section of an accretion disk of constant temperature, Latter & Ogilvie (2006) argue that the VPI (Kato 1978) is most likely to manifest itself through the destabilization of an even structured f-mode. The disturbances become unstable because the viscous perturbations transfer energy from the shear into the acoustic mode through the perturbed stress Txy'. Because f-modes are characteristically inertial-acoustic waves, they are the likely candidates for this instability since their vertical structures are the simplest which, in turn, result in minimizing dissipative losses. We observe that Txy' is proportional to the pressure fluctuation. This fluctuating stress affects the evolution of the horizontal velocity perturbation by extracting/adding energy into the disturbance. As the horizontal velocity disturbances are not in general in phase with the pressure fluctuations, especially for inertial/acoustic modes, the possibility for overstability is manifest. However, the PV-anomalies examined here are distinct from inertial-gravity and inertial-acoustic modes (e.g. Ogilvie 1998; Tevzadze et al. 2004). The horizontal velocity perturbations of PV anomalies are proportional to the radial gradient of the perturbation pressure. Since the latter quantity is proportional to a decaying exponential (i.e.
5.4 Summary and Implications
For cold disk systems, i.e. those in which magnetic effects are not active, the prospects of identifying instability mechanisms appear to be far from exhausted. We have tried to argue that certain previously considered non-magnetic instabilities need not be discarded as candidate mechanisms driving activity for disks. Indeed the SRI and PPI instabilities, which emerge as the interaction of edgewaves along cylinder/channel walls, could in principle operate in real disks so long as there exists, in general, interacting waves propagating separated from each other by a wave-evanescent region. We have demonstrated here another possible mechanism - that the existence of disk analogs of unstable Tollmien-Schlichting waves could also manifest themselves in real disk systems. We have carried out the calculation within a model shearing box in which we have imposed a single boundary on one side. True disks have boundary layers separating stars from the disk which are probably far more complicated (Regev & Bertout 1995) than the model we have presented here. Nonetheless, far from being a proof, we have demonstrated in this asymptotically simplified model that such a dynamical processes is, at least, feasible. It is no stretch of the imagination to suppose that analogous unstable waves may exist near the vicinity of the star-disk boundary layer. We add a final reflection. Classical unstable T-S waves emerge in flows with compliant boundaries showing that such instabilities are robust and persist even if the boundaries have a certain amount of elasticity to them (Carpenter & Garrad 1985) - although compliant walls delay the onset of instability to higher Reynolds numbers. As a star-disk boundary is probably not a rigid body transition, it would be beneficial to investigate and/or model these disk analog T-S waves by considering starside boundary conditions that are appropriately compliant as well.
The perspective we have adopted therefore can be broken down
into two parts. The first is that (as in the recent studies
of Kleiber & Glatzel 1999 and Latter & Ogilvie 2006)
we have expanded the exploration of the possible
destabilizing role viscosity can play. Viscosity does not always have to
stabilize disturbances as there are velocity profiles, dictated by
boundary conditions, wherein destabilization occurs counter to one's usual
physical intuition.
The
second is that experimentation with boundary conditions, even
within the context of the shearing box environment, followed
by concerted effort toward understanding and clarifying their
effects is a worthwhile endeavor given our lack of complete
knowledge about the boundaries of real disk systems (a situation
which is strongly contrasted by what is encountered in laboratory/terrestrial
flows).
If turbulent stresses in
cold disks are driven by the MRI resulting
in effective values of
![]() (Ogilvie 2001; Ogilvie & Proctor 2003; King et al. 2007),
then T-S waves like the sort here could emerge
as a secondary instability. This possibility is made
manifest because the T-S wave instability grows faster
in proportion to the value of
(Ogilvie 2001; Ogilvie & Proctor 2003; King et al. 2007),
then T-S waves like the sort here could emerge
as a secondary instability. This possibility is made
manifest because the T-S wave instability grows faster
in proportion to the value of ![]() until about
a value of 0.1.
until about
a value of 0.1.
Acknowledgements
The authors are indebted to the valuable comments and suggestions of the anonymous referee. The authors would like to thank the Israeli Science Foundation for making this research possible. O.M.U. also acknowledges that this research was partly supported by BSF grant 2004087 and ISF grant 1084/06. O.M.U. also thanks the Dead Sea Regional Council and the Ein Gedi Kibbutz for their hospitality and Phil Yecko for suggestive conversations.
Appendix A: Scaling arguments leading to the viscous large shearing box equations
The derivation of the VLSB equations follows the procedure executed in Umurhan & Regev (2004). The dimensional equations of motion in cylindrical coordinates in a frame of constant rotation are, in component form, given by the followingthe equations of mass continuity and entropy
 |
= | 0, | (A.4) |
| = | Q, | (A.5) |
with the operator definition

The
gravitational potential ![]() is written in the following unusual
form in order to effect some generality when it comes to the shear
it induces upon the steady state flow,
is written in the following unusual
form in order to effect some generality when it comes to the shear
it induces upon the steady state flow,
For the realistic Keplerian flow profile q = 3/2 and
The viscous moments are
| |
= | 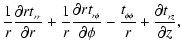 |
(A.7) |
| = |  |
(A.8) | |
| = |  |
(A.9) |
along with the viscous stresses tij,
 |
(A.10) | ||
![$\displaystyle t_{_{\phi r}} = t_{_{r\phi}} = \eta\left[ \frac{1}{
r}\frac{\part...
...mega_{_0}}{r}\right) +\frac{1}{r}\frac{\partial
u_{_r}}{\partial \phi}
\right],$](/articles/aa/full_html/2009/13/aa09604-08/img233.gif) |
(A.11) | ||
 |
(A.12) | ||
 |
(A.13) | ||
 |
(A.14) | ||
 |
(A.15) |
in which

Because the turbulent viscosity within a disk is presumed to be driven by some sort of shear process (either the MRI or a subcritical hydrodynamic transition) the bulk viscosity
 |
(A.16) |
where
We proceed from here onto non-dimensionalization. We shall
consider dynamics as taking place in a small region around the
point
![]() ,
which we shall refer to
as the box. We let
,
which we shall refer to
as the box. We let
![]() measure the non-dimensional
size of this box, i.e.,
measure the non-dimensional
size of this box, i.e.,
This motivates us to scale all the directions by R0 and to
define the nondimensional coordinates
 |
(A.17) |
where it is understood that x,y,z are now taken to be order 1 quantities.
Furthermore we suppose that all density quantities are scaled by
the reference density ![]() ,
pressure quantities are supposed
similarly scaled by
,
pressure quantities are supposed
similarly scaled by
![]() where
where
![]() is the dimensional scale of the sound speed of the box. In
parallel with this speed is the local rotation speed of the box
around the central object,
is the dimensional scale of the sound speed of the box. In
parallel with this speed is the local rotation speed of the box
around the central object,
![]() :
when q=3/2 this speed is sometimes referred to as
the local Keplerian speed of the disk. The fundamental
ansatz of cold thin disk theory is that the ratio of these two
quantities is small. We, in fact, identify
:
when q=3/2 this speed is sometimes referred to as
the local Keplerian speed of the disk. The fundamental
ansatz of cold thin disk theory is that the ratio of these two
quantities is small. We, in fact, identify
| (A.18) |
which is the classic parameter measuring the thinness or ``coldness'' of the disk (Shakura & Sunyaev 1973; and see recently Umurhan et al. 2006, for recent exploitations of this parameter). This, in turn, is a measure of the disk's vertical scaleheight
Thus we propose that all velocities observed in this rotating
frame are scaled by the soundspeed, meaning to say that

where u',w',v' are order 1 nondimensionalizations of the corresponding velocities. Note that in these scalings we are saying that all velocities observed in the rotating frame are order
Time and all advective derivatives are scaled
according to the local rotation time of the disk, i.e.
![]() .
Before putting these scalings into the
governing equations we note that
.
Before putting these scalings into the
governing equations we note that
![\begin{displaymath}\tilde\Omega_0^2 r-\frac{\partial\Psi}{\partial r}
=2\tilde\O...
...\varepsilon q x +
{\cal O}\left({\varepsilon^2}\right)\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img255.gif)
Taking into account all of the nondimensionalizations, along with writing
To obtain the viscous large shearing box equations presented in the text, i.e. (1-5), we make the following identifications and assumptions
- Drop all terms
 and higher
from (A.19-A.23).
and higher
from (A.19-A.23).
- Everywhere write
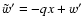 in (A.19-A.23) in order to eliminate the
sole x term on the RHS of (A.19). The expression
-qx is the background shear and will be felt by perturbations.
in (A.19-A.23) in order to eliminate the
sole x term on the RHS of (A.19). The expression
-qx is the background shear and will be felt by perturbations.
- Write the density and pressures as being comprised of
a steady portion and a time dependent perturbed portion, i.e.


- Specifically flag all Coriolis-like related effects with
the symbol
 .
.
Appendix B: Semi-infinite domain calculation details
B.1 Outer solution completion
As a result of this breakdown we write the solutions to this order according to which
side of xc one is on. Formally then we say
 |
(B.1) |
for
 |
(B.2) |
for
 |
(B.3) |
with solutions given by
![$\displaystyle \hat\Pi_{1p}^{(-)} = \frac{A_0\Lambda}{2k_{_F}i}\biggl\{
{\rm e}^...
...t[2k_{_F}(c_{_0}-x)\right]
-{\rm e}^{-xk_{_F}}\ln\bigl(c_{_0}-x\bigr)\biggr \},$](/articles/aa/full_html/2009/13/aa09604-08/img280.gif) |
(B.4) | ||
![$\displaystyle \hat\Pi_{1p}^{(+)} = \frac{A_0\Lambda}{2k_{_F}i}\biggl\{
{\rm e}^...
...t[2k_{_F}(c_{_0}-x)\right]
-{\rm e}^{-xk_{_F}}\ln\bigl(x-c_{_0}\bigr)\biggr \},$](/articles/aa/full_html/2009/13/aa09604-08/img281.gif) |
(B.5) |
where

An analysis of these solution forms for

In formally writing these solutions we purposely avoid the region described by
which we will refer to as the critical layer. The size of this bounding region is such that
B.2 Critical layer calculation and matching
The calculation will be facilitated if we consider the evolution of the residual potential vorticity quantity![$\displaystyle \Pi = \breve \Pi +
A_0 {\rm e}^{-2/q}\biggl[1 - \epsilon^{1/3}k_{...
...n^{1}\frac{1}{6}k_{_F}^3\xi^3 +
\epsilon^{4/3}\frac{1}{24}k_{_F}^2\xi^4\biggr].$](/articles/aa/full_html/2009/13/aa09604-08/img292.gif) |
The polynomial terms in the above expression are the first five terms of the series expansion of the lowest order outer solution,
 |
(B.7) |
where
 |
(B.8) |
Homogeneous solutions of the operator
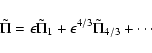
The order
With
 |
(B.10) |
In which
Operating on

It is instructive to note the expression
where
We note that there exists a phase factor proportional to
We note that the PV-anomaly arising from this
critical layer appears at order
![]() when viewed in the
unstretched coordinate frame. This is because the first non-trivial
contribution arising to the potential vorticity perturbation from this zone is
when viewed in the
unstretched coordinate frame. This is because the first non-trivial
contribution arising to the potential vorticity perturbation from this zone is
| |
= | ||
| = |
Thus, while the size of the critical layer zone is order
B.3 Matching
We must reexpress the outer solution in a ``small'' vicinity of the critical point xc. We consider first the solutions approaching from below, that is
 |
|||
![$\displaystyle \qquad
+\frac{1}{2}k_{_F}^2(x-x_c)^2
- \frac{1}{6}k_{_F}^3(x-x_c)^3 + \frac{1}{24}k_{_F}^2(x-x_c)^4 + \cdots\biggr]$](/articles/aa/full_html/2009/13/aa09604-08/img327.gif) |
|||
 |
|||
![$\displaystyle \hskip 1.0cm - k_{_F}\left(A_1^{(-)} {\rm e}^{-2/q} - B_1^{(-)} {\rm e}^{2/q}\right)(x-x_c) \biggr]$](/articles/aa/full_html/2009/13/aa09604-08/img329.gif) |
|||
| (B.14) |
while when approaching this point from above, that is as
![]() ,
we
find
,
we
find
 |
|||
![$\displaystyle \hskip 2cm - \frac{1}{6}k_{_F}^3(x-x_c)^3 + \frac{1}{24}k_{_F}^2(x-x_c)^4 + \cdots\biggr]$](/articles/aa/full_html/2009/13/aa09604-08/img334.gif) |
|||
![$\displaystyle \hskip 2cm+ {\rm e}^{-2/q}\epsilon\biggl[A_1^{(+)} - k_{_F}A_1^{(+)}(x-x_c) \biggr]$](/articles/aa/full_html/2009/13/aa09604-08/img335.gif) |
|||
| (B.15) |
Now we do the same to the critical layer solution. We restore the inner
coordinate ![]() in terms
of x-xc and take the limit of small
in terms
of x-xc and take the limit of small ![]() (as is standard practice in boundary
layer theory, Bender & Orszag 1999) revealing
(as is standard practice in boundary
layer theory, Bender & Orszag 1999) revealing
| |
= | ||
| (B.16) |
Identifications are made respecting powers of
while the remaining two terms, proportional to (x-xc)3 and (x-xc)4are satisfied given the above assignments in (B.17). At

because
To complete the matching we must prepare the final term
![$\displaystyle \epsilon\biggl[\partial_x \hat \Pi_1\biggr]_{x\rightarrow x_c - \...
...}
-\epsilon k_{_F}\left(A_1^{(-)}{\rm e}^{-2/q}
-B_1^{(-)}{\rm e}^{2/q}\right),$](/articles/aa/full_html/2009/13/aa09604-08/img347.gif) |
(B.19) |
that is, approaching
![\begin{displaymath}\epsilon\biggl[\partial_x \hat \Pi_1\biggr]_{x\rightarrow x_c...
...}}\ln\varepsilon_{+} - \epsilon k_{_F}A_1^{(+)}{\rm e}^{-2/q},
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img349.gif) |
(B.20) |
that is, approaching
Now we must match this to the corresponding expression emerging from the interior of the domain. In other words we require similarly that
in which (i) the transition in orders of
Equating the RHS of (B.21) and (B.22) and making use of the asymptotic form (B.23) we see that the offending logarithmic terms cancel leaving,
The meaning of this relationship is clear - the presence of the singular layer in the flow means that the homogeneous outer region solutions must show a jump in their derivatives (in proportion to the RHS of the above expression). Another way to interpret this is to recognize that this jump corresponds to the presence of a vortex sheet at x = xc.
The complex wavespeed may be now obtained from (B.18), (B.24)
and the boundary condition (B.6). We note that for there
to be a non-trivial solution to (B.18) and (B.24) the
following
relationship,
must be satisfied. This is the solvability condition. The second matter we note is that
![$\displaystyle \hat\Pi_{1p}^{(-)}(0) =\frac{A_0\Lambda i}{2k_{_F}}\left[\ln\left(\frac{2}{qk_{_F}}\right)
-{\rm e}^{4/q}{\rm Ei}\left(\frac{4}{q}\right)\right],$](/articles/aa/full_html/2009/13/aa09604-08/img359.gif) |
|||
![$\displaystyle \partial_x\hat\Pi_{1p}^{(-)}\Bigr\vert _{x\rightarrow 0} =-\frac{...
...c{2}{qk_{_F}}\right)
+{\rm e}^{4/q}{\rm Ei}\left(\frac{4}{q}\right)\right]\cdot$](/articles/aa/full_html/2009/13/aa09604-08/img360.gif) |
Thus, the solvability condition (B.25) together with the above
expressions used in (B.6) combine to give
The form quoted in the text follows from restoring the definition of
References
- Afshordi, N., Mukhopadhyay, B., & Narayan, R. 2005, ApJ, 629, 373 [NASA ADS] [CrossRef] (In the text)
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (Dover)
- Baines, P. G., Majumdar, S., & Mitsudera, H. 1996, J. Fluid Mech., 312, 107 [NASA ADS] [CrossRef] (In the text)
- Baines, P. G., & Mitsudera, H. 1994, J. Fluid Mech., 276, 327 [NASA ADS] [CrossRef] (In the text)
- Balmforth, N. J. 1999, J. Fluid Mech., 387, 97 [NASA ADS] [CrossRef] (In the text)
- Balmforth, N. J., & Piccolo, C. 2001, J. Fluid Mech., 449, 85 [NASA ADS] [CrossRef] (In the text)
- Balmforth, N. J., Piccolo, C., & Umurhan, O. M. 2001, J. Fluid Mech., 449, 115 [NASA ADS] [CrossRef]
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] (In the text)
- Barranco, J. A., & Marcus, P. S. 2005, ApJ, 623, 1157 [NASA ADS] [CrossRef] (In the text)
- Bayly, B. J., Orszag, S. A., & Herbert, T. 1988, Ann. Rev. Fluid Mech., 20, 359 [NASA ADS] [CrossRef]
- Bender, C. M., & Orszag, S. A. 1999, Advanced Mathematical Methods for Scientists and Engineers (Springer)
- Bodo, G., Tevzadze, A., Chagelishvili, G., et al. 2007a, A&A, 475, 51 [NASA ADS] [CrossRef] [EDP Sciences] (Bodo et al. A) (In the text)
- Bodo, G., Chagelishvili, G., Murante, G., et al. 2007b [arXiv:0705.3474v1]
- Carpenter, P. W., & Garrad, A. D. 1985, J. Fluid Mech., 155, 465 [NASA ADS] [CrossRef] (In the text)
- Case, K. M. 1960, Phys. of Fluids, 3, 143 [NASA ADS] [CrossRef] (In the text)
- Chagelishvili, G. D., Zahn, J.-P., Tevzadze, A. G., & Lominadze, J. G. 2003, A&A, 402, 401 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Charney, J. G., & Stern, M. E. 1962, J. Atmos. Sci., 19, 159 [NASA ADS] [CrossRef]
- Davies, H. C., & Bishop, C. H. 1994 J. Atm. Sci., 51, 1930
- Doering, C. R., Spiegel, E. A., & Worthing, R. A. 2000, Phy. Fluids, 12, 1955 [NASA ADS] [CrossRef] (In the text)
- Drazin, P. G., & Reid, W. H. 1984, Hydrodynamic Stability, Cambridge
- Dubrulle, B., Marie, L., Normand, Ch., et al. 2004, A&A, 429, 1 [NASA ADS] [CrossRef]
- Frank, J., King, A. R., & Raine, D. J. 2002, Accretion Power in Astrophysics (Cambridge: Cambridge Univ. Press)
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS]
- Goldreich, P., Goodman, J., & Narayan, R. 1986, MNRAS, 221, 339 [NASA ADS]
- Hayashi, Y.-Y., & Young, W. R. 1987, J. Fluid Mech., 184, 477 [NASA ADS] [CrossRef] (In the text)
- Hoskins, B. J., McIntyre, M. E., & Robertson, A. W. 1985, Quart. J. Roy. Meteor. Soc., 111, 877 [NASA ADS] [CrossRef] (In the text)
- Ioannaou, P. J., & Kakouris, A. 2001, ApJ, 550, 931 [NASA ADS] [CrossRef]
- Ji, H., Burin, M., Schartman, E., & Goodman, J. 2006, Nature, 444, 343 [NASA ADS] [CrossRef] (In the text)
- Johnson, B. M., & Gammie, C. F. 2005, ApJ, 635, 149 [NASA ADS] [CrossRef] (In the text)
- Joseph, D. D. 2003, J. Fluid. Mech., 479, 191 [NASA ADS] [CrossRef] (In the text)
- Kato, S. 1978, MNRAS, 185, 629 [NASA ADS] (In the text)
- Kersalé, E., Hughes, D. W., Ogilvie, G. I., Tobias, S. M., & Weiss, N. O. 2004, ApJ, 602, 892 [NASA ADS] [CrossRef] (In the text)
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] (In the text)
- Kleiber, R., & Glatzel, W. 1999, MNRAS, 303, 107 [NASA ADS] [CrossRef] (In the text)
- King, A. R., Pringle, J. E., & Livio, M. 2007, MNRAS, 376, 1740 [NASA ADS] [CrossRef] (KPL07) (In the text)
- Kluzniak, W., & Kita, D. 2000, Three-dimensional structure of an alpha accretion disk [arXiv:astro-ph/0006266]
- Latter, L. N., & Ogilvie, G. I. 2006, MNRAS, 372, 1829 [NASA ADS] [CrossRef] (In the text)
- Lesur, G., & Longaretti, P.-Y. 2005, A&A, 444, 25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] (In the text)
- Lions, P. L. 1993, Limits incompressible et acoustique pour des fluides visqueux, compressible et isentropique, C. R. Acad. Sci. Paris Ser. I Math, 317, 1197 (In the text)
- Lithwick, Y. 2007, ApJ, 670, 789 [NASA ADS] [CrossRef] (In the text)
- Mukhopadhyay, B., Afshordi, N., & Narayan, R., 2004, ApJ, 629, 383 [NASA ADS] [CrossRef]
- Ogilvie, G. I. 1998, MNRAS, 297, 291 [NASA ADS] [CrossRef] (In the text)
- Ogilvie, G. I. 2001, MNRAS, 325, 231 [NASA ADS] [CrossRef] (In the text)
- Ogilvie, G. I., & Proctor, M. R. E. 2003, J. Fluid Mech., 476, 389 [NASA ADS] [CrossRef]
- Papaloizou, J. C. B., & Pringle, J. E. 1984, MNRAS, 208, 721 [NASA ADS]
- Petersen, M. R., Julien, K., & Stewart, G. R. 2007a, ApJ, 658, 1236 [NASA ADS] [CrossRef] (In the text)
- Petersen, M. R., Stewart, G. R., & Julien, K. 2007b, ApJ, 658, 1252 [NASA ADS] [CrossRef]
- Regev, O., & Bertout, C. 1995, MNRAS, 272, 71-79 [NASA ADS] (In the text)
- Richard, D. 2001, Thèse de doctorat, Université Paris 7 (In the text)
- Richard, D., & Zahn, J.-P. 1999, A&A, 347, 734 [NASA ADS] (In the text)
- Schlichting, H., & Gersten, K. 2001, Boundary Layer Theory, Springer, 94 (In the text)
- Sakai, S. 1989, J. Fluid Mech., 202, 149 [NASA ADS] [CrossRef] (In the text)
- Schmid, P. J., & Henningson, D. S. 2000, Stability and Transition in Shear Flows, Springer (In the text)
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
- Shalybkov, D., & Rüdiger, G. 2005, A&A, 438, 411 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Spiegel, E. A., & Veronis, G. 1960, ApJ, 131, 442 [NASA ADS] [CrossRef] (In the text)
- Stewartson, K. 1981, IMA J. Appl. Math., 27, 133 [CrossRef] (In the text)
- Tevzadze, A. G., Chagelishvili, G. D., Zahn, J.-P., Chanishvili, R. G., & Lominadze, J. G. 2003, A&A, 407, 779 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Umurhan, O. M. 2006, MNRAS, 365, 85 [NASA ADS] [CrossRef] (In the text)
- Umurhan, O. M. 2008, A&A, 489, 953 [NASA ADS] [CrossRef] [EDP Sciences]
- Umurhan, O. M., Nemirovsky, A., Regev, O., & Shaviv, G. 2006, A&A, 446, 1 [NASA ADS] [CrossRef] [EDP Sciences]
- Umurhan, O. M., & Regev, O. 2004, A&A, 427, 855 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Yecko, P. A. 2004, A&A, 425, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Yecko, P. A., & Rossi, M. 2004, Phys. Fluids, 16, 2322 [NASA ADS] [CrossRef]
Footnotes
- ... other
![[*]](/icons/foot_motif.gif)
- By this it is meant to say that there exists a wave evanescent region separating the waves in question.
- ... (1985)
![[*]](/icons/foot_motif.gif)
- They show that the interior of the domain does not intrinsically support propagating waves as it behaves like a wave evanescent zone. However the imposition of the boundary conditions brings into existence waves that propagate along the radial boundaries of the domain.
- ... region
![[*]](/icons/foot_motif.gif)
- Examples of this process are well known in atmospheric flow (Charney & Stern 1965; Hoskins et al. 1985; Davies & Bishop 1994).
- ...

![[*]](/icons/foot_motif.gif)
- A momentary comparison to (18)
should convince the reader that
 represents a perturbed entropy
quantity (Dubrulle et al. 2005) making (25) a reasonable analog of the
linearized form of (5).
represents a perturbed entropy
quantity (Dubrulle et al. 2005) making (25) a reasonable analog of the
linearized form of (5).
- ... Number
![[*]](/icons/foot_motif.gif)
- However, note that the actual Reynolds number, denoted
by R, is a factor of
 larger than Re, i.e. R = Re
larger than Re, i.e. R = Re .
.
- ...

![[*]](/icons/foot_motif.gif)
- With respect to the other scalings we have
called on in this work, we shall formally require that
 .
.
- ... condition
![[*]](/icons/foot_motif.gif)
- Note, however, that we show in Sect. 4.3 that the results obtained in this section, including the calculation of the growth rates, would be essentially unchanged had we imposed, instead, that the radial gradient of the potential vorticity be zero at the starside boundary.
- ...
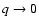
![[*]](/icons/foot_motif.gif)
- Note, however, this limit breaksdown the QHSG approximation and is not considered.
- ... particular
![[*]](/icons/foot_motif.gif)
- In other words by assuming g and N to be constant
we are able to assume solution form
 while if g and N are z-dependent one can (at best) assume
a solution in the form
while if g and N are z-dependent one can (at best) assume
a solution in the form
 where
where
 is the non-separable structure function.
is the non-separable structure function.
All Figures
 |
Figure 1:
A comparison of eigenfunctions for a variety of starside
boundary conditions. In all plots |
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
Like Fig. 1 except
|
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
Contours on the
|
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Same as Fig. 3 except: a) Zero PV-anomaly at x=0; b) Zero PV-anomaly gradient at x=0. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.









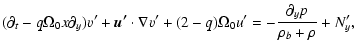





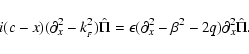
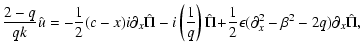

![\begin{displaymath}\dot E_{{\rm stress}} \equiv
\int\left[-\Pi u + \frac{\eta}{\rho_b}v\partial_x v\right]_0^{x_{{\rm out}}} {\rm d}y{\rm d}z.
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img113.gif)



![$\displaystyle \left(\frac{1}{i}\partial_\xi^4 - \xi\partial_\xi^2\right) \hat \...
... \epsilon^{2/3}c_1\left[\partial_\xi^2
- \epsilon^{2/3} k_{F}^2 \right]\hat\Pi.$](/articles/aa/full_html/2009/13/aa09604-08/img145.gif)
![$\displaystyle c_1 =
-\frac{2\pi}{q}{\rm e}^{4/q}\Bigl(k_{_F}^2 -\beta^2-2q\Bigr...
...\left[1+\frac{2}{q}{\rm e}^{-4/q}{\rm Ei}\left(\frac{4}{q}\right) \right] \cdot$](/articles/aa/full_html/2009/13/aa09604-08/img147.gif)
![\begin{displaymath}\sigma =
{\rm Re}^{-1}\biggl((F_\epsilon^2-1)\beta^2 - 2q\big...
...ac{2}{q}{\rm e}^{-4/q}{\rm Ei}\left(\frac{4}{q}\right)\right],
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img149.gif)
![$\displaystyle \frac{1}{2}\beta^2\left[\frac{1}{4}F_\epsilon^2 + 1 \right] > 0,$](/articles/aa/full_html/2009/13/aa09604-08/img166.gif)
![$\displaystyle k_F\dot E_{{\rm shear}}^{(1)} = \beta^4 (F_\epsilon^2 -1 - 2q/\be...
...(1 + \frac{2}{q}{\rm e}^{-4/q}{\rm Ei}\left(\frac{4}{q}\right)\right)-1\right].$](/articles/aa/full_html/2009/13/aa09604-08/img170.gif)


















![\begin{displaymath}\biggl[\partial_\xi \breve\Pi_{4/3}\biggr]^{\xi\rightarrow \D...
... -\Delta_{-}}
= \int_{-\Delta_{-}}^{\Delta_{+}}\Xi {\rm d}\xi,
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img312.gif)
![\begin{displaymath}\int_{-\Delta_{_-}}^{\Delta_{_+}}
{\Xi {\rm d}\xi}
\sim
\frac...
... e}^{-2/q}\left[\ln\Delta_{_+} - \ln\Delta{_-} + i\pi
\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img316.gif)


![$\displaystyle \epsilon\biggl[\partial_x \hat \Pi_1\biggr]^{x\rightarrow x_c + \...
...rac{\Lambda}{i{\rm e}^{2/q}}\left[\ln\varepsilon_{+}-\ln\varepsilon_{-}\right].$](/articles/aa/full_html/2009/13/aa09604-08/img351.gif)
![$\displaystyle \epsilon^{4/3}\biggl[\partial_x\breve\Pi_{4/3}\biggr]^{x\rightarr...
...arepsilon_{+}/\epsilon^{1/3}}_{\xi\rightarrow- \varepsilon_{-}/\epsilon^{1/3}}=$](/articles/aa/full_html/2009/13/aa09604-08/img352.gif)

![\begin{displaymath}\epsilon\int_{-\varepsilon_{_-}/\epsilon^{1/3}}^{\varepsilon_...
...left[\ln\varepsilon_{_+} - \ln\varepsilon_{_-} + i\pi
\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img356.gif)
![\begin{displaymath}-k_{_F}\left[A_1^{(+)} -A_1^{(-)} + B_1^{(-)}{\rm e}^{4/q}\right] =
A_0\frac{\Lambda}{i}\cdot i\pi = A_0\Lambda\pi.
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img357.gif)

![\begin{displaymath}c_1 = i\frac{\Lambda}{qk_{_F}^2}\left[q+2{\rm e}^{-4/q}{\rm Ei}\left(\frac{4}{q}\right)
-2i\pi {\rm e}^{4/q}\right].
\end{displaymath}](/articles/aa/full_html/2009/13/aa09604-08/img361.gif)