| Issue |
A&A
Volume 496, Number 3, March IV 2009
|
|
|---|---|---|
| Page(s) | 805 - 812 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811312 | |
| Published online | 30 January 2009 | |
An evolved donor star in the long-period cataclysmic variable
HS 0218+3229![[*]](/icons/foot_motif.gif)
P. Rodríguez-Gil1,2,3 - M. A. P. Torres4 - B. T. Gänsicke3 - T. Muñoz-Darias2 - D. Steeghs3,4 - R. Schwarz5 - A. Rau6 - H.-J. Hagen7
1 - Isaac Newton Group of Telescopes, Apartado de correos 321, 38700, Santa Cruz de La Palma, Spain
2 - Instituto de Astrofísica de Canarias, vía Láctea, s/n, La Laguna, 38205 Santa Cruz de Tenerife, Spain
3 - Department of Physics, University of Warwick, Coventry CV4 7AL, UK
4 - Harvard-Smithsonian Center for Astrophysics, 60 Garden St, Cambridge, MA 02138, USA
5 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
6 - Caltech Optical Observatories, Mail Stop 105-24, California Institute of Technology, Pasadena, CA 91125, USA
7 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 7 November 2008 / Accepted 20 January 2009
Abstract
Context. We present time-resolved spectroscopy and photometry of HS 0218+3229, a new long-period cataclysmic variable discovered within the Hamburg Quasar Survey. It is one of the few systems that allow a dynamical measurement of the masses of the stellar components.
Aims. We combine the analysis of time-resolved optical spectroscopy and R-band photometry with the aim of measuring the mass of the white dwarf and the donor star and the orbital inclination.
Methods. Cross-correlation of the spectra with K-type dwarf templates is used to derive the radial velocity curve of the donor star. An optimal subtraction of the broadened templates is performed to measure the rotational broadening and constrain the spectral type of the donor. Finally, an ellipsoidal model is fitted to the R-band light curve to obtain constraints upon the orbital inclination of the binary system.
Results. The orbital period of HS 0218+3229 is found to be
![]() d (
d (
![]() h), and the amplitude of the donor's radial velocity curve is
h), and the amplitude of the donor's radial velocity curve is
![]()
![]() .
Modelling the ellipsoidal light curves gives an orbital inclination in the range
.
Modelling the ellipsoidal light curves gives an orbital inclination in the range
![]() .
A rotational broadening between
.
A rotational broadening between
![]()
![]() and
and
![]()
![]() is found when assuming zero and continuum limb darkening, respectively. The secondary star has most likely a spectral type K5 and contributes
is found when assuming zero and continuum limb darkening, respectively. The secondary star has most likely a spectral type K5 and contributes ![]() 80-85% to the R-band light. Our analysis yields a mass ratio of
0.52 < q < 0.65, a white dwarf mass of
80-85% to the R-band light. Our analysis yields a mass ratio of
0.52 < q < 0.65, a white dwarf mass of
![]() ,
and a donor star mass of
,
and a donor star mass of
![]() .
.
Conclusions. We find that the donor star in HS 0218+3229 is significantly undermassive for its spectral type. It is therefore very likely that it has undergone nuclear evolution prior to the onset of mass transfer.
Key words: accretion, accretion discs - stars: binaries: close - stars: novae, cataclysmic variables
1 Introduction
Testing the current evolutionary models of the present-day Galactic population of cataclysmic variables (CVs) is not possible without a significant sample of the actual masses of the white dwarfs (i.e. the accretors) and the late-type companion stars (i.e. the donors) that form this sort of binary system. But accurate measurements of the component masses in CVs are, however, not an easy task. The donor stars are usually veiled by the extreme brightness of the accretion structures, especially the accretion disc. Furthermore, the white dwarfs are also very often hidden from view in CVs with orbital periods above the 2-3 h period gap, so optical studies aimed at dynamical mass measurements are scarce and usually make dubious assumptions. A common practice has been to assume that the amplitude of the radial velocity curve of the wings of the disc emission lines can be regarded as a reasonable estimate of the radial velocity amplitude of the white dwarf (K1), but this assumption is usually far from being true (see e.g. Shafter et al. 1995). Therefore, time-resolved studies of CVs in which the donor star and/or the white dwarf are exposed are chiefly important to our understanding of CV evolution.
HS 0218+3229 was discovered during our large-scale search for CVs in the hamburg quasar survey (HQS), based on their spectroscopic properties or, more specifically, the presence of strong emission and/or absorption lines (Gänsicke et al. 2002b). Fifty-three new CVs were found within this project, and the orbital period has been determined for the majority of them. The main result is that most of the HQS CVs have been found to have orbital periods above the period gap. Those include rarely outbursting dwarf novae, such as GY Cnc (HS 0907+1902, Gänsicke et al. 2000) or RX J0944.5+0357 (HS 0941+0411, Mennickent et al. 2002); magnetic CVs with relatively weak X-ray emission such as 1RXS J062518.2+733433 (HS 0618+7336, Araujo-Betancor et al. 2003), RX J1554.2+2721 (HS 1552+2730, Thorstensen & Fenton 2002; Gänsicke et al. 2004), and HS 0943+1404 (Rodríguez-Gil et al. 2005); a number of SW Sextantis stars (Szkody et al. 2001; Rodríguez-Gil et al. 2007,2004); one of the youngest pre-CVs known (HS 1857+5144, Aungwerojwit et al. 2007); long-period CVs (Aungwerojwit et al. 2005); and several dwarf novae (Aungwerojwit et al. 2006).
This paper presents the dynamical determination of the stellar masses in the cataclysmic variable HS 0218+3229. We present the data in Sect. 2, and an identification spectrum in Sect. 3. The orbital period is measured from the optical photometry in Sect. 4 before analysing the time-resolved spectroscopic data in Sect. 5. Modelling of the ellipsoidal modulation is carried out in Sect. 6. Finally, the system parameters of HS 0218+3229 and the overall discussion are presented in Sect. 7.
2 Observational data
2.1 Photometry
![\begin{figure}
{\includegraphics[width=7cm,clip]{1312fg01.ps} }\par\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg27.gif) |
Figure 1:
|
| Open with DEXTER | |
Astrophysikalisches Institut Potsdam.
Time series R-band photometry of HS 0218+3229 (hereafter HS 0218) was obtained on 3 nights during the period 2001 January-February using the 0.70 m telescope of the astrophysikalisches institut potsdam (AIP), Germany. The images were obtained with the camera equipped with a SITe
Fred Lawrence Whipple Observatory.
Further time-resolved R-band photometry of HS 0218 was secured on 2005 October 8-11 using the 1.2 m telescope at the fred lawrence whipple observatory (FLWO) in Arizona. The images were obtained with the KEPLERCAM mosaic camera which consists of an array of four
2.2 Optical spectroscopy
During an identification run of HQS CV candidates at the 2.2 m Calar Alto telescope on 2000 September 20, we obtained a pair of blue/red spectra of HS 0218 with the CAFOS spectrograph (Table 1). We used the B-200 and R-200 gratings in conjunction with a 2
![]() slit, which provided a spectral resolution of
slit, which provided a spectral resolution of ![]() 10 Å (FWHM). A standard reduction was performed using the CAFOS MIDAS quicklook package. The detection of strong Balmer emission lines and absorption lines of a late-type star confirmed the CV nature of HS 0218 and encouraged us to make the follow-up observations described in what follows.
10 Å (FWHM). A standard reduction was performed using the CAFOS MIDAS quicklook package. The detection of strong Balmer emission lines and absorption lines of a late-type star confirmed the CV nature of HS 0218 and encouraged us to make the follow-up observations described in what follows.
Table 1: Log of observations.
Time-resolved spectroscopy of HS 0218 was obtained with the double-armed TWIN spectrograph on the 3.5 m telescope in Calar Alto on 2002 October 28-29 (Table 1). On the first night, a total of 38 blue and red spectra were acquired using the T08 and T01 gratings, respectively, and a 1.2
![]() slit. The wavelength ranges
slit. The wavelength ranges
![]() -5560 and
-5560 and
![]() 5800-7390 were sampled at 2.2 and 1.6 Å resolution (FWHM), respectively. The gratings T05 and T06 and the same slit width were selected for the second night. This granted access to the ranges
5800-7390 were sampled at 2.2 and 1.6 Å resolution (FWHM), respectively. The gratings T05 and T06 and the same slit width were selected for the second night. This granted access to the ranges
![]() 3985-5050 and
3985-5050 and
![]() 5910-6990 at 1.1 and 1.2 Å resolution (FWHM) in the blue and the red, respectively. Spectra of the G191-B2B flux standard were taken to derive the instrument response function. Both the identification spectra and the spectra obtained on the first night showed a red continuum and absorption features originating in the photosphere of a mid-K secondary star. Hence, we also took spectra of six K stars of different spectral sub-type during the second night. For wavelength calibration we acquired spectra of a HeAr lamp throughout each night.
5910-6990 at 1.1 and 1.2 Å resolution (FWHM) in the blue and the red, respectively. Spectra of the G191-B2B flux standard were taken to derive the instrument response function. Both the identification spectra and the spectra obtained on the first night showed a red continuum and absorption features originating in the photosphere of a mid-K secondary star. Hence, we also took spectra of six K stars of different spectral sub-type during the second night. For wavelength calibration we acquired spectra of a HeAr lamp throughout each night.
Prior to optimal extraction of the individual spectra (Horne 1986), the raw images were bias-subtracted and flat-field corrected. Sky emission was removed during the optimal extraction of the spectra. The pixel-wavelength data were well fitted by a fourth-order polynomial, with an rms always smaller than one tenth of the spectral dispersion in all cases. The wavelength scale for each spectrum was derived by interpolating between the two nearest arc spectra. The accuracy of our wavelength calibration was improved by using the night-sky lines to correct for any zero-point offset.
The reduction steps and one-dimensional spectrum extraction were performed within IRAF, whilst the wavelength calibration was performed in MOLLY![]() .
.
![\begin{figure}
\par\includegraphics[height=7cm,clip]{1312fg02.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg35.gif) |
Figure 2: Discovery spectrum of HS 0218 obtained with the 2.2 m telescope at Calar Alto in September 2000 (solid line). The spectrum of a K4 V star (HD 5351) is shown as a dotted line, shifted down by 0.5 units for clarity. The template spectrum was extracted from the spectral catalogue of Jacoby et al. (1984). The absorption-line spectrum of HS 0218 is characteristic of a mid-K star. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1312fg03.ps}\includegraphics[width=8.5cm,clip]{1312fg04.ps} %
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg36.gif) |
Figure 3: R-band light curves of HS 0218+3229 obtained at the AIP ( left) and the FLWO ( right). |
| Open with DEXTER | |
3 Identification spectroscopy
One of the remarkable features of the identification spectrum of HS 0218 (Fig. 2) is its red continuum, which reveals the dominance of the companion star. The absence of strong TiO absorption bands suggests a spectral type earlier than M. In fact, the broad absorption observed at ![]() 5200 Å (produced by MgH at 5180 Å, a TiO band at
5200 Å (produced by MgH at 5180 Å, a TiO band at
![]() 4954-5200, and a jump in the continuum due to the Mg I triplet at
4954-5200, and a jump in the continuum due to the Mg I triplet at
![]() 5168-5185) constitutes a clear signature of a K-type star (McClintock & Remillard 1990, and references therein). In Sect. 5.2 we present a more accurate determination of the secondary star spectral type based on measurements of the rotational broadening of its absorption lines.
5168-5185) constitutes a clear signature of a K-type star (McClintock & Remillard 1990, and references therein). In Sect. 5.2 we present a more accurate determination of the secondary star spectral type based on measurements of the rotational broadening of its absorption lines.
4 The orbital period of HS 0218
The R-band light curves of HS 0218 (Fig. 3) exhibit a clear quasi-sinusoidal modulation with variable minima. Deeper and shallower minima alternate in a periodic basis every ![]() 3.5 h. This behaviour, together with an optical spectrum dominated by the donor star (Fig. 2), make us identify this variation with a classical ellipsoidal modulation resulting from the changing projected area of the Roche lobe with orbital phase. The deeper minima in the ellipsoidal light curve are caused by the stronger gravity darkening on the hemisphere facing the white dwarf, so they must occur at orbital phase 0.5. Therefore, the actual orbital period of HS 0218 must be twice the separation between consecutive minima, which is confirmed by the radial velocity curve of the donor star (Sect. 5.1).
3.5 h. This behaviour, together with an optical spectrum dominated by the donor star (Fig. 2), make us identify this variation with a classical ellipsoidal modulation resulting from the changing projected area of the Roche lobe with orbital phase. The deeper minima in the ellipsoidal light curve are caused by the stronger gravity darkening on the hemisphere facing the white dwarf, so they must occur at orbital phase 0.5. Therefore, the actual orbital period of HS 0218 must be twice the separation between consecutive minima, which is confirmed by the radial velocity curve of the donor star (Sect. 5.1).
As the photometry spans much longer than the spectroscopy, the analysis of the light curves provided a more accurate orbital period determination. The analysis-of-variance (AOV, Schwarzenberg-Czerny 1989) periodogram computed from our light curves is presented in Fig. 4. The highest peak is centred at
![]() (
(![]() 3.57 h), whilst the second highest lies exactly at half that frequency (
3.57 h), whilst the second highest lies exactly at half that frequency (
![]() ;
;
![]() h), which is the actual orbital frequency.
h), which is the actual orbital frequency.
In order to improve the accuracy of the orbital period we calculated a linear ephemeris from the times of all available photometric minima derived from Gaussian fits. Additionally, two measurements of the instant of zero phase (i.e. inferior cojunction of the secondary star, T0) were obtained from sine fits to the secondary star's radial velocity curves presented in Sect. 5.1, which were also included in the calculations. The measurements of the times of phase 0 (and also 0.5 for the ellipsoidal light curves) are presented in Table 2. The resulting orbital ephemeris is:
where the numbers in parentheses quote the uncertainty in the last digit.
Figure 4 also shows all the R-band data folded on the orbital period using the ephemeris given in Eq. (1). The ellipsoidal modulation is apparent. The shape of the folded light curves, however, shows significant deviations between the AIP and FLWO data. The 2001 January 8 light curve clearly displays the phase-0.5 minimum and phase-0.75 maximum shifted by ![]() -0.05 cycle with respect to the FLWO light curve. This cannot be the effect of an inaccurate orbital period determination as the phase-0 minima and phase 0.75-0 branches match very well in both sets of data. In addition, the 2001 January 16 AIP light curve exhibits a broader phase-0 minimum, with the phase 0-0.25 rising branch lagging that of the FLWO and almost equal primary and secondary minima. This behaviour indicates that the ellipsoidal modulation is actually contaminated by other sources of variation, likely originating in the accretion disc and/or the donor star itself (e.g. irradiation).
-0.05 cycle with respect to the FLWO light curve. This cannot be the effect of an inaccurate orbital period determination as the phase-0 minima and phase 0.75-0 branches match very well in both sets of data. In addition, the 2001 January 16 AIP light curve exhibits a broader phase-0 minimum, with the phase 0-0.25 rising branch lagging that of the FLWO and almost equal primary and secondary minima. This behaviour indicates that the ellipsoidal modulation is actually contaminated by other sources of variation, likely originating in the accretion disc and/or the donor star itself (e.g. irradiation).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg05.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg41.gif) |
Figure 4:
Top main panel: analysis-of-variance (AOV) periodogram computed from the R-band photometric data (Fig. 3). The periodogram shown on top was constructed from a fake sine wave with a frequency of 2 |
| Open with DEXTER | |
Table 2: Timings of phase 0 and 0.5 (light curves only).
On the other hand, the R-band light curves of HS 0218 also display higher frequency activity (see e.g. the 2005 October 10 light curve in Fig. 3). To analyse these variations we first subtracted the ellipsoidal modulation (by means of a smoothed, Fourier series-fitted version of the curves) and then computed an AOV periodogram from all the detrended light curves. The combined power spectrum does not show any predominant frequency. However, the periodogram computed from the 2005 October 9 data alone (not shown) exhibits a prominent peak at
![]() ,
which corresponds to a period of
,
which corresponds to a period of
![]() mn (=0.027 d), approximately 10% of the orbital period. The periodograms calculated from the other individual light curves (with the exception of 2005 October 8) exhibit their strongest peaks at close but lower frequencies. This might suggest the presence of quasi-periodic oscillations in HS 0218, but a much more longer light curve coverage would be needed to draw any firm conclusions.
mn (=0.027 d), approximately 10% of the orbital period. The periodograms calculated from the other individual light curves (with the exception of 2005 October 8) exhibit their strongest peaks at close but lower frequencies. This might suggest the presence of quasi-periodic oscillations in HS 0218, but a much more longer light curve coverage would be needed to draw any firm conclusions.
5 Time-resolved spectroscopy
5.1 The radial velocity amplitude of the donor star
The radial velocity curve of the secondary star in HS 0218 was measured
from the red spectra using the method of cross-correlation with the
spectrum of a template star (Tonry & Davis 1979). Five template
stars with spectral types ranging from K0 V to K5 V were acquired on
the night of 2002 October 29 to extract the radial velocities. Prior to
the cross-correlation, the spectra were re-sampled onto a common
logarithmic wavelength scale and normalised by means of a low-order
spline fit to the continuum. Individual velocities were then extracted
by cross-correlation with each template star in the range
![]() 6090-6520. We chose this spectral interval because it
contains lines useful not only for radial velocity measurements, but
also for spectral-type classification and rotational broadening
measurements (see Sect. 5.2).
6090-6520. We chose this spectral interval because it
contains lines useful not only for radial velocity measurements, but
also for spectral-type classification and rotational broadening
measurements (see Sect. 5.2).
A first look at the velocities indicates a period of ![]() 0.3 d,
which confirms the ellipsoidal nature of the R-band light curves
(Sect. 4). We therefore performed least-squares sine fits
to the radial velocity data with the period fixed at the photometric
orbital period. The resulting fit parameters are summarised in
Table 3. Although all the values are very similar, we adopt the
K5 V parameters of the radial velocity curve since the spectral type of the
donor star is shown to be most likely K5 (see Sect. 5.2):
0.3 d,
which confirms the ellipsoidal nature of the R-band light curves
(Sect. 4). We therefore performed least-squares sine fits
to the radial velocity data with the period fixed at the photometric
orbital period. The resulting fit parameters are summarised in
Table 3. Although all the values are very similar, we adopt the
K5 V parameters of the radial velocity curve since the spectral type of the
donor star is shown to be most likely K5 (see Sect. 5.2):
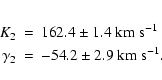
All quoted uncertainties are 1-
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg06.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg47.gif) |
Figure 5:
Radial velocity curves of the secondary star (solid dots) and the
|
| Open with DEXTER | |
Table 3:
Radial velocity parameters (errors at 1![]() ).
).
Table 4: Spectral classification and rotational broadening.
5.2 Spectral type and rotational broadening
To determine the spectral type of the donor star and the rotational broadening of its absorption lines, we used the technique outlined in Marsh et al. (1994). It is based on the search for the lowest residual obtained when subtracting a set of templates from the Doppler-corrected, average spectrum of the target.
We proceeded as follows: we used the spectra acquired during the
second night, as both target and template spectra were acquired with
the same instrumental setup. This is essential to derive a reliable
value for the rotational broadening (![]() ), in particular when
), in particular when ![]() is
of the same order as the instrumental resolution. First, the 18 target spectra were Doppler-corrected to the rest frame of the donor
star by using the radial velocity parameters derived in
Sect. 5.1. Next, we produced an average spectrum after
assigning different weights to the individual spectra to maximise the
signal-to-noise ratio of the sum. The template spectra were broadened from
70 to 110 km s-1 in steps of 1.0 km s-1 through convolution
with the spherical rotational profile of Gray (1992) with a linearised
limb-darkening coefficient of 0.5. Each broadened version of a
template spectrum was scaled by a factor f (representing the
fractional contribution of light from the secondary star) and
subtracted from the target Doppler-corrected average. Then a
is
of the same order as the instrumental resolution. First, the 18 target spectra were Doppler-corrected to the rest frame of the donor
star by using the radial velocity parameters derived in
Sect. 5.1. Next, we produced an average spectrum after
assigning different weights to the individual spectra to maximise the
signal-to-noise ratio of the sum. The template spectra were broadened from
70 to 110 km s-1 in steps of 1.0 km s-1 through convolution
with the spherical rotational profile of Gray (1992) with a linearised
limb-darkening coefficient of 0.5. Each broadened version of a
template spectrum was scaled by a factor f (representing the
fractional contribution of light from the secondary star) and
subtracted from the target Doppler-corrected average. Then a ![]() test on the residuals was performed in the range
test on the residuals was performed in the range
![]() 6090-6520 and the optimal values of f and
6090-6520 and the optimal values of f and ![]() were provided by minimising
were provided by minimising ![]() .
.
Besides the instrumental
broadening, the secondary star's photospheric lines are also smeared
due to the orbital motion of the donor star during the length of the
exposure. With 600-s exposures, the orbital smearing is ![]()
![]() km s-1. This effect can be
corrected producing a spectral template by averaging 18 smeared copies
of a template spectrum with the same weights as used to average the
spectra of the target. We performed this correction, finding no
significant difference in the values calculated for the rotational
broadening.
km s-1. This effect can be
corrected producing a spectral template by averaging 18 smeared copies
of a template spectrum with the same weights as used to average the
spectra of the target. We performed this correction, finding no
significant difference in the values calculated for the rotational
broadening.
The minimisation of
![]() (Table 4) shows that the
spectral type of the secondary star in HS 0218 is later than K1. Also, a K0-1 V donor star is rejected as the templates give f > 1. Similar results for the spectral classification were obtained
when repeating the above procedure on the 38 target spectra acquired during the first night. Additional constraints on the spectral type of the donor star are provided by the infrared colours of HS 0218 after correcting for reddening and assuming the same
(Table 4) shows that the
spectral type of the secondary star in HS 0218 is later than K1. Also, a K0-1 V donor star is rejected as the templates give f > 1. Similar results for the spectral classification were obtained
when repeating the above procedure on the 38 target spectra acquired during the first night. Additional constraints on the spectral type of the donor star are provided by the infrared colours of HS 0218 after correcting for reddening and assuming the same
![]() at
each infrared bandpass. Using 2MASS magnitudes we derive
(J-H, H-K, J-K)0=(0.63, 0.09, 0.72) based on
E(B-V)=0.071 mag (Schlegel et al. 1998). The uncertainties in the infrared
colours are 0.04 mag. The above colours reject an M-type dwarf
(J-K > 0.86, H-K > 0.165) and support a K4-K5 dwarf (see e.g. Bessell & Brett 1988). For comparison, a K5 dwarf has colours of
(0.61, 0.11, 0.72). Further visual inspection of the average spectra and templates supports a K5 spectral type based on the strength of the weak TiO bands in the spectrum and by comparing the relative intensities of the absorption lines in the interval
at
each infrared bandpass. Using 2MASS magnitudes we derive
(J-H, H-K, J-K)0=(0.63, 0.09, 0.72) based on
E(B-V)=0.071 mag (Schlegel et al. 1998). The uncertainties in the infrared
colours are 0.04 mag. The above colours reject an M-type dwarf
(J-K > 0.86, H-K > 0.165) and support a K4-K5 dwarf (see e.g. Bessell & Brett 1988). For comparison, a K5 dwarf has colours of
(0.61, 0.11, 0.72). Further visual inspection of the average spectra and templates supports a K5 spectral type based on the strength of the weak TiO bands in the spectrum and by comparing the relative intensities of the absorption lines in the interval
![]() 6400-6530. Hereafter, in accordance with the above analysis, we adopt a K5 spectral type for the donor star.
6400-6530. Hereafter, in accordance with the above analysis, we adopt a K5 spectral type for the donor star.
A rotational broadening measurement of
![]() km s-1 was
obtained from the K5 V template. However, the value of the limb-darkening coefficient for the absorption lines is unknown and this limits our ability in evaluating
km s-1 was
obtained from the K5 V template. However, the value of the limb-darkening coefficient for the absorption lines is unknown and this limits our ability in evaluating ![]() .
Limb-darkening
coefficients for the absoption lines in late-type stars are expected
to be smaller than those for the continuum (Collins & Truax 1995). Therefore, we repeated the above analysis for both a null linearised limb-darkening coefficient and for the value expected for
the continuum. The latter was selected for each template from Claret et al. (1995). We provide the
results for each template in Table 3 (Col. 6). As one can see, our uncertainty in the limb-darkening leads to values of
.
Limb-darkening
coefficients for the absoption lines in late-type stars are expected
to be smaller than those for the continuum (Collins & Truax 1995). Therefore, we repeated the above analysis for both a null linearised limb-darkening coefficient and for the value expected for
the continuum. The latter was selected for each template from Claret et al. (1995). We provide the
results for each template in Table 3 (Col. 6). As one can see, our uncertainty in the limb-darkening leads to values of ![]() of 82.4-89.4 km s-1 (K5 V template).
of 82.4-89.4 km s-1 (K5 V template).
5.3 The radial velocity amplitude of the white dwarf
We measured the radial velocity curve of the
![]() line wings by using
the double-Gaussian technique of Schneider & Young (1980). In an
ideal world, with an axisymmetric accretion disc dominating line
emission, the line wings would provide a good estimate of K1. We
obtained radial velocity curves of the
line wings by using
the double-Gaussian technique of Schneider & Young (1980). In an
ideal world, with an axisymmetric accretion disc dominating line
emission, the line wings would provide a good estimate of K1. We
obtained radial velocity curves of the
![]() wings for a number of
Gaussian (
FWHM = 200
wings for a number of
Gaussian (
FWHM = 200
![]() )
separations between 600 and
2900
)
separations between 600 and
2900
![]() in 100
in 100
![]() steps. The curve for a 1300
steps. The curve for a 1300
![]() separation
gave the best results and is shown in Fig. 5. The wings are clearly delayed
by
separation
gave the best results and is shown in Fig. 5. The wings are clearly delayed
by ![]() 0.1 cycle, but their
0.1 cycle, but their ![]() -velocity of
-velocity of
![]()
![]() (derived from a sine fit) is very similar to that of the donor star (
(derived from a sine fit) is very similar to that of the donor star (
![]()
![]() ). The sine fit gives an amplitude of the wings radial velocity curve of
). The sine fit gives an amplitude of the wings radial velocity curve of
![]()
![]() ,
which provides a mass ratio of
,
which provides a mass ratio of
![]() if assumed to be the radial velocity amplitude of the white dwarf. This mass ratio is equal to the measured from the rotational broadening of the
donor star absorption lines. Despite the phase shift that the
if assumed to be the radial velocity amplitude of the white dwarf. This mass ratio is equal to the measured from the rotational broadening of the
donor star absorption lines. Despite the phase shift that the
![]() radial velocities show (Fig. 5), the measured K1 value seems to be reliable in this case.
radial velocities show (Fig. 5), the measured K1 value seems to be reliable in this case.
6 Ellipsoidal light curve modelling
To model the ellipsoidal variation we used a binary code which uses full Roche geometry and a black body model to account for the emission of the distorted companion. In order to carry out the numerical integration the donor star surface is divided in small triangular tiles of equal area which cover completely the Roche-lobe filling star.
In this model, the disc contribution to the total light (
![]() )
is independent of the orbital phase and is scaled to a certain factor of the mean flux from the companion. The limb darkening coefficients are obtained from Al-Naimiy (1978) and the
)
is independent of the orbital phase and is scaled to a certain factor of the mean flux from the companion. The limb darkening coefficients are obtained from Al-Naimiy (1978) and the ![]() gravity darkening exponent is fixed at 0.08 (Lucy 1967). According to Gray (1992) the effective temperature of a K5 V star is 4557 K, which was adopted as the polar temperature. The synthetic ellipsoidal modulation should only depend on the orbital inclination angle, the mass ratio (
q = M2/M1, where M2 and M1 are the masses of the donor star and the compact object, respectively), and the relative disc contribution to the light curve (1-f).
In Sect. 5.2 we obtained
gravity darkening exponent is fixed at 0.08 (Lucy 1967). According to Gray (1992) the effective temperature of a K5 V star is 4557 K, which was adopted as the polar temperature. The synthetic ellipsoidal modulation should only depend on the orbital inclination angle, the mass ratio (
q = M2/M1, where M2 and M1 are the masses of the donor star and the compact object, respectively), and the relative disc contribution to the light curve (1-f).
In Sect. 5.2 we obtained
![]() by measuring the absorption lines in the range
by measuring the absorption lines in the range
![]() 6090-6520. This spectral region is contained in the R band and we can therefore use this value in our fits. However, we think that the contamination in the shape of the light curve may be due to night-to-night variations of the disc contribution (see Sect. 4). Hence, the value obtained during the spectroscopic campaign may not be the correct one for the photometric data.
6090-6520. This spectral region is contained in the R band and we can therefore use this value in our fits. However, we think that the contamination in the shape of the light curve may be due to night-to-night variations of the disc contribution (see Sect. 4). Hence, the value obtained during the spectroscopic campaign may not be the correct one for the photometric data.
In order to establish a conservative lower limit to the inclination angle (i) of the system we have fitted the light curve by using 1-f = 0, obtaining
![]() .
Since the light curves do not show eclipses we find an upper limit of
.
Since the light curves do not show eclipses we find an upper limit of
![]() from elemental trigonometry involving the maximum disc radius allowed by tidal interaction with the donor star (Paczynski 1977) and the Roche lobe radius of the latter. Thus, we obtain
from elemental trigonometry involving the maximum disc radius allowed by tidal interaction with the donor star (Paczynski 1977) and the Roche lobe radius of the latter. Thus, we obtain
![]() independently of
independently of
![]() .
The best fit to the ellipsoidal light curve was finally found for
.
The best fit to the ellipsoidal light curve was finally found for
![]() ,
q=0.62, and
,
q=0.62, and
![]() .
We have overplotted this synthetic model to the actual folded ellipsoidal curve in Fig. 4.
.
We have overplotted this synthetic model to the actual folded ellipsoidal curve in Fig. 4.
7 Discussion
7.1 Parameter estimates
Assuming that the companion star is synchronised with the binary motion and fills its Roche lobe, it is possible to calculate the mass ratio through the expression
![]() (e.g. Wade & Horne 1988). Thus we derive
0.52 < q < 0.65 from
(e.g. Wade & Horne 1988). Thus we derive
0.52 < q < 0.65 from
![]() km s-1 and the 99% confidence range for the rotational broadening (82.4-
km s-1 and the 99% confidence range for the rotational broadening (82.4-
![]() km s
km s
![]() km s-1). This mass-ratio range implies a primary velocity amplitude of 84 km s-1
< K1=qK2 < 106 km s-1. The value of
km s-1). This mass-ratio range implies a primary velocity amplitude of 84 km s-1
< K1=qK2 < 106 km s-1. The value of
![]()
![]() measured from the
measured from the
![]() line wings lies almost in the middle of this interval.
line wings lies almost in the middle of this interval.
The velocity amplitude and orbital period imply a mass function of
![]() .
Combining the values for f(M1) and our extreme limits on q and i, we constrain the masses of the
compact object and the companion star to be in the range:
.
Combining the values for f(M1) and our extreme limits on q and i, we constrain the masses of the
compact object and the companion star to be in the range:
![]() and
and
![]() .
Table 5 gives the determined system parameters for the extreme values of the inclination given by the ellipsoidal
modelling. The uncertainties in the masses for a given inclination are
dominated by the uncertainty in the value of
.
Table 5 gives the determined system parameters for the extreme values of the inclination given by the ellipsoidal
modelling. The uncertainties in the masses for a given inclination are
dominated by the uncertainty in the value of ![]() .
For
comparison, using the resulting value obtained for a limb-darkening
coefficient of 0.5 (
.
For
comparison, using the resulting value obtained for a limb-darkening
coefficient of 0.5 (
![]() km s-1), we
derive:
km s-1), we
derive:
![]() ,
,
![]() ,
,
![]() and
and
![]() km s-1. To
determine the above 1-
km s-1. To
determine the above 1-![]() uncertainties a Monte Carlo
approach was used in which we draw one million random values for the
observed quantities. We treated K2 and
uncertainties a Monte Carlo
approach was used in which we draw one million random values for the
observed quantities. We treated K2 and ![]() as being
normally distributed about their measured values with standard
deviations equal to the uncertainties on the measurements. For i the
distribution was taken to be uniform. Given the stellar masses
and orbital period, we can constrain the semi-major axis (a) of the
orbit using Kepler's Third Law, the radius of the secondary star (R2) using Eggleton's (1983) expression for the effective radius of the secondary Roche Lobe, and the luminosity of the secondary star (L2) using Stefan-Boltzmann's Law and the 4557 K
effective temperature inferred from the spectral type (Gray 1992). These quantities are listed in Table 5.
as being
normally distributed about their measured values with standard
deviations equal to the uncertainties on the measurements. For i the
distribution was taken to be uniform. Given the stellar masses
and orbital period, we can constrain the semi-major axis (a) of the
orbit using Kepler's Third Law, the radius of the secondary star (R2) using Eggleton's (1983) expression for the effective radius of the secondary Roche Lobe, and the luminosity of the secondary star (L2) using Stefan-Boltzmann's Law and the 4557 K
effective temperature inferred from the spectral type (Gray 1992). These quantities are listed in Table 5.
To constrain the distance to HS 0218 we have adopted the luminosity of the donor star given in Table 5, which, combined with the bolometric correction and the (V-R) colour of a K5 V star, yield an absolute magnitude of MR=5.96-5.65. We have calculated a dereddened magnitude of the secondary star of R=15.65-15.72 using the apparent magnitude of HS 0218 (R=15.6), AR=0.188 and a ![]() 15-20% veiling from the accretion disc (Sect. 6). Therefore, the distance modulus relation provides a distance to HS 0218 of 0.87-1.0 kpc. Note that this distance estimate must be considered as approximate given the uncertainties in our photometric calibration based on USNO A2.0 mag of field stars.
15-20% veiling from the accretion disc (Sect. 6). Therefore, the distance modulus relation provides a distance to HS 0218 of 0.87-1.0 kpc. Note that this distance estimate must be considered as approximate given the uncertainties in our photometric calibration based on USNO A2.0 mag of field stars.
Table 5: Summary of derived system parameters.
7.2 An evolved donor star
As we have demonstrated, the companion star in HS 0218 is most likely of
spectral type K5. A main-sequence K5 star has a nominal mass of
![]() (Gray 1992). The disagreement with the mass
constraints obtained above is easily explained if the secondary star
is undermassive for its spectral type, that is, has undergone nuclear
evolution before the onset of mass transfer. In fact, with a mass of
(Gray 1992). The disagreement with the mass
constraints obtained above is easily explained if the secondary star
is undermassive for its spectral type, that is, has undergone nuclear
evolution before the onset of mass transfer. In fact, with a mass of
![]() 0.33
0.33 ![]() its nuclear timescale is much greater than the
Hubble time. Previous work on donor stars in long-period CVs (see e.g. Fig. 5 in Beuermann et al. 1998) shows that most of them at long orbital periods are underluminous, and likely evolved. In Fig. 6 we plot evolutionary sequences for an initial donor star mass of 1.0
its nuclear timescale is much greater than the
Hubble time. Previous work on donor stars in long-period CVs (see e.g. Fig. 5 in Beuermann et al. 1998) shows that most of them at long orbital periods are underluminous, and likely evolved. In Fig. 6 we plot evolutionary sequences for an initial donor star mass of 1.0 ![]() and mass transfer onset at several central hydrogen abundances (Baraffe & Kolb 2000). Note that this is only for illustrative purposes and the actual initial donor mass in HS 0218 can be different. The mass of the donor star in HS 0218 is much lower than predicted by any of the sequences considered.
and mass transfer onset at several central hydrogen abundances (Baraffe & Kolb 2000). Note that this is only for illustrative purposes and the actual initial donor mass in HS 0218 can be different. The mass of the donor star in HS 0218 is much lower than predicted by any of the sequences considered.
Schenker & King (2002) show the evolution of the donor mean density
as a function of its mass (their Fig. 2) for both the ZAMS and
evolved cases. With an orbital period of 7.13 h, HS 0218 has a mean
density of 2.1 g cm-3, which results in a donor mass of ![]() 0.3
0.3 ![]() for the case of strong thermal-timescale mass transfer. Moreover, according to Schenker et al. (2002) (their Fig. 6), a donor star of spectral type K5-K7 is expected for a mass of
for the case of strong thermal-timescale mass transfer. Moreover, according to Schenker et al. (2002) (their Fig. 6), a donor star of spectral type K5-K7 is expected for a mass of ![]() 0.3
0.3 ![]() .
Both predictions for the case of an evolved donor agree well with our measurements.
.
Both predictions for the case of an evolved donor agree well with our measurements.
The binary system, therefore, formed with a companion star more massive than the white dwarf. In this scenario (
q=M2/M1 > 1), and as a consequence of mass transfer towards the white dwarf, the Roche lobe of the donor star (initially the most massive component) shrinks faster than the thermal equilibrium radius. The secondary star thus tends to expand beyond the Roche lobe to reach the thermal equilibrium radius, which triggers an episode of thermal-timescale mass transfer until the mass ratio reverses (see e.g. King et al. 2001; Schenker et al. 2002). Beyond this point, normal mass transfer starts due to either angular momentum loss (i.e. secondary Roche lobe shrinkage) of nuclear evolution of the donor star (i.e. increase of the thermal equilibrium radius) and the system becomes a normal CV. The fact that the measured white dwarf mass (
![]() )
is lower than the average value for CVs (Smith & Dhillon 1998) indicates that the transferred donor material during the thermal-timescale stage has been blown off the binary system.
)
is lower than the average value for CVs (Smith & Dhillon 1998) indicates that the transferred donor material during the thermal-timescale stage has been blown off the binary system.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg07.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg133.gif) |
Figure 6:
Spectral type, mass, and radius as a function of orbital period for four different evolutionary sequences with different initial central hydrogen abundance ( |
| Open with DEXTER | |
Nuclear evolution of the donor star prior to normal CV life should reflect in the chemical composition of the accreted material. Because of CNO processing of the material, carbon must be significantly depleted and nitrogen subsequently enriched. Unusually low C IV/N V ultraviolet line flux ratios have been observed in a number of CVs (Gänsicke et al. 2003), suggesting that a significant fraction of the present-day CV population is descendant from systems that have passed through a thermal-timescale mass transfer phase. HS 0218 is therefore a promising target for ultraviolet spectroscopy to check whether N enrichment has taken place.
Acknowledgements
This work was supported by XMM-Newton Grant NNG05GJ22G. The HQS was supported by the Deutsche Forschungsgemeinschaft through grants Re 353/11 and Re 353/22. The use of the MOLLY package developed and maintained by Tom Marsh is acknowledged. Thanks to the anonymous referee for valuable input.
References
- Al-Naimiy, H. M. 1978, Ap&SS, 53, 181 [NASA ADS] [CrossRef] (In the text)
- Araujo-Betancor, S., Gänsicke, B. T., Hagen, H.-J., Rodrí guez-Gil, P., & Engels, D. 2003, A&A, 406, 213 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aungwerojwit, A., Gänsicke, B. T., Rodríguez-Gil, P., et al. 2005, A&A, 443, 995 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aungwerojwit, A., Gänsicke, B. T., Rodríguez-Gil, P., et al. 2006, A&A, 455, 659 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aungwerojwit, A., Gänsicke, B. T., Rodríguez-Gil, P., et al. 2007, A&A, 469, 297 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baraffe, I., & Kolb, U. 2000, MNRAS, 318, 354 [NASA ADS] [CrossRef] (In the text)
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] (In the text)
- Beuermann, K., Baraffe, I., Kolb, U., & Weichhold, M. 1998, A&A, 339, 518 [NASA ADS] (In the text)
- Claret, A., Diaz-Cordoves, J., & Gimenez, A. 1995, A&AS, 114, 247 [NASA ADS] (In the text)
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] (In the text)
- Gänsicke, B. T., Fried, R. E., Hagen, H.-J., et al. 2000, A&A, 356, L79 [NASA ADS] (In the text)
- Gänsicke, B. T., Beuermann, K., & Reinsch, K., ed. 2002a, The Physics of Cataclysmic Variables and Related Objects, ASP Conf. Ser., 261
- Gänsicke, B. T., Hagen, H. J., & Engels, D. 2002b, in The Physics of Cataclysmic Variables and Related Objects, ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 190 (In the text)
- Gänsicke, B. T., Szkody, P., de Martino, D., et al. 2003, ApJ, 594, 443 [NASA ADS] [CrossRef] (In the text)
- Gänsicke, B. T., Jordan, S., Beuermann, K., et al. 2004, ApJ, 613, L141 [NASA ADS] [CrossRef]
- Gray, D. F. 1992, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) (In the text)
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] (In the text)
- Jacoby, G. H., Hunter, D. A., & Christian, C. A. 1984, ApJS, 56, 257 [NASA ADS] [CrossRef] (In the text)
- King, A. R., Schenker, K., Kolb, U., & Davies, M. B. 2001, MNRAS, 321, 327 [NASA ADS] [CrossRef]
- Lucy, L. B. 1967, Zeitschrift fur Astrophysik, 65, 89 [NASA ADS] (In the text)
- Marsh, T. R., Robinson, E. L., & Wood, J. H. 1994, MNRAS, 266, 137 [NASA ADS] (In the text)
- Mateo, M., & Schechter, P. L. 1989, in European Southern Observatory Astrophysics Symposia, ed. P. J. Grosbøl, F. Murtagh, & R. H. Warmels, 31, 69 (In the text)
- McClintock, J. E., & Remillard, R. A. 1990, ApJ, 350, 386 [NASA ADS] [CrossRef] (In the text)
- Mennickent, R. E., Tovmassian, G., Zharikov, S. V., et al. 2002, A&A, 383, 933 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Naylor, T. 1998, MNRAS, 296, 339 [NASA ADS] [CrossRef] (In the text)
- Paczynski, B. 1977, ApJ, 216, 822 [NASA ADS] [CrossRef] (In the text)
- Rodríguez-Gil, P., Gänsicke, B. T., Barwig, H., Hagen, H.-J., & Engels, D. 2004, A&A, 424, 647 [NASA ADS] [CrossRef] [EDP Sciences]
- Rodríguez-Gil, P., Gänsicke, B. T., Hagen, H.-J., et al. 2005, A&A, 440, 701 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rodríguez-Gil, P., Gänsicke, B. T., Hagen, H.-J., et al. 2007, MNRAS, 377, 1747 [NASA ADS] [CrossRef]
- Schenker, K., & King, A. R. 2002, in The Physics of Cataclysmic Variables and Related Objects, ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 242 (In the text)
- Schenker, K., King, A. R., Kolb, U., Wynn, G. A., & Zhang, Z. 2002, MNRAS, 337, 1105 [NASA ADS] [CrossRef] (In the text)
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Schneider, D. P., & Young, P. 1980, ApJ, 238, 946 [NASA ADS] [CrossRef] (In the text)
- Schwarzenberg-Czerny, A. 1989, MNRAS, 241, 153 [NASA ADS] (In the text)
- Shafter, A. W., Veal, J. M., & Robinson, E. L. 1995, ApJ, 440, 853 [NASA ADS] [CrossRef] (In the text)
- Smith, D. A., & Dhillon, V. S. 1998, MNRAS, 301, 767 [NASA ADS] [CrossRef] (In the text)
- Steeghs, D., & Jonker, P. G. 2007, ApJL, 669, L85 [NASA ADS] [CrossRef]
- Szkody, P., Gänsicke, B., Fried, R. E., Heber, U., & Erb, D. K. 2001, PASP, 113, 1215 [NASA ADS] [CrossRef]
- Thorstensen, J. R., & Fenton, W. H. 2002, PASP, 114, 74 [NASA ADS] [CrossRef]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
HS 0218+3229
![[*]](/icons/foot_motif.gif)
- Based in part on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC). Observations were also obtained at the FLWO Observatory, a facility of the Smithsonian Institution.
- ...IRAF
![[*]](/icons/foot_motif.gif)
- IRAF is distributed by the National Optical Astronomy Observatories, which is operated by the Association of Universities for Research in Astronomy, Inc., under contract with the National Science Foundation.
- ...MOLLY
![[*]](/icons/foot_motif.gif)
- Written by T. R. Marsh, http://www.warwick.ac.uk/go/trmarsh
All Tables
Table 1: Log of observations.
Table 2: Timings of phase 0 and 0.5 (light curves only).
Table 3:
Radial velocity parameters (errors at 1![]() ).
).
Table 4: Spectral classification and rotational broadening.
Table 5: Summary of derived system parameters.
All Figures
![\begin{figure}
{\includegraphics[width=7cm,clip]{1312fg01.ps} }\par\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg27.gif) |
Figure 1:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=7cm,clip]{1312fg02.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg35.gif) |
Figure 2: Discovery spectrum of HS 0218 obtained with the 2.2 m telescope at Calar Alto in September 2000 (solid line). The spectrum of a K4 V star (HD 5351) is shown as a dotted line, shifted down by 0.5 units for clarity. The template spectrum was extracted from the spectral catalogue of Jacoby et al. (1984). The absorption-line spectrum of HS 0218 is characteristic of a mid-K star. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1312fg03.ps}\includegraphics[width=8.5cm,clip]{1312fg04.ps} %
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg36.gif) |
Figure 3: R-band light curves of HS 0218+3229 obtained at the AIP ( left) and the FLWO ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg05.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg41.gif) |
Figure 4:
Top main panel: analysis-of-variance (AOV) periodogram computed from the R-band photometric data (Fig. 3). The periodogram shown on top was constructed from a fake sine wave with a frequency of 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg06.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg47.gif) |
Figure 5:
Radial velocity curves of the secondary star (solid dots) and the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1312fg07.ps}
\end{figure}](/articles/aa/full_html/2009/12/aa11312-08/Timg133.gif) |
Figure 6:
Spectral type, mass, and radius as a function of orbital period for four different evolutionary sequences with different initial central hydrogen abundance ( |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


