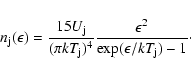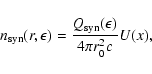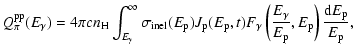| Issue |
A&A
Volume 496, Number 3, March IV 2009
|
|
|---|---|---|
| Page(s) | 751 - 758 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200810871 | |
| Published online | 09 February 2009 | |
Multi-waveband photons and high energy neutrinos from the Crab nebula
X. C. Yang - L. Zhang
Department of Physics, Yunnan University, 650091 Kunming, PR China
Received 28 August 2008 / Accepted 12 January 2009
Abstract
We study multi-waveband photon emission properties and
possible high-energy neutrino emission from the Crab nebula produced
by pulsar's accelerated heavy nuclei. Heavy nuclei are accelerated
in the outer magnetosphere of the Crab pulsar, and then suffer
partial photo-disintegration in the non-thermal radiation fields of
the pulsar's outer magnetosphere. The products (protons and
neutrons) of the photo-disintegration and surviving heavier nuclei
are injected into the expanding supernova remnant in which the
surviving heavier nuclei are further accelerated in the pulsar wind
zone. In such a case, relativistic hadrons and leptons are produced;
the hadrons consist of direct protons and the protons produced
through neutron decay in nuclei disintegration process, the leptons
consist of positrons accelerated in a realistic magneto-sonic
lepton-heavy iron plasma shock, electrons from the neutron decay,
direct electrons, and secondary electron/positron pairs in a
proton-proton interaction. We calculate the photo-disintegration
rate for a nucleus of atomic number A releasing i nucleons and the
hadronic and leptonic spectra in the Crab nebula. We then calculate
the multi-waveband non-thermal photon spectrum and possible
high-energy neutrino spectrum of the Crab nebula. Our results
indicate that the photon spectrum up to ![]() 10 TeV has a leptonic
origin, but it is difficult to distinguish leptonic and hadronic
origins of the spectrum with energy greater than 10 TeV.
10 TeV has a leptonic
origin, but it is difficult to distinguish leptonic and hadronic
origins of the spectrum with energy greater than 10 TeV.
Key words: radiation mechanisms: non-thermal - ISM: individual objects: Crab nebula - gamma rays: theory
1 Introduction
Pulsar wind nebulae (PWNe) are generally believed to be a kind of
Galactic cosmic ray source. The Crab nebula, being a well
established gamma-ray source with a complex spectrum extending up to
at least ![]() 80 TeV energies, is a possible object in which the
particles can be accelerated up to
80 TeV energies, is a possible object in which the
particles can be accelerated up to ![]() 1015-16 eV (e.g. de Jager & Harding 1992; Aharonian & Atoyan 1995). For the Crab
nebula, however, there are two possible kinds of models to explain
the observed TeV emission properties: leptonic origin models (e.g.
Jager & Harding 1992; Atoyan & Aharonian 1996; Zhang et al. 2008)
and hadronic origin models (e.g. Cheng et al. 1990; Atoyan &
Aharonian 1996; Bednarek & Prothero 1997; Bednarek & Bartosik
2003; a review see Bednarek 2007).
1015-16 eV (e.g. de Jager & Harding 1992; Aharonian & Atoyan 1995). For the Crab
nebula, however, there are two possible kinds of models to explain
the observed TeV emission properties: leptonic origin models (e.g.
Jager & Harding 1992; Atoyan & Aharonian 1996; Zhang et al. 2008)
and hadronic origin models (e.g. Cheng et al. 1990; Atoyan &
Aharonian 1996; Bednarek & Prothero 1997; Bednarek & Bartosik
2003; a review see Bednarek 2007).
Photon emission with energy up to several tens of TeV from the Crab nebula has been usually interpreted with the framework of synchrotron self-Compton (SSC) model. In such a model, relativistic leptons inside the nebula produce soft synchrotron photons, and these soft photons are next up-scattered by the same leptons to gamma-ray energies through an inverse Compton (IC) process, possible soft photons also include microwave background radiation (MBR), infrared or the optical background inside the nebula. This model has been successfully applied to the best studied TeV gamma-ray source-the Crab nebula and other TeV PWNe (de Jager & Harding 1992; Atoyan & Aharonian 1996; Zhang et al. 2008). On the other hand, the self-consistent, time dependent hadronic-leptonic model has been proposed to account for the high energy processes inside PWNe (e.g. Bednarek & Prothero 1997; Bednarek & Bartosik 2003, 2005). In such a model, heavy nuclei are accelerated in the pulsar magnetosphere, and then suffer partial photo-disintegration in the non-thermal radiation fields of pulsar's outer magnetosphere, leading to the production of relativistic protons and neutrons. These protons and neutrons, as well as surviving heavier nuclei, are injected into the expanding supernova remnant. Inside the remnant, relativistic hadrons consist of direct protons and the protons produced through neutron decay in the nuclei disintegration process, the leptons are excited by the relativistic nuclei and consist of electrons from the neutron decay, positrons accelerated in the realistic magneto-sonic lepton-heavy iron plasma shock, and secondary electron/positron pairs in the proton-proton interaction.
In this paper we study the production of non-thermal photons and
high-energy neutrinos in the Crab nebula based on the model of
Bednarek & Protheroe (1997) and Bednarek & Bartosik (2003). In our
treatment, we consider the relativistic proton spectrum from both
direct proton production and indirect proton production from neutron
decay through the disintegration process. We also consider four
kinds of leptons: the positrons accelerated in a realistic
magneto-sonic lepton-heavy iron plasma shock (Hoshino & Arons
1991; Hoshino et al. 1992; Gallant & Arons 1994), electrons
accompanying neutron decay, direct electrons, and secondary
e![]() pairs in proton-proton (pp) collisions (We call them
nuclei-excited leptons except for the direct electrons, which
accompany the nuclei). Different from the work in Bednarek &
Bartosik (2003), we include the direct proton contribution which
dominates the high-energy end of the proton spectrum, and use the
complete form of the positron spectrum (i.e. a Maxwellian
distribution plus a power-law tail) given by Hishino et al. (1992).
Using spectra of both hadrons and leptons, we calculate the
non-thermal spectrum of the Crab nebula, where the inclusive cross
sections of stable secondary particles produced by proton-proton
interaction, in parameterized formulae given by Kelner et al.
(2006), are used. The organization of this paper is as follows. We
describe the model in Sect. 2, and apply the model to the Crab nebula
in Sect. 3. We give our conclusions and discussion in Sect. 4.
pairs in proton-proton (pp) collisions (We call them
nuclei-excited leptons except for the direct electrons, which
accompany the nuclei). Different from the work in Bednarek &
Bartosik (2003), we include the direct proton contribution which
dominates the high-energy end of the proton spectrum, and use the
complete form of the positron spectrum (i.e. a Maxwellian
distribution plus a power-law tail) given by Hishino et al. (1992).
Using spectra of both hadrons and leptons, we calculate the
non-thermal spectrum of the Crab nebula, where the inclusive cross
sections of stable secondary particles produced by proton-proton
interaction, in parameterized formulae given by Kelner et al.
(2006), are used. The organization of this paper is as follows. We
describe the model in Sect. 2, and apply the model to the Crab nebula
in Sect. 3. We give our conclusions and discussion in Sect. 4.
2 Leptons and hadrons produced in the nebula
We describe the basic physics processes which produce non-thermal emission from the Crab nebula in the framework of the hadronic-leptonic model.
2.1 Nucleon injection in the pulsar magnetosphere
Rapidly rotating neutron stars are known to convert a significant
part of their rotation energy into radiation and the emission is
observable as a periodic signal. It is possible that rotating
magnetospheres of a neuron star can accelerate not only leptons but
also nuclei extracted from the positively charged polar cap region
(Bednarek & Bartosik 2004). The presence of heavy nuclei can
explain the high energy phenomena observed around a pulsar (Gil et al. 2003). The amount of irons accelerated in the inner
magnetosphere and pulsar wind zone, and injected in the pulsar wind
nebula, can be written as (Bednarek & Protheroe 1997)
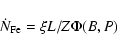 |
(1) |
where
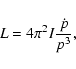
and
is the potential difference across the outer gap (Cheng et al. 1990), where I is the neutron star moment of inertia which is assumed to be
where n is the braking index (e.g. Gaensler & Slane 2006).
2.2 Photodisintegration of nuclei in the pulsar soft photon field
It has been proposed that there is the possibility of
photodisintegration of Fe nuclei during their propagation through
the soft photon field from the Crab pulsar (Bednarek & Protheroe
1997). The Fe nuclei escape from the polar cap surface and move
along magnetic field lines to enter the outer gap where they can be
accelerated in the outer gap potential, as in the model of Cheng et al. (1986a). Since nuclei have much larger Larmor radii and much
lower synchrotron and curvature radiations, they easily propagate
out across the field lines along the outer gap. The nuclei suffer
disintegration in collisions with the nonthermal radiation field in
the outer gap produced by accelerated electron and positron
cascades; the dimension of the outer gap is of the order of the
radius of the light cylinder, namely,
![]() cm (Cheng et al. 1986b). A single proton
or neutron emits in each nucleus disintegration, with the same
Lorentz factor of the nucleus. The nucleons injected into the
nebula, both the directly emitted protons and protons from neutron
decay, are trapped and accumulate in the nebula.
cm (Cheng et al. 1986b). A single proton
or neutron emits in each nucleus disintegration, with the same
Lorentz factor of the nucleus. The nucleons injected into the
nebula, both the directly emitted protons and protons from neutron
decay, are trapped and accumulate in the nebula.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0871fig1.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg14.gif) |
Figure 1: Reciprocal mean free path for 2656Fe in the Crab magnetosphere. |
| Open with DEXTER | |
The photo-disintegration rate for a nucleus of atomic number Areleasing i nucleons can be written as
where
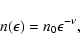 |
(5) |
where n0 is estimated using
2.3 Proton spectrum
When the photodisintegration rate for a nucleus of atomic number Areleasing i nucleons is given, the number of the i nucleons per
unit energy can be estimated. For the treatment of entangled
acceleration and disintegration process, we assume the nuclear
Lorentz factor at position s is
![]() ,
where s is
distance relative to the inner point of outer gap. For simplicity,
the parallel component of the electrical field is assumed constant,
as
,
where s is
distance relative to the inner point of outer gap. For simplicity,
the parallel component of the electrical field is assumed constant,
as
![]() ,
so we have
,
so we have
![]() and
and
![]() .
Therefore, the number of i nucleons at energy
Ei per unit energy per nucleus is approximated as
.
Therefore, the number of i nucleons at energy
Ei per unit energy per nucleus is approximated as
where i=n, p, and c is the light speed.
We now can construct and compute the total proton spectrum present
in the Crab nebula including both the contribution of neutrons and
protons. The present spectrum of protons from accelerated nuclei
disintegrating in the nebula is the result of trapping and
accumulation from the birth of pulsar to the present time and
depends on the pulsar evolution since its birth, collisions and
absorption by matter; this is estimated by optical depth. Using
initial period P0=19 ms and braking index n=2.5 for the Crab
pulsar (Lyne et al. 1993), the pulsar period evolves as Eq. (3).
During the evolution of the Crab pulsar, the energy losses are
mainly due to pp collision and adiabatic expansion. For the
present Lorentz factor
![]() at time
at time
![]() ,
its
Lorentz factor at time t can be estimated as (Bednarek &
Protheroe 1997)
,
its
Lorentz factor at time t can be estimated as (Bednarek &
Protheroe 1997)
where the
The first term is the contribution from neutrons initially decaying inside the nebula, and the second term gives the contribution of neutron initially decaying outside the nebula.
The direct contribution of proton emission is different from the
disintegrated neutron component; all successive protons emitted from
nuclei disintegrating and accelerating in the outer gap could be
accelerated continuously and achieve almost the same energy
determined by the outer gap potential
![]() ,
therefore ultimately the direct proton
number dN with energy
,
therefore ultimately the direct proton
number dN with energy
![]() at pulsar period P is the
sum of the differential energy spectra of disintegrated protons from
E=0 to
at pulsar period P is the
sum of the differential energy spectra of disintegrated protons from
E=0 to
![]() ,
,
![]() ,
i.e.
,
i.e.
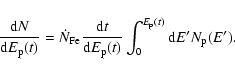 |
(9) |
Taking account of the energy loss, we reach the direct proton contribution of the energy spectrum as
where
The present proton energy spectrum has contributions both of neutron
and proton components, the former is result of accumulation since
the pulsar birth and the latter is the contribution at given time
(or P). Therefore, the total proton spectrum can be written as
In Fig. 2, the total proton energy spectrum (solid line) is shown, which is the sum of the proton spectrum (dashed line) from neutron decay and the direct proton spectrum (dotted line). Although the cross section of neutrons and protons is similar, the present proton spectrum at low energy is mainly the contribution of low energy neutron decay accumulated in the pulsar evolution period, but at higher energy the direct proton emission contribution is greater than that of neutron decay. The results show that neglecting direct proton emission is not accurate. Following Bednarek & Protheroe (1997), we can check whether the protons remain in the nebula or diffuse into the galactic environment; the typical diffusion distance to the present time is
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0871fig2.eps}
\par\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg70.gif) |
Figure 2: Present proton spectrum in the Crab nebula. The solid line represents the total proton spectrum, dashed and dotted lines represent the spectra of the protons from neutron decay (Eq. (8)) and the direct protons (Eq. (10)). |
| Open with DEXTER | |
2.4 Leptonic spectra excited by nuclei
In a PWN, leptons are excited by relativistic nuclei and consist of four components: positrons accelerated in a realistic magneto-sonic lepton-heavy iron plasma shock, electrons from neutron decay, direct electrons, and secondary electron/positron pairs in a proton-proton interaction (Bednarek & Bartosik 2003). We now give the spectra of the four kinds of leptons and show that the last three components are negligible compared to the first component.
For the first component, according to Hoshino et al. (1992),
preferential non-thermal heating of positrons occurs in the
realistic, magnetosonic, electron-positron-heavy ion shock. The
gyrating reflected heavy ions dissipate their energy in the form of
left-handed magnetosonic waves which are resonantly absorbed by the
positron behind the iron reflection region. The positron energy
spectrum can be described by a Maxwellian distribution with a
supra-thermal power-law tail, i.e. (Hoshino et al. 1992)
![\begin{displaymath}\left[\frac{{\rm d}N}{{\rm d}E_0{\rm d}t}\right]_1=\frac{N^*}...
...ac{m_{\rm e}c^2}{T_{\rm
e}}(\gamma-1)\right]+F(\gamma)\right\}
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img71.gif) |
(12) |
with
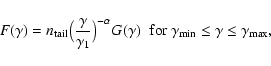 |
(13) |
and
![\begin{displaymath}\int [{\rm d}N/{\rm d}E_0{\rm d}t]_1E_0{\rm d}E_0=\chi\dot N_{\rm Fe}E_{\rm Fe}
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img83.gif) |
(14) |
where
For the second component, electrons are produced through the neutron
decay disintegrated from nuclei (
![]() ), where their Lorentz factors are
assumed to be equal to those of their parent nuclei. In this case,
the electron spectrum can be approximated as
), where their Lorentz factors are
assumed to be equal to those of their parent nuclei. In this case,
the electron spectrum can be approximated as
![\begin{displaymath}\left[\frac{{\rm d}N}{{\rm d}E_0{\rm d}t}\right]_2\approx\fra...
...\rm n}(E_{\rm n})[1-\exp(vt/c\gamma_{\rm
n}(t)\tau_{\rm n})] ,
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img86.gif) |
(15) |
where
According to Bednarek (2003), we consider the direct electron
spectrum. We assume that the spin down energy transfer ![]() to
monoenergy electrons with primary energy
to
monoenergy electrons with primary energy
![]() ,
therefore the direct electron spectrum is given by
,
therefore the direct electron spectrum is given by
![\begin{displaymath}\left[\frac{{\rm d}N}{{\rm d}E_0{\rm d}t}\right]_3\approx\frac{L(1-\xi)}{Z_{\rm
e}\Phi(B,P)}\delta(E-E_0),
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img93.gif) |
(16) |
where
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{0871fig3.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg96.gif) |
Figure 3: Present spectra of leptons (solid line) in the Crab nebula. For comparison, we plot the spectra of the Maxwellian distribution (dash-dash dotted line) and the power-law tail (dotted line); dashed, dot-dot dashed, and dot dashed lines represent the second to fourth component spectra. |
| Open with DEXTER | |
The leptons with an energy E0 at an earlier time t are injected into the nebula, and the energy E of the leptons inside the nebula at the present time
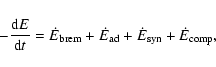 |
(18) |
where
The leptonic spectrum at the present time is obtained by summing
over the spectra from leptons injected at an early time and over all
the time up to the time of the present observation, which is given
by Bednarek & Bartisik (2003) (also see Bednarek 2007):
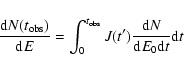 |
(19) |
where
3 Photon emission inside the nebula
Having calculated the spectra of both leptons and hadrons, which
depend on the time of evolution after the supernova explosion, we
can compute the photon spectra produced by the leptons in different
radiation processes and the hadrons in pp interactions inside the
nebula. The main leptonic processes which produce photons inside the
nebula include synchrotron radiation, bremsstrahlung, and inverse
Compton (IC) scattering. It is possible that photons produced by
inverse Compton scattering of the high-energy leptons on synchrotron
photons, microwave background photons, and infrared photons reach to
very high energies. Despite different accuracies of IC cross section
determination, as well as different distributions of magnetic fields
and photon fields in nebula used in the past by different authors,
the conclusion is unambiguous that the lepton component has a
significant contribution to TeV ![]() rays (e.g. Gould 1965;
Jones 1968; Rieke & Weekes 1969; Kennel et al. 1984; de Jager
& Harding 1992; Atoyan & Aharonian 1996; Zhang et al. 2008). On
the other hand, hadrons produce high-energy photons and neutrinos in
p-p interactions. Below, we briefly describe the relevant processes
and give our results for the Crab nebula.
rays (e.g. Gould 1965;
Jones 1968; Rieke & Weekes 1969; Kennel et al. 1984; de Jager
& Harding 1992; Atoyan & Aharonian 1996; Zhang et al. 2008). On
the other hand, hadrons produce high-energy photons and neutrinos in
p-p interactions. Below, we briefly describe the relevant processes
and give our results for the Crab nebula.
3.1 Photons produced by leptonic processes
For the synchrotron radiation, the emissivity is given by
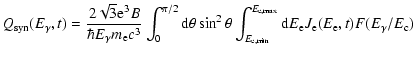 |
(20) |
where
The electron-nucleon bremsstrahlung emissivity can be written as
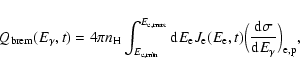 |
(21) |
where
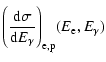 |
= | 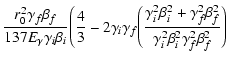 |
|
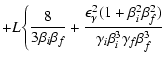 |
|||
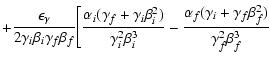 |
|||
![$\displaystyle +\frac{2\epsilon_{\gamma}}{\gamma_{i}\beta_{i}^{2}\gamma_{f}\beta_{f}^{2}}\Bigg]\Bigg\}\Bigg)$](/articles/aa/full_html/2009/12/aa10871-08/img124.gif) |
(22) |
with
![\begin{displaymath}\alpha_{i(f)}=\ln\left[\gamma_{i(f)}^{2}(1+\beta_{i(f)})^{2}\right]
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img125.gif) |
(23) |
and
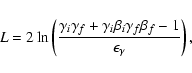 |
(24) |
where
For the inverse Compton process, we use the full Klein-Nishina cross
section for relativistic electrons to calculate the emissivity. The
emissivity can be written as
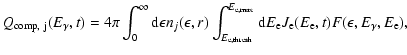 |
(25) |
where
The energy density of the synchrotron photons is (Atoyan & Aharonian 1996)
with
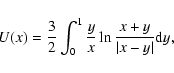 |
(28) |
where
![$\displaystyle F(\epsilon, E_{\gamma}, E_{\rm e})={3\sigma_{\rm T}\over 4 (E_{\r...
...psilon}\Big[2q\ln q +(1+2q)(1-q)
+{(\Gamma q)^2(1-q)\over 2(1+\Gamma q)}\Big] ,$](/articles/aa/full_html/2009/12/aa10871-08/img142.gif) |
(29) |
with
3.2 Photons and neutrinos produced by hadronic processes
Table 1: Main parameters for calculating photon and neutrino production.
The protons accumulated in a PWN can generate high-energy photons and neutrinos in p-p interactions (where
![\begin{displaymath}\sigma_{\rm inel}(E_{\rm
p})=34.3+1.88L+0.25L^{2}\times\left[...
...(\frac{E_{\rm th}}{E_{\rm
p}}\right)^{4}\right]^2\;\mbox{mb} ,
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img157.gif) |
(31) |
where
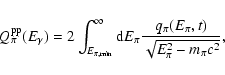 |
(32) |
where
where
In the p-p collision, the pion emissivities satisfy the following
relationship:
![]() .
The muonic neutrinos are produced at the decay of charged pions
.
The muonic neutrinos are produced at the decay of charged pions
![]() ,
and the corresponding third particle
decay yields muonic and electronic neutrinos as the mode
,
and the corresponding third particle
decay yields muonic and electronic neutrinos as the mode
![]() .
Taking neutrino oscillations into
account, all muonic neutrinos and electronic neutrinos are
incorporated and the emissivity of the muonic neutrinos is
.
Taking neutrino oscillations into
account, all muonic neutrinos and electronic neutrinos are
incorporated and the emissivity of the muonic neutrinos is
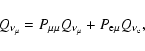 |
(34) |
where
3.3 Calculation results
We now calculate the photon spectrum and muonic neutrino flux for
the Crab nebula. For the photons produced in the nebula, the
spectrum observed on the Earth can be expressed as
| (35) |
where
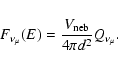 |
(36) |
We calculated the multiwaveband photon and high energy neutrino spectra of the Crab nebula and the main parameters used here are listed in Table 1. In Fig. 4, we show the comparison of the predicted photon spectrum with the observed data for the Crab nebula. The radio data are taken from Baars & Hartsuijker (1972), millimeter and IR data from Strom & Greidanus (1992), Bandiera et al. (2002), and Green et al. (2004), soft X-ray to
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0871fig4.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg190.gif) |
Figure 4:
Comparison of the calculated spectrum with observed data
for the Crab nebula. The radio data are taken from Baars &
Hartsuijker (1972), millimeter and IR data from Strom &
Greidanus (1992), Bandiera et al. (2002), and Green et al. (2004),
soft X-ray to |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0871fig5.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg191.gif) |
Figure 5: Comparison of the calculated spectrum with observed high-energy data for the Crab nebula. Symbols are the same as in Fig. 4. |
| Open with DEXTER | |
In Fig. 6, we show the predicted muonic neutrino flux
observed on the Earth and the atmospheric neutrino background
(Lipari 1993) within ![]() as indicated by the shaded band.
Compared to the result given by Bednarek (2003), our result is
slightly lower. Bednarek (2003) estimated that the number of
as indicated by the shaded band.
Compared to the result given by Bednarek (2003), our result is
slightly lower. Bednarek (2003) estimated that the number of ![]() neutrinos observed by the 1 km2 detector during 1 year is about 1.3 for the Crab nebula.
neutrinos observed by the 1 km2 detector during 1 year is about 1.3 for the Crab nebula.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0871fig6.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg193.gif) |
Figure 6:
Predicted spectrum of muonic neutrinos observed on the
Earth. The atmospheric neutrino background within |
| Open with DEXTER | |
4 Discussion and conclusion
We have studied multi-waveband photon emission and possible high-energy neutrino emission from the Crab nebula in the framework of the hadronic-leptonic model. In this model, we considered nucleon injection in the pulsar magnetosphere, proton production by the photo-disintegration process, and leptonic production excited by the nuclei in detail. The proton spectrum consists of two components: the proton component from neutron decay and the direct emitting proton component. The first component dominates over the second component in the lower energy region, but the second component has its main contribution in the higher energy region (see Fig. 2). It should be noted that previous works (e.g. Bednarek & Prothero 1997; Bednarek & Bartosik 2003) did not consider the contribution of the second component. For the leptons excited by the nuclei, the spectrum consists of four components: positrons accelerated in realistic magneto-sonic lepton-heavy iron plasma shocks, electrons from neutron decay, direct electrons, and secondary electron/positron pairs in the pp interaction (see Fig. 3), it can be seen from this figure that the first component dominates over other components, which is different from that given by Bednarek & Bartosik (2003) since the complete form of the positron spectrum given by Hoshino et al. (1992) is included in our calculation.
After determining the spectra of both hadrons and leptons, we
calculated the multi-waveband photon spectrum of the Crab nebula
(see Figs. 4 and 5). The calculated spectrum
up to TeV energy could be explained by upscattering soft photon
fields by realistic leptons accompanying nuclei, where the soft
photon fields mainly include synchrotron radiation, microwave
background, infrared and optical photons. However our predicted
spectrum reveals that the hadronic component has an important
contribution to gamma rays in the energy range above several TeV.
Bednarek & Bartosik (2003) found that the emission from the Crab
nebula can be well fitted by the composition of the ![]() -ray
emission produced by leptons (<10 TeV) and nuclei (>10 TeV).
Compared to the results of Bednarek & Bartosik (2003), our results
show that it is difficult to clearly distinguish leptonic and
hadronic origins in the
-ray
emission produced by leptons (<10 TeV) and nuclei (>10 TeV).
Compared to the results of Bednarek & Bartosik (2003), our results
show that it is difficult to clearly distinguish leptonic and
hadronic origins in the ![]() 10 TeV energy range (see Fig. 5). For the
10 TeV energy range (see Fig. 5). For the ![]() neutrino emission, our predicted
flux (see Fig. 6) is lower than that given by
Bednarek (2003).
neutrino emission, our predicted
flux (see Fig. 6) is lower than that given by
Bednarek (2003).
We now discuss the possible influence of our treatments on the
predicted photon and neutrino fluxes. In this paper, we have given
the treatment of disintegration as accelerating along the magnetic
line with a non-perpendicular electric field in the outer gap. The
nucleon energy spectrum from nucleus disintegration is calculated
simply by Eq. (6) assuming a constant electronic
field. Because the real
![]() near the outer
range of the gap should be larger than our average value, the
calculation will mainly underestimate the the proton energy spectrum
at high energy. If detailed information about
near the outer
range of the gap should be larger than our average value, the
calculation will mainly underestimate the the proton energy spectrum
at high energy. If detailed information about
![]() is known, the nucleon energy spectrum could
be calculated precisely as could its more distinct contribution to
the very high photon spectrum. It should be noted that the direct
proton contribution at high energy is significant irrespective of
the calculation technique. Another factor which could effect the
nucleon energy spectrum and thus the maximum positron energy is that
the kinetic energy of nuclei entering the outer gap is assumed to be
zero; this could lead to a decrease in the disintegration rate and
thus nuclei maximum energy (or maximum positron energy), resulting
in the decrease of fluxes at high energy of pp photon emission and
synchrotron radiation.
is known, the nucleon energy spectrum could
be calculated precisely as could its more distinct contribution to
the very high photon spectrum. It should be noted that the direct
proton contribution at high energy is significant irrespective of
the calculation technique. Another factor which could effect the
nucleon energy spectrum and thus the maximum positron energy is that
the kinetic energy of nuclei entering the outer gap is assumed to be
zero; this could lead to a decrease in the disintegration rate and
thus nuclei maximum energy (or maximum positron energy), resulting
in the decrease of fluxes at high energy of pp photon emission and
synchrotron radiation.
Acknowledgements
This work is partially supported by the National Natural Science Foundation of China under grant 10778702 and a 973 Program (2009CB824800).
References
- Aharonian, F. A., & Atoyan, A. M. 1995, Astropart. Phys., 3, 275 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F. A., & Atoyan, A. M. 2000, A&A, 362, 937 [NASA ADS] (In the text)
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2004, ApJ, 614, 897 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, ApJ, 674, 1037 [NASA ADS] [CrossRef] (In the text)
- Alvarez, R. A., Berman, B. L., Faul, D. D., Lewis Jr, F. H., & Meyer, P. 1979, Phys. Rev., Part C, Nucl. Phys., 20, 128
- Atoyan, A. M., & Aharonian, F. A., 1996, MNRAS, 278, 525 [NASA ADS] (In the text)
- Baars, J. W., & Hartsuijker, A. P. 1972, A&A, 17, 172 [NASA ADS] (In the text)
- Bandiera, R., Neri, R., & Cesaroni, R. 2002, A&A, 386, 1044 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bednarek, W. 2003, A&A, 407, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bednarek, W. 2007, Ap&SS, 309, 179 [NASA ADS] [CrossRef] (In the text)
- Bednarek, W., & Protheroe, R. J. 1997, , 79, 2616 (In the text)
- Bednarek, W., & Bartosik, M. 2003, A&A, 405, 689 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bednarek, W., & Bartosik, M. 2004, A&A, 423, 405 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bednarek, W., & Bartosik, M. 2005, J. Phys. G Nucl. Phys., 31, 1465 [NASA ADS] [CrossRef] (In the text)
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S., Cheung, T., Lau, M. M., Yu, K. N. & Kwok, P. W. 1990, J. Phys. G Nucl. Phys., 16, 1115 [NASA ADS] [CrossRef]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986a, ApJ, 300, 500 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S., Ho, C., & Ruderman, M. 1986b, ApJ, 300, 522 [NASA ADS] [CrossRef] (In the text)
- de Jager, O. C., & Harding, A. K. 1992, ApJ, 396, 161 [NASA ADS] [CrossRef] (In the text)
- Danos, M., & Fuller, E. G. 1965, Ann. Rev. Nucl. Part. Sci., 15, 29 [NASA ADS] [CrossRef]
- Davidson, K., & Fesen, R. A. 1985, ARA&A, 23, 119 [NASA ADS] [CrossRef] (In the text)
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] (In the text)
- Gallant, Y. A., & Arons, J. 1994, ApJ, 435, 230 [NASA ADS] [CrossRef] (In the text)
- Gil, J., Melikidze, G. I., & Geppert, U. 2003, A&A, 407, 315 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gould, R. J. 1975, ApJ, 196, 689 [NASA ADS] [CrossRef] (In the text)
- Gould, R. J. 1965, Phys. Rev. Lett., 15, 577 [NASA ADS] [CrossRef] (In the text)
- Green, D. A., Tuffs, R. J., & Popescu, C. C. 2004, MNRAS, 355, 1315 [NASA ADS] [CrossRef] (In the text)
- Hoshino, M., & Arons, J. 1991, Phys. Fluids B, 3, 818 [NASA ADS] [CrossRef] (In the text)
- Hoshino, M., Arons, J., Gallant, Y. A., & Langdon, A. B. 1992, ApJ, 390, 454 [NASA ADS] [CrossRef] (In the text)
- Jones, F. C. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] (In the text)
- Karakula, S., & Tkaczyk, W. 1993, Astropart. Phys., 1, 229 [NASA ADS] [CrossRef] (In the text)
- Katz, L., & Cameron, A. G. W. 1951, Canadian J. Phys., 29, 518
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] (In the text)
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 710 [NASA ADS] [CrossRef] (In the text)
- Kuiper, L., Hermsen, W., Cusumano, G., et al. 2001, A&A, 378, 918 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Koch, H. W., & Motz, J. W. 1959, Rev. Mod. Phys., 31, 920 [NASA ADS] [CrossRef] (In the text)
- Lipari, P. 1993, Astropart. Phys., 1, 195 [NASA ADS] [CrossRef] (In the text)
- Lyne, A. G., Pritchard, R. S., & Graham-Smith, F. 1993, MNRAS, 265, 1003 [NASA ADS] (In the text)
- Puget, J. L., Stecker, F. W., & Bredekamp, J. H. 1976, ApJ, 205, 638 [NASA ADS] [CrossRef] (In the text)
- Rieke, G. H., & Weekes, T. C. 1968, ApJ, 155, 429 [NASA ADS] [CrossRef]
- Ribordy, M., et al. (IceCube Collaboration) 2006, Physics of Atomic Nuclei, 69, 1899
- Stecker, F. W., & Salamon, M. H. 1999, ApJ, 512, 521 [NASA ADS] [CrossRef] (In the text)
- Strom, R. G., & Greidanus, H. 1992, Nature, ,358, 654 (In the text)
- Zhang, L., Chen, S. B., & Fang, J. 2008, ApJ, 676, 1210 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Main parameters for calculating photon and neutrino production.
All Figures
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0871fig1.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg14.gif) |
Figure 1: Reciprocal mean free path for 2656Fe in the Crab magnetosphere. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0871fig2.eps}
\par\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg70.gif) |
Figure 2: Present proton spectrum in the Crab nebula. The solid line represents the total proton spectrum, dashed and dotted lines represent the spectra of the protons from neutron decay (Eq. (8)) and the direct protons (Eq. (10)). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{0871fig3.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg96.gif) |
Figure 3: Present spectra of leptons (solid line) in the Crab nebula. For comparison, we plot the spectra of the Maxwellian distribution (dash-dash dotted line) and the power-law tail (dotted line); dashed, dot-dot dashed, and dot dashed lines represent the second to fourth component spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0871fig4.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg190.gif) |
Figure 4:
Comparison of the calculated spectrum with observed data
for the Crab nebula. The radio data are taken from Baars &
Hartsuijker (1972), millimeter and IR data from Strom &
Greidanus (1992), Bandiera et al. (2002), and Green et al. (2004),
soft X-ray to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0871fig5.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg191.gif) |
Figure 5: Comparison of the calculated spectrum with observed high-energy data for the Crab nebula. Symbols are the same as in Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0871fig6.eps}
\end{figure}](/articles/aa/full_html/2009/12/aa10871-08/Timg193.gif) |
Figure 6:
Predicted spectrum of muonic neutrinos observed on the
Earth. The atmospheric neutrino background within |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



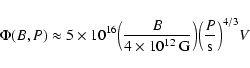
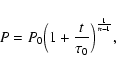
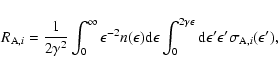
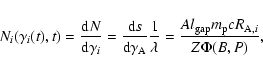
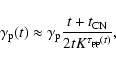
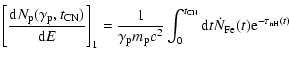
![$\displaystyle \quad\times\Bigg[N_{\rm n}(\gamma_{\rm p}(t),t)\gamma_{\rm p}(t)[1-\exp(vt/c\gamma_{\rm p}(t)\tau_{\rm n})]$](/articles/aa/full_html/2009/12/aa10871-08/img48.gif)
![$\displaystyle \quad+\int_{t}^{t_{\rm CN}}{\rm d}t^{\prime}N_{\rm n}(\gamma_{\rm...
...(t^{\prime})\tau_{\rm n})}{c\gamma_{\rm p}(t^{\prime})\tau_{\rm n}}\Bigg] \cdot$](/articles/aa/full_html/2009/12/aa10871-08/img49.gif)
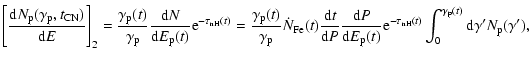
![\begin{displaymath}\frac{{\rm d}N_{\rm p}}{{\rm d}E}=\Bigg[\frac{{\rm d}N_{\rm p...
...N_{\rm p}(\gamma_{\rm p}, t_{\rm
CN})}{{\rm d} E}\Bigg]_2\cdot
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img61.gif)
![\begin{displaymath}\frac{{\rm d}N}{{\rm d}E_0{\rm d}t}=\left[\frac{{\rm d}N}{{\r...
...ht]_2+\left[\frac{{\rm d}N}{{\rm d}E_0{\rm d}t}\right]_3 \cdot
\end{displaymath}](/articles/aa/full_html/2009/12/aa10871-08/img97.gif)