EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 496 / No 3 (March IV 2009) A&A, 496 3 (2009) 855-861 Full HTML
Free Access
Issue
A&A
Volume 496, Number 3, March IV 2009
Page(s) 855 - 861
Section The Sun
DOI https://doi.org/10.1051/0004-6361:200810862
Published online 20 January 2009

On solar cycle predictions and reconstructions

R. Brajsa1,[*] - H. Wöhl2 - A. Hanslmeier3 - G. Verbanac4 - D. Ruzdjak1 - E. Cliver5 - L. Svalgaard6 - M. Roth7


1 - Hvar Observatory, Faculty of Geodesy, University of Zagreb, Kaciceva 26, 10000 Zagreb, Croatia
2 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
3 - Institut für Physik, IGAM, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
4 - Geophysical Institute, Faculty of Science, University of Zagreb, Horvatovac bb, 10000 Zagreb, Croatia
5 - Space Vehicles Directorate, Air Force Research Laboratory, Hanscom Air Force Base, MA, USA
6 - Stanford University, HEPL, Stanford, CA 94305-4085, USA
7 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany

Received 26 August 2008 / Accepted 16 December 2008

Abstract
Context. Generally, there are two procedures for solar cycle predictions: the empirical methods - statistical methods based on extrapolations and precursor methods - and methods based on dynamo models.
Aims. The goal of the present analysis is to forecast the strength and epochs of the next solar cycle, to investigate proxies for grand solar minima and to reconstruct the relative sunspot number in the Maunder minimum.
Methods. We calculate the asymmetry of the ascending and descending solar cycle phases (Method 1) and use this parameter as a proxy for solar activity on longer time scales. Further, we correlate the relative sunspot numbers in the epochs of solar activity minima and maxima (Method 2) and estimate the parameters of an autoregressive moving average model (ARMA, Method 3). Finally, the power spectrum of data obtained with the Method 1 is analysed and the Methods 1 and 3 are combined.
Results. Signatures of the Maunder, Dalton and Gleissberg minima were found with Method 1. A period of about 70 years, somewhat shorter than the Gleissberg period was identified in the asymmetry data. The maximal smoothed monthly sunspot number during the Maunder minimum was reconstructed and found to be in the range 0-35 (Method 1). The estimated Wolf number (also called the relative sunspot number) of the next solar maximum is in the range 88-102 (Method 2). Method 3 predicts the next solar maximum between 2011 and 2012 and the next solar minimum for 2017. Also, it forecasts the relative sunspot number in the next maximum to be $90 \pm 27$. A combination of the Methods 1 and 3 gives for the next solar maximum relative sunspot numbers between 78 and 99.
Conclusions. The asymmetry parameter provided by Method 1 is a good proxy for solar activity in the past, also in the periods for which no relative sunspot numbers are available. Our prediction for the next solar cycle No. 24 is that it will be weaker than the last cycle, No. 23. This prediction is based on various independent methods.

Key words: Sun: activity

1 Introduction

Understanding the solar activity cycle remains a key unsolved problem in solar physics (along with, e.g., heating of the solar corona and solar flares). It is not only an outstanding theoretical problem, but also an important practical issue, since solar activity and the radiation output related to it influences the biosphere, space weather and technology on the Earth (Eddy 1976; Hoyt & Schatten 1997; Feynman & Gabriel 2000; Lang 2000; Soon & Yaskell 2003; Feynman 2007; Hanslmeier 2007).

At present it is still not fully clear whether solar activity is purely stochastic or weakly chaotic (Stix 2002; Ossendrijver 2003; Rüdiger & Hollerbach 2004). A distinction between these two characters (Carbonell et al. 1994; Ossendrijver & Hoyng 1996; Duhau 2003; Charbonneau 2005; Letellier et al. 2006; Usoskin et al. 2007; Yeates et al. 2008) can be important for the interpretation of the long-term modulation of the solar activity (e.g., the Gleissberg cycle with a period of about 100 years, Feynman & Fougere 1984; Feynman & Gabriel 1990; Duhau 2003) and understanding the prolonged periods of extremely low activity, as in the Maunder minimum (e.g., Ruzmaikin 1985; Charbonneau 2005; Hiremath 2006; Volobuev 2006). In this context a very important but difficult task is to predict a possible return of the Maunder-type grand solar minima.

Solar cycle prediction is not an easy task and there exists a variety of methods based on different observational data and theoretical assumptions (Wilson 1994; Beck et al. 1995; Hathaway et al. 1999; Ossendrijver 2003; Schüssler 2007). Currently there are two basic classes of methods for the solar cycle predictions; these are the empirical methods and methods based on dynamo models (e.g., Schüssler 2007). The empirical methods (e.g., Hathaway et al. 1999) can be further devided into two subgroups, the statistical methods based on extrapolation (e.g., Kane 2007b) and precursor methods (e.g., Wilson 1990b). The other class of methods is based on various dynamo models (e.g., Cameron & Schüssler 2007; Choudhuri et al. 2007; Dikpati 2007; Jiang et al. 2007), but can also be combined with some precursor features (e.g. polar magnetic field of the Sun around solar minimum, Svalgaard et al. 2005). Further, various combinations of different methods were proposed (e.g., Hanslmeier et al. 1999; Lantos 2006a,b) and finally, a nonuniform latitude distribution of solar activity and North-South asymmetry were also used for predicting future solar activity (e.g., Javaraiah 2007; Kane 2007a).

We should, however, point out that there are important difficulties in predicting the solar cycle using mean-field dynamo models (Bushby & Tobias 2007; Cameron & Schüssler 2008). These difficulties arise from the significant modulation of the solar activity cycle caused by either stochastic or deterministic processes. Long-term prediction is impossible even if a model used for the prediction would be correct in all details. Moreover, even short-term prediction from mean-field models is problematic because of fundamental uncertainties in the form and amplitude of the transport coefficient and nonlinear response. All this makes the fine tuning of various dynamo models controversial for predicting future solar activity.

Generally, it can be said that for the next solar cycle (No. 24) the empirical methods predict lower amplitudes (Schatten 2005; Svalgaard et al. 2005; Du & Du 2006; Javaraiah 2007; Hiremath 2008) and the methods based on dynamo models higher amplitudes (Dikpati & Gilman 2006; Dikpati et al. 2006, 2008b). However, this distinction is not a strict one, and in both classes of methods opposite examples can be found. So an empirical method based on geomagnetic precursors forecasts a high amplitude for the next solar cycle (Hathaway & Wilson 2006) and a solar dynamo model predicts a low amplitude (Choudhuri et al. 2007; Jiang et al. 2007). Finally, various combined methods predict a low amplitude for the next solar maximum (Schatten 2003; Schatten & Tobiska 2003; Lantos 2006a). In summary, the topic of solar cycle prediction is still inconclusive to a large extent, which represents additional motivation for further research.

In the present study three different empirical methods for solar cycle prediction and reconstruction are used. We calculate the asymmetry of the ascending and descending solar cycle phases (Method 1) and use this parameter as a proxy for solar activity on longer time scales. Further, we correlate the relative sunspot numbers in the epochs of solar activity minima and maxima (Method 2). Finally, we estimate the parameters of an autoregressive moving average model (ARMA, Method 3).

With Method 1 we search for indications of grand solar minima in the past. It also enables the reconstruction of the relative sunspot number in the Maunder minimum. With this method a prediction for the amplitude of the next solar cycle is possible only if the epochs of future minima and maxima can be independently estimated. Method 2 provides a prediction of the amplitude of the next activity maximum on the basis of the relative sunspot number in the preceding minimum. Finally, with Method 3 predictions of the amplitude and epochs of the next solar cycle are possible.

2 The data set

Table 1:   The solar cycle number, the epochs of solar minima and maxima ( $T_{\rm min}$ and $T_{\rm max}$, respectively), the extreme values of the monthly smoothed relative sunspot numbers in corresponding epochs ( $R_{\rm min}$ and $R_{\rm max}$, respectively) and the asymmetry values (A, A1, A2, and A3).

Our basic data set consists of the epochs of solar minima and maxima, $T_{\rm min}$ and $T_{\rm max}$, respectively, from the year 1610 up to now. The starting point was the table published by Gleissberg et al. (1979). The epochs of solar minima and maxima were determined by Wolf for the years up to 1889, by Wolfer for the years up to 1923, by Brunner for the years up to 1944, and by Waldmeier for later years. We have checked, slightly corrected and enlarged this data set using monthly smoothed relative sunspot number beginning from 1750. This data series can be found at the solar influences data analysis center (SIDC) of the Royal Observatory of Belgium (SIDC-team). The data set used in the present work is reproduced in Table 1 (we note that the asymmetries, A, A1, A2, and A3, written in the right-hand part of the table, are calculated according to Method 1, described in the next section).

We now briefly discuss the errors in the determination of the epochs of solar minima and maxima, $T_{\rm min}$ and $T_{\rm max}$. According to Gleissberg et al. (1979) these errors are in modern times of the order of 0.2 years and for the Maunder minimum about three times larger, i.e. slightly more than half a year. In agreement with that, Wolf himself (1893) estimated the errors of the minimum and maximum epochs in the 17th century to be less than 1 year.

3 The reduction methods

3.1 Method 1: the asymmetry A of the ascending (T) and descending (U) solar cycle phases

The asymmetry of the ascending and the descending solar cycle phases is determined according to Gleissberg et al. (1979). Using the time of ascent from the minimum epoch to the maximum epoch (T) and the time of descent from the maximum epoch to the next minimum epoch (U) the asymmetry is calculated with:

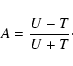\begin{displaymath}{A} = {{U - T} \over {U + T}}\cdot \end{displaymath} (1)

The asymmetry A is positive if the activity maximum occurs in the first half of the cycle and negative if it falls in the second half. The A values were calculated using Eq. (1) for all available data and listed in Table 1.

Further, various smoothing procedures were applied:

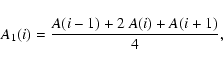\begin{displaymath}{A_1(i)} = {A(i-1) + 2 ~ A(i) + A(i+1) \over 4}, \end{displaymath} (2)


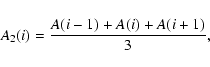\begin{displaymath}{A_2(i)} = {A(i-1) + A(i) + A(i+1) \over 3}, \end{displaymath} (3)

as well as the smoothing method of Gleissberg et al. (1979). With this method the moving averages of every four consecutive A values are computed and from this series again the means of every two adjacent values are calculated. In such a way the smoothed values A3were obtained:

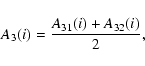\begin{displaymath}{A_3(i)} = {A_{31}(i) + A_{32}(i) \over 2}, \end{displaymath} (4)

with


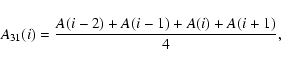\begin{displaymath}{A_{31}(i)} = {A(i-2) + A(i-1) + A(i) + A(i+1) \over 4}, \end{displaymath} (5)

and


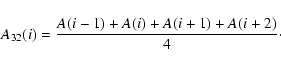\begin{displaymath}{A_{32}(i)} = {A(i-1) + A(i) + A(i+1) + A(i+2) \over 4}\cdot \end{displaymath} (6)

In Eqs. (2)-(6), A(i-1) is the asymmetry of the solar cycle preceding to the cycle iand A(i+1) the asymmetry of the solar cycle following the ith cycle. In a similar way A(i-2) and A(i+2) are also defined.

All these asymmetry values, A, A1, A2, and A3, calculated in the above described way are presented in the right-hand part of Table 1. From the smoothing procedures it is clear that the first and the last entries cannot be calculated for A1 and A2, which holds for the first two and last two entries in the case of A3. ``NaN'' stands for no data available or the value cannot be calculated and the epoch of the actual solar minimum is only an approximation.

3.2 Method 2: the correlation of the relative sunspot numbers in the solar minima R min and maxima R max

This method is based on the assumed linear relationship between relative sunspot numbers in the minimum (at the beginning of the activity cycle, $R_{\rm min}$) and in maximum epochs ( $R_{\rm max}$) of solar cycles (e.g., Wilson 1990b). For the correlation, series of the extreme values (measured in minimum and maximum epochs) of the monthly smoothed relative sunspot number, beginning from 1750 (Table 1), were used. This method enables predicting of $R_{\rm max}$ on the basis of the preceding $R_{\rm min}$.

3.3 Method 3: the autoregressive moving average model, ARMA

Especially interesting for forecasting are models where the true state x(t)and its forecasted value $\hat{x}(t)$ deviate from each other by $\epsilon$ which is a Gaussian distributed random variable. That means that the difference $x(t)-\hat{x}(t)$ between true state and the predicted value does not contain information on the stochastic process that produced the time series x(t). Such a general process can be described by the equation


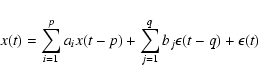\begin{displaymath}x(t)=\sum_{i=1}^p a_i x(t-p) + \sum_{j=1}^q b_j \epsilon(t-q) + \epsilon(t) \end{displaymath} (7)

with $\epsilon \sim WN(0,\sigma^2)$ and is called an ARMA[p,q] (autoregressive moving average) process (Brockwell & Davies 1996). An ARMA process is a superposition of an autoregressive process (AR[p]) and a moving average process (MA[q]). The parameters pand q are the orders of the process, i.e., they define which time step values from the past influence the present state. The coefficients ai and bj define how strong this influence from the past is. The random variables $\epsilon$ obey a white noise (Gaussian) probability distribution $WN(0,\sigma^2)$with the maximum at 0 and a variance of $\sigma^2$. We use such an ARMA process to model the sunspot number.

In the following we describe briefly the procedure for estimating the ARMA parameters ai and bj and determining the orders p and q from the time series of sunspot numbers. More details can be found in Durbin & Koopman (2001) and Gardner et al. (1980). First we use initial estimates from the Yule-Walker equations, i.e., we assume q=0. Second, the residues from such an AR[p] fit are used as first guesses for $\epsilon(t)$. Third, we minimize


\begin{displaymath}\sum_t (\epsilon(t))^2 = \sum_t \Big( x(t) - \Big[\sum_i a_i x(t-i) + \sum_j b_j \epsilon(t-j)\Big] \Big)^2 \end{displaymath} (8)

to obtain better estimates for the parameters ai and bj. We decide on the model orders p and q by increasing the orders until the residues are compatible with white noise, i.e., additional parameters do not add additional information on the process to the model.

Once we obtain the ARMA model on the basis of the last 358 yearly values we use it for forecasting the next 12 yearly values. The yearly values of the relative sunspot number for the period 1650-1699 were taken from Eddy (1976) and since the year 1700 from Waldmeier (1961). We note that the values published by Waldmeier (1961) were reproduced by Hoyt & Schatten (1998, the RZ values in their Appendix 2). The contemporary data are taken from the Solar Influences Data Analysis Center (SIDC) of the Royal Observatory of Belgium (http://sidc.oma.be).

4 Results

4.1 Method 1: the asymmetry A

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig1.eps} \end{figure} Figure 1:

The asymmetry parameter A as a function of the cycle number. The parameters of the linear least-square fit are also given.
Open with DEXTER

First we analyse the asymmetry parameters as a function of the cycle number, i.e., the time. These dependencies are presented in Figs. 1 and 2 for the asymmetry parameters A and A3, respectively. In Fig. 3 the power spectrum as a function of the inverse cycle number, i.e. time, for the asymmetry data series from Fig. 1 is presented. The Fourier analysis following the method of Deeming (1975) was applied to the asymmetry parameter A as a function of the inverse cycle number. The highest peak in Fig. 3 corresponds to the period of about 70 years, which is slightly shorter than the period of the Gleissberg cycle.

The asymmetry parameter A3, smoothed according to the method of Gleissberg et al. (1979), is presented as a function of the solar cycle number in Fig. 2. The minima in the smoothed curve clearly indicate the Maunder minimum (cycles -9 to -4; 1645-1715), the Dalton minimum (cycles 5 to 7; 1800-1830) and the modern (Gleissberg) minimum (cycles 12 to 14; 1880-1915). So, the asymmetry parameter A3 is a good proxy for grand solar minima.

Concerning the asymmetry data presented in Fig. 2 we should make two comments. (i) The trend of increasing asymmetry with time is consistent with the well-known fact that during the analysed time interval the solar activity also increased on average (e.g., Schatten 2003, Fig. 1; McCracken et al. 2004, Fig. 1c). The Gleissberg and the Schwabe cycles are superimposed on this increasing trend in solar activity. We can understand the increasing trend in the asymmetry in terms of a linear relation between the cycle amplitude and corresponding asymmetry, as will be discussed later in this section. (ii) The minimum of the asymmetry curve related to the Gleissberg minimum occured in cycles 14 to 16, rather than in cycles 12 to 14, when the Gleissberg minimum took place. For this time shift we have no simple explanation, except that there are some indications that the Gleissberg minimum was prolonged for one or two decades (i.e., in the 1920s and 1930s).

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig2.eps} \end{figure} Figure 2:

Similar to Fig. 1, here presented for the smoothed values A3.
Open with DEXTER

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig3.eps} \end{figure} Figure 3:

The power spectrum as a function of the inverse cycle number for the data series presented in Fig. 1. The highest peak corresponds to the period of about 70 years.
Open with DEXTER

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig4.eps} \end{figure} Figure 4:

The asymmetry parameter A1 as a function of the maximal smoothed monthly relative sunspot number, for all solar cycles with available sunspot number data. The parameters of the linear least-square fit are also given.
Open with DEXTER

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig5.eps} \end{figure} Figure 5:

Similar to Fig. 4, here presented for the values A3.
Open with DEXTER

We now consider the four asymmetry parameters as a function of the highest relative sunspot number, $R_{\rm max}$, represented by the smoothed monthly values (Table 1). The correlation coefficients are 0.65, 0.64, 0.57, 0.53, for the values of A, A1, A2, and A3, respectively. We now apply the linear least-square fit to these data series of the general form:

\begin{displaymath}A = a + b ~ R_{\rm max}, \end{displaymath} (9)

where a and b are the fit parameters. Two examples of these dependencies are presented in Figs. 4 and 5, for the cases $A_1(R_{\rm max})$ and $A_3(R_{\rm max})$, respectively. We now solve Eq. (9) for $R_{\rm max}$:

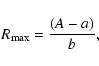\begin{displaymath}R_{\rm max} = \frac{(A - a)}{b}, \end{displaymath} (10)

which enables a reconstruction of the relative sunspot number in the epochs when the asymmetry is known. For the Maunder minimum we get values $R_{\rm max} = 0$, $R_{\rm max} = 23$, and $R_{\rm max} = 35$, for different combinations of the fit parameters a and b and the asymmetry values from Table 1. We stress that in some cases the reconstructed relative sunspot numbers are negative, so that not all combinations of the fit parameters and asymmetry values are possible. It is also important to note that these are only crude reconstructed values of the relative sunspot number. The reconstructed values for the Maunder minimum are lower than any peak $R_{\rm max}$ values in the solar cycles thereafter, as can be seen in Table 1.

4.2 Method 2: the correlation of R min and R max

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig6.eps} \end{figure} Figure 6:

The peak smoothed monthly relative sunspot number as a function of the same quantity in the preceding solar minimum, for all solar cycles with the data available. The parameters of the linear least-square fit are also given.
Open with DEXTER

In Fig. 6 we present a relationship between $R_{\rm min}$ and $R_{\rm max}$for all solar cycles with available data (Table 1). As can be seen in the figure the solar cycle No. 19 represents a kind of an outlier, outside of the bulk of data points. The solar activity maximum in 1958 had the highest $R_{\rm max}$ value which was preceded by the unusually low minimum. So, in the further analysis we exclude the data point from the solar cycle No. 19. That solar cycle was a special case, possibly even an anomaly (Wilson 1990a), not only because of the extremely low minimum at its beginning, but also due to extreme North-South asymmetry of the activity, as reported by Temmer et al. (2006). This pronounced North-South asymmetry might be a signature of a weak mixed-parity dynamo mode (Sokoloff & Nesme-Ribes 1994). One mixed-parity solution is related to ordinary Schwabe cycles, while the other one is relevant for grand minima. It is interesting, however, that the anomalous behaviour of cycle No. 19 cannot be recognized in the cycle asymmetry data (Figs. 1 and 2).

Without the data point from solar cycle No. 19 we obtain the following linear relationship:

\begin{displaymath}R_{\rm max} = 67.4 ~ (\pm10.6) + 6.9 ~ (\pm1.5) ~ R_{\rm min}, \end{displaymath} (11)

with the correlation coefficient of 0.72. Equation (11) enables a prediction of the amplitude of the next solar activity maximum, if the $R_{\rm min}$ is known (or can be estimated). For the estimated $R_{\rm min}$ values in the current solar minimum of 5, 4, and 3, we obtain $R_{\rm max}$ values of 102, 95, and 88 for the next maximum, according to Eq. (11).

For comparison, we repeat one of the formulae obtained by Wilson (1990b):


\begin{displaymath}R_{\rm max} = 81.7 + 5.46 ~ R_{\rm min}. \end{displaymath} (12)

4.3 Method 3: the ARMA model

 \begin{figure} \par\includegraphics[width = 9 cm]{0862fig7.eps} \end{figure} Figure 7:

The observed (marked by x symbol and the full line) and predicted (marked by diamond symbol and the dotted line) yearly values of the relative sunspot number using the ARMA method.
Open with DEXTER

After successful fitting of a model (p=6, q=6) the estimated process is used to predict the key quantities for the next solar cycle. We estimate on the basis of the yearly predictions that the next solar activity maximum will take place between 2011 and 2012, while the minimum thereafter should occur in 2017. The model predicts the height of the next maximum in the sunspot number to be $R_{\rm max} = 90 \pm 27$. The observed yearly values of the relative sunspot number and the predicted ones, using the ARMA method, are presented in Fig. 7.

4.4 Combined method 1 (the asymmetry A) and method 3 (the ARMA model)

Finally, we can combine the ARMA method (Method 3) and the asymmetry method (Method 1) to predict the strength of the next solar maximum using the hypothesis that the actual solar minimum occurrs at $T_{\rm min} = 2008.5$. From the ARMA model we get $T_{\rm max}=2012.0$ and $T_{\rm min}=2017.0$ (Sect. 4.3.). Now using Eq. (1) from Sect. 3.1., the asymmetry parameter can be calculated as A = 0.176. Inserting this value into Eq. (10) we obtain for $R_{\rm max}$ the values 99, 93, 92, and 78, for the A, A1, A2, and A3 cases, respectively.

5 Summary, discussion and conclusions

Signatures of the Maunder (1645-1715), Dalton (1800-1830) and Gleissberg (1880-1915) minima were found with Method 1. A period of about 70 years, somewhat shorter than the Gleissberg period was identified in the power spectrum of the asymmetry data as a function of time. The maximal smoothed monthly sunspot number during the Maunder minimum was reconstructed and found to be in the range 0-35 (Method 1). The forcasted strength of the next solar maximum is in the range 88-102 (Method 2). The ARMA method (Method 3) predicts the next solar maximum between 2011 and 2012 and the next solar minimum for 2017. Also, it forecasts the relative sunspot number in the next maximum to be $90 \pm 27$. So, we forecast a relatively weak, but also a relatively short 24th solar cycle. We stress, however, that the temporal uncertainty in forecasting $T_{\rm min}$ and $T_{\rm max}$ with ARMA is limited by the fact that we used here the yearly sunspot number values. In a subsequent paper we plan to use the monthly values which will improve the precision of the predicted epochs. An ARMA process is a linear stationary stochastic process. The sunspot number is probably the result of a more complex system. By modelling this system with an ARMA model we assume that this system is only weakly non-stationary and non-linear. A longer time series of the sunspot numbers is requested to show whether this assumption is correct. A combination of Methods 1 and 3 gives for the next solar maximum relative sunspot numbers between 78 and 99.

Our prediction for the next solar maximum is in the range from $R_{\rm max} = 78$ to $R_{\rm max} = 102$, depending on the chosen method, combination of the methods and precursor parameters. Many other predictions obtained applying the empirical or combined methods are within this span (Schatten 2003, 2005; Kane 2007b), just below our lower limit (Svalgaard et al. 2005; Javaraiah 2007), slightly above our higher limit (Lantos 2006a; Du & Du 2006; Hiremath 2008), or significantly above it (Kane 2007a). Our prediction is in qualitative agreement with a forecast based on a dynamo model (Choudhuri et al. 2007; Jiang et al. 2007). It is in a qualitative and quantitative disagreement with predictions based on other dynamo models (Dikpati & Gilman 2006; Dikpati et al. 2006, 2008b) and with one empirical forecast (Hathaway & Wilson 2006).

Concerning the start of the cycle No. 24, we can now ignore or even reject some earlier predictions which put it in early 2007 (Du 2006; Lantos 2006a). Our prediction that the next maximum should occur between 2011 and 2012 is roughly in agreement with another forecast (Lantos 2006a) obtained with a combined method.

The asymmetry parameter provided by Method 1 is a good proxy for solar activity in the past, also in the periods for which no relative sunspot numbers are available. Our prediction for the next solar cycle No. 24 is that it will be weaker than the last cycle, No. 23. This prediction is based on various independent methods and is consistent with only a small probability that the high level of solar activity during the last 65 years will continue in the next decades (Schatten & Tobiska 2003; Solanki et al. 2004; Usoskin et al. 2007). On the other hand, we should mention the possibility that the commonly used sunspot number series for the last 165 years is not calibrated correctly (Cliver & Svalgaard 2007; Svalgaard & Cliver 2007). In the case that this will prove true, the secular increase of the solar activity in the 20th century would be called into question and our prediction for the next solar maximum would be affected too. However, the times of activity minima and maxima will not change. We plan to include the analysis of the corrected sunspot number series in our future research. Also, the existing long-term series of 10Be and 14C data (e.g., Beer et al. 2006; Vonmoos et al. 2006; Abreu et al. 2008) might be suitable for an application of the empirical methods. It is not surprising that in the 10Be time-series the Maunder, Dalton and Gleissberg grand minima were clearly identified (McCracken et al. 2004) and it would be interesting to see if these data would forecast upcoming grand minima. An analysis of correctly calibrated data sets from these terrestrial proxies could also provide a better insight into whether or not the system is weakly non-stationary and weakly non-linear, as earlier discussed.

Further we can raise the question of whether the cycle asymmetry, as defined by Gleissberg et al. (1979) and applied in the present analysis (Method 1), is at all an important proxy of the solar activity on the larger temporal scale. We propose that it is indeed the case, in spite of some other opinions. For instance, Hathaway et al. (1994) claimed that such an asymmetry is not only not very important, but also that its variation from cycle to cycle is small and not indicative of solar maxima. In the present analysis we present evidence for an opposite conclusion.

A final question is related to the possible physical interpretation (or justification) of the study of the asymmetry parameter. Our analysis of the asymmetry and its proportionality to the cycle strength is obviously related to, but is not the same as the Waldmeier effect. This effect states that stronger cycles have shorter rising times (e.g., Wilson 1990c; Hathaway et al. 2002; Lantos 2006b) and is one of Waldmeier's rules (for a detailed review see e.g. Beck et al. 1995). The Waldmeier effect was found to be a result of (or at least consistent with) various dynamo models, starting with non-linear dynamo waves (Stix 1972), various fluctuations in the mean field dynamo theory (Hoyng 1993; Ossendrijver & Hoyng 1996) up to the more recent fine tuning of the flux transport dynamo models (Cameron & Schüssler 2007). On the other hand, it was even considered that the Waldmeier effect might be an artifact of the definition of the relative sunspot number (Dikpati et al. 2008a), since it is much less pronounced in the sunpot area data sets.

Acknowledgements

This work is sponsored by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant number FA8655-07-1-3093. Also, the support from the Austrian-Croatian Bilateral Scientific Project No. 1 is acknowledged. We would like to thank Manfred Schüssler and Jasa Calogovic for helpful comments and discussions, as well as the anonymous referee for many suggestions which have led to an improvement of the paper.

References

Footnotes

...[*]
Alexander von Humboldt Research Fellow.

All Tables

Table 1:   The solar cycle number, the epochs of solar minima and maxima ( $T_{\rm min}$ and $T_{\rm max}$, respectively), the extreme values of the monthly smoothed relative sunspot numbers in corresponding epochs ( $R_{\rm min}$ and $R_{\rm max}$, respectively) and the asymmetry values (A, A1, A2, and A3).

All Figures

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig1.eps} \end{figure} Figure 1:

The asymmetry parameter A as a function of the cycle number. The parameters of the linear least-square fit are also given.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig2.eps} \end{figure} Figure 2:

Similar to Fig. 1, here presented for the smoothed values A3.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig3.eps} \end{figure} Figure 3:

The power spectrum as a function of the inverse cycle number for the data series presented in Fig. 1. The highest peak corresponds to the period of about 70 years.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig4.eps} \end{figure} Figure 4:

The asymmetry parameter A1 as a function of the maximal smoothed monthly relative sunspot number, for all solar cycles with available sunspot number data. The parameters of the linear least-square fit are also given.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig5.eps} \end{figure} Figure 5:

Similar to Fig. 4, here presented for the values A3.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig6.eps} \end{figure} Figure 6:

The peak smoothed monthly relative sunspot number as a function of the same quantity in the preceding solar minimum, for all solar cycles with the data available. The parameters of the linear least-square fit are also given.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width = 9 cm]{0862fig7.eps} \end{figure} Figure 7:

The observed (marked by x symbol and the full line) and predicted (marked by diamond symbol and the dotted line) yearly values of the relative sunspot number using the ARMA method.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.