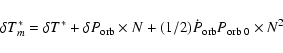Timing of the 2008 outburst of SAX J1808.4–3658 with XMM-Newton: a stable orbital-period derivative over ten years

L. Burderi; A. Riggio; T. Di Salvo; A. Papitto; M. T. Menna; A. D'Aì; R. Iaria

doi:10.1051/0004-6361/200811542

Home

All issues

Volume 496 / No 2 (March III 2009)

A&A, 496 2 (2009) L17-L20

Full HTML

Free Access

Issue		A&A Volume 496, Number 2, March III 2009


Page(s)		L17 - L20
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200811542
Published online		24 February 2009

LETTER TO THE EDITOR

Timing of the 2008 outburst of SAX J1808.4-3658 with XMM-Newton: a stable orbital-period derivative over ten years

L. Burderi¹ - A. Riggio¹ - T. Di Salvo² - A. Papitto^3,4 - M. T. Menna⁴ - A. D'Aì² - R. Iaria²

1 - Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu, KM 0.7, Monserrato 09042, Italy
2 - Dipartimento di Scienze Fisiche ed Astronomiche, Università di Palermo, via Archirafi 36, Palermo 90123, Italy
3 - Dipartimento di Fisica, Università degli Studi di Roma ``Tor Vergata'', via della Ricerca Scientifica 1, 00133 Roma, Italy
4 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, Monteporzio Catone 00040, Italy

Received 17 December 2008 / Accepted 16 February 2009

Abstract
We report on a timing analysis performed on a 62-ks long XMM-Newton observation of the accreting millisecond pulsar SAX J1808.4-3658 during the latest X-ray outburst that started on September 21, 2008. By connecting the time of arrivals of the pulses observed during the XMM-Newton observation, we derived the best-fit orbital solution and a best-fit value of the spin period for the 2008 outburst. Comparing this new set of orbital parameters and, in particular, the value of the time of ascending-node passage with the orbital parameters derived for the previous four X-ray outbursts of SAX J1808.4-3658 observed by the PCA onboard RXTE, we find an updated value of the orbital period derivative, which turns out to be $\dot P_{\rm orb} = (3.89 \pm 0.15)$ $\times$ 10^-12 s/s. This new value of the orbital period derivative agrees with the previously reported value, demonstrating that the orbital period derivative in this source has remained stable over the past ten years. Although this timespan is not sufficient yet for confirming the secular evolution of the system, we again propose an explanation of this behavior in terms of a highly non-conservative mass transfer in this system, where the accreted mass (as derived from the X-ray luminosity during outbursts) accounts for a mere 1% of the mass lost by the companion.

Key words: stars: neutron - stars: magnetic fields - X-rays: binaries - X-rays: individuals: SAX J1808.4-3658

1 Introduction

Accreting millisecond pulsars (AMSP) are generally interpreted as the evolutionary link between low-mass X-ray binaries and rotation-powered millisecond radio pulsars. According to the recycling scenario, the last are in fact formed after a phase of mass accretion from a low-mass companion star, which ultimately spins the neutron star up to ms periods (Alpar et al. 1982). SAX J1808.4-3658 was the first AMSP discovered (Wijnands & van der Klis 1998). In ten years the population of AMSP has grown to ten sources, all residing in close and transient binaries, but SAX J1808.4-3658 can still be considered the cornerstone of its class as it has repeatedly gone in outburst almost every two years after its first detection, making it the most observationally rich source of its class. Its timing and orbital properties have been extensively studied; while the timing behavior of the spin frequency is still debated because of the presence of timing noise in the phase delays (see Burderi et al. 2006, B06 hereinafter; Hartman et al. 2008, H08), there is good agreement as regards the orbital parameters of this source, which are now known with extreme precision (H08; Di Salvo et al. 2008, DS08).

In particular, a timing of the past four outbursts of SAX J1808.4-3658 observed with the PCA onboard the RXTE satellite (spanning more than 7 years from April 1998 to October 2005) has allowed the orbital period of this source to be derived with relative uncertainty $\Delta P_{\rm orb} / P_{\rm orb}$ of $\sim$ 2 $\times$ 10^-9 (dS08, H08). More interesting, the orbital period of the source shows a significant derivative, which indicates that it is increasing at a large, as well as puzzling, rate of $\dot P_{\rm orb} = (3.5 \pm 0.2)$ $\times$ 10^-12 s/s. The value of the orbital period derivative is at least one order of magnitude greater than what is expected for conservative mass transfer driven by gravitational radiation (GR; DS08, H08).

To continue the monitoring of the orbital period derivative and to further improve the orbital solution for this interesting system, we analyzed a 62 ks XMM-Newton Target of Opportunity (ToO) observation of this source, performed during the latest outburst in October 2008.

2 Timing analysis and results

SAX J1808.4-3658 was found in outburst on 2008 September 21 by RXTE, and since then it has been the object of an intensive observational campaign. XMM-Newton observed SAX J1808.4-3658 as a ToO observation for 62 ks on 2008 October 1 (start time MJD 54 739.99517), roughly one week after the assumed outburst peak. In this paper we concentrate on the pn data, which have the best statistics for timing analysis. A detailed description of the XMM-Newton observation and data reduction has already been reported in Papitto et al. (2009). The arrival times of all the pn events were referred to the solar system barycenter by using the barycen tool in SAS v.8.0.0. As the best estimate for the source coordinates, we considered the position of the radio counterpart, which has an uncertainty of 0.4 arcsec (90% c.l., Rupen et al. 2002) and is compatible with the optical counterpart (Giles et al. 1999).

We used the XMM-Newton/pn data to improve the orbital solution for SAX J1808.4-3658. To this aim we also re-analyzed the previous four outbursts of this source observed by RXTE/PCA, namely 1998 April (Obs. ID P30411), 2000 February (Obs. ID P40035), 2002 October (Obs. ID P70080), and 2005 June (Obs. ID P91056 and Obs. ID P91418) outbursts, respectively (see H08 for a detailed description of these observations). With this new analysis we present a more conservative treatment of the errors on the phase delays, to avoid any possible underestimation of the uncertainties on the orbital parameters caused by the phase changes and shifts that are known to occur during outbursts.

For each outburst, we repeat the analysis performed by DS08, with a few differences. Differential corrections to the adopted orbital parameters were found by fitting the pulse phases as a function of time for each outburst (see e.g. Fig. 1). In general, any residual orbital modulation is superposed onto a long-term variation in the phases, e.g. caused by a variation of the spin. However, SAX J1808.4-3658 shows very complex behavior of the pulse phases with time, with phase shifts, probably caused by variations in the pulse shape, that are difficult to interpret (see e.g. B06, H08). To model this complex behavior of the pulse phases with time, we fit the phases of each of these intervals with the formula for the differential corrections to the orbital parameters (see e.g. Deeter et al. 1981) plus a polynomial (up to $8{\rm th}$ degree, depending on the irregular behavior of the pulse phases). This technique is complementary to the technique adopted in dS08, where we preferred to restrict the fit of the differential corrections to the orbital parameters to intervals in which the long-term variation and/or phase shifts were negligible and considered consecutive intervals with a duration of at least 4 orbital periods (depending on the statistics), fitting the phases of each of these intervals only with the formula for the differential corrections of the orbital parameters. We have verified that the two techniques give similar orbital corrections, but we now obtain somewhat larger uncertainties on the derived orbital parameters.

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig1.ps} \end{figure}$

Figure 1:

Phase delays (in $\mu$ s) vs. time during the XMM-Newton observation after the first iteration. To show for clarity the orbital correction against an horizontal line, the frequency adopted for the folding is the best-fit spin frequency of the 2008 outburst. The orbital modulation is clearly visible ( top panel) and is well-fitted by our orbital solution, as can be seen in the post-fit residuals ( middle and bottom panels).

Open with DEXTER

Over the 10-year base line SAX J1808.4-3658 has been observed, the measured $\dot{P}_{{\rm orb}}$ should have produced $\approx$ 1 ms change in $P_{{\rm orb}}$ . However, the uncertainty on the individual $P_{{\rm orb}}$ determinations from the local orbital solution during each outburst are about 0.5-2.0 ms (see also H08); accordingly, no significant corrections to $P_{{\rm orb}}$ have been directly observed. Thus we fix our parameter $P_{{\rm orb,0}} = 7249.156499$ s (dS08) and improve its measure below using the same technique as in dS08. For each of the five outbursts, we find similar corrections for the projected semimajor axis of the neutron star orbit and upper limits on the eccentricity. We hence combine the measurements corresponding to each of the outbursts by computing the error-weighted means of the corrections to the projected semimajor axis and of the upper limits on the eccentricity. On the other hand, we find that the correction to the predicted times of passage of the NS at the ascending node at the beginning of each outburst, $T^*_{m \; {\rm predicted}} = T^*_0 + N P_{\rm orb\; 0}$ , is different among the five outbursts. Here T^*₀ is the time of ascending node passage given by dS08, and the integer N is the exact number of orbital cycles elapsed between two different ascending node passages; i.e., N is the closest integer to $(T^*_m - T^*_0)/ P_{\rm orb \;0}$ under the assumption that $\vert T^*_m - T^*_{m \; {\rm predicted}} \vert\ll P_{\rm orb \; 0}$ that we have verified a posteriori, and m = 1998, 2000, 2002, 2005, and 2008. These points show a clear parabolic trend that we fitted to the formula

$\begin{displaymath}% \delta T^*_m = \delta T^* + \delta P_{\rm orb} \times N + (1/2) \dot P_{\rm orb} P_{\rm orb \; 0} \times N^2 \end{displaymath}$

(1)

where $\delta T^*$ , $\delta P_{\rm orb}$ , and $\dot{P}_{{\rm orb}}$ (the orbital period derivative) are the fit parameters. To compute the correct errors on the derived parameters, we also considered the errors induced by the uncertainties in the time coordinate (which we assumed to be half of the duration of each outburst) following the standard procedure for the propagation of these errors (see e.g. Bevington & Robinson 2003).

We iterate the method described above until the upper limit on the eccentricity, as well as the corrections on the projected semimajor axis, the orbital period, and its derivative were all compatible with zero within the computed errors. In Fig. 1 we plot the phase delays obtained for the XMM-Newton/pn data with the orbital solution of DS08 neglecting the orbital-period derivative. The sinusoidal oscillation is clearly visible (top panel) and mainly stems from the $\sim$ 35 s delay in the ascending node passage with respect to the one predicted with a constant orbital period. In the middle panel, we show the time residuals after our first improvement of the orbital solution (reduced $\chi^2 = 1.86$ for 49 d.o.f.). In the bottom panel, the time residuals are shown with respect to the final orbital solution shown in Table 1 (reduced $\chi^2 = 1.07$ for 72 d.o.f.). In this case more points are visible in the residuals. This is caused by how improving the orbital solution results in a higher statistical significance for each point, making acceptable phase-points that were rejected with our previous solution. In Fig. 2 we plot the final $\delta T^*_m$ 's vs. time, together with the best-fit parabola. The fit was good with a reduced $\chi^2 = 1.55$ (for 2 d.o.f.). This corresponds to a probability of $21\%$ of obtaining a $\chi^2$ that is larger than the one we found. Our result is therefore acceptable, since the probability we obtained is well above the conventionally accepted significance level of $5\%$ (see e.g. Bevington & Robinson 2003).

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig2.ps} \end{figure}$	Figure 2: Differential correction to the time of passage of the neutron star at the ascending node for each of the five outbursts analyzed ( top panel) and residuals with respect to the best fit parabola ( bottom panel).
Open with DEXTER

In agreement with previous results, we find a highly significant derivative of the orbital period, which indicates that the orbital period in this system is increasing at a rate of $\dot P_{\rm orb} = (3.89 \pm 0.15)$ $\times$ 10^-12 s/s. The best-fit values for the orbital parameters are shown in Table 1. With these new ephemerides, we correct the events of the XMM-Newton ToO observation of 2008 October 1 and fit the 700 s folded phase delays of the fundamental with a straight line to obtain the correction to the spin frequency adopted for the folding. The fit is acceptable with a reduced $\chi^2 = 1.16$ (for 71 d.o.f.). The best-fit spin frequency of the 2008 outburst is also reported in Table 1.

3 Discussion

In this paper we present a timing analysis of the XMM-Newton observation performed during the last outburst of the AMSP SAX J1808.4-3658, together with a re-analysis of the past four outbursts from this source observed by RXTE/PCA. We find that the measures of the time of ascending node passage for the last 5 outbursts from this source are again perfectly fitted by a parabola; from this fitting, we find a derivative of the orbital period, $\dot P_{\rm orb} = (3.89 \pm 0.15)$ $\times$ 10^-12 s/s, which agrees with previous measures (H08; DS08; see also Patruno et al. 2008; and Hartman et al. 2009, who report a similar value using RXTE data taken during the 2008 outburst). The conclusion from these measurements is that the orbital-period derivative in this system has been stable over the past ten years. This supports the hypothesis that the system is following a non-conservative secular binary evolution (see DS08).

Table 1: Best-fit orbital solution for SAX J1808.4-3658 derived from the analysis of the five outbursts observed from 1998 to 2008.

H08 note that the orbital parameters of SAX J1808.4-3658 are very similar to those of the so-called black-widow millisecond pulsars, which show large and variable $\dot{P}_{{\rm orb}}$ (see e.g. Doroshenko et al. 2001; Arzoumanian et al. 1994). In those cases $\dot{P}_{{\rm orb}}$ changes have been ascribed to gravitational quadrupole coupling, i.e. a variable quadrupole moment of the companion that is caused by a cyclic spin-up and spin-down in the upper layers of the companion (Applegate & Shaham 1994). In this scenario, the companion star must be partially non-degenerate, convective, and magnetically active, so that the wind of the companion star will result in a strong torque, which tends to slow the star down. This torque is then transferred to the orbit via gravitational interaction. Typical timescales for the orbital period (roughly sinusoidal) modulation are about 5-6 yr (Applegate 1992). However, SAX J1808.4-3658 has been monitored since its discovery as a millisecond pulsar in 1998 and does not show any evidence of this complex behavior in its orbital period. Instead, its $\dot{P}_{{\rm orb}}$ has been remarkably stable over this time. We cannot exclude, however, that its $\dot{P}_{{\rm orb}}$ might exhibit more complex behavior on decade-long time scales.

The value of the orbital period derivative of SAX J1808.4-3658 clearly indicates that the binary system is expanding at a rate that is more than one order of magnitude higher than what is predicted by conservative mass transfer driven by GR (H08; DS08). In fact, the angular momentum losses caused by GR have the effect of reducing the binary orbital period. The transfer of mass from the secondary to the neutron star indeed has the effect of expanding the system (since the secondary star is lighter than the neutron star, e.g. Verbunt 1993). Following DS08, angular momentum conservation together with the third Kepler's law and considering the GR angular momentum losses, give the orbital period derivative:

$\displaystyle % \dot P_{-12}$	=	$\displaystyle 0.138 m_1^{5/3} q_{0.1} (1 + 0.1 q_{0.1})^{-1/3} P_{\rm 2h}^{-5/3}$
		$\displaystyle +~ 6.840 m_1^{-1} q_{0.1}^{-1} P_{\rm 2h} \; g(\beta,q,\alpha)\; \dot m_{-9}$	(2)

where $\dot P_{-12}$ is $\dot{P}_{{\rm orb}}$ in units of 10^-12 s/s, $m_1 = M_1/M_\odot$ , q_0.1 is the mass ratio q = m₂ / m₁ in units of 0.1, $P_{\rm 2h} = P_{\rm orb}/2{\rm h}$ , $\dot m_{-9} = - \dot M_2/(10^{-9}~M_\odot/{\rm yr})$ , $\beta$ is the fraction of the mass lost by the companion that is accreting onto the neutron star, $\alpha$ the specific angular momentum of the mass lost by the system written in units of the specific angular momentum of the companion ( $\alpha = [1-0.462 (1+q)^{2/3} q^{1/3}]^2 \simeq 0.7$ for matter leaving the system with the specific angular momentum of the inner Lagrangian point), and $g(\beta,q,\alpha) = 1 - \beta q - (1-\beta) (\alpha + q/3)/(1+q)$ . Inserting our derived value $\dot P_{-12} = 3.89$ into this equation, we can derive $\dot m_{-9}$ vs. m₂ = q m₁. The corresponding curves (very insensitive to the adopted values m₁ = 1.1, 1.56, 2.2) are shown in Fig. 3 and labeled with $\beta =1$ for the conservative mass transfer case. In the same figure the horizontal line at $\dot m_{-9} = 0.017$ is the time-averaged mass accretion rate derived from the X-ray luminosity observed during outbursts and quiescence periods in the last ten years (which could even be an overestimate by a factor 2 of the actual mass accretion rate, cf. Galloway & Cumming 2006). The crossing point of these curves, which is the necessary solution imposed by the conservation of angular momentum, falls in the forbidden region at $m_2 \sim 0.003$ .

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig3.ps} \end{figure}$	Figure 3: Mass-loss rate of the companion of SAX J1808.4-3658 in conservative ( $\beta =1$ ) and highly non-conservative ( $\beta = 0.01$ ) scenarios. The gray area on the left is forbidden because the radius of the (Brown Dwarf) companion is greater than its Roche Lobe. The gray area on the right shows the constraints on the companion mass imposed by the mass function of the system.
Open with DEXTER

We can further impose the obvious constraint $R_2 \leq R_{\rm RL_2}$ , where R₂ is the radius of the companion and $R_{\rm RL_2} = 1.2$ $\times$ $10^{10} m_2^{1/3} P_{\rm 2h}^{2/3}$ cm is the radius of the Roche Lobe of the companion. Adopting results from detailed numerical calculations of the mass radius relation for low main sequence stars and brown dwarfs of minimum radius (namely cold, or older than 5 Gyr, Chabrier & Baraffe 2000), the gray area on the left in Fig. 3 indicates the region excluded by the violation of this constraint and shows that a conservative solution is impossible. Companion masses below $0.02~M_\odot$ are also excluded by the constraints imposed by the mass function of the system for reasonable values of the neutron star mass.

In line with DS08, we thus propose a highly non-conservative scenario in which the mass-loss rate from the companion is stable at a level of $\dot m_{-9} \sim 1$ , with accretion episodes lasting a few tens of days, separated by quiescent phases in which the same rate of mass is ejected by the system. In this hypothesis, we calculate that $\beta = 9.5$ $\times$ 10^-3. The corresponding lines (which are again computed for m₁ = 1.1, 1.56, 2.2) are shown in Fig. 3 and labeled with $\beta = 0.01$ . The crossing point between the non-conservative lines and the horizontal line for $\dot m_{-9} = 1.8$ (from B06) at $m_2 \sim 0.08$ is outside the forbidden area and demonstrates that our proposed scenario is, in principle, viable. The ejection of matter out of the system via a pulsar wind will not imply an extra spin down for the pulsar, since in our model matter is ejected by the radiation pressure of the pulsar, well outside the light cylinder radius (where the electromagnetic radiation from the pulsar is no longer connected to the neutron star magnetic field). Also, any possible spin down caused by the propeller effect at the end of an outburst may be averaged to zero by a spin up, because of the accretion inside the corotation radius, that is expected at the beginning of an outburst.

In conclusion, to explain the large and stable orbital period derivative in the case of SAX J1808.4-3658, we propose that mass is expelled at a high rate from the system with the specific angular momentum of the inner Lagrangian point (or, eventually, of an outer disk, if present, e.g. Deloye et al. 2008). These results strengthen the hypothesis that SAX J1808.4-3658 belongs to the population of the so-called ``hidden'' millisecond pulsars, whose radio emission is completely blocked by material engulfing the system that is continuously replenished by the mass outflow driven by companion irradiation. In the case of SAX J1808.4-3658, irradiation is probably caused by the power emitted by the magneto-dipole rotator, which may also explain why, although the companion star is transferring mass at a high rate, this mass does not accrete onto the neutron star (see DS08 for a more detailed discussion). If this is the case, $\sim$ $99\%$ of the transferred mass in this system is not directly observable. Although 10 years is not long enough to confirm that the system is in a stationary (secular) orbital evolution, the next few years will be important for confirming the stability of the orbital period derivative or to observe $\dot P$ reversal as in classical black-widow pulsars.

Acknowledgements

We thank the XMM-Newton team who supported this ToO observation, and the referee for useful discussions.

References

Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] (In the text)
Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] (In the text)
Applegate, J. H., & Shaham, J. 1994, ApJ, 436, 312 [NASA ADS] [CrossRef] (In the text)
Arzoumanian, Z., Fruchter, A. S., & Taylor, J. H. 1994, ApJ, 426, L85 [NASA ADS] [CrossRef]
Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences, 3r [NASA ADS]d edn. (Boston, MA: McGraw-Hill) (In the text)
Burderi, L., Di Salvo, T., Menna, M. T., Riggio, A., & Papitto, A. 2006, ApJ, 653, L133 [NASA ADS] [CrossRef] (In the text)
Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] (In the text)
Deeter, J. E., Pravdo, S. H., & Boynton, P. E. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] (In the text)
Deloye, C. J., Heinke, C. O., Taam, R. E., & Jonker, P. G. 2008, MNRAS, 391, 1619 [NASA ADS] [CrossRef] (In the text)
Di Salvo, T., Burderi, L., Riggio, A., Papitto, A., & Menna, M. T. 2008, MNRAS, 389, 1851 [NASA ADS] [CrossRef] (In the text)
Doroshenko, O., Löhmer, O., Kramer, M., et al. 2001, A&A, 379, 579 [NASA ADS] [CrossRef] [EDP Sciences]
Galloway, D. K., & Cumming, A. 2006, ApJ, 652, 559 [NASA ADS] [CrossRef] (In the text)
Giles, A. B., Hill, K. M., & Greenhill, J. G. 1999, MNRAS, 304, 47 [NASA ADS] [CrossRef] (In the text)
Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2008, ApJ, 675, 1468 [NASA ADS] [CrossRef] (In the text)
Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2009, ApJ, submitted (In the text)
Papitto, A., Di Salvo, T., D'Ai, A., et al. 2009, A&A, 493, L39 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Patruno, A., Hartman, J. M., Wijnands, R., et al. 2008, The Astronomer's Telegram, 1760, 1 [NASA ADS] (In the text)
Rupen, M. P., Dhawan, V., Mioduszewski, A. J., Stappers, B. W., & Gaensler, B. M. 2002, IAU Circ., 7997, 2 (In the text)
Verbunt, F. 1993, ARA&A, 31, 93 [NASA ADS] [CrossRef] (In the text)
Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] (In the text)

Footnotes

... dS08: The actual T^*₀ used in this work is the T^*₀ of dS08 decremented by 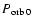$P_{\rm orb \; 0}$ in order to have the time of ascending node passage just before the beginning of RXTE data of the 1998 outburst which occurred at T₀ = 50 914.8099 MJD.

All Tables

Table 1: Best-fit orbital solution for SAX J1808.4-3658 derived from the analysis of the five outbursts observed from 1998 to 2008.

All Figures

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig1.ps} \end{figure}$	Figure 1: Phase delays (in $\mu$ s) vs. time during the XMM-Newton observation after the first iteration. To show for clarity the orbital correction against an horizontal line, the frequency adopted for the folding is the best-fit spin frequency of the 2008 outburst. The orbital modulation is clearly visible ( top panel) and is well-fitted by our orbital solution, as can be seen in the post-fit residuals ( middle and bottom panels).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig2.ps} \end{figure}$	Figure 2: Differential correction to the time of passage of the neutron star at the ascending node for each of the five outbursts analyzed ( top panel) and residuals with respect to the best fit parabola ( bottom panel).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{1542_fig3.ps} \end{figure}$	Figure 3: Mass-loss rate of the companion of SAX J1808.4-3658 in conservative ( $\beta =1$ ) and highly non-conservative ( $\beta = 0.01$ ) scenarios. The gray area on the left is forbidden because the radius of the (Brown Dwarf) companion is greater than its Roche Lobe. The gray area on the right shows the constraints on the companion mass imposed by the mass function of the system.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.