| Issue |
A&A
Volume 496, Number 2, March III 2009
|
|
|---|---|---|
| Page(s) | 333 - 342 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200811091 | |
| Published online | 09 February 2009 | |
The new intermediate long-bursting source XTE J1701-407
M. Falanga1,2 - A. Cumming3 - E. Bozzo4,5 - J. Chenevez6
1 - CEA Saclay, DSM/IRFU/Service d'Astrophysique
(CNRS FRE 2591), 91191 Gif-sur-Yvette, France
2 - AIM - Unité Mixte de Recherche CEA - CNRS -
Université Paris 7, Paris, France
3 - Physics Department, McGill University, 3600 rue University,
Montreal QC, H3A 2T8, Canada
4 - INAF - Osservatorio Astronomico di Roma, Via Frascati 33, 00044
Rome, Italy
5 - Dipartimento di Fisica - Universitá di Roma Tor Vergata, via
della Ricerca Scientifica 1, 00133 Rome, Italy
6 - National Space Institute, Technical University of Denmark,
Juliane Maries Vej 30, 2100
Copenhagen, Denmark
Received 6 October 2008 / Accepted 17 December 2008
Abstract
Aims. XTE J1701-407 is a newly discovered X-ray transient source. We investigate its flux variability and study the intermediate long- and short-bursts discovered by Swift on July 17, and 27, 2008, respectively.
Methods. Only one intermediate long-burst, of duration ![]() 18 min and ten days later a short burst, have been recorded from XTE J1701-407. We analyzed the public available data from Swift and RXTE, and compared the observed properties of the intermediate long-burst with theoretical ignition condition and light curves to investigate the possible nuclear-burning processes.
18 min and ten days later a short burst, have been recorded from XTE J1701-407. We analyzed the public available data from Swift and RXTE, and compared the observed properties of the intermediate long-burst with theoretical ignition condition and light curves to investigate the possible nuclear-burning processes.
Results. The intermediate long-burst may have exhibited a photospheric radius expansion, allowing us to derive the source distance at 6.2 kpc, assuming the empirically derived Eddington luminosity for pure helium. The intermediate long-burst decay was described most accurately by using two exponential functions with e-folding times of
![]() s and
s and
![]() s. The bursts occurred at a persistent luminosity of
s. The bursts occurred at a persistent luminosity of
![]() erg s-1 (
erg s-1 (![]() 2.2% of the Eddington luminosity). For the intermediate long-burst, the mass accretion rate per unit area onto the neutron star was
2.2% of the Eddington luminosity). For the intermediate long-burst, the mass accretion rate per unit area onto the neutron star was
![]() g cm-2 s-1, and the total energy released was
g cm-2 s-1, and the total energy released was
![]() erg. This corresponds to an ignition column depth of
erg. This corresponds to an ignition column depth of
![]() g cm-2, for a pure helium burning. We find that the energetics of this burst can be modeled in different ways, as (i) pure helium ignition, as the result of either pure helium accretion or depletion of hydrogen by steady burning during accumulation; or (ii) as ignition of a thick layer of hydrogen-rich material in a source of low metallicity. However, comparison of the burst duration with model light curves suggests that hydrogen burning plays an important role during the burst, and therefore that this source is a low accretion-rate burster with a low metallicity in the accreted material.
g cm-2, for a pure helium burning. We find that the energetics of this burst can be modeled in different ways, as (i) pure helium ignition, as the result of either pure helium accretion or depletion of hydrogen by steady burning during accumulation; or (ii) as ignition of a thick layer of hydrogen-rich material in a source of low metallicity. However, comparison of the burst duration with model light curves suggests that hydrogen burning plays an important role during the burst, and therefore that this source is a low accretion-rate burster with a low metallicity in the accreted material.
Key words: stars: binaries: close - stars: individual: XTE J1701-407 - stars: neutron - X-rays: bursts
1 Introduction
Type-I X-ray bursts are among the most evident signatures of
the presence of a neutron star (NS) in low mass X-ray binaries.
These bursts are thermonuclear explosions that occur on the surface of
accreting NSs and are triggered by unstable hydrogen and/or helium burning
(see, e.g., Lewin et al. 1993; Strohmayer & Bildsten 2006, for reviews). Type-I X-ray bursts were predicted theoretically by Hansen & Van Horn (1975),
and several thousand bursts have been observed to date
(see, e.g., Cornelisse et al. 2003; Galloway et al. 2006a; Chelovekov et al. 2006).
From the duration of the bursts measured by their decay
parameter ![]() (see e.g., Galloway et al. 2006a) three main branches are distinguishable:
normal bursts, intermediate long-bursts, and superbursts
(see Fig. 7 in Falanga et al. 2008, and references therein). These bursts
can be described in terms of different fuel types, accretion rates, and they,
therefore, also exhibit different recurrence times
(e.g., Galloway et al. 2006a; Strohmayer & Bildsten 2006; Cumming & Macbeth 2004).
Thanks to the long Galactic plane scan carried out with BeppoSAX, INTEGRAL, and
Swift, a number of rare, intermediate long-bursts and superbursts have
been observed.
In most cases, the rise of the burst was
(see e.g., Galloway et al. 2006a) three main branches are distinguishable:
normal bursts, intermediate long-bursts, and superbursts
(see Fig. 7 in Falanga et al. 2008, and references therein). These bursts
can be described in terms of different fuel types, accretion rates, and they,
therefore, also exhibit different recurrence times
(e.g., Galloway et al. 2006a; Strohmayer & Bildsten 2006; Cumming & Macbeth 2004).
Thanks to the long Galactic plane scan carried out with BeppoSAX, INTEGRAL, and
Swift, a number of rare, intermediate long-bursts and superbursts have
been observed.
In most cases, the rise of the burst was ![]() 1 s, whereas the decay was
approximately exponential, with a duration of a few seconds for normal bursts,
tens of minutes for intermediate long-bursts, and up to several hours for
superbursts
(e.g., Molkov et al. 2005; Falanga et al. 2008; Kuulkers 2004; Chenevez et al. 2007,2006; in 't Zand et al. 2005,2004).
The recurrence time of type-I X-ray busts ranges from few hours to years, depending
on the nuclear reactions involved (see, e.g., Lewin et al. 1993; Strohmayer & Bildsten 2006, for
reviews).
1 s, whereas the decay was
approximately exponential, with a duration of a few seconds for normal bursts,
tens of minutes for intermediate long-bursts, and up to several hours for
superbursts
(e.g., Molkov et al. 2005; Falanga et al. 2008; Kuulkers 2004; Chenevez et al. 2007,2006; in 't Zand et al. 2005,2004).
The recurrence time of type-I X-ray busts ranges from few hours to years, depending
on the nuclear reactions involved (see, e.g., Lewin et al. 1993; Strohmayer & Bildsten 2006, for
reviews).
Table 1: Log of RXTE and Swift observations and best-fit spectral parameters of the persistent emission. An absorbed power-law model is used to fit these spectra.
In this paper, we report on an intermediate long-burst from the
X-ray transient XTE J1701-407. This source was discovered by the Rossi X-ray Timing Explorer (RXTE)
during a routine Galactic bulge scan on June 8, 2008 (Markwardt et al. 2008a).
At the time of discovery, the source spectrum was most accurately reproduced by
an absorbed power-law model with photon index ![]() 2.2 and a
neutral absorption column of
2.2 and a
neutral absorption column of ![]()
![]() cm-2,
the measured flux was
cm-2,
the measured flux was ![]()
![]() erg cm-2 s-1in the 2-10 keV band (Markwardt et al. 2008a). Swift/XTE follow-up
observations on June 11, 2008
found both spectral and source flux measurements consistent with
the RXTE/PCA results (Degenaar & Wijnands 2008).
On July 17, 2008, the Swift/BAT camera detected a short flare consistent with the
position of XTE J1701-407, and
erg cm-2 s-1in the 2-10 keV band (Markwardt et al. 2008a). Swift/XTE follow-up
observations on June 11, 2008
found both spectral and source flux measurements consistent with
the RXTE/PCA results (Degenaar & Wijnands 2008).
On July 17, 2008, the Swift/BAT camera detected a short flare consistent with the
position of XTE J1701-407, and ![]() 97 s later Swift/XRT measured a decaying
X-ray flux (Barthelmy et al. 2008). Based on this BAT data, the X-ray
spectrum was consistent with those observed for thermonuclear X-ray
bursts, therefore, this flare was proposed to be a type-I
burst (Markwardt et al. 2008b).
Based on the Swift/XRT time-resolved spectrum during flux
decay, Linares et al. (2008a) measured the cooling tail and confirmed that the
flare was an intermediate, long, type-I X-ray
burst. This led to the classification of XTE J1701-407 as a NS low-mass X-ray
binary (Linares et al. 2008b,a).
Ten days later, i.e., on July 27, BAT observed in the 15-350 keV band, a
short burst lasting
97 s later Swift/XRT measured a decaying
X-ray flux (Barthelmy et al. 2008). Based on this BAT data, the X-ray
spectrum was consistent with those observed for thermonuclear X-ray
bursts, therefore, this flare was proposed to be a type-I
burst (Markwardt et al. 2008b).
Based on the Swift/XRT time-resolved spectrum during flux
decay, Linares et al. (2008a) measured the cooling tail and confirmed that the
flare was an intermediate, long, type-I X-ray
burst. This led to the classification of XTE J1701-407 as a NS low-mass X-ray
binary (Linares et al. 2008b,a).
Ten days later, i.e., on July 27, BAT observed in the 15-350 keV band, a
short burst lasting ![]() 10 s (Sakamoto et al. 2008).
Kilohertz quasi-periodic oscillations were observed at
10 s (Sakamoto et al. 2008).
Kilohertz quasi-periodic oscillations were observed at ![]() 1150 Hz
(see Strohmayer et al. 2008, for details). The most accurate
position of the source was provided by Swift at
1150 Hz
(see Strohmayer et al. 2008, for details). The most accurate
position of the source was provided by Swift at
![]() = 17
= 17![]() 01
01![]() 44
44
![]() 3 and
3 and
![]() = -40
= -40
![]() 51
51
![]() 29
29
![]() 9 with an
estimated accuracy of 1
9 with an
estimated accuracy of 1
![]() 7 (Starling & Evans 2008).
No infrared counterpart candidate was found at this position (Kaplan & Chakrabarty 2008).
7 (Starling & Evans 2008).
No infrared counterpart candidate was found at this position (Kaplan & Chakrabarty 2008).
2 Data analysis and results
In the present study, we used publicly available data from Swift and
RXTE observatories. The dataset include RXTE target of
opportunity observations, performed after the discovery of the source
(observation ID. 93444), as well as Swift follow-up observations
(ID. 0031221001, 0031221002, and 00317205001). The Swift data set
also includes the intermediate long-burst discovered on July 17,
(ID. 00317205000) and the short burst from July 27, 2008 (ID. 00318166000).
The total effective exposure time is 75.4 ks (30 pointings) and 1.1 ks
for RXTE/PCA and Swift, respectively. In Table 1, we report
the detailed observations log.
Data reduction of the RXTE Proportional Counter Array
(PCA; 2-60 keV, Jahoda et al. 1996) and the High Energy X-ray Timing
Experiment (HEXTE; 15-250 keV, Rothschild et al. 1998) was performed according
to the default selection criteria for background-subtraction, light-curve, and
spectrum extraction. We used only PCU2 data.
We used Swift/XRT data in both Windowed Timing (WT) and Photon
Counting (PC) mode. However, in the following, we report only
on WT data, since we found that PC data were strongly affected by
pile-up, and quasi-simultaneous observations carried out in WT mode
were available. We reduced all the XRT data by using the version of
the xrtpipeline (version 0.11.6) included in
the Heasoft package 6.4, and the latest calibration files available.
Source events in WT mode
were extracted from rectangle regions with widths of 40 pixels and
heights of 20 pixels![]() .
Ancillary response files were generated with xrtmkarf and
accounted for different extraction regions, vignetting, and
point-spread function.
For the Swift/BAT data analysis, we used the batgrbproduct tool included
in the Heasoft package 6.4. Time-resolved spectra and light curves (see
Sect. 2.2)
were extracted by using the batbinevt, batupdatephakw,
batphasyserr, and batdrmgen tools.
.
Ancillary response files were generated with xrtmkarf and
accounted for different extraction regions, vignetting, and
point-spread function.
For the Swift/BAT data analysis, we used the batgrbproduct tool included
in the Heasoft package 6.4. Time-resolved spectra and light curves (see
Sect. 2.2)
were extracted by using the batbinevt, batupdatephakw,
batphasyserr, and batdrmgen tools.
2.1 Persistent emission
Spectra obtained from RXTE/PCA and Swift/XRT observations were fit
separately by using a photoelectrically-absorbed power-law
model. The best-fit model parameters for the absorption column, ![]() ,
are
between
,
are
between ![]() and
and
![]() cm-2 and a power-law index
cm-2 and a power-law index
![]() the corresponding unabsorbed fluxes
are between
the corresponding unabsorbed fluxes
are between
![]() and
and
![]() in the 2-20 keV energy band. In Table 1, we report
all the persistent spectral parameters. All uncertainties correspond to a 90%
confidence level. PCA spectra were extracted in the 2-20 keV energy
band; the source was detected only at low significance in the HEXTE
(15-50 keV band). A fit to the joint broad-band PCA/HEXTE
(2-50 keV) spectrum did not lead to a significant improvement in the
determination of the model parameters; in the following we
therefore, report only results for the PCA data. Swift/XRT spectra were extracted in the
2-10 keV band. All the measured unabsorbed fluxes were extrapolated to the
0.3-100 keV band by generating dummy responses (XSPEC version
11.3.2ag), and are shown in Fig. 1. We also included
in this figure fluxes derived from RXTE bulge
observations
in the 2-20 keV energy band. In Table 1, we report
all the persistent spectral parameters. All uncertainties correspond to a 90%
confidence level. PCA spectra were extracted in the 2-20 keV energy
band; the source was detected only at low significance in the HEXTE
(15-50 keV band). A fit to the joint broad-band PCA/HEXTE
(2-50 keV) spectrum did not lead to a significant improvement in the
determination of the model parameters; in the following we
therefore, report only results for the PCA data. Swift/XRT spectra were extracted in the
2-10 keV band. All the measured unabsorbed fluxes were extrapolated to the
0.3-100 keV band by generating dummy responses (XSPEC version
11.3.2ag), and are shown in Fig. 1. We also included
in this figure fluxes derived from RXTE bulge
observations![]() (Swank & Markwardt 2001).
In these cases, the conversion
between RXTE count rate and flux was obtained using the spectra results
and the values reported by Markwardt et al. (2008a).
(Swank & Markwardt 2001).
In these cases, the conversion
between RXTE count rate and flux was obtained using the spectra results
and the values reported by Markwardt et al. (2008a).
 |
Figure 1: Flux history of the X-ray transient XTE J1701-407. Open squares represent fluxes derived from RXTE bulge observations in the period from March 31, to September 2, 2008. Fluxes derived from RXTE/PCA and Swift/XRT target of opportunity and follow-up observations are marked with filled squares and stars, respectively. The arrow indicates the time of the type-I X-ray burst. |
| Open with DEXTER | |
The ligh curve and spectral analysis illustate that XTE J1701-407 experienced flaring activity for a few days, during which the X-ray flux varied by over a factor of 2-3. This variability can be ascribed to changes in the mass accretion rate or in the position of the source within its colour-colour diagram (CCD, see e.g., Hasinger & van der Klis 1989). The latter possibility is investigated in Fig. 2. The CCD was produced by using background-subtracted RXTE/PCA ligh curves with a 516 s time resolution. The soft colour is defined to be the logarithm of the ratio of the count rates in the energy band 2.1-3.7 keV to that for band 3.7-5.7 keV, whereas for the hard colour the ratio of the energy band 5.7-9.8 keV to 9.8-18.9 keV is used. No obvious transition between a hard to a soft state is observed. To reduce the errors in the colours, we generated a hard intensity diagram (HID) based on the net count rates in the 2.1-5.7 keV and 5.7-18.9 keV energy ranges with a 516 s time bin. However, the source behaviour was not traced with significantly higher quality in the HID, because the statistical uncertainties are not reduced significantly along the two axes. In Fig. 2, we show the HID. Future observations are thus required to investigate further the origin of flux variations in XTE J1701-407.
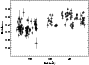 |
Figure 2: HID of XTE J1701-407. The hardness is the ratio of the count rates in the 5.7-18.9 keV to 2.1-5.7 keV and the intensity is in the 2.1-18.9 keV count rate. Each point corresponds to 516 s of integration time. |
| Open with DEXTER | |
2.2 Intermediate long-burst light curves and spectra
In Fig. 3, we show the Swift/BAT 15-25 keV (upper panel)
and XRT 0.3-10 keV (lower panel) light curve of the intermediate long-burst.
The burst start time is the time at which
the BAT X-ray intensity of the source increased to 10% of its peak value above
the persistent intensity level. The XRT light curve starts with a
delay of 133 s after the beginning of the burst observed by BAT. The
BAT light curve exhibit a slow rise time![]() of
of ![]() 45 s.
The XRT decay time from the burst is best-fit by using two exponential functions
with e-folding times of
45 s.
The XRT decay time from the burst is best-fit by using two exponential functions
with e-folding times of
![]() s and
s and
![]() s,
respectively (see also Linares et al. 2008a).
The total duration of the burst, i.e. the time to evolve away from and return to the persistent state, was of
s,
respectively (see also Linares et al. 2008a).
The total duration of the burst, i.e. the time to evolve away from and return to the persistent state, was of ![]() 86 s and
86 s and
![]() 18 min in the BAT (15-25 keV) and the XRT (0.3-10 keV) light curves, respectively.
18 min in the BAT (15-25 keV) and the XRT (0.3-10 keV) light curves, respectively.
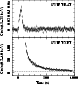 |
Figure 3:
The intermediate, long, type-I X-ray bursts detected from XTE J1701-407 on
July 17, 2008. The time T0 expressed in UTC corresponds to
|
| Open with DEXTER | |
Type-I X-ray bursts are produced by unstable burning of
accreted matter on the surface of the NS. The emission can
be described well by black-body radiation with temperatures,
![]() ,
in the energy range of a few keV. The energy-dependent
decay time of these bursts is attributed to the cooling of the NS
photosphere resulting in a gradual softening of the burst spectrum. For a review,
see, e.g. Lewin et al. (1993); Strohmayer & Bildsten (2006). The time-resolved spectral analysis
of the burst was carried out by using BAT and XRT data in the
15-35 keV and 0.3-10 keV bands, respectively. Burst spectra
were described reliably by a simple photoelectrically-absorbed black-body,
BB, model. For all these spectral fits, the
,
in the energy range of a few keV. The energy-dependent
decay time of these bursts is attributed to the cooling of the NS
photosphere resulting in a gradual softening of the burst spectrum. For a review,
see, e.g. Lewin et al. (1993); Strohmayer & Bildsten (2006). The time-resolved spectral analysis
of the burst was carried out by using BAT and XRT data in the
15-35 keV and 0.3-10 keV bands, respectively. Burst spectra
were described reliably by a simple photoelectrically-absorbed black-body,
BB, model. For all these spectral fits, the ![]() value was frozen at
value was frozen at
![]() cm-2 derived from the pre-burst persistent
emission (see Table 1).
The inferred BB temperature,
cm-2 derived from the pre-burst persistent
emission (see Table 1).
The inferred BB temperature,
![]() ,
apparent BB radius at 6.2 kpc (see Sect. 3.1),
,
apparent BB radius at 6.2 kpc (see Sect. 3.1),
![]() ,
and
bolometric luminosity are shown in Fig. 5 and in Table 3.
The burst fluence is calculated from bolometric
fluxes,
,
and
bolometric luminosity are shown in Fig. 5 and in Table 3.
The burst fluence is calculated from bolometric
fluxes,
![]() ;
these correspond to the observed 2-10 keV Swift/XTR fluxes
extrapolated to the 0.1-100 keV energy range.
The peak flux,
;
these correspond to the observed 2-10 keV Swift/XTR fluxes
extrapolated to the 0.1-100 keV energy range.
The peak flux,
![]() ,
is derived from the BAT 15-35 keV
light curve spectra and extrapolated to the 0.1-100 keV energy range.
All the measured unabsorbed fluxes were extrapolated to the
0.1-100 keV band by generating dummy responses (XSPEC version
11.3.2ag). This is justifiable for the XRT data since the
black-body temperature is well inside the spectra bandpass. However,
during the main peak a black-body temperature reaches a maximun in the energy range
2-3 keV (see e.g., Falanga et al. 2008, and references therein), and
therefore extrapolating the black-body spectra outside
the BAT bandpass. For the best-fit black-body model to the BAT (15-35 keV) burst peak spectrum,
we found
,
is derived from the BAT 15-35 keV
light curve spectra and extrapolated to the 0.1-100 keV energy range.
All the measured unabsorbed fluxes were extrapolated to the
0.1-100 keV band by generating dummy responses (XSPEC version
11.3.2ag). This is justifiable for the XRT data since the
black-body temperature is well inside the spectra bandpass. However,
during the main peak a black-body temperature reaches a maximun in the energy range
2-3 keV (see e.g., Falanga et al. 2008, and references therein), and
therefore extrapolating the black-body spectra outside
the BAT bandpass. For the best-fit black-body model to the BAT (15-35 keV) burst peak spectrum,
we found
![]() (
(
![]() ,
7 d.o.f.). We
fixed an upper and lower boundary black-body temperature of 2 and 3 keV, respectively, the normalization remaining as a free parameter. Note
the lower boundary is also consistent to be higher as the first XRT
black-body temperature of
,
7 d.o.f.). We
fixed an upper and lower boundary black-body temperature of 2 and 3 keV, respectively, the normalization remaining as a free parameter. Note
the lower boundary is also consistent to be higher as the first XRT
black-body temperature of
![]() (see Table 3).
We found an unacceptable fit by using a black-body function of 2 keV burst peak temperature
(
(see Table 3).
We found an unacceptable fit by using a black-body function of 2 keV burst peak temperature
(
![]() ,
8 d.o.f.), whereas a slightly more reliable fit was
obtained by using a temperature of 3 keV (
,
8 d.o.f.), whereas a slightly more reliable fit was
obtained by using a temperature of 3 keV (
![]() ,
8 d.o.f.). In Fig. 4, we show the
BAT data with the different black-body models corresponding to the different fits. In this
case, the best-fit model parameters and the extrapolated peak flux are
acceptable values to an accuracy of within 20%, which is inside our BAT extrapolation error box. In Table 2, we report all the measured
burst parameters.
,
8 d.o.f.). In Fig. 4, we show the
BAT data with the different black-body models corresponding to the different fits. In this
case, the best-fit model parameters and the extrapolated peak flux are
acceptable values to an accuracy of within 20%, which is inside our BAT extrapolation error box. In Table 2, we report all the measured
burst parameters.
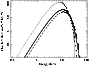 |
Figure 4:
Swift/BAT (15-35 keV) data of the intermediate long peak black-body spectra
and best-fit model,
|
| Open with DEXTER | |
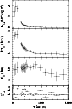 |
Figure 5:
Evolution of the spectral parameters, as inferred from Swift/BAT (first
86 s) and Swift/XRT (833 s) observations. The bolometric
luminosity is calculated by assuming a distance of 6.2 kpc, see
Sect. 3.1.
The bottom panel shows the
|
| Open with DEXTER | |
Table 2: Parameters of the Intermediate long-burst.
From the time-resolved spectral results, we converted the light-curve
count rates to flux and also found in this case that a double-exponential
function was required to fit
the intermediate long-burst decay. The derived e-folding times are
![]() s and
s and
![]() s, respectively with
s, respectively with
![]() (for 163 d.o.f.). In this fit, we also included
the first two BAT data points. We note, using only the XRT data
points, we found the same results within the error bars.
A single exponential function was found to be inadequate with
(for 163 d.o.f.). In this fit, we also included
the first two BAT data points. We note, using only the XRT data
points, we found the same results within the error bars.
A single exponential function was found to be inadequate with
![]() (166 d.o.f.). To compare the decay
tail with the
intermediate long X-ray burst from 2S 0918-549 and SLX 1737-282
(Falanga et al. 2008; in 't Zand et al. 2005), and with the decay cooling model
from Cumming & Macbeth (2004), we fitted the data with a power-law, and found an
index of
(166 d.o.f.). To compare the decay
tail with the
intermediate long X-ray burst from 2S 0918-549 and SLX 1737-282
(Falanga et al. 2008; in 't Zand et al. 2005), and with the decay cooling model
from Cumming & Macbeth (2004), we fitted the data with a power-law, and found an
index of
![]() with a
with a
![]() (167 d.o.f.). In
Fig. 6, we show the double-exponential best-fit model (upper
panel) and, in a log-log scale, the power-law best-fit function (lower panel)
to the data. The double-exponential model fit is statistically
preferred over an power-law fit by the F-test probability of
(167 d.o.f.). In
Fig. 6, we show the double-exponential best-fit model (upper
panel) and, in a log-log scale, the power-law best-fit function (lower panel)
to the data. The double-exponential model fit is statistically
preferred over an power-law fit by the F-test probability of
![]() .
Similar values of
.
Similar values of
![]() s and
s and
![]() s or power-law index
s or power-law index
![]() can be
obtained from the fit to the bolometric luminosity reported in
Fig. 5. In this case the double-exponential function fit is
also statistically preferred over a power-law function fit by the F-test probability of
can be
obtained from the fit to the bolometric luminosity reported in
Fig. 5. In this case the double-exponential function fit is
also statistically preferred over a power-law function fit by the F-test probability of
![]() .
.
The decay time determined with the light curve in unit of count rates
is restricted to the XRT 0.3-10 keV energy band. This decay time does
not take account of the different rise and cooling effects for different energy
bands during the outburst, where by converting the rates to bolometric flux or luminosity
using the time-resolved spectral results, a more realistic decay time
can be obtained. Therefore, in the following we consider only
![]() s and
s and
![]() s, or the power-law
index -2.14.
In Table 2, we report the
s, or the power-law
index -2.14.
In Table 2, we report the
![]() s, which is valid only
if one exponential function describes the decay tail. In our case, this value
is consistent within the error bars if we consider the double exponential decay to be
s, which is valid only
if one exponential function describes the decay tail. In our case, this value
is consistent within the error bars if we consider the double exponential decay to be
![]() ,
where
,
where
![]() and Fx is the peak
flux for
and Fx is the peak
flux for ![]() .
.
 |
Figure 6: Top panel: we show the BAT and XRT intermediate long-burst light curve with the double-exponential best-fit model curve. Bottom panel: the same data presented in a log-log scale with the power-law best-fit model. |
| Open with DEXTER | |
Table 3: Fit parameters of the time-averaged BAT and XRT burst spectra.
2.3 Short-burst light curves and spectra
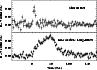 |
Figure 7: Top panel: the short type-I X-ray burst detected from XTE J1701-407 on July 27, 2008. For comparison of the rise time and duration we show also the intermediate long-burst (see also Fig. 3). The Swift/BAT (15-25 keV) light curves are shown with a time bin of 2 s. |
| Open with DEXTER | |
In Fig. 7, we show the Swift/BAT
15-25 keV short-burst light curve. The time T0 expressed in UTC
corresponds to
![]() .
The rise time is
.
The rise time is ![]() s, where the total duration is
s, where the total duration is
![]() 8 s. To determine the rise time and burst duration, we rebinned
the light curve into bins of 1 s. For this short burst, the XRT light curve starts with a
delay of 180 s after the beginning of the burst as seen by BAT. In the
XRT data (0.3-10 keV), the burst was not detected, so the total
duration of this burst must be considered <180 s.
In Fig. 7, we show the short burst, and
for comparison we also plot the intermediate long-burst observed by BAT.
8 s. To determine the rise time and burst duration, we rebinned
the light curve into bins of 1 s. For this short burst, the XRT light curve starts with a
delay of 180 s after the beginning of the burst as seen by BAT. In the
XRT data (0.3-10 keV), the burst was not detected, so the total
duration of this burst must be considered <180 s.
In Fig. 7, we show the short burst, and
for comparison we also plot the intermediate long-burst observed by BAT.
Given the short duration and statistic of the burst light curve, we
were unable to study a time-resolved spectral analysis.
Here, we report the burst spectrum analysis integrated over intervals of 6 s in
order to be able to measure as accurately as possible the peak flux.
Burst spectra were well fit by a simple black-body model.
The inferred BB temperature,
![]() keV with an
unabsorbed, bolometric peak fluxes,
keV with an
unabsorbed, bolometric peak fluxes,
![]() (0.1-100 keV). The burst occurred at a
flux persistent level of
(0.1-100 keV). The burst occurred at a
flux persistent level of
![]() erg cm-2 s-1. This short burst occurred at a persistent emission
level comparable to that of the intermediate long-burst.
erg cm-2 s-1. This short burst occurred at a persistent emission
level comparable to that of the intermediate long-burst.
3 Discussion
3.1 Source distance, persistent flux, and accretion rate
When a burst undergoes a photospheric-radius expansion (PRE), the source
distance can be determined based on the assumption that the bolometric
peak luminosity is saturated at the Eddington limit,
![]() ,
(e.g., Lewin et al. 1993; Kuulkers et al. 2003). During the PRE episode, while the
bolometric luminosity remains constant at the Eddington
value, the high energy flux may display a double-peak profile and/or a
delay in the rise time (e.g., Galloway et al. 2006a; Falanga et al. 2007; Kuulkers et al. 2002).
The BAT light curve shows a slow rise time of
,
(e.g., Lewin et al. 1993; Kuulkers et al. 2003). During the PRE episode, while the
bolometric luminosity remains constant at the Eddington
value, the high energy flux may display a double-peak profile and/or a
delay in the rise time (e.g., Galloway et al. 2006a; Falanga et al. 2007; Kuulkers et al. 2002).
The BAT light curve shows a slow rise time of ![]() 45 s, which is
typically observed at high energy in intermediate long helium bursts with PRE
(e.g., Molkov et al. 2005; Falanga et al. 2008; Kuulkers et al. 2002).
45 s, which is
typically observed at high energy in intermediate long helium bursts with PRE
(e.g., Molkov et al. 2005; Falanga et al. 2008; Kuulkers et al. 2002).
Since Swift/XRT missed the first 133 seconds of the burst from XTE J1701-407, we
are unable to determine directly whether this burst experienced a PRE. This issue cannot be
resolved with BAT time-resolved spectral analysis due to limited
statistics (see Fig. 5). However, by comparing with other PRE bursts
exhibiting this slow rise time at high energy, we infer that the observed profile
in the BAT light curve is evidence of a PRE during the first ![]() 50 s of the intermediate
long-burst, which should correspond to the timescale for the photosphere to fall back to the
neutron star surface. For the short burst, no conclusion can be drawn about whether a PRE
event has occurred (see Fig. 7).
50 s of the intermediate
long-burst, which should correspond to the timescale for the photosphere to fall back to the
neutron star surface. For the short burst, no conclusion can be drawn about whether a PRE
event has occurred (see Fig. 7).
Another possibility is that the burst has an intrinsically long rise time. For example, the mixed H/He bursts observed from GS 1826-24 (Galloway et al. 2004) do not exhibit PRE, but have a rise lasting 10 s, constrained by hydrogen burning (Heger et al. 2007). The duration of the bursts from GS 1826-24 is far shorter than the long-burst from XTE J1701-407. It is unclear whether a long-duration, mixed H/He burst could have a 50 s rise (see discussion of light curves in Sect. 3.5). The fact that helium burning can be extremely rapid, whereas hydrogen burning involves slow, weak interactions means that the rise time is longer when hydrogen is present, and PRE is far less likely. For example, Fujimoto et al. (1987) derived a critical, helium fraction that is necessary to achieve PRE.
Assuming a bolometric peak luminosity equal to
the Eddington value for a He type-I X-ray burst
(
![]() erg-1, as
empirically derived by Kuulkers et al. 2003),
we obtain the source distance of
erg-1, as
empirically derived by Kuulkers et al. 2003),
we obtain the source distance of
![]() kpc.
For comparison, the theoretical value of this distance
(e.g., Lewin et al. 1993) found by assuming a He atmosphere
and canonical NS parameters (1.4 solar mass and radius of 10 km), is
kpc.
For comparison, the theoretical value of this distance
(e.g., Lewin et al. 1993) found by assuming a He atmosphere
and canonical NS parameters (1.4 solar mass and radius of 10 km), is
![]() kpc.
We note that the source could be closer if the peak luminosity of the burst was lower than the pure-helium, Eddington limit. For example, we cannot exclude the possibility of the burst not exhibiting PRE, in which case the peak luminosity could have been sub-Eddington. Alternatively, assuming the peak luminosity to be the Eddington luminosity for solar composition
(X0=0.7) infers a distance of
kpc.
We note that the source could be closer if the peak luminosity of the burst was lower than the pure-helium, Eddington limit. For example, we cannot exclude the possibility of the burst not exhibiting PRE, in which case the peak luminosity could have been sub-Eddington. Alternatively, assuming the peak luminosity to be the Eddington luminosity for solar composition
(X0=0.7) infers a distance of ![]() 4 kpc. In the following, we consider
4 kpc. In the following, we consider
![]() kpc to be a fiducial distance, and comment on how our conclusions would change if the source was closer.
kpc to be a fiducial distance, and comment on how our conclusions would change if the source was closer.
The best-fit model solution of the 2-20 keV persistent emission spectrum of
XTE J1701-407 is an absorbed, simple, power-law model with
![]() .
Assuming a distance of 6.2 kpc, the estimated intermediate long-burst,
pre-burst persistent unabsorbed flux between 0.1-100 keV,
.
Assuming a distance of 6.2 kpc, the estimated intermediate long-burst,
pre-burst persistent unabsorbed flux between 0.1-100 keV,
![]() erg cm-2 s-1, translates
into a bolometric luminosity of
erg cm-2 s-1, translates
into a bolometric luminosity of
![]() erg s-1, or
erg s-1, or ![]()
![]() .
.
The local accretion rate per unit area is then given by
![]() ,
or
,
or
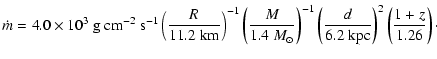 |
(1) |
A convenient unit of accretion rate is the Eddington accretion rate. Here, we define the local Eddington accretion rate to be
3.2 The energy, ignition depth, and recurrence time of the long-burst
The observed energy of the long-burst allows us to estimate the
ignition depth. The measured fluence
of the burst is
![]() ,
corresponding to a
net burst energy release of
,
corresponding to a
net burst energy release of
![]() .
The ignition depth is given by
.
The ignition depth is given by
![]() ,
or
,
or
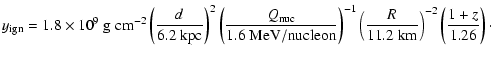 |
(2) |
The value of
At an accretion rate of
![]() ,
the
recurrence time corresponding to a column depth of
,
the
recurrence time corresponding to a column depth of
![]() (pure helium composition) is
(pure helium composition) is
![]() ,
or for
,
or for
![]() (solar composition) is
(solar composition) is
![]() days. These derived recurrence times are independent of the assumed distance. The intermediate
long-burst, which was the first
observed burst, occurred 40 days after the detection of XTE J1701-407.
The effective exposure time on source from the
beginning of the outburst to the intermediate long-burst was 0.34 days,
and there were 0.14 days between both bursts. The elapsed time on
source was thus too short compared to the theoretically-derived
recurrence time to allow us to derive an observational measurement of the
recurrence time.
days. These derived recurrence times are independent of the assumed distance. The intermediate
long-burst, which was the first
observed burst, occurred 40 days after the detection of XTE J1701-407.
The effective exposure time on source from the
beginning of the outburst to the intermediate long-burst was 0.34 days,
and there were 0.14 days between both bursts. The elapsed time on
source was thus too short compared to the theoretically-derived
recurrence time to allow us to derive an observational measurement of the
recurrence time.
3.3 Theoretical comparison with ignition models
Table 4: Type-I X-ray burst-ignition conditionsa.
In attempting to understand the nuclear-burning processes responsible for the long-burst, we compare the observed properties with type-I X-ray burst-ignition
models. The ignition conditions were calculated as described by Cumming & Bildsten (2000), apart from assuming that
![]() ,
,
![]() ,
and the energy release in hot CNO burning
,
and the energy release in hot CNO burning![]()
![]() .
The results are
shown in Table 4 for several different choices of accreted hydrogen
fraction X0, accretion rate
.
The results are
shown in Table 4 for several different choices of accreted hydrogen
fraction X0, accretion rate ![]() ,
and flux from the crust
,
and flux from the crust
![]() .
The ignition conditions are calculated by modeling the
temperature profile of the accumulated fuel layer, and adjusting the
thickness of the layer until conditions for thermal runaway are achieved
at the base. These models do not include the effects of previous
bursts on the ignition conditions (e.g. Woosley et al. 2004), and we do
not include gravitational sedimentation, which is important at low
accretion rates (Peng et al. 2007). In the following, we consider three
possibilities: 1) accretion of pure
helium; 2) hydrogen-rich matter at solar; and 3) low metallicity.
.
The ignition conditions are calculated by modeling the
temperature profile of the accumulated fuel layer, and adjusting the
thickness of the layer until conditions for thermal runaway are achieved
at the base. These models do not include the effects of previous
bursts on the ignition conditions (e.g. Woosley et al. 2004), and we do
not include gravitational sedimentation, which is important at low
accretion rates (Peng et al. 2007). In the following, we consider three
possibilities: 1) accretion of pure
helium; 2) hydrogen-rich matter at solar; and 3) low metallicity.
3.3.1 Pure helium accretion
For pure helium accretion, the accumulating
fuel layer is heated from below by a flux
![]() originating in the
crust, where
originating in the
crust, where ![]() is the energy per accreted nucleon flowing outwards from the crust.
We assume the accretion rate to be the observed value
is the energy per accreted nucleon flowing outwards from the crust.
We assume the accretion rate to be the observed value
![]() %, and adjust the value of
%, and adjust the value of ![]() until we achieve
ignition at the inferred column for pure helium burning
until we achieve
ignition at the inferred column for pure helium burning
![]() (and therefore obtain the observed burst energy). A flux from below
(and therefore obtain the observed burst energy). A flux from below
![]() MeV/nucleon reproduces the observed burst energy at 2.2%
Eddington. We also include models with
MeV/nucleon reproduces the observed burst energy at 2.2%
Eddington. We also include models with
![]() and 0.7 MeV/nucleon in
Table 4 to illustrate the sensitivity of the ignition depth to the
amount of heat from below. We note that since the combination
and 0.7 MeV/nucleon in
Table 4 to illustrate the sensitivity of the ignition depth to the
amount of heat from below. We note that since the combination
![]() defines the total flux heating the layer, an increase or decrease in
defines the total flux heating the layer, an increase or decrease in
![]() while keeping
while keeping ![]() fixed is equivalent to increasing or decreasing
fixed is equivalent to increasing or decreasing
![]() with
with ![]() fixed. Therefore, if the inferred accretion rate is
lower by some factor, the value of
fixed. Therefore, if the inferred accretion rate is
lower by some factor, the value of ![]() needed to match the
observed energy will be higher by the same factor. Similarly, a source distance of less than
needed to match the
observed energy will be higher by the same factor. Similarly, a source distance of less than
![]() can be described accurately by increasing
can be described accurately by increasing ![]() .
.
The outward flux expected from the crust depends on the accretion rate
and the core neutrino emissivity (Brown 2000), which ranges from
![]() MeV per nucleon at high accretion rates to
MeV per nucleon at high accretion rates to
![]() MeV
per nucleon at low accretion rates. The value depends on how much of
the total
MeV
per nucleon at low accretion rates. The value depends on how much of
the total ![]() 1.5 MeV per nucleon heat released in the crust by
pycnonuclear and electron capture reactions (Haensel & Zdunik 2008,1990),
is conducted into the core and released as neutrinos, compared to
being conducted outwards. Our calculated value of 0.5 MeV/nucleon
is reasonable for an accretion rate of 2.2% Eddington; for
example, the models calculated by Cumming et al. (2006) for
persistently accreting sources have
1.5 MeV per nucleon heat released in the crust by
pycnonuclear and electron capture reactions (Haensel & Zdunik 2008,1990),
is conducted into the core and released as neutrinos, compared to
being conducted outwards. Our calculated value of 0.5 MeV/nucleon
is reasonable for an accretion rate of 2.2% Eddington; for
example, the models calculated by Cumming et al. (2006) for
persistently accreting sources have
![]() to 0.9 MeV/nucleon at this
accretion rate. Galloway & Cumming (2006b) modelled the X-ray bursts
observed from SAX J1808.4-3658 and found
to 0.9 MeV/nucleon at this
accretion rate. Galloway & Cumming (2006b) modelled the X-ray bursts
observed from SAX J1808.4-3658 and found
![]() MeV/nucleon for
MeV/nucleon for
![]() %
%
![]() .
.
3.3.2 Accretion of hydrogen rich matter with solar metallicity
We next, consider that the source accretes hydrogen-rich
matter with the solar hydrogen fraction X0=0.7 and a
metallicity similar to solar, with mass fraction of CNO elements
![]() .
In that case, the hydrogen burns at a fixed rate
during accumulation of the fuel layer, by the beta-limited hot CNO
cycle of Hoyle & Fowler (1965). The hydrogen depletes at a column depth of
.
In that case, the hydrogen burns at a fixed rate
during accumulation of the fuel layer, by the beta-limited hot CNO
cycle of Hoyle & Fowler (1965). The hydrogen depletes at a column depth of
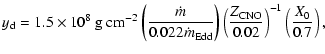 |
(3) |
which is lower than the inferred, ignition depth, so that a thick layer of pure helium accumulates and ignites beneath a steady hydrogen-burning shell. Therefore, even though solar composition material is accreted, the mean hydrogen fraction at ignition in the fuel layer is low, implying that
For a CNO mass fraction of
![]() ,
the observed burst energy
is obtained for an accretion rate three times lower than inferred from
the observed X-ray luminosity
,
the observed burst energy
is obtained for an accretion rate three times lower than inferred from
the observed X-ray luminosity
![]() % (model 5
in Table 4). At an accretion rate of 2.2% Eddington,
the burst energy is a factor of seven too small (model 4). Reducing the distance to the source does not help because it would change both the inferred
% (model 5
in Table 4). At an accretion rate of 2.2% Eddington,
the burst energy is a factor of seven too small (model 4). Reducing the distance to the source does not help because it would change both the inferred ![]() and burst energy by the same factor.
and burst energy by the same factor.
3.3.3 Accretion of hydrogen-rich matter of low metallicity
In the third scenario, we consider that the material is hydrogen-rich, but with a low
metallicity. Model 6 has a burst energy close to the observed energy
at the inferred accretion rate of 2.2% Eddington, with a CNO mass
fraction Z=10-3, approximately 10% of the solar metallicity. In this
case, the amount of hot CNO burning is reduced substantially, so that
hydrogen permeates the entire fuel layer at ignition. Hot CNO burning
still operates at a low level and causes some preheating of the fuel
layer. The hydrogen increases the amount of nuclear release during the
burst, giving
![]() MeV/nucleon, and an ignition depth three
times smaller than for the pure helium case. The low metallicity ignition
is less sensitive to
MeV/nucleon, and an ignition depth three
times smaller than for the pure helium case. The low metallicity ignition
is less sensitive to ![]() than the pure helium ignition. Model 7,
which has the same conditions as model 6, but with
than the pure helium ignition. Model 7,
which has the same conditions as model 6, but with
![]() rather
than
rather
than
![]() ,
has a burst energy within almost 20% of the observed
value. As for to the pure-helium ignitions, a closer distance can be accommodated by varying
,
has a burst energy within almost 20% of the observed
value. As for to the pure-helium ignitions, a closer distance can be accommodated by varying ![]() .
.
One caveat regarding the low-metallicity ignition-models is that there
can be substantial heating of the accumulating fuel layer because of
nuclear reactions associated with the ashes of previous
bursts. Woosley et al. (2004) found that the burst behaviour at
accretion rates of ![]() 0.1 Eddington was insensitive to the
metallicity of the accreted material due to this effect. However, they
found that at lower accretion rates there was good agreement with the
ignition models presented here (see Woosley et al. 2004, Table 9).
0.1 Eddington was insensitive to the
metallicity of the accreted material due to this effect. However, they
found that at lower accretion rates there was good agreement with the
ignition models presented here (see Woosley et al. 2004, Table 9).
3.3.4 Summary of ignition models
We present three ignition models in Table 4 that reproduce the observations. Models 1 and 6 have the correct burst energy and accretion rate. They correspond to accretion of pure helium (model 1), for which the layer is heated by the outward flux from the neutron star crust, and for accretion of hydrogen-rich material with low metallicity (model 6), for which a low level of hydrogen burning preheats the layer during accumulation, but the hydrogen fraction at ignition is significant and makes a substantial contribution to the burst energetics. Third, model 5 has the correct burst energy, but an accretion rate three times lower than observed. Given the uncertainties in translating the observed X-ray luminosity to accretion rate, it seems worthwhile considering this model further. In this model, the accreted composition is hydrogen-rich with a solar metallicity. This leads to depletion of the hydrogen by the hot CNO cycle and the build-up of a thick layer of pure helium beneath the hydrogen shell.
There is a fourth possibility, which is that the source is accreting hydrogen-rich material, but that the hydrogen burns unstably in a series of short flashes. The helium produced in the short flashes accumulates and creates a pure helium layer that ignites to generate the long burst. This is similar to model 5, but with unstable rather than stable hydrogen burning.
One way of distinguishing between the various possible explanations of the burst
energetics would be a recurrence-time measurement, since, as shown in
Table 4, the different scenarios predict different recurrence times. This is equivalent to a measurement of the ![]() parameter
parameter![]() for the bursts, which would indicate the fuel type
(e.g.
for the bursts, which would indicate the fuel type
(e.g.
![]() for solar hydrogen abundance as found for
example in GS 1826-24, Galloway et al. 2004).
for solar hydrogen abundance as found for
example in GS 1826-24, Galloway et al. 2004).
While this paper was in preparation, a similar analysis of the
intermediate burst from XTE J1701-407 was carried out and reported by Linares et al. (2008b).
The bolometric peak flux for the long-burst
and therefore the limits on the source distance are consistent
with the values that we obtain here. However, the persistent luminosity and
burst energy measured by Linares et al. (2008b) are a factor of two lower
than our values.
These values are used to interpret the long-burst, resulting in an
accretion rate of
![]() %
%
![]() ,
and a burst energy of
,
and a burst energy of
![]() ,
both a factor of two
lower than the values we find in this paper. Repeating the ignition
calculations presented earlier for this lower accretion rate, we find
that accretion of solar
composition material (X0=0.7) produces a burst
energy of
,
both a factor of two
lower than the values we find in this paper. Repeating the ignition
calculations presented earlier for this lower accretion rate, we find
that accretion of solar
composition material (X0=0.7) produces a burst
energy of
![]() for
for
![]() MeV/nucleon, and
MeV/nucleon, and
![]() for
for
![]() MeV/nucleon.
Therefore, accretion of solar composition
naturally explains the burst energetics for these values of
MeV/nucleon.
Therefore, accretion of solar composition
naturally explains the burst energetics for these values of ![]() and
and ![]() .
For pure helium accretion at this rate, we find that
.
For pure helium accretion at this rate, we find that
![]() MeV/nucleon is required to achieve a burst energy of
MeV/nucleon is required to achieve a burst energy of
![]() (lower values of
(lower values of ![]() result in a deeper
ignition and more energetic burst). Although this is a higher value
than expected for this accretion rate, it
is within the range of the total energy released in the crust
(Haensel & Zdunik 2008). In addition, since the flux heating the layer is
proportional to
result in a deeper
ignition and more energetic burst). Although this is a higher value
than expected for this accretion rate, it
is within the range of the total energy released in the crust
(Haensel & Zdunik 2008). In addition, since the flux heating the layer is
proportional to
![]() ,
the requirements on
,
the requirements on ![]() can be relaxed if the
true accretion rate is higher than assumed here. Therefore, we find
that the energetics argument provided by Linares et al. (2008b) against
explaining this burst as pure helium is overstated.
can be relaxed if the
true accretion rate is higher than assumed here. Therefore, we find
that the energetics argument provided by Linares et al. (2008b) against
explaining this burst as pure helium is overstated.
3.4 Constraints from the light curve
The shape and duration of the light curve offer another way to determine the composition of the fuel that burns during
the burst. While no models are available with exactly the same burst energy, the
low-accretion rate models from Woosley et al. (2004) are within a
factor of two to four in energy and accretion rate, and so we compare these models with the
observed light curve. These models assume that
![]() ,
corresponding to a local accretion
rate
,
corresponding to a local accretion
rate ![]() %
%
![]() .
.
First, we compare the observed light curve with burst 2 from model zm
of Woosley et al. (2004) (solid curve in Fig. 8). This model
describes the accretion of hydrogen-rich (
![]() )
material of low
metallicity,
Z=10-3, and so is similar to model 6 in Table 4.
The burst has a
total energy release of
)
material of low
metallicity,
Z=10-3, and so is similar to model 6 in Table 4.
The burst has a
total energy release of
![]() ,
just less
than a factor of two lower than the observed burst. The recurrence
time is 3.0 days, and ignition column
,
just less
than a factor of two lower than the observed burst. The recurrence
time is 3.0 days, and ignition column
![]() .
The ignition column is just less than a factor of two
smaller than the observed burst. The peak luminosity of this
burst is close to the Eddington luminosity for solar composition,
suggesting that its distance may be closer than the
.
The ignition column is just less than a factor of two
smaller than the observed burst. The peak luminosity of this
burst is close to the Eddington luminosity for solar composition,
suggesting that its distance may be closer than the
![]() assumed here. A closer distance would ensure that these light curves in closer agreement.
The model light curve has a steep decline at late
times, which is steeper than the observed decline. An extra factor of
two in ignition column would provide the correct burst energy and
lengthen the model-burst light curve, bringing it into closer agreement
with that of the observed burst. Another point to note is that this burst has
a slow rise time, lasting for several seconds, as expected for a low
helium mass fraction (Fujimoto et al. 1987).
assumed here. A closer distance would ensure that these light curves in closer agreement.
The model light curve has a steep decline at late
times, which is steeper than the observed decline. An extra factor of
two in ignition column would provide the correct burst energy and
lengthen the model-burst light curve, bringing it into closer agreement
with that of the observed burst. Another point to note is that this burst has
a slow rise time, lasting for several seconds, as expected for a low
helium mass fraction (Fujimoto et al. 1987).
 |
Figure 8:
Model light curves compared with the observed light curve. The solid
curve shows burst 2 from model zm of Woosley et al. (2004). This burst has an
ignition column
and energy a factor of 2 smaller than the observed burst. The dashed
curve shows burst 3 from model Zm of Woosley et al. (2004). This burst has an
ignition column
a factor of three to four times smaller than the observed burst. The
observed bolometric flux has been converted to luminosity using a
distance of 6.2 kpc. Redshift corrections have been applied to the
theoretical light curves, with 1+z=1.26. The dotted curves show two
cooling models calculated following Cumming & Macbeth (2004), for
(left to right)
|
| Open with DEXTER | |
The dashed curve in Fig. 8 shows burst 3 from
model Zm of Woosley et al. (2004). This model has hydrogen-rich matter with solar metallicity,
Z=0.02, and so is similar to model 5 of Table 4.
The hydrogen burns
away in a thin shell, leaving a pure helium layer that ignites. This
burst has a total energy release of
![]() ,
a
factor of 4 smaller than observed. The recurrence time is 4.5 days,
and ignition column depth
,
a
factor of 4 smaller than observed. The recurrence time is 4.5 days,
and ignition column depth
![]() .
The
burst brightens to close to the pure helium Eddington luminosity. The
duration of the burst is shorter than the observed burst by a factor
of
.
The
burst brightens to close to the pure helium Eddington luminosity. The
duration of the burst is shorter than the observed burst by a factor
of ![]() 5-10. The slope of the decay is shallower than the
observed slope. The rise time of this burst is short, a fraction
of a second, in contrast to the much slower rise of the hydrogen-rich
burst (model zm; solid line in Fig. 8).
5-10. The slope of the decay is shallower than the
observed slope. The rise time of this burst is short, a fraction
of a second, in contrast to the much slower rise of the hydrogen-rich
burst (model zm; solid line in Fig. 8).
We also include some cooling models calculated
following Cumming & Macbeth (2004). For a given ignition column, an
energy release per gram of 1.6 MeV per nucleon is deposited in the
layer, as would be appropriate if the helium burned to iron-group
elements at each depth at the start of the burst. We also
computed models for a lighter ash and correspondingly smaller energy
deposition (Woosley et al. (2004) find that the burning does not go all the
way to iron group in their model zM), but the differences are small,
and this does not change our conclusions. The cooling of the layer is
then followed, the flux from the surface being limited to the Eddington
luminosity for pure helium![]() . We show two
examples in Fig. 8. The first has
. We show two
examples in Fig. 8. The first has
![]() to match the Woosley et al. (2004) model
Zm burst. The second has
to match the Woosley et al. (2004) model
Zm burst. The second has
![]() as needed to reproduce the observed burst energy
(models 1 and 5 in Table 4). The shape of the cooling
models agrees well with the model Zm light curve, and agrees to within a
factor of two on the cooling timescale. Even allowing for this factor
of two in the
as needed to reproduce the observed burst energy
(models 1 and 5 in Table 4). The shape of the cooling
models agrees well with the model Zm light curve, and agrees to within a
factor of two on the cooling timescale. Even allowing for this factor
of two in the
![]() model, the
cooling occurs more rapidly than for the observed light curve.
model, the
cooling occurs more rapidly than for the observed light curve.
In summary, although the models from Woosley et al. (2004) are not of exactly the same ignition conditions as implied by the observations of XTE J1701-407, our comparison suggests that pure helium ignition at the inferred ignition column depth (with or without a small overlying hydrogen-burning shell) have cooling times that are shorter than the observed light curve. On the other hand, a hydrogen-rich composition throughout the layer, as expected for low metallicity, produces a longer-lasting light curve that is more consistent with the observed cooling time. This conclusion does not depend on the assumed distance to the source. Both helium and hydrogen-rich burst models reach the Eddington luminosity (either the pure helium or solar composition Eddington luminosity respectively), and therefore could explain the PRE suggested by the similarity between the observed BAT light curve and other intermediate long-bursts (see Sect. 3.1). If the slow rise time is intrinsic to the burst and not due to PRE, the hydrogen-rich model is preferred since the presence of hydrogen leads to a far slower rise time than for pure helium (Fig. 8). The double exponential nature of the decay may also argue for hydrogen burning during the burst. The burst profiles from GS 1826-24 (Galloway et al. 2004) are described well by a double exponential decay. Further modeling is required to study the expected burst profiles of hydrogen-rich bursts produced as a result of low-metallicity accretion.
3.5 Origin of the short burst
We have focused on the long-duration burst, which has a well-measured fluence and therefore energy. For the short burst, we can only place an upper limit on its fluence. At low accretion rates, unstable ignition of hydrogen can produce to short-duration bursts (e.g., Chenevez et al. 2007; Strohmayer & Bildsten 2006). Linares et al. (2008b) suggested that this is the origin of the short burst from XTE J1701-407, and that either (i) hydrogen-ignited short bursts produce the helium fuel for the long-burst; or that (ii) the source accretes close to the boundary between unstable and stable hydrogen burning, and stable hydrogen-burning produces the helium for the long-burst. The comparison with ignition models and model light curves that we have made earlier suggests that hydrogen survives to the ignition depth, implying a low metallicity in the accreted layer. Unfortunately, this would presumably ensure that a thermal instability driven by CNO burning would be less likely.
For the low-metallicity model or for pure helium accretion, another
explanation is that the local accretion rate was higher at the time of
the short burst. The ignition depth is sensitive to the base flux
or equivalently to the product
![]() (see for example Fig. 8 of
in 't Zand et al. 2005). The persistent flux at the time of the short burst
from XTE J1701-407 was slightly higher than at the time of the long-burst, even
at 30%, insufficient to produce a significant reduction in the ignition column
depth. We note that short bursts were observed from
the intermediate long X-ray burster 2S 0918-549, a suspected
ultracompact binary and therefore accreting hydrogen-deficient
matter. Therefore, it is unclear to us that the observation of the
short burst excludes pure helium accretion in XTE J1701-407, as argued by
Linares et al. (2008b).
(see for example Fig. 8 of
in 't Zand et al. 2005). The persistent flux at the time of the short burst
from XTE J1701-407 was slightly higher than at the time of the long-burst, even
at 30%, insufficient to produce a significant reduction in the ignition column
depth. We note that short bursts were observed from
the intermediate long X-ray burster 2S 0918-549, a suspected
ultracompact binary and therefore accreting hydrogen-deficient
matter. Therefore, it is unclear to us that the observation of the
short burst excludes pure helium accretion in XTE J1701-407, as argued by
Linares et al. (2008b).
4 Conclusions
We have compared the observed properties of the long duration burst
from XTE J1701-407 with models of type-I X-ray burst -ignition
conditions and light curves. We have shown that the observed burst energy
could be understood as (i) pure helium ignition, either as a result of
pure helium accretion or depletion of hydrogen by steady burning
during accumulation; or (ii) ignition of a thick layer of
hydrogen-rich material with low metallicity. Comparing
with model light-curves, we find that the pure helium ignitions cool
faster than observed. On the other hand, a hydrogen-rich layer corresponds to a
longer-duration light curve with a steep decline in the tail of the
burst, more closely matching the observed light curve. Therefore, we suggest that the
intermediate long-burst from XTE J1701-407 was powered by unstable burning of
a thick layer of hydrogen-rich matter with low metallicity.
Long X-ray bursts caused by pure helium ignitions beneath a hydrogen
shell have been identified, as for example by
Galloway & Cumming (2006b), who argued that this occurred in
SAX J1808.4-3658. However, to our knowledge, XTE J1701-407 would be the first
example of a source that exhibits long-bursts driven by a thick layer of
hydrogen-rich material. The bursts from GS 1826-24 are believed to be
powered by rp-process hydrogen burning, giving long ![]() 100 s tails, but the ignition depth in those bursts is an order of
magnitude smaller than inferred for the long-burst from XTE J1701-407,
so that hydrogen can survive until helium ignition, even for solar
metallicity. At the low accretion rate in XTE J1701-407, this is not
the case: low metallicity is required to reduce the rate of hot CNO
burning and allow hydrogen to survive until helium ignites.
This implies either that this source is a burster accreting
low-metallicity H-rich material at a low rate, or another possibility
is that heavy elements are able to sediment out from the accumulating
layer at this low accretion rate (Peng et al. 2007), reducing its
effective metallicity. If so, future studies of this source could be
used to test the physics of sedimentation at low accretion rates.
100 s tails, but the ignition depth in those bursts is an order of
magnitude smaller than inferred for the long-burst from XTE J1701-407,
so that hydrogen can survive until helium ignition, even for solar
metallicity. At the low accretion rate in XTE J1701-407, this is not
the case: low metallicity is required to reduce the rate of hot CNO
burning and allow hydrogen to survive until helium ignites.
This implies either that this source is a burster accreting
low-metallicity H-rich material at a low rate, or another possibility
is that heavy elements are able to sediment out from the accumulating
layer at this low accretion rate (Peng et al. 2007), reducing its
effective metallicity. If so, future studies of this source could be
used to test the physics of sedimentation at low accretion rates.
Acknowledgements
We thank Alexander Heger for providing the burst light curves from Woosley et al. (2004) shown in Fig. 7. M.F. acknowledges the French Space Agency (CNES) for financial support. J.C. acknowledges financial support from ESA-PRODEX, Nr. 90057, and E.B. acknowledges ASI and MIUR. A.C. acknowledges support from the National Sciences and Engineering Research Council of Canada (NSERC), Le Fonds Québécois de la Recherche sur la Nature et les Technologies (FQRNT), and the Canadian Institute for Advanced Research (CIFAR). A.C. is an Alfred P. Sloan Research Fellow.
References
- Barthelmy, S. D., et al. 2008, GCN Circ., 7985 [NASA ADS] (In the text)
- Brown, E. F. 2000, ApJ, 531, 988 [NASA ADS] [CrossRef] (In the text)
- Chelovekov, I. V., Grebenev, S. A., & Sunyaev, R. A. 2006, AstL, 32, 456 [NASA ADS]
- Chenevez, J., Falanga, M., Brandt, S., et al. 2006, A&A, 449, L5 [NASA ADS] [CrossRef] [EDP Sciences]
- Chenevez, J., Falanga, M., Kuulkers, E., et al. 2007, A&A, 469, L27 [NASA ADS] [CrossRef] [EDP Sciences]
- Cornelisse, R., in 't Zand, J. J. M., Verbunt, F., et al. 2003, A&A, 405, 1033 [NASA ADS] [CrossRef] [EDP Sciences]
- Cumming, A., & Bildsten, L. 2000, ApJ, 544, 453 [NASA ADS] [CrossRef] (In the text)
- Cumming, A., & Bildsten, L. 2001, ApJ, 559, L127 [NASA ADS] [CrossRef]
- Cumming, A., & Macbeth, J. 2004, ApJ, 603, L37 [NASA ADS] [CrossRef]
- Cumming, A., Macbeth, J., in 't Zand, J. J. M., Page, D. 2006, ApJ, 646, 429 [NASA ADS] [CrossRef] (In the text)
- Degenaar, N., & Wijnands, R. 2008, Astr. Tel., 1572 (In the text)
- Falanga, M., Poutanen, J., Bonning, E. W., et al. 2007, A&A, 464, 1069 [NASA ADS] [CrossRef] [EDP Sciences]
- Falanga, M., Chenevez, J., Cumming, A., et al. 2008, A&A, 484, 43 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fujimoto, M. Y., Sztajno, M., Lewin, W. H. G., & van Paradijs, J. 1987, ApJ, 319, 902 [NASA ADS] [CrossRef] (In the text)
- Galloway, D. K., Cumming, A., Kuulkers, E., et al. 2004, ApJ, 601, 466 [NASA ADS] [CrossRef] (In the text)
- Galloway, D. K., Muno, M. P., Hartman, J. M., et al. 2006a, ApJS, submitted, [arXiv:astro-ph/0608259]
- Galloway, D. K., & Cumming, A. 2006b, ApJ, 652, 559 [NASA ADS] [CrossRef] (In the text)
- Hansen, C. J., & Van Horn, H. M. 1975, ApJ, 195, 735 [NASA ADS] [CrossRef] (In the text)
- Haensel, P., & Zdunik, J. L. 1990, A&A, 227, 431 [NASA ADS]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences]
- Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] (In the text)
- Heger, A., Cumming, A., Galloway, D. K., & Woosley, S. E. 2007, ApJ, 671, L141 [NASA ADS] [CrossRef] (In the text)
- Hoyle, R., & Fowler, W. A. 1965, in Quasi-Stellar Sources and Gravitational Collapse, ed. I. Robinson, A. Schild, & E. L. Shucking (Chicago: Univ. Chicago Press), 17 (In the text)
- in't Zand, J. J. M., Cornelisse, R., & Cumming, A. 2004, A&A, 426, 257 [NASA ADS] [CrossRef] [EDP Sciences]
- in 't Zand, J. J. M., Cumming, A., van der Sluys, M. V., et al. 2005, A&A, 441, 675 [NASA ADS] [CrossRef] [EDP Sciences]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS] (In the text)
- Kaplan, D., & Chakrabarty, D. 2008, Astr. Tel., 1630 (In the text)
- Kuulkers, E. 2004, Nucl. Phys. B, 132, 466 [CrossRef]
- Kuulkers, E., Homan, J., van der Klis, M., et al. 2002, A&A, 382, 947 [NASA ADS] [CrossRef] [EDP Sciences]
- Kuulkers, E., den Hartog, P. R., in't Zand, J. J. M., et al. 2003, A&A, 399, 663 [NASA ADS] [CrossRef] [EDP Sciences]
- Lewin, W. H. G. L., van Paradijs, J., & Taam, R. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef]
- Linares, M., et al. 2008a, Astr. Tel., 1618 (In the text)
- Linares, M., et al. 2008b, MNRAS, in press [arXiv:0808.3950]
- Markwardt, C. B., Pereira, D., & Swank, J. H. 2008a, Astr. Tel., 1569 (In the text)
- Markwardt, C. B., Cummings, J., & Krimm, H. 2008b, Astr. Tel., 1616 (In the text)
- Molkov, S., Revnivtsev, M., Lutovinov, A., & Sunyaev, R. A. 2005, A&A, 434, 1069 [NASA ADS] [CrossRef] [EDP Sciences]
- Peng, F., Brown, E. F., & Truran, J. W. 2007, ApJ, 654, 1022 [NASA ADS] [CrossRef] (In the text)
- Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] (In the text)
- Sakamoto, T., et al. 2008, GCN circ., 8034 [NASA ADS] (In the text)
- Starling, R., & Evans, P. 2008, Astr. Tel., 1621 (In the text)
- Strohmayer, T. E., & Bildsten, L. 2006, in Compact stellar X-ray sources, ed. W. H. G. Lewin, & M. van der Klis (Cambridge: Cambridge University Press)
- Strohmayer, T. E., Markwardt, C. B., & Swank, J. H. 2008, Astr. Tel., 1635 (In the text)
- Swank, J., & Markwardt, C. 2001, in New Century of X-ray Astronomy, ed. H. Inoue, & H. Kunieda (San Francisco: ASP), ASP Conf. Ser., 251, 94 (In the text)
- Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 1389 [NASA ADS] [CrossRef]
- Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... 20 pixels
![[*]](/icons/foot_motif.gif)
- See also the XRT analysis manual at http://swift.gsfc.nasa.gov/docs/swift/analysis/xrt_swguide_v1_2.pdf
- ...
observations
![[*]](/icons/foot_motif.gif)
- http://lheawww.gsfc.nasa.gov/users/craigm/galscan/main.html
- ... time
![[*]](/icons/foot_motif.gif)
- The rise time is defined as the time spent between the start of the burst and the point at which the 90% of the peak burst intensity is reached.
- ... burning
![[*]](/icons/foot_motif.gif)
- Here we adopt the
value of
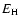 from Wallace & Woosley (1981), which includes
neutrino losses. These were not included by Cumming & Bildsten (2000).
from Wallace & Woosley (1981), which includes
neutrino losses. These were not included by Cumming & Bildsten (2000).
- ...
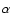 parameter
parameter![[*]](/icons/foot_motif.gif)
- The
quantity
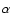 is defined as the
ratio of the total energy emitted in the persistent flux to that
emitted in a burst,
is defined as the
ratio of the total energy emitted in the persistent flux to that
emitted in a burst,
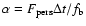 ,
where
,
where 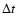 is the
time interval between two bursts.
is the
time interval between two bursts.
- ... helium
![[*]](/icons/foot_motif.gif)
- As noted by Woosley et al. (2004), the shape of the light curve as the luminosity begins to decline below the Eddington luminosity is probably not accurately reproduced by these models, which do not follow the outer layers in detail. We will improve our treatment of this in future work. However, we expect that the late time cooling is not sensitive to this.
All Tables
Table 1: Log of RXTE and Swift observations and best-fit spectral parameters of the persistent emission. An absorbed power-law model is used to fit these spectra.
Table 2: Parameters of the Intermediate long-burst.
Table 3: Fit parameters of the time-averaged BAT and XRT burst spectra.
Table 4: Type-I X-ray burst-ignition conditionsa.
All Figures
 |
Figure 1: Flux history of the X-ray transient XTE J1701-407. Open squares represent fluxes derived from RXTE bulge observations in the period from March 31, to September 2, 2008. Fluxes derived from RXTE/PCA and Swift/XRT target of opportunity and follow-up observations are marked with filled squares and stars, respectively. The arrow indicates the time of the type-I X-ray burst. |
| Open with DEXTER | |
| In the text | |
 |
Figure 2: HID of XTE J1701-407. The hardness is the ratio of the count rates in the 5.7-18.9 keV to 2.1-5.7 keV and the intensity is in the 2.1-18.9 keV count rate. Each point corresponds to 516 s of integration time. |
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
The intermediate, long, type-I X-ray bursts detected from XTE J1701-407 on
July 17, 2008. The time T0 expressed in UTC corresponds to
|
| Open with DEXTER | |
| In the text | |
 |
Figure 4:
Swift/BAT (15-35 keV) data of the intermediate long peak black-body spectra
and best-fit model,
|
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
Evolution of the spectral parameters, as inferred from Swift/BAT (first
86 s) and Swift/XRT (833 s) observations. The bolometric
luminosity is calculated by assuming a distance of 6.2 kpc, see
Sect. 3.1.
The bottom panel shows the
|
| Open with DEXTER | |
| In the text | |
 |
Figure 6: Top panel: we show the BAT and XRT intermediate long-burst light curve with the double-exponential best-fit model curve. Bottom panel: the same data presented in a log-log scale with the power-law best-fit model. |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Top panel: the short type-I X-ray burst detected from XTE J1701-407 on July 27, 2008. For comparison of the rise time and duration we show also the intermediate long-burst (see also Fig. 3). The Swift/BAT (15-25 keV) light curves are shown with a time bin of 2 s. |
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Model light curves compared with the observed light curve. The solid
curve shows burst 2 from model zm of Woosley et al. (2004). This burst has an
ignition column
and energy a factor of 2 smaller than the observed burst. The dashed
curve shows burst 3 from model Zm of Woosley et al. (2004). This burst has an
ignition column
a factor of three to four times smaller than the observed burst. The
observed bolometric flux has been converted to luminosity using a
distance of 6.2 kpc. Redshift corrections have been applied to the
theoretical light curves, with 1+z=1.26. The dotted curves show two
cooling models calculated following Cumming & Macbeth (2004), for
(left to right)
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


