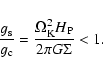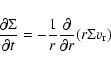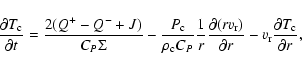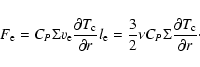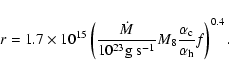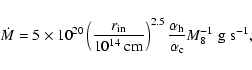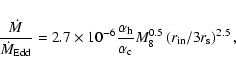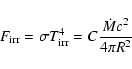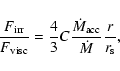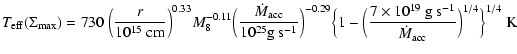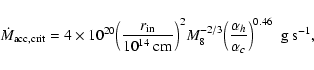| Issue |
A&A
Volume 496, Number 2, March III 2009
|
|
|---|---|---|
| Page(s) | 413 - 421 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810928 | |
| Published online | 30 January 2009 | |
The thermal-viscous disk instability model in the AGN context
J.-M. Hameury1 - M. Viallet1 - J.-P. Lasota2,3
1 - Observatoire de Strasbourg, CNRS/Université Louis Pasteur, 11 rue
de l'Université, 67000 Strasbourg, France
2 -
Institut d'Astrophysique de Paris, UMR 7095 CNRS, UPMC Univ. Paris 6, 98bis Bd Arago,
75014 Paris, France
3 -
Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków,
Poland
Received 7 September 2008 / Accepted 16 December 2008
Abstract
Context. Accretion disks in AGN should be subject to the same type of instability as in cataclysmic variables (CVs) or in low-mass X-ray binaries (LMXBs), which leads to dwarf nova and soft X-ray transient outbursts. It has been suggested that this thermal/viscous instability can account for the long-term variability of AGNs.
Aims. We test this assertion by systematically studying how the disk instability model (DIM) is applied to AGNs.
Methods. We use the adaptative grid numerical code we developed in the context of CVs, enabling us to fully resolve the radial structure of the disk.
Results. We show that, because the Mach numbers are very large in AGN disks, the heating and cooling fronts are so narrow that they cannot be resolved by the numerical codes that have been used until now. In addition, these fronts propagate on much shorter time scales than the viscous time. As a result, a sequence of heating and cooling fronts propagate back and forth in the disk, leading only to small variations in the accretion rate onto the black hole, with short quiescent states only occurring for very low mass-transfer rates. Truncation of the inner part of the disk by e.g. an ADAF does not alter this result, but enables longer quiescent states. Finally we discuss the effects of irradiation by the central X-ray source and show that, even for extremely high irradiation efficiencies, outbursts are not a natural outcome of the model.
Key words: accretion, accretion disks - instabilities - stars: dwarf novae - galaxies: active
1 Introduction
Accretion disks are found in a wide variety of astronomical objects,
from young stars to active galactic nuclei (AGNs). Among these,
close binaries have deserved special attention, because they are
nearby, and they vary on short timescales that enable time-dependent
studies of their light curves. In particular, a number of these
systems show large outbursts, such as dwarf novae, which are a
subclass of cataclysmic variables in which a low-mass companion
transfers mass onto a white dwarf. These systems undergo outbursts
lasting at least a few days, during which their brightness increases
by several magnitudes (see e.g. Warner 1995, for a review). The
outbursts are believed to be due to a thermal-viscous accretion
disk instability (Meyer & Meyer-Hofmeister 1981) that arises when the disk effective
temperature becomes ![]() 104 K, enough for hydrogen to become
partially ionized and opacities to depend strongly on temperature
(see Lasota 2001, for a review of the model). Similarly, soft X-ray
transients, which are a subclass of low-mass X-ray binaries in which
the compact object is either a black hole or a neutron star also
show outbursts, but their amplitude is greater and the time scales
longer than for dwarf novae. The ionization instability of the
accretion disk is also thought to be cause of the outbursts: the
difference with dwarf novae stems from the difference in the mass of
the compact object (and thus in the depth of the gravitational
potential well) and from the effect of illumination of the disk,
which is much more important in the case of X-ray binaries
(see e.g. Dubus et al. 2001).
104 K, enough for hydrogen to become
partially ionized and opacities to depend strongly on temperature
(see Lasota 2001, for a review of the model). Similarly, soft X-ray
transients, which are a subclass of low-mass X-ray binaries in which
the compact object is either a black hole or a neutron star also
show outbursts, but their amplitude is greater and the time scales
longer than for dwarf novae. The ionization instability of the
accretion disk is also thought to be cause of the outbursts: the
difference with dwarf novae stems from the difference in the mass of
the compact object (and thus in the depth of the gravitational
potential well) and from the effect of illumination of the disk,
which is much more important in the case of X-ray binaries
(see e.g. Dubus et al. 2001).
It was realized long ago (Lin & Shields 1986) that the same instability
could be present in accretion disks around AGNs; it was found that,
at radii ![]() 1015 - 16 cm where the effective temperature is
indeed of a few thousand degrees, the disk should be unstable. For
the parameters of AGNs, the implied timescales are
104 - 107 yr,
making the direct observation of the instability impossible, but
predicting that in many systems the disk should not be in viscous
equilibrium and that many AGNs should be in a quiescent state
(see Siemiginowska et al. 1996; Siemiginowska & Elvis 1997). It was also immediately realized that, as in
dwarf-novae, the character of putative AGN outbursts strongly
depends on the assumptions one makes about the disk viscosity
(Mineshige & Shields 1990). However, while one is guided in the case of
dwarf-novae by the observed outburst properties when fixing
the viscosity prescription, it is not even clear in the case of AGN
that outbursts are present, as the variability of these objects
could be just due to mass-supply variations. This state of affairs
gave rise to various, more or less arbitrary, prescriptions for how
viscosity varies (or not) with the state of the accretion flow
(Janiuk et al. 2004; Mineshige & Shields 1990; Menou & Quataert 2001). In addition, results of numerical
calculations of AGN outbursts were marred by the insufficient
resolution of the grids used. As shown by Hameury et al. (1998), low grid
resolution often leads to unreliable results
1015 - 16 cm where the effective temperature is
indeed of a few thousand degrees, the disk should be unstable. For
the parameters of AGNs, the implied timescales are
104 - 107 yr,
making the direct observation of the instability impossible, but
predicting that in many systems the disk should not be in viscous
equilibrium and that many AGNs should be in a quiescent state
(see Siemiginowska et al. 1996; Siemiginowska & Elvis 1997). It was also immediately realized that, as in
dwarf-novae, the character of putative AGN outbursts strongly
depends on the assumptions one makes about the disk viscosity
(Mineshige & Shields 1990). However, while one is guided in the case of
dwarf-novae by the observed outburst properties when fixing
the viscosity prescription, it is not even clear in the case of AGN
that outbursts are present, as the variability of these objects
could be just due to mass-supply variations. This state of affairs
gave rise to various, more or less arbitrary, prescriptions for how
viscosity varies (or not) with the state of the accretion flow
(Janiuk et al. 2004; Mineshige & Shields 1990; Menou & Quataert 2001). In addition, results of numerical
calculations of AGN outbursts were marred by the insufficient
resolution of the grids used. As shown by Hameury et al. (1998), low grid
resolution often leads to unreliable results![]() .
.
The aim of the present article is to systematically study how the disk-instability model (DIM) can be applied to AGNs. Instabilities other than the thermal-viscous instability may exist in AGN disks (beyond the MRI instability thought to be the source of viscosity, Balbus & Hawley 1991) and in particular the gravitational instability that arises when self-gravity exceeds the combined action of pressure and Coriolis forces (Safronov 1960; Toomre 1964); conditions for the onset of this instability are met at large distances from the black hole (see e.g. Shlosman 1990). The outcome of this instability in the AGN case is most probably the fragmentation of the accretion disk (see e.g. Rafikov 2007; Gammie 2001; Goodman 2003) since the cooling time is likely to be short in the AGN case. Duschl & Britsch (2006) suggest that the gravitational instability might instead be a source of turbulence, which could be the case if the non linear development of the instability does not lead to fragmentation, not a likely outcome in the AGN case as mentioned above. Other local or global instabilities may arise, such as the Lightman-Eardley instability (Lightman & Eardley 1974), but it is far beyond the scope of this paper to discuss them all, and we consider parameters such as these instabilities do not occur.
2 Vertical disk structure
We recall here the vertical-structure equations adapted to AGN
parameters. We consider only the case where the viscosity ![]() is
proportional to the gas pressure (not the total pressure, in order
to avoid the Lightman & Eardley 1974, instability). The vertical
structure of an
is
proportional to the gas pressure (not the total pressure, in order
to avoid the Lightman & Eardley 1974, instability). The vertical
structure of an ![]() disk in which the viscosity
disk in which the viscosity ![]() is
assumed to be proportional to the gas pressure is given by the
standard disk equations (see e.g. Frank et al. 2002, and references
therein):
is
assumed to be proportional to the gas pressure is given by the
standard disk equations (see e.g. Frank et al. 2002, and references
therein):
where
 |
(5) |
When the radiative gradient is superadiabatic,
 |
(6) |
which ensures that
We have neglected the disk self gravity. This approximation is valid
as long as the ratio of self gravity to that of the central object
is low:
If this not the case, the disk is gravitationally unstable, which, as mentioned in the introduction, is likely to lead to fragmentation if the cooling time is short enough, or may significantly change the angular momentum transport by introducing non local terms (see e.g. Balbus & Papaloizou 1999; Lin & Pringle 1987). In both cases, the thermal-viscous instability can no longer apply (in the first case for obvious reasons, and in the second one because non local effects cannot be approximated by viscosity, which is local); in our calculations, we always make sure that the condition (7) is fulfilled.
The parameter
![]() is an effective viscosity, equal to
the standard viscosity coefficient
is an effective viscosity, equal to
the standard viscosity coefficient ![]() when the disk is in
thermal equilibrium, but it also accounts for the time-dependent
terms that are assumed to also be proportional to the pressure
(see Hameury et al. 1998, for a detailed discussion).
when the disk is in
thermal equilibrium, but it also accounts for the time-dependent
terms that are assumed to also be proportional to the pressure
(see Hameury et al. 1998, for a detailed discussion).
The equation of state of matter is interpolated from the tables of Fontaine et al. (1977); in the low temperature regime (below 2000 K), which is not covered by these tables, Saha equations are solved iteratively, as described by Paczynski (1969). The Rosseland mean opacities are taken from Cox & Tabor (1976) above 10 000 K, and from Alexander (1975) below (more modern opacities introduce changes that are not important in the present context, see Lasota et al. 2008).
The boundary conditions are
![]() and Fz = 0 at the
disk midplane, and
and Fz = 0 at the
disk midplane, and
![]() at the surface. The standard
photospheric condition
at the surface. The standard
photospheric condition
![]() has to be
slightly modified, as (1) radiation pressure can de dominant; and
(2) gz can vary in the photosphere. Integrating the vertical
hydrostatic equilibrium equation and using the Eddington
approximation leading to
has to be
slightly modified, as (1) radiation pressure can de dominant; and
(2) gz can vary in the photosphere. Integrating the vertical
hydrostatic equilibrium equation and using the Eddington
approximation leading to
![]() where
where ![]() is the optical depth, one obtains
is the optical depth, one obtains
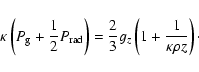 |
(8) |
The term
![\begin{figure}
\par\mbox{\resizebox{8cm}{!}{\includegraphics[angle=-90]{10928f1a.eps}}\resizebox{8cm}{!}{\includegraphics[angle=-90]{10928f1b.eps}} }\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg47.gif) |
Figure 1:
Examples of S curves in the |
| Open with DEXTER | |
The thermal equilibrium corresponds to Q+=Q-, where Q+
and Q- are the surface heating and cooling rates, respectively (see
Eq. (14) below). Figure 1 presents two
examples of thermal equilibrium curves in the ![]() -
-
![]() plane, showing the characteristic S shape. Also plotted are
the conditions
plane, showing the characteristic S shape. Also plotted are
the conditions
![]() and h/r=0.1. As can be
seen, self gravity becomes important at radii larger than
and h/r=0.1. As can be
seen, self gravity becomes important at radii larger than
![]() cm, in agreement with the findings of Cannizzo & Reiff (1992)
and Cannizzo (1992). The condition that self gravity be small can be
quite severe; for example, we note that in several of the
simulations by Janiuk et al. (2004) this condition is not fulfilled and the
corresponding results are therefore invalidated. The thin disk
approximation condition (
cm, in agreement with the findings of Cannizzo & Reiff (1992)
and Cannizzo (1992). The condition that self gravity be small can be
quite severe; for example, we note that in several of the
simulations by Janiuk et al. (2004) this condition is not fulfilled and the
corresponding results are therefore invalidated. The thin disk
approximation condition (![]() )
is usually less stringent; it
may, however, break for high accretion rates, in which case
radiation pressure gradient almost balances vertical gravity in a
significant fraction of the disk vertical extent.
)
is usually less stringent; it
may, however, break for high accretion rates, in which case
radiation pressure gradient almost balances vertical gravity in a
significant fraction of the disk vertical extent.
The values
![]() and
and
![]() that are the
minimimun (resp. maximum) values of
that are the
minimimun (resp. maximum) values of ![]() on the upper (resp.
lower) branches of the S curve can be fitted by
on the upper (resp.
lower) branches of the S curve can be fitted by
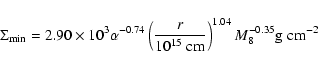 |
(9) |
and by
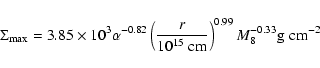 |
(10) |
where
It should also be noted that, because we are restricted to a region
where self gravitation is small, the disk extension, as measured by
the ratio
![]() is not very large. For the case
of a 108
is not very large. For the case
of a 108 ![]() black hole, this is about 100, i.e. comparable
to disks in CVs, but much smaller than for LMXBs. It is also worth
noting that the disk thickness H,
black hole, this is about 100, i.e. comparable
to disks in CVs, but much smaller than for LMXBs. It is also worth
noting that the disk thickness H,
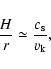 |
(11) |
where
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{10928f2.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg61.gif) |
Figure 2:
Vertical structure of the accretion disks, for
|
| Open with DEXTER | |
2.1 Critical points and the viscosity prescription
It should be noted that, for some choices of parameters, the
equilibrium curves show two ``wiggles'' (see e.g. the case
![]() at r=1015 cm, Fig. 1) on the lower branch.
This also happens in accretion disks around stellar mass black
holes, but, in contrast to Janiuk et al. (2004), we do not find that this
is always the case for AGNs. This discrepancy can be due to a
difference in the treatment of convection or to different opacities.
The small wiggle at low temperature is not related to a strong
change in the opacities, but instead to a strong change in the
adiabatic gradient when molecular hydrogen becomes partially
dissociated, as is shown by Fig. 2. Two vertical
structures, corresponding to the same r,
at r=1015 cm, Fig. 1) on the lower branch.
This also happens in accretion disks around stellar mass black
holes, but, in contrast to Janiuk et al. (2004), we do not find that this
is always the case for AGNs. This discrepancy can be due to a
difference in the treatment of convection or to different opacities.
The small wiggle at low temperature is not related to a strong
change in the opacities, but instead to a strong change in the
adiabatic gradient when molecular hydrogen becomes partially
dissociated, as is shown by Fig. 2. Two vertical
structures, corresponding to the same r, ![]() ,
and
,
and ![]() ,
but two different effective temperatures on the upper and lower
stable branches of the small wiggle of Fig. 1,
differ essentially by a much stronger temperature gradient in the
disk midplane. In one case,
,
but two different effective temperatures on the upper and lower
stable branches of the small wiggle of Fig. 1,
differ essentially by a much stronger temperature gradient in the
disk midplane. In one case,
![]() ,
while
,
while
![]() in the other. This effect occurs only if
molecular hydrogen becomes partially dissociated in the convective
zone. Since the opacities are relatively low for the corresponding
temperatures and densities, there are cases where the transition
between molecular and atomic hydrogen occurs in a radiative zone, in
which case no wiggle is found.
in the other. This effect occurs only if
molecular hydrogen becomes partially dissociated in the convective
zone. Since the opacities are relatively low for the corresponding
temperatures and densities, there are cases where the transition
between molecular and atomic hydrogen occurs in a radiative zone, in
which case no wiggle is found.
In the standard dwarf-nova model, it is assumed that the
![]() -parameter changes rapidly when the disk temperature reaches
the ionization instability; this is required for the amplitude of
the modeled outburst to be comparable to the observed one. It is
often stated that the physical reason for such a change is the
change in the ionization parameter of the gas, hence
-parameter changes rapidly when the disk temperature reaches
the ionization instability; this is required for the amplitude of
the modeled outburst to be comparable to the observed one. It is
often stated that the physical reason for such a change is the
change in the ionization parameter of the gas, hence ![]() is
assumed to remain constant when transiting this secondary wiggle.
This also seems to be a reasonable hypothesis in the AGN case, and
does not require the physics of accretion disk to be different in
different environments, even though the temperatures and densities
are similar. In the following, contrary to Janiuk et al. (2004), we assume
therefore that the critical
is
assumed to remain constant when transiting this secondary wiggle.
This also seems to be a reasonable hypothesis in the AGN case, and
does not require the physics of accretion disk to be different in
different environments, even though the temperatures and densities
are similar. In the following, contrary to Janiuk et al. (2004), we assume
therefore that the critical
![]() of the cold stable
branch corresponds to the ionization instability and that the lower
wiggle is not associated with a change in
of the cold stable
branch corresponds to the ionization instability and that the lower
wiggle is not associated with a change in ![]() .
This point is of
importance, since as shown by Hameury (2002), the shape of the
resulting S curve and hence the outcome of the model is by far
dominated by the change in the viscosity parameter
.
This point is of
importance, since as shown by Hameury (2002), the shape of the
resulting S curve and hence the outcome of the model is by far
dominated by the change in the viscosity parameter ![]() .
.
Finally, one should point out that whatever arguments are used to
justify the change in ![]() ,
i.e. the use of an
,
i.e. the use of an
![]() and an
and an
![]() ,
the real reason is the necessity to produce the required outburst
amplitude. It has been argued (Gammie & Menou 1998) that the difference
between viscosities in the high and low (quiescent) states of
dwarf-nova disks is due to the ``decay'' of the MRI mechanism that
is supposed to be the source of turbulence in accretion disks
(Balbus & Hawley 1991). In the environment of AGN disks, the MRI is supposed
to be operating also in cold disks, which was used to argue that
,
the real reason is the necessity to produce the required outburst
amplitude. It has been argued (Gammie & Menou 1998) that the difference
between viscosities in the high and low (quiescent) states of
dwarf-nova disks is due to the ``decay'' of the MRI mechanism that
is supposed to be the source of turbulence in accretion disks
(Balbus & Hawley 1991). In the environment of AGN disks, the MRI is supposed
to be operating also in cold disks, which was used to argue that
![]() in this case
(Menou & Quataert 2001).
in this case
(Menou & Quataert 2001).
However, as noted by Steven Balbus (private communication), because of the fact that numerical simulations treat the turbulent dynamics of disks at a level far beyond anything that can be approached with strictly analytic techniques, there has been a tendency to grant simulations a level of certainty that they do not merit yet. A careful treatment of realistic energetics still remains beyond the capabilities of current codes, and even simple polytropic shearing box calculations need to be run at much higher resolutions and for much longer times than were once thought necessary.
Therefore the values of critical Reynolds numbers deduced only from numerical simulations (Gammie & Menou 1998; Menou & Quataert 2001) are highly uncertain and we opted for using the standard dwarf-nova DIM also in AGNs.
3 Disk evolution
3.1 Basic equations
The standard equations for mass and angular momentum conservation in
a geometrically thin accretion disk can be written as
and
where
The energy conservation equation is taken as (see Hameury et al. 1998; Cannizzo 1993, for
details):
where
| (15) |
where
These are identical to the equations of a disk in a binary system, except that there are no tidal torques and no tidal dissipation.
The inner boundary condition is also unchanged from the binary
case:
| (17) |
where
| (18) |
so that this allows for the disk to be both in the hot or cold states (see below for a more detailed discussion on the effect of using this boundary condition).
The outer boundary condition is more problematic, as the disk
extends to large distances where all the usual approximations are
invalid (thin disk, neglect of self gravity, etc.). We instead
assume that at some distance
![]() cm for M =
108
cm for M =
108 ![]() ,
the mass-transfer rate is given and constant. This
approximation is valid provided that the heating front does not
reach this outer radius.
,
the mass-transfer rate is given and constant. This
approximation is valid provided that the heating front does not
reach this outer radius.
The heat Eq. (14) requires two additional boundary
conditions. As discussed in Hameury et al. (1998), these are of little
importance, and we take J=0 at
![]() and
and
![]() .
.
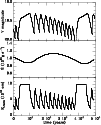 |
Figure 3:
Time evolution of an accretion disk with the following
parameters: black hole mass: 108 |
| Open with DEXTER | |
3.2 Results
Figure 3 shows an example of the evolution of the
accretion disk. We have considered here a 108 ![]() black
hole accreting at 1024 g s-1, about one hundredth of the
Eddington limit:
black
hole accreting at 1024 g s-1, about one hundredth of the
Eddington limit:
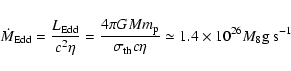 |
(19) |
where
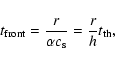 |
(20) |
where
It must also be noted that the front occasionally reaches the outer disk edge; then the outer boundary condition that dictates in particular that there is no outward mass flow is not valid, so that the correct sequence is probably different. The back and forth propagation of heating fronts on a short time scale is, however, a firm prediction of the model.
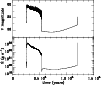 |
Figure 4:
Time evolution of an accretion disk with the following
parameters: black hole mass: 108 |
| Open with DEXTER | |
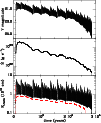 |
Figure 5: Details of the outburst shown in Fig. 4. Top panel: visual magnitude; intermediate panel: accretion rate onto the black hole; lower panel: radius at which the transition between the hot and cold regimes takes place. The red-dashed line is the semi-analytic value of the minimum transition radius given by Eq. (23). |
| Open with DEXTER | |
For lower mass-transfer rates, the outer part of the disk can remain
on the cold, stable branch, in which case the front propagation is
restricted to the innermost parts of the disk. Figures 4
and 5 show the evolution
of a disk with the same parameters as in Fig. 3, but
with a mass-transfer rate of
![]() g s-1,
g s-1,
![]() times the Eddington limit. As can be seen in
Fig. 5, heating and cooling fronts propagate in a
restricted fraction of the accretion disk. They do not reach radii
larger than that at which the disk can sit on the stable cool
branch, given the externally imposed mass-transfer rate. They also
do not reach the innermost regions where the surface density always
remains high enough for the disk to be stable on the hot branch,
except when entering a quiescence period, which happens when the
disk finally empties on a much longer viscous time. The active phase
lasts for
times the Eddington limit. As can be seen in
Fig. 5, heating and cooling fronts propagate in a
restricted fraction of the accretion disk. They do not reach radii
larger than that at which the disk can sit on the stable cool
branch, given the externally imposed mass-transfer rate. They also
do not reach the innermost regions where the surface density always
remains high enough for the disk to be stable on the hot branch,
except when entering a quiescence period, which happens when the
disk finally empties on a much longer viscous time. The active phase
lasts for
![]() yr in the case presented here, with more than
400 consecutive oscillations. These are not random, but show relatively
regular sequences of decreasing oscillations that are interrupted by
an oscillation with a larger amplitude, clearly visible in
Fig. 5. Note also some sort of hierarchical
structure for these oscillations. Figure 6 shows
the radial structure of the disk during the oscillating phase
(compare wih Fig. 2 of Dubus et al. 2001). The semi-stable inner and
outer regions are clearly visible. The central unstable zone is
divided into two parts: an inner unstable one, and an outer
marginally stable one, where
yr in the case presented here, with more than
400 consecutive oscillations. These are not random, but show relatively
regular sequences of decreasing oscillations that are interrupted by
an oscillation with a larger amplitude, clearly visible in
Fig. 5. Note also some sort of hierarchical
structure for these oscillations. Figure 6 shows
the radial structure of the disk during the oscillating phase
(compare wih Fig. 2 of Dubus et al. 2001). The semi-stable inner and
outer regions are clearly visible. The central unstable zone is
divided into two parts: an inner unstable one, and an outer
marginally stable one, where
![]() ,
resulting from the successive passage of heating fronts that die at
radii decreasing with time. A leftover of the death of these fronts
is the little wiggle in
,
resulting from the successive passage of heating fronts that die at
radii decreasing with time. A leftover of the death of these fronts
is the little wiggle in ![]() that gets smoothed with time as a
result of diffusion, or when a heat front is able to reach this
region. Note also the spike in the unstable region, which carries a
small amount of mass that will cause the small wiggles in the
marginally stable region.
that gets smoothed with time as a
result of diffusion, or when a heat front is able to reach this
region. Note also the spike in the unstable region, which carries a
small amount of mass that will cause the small wiggles in the
marginally stable region.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{10928f6.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg106.gif) |
Figure 6:
Radial structure of the disk. The blue solid line represents
the surface density, the red dashed one the central temperature.
The dotted lines are the critical
|
| Open with DEXTER | |
3.3 Minimum radius reached by cooling fronts
The minimum radius reached by the cooling front can be determined by
noting that the front propagates down to a point where
![]() and that the innermost parts of
the disk are in quasi viscous equilibrium. This means that the
surface density is determined by the accretion rate which is almost
constant in this hot inner region. This is equivalent to stating
that, at the reflection point, the dissipation rate Q+ is
and that the innermost parts of
the disk are in quasi viscous equilibrium. This means that the
surface density is determined by the accretion rate which is almost
constant in this hot inner region. This is equivalent to stating
that, at the reflection point, the dissipation rate Q+ is
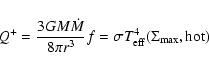 |
(21) |
where
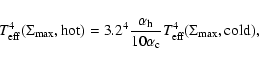 |
(22) |
which is also a very good approximation even for
Figure 6 shows that there are two points where
From Eq. (23), it appears that, for low enough ![]() or
large enough
or
large enough
![]() ,
the cooling front can reach the inner
radius, in which case the system will enter a quiescence phase. More
precisely, this happens when Eq. (23) has no solution.
Simple algebra shows that the critical
,
the cooling front can reach the inner
radius, in which case the system will enter a quiescence phase. More
precisely, this happens when Eq. (23) has no solution.
Simple algebra shows that the critical ![]() is
is
and the corresponding critical radius is
which shows that, if the disk is not truncated, low states will be found only for low mass-transfer rates, whatever the black hole mass.
The critical rate given by Eq. (25) refers to the
accretion rate onto the black hole and not to the mass-transfer
rate. For high mass-transfer rates, both are almost equal, as seen
above (see e.g. Fig. 3). For lower values of
![]() ,
they may differ by up to one order of
magnitude, as shown for example in Fig. 4 where the
accretion rate at maximum is 10 times higher than the mass supply
rate to the disk. In this case,
,
they may differ by up to one order of
magnitude, as shown for example in Fig. 4 where the
accretion rate at maximum is 10 times higher than the mass supply
rate to the disk. In this case, ![]() ultimately falls below the
critical value given by Eq. (25), and the disk enters a
quiescent state. The duration of this state is short, however, close
to the duration of the outburst state, as the average mass accretion
rate during the active state is
ultimately falls below the
critical value given by Eq. (25), and the disk enters a
quiescent state. The duration of this state is short, however, close
to the duration of the outburst state, as the average mass accretion
rate during the active state is ![]()
![]() g s-1,
i.e. not very different from the steady mass-transfer rate. (The
duty cycle expected for an outburst with an average accretion rate
2.85 times higher than the transfer rate is 0.35, very close to the
value given by the simulation (0.30), showing that the disk is
almost relaxed.) We therefore expect that outbursts exist only for
low mass-transfer rates, that these outbursts are weak - never
reaching anything close to the Eddington limit - and that the duty
cycle cannot be large.
g s-1,
i.e. not very different from the steady mass-transfer rate. (The
duty cycle expected for an outburst with an average accretion rate
2.85 times higher than the transfer rate is 0.35, very close to the
value given by the simulation (0.30), showing that the disk is
almost relaxed.) We therefore expect that outbursts exist only for
low mass-transfer rates, that these outbursts are weak - never
reaching anything close to the Eddington limit - and that the duty
cycle cannot be large.
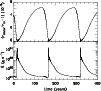 |
Figure 7:
Instability of the inner disk edge when the boundary condition
|
| Open with DEXTER | |
3.4 Innermost disk instability
The very inner parts of the disk, where the density is very low
because of the inner boundary condition should therefore be on the
cold branch. The transition between this cold region and more
distant, hotter regions should also be unstable; indeed, when one
assumes that the inner boundary condition is not
![]() at
at
![]() ,
but is smaller than
,
but is smaller than
![]() ,
oscillations are found. For the sake of
completeness, we show in Fig. 7 the effect of these
oscillations in such a case. Cooling/heating fronts propagate in a
very restricted region, whose radial extent is greater than the
vertical scale height so that the thin disk approximation is still
valid, but presumably much smaller than the zone from which matter
flows into the black hole. Also, this region is so small that the
total disk luminosity remains constant. These oscillations are
possible only when the width of heating/cooling fronts is less than
the width of the region over which
,
oscillations are found. For the sake of
completeness, we show in Fig. 7 the effect of these
oscillations in such a case. Cooling/heating fronts propagate in a
very restricted region, whose radial extent is greater than the
vertical scale height so that the thin disk approximation is still
valid, but presumably much smaller than the zone from which matter
flows into the black hole. Also, this region is so small that the
total disk luminosity remains constant. These oscillations are
possible only when the width of heating/cooling fronts is less than
the width of the region over which ![]() catches the boundary
condition
catches the boundary
condition ![]() ,
which is one to a few percent of
,
which is one to a few percent of
![]() (see Fig. 6), otherwise fronts would simply not
exist. This is quite possible in the AGN case, because the fronts
are so narrow and contrasts with the CV or LMXB case where the
reverse is true and the condition
(see Fig. 6), otherwise fronts would simply not
exist. This is quite possible in the AGN case, because the fronts
are so narrow and contrasts with the CV or LMXB case where the
reverse is true and the condition
![]() does not have such an
effect. There oscillations are most probably not physical, because
one assumes that (i) there is absolutely no torque at the inner disk
edge; and (ii) that matter is lost from the disk only at
does not have such an
effect. There oscillations are most probably not physical, because
one assumes that (i) there is absolutely no torque at the inner disk
edge; and (ii) that matter is lost from the disk only at
![]() .
It is very likely that the mechanisms leading to accretion at
the inner disk edge (e.g. evaporation, etc.) will smooth
oscillations there. To avoid these and to ease the numerical
computations, we have assumed that
.
It is very likely that the mechanisms leading to accretion at
the inner disk edge (e.g. evaporation, etc.) will smooth
oscillations there. To avoid these and to ease the numerical
computations, we have assumed that ![]() is not vanishingly small
at the inner disk edge, but that instead it is very slightly larger
than
is not vanishingly small
at the inner disk edge, but that instead it is very slightly larger
than
![]() .
.
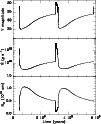 |
Figure 8:
Long-term evolution on an AGN accretion disk when
|
| Open with DEXTER | |
3.5 Disk truncation
Disk truncation could be a solution to the absence of large
outbursts. This was found to be an essential ingredient of the soft
X-ray transient model (see e.g. Menou et al. 2000; Dubus et al. 2001). Truncation
can be the result of the formation of an advection-dominated
accretion flow (ADAF) or of one of its variants (see e.g. Narayan & McClintock 2008; Kato et al. 1998, for
reviews of the ADAF), the important feature being that
the flows becomes hot, geometrically thick, and optically thin close
to the black hole. For the outburst cycle to be modified, one needs
the disk not to extend down to the innermost stable orbit, but
instead be truncated at a radius comparable to the minimum radius
reached by the cooling front. The inner disk radius will then depend
on the mass accretion rate onto the black hole. Many prescriptions
can be derived; what really matters is whether Eq. (23)
can be satisfied or not, since the details of the variations
of
![]() as a function of
as a function of ![]() are not important.
are not important.
Figures 8 and 9 show an example in which
![]()
![]() .
As can be seen, quiescent states are found, as well
as active states that are not very bright though - only brighter
than the active states for non truncated disks by a factor
.
As can be seen, quiescent states are found, as well
as active states that are not very bright though - only brighter
than the active states for non truncated disks by a factor ![]() 2,
resulting in duty cycles that also differ by factors
2,
resulting in duty cycles that also differ by factors ![]() 2.
2.
3.6 Disk irradiation
Disk irradiation plays an essential role in soft X-ray transients
(see e.g. van Paradijs 1996; Dubus et al. 2001, and references therein) and sometimes
in CVs, see e.g. Hameury et al. (1999), and could also play an important
role in the AGN context. We follow here the same procedure as in the
case of irradiated disks in SXTs (Dubus et al. 2001). We assume that the
irradiation flux
![]() onto the disk is given by
onto the disk is given by
where C is a constant. In the case of SXTs,
which clearly shows, because we are interested in regions much closer to the black hole than in the case of SXTs, that C must be large if irradiation is to have any effect at all. To affect the central temperature of the disk,
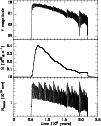 |
Figure 9: The outburst shown in Fig. 8. The two upper panels are the same as in Fig. 8, and the lower panel shows the transition radius between the inner hot disk and the cooler outer parts. |
| Open with DEXTER | |
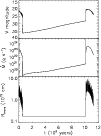 |
Figure 10: Time evolution of an irradiated disk, with parameters identical to those of Fig. 4; here C=0.01. Top panel: V magnitude; intermediate panel: accretion rate onto the black hole; lower panel: transition radius between the hot, inner disk and the cool outer disk. |
| Open with DEXTER | |
We then calculated a grid of vertical disk structures to determine
the effective temperature as a function of ![]() ,
,
![]() ,
,
![]() ,
as described in Sect. 2, with a modified boundary
condition at the disk surface:
,
as described in Sect. 2, with a modified boundary
condition at the disk surface:
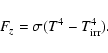 |
(28) |
As in the case of SXTs, the effect of irradiation is a stabilization of the disk when the irradiation temperature is high enough, typically higher than
A reasonably good fit to the effective temperature at
![]() is given by
is given by
in a situation where the disk is in viscous equilibrium, hence
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=90]{10928f11.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg143.gif) |
Figure 11:
Example of the disk radial structure in the irradiated
case. The blue solid line is the surface density, the red dashed
line is the central temperature. The blue dotted lines represent
|
| Open with DEXTER | |
Figure 10 shows the time evolution of an irradiated
disk with the same parameters as in Fig. 4, apart
from the irradiation factor C set to 0.01. As can be seen, even in
this maximally irradiated disk, the time evolution is not very
different from that of an unirradiated disk. There is still a
succession of rapid oscillations of the luminosity, with a
heating/cooling front propagating back and forth. The main
difference is here that the disk enters into a quiescent phase more
rapidly than in the unirradiated case, but one should note that the
initial structure was not exactly the same in both cases, and that
because of the huge computing time required to follow the disk
oscillations, a relaxed state cannot be attained in practice.
However, the radial disk structure obtained at the end of active
phases in the irradiated and unirradiated cases do not differ much,
with an outer disk on the cold stable branch, and most of the disk
having
![]() .
This similarity, and the fact
that the unirradiated disk was almost relaxed makes us confident
that, here also, the disk is close to relaxation.
.
This similarity, and the fact
that the unirradiated disk was almost relaxed makes us confident
that, here also, the disk is close to relaxation.
Figure 11 shows the radial structure of the disk at
time
![]() yr, when 3/4 of the first outburst have
elapsed. It clearly shows the impact of irradiation on the innermost
part of the disk, which is due both to a high irradiation
temperature and to the decreasing viscous dissipation close to the
inner disk edge (the f factor).
yr, when 3/4 of the first outburst have
elapsed. It clearly shows the impact of irradiation on the innermost
part of the disk, which is due both to a high irradiation
temperature and to the decreasing viscous dissipation close to the
inner disk edge (the f factor).
The conclusion that quiescent states are only possible for low
mass-transfer rates is very general. An analysis similar to that
described above in the non irradiated case leads to the conclusion
that the disk can enter into quiescence only if the mass accretion
rate is less than
which is accurate to within a factor 2 when compared to the results of the numerical simulations. Although the dependence on M8,
4 Conclusion
We have shown that the accretion disks in AGNs can indeed be subject to the same thermal-viscous instability as in dwarf novae and soft X-ray transients, but the outcome of this instability is very different. This contrasts with previous findings that large amplitude outbursts reaching the Eddington limit were possible, and the reason for this discrepancy is the poor spatial resolution of the numerical codes that have been used to model the disk. In AGNs, the disk opening angle is much less than in DNs or SXTs, because the Keplerian velocity is not low compared to the speedof light, whereas the sound speed is, by construction, the same in both cases. This results in very thin transition fronts, which are quite difficult to follow numerically.
We do, however, predict time variations of the AGN luminosity by a few magnitudes on time scales ranging from a few thousand (the propagation time of a thermal front in the disk) to a few million years (the typical quiescent/outburst time), and these oscillations are enhanced by a possible truncation of the innermost parts of the disk. However, because of their small amplitudes and duty cycles, these variations cannot explain the statistical properties of quasar and AGN luminosity distribution.
One should also stress that, for high mass-transfer rates, the transition front can reach regions in the disk where self-gravitation becomes important, and there the assumption of a homogeneous disk becomes quite questionable, as a result of the development of a gravitational instability that is likely to result in the fragmentation of the disk.
References
- Alexander, D. R. 1975, ApJS, 29, 363 [NASA ADS] [CrossRef] (In the text)
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 521, 650 [NASA ADS] [CrossRef] (In the text)
- Balbus, S. A., & Papaloizou, J. C. B. 1999, ApJ, 376, 214 [CrossRef]
- Cannizzo, J. K. 1992, ApJ, 385, 94 [NASA ADS] [CrossRef] (In the text)
- Cannizzo, J. K. 1993, ApJ, 419, 318 [NASA ADS] [CrossRef]
- Cannizzo, J. K., & Reiff, C. M. 1992, ApJ, 385, 87 [NASA ADS] [CrossRef] (In the text)
- Cox, A. N., & Tabor, J. E. 1976, ApJS, 31, 271 [NASA ADS] [CrossRef] (In the text)
- Dubus, G., Hameury, J.-M., & Lasota, J.-P. 2001, A&A, 373, 251 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Duschl, W. J. 1986, A&A, 163, 61 [NASA ADS] (In the text)
- Duschl, W. J., & Britsch, M. 2006, A&A, 653, L89 [NASA ADS] (In the text)
- Fontaine, G., Graboske, H. C. Jr., & Van Horn, H. M. 1977, ApJS, 35, 293 [NASA ADS] [CrossRef] (In the text)
- Frank, J., King, A. R., & Raine, D. 2002, Accretion Power in Astrophysics, 3r [NASA ADS]d edn. (Cambridge University Press) (In the text)
- Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef]
- Gammie, C. F., & Menou, K. 1998, ApJ, 492, L75 [NASA ADS] [CrossRef] (In the text)
- Goodman, J. 2003, MNRAS, 339, 937 [NASA ADS] [CrossRef]
- Hameury, J. M. 2002, in The physics of cataclysmic variables and related objects, ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 377 (In the text)
- Hameury, J.-M., Lasota, J.-P., MCClintock, J. E., & Narayan, R. 1997, ApJ, 489, 234 [NASA ADS] [CrossRef] (In the text)
- Hameury, J.-M., Menou, K., Dubus, G., Lasota, J.-P., & Huré, J. M. 1998, MNRAS, 298, 1048 [NASA ADS] [CrossRef] (In the text)
- Hameury, J.-M., Lasota, J.-P., & Dubus, G. 1999, MNRAS, 303, 39 [NASA ADS] [CrossRef] (In the text)
- Janiuk, A., Czerny, B., Siemiginowska, A., & Szczerba, R. 2004, ApJ, 602, 595 [NASA ADS] [CrossRef]
- Kato, S., Fukue, J., & Mineshige, S. 1998, Black-hole accretion disks (Kyoto University Press)
- Lasota, J.-P. 2001, New Astron. Rev., 45, 449 [NASA ADS] [CrossRef] (In the text)
- Lasota, J.-P., Dubus, G., & Kruk, K. 2008, A&A, 486, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [NASA ADS] [CrossRef] (In the text)
- Lin, D. N. C., & Pringle, J. E. 1987, MNRAS, 225, 607 [NASA ADS]
- Lin, D. N. C., & Shields, G. 1986, ApJ, 305, 28 [NASA ADS] [CrossRef] (In the text)
- Mayer, M., & Pringle, J. E. 2006, MNRAS, 368, 379 [NASA ADS]
- Menou, K., & Quataert, E. 2001, ApJ, 552, 204 [NASA ADS] [CrossRef]
- Menou, K., Hameury, J. M., & Stehle, R. 1999, MNRAS, 305, 79 [NASA ADS] [CrossRef] (In the text)
- Menou, K., Hameury, J. M., Lasota, J. P., & Narayan, R. 2000, MNRAS, 314, 498 [NASA ADS] [CrossRef]
- Meyer, F., & Meyer-Hofmeister, E. 1981, A&A, 104, L10 [NASA ADS] (In the text)
- Mineshige, S., & Shields, G. A. 1990, ApJ, 351, 47 [NASA ADS] [CrossRef] (In the text)
- Narayan, R., & McClintock, J. E. 2008, New Astron. Rev., 51, 733 [NASA ADS] [CrossRef]
- Paczynski, B. 1969, Acta Astron., 19, 1 [NASA ADS] (In the text)
- Rafikov, R. R. 2007, ApJ, 682, 542 [NASA ADS] [CrossRef]
- Safronov, V. S. 1960, Ann. Astrophys., 23, 979 [NASA ADS]
- Shlosman, I., Begelman, M., & Frank, J. 1990, Nature, 345, 679 [NASA ADS] [CrossRef] (In the text)
- Siemiginowska, A., & Elvis, M. 1997, ApJ, 482, L9 [NASA ADS] [CrossRef]
- Siemiginowska, A., Czerny, B., & Kostyunin, V. 1996, ApJ, 458, 491 [NASA ADS] [CrossRef]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef]
- van Paradijs, J. 1996, ApJ, 464, L139 [NASA ADS] [CrossRef]
- Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge University Press) (In the text)
Footnotes
- ... results
![[*]](/icons/foot_motif.gif)
- Mayer & Pringle (2006) make the mischievous remark in this context that ``mathematical convergence does not necessarily imply more accurate modeling of physical reality''. While this might be true, it is clear that the lack of convergence of a mathematical model makes it useless for physical applications.
All Figures
![\begin{figure}
\par\mbox{\resizebox{8cm}{!}{\includegraphics[angle=-90]{10928f1a.eps}}\resizebox{8cm}{!}{\includegraphics[angle=-90]{10928f1b.eps}} }\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg47.gif) |
Figure 1:
Examples of S curves in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{10928f2.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg61.gif) |
Figure 2:
Vertical structure of the accretion disks, for
|
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
Time evolution of an accretion disk with the following
parameters: black hole mass: 108 |
| Open with DEXTER | |
| In the text | |
 |
Figure 4:
Time evolution of an accretion disk with the following
parameters: black hole mass: 108 |
| Open with DEXTER | |
| In the text | |
 |
Figure 5: Details of the outburst shown in Fig. 4. Top panel: visual magnitude; intermediate panel: accretion rate onto the black hole; lower panel: radius at which the transition between the hot and cold regimes takes place. The red-dashed line is the semi-analytic value of the minimum transition radius given by Eq. (23). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{10928f6.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg106.gif) |
Figure 6:
Radial structure of the disk. The blue solid line represents
the surface density, the red dashed one the central temperature.
The dotted lines are the critical
|
| Open with DEXTER | |
| In the text | |
 |
Figure 7:
Instability of the inner disk edge when the boundary condition
|
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Long-term evolution on an AGN accretion disk when
|
| Open with DEXTER | |
| In the text | |
 |
Figure 9: The outburst shown in Fig. 8. The two upper panels are the same as in Fig. 8, and the lower panel shows the transition radius between the inner hot disk and the cooler outer parts. |
| Open with DEXTER | |
| In the text | |
 |
Figure 10: Time evolution of an irradiated disk, with parameters identical to those of Fig. 4; here C=0.01. Top panel: V magnitude; intermediate panel: accretion rate onto the black hole; lower panel: transition radius between the hot, inner disk and the cool outer disk. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=90]{10928f11.eps}}
\end{figure}](/articles/aa/full_html/2009/11/aa10928-08/Timg143.gif) |
Figure 11:
Example of the disk radial structure in the irradiated
case. The blue solid line is the surface density, the red dashed
line is the central temperature. The blue dotted lines represent
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.