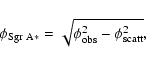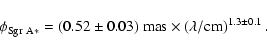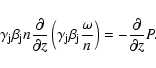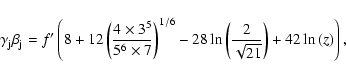Jet-lag in Sagittarius A*: what size and timing measurements tell us about the central black hole in the Milky Way

H. Falcke; S. Markoff; G. C. Bower

doi:10.1051/0004-6361/20078984

Free Access

Issue		A&A Volume 496, Number 1, March II 2009


Page(s)		77 - 83
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/20078984
Published online		30 January 2009

Jet-lag in Sagittarius A*: what size and timing measurements tell us about the central black hole in the Milky Way

H. Falcke^1,2 - S. Markoff³ - G. C. Bower⁴

1 - Department of Astrophysics, Institute for Mathematics, Astrophysics and Particle Physics, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
2 - ASTRON, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
3 - Astronomical Institute ``Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098SJ Amsterdam, The Netherlands
4 - UC Berkeley, 601 Campbell Hall, Astronomy Department & Radio Astronomy Lab, Berkeley, CA 94720, USA

Received 3 November 2007 / Accepted 28 December 2008

Abstract
Context. The black hole at the Galactic Center, Sgr A*, is the prototype of a galactic nucleus at a very low level of activity. Its radio through submm-wave emission is known to come from a region close to the event horizon, however, the source of the emission is still under debate. A successful theory explaining the emission is based on a relativistic jet model scaled down from powerful quasars.
Aims. We want to test the predictive power of this established jet model against newly available measurements of wavelength-dependent time lags and the size-wavelength structure in Sgr A*.
Methods. Using all available closure amplitude VLBI data from different groups, we again derived the intrinsic wavelength-dependent size of Sgr A*. This allowed us to calculate the expected frequency-dependent time lags of radio flares, assuming a range of in- and outflow velocities. Moreover, we calculated the time lags expected in the previously published pressure-driven jet model. The predicted lags are then compared to radio monitoring observations at 22, 43, and 350 GHz.
Results. The combination of time lags and size measurements imply a mildly relativistic outflow with bulk outflow speeds of $\gamma\beta\simeq0.5{-}2$ . The newly measured time lags are reproduced well by the jet model without any major fine tuning.
Conclusions. The results further strengthen the case for the cm-to-mm wave radio emission in Sgr A* as coming from a mildly relativistic jet-like outflow. The combination of radio time lag and VLBI closure amplitude measurements is a powerful new tool for assessing the flow speed and direction in Sgr A*. Future VLBI and time lag measurements over a range of wavelengths will reveal more information about Sgr A*, such as the existence of a jet nozzle, and measure the detailed velocity structure of a relativistic jet near its launching point for the first time.

Key words: black hole physics - galaxies: active - galaxies: jets - galaxies: nuclei - Galaxy: center - radio continuum: general

1 Introduction

The Galactic center hosts by far the best constrained super-massive black hole candidate: the compact radio source Sgr A* (see Melia & Falcke 2001, for a review). Its mass is believed to be around $4\times10^6~M_\odot$ based on stellar proper motion measurements (Schödel et al. 2002; Ghez et al. 2005). Linear polarization measurements indicate that it is extremely underfed, with an accretion rate of less than $10^{-7}~M_\odot/{\rm yr}$ (Macquart et al. 2006; Marrone et al. 2007; Agol 2000; Bower et al. 2005). The accretion rate and low radio flux put Sgr A* at the tail end of the local luminosity function (Nagar et al. 2005) of low-luminosity active galactic nuclei (LLAGN). This makes Sgr A* an ideal laboratory to study supermassive black hole physics in the quasi-quiescent state in which most galactic nuclei exist today.

Sgr A* has been detected at radio (Balick & Brown 1974) and now near-infrared (Genzel et al. 2003) and X-ray wavelengths (Baganoff et al. 2001). The radio spectrum of the source is variable, slightly inverted, and peaking in a submm-bump which originates close to the event horizon (Eckart et al. 2006; Melia & Falcke 2001; Zylka et al. 1992; Falcke et al. 1998,2000; Miyazaki et al. 2004). The latter is of particular importance since it may eventually allow imaging of the shadow cast by the event horizon (Huang et al. 2007; Falcke et al. 2000; Broderick & Loeb 2006). However, until recently no structural information was available for Sgr A*. At wavelengths shorter than that of the submm-bump, the resolution of current telescopes is insufficient and at long wavelengths, where high-resolution very long baseline interferometry (VLBI) techniques can be used, the source structure is blurred by interstellar scattering.

This ambiguity has led to a longstanding debate about the actual nature of the Sgr A* emission. One class of models suggests that the radio through X-ray emission is caused by accreting hot plasma flowing into the black hole (Narayan et al. 1998; Quataert & Gruzinov 2000; Melia 1992). On the other hand, it has been suggested that Sgr A* resembles the compact radio cores of active galactic nuclei (AGN) and therefore most of the emission is associated with a (mildly) relativistic outflow or jet (Reynolds & McKee 1980; Falcke & Biermann 1999; Falcke et al. 1993; Yuan et al. 2002; Falcke & Markoff 2000).

Only recently have measurements of the intrinsic size of Sgr A* become available (Shen et al. 2005; Doeleman et al. 2008; Bower et al. 2004), providing crucial new input. The new intrinsic size measurements agree well with the predictions of the traditional jet model (Markoff et al. 2007; Bower et al. 2004), however, a direct confirmation of an outflow is still lacking.

Clearly, additional information is required to determine the speed and direction of the flow responsible for the emission in Sgr A*. Such additional information has now become available with the first reliable time lag measurements of radio outbursts at different wavelengths (Yusef-Zadeh et al. 2008,2006a).These observations show that high radio frequencies lead the lower radio frequencies by some 20 min around 43 GHz. Because the radio emission is considered to be optically thick due to its flat-to-inverted spectrum, and the synchrotron loss timescale is much longer, the radio flux variations are tracing actual adiabatic expansion or contraction of the emitting plasma. This scenario is in marked contrast to observations in the optically thin part of the spectrum at near-infrared (NIR) and X-ray bands, where the cooling time scales are faster than adiabatic. At these higher frequencies, observations (Marrone et al. 2008; Dodds-Eden et al. 2008) show a near simultaneity between NIR and X-ray flares within minutes and a delay between X-ray/NIR with respect to the radio emission on ther order of hours. The expectation therefore is that radio timing observations trace bulk plasma properties, while X-ray/NIR variability is dominated by heating and cooling of particle energy distributions in the plasma. Which physical parameters determine a potential lag between X-rays/NIR and radio/submm (Marrone et al. 2008), is not immediately obvious.

In this paper we focus on the radio time lag data and size measurements to obtain information on the plasma flow speed. To do this we re-derive the intrinsic size of Sgr A* by combining all existing VLBI data in Sect. 2.1, thereby resolving some of the apparent discrepancies between the results of different groups in the literature. We then compute the predicted time lags for various inflow/outflow speeds in Sect. 2.3 and present time lag predictions of the canonical jet model in Sect. 2.4. Here we also present the only analytical velocity profile of a pressure-driven jet in a closed form. The predictions are then compared with the data under the assumption that the region causing the variability roughly follows a similar size-frequency relation as seen by VLBI, tracing the bulk of the plasma. Our main conclusions are then summarized and discussed in Sect. 3.

2 Size and time lag data in Sgr A*

2.1 VLBI size of Sgr A*

The radio size of Sgr A* is extremely difficult to determine for several reasons. The radio source itself is very compact and hence VLBI techniques have to be used, where radio telescopes with separations of several thousand kilometers are combined to obtain interferometric information of the source structure. However, the major high-frequency VLBI telescopes are in the Northern hemisphere, making Sgr A* a low-elevation source which is difficult to calibrate. Moreover, the source is located in the Galactic center behind a large scattering screen that broadens the intrinsic source size significantly at long wavelengths. To escape scattering effects requires observing at shorter wavelengths, which are even more difficult to calibrate. Hence, the breakthrough for the detection of the intrinsic size (Bower et al. 2004) came via the introduction of closure amplitude analysis (Doeleman et al. 2001), a method relatively insensitive to common station-based calibration errors.

Closure amplitudes provide good means to measure the source size with very high accuracy, especially if the source structure is simple. Since the broadening of the source structure by scattering follows a $\lambda ^2$ law (van Langevelde et al. 1992; Lo et al. 1998; Davies et al. 1976; Bower et al. 2004) the actual source size $\phi_{\rm Sgr~A*}$ is given by

$\begin{displaymath} \phi_{\rm Sgr~A*}=\sqrt{\phi_{\rm obs}^2-\phi_{\rm scatt}^2}, \end{displaymath}$

(1)

where $\phi_{\rm obs}$ and $\phi_{\rm scatt}$ are the actually observed and the expected scattering size respectively. $\phi_{\rm scatt}$ can be obtained by measuring the source size at long wavelengths, where the intrinsic size is negligible, and extrapolating with a $\lambda ^2$ -dependence to shorter wavelengths. The validity of this extrapolation of the $\lambda ^2$ -law has been discussed by Bower et al. (2004) and demonstrated using the measured Gaussianity of the scattered image.

In the following we employ this procedure using all currently available data, and discuss the origin of apparently conflicting results for the wavelength-size structure of Sgr A*.

There are currently only four papers which contain reliable major and minor axes for Sgr A*: Bower et al. (2004) for $\lambda$ 6 cm to $\lambda$ 7 mm data, Bower et al. (2006) for $\lambda$ 24 cm to $\lambda$ 17 cm data, and Shen et al. (2005) and Shen (2006) for $\lambda$ 3 mm and $\lambda$ 7 mm data. Sizes at wavelengths longer than 20 cm are from VLBA closure-amplitude measurements and at longer wavelengths high-quality VLA data is available. There is also a closure amplitude size at $\lambda$ 3 mm from Doeleman et al. (2001), however, that was only reliably obtained for a circular Gaussian source and has been superseded by Shen (2006), who fit an elliptical Gaussian. In addition there was one older measurement at $\lambda$ 1.3 mm, by Krichbaum et al. (1998), based on a single baseline detection. The latter has now been superceded by a more recent detection by Doeleman et al. (2008), based on three baselines and higher signal-to-noise ratio. The $\lambda$ 1.3 mm observations yield the smallest sizes and the largest excursion from the scattering law. We therefore include these data points in our analysis for completeness, even though they do not represent a closure amplitude measurement and one cannot distinguish between major and minor axis. Their inclusion, however, does not change our results significantly.

Figure 1 shows the size data of Sgr A* as function of wavelength together with the scattering law from Bower et al. (2006), $\phi_{\rm scatt}=(1.31\pm0.02)~{\rm mas}\;(\lambda/{\rm cm})^2$ . One can clearly see how the overall size of Sgr A* follows the $\lambda ^2$ -law closely at long wavelengths.

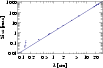$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig1.ps}} \end{figure}$	Figure 1: Measured radio source size (major axis) of Sgr A* as function of observing wavelength in centimeters.
Open with DEXTER

The next step is to subtract the scattering law in quadrature from the observed size according to Eq. (1). For this, the exact normalization of the scattering law is vitally important. The normalizations used by Bower et al. (2006) and Shen et al. (2005) differ only slightly. This has little impact on the intrinsic source size at $\lambda$ 3 mm and $\lambda$ 7 mm, but markedly affects the size at longer wavelengths. As Bower et al. (2006) showed, this changes the size-vs.-wavelength relation (size $\propto$ $\lambda^{m}$ ). Bower et al. (2006) find power laws in the range between m=1.3 and m=1.7(Shen et al. 2005), who use only short-wavelength data, find m=1.09.

The biggest problem, therefore, is the systematic uncertainty introduced by the inclusion or non-inclusion of long-wavelength data sets. We investigate this uncertainty in the following discussion. Note however that the difference in the scattering law primarily affects intrinsic sizes at long wavelengths; short wavelength sizes are largely unaffected because the contribution of the scattering angle to the observed size is much less.

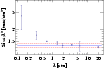$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig2.ps}} \end{figure}$	Figure 2: Measured radio source size (major axis) of Sgr A* divided by $\lambda ^2$ as function of observing wavelength in cm. The solid line represents the average scattering law used here, where the dashed lines indicated the 3 $\sigma$ limits found by randomly dropping one data point.
Open with DEXTER

2.2 Robustness of the Sgr A* size measurements

Figure 2 shows the observed sizes divided by $\lambda ^2$ . Here we have averaged the data for the various observing bands, in order to avoid having the final fit be biased by the number of observations in one band. For the averaging we divided the sizes by $\lambda ^2$ to take out the frequency dependence, and weighted them by their error bars. This gives us one data point per band. In particular, all 20 cm data from Bower et al. (2006) are averaged into one point here. The error bars we show are the standard deviations of the measurements in one band, where multiple measurements were available. In principle this should be a more robust measure of the error.

The non-homogeneous error distribution is problematic, but as it is a limit of the available observational data base, it cannot be overcome. The three data points at $\lambda$ 7 mm, $\lambda$ 3.5 cm, and $\lambda$ 20 cm tend to dominate any fitting and a combined multi-parameter fit of scattering-law and intrinsic size does not converge. Therefore it is customary to only fit the scattering law to long-wavelength data. The range of currently used scattering laws then depends exclusively on which data to include. Any unknown systematic error at $\lambda$ 3.5 cm or $\lambda$ 20 cm would drastically affect the result. To quantify the robustness of the inferred sizes, we performed a series of weighted fits to the data below $\lambda$ 1 cm, with one random data point dropped. Doing this we find a range of possible scattering laws (Fig. 2) given by

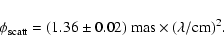$\begin{displaymath}\phi_{\rm scatt}=(1.36\pm0.02)~{\rm mas}\times(\lambda/{\rm cm})^2. \end{displaymath}$

(2)

This includes the best-fit scattering laws used by Bower et al. (2006) and Shen et al. (2005) within 3 $\sigma$ limits, which have scaling factors of $1.31\pm0.02$ and $1.39\pm0.02$ respectively.

Subtraction of this scattering law in quadrature yields a slightly revised intrinsic size as shown in Fig. 3. The sizes at $\lambda$ 2 cm and $\lambda$ 3.5 cm are relatively sensitive to the scattering law and therefore ``negative'' source sizes are possible within the errors. Negative sizes are treated as lower limits around zero with the respective error bars. We fit the error-weighted intrinsic source size with a powerlaw function, yielding:

$\begin{displaymath} \phi_{\rm Sgr~A*}=(0.52\pm0.03)~{\rm mas}\times\left({\lambda/{\rm cm}}\right)^{1.3\pm0.1}. \end{displaymath}$

(3)

Again, this is consistent with the previous results and will be used in the following analysis. We have further verified this result by running a Monte Carlo simulation, excluding the 1.3 mm data, by randomly varying the observed data and the scattering law within the errors quoted here. To each of these trials we then fitted the intrinsic size law and determined the slope parameter m. We find that the distribution of m is non-Gaussian, with a more extended tail towards smaller values. The median, however, is again at m=1.44-0.19+0.16, where the errors are the 25% and 75% quantiles, respectively. These may be the more realistic error estimates than the ones from the simple analytic fitting.

To improve on this result in the future, more and better closure-amplitude size measurements need to be obtained at longer wavelengths, especially at $\lambda$ 2 and $\lambda$ 6 cm.

In any case, the combined set of currently available data and the error analysis confirm previous conclusions that there is a wavelength-dependent photosphere in Sgr A* from a stratified medium. As expected for optically thick synchrotron radiation, the optical depth is indeed frequency dependent. This means that observations of Sgr A* at two different radio wavelengths provide information about two different spatial scales where the emission originates.

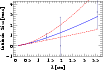$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig3.ps}} \end{figure}$	Figure 3: Intrinsic radio source size (major axis) of Sgr A* obtained by subtracting the scattering diameter in quadrature. The solid line represents the best fit powerlaw. The upper and lower dashed lines are the intrinsic sizes fitted by Bower et al. (2006) and Shen et al. (2005) respectively.
Open with DEXTER

2.3 Variability and time lags

In addition to the size measurement, we now have another new crucial parameter: the time lags between different wavelengths during small-scale variability outbursts. In the absence of direct imaging of source substructure, this provides the only means to determine flow or signal speeds in Sgr A*.

The overall variability of Sgr A* has been established for a long time. The most comprehensive data sets stem from long-term monitoring programs with the Green Bank Interferometer (Falcke 1999) and the VLA (Herrnstein et al. 2004) at cm wavelengths. The reported rms variations of the radio spectrum are 2.5%, 6%, 16%, 17%, and 21% at wavelengths of 13, 3.6, 2, 1.3, and 0.7 cm respectively. Macquart & Bower (2006) argue that most of the variation at longer timescales (several days) and at long wavelengths is due to interstellar scintillation. However, for time scales less than four days the variations may be intrinsic with an rms of $\sim$ $10\%$ for wavelengths 0.7-3 cm. Variability is also seen at mm and sub-mm wavelengths (Marrone et al. 2008; Zylka et al. 1995; Zhao et al. 2003; Mauerhan et al. 2005; Miyazaki et al. 2004) with yet larger rms variations and outbursts of a factor of several over the quiescent level.

In most cases, where multiple wavelengths were observed, the time coverage was not dense enough to find a reliable time lag between two wavelengths, despite several attempts. Recently, Yusef-Zadeh et al. (2006a) and Yusef-Zadeh et al. (2008) published data obtained with the VLA in fast switching mode allowing quasi-simultaneous high-time resolution measurements of time variability in Sgr A* at two different wavelengths. They find a lag between $\lambda$ 1.3 and 0.7 cm on the order of 20 min. Taking the weighted average of Table 1 in Yusef-Zadeh et al. (2008) one finds a lag of $21\pm3$ min. Millimeter and submm-millimeter wave timing observations by the same group are less significant, but seem to go in the same direction, with a lag between 22 and 350 GHz of $65\pm+10-23$ min (Yusef-Zadeh et al. 2008).

The sign of the lag between 43 and 22 GHz ( $\lambda\lambda$ 0.7 and 1.3 cm) is such that the shorter wavelengths lead the longer ones. Keeping in mind that shorter wavelength emission originates at smaller size regions, this immediately implies that bursts propagate outwards from small to larger scales.

Given that we know the projected size $s=\phi_{\rm Sgr~A*}D_{\rm GC}$ of Sgr A* from observations - $D_{\rm GC}$ is the Galactic center distance D=8 kpc (Eisenhauer et al. 2003) - the time lag provides a straightforward estimate for the flow speed. Using equation Eq. (3) we find that the intrinsic size of Sgr A* is $\phi_1=0.73$ mas and $\phi_2=0.32$ mas or $s_1=8.8\times10^{13}$ cm and $s_2=3.9\times10^{13}$ cm at $\lambda1.3$ cm and $\lambda7$ mm respectively. Hence, $\Delta s$ is $\sim$ 27 light minutes. Given a time lag on the order of $\Delta \tau=20$ min the flow velocity is $v=(s_1-s_2)/\Delta \tau=1.4 c$ . Therefore, Sgr A* needs to a harbor at least a mildly relativistic outflow, even if one allows for an error of $\sim$ 50%. Projection effects would tend to increase this value even further.

Alternatively, if one has a model for a flow speed v(s) one can predict the time lags with $\Delta\tau=(s_1/v(s_1) - s_2/v(s_2))$ . The easiest model is one with a constant flow speed $v(s)=\rm const$ . To allow for relativistic speeds we write this as $v(s)=\gamma\beta c$ , where $\gamma=\sqrt{1-\beta^2}~^{-1}$ and $\beta=v/c$ . For this subsection, we will ignore projection effects for the sake of simplicity. The time lag then is $\Delta \tau=D_{\rm GC}\Delta \phi_{\rm Sgr A*}/\gamma\beta c$ . Figure 4 shows the time lags for proper speeds $\gamma\beta$ in the range 0.5-2 c for the measured size-wavelength relation.

We note that the source size in Sgr A* is close to linear with wavelength, hence, for constant velocity one expects a linear increase of the time lags with decreasing wavelength relative to a fixed reference wavelength. For comparison, we also show the time lags if the outflow would propagate always with the (Newtonian) escape speed ( $\sqrt{2 GM/r}$ ) for a $3.6\times10^6~M_\odot$ black hole. Here the time lags would become longer and grow nonlinearly towards shorter wavelengths, since the escape speed is significantly slower than the speed of light. Figure 4 shows that a gravitationally bound flow would predict much longer time lags than what is actually observed.

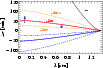$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig4.ps}} \end{figure}$

Figure 4:

Expected time lag of Sgr A* versus wavelength relative to $\lambda$ 1.3 cm (22 GHz) for the observed size-wavelength relation and a proper flow or signal speed of $\gamma \beta =1$ (red, solid line) or $\gamma \beta =0.5$ and 2 (orange, dashed). The data points are measured time lags from Yusef-Zadeh et al. (2008). The top black solid line shows the Newtonian time lag for an outflow just at the escape speed. Long lags above that line would correspond to gravitationally bound outflows.

Open with DEXTER

2.4 Time lags in the jet model

Given that the time lags suggest a mildly relativistic outflow, it seems appropriate to investigate what an actual jet model predicts. The basic jet model for Sgr A* (Falcke et al. 1993; Falcke & Markoff 2000) naturally fits the spectrum, properly predicted the low accretion rate of Sgr A* now inferred from polarization, and also was able to explain the VLBI size (Markoff et al. 2007). The only major property that could not be tested so far is in fact the flow speed.

So far, the underlying assumption for the jet model has been that Sgr A* is not a strongly relativistic outflow. Energetically this is an optimal solution in terms of the ratio between total jet power and emitted synchrotron radiation (Falcke et al. 1993). On the other hand, the sound speed for a relativistic plasma as well as the escape speed from the black hole are on the order of $\sim$ 0.5c, which sets a lower bound for a supersonic jet in Sgr A*.

In the standard Blandford & Königl (1979) model for the flat-spectrum radio emission of compact jets, a constant velocity is assumed and introduced as a free parameter. Falcke (1996) pointed out that this is in principle inconsistent, since the longitudinal pressure gradient would inevitably lead to some acceleration of a modestly relativistic jet. As a first-order assumption the velocity was then assumed to be simply given by a purely pressure-driven wind in the supersonic regime. This approach had the advantage that the actual acceleration mechanism of the jet, which is likely magnetohydrodynamic in origin, could be treated as a black box.

Simulations of the actual acceleration process are actually very difficult and time consuming (e.g., Meier et al. 2001; De Villiers et al. 2005). However, they all start with some initial magnetohydrodynamic collimation regime (here referred to as the ``nozzle''). After passing through the fast magnetosonic point, the flow eventually becomes over-pressured in a phase where the jet expands more or less freely into the ambient medium. The latter situation is mainly addressed by simulations of pc-scale jets observed with VLBI (e.g., Mimica et al. 2008).

Since for our simple Sgr A* jet model only the part after the sonic point was considered, the only main parameter is then the location of the sonic point and the sound speed. For powerful, relativistic jets the sonic point is expected to be up to thousands of Schwarzschild radii away from the central engine (Marscher et al. 2008) while for Sgr A* a relatively small value, of a few Schwarzschild radii, seems required by the data (Markoff et al. 2007). The magnetized plasma is here treated as a single-component fluid with adiabatic index 4/3 - i.e., in the relativistic limit of a ``photon gas''. The supersonic jet evolution is then calculated from the modified, relativistic Euler equation for a freely expanding jet propagating along the z axis in a cylindrical coordinate system, which we reproduce here from Falcke (1996):

$\begin{displaymath} \ensuremath{\gamma_{\rm j}\beta_{\rm j}} n {\partial\over\pa... ...a_{\rm j}} {\omega\over n}\right)=-{\partial\over\partial z}P. \end{displaymath}$

(4)

$\omega=m_{\rm p}nc^2+U_{\rm j}+P_{\rm j}$ is the enthalpy density of the jet, $U_{\rm j}$ is the internal energy density, n is the particle density, and $P_{\rm j}=(\Gamma-1)U_{\rm j}$ is the pressure in the jet (all in the local rest frame). With a ``total equipartition'' assumption one gets $U_{\rm j}\simeq m_{\rm p}nc^2$ , hence $\omega=(1+\Gamma)U_{\rm j}$ and ${\omega/n}=(1+\Gamma)m_{\rm p} c^2=\rm const.$ at the sonic point z=z₀. In the free jet with conical shape the energy density evolves as $U_{\rm j}\propto \left(\ensuremath{\gamma_{\rm j}\beta_{\rm j}}\right)^{-\Gamma}z^{-2}$ . The final equation is then given by Eq. (2) in Falcke (1996).

Note that for simplicity this equation lacks a gravitational term. This term becomes negligible quickly at larger distances and for unbound flows corresponding to typical radio frequencies for Sgr A*. This is clearly a deficiency when discussing the nozzle region in detail. In the following we will subsume this effect in the nozzle size as a free parameter.

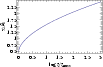$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig5.ps}} \end{figure}$	Figure 5: The proper flow speed (Eq. (5)) of a pressure driven jet plotted versus the logarithm of the distance, in units of the nozzle size $z_{\rm nozz}$ , along the z-axis.
Open with DEXTER

Previously the solution of the equation was only available numerically in the code. In in the following we present it in a closed form that allows testing it against time lag observations. For an adiabatic index of $\Gamma=4/3$ the solution (see Fig. 5) is given implicitly as

$\begin{displaymath} \gamma_{\rm j}\beta_{\rm j}=f^\prime\left(8+12\left({4\times... ...)^{1/6}-28\ln\left({2\over\sqrt{21}}\right)+42\ln{(z)}\right), \end{displaymath}$

(5)

where f'(y)=x is the inverse function of f such that f(x)=y, $x=\gamma_{\rm j}\beta_{\rm j}$ , and

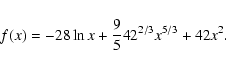$\begin{displaymath}f(x)=-28 \ln x+{9\over5}42^{2/3}x^{5/3}+42x^2. \end{displaymath}$

(6)

$\gamma_{\rm j}$ and $\beta_{\rm j}c$ are the bulk jet Lorentz factor and velocity, $z=Z/z_{\rm nozz}$ is the dimensionless length along the jet axis (Z), and $z_{\rm nozz}$ marks the location of the jet nozzle. The equation thus has a critical point at z=1, where $\gamma_{\rm j}\beta_{\rm j}$ equals the proper sound speed $\gamma_{\rm s}\beta_{\rm s}=\sqrt{\Gamma(\Gamma-1)(\Gamma+1)^{-1}}$ , and is only valid in the supersonic regime z>1.

This relatively simple quasi-analytical description had first been developed for M 81* and was then integrated into the Sgr A* jet papers thereafter. While naturally overly simplified, we retain it here, treating it as a published prediction. However, one should not consider this as the only possible solution, but rather as representative of a broader class of models for modestly relativistic accelerating jets.

Using this description we now calculate the time lags based on the assumption that any flare is essentially due to an increase in the accretion power. This increased accretion will turn into an increased outflow rate, based on the ``jet-disk symbiosis''-ansatz of a linear coupling between inflow and outflow rate (Falcke & Biermann 1995). The increased power and mass flow will then propagate along the jet essentially with the local flow speed. Here we ignore the slightly increased acceleration due to the increased longitudinal pressure gradient in an overdense region, which would be a second order effect.

We note that earlier we have argued that the X-ray flares in Sgr A* are not due to a similar increase in accretion, but rather due to additional heating or acceleration of the internal particle distributions (Markoff et al. 2001). This is entirely consistent with our approach here, since in the same paper we showed that such heating processes only marginally affect the radio flux in the optically thick region. Hence simultaneous radio-X-ray flare are not necessarily required. Radio flares, however, required an actual increase in accretion rate as also argued here. Of course, it is not inconceivable that a sudden increase in accretion rate also leads to additional heating and particle accreleration in the inner region of disk and jet.

Indeed, recent observations Marrone et al. (2008) seem to show that there is a rather long lag (on the order of hours) between X-ray/IR-flares and radio flares. This time scale is much longer than free-fall or rotational time scales and consistent with viscous processes in the accretion flow linking the two types of flares.

The predicted radio time lags in the jet model are then calculated as

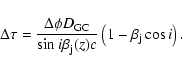$\begin{displaymath}\Delta\tau={\Delta \phi D_{\rm GC} \over \sin i \beta_{\rm j}(z) c}\left(1-\beta_{\rm j} \cos i\right). \end{displaymath}$

(7)

$\Delta \phi=\phi_{\rm Sgr~A*}(\lambda_0)-\phi_{\rm Sgr A*}(\lambda)$ and $\lambda_0=1.35$ cm is chosen as the reference wavelength. This formulation recovers the well-known formula for apparent superluminal motion ( $\beta_{\rm app}=\Delta \phi D/\Delta\tau$ ), if the implied flares were observed as moving blobs.

For the dimensionless length we take $z=\phi_{\rm Sgr~A*}(\lambda)/\phi_{\rm Sgr~A*}(\lambda_{\rm nozz})$ with $\lambda_{\rm nozz}=0.8$ mm. The latter represents the next observing band above the highest currently available VLBI measurements and corresponds to a projected size of about $4 R_{\rm g}$ ( $R_{\rm g}=GM_{\bullet}/c^2$ ), for a black hole mass of $M_\bullet=3.6\times10^6~M_{\odot}$ . This is also the typical nozzle size used in spectral fits (e.g., Markoff et al. 2007; Falcke & Markoff 2000).

Figure 6 shows the expected time lag for the measured size and the velocity field of the pressure-driven jet. The prediction is consistent with the 21 min time lag found between $\lambda$ 7 mm and $\lambda$ 1.3 cm. We stress that this is based solely on the combination of the observed sizes and the previously published velocity field for the jet model.

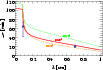$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig6.ps}} \end{figure}$	Figure 6: Expected time lag of Sgr A* versus wavelength relative to $\lambda$ 1.3 cm (22 GHz) for the observed size-wavelength relation and a flow speed according to the jet model for three inclination angles. The data points are the same as in Fig. 4.
Open with DEXTER

Quite noticeable is the quick rise of the time lag, relative to $\lambda$ 1.3 cm, towards shorter wavelengths. The rise comes from the fact that the jet first needs to accelerate beyond the nozzle, which yields initially slower flow velocities and accordingly longer time lags. This should be a characteristic signal of a nozzle, which future time lag measurements could help to identify. Of course, one has to bear in mind that the model is overly simplistic and in reality this feature may look less drastic. In particular, general relativistic effects will start to play an important role. Also, the exact location of this kink is very sensitive to the size of the nozzle, which is a free parameter within a factor of two or so and therefore difficult to predict. On the other hand, an exact localization of the kink would effectively constrain the nozzle size.

For future use, we also extrapolate the predicted time lag to longer wavelengths (Fig. 7). One can see that the lag becomes on the order of a day at cm wavelengths. This may therefore be difficult to observe, given the limited observability of Sgr A* in the Northern hemisphere, but would certainly provide crucial information on the large-scale structure of Sgr A* that is otherwise impossible to obtain due to the strong scatter broadening.

In addition we consider the effect of the range of possible size-wavelength relations for Sgr A* in Fig. 8. Not surprisingly the time lags do not show much of a difference at short wavelengths, but differ markedly at long wavelengths.

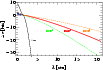$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig7.ps}} \end{figure}$	Figure 7: Same as Fig. 6 but extended to longer wavelengths. For reference we also show the time lags for a marginally bound outflow as in Fig. 4.
Open with DEXTER

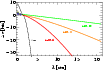$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig8.ps}} \end{figure}$	Figure 8: Same as Fig. 7 but now we show the time lags for a jet model inclined by $60^\circ$ for the different size-wavelength laws considered. This has a significant effect at long cm waves.
Open with DEXTER

3 Summary and discussion

By now Sgr A* is probably the best studied supermassive black hole with imaging and timing information on scales very close to the event horizon over a wide range of frequencies. New VLBI measurements, which we have here revisited, have confirmed theoretical predictions that Sgr A* has a frequency-dependent photosphere at radio wavelengths, with sizes scaling roughly as $\lambda^{1.3\pm0.1}$ .

The time lag of individual bursts seen at different wavelengths provides a powerful new tool to constrain the physics at work in Sgr A*. Combining this timing data with the increasingly better intrinsic size measurements obtained with VLBI can significantly constrain flow speeds. The latter is otherwise not measurable with direct imaging due to the extreme scatter broadening in the Galactic center.

The well-established lag of $\sim$ 20 min between $\lambda7$ mm and $\lambda1.3$ cm found by Yusef-Zadeh et al. (2006b), together with the intrinsic size difference of $\sim$ 27 light minutes at these wavelengths, already suggests that the radio emitting plasma is unbound and flows out with mildly relativistic speeds.

This is in contrast with the conclusions by Yusef-Zadeh et al. (2006b) who derive a subsonic and sub-relativistic outflow from the same time lag data. However, the authors base their conclusions solely on a fit of their light curve to a simple van der Laan (1966) model without ever considering the VLBI size measurements. As mentioned by these authors, the van der Laan model describes the adiabatic expansion of a spherical plasma blob and cannot describe bulk outflow, which we now know is a major factor in the extragalactic radio sources it was developed for. The van der Laan model predicts source sizes of 8 Schwarzschild radii (e.g., Fig. 3 in Yusef-Zadeh et al. 2006b) at 22 GHz while the measured radio size at 22 GHz is 80 Schwarzschild radii. The variations of $\ga$ $20\%$ of the total flux would thus have to be produced by a region that is only $\sim$ 0.1% of the total volume compared to the bulk of the plasma. We find this scenario unlikely.

The pressure-driven jet model (Falcke & Markoff 2000), that has been successfully used to fit size and spectrum of Sgr A* already, is quite consistent with the combined size and time lag data. No particular adjusting of parameters is necessary with respect to published jet models. The main free parameters are the nozzle size and the inclination angle, for which we have used canonical values. Coincidentally, both parameters do not affect the $\lambda$ 7 mm- $\lambda1.3$ cm lag very much. However, as one can see in the figures, these parameters will become important once time lags at other wavelengths are available.

The sensitivity to parameters can be turned around to state that measurements at other wavelengths in the future will provide invaluable information about the structure of Sgr A*. If time lags can be found at $\lambda$ 2 cm or $\lambda$ 3.5 cm, this would constrain inclination angle and the size-wavelength relation much better and even more clearly distinguish between models.

Moreover, time lags at $\lambda$ 3 mm and $\lambda$ 1 mm could start to show evidence for the acceleration region of the outflow (``the nozzle''), which would be a unique diagnostic for jet and accretion physics. However, here one has to caution that our simple analytic treatment naturally breaks down near the nozzle region and in the vicinity of the black hole. More sophisticated numerical magnetohydrodynamic calculations (e.g., Hawley & Krolik 2006) are clearly needed to understand the submm-wave emission. Also, since the jet likely originates from an inflow somewhere close to the nozzle region, this inflow could also contribute to the submm-bump emission (e.g., Yuan et al. 2002). These additional emission components might eventually decrease the coherence of outbursts across wavelength in the submm & mm-wave region.

So far we only have a single reliable time lag from $\lambda7$ mm to $\lambda$ 1.3 cm on which to base conclusions, with corroborating evidence from a tentative $\lambda$ 0.8 mm to $\lambda$ 1.3 cm lag. Therefore further time lag measurements at these and other wavelengths and VLBI closure amplitude measurements at long wavelengths are highly desirable. The former is challenging since the expected time scales at longer wavelengths are on the order of a typical observing run. The latter is challenging because typical VLBI arrays resolve out Sgr A* at long wavelengths and long baselines. Nonetheless, these observations are certainly worth the effort. They promise a wealth of detailed information about how plasma behaves very close to the event horizon of a supermassive black hole. Such coordinated multi-wavelength studies will eventually allow a range of more sophisticated models to be tested in great detail.

References

Agol, E. 2000, ApJ, 538, L121 [NASA ADS] [CrossRef]
Baganoff, F. K., Bautz, M. W., Brandt, W. N., et al. 2001, Nature, 413, 45 [NASA ADS] [CrossRef] (In the text)
Balick, B., & Brown, R. L. 1974, ApJ, 194, 265 [NASA ADS] [CrossRef] (In the text)
Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] (In the text)
Bower, G. C., Falcke, H., Herrnstein, R. M., et al. 2004, Science, 304, 704 [NASA ADS] [CrossRef]
Bower, G. C., Falcke, H., Wright, M. C., & Backer, D. C. 2005, ApJ, 618, L29 [NASA ADS] [CrossRef]
Bower, G. C., Goss, W. M., Falcke, H., Backer, D. C., & Lithwick, Y. 2006, ApJ, 648, L127 [NASA ADS] [CrossRef] (In the text)
Broderick, A. E., & Loeb, A. 2006, MNRAS, 367, 905 [NASA ADS] [CrossRef] (In the text)
Davies, R. D., Walsh, D., & Booth, R. S. 1976, MNRAS, 177, 319 [NASA ADS]
De Villiers, J.-P., Hawley, J. F., Krolik, J. H., & Hirose, S. 2005, ApJ, 620, 878 [NASA ADS] [CrossRef]
Dodds-Eden, K., Bartko, H., Eisenhauer, F., Falcke, H., & Genzel, R. 2008, ApJ, submitted
Doeleman, S., Weintroub, J., Rogers, A. E. E., et al. 2008, Nature, 455, 78 [NASA ADS] [CrossRef]
Doeleman, S. S., Shen, Z.-Q., Rogers, A. E. E., et al. 2001, AJ, 121, 2610 [NASA ADS] [CrossRef] (In the text)
Eckart, A., Baganoff, F. K., Schödel, R., et al. 2006, A&A, 450, 535 [NASA ADS] [CrossRef] [EDP Sciences]
Eisenhauer, F., Schödel, R., Genzel, R., et al. 2003, ApJ, 597, L121 [NASA ADS] [CrossRef] (In the text)
Falcke, H. 1996, ApJ, 464, L67 [NASA ADS] [CrossRef] (In the text)
Falcke, H. 1999, in The Central Parsecs of the Galaxy, ed. H. Falcke, A. Cotera, W. Duschl, F. Melia, & M. J. Rieke (San Francisco: ASP), ASP Conf. Ser., 186, 113 (In the text)
Falcke, H., & Biermann, P. L. 1995, A&A, 293, 665 [NASA ADS] (In the text)
Falcke, H., & Biermann, P. L. 1999, A&A, 342, 49 [NASA ADS]
Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS]
Falcke, H., Mannheim, K., & Biermann, P. L. 1993, A&A, 278, L1 [NASA ADS]
Falcke, H., Goss, W. M., Matsuo, H., et al. 1998, ApJ, 499, 731 [NASA ADS] [CrossRef]
Falcke, H., Melia, F., & Agol, E. 2000, ApJ, 528, L13 [NASA ADS] [CrossRef]
Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934 [NASA ADS] [CrossRef] (In the text)
Ghez, A. M., Salim, S., Hornstein, S. D., et al. 2005, ApJ, 620, 744 [NASA ADS] [CrossRef]
Hawley, J. F., & Krolik, J. H. 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] (In the text)
Herrnstein, R. M., Zhao, J.-H., Bower, G. C., & Goss, W. M. 2004, AJ, 127, 3399 [NASA ADS] [CrossRef] (In the text)
Huang, L., Cai, M., Shen, Z.-Q., & Yuan, F. 2007, MNRAS, 379, 833 [NASA ADS] [CrossRef]
Krichbaum, T. P., Graham, D. A., Witzel, A., et al. 1998, A&A, 335, L106 [NASA ADS] (In the text)
Lo, K. Y., Shen, Z. Q., Zhao, J. H., & Ho, P. T. P. 1998, ApJ, 508, L61 [NASA ADS] [CrossRef]
Macquart, J.-P., & Bower, G. C. 2006, ApJ, 641, 302 [NASA ADS] [CrossRef] (In the text)
Macquart, J.-P., Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 2006, ApJ, 646, L111 [NASA ADS] [CrossRef]
Markoff, S., Falcke, H., Yuan, F., & Biermann, P. L. 2001, A&A, 379, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Markoff, S., Bower, G. C., & Falcke, H. 2007, MNRAS, 379, 1519 [NASA ADS] [CrossRef]
Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef]
Marrone, D. P., Baganoff, F. K., Morris, M. R., et al. 2008, ApJ, 682, 373 [NASA ADS] [CrossRef]
Marscher, A. P., Jorstad, S. G., D'Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] (In the text)
Mauerhan, J. C., Morris, M., Walter, F., & Baganoff, F. K. 2005, ApJ, 623, L25 [NASA ADS] [CrossRef]
Meier, D. L., Koide, S., & Uchida, Y. 2001, Science, 291, 84 [NASA ADS] [CrossRef]
Melia, F. 1992, ApJ, 387, L25 [NASA ADS] [CrossRef]
Melia, F., & Falcke, H. 2001, ARA&A, 39, 309 [NASA ADS] [CrossRef] (In the text)
Mimica, P., Aloy, M. A., Agudo, I., et al. 2008, ArXiv e-prints (In the text)
Miyazaki, A., Tsutsumi, T., & Tsuboi, M. 2004, ApJ, 611, L97 [NASA ADS] [CrossRef]
Nagar, N. M., Falcke, H., & Wilson, A. S. 2005, A&A, 435, 521 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Narayan, R., Mahadevan, R., Grindlay, J. E., Popham, R. G., & Gammie, C. 1998, ApJ, 492, 554 [NASA ADS] [CrossRef]
Quataert, E., & Gruzinov, A. 2000, ApJ, 539, 809 [NASA ADS] [CrossRef]
Reynolds, S. P., & McKee, C. F. 1980, ApJ, 239, 893 [NASA ADS] [CrossRef]
Schödel, R., Ott, T., Genzel, R., et al. 2002, Nature, 419, 694 [NASA ADS] [CrossRef]
Shen, Z.-Q. 2006, J. Phys. Conf. Ser., 54, 377 [NASA ADS] [CrossRef] (In the text)
Shen, Z.-Q., Lo, K. Y., Liang, M.-C., Ho, P. T. P., & Zhao, J.-H. 2005, Nature, 438, 62 [NASA ADS] [CrossRef]
van der Laan, H. 1966, Nature, 211, 1131 [NASA ADS] [CrossRef] (In the text)
van Langevelde, H. J., Frail, D. A., Cordes, J. M., & Diamond, P. J. 1992, ApJ, 396, 686 [NASA ADS] [CrossRef]
Yuan, F., Markoff, S., & Falcke, H. 2002, A&A, 383, 854 [NASA ADS] [CrossRef] [EDP Sciences]
Yusef-Zadeh, F., Roberts, D., Wardle, M., Heinke, C. O., & Bower, G. C. 2006a, ApJ, 650, 189 [NASA ADS] [CrossRef]
Yusef-Zadeh, F., Wardle, M., Roberts, D. A., et al. 2006b, in BAAS, 38, 1062 (In the text)
Yusef-Zadeh, F., Wardle, M., Heinke, C., et al. 2008, ApJ, 682, 361 [NASA ADS] [CrossRef]
Zhao, J.-H., Young, K. H., Herrnstein, R. M., et al. 2003, ApJ, 586, L29 [NASA ADS] [CrossRef]
Zylka, R., Mezger, P. G., & Lesch, H. 1992, A&A, 261, 119 [NASA ADS]
Zylka, R., Mezger, P. G., Ward-Thompson, D., Duschl, W. J., & Lesch, H. 1995, A&A, 297, 83 [NASA ADS]

All Figures

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig1.ps}} \end{figure}$	Figure 1: Measured radio source size (major axis) of Sgr A* as function of observing wavelength in centimeters.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig2.ps}} \end{figure}$	Figure 2: Measured radio source size (major axis) of Sgr A* divided by $\lambda ^2$ as function of observing wavelength in cm. The solid line represents the average scattering law used here, where the dashed lines indicated the 3 $\sigma$ limits found by randomly dropping one data point.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig3.ps}} \end{figure}$	Figure 3: Intrinsic radio source size (major axis) of Sgr A* obtained by subtracting the scattering diameter in quadrature. The solid line represents the best fit powerlaw. The upper and lower dashed lines are the intrinsic sizes fitted by Bower et al. (2006) and Shen et al. (2005) respectively.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig4.ps}} \end{figure}$	Figure 4: Expected time lag of Sgr A* versus wavelength relative to $\lambda$ 1.3 cm (22 GHz) for the observed size-wavelength relation and a proper flow or signal speed of $\gamma \beta =1$ (red, solid line) or $\gamma \beta =0.5$ and 2 (orange, dashed). The data points are measured time lags from Yusef-Zadeh et al. (2008). The top black solid line shows the Newtonian time lag for an outflow just at the escape speed. Long lags above that line would correspond to gravitationally bound outflows.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig5.ps}} \end{figure}$	Figure 5: The proper flow speed (Eq. (5)) of a pressure driven jet plotted versus the logarithm of the distance, in units of the nozzle size $z_{\rm nozz}$ , along the z-axis.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig6.ps}} \end{figure}$	Figure 6: Expected time lag of Sgr A* versus wavelength relative to $\lambda$ 1.3 cm (22 GHz) for the observed size-wavelength relation and a flow speed according to the jet model for three inclination angles. The data points are the same as in Fig. 4.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig7.ps}} \end{figure}$	Figure 7: Same as Fig. 6 but extended to longer wavelengths. For reference we also show the time lags for a marginally bound outflow as in Fig. 4.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{8984fig8.ps}} \end{figure}$	Figure 8: Same as Fig. 7 but now we show the time lags for a jet model inclined by $60^\circ$ for the different size-wavelength laws considered. This has a significant effect at long cm waves.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.